Pochodna funkcji

Pochodna funkcji y = f(x) jest określona jako 
granica stosunku przyrostu funkcji y do 
odpowiadającego mu przyrostu zmiennej 
niezależnej x, gdy jej przyrost 



x dąży do zera:

Pochodna funkcji y = f(x) jest oznaczana 
symbolami f’(x), 

y’ lub        . 

Różniczka funkcji - to iloczyn pochodnej 
pomnożonej przez różniczkę zmiennej niezależnej:

 

 



  

x

x

f

x

x

f

x

f

x















0

lim

'

dx

dy

 

dx

x

f

dy

'



 

 

Różniczka funkcji wielu zmiennych

Pochodna cząstkowa funkcji wielu zmiennych y = 
f(x

1

,x

2

,...,x

n

) to:

Pochodne cząstkowe oblicza się zgodnie z regułami 
obliczania pochodnych jednej zmiennej, traktując 
pozostałe zmienne jak stałe.  

Różniczka funkcji wielu zmiennych to:

n

n

dx

x

y

dx

x

y

dx

x

y

dy





















 

...

 

2

2

1

1



 



i

n

i

n

i

i

x

i

x

x

x

x

x

f

x

x

x

x

x

f

x

y

i



















,...,

,...,

,

,...,

,...,

,

lim

2

1

2

1

0

 

 

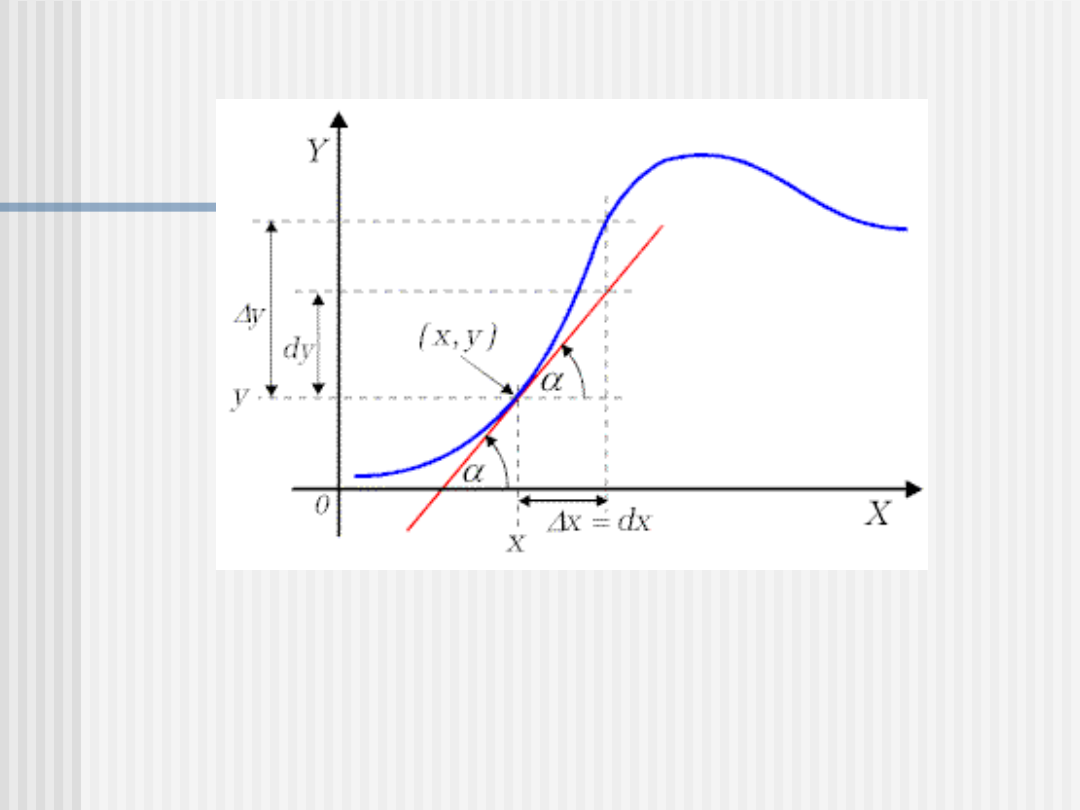
Geometryczna interpretacja 
pochodnej

 

Wartość pochodnej funkcji w danym punkcie, równa 
jest tangensowi kąta pomiędzy osią X, a styczną do 
krzywej y = f(x) 
w punkcie o współrzędnych (x,y). Kąt ten liczy się od 
dodatniej półosi X w kierunku przeciwnym do ruchu 
wskazówek zegara
(w ekstremum, tj. maksimum lub minimum, y’ = 0). 

 

 

Reguły różniczkowania

• Pochodna sumy (różnicy) funkcji f = f(x) i g = g(x):

• Pochodna iloczynu dwóch funkcji:

• Stałą c można wynieść przed znak pochodnej: 





'

 

'

'

 

g

f

g

f











'

 

'

'

g

f

g

f

g

f











'

)'

(

cf

cf 

 

 

Reguły różniczkowania – cd.

• Pochodna ilorazu funkcji:

• Pochodna funkcji złożonej, tj. gdy y = f(u) i u = g(x):  

2

'

'

g

g

f

g

f

g

f

'





















   

x

g

u

f

dx

dy

'

'





 

 

Przykłady pochodnych

x

y

x

y

x

y

x

y

a

a

y

a

y

x

y

x

x

y

e

y

x

e

y

nx

y

dx

dy

x

y

x

x

x

x

n

n

sin

'

   

;

  

cos

cos

'

   

;

  

sin

ln

'

   

;

  

1

'

   

;

  

)

0

(

  

ln

'

   

;

  

exp

'

   

;

  

1



































 

 

Funkcja pierwotna

Funkcja pierwotna F(x) danej funkcji y = f(x) - to 
taka funkcja, której pochodna jest równa f(x) lub, co 
jest równoważne, której różniczka równa jest f(x)dx: 
 

 

 

 

 

 

dx

x

f

x

dF

x

f

dx

x

dF

x

F







   

; 

'

Ponieważ pochodna stałej równa jest zeru, to dla dowolnej stałej C:

 





 

x

F

C

x

F

'

'



Jeśli więc funkcja F(x) jest funkcją pierwotną danej 
funkcji f(x), to każda funkcja różniąca się od F(x) o 
stałą wartość C jest także funkcją pierwotną funkcji 
f(x). Funkcja f(x) ma więc nieskończenie wiele 
funkcji pierwotnych różniących się o wartość 
dowolnej stałej. 

 

 

Całka nieoznaczona

Zbiór wszystkich funkcji pierwotnych danej funkcji 
f(x) nazywamy całką nieoznaczoną funkcji f(x), co 
zapisujemy 
w postaci

:

 

 

 

 

x

f

x

F

C

x

F

dx

x

f









'

    

;

  

Całkę wyznaczamy z dokładnością do dowolnej 
stałej, którą nazywamy stałą całkowania. 

 

 

Reguły całkowania

 

• Stały czynnik c  można wynieść przed 
znak całki:

 

 

dx

x

f

c

dx

x

f

c









• Całka sumy (różnicy) funkcji równa jest sumie 
(różnicy) całek poszczególnych składników:





dx

g

dx

f

dx

g

f

















• Całkowanie metodą podstawienia:

 

 

 

 

dx

t

g

t

g

f

dx

x

f

'









• Całkowanie przez 
części:













df

g

fg

dg

f

 

 

Całka oznaczona

Całka oznaczona funkcji f(x) w przedziale od 
granicy dolnej a do granicy górnej b  wynosi:

 

 

 

a

F

b

F

dx

x

f

b

a







Dla wyznaczenia całki oznaczonej w granicach od a 
do b należy znaleźć funkcję pierwotną F(x) dla danej 
funkcji f(x), wyznaczyć wartości tej funkcji w 
punktach x = a oraz x = b, 
a następnie obliczyć różnicę F(b) – F(a). 

 

 

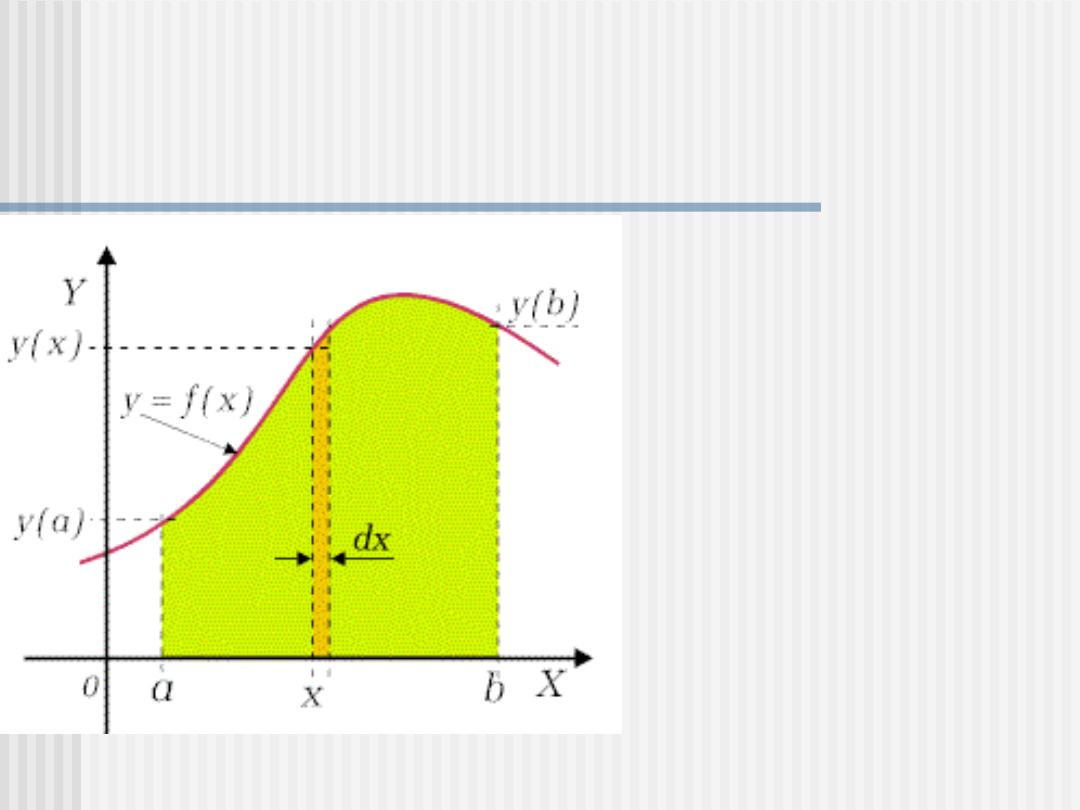
Geometryczna interpretacja 

całki oznaczonej

Wyrażenie f(x)dx 
reprezentowane jest 
przez pole 
elementarnego paska 
o szerokości dx i 
wysokości y(x), zaś 
całka oznaczona jest 
równa polu figury pod 
krzywą y = f(x) i 
ograniczonej rzędnymi 
w punktach y(a) oraz 
y(b). 

 

 

Przykłady całek (bez stałej 
całkowania)

 

















































x

dx

x

x

dx

x

a

a

a

a

dx

a

e

dx

e

x

x

dx

n

n

x

dx

x

x

x

x

x

n

n

sin

cos

cos

sin

1

,

0

   

;

  

ln

ln

1

   

;

  

1

1