1

DUALIZM KORPUSKULARNO - FALOWY

PROMIENIE RENTGENOWSKIE

Powstają one podczas hamowania rozpędzonych elektronów na powierzchni
metalowej elektrody. Promienie te są falą elektromagnetyczną o długości
10

-12

m - 10

-8

m. Zostały one odkryte w 1895r. przez Wilhelma Roentgena.

1. Mechanizm powstawania.

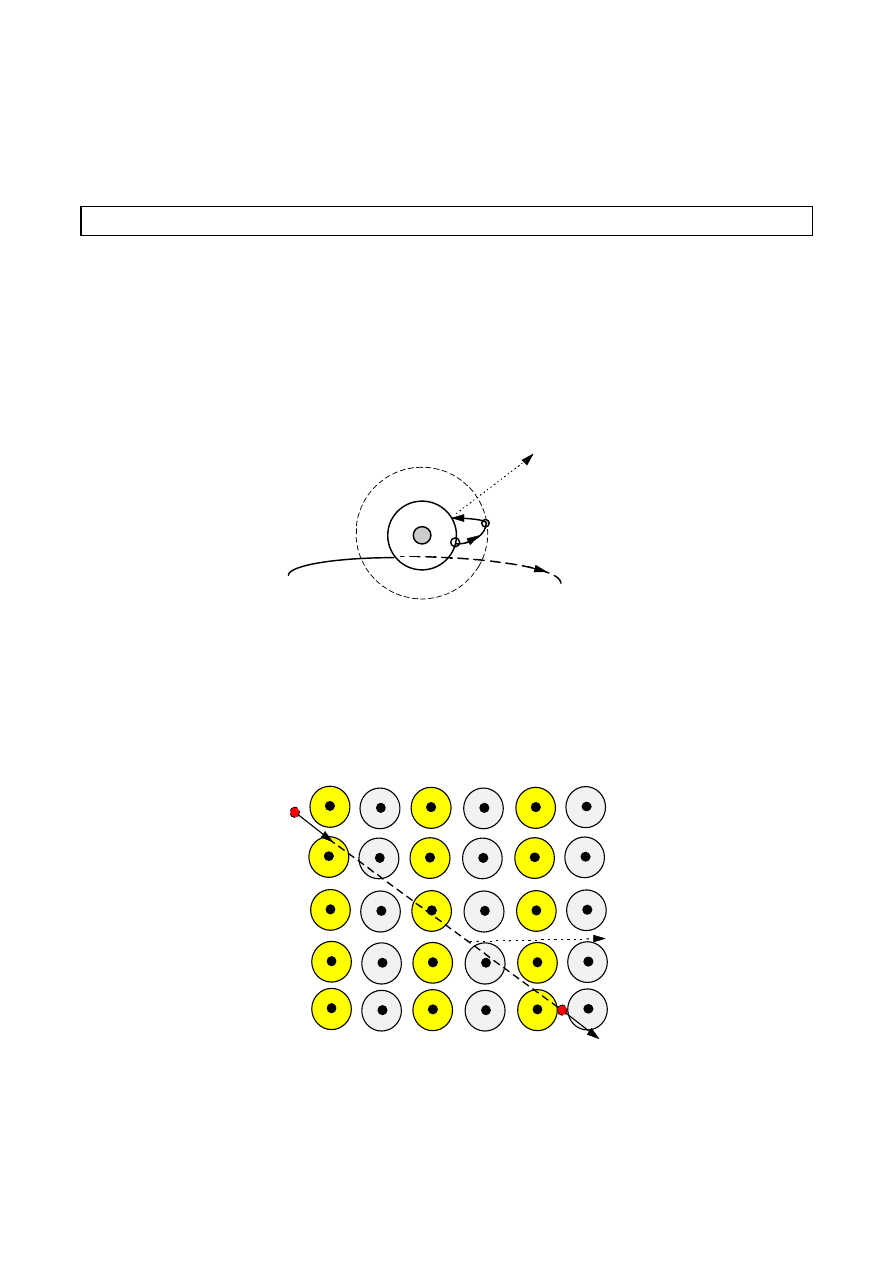
Rozpędzony elektron padając na powierzchnię elektrody zawierającej atomy ciężkich
pierwiastków powoduje silne wzbudzenie atomów.

W wyniku przejścia atomu wzbudzonego do stanu podstawowego następuje emisja
kwantu promieniowania rentgenowskiego (prom. X ). Tak wytworzone
promieniowanie zawiera tylko niektóre długości fali, a zatem ma ono widmo liniowe.
Promieniowanie to nazywamy również charakterystycznym. Jego widmo zależy od
rodzaju materiału, który je emituje.

Jeśli rozpędzony elektron nie może przekazać swojej energii atomom sieci
krystalicznej bombardowanego materiału, to doznając hamowania sam staje się
ź

ródłem promieniowania X. Tak wytworzone promieniowanie zawiera wszystkie

X

X

e

2

długości fal, ma zatem widmo ciągłe i nazywamy je promieniowaniem hamowania.
Niezależnie od sposobu wytworzenia, energia promieniowania nie może być większa
od energii elektronu uderzającego w anodę lampy rentgenowskiej. Ponieważ szybkie
elektrony są uzyskiwane w wyniku przyspieszania w polu elektrycznym przy
pomocy napięcia U, stąd otrzymujemy:

eU

h

≥≥≥≥ νννν

eU

h

c

≥≥≥≥

λλλλ

λλλλ

min

====

hC

eU

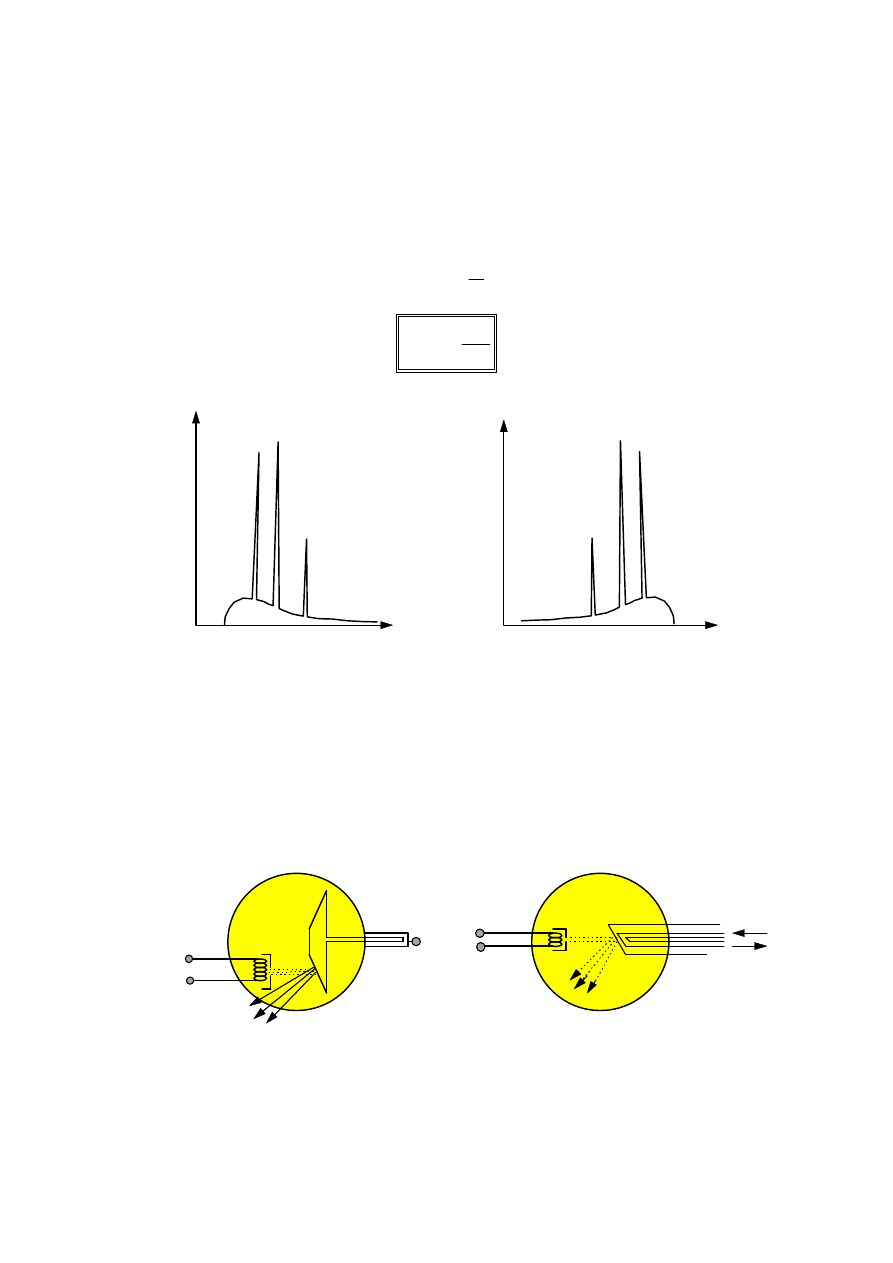
Na wykresach przedstawiono zależność natężenia promieniowania rentgenowskiego
od długości fali i od częstotliwości. Widoczne maksima składają się na widmo
charakterystyczne.

2. Lampy rentgenowskie.

Większość energii, którą niosą rozpędzone elektrony jest przekazywana sieci
krystalicznej anody lampy rentgenowskiej (99%). Aby nie dopuścić do uszkodzenia
anody stosuje się anody obrotowe lub chłodzone cieczą.

I

I

λλλλ

min

λλλλ

νννν

max

νννν

+

-

∼∼∼∼

∼∼∼∼

-

+

3

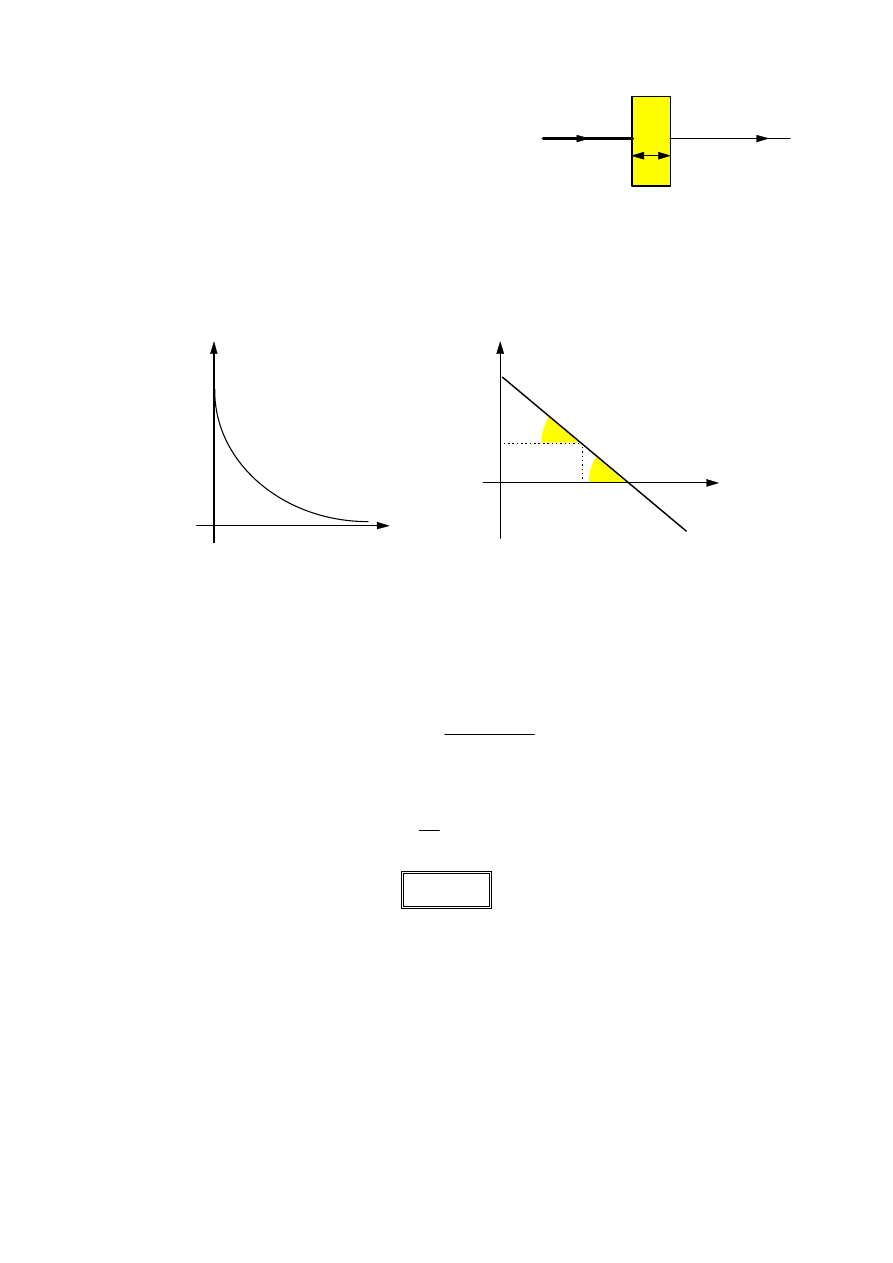
3. Pochłanianie promieni rentgenowskich.

Jeśli na przeszkodę o szerokości d pada wiązka promieni X o natężeniu I

0

a po

przejściu przez przeszkodę natężenie promieniowania wynosi I, to zależność
natężenia promieniowania przechodzącego od grubości warstwy pochłaniającej ma
postać:

Za miarę pochłaniania przyjmuje się tangens kąta nachylenia wykresu zależności
ln

I

od d. Wielkość tą nazywamy współczynnikiem pochłaniania. Wartość tego

współczynnika zależy od rodzaju materiału i jest tym większa im cięższe pierwiastki
wchodzą w skład materiału pochłaniającego.

µµµµ

ββββ

====

====

−−−−

tg

I

I

d

ln

ln

0

ln

I - ln

I

0

= -

µµµµ

d

ln

I

I

d

0

==== −−−−µµµµ

I

I e

d

====

−−−−

0

µµµµ

Szczególnie duży współczynnik pochłaniania ma ołów i jego związki.

4. Własności falowe promieni rentgenowskich.

O własnościach falowych promieniowania świadczy przede wszystkim interferencja.
Dobrze widoczne maksima interferencyjne powstają wtedy, gdy fale cząstkowe są w
odległościach wzajemnych niewiele większych od długości fali. Interferencję
promieni rentgenowskich można uzyskać przy odbiciu promieni od powierzchni

I

o

I

d

I

ln I

ln I

0

I

0

ln I

αααα

d

d

d

4

kryształu. Atomy w kryształach tworzą regularne powierzchnie odległe od siebie o
około 10

-10

m - 10

-9

m

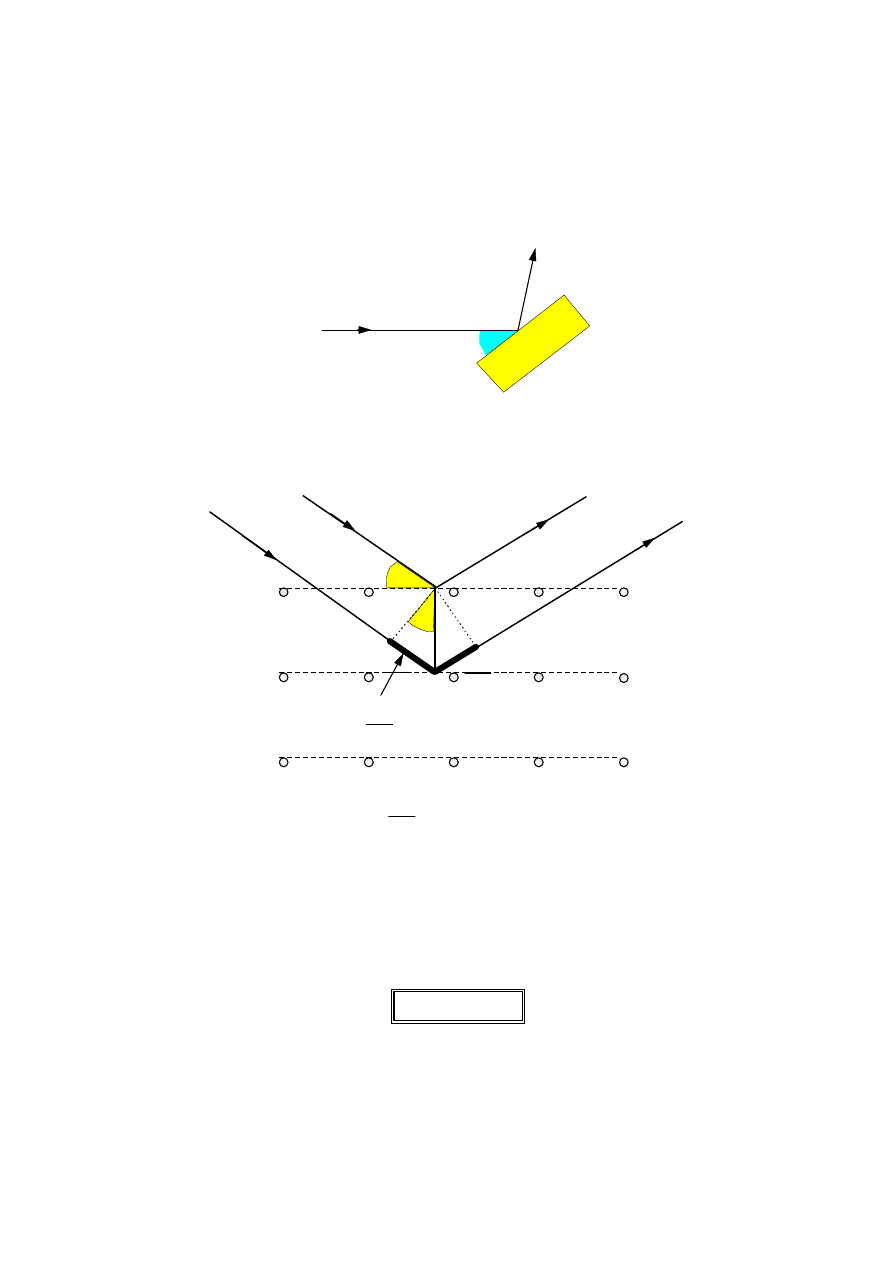
. Kierując wiązkę promieni rentgenowskich na powierzchnię

monokryształu można stwierdzić, że przy pewnym kącie padania

ϑϑϑϑ

, promienie

zostają odbite od powierzchni kryształu jak od lustra, podczas gdy przy innym kącie
padania ulegają pochłonięciu.

Jeśli kryształ jest obracany, to lustrzane odbicie powstaje dla szeregu kątów

ϑϑϑϑ

n

.

Tłumaczymy to interferencją promieni odbitych od różnych warstw atomów.

∆∆∆∆

x

d

n

2

====

sin

ϑϑϑϑ

∆∆∆∆

x

d

n

====

2 sin

ϑϑϑϑ

Korzystając z warunku interferencyjnego wzmocnienia otrzymujemy:

n

d

n

λλλλ

ϑϑϑϑ

====

2 sin

warunek Bragga

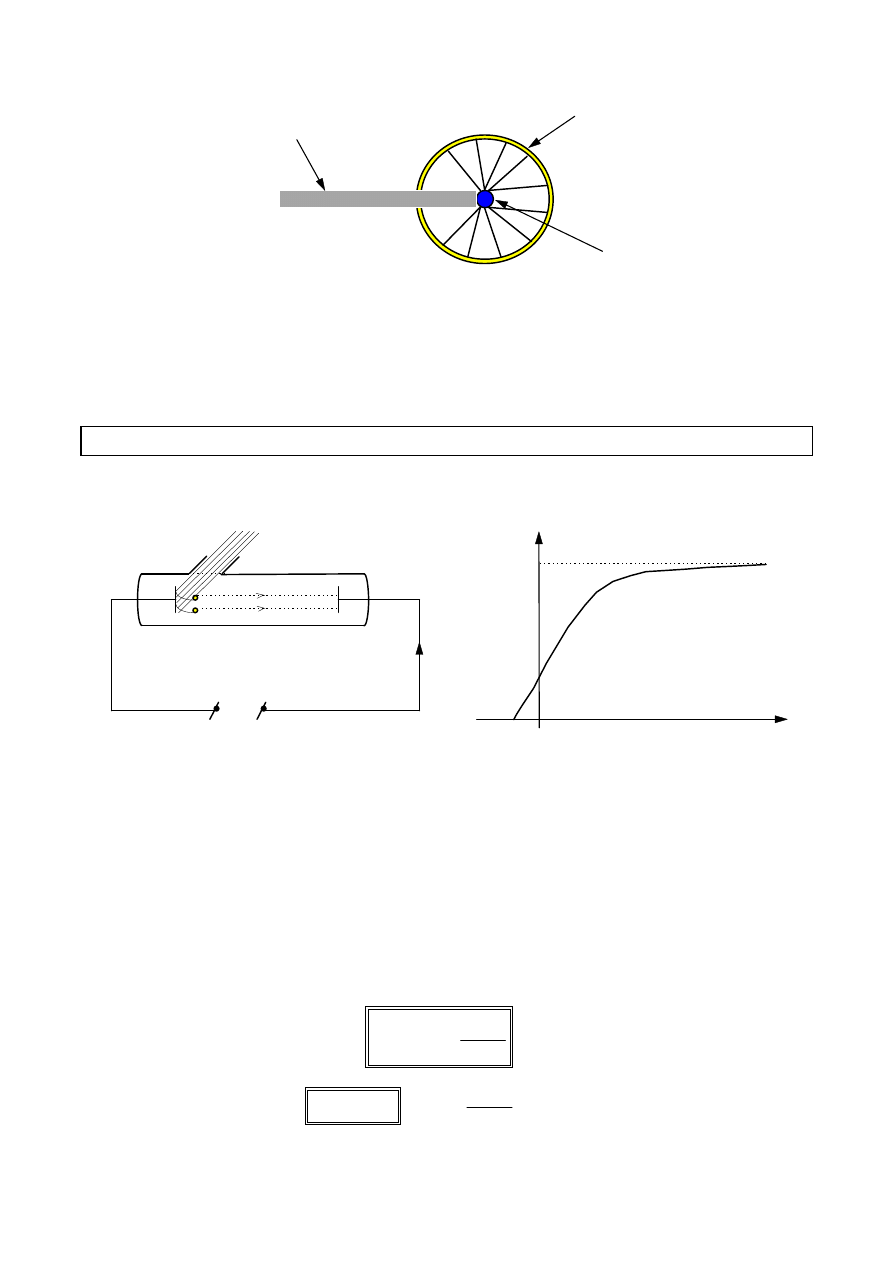
Jeśli promienie padają na pręcik pokryty proszkiem polikrystalicznym, to
jednocześnie powstają wszystkie możliwe maksima interferencyjne. Można je
zarejestrować na kliszy fotograficznej.

ϑϑϑϑ

ϑϑϑϑ

n

ϑϑϑϑ

n

d

∆∆∆∆

x

2

5

Maksima interferencyjne powstają przy odbiciu promieni

X

od tych

mikrokryształów, które spełniają warunek Bragga.

ZJAWISKO FOTOELEKTRYCZNE ZEWN

Ę

TRZNE

Ś

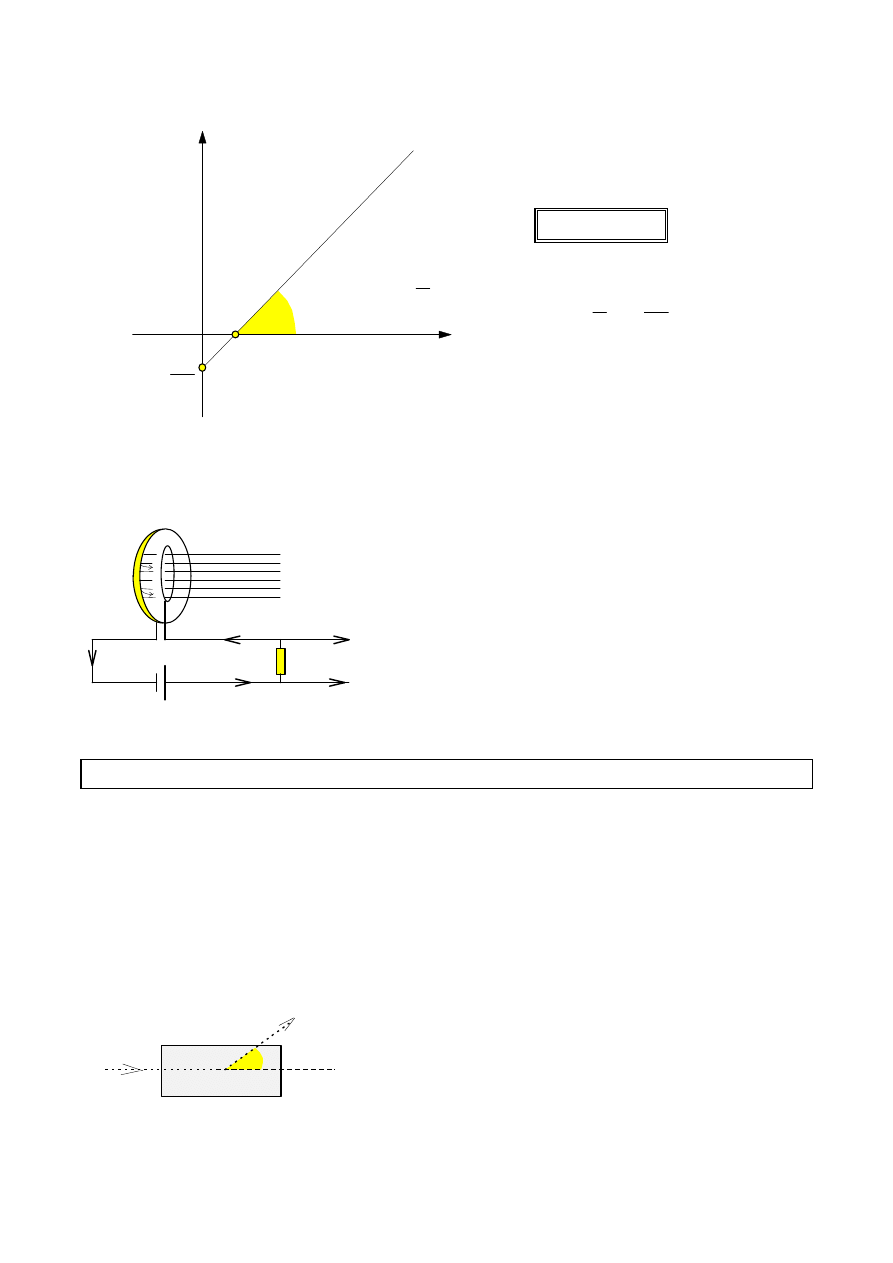
wiatło padające na powierzchnię przewodnika wybija z niego elektrony.

Badając natężenie prądu płynącego w obwodzie przedstawionym na rysunku
stwierdzono, że prąd przestaje płynąć jeśli długość fali promieniowania padającego
na katodę staje się dłuższa od pewnej długości granicznej. Aby wyjaśnić istnienie
długofalowej granicy zjawiska fotoelektrycznego trzeba było przyjąć, że światło nie
jest zwykłą falą, a składa się z paczek fal, tzw. fotonów. Każdy foton niesie kwant
energii ( porcję energii ) o wartości

h

νννν.

Wybicie elektronu z powierzchni metalu jest

możliwe wtedy, gdy energia kwantu jest większa od tzw. pracy wyjścia elektronu
(

W

).Praca wyjścia określa najmniejszą energię potrzebną do wyrwania elektronu z

powierzchni metalu i jest zależna od rodzaju metalu.

h

W

mV

νννν ====

++++

2

2

h

W

gr

νννν ====

mV

eU

h

2

2

====

wiązka padająca

klisza fotograficzna

pręcik pokryry
proszkiem polikrtstalicznym

wiązka światła

napięcie

hamowania

prąd

nasycenia

I

n

I

U

h

-

+

U

U

6

ν

ν

ν

ν

gr

- częstość graniczna

U

h

- napięcie hamowania

h

W

eU

h

νννν ====

++++

U

h

e

W

e

h

====

−−−−

νννν

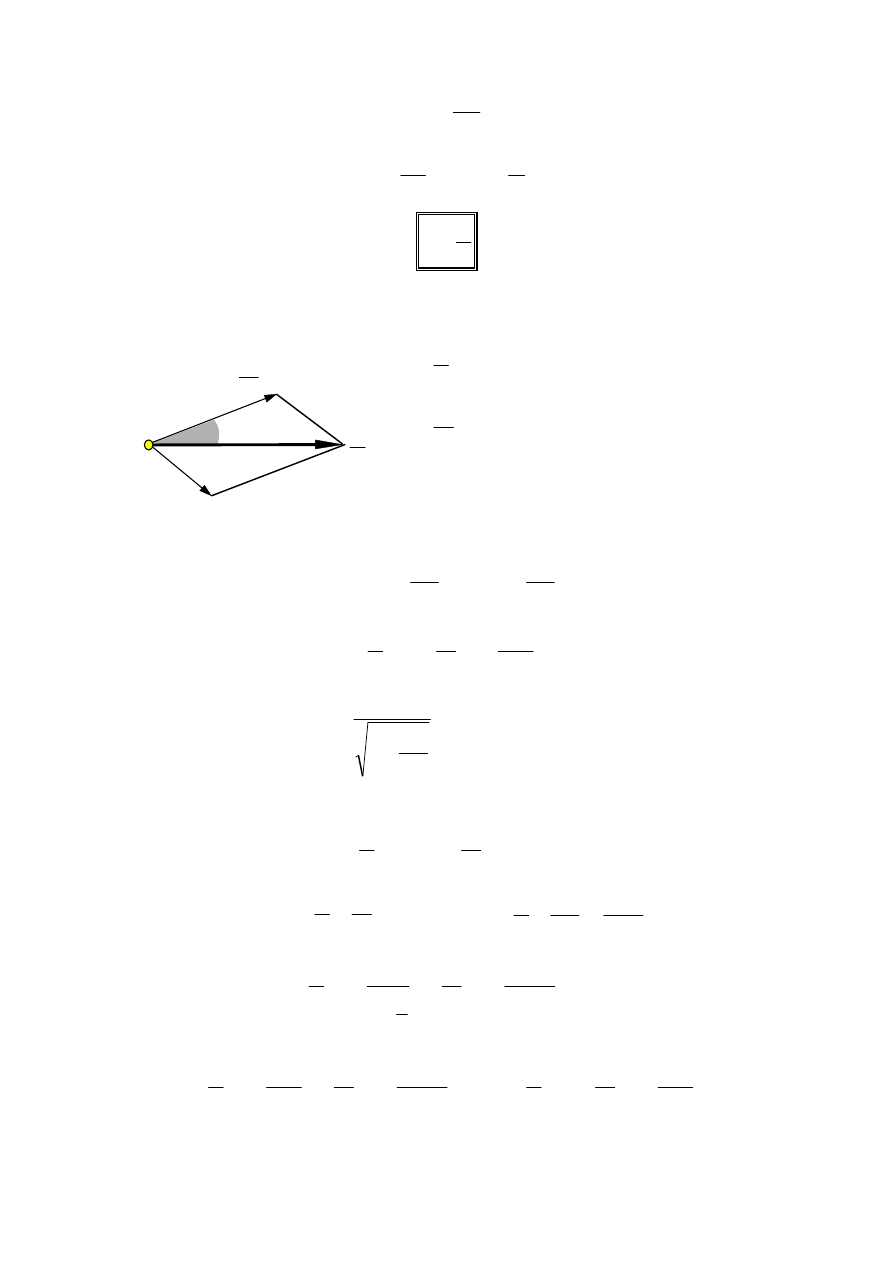
Zjawisko fotoelektryczne jest praktycznie
wykorzystane w komórce fotoelektrycznej.
Gdy na fotokomórkę pada strumień światła, to
z katody są wybijane elektrony. Pod wpływem
napięcia zewnętrznego przepływają one do
anody. W obwodzie płynie prąd. Spadek
napięcia na oporze

R

po wzmocnieniu może

posłużyć do uruchomienia np. urządzenia
alarmowego.

EFEKT COMPTONA

W 1923 r. Compton stwierdził, że promieniowanie rentgenowskie rozproszone w
bloku grafitowym ma długość fali większą od promieniowania padającego. Przyjęto,
ż

e strata energii fotonu jest efektem zderzenia fotonu z elektronem. Wszystkie

zderzenia zachodzą jednak zgodnie z zasadą zachowania pędu. Powstał więc
problem: co należy uważać za pęd fotonu?

Foton porusza się z prędkością światła, a zatem
jego pęd:

p = m c

Foton nie ma masy spoczynkowej, ale ma energię
i zgodnie ze wzorem Einsteina można mu
przypisać masę:

h

mc

νννν ====

2

U

h

−−−−

W

e

αααα

νννν

gr

νννν

tg

h

e

αααα

∼∼∼∼

zależność napięcia hamowania od częstotliwości fali
ś

wietlnej

komórka fotoelektryczna

e
e

U

λλλλ

′′′′

>>>>λλλλ

λλλλ

α

αα

α

blok grafitu

7

m

h

C

==== νννν

2

p

h

C

====

νννν

νννν

λλλλ

====

C

p

h

====

λλλλ

Zderzenie fotonu z elektronem zachodzi zgodnie z zasadą zachowania energii i
zasadą zachowania pędu.

h

λλλλ

- pęd fotonu przed zderzeniem

h

λλλλ

'

- pęd fotonu po zderzeniu

p

- pęd odrzuconego elektronu

Korzystając z zasady zachowania energii i zasady

zachowania pędu otrzymujemy:

m C

hC

mC

hC

0

2

2

++++

====

++++

λλλλ

λλλλ

'

p

h

h

h

2

2

2

2

2

====











++++











−−−−

λλλλ

λλλλ

λλ

λλ

λλ

λλ

ϕϕϕϕ

'

'

cos

p

mV

m V

V

C

p

m C

m C

====

====

−−−−

⇒

⇒

⇒

⇒

====

−−−−

0

2

2

2

2

2

0

2

2

1

Rozwiązując powyższy układ równań otrzymujemy:

h

m C

h

mC

λλλλ

λλλλ

++++

====

++++

0

'

mC

h

h

m C

====

−−−−











++++

λλλλ λλλλ

'

0

h

h

h

λλλλ λλλλ

λλ

λλ

λλ

λλ

−−−−

====

'

'

∆λ

∆λ

∆λ

∆λ

m C

h

h

h

h

m C

m C

2

2

2

2

2

0

0

2

2

2

2

====











−−−−

++++











++++

++++

λλλλ

λλ

λλ

λλ

λλ

λλλλ

λλ

λλ

λλ

λλ

'

'

'

∆λ

∆λ

∆λ

∆λ

p

h

h

h

h

m C

h

h

h

2

2

2

2

0

2

2

2

2

2

2

====











−−−−

++++











++++

====











++++











−−−−

λλλλ

λλ

λλ

λλ

λλ

λλλλ

λλ

λλ

λλ

λλ

λλλλ

λλλλ

λλ

λλ

λλ

λλ

ϕϕϕϕ

'

'

'

'

'

cos

∆λ

∆λ

∆λ

∆λ

2

⋅⋅⋅⋅

h

⋅⋅⋅⋅∆λ

∆λ

∆λ

∆λ⋅⋅⋅⋅

m

0

⋅⋅⋅⋅

C = 2h

2

- 2h

2

cos

ϕϕϕϕ

ϕ

p

h

λλλλ

h

′′′′

λλλλ

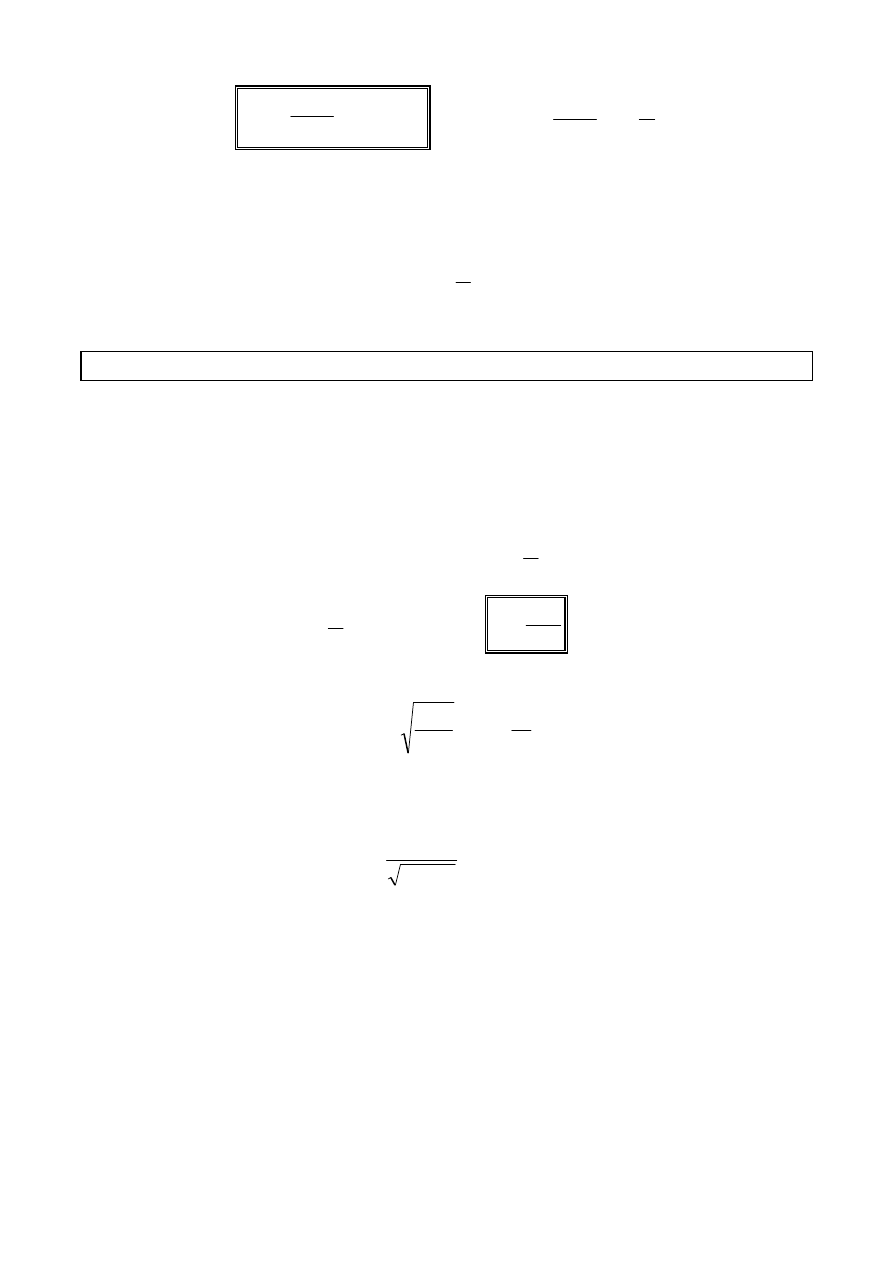
8

((((

))))

∆λ

∆λ

∆λ

∆λ ====

−−−−

h

m C

0

1

cos

ϕϕϕϕ

lub

∆λ

∆λ

∆λ

∆λ ====

2

2

0

2

h

m C

sin

ϕϕϕϕ

Doświadczalnie zmierzona zmiana długości fali

∆λ

∆λ

∆λ

∆λ

okazała się zgodna z

przewidywaną. Oznacza to, że foton może być traktowany jak cząstka o pędzie

p

h

====

λλλλ

.

DUALIZM KORPUSKULARNO - FALOWY

Zjawisko fotoelektryczne i efekt Comptona świadczą o korpuskularnych
własnościach promieniowania. Stwierdzenie tego faktu zrodziło przypuszczenie, że
cząstki mogą mieć własności falowe. Przyjęto, że jeśli foton i cząstka mają
jednakowe pędy, to powinny im odpowiadać jednakowe długości fali.

p

cz

=

m V

p

h

f

====

λλλλ

h

mV

λλλλ

====

λλλλ ====

h

mV

Elektron przyspieszony napięciem

150V

uzyskuje prędkość:

V

eU

m

m

s

====

≈≈≈≈

2

10

7

Takiemu elektronowi można przypisać długość fali:

λλλλ ====

≈≈≈≈

−−−−

h

emU

m

2

10

10

Jest to przeciętna długość fali promieniowania rentgenowskiego. Potwierdzeniem
słuszności takiego rozumowania jest uzyskanie charakterystycznych maksimów
interferencyjnych wiązki elektronowej odbitej od powierzchni kryształu.
Analogiczne widmo interferencyjne można uzyskać przy użyciu promieni
rentgenowskich.

Fale skojarzone z ruchomą cząstką są nazywane falami materii lub falami de
Broglie’a, ponieważ z hipotezą fal materii wystąpił jako pierwszy fizyk francuski,

9

profesor Sorbony, członek Akademii Francuskiej - Louis Victor de Broglie. Teoria ta
powstała w roku 1924. W roku 1929 L.V.de Broglie otrzymał nagrodę Nobla.
Fale materii nie mają natury jakichkolwiek znanych fal. Traktowanie elektronu, czy
innej cząstki materialnej jako pewnego rodzaju fali wydaje się dziwne, ponieważ
stanowi dysonans z mocno utrwalonym modelem cząstki materialnej jako punktu.
Obraz ten jednak jest fałszywy. Nie pierwszy to raz w historii fizyki wyobraźnia,
ukształtowana w określonych warunkach stanowi przeszkodę w poznawaniu świata.
Istotą dualizmu korpuskularno-falowego jest podwójne traktowanie zarówno fal jak i
cząstek. Fali o długości

λλλλ

można przypisać pęd - wielkość charakterystyczną dla

cząstek:

p

h

====

λλλλ

Cząstce o pędzie

p

można przypisać długość fali - wielkość charakterystyczną dla

fal:

λλλλ ====

h

p

Falowe traktowanie materii jest podstawą mechaniki falowej.

ZASADA NIEOZNACZONOŚCI HEISENBERGA

1

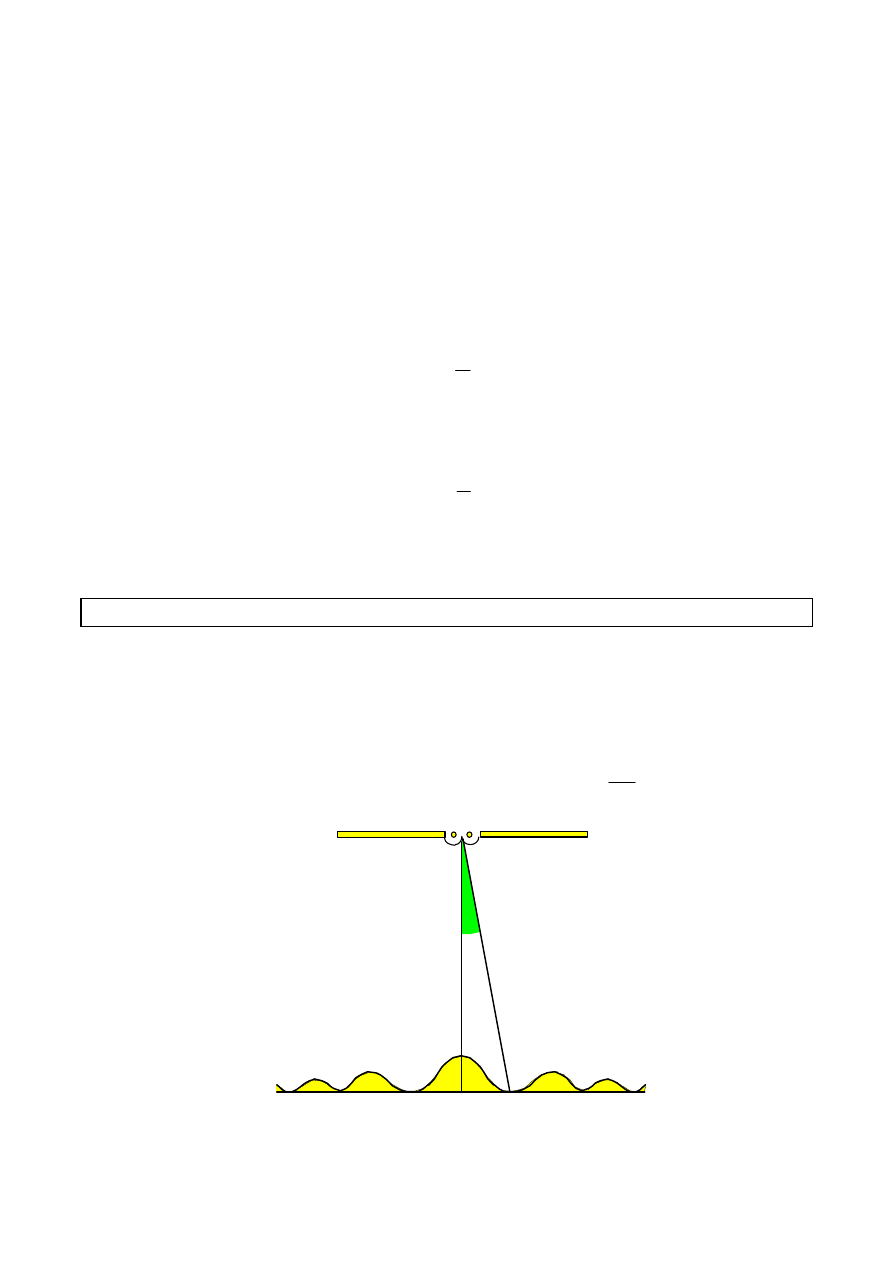
. Interferencja światła przy przejściu przez szczelinę.

Każdy punkt szczeliny o szerokości

∆∆∆∆

x

jest źródłem fali cząsteczkowej. Fale te

nakładają się, w wyniku czego powstają charakterystyczne maksima interferencyjne.

Najsilniejszym źródłem fal są punkty położone w odległości

∆∆∆∆

x

2

.

Pierwsze minimum powstaje pod kątem

αααα

spełniającym warunek:

∆∆∆∆

x

αααα

10

λλλλ

αααα

2

2

==== ∆∆∆∆

x

sin

λλλλ

αααα

==== ∆∆∆∆

x sin

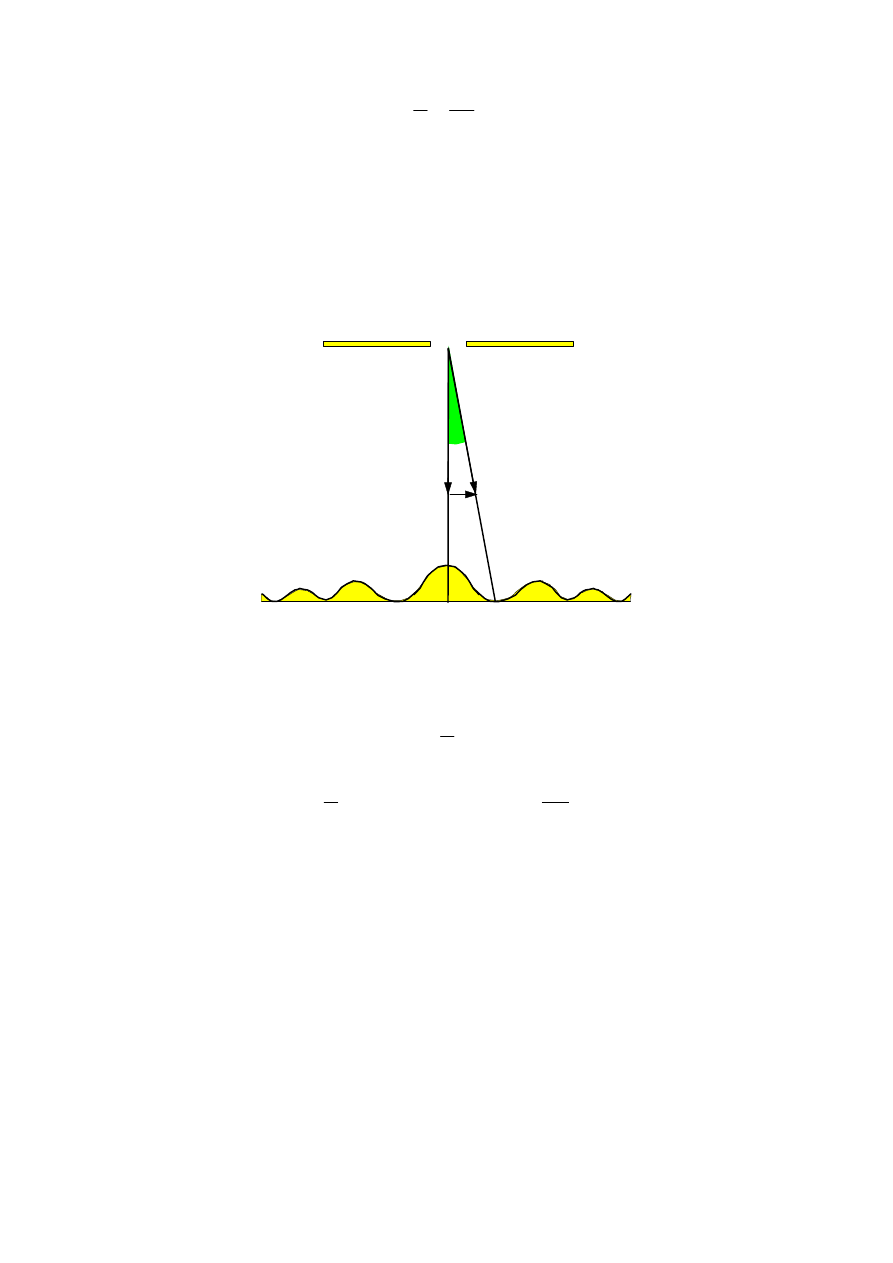
2. Przechodzenie wiązki cząstek przez szczelinę.

Strumień cząstek, np. elektronów przechodząc przez szczelinę o szerokości

∆∆∆∆

x

również ulega interferencji, tworząc analogiczne maksima interferencyjne. Cząstka o
pędzie

p

przechodząc przez szczelinę doznaje zmiany pędu w kierunku

równoległym

do

szczeliny

∆∆∆∆

p

x

.

Dla cząstek tworzących pierwsze minimum interferencyjne otrzymujemy:

∆∆∆∆

p

x

= p sin

αααα

Traktując cząstki jak fale o długości

λλλλ ====

h

p

otrzymujemy:

h

p

x

p

h

x

====

⇒

⇒

⇒

⇒

====

∆∆∆∆

∆∆∆∆

sin

sin

αααα

αααα

∆∆∆∆

∆∆∆∆

p

x

h

x

⋅⋅⋅⋅

====

Cząstki tworzące maksimum pierwszego rzędu i dalsze doznają jednak większego
odchylenia. Dla tych cząstek spełniona jest nierówność:

∆

∆

∆

∆

p

x

⋅⋅⋅⋅

∆

∆

∆

∆

x

≥≥≥≥

h

3. Odchylenie standardowe ( średnie kwadratowe odchylenie ).

Przy szczelinie o szerokości

∆∆∆∆

x

, odchylenia cząstek, wynikające ze zmiany ich pędu

mają charakter przypadkowy. Jeśli przez szczelinę przechodzi

n

cząstek, przy czym

αααα

r

p

0

r

p

∆∆∆∆

r

p

x

∆∆∆∆

x

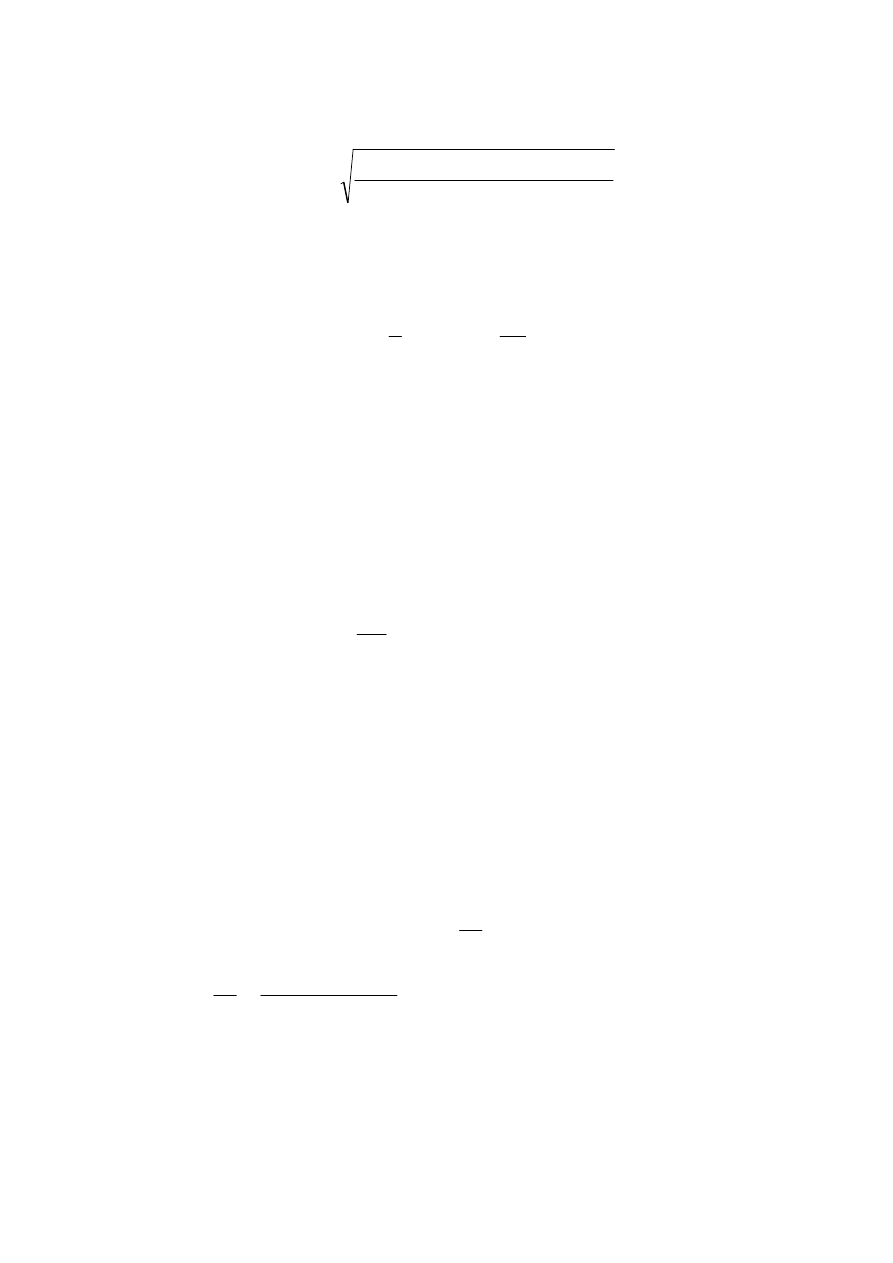
11

kolejne cząstki doznają zmian pędu

∆∆∆∆

p

1

,

∆∆∆∆

p

2

, ...... to średnia, standardowa zmiana

pędu wynosi:

∆∆∆∆

∆∆∆∆

∆∆∆∆

∆∆∆∆

∆∆∆∆

p

p

p

p

p

n

n

==== ±±±±

++++

++++

++++

++++

1

2

2

2

3

2

2

. . . . . .

4. Nieoznaczoność pędu i położenia.

Jeśli przez

∆∆∆∆

p

i przez

∆∆∆∆

x

oznaczymy odpowiednio standardowe odchylenie pędu i

standardowe odchylenie położenia cząstki, to nierówność przyjmuje postać:

∆∆∆∆ ∆∆∆∆

p x

≥≥≥≥

h

2

;

h

====

h

2

ππππ

Powyższa nierówność stanowi matematyczny zapis tzw. zasady nieoznaczoności
Heisenberga. Została ona sformułowana w roku 1927 przez profesora uniwersytetów
w Lipsku i Berlinie - Wernera Carla Heisenberga ( 1901 - 1976 ).

Wielkości

∆∆∆∆

p

i

∆∆∆∆

x

określają statystyczną niepewność określenia pędu i położenia

cząstki. Im dokładniej określone jest położenie cząstki, tym mniej dokładnie można
określić jej pęd i odwrotnie.

5. Nieoznaczoność energii i czasu.

Nieokreśloność nie dotyczy tylko położenia i pędu.

dp dx

m dV dx

m

dV

dt

dx dt

m a dx dt

F dx dt

dE dt

⋅⋅⋅⋅

==== ⋅⋅⋅⋅

⋅⋅⋅⋅

==== ⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

==== ⋅⋅⋅⋅ ⋅⋅⋅⋅

⋅⋅⋅⋅

==== ⋅⋅⋅⋅

⋅⋅⋅⋅ ====

⋅⋅⋅⋅

Iloczyn zmiany pędu i zmiany położenia jest równoważny zatem iloczynowi zmiany
energii i czasu, w którym ta zmiana nastąpiła.

∆∆∆∆

p

⋅⋅⋅⋅∆∆∆∆

x =

∆∆∆∆

E

⋅⋅⋅⋅∆∆∆∆

t

Dla przykładu: Stan wzbudzenia atomu charakteryzuje energia wzbudzenia i czas, w
którym atom pozostaje w stanie wzbudzonym. Jeśli czas wzbudzenia atomu wynosi
10

-8

s

, to niepewność w określeniu energii tego stanu wynosi:

∆∆∆∆

∆∆∆∆

E

t

≥≥≥≥

h

h

∆∆∆∆

t

J s

s

J

eV

====

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

−−−−

−−−−

−−−−

−−−−

6 626 10

2

10

1 0546 10

6 58 10

34

8

26

8

,

,

,

ππππ

∆∆∆∆

E

≥≥≥≥

6,58

⋅⋅⋅⋅

10

-8

eV

Oznacza to, że dokładność określenia energii stanu wzbudzonego jest rzędu 10

-7

eV

.

Zasada nieoznaczoności Heisenberga nie ma nic wspólnego z niedokładnością

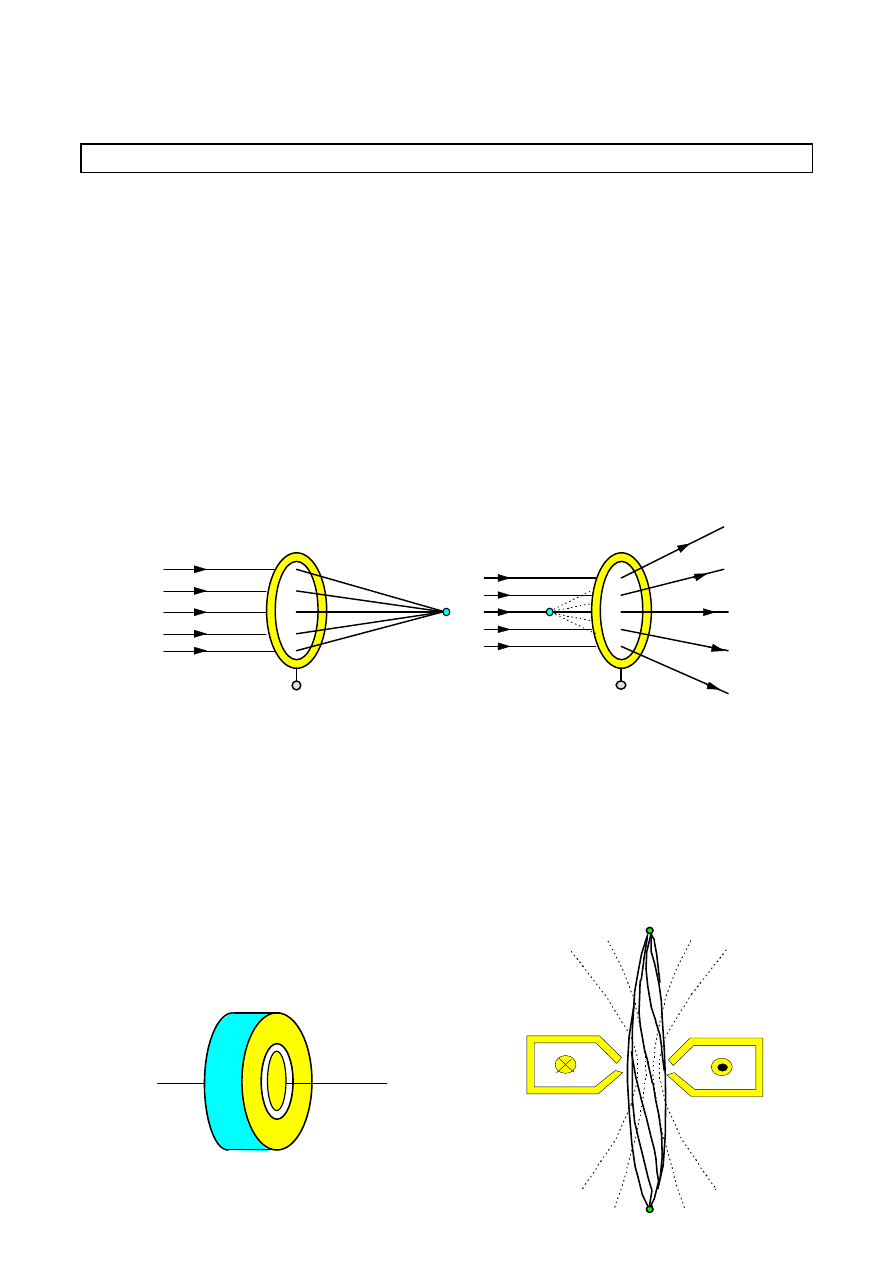
12

przyrządów pomiarowych, lecz jest fundamentalną własnością mikroświata,
wynikającą z falowej natury cząstek.

MIKROSKOP ELEKTRONOWY

Mikroskop optyczny pozwala rozróżniać szczegóły odległe od siebie o długość fali
ś

wiatła użytego do obserwacji. Najlepsza zdolność rozdzielcza, którą można uzyskać

przy pomocy światła nadfioletowego, wynosi 10

-7

m

. Wiązce elektronów

przyspieszonych napięciem 50 - 100 kV odpowiada długość fali de Broglie’a rzędu
10

-12

m

.

W mikroskopie elektronowym strumień elektronów pełni funkcję światła. Uzyskanie
odwzorowania przedmiotu przy użyciu wiązki elektronów jest możliwe przy użyciu
tzw. soczewek elektronowych. Istnieją soczewki elektrostatyczne i soczewki
magnetyczne.

Soczewkę

elektrostatyczną

stanowi

pierścień

wytwarzający

niejednorodne pole elektryczne.

Ogniskowanie strumienia elektronów można również uzyskać przy użyciu
odpowiednio ukształtowanego pola magnetycznego.

Strumień elektronów wychodzący z punktu P wpada w obszar niejednorodnego
pola magnetycznego. Pole to powoduje odchylanie elektronów, które poruszają się
po torach śrubowych i po przejściu przez obszar pola zostają skupione w punkcie P’.

F

F

_

+

soczewka skupiająca

soczewka rozpraszająca

soczewka magnetyczna

P

p’

13

Soczewki elektrostatyczne lub magnetyczne w mikroskopie elektronowym pełnią
takie same funkcje jak soczewki optyczne w mikroskopie optycznym. W odróżnieniu
od mikroskopu optycznego, w mikroskopie elektronowym obraz jest rzeczywisty i
powstaje na ekranie pokrytym substancją fluoryzującą.

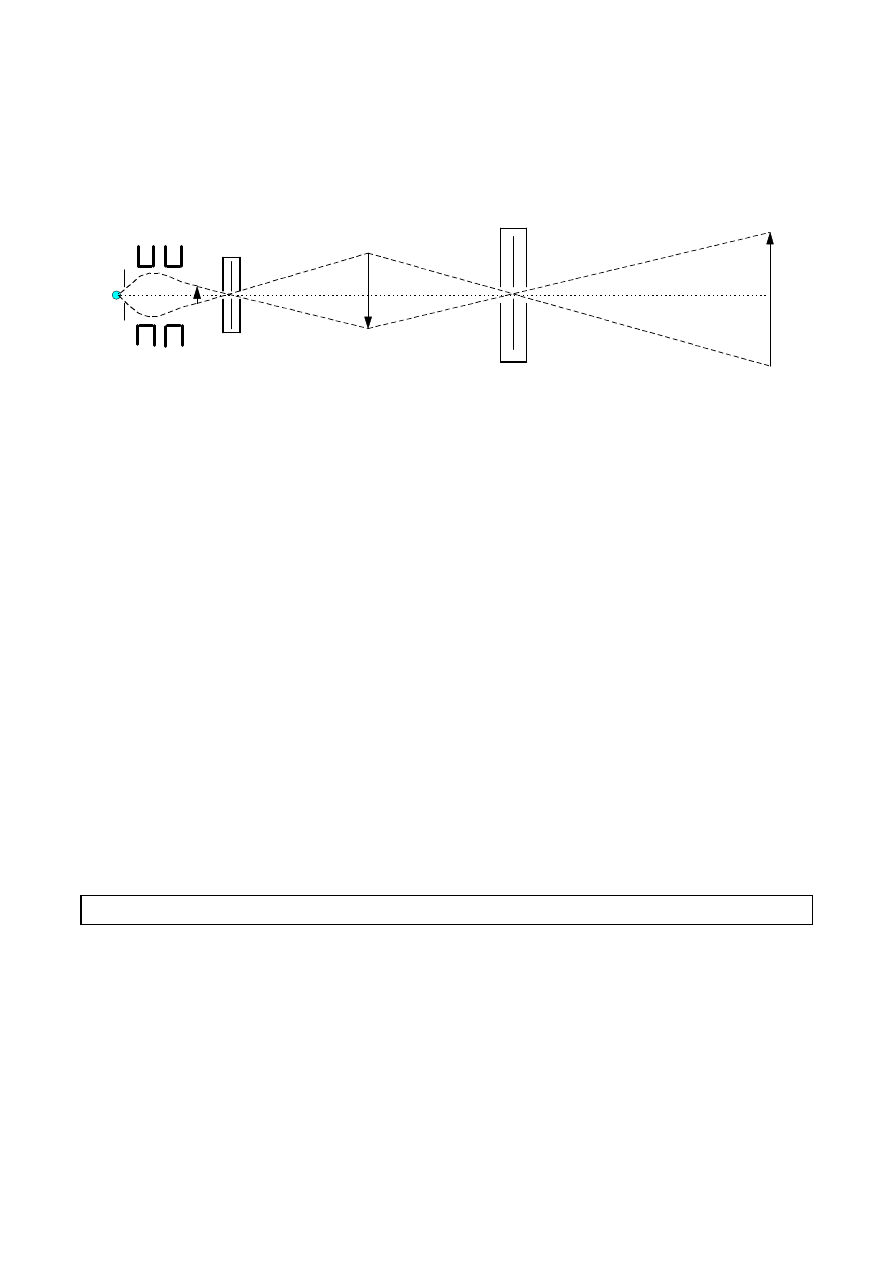
Schemat mikroskopu elektronowego

Ź

ródłem elektronów jest żarząca się spiralka (Z). Elektrony te przyspieszone

napięciem kilkudziesięciu tysięcy woltów przechodzą przez tzw. kondensor
elektronowy (K), dzięki któremu zostają one skupione na przedmiocie (P). Elektrony
przenikają przez przedmiot, po czym są zbierane przez soczewkę elektronową (S

1

)

wytwarzający powiększony obraz przedmiotu (P

1

). Obraz ten jest jeszcze raz

powiększony przez soczewkę elektronową (S

2

). Ostateczny obraz przedmiotu (P

2

)

powstaje na ekranie fluoryzującym, względnie na kliszy fotograficznej.

Zdolność rozdzielczą mikroskopów elektronowych ogranicza przede wszystkim
aberracja

sferyczna

soczewek

elektronowych.

Przy pomocy mikroskopu

elektronowego uzyskuje się praktycznie powiększenia do 500 tys. razy. Pierwszy
mikroskop elektronowy zbudowali M.Knoll i E.A. Ruska w 1931 r. w Berlinie.
Obecnie mikroskopy elektronowe buduje się w wielu krajach. Pozwalają one na
uzyskanie zdolności rozdzielczej rzędu 10

-10

m

. Za pomocą mikroskopu

elektronowego możliwe jest badanie wirusów, lub badanie struktur krystalicznych
czy molekularnych.

EMISJA I ABSORPCJA PROMIENIOWANIA

Wszystkie ciała o temperaturze wyższej od temperatury zera bezwzględnego
wysyłają promieniowanie zwane temperaturowym.

1. Zdolność emisyjna.

P

2

P

1

S

2

S

1

P

K

-

+

-

+

Z

14

Miarą zdolności emisyjnej ciała jest stosunek
energii wypromieniowanej przez ciało w
jednostce czasu, w elementarnym przedziale
długości fal do powierzchni emitującej to
promieniowanie.

Zdolność

emisyjna

jest

funkcją długości fali i temperatury.

(((( ))))

e

T

dW

dt dS d

λλλλ

λλλλ

,

====

⋅⋅⋅⋅

⋅⋅⋅⋅

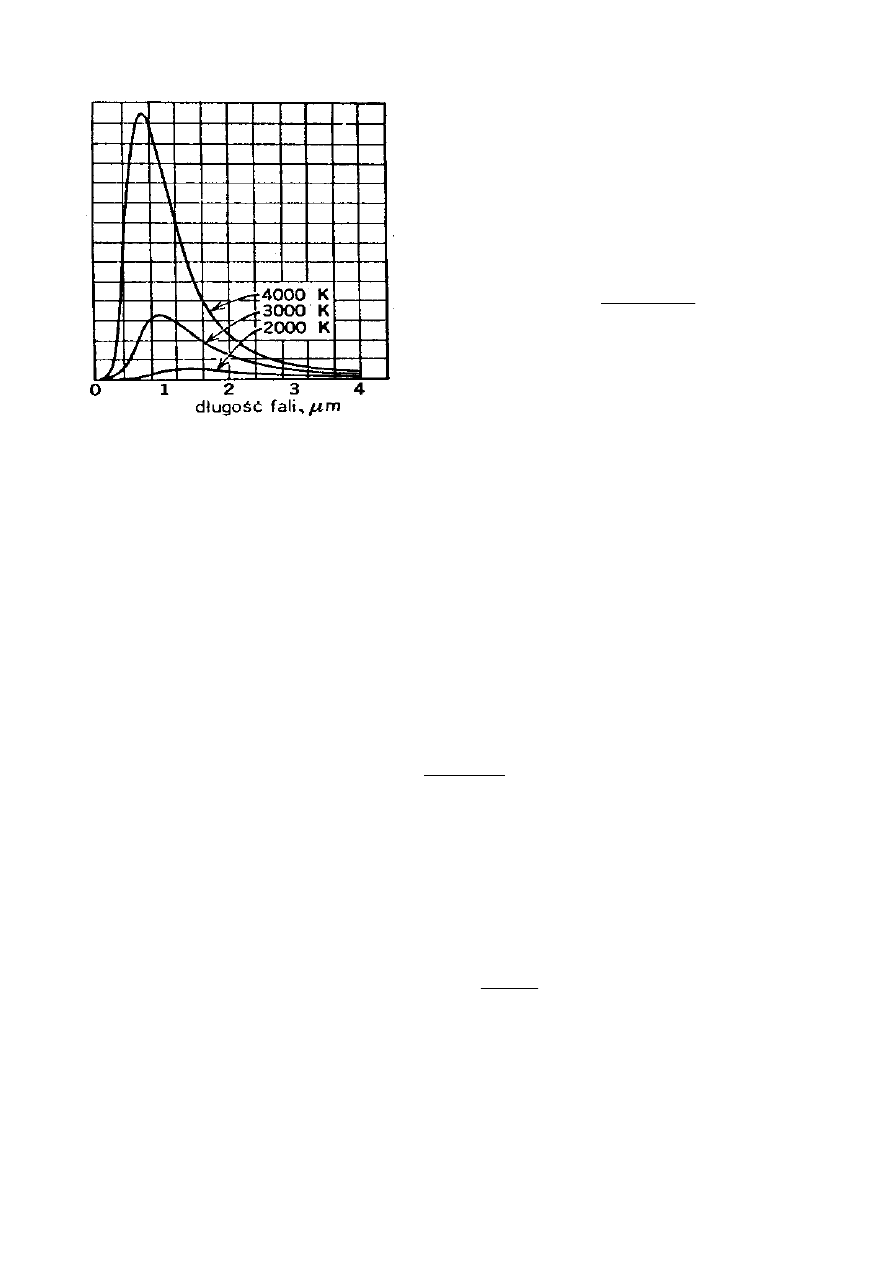
Zależność zdolności emisyjnej ciała od

długości fali, przy ustalonej temperaturze zależy od rodzaju ciała.

2. Całkowita zdolność emisyjna. Prawo Stefana Boltzmanna.

Przez całkowitą zdolność emisyjną rozumiemy następującą sumę:

E

e d

e d

e

d

o

====

++++

++++

====

∞

∞

∞

∞

∫∫∫∫

1

1

2

2

0

λλλλ

λλλλ

λλλλ λλλλ

. . . . . . .

( )

Graficznym obrazem takiej sumy jest pole figury zawartej po wykresem zdolności
emisyjnej ciała. Zgodnie z prawem Stefana - Boltzmanna całkowita zdolność
emisyjna jest wprost proporcjonalna do czwartej potęgi temperatury bezwzględnej
ciała.

Współczynnik

σσσσ

ma ustaloną wartość dla tzw. ciała doskonale czarnego. Jest to

ciało, dla którego cechy charakterystyczne powierzchni nie mają wpływu na emisję
promieniowania. Własności zbliżone do ciała doskonale czarnego mają sadze, czy
powierzchnia pokryta tlenkiem toru. Dla ciała doskonale czarnego:

σσσσ ====

⋅⋅⋅⋅

−−−−

5 67 10

8

2

4

,

W

m K

Całkowita zdolność emisyjna dla ciał rzeczywistych jest określona wzorem:

E = k

σ

σ

σ

σ

T

4

E

0

=

δ

δ

δ

δ

T

4

15

gdzie wartość współczynnika k zależy od rodzaju ciała.

3. Prawo Wiena.

Prawo to określa długość fali, której odpowiada maksimum zdolności emisyjnej
ciała. Długość fali odpowiadającej zdolności emisyjnej jest odwrotnie
proporcjonalna do temperatury bezwzględnej ciała.

λλλλ

m

C

T

====

Dla ciała doskonale czarnego c = 2,866

⋅⋅⋅⋅

10

-9

m

⋅⋅⋅⋅

K

4. Zdolność absorpcyjna.

Marą zdolności absorpcyjnej jest stosunek energii pochłoniętej przez ciało do energii
padającej. Jest ona również funkcją długości fali i temperatury. Dla ciała doskonale
czarnego a(

λ,

λ,

λ,

λ,

T ) = 1

5. Prawo Kirchhoffa.

Stosunek zdolności emisyjnej do zdolności absorpcyjnej jest dla wszystkich ciał
jednakowy.

(((( ))))

(((( )))) (((( ))))

e

T

a

T

f

T

λλλλ

λλλλ

λλλλ

,

,

,

====

;

f

T

hc

e

hc

kT

( , )

λλλλ

ππππ

ππππ

λλλλ

====

−−−−

2

1

1

2

5