POLA I FALE

ELEKTROMAGNETYCZNE

Drgania (zmiany) natężeń pól elektrycznego i magnetycznego w
przestrzeni (w próżni lub w ośrodkach materialnych)

Częstotliwości

przemysłowe (50Hz)

Energetyka
Zasilanie urządzeń

Fale radiowe

Radiokomunikacja

(

λλλλ→

→

→

→km ÷÷÷÷ m)

Radiodyfuzja, TV

Mikrofale

Telekomunikacja

(

λλλλ→

→

→

→dcm ÷÷÷÷ mm)

i TV Satelitarna,
Radiolokacja,
Radionawigacja
Łączność naziemna (radiolinie)

Fale świetlne

Łączność światłowodowa

(

λλλλ < µµµµm)

Transmisja dużej ilości danych
między komputerami

Inne zastosowania:

- grzanie (suszenie, niszczenie szkodników)
- ruch drogowy (radary antykolizyjne, pomiar prędkości)
- precyzyjne pomiary geodezyjne
- technika jądrowa (akceleratory)
- medycyna (spektroskopia, tomografia, napromieniowanie)

Przedmiot Pola i fale będzie głównie rozwijany i wykorzystywany w
następnych semestrach w przedmiotach:

- podstawy techniki w.cz.
- anteny i propagacja fal
- analiza i synteza układów mikrofalowych

POLA i FALE AKUSTYCZNE

Drgania cząstek materialnych w środowiskach sprężystych.

Akustyka

fizyczna

Promieniowanie

i rozchodzenie sie

dzwieku w srodowiskach

materialnych

Akustyka

Ultra-
akustyka
Elektro-
akustyka

Uderzenia

Wibracje

Szum

Akustyka

wnetrz

Gamy

muzyczne

Instrumenty

Komuni-

kacja

Psycho-

akustyka

Sluch

Bioakustyka

Oceanografia

Akustyka

podwodna

Fizyka ziemi

i

atmosfery

Nauki

o ziemi

Technika

Elektrotechnika

i

chemia

Mechanika

Architektura

Sztuki

wizualne

Muzyka

Mowa

Psychologia

Medycyna

Fizjologia

Biologia

Sztuka

Rysunek przytoczony w/g książki Z. Żyszkowski: Podstawy elektroakustyki :WNT, Warszawa
1984, ss. 22

Pola i fale akustyczne są szeroko omawiane w przedmiocie:
- Podstawy elektroakustyki

ANALIZA WEKTOROWA

pseudowektor:

∇

∇

∇

∇ ====

++++

++++

&

&

&

i

x

i

y

z

x

y

∂∂∂∂

∂∂∂∂

∂∂∂∂

∂∂∂∂

∂∂∂∂

∂∂∂∂

i

z

operacje wektorowe:

grad U

i

U

x

i

U

y

U

z

U

x

y

====

++++

++++

==== ∇

∇

∇

∇

&

&

∂∂∂∂

∂∂∂∂

∂∂∂∂

∂∂∂∂

∂∂∂∂

∂∂∂∂

div A

A

x

A

y

A

z

A

x

y

z

&

&

====

++++

++++

==== ∇

∇

∇

∇ ⋅⋅⋅⋅

∂∂∂∂

∂∂∂∂

∂∂∂∂

∂∂∂∂

∂∂∂∂

∂∂∂∂

rotA

i

i

i

x

y

z

A

A

A

A

x

y

z

x

y

z

&

&

&

&

&

====

==== ∇

∇

∇

∇ ××××

∂∂∂∂

∂∂∂∂

∂∂∂∂

∂∂∂∂

∂∂∂∂

∂∂∂∂

Laplasjan U

U

x

U

y

U

z

U

2

2

2

2

2

2

2

====

++++

++++

==== ∇

∇

∇

∇

∂∂∂∂

∂∂∂∂

∂∂∂∂

∂∂∂∂

∂∂∂∂

∂∂∂∂

∇

∇

∇

∇

==== ∇

∇

∇

∇

++++ ∇

∇

∇

∇

++++ ∇

∇

∇

∇

2

2

2

2

&

&

&

&

A

i

A

i

A

i

A

x

x

y

y

z

z

Wybrane tożsamości wektorowe

(

)

∇⋅ ∇ ×

=

&

A

0

pole wirowe jest bezźródłowe

(

)

∇ × ∇

=

U

0

pole potencjalne jest bezwirowe

(

)

∇⋅ ∇

= ∇

U

U

2

(

) ( )

∇ × ∇ ×

= ∇ ∇⋅

− ∇

&

&

&

A

A

A

2

Tw. Gaussa:

∇ ⋅

=

⋅

∫∫∫

∫∫

&

& &

A dV

A n dS

V

S

Tw. Stokesa:

&

&

& &

A d l

A n dS

l

S

⋅

=

∇ × ⋅

∫

∫∫

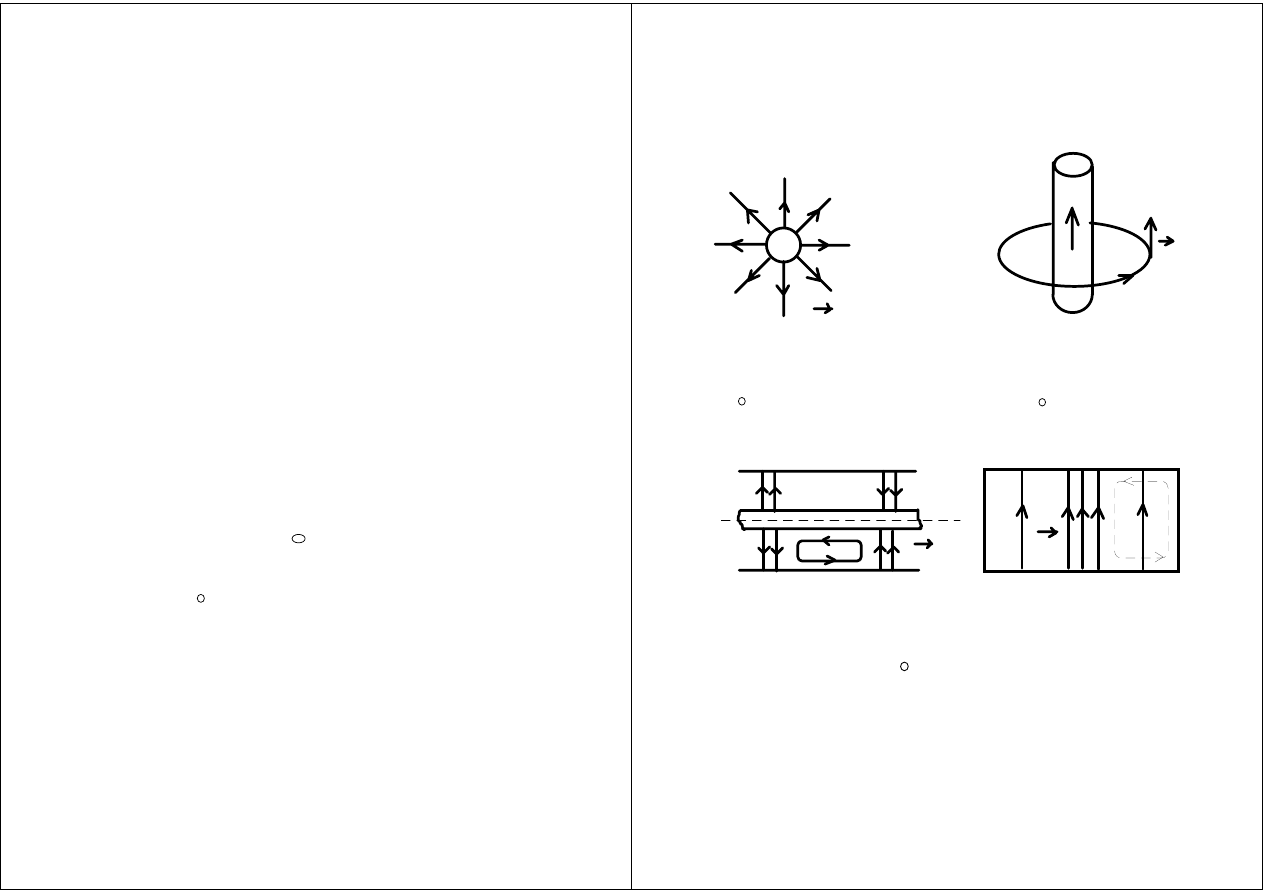
Pola wektorowe

+

E

J

H

l

Pole bezwirowe

Pole wirowe

&

&

E

⋅

=

∫

d l

0

l

&

&

H

J

⋅

=

∫

d l

l

l

E

E

l

Pole wirowe

&

&

E

⋅

≠

∫

d l

0

l

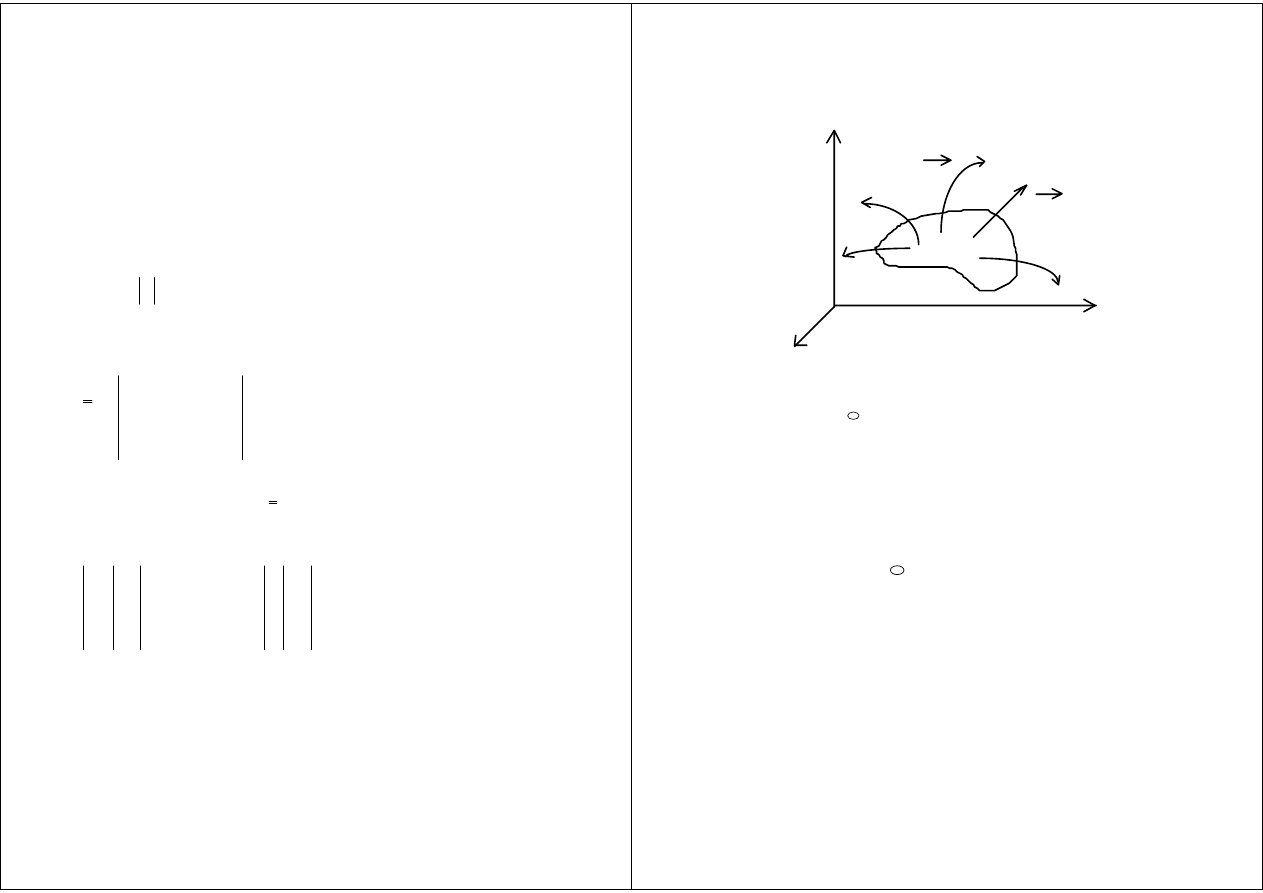
Rodzaje ośrodków

&

&

D

E

==== εεεε

&

&

B

H

==== µµµµ

&

&

J

E

==== σσσσ

(

)

ε = f x y z

, ,

- niejednorodny

( )

ε

= f

&

E

- nieliniowy

( )

ε

ω

= f

- dyspersyjny

εεεε

εεεε

εεεε

εεεε

εεεε

εεεε

εεεε

εεεε

εεεε

εεεε

====

11

12

13

21

22

23

31

32

33

- anizotropowy

Żyrotropowy, gdy

εεεε

εεεε

→

→

→

→

pod wpływem stałego

&

B

D

D

D

E

E

E

x

y

z

x

y

z

====

⋅⋅⋅⋅

εεεε

εεεε

εεεε

εεεε

εεεε

εεεε

εεεε

εεεε

εεεε

11

12

13

21

22

23

31

32

33

Prawo Gaussa

x

z

y

s

v

D

n

& &

D

⋅

=

=

∫∫∫

∑

∫∫

n dS

q

dV

V

S

ρ

∇⋅

=

∫∫∫

∫∫∫

&

D dV

dV

V

V

ρ

∇

∇

∇

∇ ⋅⋅⋅⋅

====

&

D

ρρρρ

& &

B

⋅

=

∫∫

n dS

S

0

∇

∇

∇

∇ ⋅⋅⋅⋅ ====

&

B

0

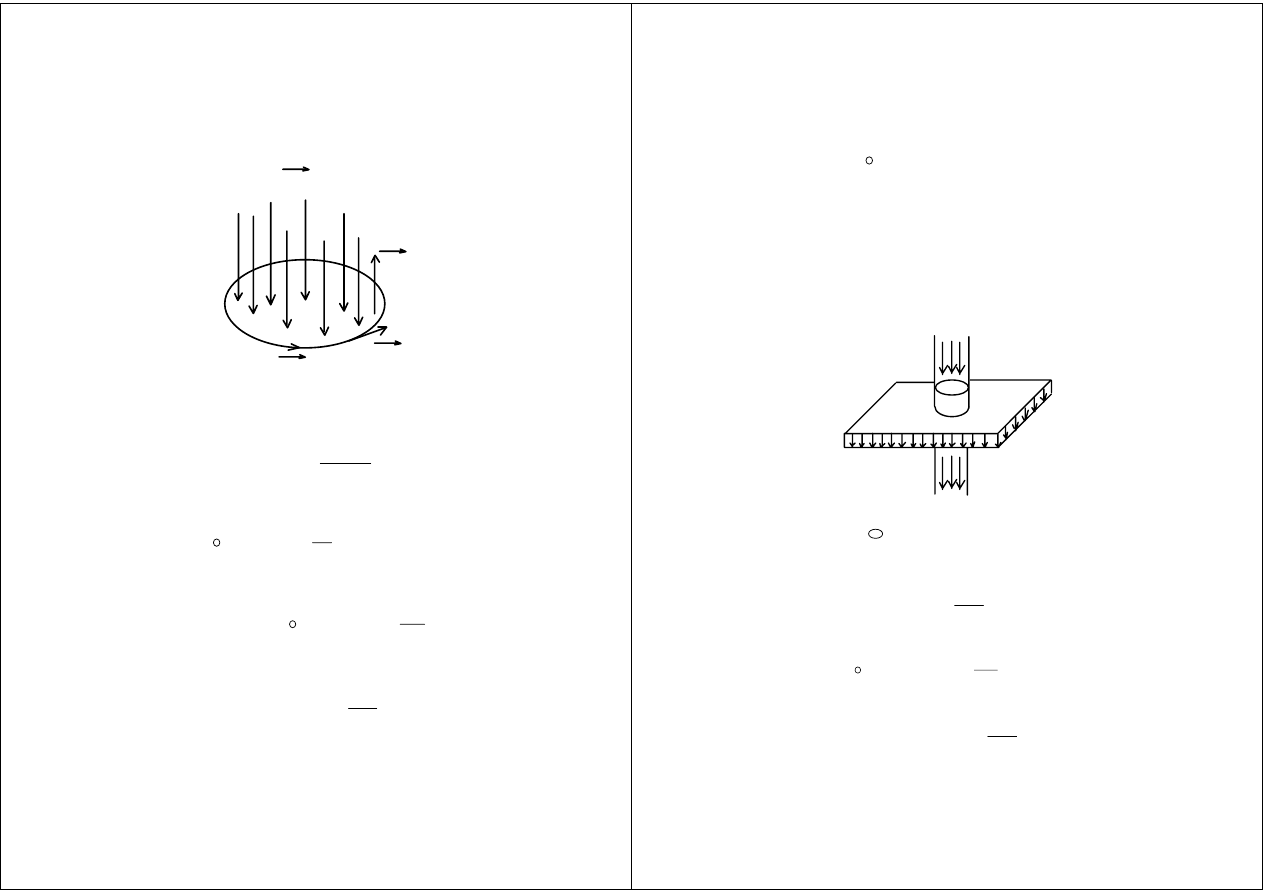
Prawo Faradaya

B

S

l

dl

n

V

d

d t

m

==== −−−−

Φ

Φ

Φ

Φ

&

&

& &

E

B

⋅

= −

⋅

∫∫

∫

d l

d

d t

n d S

S

l

∇ × ⋅

=

⋅

= −

⋅

∫∫

∫∫

∫

& &

&

&

&

&

E

E

B

n dS

d l

t

n dS

S

l

∂

∂

S

∇

∇

∇

∇ ×××× ==== −−−−

&

&

E

B

∂∂∂∂

∂∂∂∂ t

Prawo Ampera

&

&

& &

H

J

⋅

=

⋅

∫∫

∫

dl

n dS

S

l

&

&

J

E

σσσσ

σσσσ

====

-

(prąd przewodzenia)

&

&

J

ρρρρ

ρρρρ

==== V

- (prąd unoszenia)

&

&

&

J

J

J

====

++++

σσσσ

ρρρρ

- (prąd związany z ruchem ładunków)

+

+

+

+

+

+

+

+

+

+

+

+

+

+q

-q

S

J

p

J

p

J

d

& &

D

D

⋅

= ⋅ =

∫∫

n dS

S

q

S

&

&

J

D

d

t

==== ∂∂∂∂

∂∂∂∂

&

&

&

&

&

H

J

D

⋅

=

+









 ⋅

∫∫

∫

d l

t

n dS

S

l

∂

∂

∇

∇

∇

∇ ××××

==== ++++

&

&

&

H

J

D

∂∂∂∂

∂∂∂∂ t

Równania Maxwella

∇

∇

∇

∇ ×××× ==== −−−−

&

&

E

B

∂∂∂∂

∂∂∂∂ t

∇

∇

∇

∇ ××××

==== ++++

&

&

&

H

J

D

∂∂∂∂

∂∂∂∂ t

∇

∇

∇

∇ ⋅⋅⋅⋅

====

&

D

ρρρρ

∇

∇

∇

∇ ⋅⋅⋅⋅ ====

&

B

0

∇

∇

∇

∇ ⋅⋅⋅⋅ ==== −−−−

&

J

∂∂∂∂ ρρρρ

∂∂∂∂ t

Równania falowe w dielektryku

idealnym

∇

∇

∇

∇ ×××× ==== −−−−

∇

∇

∇

∇ ⋅⋅⋅⋅ ====

∇

∇

∇

∇ ××××

====

∇

∇

∇

∇ ⋅⋅⋅⋅ ====

&

&

&

&

&

&

E

H

E

H

E

H

µµµµ ∂∂∂∂

∂∂∂∂

εεεε ∂∂∂∂

∂∂∂∂

t

t

0

0

(

) ( )

∇ × ∇ ×

= ∇ ∇ ⋅

− ∇

&

&

&

E

E

E

2

∇

∇

∇

∇

−−−−

====

2

2

2

0

&

&

E

E

µµµµ εεεε ∂∂∂∂

∂∂∂∂ t

∇

∇

∇

∇

−−−−

====

2

2

2

0

&

&

H

H

µµµµ εεεε ∂∂∂∂

∂∂∂∂ t

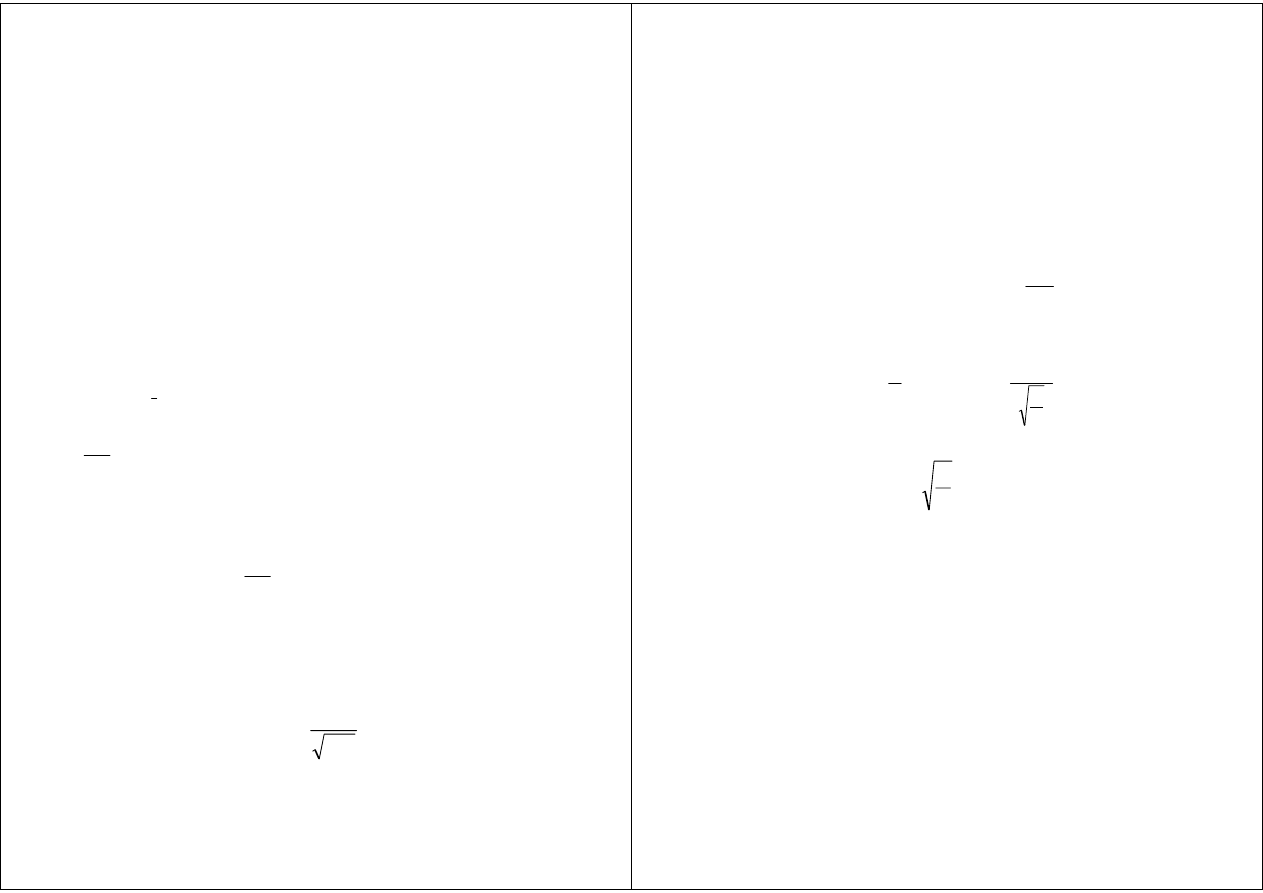
Fala płaska

→

równanie płaszczyzny prostopadłej do wektora k:

& &

k r

const

⋅⋅⋅⋅ ====

→

płaszczyzna poruszająca się w kierunku k z prędkością v :

& &

k r

v t

const

⋅⋅⋅⋅ −−−−

====

(

) (

)

&

& & &

& & &

E

F

=

⋅ −

+

⋅ +

k

r

v t

k

r

v t

φ

(

)

(

)

&

& &

&

E

F

F

=

⋅ −

=

+

+

−

k r

v t

k x k y k z v t

x

y

z

(

)

(

)

∂

∂

2

2

x

k x k y k z vt

k

' ' k r

v t

x

y

z

x

2

&

& & &

F

F

+

+

−

=

⋅ −

(

)

(

) (

)

∇

=

+ +

⋅ −

=

⋅ −

2

&

& & &

& & &

F

F

F

k

k

k

' ' k r

v t

' ' k r

v t

x

2

y

2

x

2

(

)

∂

∂

2

2

2

&

& & &

F

F

t

v

' ' k

r

vt

=

⋅ −

(

)

(

)

& & &

F' ' k

r

v t

v

⋅ −

−

=

1

0

2

µ ε

v

====

1
µµµµ εεεε

Fala TEM

∇

∇

∇

∇ ⋅⋅⋅⋅ ====

⋅⋅⋅⋅ ====

&

&

&

F

F

' k

0

& &

& &

E

H

⋅⋅⋅⋅ ====

⋅⋅⋅⋅ ====

k

,

k

,

fala poprzeczna

0

0

∇

∇

∇

∇ ×××× ==== ××××

==== −−−−

&

&

&

&

F

F

H

k

'

t

µµµµ ∂∂∂∂

∂∂∂∂

(

)

&

&

&

&

&

H

F

E

= −

×

=

×

∫

1

µ

µ

ε

k

' dt

k

&

&

&

E

H

====

××××

µµµµ

εεεε

k

Impedancja falowa

Z

E

H

Z

f

====

====

⊥

⊥⊥

⊥

⊥

⊥⊥

⊥

,

µµµµ

εεεε

Z

0

0

0

120

====

====

µµµµ

εεεε

ππππ Ω

Ω

Ω

Ω

H

E

y

x

z

Fale akustyczne

fale w cieczy:

∇

∇

∇

∇

−−−−

====

2

2

2

0

P

k

P

t

ρρρρ ∂∂∂∂

∂∂∂∂

P - ciśnienie akustyczne
ρρρρ - gęstość środowiska [kg/m3]

k - sprężystość (sztywność) objętościowa

v

k

====

ρρρρ

prędkość fali akustycznej

fale w strunie:

∂∂∂∂

∂∂∂∂

ρρρρ ∂∂∂∂

∂∂∂∂

2

2

2

2

0

U

l

E

U

t

x

−−−−

====

E - moduł sprężystości Younga [kg/m s2]
lx - wymiar wzdłż struny

U(lx)

U(lx-vτ )

l x

v

τ

t = t

0

τ

t = t

+

0

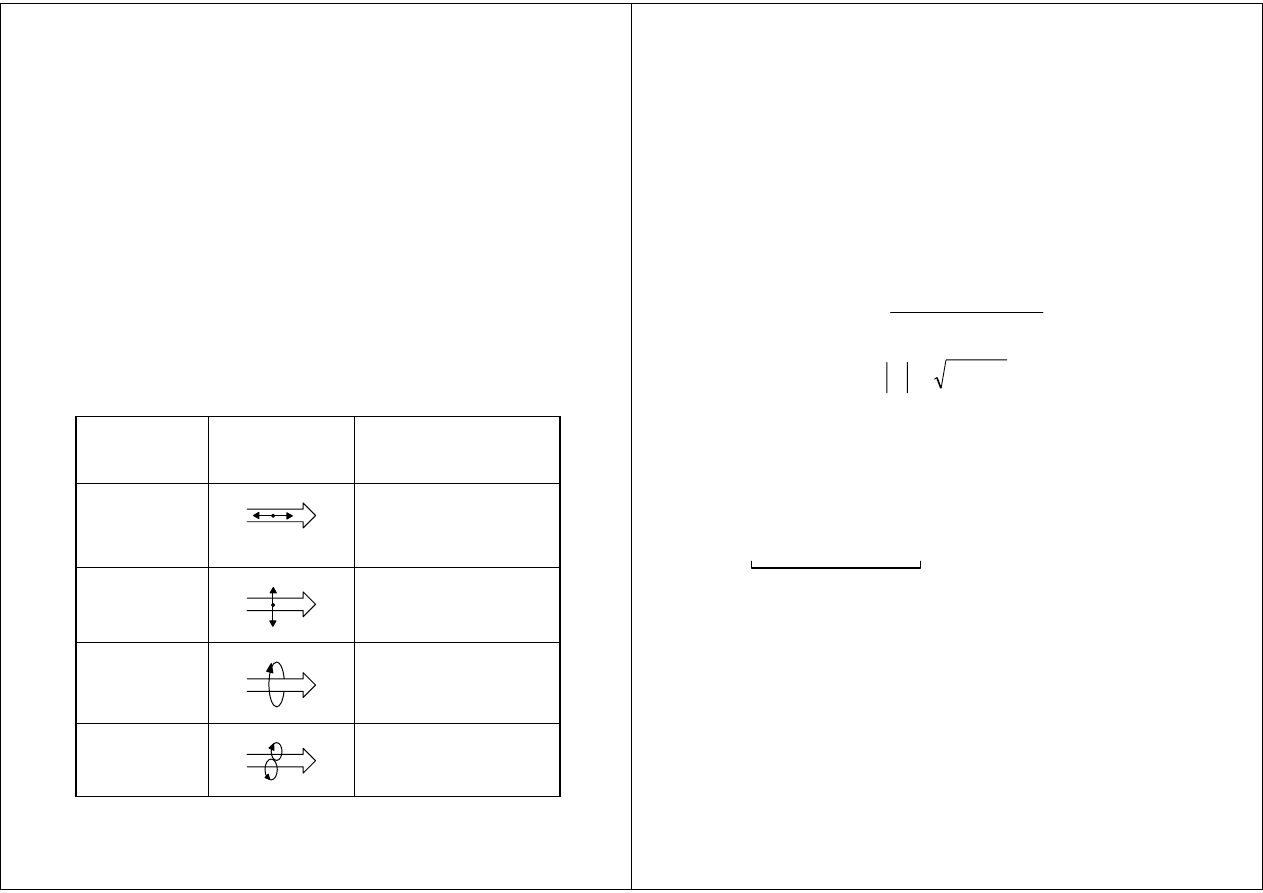
Rodzaje fal

fale elektromagnetyczne :

TEM,

Ez = 0, Hz = 0 - ośrodki nieograniczone

linie dwu- i wieloprzewodowe

H

Ez = 0

Hz ≠≠≠≠ 0 - falowody o przewodzących

E

Hz = 0 Ez ≠≠≠≠ 0

ściankach

EH, HE Ez ≠≠≠≠ 0

Hz ≠≠≠≠ 0 - światłowody,

falowody dielektryczne

fale akustyczne :

Rodzaj fali

Ruch cząstek
względem czoła fali

Ośrodek

Podłużna

gazy
ciecze
ciała stałe

Poprzeczna

ciała stałe
(np. struna)

Rayleigha

powierzchnia ciała stałego

Giętna

ciała stałe (belki, płyty)

Wektory zespolone

cos

ω

ω

ω

ω

ω

ω

ω

ω

t

e

j t

→

→

→

→

&

&

A

A

(x, y, z, t)

(x, y, z) e

j t

====

ω

ω

ω

ω

(

)

&

&

A

=

⋅

Re

e

j

t

A

ω

&

&

&

A

=

e

e

j t

j t

A

A

ω

ω

ω

ω

ω

ω

ω

ω

++++

∗∗∗∗ −−−−

2

&

& &

A

====

⋅⋅⋅⋅

∗∗∗∗

A A

Np:

(

)

(

)

[

]

&

&

&

E

=

−

+

−

E

i cos

t

z

i sin

t

z

x

y

0

2

ω

β

ω

β

(

)

&

&

&

E

E

y

=

−

⋅

−

0

2 i

j i

e

e

x

j z

j

t

β

ω

amplituda zespolona

&

&

E

= Re ( )

E

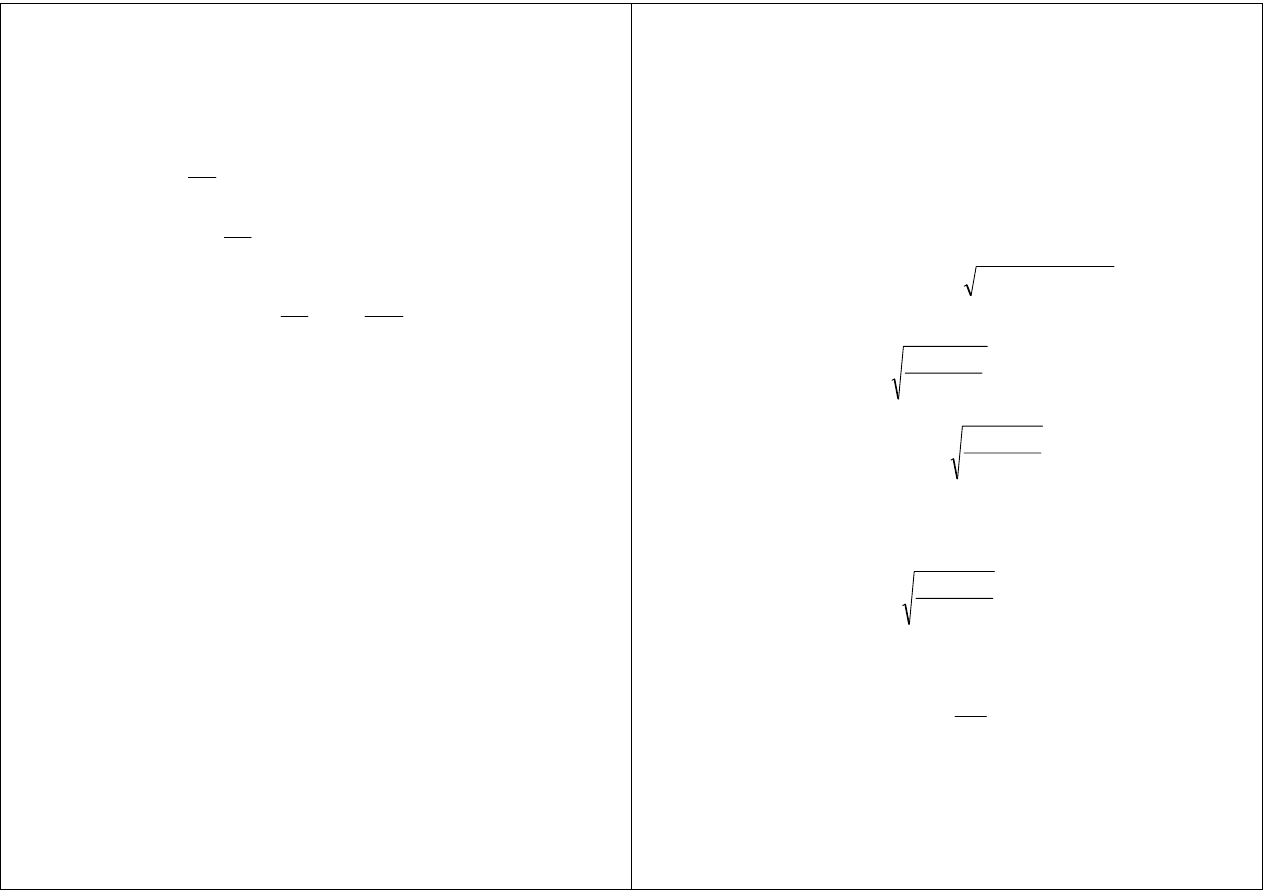
Fala płaska w dielektryku stratnym

∇

∇

∇

∇ ××××

−−−−

∇

∇

∇

∇ ⋅⋅⋅⋅ ====

∇

∇

∇

∇ ××××

====

++++

∇

∇

∇

∇ ⋅⋅⋅⋅ ====

&

*

&

&

&

&

&

E

H

E

H

E

E

H

=

t

,

t

,

µµµµ ∂∂∂∂

∂∂∂∂

σσσσ

εεεε ∂∂∂∂

∂∂∂∂

0

0

∇

∇

∇

∇

−−−−

−−−−

====

2

2

2

0

&

&

&

E

E

E

µµµµ σσσσ ∂∂∂∂

∂∂∂∂

µµµµ εεεε ∂∂∂∂

∂∂∂∂

t

t

(

)

∇ ×

=

+

∇ ⋅

=

∇ ×

= −

∇ ⋅

=

&

&

&

&

&

&

H

E

H

E

H

E

σ

ω ε

ω µ

j

,

j

,

0

0

&

&

&

&

&

& &

&

&

&

& &

E

E e

E

E

E

E

====

==== ⋅⋅⋅⋅

∇

∇

∇

∇ ⋅⋅⋅⋅ ==== −−−− ⋅⋅⋅⋅

∇

∇

∇

∇ ×××× ==== −−−− ××××

−−−− ⋅⋅⋅⋅

0

γγγγ

γγγγ

γγγγ

γγγγ

γγγγ

r

,

gdzie

k

,

(

)

&

&

&

& &

&

&

&

& &

γ

σ

ω ε

γ

γ

ω µ

γ

×

= −

+

⋅

=

×

=

⋅ =

H

E

H

E

H

E

j

,

j

,

0

0

(

)

&

&

&

&

&

γ

γ

ω µ γ

×

×

=

×

E

H

j

(

)

−

= −

+

γ

ω µ σ

ω ε

2

&

&

E

E

j

j

(

)

γ

ω µ σ

ω ε

2

=

+

j

j

stała propagacji

(

)

γ

ω µ σ

ω ε

=

+

j

j

&

&

&

H

E

====

++++

××××

σσσσ

ω

ω

ω

ω εεεε

ω

ω

ω

ω µµµµ

j

j

k

&

&

&

E

H

====

××××

++++

k

j

j

ω

ω

ω

ω µµµµ

σσσσ

ω

ω

ω

ω εεεε

Impedancja właściwa ośrodka :

Z

j

j

====

++++

ω

ω

ω

ω µµµµ

σσσσ

ω

ω

ω

ω εεεε

Impedancja falowa:

Z

E

H

f

====

⊥

⊥⊥

⊥

⊥

⊥⊥

⊥

Z

Z

f

====

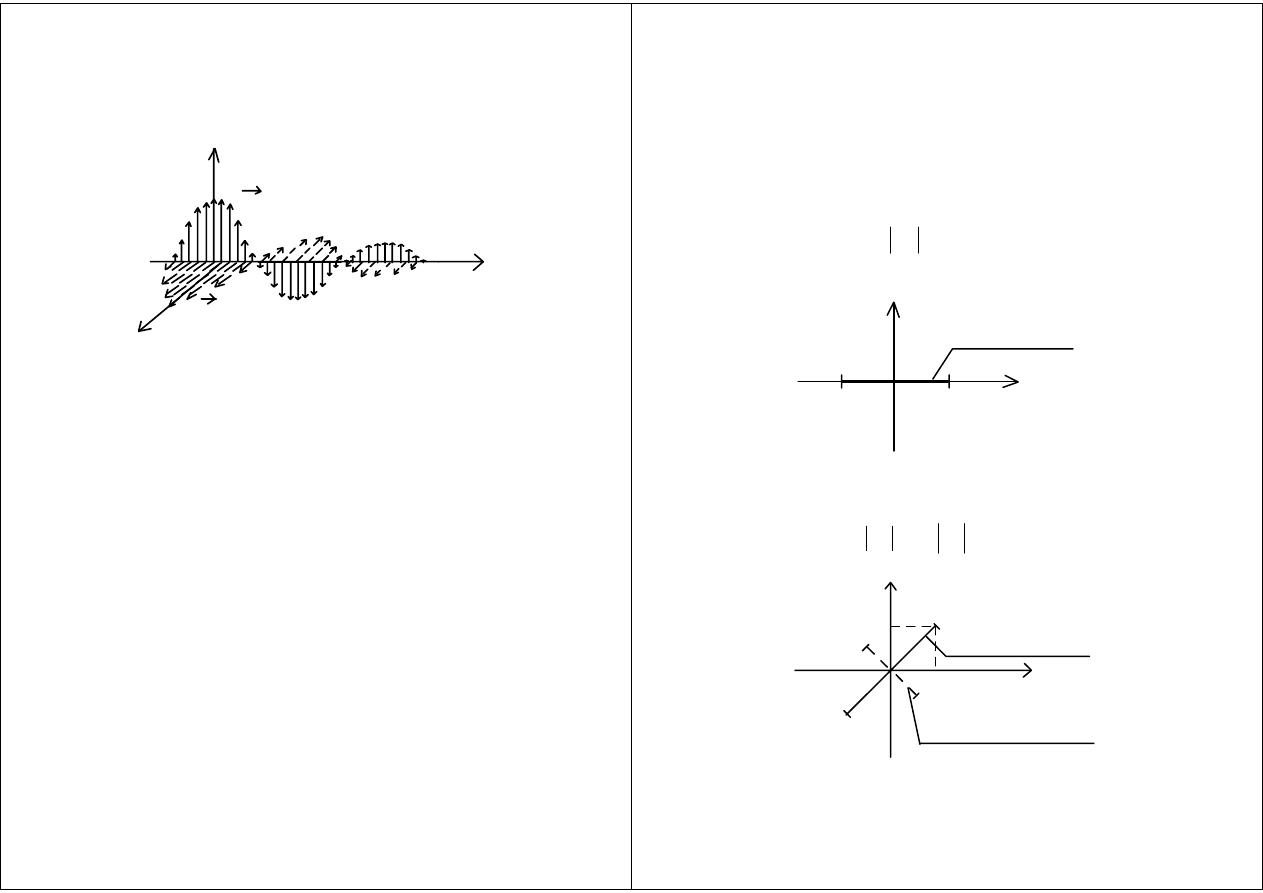
y

z

y

E

H

Polaryzacja fali

Polaryzacja liniowa

dla k

i

z

&

&

====

(

)

(

)

&

&

E

E

x, y, z, t

i

cos

t

z

e

x

x

x

z

=

−

+

−

ω

β

ϕ

α

Miejsce geometryczne

koncow wektora

' '

I

E

I

E (t)

y

x

x

(

)

[

]

(

)

&

&

&

E

E

E

x, y, z, t

i

i

cos

t

z

e

x

x

y

y

z

=

+

⋅

−

+

−

ω

β

ϕ

α

I

E

I

I

E

I

Miejsce geometryczne
koncow wektora

'

'

Miejsce geometryczne
koncow wektora

'

'

E

H

y

x

x

y

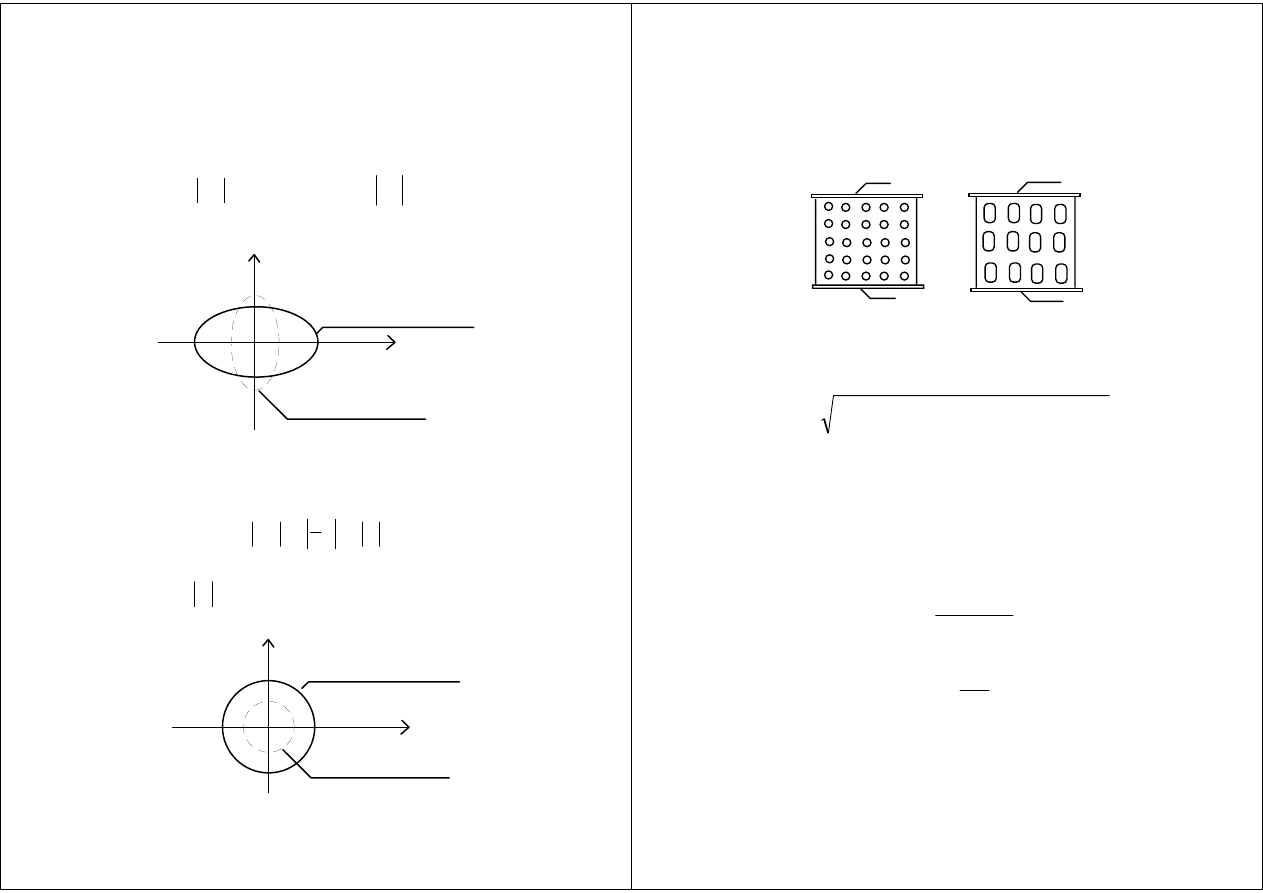
Polaryzacja eliptyczna

dla z = 0

(

)

(

)

&

&

&

E

E

E

(t)

i

cos

t

i

sin

t

x

x

y

y

=

+

+

+

ω

ϕ

ω

ϕ

I

E

I

I

Miejsce geometryczne
koncow wektora

' '

Miejsce geometryczne

koncow wektora

' '

E

H

y

x

I

E y

x

Polaryzacja kołowa

E

E

E

x

y

====

====

( )

(

)

(

)

[

]

&

&

&

E

E

t

i cos

t

i sin

t

x

y

=

+

+

+

ω

ϕ

ω

ϕ

I

E

I

Miejsce geometryczne
koncow wektora

' '

E

Miejsce geometryczne

koncow wektora

' '

H

y

x

Fala w ośrodkach rzeczywistych

-

+

-

+

-

+

-

+

-

+

-

+

-

+

-

+

-

+

-

+

-

+

-

+

a)

b)

q = 0

q = 0

+q

-q

&

&

&

D

E

P

====

++++

εεεε

0

(

)

(

)

[

]

γ

ω µ

µ σ

ω ε

ε

=

−

+

−

j

j

j

j

'

''

'

''

(

) (

)

&

&

&

&

&

J

E

E

E

E

=

+

−

=

+

+

σ

ω ε

ε

σ ω ε

ω ε

j

j

j

'

''

''

'

tg

δδδδ

σσσσ ω

ω

ω

ω εεεε

ω

ω

ω

ω εεεε

====

++++

''

'

tg

σσσσ

σσσσ

ω

ω

ω

ω εεεε

≈≈≈≈

σσσσ

σσσσ ω

ω

ω

ω εεεε

zast

==== ++++

''

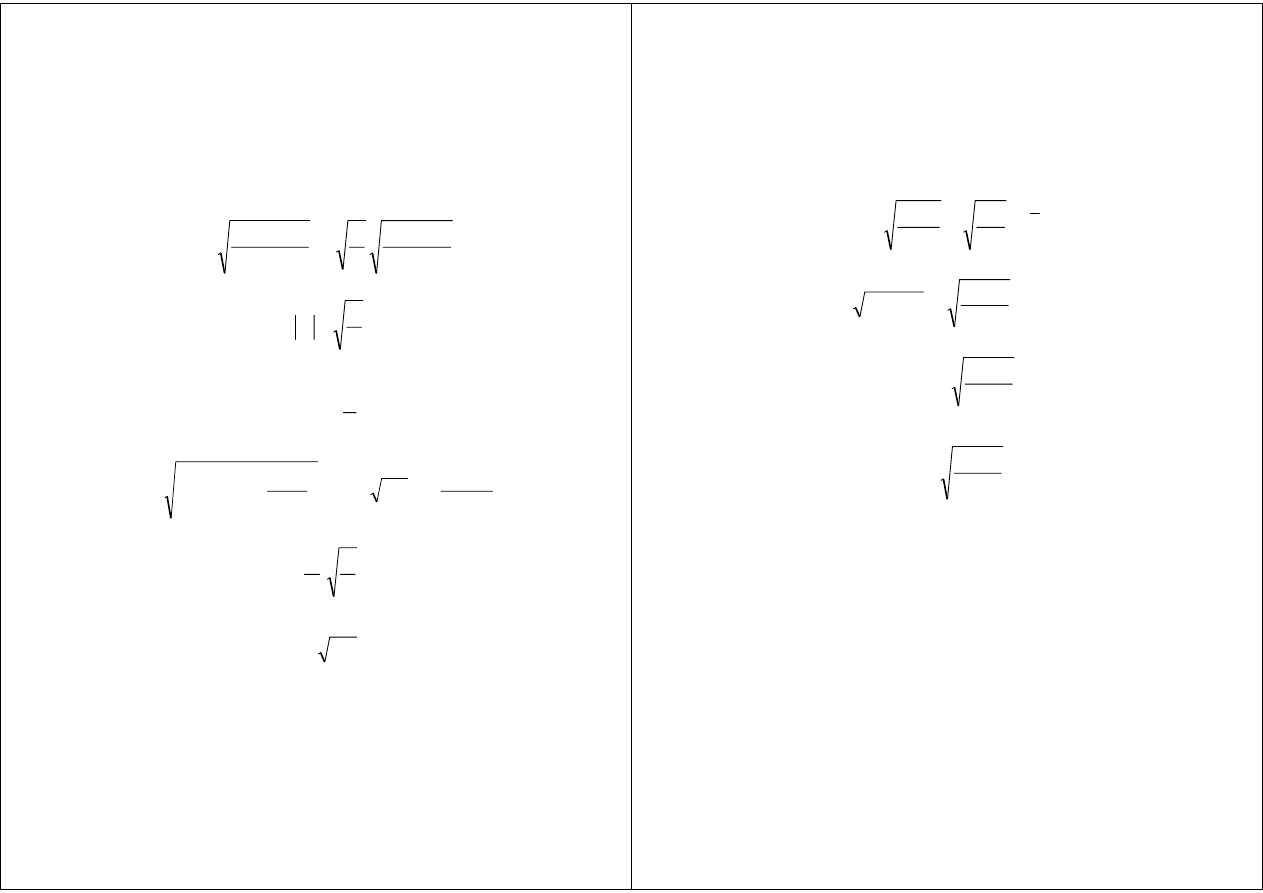
Ośrodki małostratne

σσσσ

ω

ω

ω

ω εεεε

δδδδ

<<<<<<<<

<<<<<<<<

;

tg

1

Z

j

j

j tg

====

++++

====

−−−−

ω

ω

ω

ω µµµµ

σσσσ

ω

ω

ω

ω εεεε

µµµµ

εεεε

δδδδ

1

1

Z

Arg Z

≈≈≈≈

====

µµµµ

εεεε

δδδδ

2

γ

ω µ ε

σ

ω ε

ω µ ε

σ

ω ε

= −

+









 ≈

+











2

1

1

2

j

j

j

αααα σσσσ µµµµ

εεεε

ββββ ω

ω

ω

ω µµµµ εεεε

≈≈≈≈

≈≈≈≈

2

Quasiprzewodniki

σσσσ

ω

ω

ω

ω εεεε

>>>>>>>>

Z

j

e

j

≈≈≈≈

====

ω

ω

ω

ω µµµµ

σσσσ

ωµ

ωµ

ωµ

ωµ

σσσσ

ππππ
4

(

)

γ

ω µσ

ω µσ

≈

=

+

j

j

2

1

αααα ββββ

ω

ω

ω

ω µµµµ σσσσ

δδδδ

ω

ω

ω

ω µµµµ σσσσ

≈≈≈≈ ≈≈≈≈

====

2

2

w

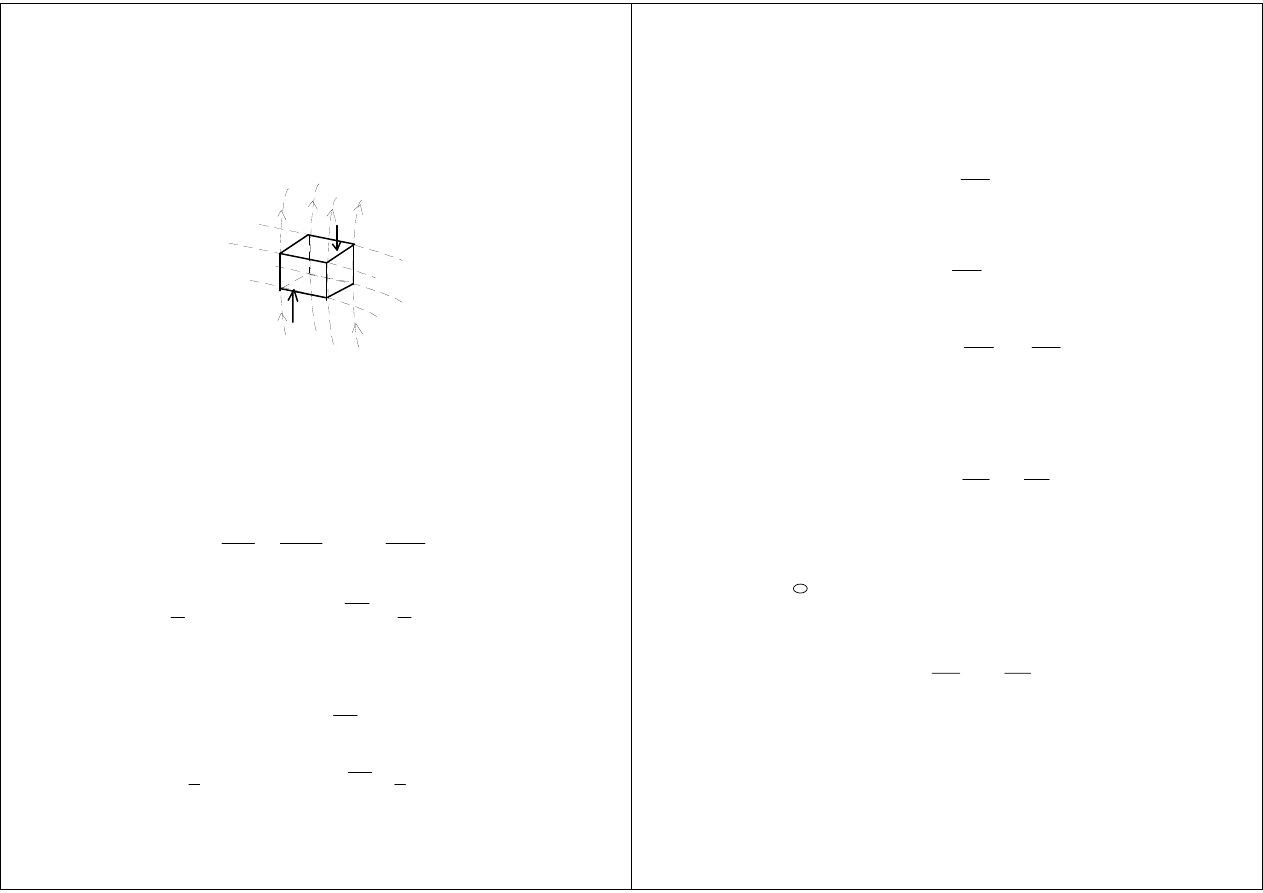
Moc strat i energia magazynowana

p

E

J =

E

q

q

====

⋅⋅⋅⋅

&

&

σσσσ

2

S

1

S

2

S

3

{

∆

l

ϕ

1

ϕ

2

Q

d S

d S

S

S

2

n

2

=

⋅

≈

⋅

≈

∫∫

∫∫

&

&

&

&

D

D

D

S

1

1

U

E

E

=

d l

l

& &

⋅

=

∫

∆

W

Q

V

V

e

n

====

====

==== ⋅⋅⋅⋅

U

D E

D E

2

2

2

∆∆∆∆

∆∆∆∆

& &

(

)

w

w

Re

e

e

=

⋅

=

⋅

∗

1

2

1

4

& &

& &

D E

E D

W

I

m

==== φφφφ

2

(

)

w

w

Re

m

m

=

⋅

=

⋅

∗

1

2

1

4

& &

& &

B H

H B

Twierdzenie Poyntinga

∇

∇

∇

∇ ××××

∇

∇

∇

∇ ××××

++++

&

&

&

&

&

E

B

H

D

J

= -

t

=

t

∂∂∂∂

∂∂∂∂

∂∂∂∂

∂∂∂∂

&

& &

& &

&

&

&

& &

E

H H

E E

D

H

B

J E

⋅⋅⋅⋅∇

∇

∇

∇ ××××

⋅⋅⋅⋅∇

∇

∇

∇ ××××

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

-

=

t

+

t

+

∂∂∂∂

∂∂∂∂

∂∂∂∂

∂∂∂∂

(

)

∇⋅ ×

= ⋅∇×

⋅∇×

& &

&

& &

&

E H

H

E E

H

-

(

)

∇⋅ ×

+ ⋅

⋅

⋅

=

& &

& & &

&

&

&

E H

E J

E

D

H

B

+

t

+

t

∂

∂

∂

∂

0

(

)

& &

&

& &

&

&

&

&

E H

E J

E

D

H

B

×

⋅

+

⋅

+

+

⋅

+ ⋅











=

∫∫

∫∫∫

∫∫∫

S

V

V

d S

d V

t

t

d V

∂

∂

∂

∂

0

( )

&

&

& &

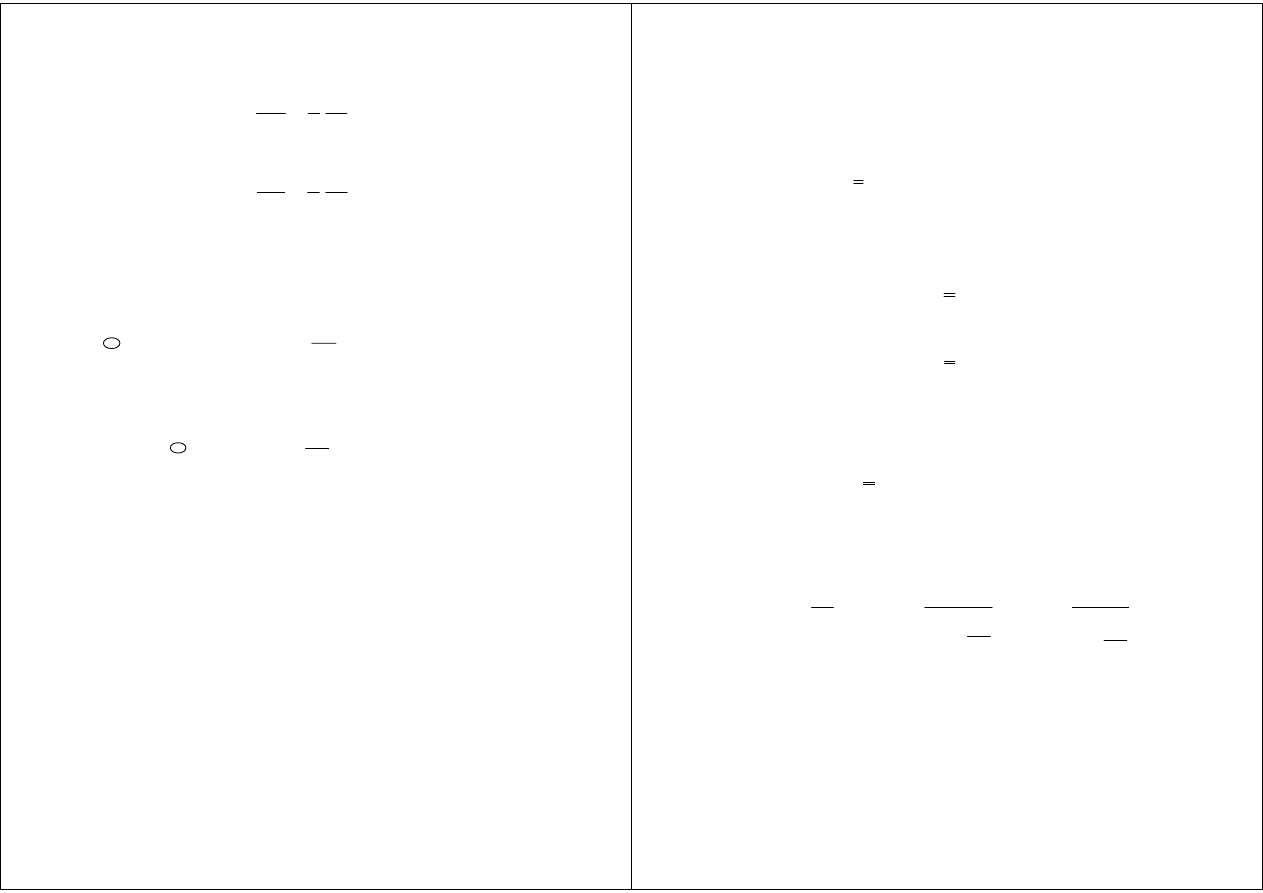
E

D

E D

⋅

=

⋅

∂

∂

∂

∂

t

t

1

2

( )

&

&

& &

H

B

H B

⋅

=

⋅

∂

∂

∂

∂

t

t

1

2

&

&

&

S

E

H

=

××××

(

)

&

&

S

p

q

⋅

+

+

+

=

∫∫∫

∫∫

∫∫∫

d S

dV

t

w

w

dV

V

S

e

m

V

∂

∂

0

(

)

&

&

S

P

q

⋅

+

+

+

=

∫∫

dS

t

W

W

e

m

S

∂

∂

0

Fale w ośrodku żyrotropowym

ε

ε

ε

ε

ε

ε

= −





















j

j

y

y

z

0

0

0

0

&

&

*

&

E

D

H

B

=

=

χχχχ

νννν

⋅⋅⋅⋅

⋅⋅⋅⋅

χ

χ

χ

χ

χ

χ

= −





















j

j

y

y

z

0

0

0

0

χχχχ

εεεε

χχχχ

εεεε

εεεε
εεεε

χχχχ

εεεε

εεεε

εεεε

z

z

y

y

y

y

====

====

−−−−

====

−−−−

1

1

1

2

2

,

,

(

)

(

)

(

)

(

)

&

&

&

&

&

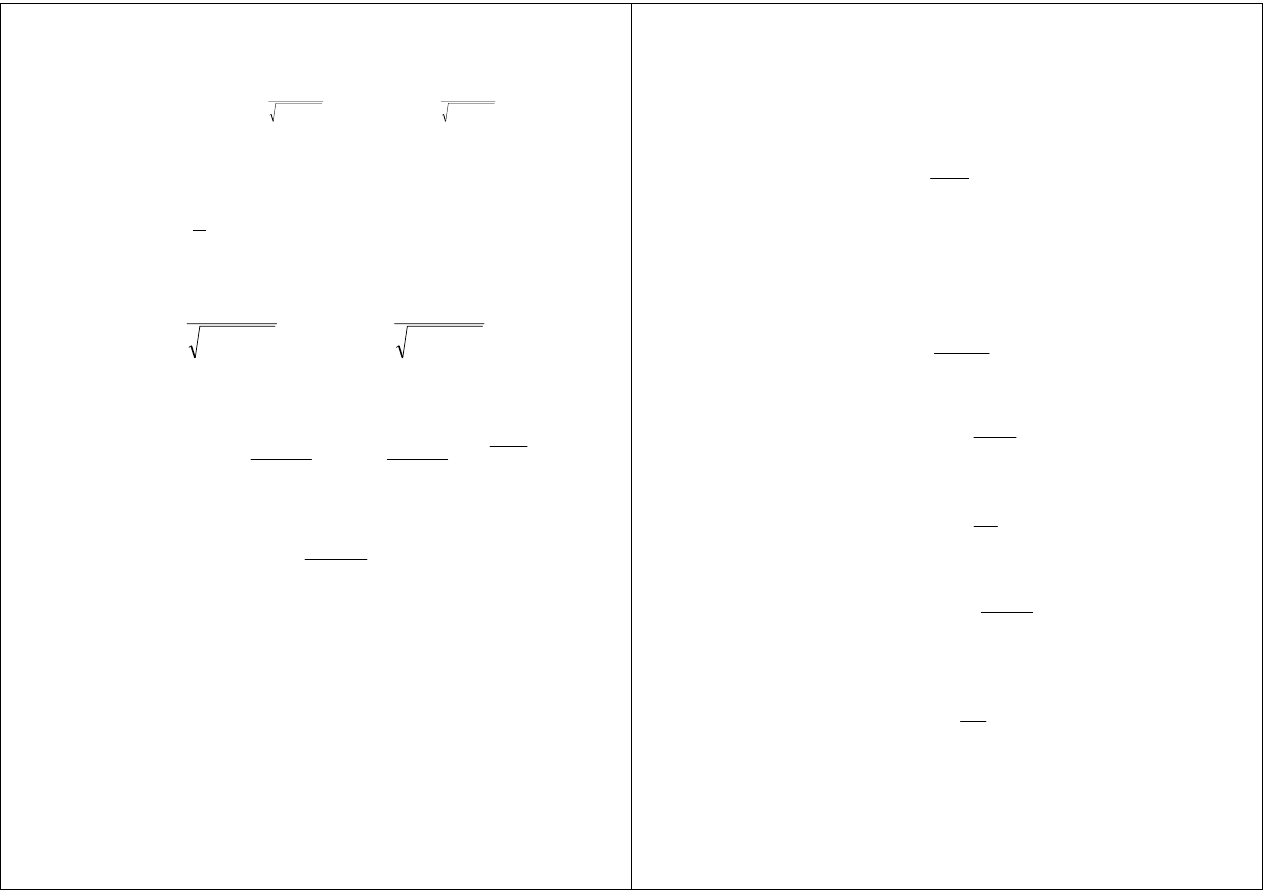
D

D

=

−

+

+

















−

−

−

−

0

i

j i e

i

j i

e

x

y

j

z

x

y

j

z

y

y

ω

ν χ χ

ω

ν χ χ

( )

(

)

(

)

[

]

&

&

&

&

&

D

D

l

i

j i e

i

j i

e

x

y

j

x

y

j

=

−

+

+

−

−

1

2

0

1

2

φ

φ

(

)

(

)

φ

ω

ν χ χ

φ

ω

ν χ χ

1

2

=

+

=

−

l

l

y

y

( )

&

&

&

D

D

l

i cos

i sin

e

x

1

y

j

=

−

+

−









−

+

0

2

1

2

2

2

2

1

2

φ φ

φ φ

φ φ

ψ

ψ

ψ

ψ

φφφφ

φφφφ

====

−−−−

1

2

2

Fale w plaźmie

&

&

&

F

E

0

=

V

t

e

m

e

∂∂∂∂

∂∂∂∂

====

0

j

V

e

ω

ω

ω

ω m

e E

0

&

&

====

0

&

&

&

J

ne

u

====

====

ρρρρ V

V

e

e

0

&

&

J

ne

m

E

u

====

0

2

0

j

ω

ω

ω

ω

&

&

J

n e

m

E

=

−











j

j

ω ε

ω

0

0

2

0

&

&

J

E

=

−



























j

p

ω ε

ω

ω

0

2

1

gdzie:

p

2

ω

ω

ω

ω

εεεε

====

ne

m

0

2

0

0























−

=

2

0

1

ω

ω

ε

ε

p

p

ω

ω

p

β

β

0

α

β

0

|γ|

β

0

1

1

1

1

ω

ω

p

|Ζ|

Ζ

0

Re

Im

(

)

m

e

e

0

0

∂

∂

&

&

&

&

V

t

+ V

0

=

×

E

B

e

ε ε

ε

ε

ε

ε

ε

=

−





















0

11

12

12

11

33

0

0

0

0

εεεε

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

11

2

2

2

1

==== −−−−

−−−−

p

c

(

)

ε

ω ω

ω ω

ω

12

2

2

2

= −

−

j

p

c

c

ε

ω

ω

33

2

1

= −











p

ω

ω

ω

ω

c

e

m

====

≈≈≈≈

⋅⋅⋅⋅

0

11

1 75 10

B

B

0

0

,

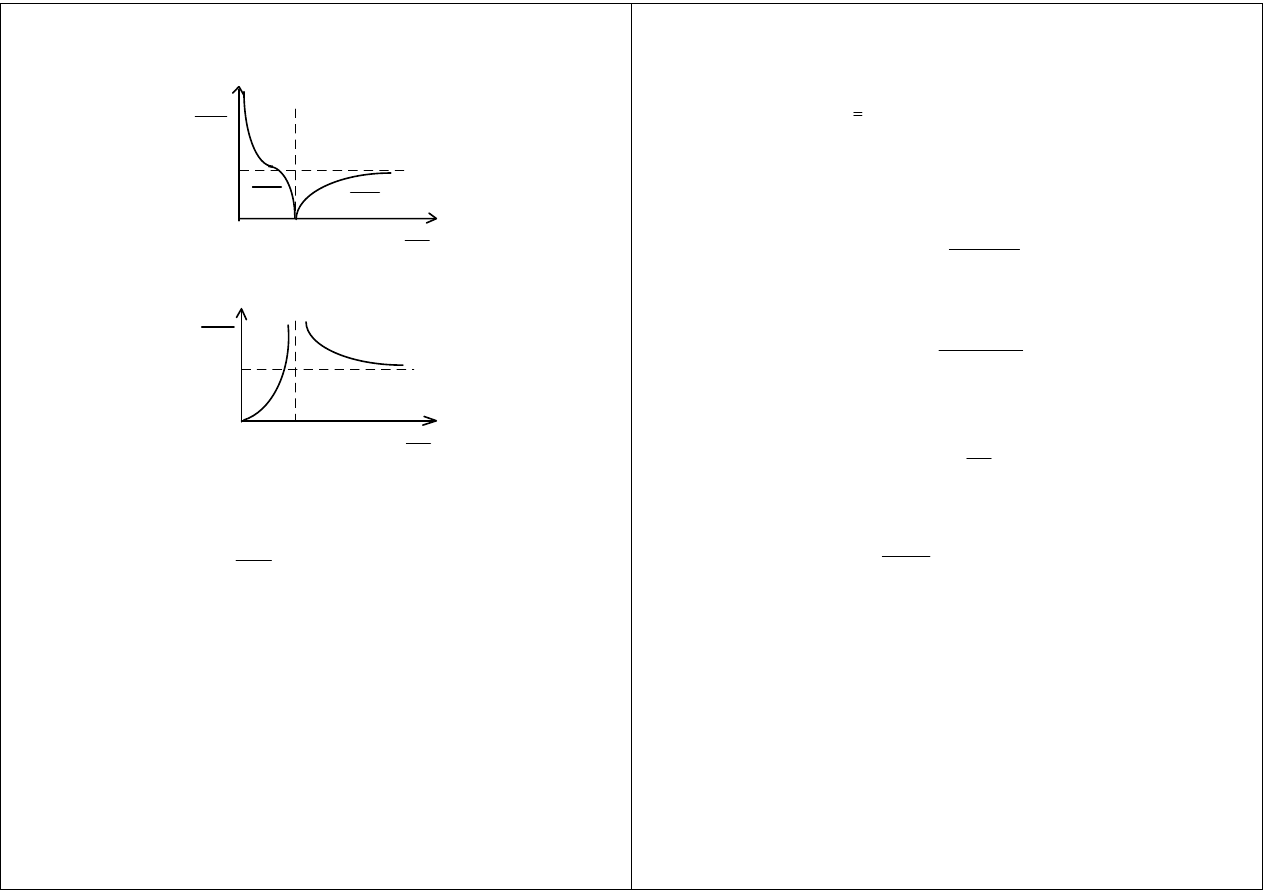
Prędkość fazowa i grupowa

&

&

V

k

f

==== ω

ω

ω

ω

ββββ

V

d

d

g

==== ω

ω

ω

ω

ββββ

π/(β

1

−β

2

)

E

1

+ E

2

0

0

E

1

E

2

0

0

−

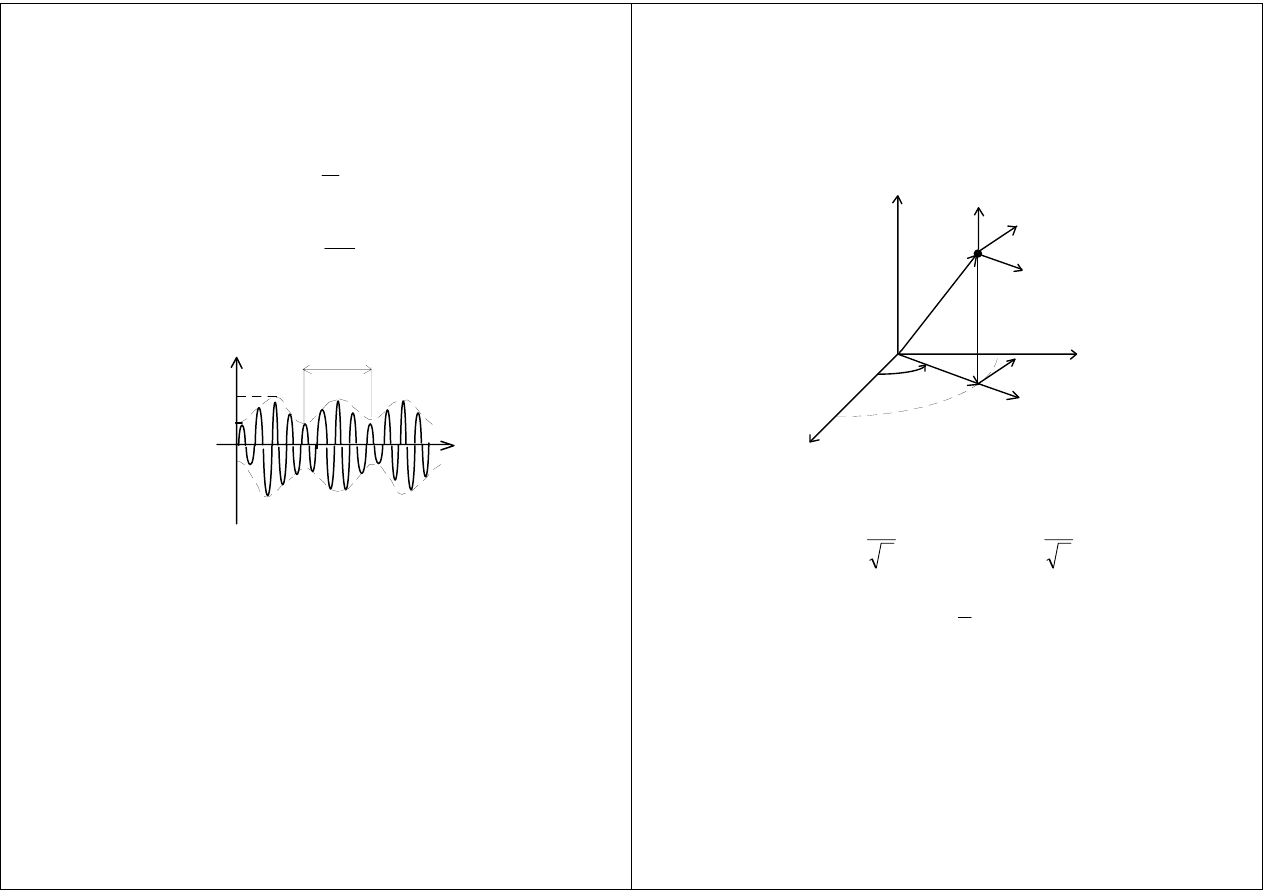
Fale cylindryczne

z

x

y

P

i

i

i

i

i

r

z

ϕ

ϕ

ρ

ρ

ϕ

ρ

0

E

H

z

÷÷÷÷

÷÷÷÷

1

1

ρρρρ

ρρρρ

ϕϕϕϕ

S

1

÷÷÷÷

ρρρρ

S

- powierzchniowa gęstość mocy

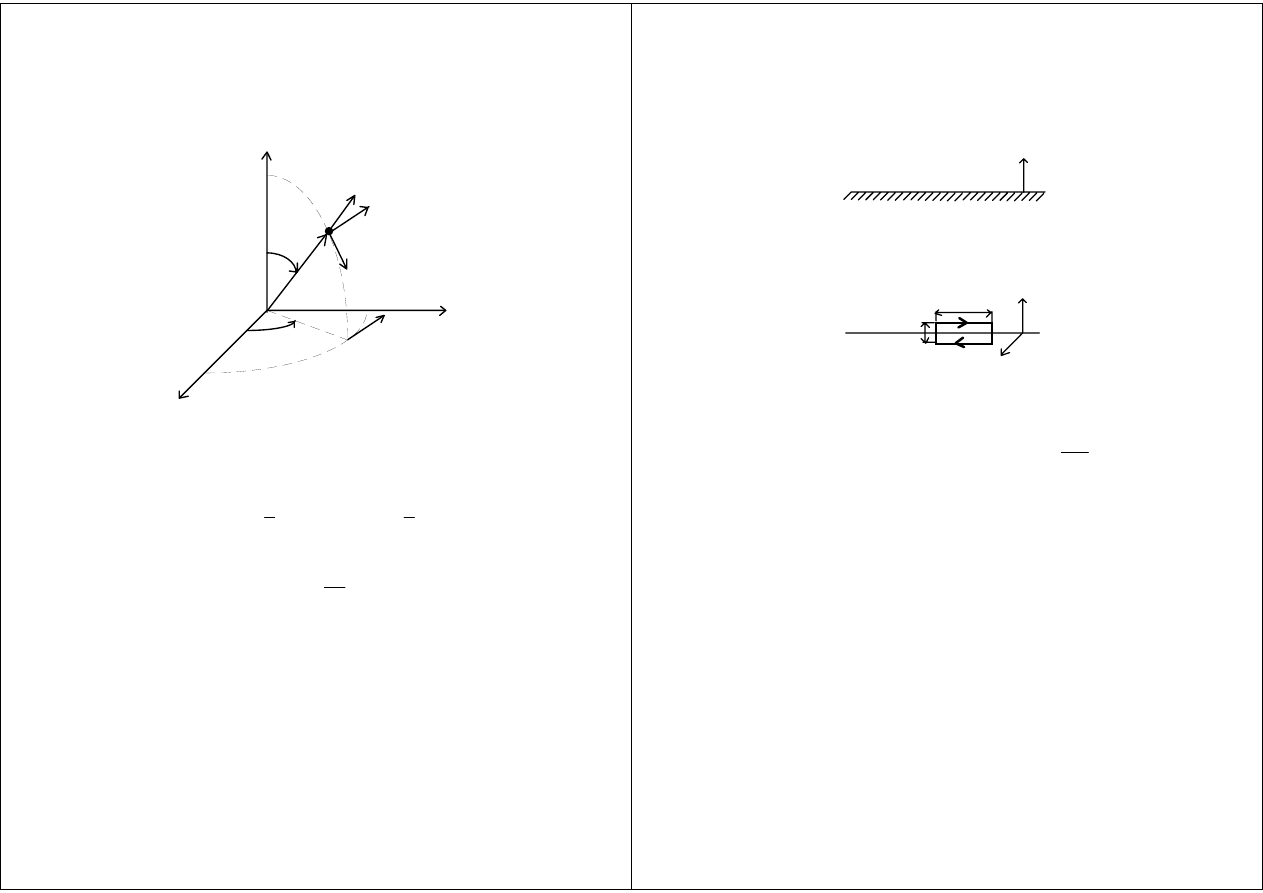
Fale kuliste

z

x

y

P

i

r

i

ϕ

ϕ

ϕ

0

i

i

r

θ

θ

E

r

H

r

θθθθ

ϕϕϕϕ

÷÷÷÷

÷÷÷÷

1

1

S

1

r

2

÷÷÷÷

Warunki brzegowe

n

ε µ σ

,

,

ε µ σ

1

1

1

,

,

2

2

2

E

E

H

H

2

2

1

1

,

,

Oœrodek 2

Oœrodek 1

n

p

∆

δ

l

l

Oœrodek 2

Oœrodek 1

E

E

E

E

B

2 t

/ n

t

/ n

l

l

l

l

t

l

l

⋅

−

−

+

=











⋅

∆

∆

∆

2 1

1

1 2

δ

δ

∂

∂

δ

E

E

2

1

0

t

t

−−−−

====

(

)

&

&

&

n

×

−

=

E

E

2

1

0

(

)

&

&

&

&

n

s

×

−

=

H

H

J

2

1

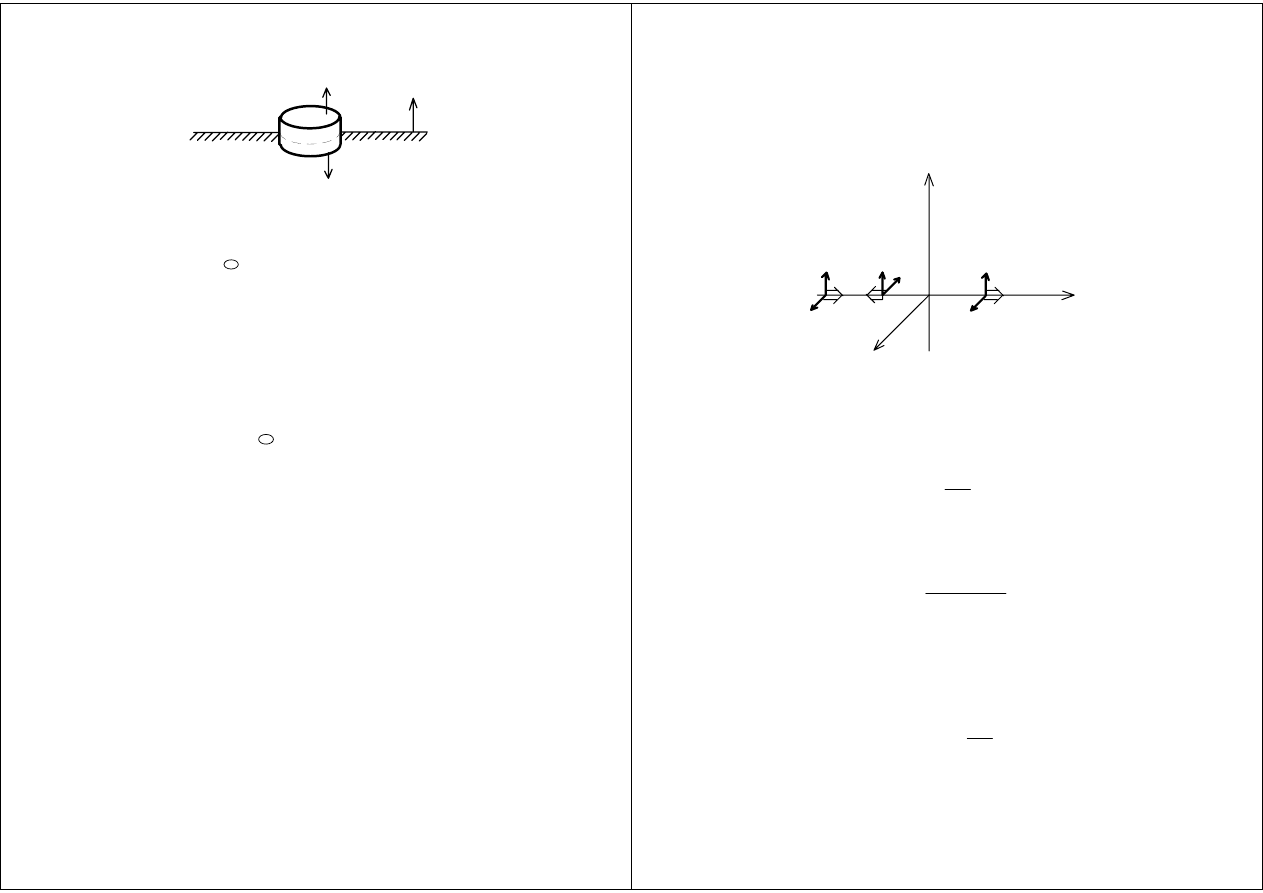
v

n

2

=

n

n

n

=

n

1

-

2

Oœrodek

Oœrodek 1

& &

D

⋅

=

⋅

∫∫

∫∫∫

n dS

d V

S

V

ρ

(

)

&

&

&

D

D

2

1

−

⋅ =

n

s

ρ

& &

B

⋅

=

∫∫

n dS

S

0

(

)

&

&

&

B

B

2

1

0

−

⋅ =

n

Fala padająca prostopadle

na granicę ośrodków

Oœrodek 1

Oœrodek 2

ε

ε

µ

µ

σ

σ

1

1

1

2

2

2

,

,

,

,

E

H

E

H

H

E

1

1

1

1

2

2

+

+

-

-

x

y

z

0

&

&

&

&

E

E

H

E

1

0

1

0

1

1

1

++++

−−−−

++++

−−−−

====

====

i

e

i

Z

e

x

z

y

z

γγγγ

γγγγ

(

)

(

)

Γ =

=
=

−

+

E

E

1

1

0

0

z

z

&

&

&

&

E

E

H

E

1

0

1

0

1

1

1

−−−−

−−−−

====

==== −−−−

i

e

i

Z

e

x

z

y

z

ΓΓΓΓ

ΓΓΓΓ

γγγγ

γγγγ

(

)

(

)

&

&

&

&

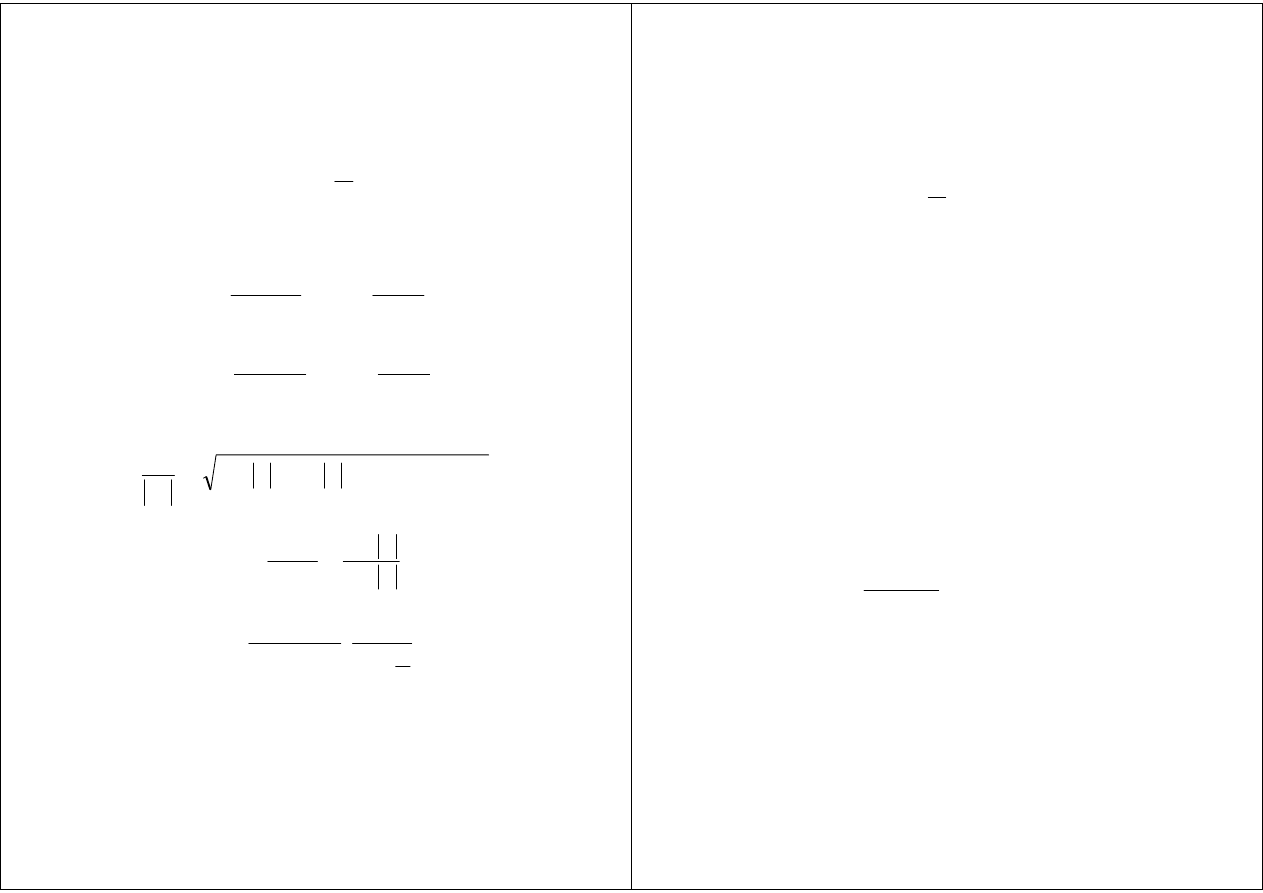
E

E

H

E

2

0

2

0

1

1

1

2

2

=

+

=

−

−

−

i

e

i

Z

e

x

z

y

z

Γ

Γ

γ

γ

(

)

(

)

(

)

(

)

T

E

E

T

H

H

e

m

z

z

Z

Z

Z

z

z

Z

Z

Z

=

=

=

= + =

+

=

=

=

= − =

+

+

+

2

1

2

2

1

2

1

1

2

1

0

0

1

2

0

0

1

2

Γ

Γ

(

)

E

1

0

2

1

1

2

2

x

cos

z

E

=

+

+

+

Γ

Γ

β

ψ

ρρρρ ====

====

++++
−−−−

E

E

1

1

1
1

max

min

ΓΓΓΓ
ΓΓΓΓ

(

)

(

)

ρ

ρ

1

2

4

Re

Re

T

1

1

2

2

p

+

+

=

×

×

=

∗

+

+

∗

H

E

H

E

W przypadku fali akustycznej

w ośrodku płynnym bezstratnym :

Z

p

V

c

====

==== ρρρρ

0

Z - oporność właściwa
p - ciśnienie
V - prędkość ruchu elementu mechanicznego
ρρρρ

0

- gęstość ośrodka w stanie spoczynku

c - prędkość rozchodzenia się fali akustycznej

Warunki brzegowe:

V

1 =

V

2

p

1 =

p

2

Współczynnik odbicia:

ΓΓΓΓ ====

−−−−
++++

Z

Z

Z

Z

2

1

2

1

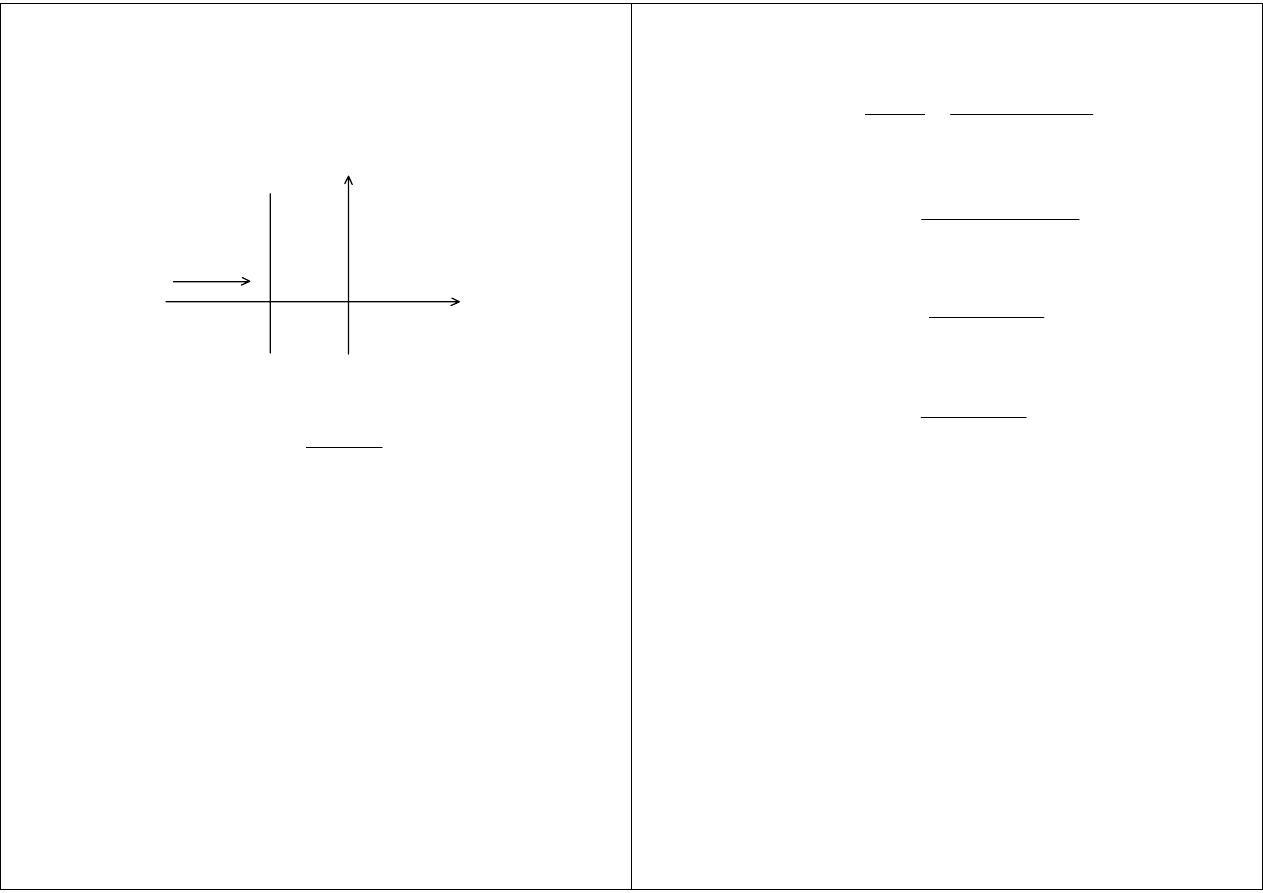
Fala padająca na ośrodek

składający się z trzech warstw

Z

2

1

x

z

0

-l

Z

Z

Kierunek

padania fali

1

2

3

Oœrodek

Oœrodek

Oœrodek 3

ΓΓΓΓ

2 3

3

2

3

2

,

Z

Z

Z

Z

====

−−−−
++++

Z( z)

( z)

( z)

( z)

( z)

( z)

( z)

====

====

++++
++++

⊥

⊥⊥

⊥

⊥

⊥⊥

⊥

⊥

⊥⊥

⊥

++++

⊥

⊥⊥

⊥

−−−−

⊥

⊥⊥

⊥

++++

⊥

⊥⊥

⊥

−−−−

E

H

E

E

H

H

Z ( z)

Z

e

e

e

e

j

z

,

j

z

j

z

,

j

z

2

2

2 3

2 3

2

2

2

2

====

++++
−−−−

−−−−

−−−−

ββββ

ββββ

ββββ

ββββ

ΓΓΓΓ
ΓΓΓΓ

( )

Z z

Z

Z

j Z tg

z

Z

j Z tg

z

2

2

3

2

2

2

3

2

=

−

−

β
β

( )

( )

Γ

1 2

2

1

2

1

,

Z

l

Z

Z

l

Z

=

− −
− +

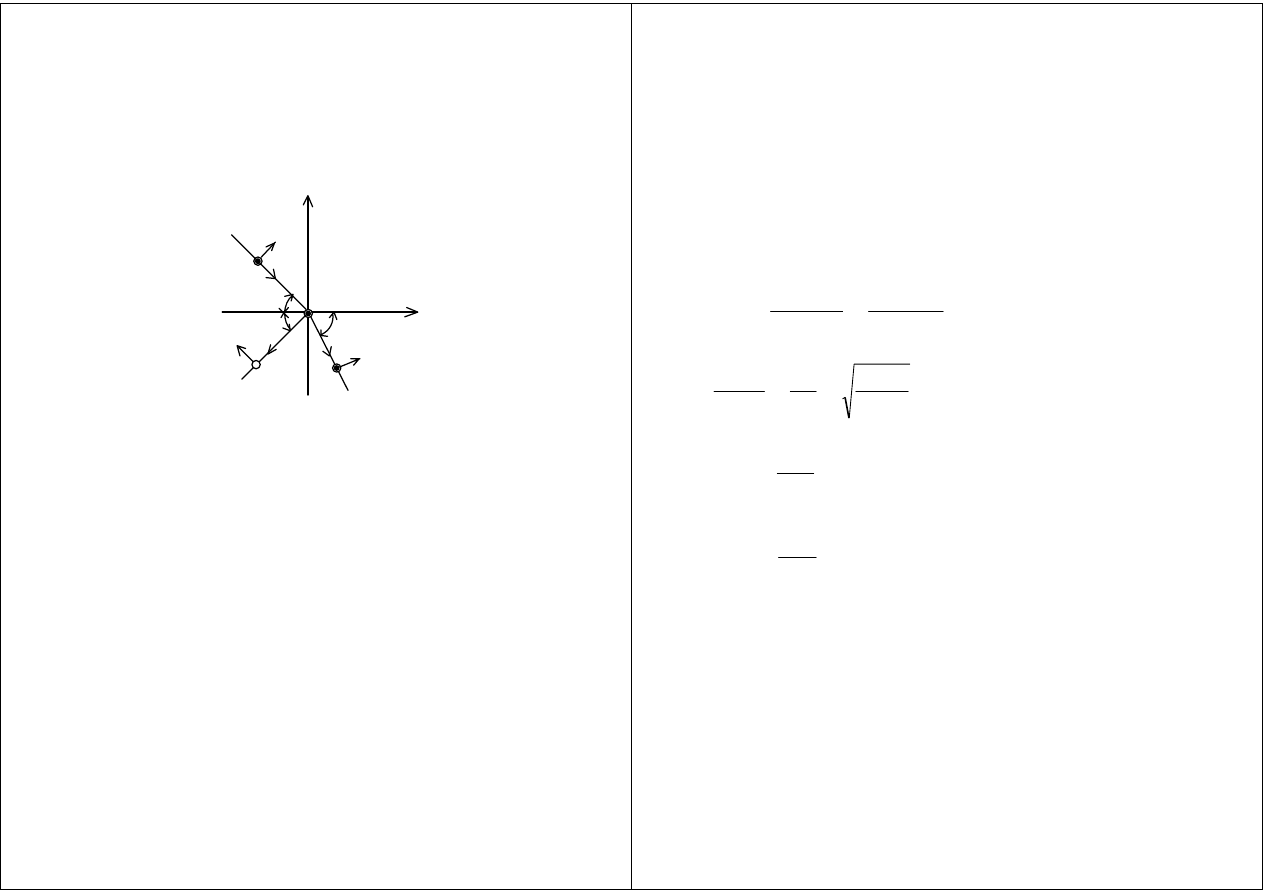
Fala płaska padająca ukośnie na granicę

dwóch ośrodków

x

x

z

Oœrodek 1

Oœrodek 2

y

ε

1

µ

1

σ

1

,

,

ε

2

µ

2

σ

2

,

,

θ

2

+

θ

θ

1

+

1

−

E

E

E

H

H

H

1

+

1

+

1

-

1

-

2

2

Fala o polaryzacji równoległej

(

)

+

+

+

−

+

+

=

1

1

1

sin

x

cos

z

t

j

0

y

1

e

i

(t)

θ

θ

γ

ω

H

H

&

&

(

)

(

)

−

−

+

+

−

Γ

−

=

1

1

1

sin

x

cos

z

t

j

0

y

1

e

i

(t)

θ

θ

γ

ω

H

H

&

&

( )

(

)

2

2

2

sin

x

cos

z

t

j

0

y

2

e

1

i

(t)

θ

θ

γ

ω

+

−

+

Γ

−

=

H

H

&

&

( )

2

2

1

1

1

1

sin

x

sin

x

sin

x

e

1

e

e

θ

γ

θ

γ

θ

γ

Γ

−

=

Γ

−

−

+

sin

sin

θθθθ

θθθθ

1

1

++++

−−−−

====

γγγγ

θθθθ

γγγγ

θθθθ

1

1

2

2

sin

sin

++++

====

ββββ

θθθθ

ββββ

θθθθ

1

1

2

2

sin

sin

====

V

sin

sin

V

f x

f x

1

1

1

2

2

2

====

====

====

ω

ω

ω

ω

ββββ

θθθθ

ω

ω

ω

ω

ββββ

θθθθ

sin

sin

V

V

θθθθ

θθθθ

εεεε µµµµ

εεεε µµµµ

1

2

1

2

2

2

1

1

====

====

Z

Z cos

f z

x

y

1

1

1

1

1

====

====

++++

++++

E

H

θθθθ

Z

Z cos

f z

x

y

2

2

2

2

2

====

====

++++

++++

E

H

θθθθ

ΓΓΓΓ ====

−−−−
++++

====

−−−−
++++

Z

Z

Z

Z

Z cos

Z cos

Z cos

Z cos

f z

f z

f z

f z

2

1

2

1

2

2

1

1

2

2

1

1

θθθθ

θθθθ

θθθθ

θθθθ

(

)

(

)

1

2

1

2

tg

tg

θ

θ

θ

θ

+

−

=

Γ

θθθθ

εεεε

εεεε

1

2

1

B

arc tg

====

Fala o polaryzacji prostopadłej

ΓΓΓΓ

⊥

⊥⊥

⊥

====

−−−−
++++

====

−−−−

++++

Z

Z

Z

Z

Z

cos

Z

cos

Z

cos

Z

cos

f z

f z

f z

f z

2

1

2

1

2

2

1

1

2

2

1

1

θθθθ

θθθθ

θθθθ

θθθθ

(

)

(

)

1

2

1

2

sin

sin

θ

θ

θ

θ

+

−

=

Γ

⊥

Statyczny potencjał skalarny

&

E

U

==== −−−− ∇

∇

∇

∇

0

l

d

E

S

d

E

l

S

=

⋅

=

×

∇

∫

∫∫

&

&

&

&

∇

∇

∇

∇

∇

∇

∇

∇

++++

U =

U

U

0

β γ

∇

∇

∇

∇ ⋅⋅⋅⋅ ====

&

E

ρρρρ

εεεε

∇

∇

∇

∇

==== −−−−

2

U

ρρρρ

εεεε

V

r

r

r-r

1

1

0

P

x

y

z

ρ

(x,y,z)

( )

1

r

r

q

4

1

r

U

−

=

ε

π

( )

( )

∫∫∫

−

=

V

1

1

V

d

r

r

r

4

1

r

U

ρ

ε

π

Magnetyczny potencjał wektorowy

&

&

B

A

==== ∇

∇

∇

∇ ××××

(

)

ψ

∇

×

∇

=

×

∇

+

A

A

&

&

∇

∇

∇

∇ ⋅⋅⋅⋅

====

∇

∇

∇

∇ ⋅⋅⋅⋅

====

&
&

A

A

'

0

f

(

)

0

©

A

A

=

∇

+

⋅

∇

=

⋅

∇

ϕ

&

&

∇

∇

∇

∇

==== −−−−

2

ϕϕϕϕ

f

∇

∇

∇

∇ ××××

====

&

&

H

J

∇

∇

∇

∇

==== −−−−

2

&

&

A

J

µµµµ

( )

( )

∫∫∫

−

=

V

1

1

V

d

r

r

r

J

4

r

A

&

&

π

µ

Potencjały elektrodynamiczne

∇

∇

∇

∇ ×××× ==== −−−−

==== ∇

∇

∇

∇ ××××

&

&

&

&

E

B

B

A

∂∂∂∂

∂∂∂∂ t

∇

∇

∇

∇ ×××× ==== −−−− ∇

∇

∇

∇ ××××

&

&

E

A

∂∂∂∂

∂∂∂∂ t

0

t

A

E

=









+

×

∇

∂

∂

&

&

&

&

E

A

U

++++

==== −−−− ∇

∇

∇

∇

∂∂∂∂

∂∂∂∂ t

&

&

E

A

U

==== −−−−

−−−− ∇

∇

∇

∇

∂∂∂∂

∂∂∂∂ t

∇

∇

∇

∇ ××××

====

++++

&

&

&

H

E

J

εεεε ∂∂∂∂

∂∂∂∂ t

( )

2

2

2

t

A

t

U

J

A

A

∂

∂

ε

µ

∂

∂

ε

µ

µ

&

&

&

&

−

∇

−

=

∇

−

⋅

∇

∇

∇

∇

∇

∇ ⋅⋅⋅⋅

==== −−−−

&

A

U

µµµµ εεεε ∂∂∂∂

∂∂∂∂ t

∇

∇

∇

∇

−−−−

==== −−−−

2

2

&

&

&

A

A

J

2

µµµµ εεεε ∂∂∂∂

∂∂∂∂

µµµµ

t

∇

∇

∇

∇ ⋅⋅⋅⋅

====

&

D

ρρρρ

∇

∇

∇

∇

−−−−

==== −−−−

2

2

U

U

2

µµµµ εεεε ∂∂∂∂

∂∂∂∂

ρρρρ

εεεε

t

( )

∫∫∫

−









−

−

=

V

1

1

1

dV

r

r

V

r

r

t

,

r

J

4

t

r,

A

&

&

π

µ

( )

∫∫∫

−









−

−

=

V

1

1

1

dV

r

r

V

r

r

t

,

r

4

1

t

r,

U

ρ

ε

π

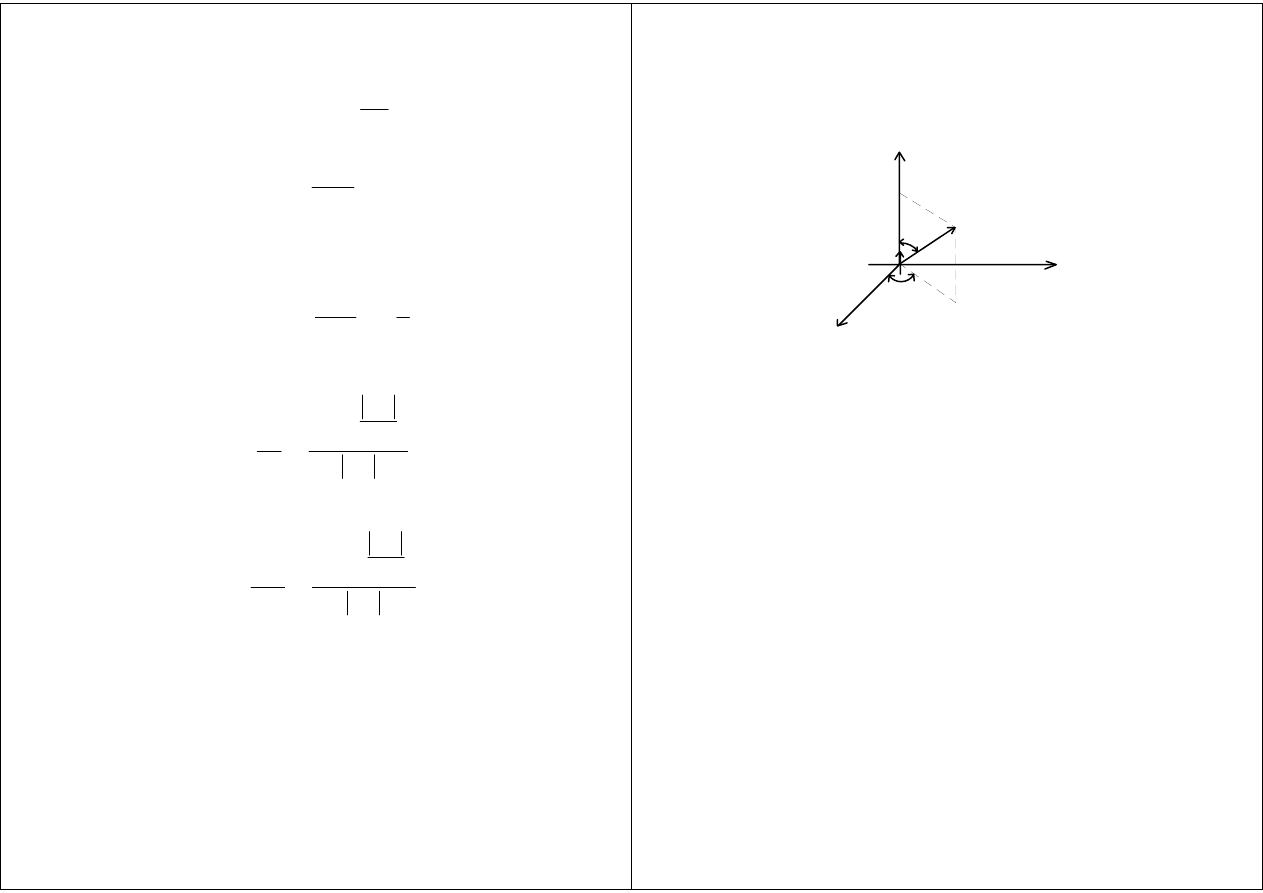
Pola w sąsiedztwie dipola Hertza

Θ

ϕ

r

I

x

y

z

q

q e

j t

====

0

ω

ω

ω

ω

I

q j e

jI e

j t

j t

==== −−−−

==== −−−−

0

0

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

l

<<<<<<<<

λλλλ

( )

(

)

(

)

(

)

r

t

j

0

r

r

t

j

0

z

e

r

4

l

I

j

sin

i

cos

i

e

r

4

l

I

j

i

r

β

ω

θ

β

ω

π

µ

θ

θ

π

µ

−

−

−

−

=

=

−

=

&

&

&

&

A

&

&

&

H

B

A

====

====

∇

∇

∇

∇ ××××

1

1

µµµµ

µµµµ

(

)

r

t

j

2

0

e

r

1

j

r

sin

4

l

I

i

β

ω

ϕ

β

θ

π

−











 −

=

&

&

H

&

&

E

H

====

∇

∇

∇

∇ ××××

1

j

ω

ω

ω

ω εεεε

(

)





































+

−

−

+

+













−

−

=

−

r

r

j

r

1

sin

i

r

j

r

1

cos

2

i

e

4

l

I

2

2

3

2

3

r

r

t

j

0

ω

β

ω

β

ω

θ

ω

β

ω

θ

ε

π

θ

β

ω

&

&

&

E

&

&

H

≈≈≈≈

−−−−

i

I l

r

sin e

j

t

r

ϕϕϕϕ

ω

ω

ω

ω

ββββ

ββββ

ππππ

θθθθ

0

4

β

γ

&

&

E

≈≈≈≈

−−−−

i

I l

r

sin e

j

t

r

θθθθ

ω

ω

ω

ω

ββββ

ββββ

ππππ εεεε ω

ω

ω

ω

θθθθ

0

2

4

β γ

(

)

θ

θ

ω

ε

π

θ

ω

sin

i

cos

2

i

e

r

4

l

I

r

t

j

3

0

&

&

&

+

−

=

E

( ) ( )

max

S

,

S

,

F

θ

ϕ

θ

ϕ

=

( )

θ

θ

ϕ

2

sin

,

F

=

a)

Direktor

λ/2

Reflektor

b)

c)

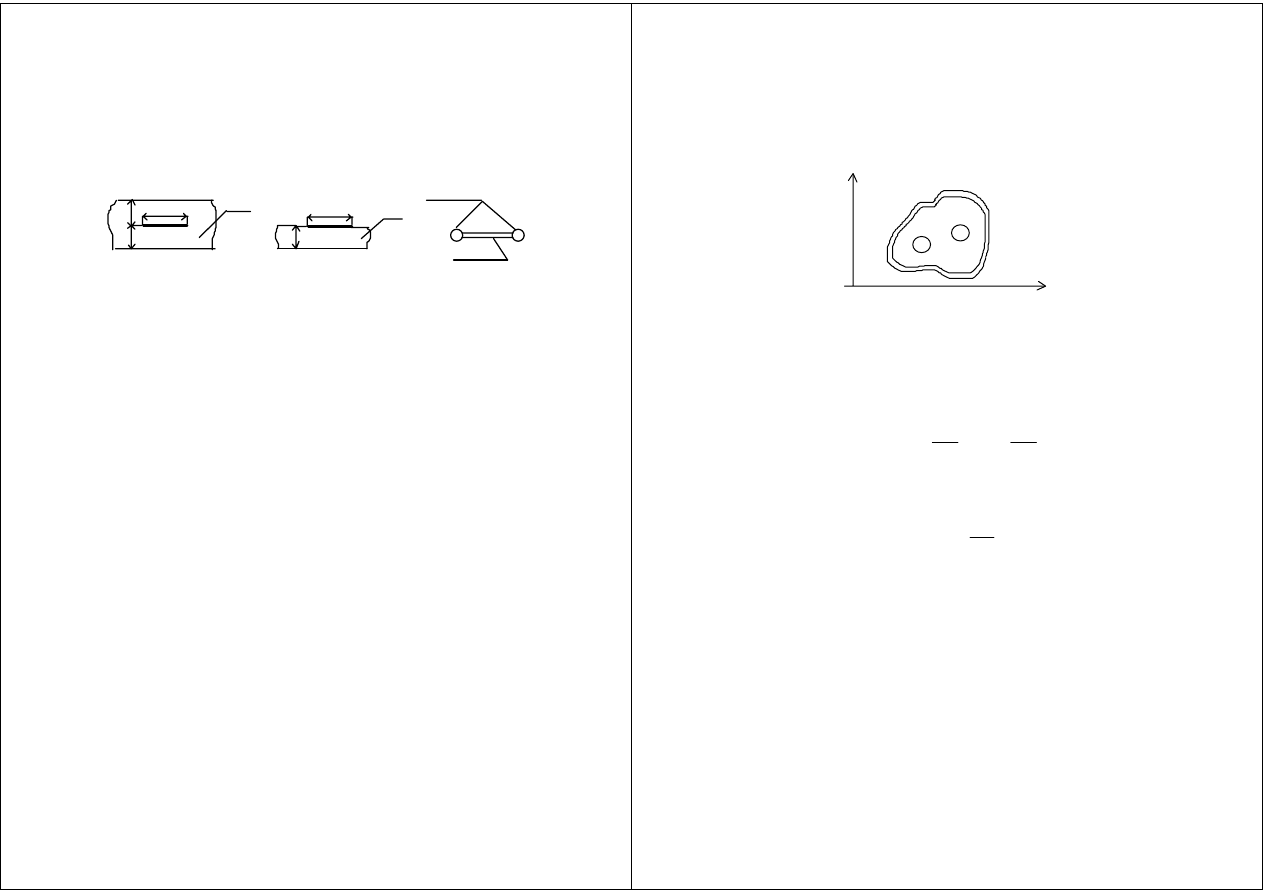
Przykłady linii TEM

b

b

w

b

w

Przewody

Izolacja

w

w

ε

ε

a)

b)

c)

- fala typu TEM , E

z

= 0, H

z

= 0

- fala typu E (zwana też TM)

E

z

≠≠≠≠ 0, H

z

= 0

- fala typu H (zwana też TE)

E

z

= 0, H

z

≠≠≠≠ 0

- fala typu EH, E

z

≠≠≠≠0, H

z

≠≠≠≠ 0

Prowadnice falowe TEM

y

x

0

∇

∇

∇

∇ ==== ∇

∇

∇

∇ ++++ ∇

∇

∇

∇

⊥

⊥⊥

⊥

z

∇

∇

∇

∇ ====

++++

⊥

⊥⊥

⊥

&

&

i

x

i

y

x

y

∂∂∂∂

∂∂∂∂

∂∂∂∂

∂∂∂∂

∇

∇

∇

∇ ====

z

z

i

z

& ∂∂∂∂

∂∂∂∂

(

)

(

)

⊥

⊥

⊥

+

=

×

∇

+

∇

E

H

&

&

ε

ω

σ

j

z

(

)

⊥

⊥

⊥

−

=

×

∇

+

∇

H

E

&

&

µ

ω

j

z

(

)

⊥

⊥

+

=

×

∇

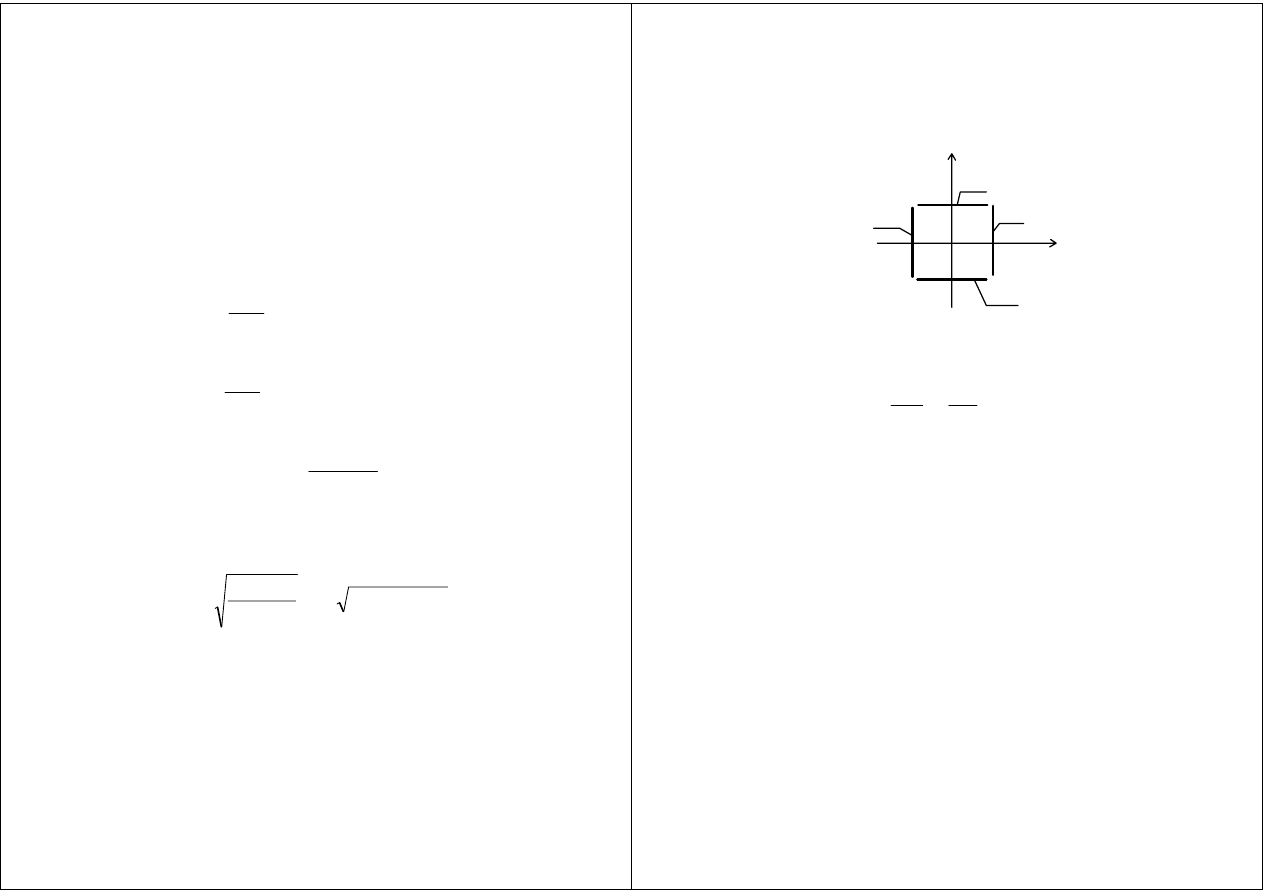
E

H

&

&

ε

ω

σ

j

z

∇

∇

∇

∇ ××××

==== −−−−

⊥

⊥⊥

⊥

⊥

⊥⊥

⊥

z

j

&

&

E

H

ω

ω

ω

ω µµµµ

∇

∇

∇

∇ ××××

====

⊥

⊥⊥

⊥

⊥

⊥⊥

⊥

&

H

0

∇

∇

∇

∇ ××××

====

⊥

⊥⊥

⊥

⊥

⊥⊥

⊥

&

E

0

∂∂∂∂

∂∂∂∂

γγγγ

2

2

2

0

z

&

&

E

E

⊥

⊥⊥

⊥

⊥

⊥⊥

⊥

−−−−

====

∂∂∂∂

∂∂∂∂

γγγγ

2

2

2

0

z

&

&

H

H

⊥

⊥⊥

⊥

⊥

⊥⊥

⊥

−−−−

====

&

&

&

H

E

⊥

⊥⊥

⊥

⊥

⊥⊥

⊥

====

××××

i

Z

z

f

&

&

&

E

H

⊥

⊥⊥

⊥

⊥

⊥⊥

⊥

====

⋅⋅⋅⋅

××××

Z

i

f

z

(

)

(

)

ε

ω

σ

µ

ω

γ

ε

ω

σ

µ

ω

j

j

,

j

j

Z

f

+

=

+

=

∇

∇

∇

∇ ⋅⋅⋅⋅ ====

⊥

⊥⊥

⊥

2

0

U

Metoda rozdzielenia zmiennych

+1

+1

-1

-1

y

x

U = 0

U = 0

U = +1

U = -1

( ) ( ) ( )

y

Y

x

X

y

x,

U

⋅

=

−−−−

====

====

X

X

Y

Y

''

''

p

2

X

X

''

p

++++

====

2

0

Y

Y

''

p

−−−−

====

2

0

X

A

B

====

++++

−−−−

e

e

jp x

jp x

Y

C

D

====

++++

−−−−

e

e

jp y

jp y

X

A'cospx

B'sinpx

====

++++

Y

C'coshpy

D'sinhpy

====

++++

( )

( ) ( )

∑

=

k

k

k

k

y

Y

x

X

C

y

x,

U

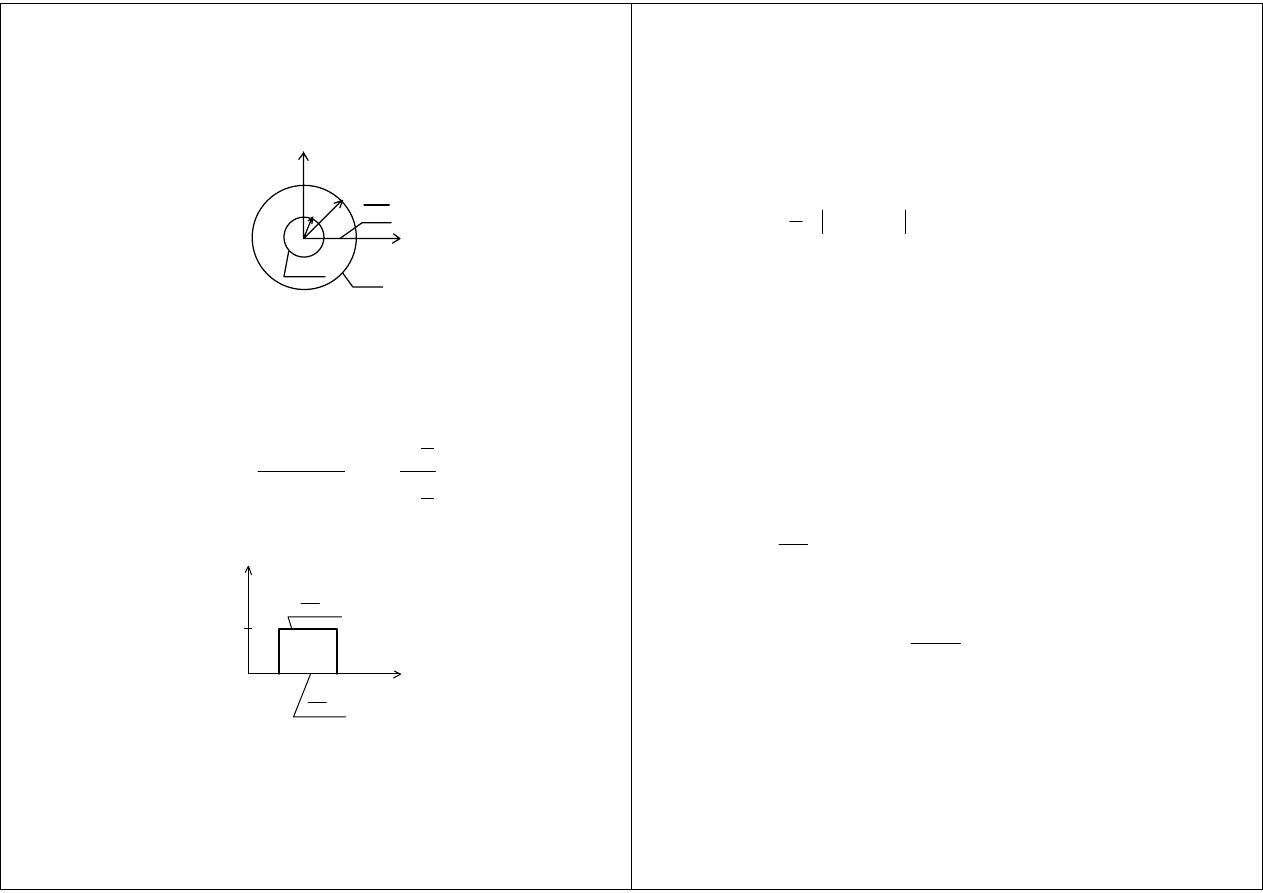
Metoda odwzorowań konforemnych

b

a

U=U

0

U=0

ο)

U

ο)

n

x

y

= 0

W

ln z

====

U = U

U

0

0

ln

ln a

lnb

ln a

ln

a

ln

b

a

ρρρρ

ρρρρ

−−−−
−−−−

====

U

1

=ln b

U

2

=ln a

U=U

0

U=0

)

o

)

o

U

n = 0

)

o

)

o

U

n

= 0

u

v

2

π

Metoda Ritza (wariacyjna)

Funkcjonał ;

Funkcja

⇒

⇒

⇒

⇒

Liczba

dS

y)

x,

U(

2

W

2

S

1

e

∫∫

⊥

∇

=

ε







 osiąga minimum !

U

0

- spełnia zadane warunki brzegowe

U

k

- spełnia zerowe warunki brzegowe, k = 1,2 ....N

( ) ( )

( )

∑

=

+

=

N

1

k

k

k

0

y

x,

U

y

x,

U

y

x,

U

α

(

)

N

2

1

1

e

......

,

W

α

α

α

φ

=

Warunek stacjonarności funkcjonału W

e1

:

∂∂∂∂ φφφφ

∂∂∂∂ αααα

k

==== 0

⇒

⇒

⇒

⇒

oblicza się

αααα

k

Uwaga:

C

e

1

1

2

2

====

W

U

;

Po podstawieniu przybliżonego rozwiązania na U(x,y)
otrzymuje się zawyżoną wartość W

e1

oraz C

1

(tzn.

ograniczenie od góry)

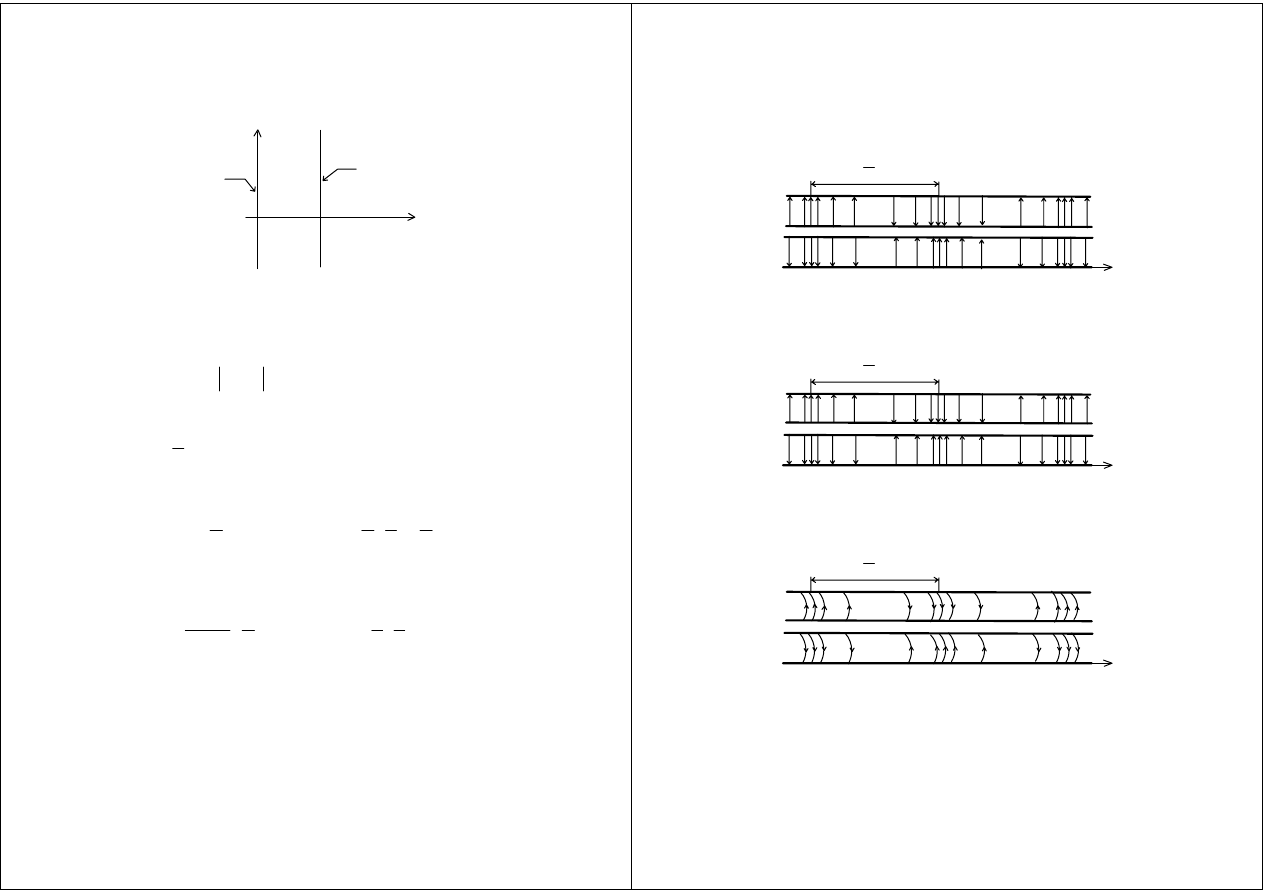
Przykład

0

y

z

U = 0

U

0

1

Funkcjonał:

U = U

0

[

αααα x + (1 - αααα) x

2

]

spełnia warunki brzegowe dla każdego

αααα.

(

)

2

2
0

2

x

2

x

2

U

U

α

α

−

+

=

∇

⊥

(

)

∫

+

−

+

−

+

=

1

0

2

2

2

2

2

2

2
0

1

e

x

d

x

4

x

8

x

4

x

4

x

4

U

2

W

α

α

α

α

α

ε













+

−

+

−

+

=

2

2

2

2
0

1

e

3

4

3

8

3

4

2

2

U

2

W

α

α

α

α

α

ε

0

3

8

3

8

4

2

2

U

2

W

2
0

1

e

=













+

−

−

+

=

α

α

α

ε

α

∂

∂

αααα = 1

czyli, zgodnie z przewidywaniami :

U = U

0

x

a)

z

x x x x x x

x

x x x x

x

o

o

o

o

o

o

o

o

o

o

o

o

o

o o o

o

o o

o

o

o

o

o

x

x x x x x x

x

x x x x

x

λ
2

o

o o o

o

o o

o

o

o

o

o

x

x x x x x x

x x x x

x

o

b)

z

x x x x x x

x

x

x x x

x

o

o

o o o

o

o o

o

o

o

o

o

x

x

x

x

x

x

x

x

x

x

x

x

x

λ

2

o

o

o o

o

o

o

o

o

o

o

o

c)

z

λ

2

o

o o

o

o o

o

o o o

o

o

o o

o

o

x

x x

x

x

x

x x

x

x

x x

x

x

x

x x

x

x x

x

o

o

o

o o

o o

o

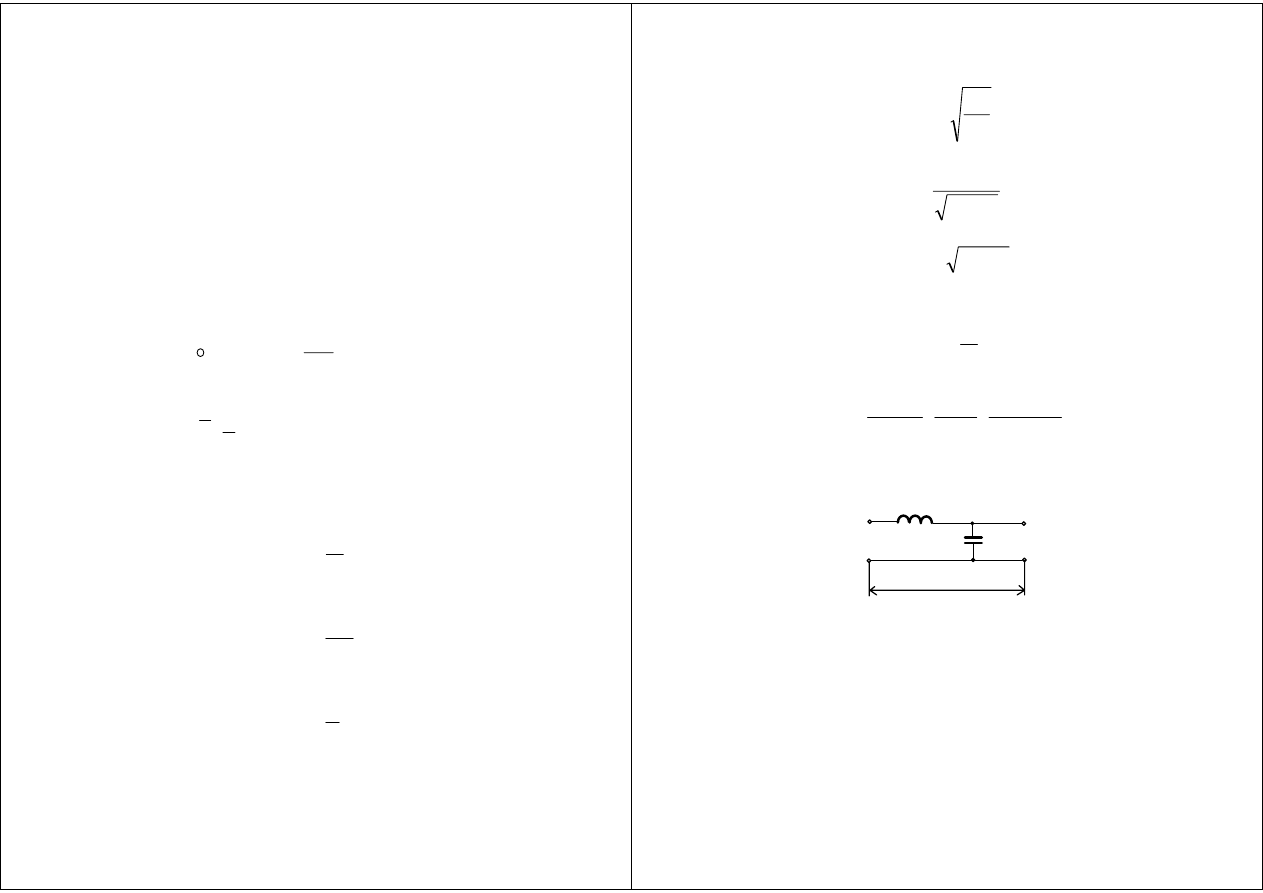
Rozkład pola elektromagnetycznego w linii współosiowej
a) dla fali bieżącej
b) dla fali stojącej
c) dla fali bieżącej - linia o stratnych ściankach

Parametry obwodowe linii TEM

∫

⋅

=

B

A

B

A,

l

d

E

U

&

&

0

I

S

d

t

D

+

J

l

d

H

k

k

S

l

=

=

⋅









=

⋅

∑

∫∫

∫

&

&

&

&

&

∂

∂

( ) ( )

∫∫

⋅

×

=

∗

S

0

0

S

d

y

x,

y

x,

Re

2

1

P

&

&

&

H

E

Z

U

I

C

Q

U

L

I

c

====

====

====

1

1

1

φφφφ

Z

L
C

c

1

1

====

V

1

L C

1

1

====

γγγγ

ω

ω

ω

ω

==== j

L C

1

1

(

)

l

L

j

l

V

Z

j

l

tg

Z

j

Z

1

c

c

w

∆

=

∆

≈

∆

=

ω

ω

β

(

)

l

C

j

1

l

j

V

Z

l

tg

j

Z

Z

1

c

c

w

∆

=

∆

≈

∆

=

ω

ω

β

L

1

∆ l

C

1

∆ l

∆ l

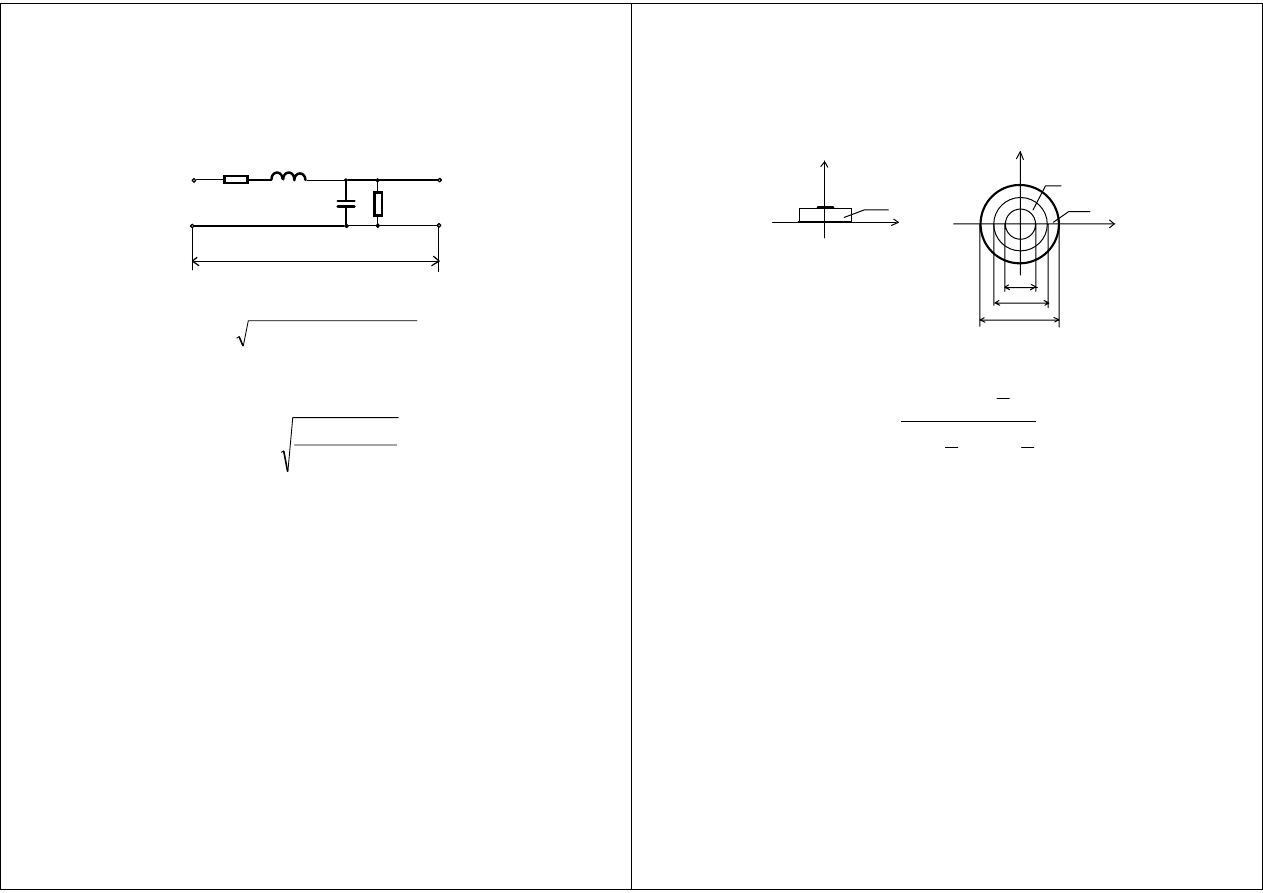
Stratne linie TEM

L

1

∆ l

C

1

∆ l

∆ l

R

1

∆ l

1

∆ l

G

(

)(

)

1

1

1

1

G

C

j

R

L

j

+

+

=

ω

ω

γ

Z

j L

R

j C

G

c

====

++++
++++

ω

ω

ω

ω
ω

ω

ω

ω

1

1

1

1

Niejednorodne linie TEM

2c

2b

2a

y

y

x

x

U = U

0

U =

0

ε

w

ε

w

= 1

>1

ε

1

ε

2

εεεε

εεεε εεεε

εεεε

εεεε

z

ln

a

c

ln

b

c

ln

a

b

====

++++

1

2

2

1

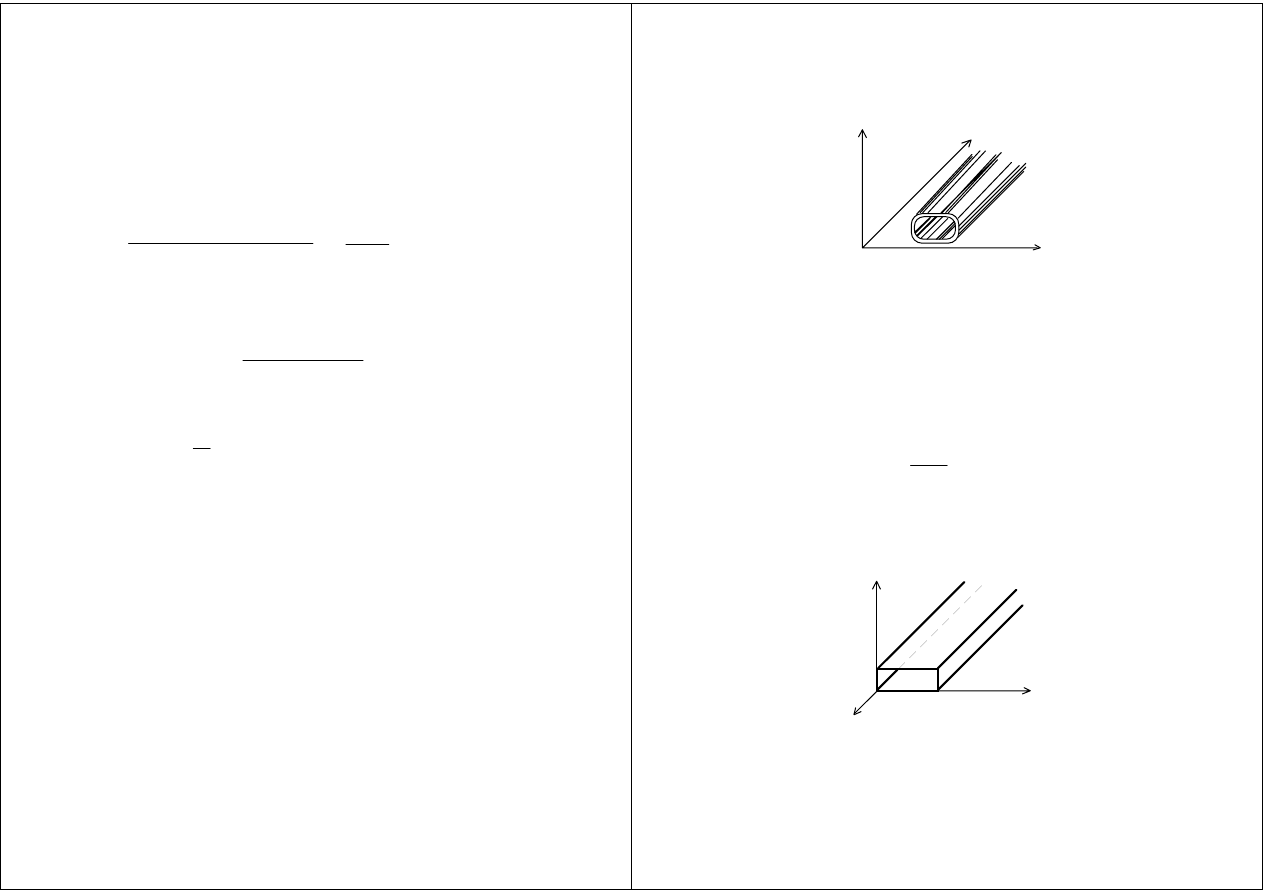
Fale akustyczne w rurach

Dla rury o gładkich ściankach, o przekroju S, wypełnionej
powietrzem o gęstości

ρρρρ

0

; akustyczna impedancja falowa

Z

f

=

ciœnienie akustyczne

prêdkoœæ objêtoœciowa

= ρ

ρρρ

0

c

S

gdzie: c - prędkość dźwięku w powietrzu

Z

Z

Z

j tg

l

Z

jZ tg l

c

we

f

k

f

k

====

++++

++++

====

ββββ

ββββ

ββββ

ω

ω

ω

ω

Falowody

x

z

y

0

E

H

t

n

====

====

0

0

∂∂∂∂

∂∂∂∂

H

t

n

==== 0

z

x

y

0

a

b

∇

∇

∇

∇

−−−−

====

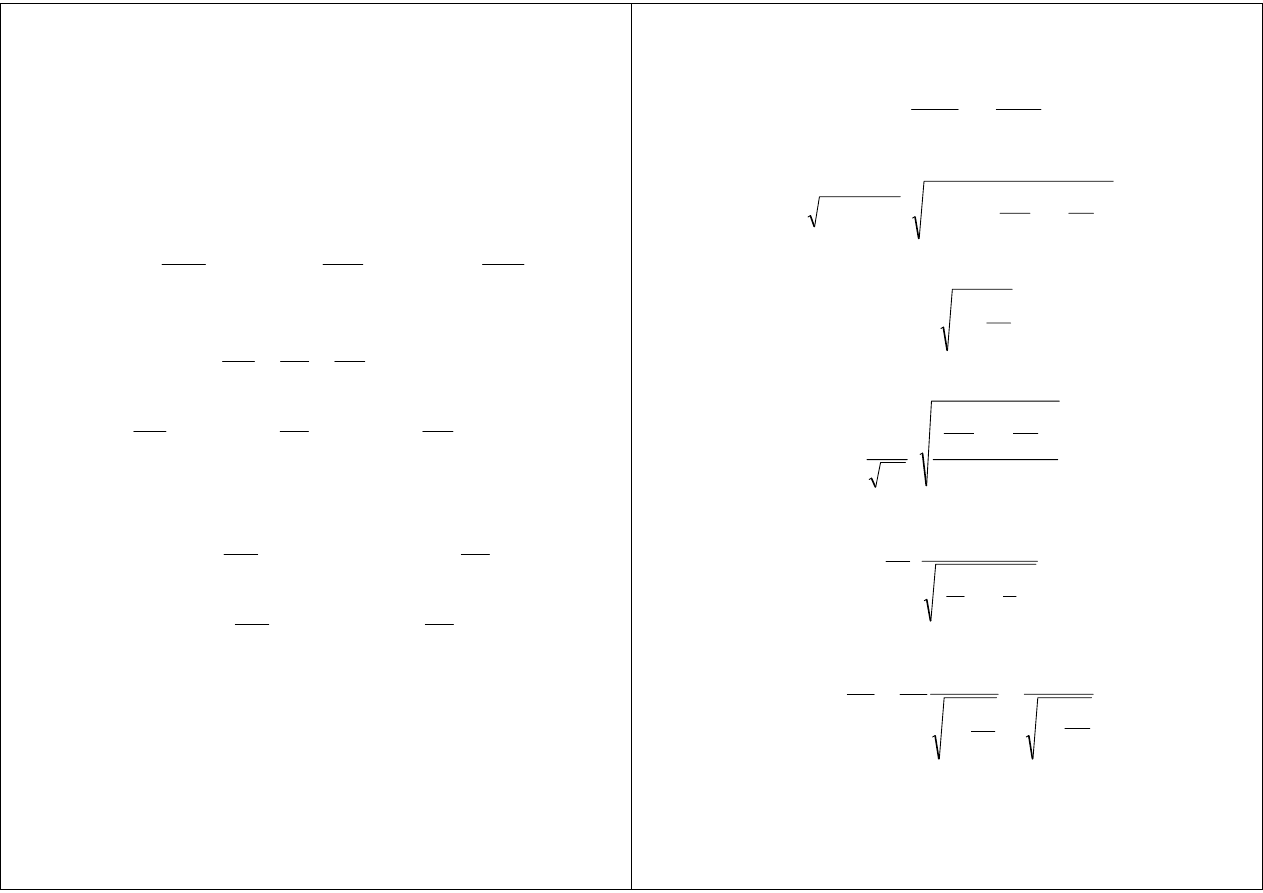
2

2

0

E

E

z

z

γγγγ

( ) ( ) ( )

z

y

x

z

Z

Y

X

E

=

X Y Z

X Y

Z

X Y Z

XYZ

''

''

''

++++

++++

−−−−

====

γγγγ

2

0

X

X

Y

Y

Z

Z

''

d

dx

''

d

d y

''

d

d z

====

====

====

2

2

2

2

2

2

X

X

Y

Y

Z

Z

''

''

''

++++

++++

==== γγγγ

2

X

X

Y

Y

Z

Z

''

''

''

x

y

z

====

====

====

γγγγ

γγγγ

γγγγ

2

2

2

γγγγ

γγγγ

γγγγ

γγγγ

x

y

z

2

2

2

2

++++

++++

====

X

C

Y

C

====

====

x

y

sin

m

a

x

sin

n

b

y

ππππ

ππππ

γγγγ

ππππ

γγγγ

ππππ

x

y

j

m

a

j

n

b

====

====

Z

C

====

−−−−

z

z

e

z

γγγγ

E

E

z

z

z

sin

m x

a

sin

n y

b

e

z

====

−−−−

0

ππππ

ππππ

γγγγ

2

2

2

2

y

2

x

2

z

b

n

a

m













+













+

−

=

−

−

=

π

π

µ

ε

ω

γ

γ

γ

γ

ββββ

ββββ

ββββ
ββββ

z

g

====

−−−−

1

2

2

ε

µ

π

π

ε

µ

β

ω

2

2

g

g

b

n

a

m













+













=

=

2

2

g

g

b

n

a

m

2

2













+













=

=

β

π

λ

λλλλ

ππππ

ββββ

ππππ

ββββ

ββββ
ββββ

λλλλ

λλλλ

λλλλ

z

z

g

g

====

====

−−−−

====

−−−−

2

2

1

1

1

2

2

2

2

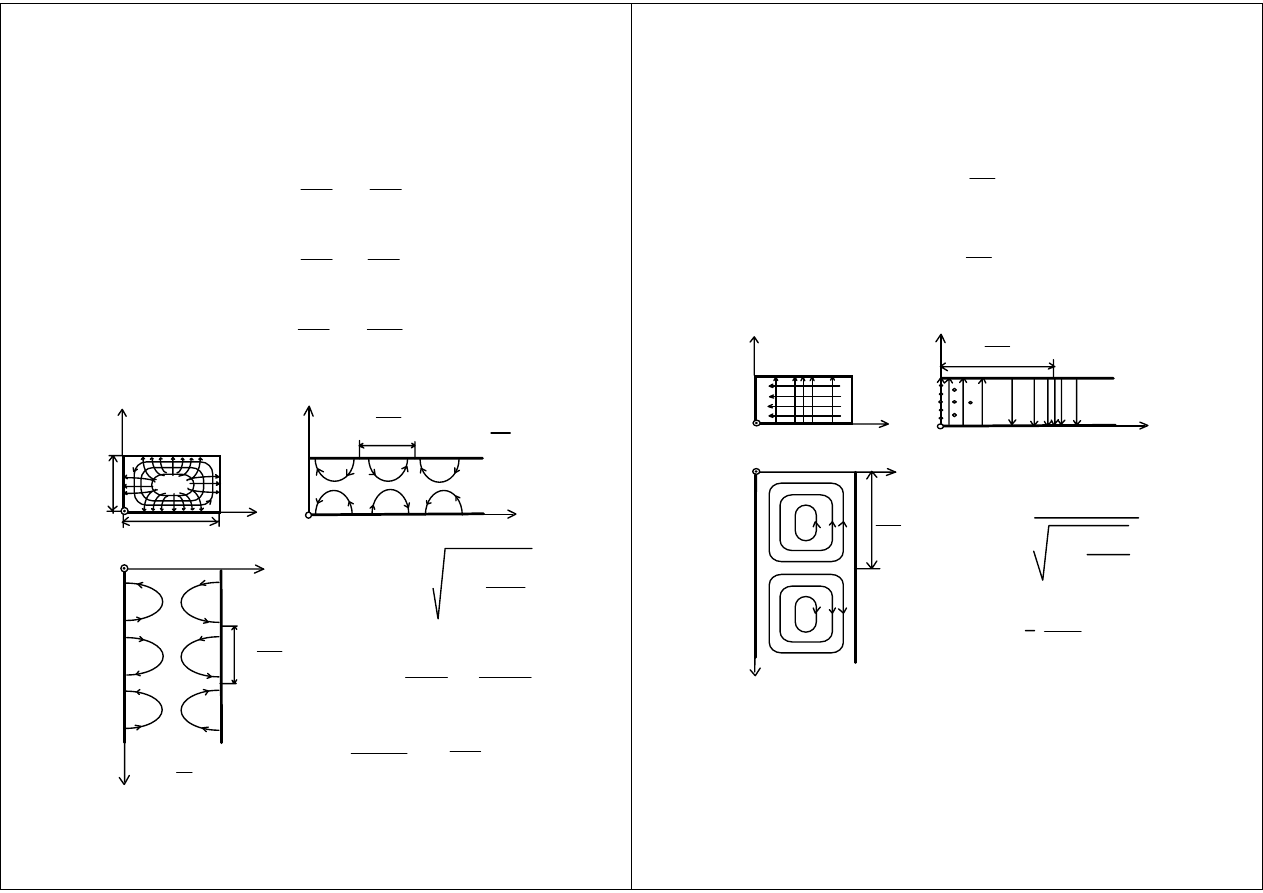
Rodzaj E

11

E

E

x

x

z

cos

x

a

sin

y

b

e

z

==== −−−−

−−−−

0

ππππ

ππππ

γγγγ

E

E

y

y

z

sin

x

a

cos

y

b

e

z

==== −−−−

−−−−

0

ππππ

ππππ

γγγγ

E

E

z

z

z

j

sin

x

a

sin

y

b

e

z

====

−−−−

0

ππππ

ππππ

γγγγ

b

a

z

x

y

x

o o

xx

o

xx

oo

x

o

x

z

y

x

x

oo

xx

o

o

xx

oo

x

y

x

z

y = b

2

λ

2

λ

2

x

=

a

2

z

z

Z

f

= Z

1 - λ

λλλ

2222

λλλλ

g

2

Z

f

=

E

H

x

y

E

H

=

-

y

x

H

H

x0

y0

=

a

b

Rodzaj H

10

(podstawowy)

z

0

x

x

z

e

a

x

sin

γ

π

−













−

= H

H

z

0

z

z

z

e

a

x

cos

j

γ

π

−













= H

H

x

y

x

z

y

x

y

x

z

λ

2

z

λ

2

z

z

o o o o o

o o o

o

x x x x x

x x x

x x x

x

x

x

x
x

x

o

o
o
o

x

x

x

x

x

Z

f

=

Z

2

1 -

λλλλ

λλλλ

2

g

Z

f

=

x
x

x

x

x

x

x

x

x

E

x

H

y

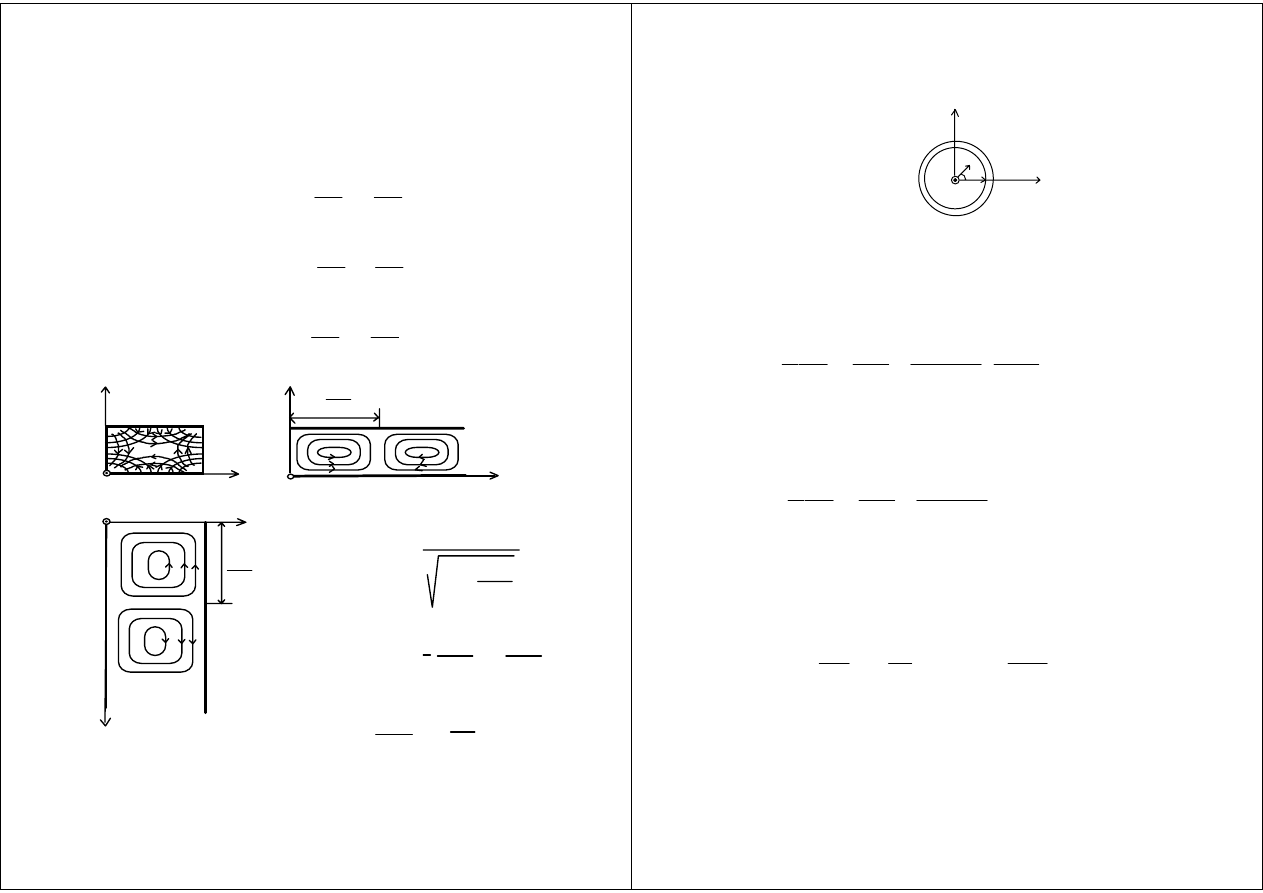
Rodzaj H

11

H

H

x

x

z

sin

x

a

cos

y

b

e

z

==== −−−−

−−−−

0

ππππ

ππππ

γγγγ

H

H

y

y

z

cos

x

a

sin

y

b

e

z

==== −−−−

−−−−

0

ππππ

ππππ

γγγγ

H

H

z

z

z

j

cos

x

a

cos

y

b

e

z

====

−−−−

0

ππππ

ππππ

γγγγ

x

y

x

z

y

x

y

x

z

λ

2

z

λ

2

z

z

o

o

o

o

o o o

o

x

x
x

x

x

xx

o o

o o

x x

x x x

x

x

x

~

~ 0

~

~ 0

y

Z

f

=

Z

1 -

λ

2

λ

g

2

Z

f

=

y

y

x

x

E

E

H

H

=

y0

x0

E

E

=

b

a

y

x

z

0

ϕ

ρ

a

Rodzaje E

∇

∇

∇

∇

−−−−

====

2

2

0

E

E

z

z

γγγγ

0

z

1

1

z

2

2

z

2

2

z

2

2

z

=

−

+

+









E

E

E

E

γ

∂

∂

ϕ

∂

∂

ρ

ρ

∂

∂

ρ

ρ

∂

∂

ρ

( ) ( )

z

z

z

e

R

γ

ϕ

φ

ρ

−

=

E

(

)

0

1

1

z

2

2

z

2

z

2

2

z

=

−

+

+









E

E

E

γ

γ

ϕ

∂

∂

ρ

ρ

∂

∂

ρ

ρ

∂

∂

ρ

ββββ

g

2

ρρρρ

ρρρρ

ρρρρ ββββ

φφφφ

φφφφ

2

2

2

2

R''

R

R'

R

''

m

g

++++

++++

====

−−−−

====

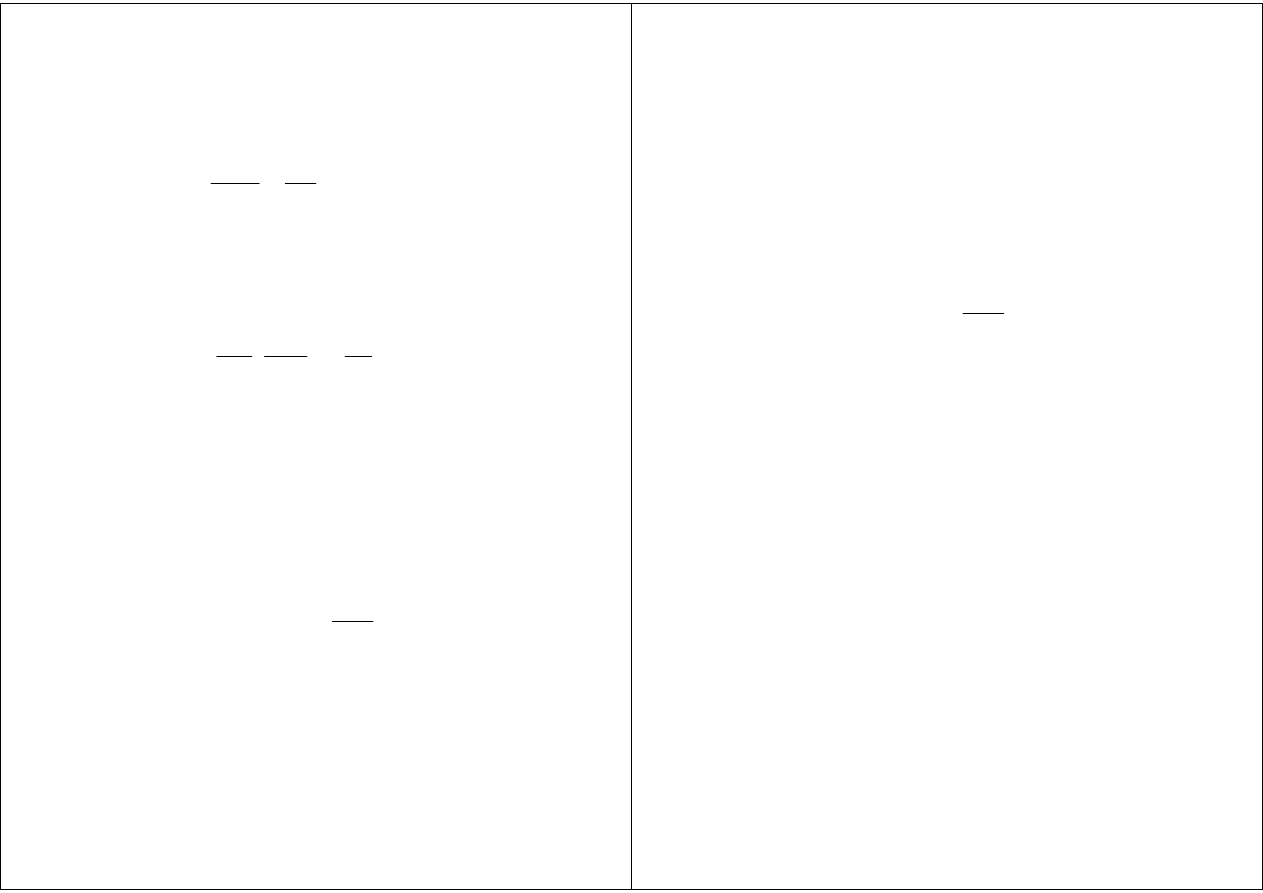
φφφφ

φφφφ

''

m

++++

====

2

0

(

)

0

m

R

R©

R

©

R©

2

2

g

2

2

=

−

+

+

β

ρ

ρ

ρ

φφφφ

ϕϕϕϕ

ϕϕϕϕ

====

++++

A cosm

B sin m

'

'

φφφφ

ϕϕϕϕ

==== A cosm

0

R

m

1

d

R

d

1

d

R

d

2

2

2

2

=









ℵ

−

+

ℵ

ℵ

+

ℵ

gdzie:

g

ℵ

ℵ

ℵ

ℵ ==== ββββ ρρρρ

2

( )

z

g

m

0

z

z

z

e

m

cos

J

γ

ϕ

ρ

β

−

=E

E

( )

0

a

J

g

m

=

β

ββββ

g,m,n

m,n

a

====

ℵ

ℵ

ℵ

ℵ

ℵ

ℵ

ℵ

ℵ

01

= 2.405

ℵ

ℵ

ℵ

ℵ

11

= 3.832

Rodzaje H

( )

z

g

m

0

z

z

z

e

m

cos

J

γ

ϕ

ρ

β

−

=H

H

( )

0

a

J

g

©
m

=

β

ββββ

g,m,n

m,n

'

a

====

ℵ

ℵ

ℵ

ℵ

ℵ

ℵ

ℵ

ℵ ====
ℵ

ℵ

ℵ

ℵ ====
ℵ

ℵ

ℵ

ℵ ====

01

11

21

3 832

1 841

3 054

'

'

'

.

.

.

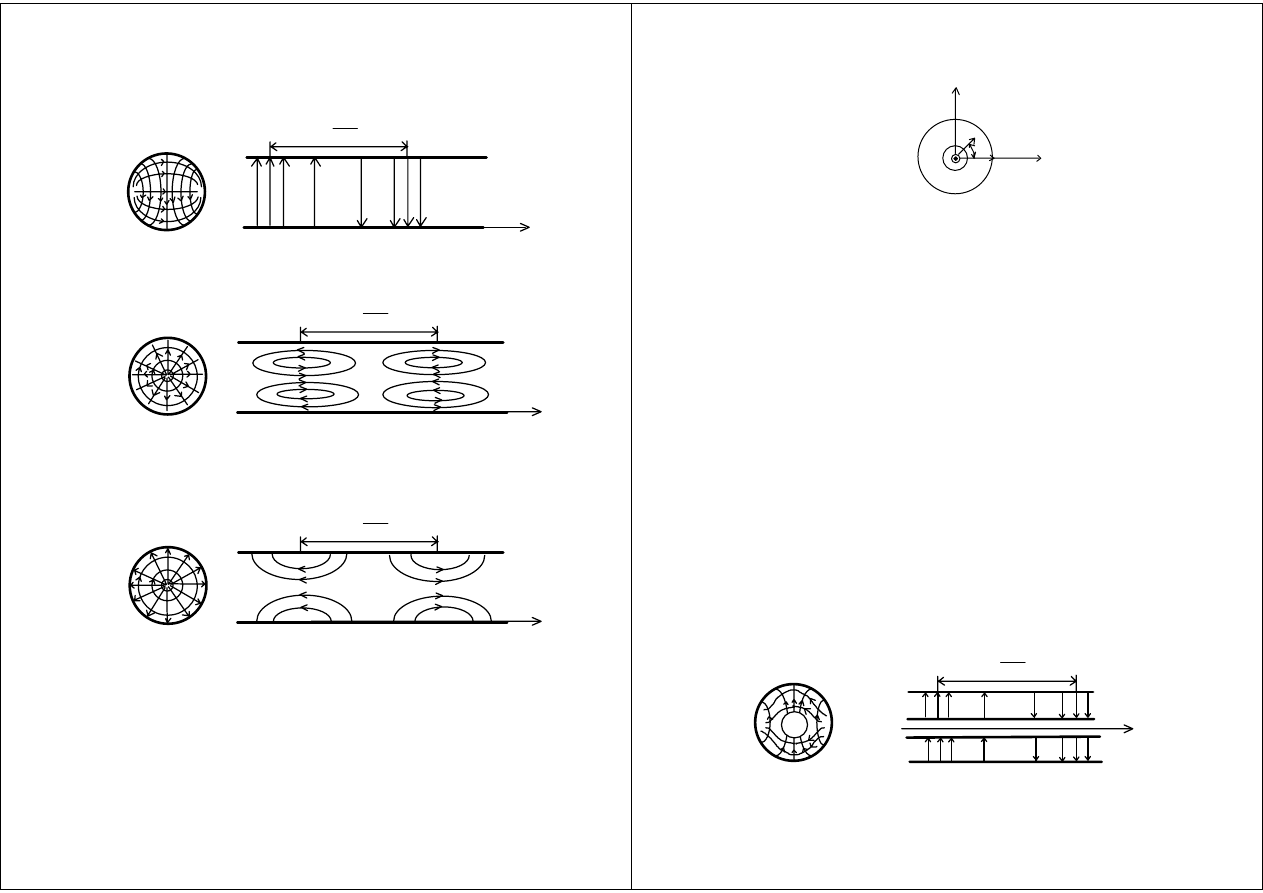
H

11

(rodzaj podstawowy)

o

o

x

x

o

o

o

o

o

o

x

x

x

x

x

x

λ

z

2

z

H

01

λ

z

2

z

o
o

x x

x x

o
o

o o
o o

x

x

x
x

E

01

λ

z

2

z

o

o

x x

x x

o

o

o o
o o

x

x

x
x

y

x

ϕ

ρ

a

b

z

( )

( )

[

]

z

g

m

g

m

z

z

e

m

cos

N

J

γ

ϕ

ρ

β

ρ

β

−

+

=

B

A

E

Rodzaje E:

( )

( )

0

a

N

a

J

g

m

g

m

=

+

β

β

B

A

( )

( )

0

b

N

b

J

g

m

g

m

=

+

β

β

B

A

Rodzaje H:

( )

( )

0

a

N

a

J

g

©
m

g

©
m

=

+

β

β

B

A

( )

( )

0

b

N

b

J

g

©
m

g

©
m

=

+

β

β

B

A

Rodzaj podstawowy H

11

λ

z

2

z

o o o o

o o

o o

o

o o

x
x

o
o

x x

o

o

x x

x

x x

x x x x

x x

o

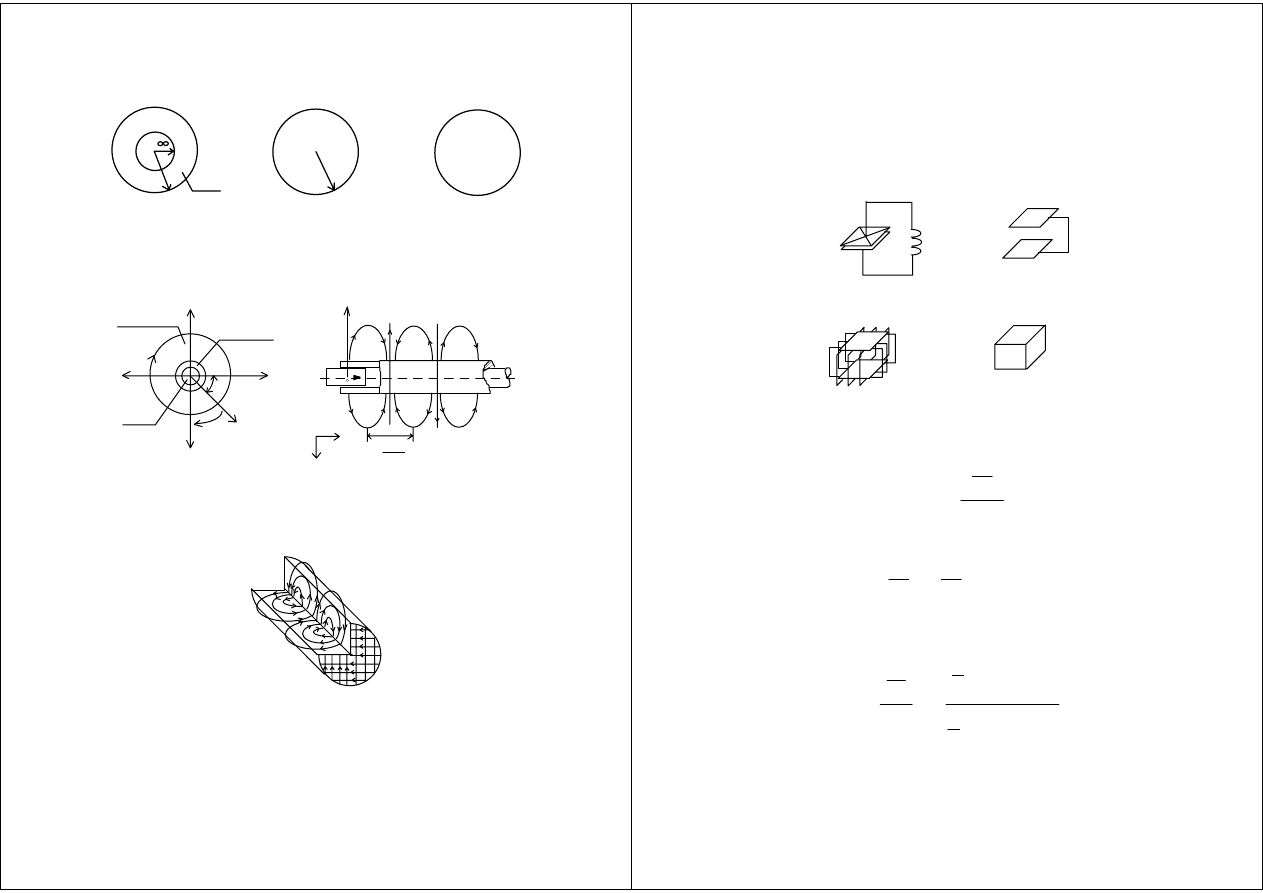
σ =

b

a

σ = 0

ε >ε

0

ε = ε

0

σ

σ >>ωε

< oo

a

ε = ε

0

ε = ε

0

ε > ε

σ = 0

o

Falowody:

Goubau

drutowy

dielektryczny

Powietrze

Dielektryk

Metal

H

E

Hθ

θ

r

H

E

o

o

o

o

λ

z

2

E

E

z

r

z

r

Pole E

01

w falowodzie Goubau

Pole HE

11

w falowodzie dielektrycznym

Rezonatory

c)

d)

a)

b)

Q

W

P T

q

==== 2ππππ

W

W

0

m

e

−−−−

====

∫∫∫

∫∫∫

∗

∗

⋅

⋅

=

=

V

V

q

V

d

T

2

1

V

d

4

1

4

T

P

W

2

Q

J

E

D

E

&

&

&

&

π

π

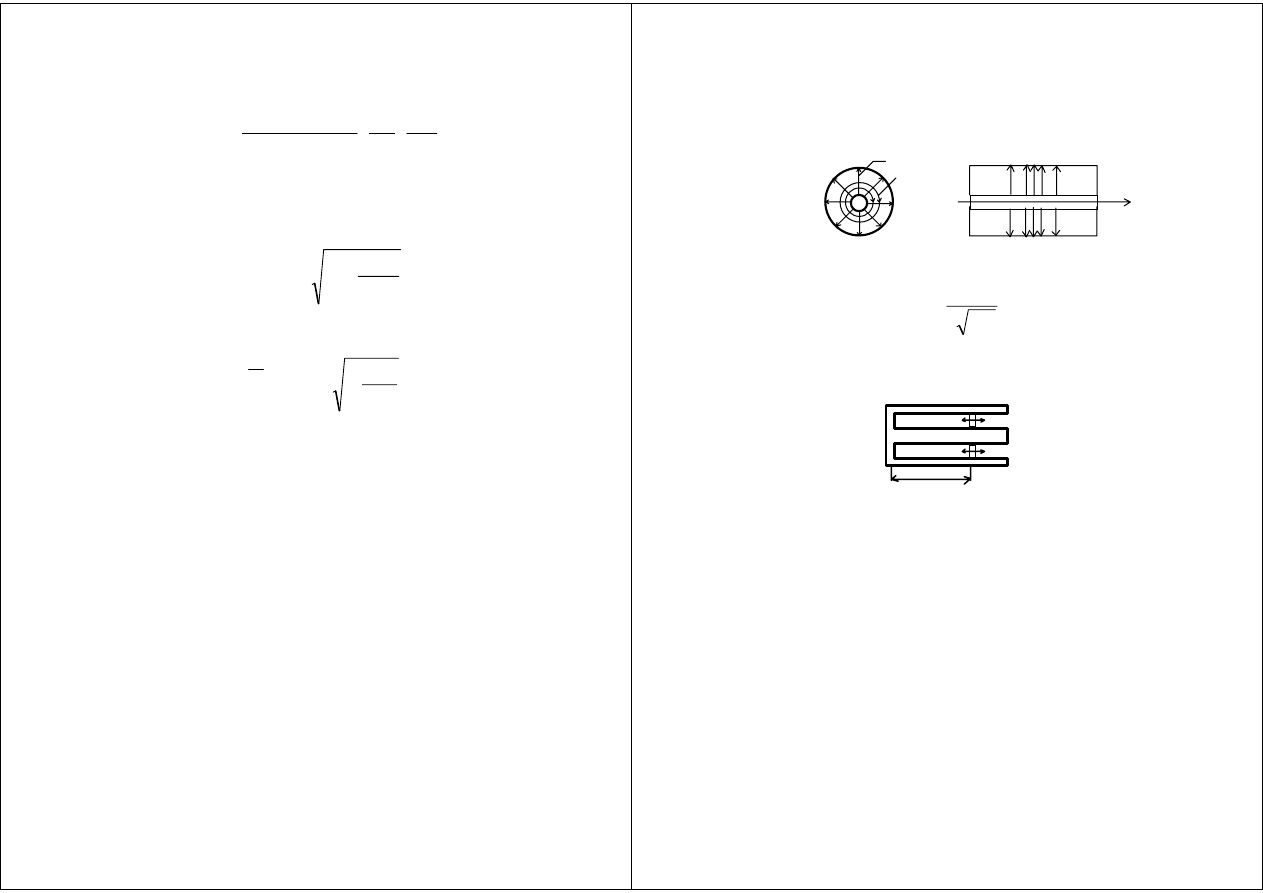
δ

σ

ε

ω

σ

ε

π

tg

1

V

d

T

V

d

2

Q

V

V

=

=

⋅

⋅

=

∫∫∫

∫∫∫

∗

∗

E

E

E

E

&

&

&

&

ω

ω

ω

ω

ω

ω

ω

ω

νννν

νννν

'

Q

====

−−−−

1

1

4

2

























−

−

t

Q

4

1

1

cos

e

~

E

2

r

t

Q

2

r

ω

ω

Rezonator współosiowy

E

x x x x

x x x

x x

o o o o

o o o
o o

x x x x

x x x

x x

o o o o

o o o

o o

E

H

0

l

z

H

ω

ω

ω

ω

ππππ

µµµµ εεεε

νννν

====

l

l

Przestrajanie rezonatora współosiowego

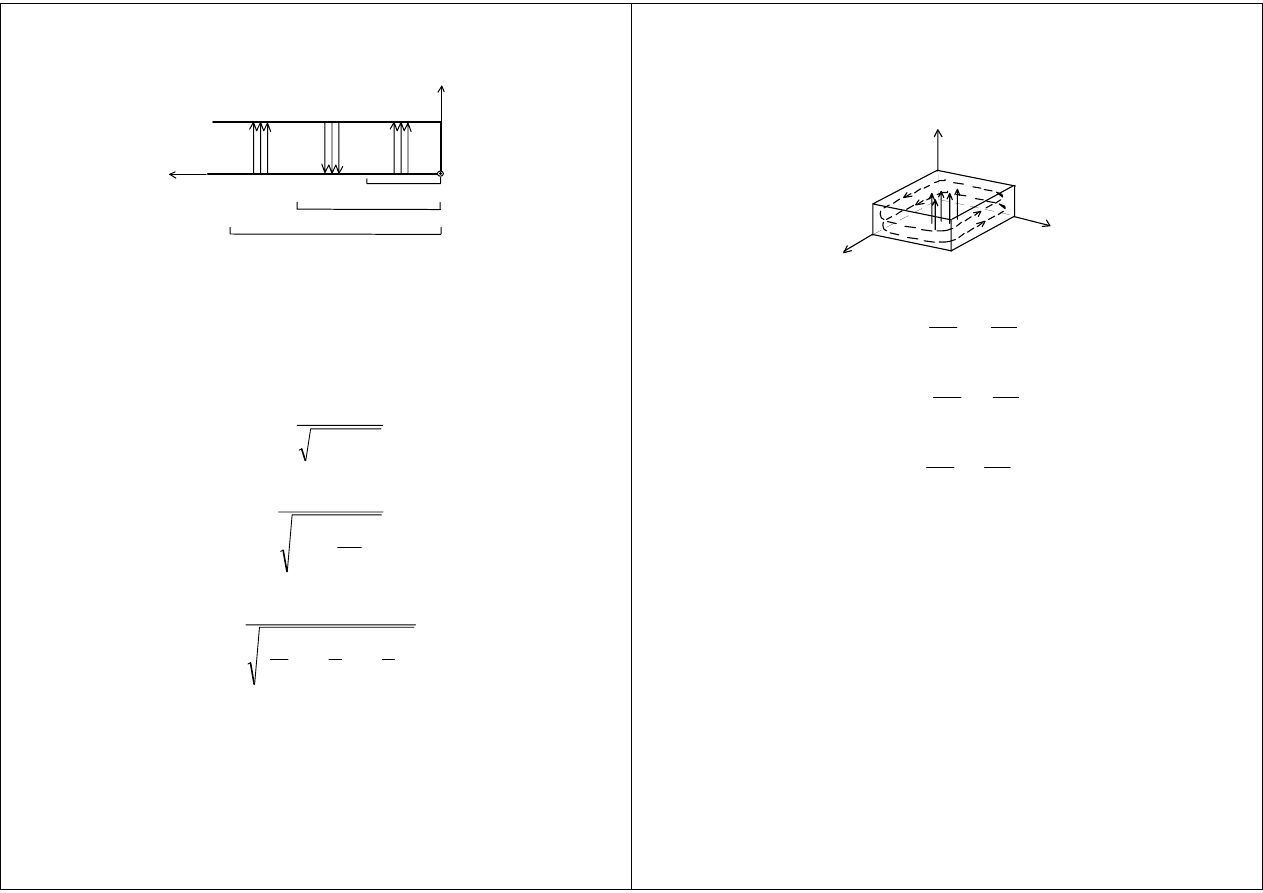
0

z

y

x

x

x

x

x

x

x

x

x

o
o
o
o

o
o
o
o

x

x

x

x

o
o
o
o

H

H

H

101

102

103

ββββ

ππππ

z

l

p

====

ββββ

ββββ

ββββ

g

z

2

2

2

++++

====

λλλλ

ππππ

ββββ

ββββ

νννν

====

++++

2

2

2

g

z

2

2

g

l

p

2













+

=

π

β

π

λ

ν

2

2

2

l

p

b

n

a

m

2













+













+













=

ν

λ

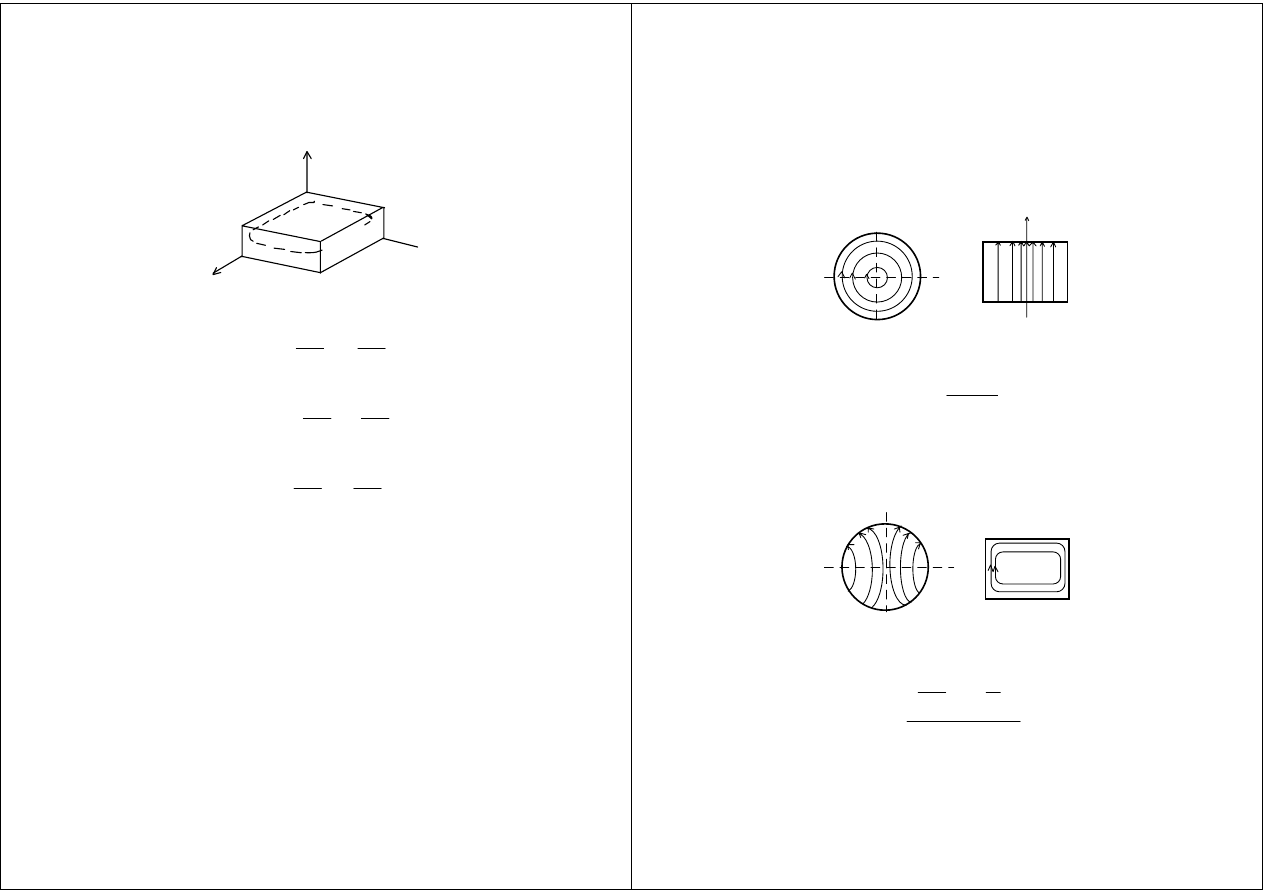
Rodzaj H

101

y

z

x

H

E

E

E

y

y

sin

x

a

sin

z

l

cos t

====

0

ππππ

ππππ

ω

ω

ω

ω

H

H

x

x 0

sin

x

a

cos

z

l

sin

t

==== −−−−

ππππ

ππππ

ω

ω

ω

ω

νννν

H

H

z

z

cos

x

a

sin

z

l

sin

t

====

0

ππππ

ππππ

ω

ω

ω

ω

νννν

Rodzaj E

110

y

z

x

E

E

z

z

sin

x

a

sin

y

b

cos t

====

0

ππππ

ππππ

ω

ω

ω

ω

H

H

y

y

cos

x

a

sin

y

b

sin

t

==== −−−−

0

ππππ

ππππ

ω

ω

ω

ω

νννν

H

H

x

x

sin

x

a

cos

y

b

sin

t

====

0

ππππ

ππππ

ω

ω

ω

ω

νννν

Rezonatory kołowe

Rodzaj E

010

o

o

o

o

o

o o

o

o

o

o

o

o

o

o

o

H

E

z

x x

x x
x x
x x

x x

x x

x
x
x

x
x

x

o o
o o
o o

o o

o o

o o

o

o
o
o

o

o

E

H

ω

ω

ω

ω

µµµµ εεεε

νννν

2

01

2

2

====

ℵ

ℵ

ℵ

ℵ

a

Rodzaj H

111

x x x x x

x x x

x x x E

H

o

o

o

o

o

o

o

o

o

x

x x

x x

x

x

x

x

E

H

µε

π

ω

ν

2

2

©

11

2

l

a













+







ℵ

=

E

x x x

x x x

x x x

x x x

x x x

o o o

o o o

o o o

o o o

o o o

H

E

H

o

o

o

o

o

o o

o

o

o

o o

o

o

o

o

o

o

o

o

o
o

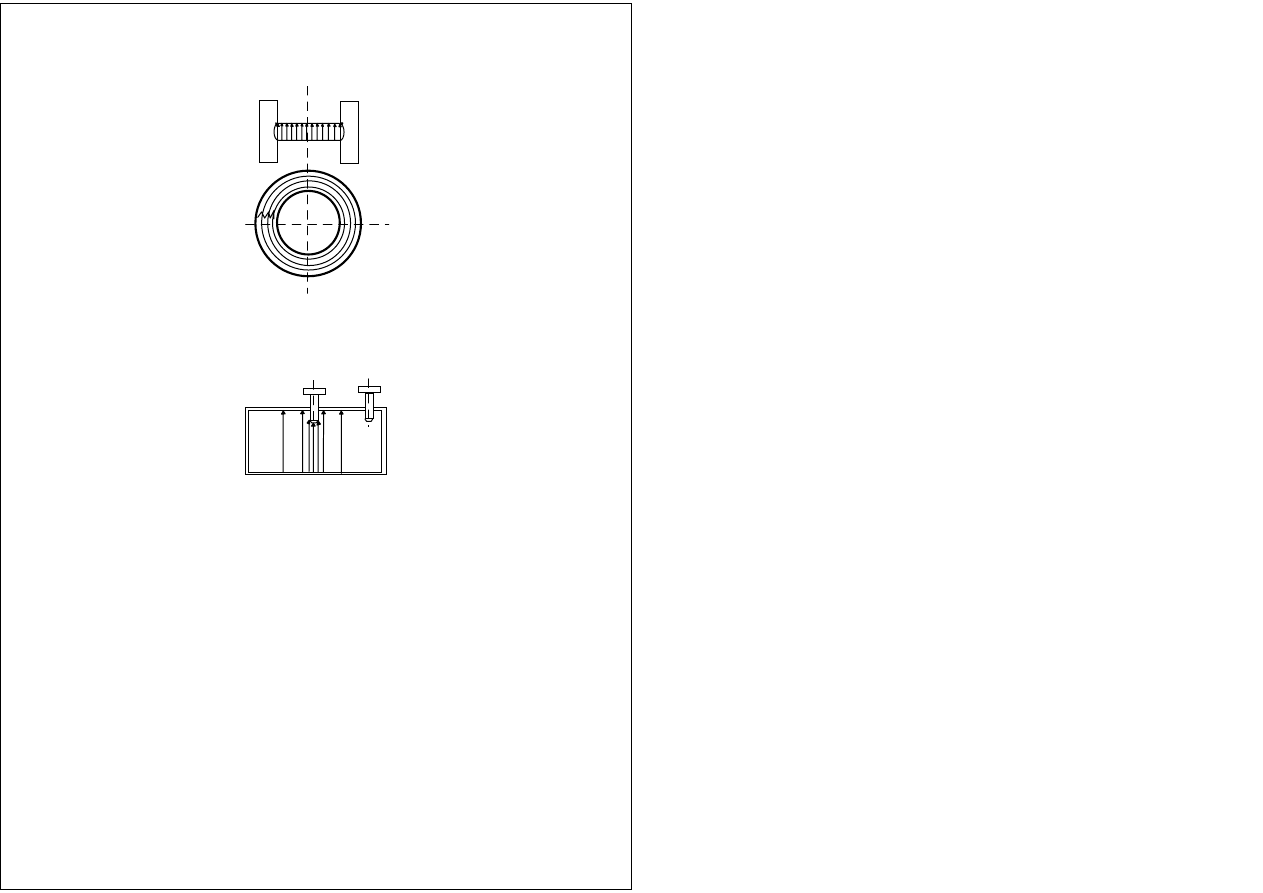
Rezonator toroidalny

x
x

x

x

x

x

x

x

x

o

o

o

o

o
o

o
o
o

A

B

E

H

Przestrajanie rezonatora kołowego