Regulacja prędkości silników indukcyjnych
Andrzej Kapłon
Katedra Energoelektroniki, Politechnika Świętokrzyska
Wstęp. Maszyny indukcyjne w napędzie.
Maszyna indukcyjna jest tzw. „koniem pociągowym” przemysłu. Jest to silnik prądu
przemiennego, przeważnie trójfazowy lub dla małych mocy jednofazowy. Przemysłowe
(konwencjonalne) silniki indukcyjne są zasilane z sieci o stałym napięciu i częstotliwości w
przypadku nieregulowanych napędów, tj. dla napędów o stałej w przybliżeniu prędkości
wirowania. W napędach regulowanych (tj. napędach o zmienianej wartości prędkości) silniki
indukcyjne są zasilane z przekształtników, napięciem o regulowanej amplitudzie i
częstotliwości.
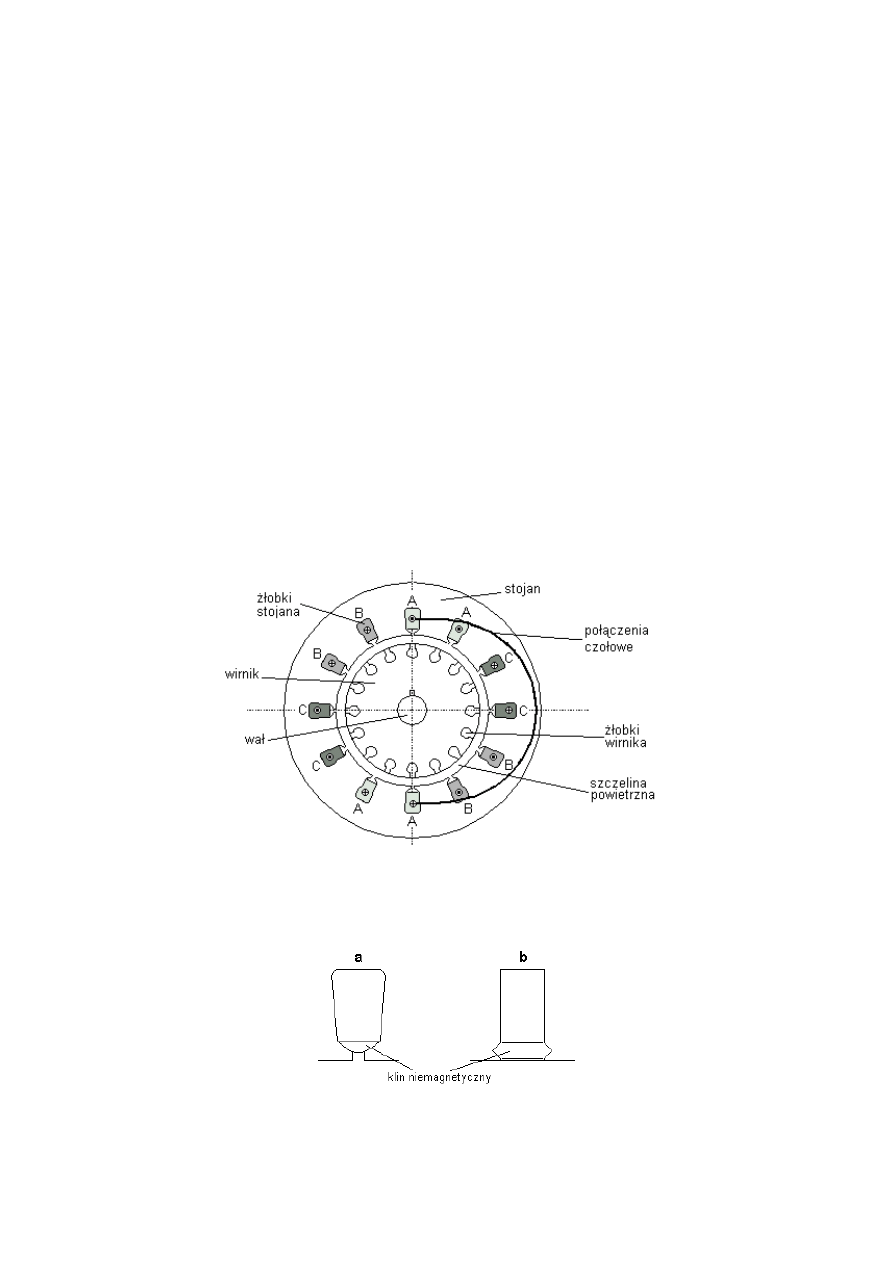
Podobnie jak silnik prądu stałego, silnik indukcyjny zbudowany jest ze stojana (części
nieruchomej) i wirnika (części wirującej) zamocowanego na łożyskach mechanicznych i
odseparowanego od stojana szczeliną powietrzną.
Stojan i jego pole wirujące
Stojan zbudowany jest zasadniczo w postaci rdzenia spakietowanego z blach
magnetycznych o grubości od 0.1 mm do 0.5 mm z wyciętymi na obwodzie żłobkami.
Żłobki wypełnione są cewkami połączonymi w odpowiedni sposób tworząc tzw. uzwojenie
prądu przemiennego strony pierwotnej (wzbudnika) (Rys. 1).
Rys. 1. Przekrój poprzeczny dwubiegunowego silnika indukcyjnego.
Żłobki stojana są przeważnie: półzamknięte (Rys. 2) dla małych i średnich mocy (do
100 kW) lub otwarte dla mocy powyżej 100 KW.
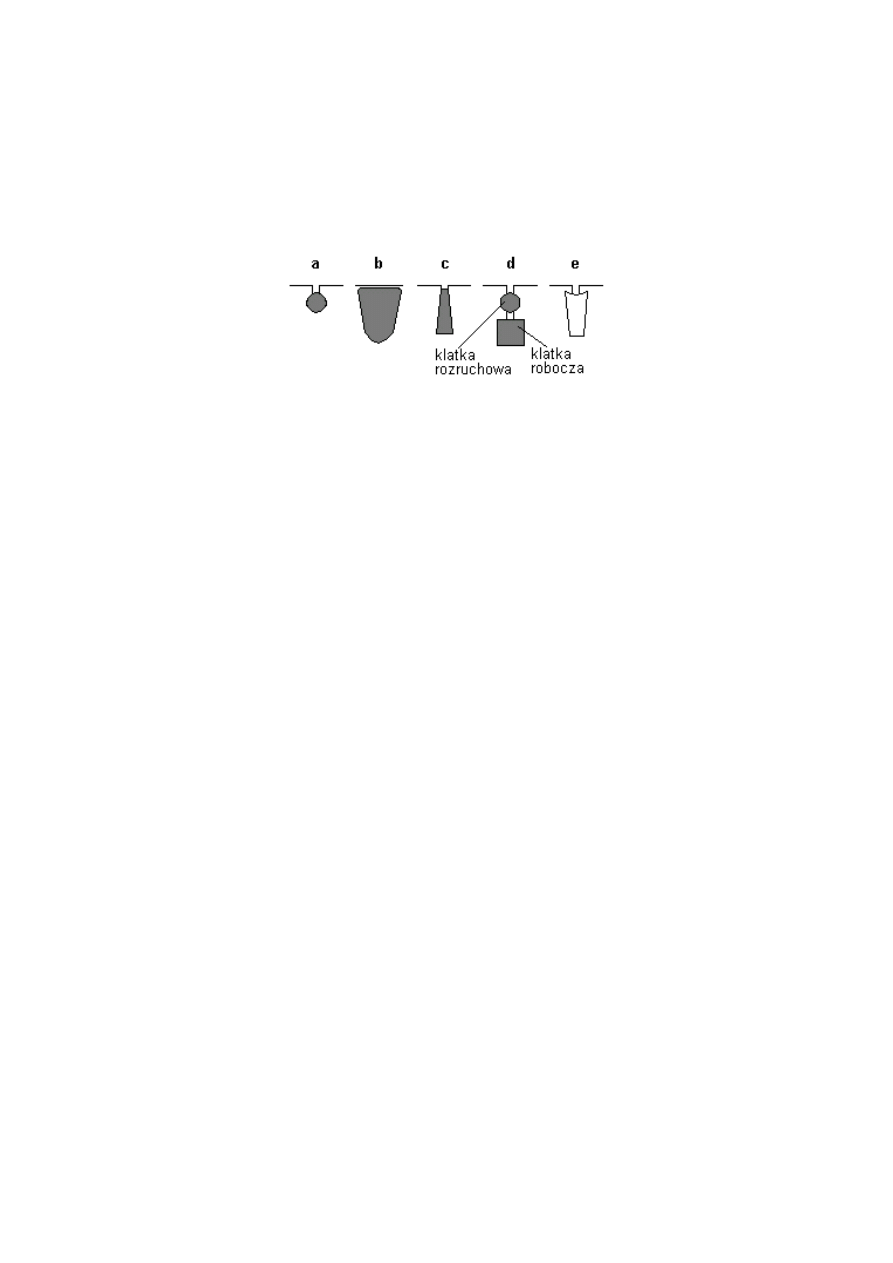
Rys. 2. Kształt żłobków: a) półotwarte (małe moce), b) otwarte (duże moce).
W przypadku silników pierścieniowych żłobki wirnika są przeważnie półzamknięte podczas
gdy stojana otwarte w celu zapewnienia stosunkowo małej szczeliny (mniej niż 2 mm)
powietrznej nawet dla bardzo dużych mocy (MW i powyżej).
W przypadku silników klatkowych przy stałej częstotliwości zasilania kształt żłobków
wirnika zależy od mocy i wielkości momentu rozruchowego.
Rys. 3. Przykładowe kształty żłobków wirnika:
a półotwarte okrągłe - dla silników małych mocy i zmiennej częstotliwości zasilania
b zamknięte – dla silników wysokoobrotowych i cichobieżnych
c głębokie, z silnym efektem wypierania prądu - dla silników o podwyższonym momencie
rozruchowym przy stałej częstotliwości zasilania
d dwuklatowe - dla silników o podwyższonym momencie rozruchowym przy stałej
częstotliwości zasilania
e dla silników wysokoobrotowych i przy zmiennej częstotliwości zasilania
Okrągłe półzamknięte żłobki (rys. 3a) nie wykazują efektu wypierania prądu przy rozruchu i
mogą być użyte przy stałej częstotliwości zasilania dla silników małej mocy i małym
momencie rozruchowym oraz dla zmiennej prędkości, jeśli efekt wypierania jest do
pominięcia.
Efekt wypierania prądu polega na zwiększeniu gęstości prądu w górnej części żłobka przy
wyższych częstotliwościach prądu wirnika (na początku rozruchu f
2
= f
1
). Powoduje to
zwiększanie rezystancji wirnika oraz co jest mniej istotne zmniejszenie indukcyjności
rozproszenia żłobka (rys. 3c,d). Podwójna klatka jest stosowana w silnikach średniej mocy dla
zredukowania prądu rozruchowego i zwiększenia momentu rozruchowego silnika. Efekt
wypierania prądu głębokich żłobków lub podwójnej klatki zwiększa rezystancję wirnika i
straty w punkcie pracy znamionowym co powoduje, że tego typu silniki nie są wskazane do
pracy w napędach z regulacją prędkości. W napędach z regulacją prędkości (częstotliwości)
wskazane są silniki o kształcie żłobków jak na rys. 3e wykazujących małe straty w wirniku.
Trójfazowe uzwojenie może być umieszczone w żłobkach jedno- lub dwuwarstwowo.
Wszystkie cewki są w ogólnym przypadku jednakowe i mają rozpiętość bliską lub równą
podziałce biegunowej
τ stanowiącej połowę okresu siły magnetomotorycznej cewki lub fazy.
Ilość biegunów na długości obwodu stojana jest równa 2p.
Pod każdym biegunem rozłożone są trzy strefy, po jednej dla każdej fazy. Każda strefa
zawiera q żłobków na biegun i fazę (q=2
÷8, przeważnie liczba naturalna). Sąsiednie strefy są
przesunięte w przestrzeni o kąt mechaniczny 2
π/3p, co odpowiada 2/3 podziałki biegunowej τ
uzwojenia.
Jeśli jednej podziałce biegunowej
τ odpowiada połowa okresu (180° elektrycznych),
to pomiędzy kątem elektrycznym
α
e
i kątem mechanicznym
α
m
zachodzi relacja
m
b
e
p
α
α =
(1)
Siła magnetomotoryczna (
sa
Θ ) każdej cewki fazy ma formę funkcji skokowej (Rys. 2), w
której można wyodrębnić składową podstawową
1
sa
Θ o rozkładzie sinusoidalnym o
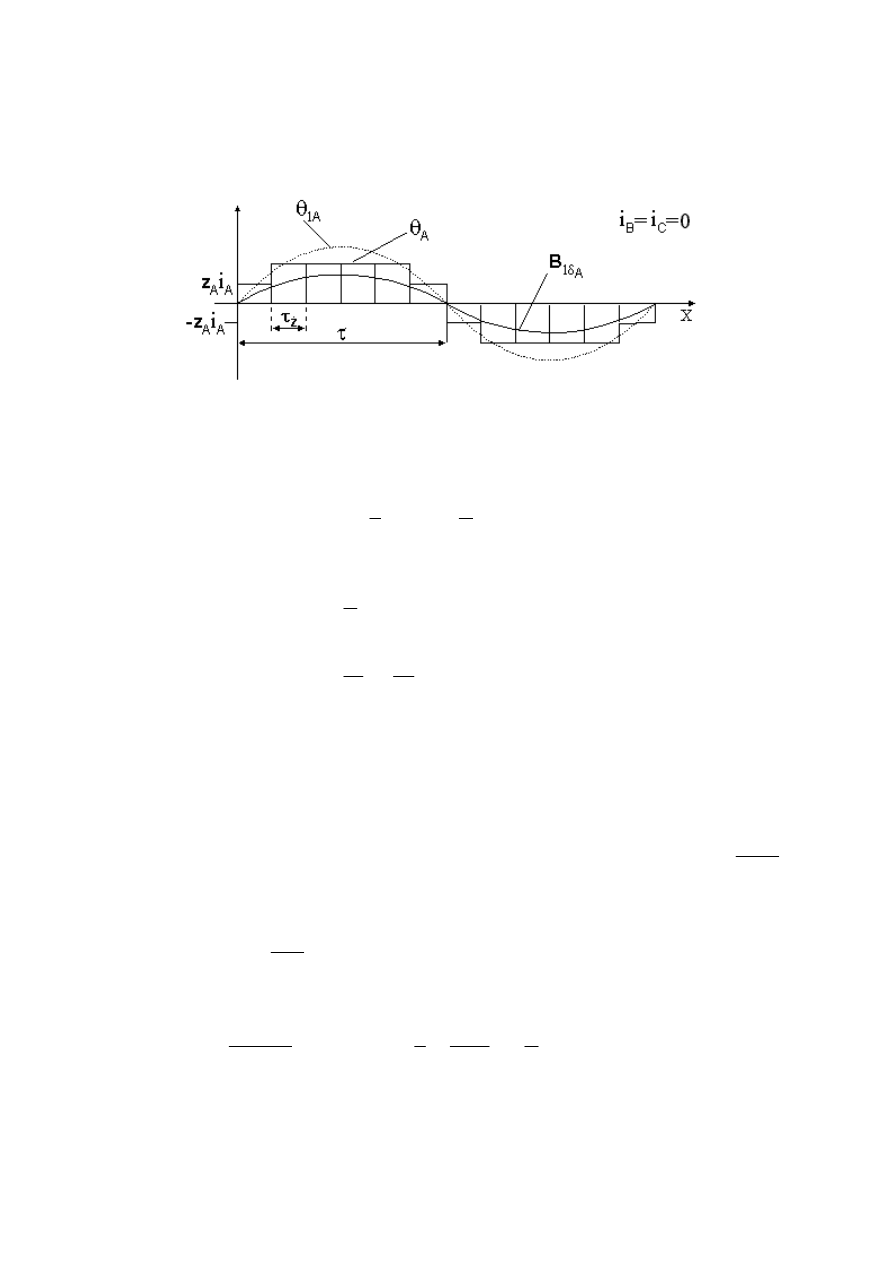
półokresie
τ. W rozkładzie tym występują także wyższe harmoniczne pola wzmocnione
jeszcze bardziej otwarciem żłobków stojana i wirnika. Wyższe harmoniczne pola produkują
pasożytnicze momenty maszyny.
Rys. 4. Siła magnetomotoryczna i indukcja w szczelinie powietrznej dla fazy a silnika.
Wypadkowy przepływ od trzech uzwojeń o rozłożeniu sinusoidalnym przesuniętych w
przestrzeni względem siebie o kąt elektryczny 2
π/3 i zasilonych sinusoidalnymi prądami
przesuniętymi w czasie o kąt 2
π/3 jest określony:
)
t
x
cos(
)
t
,
x
(
Am
s
1
1
2
3
ω
τ
π
−
Θ
=
Θ
(2)
Jest to fala poruszająca się wzdłuż obwodu stojana z prędkością liniową
ν
s
wyznaczoną z
warunku:
0
1
=
− t
x
ω
τ
π
(3)
Po zróżniczkowaniu otrzymamy ostatecznie:
1
1
2 f
dt
dx
τ
π
ω
τ
=
=
(4)
gdzie
δ
s
jest zastępczą grubością szczeliny powietrznej uwzględniającą żłobkowanie wirnika i
stojana, nasycenie obwodu magnetycznego.
Tak więc, trójfazowe uzwojenie stojana wytwarza biegnące w szczelinie powietrznej
pole magnetyczne o liniowej prędkości synchronicznej
1
2 f
s
τ
υ =
. Prędkość ta jest związana
z prędkością kątową ruchu obrotowego poprzez promień otworu stojana r:
r
f
s
1
2
τ
ω =
.
Uwzględniając, że
b
p
r
D
2
2
τ
π =
=
prędkość kątowa synchroniczna pola jest określona
zależnością:
b
s
p
f
1
2
π
ω =
1
1
2
f
π
ω =
m
I
1
1
z
(5)
Przy założeniu jednakowej szczeliny powietrznej wzdłuż obwodu (przy zerowym
prądzie wirnika) indukcja magnetyczna w szczelinie jest określona wzorem
s
s
o
)
t
,
x
(
)
t
,
x
(
B
δ
µ
δ
Θ
≈
)
t
x
cos(
I
z
)
t,
x
(
B
s
m
o
1
1
1
2
3
ω
τ
π
δ
µ
δ
−
≈
(6)

1.1
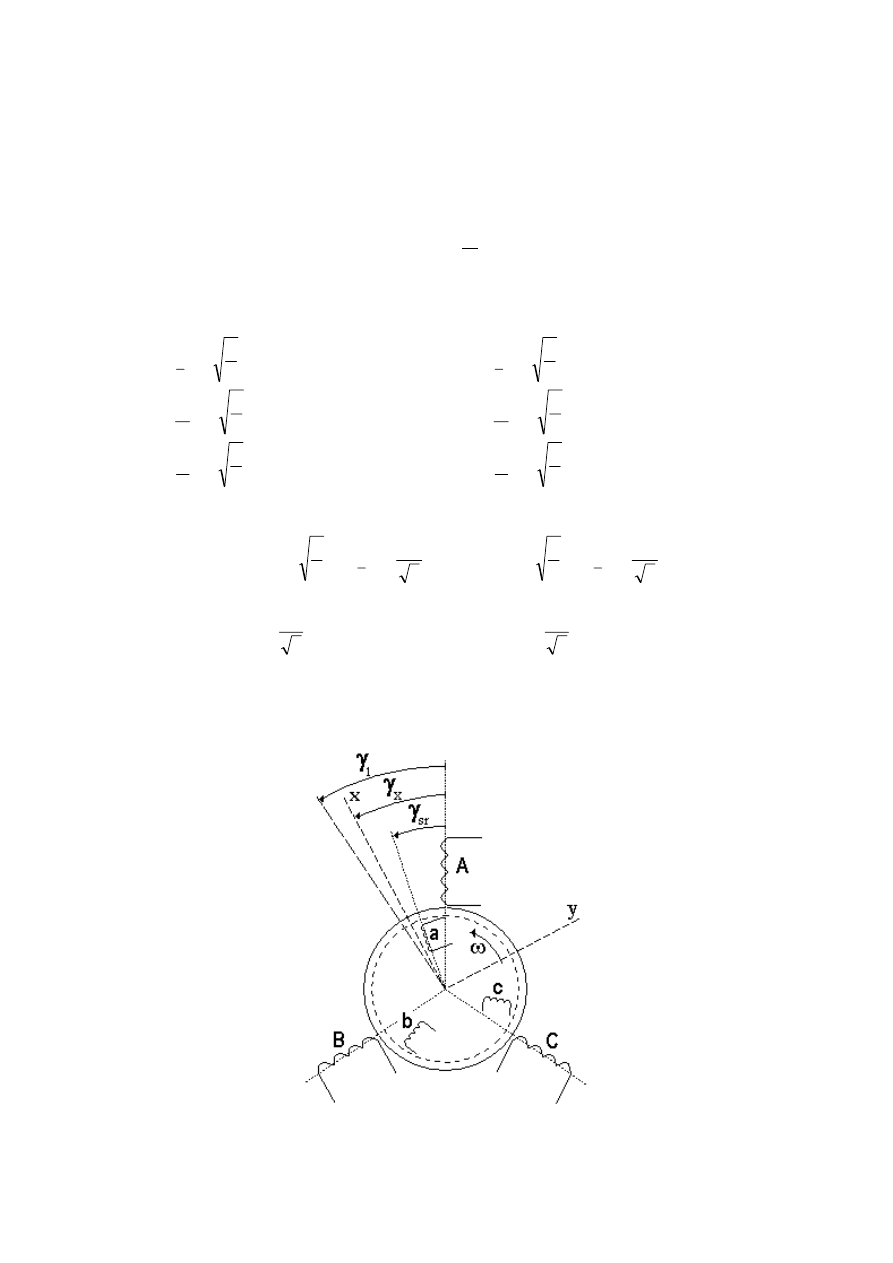
Model maszyny we współrzędnych fazowych
Na rysunku 3 przedstawiono schematycznie układ faz trójfazowej maszyny indukcyjnej z
uzwojonym wirnikiem. Rozłożone pasma fazowe są przedstawione za pomocą skupionych
cewek, których indukcyjności własne nie zależą od położenia wirnika. Indukcyjności te
zawierają część główną
r
s
L
,
L
δ
δ
, która jest związana ze strumieniem głównym w szczelinie
obejmującym zezwoje odpowiednich pasm fazowych stojana i wirnika oraz rozproszenia
r
s
L
,
L
σ
σ
, które związane są ze strumieniami rozproszenia zamykającymi się w żłobkach, w
obszarze (przeważnie w powietrzu) od połączeń czołowych tylko pojedynczego pasma
fazowego.
Rys. 3. Trójfazowa maszyna indukcyjna.
Przy założeniu, że rozkład indukcji magnetycznej w szczelinie powietrznej oraz okładu
prądu wzdłuż obwodu maszyny każdej fazy są sinusoidalne to indukcyjności wzajemne
pomiędzy poszczególnymi fazami są funkcjami cosinusa kąta elektrycznego zawartego
między osiami dwóch uzwojeń.
Indukcyjności wzajemne pomiędzy poszczególnymi fazami stojana i wirnika zależą od
elektrycznego kąta położenia wirnika
m
b
sr
p
γ
γ =
Indukcyjności te tworzą tzw. macierz indukcyjności
[
]
)
(
sr
γ
L
:
[
]
=
c
cb
ca
cC
cB
cA
bc
b
ba
bC
bB
bA
ac
ab
a
aC
aB
aA
Cc
Cb
Ca
C
CB
CA
Bc
Bb
Ba
BC
B
BA
Ac
Ab
Aa
AC
AB
A
sr
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
)
(
γ
L
(1)
gdzie:
s
s
C
B
A
L
L
L
L
L
σ
δ
+
=
=
=
,
r
r
c
b
a
L
L
L
L
L
σ
δ
+
=
=
=
sr
sr
cC
Cc
bB
Bb
aA
Aa
cos
Lˆ
L
L
L
L
L
L
γ
δ
=
=
=
=
=
=
)
cos(
Lˆ
L
L
L
L
L
L
sr
sr
aC
Ca
cB
Bc
bA
Ab
3
2
π
γ
δ
−
=
=
=
=
=
=

)
cos(
Lˆ
L
L
L
L
L
L
sr
sr
bC
Cb
aB
Ba
cA
Ac
3
2
π
γ
δ
+
=
=
=
=
=
=
r
s
sr
L
L
Lˆ
δ
δ
δ
=
ż
s
ż
s
CA
BC
AB
M
L
M
cos
L
L
L
L
+
−
=
+
=
=
=
2
3
2
δ
δ
π
żr
r
żr
r
ca
bc
ab
M
L
M
cos
L
L
L
L
+
−
=
+
=
=
=
2
3
2
δ
δ
π
oraz:
żr
ż
M
,
M
- indukcyjność wzajemna (wartość ujemna) związana ze wspólnym strumieniem
rozproszenia żłobkowego między sąsiednimi pasmami fazowymi odpowiednio stojana i wirnika; dla
uzwojeń dwuwarstwowych o skróconym poskoku (dla uzwojeń średnicowych
0
=
żr
ż
M
,
M
).
Równania stanu elektromagnetycznego maszyny indukcyjnej, po sprowadzeniu strony
wtórnej na pierwotną, w zapisie macierzowym przyjmują postać:
[ ] [ ] [ ]
[ ]
Ψ
i
r
U
dt
d
+
⋅
=
(2a)
[ ] [
] [ ]
i
L
Ψ
⋅
=
)
(
sr
γ
(2b)
przy czym:
[ ]
[
]
T
c
b
a
C
B
A
U
,
U
,
U
,
U
,
U
,
U
•
•
•
=
U
;
[ ]
[
]
T
c
b
a
C
B
A
i
,
i
,
i
,
i
,
i
,
i
•
•
•
=
i
;
[ ]
[
]
•
•
•
=
c
b
a
C
B
A
r
,
r
,
r
,
r
,
r
,
r
diag
r
Moc elektromagnetyczna
e
P :
[ ]
[
] [ ]
ω
γ
γ
ω
⋅
⋅
⋅
⋅
=
⋅
=
i
L
i
sr
sr
T
m
e
e
d
)
(
d
M
P
2
1
(3)
oraz wynikający z niej moment elektromagnetyczny:
[ ]
[
] [ ]
i
L
i
⋅
⋅
⋅
⋅
=
sr
sr
T
b
e
d
)
(
d
p
M
γ
γ
2
1
(4)
gdzie:
m
b
sr
p
dt
d
ω
ω
γ
=
=
,
m
ω
(
30
n
m
⋅
=
π
ω
) – odpowiednio elektryczna, mechaniczna prędkość
kątowa wirnika.
Z równania (4) wynika, że moment elektromagnetyczny powstaje w maszynie
elektrycznej, gdy co najmniej jeden element macierzy indukcyjności zależy od kąta położenia
wirnika. W symetrycznej maszynie asynchronicznej są to indukcyjności wzajemne między
stojanem i wirnikiem, w symetrycznej maszynie synchronicznej z biegunami wydatnymi –
indukcyjności wzajemne między uzwojeniami stojana a wirnika oraz indukcyjności własne
uzwojenia twornika, a w maszynie synchronicznej reluktancyjnej z wirnikiem nieuzwojonym
– tylko indukcyjności własne i wzajemne uzwojeń stojana.
Równania te uzupełnione równaniem ruchu dla stanu elektromechanicznego (przy stałym
momencie bezwładności J):
dt
d
p
J
M
M
b
st
e
ω
=
−
(5)
rozwiązują stan elektrodynamiczny maszyny. Równanie na moment elektromagnetyczny (4)
wiąże równania stanów: elektromagnetycznego i mechanicznego.
Przy znanym przebiegu prędkości obrotowej maszyny układ ten jest układem równań
liniowych, a przy prędkości stałej układem równań o współczynnikach okresowo zmiennych
w czasie. Jeżeli prędkość obrotowa wynika z równań stanu elektrodynamicznego, to wówczas
równania różniczkowe są nieliniowe (nieliniowość strukturalna). Rozwiązanie tego układu
równań, o zmiennych współczynnikach (indukcyjności są funkcją kąta położenia wirnika),
jest możliwe z użyciem metod numerycznych i jest stosowane w szczególnych przypadkach
analizy stanów nieustalonych napędów indukcyjnych.
1.2 Model maszyny we współrzędnych dwuosiowych
Wprowadźmy jednostkowy wektor obrotu
3
2
π
j
e
a
=
.
Fazory przestrzenne prądów, strumieni skojarzonych, napięć stojana i wirnika, przy założeniu
ortogonalności transformacji układu współrzędnych, określimy jako wektory zespolone
postaci:
(
)
C
B
A
s
i
a
i
a
i
I
⋅
+
⋅
+
=
2
3
2
oraz
(
)
•
•
•
•
⋅
+
⋅
+
=
c
b
a
r
i
a
i
a
i
I
2
3
2
(5a)
(
)
C
B
A
s
a
a
ψ
ψ
ψ
⋅
+
⋅
+
=
Ψ
2
3
2
oraz
(
)
•
•
•
•
⋅
+
⋅
+
=
Ψ
c
b
a
r
a
a
ψ
ψ
ψ
2
3
2
(5b)
(
)
C
B
A
s
u
a
u
a
u
U
⋅
+
⋅
+
=
2
3
2
oraz
(
)
•
•
•
•
⋅
+
⋅
+
=
c
b
a
r
u
a
u
a
u
U
2
3
2
(5c)
Dla przekształcenia odwrotnego zależności np. prądy dla fazy A stojana i fazy a wirnika są
określone następująco:
[ ]
3
3
2
0
s
s
A
I
I
Re
i
+
⋅
=
oraz
[ ]
3
3
2
0
•
•
•
+
⋅
=
r
r
a
I
I
Re
i
, (6)
gdzie prądy składowej zerowej zapewniające izomorfizm przekształcenia są określone:
(
)
C
B
A
s
i
i
i
I
+
+
=
3
1
0
oraz
(
)
•
•
•
•
+
+
=
c
b
a
r
i
i
i
I
3
1
0
(7)
W przypadku maszyny symetrycznej i przy połączeniu uzwojeń w gwiazdę bez przewodu
zerowego prądy składowej zerowej są równe zeru.
Rys. 4. Trójfazowa maszyna indukcyjna.
Należy zauważyć, że w nowym układzie współrzędnych, wszystkie fazory stojana i
wirnika wirują z tą samą prędkością (w stanie ustalonym pracy z prędkością
(
)
x
ω
ω −
1
, gdzie
1
ω -prędkość pola,
x
ω -prędkość nowego układu współrzędnych). Nowy układ współrzędnych
wiruje z kolei względem starych układów odpowiednio z prędkościami:
x
ω oraz
(
)
ω
ω −
x
.
Stan elektromagnetyczny:
1
1
1
1
1
1
1
1
I
r
E
j
dt
d
I
r
U
x
⋅
+
=
Ψ
+
Ψ
+
⋅
=
ω
(11a)
(
)
•
•
•
•
•
•
•
•
⋅
+
=
Ψ
−
+
Ψ
+
⋅
=
2
2
2
2
2
2
2
2
I
r
E
j
dt
d
I
r
U
x
ω
ω
(11b)
•
⋅
+
⋅
=
Ψ
2
1
1
1
I
L
I
L
µ
(11c)
1
2
2
2
I
L
I
L
⋅
+
⋅
=
Ψ
•
•
•
µ
(11d)
gdzie:
1
1
1
1
1
2
3
ż
s
ż
M
L
L
M
L
L
L
−
+
=
−
+
=
σ
δ
σ
µ
,
•
•
•
•
•
−
+
=
−
+
=
2
2
2
2
2
2
3
ż
s
ż
M
L
L
M
L
L
L
σ
δ
σ
µ
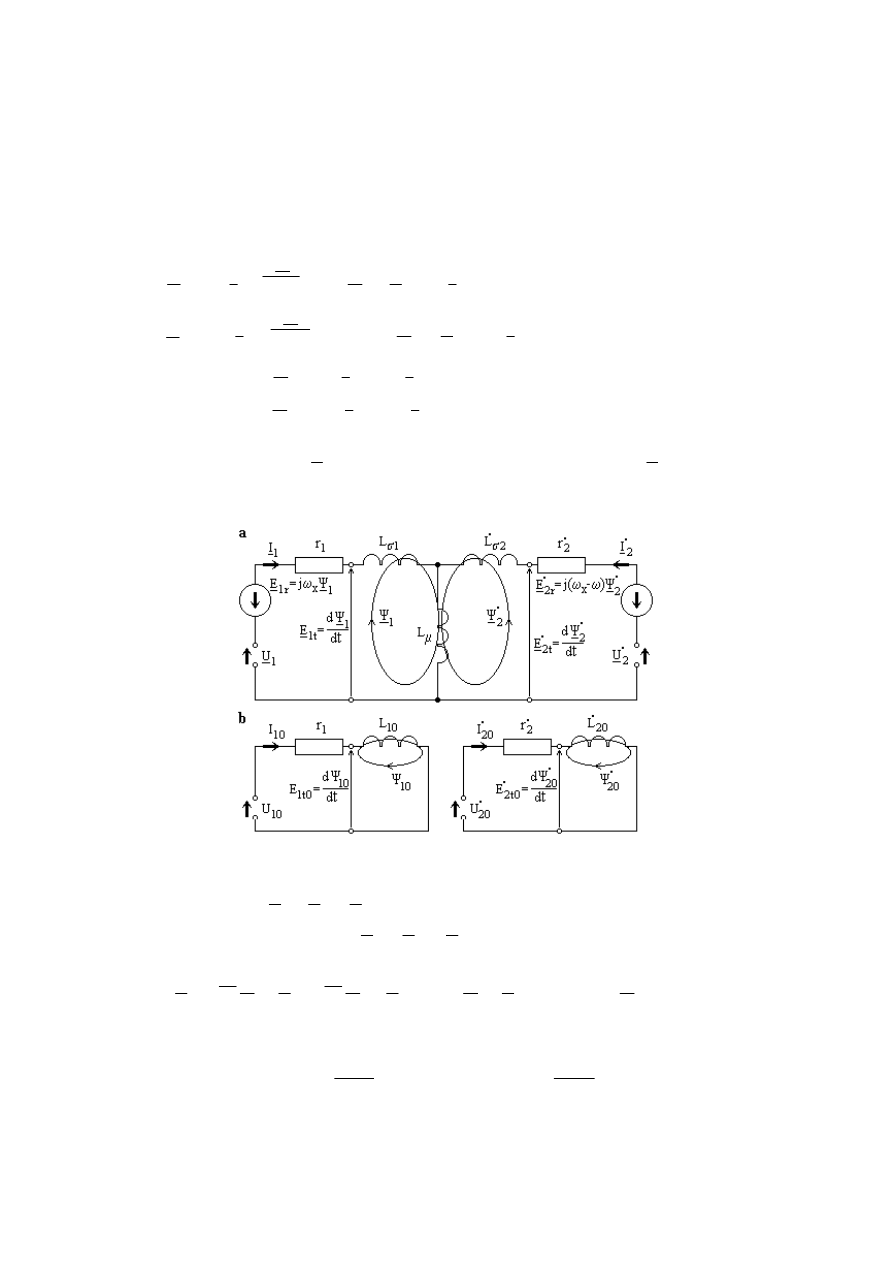
Równaniom (11) odpowiada schemat zastępczy na rys. 5a.
Rys. 5. Schemat zastępczy maszyny indukcyjnej
W równaniach (11):
r
t
E
E
E
1
1
1
+
=
- oznacza napięcie indukowane w stojanie złożone z
napięcia transformacji i rotacji;
•
•
•
+
=
r
t
E
E
E
2
2
2
- odpowiednio napięcie indukowane w
wirniku:
(
)
•
•
•
•
Ψ
−
=
Ψ
=
Ψ
=
Ψ
=
2
2
1
1
2
2
1
1
,
,
,
ω
ω
ω
x
r
x
r
t
t
j
E
j
E
dt
d
E
dt
d
E
(12)
Dla składowych zerowych obowiązują oddzielne równania:
dt
d
I
r
U
10
10
1
10
Ψ
+
⋅
=
,
dt
d
I
r
U
•
•
•
•
Ψ
+
⋅
=
20
20
2
20
(13)
Schemat zastępczy dla składowej zerowej (rys. 5b) łączy zależność między strumieniem
skojarzonym, prądem i napięciem składowych zerowych. Wynika z niego, że trójprzewodowe

zasilanie uzwojeń bez przewodu neutralnego powoduje zerowanie prądu, a w konsekwencji
strumienia i napięcia składowej zerowej.
W równaniach stanu elektromagnetycznego (11) wyrażonych na płaszczyźnie liczb
zespolonych x,y (rys. 4), wirującej z arbitralną prędkością
x
ω , można wyróżnić operator
indukowania napięcia w obwodzie wirnika określonego w dziedzinie czasowej przez
(
)
ω
ω −
+
=
x
t
j
dt
d
D
. Wtedy równania te przyjmą postać:
(
)
1
1
1
1
Ψ
+
+
⋅
=
ω
j
D
I
r
U
t
(14a)
•
•
•
•
Ψ
+
⋅
=
2
2
2
2
t
D
I
r
U
(14b)
Z uwagi na arbitralne przyjęcie prędkości wirowania układu x,y rozłożenie napięcia
indukowanego na napięcie rotacji i transformacji ma znaczenie czysto formalne i wynika to ze
względnego odczuwania napięcia indukowanego przez obserwatora związanego z przyjętym
układem odniesienia, którym jest płaszczyzna liczb zespolonych x,y wirująca z prędkością
x
ω .Przez dobór prędkości wirowania
x
ω można otrzymać różne postacie równań
napięciowo-prądowych (11,13) i odpowiednio schematy zastępcze:
- przy
ω
ω =
x
znika napięcie rotacji w wirniku, co odpowiada transformacji „na
płaszczyznę wirnika”, nazywanej transformacją A.L.E. Blondela - R.H. Park’a, oznaczaną
d,q,0
- przy 0
=
x
ω
znika napięcie rotacji w stojanie, co odpowiada transformacji „na płaszczyznę
stojana”, nazywanej transformacją E. Clark - H.C. Stanley’a, oznaczaną x,y
- przy
1
ω
ω =
x
dokonujemy transformacji „na płaszczyznę synchroniczną” oznaczaną
0
,
,
β
α
.
Przyjęcie płaszczyzny wirnika jako płaszczyzny odniesienia jest często preferowane w
analizie maszyny indukcyjnej ze względu na stosunkowo najprostszą relację wiążącą fazory
strumienia i prądu, korzystną w szczególności przy bardziej skomplikowanych schematach
zastępczych obwodów wirnika.
1.3 Moment elektromagnetyczny
Moment elektromagnetyczny (4) w zapisie fazorowym jest określony następująco:
(
)
Ψ
⋅
⋅
⋅
=
⋅
Ψ
⋅
⋅
=
∗
•
•
∗
2
2
1
1
I
j
Re
p
I
j
Re
p
M
b
b
e
(15a)
lub
(
)
⋅
Ψ
⋅
=
Ψ
⋅
⋅
=
∗
•
•
∗
2
2
1
1
I
Im
p
I
Im
p
M
b
b
e
(15b)
W zależnościach (15) przy uwzględnieniu (11c,d) można wyeliminować jedną z wielkości
Ψ
bądź I i otrzymać równoważne postacie wyrażenia na moment elektromagnetyczny:
(
)
(
)
∗
∗
Ψ
⋅
⋅
=
⋅
Ψ
⋅
⋅
=
1
1
1
1
I
Im
p
I
j
Re
p
M
b
b
e
(16a)
(
)
⋅
⋅
⋅
=
⋅
⋅
⋅
⋅
=
∗
•
∗
•
2
1
1
2
I
I
Im
L
p
I
I
j
Re
L
p
M
b
b
e
µ
µ
(16b)
(
)
Ψ
⋅
Ψ
⋅
⋅
⋅
⋅
=
Ψ
⋅
Ψ
⋅
⋅
⋅
⋅
⋅
=
∗
•
∗
•
2
1
2
1
1
2
2
1
Im
L
L
L
p
j
Re
L
L
L
p
M
b
b
e
σ
σ
µ
µ
(16c)
⋅
Ψ
⋅
=
Ψ
⋅
⋅
⋅
=
∗
•
•
∗
•
•
2
2
2
2
I
Im
p
I
j
Re
p
M
b
b
e
(16d)
(
)
⋅
Ψ
⋅
⋅
=
Ψ
⋅
⋅
⋅
⋅
=
∗
•
∗
•
2
1
1
1
2
1
I
Im
L
L
p
I
j
Re
L
L
p
M
b
b
e
µ
µ
(16e)
(
)
Ψ
⋅
⋅
⋅
=
⋅
Ψ
⋅
⋅
⋅
=
∗
•
∗
•
2
1
2
1
2
2
I
Im
L
L
p
I
j
Re
L
L
p
M
b
b
e
µ
µ
(16f)
gdzie:
2
1
2
1
L
L
L
µ
σ
−
=
. p
b
– liczba par biegunów
2 Równania stanu elektrodynamicznego maszyny indukcyjnej
Równania (11) opisują stan elektromagnetyczny maszyny. Równania te uzupełnione
równaniem ruchu dla stanu elektromechanicznego (przy stałym momencie bezwładności J):
dt
d
p
J
M
M
b
st
e
ω
=
−
(17)
rozwiązują stan elektrodynamiczny maszyny. Równanie na moment elektromagnetyczny (16)
wiąże równania stanów: elektromagnetycznego i mechanicznego.
Równania (11a,b;16) można zapisać w innej postaci wykorzystując dekompozycję
zespolonych fazorów przestrzennych na dwie składowe w płaszczyźnie zespolonej d,q
wirującej z prędkością
x
ω :
q
d
U
j
U
U
1
1
1
⋅
+
=
;
q
d
I
j
I
I
1
1
1
⋅
+
=
;
q
d
j
1
1
1
Ψ
⋅
+
Ψ
=
Ψ
(17a)
•
•
•
⋅
+
=
q
d
U
j
U
U
2
2
2
;
•
•
•
⋅
+
=
q
d
I
j
I
I
2
2
2
;
•
•
•
Ψ
⋅
+
Ψ
=
Ψ
q
d
j
2
2
2
(17b)
Uwzględniając zależności (17) w równaniach (11a,b;16) otrzymamy:
q
x
d
d
d
dt
d
I
r
U
1
1
1
1
1
Ψ
−
Ψ
+
⋅
=
ω
(18a)
d
x
q
q
q
dt
d
I
r
U
1
1
1
1
1
Ψ
+
Ψ
+
⋅
=
ω
(18b)
(
)
•
•
•
•
•
Ψ
−
−
Ψ
+
⋅
=
q
x
d
d
d
dt
d
I
r
U
2
2
2
2
2
ω
ω
(18c)
(
)
•
•
•
•
•
Ψ
−
+
Ψ
+
⋅
=
d
x
q
q
q
dt
d
I
r
U
2
2
2
2
2
ω
ω
(18d)
(
)
(
)
d
q
q
d
b
d
q
q
d
b
e
I
I
I
I
L
p
I
I
p
M
1
2
1
2
1
1
1
1
⋅
−
⋅
⋅
⋅
=
⋅
Ψ
−
⋅
Ψ
⋅
=
µ
(19)
Z definicji fazorów przestrzennych (5) oraz porównania (2) i (18) wynika transformacja
wielkości fazowych stojana i wirnika maszyny indukcyjnej do układu dwuosiowego:
9
dla wielkości stojana
[
]
⋅
=
C
B
A
x
q
d
u
u
u
)
(
P
U
U
U
γ
10
1
1
;
[
]
⋅
=
C
B
A
x
q
d
i
i
i
)
(
P
I
I
I
γ
10
1
1
;
[
]
⋅
=
Ψ
Ψ
Ψ
C
B
A
x
q
d
)
(
P
ψ
ψ
ψ
γ
10
1
1
(20a)
9
dla wielkości wirnika
[
]
⋅
′
=
•
•
•
•
•
•
c
b
a
x
q
d
u
u
u
)
(
P
U
U
U
γ
20
2
2
;
[
]
⋅
′
=
•
•
•
•
•
•
c
b
a
x
q
d
i
i
i
)
(
P
I
I
I
γ
20
2
2
;
[
]
⋅
′
=
Ψ
Ψ
Ψ
•
•
•
•
•
•
c
b
a
x
q
d
)
(
P
ψ
ψ
ψ
γ
20
2
2
(20b)

gdzie macierze transformacji:
[
]
( )
( )
+
−
−
−
−
+
−
⋅
=
2
1
2
1
2
1
3
2
3
2
3
2
3
2
3
2
π
γ
π
γ
γ
π
γ
π
γ
γ
γ
x
x
x
x
x
x
x
sin
sin
sin
cos
cos
cos
)
(
P
(21a)
[
]
(
)
(
)
+
−
−
−
−
−
−
−
+
−
−
−
−
⋅
=
′
2
1
2
1
2
1
3
2
3
2
3
2
3
2
3
2
π
γ
γ
π
γ
γ
γ
γ
π
γ
γ
π
γ
γ
γ
γ
γ
sr
x
sr
x
sr
x
sr
x
sr
x
sr
x
x
sin
sin
sin
cos
cos
cos
)
(
P
(21b)
przy czym:
dt
t
x
x
∫
=
0
ω
γ
,
(
) (
)
dt
t
x
sr
x
∫
−
=
−
0
ω
ω
γ
γ
Transformacja odwrotna ze względu na ortogonalność przekształcenia jest określona:
[
]
[
]
T
x
x
)
(
P
)
(
P
γ
γ
=
−1
oraz
[
]
[
]
T
x
x
)
(
P
)
(
P
γ
γ
′
=
′
−1
(22)
2.1 Model maszyny w stanie ustalonym
W układzie współrzędnych synchronicznych (
1
ω
ω =
x
), w stanie ustalonym wszystkie
fazory przestrzenne są wskazami nieruchomymi, co oznacza zerowanie pochodnych tych
wielkości. Stąd równania (11a,b) zapiszemy w postaci:
1
1
1
1
1
Ψ
⋅
+
⋅
=
ω
j
I
r
U
(26a)
2
2
2
2
2
1
2
2
2
Ψ
⋅
+
⋅
=
Ψ
⋅
+
⋅
=
ω
ω
j
I
r
s
j
I
r
U
(26b)
gdzie:
1
1
ω
ω
−
=
s
;
ω
ω
ω
−
=
1
2
Po wydzieleniu w równaniach (11c,d) prądu magnesującego otrzymamy:
µ
µ
σ
I
L
I
L
⋅
+
⋅
=
Ψ
1
1
1
;
µ
µ
σ
I
L
I
L
⋅
+
⋅
=
Ψ
2
2
2
,
2
1
I
I
I
+
=
µ
(26c)
Równania postaci (26) można również otrzymać w układzie współrzędnych
wirujących z dowolną prędkością
x
ω , jeśli przyjąć że w stanie ustalonym w równaniach
(11a,b)
(
)
x
j
dt
d
ω
ω −
=
1
. Tak więc forma równań stanu ustalonego nie zależy od prędkości
wirowania układu współrzędnych.
Równania (26) stanowią podstawę zbudowania klasycznego schematu dla stanu ustalonego
maszyny (rys. 8) dla fazorów przestrzennych.
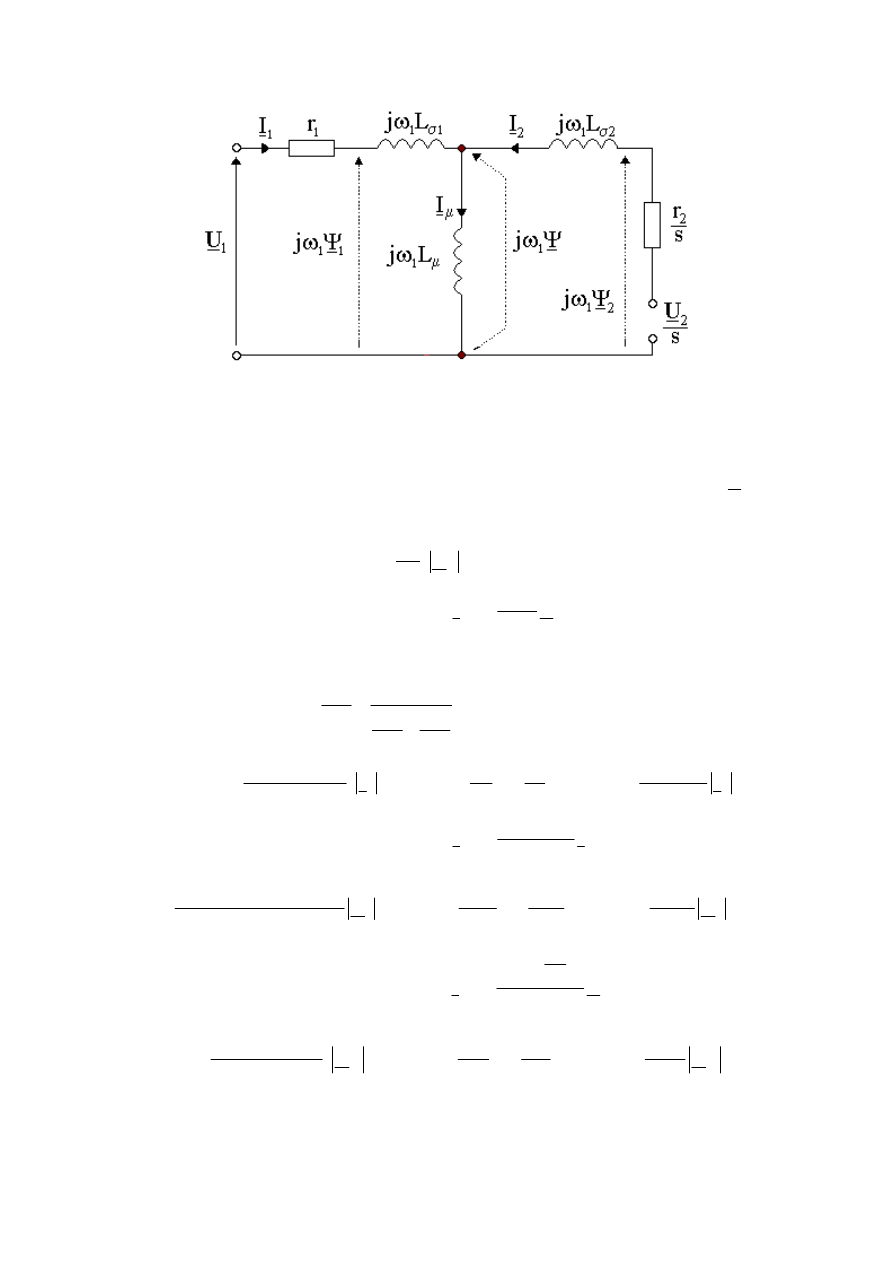
Rys. 8. Schemat zastępczy maszyny indukcyjnej dla stanu ustalonego dla fazorów przestrzennych
2.2 Charakterystyki elektromechaniczne maszyny indukcyjnej
Wykorzystując zależności 16 oraz relacje pomiędzy poszczególnymi wielkościami
elektromagnetycznymi wynikające ze schematu zastępczego (rys. 8), przy warunku
0
2
=
U
,
można otrzymać inne postacie momentu elektromagnetycznego:
9
2
2
2
2
Ψ
⋅
⋅
=
r
p
M
b
e
ω
(27)
(po wstawieniu w (16d) zależności na prąd
2
2
2
2
Ψ
⋅
−
=
r
j
I
ω
)
9
2
2
2
2
2
ω
ω
ω
ω
k
k
k
e
M
M
+
=
♦
(
)
2
1
2
2
2
2
2
2
2
2
I
L
r
r
L
p
M
b
e
⋅
+
⋅
⋅
=
ω
ω
µ
;
2
2
2
2
1
T
L
r
k
±
=
±
=
ω
;
(
)
2
1
1
2
1
I
L
p
M
b
k
σ
−
=
(28)
(po wstawieniu w (16b) zależności na prąd
1
2
2
2
2
2
I
L
j
r
L
j
I
ω
ω
µ
+
−
=
)
♦
(
)
(
)
[
]
2
1
2
2
2
2
2
2
1
2
2
2
1
Ψ
⋅
+
⋅
−
⋅
⋅
⋅
=
L
r
L
L
r
p
M
b
e
σ
ω
σ
ω
;
2
2
2
2
1
T
L
r
k
σ
σ
ω
±
=
±
=
;
2
1
1
2
1
Ψ
−
=
L
p
M
b
k
σ
σ
(29)
(po wstawieniu w (16e) zależności na prąd
1
2
2
2
1
2
2
Ψ
+
−
=
σ
ω
ω
µ
L
j
r
L
L
j
I
)
♦
(
)
2
2
2
2
2
2
2
2
µ
σ
ω
ω
Ψ
⋅
+
⋅
=
L
r
r
p
M
b
e
;
σ
σ
ω
2
2
2
2
1
T
L
r
k
±
=
±
=
;
2
2
2
1
µ
σ
Ψ
=
L
p
M
b
k
(30)
(po wstawieniu w (27) zależności na strumień
µ
σ
ω
Ψ
+
−
=
Ψ
2
2
2
2
2
L
j
r
r
, gdzie:
µ
µ
µ
I
L
⋅
=
Ψ
- strumień główny)
9
1
2
2
2
1
2
2
ω
ω
ω
ω
ω
ω
ω
ω
k
k
k
k
k
e
a
a
M
M
+
+
+
=
;
(
)
2
1
1
1
1
1
2
1
1
1
1
2
L
r
L
L
r
c
r
a
ω
σ
+
−
⋅
=
(
)
2
1
2
1
2
1
2
2
1
1
1
2
2
1
1
2
1
2
1
2
2
2
1
U
L
L
r
r
c
r
L
c
L
L
r
r
r
p
M
b
e
⋅
+
+
+
+
−
=
µ
σ
σ
σ
µ
ω
ω
ω
ω
ω
ω
ω
(
)
2
2
1
1
2
2
2
1
1
2
1
1
1
2
1
2
1
1
c
σ
σ
µ
σ
ω
ω
ω
L
c
L
L
L
r
L
r
r
k
+
+
+
+
⋅
±
=
(31)
(
)
1
1
1
2
2
1
1
1
2
2
1
1
2
1
2
2
2
1
1
1
1
2
1
1
1
+
+
+
+
±
−
=
L
r
L
c
L
L
L
r
L
L
r
U
c
p
M
b
kg
ks
ω
ω
ω
σ
σ
µ
σ
σ
(po uwzględnieniu w (27) zależności pomiędzy fazorami
1
U i
2
Ψ
(
)
+
+
+
+
−
⋅
Ψ
=
µ
σ
σ
σ
µ
ω
ω
ω
ω
ω
ω
ω
L
L
r
r
c
r
j
L
c
L
L
r
r
r
U
1
2
1
2
2
1
1
1
2
1
1
2
1
2
1
2
1
2
2
1
;
µ
σ
L
L
c
1
1
1
+
=
)
Uwzględniając w (31)
0
2
1
1
1
1
≈
µ
σ
σ
µ
ω
L
L
;
L
L
;
L
r
otrzymamy znane wyrażenie na moment
elektromagnetyczny maszyny indukcyjnej:
(
)
2
1
2
2
1
1
2
2
2
1
1
1
2
2
2
1
U
L
c
L
r
c
r
r
p
M
b
e
⋅
+
+
+
=
σ
σ
ω
ω
ω
ω
(32a)
Pulsacja krytyczna oraz krytyczny moment elektromagnetyczny wynoszą odpowiednio:
(
)
(
)
2
2
1
1
1
1
2
2
2
1
1
2
1
1
2
1
2
1
1
1
c
+
+
±
=
+
+
±
=
σ
σ
σ
σ
ω
σ
ω
ω
L
c
L
r
T
L
c
L
r
r
k
(32b)
(
)
+
+
±
=
2
2
1
1
2
1
2
1
1
1
2
1
1
2
σ
σ
ω
ω
L
c
L
r
r
c
U
p
M
b
kg
ks
(32c)
Podstawiając za
u
uˆ
U
3
2
3
1
=
=
(u – wartość skuteczna napięcia fazowego)
przedstawimy wyrażenia (31,32) w zależności od wartości skutecznej napięcia fazowego.
Przy pominięciu rezystancji stojana (
0
1
=
r
) równania (31) przyjmą postać równań (29),
przy czym należy uwzględnić:
2
1
2
1
1
L
c
L
c
L
σ
σ
σ
=
+
Poślizgową charakterystykę momentu elektromagnetycznego (31) silnika indukcyjnego
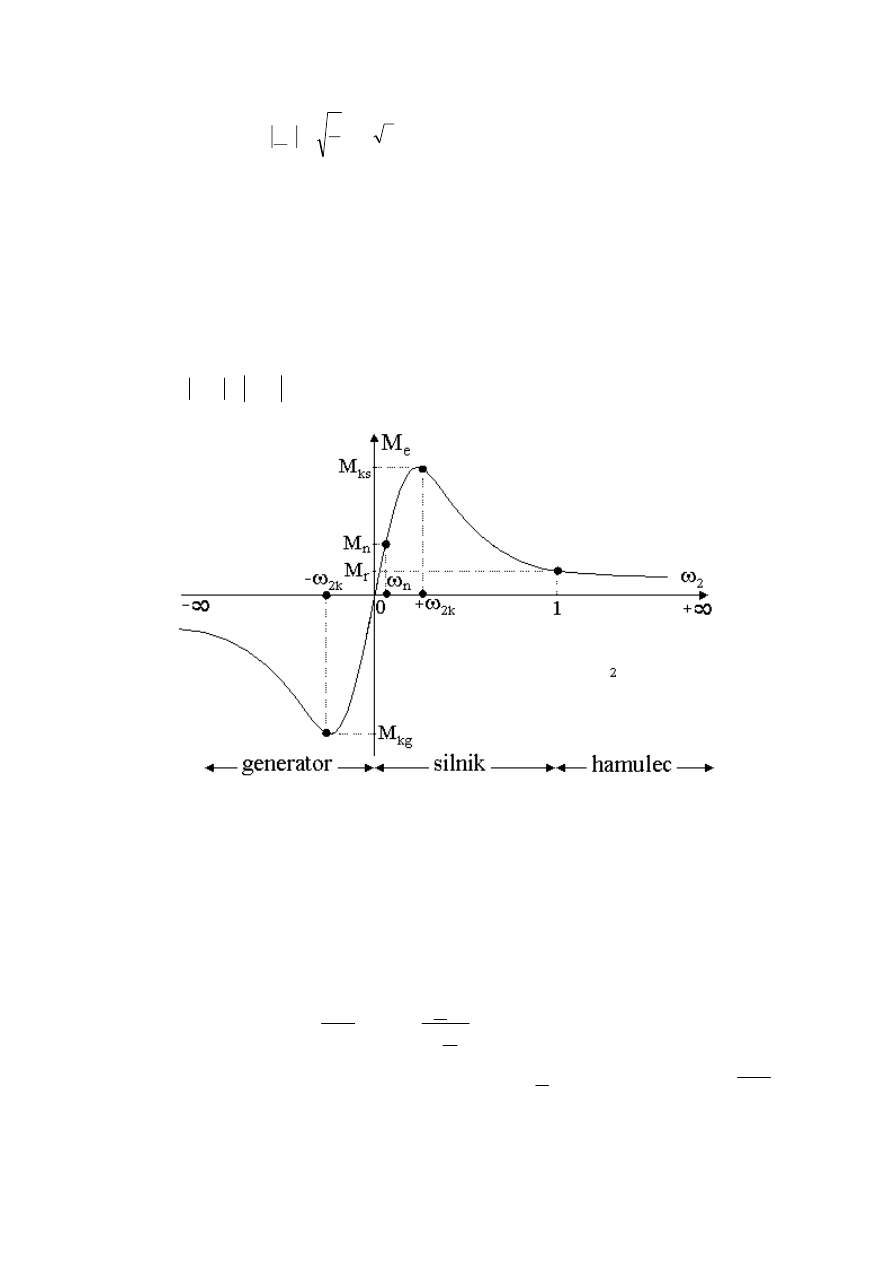
przy stałym napięciu i częstotliwości zasilania pokazano na rysunku 11. Przy pulsacjach
krytycznych (
k
k
,
2
2
ω
ω
−
+
) występują maksymalne wartości momentu elektromagnetycznego
(moment krytyczny:
0
0
<
>
kg
ks
M
,
M
) odpowiednio dla pracy silnikowej i generatorowej,
przy czym
kg
ks
M
M
<
.
Rys. 9. Poślizgowa charakterystyka momentu elektromagnetycznego silnika indukcyjnego przy stałym
napięciu i częstotliwości zasilania
3 Sposoby regulacji prędkości
W wielu zastosowaniach wymagana jest regulacja prędkości silnika indukcyjnego.
Regulacja ta powinna jednocześnie zapewniać wysoką sprawność przetwarzania mocy
elektrycznej w mechaniczną.
Prędkość idealnego biegu jałowego silnika indukcyjnego jest określona wzorem:
2
1
2
1
2
1
,
1
2
ω
ω
ω
ω
π
ω
+
=
Ψ
ℑ
+
=
U
m
p
f
b
o
(37)
Dla silników klatkowych napięcie źródła zasilania wirnika
0
2
=
U
, co implikuje
p
f
o
1
2
π
ω =
.
Zgodnie z równaniem (37) mamy trzy sposoby regulacji prędkości kątowej silników
indukcyjnych:

• zmiana częstotliwości zasilania stojana f
1
• zmiana liczby par biegunów
b
p
• zasilanie wirnika silnika pierścieniowego (
0
2
≠
U
) lub zmiana częstotliwości prądów
wirnika f
2
Podczas gdy zmiana liczby par biegunów wymaga specjalnego uzwojenia Dahlander’a , to
dwie pozostałe metody wymagają zmiany częstotliwości i modułu napięcia uzyskiwanych
poprzez stosowanie przekształtników zasilających stojan lub wirnik.
Generalnie istnieje wiele metod określających relacje pomiędzy napięciem
1
U lub prądem
1
I (
µ
I
) a częstotliwością
1
f dla zapewnienia żądanej jakości sterowania.
Jednak w zasadzie tylko trzy metody są stosowane w praktyce:
•
1
1
f
U
- sterowanie skalarne;
• sterowanie przy stałym strumieniu stojana
1
Ψ lub wirnika
2
Ψ - sterowanie
wektorowe;
• bezpośrednie sterowanie momentem i strumieniem.
4 Sterowanie skalarne
W sterowaniu skalarnym zmianom częstotliwości towarzyszą odpowiednie zmiany
napięcia lub prądu stojana prowadzące w sposób pośredni lub bezpośredni do stabilizacji
strumienia głównego, stojana lub wirnika. Dla każdej z tych metod istnieją algorytmy
sterowania wyprowadzone w oparciu o znajomość charakterystyk momentu
elektromagnetycznego krytycznego oraz poślizgu krytycznego w funkcji częstotliwości
napięcia (lub prądu) stojana.
Sterowanie skalarne stosowane jest przeważnie do napędów o małych wymaganiach
dynamicznych, względnie w przypadkach zasilania wspólnego grupowego silników o różnym
stanie obciążenia. Przy zasilaniu indywidualnym z reguły stosuje się sterowanie wektorowe.
Wśród metod sterowania skalarnego ze stabilizacją strumienia stojana lub wirnika można
wyróżnić:
- pośrednią metodę sterowania amplitudy strumienia skojarzonego stojana poprzez
zmianę amplitudy napięcia stojana,
- pośrednią metodę sterowania amplitudy strumienia skojarzonego stojana lub wirnika
poprzez zmianę amplitudy prądu stojana,
- bezpośrednią metodę sterowania amplitudy strumienia skojarzonego stojana (wirnika),
- sterowanie według określonej funkcji
( )
1
1
f f
U
=
4.1 Pośrednia metoda stabilizacji strumienia poprzez zmianę amplitudy napięcia
stojana
Algorytm sterowania
( )
1
1
f f
U
=
w tej metodzie można wyprowadzić na podstawie
wzorów na moment elektromagnetyczny dla wymuszenia od napięcia i strumienia stojana:
(
)
2
1
2
2
1
1
1
2
2
2
2
1
1
1
2
1
2
2
2
2
1
1
1
U
r
L
r
L
L
L
r
r
L
r
p
L
M
b
e
⋅
+
+
−
⋅
⋅
⋅
=
ω
ω
ω
σ
ω
ω
ω
µ
(
)
2
1
2
2
2
2
2
2
2
2
2
1
1
Ψ
⋅
+
⋅
⋅
⋅
=
L
r
L
r
p
L
M
b
e
ω
σ
ω
µ
Otrzymamy zasadę sterowania amplitudą napięcia:
(
)
1
2
2
2
2
2
2
2
1
1
1
2
2
2
2
1
1
1
2
1
1
1
Ψ
⋅
+
+
+
−
=
r
L
r
L
r
L
L
L
r
r
U
ω
σ
ω
ω
ω
σ
ω
ω
(38)
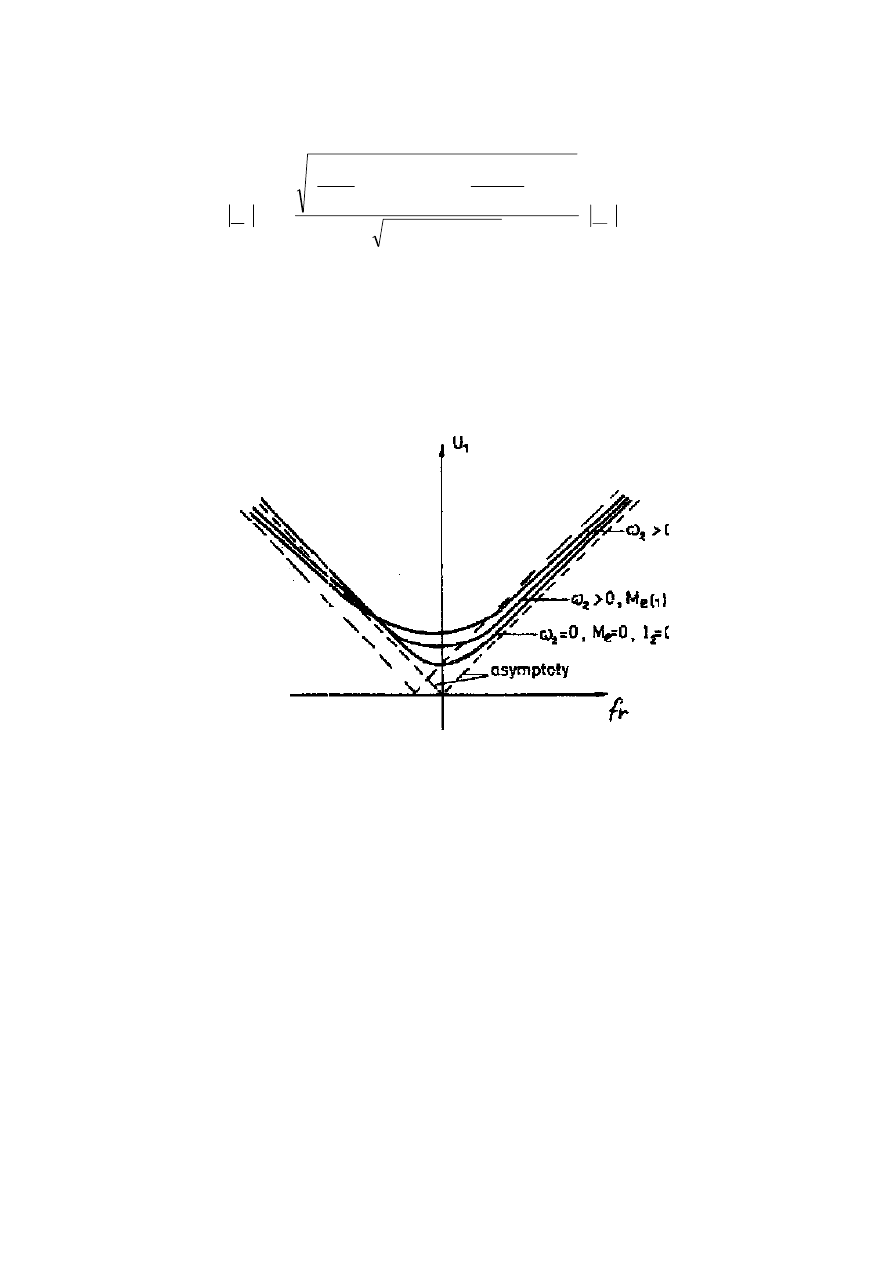
Sterowanie według zależności (38) zapewnia korekcję amplitudy napięcia stojana o
wartość spadku napięcia na rezystancji i reaktancji rozproszenia uzwojenia stojana. Ponadto
realizowana jest także kompensacja wpływu obciążenia silnika poprzez przesuwanie tych
charakterystyk w zależności od pulsacji
2
ω
niezbędnej do wytworzenia momentu
elektromagnetycznego
( )
ω
e
M
silnika. Konieczność przesuwania charakterystyk (rys. 13) jest
podstawową wadą i komplikuje układ sterowania (rys. 14).
Rys. 13. Charakterystyki
( )
1
1
f f
U
=
silnika indukcyjnego
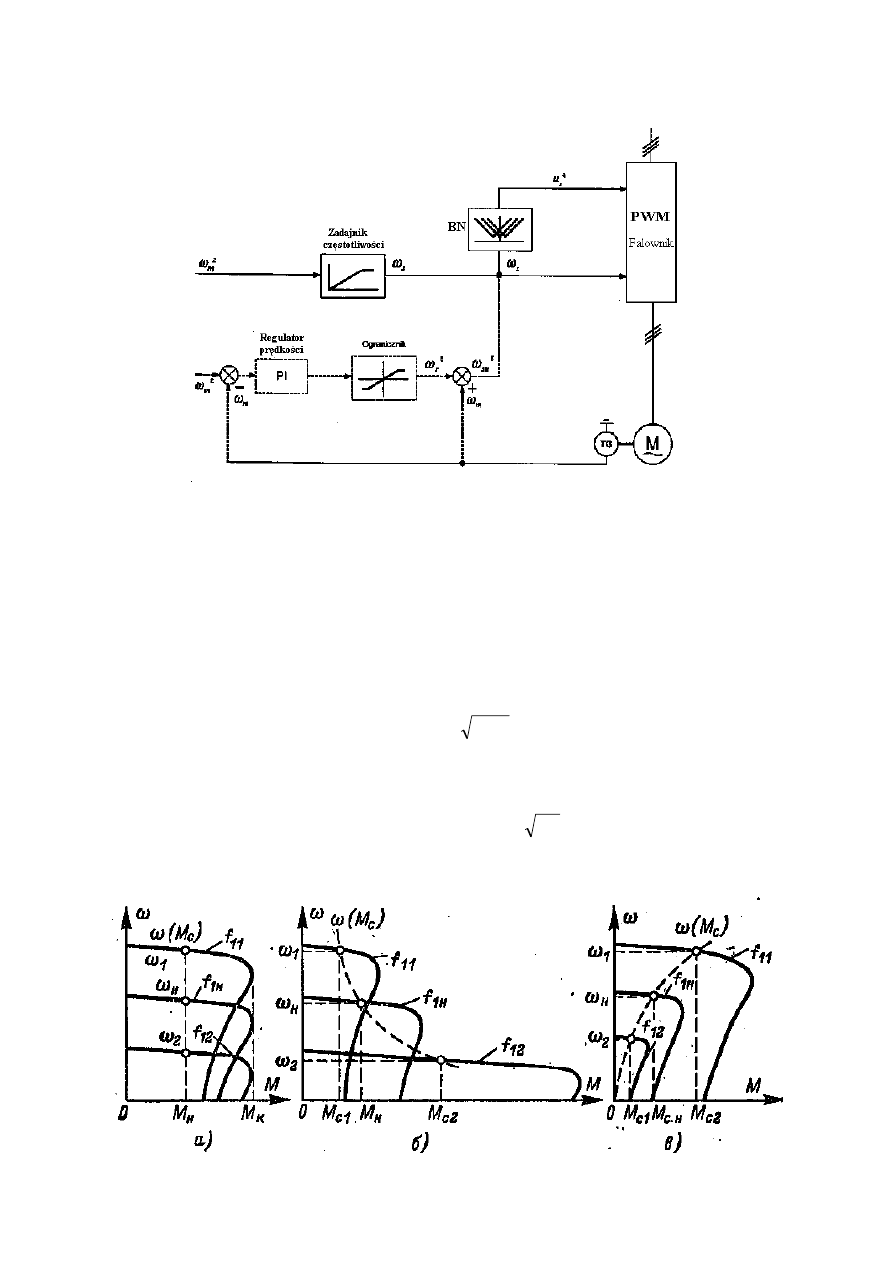
Rys. 14. Struktura sterowania
4.2 U
1
/f
1
– z warunku stałej przeciążalności
Przy wyborze relacji pomiędzy amplitudą a częstotliwością (pulsacją) napięcia
zasilającego stojan silnika indukcyjnego można wyjść z warunku jednakowej przeciążalności
λ silnika określonej jako stosunek momentu krytycznego
k
M do momentu obciążenia
st
M .
W takim przypadku, pomijając spadek napięcia na rezystancji stojana zasada
częstotliwościowej regulacji prędkości kątowej silnika indukcyjnego w jednostkach
względnych jest określona następująco:
∗
∗
∗
⋅
=
st
M
f
u
1
1
(40)
Uwzględniając w (40) charakterystyki mechaniczne mechanizmów stosowanych w praktyce
otrzymamy uproszczone zasady sterowania dla typowych obciążeń (rys. 16):
- dla obciążenia stałomomentowego:
∗
∗
=
1
1
f
u
(41a)
- dla obciążenia stałomocowego:
∗
∗
=
1
1
f
u
(41b)
- dla obciążenia wentylatorowego:
2
1
1
∗
∗
= f
u
(41c)
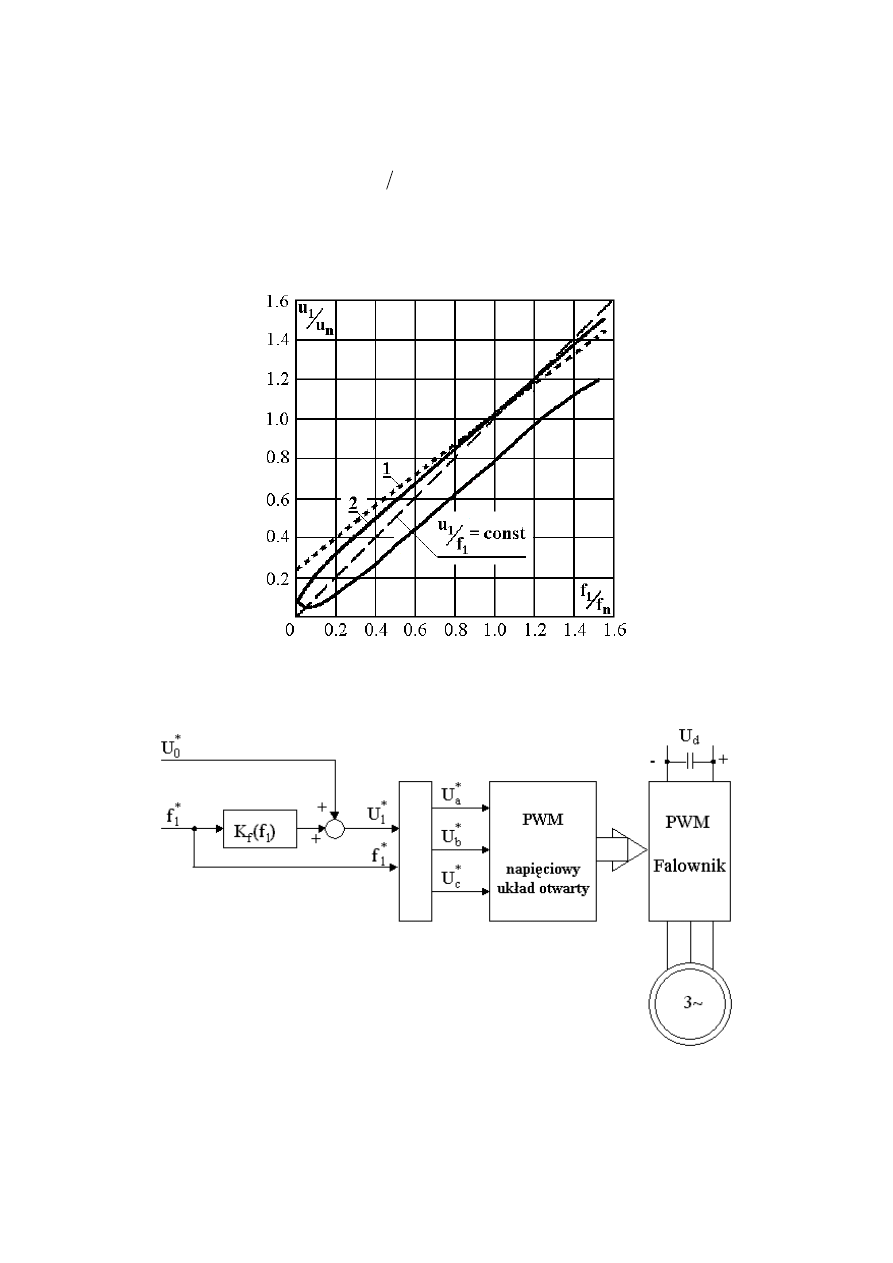
Rys. 16. Charakterystyki mechaniczne silnika indukcyjnego przy częstotliwościowej regulacji
prędkości.
W praktyce sterowanie skalarne
1
1
f
U
oznacza sterowanie według zależności:
1
1
f
K
U
U
f
o
+
=
(42)
0
U zwane napięciem kompensującym osiąga wartość kilku procent napięcia znamionowego,
wyższe wartości dla mniejszych mocy (rys. 17).
Rys. 17. Zmiana napięcia przy regulacji częstotliwościowej przy stałym momencie obciążenia
z zachowaniem stałej przeciążalności: 1 - silnik 50 W, 2 – silnik 14 kW
Rys. 21. Układ otwarty sterowania skalarnego U
1
/f
1
.
Powyżej prędkości znamionowej napięcie zasilające pozostaje stałe (równe
znamionowemu), a moment krytyczny ulega zmniejszeniu przy zachowaniu warunku stałej
mocy (rys. 15).
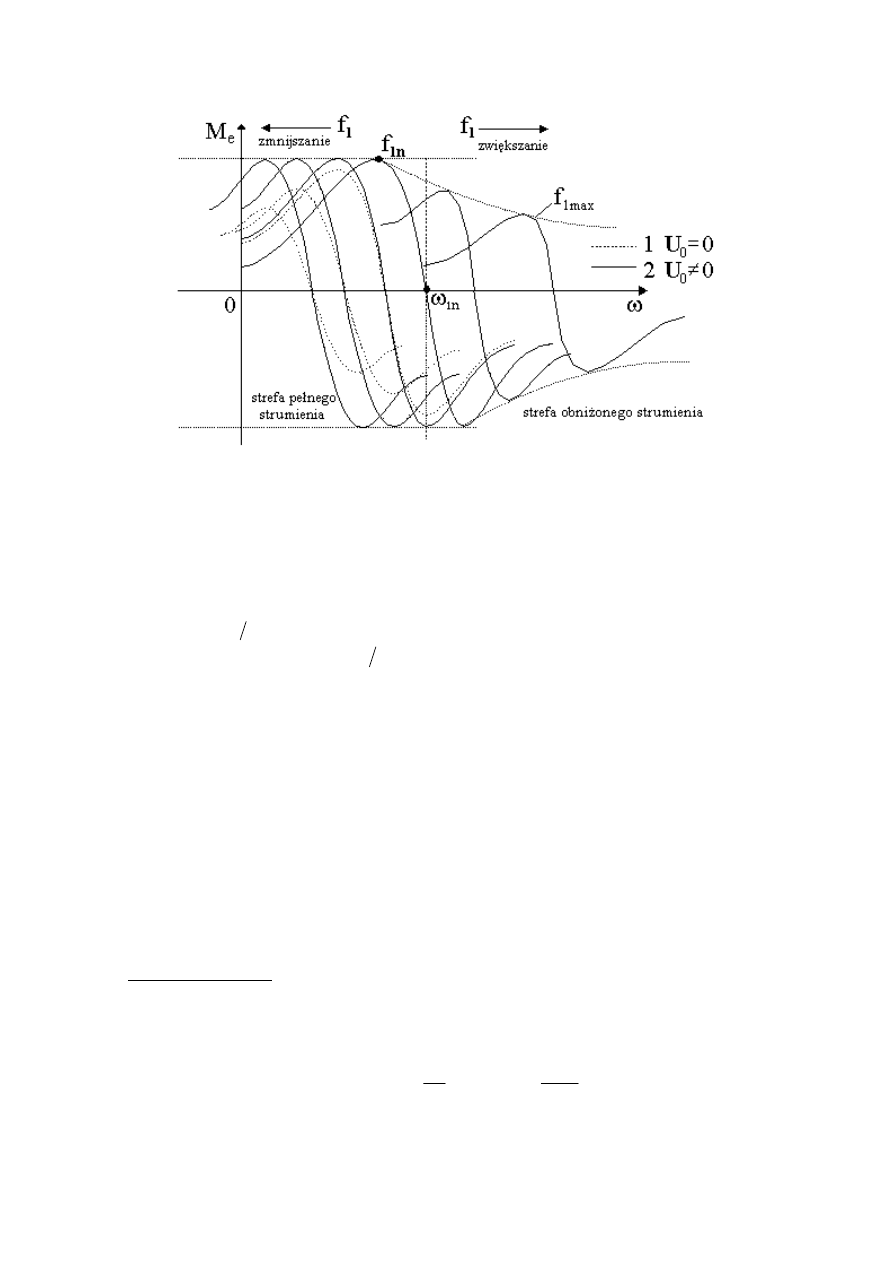
Rys. 15. Charakterystyki mechaniczne dla sterowania U
1
/f
1.
W tego typu układach, dla zachowania stabilności układu, zmiana częstotliwości odbywa
się stosunkowo wolno. Większe skłonności do niestabilnej pracy wykazują silniki
dwubiegunowe. Ponadto, wzrost momentu obciążenia powoduje spadek prędkości kątowej.
Temu ostatniemu można zapobiec stosując kompensancję częstotliwości poślizgu. Zasada
kompensacji poślizgu polega na wzroście wielkości zadanej o wyznaczoną dla danego
momentu obciążenia wartość częstotliwości poślizgu.
Sterowanie
1
1
f
U
jest stosowane w napędach o małych wymaganiach dynamicznych i
zakresie regulacji prędkości
15
3
÷
=
min
m
max
m
ω
ω
, tzn. napędach pomp, wentylatorów, dla
których moment obciążenia jest funkcją prędkości, co wpływa na kształtowanie napięcia
1
U
w funkcji częstotliwości
1
f w taki sposób, aby uzyskać maksymalną sprawność układu
napędowego. Stosowanie czujników ruchu jest zbyteczne.
5 Sterowanie wektorowe
5.1 Pośrednie odsprzęganie prądu.
W sterowaniu wektorowym zmiennymi wejściowymi są zadany strumień
z
µζ
Ψ
i zadany
moment
z
e
M . W konsekwencji maszyna indukcyjna jest układem dwu-wejściowym. Wartość
z
µζ
Ψ
jest stała albo jest funkcją prędkości lub momentu, w zależności od postawionego
kryterium optymalizacji dla danej aplikacji.
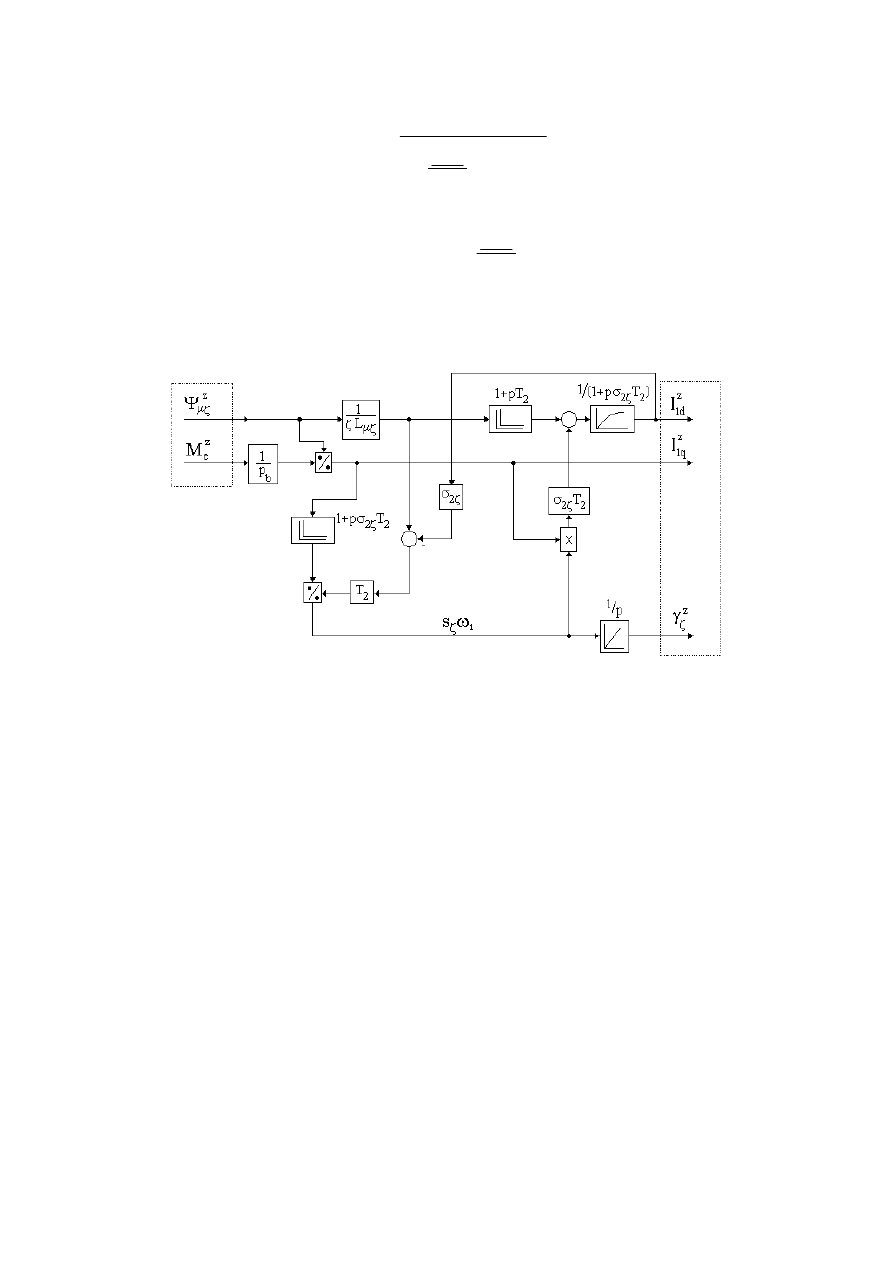
Odsprzężenie prądu polega więc na określeniu zadanych składowych fazora prądu stojana
z
q
z
d
I
,
I
1
1
prądu stojana bazując na zadanych wielkościach wejściowych. Wielkość zadana
prądu może być wielkością wyjściową zamkniętego układu regulacji prędkości lub położenia
lub żądaną wartością (zależną od prędkości lub czasu) w napędach trakcyjnych.
Oznaczając:
2
2
2
2
2
1
L
L
,
r
L
T
ζ
σ
µ
ζ
−
=
=
(87)
równanie (82b) z uwzględnieniem (84) i (87) można rozpisać:
(
)
−
Ψ
+
=
d
q
I
L
T
I
pT
s
1
2
2
1
2
2
1
1
ζ
µ
µζ
ζ
ζ
σ
ζ
σ
ω
(88)
(
)
(
)
q
d
I
T
s
L
pT
I
pT
1
2
2
1
2
1
2
2
1
1
ζ
ζ
µ
µζ
ζ
σ
ω
ζ
σ
+
Ψ
⋅
+
=
⋅
+
Równania (86) i (88) są uogólnioną postacią odsprzężenia prądu i w postaci schematu
blokowego są przedstawione na rysunku 23.
Rys. 23. Schemat blokowy metody rozdzielenia wektora prądu względem wektora strumienia
głównego w pośredniej metodzie rozdzielenia zmiennych.
Efektem tego odsprzężenia jest możliwość kształtowania strumienia w maszynie za pomocą
składowej prądu falownika
z
d
I
1
oraz niezależnego kształtowania momentu za pomocą
składowej prądu falownika
z
q
I
1
.
Przyjmując odpowiednie wartości współczynnika sprowadzenia
ζ można dokonywać
wymuszania prądów
z
q
z
d
I
,
I
1
1
przy orientacji względem dowolnego strumienia.
Metoda orientacji według uogólnionego wektora strumienia pola.
Sterowanie wektorowe oznacza niezależne (rozdzielne) sterowanie strumienia i momentu
poprzez składowe prądu stojana, za pomocą skoordynowanej zmiany amplitudy, fazy i
częstotliwości napięcia zasilającego. Ze względu na stosunkowo wolne zmiany strumienia,
szczególnie przy sterowaniu prądowym, ustalenie strumienia daje możliwość otrzymania
szybkiej odpowiedzi moment/prąd (oraz moment), a w konsekwencji szybkiej odpowiedzi
prędkości (położenia). Z drugiej strony, regulowanie wartości strumienia jest podstawowym
sposobem zapobiegania nasycania obwodu magnetycznego (a w związku z tym powstawaniu
dużych strat w rdzeniu) i redukcji strat w rdzeniu poprzez osłabianie pola przy małych
obciążeniach.
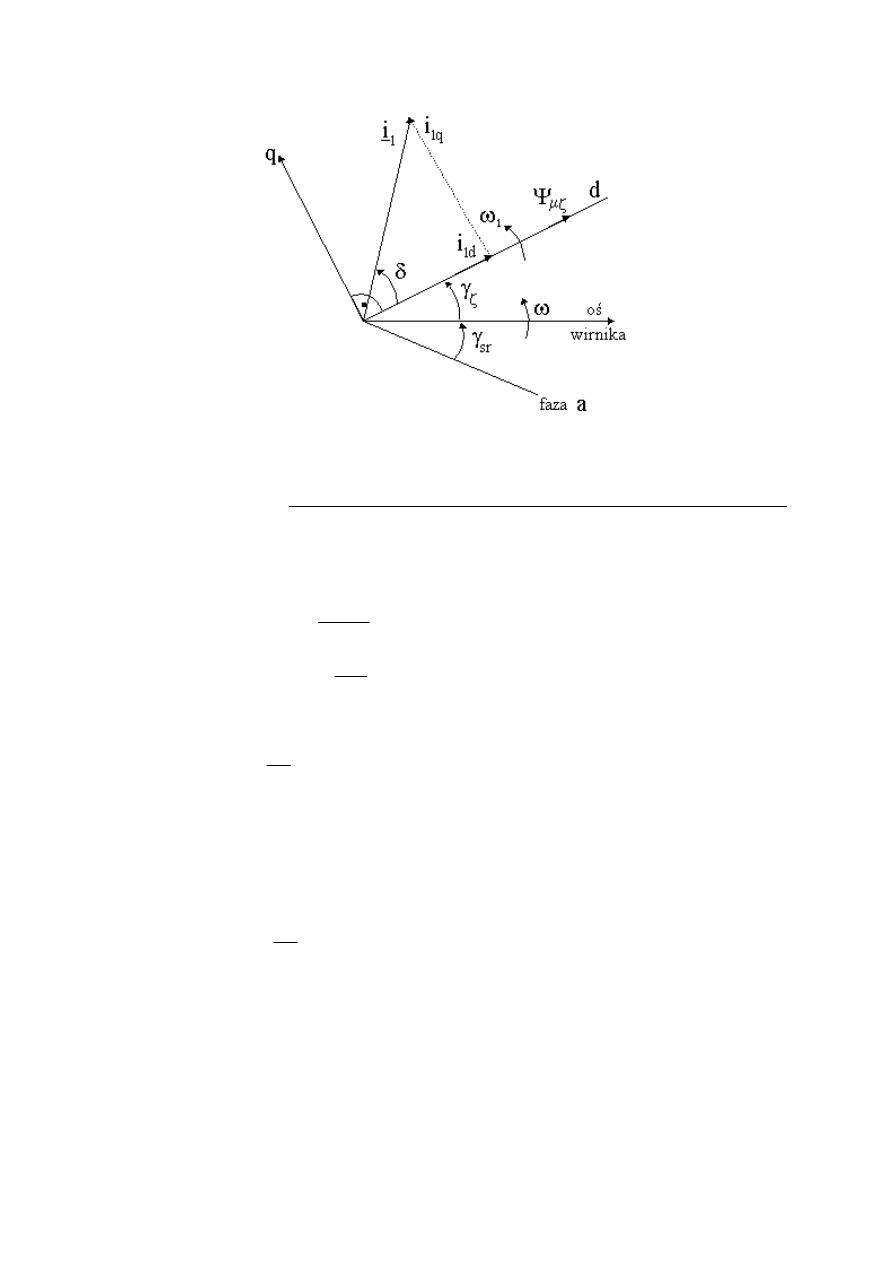
Rys. 16. Współrzędne w sterowaniu polowo-zorientowanym.
Z rysunku 16 wynika, że
q
I
1
jest momentową składową, podczas gdy
d
I
1
strumieniową
składową prądu stojana. To rozdzielne sterowanie stanowi esencję sterowania wektorowego.
Utrzymując stałym strumień
µζ
Ψ maszyny, sterowanie momentem oznacza sterowanie
składową
q
I
1
a sterowanie strumieniem składową
d
I
1
.
δ
µζ
sin
1
1
1
⋅
=
⋅
Ψ
⋅
=
I
I
,
I
p
M
q
q
b
e
(48)
Z wyrażenia na poślizg
1
1
ω
ω
ω
ζ
−
=
s
oraz z rysunku 16 wynika także:
1
d
d
ω
γ
ζ
ζ
s
t
=
(49)
Orientacja względem strumienia wirnika.
Przyjęcie
2
L
L
µ
ζ =
powoduje
0
2
=
ζ
σ
, a w konsekwencji formalne pokrywanie się
sprowadzonego strumienia wirnika ze strumieniem uogólnionym:
ζ
µζ
2
Ψ
=
Ψ
.
Należy zauważyć (rys. 24), że na sterowanie to, zależące od parametrów
2
T
,
,
L
ζ
µ
, wpływa
zarówno nasycanie obwodu magnetycznego (
2
T
,
L
µ
) jak i temperatura wirnika (
2
T ).
Orientacja względem strumienia stojana.
Przyjęcie
µ
ζ
L
L
1
=
powoduje formalne pokrywanie się strumienia stojana ze
strumieniem uogólnionym:
1
Ψ
=
Ψ
µζ
.
Orientacja względem strumienia głównego.
Przyjęcie 1
=
ζ
powoduje formalne pokrywanie się strumienia głównego ze
strumieniem uogólnionym:
µ
µζ
Ψ
=
Ψ
.
Metoda rozdzielenia składowych prądu jest pośrednią metodą sterowania. Wymaga
ona znajomości parametrów maszyny i wymaga wykonywania obliczeń w trybie
rzeczywistym (z reguły z zastosowaniem procesorów sygnałowych), których objętość zależy
od stopnia skomplikowania metody. Najprostsze relacje pozostają dla sterowania z orientacją
według strumienia wirnika.
Bez względu na stopień skomplikowania algorytmu sterowania pośrednia metoda
sterowania, zależąc od parametrów
2
T
,
,
L
ζ
µ
, jest wrażliwa zarówno na nasycanie się obwodu
magnetycznego (
2
T
,
L
µ
) jak i nagrzewania wirnika (
2
T ).
5.2 Bezpośrednia metoda odsprzęgania prądu.
W wyprowadzonej wyżej pośredniej metodzie rozdzielenia jest stosunkowo
skomplikowana dla orientacji względem strumienia stojana oraz mniej dla orientacji
względem strumienia wirnika, nie mniej jednak obie wymagają znajomości podstawowych
parametrów schematu zastępczego maszyny, a w związku z tym silnie zależą od nasycania się
obwodu magnetycznego i temperatury.
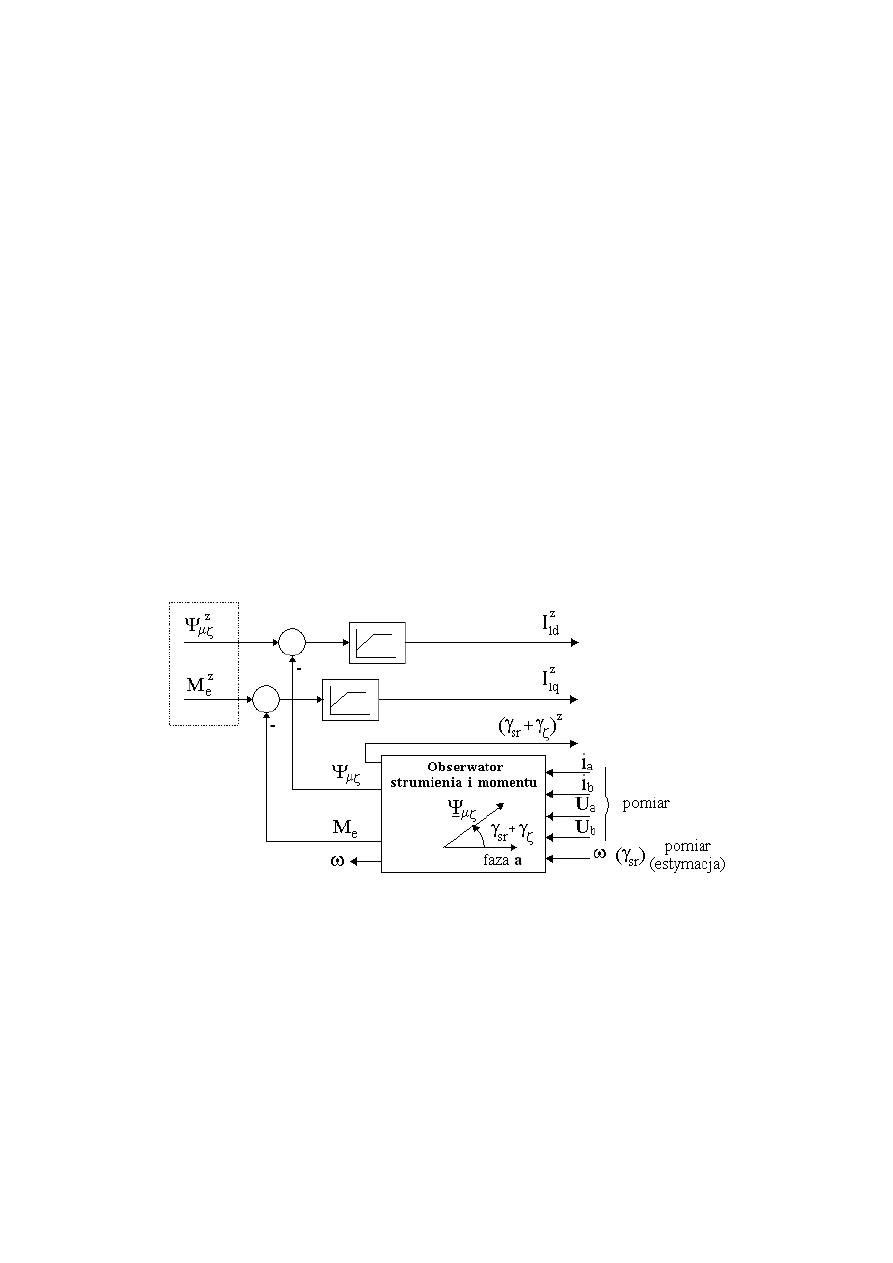
Bezpośrednia metoda polega sterowaniu strumieniem i momentem w zamkniętym
układzie sterowania na bazie estymacji (lub pomiarze) momentu i strumienia maszyny
stanowiących sprzężenia zwrotne. Dalej pozostaje problem błędów oszacowania parametrów
maszyny, przeniesionych w tej metodzie do estymatorów, ale w tym przypadku łatwiej jest
zminimalizować ich wpływ na jakość sterowania.
Koncepcję bezpośredniej metody rozdzielenia zmiennych przedstawiono na
rysunku 25.
Rys. 25. Bezpośrednia metoda rozdzielenia zmiennych.
6 Bezpośrednie sterowanie momentem i strumieniem (DTFC)
DTFC jest powszechnie używanym skrótem dla metody bezpośredniego sterowania
momentem i strumieniem (direct torque and flux control).
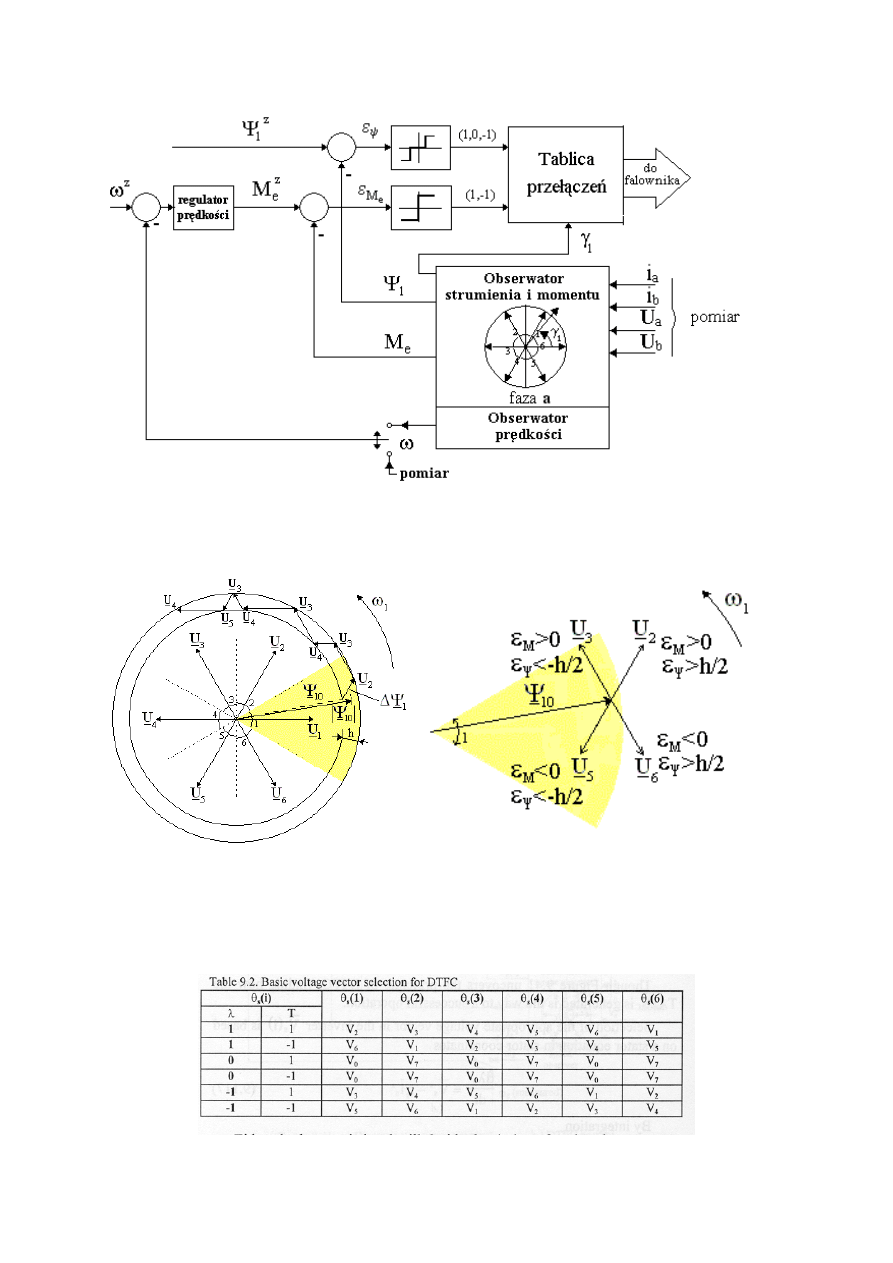
Rys. 25. a) Bezpośrednie sterowanie wektorem prądu, b) sterowanie DTFC
a
b
Rys. 26. a) trajektoria fazora przestrzennego strumienia stojana,
b) sposób określania startowego położenia fazora strumienia.
Tablicę optymalnych przełączeń napięć w DTFC zbudowano w oparciu o stany
przerzutników błędu strumienia i błędu momentu (Tabela 1).

ε
Ψ
ε
M
γ
s
(1)
γ
s
(2)
γ
s
(3)
γ
s
(4)
γ
s
(5)
γ
s
(6)
1
1
V
2
V
3
V
4
V
5
V
6
V
1
1
-1
V
6
V
1
V
2
V
3
V
4
V
5
0
1
V
0
V
7
V
0
V
7
V
0
V
7
0
-1
V
0
V
7
V
0
V
7
V
0
V
7
-1
1
V
3
V
4
V
5
V
6
V
1
V
2
-1
-1
V
5
V
6
V
1
V
2
V
3
V
4
Dla napędów DTFC bez czujników pomiarowych potrzebne są oba obserwatory:
strumienia i prędkości. Odpowiedź momentu jest rzędu 1-5 ms (podobnie jak dla układów z
czujnikami) jest otrzymywana dla zakresu regulacji 100 i błędzie względnym regulacji 0.1%.
7 Wnioski
1. Silniki indukcyjne są używane w napędach z regulacją momentu, prędkości i położenia, w
układach bez oraz z czujnikami ruchu (prędkości lub/i położenia).
2. Efekt wypierania prądu w prętach wirnika jest wykorzystany w napędach o dużym
momencie rozruchowym przy stałej częstotliwości napięcia zasilającego.
3. Indukcyjności wzajemne pomiędzy stojanem i wirnikiem zmieniają się sinusoidalnie od
położenia wirnika, co powoduje utrudnienie analizy stanów przejściowych równań
napięciowo-prądowych we współrzędnych fazowych (trójosiowych) poprzez
wprowadzenie do układu równań współczynników zależnych od kąta położenia.
4. Model maszyny we współrzędnych dwuosiowych (d,q lub
α,β) w wyniku wprowadzenia
fazorów przestrzennych powoduje ustalenie współczynników.
5. W stanie ustalonym pracy (w silniku ze zwartym wirnikiem) fazory przestrzenne wirnika:
prąd i strumień są do siebie wzajemnie prostopadłe.
6. Przy stałej prędkości model dwufazowy silnika jest modelem rzędu drugiego z dwoma
zespolonymi wartościami własnymi, jednej dla stojana i drugiej dla wirnika. Zależą one
od prędkości wirnika i prędkości układu odniesienia, lecz ich części rzeczywiste są w
ogólnym przypadku ujemne.
7. W stanie ustalonym model fazorowy jest reprezentowany tym samym układem równań
bez względu na prędkość układu odniesienia.
8. Silnik pracuje w trzech podstawowych stanach pracy: silnikowym, generatorowym i
hamowania. Charakterystyki elektromechaniczne są krzywoliniowe i posiadają dwa
maksima momentu (dla pracy silnikowej i generatorowej).
9. Przy hamowaniu dynamicznym prądem stałym maksimum momentu dla silnika
klatkowego na charakterystyce mechanicznej występuje przy małej prędkości kątowej
wirnika, jako że pulsacja prądów wirnika jest równa elektrycznej prędkości kątowej
wirnika.
10. Metody sterowania prędkością przy zasilaniu z falownika wymagają zmiany zarówno
częstotliwości prądów stojana lub wirnika jak i napięcia.
11. Dla ograniczonego zakresu regulacji (
±30% w górę i w dół od prędkości idealnego biegu
jałowego) zasilanie z falownika obwodów wirnika silnika pierścieniowego (ze względu na
mniejszą moc znamionową falownika) jest szczególnie polecane, zwłaszcza dla napędów
dużych mocy.
12. Sterowanie skalarne daje możliwość regulacji bez czujników ruchu w zakresie regulacji
prędkości do 20, w układach ze sprzężeniem zwrotnym do 100 dla wolnych napędów
(słabe wymagania dynamiki napędu).

13. W przypadku szybkich napędów (duża dynamika) niezbędne jest stosowanie linearyzacji
charakterystyk mechanicznych silnika lub rozdzielnej regulacji strumienia i momentu.
14. Sterowanie wektorowe (VC), bezpośrednie sterowanie momentem i strumieniem (DTFC)
oraz linearyzacja za pomocą sprzężeń zwrotnych pozwalają regulowane napędy o dużych
własnościach dynamicznych.
15. Sterowanie wektorowe (VC) bazuje na orientacji fazora prądu stojana względem fazora
strumienia (stojana, wirnika lub głównego), a w konsekwencji na wyodrębnieniu
składowej prądu strumieniowej oraz składowej prądu momentowej.
16. Orientacja względem strumienia wirnika prowadzi do uproszczonego schematu
rozdzielenia prądu, natomiast orientacja względem strumienia stojana do uproszczonego
schematu rozdzielenia napięcia.
17. Tylko przy sterowaniu ze stabilizacją strumienia wirnika charakterystyki mechaniczne
silnika są liniowe (jak dla maszyny prądu stałego) i z tego powodu są idealne do
sterowania w napędzie elektrycznym.
18. Błędy w wyznaczeniu parametrów silnika najsilniej wpływają na jakość sterowania przy
orientacji względem strumienia wirnika.
19. Rozdzielenie prądu względem strumienia jest możliwe metodą pośrednią (feedforward -
wprost ze schematu zastępczego) lub metodą bezpośrednią wykorzystującą obserwatory
stanu (strumienia, prędkości i położenia) w układzie ze sprzężeniami.
20. Regulatory prądu stałego (fazorowe, współrzędne synchroniczne d,q) w porównaniu do
regulatorów prądów fazowych są mniej wrażliwe na zmiany parametrów silnika oraz
bardziej stabilne częstotliwościowo.
21. Rozdzielenie prądu jest stosowane w pierwszej strefie regulacji natomiast dla wyższych
prędkości (II strefa regulacji) stosowane jest rozdzielenie napięcia (pozwala uwzględnić
wpływ napięcia rotacji).
22. Osłabianie pola obejmuje dwa obszary. Pierwszy dla stałej mocy, gdy kąt fazowy fazora
prądu i pulsacja prądu wirnika rosną do osiągnięcia maksymalnego kąta
moment/strumień. Drugi obszar (dla wyższych prędkości) występuje przy stałej pulsacji
prądów wirnika co nie zapewnia stałej mocy.
23. Istnieje ograniczenie prądowe dla niskich prędkości i ograniczenie napięciowe dla
wyższych.
24. Szerszy zakres regulacji prędkości mają napędy z silnikami o mniejszej indukcyjności
przejściowej (zwarcia – stanowiącej sumaryczną indukcyjność rozproszenia).
25. Wektorowe metody sterowania (rozdzielenie prądu lub/i napięcia) są realizowane w
falownikach napięcia ze sterowaniem PWM w układach otwartych lub zamkniętych
(nadążne kształtowanie prądu).
26. W metodzie bezpośredniego sterowania momentem i strumieniem(DTFC) błędy regulacji
momentu i strumienia są wykorzystane do utworzenia optymalnej tablicy przełączeń.
27. Sterowanie skalarne
1
1
f
U
ma skłonności do pracy niestabilnej, szczególnie z silnikami
dwubiegunowymi.
28. Zwiększanie dokładności stabilizacji prędkości w sterowaniu skalarnym odbywa się za
pomocą kompensacji poślizgu.

Wyszukiwarka
Podobne podstrony:
Maszyna indukcyjna 2
Podstawowe zależności z teorii maszyn indukcyjnych
Zasada działania maszyny indukcyjnej a
Maszyny indukcyjne
Badanie maszyn indukcyjnych
antal,elektrotechnika, MASZYNY INDUKCYJNE
charakterystyki mechaniczne przy zmianie rezystancji w obwodzie wirnika maszyny indukcyjnej
Maszyny indukcyjne
Maszyna indukcyjna 1 rozwiązanie i parametry
Maszyny Indukcyjne
maszyny indukcyjny1
Maszyny elektryczne 03 MASZYNY INDUKCYJNE ASYNCHRONICZNE
Maszyny indukcyjne
Budowa maszyn indukcyjnych 2, ۞ Nauka i Technika, Elektrotechnika, Maszyny elektryczne
Maszyny Elektryczne - Zadanie 7,8, Maszyna Indukcyjna Trójfazowa
Ćwiczenie A2, Maszyna indukcyjna trójfazowa klatkowa a2 f
Ćwiczenie A2, Maszyna indukcyjna trójfazowa klatkowa a2 pr
Maszyna indukcyjna 1
Badanie maszyn indukcyjnych silnik klatkowy i pierścieniowy
więcej podobnych podstron