Projekt „Program Rozwojowy Potencjału Dydaktycznego Politechniki Świętokrzyskiej w Kielcach: kształcenie na miarę sukcesu”

Program Operacyjny Kapitał Ludzki Priorytet IV Działanie 4.1 Poddziałanie 4.1.1

Umowa UDA-POKL.04.01.01-00-175/08-02

Politechnika Świętokrzyska

25-314 Kielce

Al. Tysiąclecia Państwa Polskiego 7

Biuro Projektu - bud. B pok. 324

Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego

Maszyny elektryczne – wykład multimedialny

Część III

Autorzy:

Prof. dr hab. inż. Roman Nadolski

Dr inż. Jan Staszak

Dr inż. Krzysztof Ludwinek

Mgr inż. Zbigniew Gawęcki

Lata realizacji 2008-2011

SPIS TREŚCI

3 Maszyny indukcyjne asynchroniczne

3.1 Budowa maszyny indukcyjnej

3.2 Zasada działania

3.3 Schemat zastępczy i wykres wskazowy

3.4 Podstawowe stany pracy maszyny indukcyjnej

3.4.1 Stan jałowy

3.4.2 Stan zwarcia

3.4.3 Bilans mocy

3.5 Moment elektromagnetyczny, charakterystyka mechaniczna silnika

indukcyjnego

3.6 Regulacja prędkości obrotowej silników indukcyjnych

3.6.1 Regulacja napięcia poprzez zmianę częstotliwości

3.6.2 Regulacja prędkości przez zmianę liczby par biegunów

3.6.3 Regulacja prędkości obrotowej przez zmianę poślizgu

3.7 Rozruch silników indukcyjnych

LITERATURA

3.1 BUDOWA MASZYNY INDUKCYJNEJ

Maszyny indukcyjne mają prostą budowę i w związku z tym charakteryzują się wysoką

pewnością ruchową, łatwością obsługi i niską ceną, Najczęściej maszyny indukcyjne pracują

jako silniki, hamulce elektryczne, rzadziej jako prądnice.

Maszyna indukcyjna składa się z następujących podstawowych części:

ze stojana stanowiącego część nieruchomą, w kształcie wydrążonego walca,

z wirnika, czyli części ruchomej (wirującej) w kształcie walca,

elementów konstrukcyjnych stanowiących obudowę maszyny i umożliwiających ruch

obrotowy wirnika i zapewniających odpowiednie chłodzenie maszyny i ochronę przed

działaniem czynników zewnętrznych (pył, wilgoć itp.)

Pomiędzy częścią nieruchomą a wirującą znajduje się szczelina powietrzna o wielości

zależnej od gabarytów maszyny (od dziesiątych milimetra do kilku milimetrów). Szczelina

między stojanem a wirnikiem powinna być ze względów elektromagnetycznych jak

najmniejsza, gdyż wtedy jest mały prąd biegu jałowego. Ze względów mechanicznych

minimalna szczelina powietrzna wynosi 0,2 mm. Obwody magnetyczne stojana i wirnika

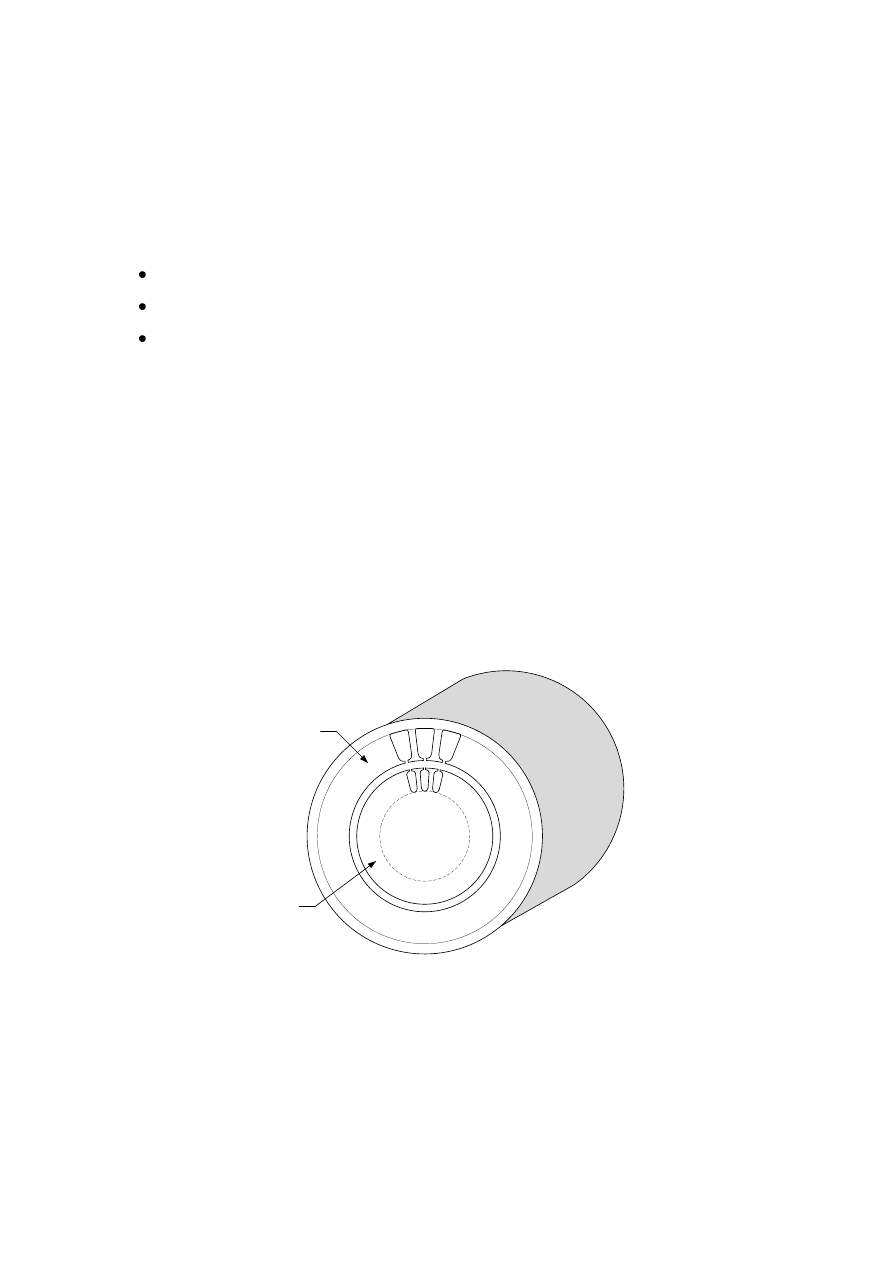
(rys 3.1.) wykonuje się z izolowanych blach elektrotechnicznych, zazwyczaj o grubości

0.5mm, natomiast wirniki dużych maszyn indukcyjnych wykonuje się z blach o większej

grubości.

1

2

Rys 3.1. Schemat budowy obwodu magnetycznego maszyny indukcyjnej: 1-wirnik, 2-stojan.

Na wewnętrznej stronie pakietu blach stojana i zewnętrznej stronie pakietu blach wirnika

wykonane są specjalne rowki zwane żłobkami (rys 3.2.) w których umieszczane są uzwojenia.

Liczba żłobków stojana i wirnika powinna być różna. Elementy obwodu magnetycznego

między żłobkami nazywane są zębami. Żłobki i zęby mogą mieć różne kształty. W małych

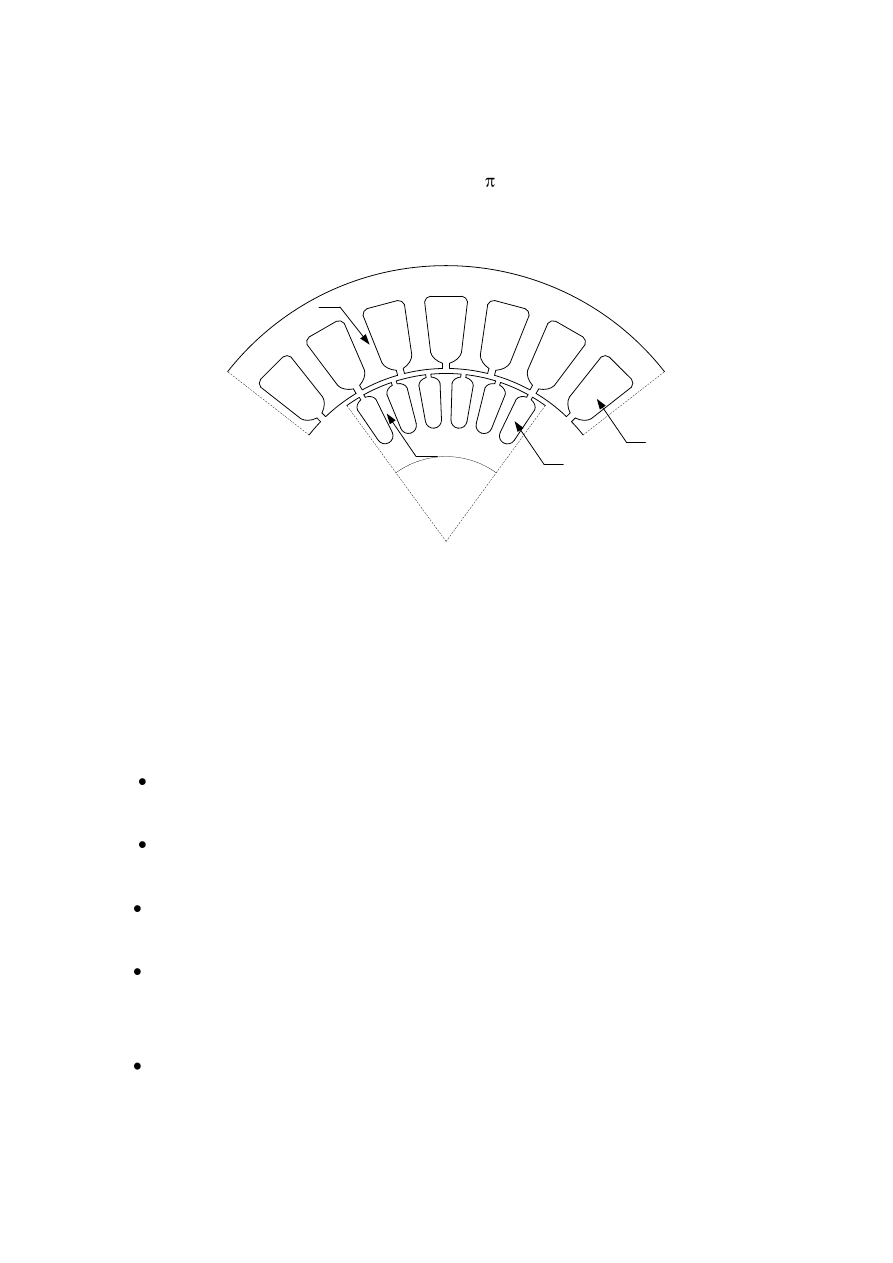
i średnich mocy kształt zębów jest prostokątny. W żłobkach stojana umieszczone jest

trójpasmowe uzwojenie wykonane z cewek z drutu nawojowego. Odległość między

początkami pasm uzwojeń trójfazowych wynosi 2/3 elektrycznych. Kąt mechaniczny będzie

p razy mniejszy, gdzie p jest liczbą par biegunów.

1

1

2

2

Rys 3.2. Wykrój blach stojana i wirnika Schemat budowy obwodu magnetycznego maszyny

indukcyjnej: 1-żłobek, 2-ząb.

W celu poprawienia oddawania ciepła z obwodu elektrycznego i magnetycznego silniki

indukcyjne wyposażone są w wentylatory, których zadaniem jest spowodowanie

intensywnego przepływu powietrza chłodzącego.

Ze względu na sposób uzwojenia stojana wśród silników indukcyjnych można wyróżnić:

silniki trójfazowe, najczęściej stosowane o trzech uzwojeniach fazowych

umieszczonych w stojanie, skojarzonych w gwiazdę lub trójkąt,

silniki jednofazowe, zwykle mniejszych mocy o jednofazowym uzwojeniu

umieszczonym w stojanie,

silniki dwufazowe o dwufazowym uzwojeniu stojana.

Ze względu na budowę wirnika silniki indukcyjne można podzielić na:

silniki klatkowe z wirnikiem tzw. zwartym, w których pręty wirnika połączone są

pierścieniami i tworzą pewnego rodzaju klatkę, pręty i pierścienie zwierające

wykonywane są zazwyczaj z aluminium, są to najpowszechniej stosowane silniki,

silniki pierścieniowe w których istnieje możliwość dołączania dodatkowych rezystancji

(np. w trakcie rozruchu) w obwód uzwojonego wirnika poprzez pierścienie ślizgowe

i szczotki.

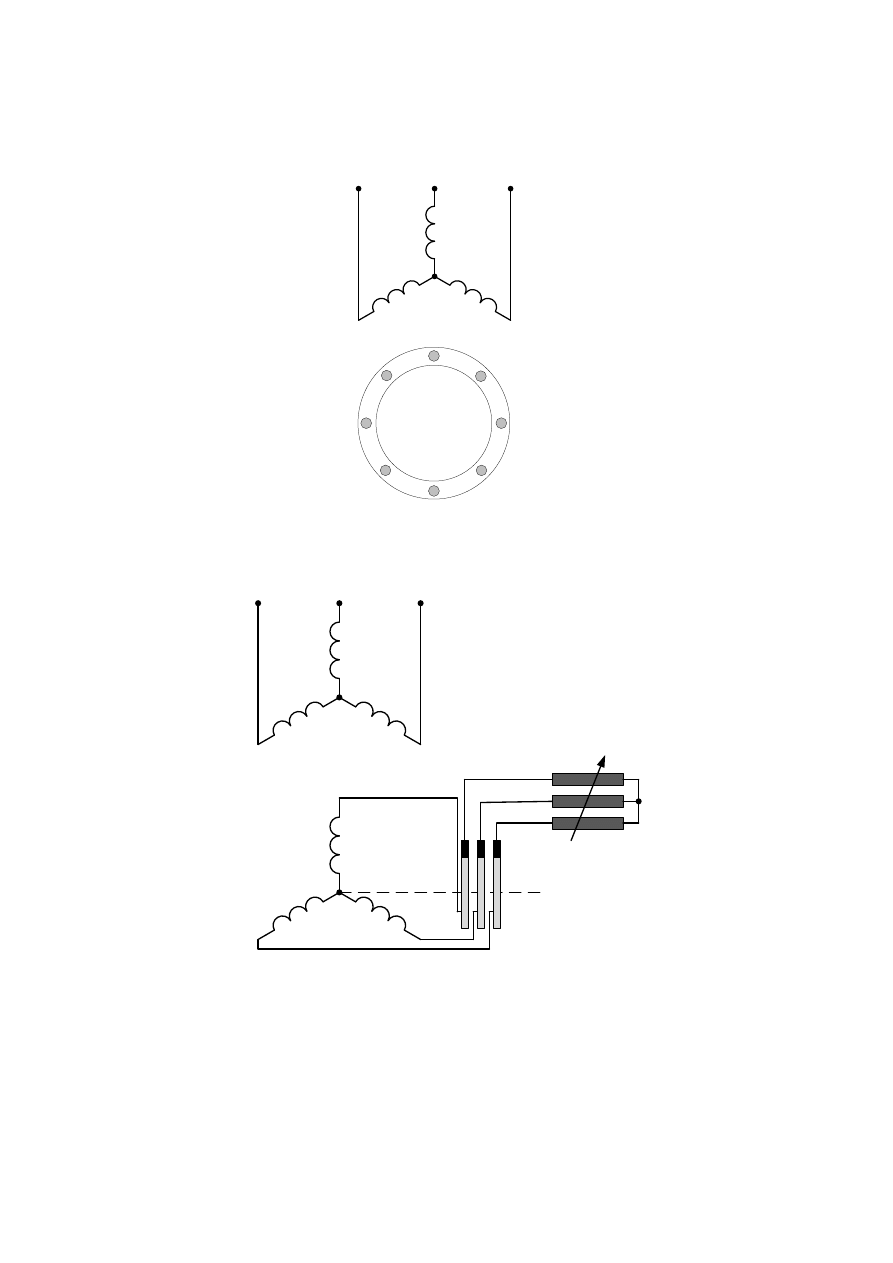
a)

U

V

W

Stojan

Wirnik

b)

U

V

W

Stojan

Wirnik

R

d

P

Rys 3.3. Schemat obwodu elektrycznego silnika indukcyjnego: a) klatkowego, b) pierścieniowego:

R

d

- rezystancja dodatkowa, P- pierścienie ślizgowe.

Rys 3.4. Widok typowego silnika klatkowego.

W grupie silników klatkowych można wyróżnić:

silniki z wirnikami jednoklatkowymi – pojedyncze uzwojenie w postaci prętów

zwarte pierścieniami (najpowszechniej stosowane),

silniki z wirnikami dwuklatkowymi – dwa uzwojenia z jednakową liczbą prętów

zwarte poprzez pierścienie (tworzą podwójną klatkę, pozwalającą uzyskać odpowiedni

poziom momentu rozruchowego),

silniki głębokożłobkowe – pojedyncze uzwojenie w postaci prętów sięgających w głąb

wirnika zwartych pierścieniami (wykorzystane zjawisko wypierania prądu do

uzyskania odpowiedniej wartości momentu rozruchowego).

a)

b)

c)

Rys 3.5. Kształt żłobków silnika klatkowego: a) żłobek silnika jednoklatkowego, b) żłobek silnika

dwuklatkowego, c) żłobek silnika głęboko żłobkowego.

Ze względu na rodzaj ruchu maszyny indukcyjne można podzielić na:

maszyny o ruchu wirującym,

maszyny o ruchu liniowym.

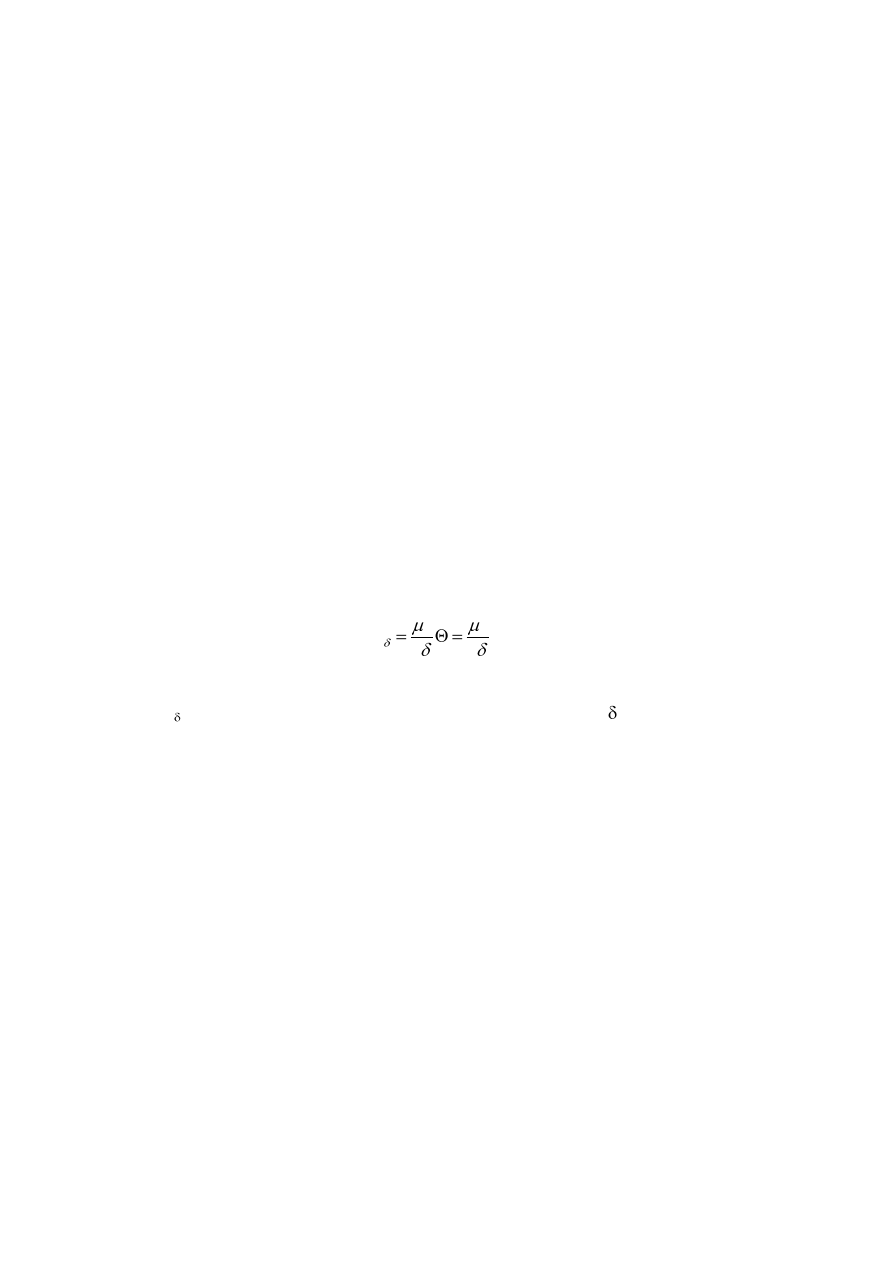
3.2 ZASADA DZIAŁANIA

Uzwojenie trójfazowe stojana, wytwarzanie pola wirującego

Pojedyncze pasmo uzwojenia trójfazowego zasilane prądem przemiennym sinusoidalnym

wytwarza pole pulsujące o częstotliwości równej częstotliwości prądu przemiennego.

Kierunek tego pola jest zawsze zgodny z osią magnetyczną uzwojenia danej fazy. Oś

magnetyczna uzwojenia jest to oś prostopadła do płaszczyzny cewki tego uzwojenia. Zwrot

pola magnetycznego będzie zależny od wartości chwilowej prądu płynącego przez uzwojenie;

przy wartości dodatniej prądu zwrot pola będzie zgodny z osią magnetyczną dodatnią, przy

wartości ujemnej prądu pole magnetyczne będzie mieć zwrot przeciwny do osi dodatniej

uzwojenia. Pole magnetyczne wyznaczamy z prawa. Przy pominięciu spadków napięć

magnetycznych w rdzeniu stojana i wirnika możemy napisać

s

s

N

i

B

2

2

0

0

(3.1)

gdzie: B – indukcja magnetyczna w szczelinie powietrznej,

– długość szczeliny

powietrznej, i

s

– wartość chwilowa prądu płynącego w uzwojeniu, N

s

– liczba zwojów

szeregowych uzwojenia jednej fazy

Z zależności (3.1) wynika, że rozkład pola magnetycznego, przy jednakowej długości

szczeliny powietrznej, jest zależny od rozkładu przepływu. Kierunek przepływu będzie

zawsze zgodny z osią magnetyczną uzwojenia a jego zwrot zależny od wartości chwilowej

prądu. Wartość chwilową prądu określamy na podstawie wykresów wskazowych prądów

fazowych. Rzut wskazu prądu fazowego na oś czasu przedstawia wartość chwilową prądu.

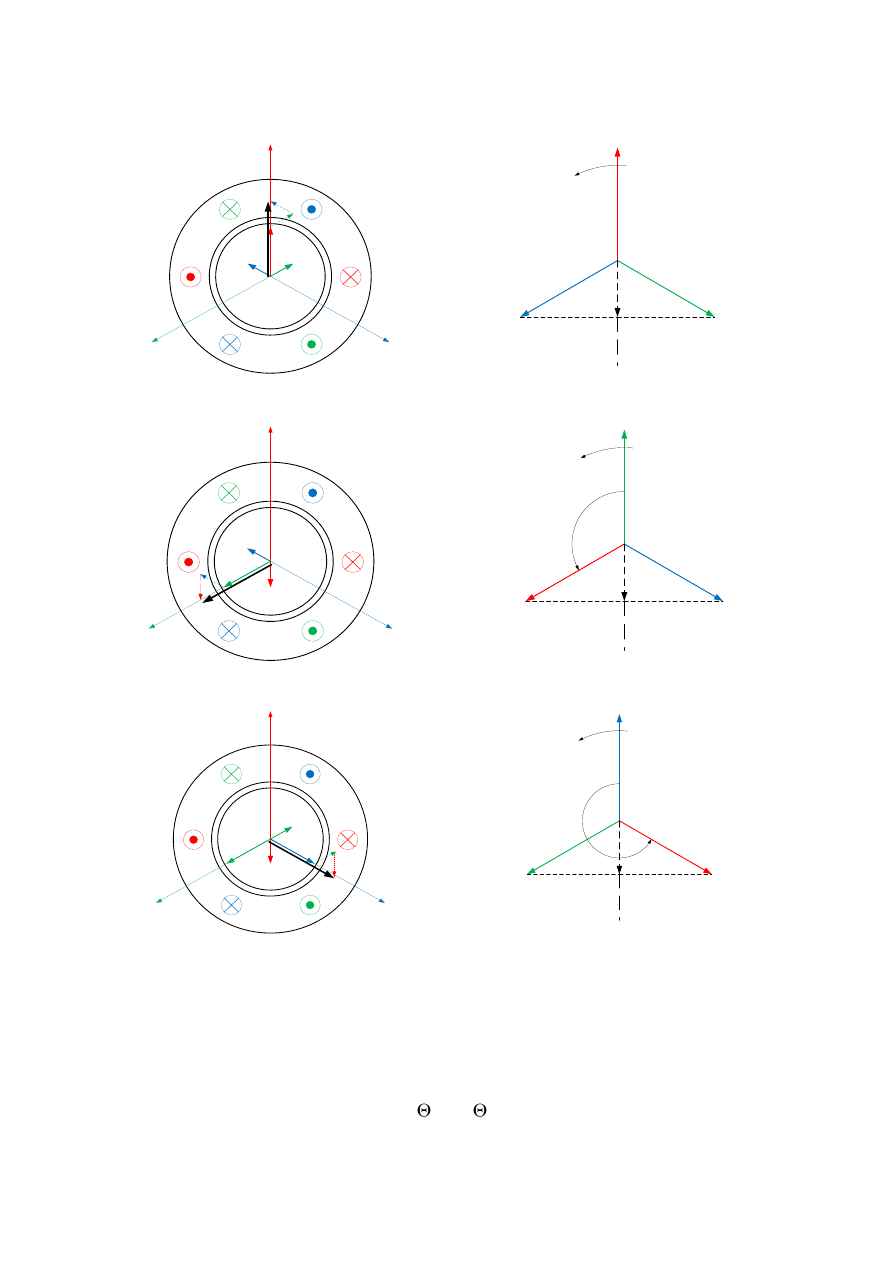
Zasadę powstawania pola magnetycznego wirującego wytworzonego przez uzwojenie

trójfazowe ilustruje rys.3.6.

a)

U

V

W

W1

W2

V2

U2

V1

U1

Θ

U

Θ

V

Θ

W

Θ

O

ś

cz

as

u

I

U

=I

m

I

V

I

W

I

V

=I

W

= ─0.5I

m

ω

s

b)

U

V

W

W1

W2

V2

U2

V1

U1

Θ

U

Θ

V

Θ

W

Θ

O

ś

cz

as

u

I

V

=I

m

I

W

I

U

I

U

=I

W

= ─0.5I

m

ω

s

α=ω

s

t=120°e

c)

U

V

W

W1

W2

V2

U2

V1

U1

Θ

U

Θ

V

Θ

W

Θ

O

ś

cz

as

u

I

W

=I

m

I

U

I

V

I

U

=I

V

= ─0.5I

m

ω

s

α=ω

s

t=240°e

Rys.3.6. Wirujące pole magnetyczne wytworzone przez uzwojenie trójfazowe.

Każdy z prądów fazowych wytwarza pole pulsujące w osi danego uzwojenia.

Określenia wypadkowego pola magnetycznego jest równoznaczne z wyznaczeniem

wypadkowego przepływu. W tym wypadku należy wykonać sumowanie przepływów

poszczególnych faz. Dla wykresu prądów przestawionych na rys.3.6. a), prąd i

u

ma wartość

maksymalną dodatnią, więc przepływ

u

=

max

będzie miał wartość maksymalną

i będzie skierowany wzdłuż osi dodatniej uzwojenia. Wartości chwilowe prądów i

v

oraz i

w

są

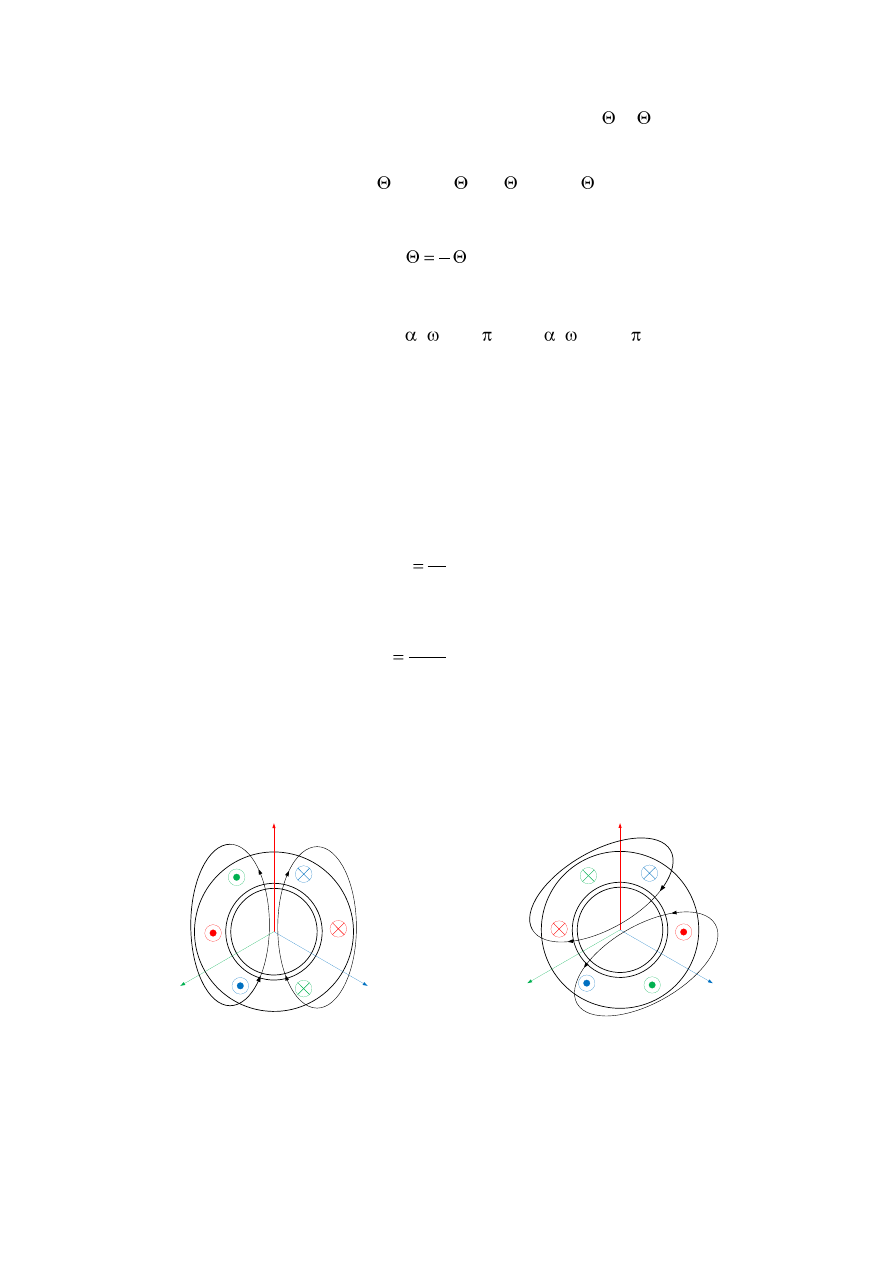
ujemne i równe połowie wartości maksymalnej. A więc przypływy

v

i

w

będą skierowane

przeciwnie do swych dodatnich osi magnetycznych a wartość tych przepływów będzie równa

połowie wartości maksymalnej czyli

v

= – 0.5

max

,

v

= – 0.5

max

. Suma poszczególnych

wynosi

max

2

3

(3.2)

A więc wypadkowy przepływ jest 1.5 razy większy od przepływu maksymalnego danej fazy.

Dla kolejnych chwil czasowych, gdy

=

s

t=2/3 oraz

=

s

t =4/3 (rys.3.6. b) i c)),

otrzymuje się inne chwilowe wartości prądów fazowych, lecz wartość przepływu

wypadkowego jest taka sama. Natomiast oś przypływu obraca się o taki sam kąt jak wektory

prądów fazowych. Powstałe w ten sposób pole magnetyczne nazywamy polem wirującym.

Prędkość obrotowa wirowania pola przypływu a tym samym i pola magnetycznego stojana

nazywana jest prędkością synchroniczną i zależna jest od częstotliwości prądów trójfazowych

oraz od liczby par biegunów i wynosi

p

f

n

s

s

[obr/s]

(3.3)

lub

p

f

n

s

s

60

[obr/min]

(3.4)

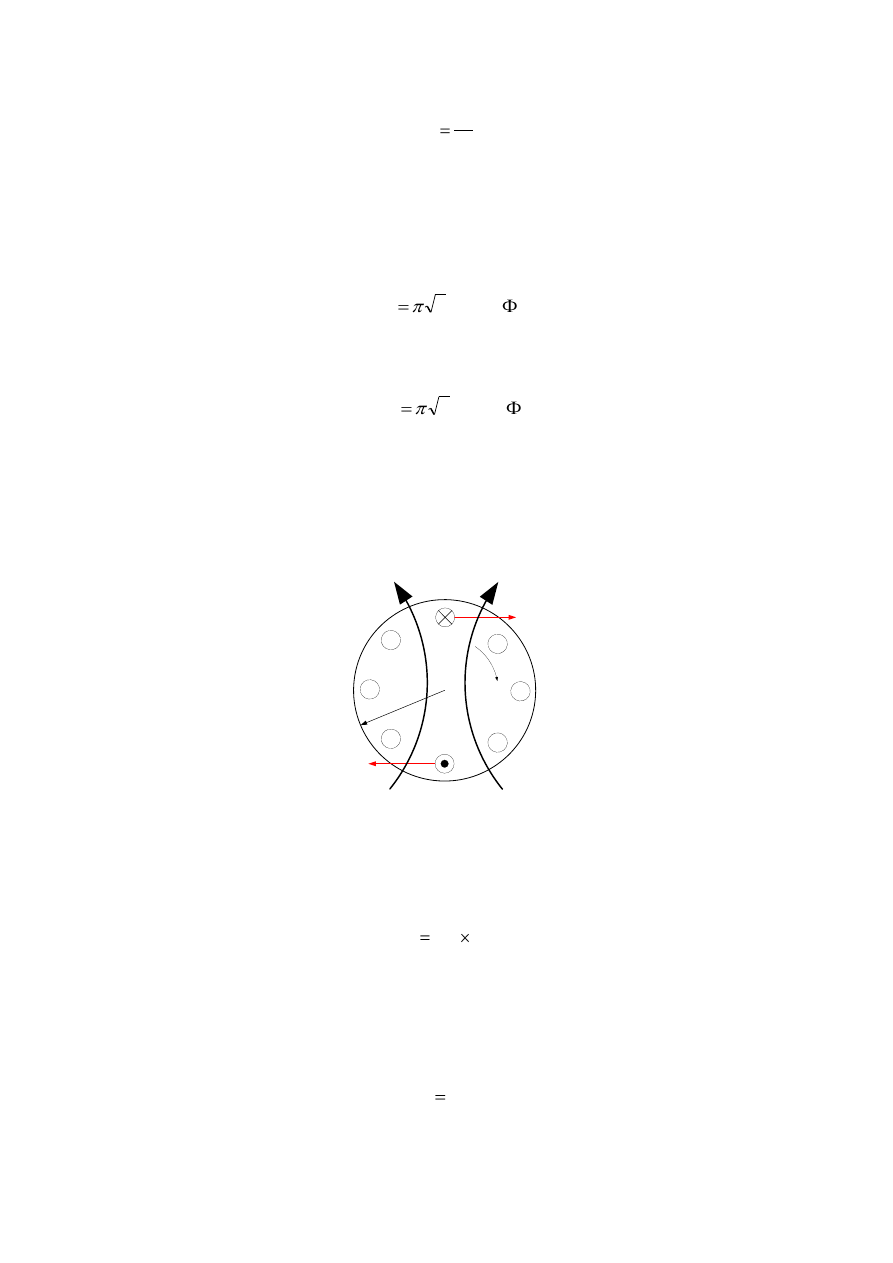
Na rys.3.7. przedstawiono obraz graficzny pola. Kierunek pola określa się posługując reguła

śruby prawoskrętnej. Kierunek prądu w uzwojeniu przedstawia wartości chwilowe prądów

fazowych.

a)

U

V

W

W1

W2

V2

U2

V1

U1

Φ

b)

U

V

W

W1

W2

V2

U2

V1

U1

Φ

Rys. 3.7. Graficzny obraz pola.

Prąd trójfazowy płynący przez trójfazowe uzwojenie stojana wytwarza pole wirujące.

Podstawowa harmoniczna tego pola wiruje z prędkością synchroniczną względem

nieruchomego stojana

p

f

n

s

s

(3.5)

gdzie:

f

s

- częstotliwość napięcia zasilającego uzwojenie stojana, p- liczba par biegunów.

Wirujący strumień magnetyczny stojana indukuje w uzwojeniu stojana wartość skuteczną

napięcia

s

ws

s

s

f

k

N

E

2

(3.6)

Jeżeli wirnik pozostaje nieruchomy, to w każdej fazie uzwojenia wirnika indukuje się

napięcie o wartości skutecznej równej

s

wr

r

r

f

k

N

E

2

0

(3.7)

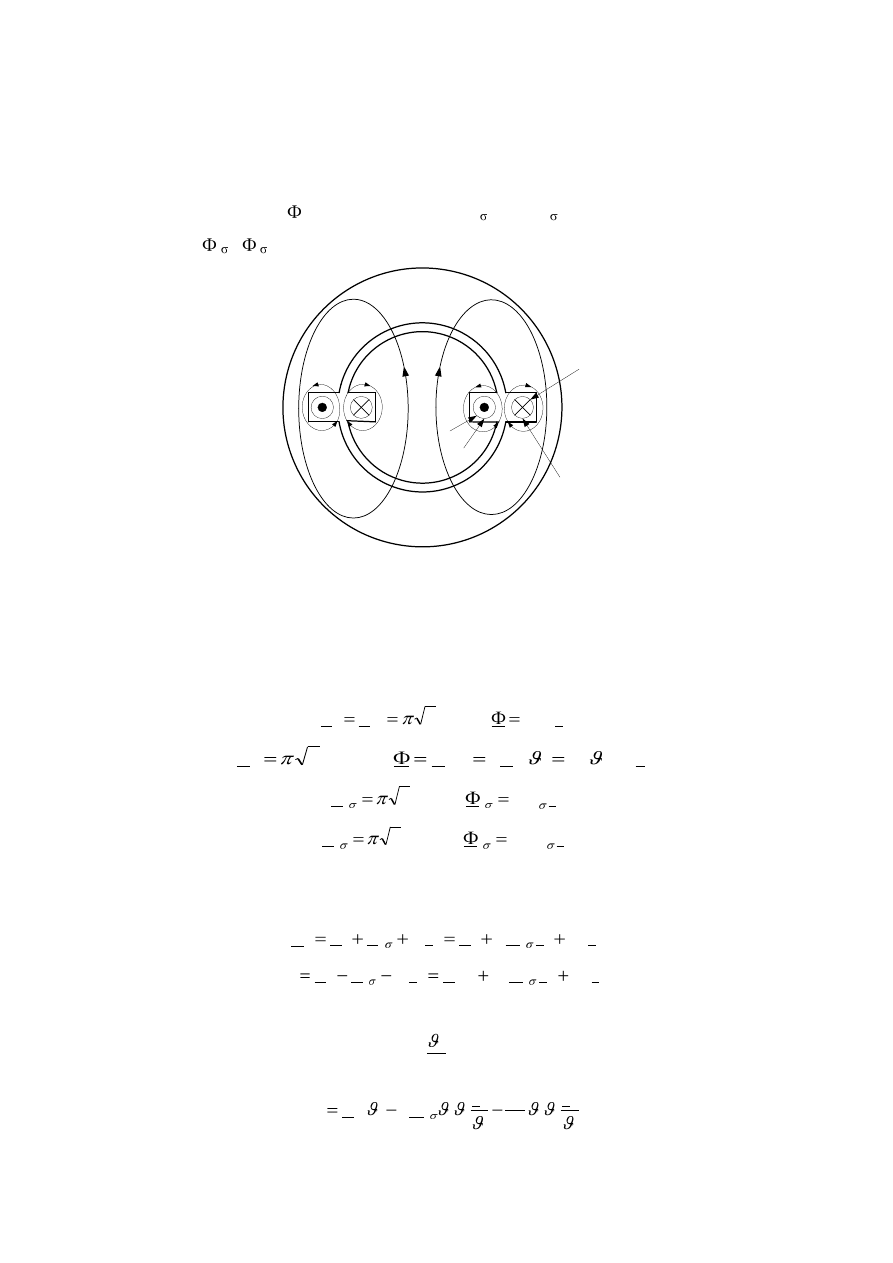
Zwrot tego napięcia określamy za pomocą reguły prawej dłoni (rys 3.8). Jeżeli prawą dłoń

ułożymy tak, aby linie pola były zwrócone prostopadle do dłoni, a kciuk odchylony w

kierunku prędkości względnej przewodu względem pola, to cztery wyprostowane palce

wskażą zwrot napięcia indukowanego E

r0

.

F

Φ

F

E

ro

, I

r

n

R

Rys.3.8. Zwroty napięcia, prądu i siły w uzwojeniu wirnika silnika indukcyjnego.

Gdy obwód elektryczny wirnika jest zamknięty, to popłynie prąd I

r

, którego zwrot jest zgodny

ze zwrotem napięcia E

r0

. Na przewód z prądem znajdujący się w polu magnetycznym działa

siła F

)

(

B

l

r

I

F

(3.8)

Zwrot tej siły wyznaczamy za pomocą reguły lewej dłoni (rys 3.8.).. Jeżeli lewa dłoń zostanie

ułożona tak, aby linie pola były skierowane do dłoni, a cztery wyprostowane palce

wskazywały kierunek prądu, to odchylony kciuk wskaże kierunek siły F. A więc powstanie

moment obrotowy

R

F

M

(3.9)

skierowany w kierunku wirowania pola magnetycznego i wirnik zacznie się obracać

z prędkością n mniejszą od prędkości synchronicznej n

s

. Przy prędkości obrotowej wirnika n

pole stojana obraca się względem wirnika z prędkością

n

n

n

s

r

(3.10)

Stosunek prędkości obrotowej pola magnetycznego stojana względem wirnika n

r

odniesiony

do prędkości pola nazywamy poślizgiem

s

s

s

n

n

n

n

n

s

1

(3.11)

Prędkość wirnika można wyrazić poprzez prędkość synchroniczną n

s

i poślizg s

)

1

(

s

n

n

s

(3.12)

Częstotliwość napięcia indukowanego w uzwojeniu wirnika zależy od prędkości od prędkości

pola względem wirnika

s

f

n

n

n

pn

pn

f

s

s

s

s

r

r

(3.13)

Napięcie indukowane w uzwojeniu wirnika przy dowolnej prędkości n wyraża się zależnością

s

E

s

f

k

N

f

k

N

E

r

s

wr

r

r

wr

r

r

0

2

2

(3.14)

Prąd I

r

płynący w uzwojeniu wirnika pod wpływem napięcia E

r

ma również częstotliwość f

r

i wytwarza własne pole magnetyczne, które wiruje względem wirnika z prędkością

s

n

s

p

f

p

f

n

s

s

r

r

(3.15)

Natomiast pole magnetyczne wirnika wiruje względem stojana z prędkością

s

s

s

r

n

s

n

s

n

n

n

)

1

(

(3.16)

Z zależności (3.5) i (3.16) wynika, że pola magnetyczne wytworzone przez uzwojenie stojana

i wirnika są względem siebie nieruchome dla każdej prędkości obrotowej wirnika, dając

wypadkowe pole magnetyczne. To wypadkowe pole magnetyczne indukuje w uzwojeniu

stojana napięcie E

s

o częstotliwości sieci f

r

i w uzwojeniu wirnika napięcie E

r

o częstotliwości f

r

. Stosunek napięć i indukowanych przy nieruchomym wirniku nazywamy

przekładnią napięciową

wr

r

ws

s

r

s

u

k

N

k

N

E

E

0

(3.17)

gdzie: N

s

k

ws

, N

r

k

wr

– efektywna liczba zwojów szeregowych jednej fazy odpowiednio

uzwojenia stojana i wirnika.

Wynika stąd, że

'

0

0

r

u

r

s

E

E

E

(3.18)

gdzie:

'

0

r

E - napięcie indukowane w uzwojeniu wirnika sprowadzone na stronę stojana, przy

czym

u

r

r

E

E

0

'

0

(3.19)

Prądy stojana i wirnika wytwarzają przepływy

s

ws

s

s

s

I

p

k

N

m

2

4

2

(3.20)

4

2

2

r

wr

r

r

r

N k

m

I

p

(3.21)

gdzie: m

s

, m

r

– odpowiednio liczba faz uzwojenia stojana i wirnika.

Strumień wypadkowy

jest wynikiem działania wypadkowego przepływu

0

0

0

0

R

(3.22)

gdzie: R

μ

– reluktancja obwodu magnetycznego.

przy czym, przepływ wypadkowego jest różnicą przepływu stojana i wirnika.

0

0

2

4

2

I

p

k

N

m

ws

s

s

r

s

(3.23)

Przepływ wypadkowy

0

jest to przepływ wytworzony przez prąd biegu jałowego I

0

, który

płynie w uzwojeniu stojan. Podstawiając zależności (3.20) i (3.21) do równania (3.23),

otrzymuje się

r

wr

r

r

s

ws

s

s

ws

s

s

I

p

k

N

m

I

p

k

N

m

I

p

k

N

m

2

4

2

2

4

2

2

4

2

0

(3.24)

stąd

'

0

r

s

i

r

s

r

ws

s

wr

r

s

r

s

I

I

I

I

I

k

N

k

N

m

m

I

I

(3.25)

gdzie:

'

r

I

- prąd wirnika sprowadzony na stronę uzwojenia stojana,

i

- przekładnia prądowa,

przy czym

i

r

r

I

I

'

(3.26)

wr

r

ws

s

r

s

i

k

N

k

N

m

m

(3.27)

3.3 SCHEMAT ZASTĘPCZY i WYKRES WSKAZOWY

W uzwojeniach stojana i wirnika oprócz napięć E

s

i E

r

, indukowanych w uzwojeniach stojana

przez strumień główny , występują napięcia E

s

oraz E

r

indukowane przez strumienie

rozproszenia

s

i

r

(rys.3.9.).

Φ

E

r

, E

rσ

Φ

rσ

Φ

sσ

I

s

I

r

E

s

, E

sσ

Rys.3.9. Obraz strumieni, napięć i prądów.

Napięcia te, podobnie jak w transformatorze można traktować jako napięcia na reaktancji

indukcyjnej

m

m

s

ws

s

r

s

I

jX

f

k

N

E

E

2

'

0

(3.28)

m

m

u

u

r

r

s

wr

r

r

I

X

js

E

s

s

E

s

f

k

N

E

'

0

0

2

(3.29)

s

s

s

s

ws

s

s

I

jX

f

k

N

E

2

(3.30)

r

r

r

s

ws

s

r

I

sX

j

s

f

k

N

E

2

(3.31)

Dla uzwojenia stojana i wirnika można sporządzić bilans napięć

s

s

s

s

s

s

s

s

s

I

R

I

X

j

E

I

R

E

E

U

(3.32)

r

r

r

r

r

r

r

r

I

R

I

X

js

s

E

I

R

E

E

0

0

(3.33)

Równaniom (3.32) i (3.33) odpowiada schemat zastępczy przestawiony na rys.3.10.

Mnożąc drugie równanie obustronnie przez

s

u

otrzymuje się

i

r

i

u

r

i

r

i

u

r

u

r

I

s

R

I

X

j

E

0

0

(3.34)

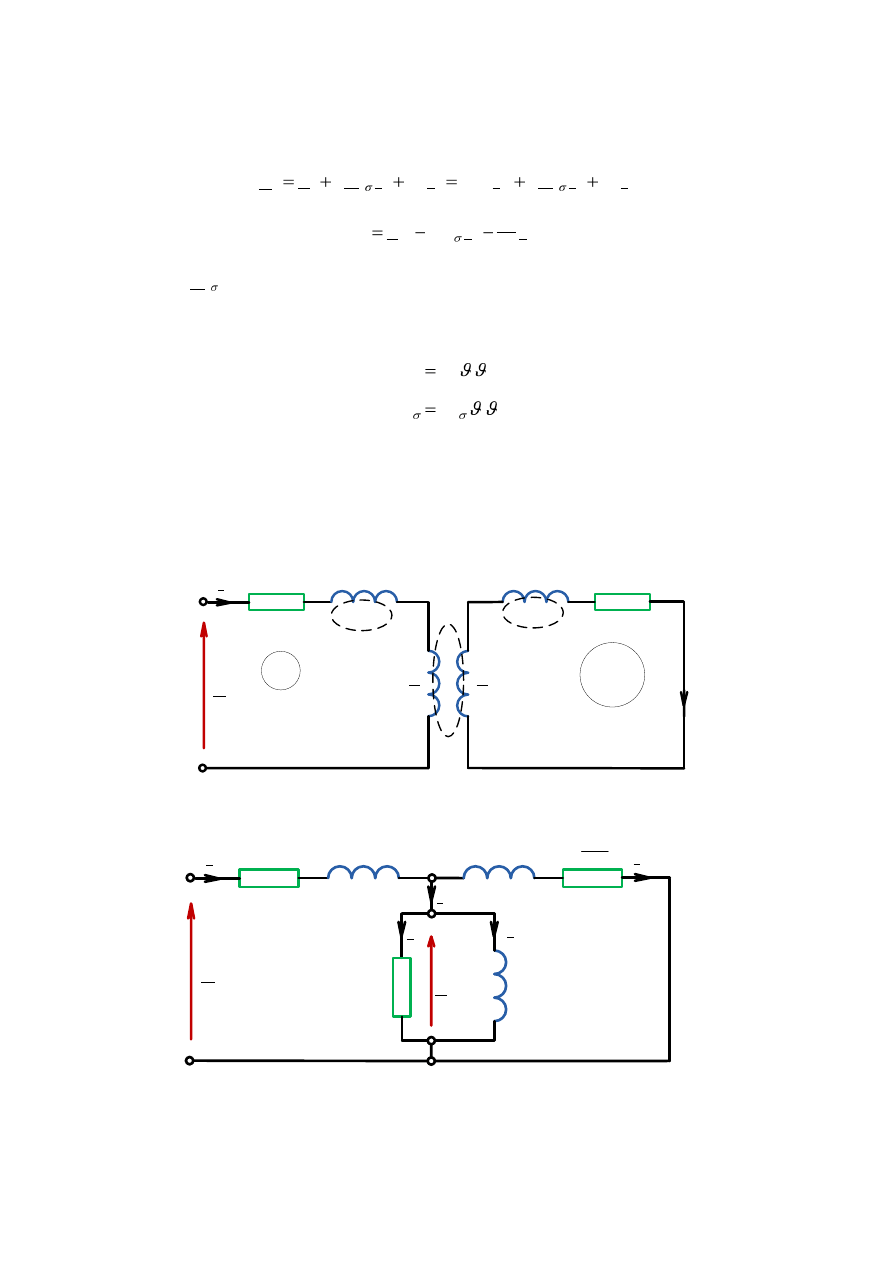
Uwzględniając zależności (3.18) i (3.28) oraz równania (3.32) i (3.34) można zapisać

w postaci

s

s

s

s

m

m

s

s

s

s

s

s

I

R

I

X

j

I

jX

I

R

I

X

j

E

U

(3.35)

'

'

'

'

'

0

0

r

r

r

r

r

I

s

R

I

jX

E

(3.36)

gdzie:

'

r

R

,

'
r

X

- odpowiednio, rezystancja i reaktancja rozproszenia wirnika sprowadzona na

stronę uzwojenia stojana, przy czym

i

u

r

r

R

R

'

(3.37)

i

u

r

r

X

X

'

(3.38)

Równaniom (3.35) i (3.36) odpowiada schemat zastępczy przedstawiony na rys.3.10. oraz

wykres wskazowy (rys 3.11.).

a)

R

s

R

r

sX

r

s

X

s

s

U

s

I

s

X

m

f

s

f

r

=sf

s

`

`

`

`

E

s

`

F

E

r

F

s

F

r

b)

R

s

R

’

r

X

’

r

s

X

s

s

R

Fe

E

s

=E’

r0

U

s

I

’

r

I

s

I

0

I

Fe

I

m

X

m

s

Rys.3.10. Schematy zastępcze maszyny indukcyjnej: a) oddzielone obwody stojana i wirnika, b)

połączenie obwodów stojana i wirnika w czwórnik z uwzględnieniem strat w rdzeniu.

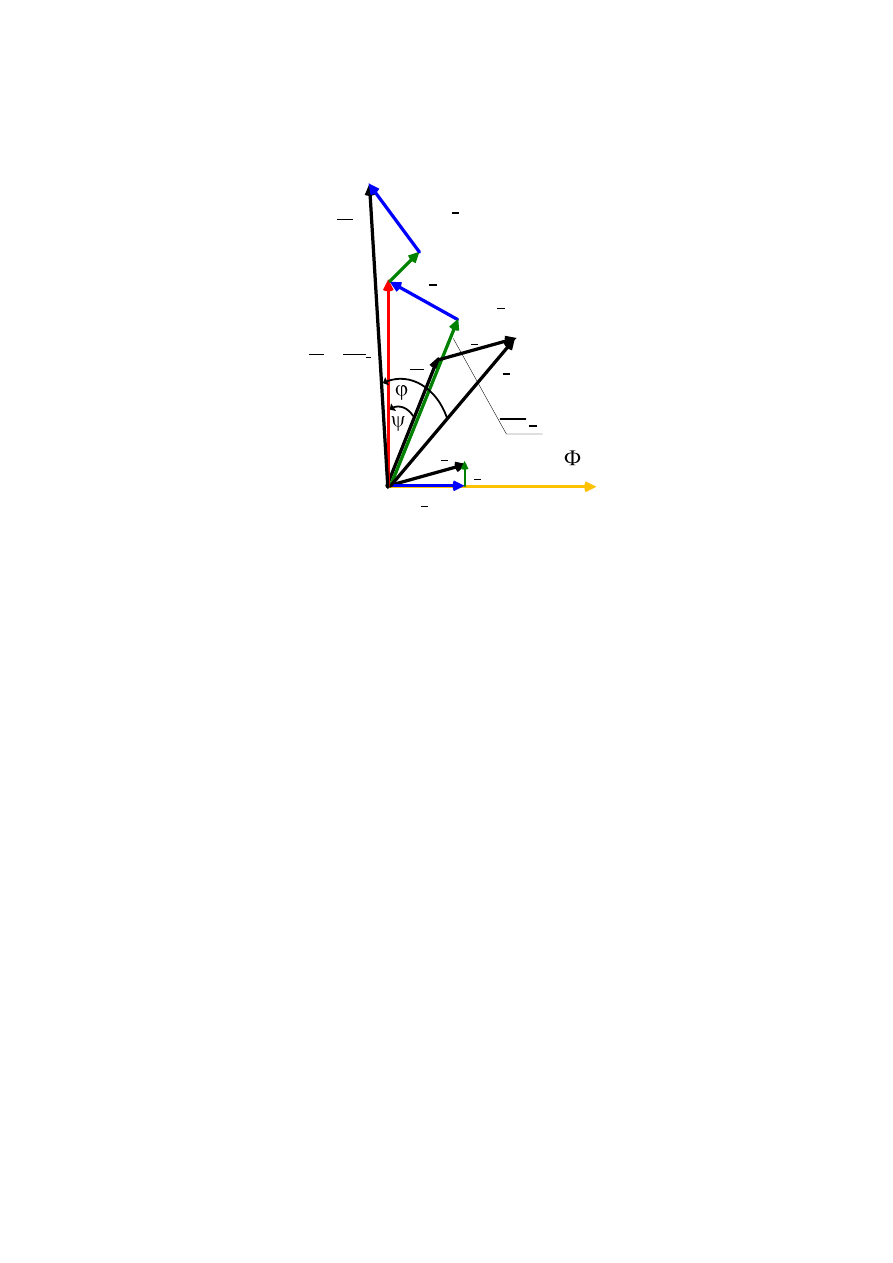
Schemat zastępczy przedstawiony na rys.3.10.b) uzupełniony jest o rezystancję R

Fe

reprezentującą straty w rdzeniu stojana.

U

s

jX’

r

s

I’

r

R

s

I

s

jX’

s

s

I

s

s

I

Fe

I

0

I

m

I’

r

I’

r

I

s

E

s

=E’

r

r

R’

r

s

I

0

Rys.3.11. Wykres wskazowy maszyny indukcyjnej dla stanu obciążenia.

3.4 PODSTAWOWE STANY PRACY MASZYNY INDUKCYJNEJ

3.4.1

Stan jałowy

Stan jałowy maszyny indukcyjnej występuje wtedy, gdy maszyna na wale nie jest

obciążona momentem mechanicznym. Pracuje ona wówczas jako silnik, którego wirnik

obraca się z prędkością bliską prędkości synchronicznej. Poślizg w tym stanie pracy jest

znikomo mały rzędu 0.001, a zatem rezystancja wirnika

s

R

r

/

, czyli można uważać że

obwód wirnika jest rozwarty (I

r

=0). Schemat zastępczy silnika i wykres wskazowy

przedstawiono na rys.3.12.

a)

R

s

X

s

s

R

Fe

E

s

U

s

I

s0

I

0

I

Fe

I

m

X

m

b)

U

s

R

s

I

0

jX

s

s

I

0

0

I

Fe

I

0i

I

m

E

s

I

0

I

mech

Rys. 3.12. Stan jałowy maszyny indukcyjnej (przy s=0): a) schemat zastępczy, b) wykres wskazowy,

W stanie jałowym moc pobierana z sieci P

0

idzie na pokrycie strat w uzwojeniu stojana P

Cu0

oraz w rdzeniu P

Fe

oraz strat mechanicznych P

m

0

0

0

0

cos

Cus

m

Fe

s

s

s

P

P

P

I

U

m

P

(3.39)

Prąd w stanie jałowym dla maszyn indukcyjnych przy zasilaniu napięciem znamionowym

wynosi I

s0

= (0.25 0.5)I

sN

, dla maszyn małych może osiągać wartość 0.7I

sN

. Współczynnik

mocy przy biegu jałowym cos

0

= 0.1 0.2.

Strat w rdzeniu oraz straty mechaniczne nazywane są stratami jałowymi P

0

i są mniejsze od

mocy biegu jałowego o wartość strat w uzwojeniu stojana

m

Fe

Cus

P

P

P

P

P

0

0

0

(3.40)

Straty w rdzeniu są zależne od kwadratu napięcia zasilającego U

s

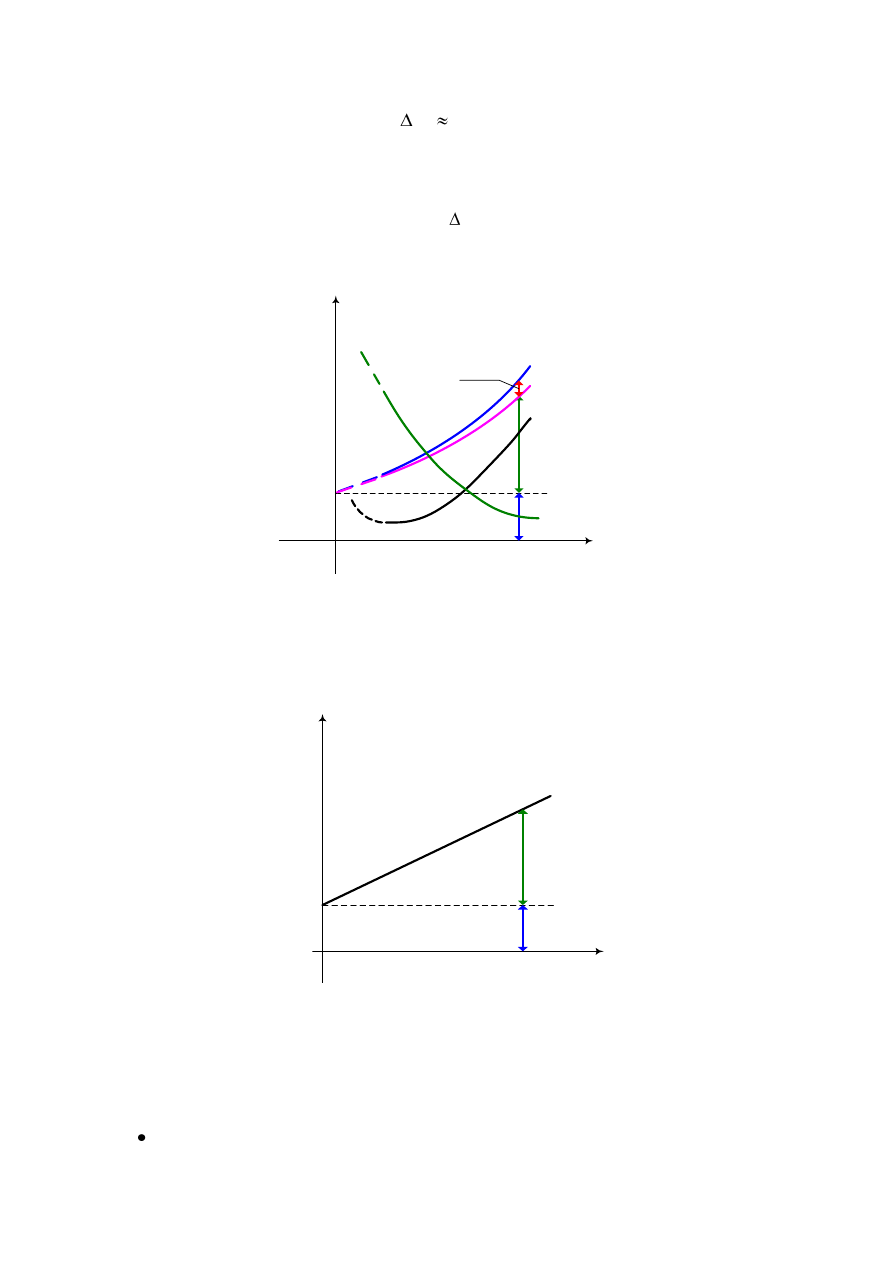
2

s

Fe

Fe

U

c

P

(3.41)

Straty mechaniczne są w przybliżeniu zależne od kwadratu prędkości obrotowej. W zakresie

niewielkich zmian prędkości są praktycznie stałe. Na rys.3.13 przedstawiono charakterystyki

biegu jałowego czyli zależność strat jałowych P

0

, prądu jałowego I

s0

, współczynnika biegu

jałowego od napięcia zasilającego.

P

0

U

sN

U

0

DP

FeN

DP

mN

DP

0

I

0

cos

f

0

DP

0

P

0

I

0

f = f

N

DP

CuN

cos

f

0

Rys. 3.13. Charakterystyki biegu jałowego.

Wykreślając straty jałowe w funkcji kwadratu napięcia, dokonujemy rozdziału strat na

straty w rdzeniu i straty mechaniczne (rys.3.14)

DP

0

U

2

sN

U

2

DP

Fe

DP

m

Rys. 3.14. Zależność strat jałowych od kwadratu napięcia – podział strat jałowych na straty w rdzeniu

i straty mechaniczne.

Na postawie pomiarów w stanie jałowym, można wyznaczyć parametry gałęzi poprzecznej

schematu zastępczego, tj. rezystancję R

Fe

reprezentującą straty w rdzeniu oraz reaktancję

magnesowania X

m

. W tym celu należy wyznaczyć

prąd reprezentujący straty mechaniczne

s

m

s

m

mech

U

P

E

P

I

(3.42)

prąd reprezentujący straty w rdzeniu

s

Fe

s

Fe

Fe

U

P

E

P

I

(3.43)

prąd magnesujący

2

2

0

)

(

mech

Fe

s

m

I

I

I

I

(3.44)

Dla obliczonych wartości prądów I

Fe

i I

m

, rezystancję R

Fe

i reaktancję magnesowania

wyznacza się z zależności

Fe

s

Fe

s

Fe

I

U

I

E

R

(3.45)

m

s

m

s

m

I

U

I

E

X

(3.46)

3.4.2

Stan zwarcia

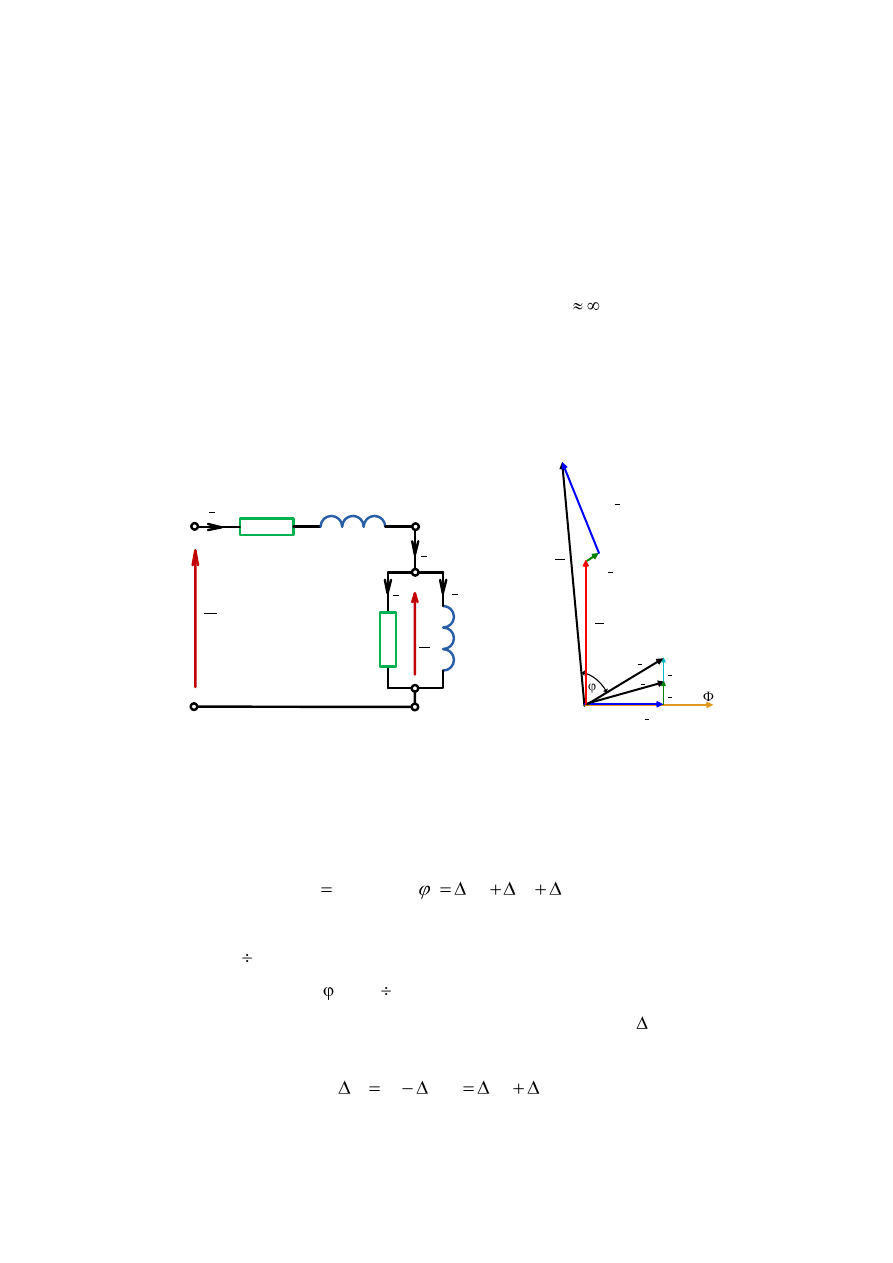
Stanem zwarcia maszyny indukcyjnej nazywamy stan, który występuje gdy uzwojenie

stojana jest zasilane a wirnik zahamowany (n =0, s =1) i zwarty. Schemat zastępczy dla stanu

zwarcia przedstawiono na rys.3.15.a). W stanie zwarcia można pominąć prąd jałowy I

0

i korzystać z uproszczonego schematu zastępczego (rys.3.15. b)), któremu odpowiada wykres

wskazowy przedstawiony na rys.3.15. c).

a)

R

s

R

’

r

X

’

r

s

X

s

s

R

Fe

E

s

=E’

r

U

s

I

sz

I

0

I

Fe

I

m

X

m

I

rz

b)

R

s

R

’

r

X

’

r

s

X

s

s

U

s

I

sz

I

’

rz

E

s

=E’

r

c)

E

s

= E’

r

z

U

s

R’

r

I’

rz

R

1

I

sz

jX’

r

s

I’

rz

jX’

s

s

I

sz

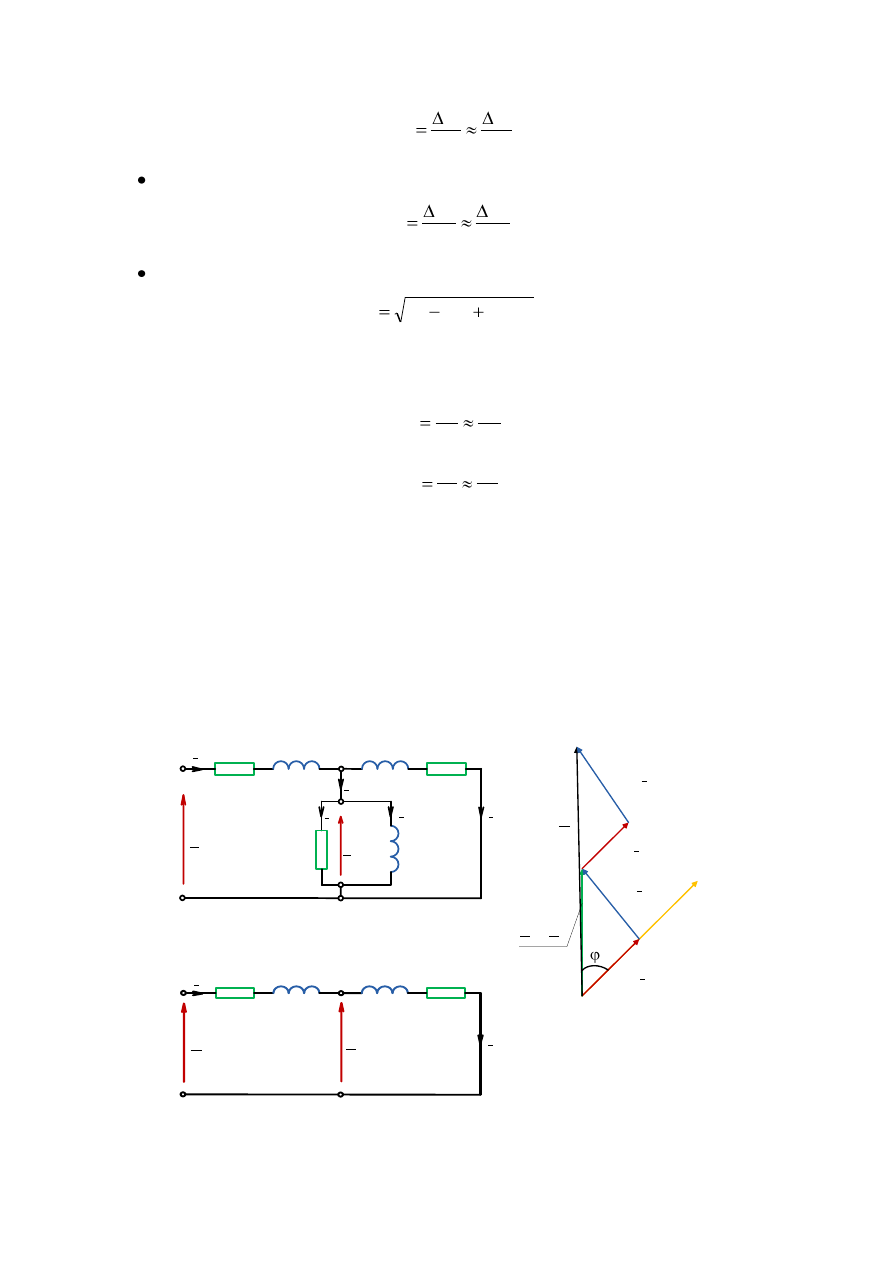
Rys. 3.15. Stan zwarcia maszyny indukcyjnej: a),b) schemat zastępczy, c) wykres wskazowy.

Na rys.3.16. przedstawiono schemat zastępczy i wykres wskazowy maszyny indukcyjnej

w formie zwartej.

a)

U

s

I

rz

R

z

X

z

I

sz

b)

z

U

s

R

z

I

z

I

z

jX

z

I

z

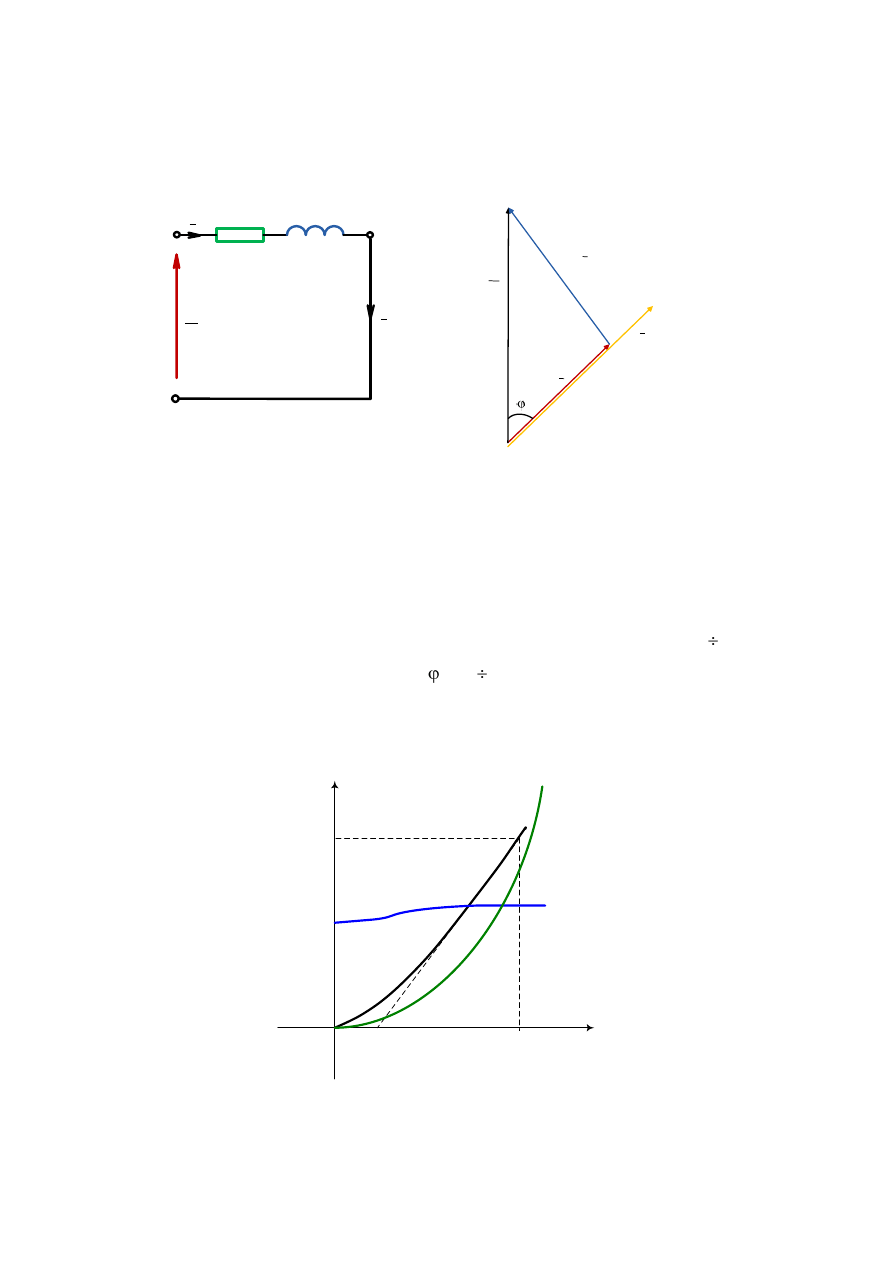
Rys. 3.16. Stan zwarcia maszyny indukcyjnej w formie zwartej: a) schemat zastępczy, b) wykres

wskazowy; R

z

=R

s

+R’

r

, X

z

=X

s

+X’

r

.

W stanie zwarcia przy zasilaniu silnika napięciem znamionowym, silnik pobiera z sieci prąd

5-8 krotnie większy od znamionowego. Stan zwarcia laboratoryjnego wykonuje się przy

takim napięciu, zwanym napięciem zwarcia, przy którym w uzwojeniu stojana płynie prąd

znamionowy. Napięcie zwarcia maszyn indukcyjnych wynosi zwykle (0.15 0.20)U

sN

.

Współczynnik mocy w stanie zwarcia cos

z

=0.2 0.4. Na rys.3.17 przedstawione są tzw.

charakterystyki zwarcia, czyli zależności prądu, mocy i współczynnika mocy od napięcia

zasilania w stanie zwarcia.

I

z

U

zN

U

z

P

z

cos

f

z

f = f

N

P

z

cos

f

z

I

z

s = 1

DU

z

Rys. 3.17. Charakterystyki stanu zwarcia.

Moc pobierana z sieci w stanie zwarcia P

z

, wobec znikomych strat w rdzeniu, idzie na

pokrycie strat obciążeniowych tj. strat w uzwojeniach stojana i wirnika, czyli

2

z

s

z z

P

m R I

(3.47)

gdzie: I

z

– prąd stojana w stanie zwarcia, R

z

– rezystancja zwarcia, przy czym

'

z

s

r

R

R

R

(3.48)

Z pomiarów w stanie zwarcia można wyznaczyć parametry gałęzi poprzecznej schematu

zastępczego, tj.

impedancję zwarcia

z

z

z

U

Z

I

(3.49)

rezystancję zwarcia

2

3

z

z

z

P

R

I

(3.50)

reaktancję zwarcia

2

2

z

z

z

X

Z

R

(3.51)

Znając rezystancję stojana R

s

, rezystancję wirnika wyznaczamy z zależności (3.48)

'

r

z

s

R

R

R

(3.52)

Nie istnieje prosta metoda pozwalająca z pomiarów wyznaczyć oddzielnie reaktancję
rozproszenia stojana X

s

i reaktancję rozproszenia wirnika

'

r

X

. Dla silników

pierścieniowych można przyjąć, że reaktancje te są sobie równe

'

2

z

s

r

X

X

X

(3.53)

Dla silników klatkowych można przyjmować następujące relacje

0.35

s

z

X

X

(3.54)

'

0.65

r

z

X

X

(3.55)

3.4.3

Bilans mocy

Silnik indukcyjny pobiera z sieci moc czynną

1

cos

s s

s

s

P

m I U

(3.56)

Odejmując od tej mocy straty w uzwojeniu stojana

s

s

s

Cus

R

I

m

P

2

(3.57)

Oraz straty w rdzeniu

2

2

s

Fe

Fe

Fe

s

Fe

U

c

R

I

m

P

(3.58)

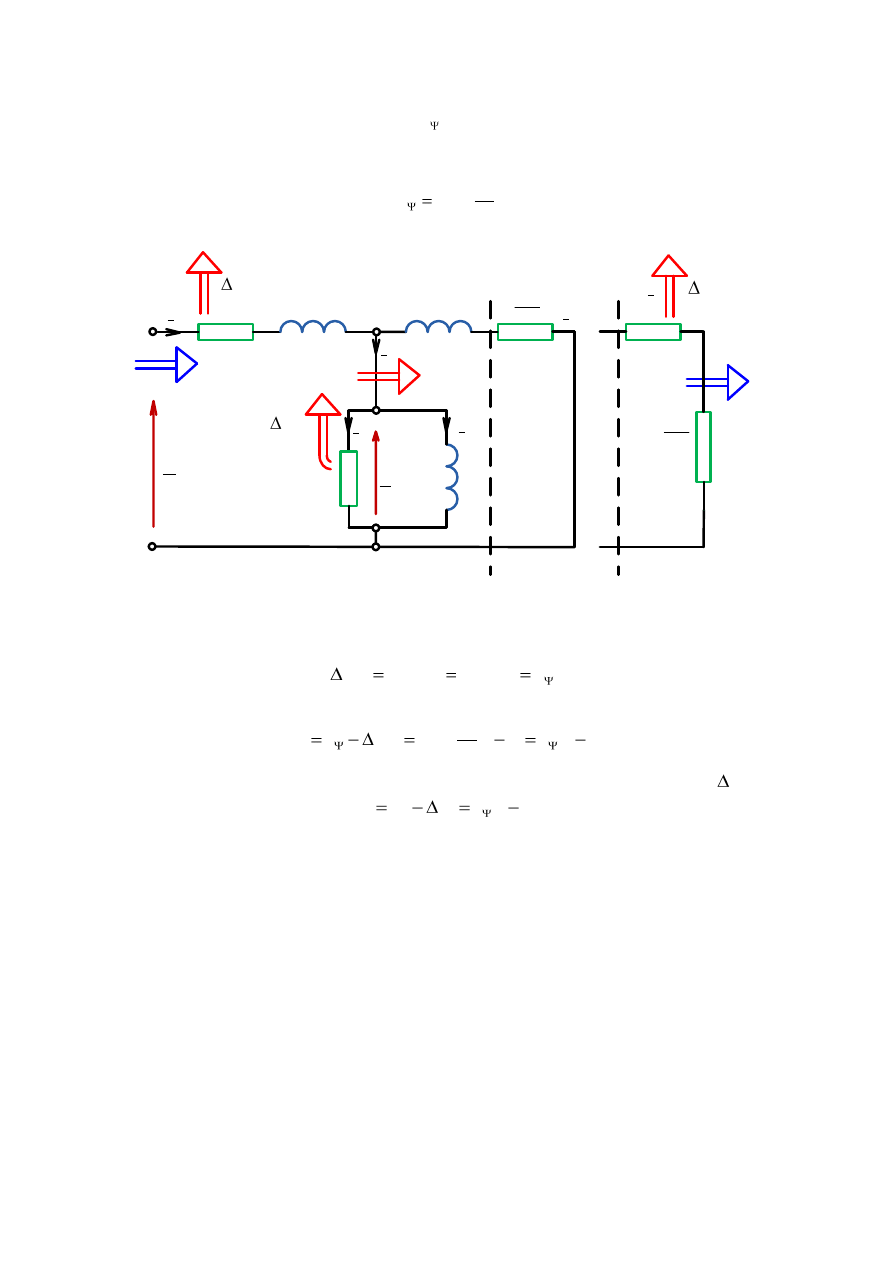
Otrzymuje się moc elektromagnetyczną P

przekazywaną ze stojana do wirnika, która

zgodnie ze schematem zastępczym (rys.3.18) wynosi

s

R

I

m

P

r

r

s

'

2

'

(3.59)

I

r

R

s

R

’

r

X

’

r

s

X

s

s

R

Fe

E

s

=E’

20

U

s

I

’

r

I

s

I

0

I

Fe

I

m

X

m

P

1

P

y

P

Fe

s

R

’

r

R

’

r

1-

s

s

P

m

P

Cur

P

cu1

Rys.3.18. Schemat zastępczy maszyny indukcyjnej ilustrujący bilans rozpływu mocy i strat mocy.

Odejmując od mocy elektromagnetycznej straty w uzwojeniu wirnika

s

P

R

I

m

R

I

m

P

r

r

s

r

r

r

Cur

'

2

'

2

(3.60)

moc mechaniczną

)

1

(

)

1

(

'

2

'

s

P

s

s

R

I

m

P

P

P

r

r

s

Cur

m

(3.61)

Moc na wale silnika

2

P jest mniejsza od mocy mechanicznej od straty mechaniczne

m

P

)

1

(

2

s

P

P

P

P

m

m

(3.62)

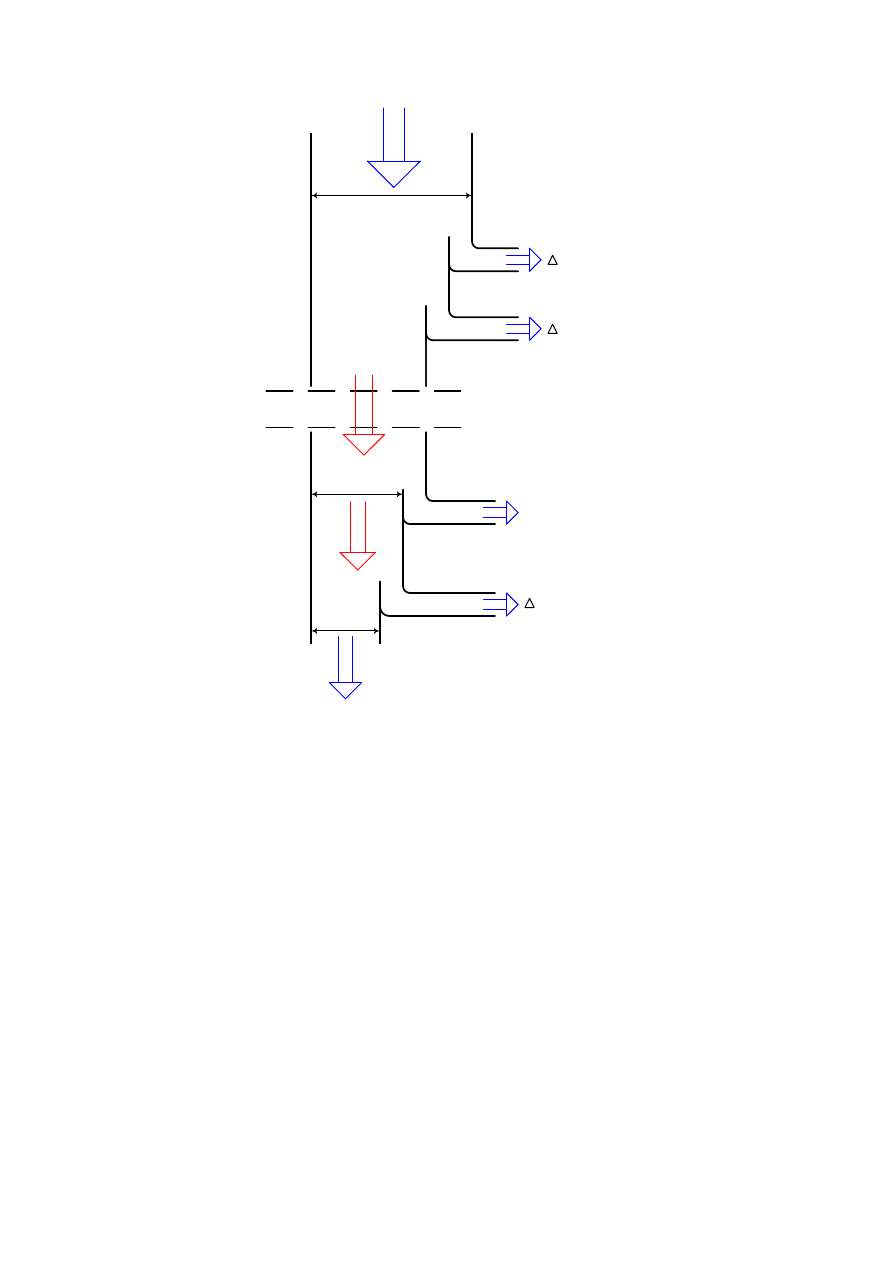
Straty mechaniczne nie są ujęte na schemacie zastępczym. Bilans mocy i strat przedstawiono

na schemacie zastępczym (rys.3.18.) oraz zilustrowano na wykresie rozpływu mocy i strat

zwanym wykresem Sankeya (rys.3.19.).

P

Cus

P

Fe

DP

Cur

+

DP

e

=Pe

P

m

P

2

P

1

P

y

P

m

w

ir

n

ik

Szczelina

powietrzna

s

to

ja

n

Rys.3.19. Wykres rozpływu mocy i strat mocy maszyny indukcyjnej – wykres Sankey’a.

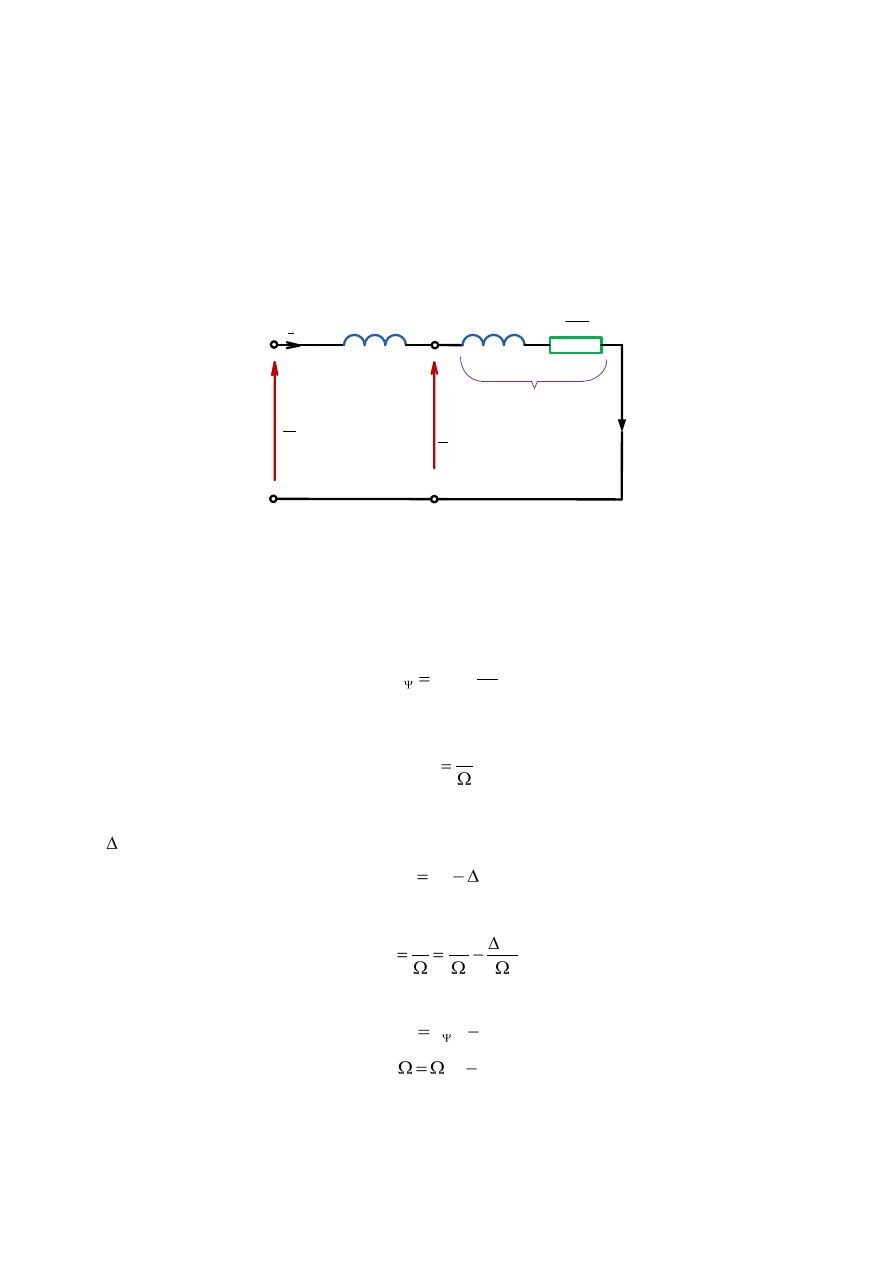
3.5 MOMENT ELEKTROMAGNETYCZNY, CHARAKTERYSTYKA

MECHANICZNA MASZYNY INDUKCYJNEJ

W celu wyprowadzenia zależności na moment elektromagnetyczny pomija się zwykle

rezystancję stojana R

s

oraz prąd biegu jałowego I

0

, otrzymując uproszczony schemat

zastępczy przedstawiony na rys.3.20.

R

’

r

X

’

r

s

X

s

s

E

s

=E’

r0

U

s

I

S

s

Z

’

r

(s)

I

’

r

≈ I

s

Rys.3.20. Schemat zastępczy silnika indukcyjnego w którym pominięto rezystancję stojana R

s

oraz prąd jałowy I

0

.

Moc elektromagnetyczna przekazywana ze stojana do wirnika, jak to wynika ze schematu

zastępczego jest równa

s

R

I

m

P

r

r

s

'

2

'

(3.63)

Moment na wale silnika jest równy

s

P

M

(3.64)

Uwzględniając, że moc na wale jest mniejsza od mocy mechanicznej o straty mechaniczne

P

m

m

m

s

P

P

P

(3.65)

równanie (3.64) można napisać w postaci

m

m

s

P

P

P

M

(3.66)

Uwzględniając, że

)

1

(

s

P

P

m

(3.67)

)

1

(

s

s

(3.68)

równanie (3.66) można napisać w postaci

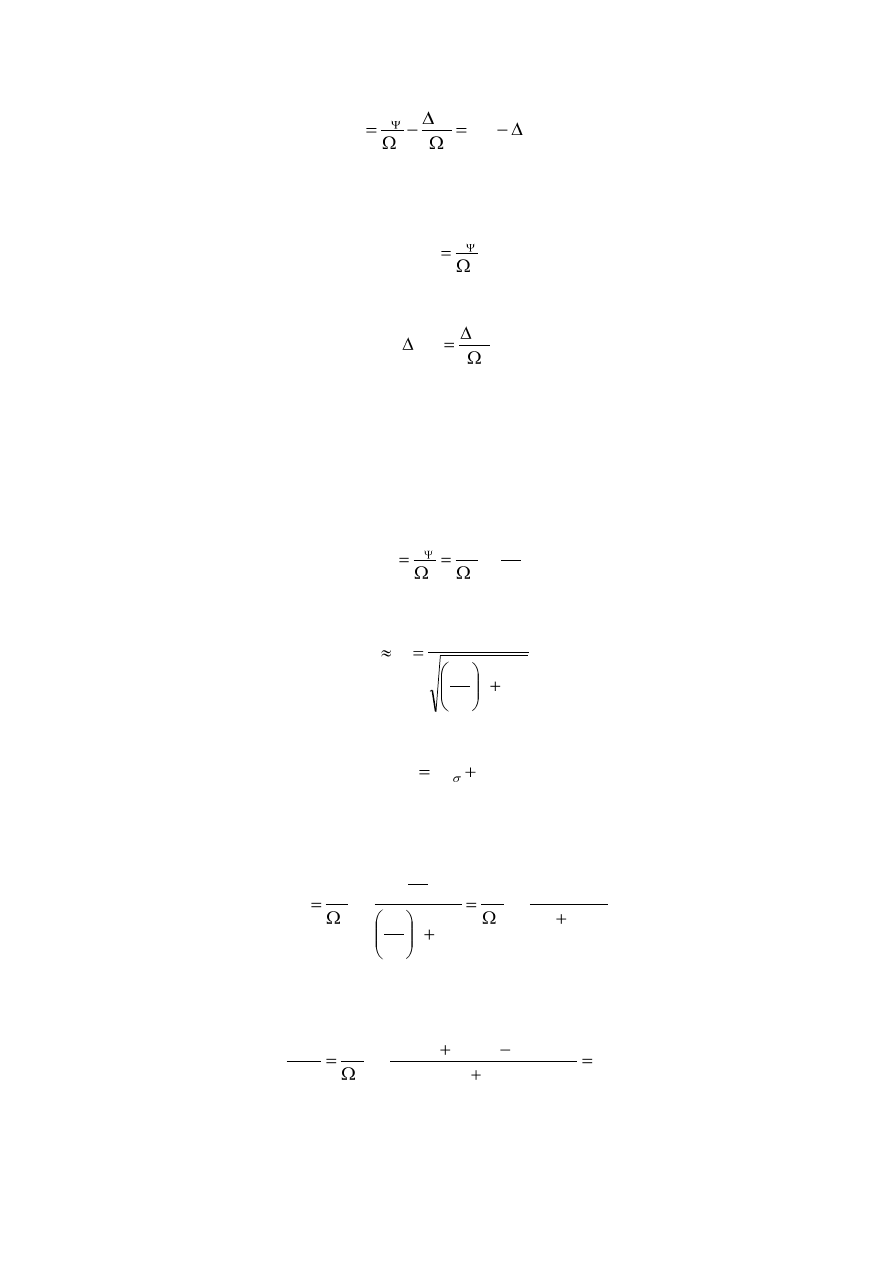
m

e

m

s

M

M

P

P

M

(3.69)

Pierwszy składnik równania (3.69) reprezentuje moment elektromagnetyczny

s

e

P

M

(3.70)

natomiast drugi składnik reprezentuje moment strat mechanicznych

m

m

P

M

(3.71)

A więc moment na wale jest mniejszy od momentu elektromagnetycznego o wartość

momentu strat mechanicznych. W silnikach o mocy powyżej 1 kW możemy pominąć moment

strat mechanicznych i przyjąć, że moment na wale jest równy momentowi

elektromagnetycznemu. Uwzględniając zależność (3.59), moment elektromagnetyczny można

wyznaczyć ze wzoru

s

R

I

m

P

M

r

r

s

s

s

e

'

2

'

(3.72)

Na podstawie uproszczonego schematu zastępczego można wyznaczyć prąd wirnika

2

2

'

'

k

r

s

s

r

X

s

R

U

I

I

(3.73)

gdzie: X

k

– reaktancja zwarcia, przy czym

'

r

s

k

X

X

X

(3.74)

Podstawiając zależność (3.73) do równania (3.72), otrzymujemy wyrażenie na moment

elektromagnetyczny silnika indukcyjnego

2

2

2

'

'

2

2

2

'

'

2

k

r

r

s

s

s

k

r

r

s

s

s

e

X

s

R

s

R

U

m

X

s

R

s

R

U

m

M

(3.75)

Obliczając pochodną momentu M

e

względem poślizgu s, wyznacza się wartość momentu

maksymalnego

0

2

)

(

2

2

2

'

'

2

2

2

2

2

'

'

2

k

r

r

k

k

r

r

s

s

s

e

X

s

R

R

X

s

X

s

R

R

U

m

ds

dM

(3.76)

stąd

k

r

k

X

R

s

'

(3.77)

Wyrażenie (3.77) nazywamy poślizgiem krytycznym. Jest to wartość poślizgu, dla którego

moment elektromagnetyczny osiąga wartość maksymalną. Podstawiając zależność (3.77) do

równania (3.75), otrzymuje się wyrażenie na moment maksymalny M

k

zwany również

momentem krytycznym

k

s

s

s

k

X

U

m

M

2

2

(3.78)

Znak (+) we wzorach (3.77) i (3.78) odnosi się do pracy silnikowej a znak (-) do pracy

prądnicowej. Uwzględniając, że

p

f

p

s

s

s

2

(3.79)

k

s

k

L

f

X

2

(3.80)

równanie na moment krytyczny przyjmie postać

2

2

8

s

s

k

s

k

f

U

L

p

m

M

(3.81)

Z zależności (3.81) wynika, że moment maksymalny jest proporcjonalny do kwadratu

wartości skutecznej napięcia fazowego stojana i odwrotnie proporcjonalny do kwadratu

częstotliwości napięcia zasilającego. Przy zachowaniu stałego stosunku

.

const

f

U

s

s

(3.82)

moment krytyczny ma stałą wartość.

Stosunek momentu przy dowolnym poślizgu (3.75) do momentu maksymalnego (3.78)

określa zależność

s

s

s

s

M

M

k

k

k

e

2

(3.83)

Wyrażenie (3.83) nosi nazwę wzoru Klossa.

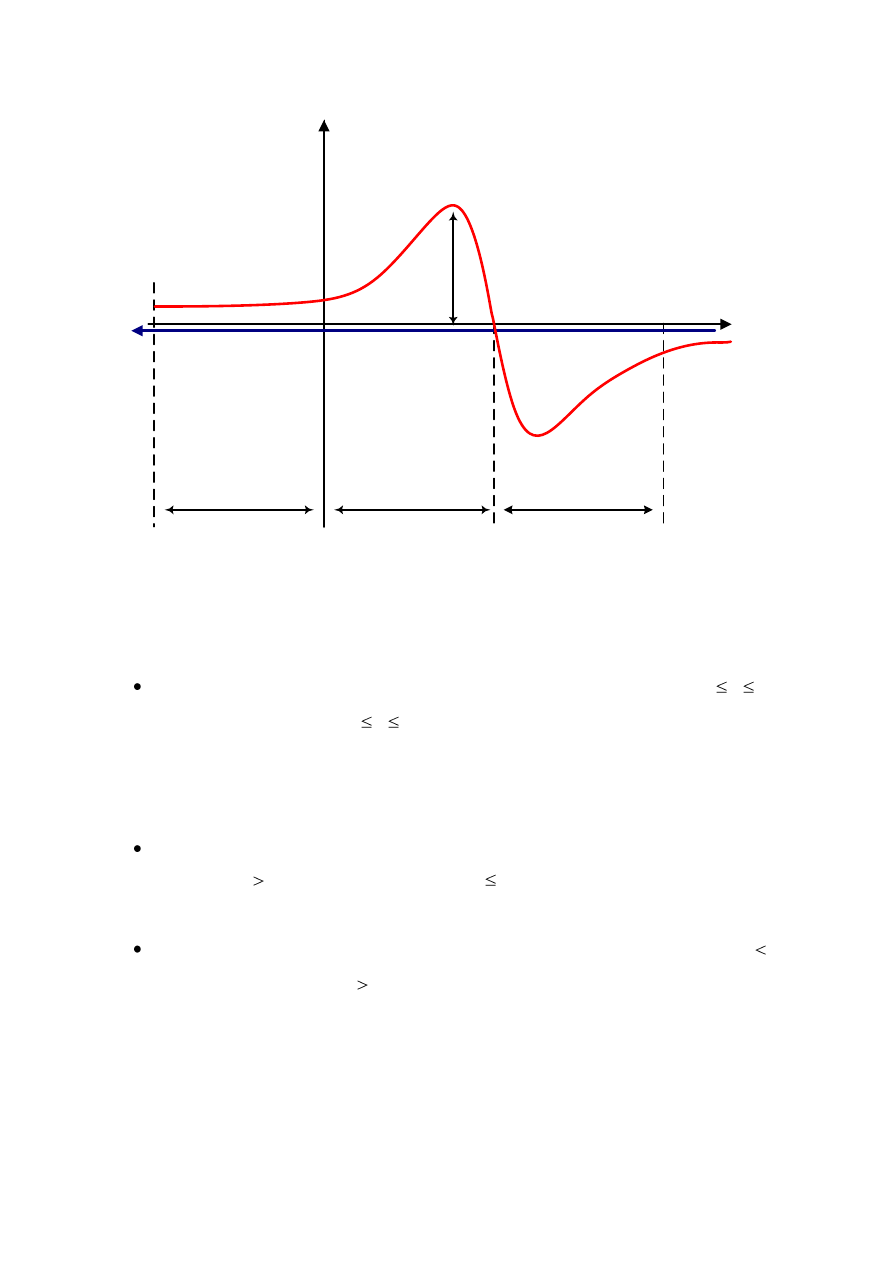
Zależność momentu elektromagnetycznego od prędkości obrotowej n lub od poślizgu s

nazywa się charakterystyką mechaniczną (rys.3.21).

0

M

M

r

hamulec

silnik

generator

s

0

1

2

-1

-n

s

M

k

n

s

s

k

2n

s

n

Rys.3.21. Charakterystyka mechaniczna maszyny indukcyjnej.

Wyróżnić tu można trzy podstawowe stany pracy silnika indukcyjnego:

praca silnikowa. Praca silnikowa występuje w zakresie prędkości obrotowej

s

n

n

0

lub w zakresie poślizgów

1

0

s

Wyróżnić tu można jeszcze stan idealnego biegu jałowego dla n = n

s

czyli s = 0 i stan zwarcia

(wirnik zahamowany) dla n = 0 czyli s = 1

praca prądnicowa (generatorowa). Praca prądnicowa występuje w zakresie prędkości

obrotowej

s

n

n

lub w zakresie poślizgów

0

s

praca hamulcowa. Praca hamulcowa występuje w zakresie prędkości obrotowej

s

n

n

lub w zakresie poślizgów

1

s

.

Przy pracy prądnicowej wirnik obraca się w kierunku wirowania pola wirującego

z prędkością większą od synchronicznej. Natomiast przy pracy hamulcowej wirnik obraca się

w kierunku przeciwnym do kierunku pola wirującego.

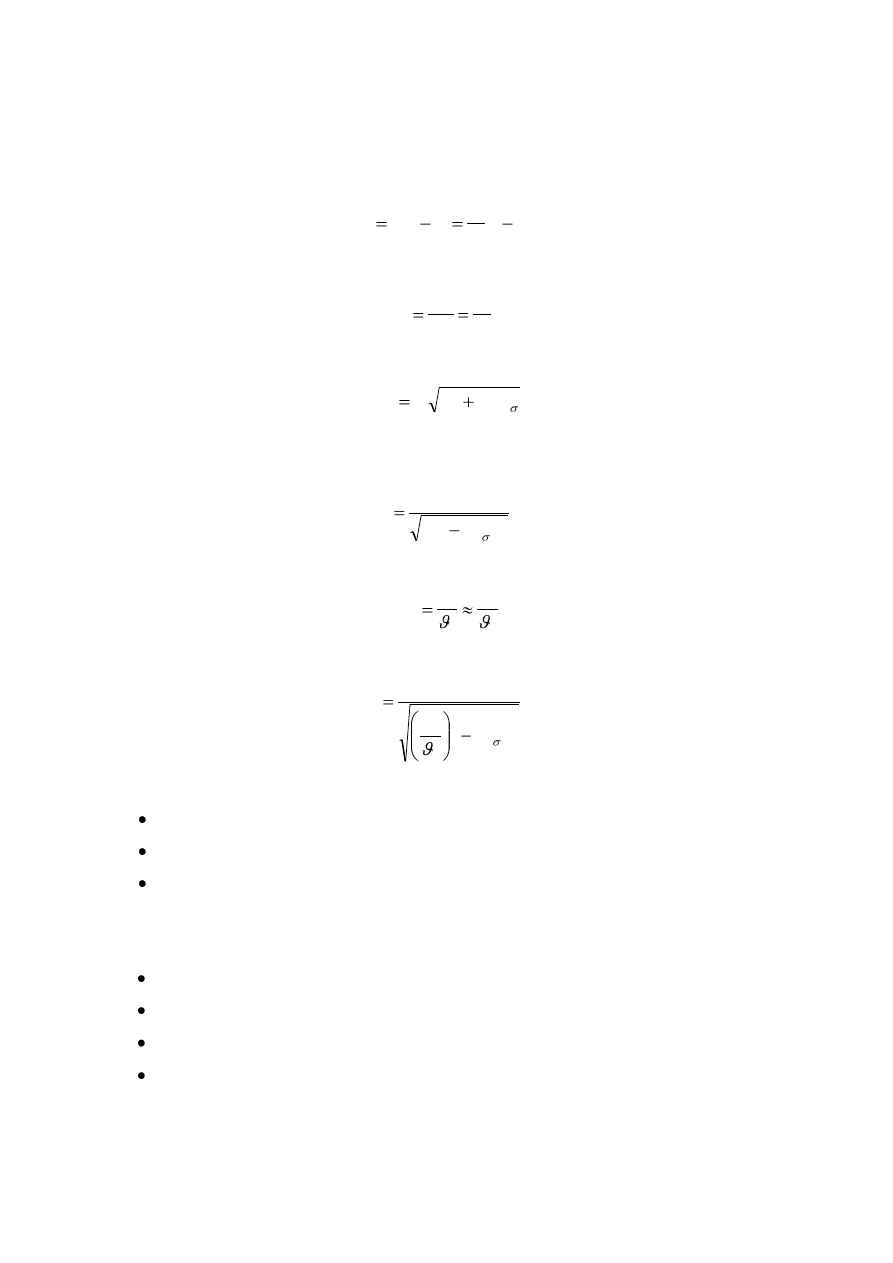
3.5 REGULACJA PRĘDKOŚCI OBROTOWEJ SILNIKÓW INDUKCYJNYCH

Prędkość obrotowa silnika zmienia się zgodnie ze wzorem (3.12) wg zależności

)

1

(

)

1

(

s

p

f

s

n

n

s

s

(3.84)

przy czym

s

r

r

r

f

f

E

E

s

0

(3. 85)

Biorąc pod uwagę, że

2

2

2

0

r

r

r

r

X

s

R

I

E

(3.86)

równanie (3.85) po przekształceniach algebraicznych ze względu na poślizg s możemy

zapisać w postaci

2

2

2

0

r

r

r

r

r

I

X

E

I

R

s

(3.87)

Uwzględniając, że

u

s

u

s

r

U

E

E

0

(3.88)

zależność (3.87) przyjmie postać

2

2

2

r

r

u

s

r

r

I

X

U

I

R

s

(3.89)

Z zależności (3.84) wynika, że prędkość obrotową można regulować przez zmianę

częstotliwości f

s

napięcia zasilającego

liczby par biegunów p

poślizgu s

Poślizg silnika, jak wynika ze wzorów (3.89), w praktyce reguluje się trzema sposobami

przez zmianę napięcia zasilającego U

s

przez zmianę rezystancji w obwodzie wirnika – silniki pierścieniowe

przez zmianę częstotliwości w obwodzie wirnika – silniki pierścieniowe

przez zmianę napięcia E

r

doprowadzonego do obwodu wirnika – silniki pierścieniowe

Przy rozpatrywaniu regulacji prędkości obrotowej przez zmianę jednego z parametrów,

pozostałe parametry przyjmuje się jako stałe.

3.6.1 Regulacja napięcia poprzez zmianę częstotliwości

Zmieniając częstotliwość napięcia zasilania silnika indukcyjnego regulujemy prędkość

synchroniczną pola wirującego, a tym samym jak to wynika ze wzoru (3.84), regulujemy

prędkość wirnika. Przebieg charakterystyk mechanicznych przy zmianach częstotliwości

i stałej wartości amplitudy napięcia zasilającego przedstawiono na rys. 3.22.

M

n

sN

0

M

kN

M

k

’

M

k

’’

f

’

< f

N

f

’’

> f

N

f = f

N

M

m

n

s

’’

n

s

’

n

N

n

’’

n

’

n

Rys.3.22. Charakterystyki mechaniczne przy zmianie częstotliwości przy U

s

=const.

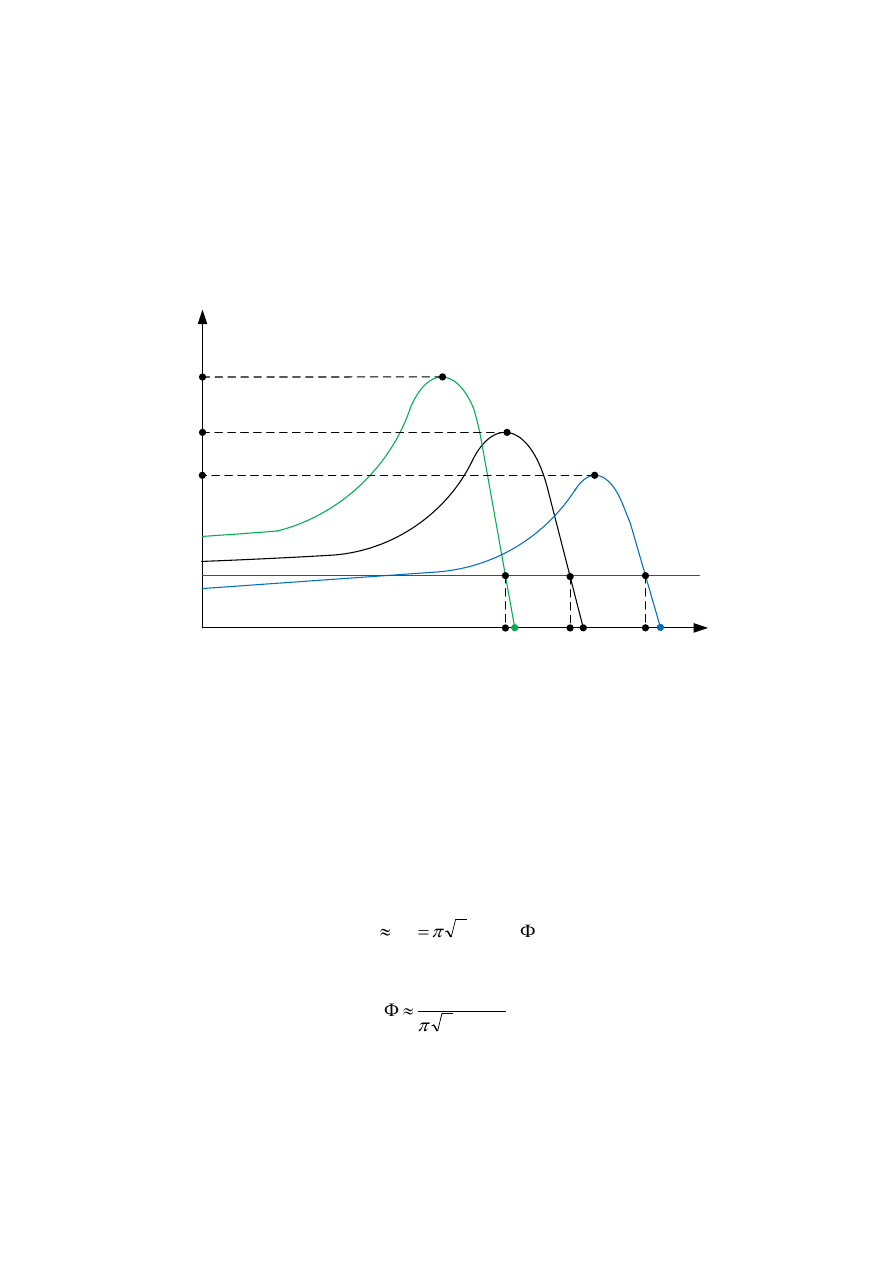
Zmniejszenie częstotliwości, przy stałym napięciu zasilającym i stałym momencie obciążenia

mechanicznego, powoduje spadek prędkości obrotowej i wzrost momentu maksymalnego.

Natomiast wzrost częstotliwości powoduje zwiększenie prędkości obrotowej zmniejszenie

momentu maksymalnego.

Przy zmniejszeniu częstotliwości strumień magnetyczny rośnie, gdyż przy stałej

wartości napięcia zasilającego U

s

, w przybliżeniu stała jest również wartość napięcia

indukowanego w stojanie E

s

s

ws

s

s

s

f

k

N

U

E

2

(3.90)

stąd

f

k

N

U

ws

s

s

2

(3.91)

Wzrost strumienia magnetycznego, przy zmniejszeniu częstotliwości i przy stałym napięciu

zasilającym, powoduje wzrost indukcji magnetycznej w rdzeniu stojana i wirnika i rosną

straty w rdzeniu, które są zależne od kwadratu indukcji.

Z zależności (3.91) wynika, że aby zachować stały strumień w maszynie, należy przy

zmianie częstotliwości utrzymywać stały stosunek napięcia zasilającego do częstotliwości,

czyli

.

const

f

U

s

s

(3.92)

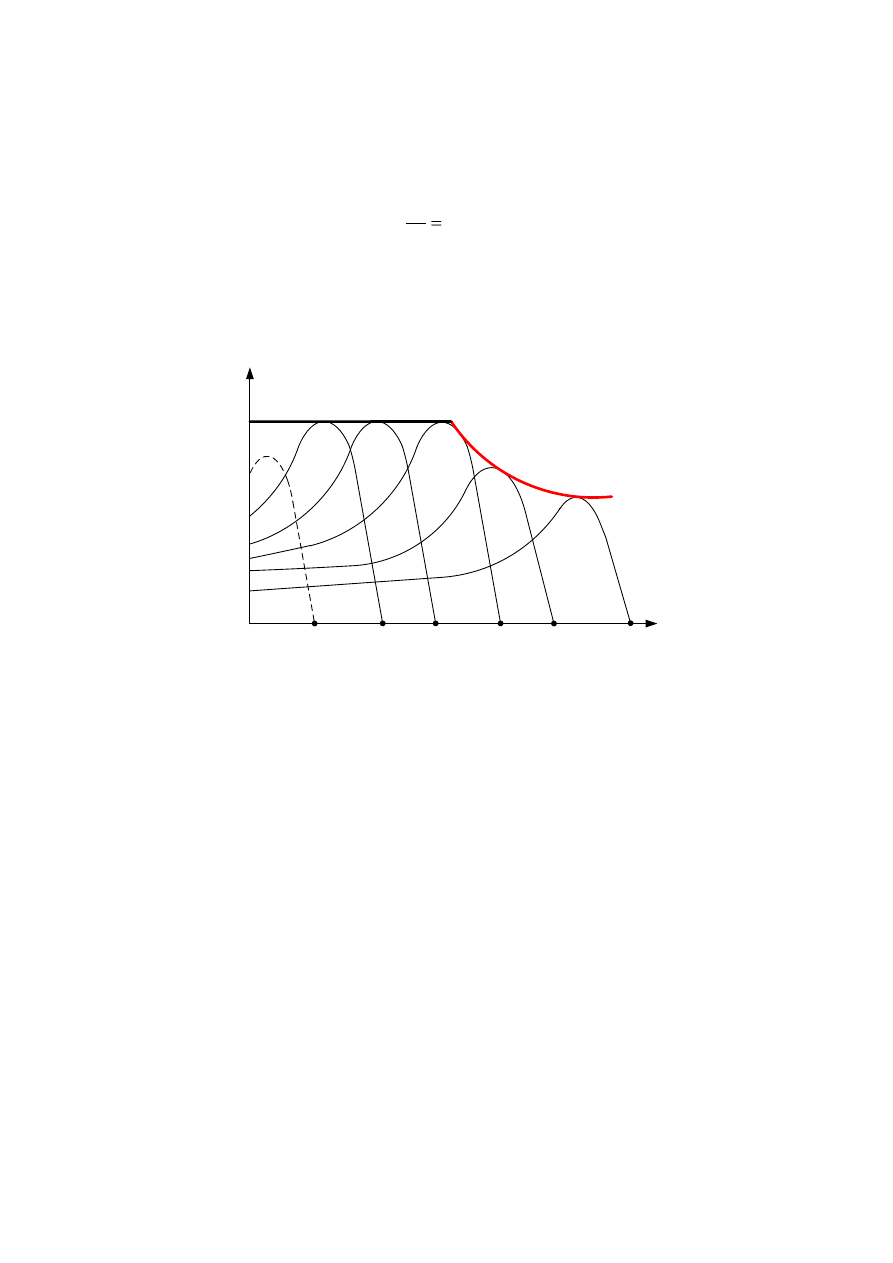
Zgodnie ze wzorem (3.81) moment maksymalny będzie miał wtedy również stałą wartość. Na

rys.3.23. przedstawiono przebieg charakterystyk mechanicznych M=f(n) dla różnych wartości

częstotliwości oraz przy zachowaniu warunku (3.92).

M

n

sN

0

M

kN

M

k

=const.

n

s100

n

P=const.

100Hz

10Hz

50Hz

75Hz

40Hz

30Hz

n

s75

n

s40

n

s30

n

s10

Rys.3.23. Przebieg charakterystyk mechanicznych M=f(n) dla różnych wartości częstotliwości.

Przy bardzo małych częstotliwościach moment maksymalny ulega zmniejszeniu, gdyż

pojawia się tu wpływ pominiętej rezystancji stojana przy malejących reaktancjach. Stały

stosunek napięcia do częstotliwości jest utrzymywany przy częstotliwościach mniejszych od

znamionowej. Przy częstotliwościach większych od znamionowej należy utrzymywać stałą

wartość napięcia zasilającego równą napięciu znamionowemu, a więc moment krytyczny

będzie wtedy malał.

3.6.2 Regulacja prędkości przez zmianę liczby par biegunów

Regulację prędkości przez zmianę liczby par biegunów stosuje się tylko w silnikach

klatkowych, gdyż wystarczy zmieniać liczbę par biegunów stojana, a uzwojenie klatkowe

wirnika automatycznie dostosowuje się pod względem liczby par biegunów do pola

wirującego stojana. W silnikach pierścieniowych należałoby zmieniać również liczbę par

biegunów w wirniku. Silniki indukcyjne, w których skokowa regulacja prędkości obrotowej

odbywa się przez zmianę liczby par biegunów nazywamy silnikami wielobiegowymi. Silniki

te znalazły zastosowanie szczególnie do napędu obrabiarek, gdyż umożliwiają zmniejszenie

kosztów przekładni mechanicznej. Najczęściej stosowany jest silnik dwubiegowy o zakresie

regulacji 2:1. Posiada on jedno uzwojenie przełączalne w stojanie. W silnikach trójbiegowych

ułożone są w tych samych żłobkach dwa uzwojenia, z których jedno jest przełączalne.

W silnikach czterobiegowych, każde z dwóch uzwojeń jest przełączalne na dwie różne

prędkości obrotowe ( np. 3000, 1500, 1000 i 500 obr/min).

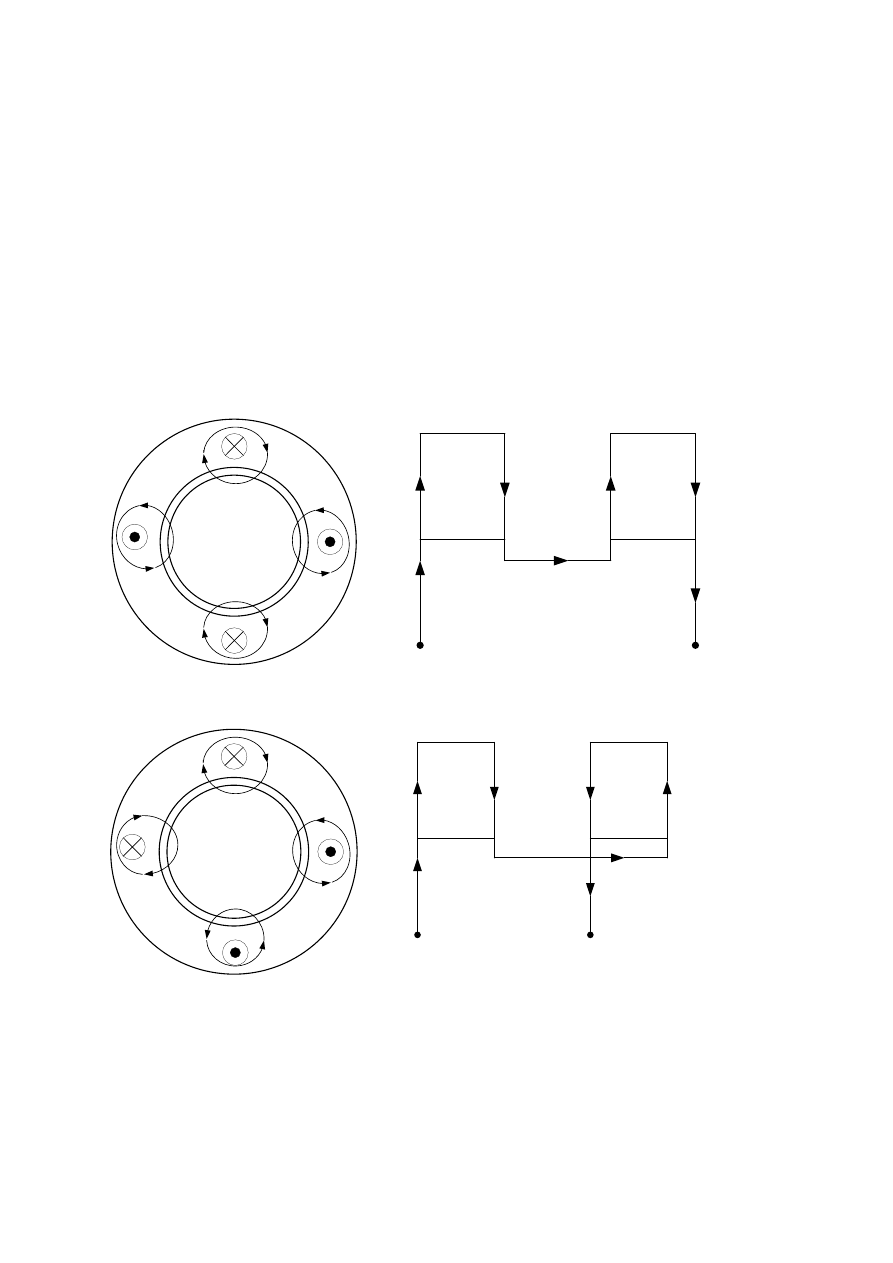
Zasadę zmiany liczby par biegunów dla jednej fazy uzwojenia stojana przedstawiono na

rys.3.24.

a)

N

N

S

S

1

2

3

4

U1

I

U2

1

2

3

4

I

I

I

I

p=2

b)

N

S

1

2

3

4

U1

I

U2

1

2

3

4

I

I

I

I

p=1

Rys.3.24. Zmiana liczby par biegunów dla jednej fazy uzwojenia stojana.

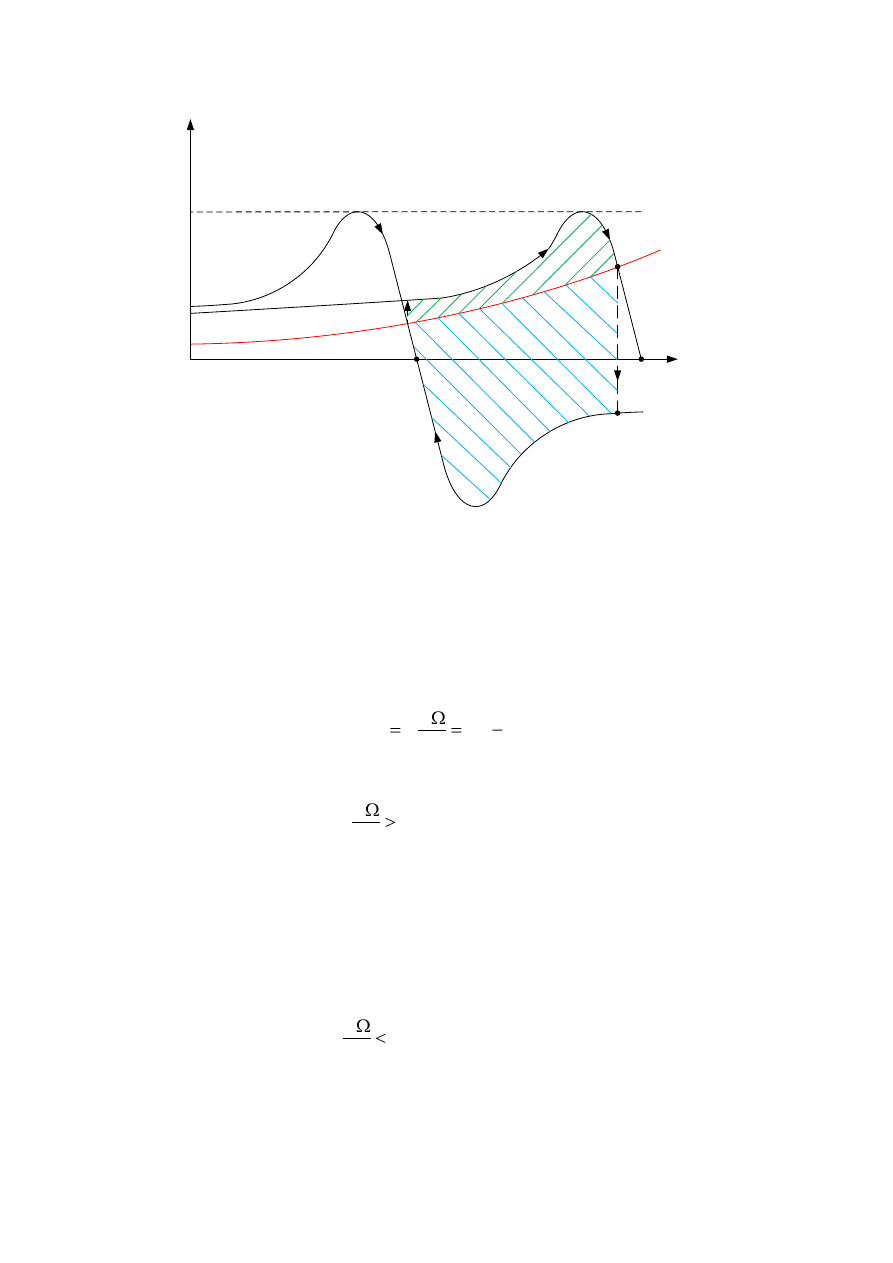
Przebieg zjawisk zachodzących przy zmianie liczby par biegunów przedstawiono na rys. 3.25

M

p=1

n

s

=1500obr/min

0

M

m

p=2

n

s

=3000obr/min

n

Rys.3.25. Charakterystyki mechaniczne przy zmianie liczby par biegunów z mniejszej na większą

i odwrotnie.

Jeżeli silnik pracuje przy prędkości odpowiadającej większej liczbie par biegunów (mniejsza

prędkość obrotowa), to w chwili przełączenia na mniejszą liczbę par biegunów (większą

prędkość), pojawia się zgodnie ze wzorem

m

e

d

M

M

t

d

d

J

M

(3.93)

nadwyżka momentu silnika nad momentem mechanicznym. Moment dynamiczny M

d

jest

wtedy większy od zera czyli

0

t

d

d

i następuje przyśpieszanie układu napędowego

i ustalenie się punktu pracy w nowym stanie równowagi.

Natomiast jeżeli silnik pracuje przy prędkości odpowiadającej mniejszej liczbie par

biegunów (większa prędkość obrotowa), to w chwili przełączenia na większą liczbę par

biegunów (mniejszą prędkość), pojawia się zgodnie ze wzorem (3.93) pojawia się nadwyżka

momentu mechanicznego nad momentem elektromagnetycznym silnika. Moment dynamiczny

M

d

jest mniejszy od zera, czyli

0

t

d

d

i następuje hamowanie układu napędowego. Wirnik

silnika posiada prędkość większą od prędkości synchronicznej pola wirującego i silnik

przechodzi do pracy generatorowej. Po zmniejszeniu się prędkości obrotowej poniżej

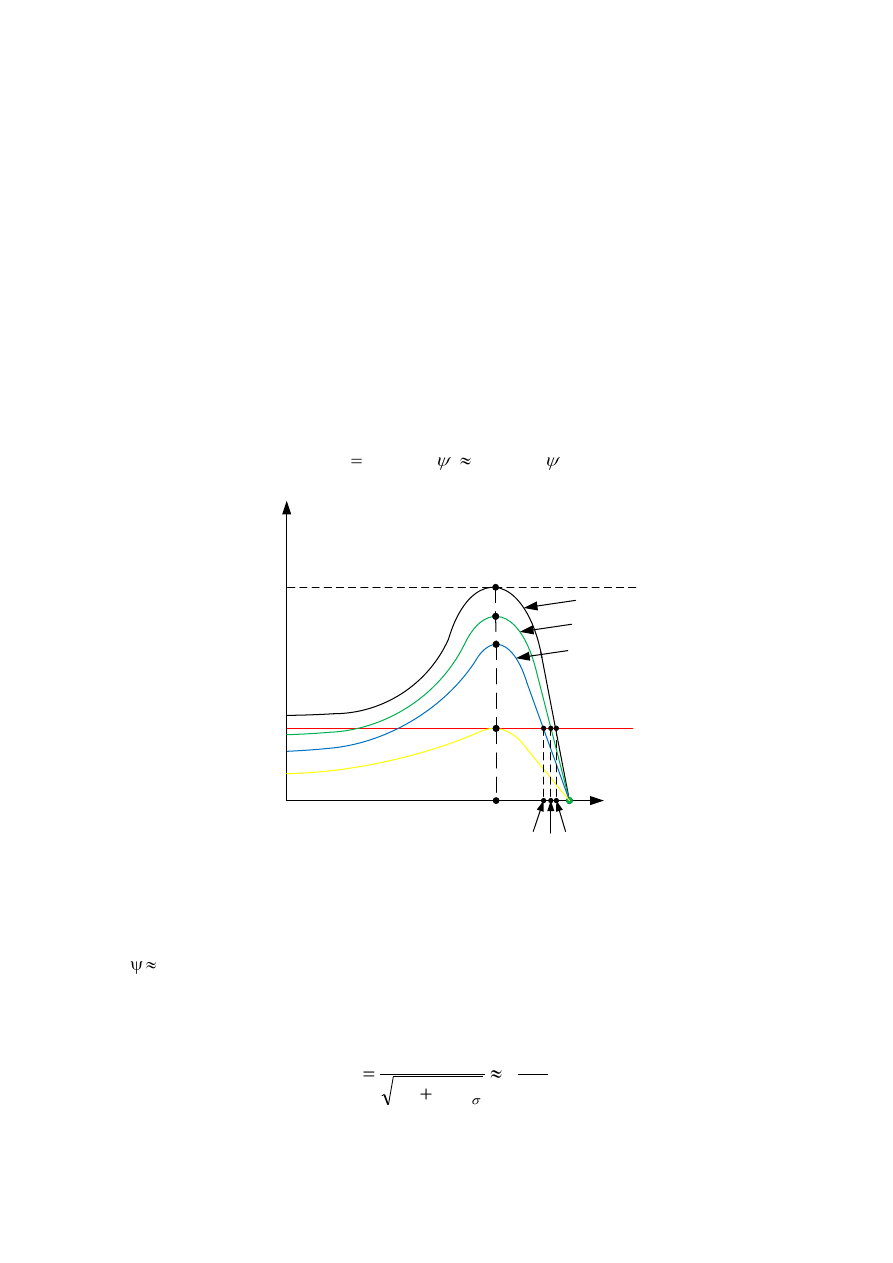
synchronicznej, kierunek momentu elektromagnetycznego ulega zmianie i maszyna

przechodzi w stan pracy silnikowej, osiągając prędkość ustaloną w nowym stanie równowagi.

3.6.3 Regulacja prędkości obrotowej przez zmianę poślizgu

Regulacja prędkości przez zmianę napięcia zasilającego

Zmiana napięcia zasilania U

s

powoduje zmianę przebiegu charakterystyk

mechanicznych (rys.3.26.). Zmniejszenie napięcia zgodnie ze wzorem (3.81) powoduje

zmniejszenie się wartości momentu maksymalnego M

k

, przy czym poślizg krytyczny s

k

nie

ulega zmianie.

Istota regulacji prędkości obrotowej wynika z zależności

r

r

s

r

r

r

I

U

c

I

cE

M

cos

cos

1

0

(3.94)

M

s

1

U=U

N

s

kr

n

s

0

M

m

U=0,9U

N

U=0,8U

N

s

N

s

1

s

2

Rys.3.26. Regulacja prędkości przez zmianę napięcia zasilającego.

Jeżeli regulacja prędkości odbywa się w małym zakresie prędkości, to można przyjąć

cos

r

const. Przy obniżeniu napięcia na zaciskach stojana i zachowaniu stałego momentu

obrotowego M=const., niezbędne jest zwiększenie prądu wirnika I

r

. Prąd wirnika określa

zależność

r

s

r

r

r

r

R

s

U

c

X

s

R

s

E

I

2

2

2

0

(3.95)

Ze wzoru (3.95) wynika, że zwiększenie prądu wirnika przy zmniejszeniu napięcia zasilania

U

s

może nastąpić przez zwiększenie poślizgu s. Wzrost prądu wirnika a więc i prądu stojana

powoduje zwiększenie strat mocy w uzwojeniach. Z tych względów niedopuszczalna jest

praca ciągła silnika przy obciążeniu znamionowym i zasilaniu napięciem obniżonym.

Wartość poślizgu s przy obniżonym napięciu dla stałego momentu obciążenia obliczamy

z zależności

.

2

2

2

'

'

2

const

X

s

R

s

R

U

m

M

k

N

r

N

r

sN

s

s

(3.96)

.

2

2

2

'

'

2

const

X

s

R

s

R

U

m

M

k

r

r

s

s

s

(3.97)

Dzieląc stronami oba wyrażenia oraz zakładając że

2

2

2

'

k

r

X

s

R

, otrzymujemy

2

sN

s

N

U

U

s

s

(3.98)

Regulacja prędkości przez zmianę rezystancji w obwodzie wirnika

Ten sposób regulacji prędkości obrotowej stosowany jest w silnikach pierścieniowych

małej mocy. Zaletą tego sposobu regulacji jest jego prostota, natomiast wadą są duże straty

energii oraz mała sztywność charakterystyk mechanicznych.

Włączanie rezystancji w obwód wirnika powoduje zmianę przebiegu charakterystyk

mechanicznych (rys.3.27). Moment maksymalny zgodnie ze wzorem (3.81) nie ulega

zmianie, zmienia się natomiast poślizg krytyczny

k

d

r

k

X

R

R

s

'

'

(3.99)

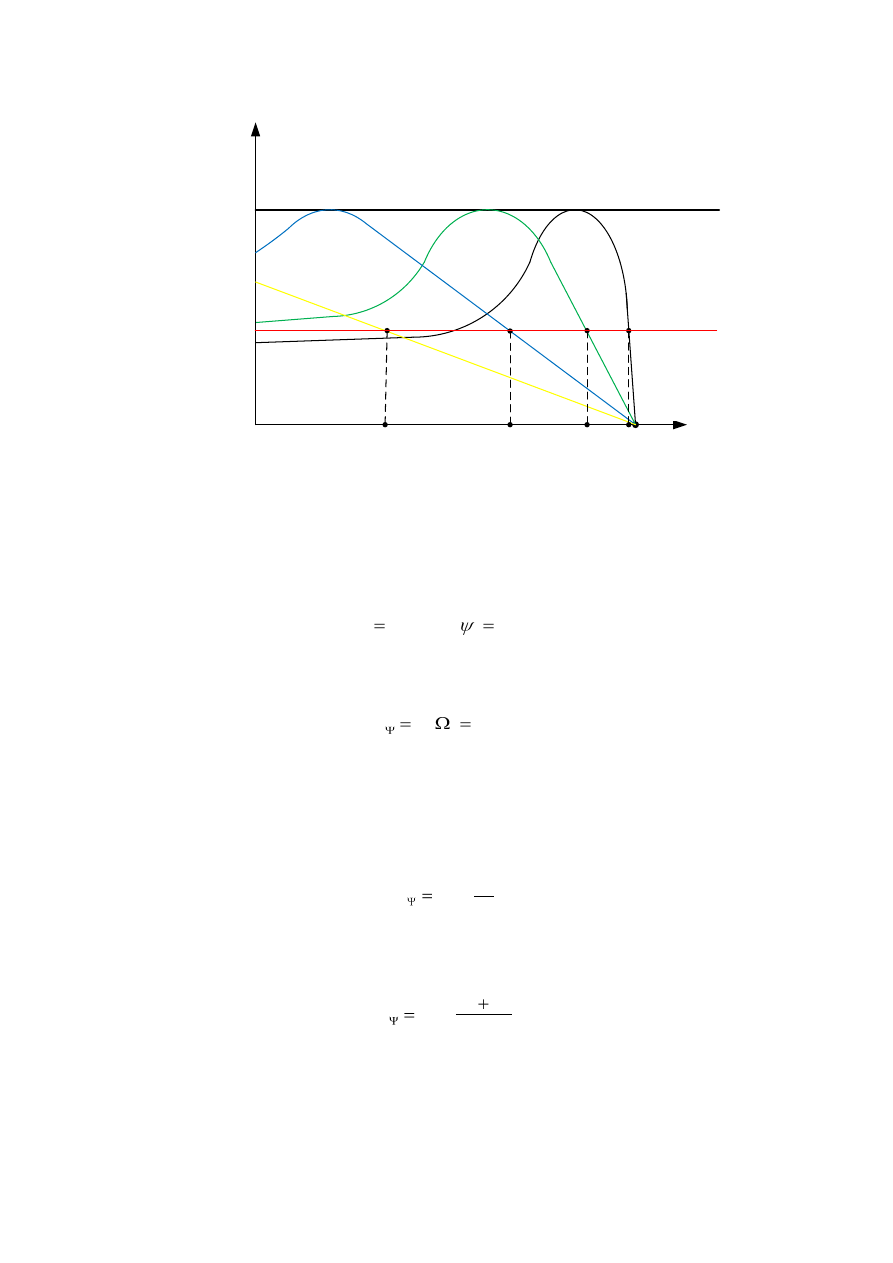
M

s

1

R

2

R

d1

R

d2

R

d3

s

3

s

2

s

1

s

N

0

M

m

M

k

=const.

Rys.3.27. Regulacja prędkości silnika indukcyjnego pierścieniowego przez zmianę rezystancji

w obwodzie wirnika.

Jeżeli przy stałym napięciu zasilania moment obciążenia mechanicznego jest stały, to

zgodnie ze wzorem

.

cos

0

const

I

cE

M

r

r

r

(3.100)

wynika warunek I

r

= const. Dla utrzymania stałej wartości prądu wirnika przy M = const.

wynika, że moc elektromagnetyczna

.

const

M

P

s

(3.101)

wobec stałej prędkości kątowej synchronicznej jest również stała.

Rezystancję R

r

regulatora prędkości w przypadku regulacji przy stałym momencie

hamującym oblicza się w następujący sposób. Stałej wartości momentu przy rezystancji

obwodu wirnika R

r

odpowiada poślizg s i stała wartość mocy elektromagnetycznej

s

R

I

m

P

r

r

r

2

(3.102)

Jeżeli w obwód wirnika zostanie włączona rezystancja dodatkowa R

d

to przy stałej wartości

momentu wystąpi poślizg s

d

, któremu odpowiada moc elektromagnetyczna

d

d

r

r

r

s

R

R

I

m

P

2

(3.103)

Wobec równości mocy elektromagnetycznej i równości prądów wirnika, znając

rezystancje wirnika R

r

i odpowiadający jej poślizg s, rezystancję dodatkową R

d

dla

osiągnięcia poślizgu s

d

obliczymy z zależności

r

d

d

R

s

s

R

1

(3.104)

Sprawność silnika przy regulacji prędkości przez zmianę rezystancji w obwodzie wirnika,

przy pominięciu strat w rdzeniu i uzwojeniu stojana oraz strat mechanicznych, będzie

w przybliżeniu równa

s

P

m

n

n

s

P

s

P

P

P

P

P

1

)

1

(

1

2

(3.105)

a więc będzie maleć ze zmniejszaniem się prędkości obrotowej. Przy prędkości obrotowej

równej połowie prędkości synchronicznej, sprawność będzie wynosić ok. 50%. Jest to

regulacja nieekonomiczna, gdyż występują duże straty energii w rezystorze regulacyjnym.

3.7 ROZRUCH SILNIKÓW INDUKCYJNYCH

Rozruchem silnika nazywa się stan pracy od chwili załączenia napięcia do chwili

osiągnięcia przez silnik ustalonej prędkości obrotowej, określonej parametrami zasilania

(amplituda i częstotliwość napięcia ) i parametrami obciążenia (moment bezwładności i

moment mechaniczny na wale maszyny)

Prąd stojana po pominięciu gałęzi poprzecznej w schemacie zastępczym(rys.3.10) przy pracy

znamionowej określony jest zależnością

2

'

2

r

s

N

r

s

sN

sN

X

X

s

R

R

U

I

(3.106)

Przy pracy znamionowej poślizg silnika s

N

jest rzędu 0.01-0.08 i rezystancja wirnika jest

duża. Natomiast przy rozruchu prędkość silnika jest równa zeru a poślizg s =1 a rezystancja

wirnika jest dużo mniejsza niż przy pracy znamionowej. Wówczas prąd stojana zwany

prądem rozruchowym wynosi

2

'

2

r

s

r

s

s

sl

X

X

R

R

U

I

(3.107)

i jest 5-8 krotnie większy od prądu znamionowego.

Rozruch silników klatkowych

Jak wynika ze wzoru (3.107) rozruchu silników klatkowych możemy dokonać następującymi

sposobami:

a) stosując rozruch bezpośredni,

b) przez włączenie dodatkowej impedancji w obwód stojana,

c) przez obniżenie napięcia zasilającego poprzez zastosowanie,

przełącznika gwiazda-trójkąt,

autotransformatora,

sterowników napięcia.

Rozruch bezpośredni

Rozruch bezpośredni jest najprostszym i dlatego najczęściej stosowanym sposobem

rozruchu silników indukcyjnych klatkowych. Wadą rozruchu bezpośredniego jest duży prąd

rozruchowy, który powoduje duże spadki napięć w sieci, co ma niekorzystny wpływ na pracę

innych odbiorników. Przepisy ograniczają moc znamionową silników uruchomianych

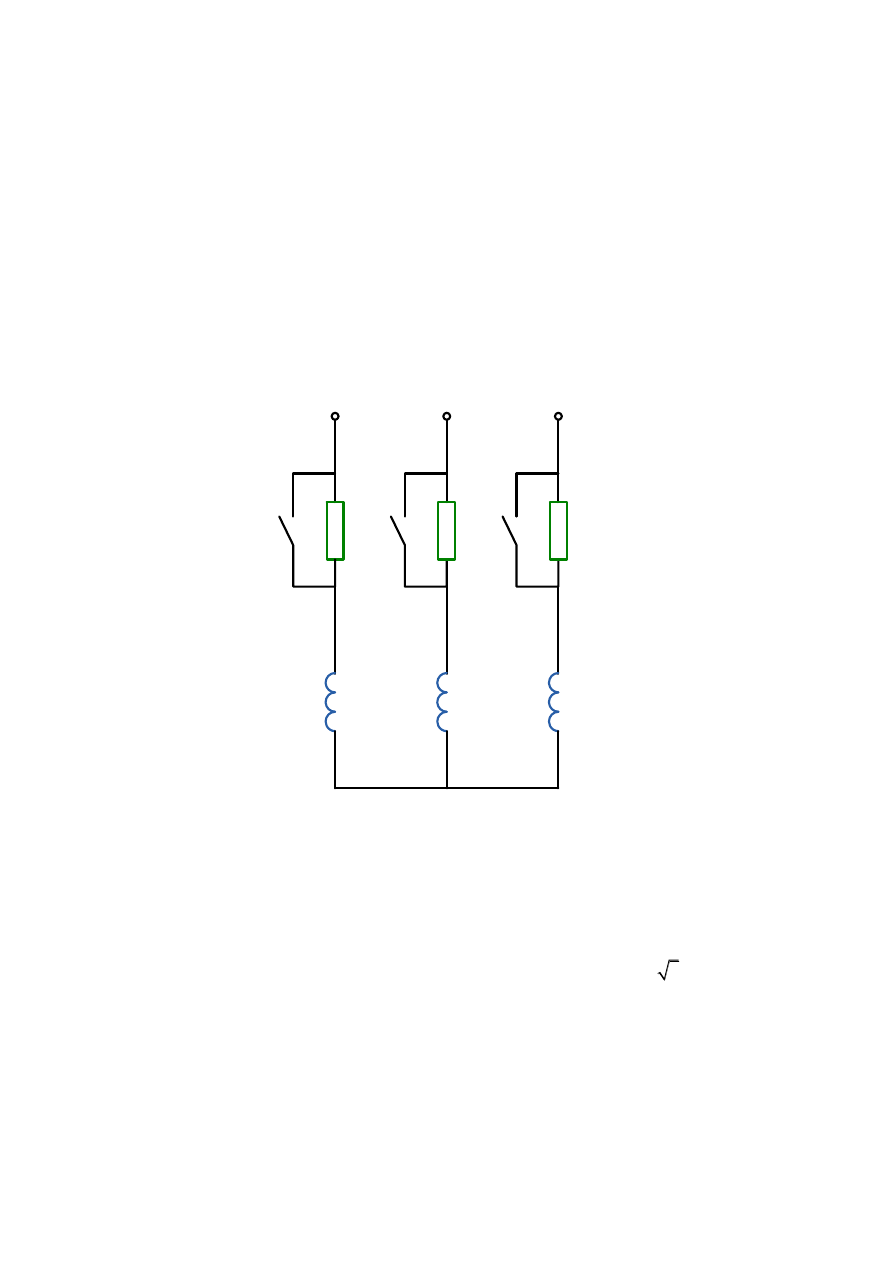
bezpośrednio z sieci publicznych niskiego napięcia , w których dopuszczalny spadek napięcia

wynosi 5%, do mocy nie większej od 5.5kW.

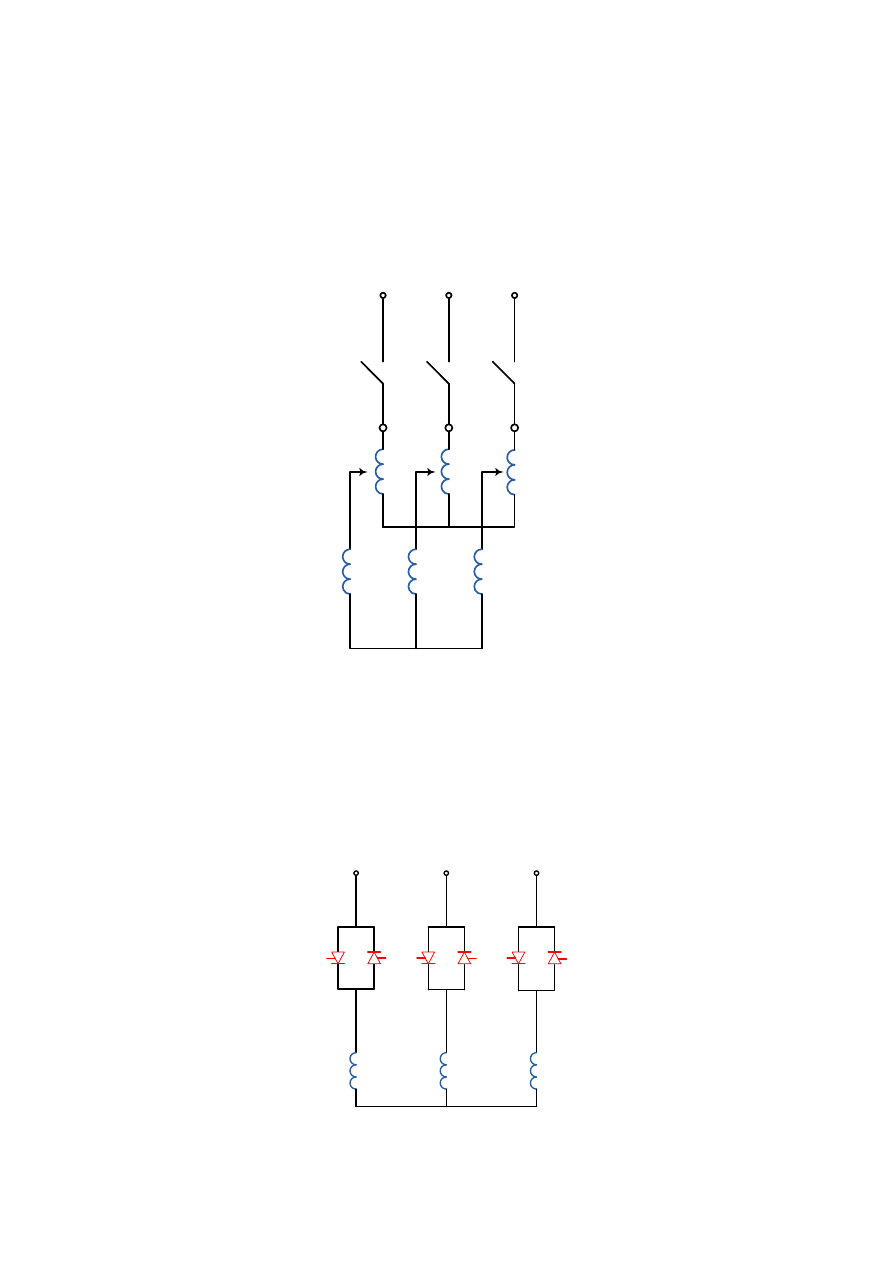
Rozruch przez włączenie dodatkowych impedancji w obwód stojana

Włączenie dodatkowych impedancji (rys.3.28.), zwykle rezystorów lub dławików,

szeregowo w obwód stojana może być traktowane jako zwiększenie całkowitej impedancji

silnika, co powoduje zmniejszenie prądu rozruchowego. Jednocześnie występuje spadek

napięcia na włączanej impedancji i maleje napięcie na zaciskach silnika a zatem zmniejsza się

moment rozruchowy.

L

1

L

2

L

3

U

1

U

2

V

1

V

2

W

1

W

2

K

(R

d

, X

d

)

K

K

Rys.3.28. Rozruch silnika klatkowego poprzez włączenie impedancji w obwód uzwojenia stojana.

Rozruch za pomocą przełącznika gwiazda-trójkąt

Jest to najczęściej stosowany sposób rozruchu silników małej i średniej mocy

o napięciach zasilających poniżej 1 kV. Podczas rozruchu uzwojenie stojana najpierw łączy

się w gwiazdę (rys.3.29.), wówczas napięcie fazowe uzwojenia stojana jest 3 razy mniejsze

od napięcia znamionowego.

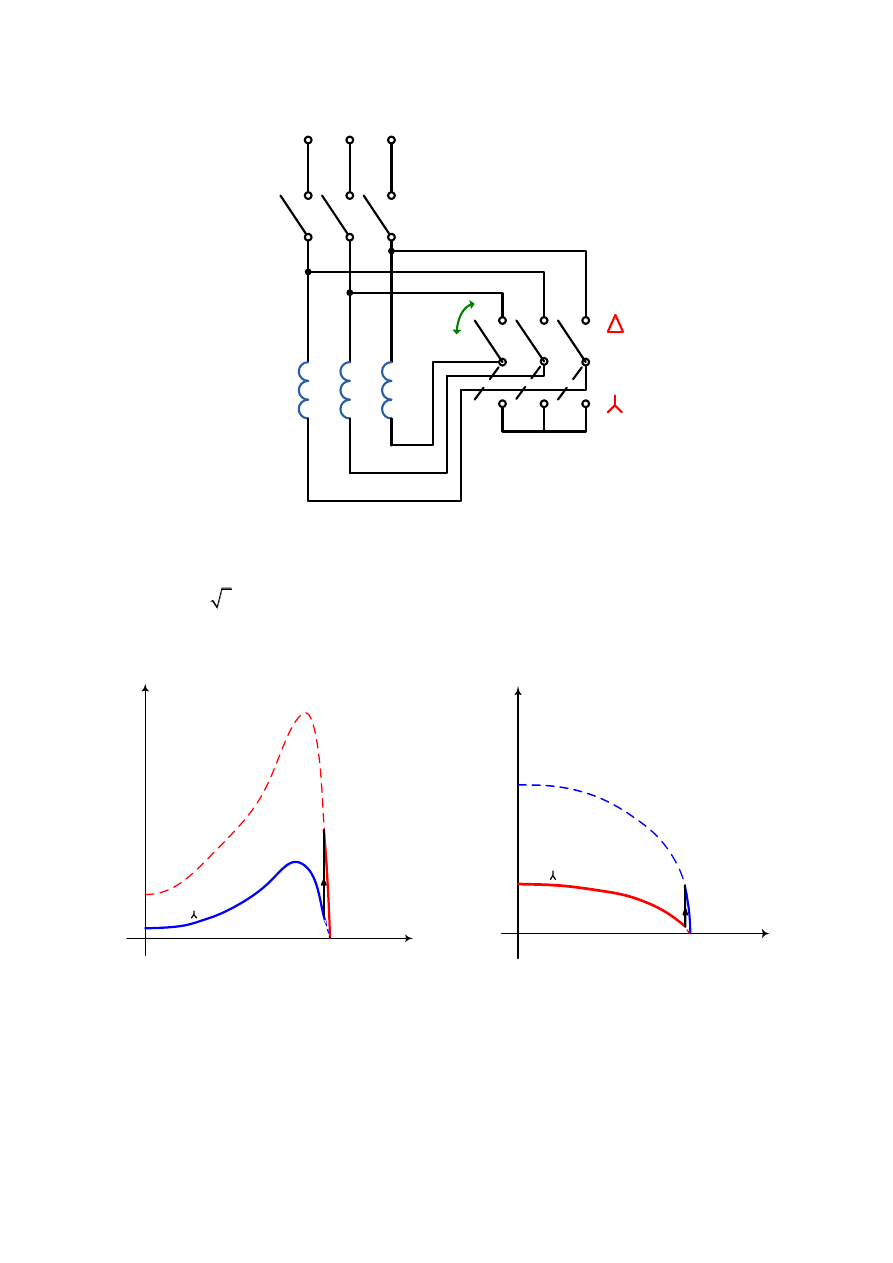
U1

V1 W1

U2

V2 W2

K

L1

L2

L3

Rys.3.29. Schemat układu połączeń do rozruchu silnika indukcyjnego klatkowego za pomocą

przełącznika gwiazda-trójkąt

Tym samym moment rozruchowy zmniejsza się 3-krotnie (rys.3.30.a)), zaś prąd fazowy
zmniejsza się 3 (rys.3.30b)) razy a prąd pobierany z sieci zmniejsza się 3-krotnie.

a)

M

n

s

M

M

D

n

b)

I

s

n

s

I

I

D

Rys.3.30. Przebieg momentu i prądu rozruchowego przy rozruchu za pomocą przełącznika gwiazda-

trójkąt; a) przebieg momentu w funkcji prędkości obrotowej, b) przebieg prądów przewodowych w

funkcji prędkości obrotowej,

Przy prędkości obrotowej zbliżonej do prędkości znamionowej, uzwojenie stojana łączy się w

trójkąt co odpowiada pracy normalnej silnika.

Rozruch za pomocą autotransformatora

Rozruch za pomocą autotransformatora (rys.3.31) jest stosowany do silników dużej

mocy i wysokim napięciu znamionowym. Przy rozruchu z zastosowaniem autotransformatora,

prąd pobierany z sieci jak i moment rozruchowy maleje z kwadratem napięcia zasilającego

uzwojenie stojana.

U

1

U

2

V

1

V

2

W

1

W

2

K

Atr.

L

1

L

2

L

3

Rys.3.31. Schemat układu połączeń do rozruchu silnika indukcyjnego klatkowego za pomocą

autotransformatora.

Rozruch za pomocą sterowników napięcia

Schemat układu do rozruchu silnika indukcyjnego za pomocą sterowników napięcia

przedstawiono na rys.3.32.

L1

T1

T4

T3

T6

T2

U2

V2

W1

W2

T5

V1

U1

L2

L3

Rys.3.32. Układ do rozruchu silnika indukcyjnego klatkowego za pomocą sterowników napięcia.

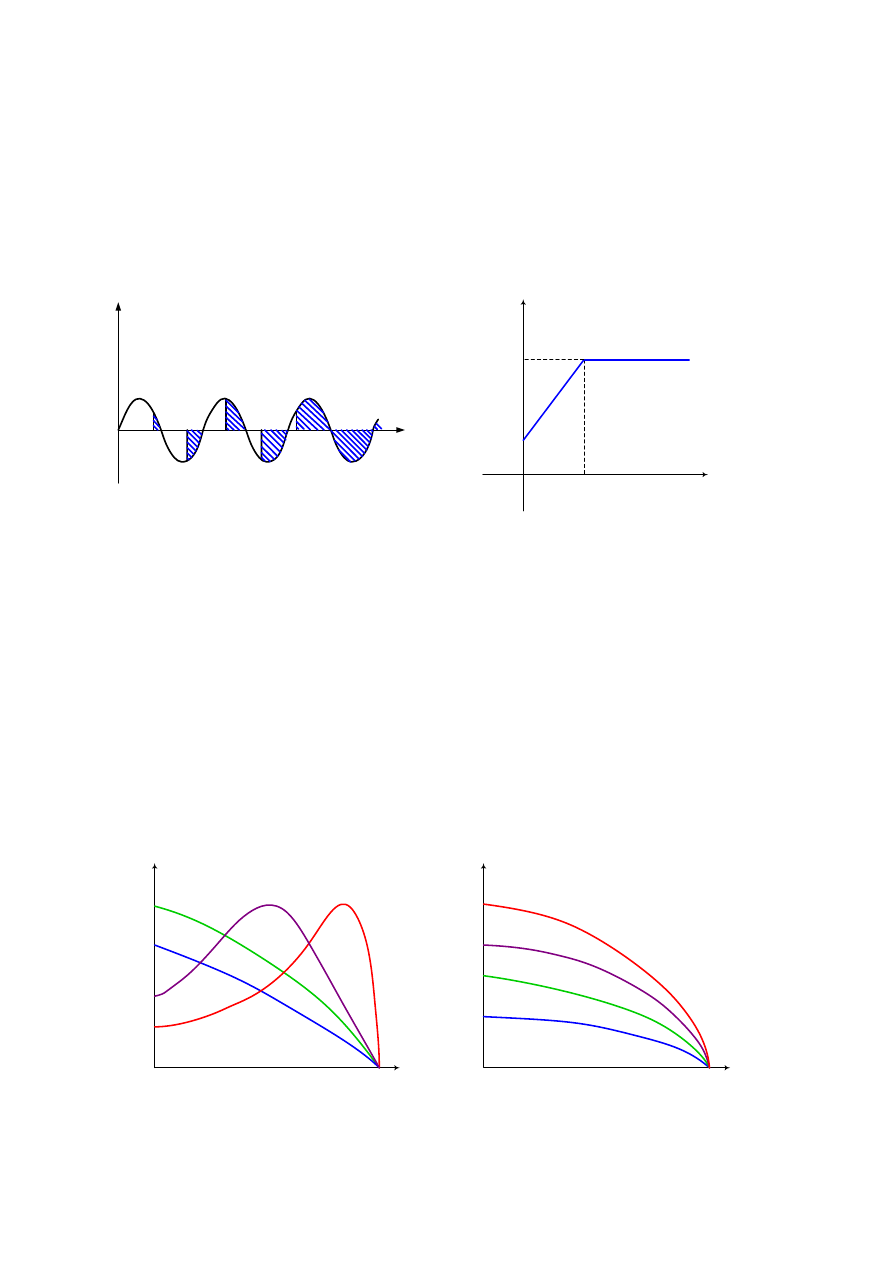
Sterowniki napięcia są to układy energoelektroniczne zbudowane w oparciu

o elementy półprzewodnikowe najczęściej tyrystory pracujące w układzie antyrównoległym.

Podczas rozruchu amplituda napięcia podawanego na uzwojenie silnika zmienia się w czasie

np. w sposób liniowy (rys.3.33), co uzyskuje się poprzez regulację kąta wysterowania

tyrystorów.

a)

U

t

b)

U

t

U

sN

U

min

t

1

Rys.3.33. Przebieg napięcia zasilania podczas rozruchu silnika indukcyjnego za pomocą

sterowników napięcia; a) zasada regulacji napięcia, b) przebieg amplitudy napięcia w funkcji czasu.

Rozruch silników pierścieniowych

Rozruch silników pierścieniowych przeprowadza się przez włączenie rezystancji

w obwód wirnika. Włączenie rezystancji w obwód wirnika powoduje ze zgodnie ze wzorem

(3.99) zwiększenie się poślizgu krytycznego oraz zmniejszenie prądu rozruchowego stojana,

przy czym moment maksymalny nie ulega zmianie. Wzrost rezystancji dodatkowej powoduje

przesuwanie się maksimum momentu w kierunku rosnących wartości poślizgów przy

równoczesnym zmniejszaniu się prądu rozruchowego (rys.3.34.).

a)

M

n

R

d3

R

d2

R

d1

R

r

n

s

b)

R

d1

R

d2

R

d3

R

r

I

s

n

n

s

Rys.3.34. Wpływ rezystancji dodatkowej Rd na przebieg momentu i pradu silnika indukcyjnego

pierścieniowego; a) przebiegi momentu w funkcji prędkości, b) przebiegi prądu w funkcji prędkości

obrotowej.

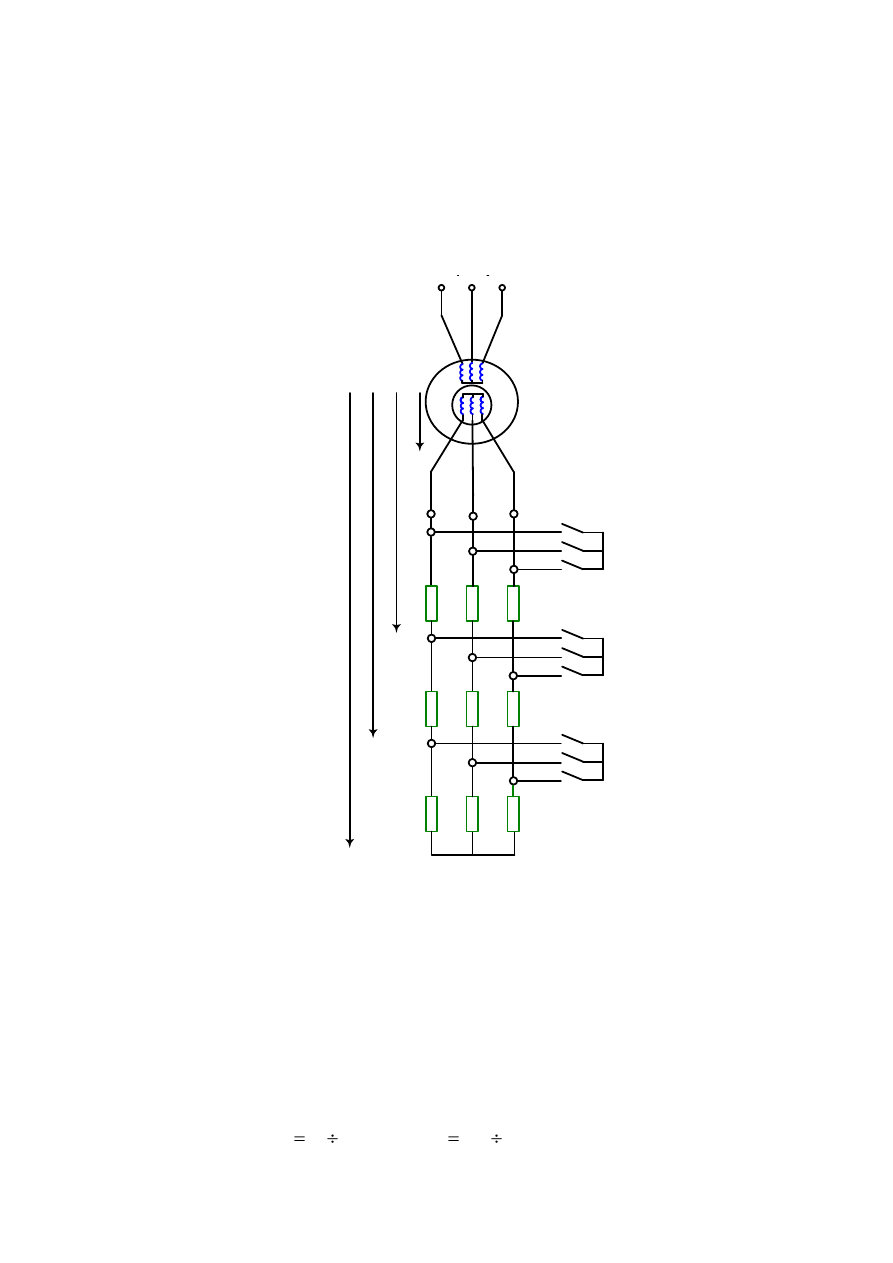
Można tak dobrać wartość rezystancji włączonej w obwód wirnika, że moment

maksymalny wystąpi przy poślizgu s =1. Wówczas moment rozruchowy będzie równy

momentowi maksymalnemu. Dalsze zwiększanie rezystancji powoduje zmniejszanie się

momentu rozruchowego. W praktyce rozruchu silnika pierścieniowego dokonuje się za

pomocą rezystora sekcyjnego zwanego rozrusznikiem rezystorowym (rys.3.35).

L1 L2

L3

R

d

3

R

d

2

R

d

1

K

L

M

K

1

R

r

K

2

K

3

R

r1

R

r2

R

r3

Rys.3.35. Schemat połączeń do rozruchu silnika indukcyjnego pierścieniowego za pomocą

rozrusznika rezystorowego wielostopniowego.

Rozruszniki rezystorowe wielostopniowe pozwalają dowolnie kształtować przebieg

charakterystyk rozruchowych silnika, stosownie do przebiegu momentu hamującego.

Rezystancje na poszczególnych stopniach rozruchowych dobiera się tak, aby w czasie

rozruchu moment zmieniał się na każdym stopniu od wartości maksymalnej M

max

do wartości

minimalnej M

min

(rys.3.26.a)), przy czym wartość minimalna momentu musi być większa od

momentu hamującego. Przy doborze wartości granicznych momentu rozruchowego należy

zachować warunki:

N

M

M

)

5

,

2

2

(

max

,

N

M

M

)

2

.

1

1

.

1

(

min

.

R

d1

R

d2

R

d3

R

r

I

s

n

M

n

R

d3

R

d2

R

d1

R

r

M

max

M

min

M

m

I

max

I

min

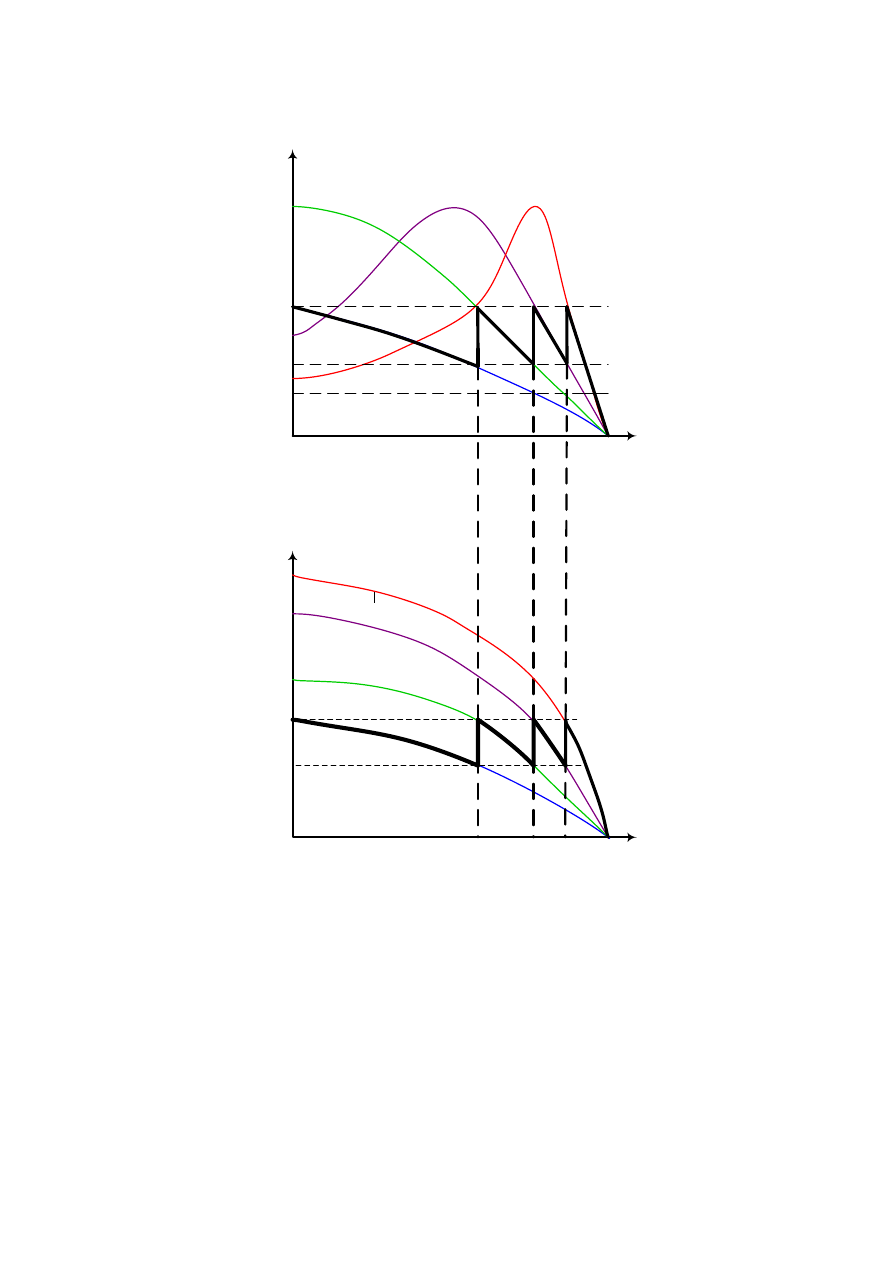
Rys.3.36. Przebiegi momentu i prądu silnika indukcyjnego pierścieniowego przy zastosowaniu

rozrusznika rezystorowego wielostopniowego.

Im mniejsze są różnice między momentem maksymalnym a minimalnym tym większa musi

być liczba stopni rozruchowych i rozruch jest bardziej płynny.

Zamiast rozruchu za pomocą rozrusznika wielostopniowego można zastosować rozruch

rezystorowy za pomocą tyrystorowego modulatora rezystancji (rys.3.37.).

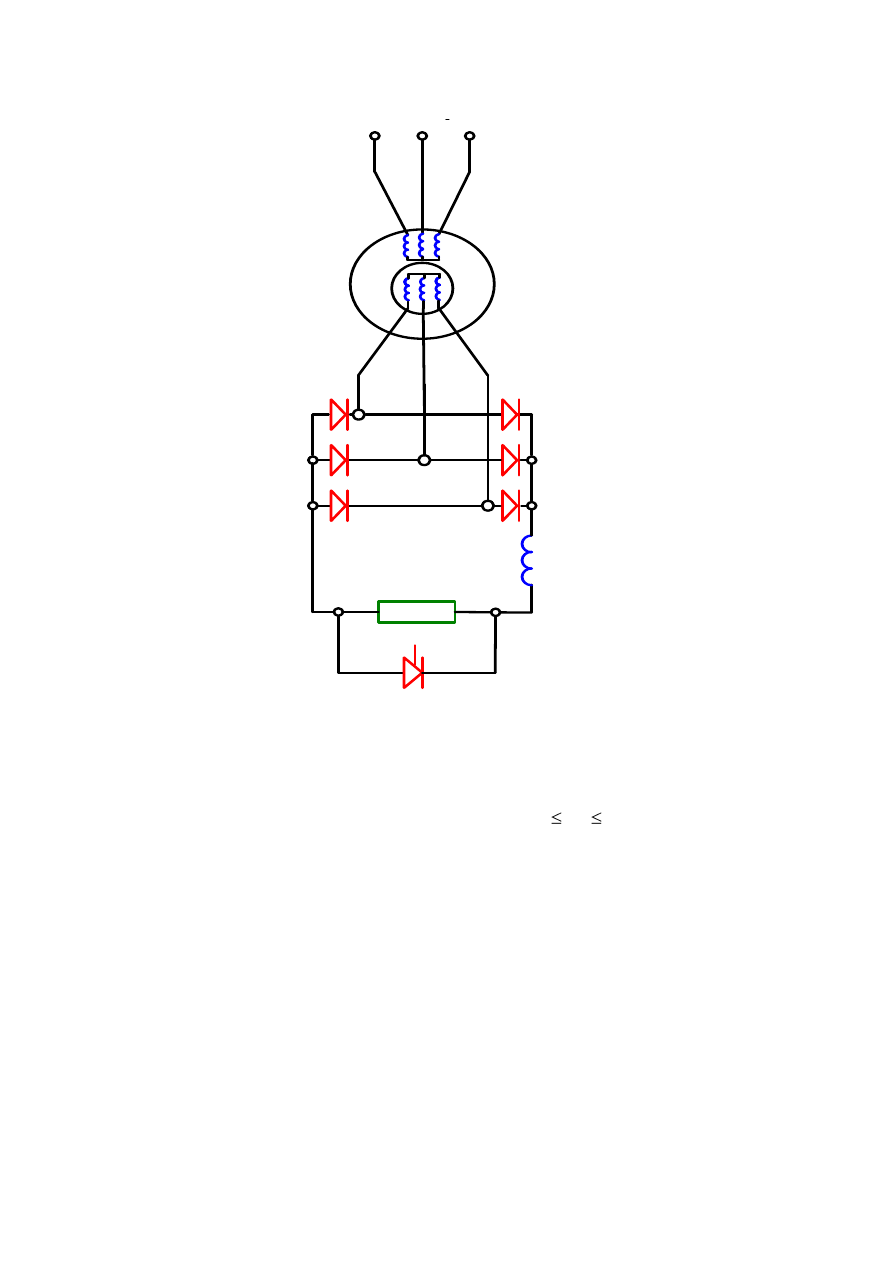
R

D

1

D

3

D

5

D

4

D

6

D

2

T

L

d

L1

L2

L3

Rys.3.37. Rozruch silnika indukcyjnego pierścieniowego za pomocą

tyrystorowego modulatora

rezystancji

Modulator rezystancji jest włączony w obwód wirnika poprzez prostownik diodowy

mostkowy. Równoległe włączenie modulatora do rezystancji R umożliwia uzyskanie

rezystancji modulowanej R

m

, zmieniającej się w granicach 0 R

m

R.

LITERATURA

[1]

Bajorek Z.: Maszyny elektryczne, WNT, Warszawa 1983

[2]

Chapman S.J.: Electric machinery fundamentals, Third Edition, McGraw-Hill Book

Company, Singapore 1999.

[3]

Fitzgerald A. E., Kingsley Ch. Jr., Stephen D. Umans S.D.: Electric machinery, Sixth

edition, McGraw-Hill, USA, New York, 2003.

[4]

Gieras J.F., Wing M.: Permanent magnet motor technology. Design and Application,

Second Edition, Marcel Dekker Inc., New York 2002.

[5]

Krause P.C.: Analysis of electric machinery, McGraw-Hill Book Company, New York

1986.

[6]

Kurdziel R.: Podstawy elektrotechniki, WNT, Warszawa 1972

[7]

Latek W.: Teoria maszyn elektrycznych, WNT, Warszawa 1987

[8]

Plamitzer A.: Maszyny elektryczne, WNT, Warszawa 1982

Projekt „Program Rozwojowy Potencjału Dydaktycznego Politechniki Świętokrzyskiej w Kielcach: kształcenie na miarę sukcesu”

Program Operacyjny Kapitał Ludzki Priorytet IV Działanie 4.1 Poddziałanie 4.1.1

Umowa UDA-POKL.04.01.01-00-175/08-02

Politechnika Świętokrzyska

25-314 Kielce

Al. Tysiąclecia Państwa Polskiego 7

Biuro Projektu - bud. B pok. 324

Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego