1

Geochemia analityczna II

Przykłady obliczeń

Tematyka ćwiczeń.

•

Przeliczanie analizy na wzór chemiczny minerału

•

Projekcja skały w trójkącie klasyfikacyjnym

•

Przeliczanie wyników analiz podanych w pierwiastkach na tlenki

•

Obliczanie zawartości pierwiastka w rudzie

Przeliczanie analizy na wzór chemiczny minerału

Jaki

jest

cel

wykonywania

analizy

chemicznej

minerału

i

przeliczania jej na jego wzór strukturalny?
- analiza mikroskopowa dostarcza ogólnych danych identyfikacyjnych

interesuj

ą

cego nas minerału (np. plagioklaz, oliwin, amfibol,

piroksen),

ale

nie

umo

ż

liwia

jego

dokładnego

rozpoznania

(plagioklaz: albit czy anortyt; oliwin: forsteryt czy fajalit;
amfibol: np. hornblenda czy glaukofan itd.). Na podstawie wyników
analizy chemicznej od razu wiadomo, który to dokładnie minerał i
jaki jest jego wzór strukturalny;

- niektóre metody datowania (np. uranowa) bazuj

ą

na wynikach analizy

chemicznej minerałów;

- wyznaczanie temperatur i ci

ś

nie

ń

, w których powstaj

ą

skały opiera

si

ę

m.in. na analizach chemicznych minerałów wchodz

ą

cych w ich

skład;

- odtworzenie warunków powstawania niektórych skał magmowych jest

interpretowane na podstawie wyników analiz chemicznych minerałów
wchodz

ą

cych w ich skład.

Współczesna chemia analityczna oferuje nam wiele ró

ż

nych technik

u

ż

ytecznych

dla

analizy

składu

chemicznego

minerałów.

Analiz

ę

chemiczn

ą

minerału mo

ż

na wykona

ć

stosuj

ą

c metody klasyczne lub

instrumentalne. Po

ś

ród nich najbardziej rozpowszechnione s

ą

:

1)

analiza „na mokro” (klasyczna metoda, rozpuszczenie próbki
minerału w kwasach i oznaczenie zawarto

ś

ci jego składników w

otrzymanym roztworze);

2)

analiza instrumentalna metodami spektroskopowymi np. metod

ą

fluorescencji rentgenowskiej XRF (o

ś

wietlanie promieniami X

próbki sproszkowanego minerału powoduje,

ż

e pierwiastki obecne w

próbce

wysyłaj

ą

własne

promieniowanie

pozwalaj

ą

ce

je

zidentyfikowa

ć

i oznaczy

ć

ilo

ś

ciowo ich zawarto

ść

);

3)

analiza metodami mikroanalitycznymi (najcz

ęś

ciej stosowana jest

technika

mikrosondy

elektronowej,

w

której

o

ś

wietlanie

polerowanego preparatu mikroskopowego elektronami powoduje,

ż

e

pierwiastki

obecne

w

próbce

wysyłaj

ą

charakterystyczne

promieniowanie X pozwalaj

ą

ce je zidentyfikowa

ć

i oznaczy

ć

ilo

ś

ciowo ich zawarto

ść

, przy czym próbka mo

ż

e by

ć

bardzo mała,

do kilku mikrometrów

ś

rednicy).

Ka

ż

da z wymienionych technik ma swoje wady i zalety i inne

wymagania, co do wielko

ś

ci próbki i jej preparatyki. Na przykład do

2

zalet metod „na mokro” nale

ż

y to,

ż

e pozwalaj

ą

one oznaczy

ć

zawarto

ś

ci

pierwiastków na ró

ż

nych stopniach utlenienia (na przykład Fe

+2

i Fe

+3

,

czy S

-2

i S

+6

). W metodzie klasycznej mo

ż

liwe jest tak

ż

e oznaczenie

ilo

ś

ci wody wyst

ę

puj

ą

cej w minerale w postaci grup OH

-

(woda H

2

O

+

). Z

kolei zalet

ą

mikrosondy elektronowej jest mo

ż

liwo

ść

analizy bardzo

małych próbek, dzi

ę

ki czemu unika si

ę

mo

ż

liwych wpływów zanieczyszcze

ń

czy niehomogeniczno

ś

ci. Istniej

ą

oczywi

ś

cie metody instrumentalne,

pozwalaj

ą

ce oznaczy

ć

pierwiastki na ró

ż

nych stopniach utlenienia. Nie

ma jednak jednej uniwersalnej metody instrumentalnej, przy pomocy
której mo

ż

na wykona

ć

analiz

ę

chemiczn

ą

i jednocze

ś

nie wyznaczy

ć

stopnie utlenienia pierwiastków wchodz

ą

cych w skład analizowanego

minerału. Przewaga analiz instrumentalnych nad klasycznymi polega
głównie na znacznie krótszym czasie wykonania analizy.
Zarówno

w

metodach

klasycznych,

jak

i

w

wi

ę

kszo

ś

ci

metod

instrumentalnych musimy dysponowa

ć

odpowiednio du

żą

ilo

ś

ci

ą

próbki

minerału, który b

ę

dziemy analizowa

ć

. Minerał musi by

ć

pozbawiony

jakichkolwiek domieszek i wrostków innych minerałów oraz oznak
zwietrzenia i przemian. Czasami jest bardzo trudno uzyska

ć

wi

ę

ksz

ą

ilo

ść

"czystego" materiału. Do analizy klasycznej potrzebne jest 100 -

500 mg próbki a do XRF nawet 4 g. Je

ś

li minerał, wyst

ę

puj

ą

cy w

polimineralnej próbce widoczny jest dopiero pod mikroskopem, do
analizy stosuje si

ę

mikrosond

ę

elektronow

ą

. Zdolno

ść

rozdzielcza

wi

ą

zki elektronowej wynosi około 1

µ

m, co oznacza,

ż

e mo

ż

na oznaczy

ć

skład chemiczny niewielkich ziaren minerału o rozmiarach rz

ę

du

mikrometrów.

Za wyj

ą

tkiem metali rodzimych wszystkie minerały składaj

ą

si

ę

z

dwóch lub wi

ę

cej pierwiastków. Przedstawianie ich składu przy pomocy

wzorów

chemicznych

ma

na

celu

zawarcie

w

pojedynczym

zapisie

informacji o tym, z jakich pierwiastków zbudowany jest minerał, w
jakich wyst

ę

puj

ą

one proporcjach atomowych, oraz w jaki sposób s

ą

ze

sob

ą

poł

ą

czone. Taki zapis nazywa si

ę

wzorem strukturalnym lub pół

strukturalnym minerału:

Oliwin

(Mg,Fe)

2

SiO

4

Dolomit

CaMg(CO

3

)

2

Gips

CaSO

4

.

2H

2

O

Apatyt

Ca

5

(PO

4

)

3

(F,Cl,OH)

Przy zapisie tym obowi

ą

zuj

ą

standardowe zasady zapisu wzorów

chemicznych. Kationy s

ą

wyliczone najpierw, po nich aniony i kompleksy

anionów (takie jak grupy SiO

4

, CO

3

, SO

4

czy PO

4

). Lu

ź

no zwi

ą

zane

składniki s

ą

wypisywane na ko

ń

cu wzoru (np. woda w strukturze gipsu

czy fluor, chlor i grupy hydroksylowe w apatycie). Dolne indeksy przy
symbolach i nawiasach wskazuj

ą

na wzgl

ę

dn

ą

ilo

ść

atomów lub grup

atomów uj

ę

tych w nawias, jak w przykładzie oliwinu czy apatytu.

Przecinkami oddziela si

ę

pierwiastki lub grupy pierwiastków wzajemnie

si

ę

podstawiaj

ą

ce na przykład na zasadzie diadochii. Podstawienia

izomorficzne, czyli wzajemna substytucja (zast

ę

powanie) pierwiastków w

strukturze

minerału

jest

efektem

podobie

ń

stwa

ładunku,

promieni

jonowych i elektroujemno

ś

ci. Na przykład Mg

2+

(promie

ń

jonowy 0,080 nm)

i Fe

2+

(promie

ń

jonowy 0,069 nm) podstawiaj

ą

si

ę

wzajemnie w strukturze

oliwinu (Mg, Fe)[SiO

4

]. W składzie oliwinu mo

ż

e wi

ę

c by

ć

obecny albo

magnez, albo

ż

elazo albo oba pierwiastki naraz. Substytucja tego

rodzaju nazywana jest izowalentn

ą

gdy

ż

zast

ę

puj

ą

si

ę

jony o tej samej

warto

ś

ciowo

ś

ci. W przypadku substytucji heterowaletnej zast

ę

puj

ą

si

ę

jony o ró

ż

nych warto

ś

ciowo

ś

ciach, np. jony sodu Na

+

podstawiaj

ą

ce jony

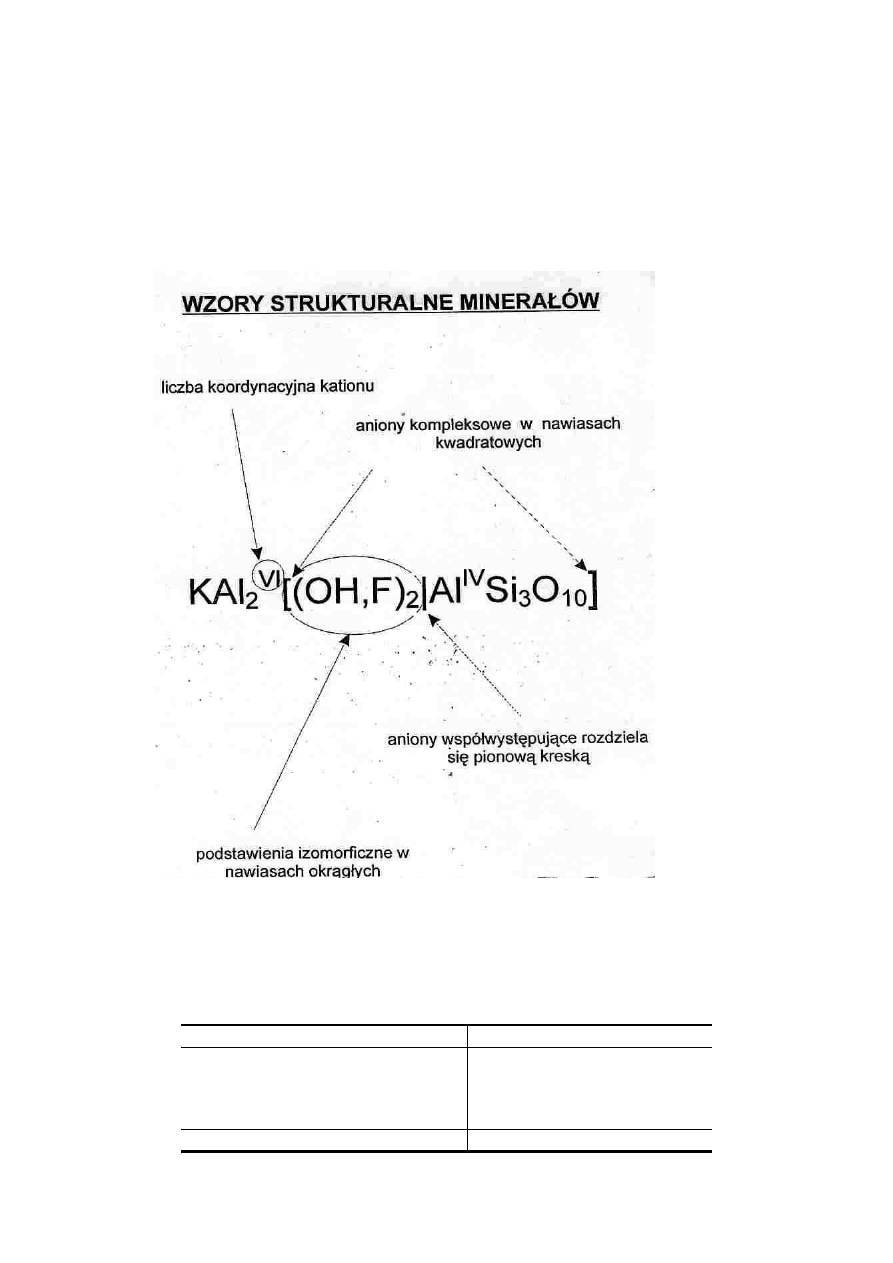
3

wapnia Ca

+2

i jednocze

ś

nie jony krzemu Si

+4

podstawiaj

ą

ce jony glinu Al

+3

w szeregu plagioklazów albit–anortyt:

Na

[Al

Si

Si

2

O

8

] -

Ca

[Al

Al

Si

2

O

8

].

Wyniki

analizy

prezentuje

si

ę

w

postaci

zawarto

ś

ci

wagowej

pierwiastków lub ich tlenków. Ró

ż

nice w zapisie wyników analizy

chemicznej zale

żą

od tego, czy minerał jest beztlenowy, na przykład

siarczek: galena PbS, Piryt FeS

2

, czy tlenowy, na przykład siarczan:

anhydryt CaSO

4

; krzemian: oliwin (Fe,Mg)SiO

4

; glinokrzemian: piroksen

Ca(Mg,Fe)(Si,Al)

2

O

6

.

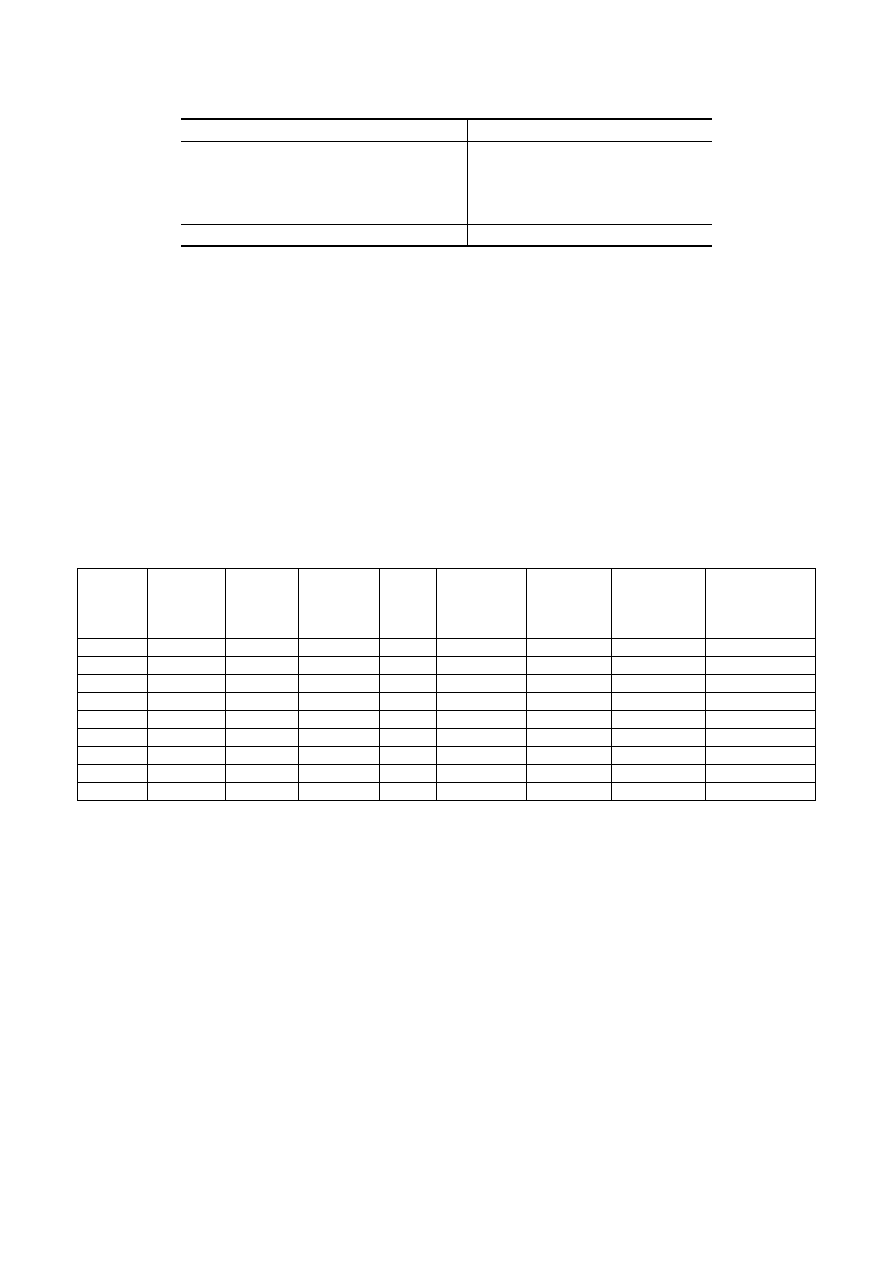
Przykład zapisu wyników analizy chemicznej

minerału beztlenowego – sfalerytu:

Składnik

% wag

Fe

7,99

Cd

1,23

Zn

57,38

S

32,99

Suma

99,59

4

Przykład zapisu wyników analizy chemicznej

minerału tlenowego – oliwinu

Ilo

ś

ciowa analiza chemiczna minerału dostarcza nam informacji o

składzie pierwiastkowym i o wzajemnych proporcjach tych pierwiastków.
Nie podaje jednak informacji o tym gdzie i w jakich ilo

ś

ciach

poszczególne jony i atomy rozlokowane s

ą

w strukturze minerału.

Standardowo zapisana tabela wyników analizy chemicznej podaje nam
procentowy udział zawarto

ś

ci pierwiastków lub tlenków wyra

ż

ony w

procentach wagowych, które dodane do siebie powinny zamkn

ąć

si

ę

w 100%

(zazwyczaj wyst

ę

puj

ą

niewielkie odchylenia od tej sumy, wynikaj

ą

ce z

ograniczonej dokładno

ś

ci metod analitycznych). Dlatego aby skład

minerału był przedstawiony w formie wzoru strukturalnego trzeba wyniki
analizy chemicznej przeliczy

ć

.

Zasady przeliczenia mo

ż

na prze

ś

ledzi

ć

na poni

ż

szym przykładzie

wyliczenia wzoru skalenia.

Składnik Zawartość

w % wag.

Masa
molowa
tlenku

Ilość
kationów
w tlenku

Ilość
O

w

tlenku

Molowe
udziały
tlenków

Udziały
kationów

Udziały
anionów
(tlenu)

Udziały
kationów
na 8 atomów O
we wzorze

A

B

C

D

E

F = B/C

G = F

.

D

H = F

.

E

I=G*(8/H

tot

)

SiO

2

65,75

60,08

1

2

1,09437

1,09437

2,18874

2,94

Al

2

O

3

19,55

101,96

2

3

0,19174

0,38348

0,57522

1,03

Fe

2

O

3

1,08

159,68

2

3

0,00676

0,01352

0,02029

0,04

CaO

0,72

56,08

1

1

0,00927

0,00927

0,00927

0,02

Na

2

O

6,98

61,96

2

1

0,11797

0,23595

0,11797

0,63

K

2

O

6,23

94,20

2

1

0,06613

0,13227

0,06613

0,36

Suma

100,44

H

tot

=

2,977652

W kolumnie A wypisane s

ą

te składniki (pierwiastki w postaci

tlenków), które były analizowane. W kolumnie B podane s

ą

wyniki

analiz: zawarto

ś

ci wyra

ż

one w procentach wagowych tlenków, które

sumuj

ą

si

ę

w tym wypadku do 100,44% wagowych. Pierwszym krokiem jest

zamiana wyników analiz na molowe udziały tlenków przez podzielenie
procentu wagowego przez mas

ę

atomow

ą

tlenku (kolumna B dzielona przez

kolumn

ę

C). Wynik zapisany jest w kolumnie F.

Nast

ę

pnym krokiem jest zamiana molowych udziałów tlenków na udziały

kationów. Dokonuje si

ę

tego przez pomno

ż

enie ilo

ś

ci kationów w ka

ż

dym

tlenku (kolumna D) przez warto

ś

ci z kolumny F. Wynik zapisany jest w

kolumnie G (G=F*D). Na przykład dla krzemu jest to 1 razy 1,09437, dla
glinu jest to 2 razy 0,19174, dla

ż

elaza 2 razy 0,00676 itd. Nast

ę

pn

ą

kolumn

ę

, udziały tlenów, uzyskujemy podobnie mno

żą

c warto

ś

ci z kolumny

G przez ilo

ść

tlenów we wzorze ka

ż

dego przeliczanego tlenku (kolumna

E): otrzymujemy kolumn

ę

H (H=G*E). Na przykład dla tlenu w SiO

2

jest to

2 razy 1,09437, dla tlenu w Al

2

O

3

jest to 3 razy 0,19174, itd. W

Składnik

% wag

SiO

2

34,96

FeO

36,77

MnO

0,52

MgO

27,04

Suma

99,29

5

zasadzie w tym momencie mo

ż

emy napisa

ć

ju

ż

pół strukturalny wzór

skalenia wynikaj

ą

cy z analizy. Wygl

ą

da on tak:

Ca

0,009

Na

0,118

K

0,066

Fe

0,007

Al

0,192

Si

1,094

O

2,977

Poniewa

ż

przyj

ę

te

jest

podawanie

warto

ś

ci

we

wzorze

skalenia

proporcjonalnie do o

ś

miu atomów tlenu, wszystkie powy

ż

sze zawarto

ś

ci

mno

ż

ymy przez iloraz (8/H

tot

) czyli w tym wypadku przez 8/2,97765.

Powstaje kolumna I, w której wszystkie zawarto

ś

ci jonów w skaleniu

znormalizowane s

ą

do o

ś

miu tlenów. Otrzymany wzór wygl

ą

da tak:

(Ca

0,02

Na

0,63

K

0,36

)(Fe

0,04

Al

1,03

Si

2,94

)O

8

co jest bardzo bliskie idealnemu wzorowi (Ca,Na,K)[(Fe,Al,Si)

4

O

8

].

Ró

ż

nice wynikaj

ą

cz

ęś

ciowo z nieidealno

ś

ci naturalnego minerału a

cz

ęś

ciowo z bł

ę

dów analizy. Uwaga: prosz

ę

zwróci

ć

uwag

ę

w powy

ż

szej

tabeli,

ż

e zaokr

ą

gle

ń

dokonujemy dopiero na samym ko

ń

cu a w trakcie

oblicze

ń

u

ż

ywamy 4 lub 5 miejsc po przecinku.

Przeliczanie analiz chemicznych minerałów:

Przykład 1. Troilit FeS

1

% wagowe

2

masy atomowe

3

udziały atomowe

(kolumna 1/kol.2)

4

stosunki atomowe

Fe

63,53

55,85

1,137

S

36,47

32,07

1,137

1:1
wzór: FeS

Przykład 2. Chalkopiryt CuFeS

2

1

% wagowe

2

masy atomowe

3

udziały atomowe

(kolumna 1/kol.2)

4

stosunki atomowe

Cu 34,30

63,54

0,54982

1 1,08

Fe

30,59

55,85

0,54772

1 1,09

S

34,82

32,07

1,08575

2 2,17

suma: 99,71

Przykład 3. Sfaleryt ZnS z podstawieniami izomorficznymi:

1

% wagowe

2

masy atomowe

3

udziały atomowe

(kolumna 1/kol.2)

4

stosunki atomowe

Fe

18,25

55,85

0,3268

(0,3286•1)/1,0468 = 0,312

Mn 2,66

54,94

0,0484

(0,0484•1)/ 1,0468 = 0,046

Cd

0,28

112,40

0,0025

(0,0025•1)/ 1,0468 = 0,02

Zn

44,67

65,37

0,6833

(0,6833•1)/ 1,0468 = 0,653

S

33,57

32,07

1,0468

(1,0468•1)/ 1,0468 = 1

Suma stosunków atomowych Fe, Mn, Cd i Zn = 1,01

Wzór

: (Fe

0,31

Mn

0,04

Cd

0,002

Zn

0,65

)S

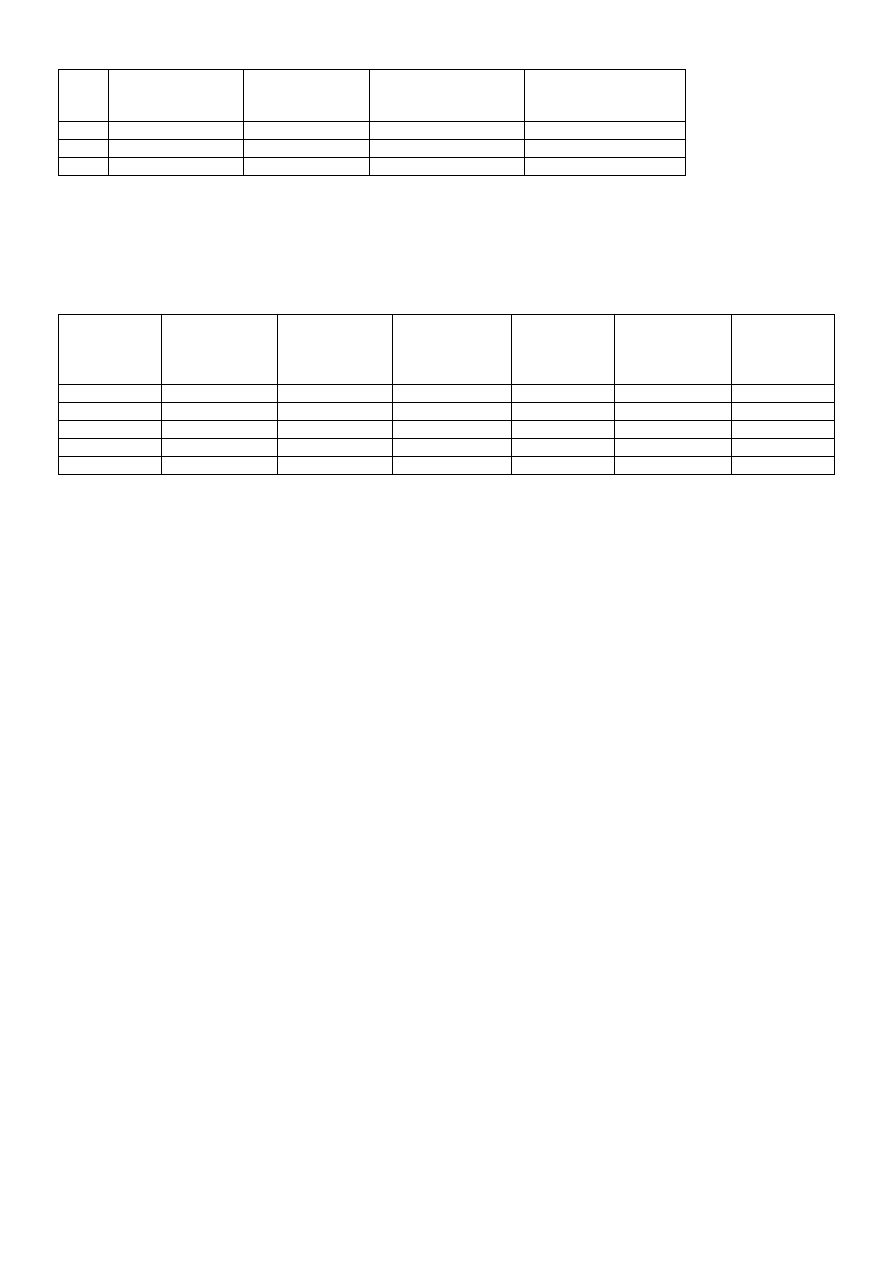
6

Przykład 4. Gips CaSO

4

•2H

2

O

1

% wagowe

2

masy molowe

3

udziały molowe

(kolumna 1/kol.2)

4

stosunki atomowe

CaO

32,44

56,08

0,57846

1,156 1

SO

3

46,61

80,08

0,58211

1,164 1

H

2

O

+

20,74

18,0

1,1522

2,304 2

Suma: 99,79

CaO•SO

3

•2H

2

O

Przykład 5. Oliwin (Mg,Fe)

2

SiO

4

1

% wagowe

2

masy molowe

3

udziały molowe

(kolumna

1/kol.2)

4a

stosunki

atomowe

kationów

4b

Stosunki

atomowe

anionów

5

liczby

kationów na 4

atomy O

SiO

2

34,96

50,09

0,58179

Si 0,5818

1,1636

0,989

FeO

71,85

71,845

0,5118

Fe

2+

0,5118

0,5118

0,879

MnO

0,52

70,94

0,00733

Mn 0,00733

0,00733

0,012

MgO

27,04

40,31

0,67080

Mg 0,6708

0,6708

1,140

Suma

99,29

2,3535

Suma FeO, MnO i MgO = 2,022


Wartości w kolumnie 4a oblicza się mnożąc wartość kolumny 3 razy ilość kationów we wzorze tlenku.
Wartość w kolumnie 4b oblicza się mnożąc wartość z kolumny 3 razy ilość tlenów we wzorze tlenku.
Obliczone liczby kationów powinny w sumie dać 2, a nie 2,022. Dlatego trzeba je dalej przeliczyć z proporcji:

Na 2,022 przypada 0,87 Fe

Na 2,022 przypada 0,012 Mn

to na 2 - x

To na 2 - x

x = (2•0,87)/2,022=0,86

x=(2•0,12)/2,022=0,011

Na 2,022 przypada 1,14 Mg

To na 2 - x
x=(2•1,14)/2,022=1,13

wzór:

(Fe

0,86

Mn

0,01

Mg

1,13

) SiO

4

Procentowy udział fajalitu i forsterytu:

Fe

0,86

0,86/1,99•100% = 43,3% Fajalitu Fe

2

SiO

4

Mg

1,13

1,13/1,99•100% = 56,7% Forsterytu Mg

2

SiO

4

Suma: 1,99

7

Przykład 6. Piroksen Ca(Mg,Fe) [(Si, Al.)

2

O

6

]

1

% wagowe

2

stosunki

atomowe

3

Stosunki

atomowe

kationów

4

liczba

tlenu

5

liczba

kationów na
6 atomów O

6

podział kationów

na pozycje

strukturalne

7

suma kationów na

pozycjach strukturalnych

SiO

2

50,38

0,8384

0,8384

1,6768

1,875

Si 1,875

Si + Al = 2,0

Al

2

O

3

3,01

0,0295

0,0590

0,0885

0,192

Al 0,125
Al 0,007

TiO

2

0,45

0,0056

0,0056

0,0112

0,012

Ti 0,12

Fe

2

O

3

1,95

0,0122

0,0244

0,0366

0,055

Fe

3+

0,055

FeO

4,53

0,00630

0,0630

0,0630

0,141

Fe

2+

0,141

MnO

0,09

0,0013

0,0013

0,0013

0,003

Mn 0,003

MgO

14,69

0,3643

0,3643

0,3643

0,815

Mg 0,815

Al+Ti+Fe

2+

+Fe

3+

+Mn+Mg

= 1,033 ≈ 1

CaO

24,32

0,4321

0,4321

0,4321

0,996

Ca 0,996

Na

2

O

0,46

0,0074

0,00148

0,0074

0,033

Na 0,033

K

2

O

0,15

0,0016

0,0032

0,0016

0,007

K 0,007

Ca+Na+K = 1,006 ≈ 1

suma

99,94

2,6828

Faktor tlenowy = 6/2,6828 = 2,236469

MgO jako MgSiO

3

(enstatyt = En)

FeO jako FeSiO

3

(ferrosilit = Fs)

CaO jako CaSiO

3

(wollastonit = Wo)

Używając proporcji molowych:

MgO =0,3644

FeO = 0,0630

CaO = 0,4321

Suma= 0,8595

%En = 42,39

%Fs = 7,33

%Wo = 50,27

Wzór:

(Ca

0,97

Na

0,03

K

0,007

)(Mg

0,815

Mn

0,003

Fe

2+

0,141

Fe

3+

0,055

Al

0,007

Ti

0,012

)[(Si

1,875

Al

0,125

)O

6

]

8

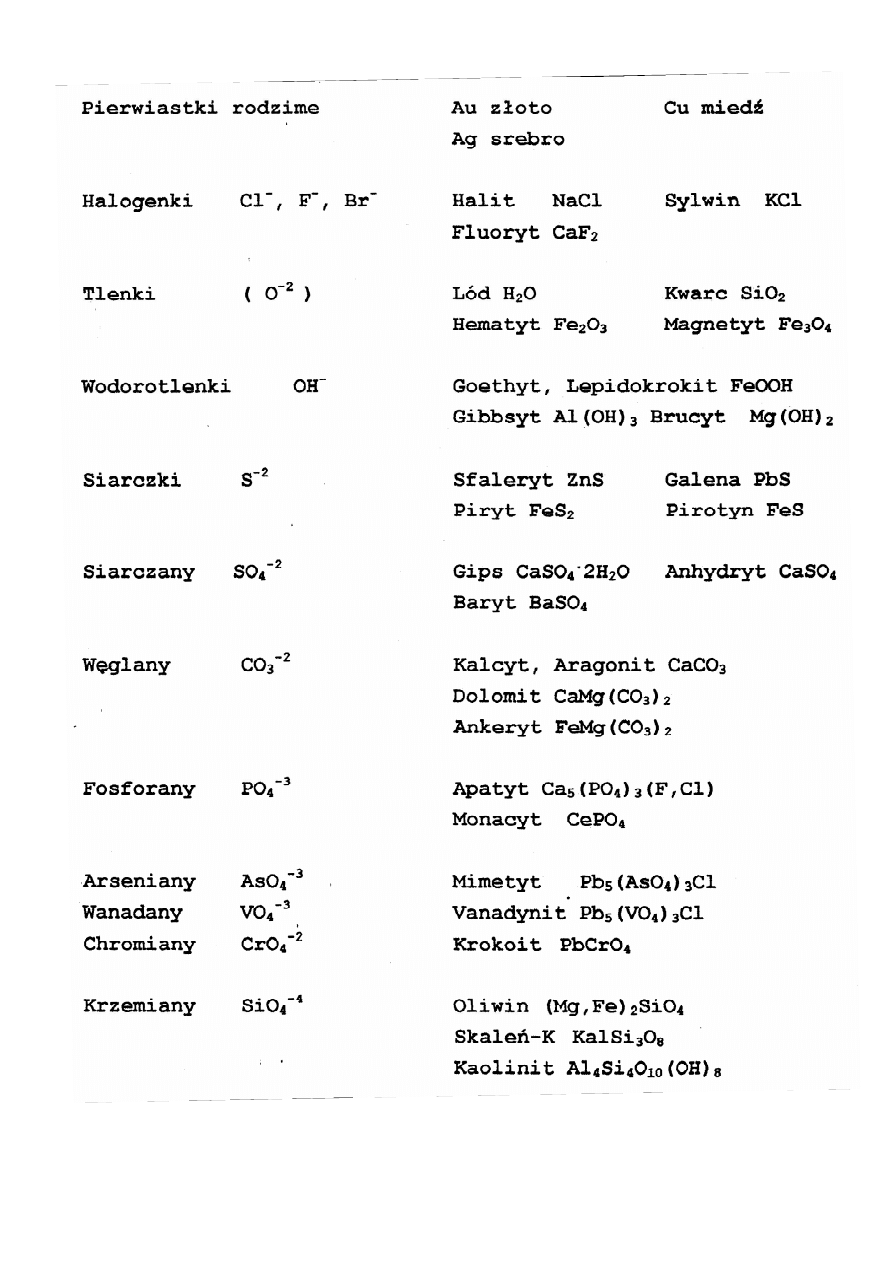
Przykłady klas chemicznych minerałów

Opracowanie konspektu:
T.Bajda i M.Manecki, 2004; M.Manecki i A.Kleszczewska 2007