PODSTAWY AUTOMATYKI

I

ROBOTYKI

Laboratorium

Sala 125

Wykonał:

Łukasz Konopacki 155796

Grupa:

poniedziałek/P, 16.10 – 18.10

Prowadzący:
Dr.inż.Ewa Szlachcic

Termin oddania sprawozdania:

Ocena:

Matlab - firmy The MathWorks to jednocześnie interakcyjne środowisko i wysokiego poziomu język
programowania przeznaczony przedewszystkim do obliczeń naukowych i inżynierskich.Pozwala na
wykonywanie skomplikowanych obliczeń numerycznych oraz wizualizacji wyników.Nazwa pakietu jest skrótem
od „MATrix LABoratory” czyli „Laboratorium Macierzowe”.Już sama nazwa wskazuje, że użytkownik operuje
tylko na jednym typie danych – macierzach ( rzeczywistych bądż zespolonych).Dlatego też nawet pojedyncze
liczby reprezentowane są w formie jednowymiarowej macierzy kwadratowej.Do ważniejszych cech Matlaba
należy dodać możliwość pracy w trybie interakcyjnym.Wyniki obliczeń są dostępne natychmiast i można je
przedstawić w postaci wykresów 2 lub 3 wymiarowcy albo map wielobarwnych.

Praca z programem :

Po uruchomieniu programu MatLab pojawia sie okno wiersza poleceń.O gotowości programu świadczą

„znaki zachęty”  >>.Wszystkie polecienie zatwierdzamy ENTER-em.

Help-system pomocy

Help temat np.(help elfun) – program pokazuje wszystkie dostępne pomoce dotyczące danej grupy.

1)

Podstawowe obliczenia

Atan(log10(log(4+2)*3))  program bez problemu obliczy nam to wyrażenie i na ekranie pokaże się
wynik ans = 0.63084

Atan  oznacza funkcję arctangens

2) Wektory:

X=[1 2 3 4]  program pokaże nam X= 1 2 3 4

Y=[1:8]  program pokaże nam Y= 1 2 3 4 5 6 7 8

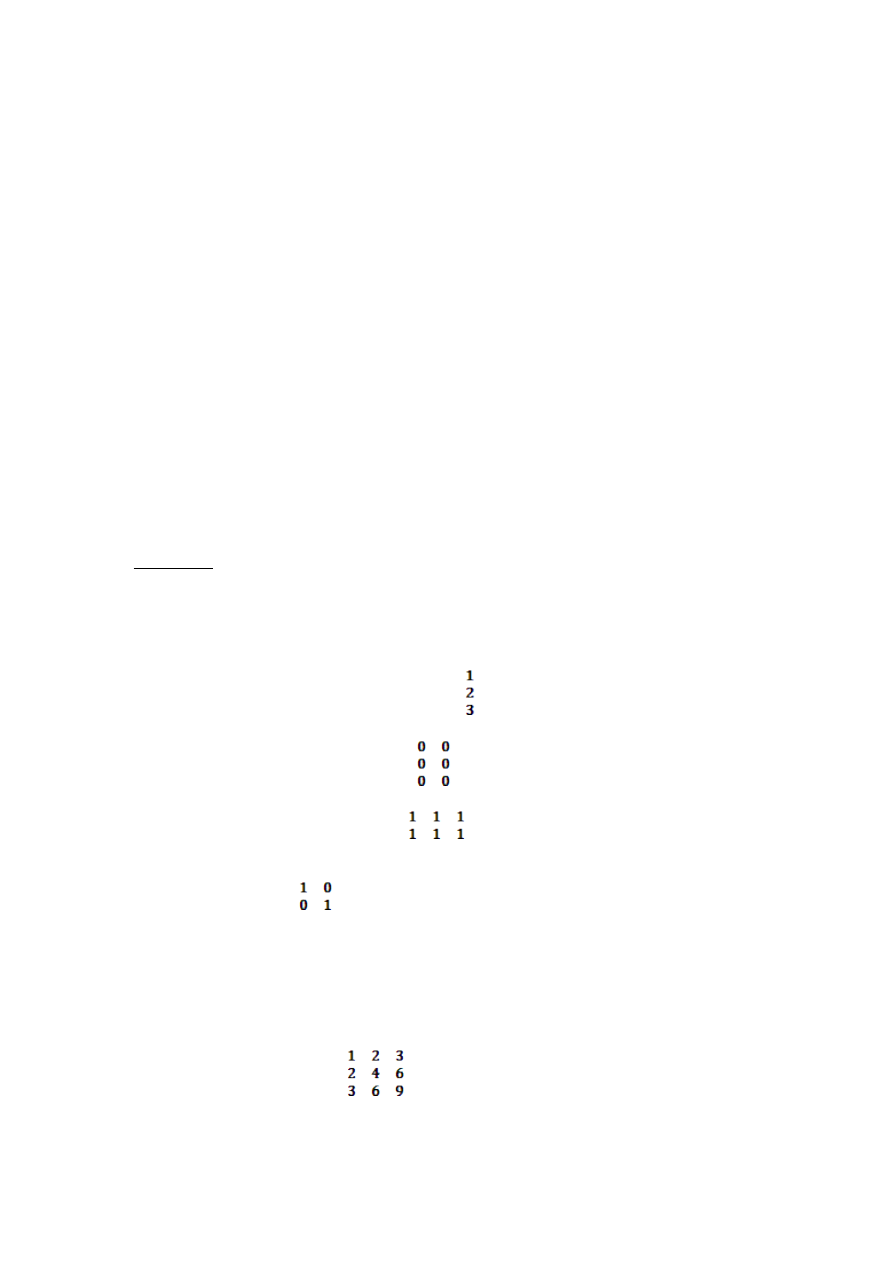
Z=[1:3:10]  program pokaże nam Z= 1 4 7 10

( pierwsza liczba odpowiada początkowi wektora,ostatnia końcowki a środkowa jest długością kroku )

a)Do każdego elementu wektora można dodać/odjąc dowolną liczbę:

B=X+1

b)Dodawanie/Odejmowanie dwóch wektorów

X=[1 2 3 4]

Y=[2 3 4 5]

Z=X+Y/Z=X-Y

Z=X*2  program pomnoży wektor/macierz razy 2

R=[1 2 3 4]  wprowadzenie wektora r

Norm(r)  obliczanie normy wektora r,w naszym przypadku ans = 5.4772

R*R’ 

3) Macierze:

Np.

A=[1,2,3,4] – wprowadzenie macierzy A  A=1 2 3

B=[1;2;3;4] – wprowadzenie macierzy B  B =

Zeros(3,2) – program wprowadzi macierz

Ones(2,3) – program wprowadz macierz

Eye(2,2) – program stworzy macierz jednostkowa z jedynkami na przekątniej i w naszym przypadku

ukaże się taka macierz

A* B – program obliczy nam pomnożenie A * B ( wartości macierzy podane wyżej )

Program pokaże nam : ans=14

B * A – program obliczy nam pomnożenie B * A( wartości macierzy podane wyżej )

Program pokaże nam :

AT=A’  transponowanie macierzy dla A = [1 2 3]

Program pokaże nam :

Det(A)  obliczanie wyznacznika macierzy,np dla A =

det(a) = 0

Inv(a)  obliczanie odwrotniej macierz,np. dla A =

inv(a)=

C=A^2  mnożenie macierzy przez siebie ( wykorzystując operator potęgi )

Np. dla macierzy

A =

Potęgą jest :

c =

C=A.^2  podnoszenie każdego elementu macierzy do kwadratu z osobna

Np. dla macierzy a =

Podniesienie każdego elementu do kwadratu jest macierz : c =

X=inv(a)*b’ 

X=A/B  rozwiązuje układ AX=B

X=B/A  rozwiązuje układ XA=B

BLAD=A*X-B’  obliczanie normy błedu np. dla A =

Oraz B =

norma błędu wynosi BLAD =

-3.5527e-0.15

-3.5527e-0.15

-1.7764e-0.15

0.0000e+000

Cond(a)  oblicza spektralną liczbę uwarunkowania macierzy kwadratowej

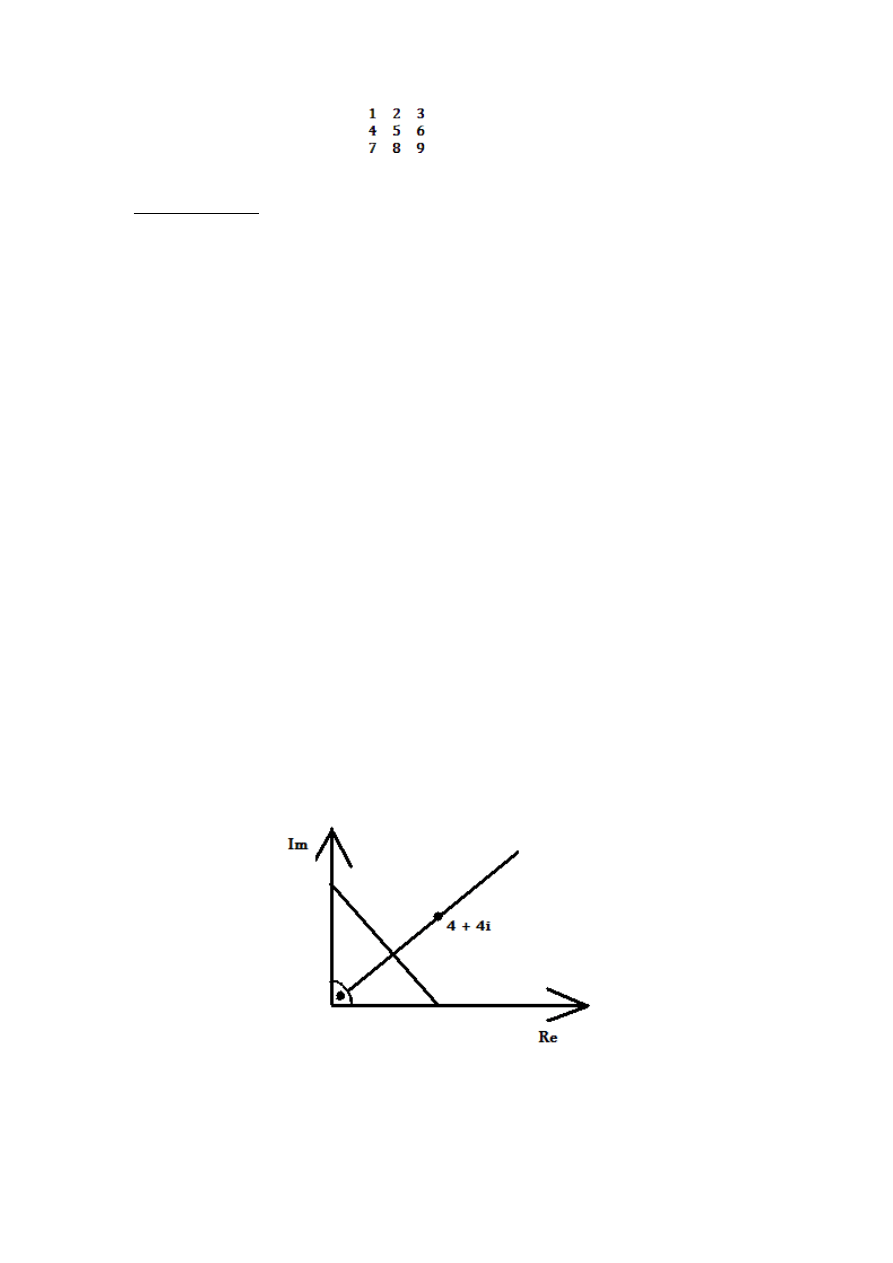
Np. dla macierzy a=

cond(a) = 5.6133e+016

4) Liczby zespolone:

Wprowadzamy dane liczby zespolonej

Np. A=complex(4,4)  program tworzy liczbę zespoloną a=4+4i

Lub A= 4+ 4i  program rownież tworzy liczbę zespoloną a=4+4i

Z=2+2i

W=5-1i

Podstawowe obliczenia : y=w+z  obliczenia programy : y=7+i

y=w-z 

y=3-3i

y=w*z 

y=12+8i

y=w/z 

y=1.0000-1.5000i

a) Obliczenie modułu liczby zespolonej

Abs(a)



ans=5.6569

Modul=Sqrt((real(a))^2+(imag(a))^2)  ans=5.5659  liczenie modulu liczby zespolonej

Po wpisaniu komendy imag(a) lub real(a)  ukażą sie nam odpowiednio liczby urojone lub
rzeczywiste dla danej funkcji

b) Liczenie stopni w Celcjuszach i Radianach

Atand(1)  ilość stopni(w Celcjuszach) w którym arctangens posiada wartość 1

Program pokaże nam : ans = 45

Atan(1)  ilość stopni(w Radianach) w którym arctangens posiada wartość 1

Program pokaże nam : ans = 0.78540

Atand(real(a)/imag(a))  liczenie stopni w Celcjuszach

Atand(imag(a)/real(a))  liczenie stopni w Celcjuszach

5) Wielomiany:

a)

f(x)= 2x

2

+ 3x +1

Aby MatLab odczytał tą funkcję musimy ją zapisać jako wektor:

D=[2 3 1]



Obliczanie miejsc zerowych funkcji wyraża się wzorem :

Roots(d)

Ans=

-1.0000 -0.5000



Liczenie wartości funkcji w danym punkcie:

Polyval(d,3)

Ans=28

Inne polecenia dotyczące wielomianów:

•

poly - tworzy wielomian na podstawie podanych pierwiastków

•

polyder - pochodna wielomianu

•

conv - mnożenie wielomianów

•

deconv - dzielenie wielomianów

6) Rysowanie:

Sin(x) 

w trójkącie prostokątnym nazywamy stosunek długości

przyprostokątnej przeciwnegłej temu kątowi do długości przeciwprostokątnej

Cos(x)  Cosiunusem kąta £ w trójkącie prostokątnym nazywamy stosunek długości
przyprostokątnej przyległej temu kątowi do długości przeciwprostokątnej

a) Wykresy dwuwymiarowe

X=[0:0.1:2*pi]  program pokaże nam wartość x = od 0.00000 do 6.200000 co 0.1

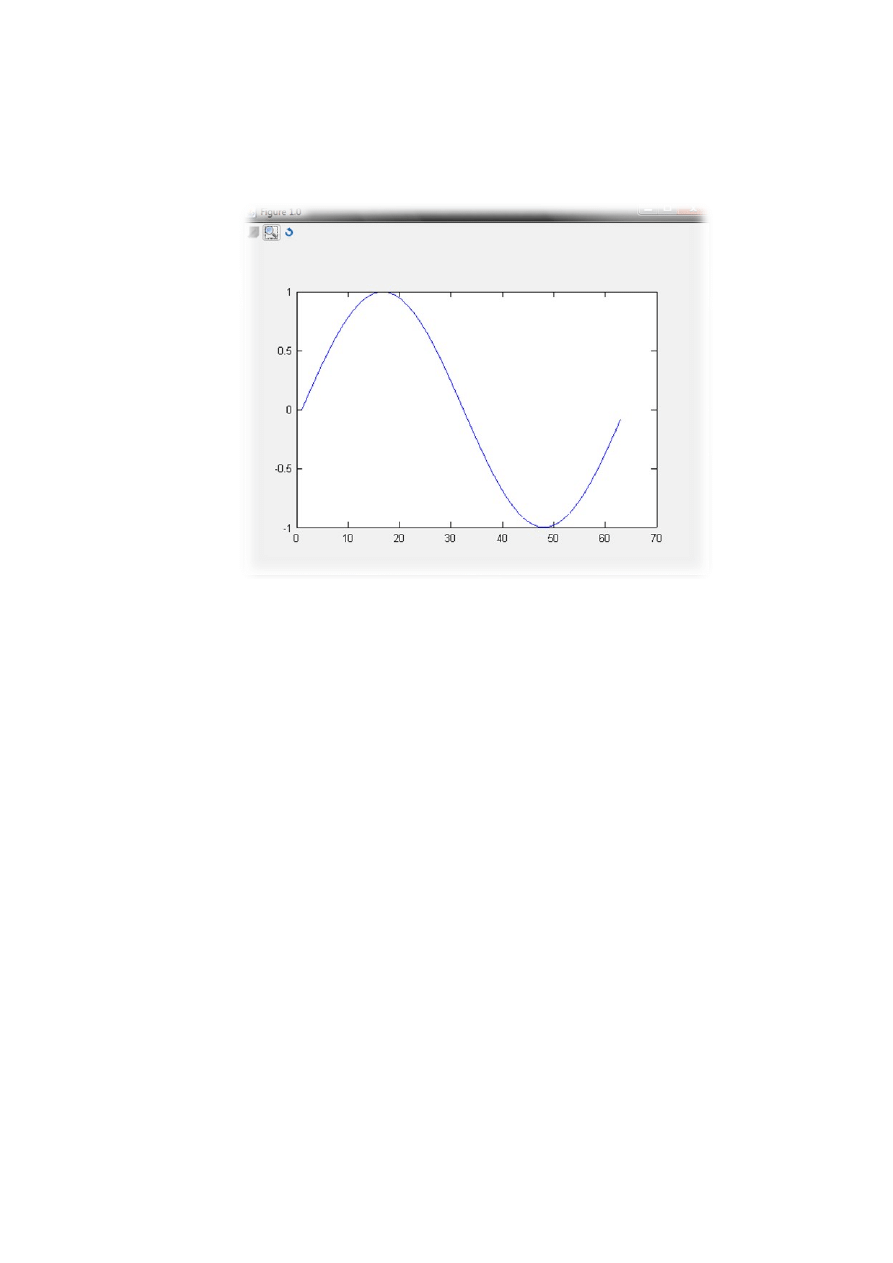
Plot(sin(x))  Po wpisaniu takiej komendy program pokaże nam wykres sinusa : jeżeli jest
potrzebna pomoc to wpisujemy komendę help plot

Parametry opisujące wykres funkcji :

y - żółty

. - punkt

m - purpurowy o - kółko
c - błękitny

x - krzyżyk

r - czerwony

+ - plus

g - zielony

- - linia ciągła

w - biały

--- linia kreskowa

k - czarny

: - linia kropkowa

Polecenia służące do opisywania wykresu:

•

title - nadaje tytuł wykresowi np.title(‘wpisujemy nazwę wykresu’)

•

xlabel - opisuje oś x np.xlabel(‘wpisujemy nazwę osi x’)

•

ylabel - opisuje oś y np.ylabel(‘wpisujemy nazwę osi y’)

•

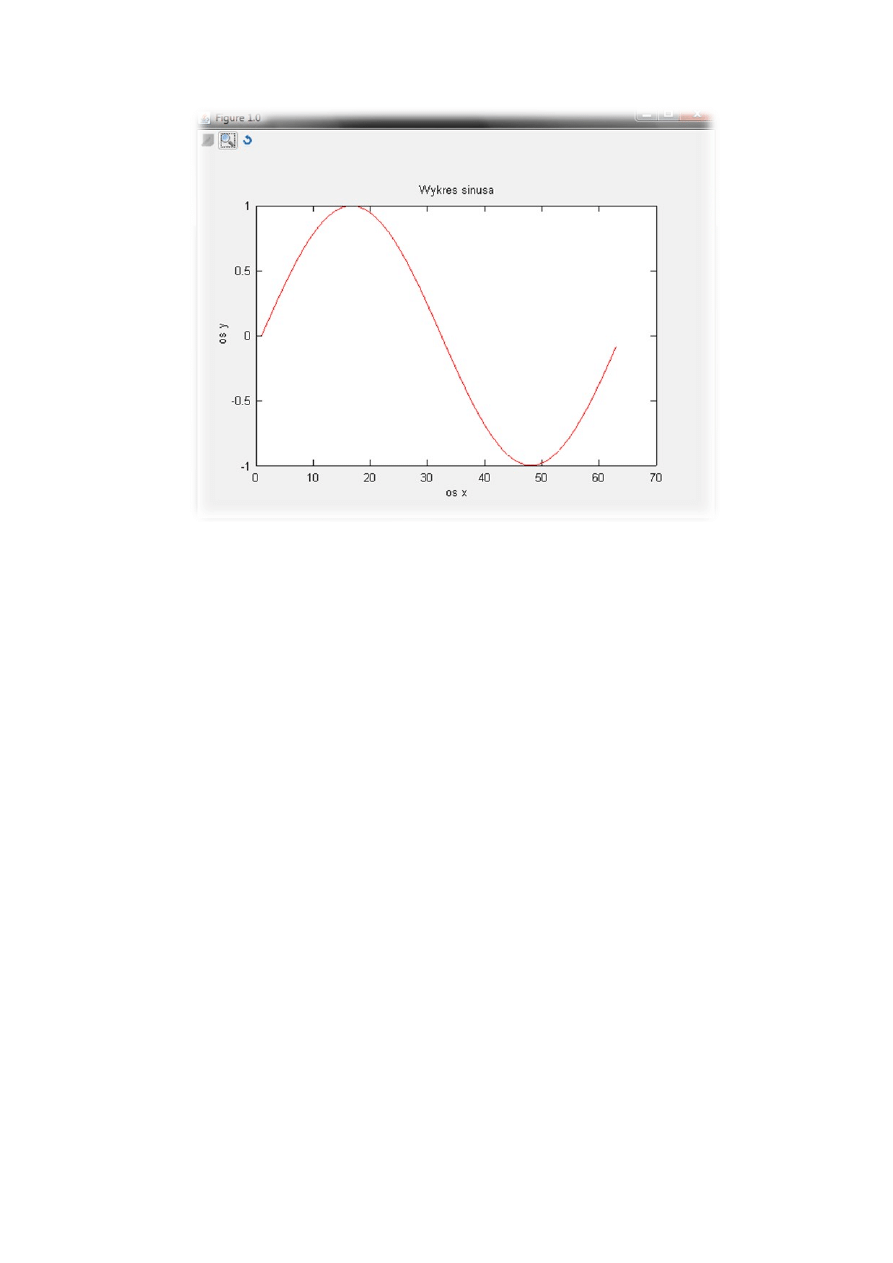
legend - umieszcza legndę na wykresie

np.dopisaniu do funkcji : plot(sin(x),’r’);xlabel(‘os x’);ylabel(‘os y)

program pokaże nam wykres taki sam jak powyżej lecz z podpisanymi osiami oraz kolor wykresu
zmieni sie na czerwony zgodnie z tabelką powyżej.

Można również narysować 2 funkcje jednocześnie na jednym wykresie

Wieć zaczniemy od komendy u=[-2*pi:0.1:2*pi]  ustalamy przedział

Plot(u,sin(u),u,cos(u))  po wpisaniu tej komendy pokaże się nam

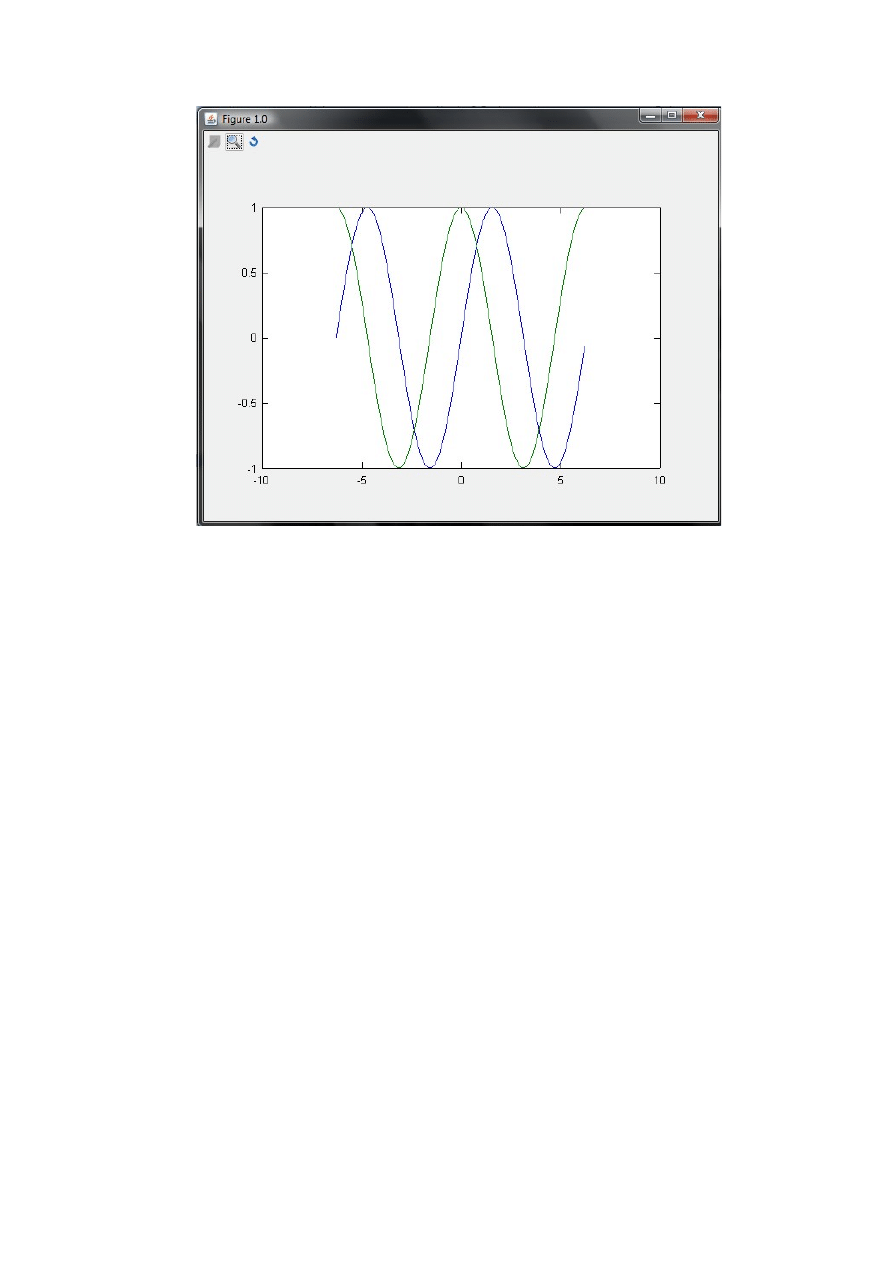
Można rownież wykorzystac polecenie surface która jest funkcją niskiego poziomu do tworzenie
obiektów graficznych.

b) Wykresy trójwymiarowe

Program MatLab umożliwia wizulalizację 3-wymiarową.Umożliwiają to funkcje krzywych
przestrzennych (plot), siatek (mesh), powierzchni (surf), oraz wykresów konturowych (contour)

Np. T=[0:0.01:1]



zakres od 0 do 1 co 0.01

Z=(sin(2*pi*t))  wykres sinusa zależnego od parametru „t”

Surf(z’*z)



polecenie rysowania wykresu 3 wymiarowego

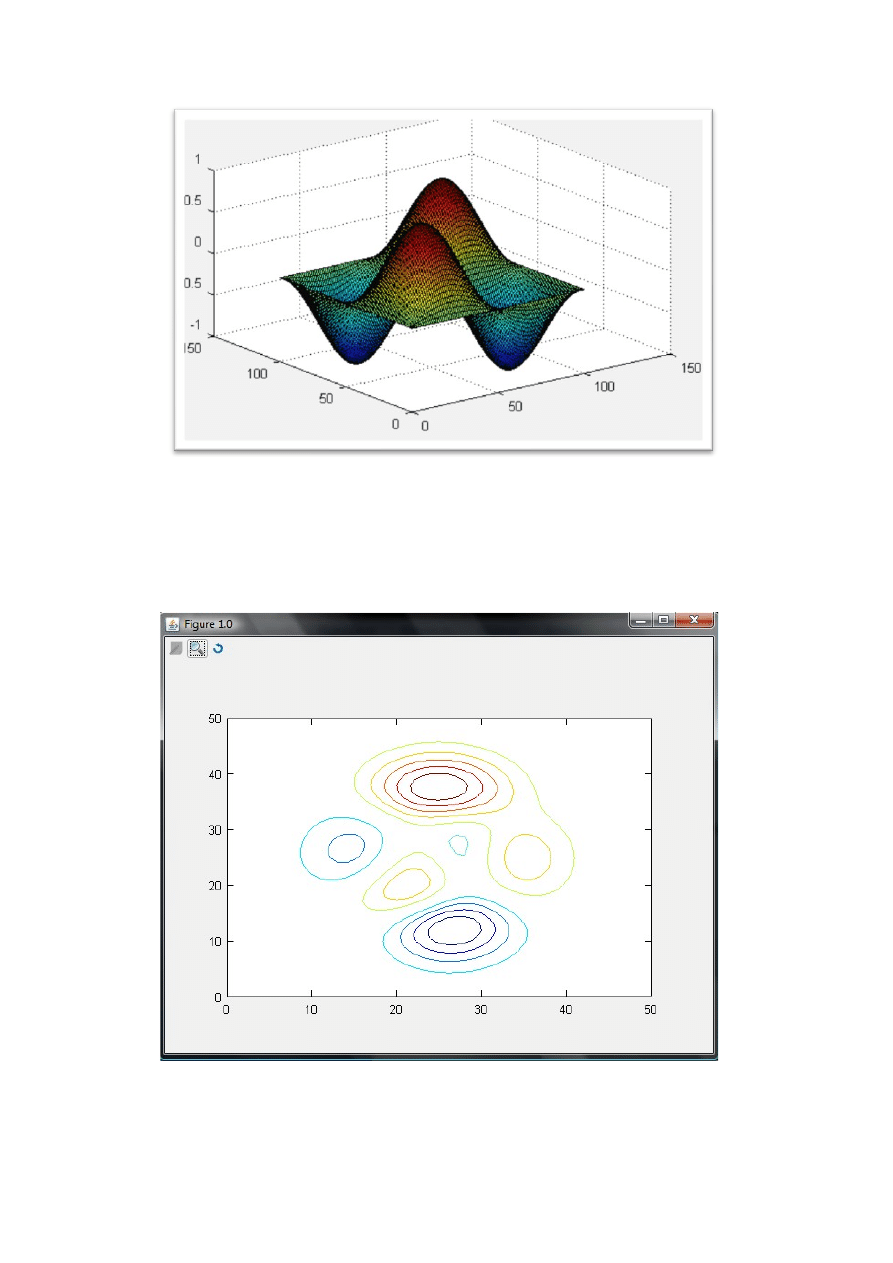
Istnieją

jeszcze inne polecenia związane z wykresami 3 wymiarowymi : np.

Z=[2 4 7 8 25 47]

Z=peaks

Contour(z)