Laboratorium numer 1. Numeryczne Algorytmy Inżynierskie, Tomasz Owerko KGIiB

Regresja nieliniowa, aproksymacja krzywych dla potrzeb obliczeń geodezyjnych i
inżynierskich:

Wstęp

The R Project for Statistical Computing –

http://www.r-project.org/

Literatura:
D. M. Bates and D. G. Watts. Nonlinear Regression Analysis and
Its Applications. Wiley, 1988.
S. E. Maxwell and H. D. Delaney (1990), "Designing experiments and
analyzing data: A model comparison perspective".

W „R” Równania które nie mogą być zlinearyzowane lub ich linearyzowana postać nie jest znana mogą
być wpasowywane za pomocą metody nls
Postać wstępna funkcji powinna być znana z teorii np. z fizyki zjawiska (termowizja, konstrukcje:
maszty, kominy, wiadukty, kładki itp.)

Zadanie 1 - wprawka:

Stworzyć ramkę jednolitych danych (o liczebności 24) wraz z odpowiadającą zmienną zależną o
pewnym losowym zaszumieniu. Narysować dane oraz krzywą teoretyczną.

Założenie:
a) Radomizujemy pomiary funkcją rnorm
b) Długość wektora opracowania = 24 (pomiar dyskretny)

len=24
x=runif(len)

// jednolicie rozłożona zmienna

y=x^2+rnorm(len,0,0.04)

// wprowadzmy szum losowy do wartości funkcji

ds=data.frame(x=x,y=y)

// tworzymy ramkę danych

ds

// wyświetlając ramkę

x y
1 0.89630372 0.82353177
2 0.02321050 -0.04986645
3 0.41016706 0.08474166
4 0.33757243 0.10262701
5 0.86798392 0.80236827
6 0.34340661 0.10700315
7 0.08304545 0.04435323
8 0.60756028 0.45617045
9 0.21540084 0.10360606
10 0.23889671 0.04242461
11 0.98617209 0.94627259
12 0.98083996 0.96310611
13 0.92455574 0.80253030
14 0.09107546 -0.00885334
15 0.61064812 0.45171589
16 0.35651122 0.11266692
17 0.96864061 0.88724460
18 0.58030270 0.28182619
19 0.42512862 0.20558007
20 0.70878168 0.48703572
21 0.92171906 0.83941377

Laboratorium numer 1. Numeryczne Algorytmy Inżynierskie, Tomasz Owerko KGIiB

22 0.98873698 1.01740812
23 0.63951224 0.43364385
24 0.69595835 0.51077657

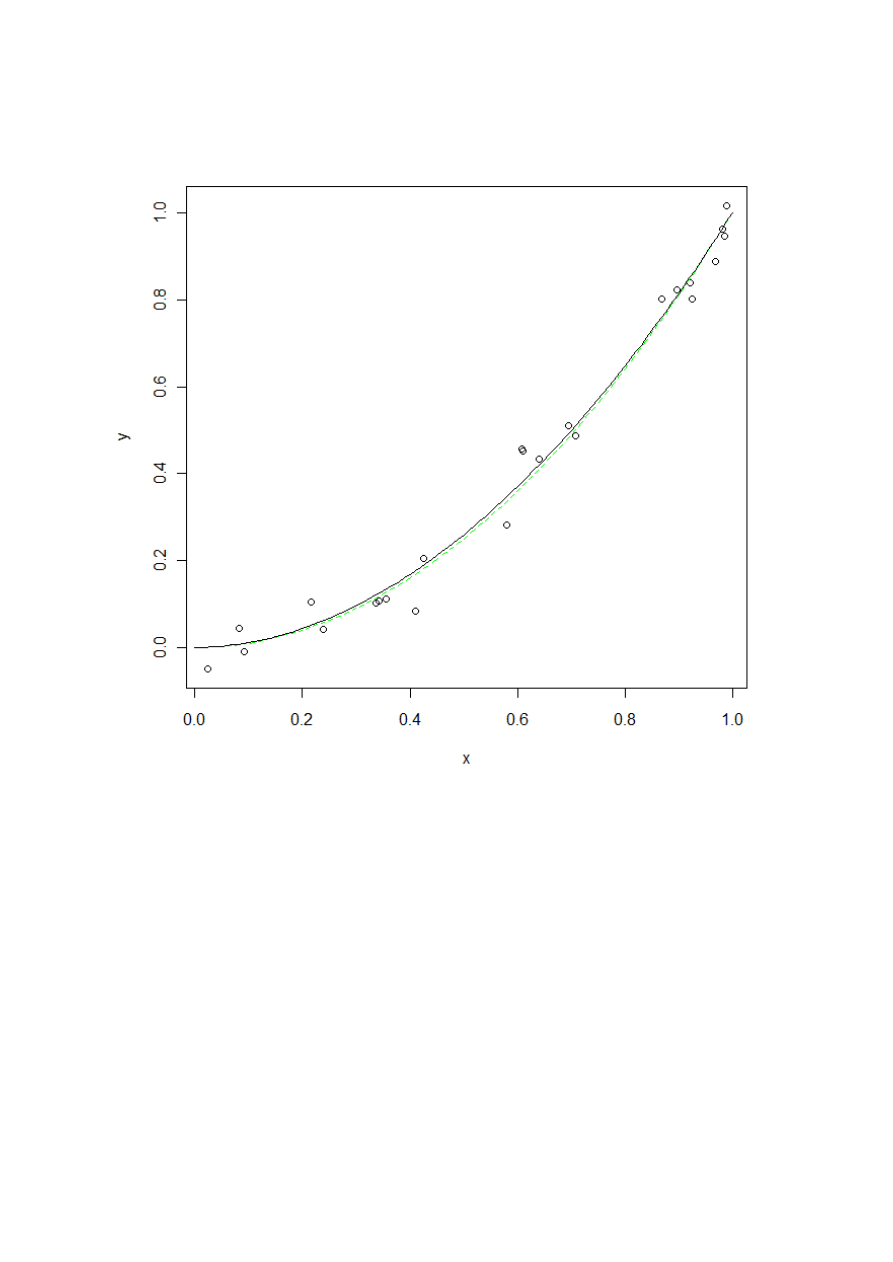
plot(y~x)

//rysujemy "dane"

s=seq(0,1,by=0.01)
s

[1] 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 0.11 0.12 0.13 0.14
[16] 0.15 0.16 0.17 0.18 0.19 0.20 0.21 0.22 0.23 0.24 0.25 0.26 0.27 0.28 0.29
[31] 0.30 0.31 0.32 0.33 0.34 0.35 0.36 0.37 0.38 0.39 0.40 0.41 0.42 0.43 0.44
[46] 0.45 0.46 0.47 0.48 0.49 0.50 0.51 0.52 0.53 0.54 0.55 0.56 0.57 0.58 0.59
[61] 0.60 0.61 0.62 0.63 0.64 0.65 0.66 0.67 0.68 0.69 0.70 0.71 0.72 0.73 0.74
[76] 0.75 0.76 0.77 0.78 0.79 0.80 0.81 0.82 0.83 0.84 0.85 0.86 0.87 0.88 0.89
[91] 0.90 0.91 0.92 0.93 0.94 0.95 0.96 0.97 0.98 0.99 1.00

lines(s,s^2,lty=2,col="green")

// funkcja "modelowa" [w praktyce nie znana!]

Laboratorium numer 1. Numeryczne Algorytmy Inżynierskie, Tomasz Owerko KGIiB

m=nls(y~I(x^potegi),data=ds,start=list(potegi=1),trace=T) )//

model wykładniczy - estymujemy (tylko) wykładnik - proces iteracyjny!

0.696303 : 1
0.08328449 : 1.647024
0.04389877 : 1.922860
0.04367553 : 1.947776
0.04367551 : 1.947541
0.04367551 : 1.947545

summary(m)

Formula: y ~ I(x^potegi)
Parameters:
Estimate Std. Error t value Pr(>|t|)
potegi 1.94755 0.07317 26.62 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.04358 on 23 degrees of freedom
Number of iterations to convergence: 5
Achieved convergence tolerance: 2.020e-07

lines(s,predict(m,list(x=s),lty=1,col="blue"))

// rysyjemy linię z wygenerowanego

modelu

Laboratorium numer 1. Numeryczne Algorytmy Inżynierskie, Tomasz Owerko KGIiB

Na nasze potrzeby:
Def 1.
RSS: residual sum of squaers - świadczy o wariancji w modelowaniu błędów
Def 2.
TSS Total sum of squares - świadczy o wariancji w modelowanych danych
Def 3.
ESS: Explained sum of squares - parametr stosowany do wyrażenia jak dobrze model (regresji) modeluje
zadane dane

Ogólnie:
TSS=ESS+RSS

Szacujemy jakość wpasowania

RSS.p=sum(residuals(m)^2)

// liczymy RSS

RSS.p

[1] 0.04367551

TSS=sum((y-mean(y))^2)

// liczymy TSS

TSS

Laboratorium numer 1. Numeryczne Algorytmy Inżynierskie, Tomasz Owerko KGIiB

[1] 3.047115

1-(RSS.p/TSS)

// jakość modelu wygenerowanego na podstawie nls

[1] 0.9856666

1-sum(x^2-y)^2/TSS

// jakość znanej funkcji (zależy od szumu)

[1] 0.9996179

Może lepszy model?

kwadracik=function(x,w,b)
+ {x^w+b}
m.2=nls(y~kwadracik(x,w,b), data=ds, start=list(w=1,b=0),trace=T)

0.696303 : 1 0
0.07191987 : 1.58621651 -0.01789465
0.04278197 : 1.85001676 -0.01101228
0.04252747 : 1.86518399 -0.01244997
0.04252742 : 1.86456054 -0.01252547
0.04252742 : 1.86458905 -0.01252242

summary(m.2)

Formula: y ~ kwadracik(x, w, b)

Parameters:
Estimate Std. Error t value Pr(>|t|)
w 1.86459 0.12930 14.420 1.08e-12 ***
b -0.01252 0.01656 -0.756 0.458
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.04397 on 22 degrees of freedom

Number of iterations to convergence: 5
Achieved convergence tolerance: 2.163e-06

RSS.pb=sum(residuals(m.2)^2)

[1] 0.04252742

1-(RSS.pb/TSS)

[1] 0.9860434

1-(RSS.p/TSS)

[1] 0.9856666

1-sum(x^2-y)^2/TSS

[1] 0.9996179

Anova

anova(m.2,m)

Analysis of Variance Table
Model 1: y ~ kwadracik(x, w, b)
Model 2: y ~ I(x^potegi)
Res.Df Res.Sum Sq Df Sum Sq F value Pr(>F)
1 22 0.052105
2 23 0.053218 -1 -0.0011123 0.4696

0.5003

Komentarz:
Pr (>F) to jest prawdopodobieństwo że odrzucenie hipotezy zerowej
(bardziej skomplikowany model nie pasuje lepiej niż prostszy)
byłoby błędem.
My wiemy że nie powinno być "b" (parametru przecięcia - bo

Laboratorium numer 1. Numeryczne Algorytmy Inżynierskie, Tomasz Owerko KGIiB

zaburzaliśmy czyste x^2!) - więc liczymy na to że wartość Pr(>F)
będzie wysoka - i tak jest.
Dalmierz:
c(t)=Csin(фt)
m(t)=sin(wt+P)
y=(C+Msin(wt+P))*sin(фt)

Przykłady do wykonania:

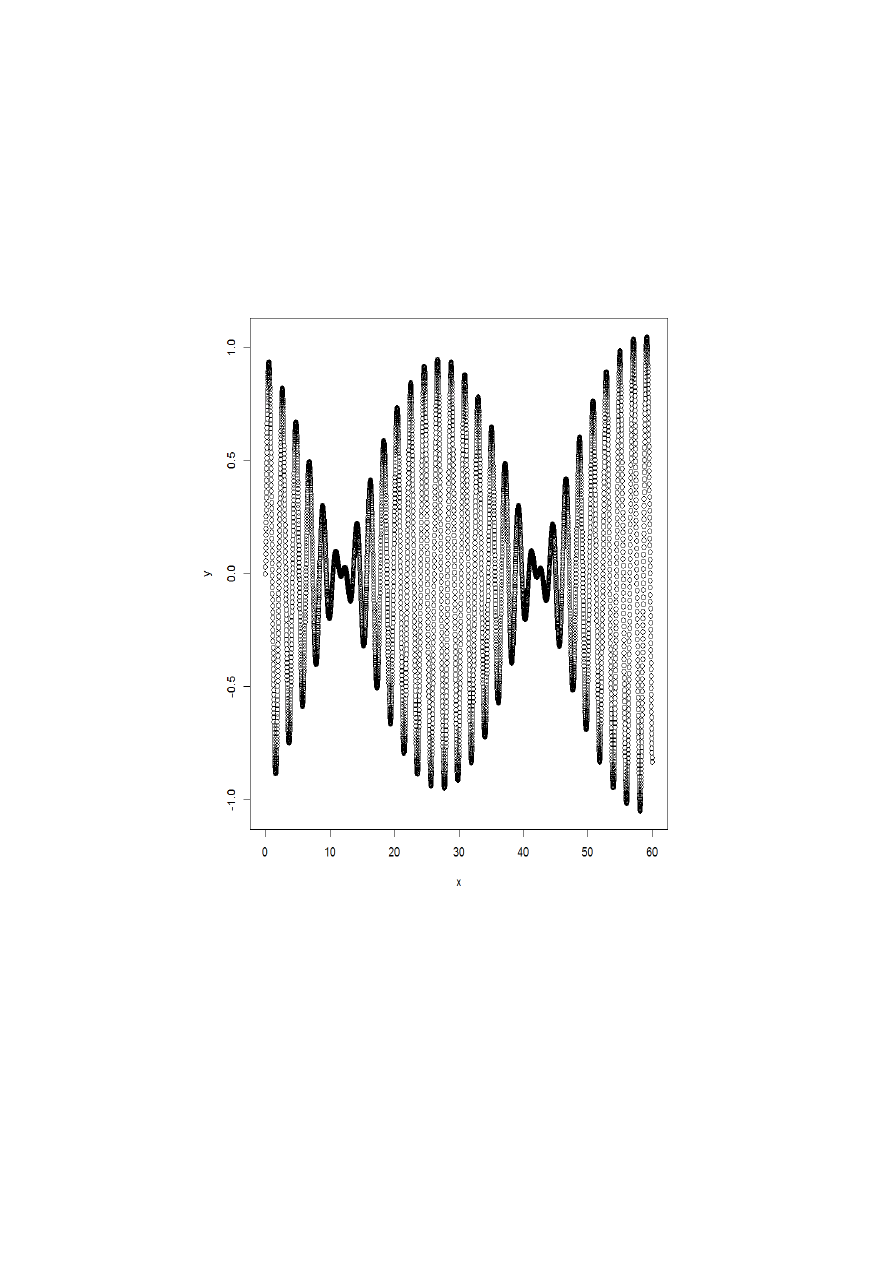
1. Modulacja Amplitudowa (dalmierze EDM)
x=seq(0,60,by=0.01)
y=(0.05+1*sin(0.1*x+2))*sin(3*x)

2. Funkcja okresowa z trendem liniowym
sinusik=function(x,a,a2,w,b2){a*x+a2*sin(w*x)+b2}