- 1 -

REGRESJA NIELINIOWA

w programie STATGRAPHICS Centurion

Przekład

Robert Wiśniewski

http://chomikuj.pl/bobwis

PODSUMOWANIE

Procedura regresji nieliniowej dopasowuje model zdefiniowany przez użytkownika wiążący jedną
zmienną zależną Y z jedną lub z kilkoma zmiennymi niezależnymi X. Model ten estymowany jest przy
korzystaniu z nieliniowej metody najmniejszych kwadratów. Dopasowany model można wykreślać,
generować na jego podstawie wartości przewidywane oraz identyfikować reszty odbiegające.

Przykładowy plik folii statystycznej StatFolio:

nonlinear reg.sgp

Przykładowy plik danych Data:

nonlin.sf3

Powyższy plik

nonlin.sf3

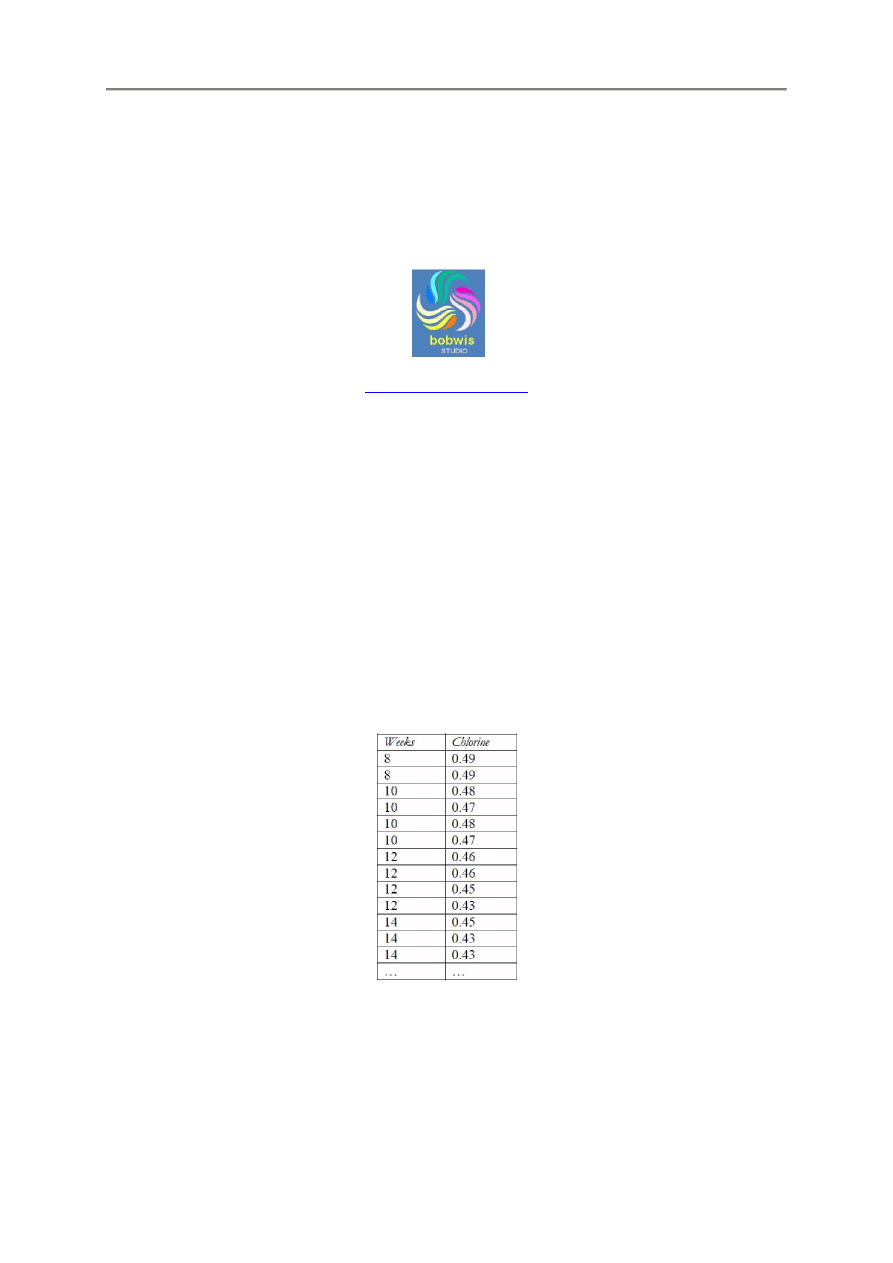
zawiera dane dotyczące zawartości chloru w próbkach produktu w funkcji

liczby tygodni upływających od daty ich produkcji.

Dane te zaczerpnięte z książki Draper and Smith (1998) zawierają, n = 44 próbek, których część
zastawiono w poniższej tablicy.

Zadaniem naszym jest dopasowanie poniższego modelu do tych danych:









8

49

0











weeks

b

e

a

a

chlorine

,

......................................... (1)

Model ten zasugerowany przez eksperta w danej dziedzinie zawiera dwie niewiadome: a – linia
asymptoty do której zmierza zmienna chlorine gdy zmienna weeks zmierza do dużych wartości
oraz b – wykładnik szybkości opóźnienia

- 2 -

WPROWADZANIE DANYCH

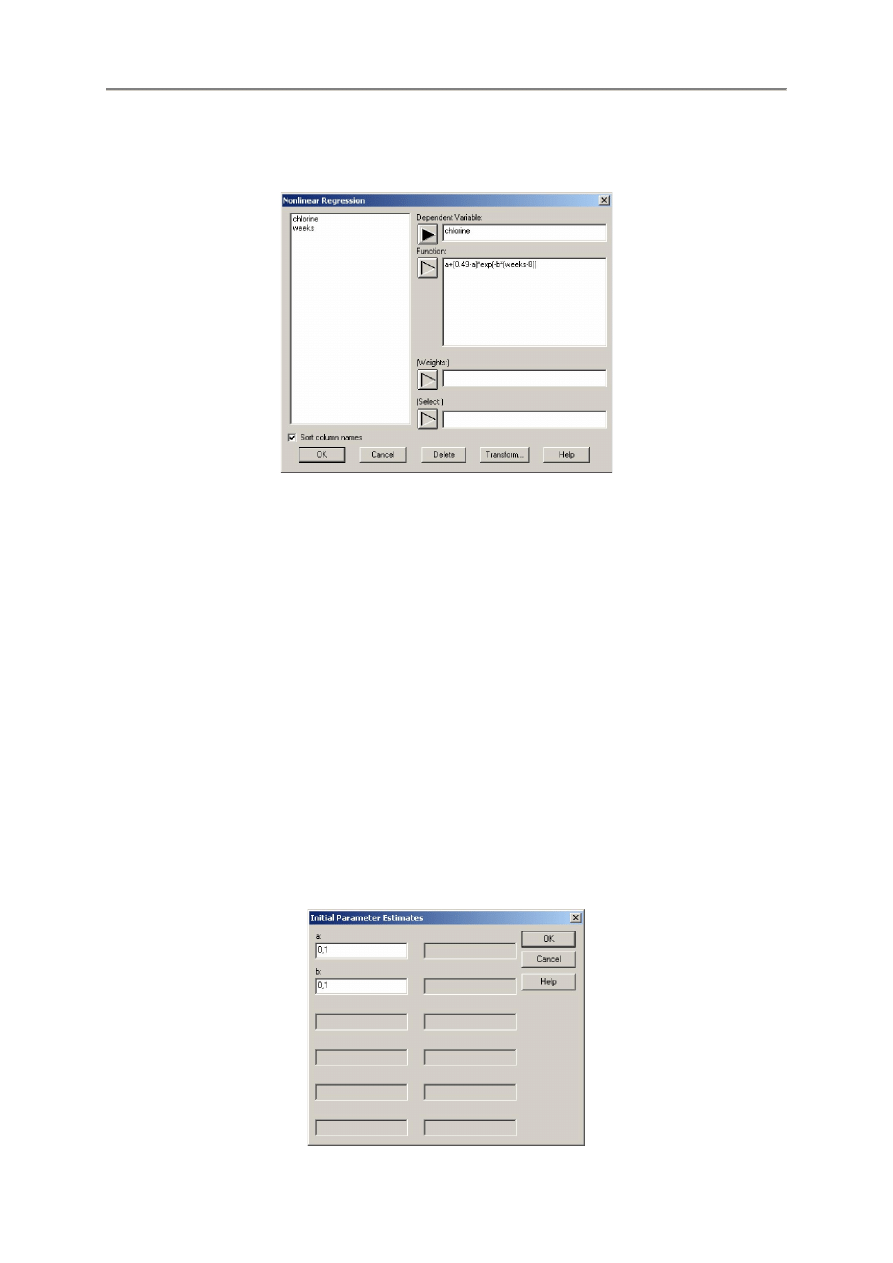
Wybieramy polecenie menu Relate | Multiple Factors | Nonlinear Regression. Otwiera się pierwsze
okienko dialogowe oczekujące wprowadzenia wymaganych danych:

 Dependend Vaiable - Zmienna zależna. Kolumna numeryczna arkusza danych zawierająca

n-wartości zmiennej Y.W

W naszym przykładzie wprowadzamy tu zmienną chlorine.

 Function – Funkcja. Wyrażenie STATGRAPHICS reprezentujące dopasowywany model

regresji. Musi on zawierać jedną lub kilka nazw kolumn reprezentujących zmienne niezależne
i może zawierać takie funkcje jak SQRT lub EXP. W naszym przykładzie wprowadzamy tu
wyrażenie w poniższej postaci:

a+(0.49-a)*exp(-b*(weeks-8))

Wszelkie nierozpoznane nazwy będą traktowane jako parametry modelu wymagające
estymacji.

 (Weight) – Waga. Opcjonalna nazwa kolumny numerycznej zawierającej wagi stosowane do

kwadratów reszt gdy korzystamy z analizy regresji za pomocą ważonej metody najmniejszych
kwadratów.

 (Select) – Selekcja – Opcjonalna fraza stosowana do wyboru podzestawu danych do analizy.

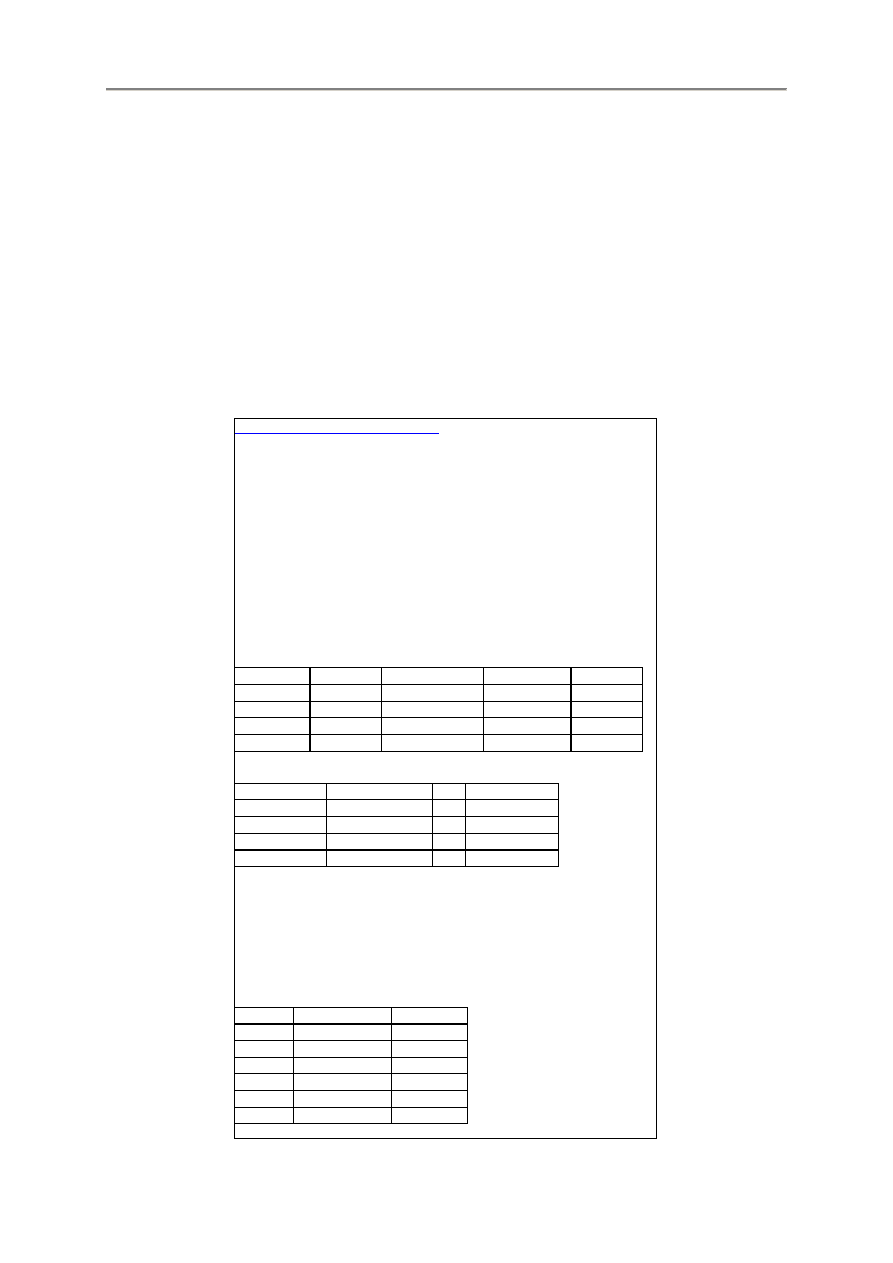
Po kliknięciu przycisku OK otwiera sie drugie okienko dialogowe oczekujące wprowadzenia wartości
początkowych każdego nieznanego parametru modelu.

- 3 -

Wprowadzamy tu wartości początkowe (pierwsze przybliżenia) każdego estymowanego parametru.

Program zacznie obliczenia od tych wartości i będzie numerycznie szukał uch estymacji, które
minimalizują resztową sumę kwadratów.

W zależności od złożoności modelu, zła estymacja może ale nie musi prowadzić do optymalnego
rozwiązania. We wszystkich stosunkowo prostych przypadkach, inteligentny wybór wartości
początkowych może znacznie zwiększyć szanse uzyskania dobrego rozwiązania.

Typowo, ważne jest aby pierwsze przybliżenia miały co najmniej poprawny znak (dodatni lub ujemny),
ponieważ w przeciwnym razie procedura szukania może się zacząć w złym kierunku.


PODSUMOWANIE ANALIZY

Po kliknięciu przycisku OK, otwiera się okno z tablicą analizy wyników.

Nonlinear Regression - chlorine

Dependent variable: chlorine (percent available)

Independent variables:
weeks (weeks since production)

Function to be estimated: a+(0.49-a)*exp(-b*(weeks-8))
Initial parameter estimates:
a = 0,1
b = 0,1

Estimation method: Marquardt
Estimation stopped due to convergence of residual sum of squares.
Number of iterations: 4
Number of function calls: 14

Estimation Results

Asymptotic

95,0%

Asymptotic

Confidence

Interval

Parameter Estimate

Standard Error Lower

Upper

a

0,390144 0,00501534

0,380022

0,400265

b

0,101644 0,0133628

0,0746763

0,128611

Analysis of Variance

Source

Sum of Squares Df

Mean Square

Model

7,982

2

3,991

Residual

0,00500168

42

0,000119088

Total

7,987

44

Total (Corr.)

0,0395

43

R-Squared =

87,3375

percent

R-Squared (adjusted for d.f.) =

87,036

percent

Standard Error of Est. =

0,0109127

Mean absolute error =

0,00769665

Durbin-Watson statistic = 1,98378
Lag 1 residual autocorrelation = 0,00702451

Residual Analysis

Estimation

Validation

n

44

MSE

0,000119088

MAE

0,00769665

MAPE

1,82283

ME

-0,000097621

MPE

-0,0826224

- 4 -

Wyniki warte w tej tablicy zawierają:

 Dane sumaryczne – Informacje o wprowadzanych danych,

 Estymowana funkcja – Przyjęty model i wartości początkowe parametrów.

 Estymowane statystyki – Stosowana metoda estymacji i liczba wykonanych iteracji oraz

liczba wywoływania funkcji.

 Estymowane parametry – Obliczone parametry modelu wraz z ich przedziałami ufności.

Przedziały ufności nie zawierające wartości 0 świadczą, że parametr modelu jest statystycznie
istotny na przyjętym poziomie istotności.

 Analiza wariancji – Dekompozycja (rozkład) zmienności zmiennej zależnej Y na sumę

kwadratów modelu i sumę kwadratów reszt (błędów).

 Statystyki – Opisowe statystyki dopasowanego modelu, w tym:

 R-Squared – Współczynnik determinacji R

2

(kwadrat współczynnika korelacji), który

reprezentuje procent zmienności zmiennej zależnej Y wyjaśniony dopasowanym modelem
regresji, mieszczący się w przedziale od 0 do 100 %. Dla danych naszego przykładu
(zmienność stężenia chloru), wartość tego współczynnika wynosi 87,3.

 Adjusted R-Squared – Dopasowany współczynnik determinacji R

2

uwzględniający liczbę

współczynników (parametrów) modelu. Wartość ta często jest stosowana do porównywania
modeli o różnej liczbie współczynników.

 Standard Error of Est. – Estymowane odchylenie standardowe reszt (odchylenia w całym

modelu). Wartość ta jest stosowana do obliczania granic przewidywania dla nowych
obserwacji.

 Mean Absolute Error – Średnia wartość bezwzględna reszt.

 Durbin-Watson Statistic – Miara seryjnej korelacji reszt. Gdy reszty zmieniają się lisowo,

wartość ta powinna być bliska 2. Małe wartości P-Value wskazują na nielosowy rozkład
reszt.

Dla danych rejestrowanych w czasie, małe wartości P-Value mogą wskazywać, że niektóre
trendy w czasie nie mogą być uwzględniane.

 Lag 1 Residual Autocorrelation – Estymowana korelacja między kolejnymi resztami

w skali od -1 do +1. Wartości odległe od 0 wskazują, na strukturę niedostatecznie
objaśnioną przez ten model.

 Residual Analysis – Analiza reszt. Gdy podgrupa wierszy arkusza danych była wykluczona

z analizy przy korzystaniu z pola Select w okienku dialogowym wprowadzania danych,
wówczas dopasowany model jest stosowany do przewidywania wartości Y tych wierszy.
Tabela ta pokazuje statystyki błędów przewidywania definiowanych następująco:

i

i

i

y

y

e

ˆ





.................................................................... (2)

i zawiera średni błąd kwadratowy MSE, średni błąd bezwzględny MAE, średni bezwzględny
błąd procentowy MAPE błąd średniej ME i błąd procentowy średniej MPE.

Te prawomocne statystyki mogą być porównywalne ze statystykami dopasowania modelu
w celu sprawdzania jak dobrze model przewiduje obserwacje leżące poza stosowanymi
danymi do jego dopasowania.

- 5 -

Dla przykładowych danych, dopasowany model ma poniższą postać:

chlorine = 0.390144 + (0.49-0.390144)exp(-0.101644(weeks-8)) ……………….. (3)

Model ten zaczyna się od zawartości chloru chlorine = 0,49 po 8 tygodniach weeks = 8 i spada
wykładniczo do asymptoty równej w przybliżeniu 0,39 w miarę wzrostu zmiennej weeks.

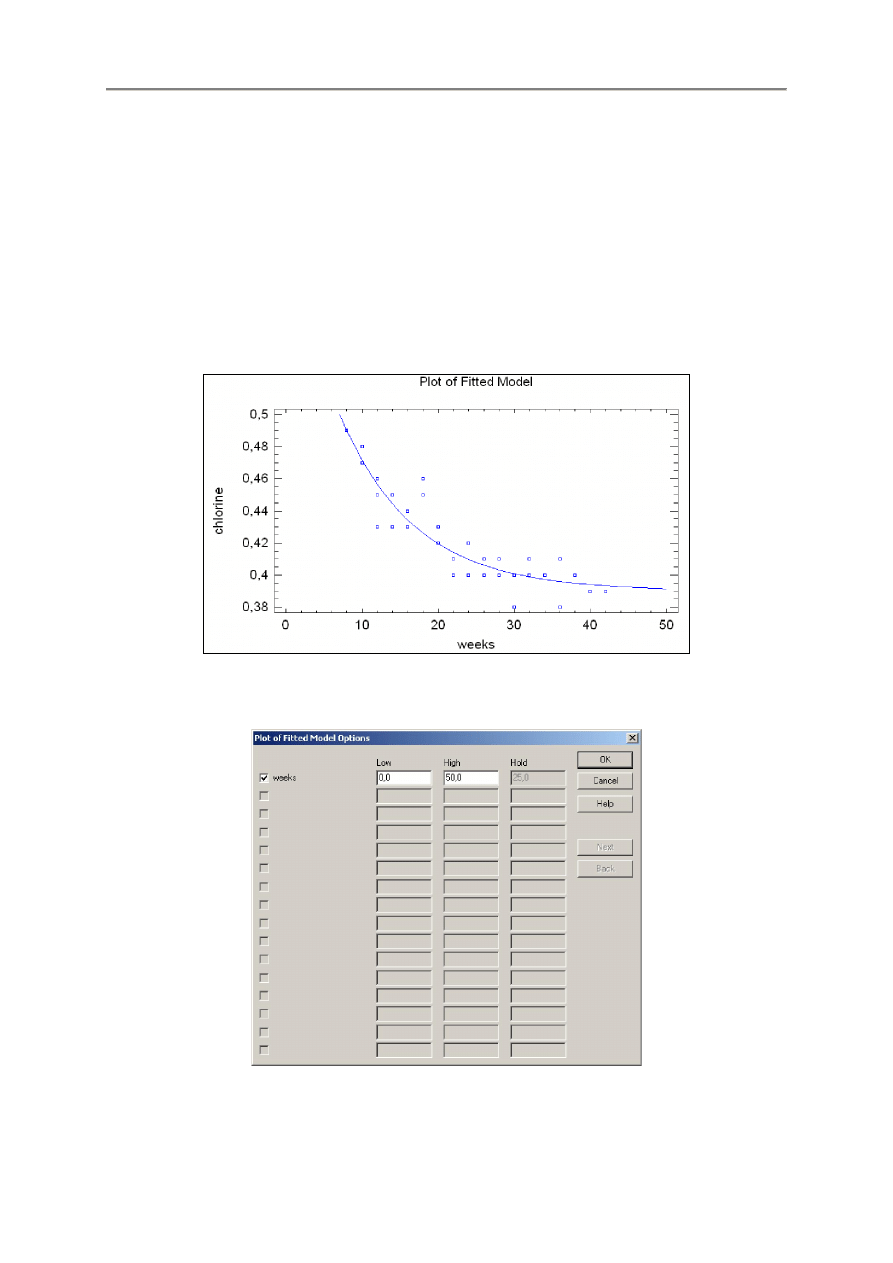
WYKRES DOPASOWANEGO MODELU

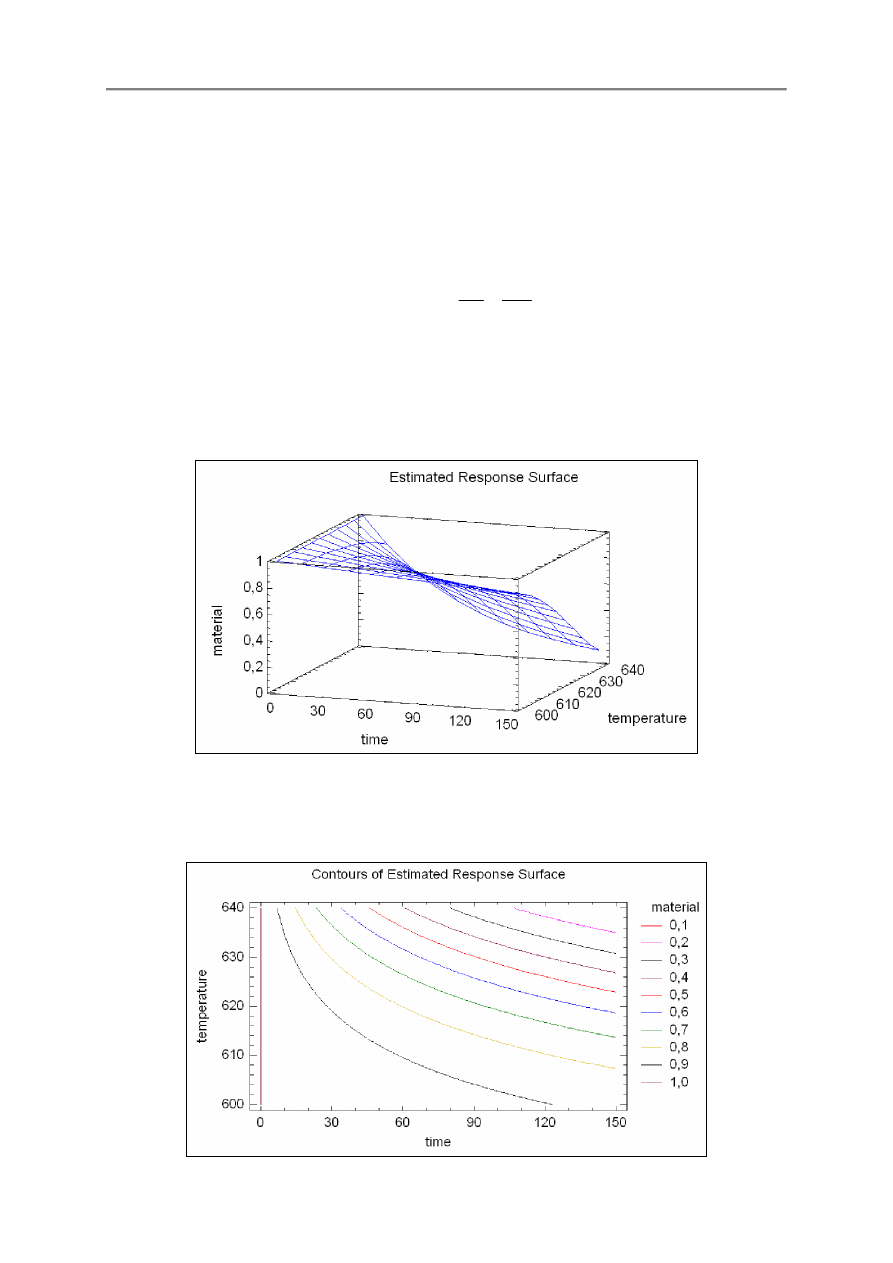
Wykres ten wyświetlany jest w lewym panelu okna wyników i pokazuje dopasowany model regresji
w funkcji jednej zmiennej niezależnej, przy innych (ewentualnych) zmiennych ustawionych na wartości
wyspecyfikowane w okienku dialogowym opcji panelu Pane Options.

Opcje panelu

Można tu wybrać jedna zmienną do wykreślania na osi poziomej wraz z jej zakresem. Dla innych
zmiennych można wprowadzać wartości zastępujące je w dopasowywanym modelu.

- 6 -

WYKRESY POWIERZCHNIOWE ODPOWIEDZI

Gdy w modelu występuje więcej niż jedna zmienna niezależna, można tworzyć wykresy
powierzchniowe Surface oraz konturowe Contour.

Przykładowo, Draper and Smith (1998) przytaczają raport z eksperymentu, w którym model opisywał
udział materiału Y pozostałego po reakcji chemicznej:

























































620

1

1

2

2

1

1

X

X

Y





exp

exp

............................................... (4)

gdzie X

i

jest czasem reakcji w minutach, a X

2

jest temperaturą reakcji w stopniach Kelvina. Dane te są

zapisane w przykładowym pliku nlreact.sf6 a ich analiza w pliku nlreact.sgp.

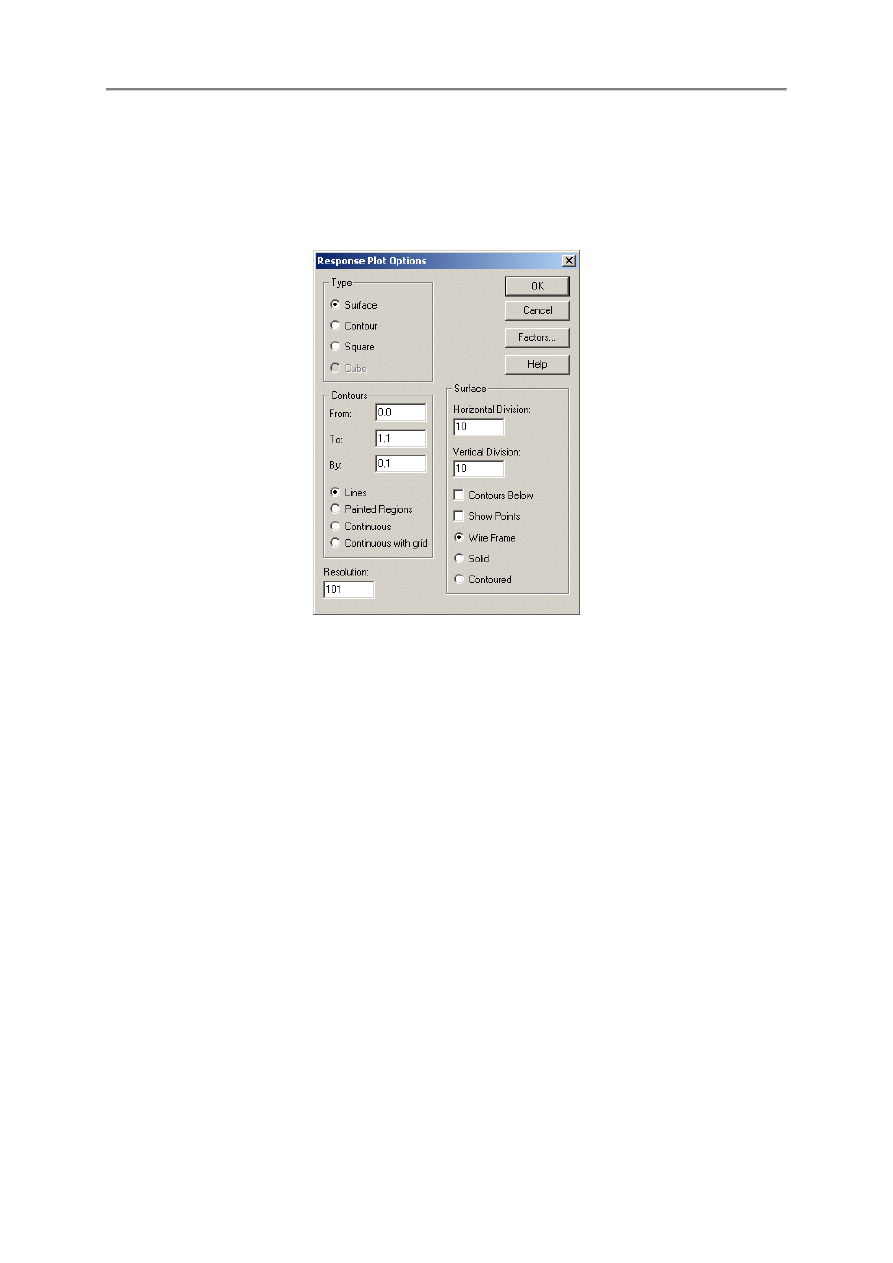
Poniżej pokazano wykres powierzchniowy dopasowanego modelu.

Na tym wykresie powierzchniowym, wysokość powierzchni reprezentuje przewidywane wartości Y.
Druga pozycja Response Surface Plots w okienku dialogowym otwieranym po kliknięciu przycisku
grafiki Graphics w pasku narzędzi analizy tworzy wykres konturowy:

- 7 -

Na wykresie konturowym w powyższym formacie, każda linia reprezentuje kombinację zmiennych
niezależnych X

1

i X

2

, które tworzą tą samą przewidywaną wartość Y.

W okienku dialogowym opcji panelu Pane Options znajdują się inne dostępne formaty.


Opcje panelu

 Type – Typ wykresu. Można tu wybrać wykres powierzchni 3D Surface. w którym wysokość

powierzchni reprezentuje wartość Y w funkcji dwóch dowolnych zmiennych niezależnych,
wykres konturowy 2D Contour, w którym barwne linie lub obszary reprezentują wartość Y
w funkcji dwóch dowolnych zmiennych niezależnych, wykres kwadratowy 2D Square,
w którego rogach wyświetlane są przewidywane wartości Y przy różnych kombinacjach dwoch
zmiennych niezależnych, lub wykres sześcienny 3D Cube w którego wierzchołkach
wyświetlane są przewidywane wartości Y przy różnych kombinacjach trzech zmiennych
niezależnych.

 Contours – Kontury. Granice i ostępy linii konturów i obszarów. Kontury mogą być rysowane

jako linie ciągłe Lines reprezentujące jedną wartość Y, malowane obszary Painted Regions
reprezentują przedziały, albo można korzystać z zakresów kolorów ciągłych Continuous.

 Resolution – Rozdzielczość. Liczba działek wzdłuż każdej osi przy których wykreślane są

wartości Y. Zwiększenie rozdzielczości może poprawić jakość wykresu, ale może przedłużyć to
czas jego rysowania.

 Surface – Powierzchnia. Dla wykresu powierzchni, jest to liczba działek wzdłuż każdej osi

między liniami stosowanym do rysowania powierzchni. Powierzchnie mogą być rysowane jako
drutowe Wire Frame (przezroczysta siatka), jako jednolita powierzchnia barwna Solid lub jako
kolorowe kontury Contoured (barwy zgodne z wartościami Y). Pole Contours Below wstawia
wykres konturowy na dole sześcianu. Pole Show Points nanosi punkty obserwacji na
powierzchnię.

 Factors. Czynniki. Przycisk ten służy do wybierania wykreślanych zmiennych. Otwiera się

wtedy okienko dialogowe podobne do opcji panelu dopasowanego wykresu Plot of Fitted
Model Options.

- 8 -

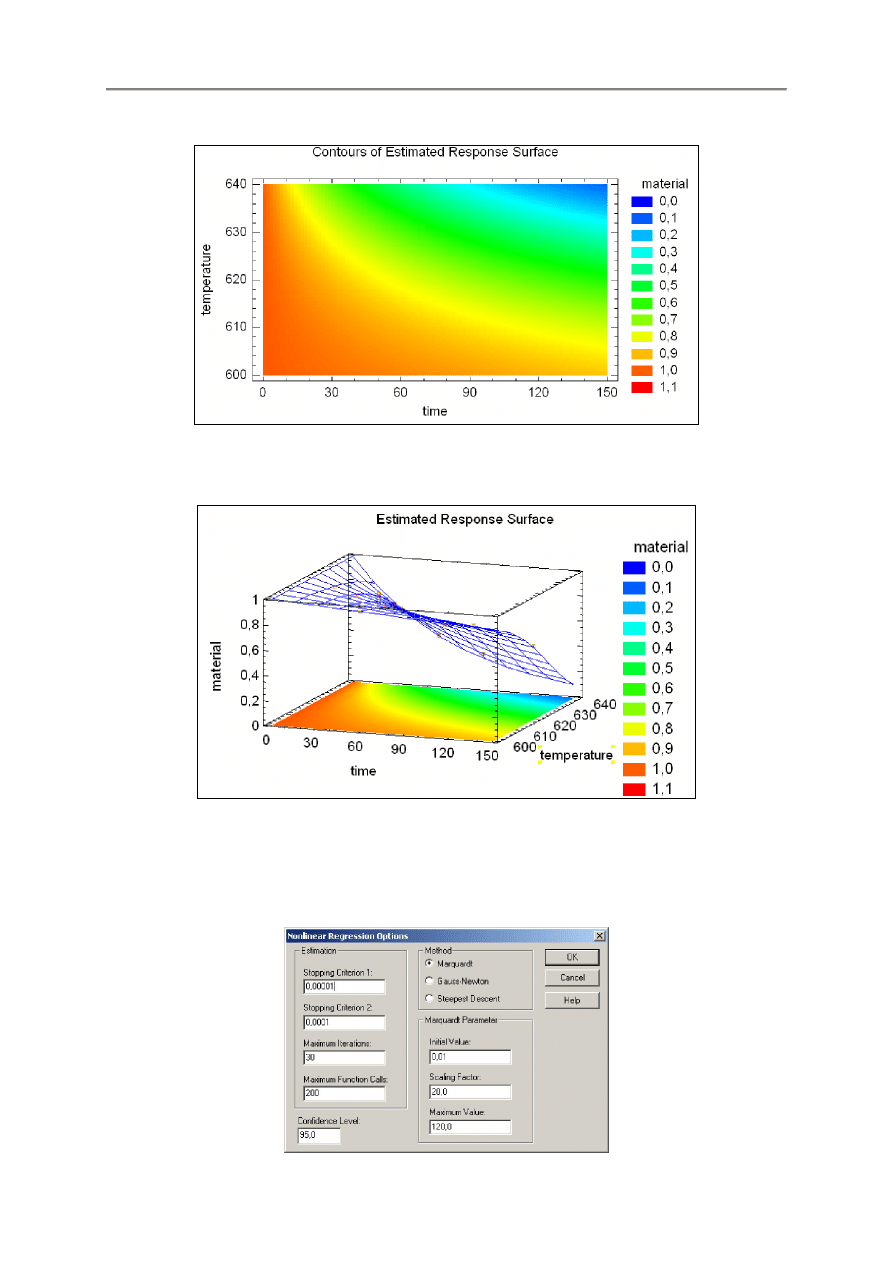
Przykład – Wykres konturowy z ciągłymi (jednolitymi) kolorami.

Przykład – Wykres powierzchniowy z konturami pod spodem i wstawionymi punktami.

OPCJE ANALIZY

Okienko dialogowe opcji analizy Analysis Options steruje algorytmem stosowanym do dopasowania
modelu regresji.

- 9 -



Method – Metoda stosowana do estymacji parametrów modelu. Metoda Gauss-Newton
korzysta z techniki linearyzacji, która dopasowuje sekwencję liniowych modeli regresji w ceu
znalezienia minimum resztowej sumy kwadratów. Metoda Steepest-Descent (metoda
najmniejszego spadku) korzysta gradientu resztowej sumy kwadratów. Natomiast domyślna
metoda Marquardt jest szybkim i przydatnym sposobem stanowiącym kompromis dwóch
poprzednich metod.



Stopping Criteriion 1 – Algorytm stosowany jako kryterium zbieżności gdy względna zmiana
resztowej sumy kwadratów jednej iteracji i następnej jest mniejsza od podanego kryterium.



Stopping Criteriion 2 – Algorytm stosowany jako kryterium zbieżności gdy względna zmiana
wszystkich estymowanych parametrów jednej iteracji i następnej jest mniejsza od podanego
kryterium.



Maximum Iterations – Estymacja zatrzymuje się gdy zbieżność nie została osiągnięta po
podanej liczbie iteracji.



Maximum Function Calls – Estymacja zatrzymuje się gdy zbieżność nie została osiągnięta
gdy funkcja liczba wywoływania funkcji przekracza podaną liczbą razy.



Marquardt Parameters – Wartoścu parametru Marquardta sterującego stopniem w jakim
dwie metody regresji rozciągają się w względem siebie. Szczegóły dotyczące algorytmu
Marquardta – patrz Box, Jenkins and Reinsel (1994).



Confidence Level – Poziom ufności (istotności). Wartość procentowa stosowana do
obliczania asymptotycznych przedziałów ufności dla współczynników modelu.

RAPORTY

Po kliknięciu przycisku tablic Tables w pasku narzędzi analizy i wybraniu opcji Reports, w panelu
wyników ukazuje się tablica zawierająca przewidywania na podstawie dopasowanego modelu regresji.
Domyślnie, tablica ta zawiera każdy wiersz arkusza danych mający pełną informację o zmiennych X,
ale nie ma wartości dla zmiennych Y. Dzięki temu można dodawać wiersze na dole arkusza danych
odpowiadające poziomom, przy których chcemy uzyskać przewidywania bez zmiany dopasowanego
modelu.

Przykładowo załóżmy, że chcemy uzyskać przewidywaną wartość zmiennej chlorine dla wartości
zmiennej weeks = 50 (ekstrapolacja za pomocą modelu). W tym celu w wierszu 45 arkusza danych
wprowadzany w pierwszej kolumnie weeks wartość 50, ale pole tego wiersza w drugiej kolumnie
chlorine pozostawiamy puste.

Po wybraniu opcji Reports (patrz wyżej) , w oknie wyników uzyskujemy poniższą tablicę:

Tablica ta zawiera poniższe pozycje:



Row – Numer wiersza w arkuszu danych zawierającego wartość zmiennej niezależnej.



Fitted – Przewidywana wartość zmiennej zależnej na postawie dopasowanego modelu.



Stand, Error – Estymowany błąd standardowy nowej obserwacji.

- 10 -



Lower / Upper 95 % CL for Ferecast – Granice ufności (dolna i górna) wartości prognozy Y.



Lower / Upper 95 % CL for Mean – Granice ufności (dolna i górna) wartości średniej Y.

Dla wiersza #45, przewidywana wartość zawartości chloru chlorine wynosi około 0,392. Nowa próbka
przy zmiennej weeks = 50 powinna być oczekiwana w przedziale od 0,368 do 0,4i6 na poziomie
istotności 95 % (pod warunkiem, że wykonana jest ekstrapolacja). Średni poziom zmiennej chlorine
po czasie weeks równym 50 tygodni jest estymowany w przedziale od 0,383 do 0,400.

Korzystając z okienka dialogowego opcji panelu Pane Options, można dołączyć do tej tablicy
dodatkowe informacje o przewidywanych wartościach i resztach stosowanych do dopasowania
modelu.


Opcje panelu

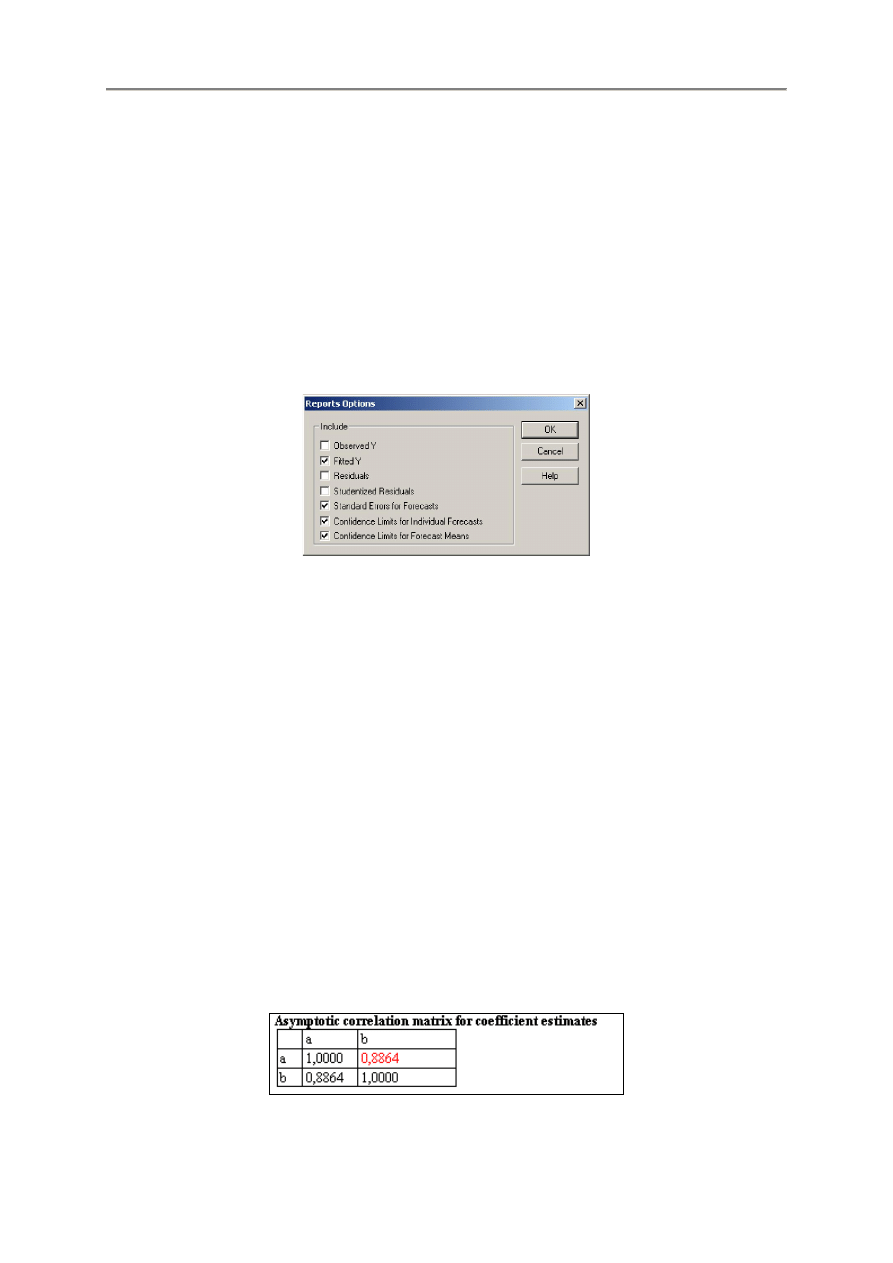
Można tu dołączać:



Observed Y – Obserwowane wartości zmiennej zależnej



Fitted Y – Przewidywane wartości zmiennej zależnej



Residuals – Zwykłe reszty (wartości obserwowane minus przewidywane)

|



Studentized Residuals – Usuwane reszty studentyzowane opisane w dokumentacji



Standard Errors for Forecast – Błędy standardowe nowych obserwacji



Confidence Limits for Indywidual Forecast – Błędy standardowe prognozy wartiości Y



Confidence Limits for Forecast Means – Błędy standardowe prognozy średnich Y.

MACIERZ KORELACJI

Po kliknięciu przycisku tablic Tables w pasku narzędzi analizy i wybraniu opcji Correlation Matrix,
w panelu wyników ukazuje się tablica zawierająca estymacje korelacji między estymowanymi
współczynnikami modelu regresji.

Tablica ta może być pomocna przy sprawdzaniu w jakim stopniu wplywy różnych zmiennych
niezależnych mogą być oddzielone jedne od drugich.

- 11 -

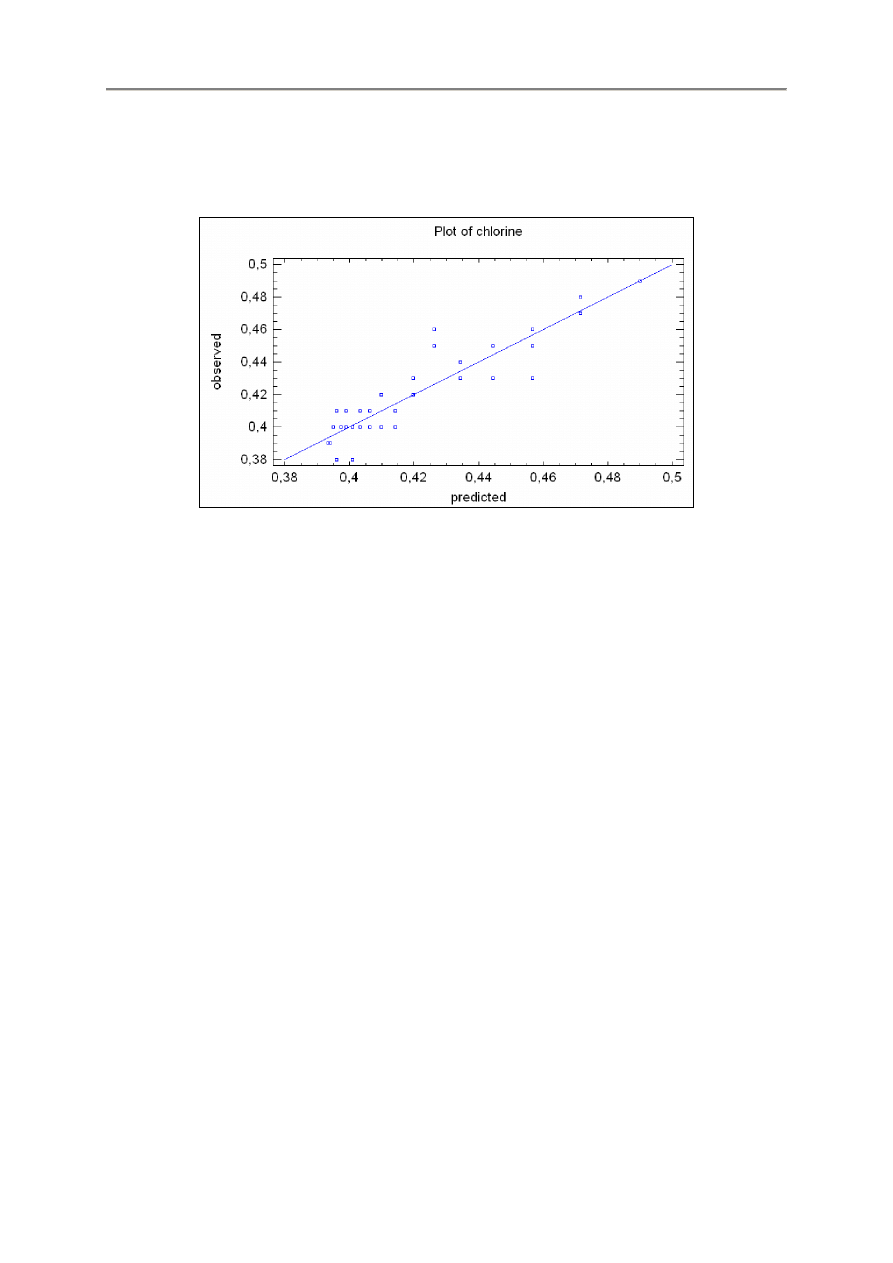
WARTOŚCI OBSERWOWANE W FUNKCJI PRZEWIDYWANYCH

Po kliknięciu przycisku grafiki Graphs w pasku narzędzi analizy i wybraniu opcji Observed versus
Predicted, w panelu wyników ukazuje się wykres pokazujący wartości obserwowane Y na osi
pionowej w funkcji wartości przewidywanych na osi poziomej.



Gdy model regresji jest dobrze dopasowany, wówczas punkty tego wykresu są losowo rozmieszczone
wzdłuż linii przekątnej.

Czasem można zauważyć pewną krzywiznę punktów na tym wykresie, co wskazuje na potrzebę
zastosowania modelu krzywoliniowego zamiast liniowego.

Wszelkie zmiany rozrzutu od dolnych do górnych wartości Y wskazują na celowość transformacji
zmiennej zależnej przed dopasowaniem modelu do danych.


WYKRESY RESZT

Tak jak we wszystkich modelach statystycznych, warto sprawdzać reszty Residuals. W analizie
regresji, reszty są definiowane następująco:

i

i

i

y

y

e

ˆ





.................................................................... (5)

tzn. reszta jest różnicą między wartością obserwowaną danej a wartością wynikającą z modelu.
Procedura regresji nieliniowej Nonlinear Regression tworzy różne typy wykresów reszt Residual
Plots w zależności od wybranych opcji w okienku dialogowym opcji wykresu reszt Residual Plot
Options otwieranym po kliknięciu przycisku Pane Options w pasku narzędzi wyników

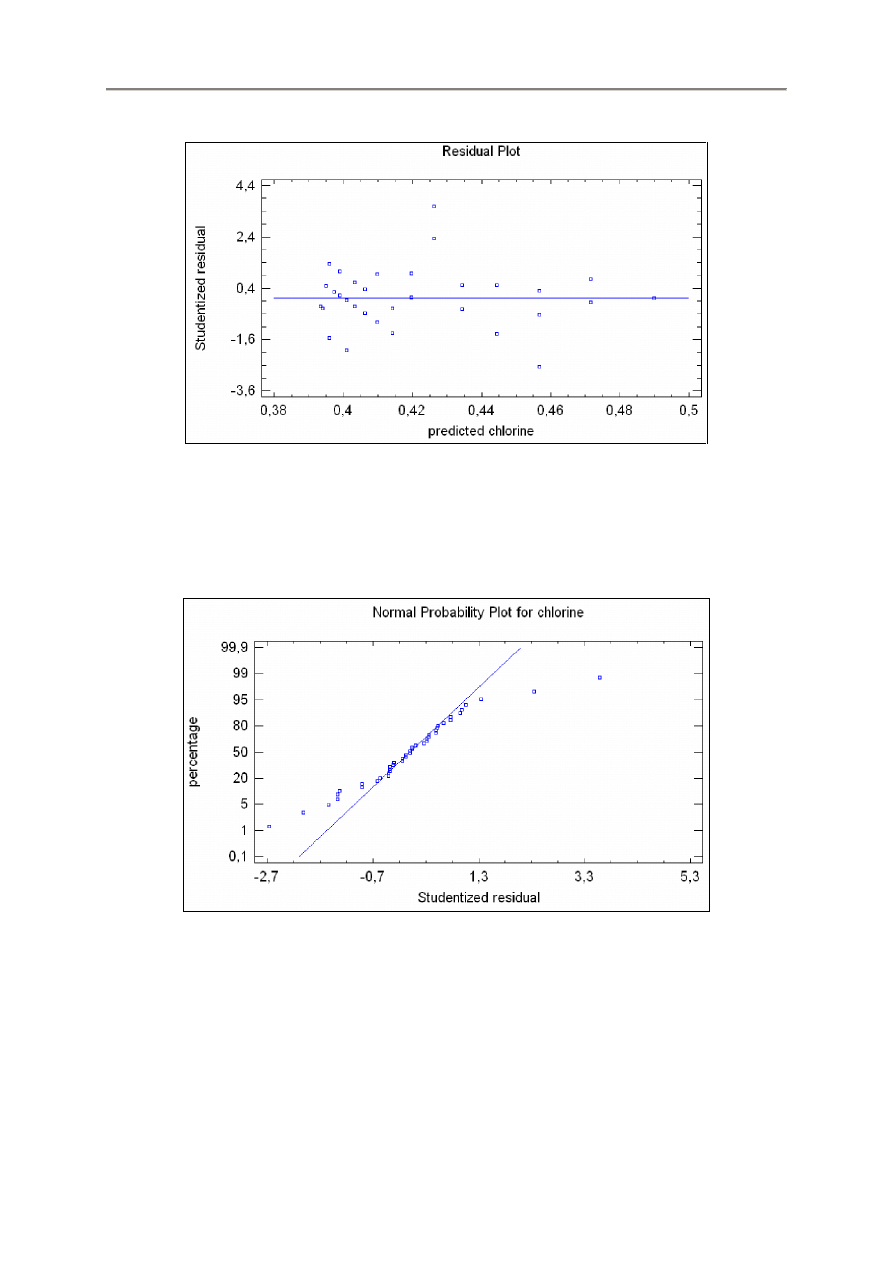
Scatterplots - Wykresy rozrzutu

Opcja ta znajdująca się w sekcji Type udostępnia sekcję Plot Versus, w której można wybrać
wielkość wyświetlaną na osi poziomej.



Predicted Values – W funkcji przewidywanych wartości, tutaj chlorine (opcja domyślna)



Row Number – W funkcji numerów wierszy



Independent Variable – W funkcji zmiennej niezależnej X (tutaj weeks).

- 12 -

Normal Probability Plot – Wykres prawdopodobieństwa normalnego

Wykres ten wybierany w sekcji Type można stosować do sprawdzania czy odchylenia wokół linii
spełniają rozkład normalny, co jest założeniem stosowanym do obliczania przedziałów przewidywania.

Gdy odchylenia spełniają rozkład normalny, układają się w przybliżeniu wzdłuż linii prostej.

Na powyższym wykresie dane odchylają się znacznie od linii prostej, co wskazuje że odchylenia są
większe w ogonach rozkładu niż powinno to mieć miejsce w rozkładzie normalnym.


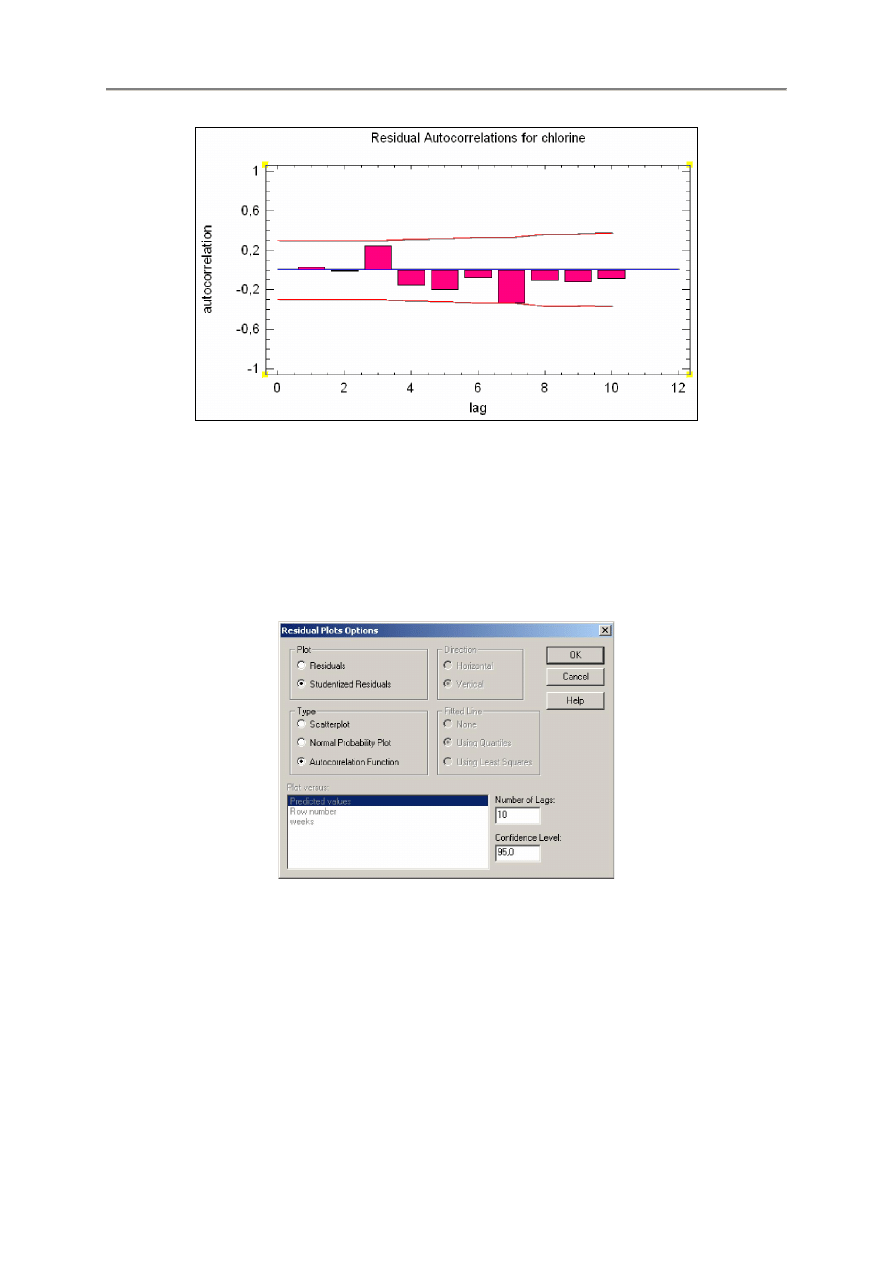
Autocorrelations Functions – Funkcje autokorelacji reszt

Wykres ten wybierany w sekcji Type oblicza korelacje między resztami w funkcji liczby wierszy między
nimi w arkuszu danych.

- 13 -

Wykres ten jest odpowiedni tylko wtedy, gdy dane były gromadzone sekwencyjnie.

Każdy słupek wykraczający poza linie granic prawdopodobieństwa może wskazywać na istotną
zależność między resztami oddzielanymi wskaźnikiem lag (na osi poziomej) co narusza założenie
o niezależności przyjęte przy dopasowywaniu modelu regresji.


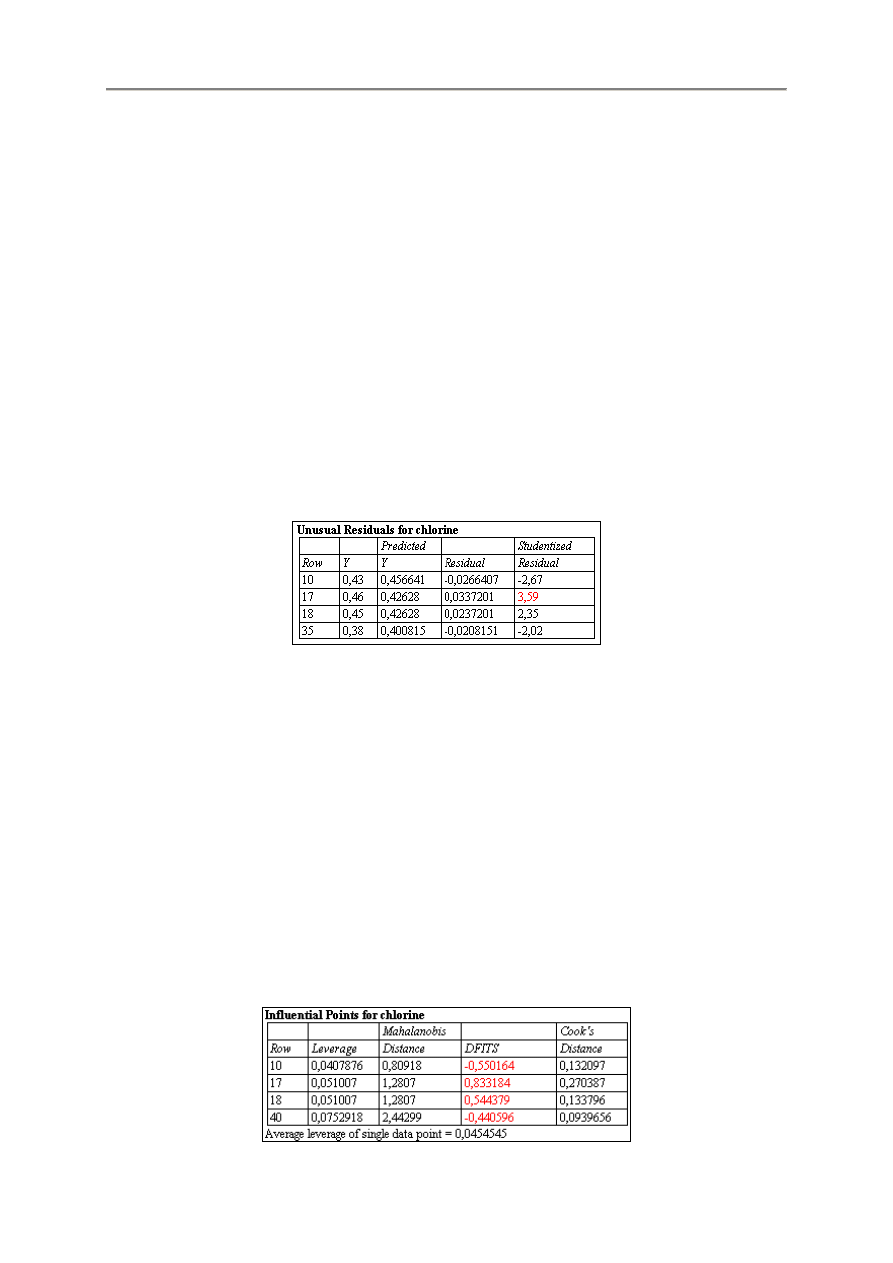
Opcje panelu



Plot – Rodzaj wykresu reszt

 Residuals – Reszty analizy regresji wykonywanej metodą najmniejszych kwadratów

 Studentized Residuals – Reszty studentyzowane. Są to różnice między wartościami

obserwowanymi y

i

, a przewidywanymi

i

y

ˆ

gdy model jest dopasowywany przy korzystaniu

ze wszystkich obserwacji oprócz i-tej, dzielonej przez estymowany błąd standardowy.

Reszty te noszą czasem nazwę reszt usuwanych zewnętrznie Externally Deleted,
ponieważ są one miarą odchyleń wartości od modelu regresji gdy jest on dopasowywany
oprócz tych punktów. Jest to ważne, ponieważ duże wartości odbiegające mogą wpływać
na model i tym samym nie odbiegają zbytnio od linii regresji.

- 14 -



Type – Typ tworzonego wykresu. Wykres rozrzutu Scatterplot stosuje się do testowania
krzywizny. Wykres prawdopodobieństwa Normal Probability Plot stosuje się do sprawdzania
czy dane pochodzą z rozkładu normalnego, a wykres funkcji autokorelacji Autocorrelations
Functions stosuje się do testowania zależności między kolejnymi resztami.



Plot Versus – Dla wykresu rozrzutu Scatterplot, wielkość wykreślana na osi poziomej



Number of Lags – Dla funkcji autokorelacji Autocorrelations Functions, maksymalna liczba
odstępów między wierszami Lags. Dla małych zestawów danych, liczba ta może być
mniejsza od podanej wartości



Confidence Level – Dla funkcji autokorelacji Autocorrelations Functions, poziom istotności
stosowany do tworzenia granic prawdopodobieństwa.

NIETYPOWE RESZTY

Po dopasowaniu modelu, celowe jest badanie reszt w celu sprawdzenia czy istnieją wartości
odbiegające Outlier, które można usuwać z danych. Opcja Unusual Residuals dostępna po
kliknięciu przycisku tablic Tables w pasku narzędzi analizy, wyświetla w oknie wyników tablicę
nietypowych reszt zawierającą wszystkie obserwacje dla których studentyzowane reszty są równe lub
większe od wartości bezwzględnej 2.

Studentyzowane reszty większe co do wartości bezwzględnej od 3 odpowiadają punktom odległym
więcej niż o 3 odchylenia standardowe od dopasowanego modelu, co jest rzadkim przypadkiem przy
rozkładzie normalnym. W naszym przykładzie, wiersz # 17 jest dalszy niż 3,5 odchylenia standardowe
od dopasowanego modelu;

UWAGA: Punkty można usuwać z analizy regresji po wybraniu wykresu dopasowanego modelu
Plot of Fitted Model i kliknięciu na punkcie i wybraniu przycisku Exclude/Include w pasku narzędzi
analizy. Wykluczone punkty będą zaznaczone znakiem



.

PUNKTY ODLEGLE

Przy dopasowywaniu modelu regresji, nie wszystkie obserwacje mają jednakowy wpływ na
estymowane parametry. W przypadku prostej analizy regresji liniowej, punkty znajdujące się przy
bardzo niskich lub bardzo wysokich wartości X, mają większy wpływ niż punkty leżące blisko średniej
wartości X. Opcja Influential Points dostępna po kliknięciu przycisku tablic Tables w pasku narzędzi
analizy, wyświetla w oknie wyników tablicę zawierającą obserwacje odległe, mające jednak silny
wpływ na dopasowany model.

- 15 -

Punkty są wstawiane na tą listę wg poniższego schematu:



Leverage – Punkty wpływowe. Mierzą jak bardzo odlegle są obserwacje od średniej ze
wszystkich n-obserwacji w przestrzeni zmiennych niezależnych. Im wyższa wartość punktu
wpływowego, tym większy jest jego wpływ na dopasowana wartość

i

y

ˆ

.

Punkty są wstawiane na tej liście, jeśli ich wartość statystyki Leverage jest większa od
3-krotnej odległości od średniej z punktów danych.



Mahalanobis Distance – Odległość Mahalanobisa. Mierzy odległość punktu od środka
zestawu punktów w przestrzeni wielu zmiennych niezależnych. Z uwagi na to, że odległość ta
jest związana ze statystyką Leverage, nie jest ona stosowana do zaznaczania punktów
w tablicy.



DFITS – Mierzy różnicę między wartością przewidywaną

i

y

ˆ

gdy model jest dopasowany wraz

lub bez i-tej danej. Punkty są wstawiane na liście gdy wartość bezwzględna DFITS
przekracza wartość 2p/n, gdzie p jest liczbą współczynników modelu regresji.

ZAPISYWANIE WYNIKÓW

Poniższe wyniki można zapisywać w arkuszu danych:

1. Predicted Values – Przewidywane wartości Y odpowiadające każdej z n-obserwacji

2. Standard Errors of Predictions – Błędy standardowe n-przewidywanych obserwacji

3. Lower Limits for Predictions – Dolne granice przewidywania każdej wartości Y

4. Upper Limits for Predictions – Górne granice przewidywania każdej wartości Y

5. Standard Errors of Means – Błędy standardowe wartości średniej Y dla wszystkich X

6. Lower Limits for Forecast Means – Dolne granice średniej wartości Y dla wszystkich X

7. Upper Limits for Forecast Means – Górne granice średniej wartości Y dla wszystkich X

8. Residuals – n-wszystkich reszt

9. Studentized Residuals –– n-wszystkich studentyzowanych reszt

10. Leverages – Punkty wpływowe odpowiadające n-wartościom X

11. DFITS – Statystyki odpowiadające n-wartościom X

12. Mahalanobis Distances – Odleglości Mahalanobisa odpowiadające n-wartościom X

13. Coefficients – Estymowane współczynniki (parametry) modelu regresji

14. Function – Łańcuch tekstowy wyrażenia STATGRAPHICS funkcji (modelu) regresji.

OBLICZENIA

Estymowane parametry są obliczane numerycznie przez minimalizacją sumy kwadratów. Macierz
wariancji / kowariancji tych współczynników jest estymowana na podstawie pochodnych cząstkowych
sąsiednich przybliżeń rozwiązania metodą najmniejszych kwadratów.