2014-04-15

1

Bezpieczeństwo

i ochrona danych

Jednokierunkowe funkcje

skrótu i ich zastosowania

Agenda

• Funkcje jednokierunkowe
• Podpis elektroniczny
• Wybrane algorytmy skrótu

– MD5, SHA

• Ataki na funkcje skrótu i podpisy

elektroniczne

• Algorytmy wymiany klucza

Funkcja jednokierunkowa

• Stworzenie praktycznego systemu szyfrowania asymetrycznego z

kluczem jawnym wymaga zastosowania funkcji jednokierunkowej
z bocznym wejściem (ang. trapdoor one-way function)

• Funkcja jednokierunkowa to taka, która przekształca swoją

dziedzinę na przedział w taki sposób, że każda wartość funkcji ma
tylko jedną odwrotność, z tym że obliczenie funkcji jest łatwe
(czas wielomianowy), a obliczenie odwrotności niewykonalne
(wysiłek obliczeniowy rośnie szybciej niż wielomianowo):

– Y=f(X) - łatwe
– X=f

-1

(Y) - niewykonalne

Funkcja jednokierunkowa z
bocznym wejściem

• Obliczenie funkcji jednokierunkowej z bocznym

wejściem jest łatwe w jednym kierunku, a niewykonalne
w drugim, chyba że są znane pewne dodatkowe
informacje, które umożliwiają obliczenie odwrotności w
czasie wielomianowym

• Y=f

k

(X) - łatwe przy znajomości k i X

• X=f

k

-1

(Y) - łatwe przy znajomości k i Y

• X=f

k

-1

(Y) - niewykonalne, gdy znamy Y, a nie znamy k

Algorytmy skrótu

• Funkcja skrótu z danych o zmiennym rozmiarze wylicza

pewien wynik H(M) o stałym rozmiarze, zwany też
wyciągiem lub skrótem komunikatu

• Wynik skrótu jest funkcją wszystkich bitów komunikatu i

zapewnia:

– wykrywanie błędów,
– uwierzytelnianie (w pewnych warunkach)

Wymagania dla kryptograficznej
funkcji skrótu

• H(x) można zastosować do dowolnej wielkości

bloku danych

• H(x) tworzy dane wyjściowe o ustalonej

długości

• H(x) jest łatwo obliczyć dla każdego x, co

ułatwia implementację sprzętową i
programową

2014-04-15

2

Wymagania dla kryptograficznej
funkcji skrótu

• Dla każdego kodu m znalezienie takiego x, że H(x)=m

nie jest wykonywalne na drodze obliczeń –
jednokierunkowość

• Dla każdego danego bloku x, znalezienie takiego y

różnego od x, dla którego H(y)=H(x) nie jest
wykonywalne na drodze obliczeń – słaba odporność na
kolizje

• Znalezienie pary (x,y), że H(y)=H(x) nie jest

wykonywalne na drodze obliczeń – (silna) odporność na
kolizje

Skrót niekryptograficzny (1)

• Dane: X = (X

0

,X

1

,X

2

,…,X

n-1

), X

i

są bajtami

• Niech hash(X) = X

0

+X

1

+X

2

+…+X

n-1

• Czy jest to bezpieczne?
• Przykład: X = (10101010,00001111)
• Skrót:10111001
• Ale również jest to skrót

Y = (00001111,10101010)

• Łatwo znaleźć kolizję, więc nie jest

bezpieczne…

Skrót niekryptograficzny(2)

• Dane: X = (X

0

,X

1

,X

2

,…,X

n-1

)

• Niech skrót będzie następujący:

h(X) = nX

0

+(n-1)X

1

+(n-2)X

2

+…+1



X

n-1

• Czy jest bezpieczny?

h(10101010,00001111)



h(00001111,10101010)

• Lecz skrót (00000001,00001111) jest taki sam

jak skrót (00000000,00010001)

• Nie jest bezpieczny, lecz wykorzystywany w

niekrytycznych aplikacjach np

.

rsync

Skrót niekryptograficzny (3)

• Cyclic Redundancy Check (CRC)
• CRC jest resztą z dzielenia
• Dobre dla wykrywania błędów
• Łatwe znalezienie kolizji
• CRC czasami, przypadkowo pojawia się w

kontekście bezpieczeństwa (WEP)

Popularne funkcje

• MD5



opracowane przez Rivest’a

– 128 bit wyjście
– MD5 – wykryto kolizje

• SHA-1



standard rządu US (podobne do

MD5)

– 160 bit wyjście
– również uważana za mało bezpieczne rozwiązanie

• Wiele innych, lecz MD5 oraz SHA-1 są

najpopularniejsze

Notacja klucza publicznego

• Podpis

Alicji dla wiadomości M

prywatnym kluczem:

[M]

Alicja

• Szyfrowanie

wiadomości M

kluczem publicznym:

{M}

Alicja

• Wtedy:

{[M]

Alicja

}

Alicja

= M

[{M}

Alicja

]

Alicja

= M

2014-04-15

3

Zastosowania funkcji skrótu:
Podpis elektroniczny

• Przypuśćmy, że Alicja podpisała M

– Alicja wysyła M oraz S = [M]

Alicja

do Boba

– Bob weryfikuje, że M = {S}

Alicja

• Jeżeli M jest duże, [M]

Alicja

jest kosztowne

obliczeniowo

• Przypuśćmy natomiast, że Alicja podpisuje

h(M), gdzie h(M) jest mniejsze niż M

– Alicja wysyła M oraz S = [h(M)]

Alicja

do Boba

– Bob sprawdza czy h(M) = {S}

Alicja

Podpisy elektroniczne

• MAC

- Message Authentication Code,

także MIC - Message Integrity Code

– to w kryptografii kod służący uwierzytelnieniu

danych.

– argumentami funkcji uwierzytelniającej są tajny

klucz oraz wiadomość.

– wartością wyjściową funkcji jest kod MAC.

Podpisy elektroniczne

• HMAC

keyed-Hash Message Authentication Code

– MAC z kluczem tajnym zapewniający zarówno

ochronę integralności jak i autentyczności
danych.

– Standardowy kod MAC zapewnia ochronę

integralności ale może podlegać sfałszowaniu jeśli
nie jest zabezpieczony dodatkowym
mechanizmem chroniącym jego autentyczność
(np. podpisem cyfrowym).

Podpisy elektroniczne

• Podpis elektroniczny zapewnia ochronę

integralności

– Podobnie jak MAC oraz HMAC

• Dlaczego?
• Alicja wysyła M oraz S = [h(M)]

Alicja

do Boba

• Jeżeli M będzie zmienione an M



lub S

zmienione na S



(przypadkowo lub celowo)

Bob wykryje to :

h(M



)



{S}

Alicja

, h(M)



{S



}

Alicja

, h(M



)



{S



}

Alicja

Niezaprzeczalność

• Podpis elektroniczny zapewnia

niezaprzeczalność

• Alicja wysyła M oraz S = [h(M)]

Alicja

do Boba

• Alicja nie może “wyprzeć się” podpisu

– Alicja nie może obronić twierdzenia, że nie

podpisała M

• Jak to działa?
• Czy tak samo jak dla MAC?

Niezaprzeczalność

• Alicja zamawia 100 laptopów u Boba
• Alicja oblicza

MAC

korzystając z klucza

symetrycznego

• Znajduje tańszą ofertę, Alicja twierdzi, że nie

składała zamówienia

• Czy Bob może udowodnić Alicji kłamstwo?

• Nie!

Ponieważ Bob również zna klucz

symetryczny, mógł zatem sfałszować zamówienie

• Problem

:

Bob wie, że Alicja złożyła zamówienie

i nie może tego udowodnić

2014-04-15

4

Niezaprzeczalność

• Alicja zamawia 100 laptopów u Boba
• Alicja

podpisuje

zamówienie korzystając z

klucza prywatnego

• Znajduje tańszą ofertę, Alicja twierdzi, że

nie składała zamówienia

• Czy Bob może udowodnić Alicji kłamstwo?

• Tak!

Tylko ktoś kto zna klucz prywatny Alicji

mógł złożyć podpis

• Jeżeli nikt go nie ukradł Alicji to jest jedną

osobą, która mogła to zrobić

Skróty i podpisy

• Alicja podpisuje h(M), wysyła M oraz

S = [h(M)]

Alicja

do Boba oraz Bob weryfikuje

h(M) = {S}

Alicja

• Bezpieczeństwo zależy od bezpieczeństwa

kryptosystemu klucza publicznego

i od

bezpieczeństwa funkcji skrótu

• Niech Intruz znajdzie kolizję: M



M taką, że

h(M



) = h(M)

• Wtedy Intruz może zamienić M na M



i

schemat podpisu jest złamany

Projekt kryptograficznej funkcji
skrótu

• Pożądana własność:

efekt lawinowy

– Zmiana dowolnego bitu powoduje zmianę około

dużej liczby bitów skrótu

• Kryptograficzne funkcje skrótu składają się z

kilku rund (analogicznie jak algorytmy
blokowe w trybie CBC)

• Potrzebujemy bezpieczeństwa i prędkości

– Efekt lawinowy po kilku rundach
– Lecz runda musi być prosta

Projekt kryptograficznej funkcji
skrótu

• Dane wejściowe rozbijane na bloki

• Kompresja

stosowana względem bloków

• Wartość bloku zależna od obecnej

wartości i od wyjścia poprzedniej rundy

– Wyjście z ostatniej rundy jest wartością

skrótu

• Dla funkcji skrótu rozważamy:

– Rozmiar bloku 512 bit
– Kompresja bloku wyjściowego 128 bit

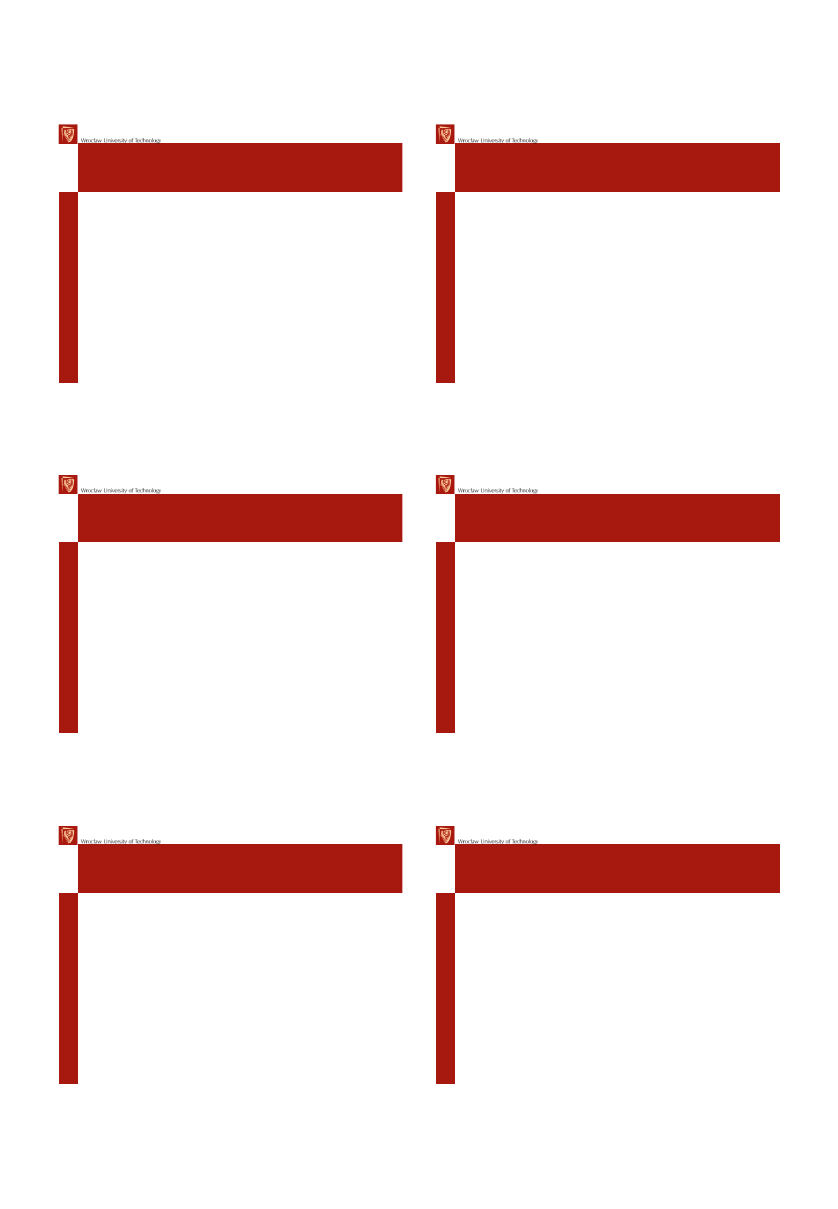
Funkcja skrótu

• Wejście lub

“wiadomości” w
blokach
M

0

,M

1

,…,M

N



1

• Dodatkowo mod 2

32

na 32-bit słowie

• Schemat Merkle-

Damgard

Funkcje skrótu: ciekawostki

• Jeżeli wiadomość jest długości pojedynczego

bloku 512-bit : h(M) = f(IV,M) gdzie f oraz IV
znane Intruzowi

• Dla 2 bloków:
h(M) = f(f(IV,M

0

),M

1

) = f(h(M

0

),M

1

)

• Ogólnie

h(M) = f(h(M

0

,M

1

,…,M

n



2

),M

n



1

)

– Jeżeli h(M) = h(M



) wtedy h(M,X) = h(M



,X) dla

dowolnego X

2014-04-15

5

HMAC

• MAC: algorytm blokowy dla integralności

– Czy możemy użyć funkcji skrótu?

• “hashed MAC”,

HMAC

, wiadomości M z

kluczem K

– Dlaczego potrzebujemy klucza?

• Jak obliczyć HMAC?

– Dwa oczywiste podejścia:

h(K,M) and h(M,K)

• Które (czy w ogóle) jest lepsze?

Jak obliczyć HMAC?

• Czy mamy obliczać HMAC jako h(K,M) ?
• Skróty obliczane w blokach
• Przypominamy: h(M

0

,M

1

) = F(h(M

0

),M

1

)

• Niech M



= (M,X)

– Wtedy h(K,M



) = F(h(K,M),X)

– Intruz może obliczyć HMAC z M



bez

znajomości K

– Kompromituje to HMAC

Jak obliczyć HMAC?

• Czy powinniśmy obliczać HMAC jako

h(M,K) ?

– Lepsze niż h(K,M) ?

• Jeżeli h(M



) = h(M) wtedy

h(M,K) = F(h(M),K) = F(h(M



),K) = h(M



,K)

• W tym przypadku, Intruz nie może

obliczyć HMAC bez znajomości K

– Lecz musi znać kolizje
– Lepsze niż h(K,M), lecz wciąż może być

lepiej

Właściwy sposób na HMAC

• Opisany w RFC 2104
• Niech B będzie długością w bajtach bloku

funkcji skrótu

• Dla popularnych funkcji B = 64

– SHA-1, MD5, Tiger, etc.

• Definiujemy
ipad = 0x36 (00110110) powtarzany B razy

opad = 0x5C (01011100) powtarzany B razy
• Wtedy

HMAC(M,K) = H(K



opad, H(K



ipad, M))

Algorytm MD5

• Algorytm MD5 (ang. Message Digest) został opracowany

przez Rona Rivesta i opublikowany jako RFC1321

• Algorytm z wejściowego komunikatu o dowolnej długości

generuje 128-bitowy skrót

• Dane wejściowe przetwarzane są w 512 bitowych

blokach

• Przykład działania
• MD5("Ala ma kota") =

91162629d258a876ee994e9233b2ad87

• MD5("Ala ma koty") =

6a645004f620c691731b5a292c25d37f

Dodawanie bitów dopełniających

• Komunikat jest dopełniany tak, by jego długość w bitach

przystawała do 448 modulo 512

• Czyli długość komunikatu musi być o 64 bity mniejsza niż

całkowita wielokrotność 512 bitów

• Na przykład jeżeli komunikat ma 2345 bitów to

najbliższa wielokrotność 512 bitów to 2560, więc
komunikat zostanie dopełniony do 2496 bitów

• Dopełnienie dodaje się zawsze, nawet gdy komunikat ma

żądaną długość

• Dopełnienie składa się z bitu 1, po którym następuje

odpowiednia liczba bitów 0

2014-04-15

6

Dodanie długości komunikatu

• Do komunikatu uzupełnionego o dopełnienie dodaje się

64-bitową reprezentację długości pierwotnego
komunikatu w bitach (przed dopełnieniem)

• Jeżeli komunikat jest dłuższy niż 2

64

to używa się tylko

młodszych 64 bitów długości

• To oznacza, że pole długości zawiera długość

początkowego komunikatu modulo 2

64

• Następnie cały komunikat wraz z dopełnieniem i

długością jest przetwarzany w blokach Y

0

, Y

1

,...,Y

L-1

, o

długości 512 bitów

Inicjalizacja bufora MD

• Do przechowywania pośrednich i końcowych wartości

funkcji skrótu stosuje się bufor 128-bitowy

• Bufor ten można zapisać jako cztery 32-bitowe rejestry

oznaczane jako A, B, C, D

• Rejestry te są na początku inicjalizowane następującymi

wartościami szesnastkowymi (najpierw młodsze oktety):

A=01234567

B=89ABCDEF
C=FEDCBA98

D=76543210

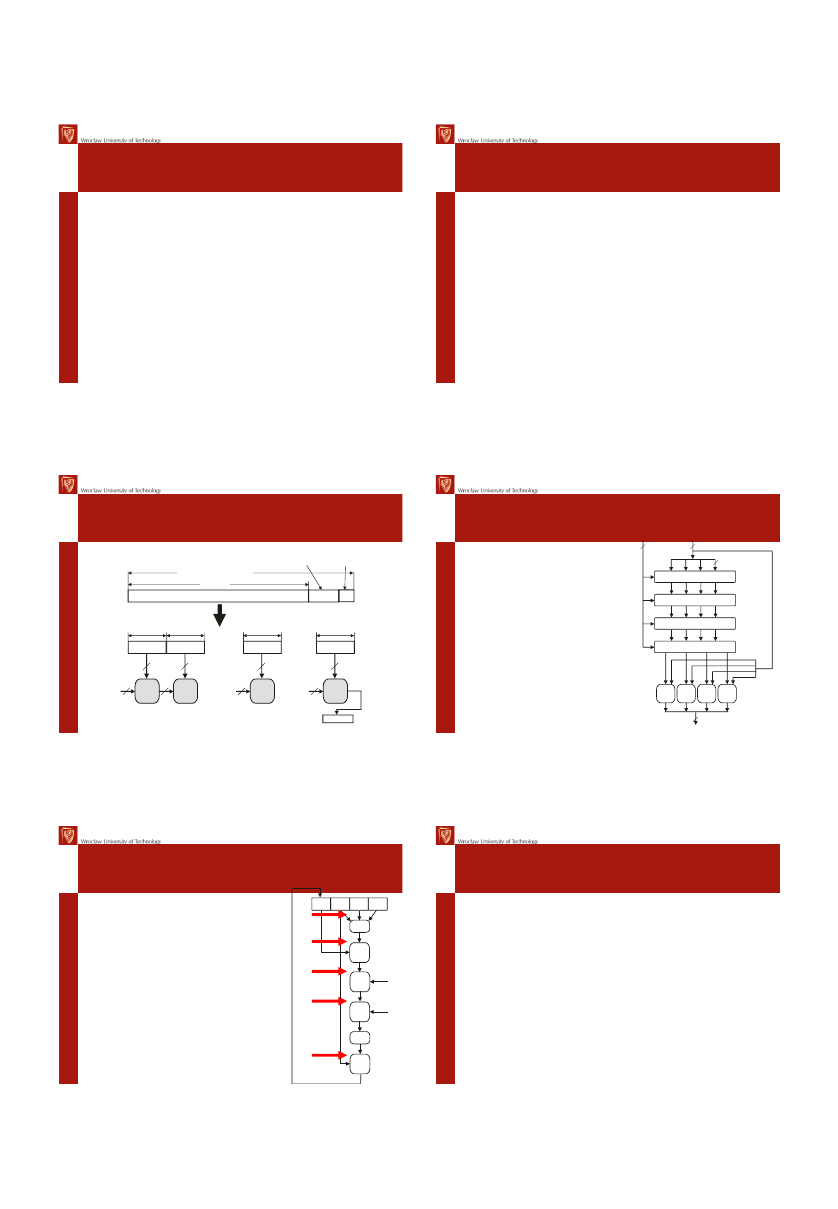
Generowanie wyciągu w MD5

Komunikat

K bitów

L

x 512 bitów=N x 32 bity

Dopełnienie

(1-512) bitów

Długość

komunikatu
(K mod 2 )

64

100...0

Y

0

Y

1

512 bitów

512 bitów

Y

q

512 bitów

Y

L-1

512 bitów

. . .

. . .

H

MD5

512

H

MD5

512

H

MD5

512

H

MD5

512

128

128

128

128

ABCD

128 bitowy wyciąg

Przetwarzanie komunikatu w 512-
bitowych blokach

• Wszystkie 4 etapy mają

podobną strukturę, lecz każdy

korzysta z innej elementarnej

funkcji logicznej oznaczanej w

specyfikacji jako F, G, H, I

• W każdym etapie jest

przetwarzany aktualny blok Y

q

oraz bufor ABCD (MD

q

)

• Dodatkowo w każdym etapie

korzysta się z kolejnych części

tablicy T[1,...,64]

skonstruowanej na podstawie

funkcji sinus

f (ABCD,Y ,T[1,...,16])

F

q

128

MD

q

A B C D

A B C D

32

f (ABCD,Y ,T[17,...,32])

G

q

A B C D

f (ABCD,Y ,T[33,...,48])

H

q

A B C D

f (ABCD,Y ,T[49,...,64])

I

q

512

Y

q

+

mod 2

32

+

mod 2

32

+

mod 2

32

+

mod 2

32

128

MD

q+1

Elementarna operacja MD5

• Każdy z kroków wykonywanych 64

razy dla każdego bloku ma postać

A



B+CLS

s

(A+g(B,C,D)+X[k]+T[i])

• Przez g oznaczamy jedną z funkcji

elementarnych F, G, H, I

• X[k] oznacza k-te 32 bitowe słowo

w przetwarzanym 512-bitowym

bloku

• T[i] oznacza i-te 32 bitowe słowo w

tablicy stałych

• Wszystkie dodawania są

realizowane modulo 2

32

A B C D

+

mod 2

32

g

+

mod 2

32

X[k]

+

mod 2

32

T[i]

CLS

s

+

mod 2

32

Elementarna operacja MD5

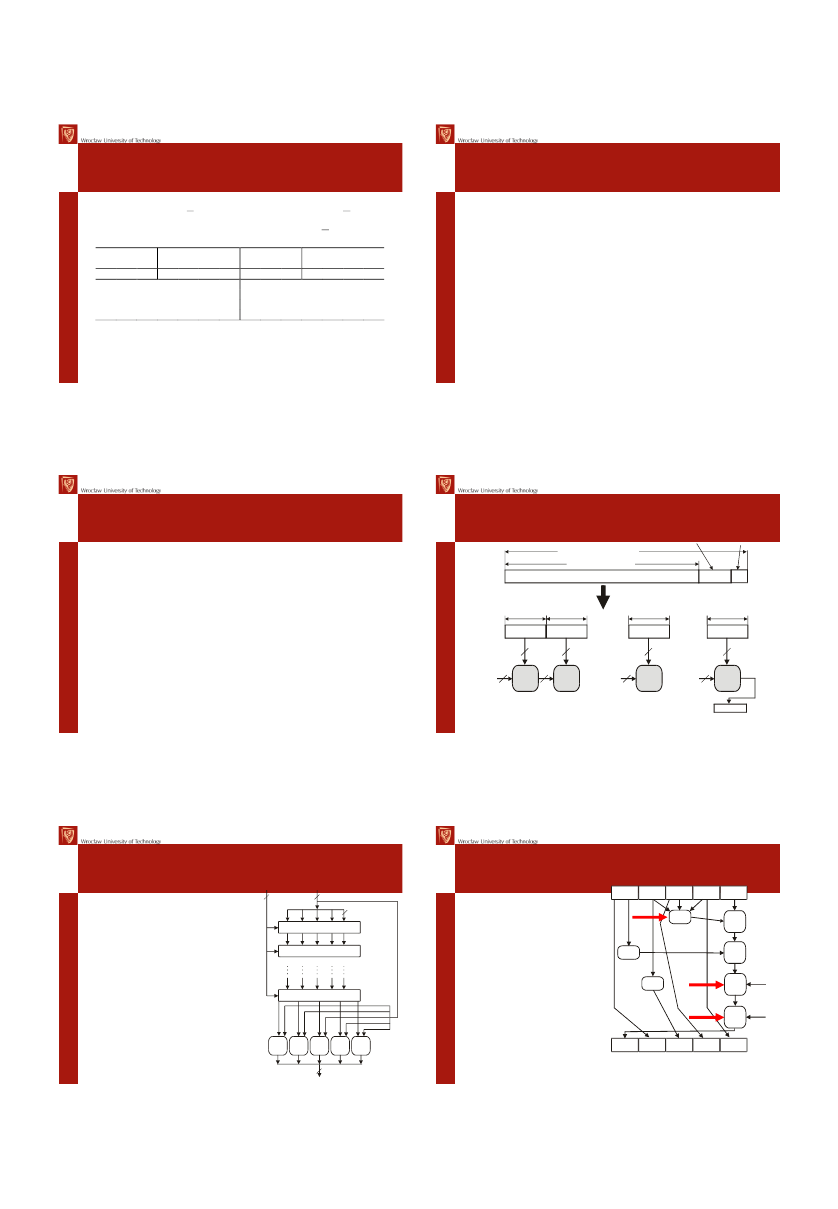
• Indeksy k do tablicy X oraz wartość przesunięcia s jest

zdefiniowana w RFC1321

• Elementarna operacja MD5 może być zapisana jako

[ABCD k s i]

• Dla etapów 1-16 A=B+CLS

s

(A+F(B,C,D)+X[k]+T[i])

[ABCD k s i] [DABC k s i] [CDAB k s i] [BCDA k s i]

[ABCD 0 7 1] [DABC 1 12 2] [CDAB 2 17 3] [BCDA 3 22 4]
[ABCD 4 7 5] [DABC 5 12 6] [CDAB 6 17 7] [BCDA 7 22 8]
[ABCD 8 7 9] [DABC 9 12 10] [CDAB 10 17 11] [BCDA 11 22 12]
[ABCD 12 7 13] [DABC 13 12 14] [CDAB 14 17 15] [BCDA 15 22 16]

2014-04-15

7

Funkcje elementarne

D)

B

(

C)

(B

D)

C,

F(B,









)

D

(C

D)

(B

D)

C,

G(B,









D

C

B

D)

C,

H(B,







)

D

(B

C

D)

C,

I(B,







bity

Funkcje

elementarne

bity

Funkcje

elementarne

B

C

D

F

G

H

I

B

C

D

F

G

H

I

0

0

0

0

0

0

1

1

0

0

0

0

1

1

0

0

1

1

0

1

0

1

0

1

0

1

0

1

0

1

0

0

1

1

0

1

1

0

1

1

0

0

0

1

1

1

0

0

1

1

1

1

1

1

1

0

Algorytm SHA

• Algorytm SHA (ang. Secure hash algorithm) został

stworzony przez Narodowy Instytut Standardów i

Technologii USA (NIST) i opublikowany jako FIPS PUB

180 w 1993 roku

• Algorytm z wejściowego komunikatu o długości

mniejszej niż 2

64

bity generuje 160-bitowy wyciąg

• Dane przetwarzane są w 512 bitowych blokach
• Od 2001 powstały cztery warianty określane jako SHA-2

(SHA-224, SHA-256, SHA-384, SHA-512)

• Ponieważ w 2004 zgłoszono udane ataki na funkcje

skrótu mające strukturę podobną do SHA-1 NIST ogłosił,

że do 2010 zaprzestanie stosować SHA-1 na rzecz

różnych wariantów SHA-2

Generowanie skrótu w SHA

• Dodawanie bitów dopełniających
• Dodanie długości komunikatu , długość musi być mniejsza

niż 2

64

• Inicjalizacja 160-bitowego bufora MD

A=67452301 B=EFCDAB89 C=98BADCFE

D=10325476 E=C3D2E1F0

• Przetwarzanie komunikatu w blokach 512-bitowych
• Otrzymanie wyniku

Generowanie skrótu w SHA

Komunikat

K bitów (<2 bitów)

64

L

x 512 bitów=N

x 32 bity

Dopełnienie

(1-512) bitów

Długość

komunikatu

(K)

100...0

Y

0

Y

1

512 bitów

512 bitów

Y

q

512 bitów

Y

L-1

512 bitów

. . .

. . .

H

SHA

512

512

512

512

160

ABCDE

160 bitowy wyciąg

160

160

160

H

SHA

H

SHA

H

SHA

Przetwarzanie komunikatu w 512-
bitowych blokach

• Podstawowym elementem

algorytmu jest przetwarzanie
bloku 512 bitowego za pomocą
80 podobnych etapów

• W każdym etapie jest

przetwarzany aktualny blok Y

q

oraz bufor ABCDE (MD

q

)

• Dodatkowo w każdym etapie

korzysta się z zdefiniowanej
stałej addytywnej K

t

: 0



t



19

ETAP (ABCDE,Y ,K )

0

q

0

160

MD

q

A B C D E

512

Y

q

+

mod 2

32

+

mod 2

32

+

mod 2

32

+

mod 2

32

160

MD

q+1

32

A B C D E

A B C D E

ETAP (ABCDE,Y ,K )

1

q

1

ETAP (ABCDE,Y ,K )

79

q

79

+

mod 2

32

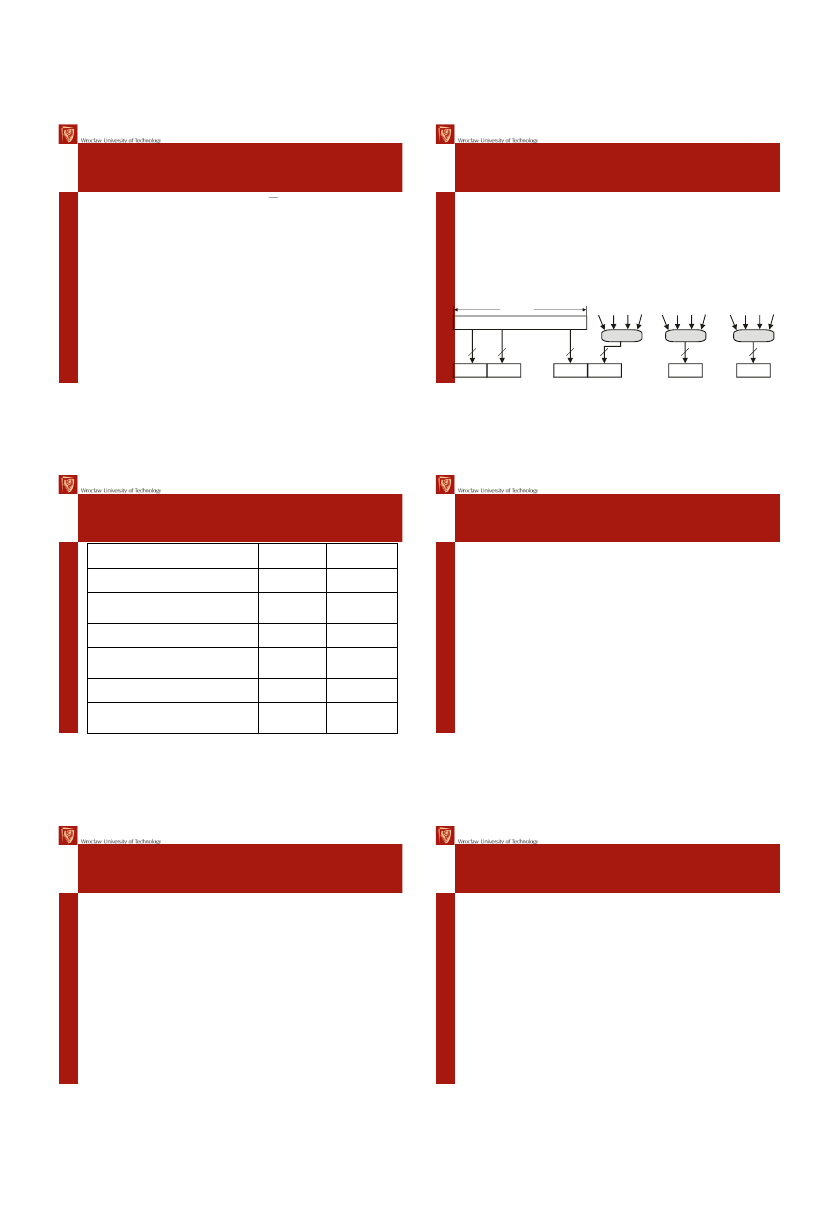
Elementarna operacja SHA

• Każdy z etapów wykonywanych

80 razy dla każdego bloku ma
postać

A, B, C, D, E



(CLS

5

(A)+f

t

(B,C,D)+E+W

t

+K

t

), A,

CLS

30

(B), C, D

• Przez f

t

oznaczamy jedną z

funkcji elementarnych

• W

t

oznacza 32 bitowe słowo w

przetwarzanym 512-bitowym
bloku

• K

t

to zdefiniowana stała

+

mod 2

32

f

t

+

mod 2

32

W

t

+

mod 2

32

CLS

30

A B C D E

+

mod 2

32

K

t

A B C D E

CLS

5

2014-04-15

8

Funkcje elementarne

D)

B

(

C)

(B

D)

C,

(B,

f

19

0













t

t

D

C

B

D)

C,

(B,

f

39

20











t

t

D)

(C

D)

(B

C)

(B

D)

C,

(B,

f

59

0

4

















t

t

D

C

B

D)

C,

(B,

f

79

60











t

t

Tworzenie sekwencji danych
wejściowych

• W

t

oznacza 32 bitowe słowo z przetwarzanego 512-

bitowym bloku

• Pierwsze 16 wartości W

t

otrzymuje się bezpośrednio z

aktualnego bloku 512-bitowego

• Pozostałe wartości są definiowane według

W

t

=W

t-16



W

t-14



W

t-8



W

t-3

. . .

Y

q

32

512 bitów

W

0

W

1

32

32

W

15

32

W

16

W

0

W W W

2

8

13

32

W

t

XOR

W

t-16

W W W

t

t

t

-14

-8

-3

XOR

32

W

79

XOR

W

63

W W W

65

71

13

. . .

. . .

Porównanie MD5 i SHA

MD5

SHA

Długość skrótu

128 bitów

160 bitów

Podstawowa jednostka

przetwarzania

512 bitów

512 bitów

Liczba kroków

64

80

Maksymalny rozmiar

komunikatu



2

64

Elementarne funkcje logiczne

4

3

Zastosowanie stałych

addytywnych

64

4

Porównanie MD5 i SHA

• Bezpieczeństwo – SHA daje dłuższy skrót, co zapewnia

większe bezpieczeństwo

• Szybkość – oba algorytmy działają podobnie. Jednak

ponieważ SHA ma dłuższy bufor działa około 25% wolniej
niż MD5

• Prostota i poręczność – SHA posiada prostszą strukturę
• Architektura – MD5 interpretuje komunikat jako

sekwencje 32-bitowych słów zapisanych w architekturze
„little-endian”, SHA stosuje architekturę „big-endian”

Bezpieczeństwo SHA

• Złożoność obliczeniowa ataku metodą brutalnej siły dla

wykrycia kolizji (wykrycie dwóch wiadomości, których

wynikiem jest ta sama funkcja skrótu) wynosi dla SHA

2

80

• Kryptologom udało się opracować atak, którego

złożoność obliczeniowa wynosi 2

69

• W związku z tym pojawiły się wątpliwości co do

bezpieczeństwa wielu systemów kryptograficznych

używających SHA (np. system podpisu elektronicznego)

• Narodowy Instytut Standardów i Technologii (NIST)

zaproponował zastąpienia szeroko używanej funkcji

haszującej SHA-1 silniejszą i mocniejszą funkcją SHA-

256 lub SHA-512

Najważniejsze cechy SHA-256

• SHA-256 daje skrót w długości 256 bitów co podnosi

znacznie bezpieczeństwo skrótu

• Dane wejściowe przetwarzane są w 512 bitowych

blokach

• Generalna zasada działania SHA-256 jest bardzo podobna

do MD5 i SHA

• Zastosowano inne funkcje na etapie przetwarzania

pojedynczych 512-bitowych bloków

2014-04-15

9

Najważniejsze cechy SHA-512

• SHA-512 daje 512 bitowy skrót. Dane wejściowe

przetwarzane są w 1024 bitowych blokach

• Komunikat jest dopełniany tak, by jego długość w bitach

przystawała do 896 modulo 1024

• Odpowiednio jak dla SHA-256 wprowadzono nowe

funkcje przetwarzające dane

SHA-3 - Algorytm Keccak

Architektura gąbki

SHA-3 - Algorytm Keccak

SHA-3 - Algorytm Keccak

SHA-3 - Algorytm Keccak

Dziękuję za uwagę