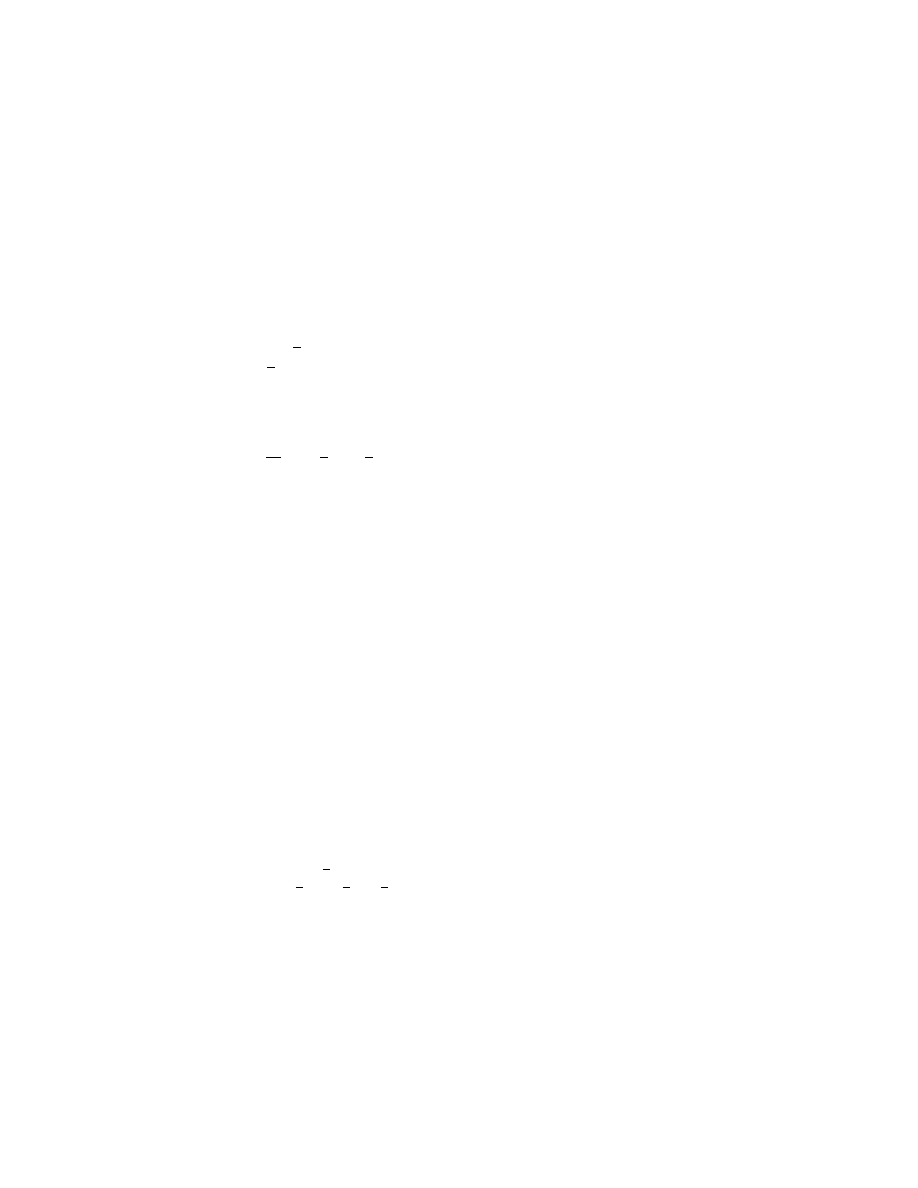
Wst ¾
ep do analizy matematycznej - arkusz zada´
n
1) Rozwi ¾
aza´c podane równania i nierówno´sci.
1) jx
3j = 5
2) j1
3xj = 0
3) j7
6xj = 2
4) j13 + 6xj < 2
5) j3x
4j
3
6) 2x
p
3 <
2
7) x
p
3
2 > 5
8) jxj = x
9) jxj = x
10) jxj
x
11) jxj
x
12)
p
13 + x
p
6
p
2
13) j4x
3j = j4x + 3j
14) j2x
3j = j7x + 32j
15) j3x
5j
x
16) j1
3xj < 2x
17) jx
5j + 4x = jx + 2j + 3
18) jx
1j + 3 jx
5j
17
19) j3
xj + 2 jx
25j < 77
20) j2
3xj + j2 + 5xj + 3 jxj < 0
2) Metod ¾
a przekszta÷
ce´
n naszkicowa´c wykresy podanych funkcji.
1) f (x) = jx + 4j
2) f (x) = jx
3j
2
3) f (x) = 5
jx + 1j
4) f (x) = 3 + j1
xj
5) f (x) = jjxj
5j
6) f (x) = 3
jjx + 1j
5j
7) f (x) = jjjxj
1j
1j
8) f (x) = 2
jjx
1j
3j
3) Rozwi ¾
aza´c podane równania i nierówno´sci.
1)
2x
2
2x + 12
0
2)
x
2
+ 4x > 0
3) x
2
+ x + x
p
5
0
4) x
2
+ x
p
2
x
p
3
p
6 = 0
5)
6x
x
2
9 > 0
6) jtj
2
+ jtj
2 = 0
7) t
2
+ jtj
2 = 0
8) u
2
9 juj
22
0
9) 4 juj + u
2
117 > 0
10) x
4
+ 6x
2
27 = 0
1
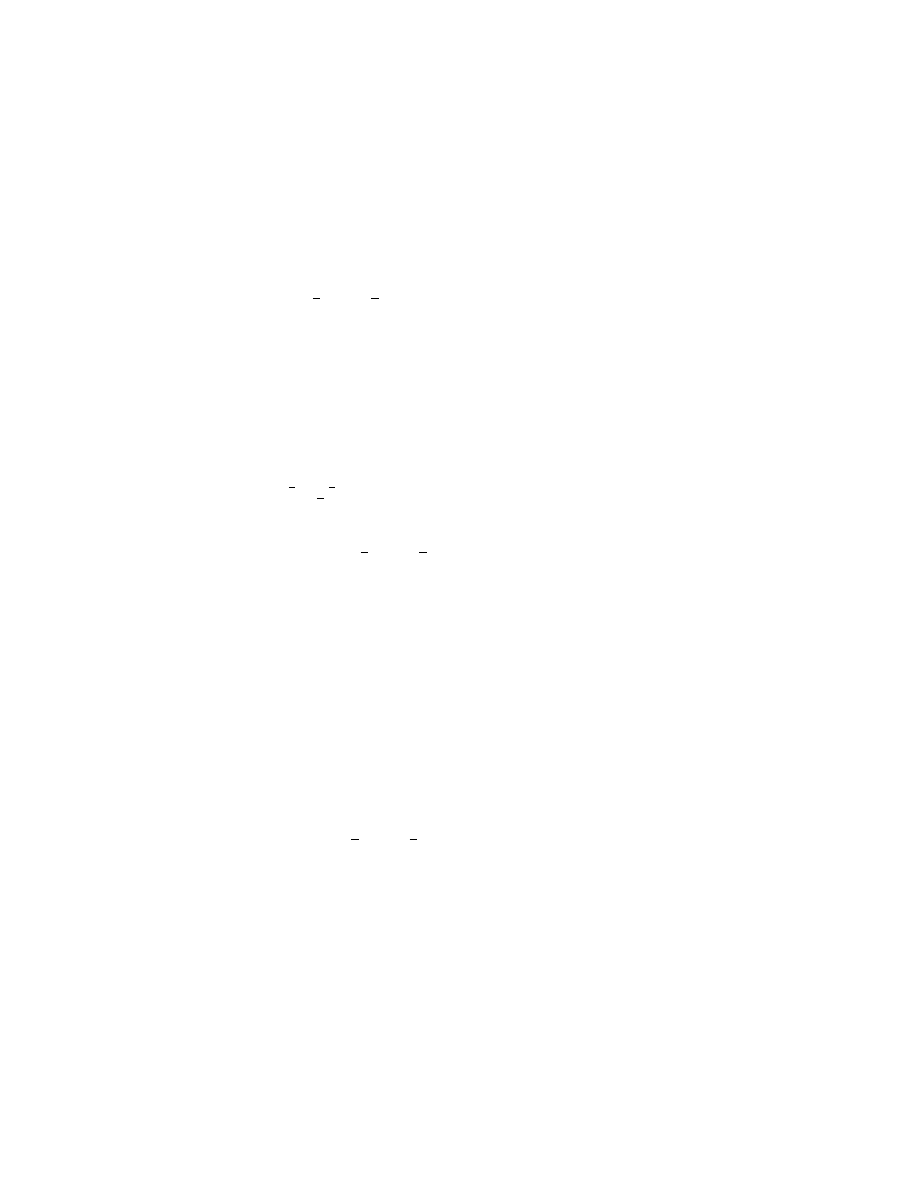
11) x
4
8x
2
9
0
12)
32 + 31x
5
+ x
10
= 0
13) t
2
+ 2t + 3 = t + 7
14) t
2
t + 3 = t
2
+ 3t
1
15) x
2
+ jx
1j
1 > 0
16) x
6
2x
3
+ 7 > 0
17)
2(x
p
2)(x +
p
3)
0
18)
x
2
+ 4x
3
4) Podan ¾
a funkcj ¾
e kwadratow ¾
a sprowadzi´c do postaci kanonicznej,
a nast ¾
epnie metod ¾
a przekszta÷
ce´
n naszkicowa´c jej wykres.
1) f (x) = x
2
+ 3x
5
2) f (x) = x
2
4x + 4
3) f (x) = x
2
5x
4) f (t) =
t
2
+ t + 6
5) f (t) =
5t
2
2t + 3
6) f (t) =
1
3
t
2
2
5
t
1
7) g(x) = x
2
p
5
3
8) g(x) =
2(x + 6)
2
+ 3
9) g(x) =
x
2
+ 3x + 7
10) g(x) =
2(x
p
2)(x +
p
3)
5) Podany wielomian
W roz÷
o·
zy´c na czynniki, a nast ¾
epnie nasz-
kicowa´c jego wykres i poda´c zbiór rozwi ¾
aza´
n równania
W (x) = 0 i
nierówno´sci W (x) < 0; W (x) > 0; W (x)
0; W (x)
0.
W (x) =
1) x
5
2)
3x + 8
3)
2x
2
14x + 36
4)
x
2
+ 3x
123
5) x
3
2x
2
+ x
6) x
3
2x
2
x
7) x
3
x
2
+ x
1
8) x
3
+ 2x
2
+ 2x + 4
9)
3(x
2
6x + 9)
10) 5(x
1)(x + 3)(x
5)
11)
(x
1)(x
p
2)(x
p
3)(x
2)
12) x
4
16
13) x
4
+ 4x
2
+ 4
14) x
4
4x
2
+ 4
15) x
8
2x
4
+ 1
16) x
3
8
17) x
3
2x
2
5x + 6
18) x
3
3x
2
10x + 24
19) 9x
3x
3
6
2

20) 5x
4x
2
+ x
3
6
21) 2x
3
3x
2
4x + x
4
+ 4
22) 14x
2
12x
2x
4
23) x
4
5x
2
6x
3
12x
14
24) 3x
2
3x
x
3
+ 1
25) 24x
2
32x
8x
3
+ x
4
+ 16
26) x
3
7
6
x
2
+
1
6
27)
16
9
x +
2
3
x
2
2x
3
8
9
28) 3x
2
p
3
3x
p
5 +
p
10
x
p
6
29)
3
98
x
83
196
x
2
1
7
x
3
+ x
4
+
9
196
30)
41
4
x +
27
4
x
2
+ x
3
3
6) Rozwi ¾
aza´c podane równania i nierówno´sci.
1)
1
x
> 9
2)
1
x
2
> 9
3)
x
1
x 2
4)
x
x 1
>
2
x
5)
x
2
x+2
jx 1j
= 0
6)
x
2
+x+12
jx+3j
0
7)
1
jx 2j
> x + 3
8)
j2x 1j
x
2
1
0
9)
3x 2
1+x
< 2 +
1 x
3+2x
10)
1
x
+
2
x 1
+
3
x 2
< 0
11)
1
x
9
x
2
0
12)
1
x
2
+x 2
+
1
x
2
+5x 6
< 0
7) Podan ¾
a funkcj ¾
e przedstawi´c w postaci f
(x) = A +
a
x B
, a nast ¾
ep-
nie (metod ¾
a przekszta÷
ce´
n) naszkicowa´c jej wykres.
f (x) =
1)
x+2
x 1
2)
2x
x+5
3)
2x 3
x+7
4)
1 x
x 3
5)
3 4x
x+5
6)
3x 1
2x+9
7)
1 7x
3 4x
8)
1
2 x
9)
3
2x+7
8) Metod ¾
a przekszta÷
ce´
n naszkicowa´c wykresy podanych funkcji.
f (x) =
1) 2
x
+ 1
2) 2
x
+ 1
3

3) 3
x 1
2
4) 3
x 1
2
5) 3
4
2 x
6) 2
2x 6
7
7) 1
3
x+2
8) 2
3x 9
5
2
9) 6
5
3
2x+2
7
10) 5
(
1
2
)
2x+5
11) 3
(0:6)
2x 5
12) 3
1 x
3
9) Rozwi ¾
aza´c podane równania i nierówno´sci.
1) (
1
3
)
2x 1
=
9
p
3
4
p
3
2) 2
x+3
>
p
8
32
3) (0:04)
x+3
9
p
625
4) 7
x
2
5x
> 1
5) (
p
3)
jx+2j
3
p
81
3
2
6) (
1
64
)
1 x
(
4
p
2)
2x
= 8
x 4
(
p
2
5
p
2
)
3 x
7) (3
x 1
)
2
p
27
3
1
x
<
9
3
x+2
((
4
p
3)
5x
)
1
8) (
p
2)
3
jx+2j
1
2
9)
1
3
jx 7j
>
1
3
x
10) 2
2x
2
11x+x
3
12
= 1
11) (
p
3)
2x
3
+4
< (
1
3
)
3x
12) 2 4
x
65 2
x
+ 32 = 0
13) 2 4
x
65 2
x
+ 32 < 0
14) (
1
9
)
jxj
30
3
jxj
81
15) 7
x
2
3x
+ 3
p
7
x
2
3x
> 4
16) 2
3
jxj
126 2
2
jxj
259 2
jxj
+ 384 = 0
17) 2
3
jxj
126 2
2
jxj
259 2
jxj
+ 384 < 0
18) 5
j2x 1j
0:24 5
jx 0:5j
+ 0:008
0
19) 3
x
4
3x+1
>
1
20) 2
1 3
jx+2j
0
21) 2
x 1
+ (
1
2
)
x
3
1
+ 1 < 0
10) Metod ¾
a przekszta÷
ce´
n naszkicowa´c wykresy podanych funkcji.
f (x) =
1) log
1
2
(x
1)
2) 3 + log
2
(x + 2)
3) 5
log(x
3)
4) jlog
0:4
(x + 5)j
5) j1
log
2
(x
1)j
6) 3
log
p
3
(x + 2) + 1
7) j1
j1
log(x
1)jj
4
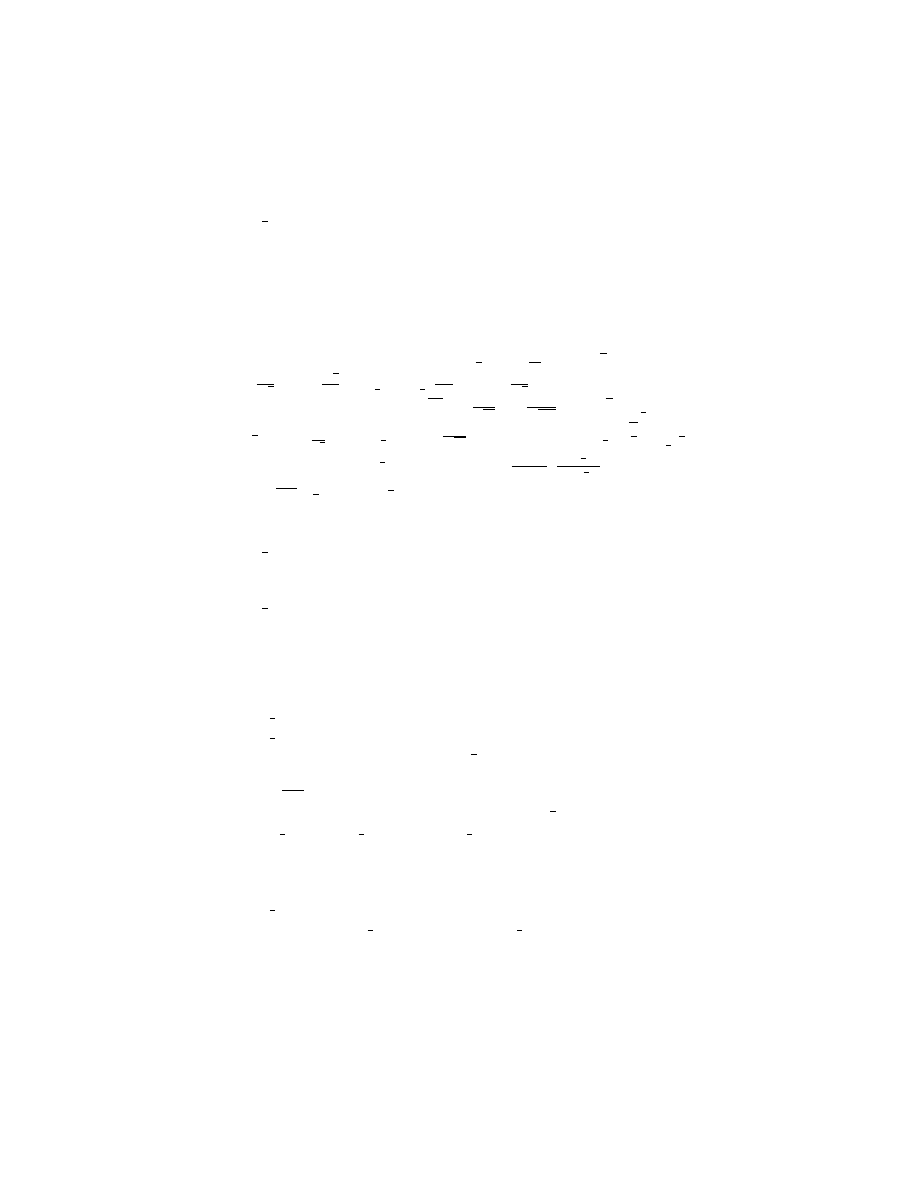
8) log
2
( x)
9) log
1
3
( x)
10) log
5
[ (x + 2)]
11) log
0:2
[ (x
6)]
12) log
3
( x + 3)
13) jlog ( x
1)j
14) 2
j1
log( x + 5)j
11) Obliczy´c
log
2
8; log
2
16; log
2
(2
5
); log
2
(2
1
); log
2
(
1
2
); log
2
(
1
64
); log
2
(
p
2); log
2
1;
log
2
(
1
3
p
2
); log
2
(
5
p
2
16
); log
1
2
2; log
1
2
(
1
128
); log
0:5
(
2
6
p
2
); log(10); log(100); log(100000);
log(10
15
); log(10
4
); log 1; log
3
p
10; log
100
p
10
; log
1
4
p
100
; log
3
p
3; log
1
3
27;
log
p
5
125; log
1
p
5
(5
3
); log
1
7
49; log
7
1
5
p
49
; log
1:5
1:5; log 10; log
2
3
6
q
9
4
; log
2
5
2
5
;
2
log
2
3
; 3
log
3
7
; 4
log
2
5
; 9
log
1
3
5
; 10
log 2
; 1000
log 3
;
log
5
27
log
5
3
;
log
p
2
27
log
p
2
9
;
2
log
4
3
; 5
log 3
log 5
; (
1
4
)
log
2
3
; 3
log
1
3
4
:
12) Rozwi ¾
aza´c podane równania i nierówno´sci.
1) log
1
2
(3
2x) <
1
2) log
3
(3x
1)
0
3) log(x
7) = 3
4) log
1
3
(jx
2j
3)
0
5) log
2
(jx + 1j + 2) = 4
6) log
2
(j2x + 1j + 1)
log
0:5
2
7) log
3
(x
1) + log
3
(x + 1)
1
8) log
3
(1
x) + log
3
(x + 1)
1
9) log(x
2)
log(4
x) = 1
log(13
x)
10) log
1
2
(x
2
+ 3x) >
2
11) log
1
2
(j3x
1j + 1)
3
12) log(2
x
4
x
)
log 8
log(2
x 1
+
1
4
)
13) log
5
x
log
5
(x
1)
2
14) log
5
(
x
x 1
)
2
15) log x + log(x + 1) + log(x + 2) > 2 log 3 + log(
2
3
)
16) 2 log
1
2
( x) + log
1
2
(x + 6)
log
1
2
(0:2)
17) log
2
x + 2 log x
3 < 0
18) log
3
2
(x + 1)
3 log
2
(x + 1) + 2
0
19) jlog
3
(x + 1)j < 1
20) log
2
1
3
(x
1)
25
21) log
5
(2x + 1) + log
1
5
(x
1) > log
5
x + log
1
5
(x + 1)
22) 2
x 1
+ log(x + 2) =
2
23) log
2
2
(jxj + 1)
4 log
2
(jxj + 1)
5
13) Obliczy´c sin ; cos ; tg ; ctg
dla
=
5
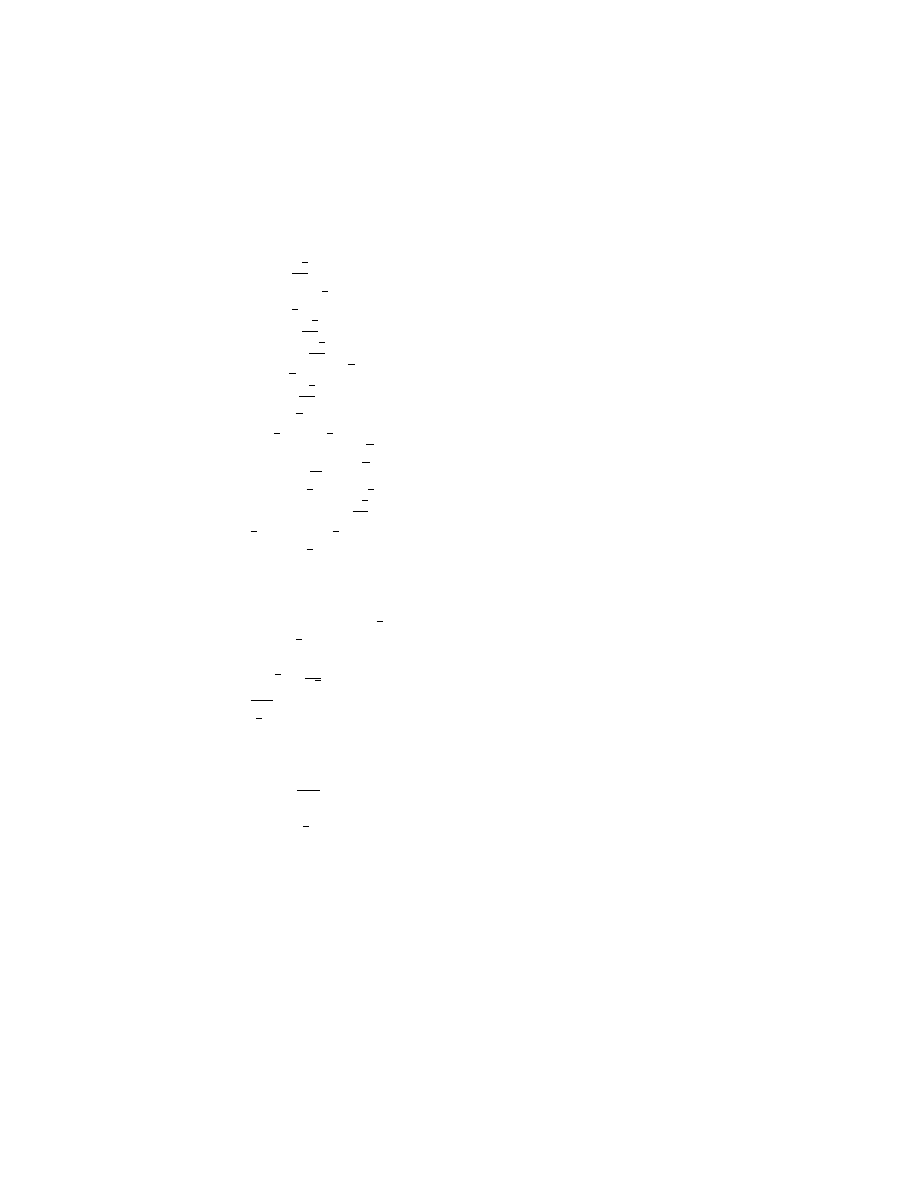
120 ; 135 ;
150 ; 240 ;
225 ; 300 ;
315 ; 330 ;
570 ; 1395 ;
2670 ; 4200 ;
6435 ; 115860 :
14) Rozwi ¾
aza´c podane równania i nierówno´sci.
1) sin x =
p
3
2
2) cos(2x) =
1
2
3) sin x >
1
2
4) jcos xj
p
2
2
5) sin(4x) <
p
7
2
6) tg(x
7
) >
p
3
7) jctgxj >
p
3
3
8) tg
2
(x +
5
) = 1
9) sin
2
(
2
7
x)
1
2
10) cos(3x
4)
p
3
11) ctg(3x
12
)
p
3
12) cos
2
x +
5
2
cos x
3
2
0
13) sin
2
x
sin x +
p
2
2
(1
sin x) > 0
14)
5
2
sin
2
x
7
2
cos x
0
15) cos
2
x
5
2
sin x
2
0
16) sin 2x = sin x
17) sin 4x + cos 2x = 0
18) cos 2x + sin
2
x = 0
19) cos 2x
cos
2
x =
3
4
20) 2
tgx
<
1
2
21) 3
cos
2
3x
1
22) 2
sin
x
3
>
1
p
2
23)
1
3
tgx
3
24) (
1
5
)
ctg2x
< 1
25) sin x = cos x
26) jsin xj = cos x
27) tgx = ctgx
28) ctgx +
1
sin x
= 0
29) tgx = sin x
30) sin x
1
2
1
6
Wyszukiwarka
Podobne podstrony:
arkusz-wstęp
2007-Wstep-Arkusz
2006 Wstep Arkusz1 3
SI wstep
Zajęcie1 Wstęp
Wstęp do psychopatologii zaburzenia osobowosci materiały
układ naczyniowy wstep
ZMPST Wstep
Dekalog 0 wstęp
1 WSTEP kineza i fizykot (2)
01 AiPP Wstep
wstęp neg
Wyklad I Problemy etyczne Wstep
więcej podobnych podstron