
DROGI SZYNOWE cz. 7

Urządzenia w wagonach, służące do przechylania nadwozi, mogą mieć różną
konstrukcję napędu. Źródło sygnału uruchamiającego zespół sterujący
przechyłem może pochodzić od:
•
krzywej przejściowej (przed wjazdem na łuk kołowy), wywołującej
przyspieszenie poprzeczne,
•
magnesów trwałych, zainstalowanych przy torze przed wjazdem na krzywą
przejściową i przy zjeździe z krzywej przejściowej,
•
taśmy magnetycznej, na której zostały uprzednio zapisane parametry
geometryczne toru na danej linii.

Najczęściej stosuje się pierwszy sposób, umieszczając w pierwszym wagonie
(sterującym) na ramie przedniego wózka, nad pierwszą osią, żyroskop i
przyspieszeniomierz do przejmowania przyspieszenia jako sygnału sterującego
przechyłem nadwozia.
Sygnał ten, po odpowiedniej analizie, wykonanej przez komputer, jest podawany
kolejno z wagonu na wagon i uruchamia sukcesywnie urządzenia przechylające
nadwozia.
Ponieważ sygnały przyspieszeń są filtrowane, zapobiega to przechyłom nadwozia,
spowodowanym oddziaływaniem nierówności poziomych toru na odcinkach
prostych.
Podczas przejazdu z odcinka prostego na krzywoliniowy bardziej wiarygodny
jest sygnał z żyroskopu, reagującego na zmianę wysokości toków szynowych.

System przyspieszeniomierzy i układy żyroskopów nie mogą reagować na
przypadkowe nierówności (poziome i pionowe) toków szynowych, stąd układ
przechyłu zaczyna działać po przekroczeniu określonej wartości
przyspieszenia bocznego na wózku.
System sterowania przechyłem współpracuje więc z drogą kolejową,
szczególną zaś rolę odgrywa tutaj odcinek krzywej przejściowej.
Należy więc prześledzić kinematykę ruchu taboru z wychylnymi nadwoziami
na krzywej przejściowej
−
z uwzględnieniem występujących przyspieszeń
poprzecznych oraz charakterystyki obrotu nadwozia. Jest to o tyle istotne,
że
−
jak wiadomo
−
krzywa przejściowa decyduje często o prędkości jazdy
pociągu.

Rozpatrując poruszanie się taboru z przechylnym nadwoziem na
krzywiznach poziomych (wzdłuż drogi x) należy uwzględnić dwa rodzaje
bocznych przyspieszeń niezrównoważonych:
•
przyspieszenia a
d
(x), rejestrowane na wózku, oraz
•
przyspieszenia a
n
(x), oddziałujące na nadwozie, powstałe po
zredukowaniu a
d
(x) na skutek obrotu nadwozia.
zredukowaniu a
d
(x) na skutek obrotu nadwozia.
Na pasażera działa przyspieszenie nieco zwiększone w porównaniu do
a
n
(x), wskutek przechyłu nadwozia na zewnątrz łuku, wywołanego
usprężynowaniem na ramie wózka.
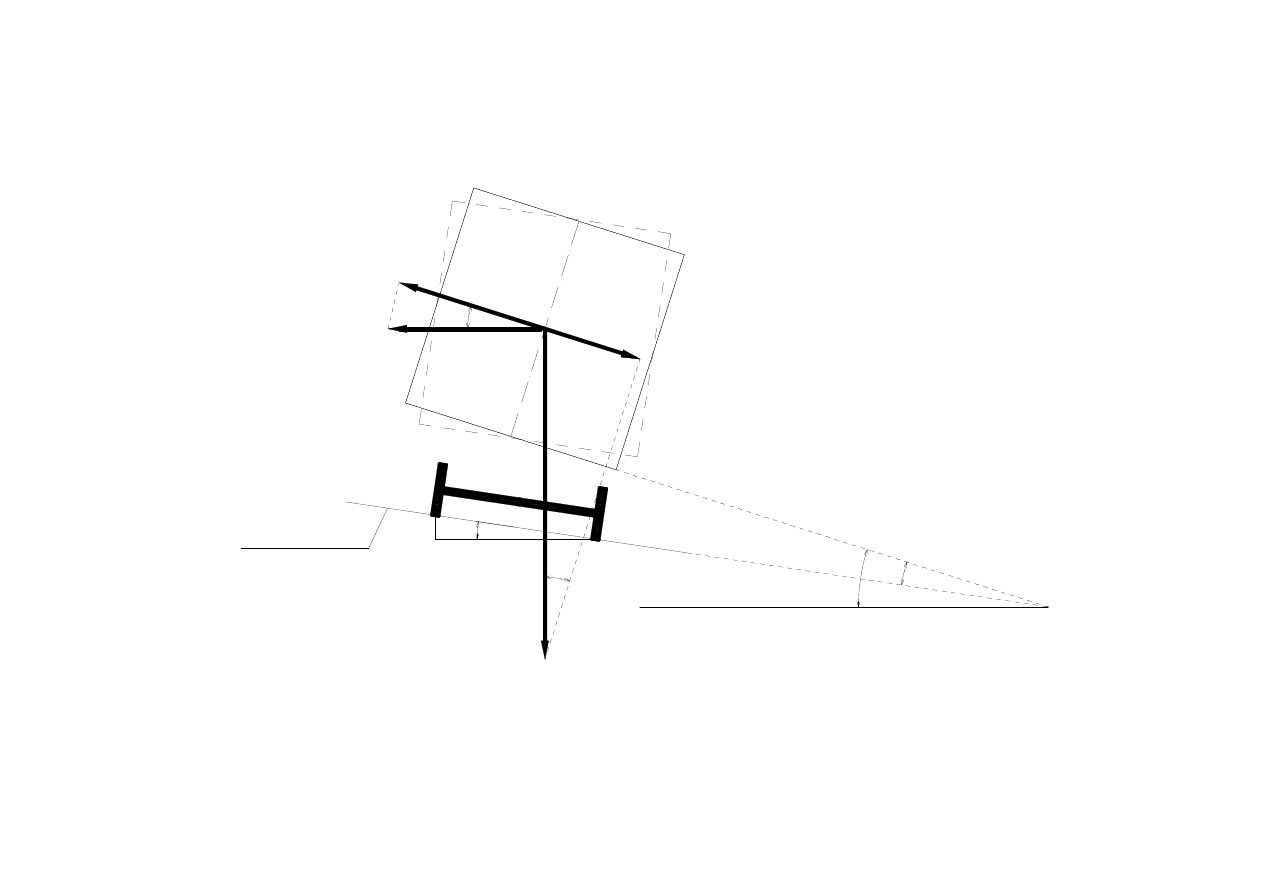
a
W
a
Z
a
R
0
ϕ + γ
Przyspieszenia poprzeczne działaj
ą
ce na przechylone nadwozie
w poje
ź
dzie szynowym poruszaj
ą
cym si
ę
po krzywi
ź
nie poziomej
ϕ
+
γ
h
s
ϕ
ϕ + γ
γ
g
Płaszczyzna toru

Działające na pasażera przyspieszenia: a
z
skierowane na zewnątrz i a
w
skierowane do wewnątrz łuku są opisywane następującymi wzorami:
)
cos(
)
6
,
3
(
2
2
γ
ϕ
+
⋅
=
R
v
a
p
z
)
sin(
γ
ϕ
+
⋅
=
g
a
w
Uwzględniając, jak poprzednio, że
)
sin(
γ
ϕ
+
⋅
=
g
a
w
s
h
=
ϕ
sin
(gdzie relacja h/s nie przekracza 0,1), a kąt
γ
jest mały
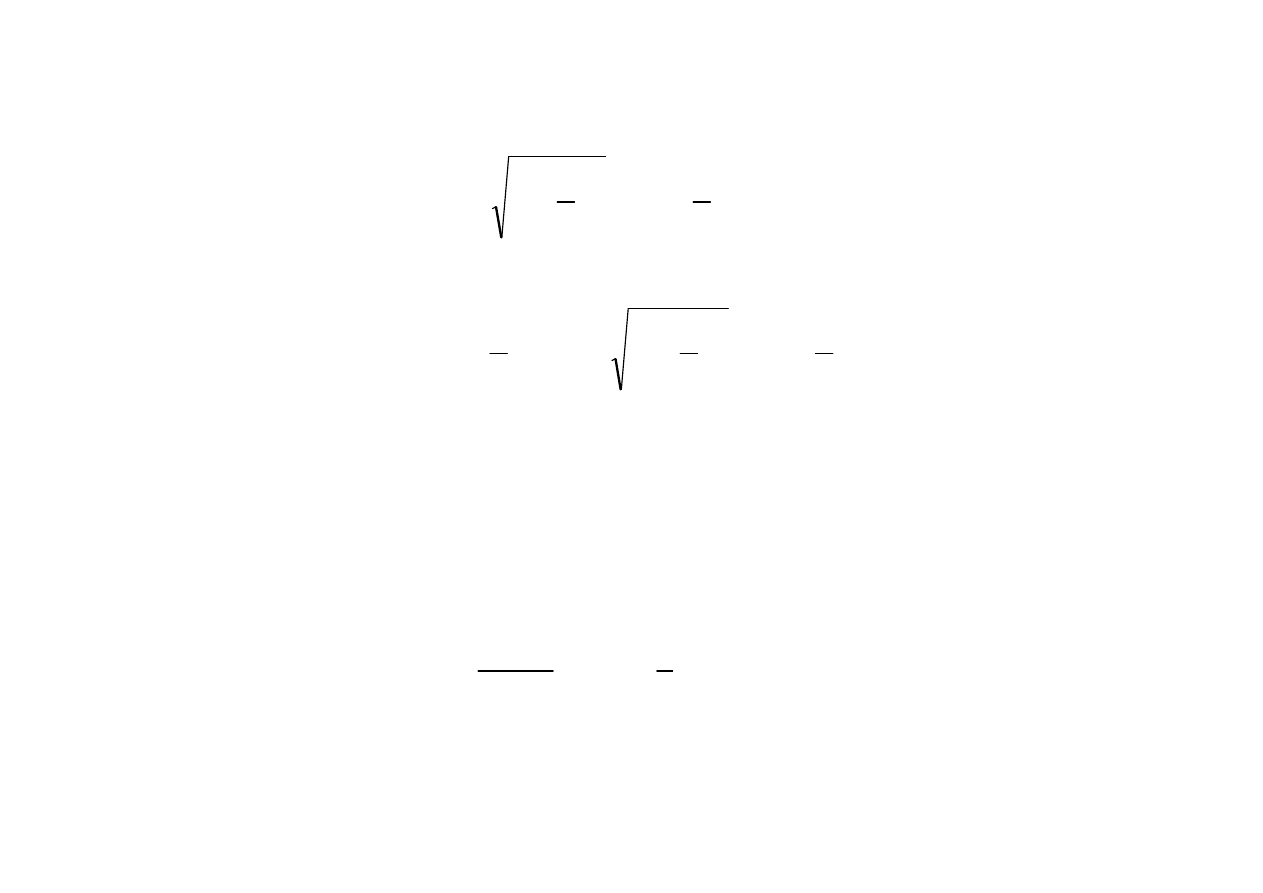
γ
γ
γ
γ
ϕ
cos
sin
cos
1
)
cos(
2
≅
⋅
−
−
=
+
s
h
s
h
γ
γ
γ
γ
γ
ϕ
sin
cos
sin
1
cos
)
sin(
2
+
⋅
≅
−
+
⋅
=
+
s
h
s
h
s
h
Przyspieszenie wypadkowe oddziałujące na przechylone nadwozie
opisuje zatem wzór
γ
γ
γ
sin
cos
cos
96
,
12
2
⋅
−
−
=
g
s
h
g
R
v
a
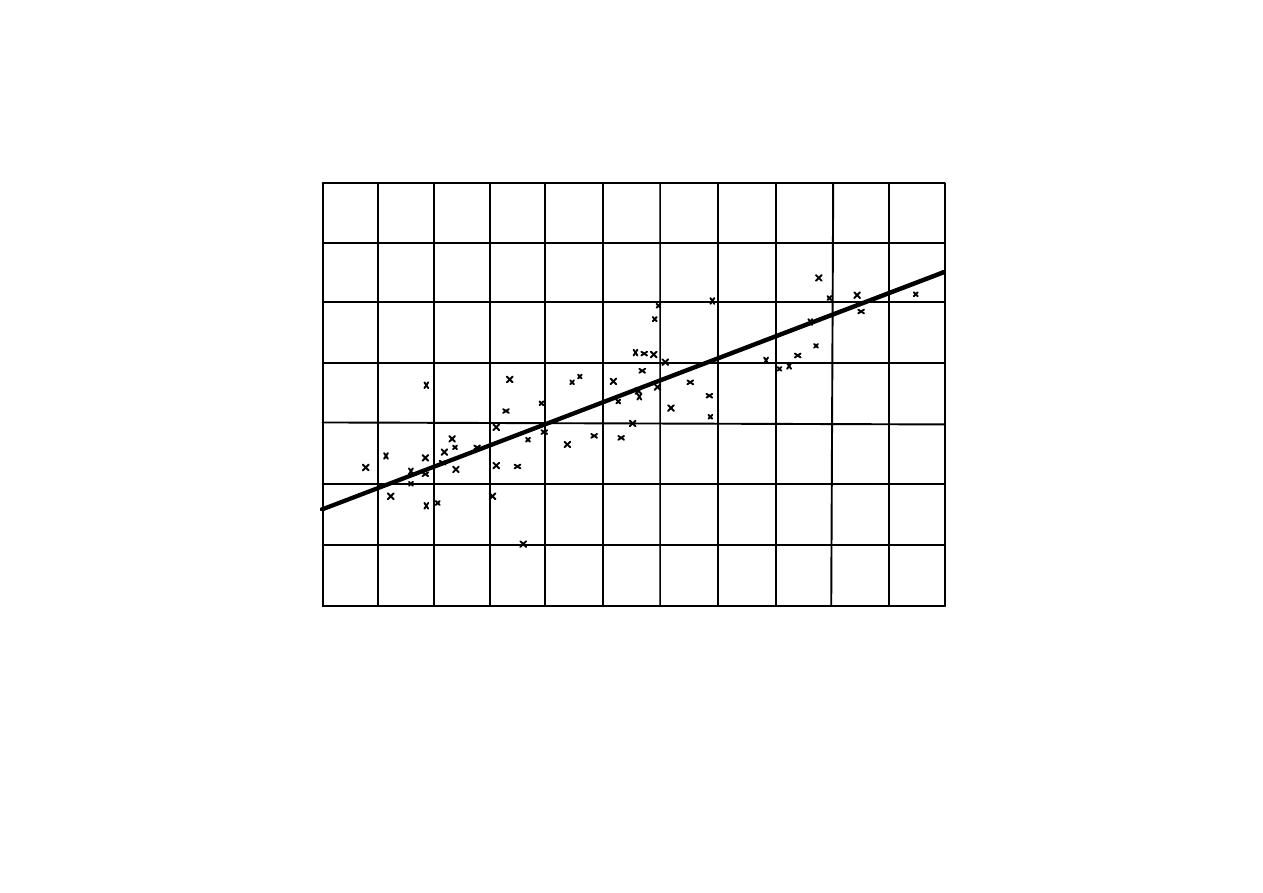
ϑ
[
0
/s]
7,00
6,00
5,00
4,00
3,00
Prędkość obrotu nadwozia wagonu ETR
−
460 w funkcji przyspieszenia
bocznego na wózku a
d
(badania eksploatacyjne na linii Warszawa
−
Gdańsk)
2,00
1,00
0,00
0,00 0,40 0,80 1,20 1,60 2,00 a
d
[m/s
2
]

Z badań eksploatacyjnych pociągu ETR
−
460 Pendolino,
przeprowadzonych na linii Warszawa
−
Gdańsk, wynika, że prędkość
obrotu nadwozia rośnie wraz ze wzrostem przyspieszenia bocznego
a
d
(x), wynikającego z prędkości jazdy v i układu geometrycznego toru,
natomiast sam obrót rozpoczyna się przy pewnej wartości a
p
< a
0
.
Zależność = f(a
d
) ma charakter liniowy.
Ponieważ dla krzywej przejściowej w postaci paraboli trzeciego stopnia
przyspieszenie a
d
jest liniową funkcją drogi x (a przy prędkości jazdy v
W tej sytuacji obrót nadwozia odbywa się ze stałym przyspieszeniem:
przyspieszenie a
d
jest liniową funkcją drogi x (a przy prędkości jazdy v
= const
−
również liniową funkcją czasu t), można przyjąć, że prędkość
obrotu nadwozia narasta liniowo na długości krzywej przejściowej.
c
d
dt
const
0
=
=
ϑ

Przyspieszenie to występuje na całym odcinku obrotu, tj. dla
x
p
−
położenie punktu początkowego odcinka obrotu
nadwozia,
l
−
długość krzywej przejściowej.
(
]
x
x
l
p
∈
,
W dalszych rozważaniach, dotyczących krzywej przejściowej, będziemy
W dalszych rozważaniach, dotyczących krzywej przejściowej, będziemy
operować zmienną niemianowaną
ξ
= =
x
l
t
T
Zakładamy też stałą prędkość przejazdu v , a więc czas przejazdu przez
krzywą przejściową wynosi
T
l
v
=
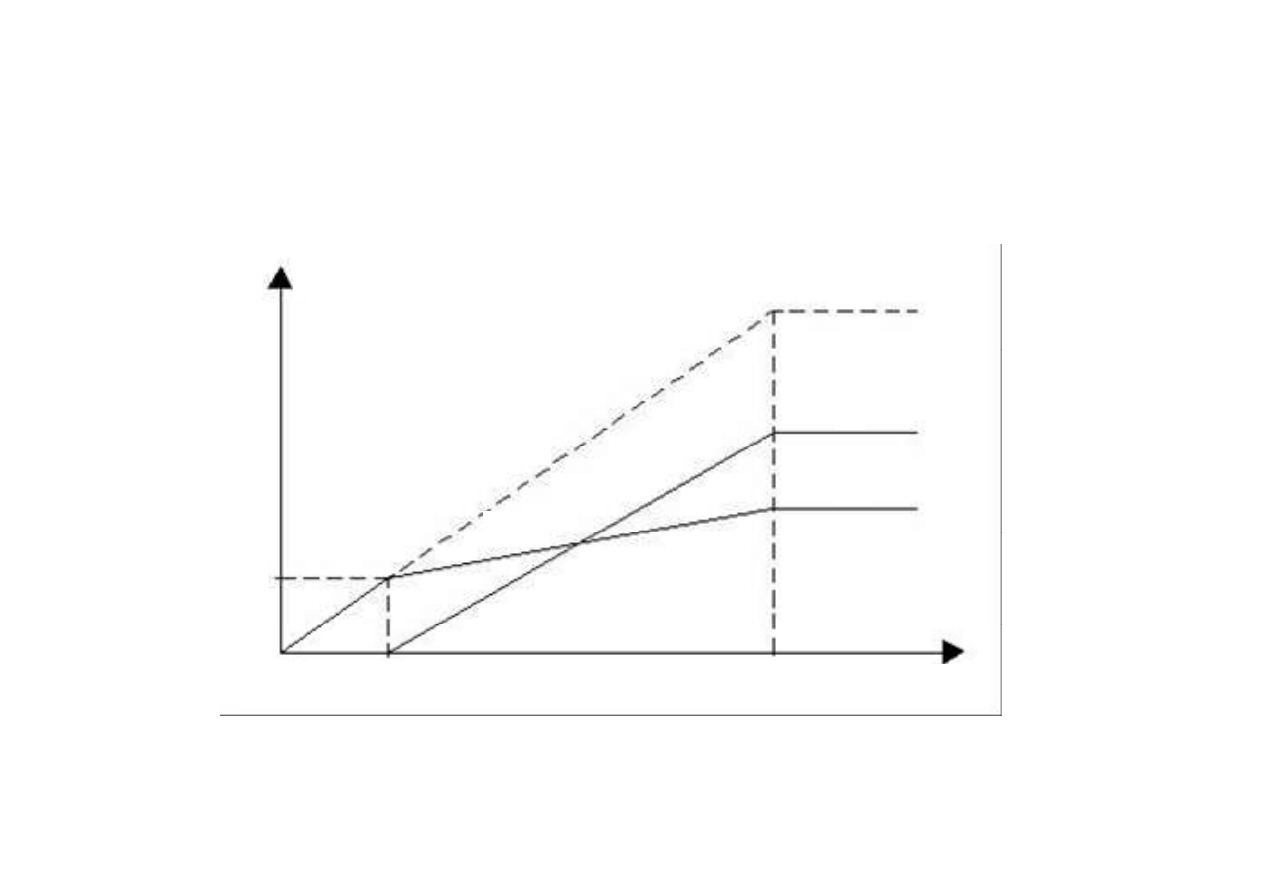
Zależności teoretyczne dla krzywej przejściowej w postaci paraboli
trzeciego stopnia
a
γ
a
m
γ
0
a
d
(
ξ
)
Wykresy przyspieszeń a
d
(
ξ
) i a
n
(
ξ
) oraz wykres kąta obrotu nadwozia
γ
(
ξ
) na długości krzywej przejściowej (schemat ideowy dla obrotu
jednostajnego)
a
p
0
ξ
p
1,0
ξ
a
0
a
n
(
ξ
)
a
d
(
ξ
)
γ
(
ξ
)
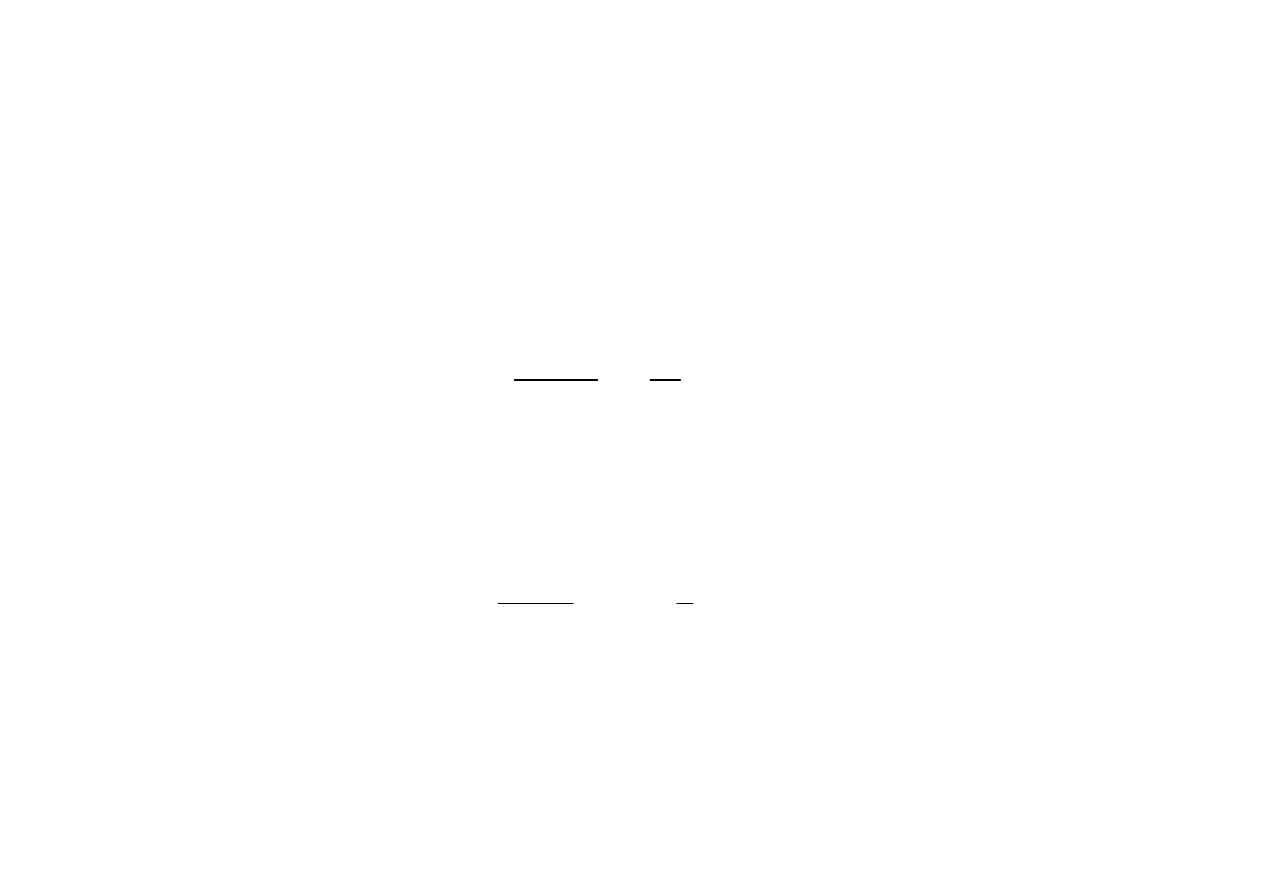
Na łuku kołowym (tj. dla
ξ
= 1) funkcje a
d
(
ξ
) , a
n
(
ξ
) i
γ
(
ξ
) przyjmują
wartości stałe.
Przyspieszenie a
m
na wózku – jak w tradycyjnym taborze – wynosi
s
h
g
R
v
a
m
0
2
96
,
12
−
=
Ponieważ jednak kąt
γ
jest mały (w rozpatrywanym przypadku
γ
= 0
÷
8
0
), więc nie popełnimy dużego błędu, jeśli kierując się względami
praktycznym przyjmiemy cos
γ
≈
1 i sin
γ
≈
γ
. Otrzymujemy wówczas
Dla przechylonego nadwozia obowiązuje wzór
γ
γ
γ
sin
cos
cos
96
,
12
2
⋅
−
−
=
g
s
h
g
R
v
a

gdzie:
γ
0
−
wartość kąta obrotu nadwozia na łuku kołowym.
0
0
2
0
96
,
12
γ
⋅
−
−
=
g
s
h
g
R
v
a
γ
0
0
1
≅
−
g
a
a
m
(
)
Boczne przyspieszenie niezrównoważone na wózku zmienia się w
sposób liniowy.
( )
ξ
ξ
⋅
=
m
d
a
a
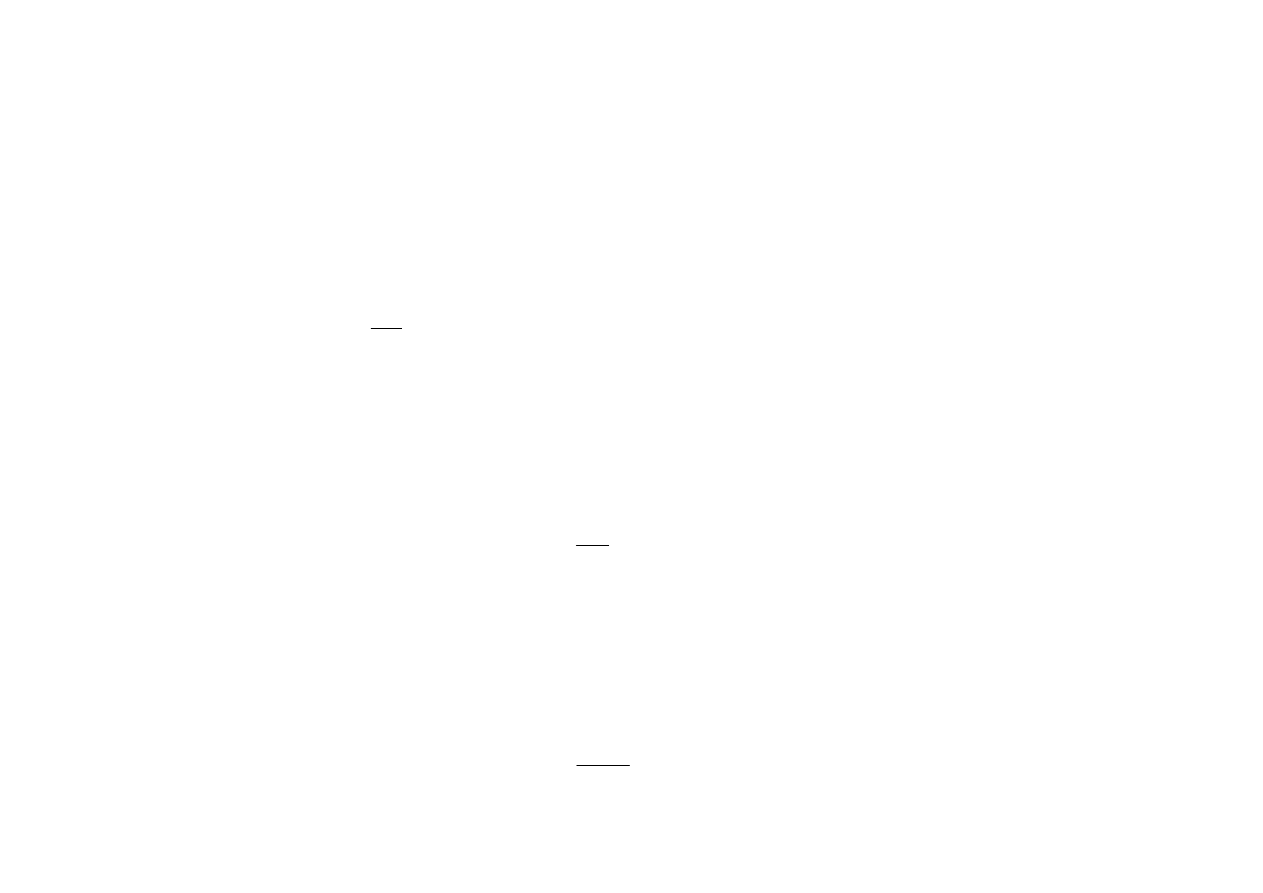
Na odcinku początkowym krzywej przejściowej, dla
nie następuje obrót nadwozia, stąd
Przyspieszenia a
n
(
ξξξξ
) na odcinku początkowym krzywej przejściowej
[ ]
ξ
ξ
∈
0,
p
gdzie
l
x
p
p
=
ξ
( )
( )
ξ
ξ
d
n
a
a
=
Jednocześnie
ξ
p
p
m
a
a
=
[ ]
a
a
p
∈
0
0
,
a
a
dop
0
≤
Prędkość zmiany przyspieszenia na tym odcinku jest wartością stałą
i wynosi
dop
m
l
v
a
ψ
ψ
≤
⋅
=
6
,
3
0

Wynika stąd pierwszy warunek na graniczną wartość przyspieszenia a
m
.
Drugi warunek na przyspieszenie wynika z wymagań konstrukcyjnych
wagonu. Chodzi o to, że niezrównoważone przyspieszenie boczne,
rejestrowane na wózku, decyduje o wielkości sił między kołem a
v
l
a
dop
m
⋅
=
ψ
ψ
6
,
3
rejestrowane na wózku, decyduje o wielkości sił między kołem a
szyną.
Utrzymanie tych sił w dopuszczalnych granicach powoduje, że w
przypadku szyn UIC60 i nacisku koła na szynę odpowiadającego
masie 20 t, dopuszczalne przyspieszenie odśrodkowe w
płaszczyźnie toru nie powinno przekraczać 1,25
÷
1,5 m/s
2
, przy
masie 16 t
−
1,6 m/s
2
, przy masie 13 t
−
1,8 m/s
2
. Dla taboru
ETR
−
460 Pendolino = 2,0 m/s
2
.

Charakterystyka obrotu nadwozia
Obrót nadwozia występuje na odcinku
(
]
ξ
ξ
∈
p
,1
Przy założeniu stałego przyspieszenia obrotu c
0
, prędkość obrotu
nadwozia narasta liniowo
ϑ
ϑ
( )
(
)
t
c t
t
p
p
=
+
−
0
natomiast kąt obrotu
γ
rośnie ruchem jednostajnie przyspieszonym
natomiast kąt obrotu
γ
rośnie ruchem jednostajnie przyspieszonym
γ
ϑ
( )
(
)
(
)
t
t
t
c t
t
p
p
p
=
−
+
−
1
2
0
2
Przechodząc na zmienną niemianowaną
ξ
oraz wykorzystując związek
m
a
l
v
0
6
,
3
ψ
=
⋅
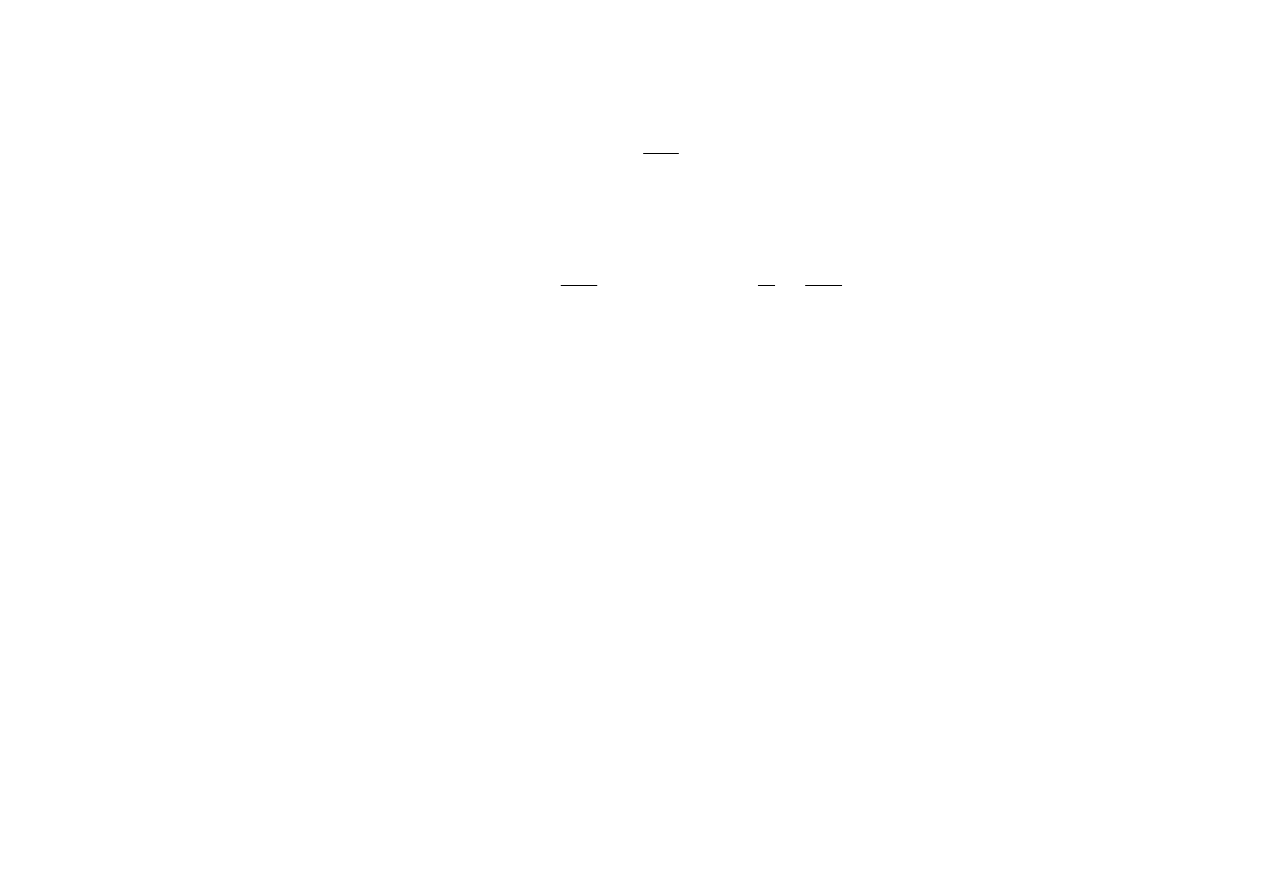
Obrót nadwozia musi być kontrolowany, gdyż powinien on
doprowadzić do uzyskania stałego kąta przechyłu
γ
0
na łuku kołowym.
ϑ ξ
ϑ
ψ
ξ ξ
( )
(
)
=
+
−
p
m
p
c
a
0
0
γ ξ
ψ
ϑ ξ ξ
ψ
ξ ξ
( )
(
)
(
)
=
−
+
−
a
c
a
m
p
p
m
p
0
0
0
2
1
2
doprowadzić do uzyskania stałego kąta przechyłu
γ
0
na łuku kołowym.
Stąd parametry funkcji obrotu nie są dowolne, lecz muszą być tak
dobrane, żeby spełniony został warunek:
dla
ξ
= 1 ,
γ
(
ξ
) =
γ
0
.
Warunek ten sprawia, że pomiędzy parametrami funkcji obrotu musi
występować zależność funkcyjna.
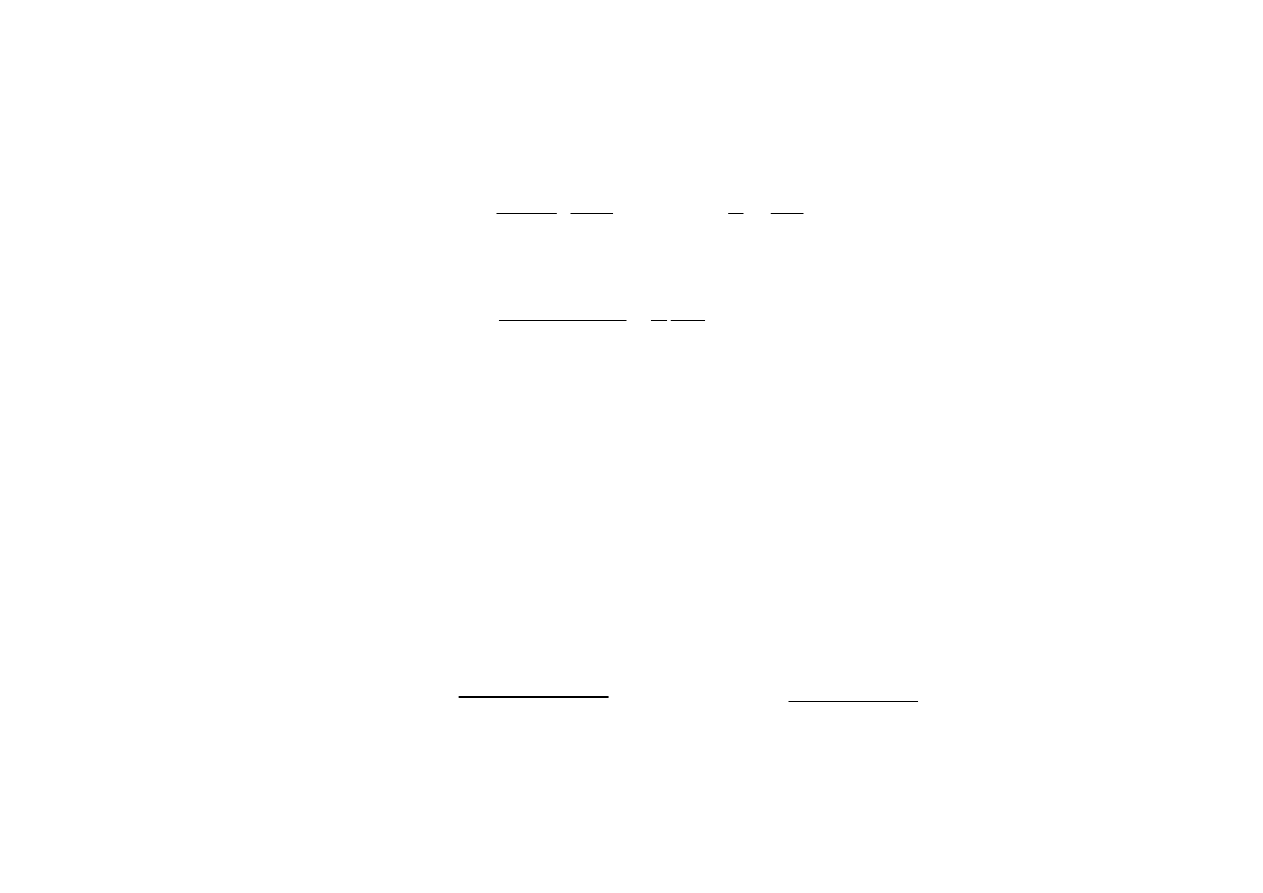
Związek ten można zapisać dwojako:
ϑ
ξ
ψ
ψ
ξ
p
p
m
m
m
p
ga
a
a
c
a
=
−
−
−
−
1
1
1
2
1
0
0
0
0
2
(
)
(
)
ϑ
ψ
ψ
p
m
m
p
m
p
a
a
g a
a
c
a
a
=
−
−
−
−
0
0
0
0
1
2
(
)
(
)
(
)
Obrót nadwozia odbywa się w sposób jednostajnie przyspieszony (lub
jednostajny), płynnie w całym przedziale, muszą być więc spełnione
Wynikają z nich górne ograniczenia
jednostajny), płynnie w całym przedziale, muszą być więc spełnione
jednocześnie dwa warunki:
c
0
0
≥
ϑ
p
≥
0
c
a
a
g a
a
m
m
p
0
0
2
0
2
2
≤
−
−
ψ
(
)
(
)
ϑ
ψ
p
m
m
p
a
a
g a
a
≤
−
−
0
0
(
)
(
)
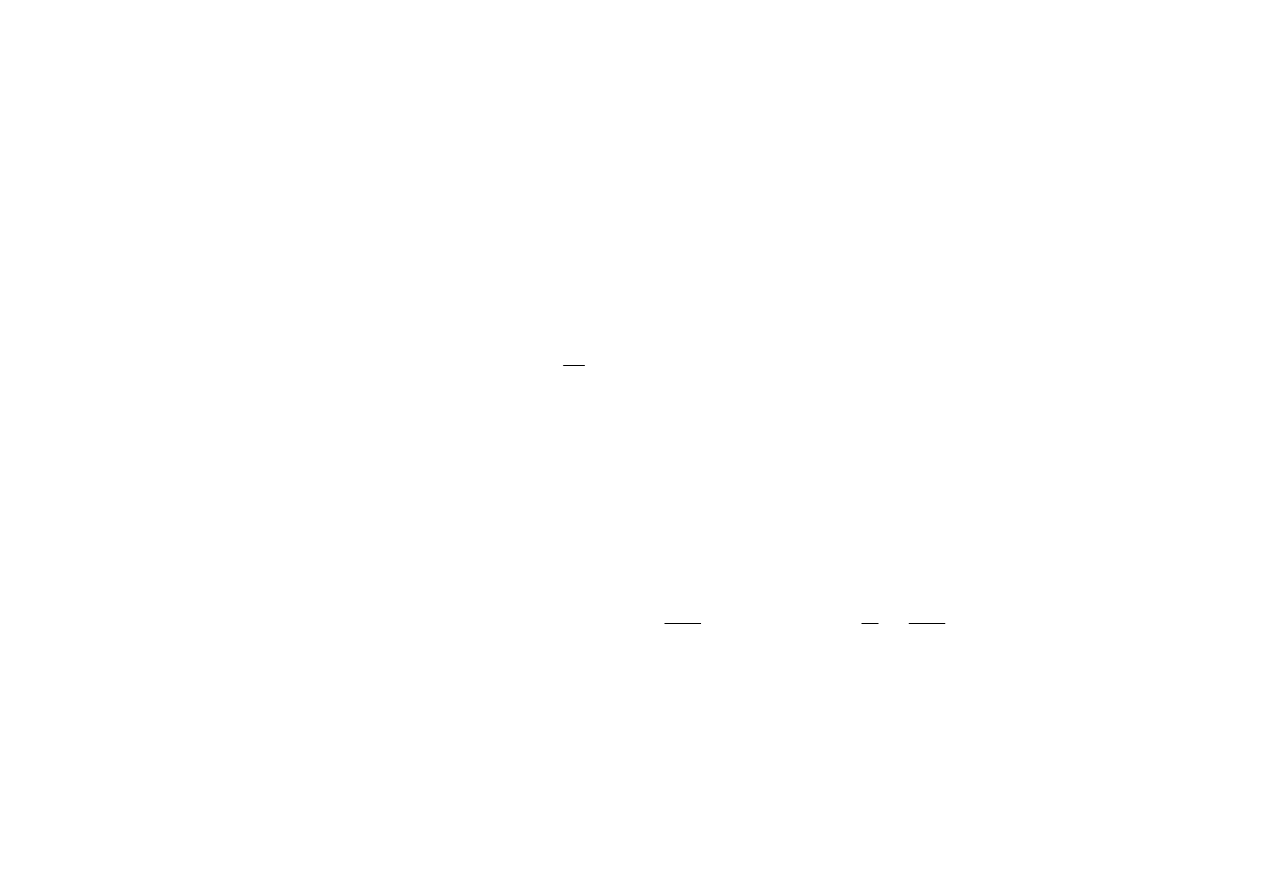
Przyspieszenia a
n
(
ξξξξ
) na odcinku obrotu nadwozia
Wzór na przyspieszenie a
n
(
ξ
) na odcinku
(
]
ξ
ξ
∈
p
,1
wynika z zależności:
[
]
)
(
)
(
1
)
(
ξ
ξ
ξ
γ
n
d
a
a
g
−
=
)
(
)
(
)
(
ξ
γ
ξ
ξ
⋅
−
=
g
a
a
d
n
a
a
g
a
c
a
n
m
m
p
p
m
p
( )
(
)
(
)
ξ
ξ
ψ
ϑ ξ ξ
ψ
ξ ξ
=
−
−
+
−
0
0
0
2
1
2

Funkcja a
n
(
ξ
) , z założenia, powinna być funkcją rosnącą (a w każdym
razie
−
nie malejącą) w przedziale
Powyższe wyrażenie maleje w sposób liniowy ze wzrostem
ξ
,
osiągając minimum dla
ξ
= 1. Wystarczy więc sprawdzić postawiony
warunek na końcu krzywej przejściowej.
(
]
ξ
p
,1
0
)
(
)
(
0
0
0
≥
−
+
−
=
p
m
p
m
m
n
a
c
a
g
a
a
d
d
ξ
ξ
ψ
ϑ
ψ
ξ
ξ
ϑ
ψ
ψ
p
m
p
c
a
a
g
+
−
≤
0
0
0
(
)
c
a
a
g a
a
p
m
p
0
0
2
0
2
2
≤
−
−
ψ
(
)
(
)
ϑ
ψ
p
m
m
p
p
m
p
g
a
a
a
a
a
a
a
a
≥
−
−
−
−
−
0
0
0
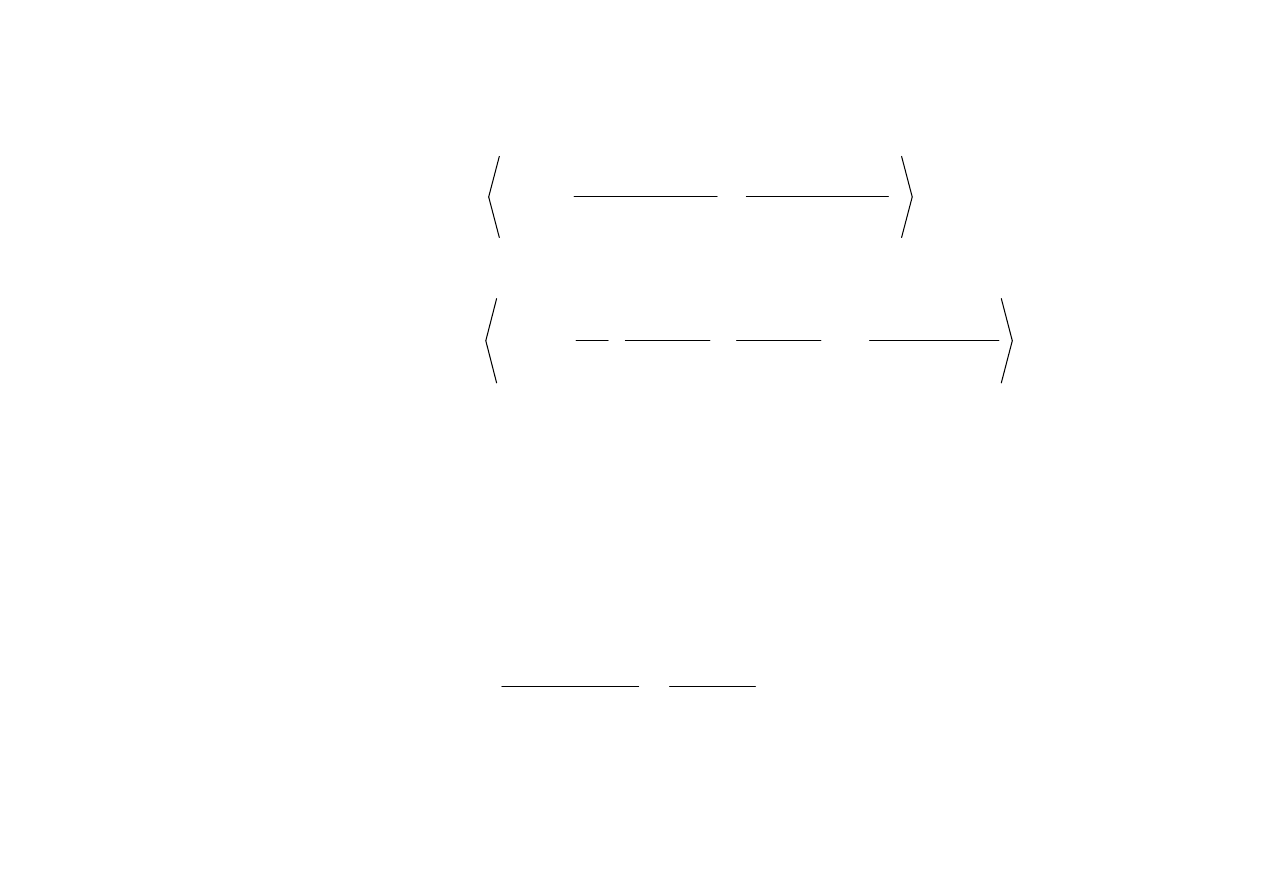
−
−
−
−
∈
2
0
2
0
2
0
2
0
0
)
(
)
(
2
,
)
(
)
(
2
min
;
0
p
m
p
p
m
m
a
a
g
a
a
a
a
g
a
a
c
ψ
ψ
)
(
)
(
;
,
0
max
0
0
0
0
0
p
m
m
p
m
p
p
m
m
p
a
a
g
a
a
a
a
a
a
a
a
a
a
g
−
−
−
−
−
−
−
∈
ψ
ψ
ϑ
Przypadek jednostajnego obrotu nadwozia
W przypadku c
0
= 0 obrót nadwozia na krzywej przejściowej odbywa
się ze stałą prędkością:
Przypadek jednostajnego obrotu nadwozia
ϑ
ψ
γ ψ
ϑ
0
0
0
0
0
=
−
−
=
−
≤
(
)
(
)
a
a
g a
a
a
a
m
m
p
m
p
dop
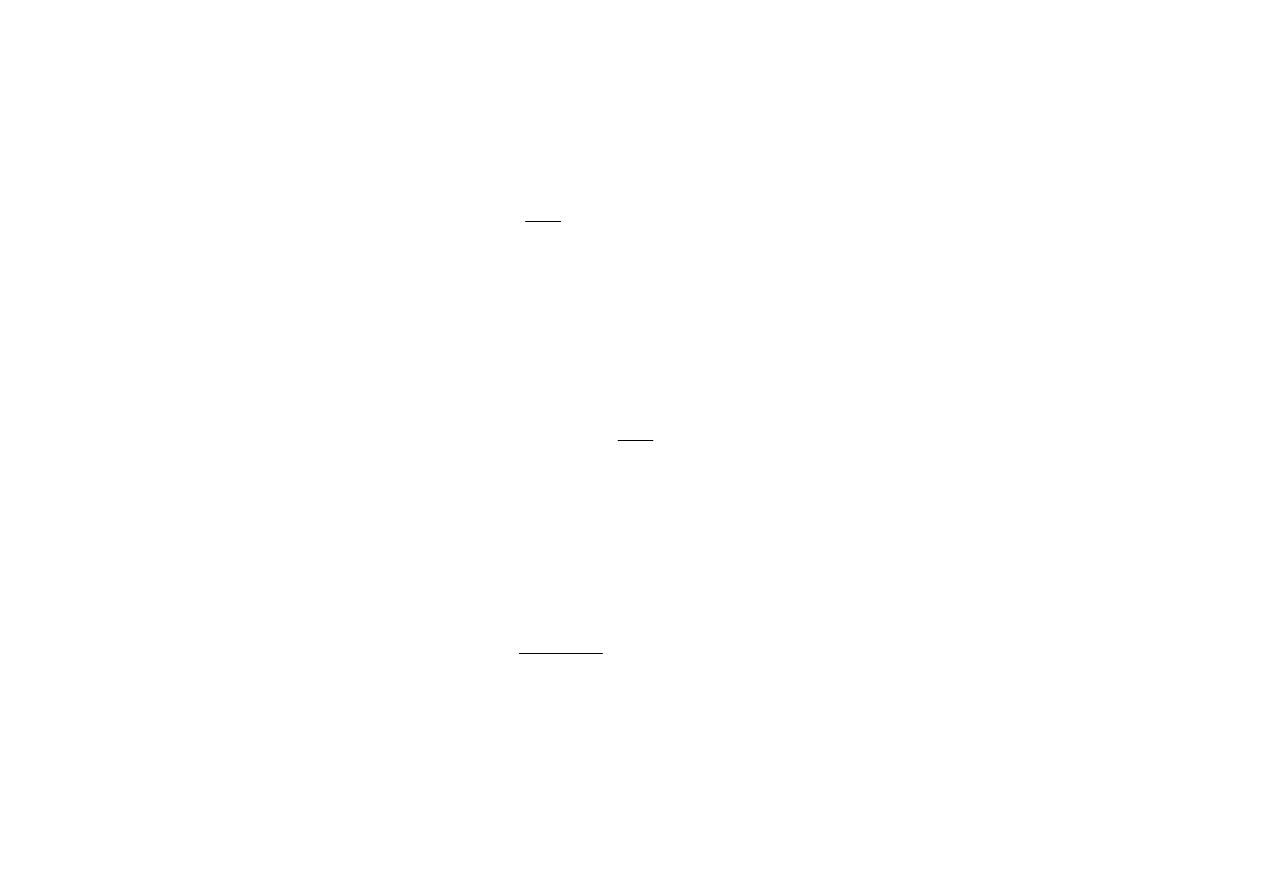
W sposób liniowy zmienia się również boczne niezrównoważone
przyspieszenie nadwozia.
Kąt obrotu zmienia się wówczas liniowo
γ ξ
ψ
ϑ ξ ξ
( )
(
)
=
−
a
m
p
0
0
a
a
g
a
n
m
m
p
( )
(
)
ξ
ξ
ψ
ϑ ξ ξ
=
−
−
0
a
a
g
n
m
p
( )
(
)
ξ
ξ
ψ
ϑ ξ ξ
=
−
−
0
0
Warunek na prędkość przyrostu przyspieszenia dla nadwozia (która to
prędkość jest wartością stałą)
ψ
ψ
ψ
n
p
m
p
dop
a
a
a
a
=
−
−
≤
0
0
jest spełniony zawsze, gdyż w przypadku wystąpienia obrotu
nadwozia
.
a
a
m
>
0

Prędkość obrotu nadwozia wynosi
Dla taboru z przechylnym nadwoziem najbardziej niekorzystny będzie
przypadek a
p
= a
0
. Łatwo wykazać, że przypadek ten może wystąpić tylko
przy jednostajnym obrocie nadwozia.
ϑ
ψ
ϑ
0
0
=
≤
g
dop
Kąt obrotu nadwozia narasta liniowo
a przyspieszenie jest na całym odcinku obrotu nadwozia wielkością
stałą.
γ ξ
ξ ξ
( )
(
)
=
−
a
g
m
p
a
a
n
( )
ξ
=
0
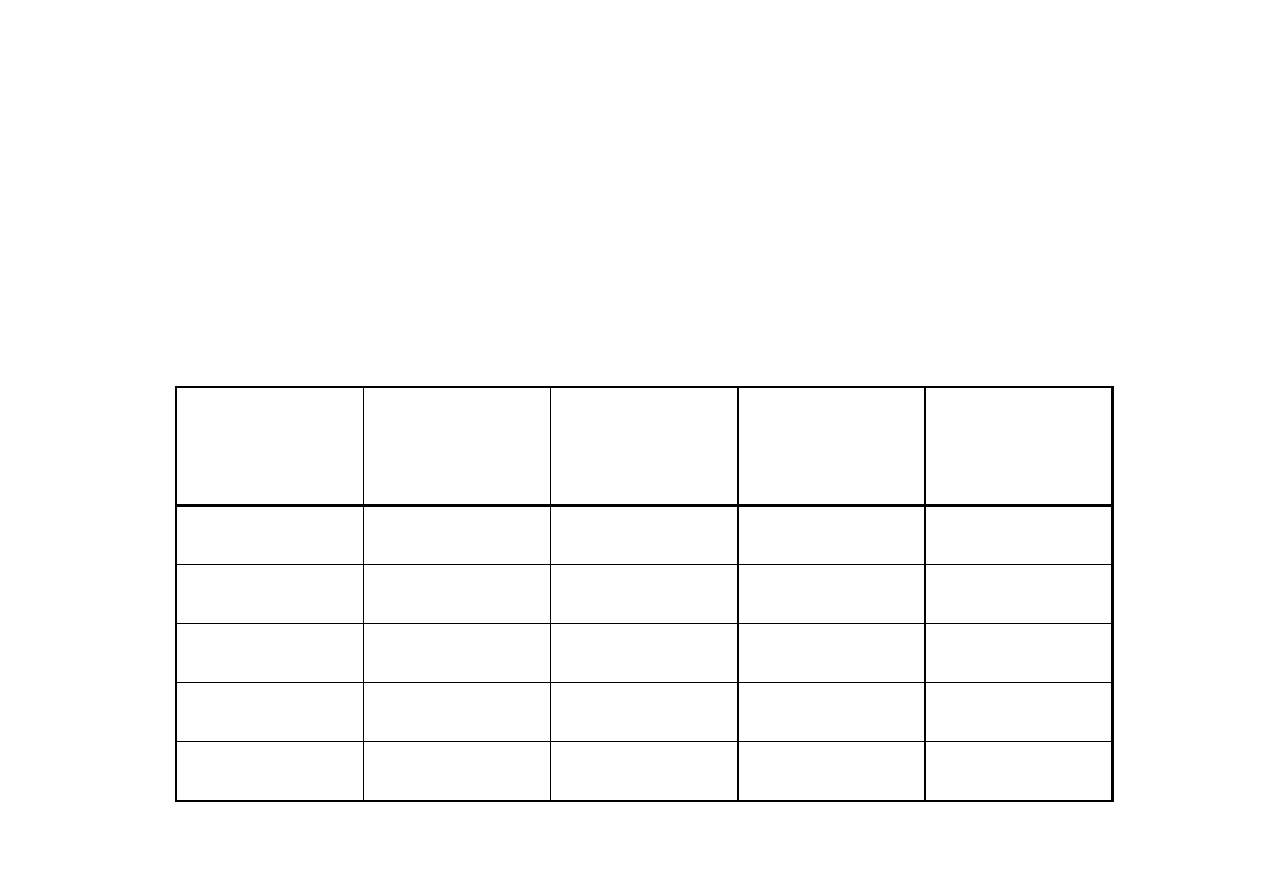
W tabeli przedstawiono wyniki obliczeń parametrów
charakteryzujących obrót nadwozia. Przyjęto następujące dane
wyjściowe: a
m
= 2,0 m/s
2
, a
0
= 0,6 m/s
2
,
ψ
0
= 0,5 m/s
3
; dla tych
danych
γ
0
= 8,12
0
.
Przykłady
a
p
min c
0
max c
0
min
max
ϑ
p
ϑ
p
ϑ
p
p
[m/s
2
]
0
[rad/s
2
]
0
[rad/s
2
]
[rad/s]
[rad/s]
0,20
0
0,00629
0,0283
0,0396
0,30
0
0,00529
0,0330
0,0420
0,40
0
0,00398
0,0382
0,0446
0,50
0
0,00227
0,0442
0,0476
0,60
0
0
0,0510
0,0510
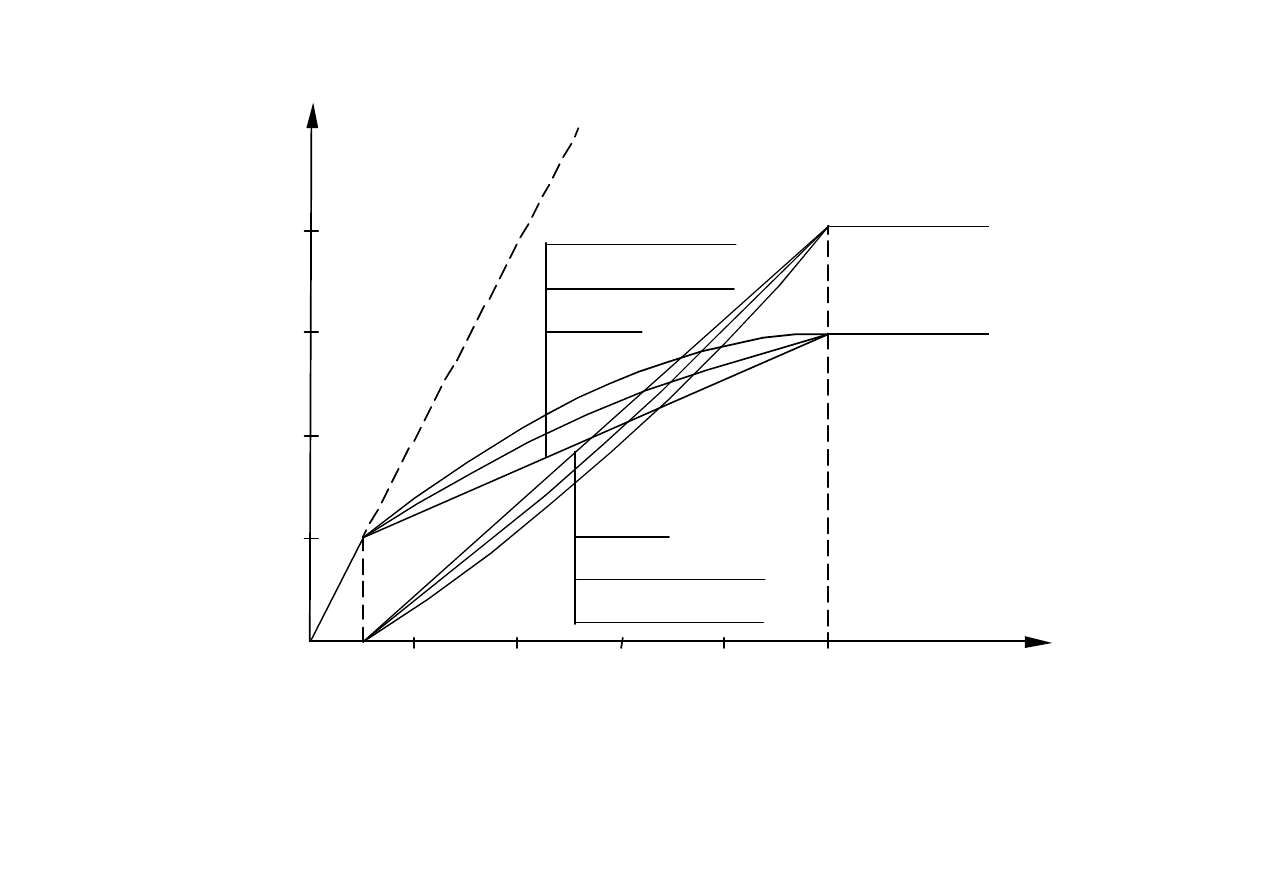
c
0
= 0,03 rad/s
2
c
0
= 0,06 rad/s
2
c
0
= 0
a
0
= 0,6 m/s
2
γ
0
= 8,12
0
a
m
= 2,0 m/s
2
a
[m/s
2
]
0,8
0,6
0,4
γ
[deg]
8
6
4
c
0
= 0,03 rad/s
2
c
0
= 0,06 rad/s
2
c
0
= 0
a
p
= 0,2 m/s
2
0,4
0,2
0,0
4
2
0
0,2 0,4 0,6
0,8
1,0
ξ
Wykresy kąta obrotu nadwozia
γ
(
ξ
) oraz niezrównoważonego
przyspieszenia bocznego a
n
(
ξ
) dla różnych wartości parametru c
0
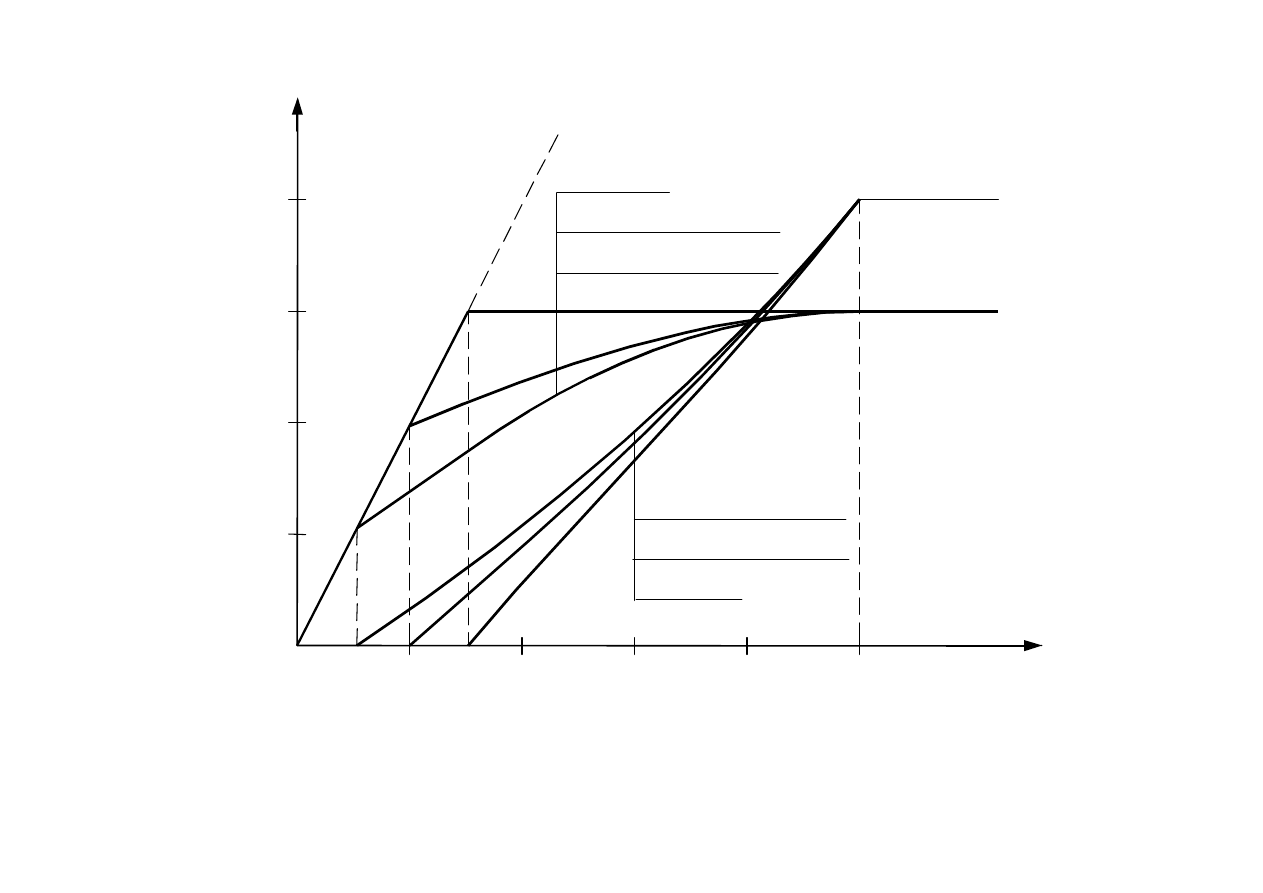
c
0
= 0,00629 rad/s
2
c
0
= 0,00398 rad/s
2
c
0
= 0
γ
0
= 8,12
0
a
0
= 0,6 m/s
2
a
m
= 2,0 m/s
2
γ
[deg]
a
[m/s
2
]
8
6
4
0,8
0,6
0,4
a
m
= 2,0 m/s
c
0
= 0,00398 rad/s
2
c
0
= 0,00629 rad/s
2
c
0
= 0
2
0,2
0
0,2
0,4
0,6
0,8
1,0
ξ
0,0
Wykresy kąta obrotu nadwozia
γ
(
ξ
) oraz niezrównoważonego
przyspieszenia bocznego a
n
(
ξ
) dla różnych wartości przyspieszenia a
p
i maksymalnych wartości c
0
c
0
= 0,0063 rad/s
2
c
0
= 0,0104 rad/s
2
c
0
= 0,0204 rad/s
2
a
m
= 2,0 m/s
2
a
m
= 1,6 m/s
2
a
m
= 1,2 m/s
2
γ
0
= 8,12
0
γ
0
= 5,83
0
γ
= 3,51
0
a
[m/s
2
]
γ
[deg]
10
8
6
4
2,0
1,6
1,2
0,8
a
m
= 0,6 m/s
2
a
p
= 0,2 m/s
2
γ
0
= 3,51
0
4
2
0
0,8
0,4
0,2
0,4
0,6
0,8
1,0
ξ
0,0
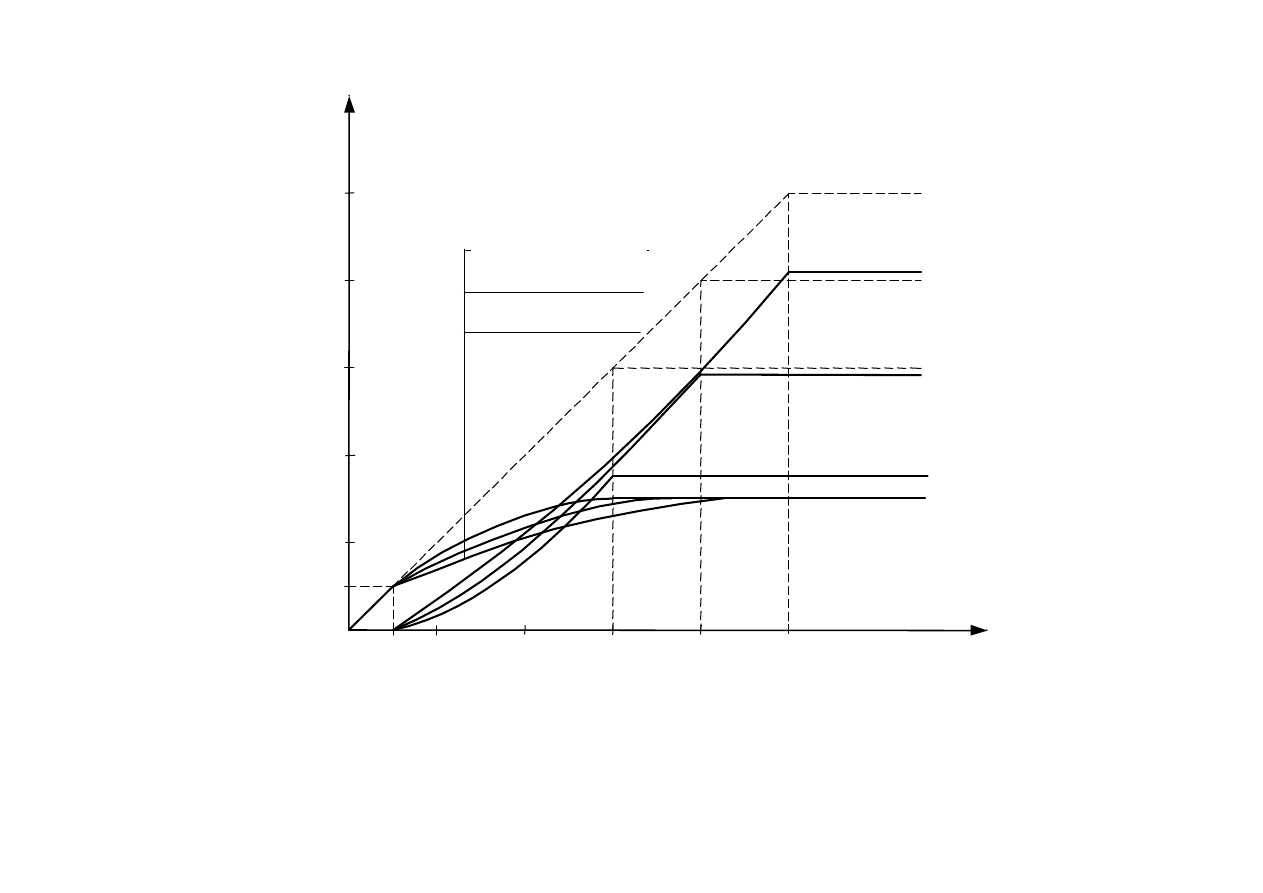
Wykresy kąta obrotu nadwozia
γ
(
ξ
) oraz niezrównoważonego
przyspieszenia bocznego a
n
(
ξ
) dla różnych wartości przyspieszenia
a
m
i maksymalnych wartości c
0
Wyszukiwarka
Podobne podstrony:
DROGI SZYNOWE PREZ 5
DROGI SZYNOWE PREZ 9
DROGI SZYNOWE PREZ 2
DROGI SZYNOWE PREZ 8
DROGI SZYNOWE PREZ 4
DROGI SZYNOWE PREZ 6
DROGI SZYNOWE PREZ 1
DROGI SZYNOWE PREZ 3
DROGI SZYNOWE PREZ 5 id 142683 Nieznany
DROGI SZYNOWE PREZ 5
DROGI SZYNOWE PREZ 2
DROGI SZYNOWE PREZ 7
DROGI SZYNOWE PREZ 9
DROGI SZYNOWE PREZ 8
Przykład opisu, Budownictwo PK, Drogi szynowe
opis kladki, Przodki IL PW Inżynieria Lądowa budownictwo Politechnika Warszawska, Semestr 4, Inżynie
Wykład IK Drogi Szynowe 2000
więcej podobnych podstron