1

Praca domowa

Metody numeryczne

Kamil Żyłko

Wydział Inżynierii Produkcji

Automatyka i robotyka

Studia magisterskie stacjonarne

Warszawa 2013

2

1.

Treść zadania Z90.

Dana jest funkcja zadana poniższą tablicą:

gdzie x

i

jest argumentem funkcji a f(x

i

) jej wartością, i=1,…, 21. Wyznacz:

a)

wielomiany interpolacyjne Newtona i Lagrange’a szóstego stopnia w przedziale [-1.5 , 1.5],

b)

wielomian interpolacyjny składający się z funkcji sklejanych trzeciego i/lub czwartego stopnia

na przedziale [-5, 5].

Przedstaw graficznie na jednym wykresie wielomiany z punktów a) i b). Porównaj błąd interpolacji w
przedziale [-1,5, 1,5].

2.

Opis metod numerycznych wykorzystanych do rozwiązania zadania.

Interpolacja stosowana jest w celu określenia wartości funkcji między znanymi punktami jej

przebiegu. Stosuje się przybliżanie funkcji za pomocą wielomianu odpowiednio wysokiego stopnia.

Można to wyznaczyć dzięki znanym wartościom funkcji w danych punktach. Tych znanych punktów

jest n+1, natomiast wyznaczany wielomian może być stopnia co najwyżej n.

a)

Metoda Newtona

Wielomian interpolacyjny metodą Newtona można zapisać jako:

ݓሺݔሻ = ෍ ܽ

௜

௡

௜ୀ଴

ෑሺݔ − ݔ

௝

௜ିଵ

௝ୀ଴

ሻ

= ܽ

଴

+ ܽ

ଵ

ሺݔ − ݔ

଴

ሻ + ܽ

ଶ

ሺݔ − ݔ

ଵ

ሻሺݔ − ݔ

଴

ሻ + ⋯ + ܽ

௡

ሺݔ − ݔ

௡ିଵ

ሻ … ሺݔ − ݔ

ଵ

ሻሺݔ − ݔ

଴

ሻ

Do wyznaczenia wielomianu można wykorzystać metodę interpolacji Newtona. W związku z tym,

że należy wyznaczyć wielomian w przedziale [-1.5 , 1.5], a punkty x

i

są w równych odległościach,

należy zastosować wzory interpolacyjne Newtona dla równoodległych wartości argumentu.

x

i

-5

-4,5

-4

-3,5

-3

-2,5

-2

f(x

i

)

1,536098

2,318505

3,663004

6,12323

10,98901

21,59244

47,61905

x

i

-1,5

-1

-0,5

0

0,5

1

1,5

f(x

i

)

120,3008

333,3333

761,9048

1000

761,9048

333,3333

120,3008

x

i

2

2,5

3

3,5

4

4,5

5

f(x

i

)

47,61905

21,59244

10,98901

6,12323

3,663004

2,318505

1,536098

3

W pierwszej kolejności mając dane wartości funkcji dla argumentów będących w równych

odległościach wyznacza się różnice między wartościami funkcji dla argumentów sąsiadujących ze

sobą. Można zapisać to jako:

∆ݕ

଴

= ݕ

ଵ

− ݕ

଴

∆ݕ

ଵ

= ݕ

ଶ

− ݕ

ଵ

…………………………..

∆ݕ

௡ିଵ

= ݕ

௡

− ݕ

௡ିଵ

Następnie wylicza się różnice między wyznaczonymi przed chwilą różnicami:

∆

ଶ

ݕ

଴

= ∆ݕ

ଵ

− ∆ݕ

଴

∆

ଶ

ݕ

ଵ

= ∆ݕ

ଶ

− ∆ݕ

ଵ

………………….

∆

ଶ

ݕ

௡ିଶ

= ∆ݕ

௡ିଵ

− ∆ݕ

௡ିଶ

Powyższą czynność powtarza się aż do momentu, w którym zostaną wyliczone wszystkie różnice

różnic i nie będzie możliwości wyznaczenia kolejnej. Ostatnia wyznaczona różnica zapisana jest jako:

∆

௡

ݕ

଴

= ∆

௡ିଵ

ݕ

଴

− ∆

௡ିଵ

ݕ

௡ି௡ିଵ

Po wyliczeniu różnic należy przejść do wyznaczania wielomianu opisanego wzorem:

ܹ݊ሺݔሻ = ݕ

଴

+ ݍ ∗ ∆ݕ

଴

+

ݍሺݍ − 1ሻ ∗ ∆

ଶ

ݕ

଴

2!

+ ⋯ +

ݍሺݍ − 1ሻ … ൫ݍ − ሺ݊ − 1ሻ൯ ∗ ∆

௡

ݕ

଴

݊!

ݍ =

ݔ

ݔ

ଵ

− ݔ

଴

b)

Metoda Lagrange’a

Wielomian interpolacyjny metodą Lagrange’a można zapisać jako:

ݓ

௙

ሺݔሻ = ෍ ݂ሺݔ

௝

௡

௝ୀ଴

ሻ݈

௝

ሺݔሻ

= ෍ ݂ሺݔ

௝

௡

௝ୀ଴

ሻ ∗

ሺݔ − ݔ

଴

ሻሺݔ − ݔ

ଵ

ሻ … ൫ݔ − ݔ

௝ିଵ

൯൫ݔ − ݔ

௝ାଵ

൯ … ሺݔ − ݔ

௡

ሻ

൫ݔ

௝

− ݔ

଴

൯൫ݔ

௝

− ݔ

ଵ

൯ … ൫ݔ

௝

− ݔ

௝ିଵ

൯൫ݔ

௝

− ݔ

௝ାଵ

൯ … ൫ݔ

௝

− ݔ

௡

൯

c)

Interpolacja za pomocą funkcji sklejanych

Niech f(x)

∈ C <a;b>. s(x) ∈ S

3

(

∆

n

) jest funkcją sklejaną stopnia trzeciego dla funkcji f(x) jeżeli

s(x

i

)=f(x

i

)=y

i.

Interpolacja funkcjami sklejanymi polega na podziale przedziału <a;b> na tyle kolejnych

przedziałów, aby każdy z nich zawierał najwyżej kilka argumentów. Punkty wspólne

4

utworzonych przedziałów nazywane są węzłami interpolacji. W tym samym węźle, czyli

stanowiącym początek jednego przedziału i koniec drugiego przedziału funkcja musi

przyjmować takie same wartości.

W każdym z tych przedziałów interpoluje się funkcję wielomianem interpolacyjnym.

3.

Obliczenia numeryczne metodami:

a)

Newtona

W związku z tym, że argumenty funkcji są równoodległe oraz dlatego, że wartości

przyjmowane przez funkcję są takie same dla argumentów ze znakiem + i ze znakiem –

należy wyznaczyć wielomian metodą Newtona dla równoodległych wartości argumentu

jedynie dla argumentów od 0 do +1,5.

W tym przedziale podane są 4 argumenty, więc wyznaczony wielomian będzie miał

postać trzeciego stopnia.

x

y

∆y

∆

ଶ

y

∆

ଷ

y

0

1000

-238.0952

0.5

761.9048

-190.4763

-428.5715

406.0153

1

333.3333

215.539

-213.0325

1.5

120.3008

ܹ݊ሺݔሻ = ݕ

଴

+ ݍ ∗ ∆ݕ

଴

+

ݍሺݍ − 1ሻ ∗ ∆

ଶ

ݕ

଴

2!

+

ݍሺݍ − 1ሻሺݍ − 2ሻ ∗ ∆

ଷ

ݕ

଴

3!

=

= 1000 + ݍ ∗ −238.0952 +

ݍሺݍ − 1ሻ ∗ −190.4763

2!

+

ݍሺݍ − 1ሻሺݍ − 2ሻ ∗ 406.0153

3!

=

= 1000 + ݍ ∗ −238.0952 + ݍሺݍ − 1ሻ ∗ −95.23815 + ݍሺݍ − 1ሻሺݍ − 2ሻ ∗ 67.66921667

ݍ =

ݔ

ݔ

ଵ

− ݔ

଴

=

ݔ

0.5 = 2ݔ

Po podstawieniu do wzoru

ܹ݊ሺݔሻ wartości 2x zamiast q otrzymujemy:

ܹሺݔሻ

= 2ݔሺ2ݔ − 1ሻሺ2ݔ − 2ሻ67.66921667 + 2ݔሺ2ݔ − 1ሻሺ−95.23815ሻ

+ 2ݔሺ−238.0952ሻ + 1000 =

= ሺ4ݔ

ଶ

− 2ݔሻሺ2ݔ − 2ሻ67.66921667 + ሺ4ݔ

ଶ

− 2ݔሻሺ−95.23815ሻ − 476.1904ݔ + 1000 =

= ሺ8ݔ

ଷ

− 8ݔ

ଶ

− 4ݔ

ଶ

+ 4ݔሻ67.66921667 − 380.9526ݔ

ଶ

+ 190.4763ݔ − 476.1904ݔ + 1000 =

= 541.3537334ݔ

ଷ

− 541.3537334ݔ

ଶ

− 270.6768667ݔ

ଶ

+ 270.6768667ݔ − 380.9526ݔ

ଶ

− 285.7141ݔ + 1000 =

= 541.3537334ݔ

ଷ

− 1192.9832ݔ

ଶ

− 15.0372333ݔ + 1000

5

Ze względu na to, że wartości przyjmowane przez funkcję są takie same dla argumentów ze

znakiem + i ze znakiem -, postać wielomianu wyznaczonego metodą Newtona jest następująca:

W(x)=

|541.3537334ݔ

ଷ

| − |1192.9832ݔ

ଶ

| − |15.0372333ݔ| + 1000

b)

Lagrange’a

x

0

0.5

1

1.5

y

1000

761.9048

333.3333

120.3008

ݓ

௙

ሺݔሻ = ෍ ݂ሺݔ

௝

௡

௝ୀ଴

ሻ݈

௝

ሺݔሻ

= ෍ ݂ሺݔ

௝

௡

௝ୀ଴

ሻ ∗

ሺݔ − ݔ

଴

ሻሺݔ − ݔ

ଵ

ሻ … ൫ݔ − ݔ

௝ିଵ

൯൫ݔ − ݔ

௝ାଵ

൯ … ሺݔ − ݔ

௡

ሻ

൫ݔ

௝

− ݔ

଴

൯൫ݔ

௝

− ݔ

ଵ

൯ … ൫ݔ

௝

− ݔ

௝ିଵ

൯൫ݔ

௝

− ݔ

௝ାଵ

൯ … ൫ݔ

௝

− ݔ

௡

൯

=

= 1000 ∗

ሺݔ − 0.5ሻሺݔ − 1ሻሺݔ − 1.5ሻ

ሺ0 − 0.5ሻሺ0 − 1ሻሺ0 − 1.5ሻ +

+761.9048 ∗

ሺݔ − 0ሻሺݔ − 1ሻሺݔ − 1.5ሻ

ሺ0.5 − 0ሻሺ0.5 − 1ሻሺ0.5 − 1.5ሻ +

+333.3333 ∗

ሺݔ − 0ሻሺݔ − 0.5ሻሺݔ − 1.5ሻ

ሺ1 − 0ሻሺ1 − 0.5ሻሺ1 − 1.5ሻ +

+120.3008 ∗

ሺݔ − 0ሻሺݔ − 0.5ሻሺݔ − 1ሻ

ሺ1.5 − 0ሻሺ1.5 − 0.5ሻሺ1.5 − 1ሻ =

= ሺ1000ݔ − 500ሻ ∗

ሺݔ − 1ሻሺݔ − 1.5ሻ

0.5ሺ−1.5ሻ

+

+761.9048ݔ ∗

ሺݔ − 1ሻሺݔ − 1.5ሻ

−0.5ሺ−0.5ሻ +

+333.3333ݔ ∗

ሺݔ − 0.5ሻሺݔ − 1.5ሻ

0.5ሺ−0.5ሻ

+

+120.3008ݔ ∗

ሺݔ − 0.5ሻሺݔ − 1ሻ

1.5ሺ0.5ሻ

=

= ሺ1000ݔ

ଶ

− 1500ݔ + 500ሻ ∗

ሺݔ − 1.5ሻ

−0.75 +

+ሺ761.9048ݔ

ଶ

− 761.9048ݔሻ ∗

ሺݔ − 1.5ሻ

0.25 +

+ሺ333.3333ݔ

ଶ

− 166.66665ݔሻ ∗

ሺݔ − 1.5ሻ

−0.25 +

+ሺ120.3008ݔ

ଶ

− 60.1504ݔሻ ∗

ሺݔ − 1ሻ

0.75 =

= −1333.333333ݔ

ଷ

+ 4000ݔ

ଶ

− 3666.666667ݔ + 1000 +

+3047.6192ݔ

ଷ

− 3047.6192ݔ

ଶ

− 4571.4288ݔ

ଶ

+ 4571.4288ݔ −

−1333.3332ݔ

ଷ

+ 666.6666ݔ

ଶ

+ 1999.9998ݔ

ଶ

− 999.9999ݔ +

+160.4010667ݔ

ଷ

− 80.20053333ݔ

ଶ

− 160.4010667ݔ

ଶ

+ 80.20053333ݔ =

= 541.3537337ݔ

ଷ

− 1192.9832ݔ

ଶ

− 15.03723367ݔ + 1000

6

Powyższa postać wielomianu ma tylko zastosowanie dla funkcji w przedziale [0, 1.5] z kolei

dla funkcji w przedziale [-1.5, 1.5]:

ݓ

௙

ሺݔሻ = |541.3537337ݔ

ଷ

| − |1192.9832ݔ

ଶ

| − |15.03723367ݔ| + 1000

c)

funkcji sklejanych

W przedziale [-5;5] znane są wartości funkcji dla 21 argumentów. W związku z tym można

dokonać podziału na 6 przedziałów, w dwóch z nich wyznaczone zostaną wielomiany

czwartego stopnia, zaś w czterech z nich wielomiany trzeciego stopnia.

Tak więc będą to przedziały: [-5;-3], [-3;-1.5], [-1.5;0], [0;1.5], [1.5;3], [3;5].

Interpolacja funkcji w przedziale [-5;-3]

x

-5

-4.5

-4

-3.5

-3

y

1,536098

2,318505

3,663004

6,12323

10,98901

ݓ

௙

ሺݔሻ = ෍ ݂ሺݔ

௝

௡

௝ୀ଴

ሻ݈

௝

ሺݔሻ

= ෍ ݂ሺݔ

௝

௡

௝ୀ଴

ሻ ∗

ሺݔ − ݔ

଴

ሻሺݔ − ݔ

ଵ

ሻ … ൫ݔ − ݔ

௝ିଵ

൯൫ݔ − ݔ

௝ାଵ

൯ … ሺݔ − ݔ

௡

ሻ

൫ݔ

௝

− ݔ

଴

൯൫ݔ

௝

− ݔ

ଵ

൯ … ൫ݔ

௝

− ݔ

௝ିଵ

൯൫ݔ

௝

− ݔ

௝ାଵ

൯ … ൫ݔ

௝

− ݔ

௡

൯

=

= 1.536098 ∗

ሺݔ + 4.5ሻሺݔ + 4ሻሺݔ + 3.5ሻሺݔ + 3ሻ

ሺ−5 + 4.5ሻሺ−5 + 4ሻሺ−5 + 3.5ሻሺ−5 + 3ሻ +

+2.318505 ∗

ሺݔ + 4ሻሺݔ + 3.5ሻሺݔ + 3ሻሺݔ + 5ሻ

ሺ−4.5 + 4ሻሺ−4.5 + 3.5ሻሺ−4.5 + 3ሻሺ−4.5 + 5ሻ +

+3.663004 ∗

ሺݔ + 3.5ሻሺݔ + 3ሻሺݔ + 5ሻሺݔ + 4.5ሻ

ሺ−4 + 3.5ሻሺ−4 + 3ሻሺ−4 + 5ሻሺ−4 + 4.5ሻ +

+6.12323 ∗

ሺݔ + 3ሻሺݔ + 5ሻሺݔ + 4.5ሻሺݔ + 4ሻ

ሺ−3.5 + 3ሻሺ−3.5 + 5ሻሺ−3.5 + 4.5ሻሺ−3.5 + 4ሻ +

+10.98901 ∗

ሺݔ + 3ሻሺݔ + 5ሻሺݔ + 4.5ሻሺݔ + 4ሻ

ሺ−3.5 + 3ሻሺ−3.5 + 5ሻሺ−3.5 + 4.5ሻሺ−3.5 + 4ሻ =

= ሺ1.536098ݔ

ଶ

+ 13.056833ݔ + 27.649764ሻ ∗

ሺݔ + 3.5ሻሺݔ + 3ሻ

1.5

+

+ሺ2.318505ݔ

ଶ

+ 17.3887875ݔ + 32.45907ሻ ∗

ሺݔ + 3ሻሺݔ + 5ሻ

−0.375

+

+ሺ3.663004ݔ

ଶ

+ 23.809526ݔ + 38.461542ሻ ∗

ሺݔ + 5ሻሺݔ + 4.5ሻ

0.25

+

+ሺ6.12323ݔ

ଶ

+ 30.61615ݔ + 91.84845ሻ ∗

ሺݔ + 4.5ሻሺݔ + 4ሻ

−0.375

+

+ሺ10.98901ݔ

ଶ

+ 87.91208ݔ + 164.83515ሻ ∗

ሺݔ + 4.5ሻሺݔ + 4ሻ

−0.375

=

= ሺ1.536098ݔ

ସ

+ 9.984637ݔ

ଷ

+ 16.129029ݔ

ଶ

+ 13.056833ݔ

ଷ

+ 84.8694145ݔ

ଶ

+ 137.0967465ݔ + 27.649764ݔ

ଶ

+ 179.723466ݔ + 290.322522ሻ ∗

1

1.5 +

7

+ሺ2.318505ݔ

ସ

+ 18.54804ݔ

ଷ

+ 34.777575ݔ

ଶ

+ 17.3887875ݔ

ଷ

+ 139.1103ݔ

ଶ

+ 260.8318125ݔ + 32.45907ݔ

ଶ

+ 259.67256ݔ + 486.88605ሻ ∗

1

−0.375 +

+ሺ3.663004ݔ

ସ

+ 34.798538ݔ

ଷ

+ 82.41759ݔ

ଶ

+ 23.809526ݔ

ଷ

+ 226.190497ݔ

ଶ

+ 535.714335ݔ + 38.461542ݔ

ଶ

+ 365.384649ݔ + 865.384695ሻ ∗

1

0.25 +

+ሺ6.12323ݔ

ସ

+ 52.047455ݔ

ଷ

+ 110.21814ݔ

ଶ

+ 30.61615ݔ

ଷ

+ 260.237275ݔ

ଶ

+ 551.0907ݔ + 91.84845ݔ

ଶ

+ 780.711825ݔ + 1653.2721ሻ ∗

1

−0.375 +

+ሺ10.98901ݔ

ସ

+ 93.406585ݔ

ଷ

+ 197.80218ݔ

ଶ

+ 87.91208ݔ

ଷ

+ 747.25268ݔ

ଶ

+ 1582.41744ݔ + 164.83515ݔ

ଶ

+ 1401.098775ݔ + 2967.0327ሻ

∗

1

−0.375 =

= 1.024065333ݔ

ସ

+ 15.36098ݔ

ଷ

+ 85.76547167ݔ

ଶ

+ 211.213475ݔ + 193.548348 +

−6.18268ݔ

ସ

− 95.83154ݔ

ଷ

− 550.25852ݔ

ଶ

− 1388.01166ݔ − 1298.3628 +

+14.652016ݔ

ସ

+ 234.432256ݔ

ଷ

+ 1388.278516ݔ

ଶ

+ 3604.395936ݔ + 3461.53878 +

−16.32861333ݔ

ସ

− 220.43628ݔ

ଷ

− 1232.810307ݔ

ଶ

− 3551.4734ݔ − 4408.7256 +

−29.30402667ݔ

ସ

− 483.51644ݔ

ଷ

− 2959.706693ݔ

ଶ

− 7956.04324ݔ − 7912.0872ሻ =

= −36.13923867ݔ

ସ

− 549.991024ݔ

ଷ

− 3268.731532ݔ

ଶ

− 9079.918889ݔ

− 9964.088472

Interpolacja funkcji w przedziale [0;1.5]

x

0

0,5

1

1,5

y

1000

761,9048

333,3333

120,3008

ݓ

௙

ሺݔሻ = ෍ ݂ሺݔ

௝

௡

௝ୀ଴

ሻ݈

௝

ሺݔሻ

= ෍ ݂ሺݔ

௝

௡

௝ୀ଴

ሻ ∗

ሺݔ − ݔ

଴

ሻሺݔ − ݔ

ଵ

ሻ … ൫ݔ − ݔ

௝ିଵ

൯൫ݔ − ݔ

௝ାଵ

൯ … ሺݔ − ݔ

௡

ሻ

൫ݔ

௝

− ݔ

଴

൯൫ݔ

௝

− ݔ

ଵ

൯ … ൫ݔ

௝

− ݔ

௝ିଵ

൯൫ݔ

௝

− ݔ

௝ାଵ

൯ … ൫ݔ

௝

− ݔ

௡

൯

=

= 1000 ∗

ሺݔ − 0.5ሻሺݔ − 1ሻሺݔ − 1.5ሻ

ሺ0 − 0.5ሻሺ0 − 1ሻሺ0 − 1.5ሻ +

+761.9048 ∗

ሺݔ − 0ሻሺݔ − 1ሻሺݔ − 1.5ሻ

ሺ0.5 − 0ሻሺ0.5 − 1ሻሺ0.5 − 1.5ሻ +

+333.3333 ∗

ሺݔ − 0ሻሺݔ − 0.5ሻሺݔ − 1.5ሻ

ሺ1 − 0ሻሺ1 − 0.5ሻሺ1 − 1.5ሻ +

+120.3008 ∗

ሺݔ − 0ሻሺݔ − 0.5ሻሺݔ − 1ሻ

ሺ1.5 − 0ሻሺ1.5 − 0.5ሻሺ1.5 − 1ሻ =

= ሺ1000ݔ − 500ሻ ∗

ሺݔ − 1ሻሺݔ − 1.5ሻ

0.5ሺ−1.5ሻ

+

+761.9048ݔ ∗

ሺݔ − 1ሻሺݔ − 1.5ሻ

−0.5ሺ−0.5ሻ +

+333.3333ݔ ∗

ሺݔ − 0.5ሻሺݔ − 1.5ሻ

0.5ሺ−0.5ሻ

+

+120.3008ݔ ∗

ሺݔ − 0.5ሻሺݔ − 1ሻ

1.5ሺ0.5ሻ

=

8

= ሺ1000ݔ

ଶ

− 1500ݔ + 500ሻ ∗

ሺݔ − 1.5ሻ

−0.75 +

+ሺ761.9048ݔ

ଶ

− 761.9048ݔሻ ∗

ሺݔ − 1.5ሻ

0.25 +

+ሺ333.3333ݔ

ଶ

− 166.66665ݔሻ ∗

ሺݔ − 1.5ሻ

−0.25 +

+ሺ120.3008ݔ

ଶ

− 60.1504ݔሻ ∗

ሺݔ − 1ሻ

0.75 =

= −1333.333333ݔ

ଷ

+ 4000ݔ

ଶ

− 3666.666667ݔ + 1000 +

+3047.6192ݔ

ଷ

− 3047.6192ݔ

ଶ

− 4571.4288ݔ

ଶ

+ 4571.4288ݔ −

−1333.3332ݔ

ଷ

+ 666.6666ݔ

ଶ

+ 1999.9998ݔ

ଶ

− 999.9999ݔ +

+160.4010667ݔ

ଷ

− 80.20053333ݔ

ଶ

− 160.4010667ݔ

ଶ

+ 80.20053333ݔ =

= 541.3537337ݔ

ଷ

− 1192.9832ݔ

ଶ

− 15.03723367ݔ + 1000

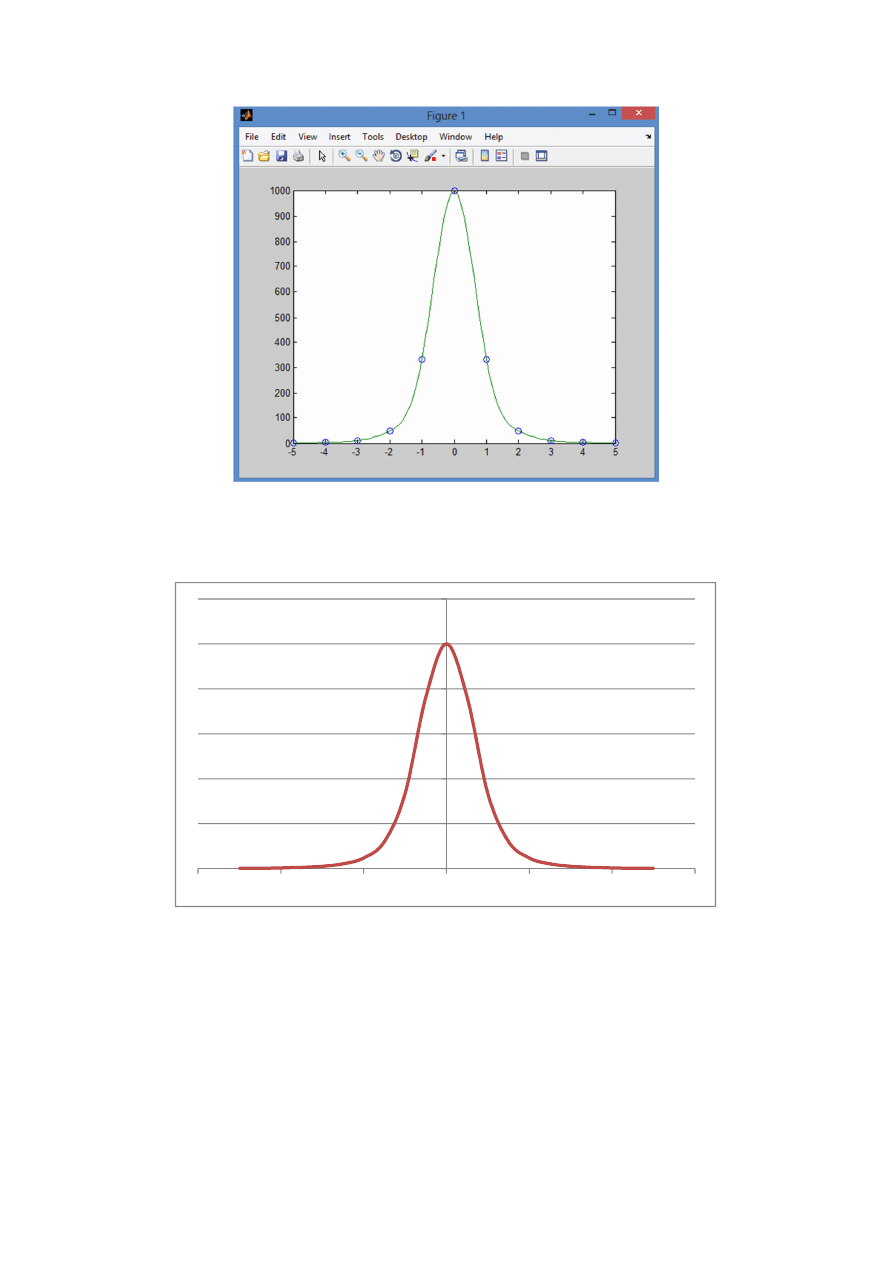
W programie Matlab możliwe jest graficzne przedstawienie rozwiązania metodą funkcji sklejanych.

Umożliwia to wpisanie następujących komend:

x = -5:5;

y = [1.536098 3.663004 10.98901 47.61905 333.3333 1000 333.3333 47.61905 10.98901 3.663004

1.536098];

cs = spline(x,[0 y 0]);

xx = linspace(-5,5,101);

plot(x,y,'o',xx,ppval(cs,xx),'-');

4.

Graficzna prezentacja wyników

Rozwiązanie metodą funkcji sklejanych wygląda następująco, po wykonaniu w programie Matlab:

9

Rozwiązanie metodą Newtona wygląda z kolei następująco:

5.

Przedstawienie otrzymanych wyników

Wielomian wyznaczony metodą Newtona ma postać:

ܹሺݔሻ = |541.3537334ݔ

ଷ

| − |1192.9832ݔ

ଶ

| − |15.0372333ݔ| + 1000

Z kolei wyznaczony metodą Lagrange’a:

ݓ

௙

ሺݔሻ = |541.3537337ݔ

ଷ

| − |1192.9832ݔ

ଶ

| − |15.03723367ݔ| + 1000

0

200

400

600

800

1000

1200

-6

-4

-2

0

2

4

6

10

Na podstawie powyższych wielomianów można wyznaczyć błąd interpolacji. Do jego określenia

można ustalić wartości jakie przyjmują funkcje dla argumentu wynoszącego: 0.1

Dla wielomianu wyznaczonego metodą Newtona wynosi ona 987,1077984034.

Dla wielomianu wyznaczonego metodą Lagrange’a wynosi ona 987,1077983667.

Błąd interpolacji liczymy więc następująco:

ߝ =

ሺଽ଼଻,ଵ଴଻଻ଽ଼ସ଴ଷସିଽ଼଻,ଵ଴଻଻ଽ଼ଷ଺଺଻ሻ

ଽ଼଻,ଵ଴଻଻ଽ଼ସ଴ଷସ

=1.013060581*10^-10