Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 5
W5 - 1
Całkowanie numeryczne
Kwadratura:
∫
∑
=
=
b
a
n
k
k
k
)
x
(
f
A
dx
)
x
(
f
0
KWADRATURY NEWTONA-COTESA
uzyskane przez interpolację wielomianem z węzłami
równoodległymi
n
a
b
h
,
n
,...,
i
,
ih
a
x
i
−
=
=
+
=
0
)
x
(
P
)
x
(
f
f
,
f
ns
a
b
dx
)
x
(
P
dx
)
x
(
f
i
n
i
i
b
a
n
i
i
i
n
b
a
=
=
−
=
≈
∫
∑
∫
=0
σ
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 5
W5 - 2
n
σ
i
ns
błąd nazwa
1 1 1
2
)
(
f
h
)
(
ξ
2
3
12
1
wzór trapezów
2 1 4 1
6
)
(
f
h
)
(
ξ
4
5
90
1
wzór Simpsona
3 1 3 3 1
8
)
(
f
h
)
(
ξ
4
5
80
3
wzór "trzech ósmych"
4 7 32 12 32
7
90
)
(
f
h
)
(
ξ
6
7
945
8
wzór Milne'a
5 19 75 50 50
75 19
288
)
(
f
h
)
(
ξ
6
7
12096
275
-
6 41 216 27 272
27 216 41
840
)
(
f
h
)
(
ξ
8
9
1400
9
wzór Weddle'a
h- długość przedziału,
ξ
- punkt pośredni
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 5
W5 - 3
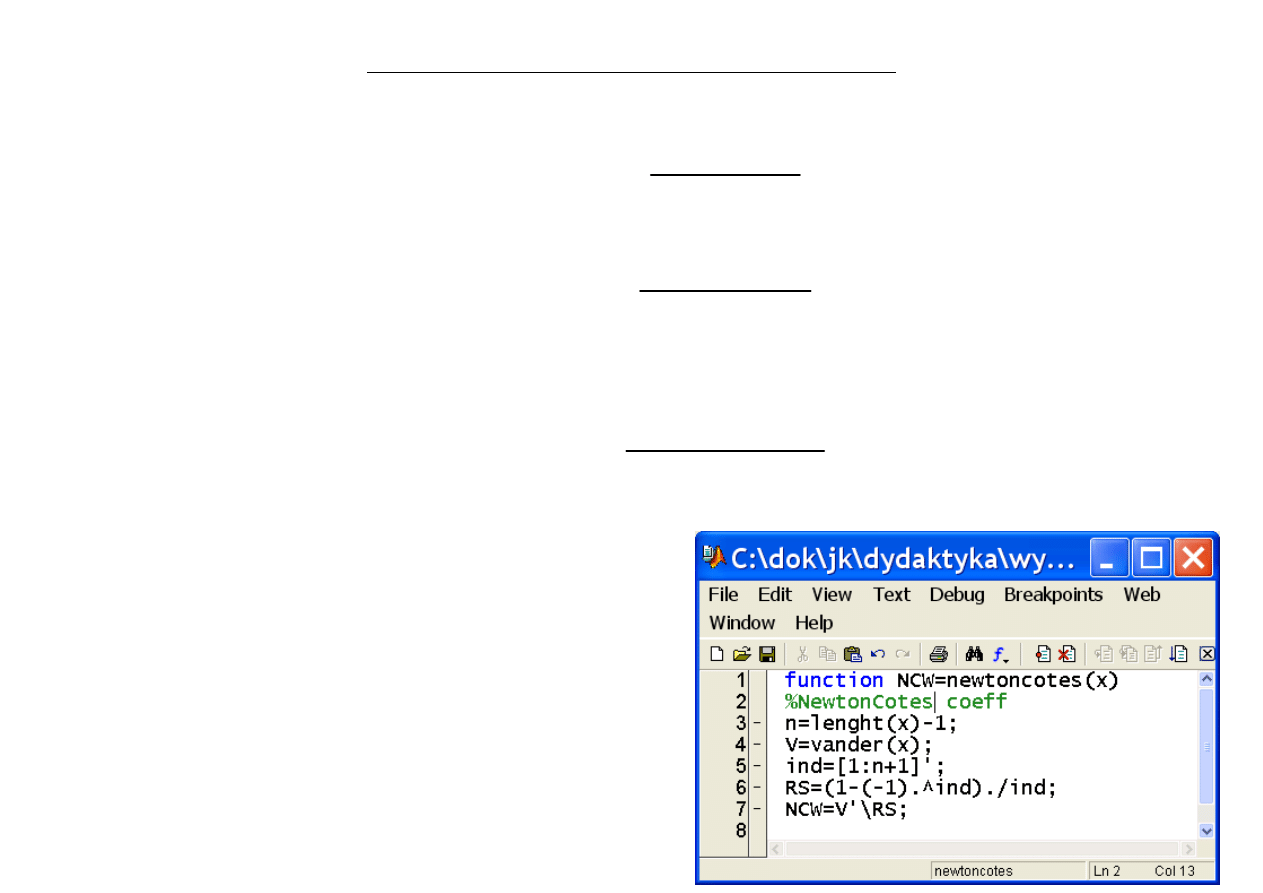
Obliczenie współczynników kwadratur Newtona-Cotesa:
Dane są węzły x
0
,x
1
,..,x
n
. Chcemy, by kwadratura całkowała dokładnie (na przedziale [–1
1])stałą:
1
1
1
1
1
1
1
1
1
0
0
0
1
1
0
0
0
)
(
x
dx
x
x
w
x
w
x
w
n
n
−
−
=
⎥
⎦
⎤
⎢
⎣
⎡
=
=
+
+
+
−
−
∫
L
oraz funkcje x, x
2
, …x
n
:
2
1
1
2
2
2
1
1
1
1
2
1
1
1
1
1
1
0
0
)
(
x
dx
x
x
w
x
w
x
w
n
n
−
−
=
⎥
⎦
⎤
⎢
⎣
⎡
=
=
+
+
+
−
−
∫
L
…………………………………
1
1
1
1
1
1
1
1
1
1
1
1
0
0
+
−
−
=
⎥
⎦
⎤
⎢
⎣
⎡
+
=
=
+
+
+
+
−
−
+
∫
n
)
(
n
x
dx
x
x
w
x
w
x
w
n
n
n
n
n
n
n
n
L
W postaci macierzowej:
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 5
W5 - 4
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
+
−
−
−
−
−
−
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
+
1
1
1
2
1
1
1
1
1
1
2
1
0
1
0
1
1
1
1
1
0
0
0
1
0
0
n
)
(
)
(
)
(
w
w
w
x
x
x
x
x
x
x
x
x
n
n
n
n
n
n
n
M
M
L
M
M
M
M
K
L
transponowana macierz Vandermode’a
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 5
W5 - 5
Kwadratura Newtona-Cotes’a o n+1 węzłach obliczy dokładnie całkę wielomianu
stopnia n. Można zmienić układ węzłów, tak by zwiększyć stopień wielomianu
całkowanego dokładnie przez kwadraturę korzystającą z n węzłów.
Kwadratury Gaussa pozwalaja na dokładne całkowanie wielomianów stopnia do
2n-1 przy n węzłach.
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 5
W5 - 6
Kwadratury złożone
n
a
b
h
,
n
,...,
i
,
ih
a
x
i
−
=
=
+
=
0
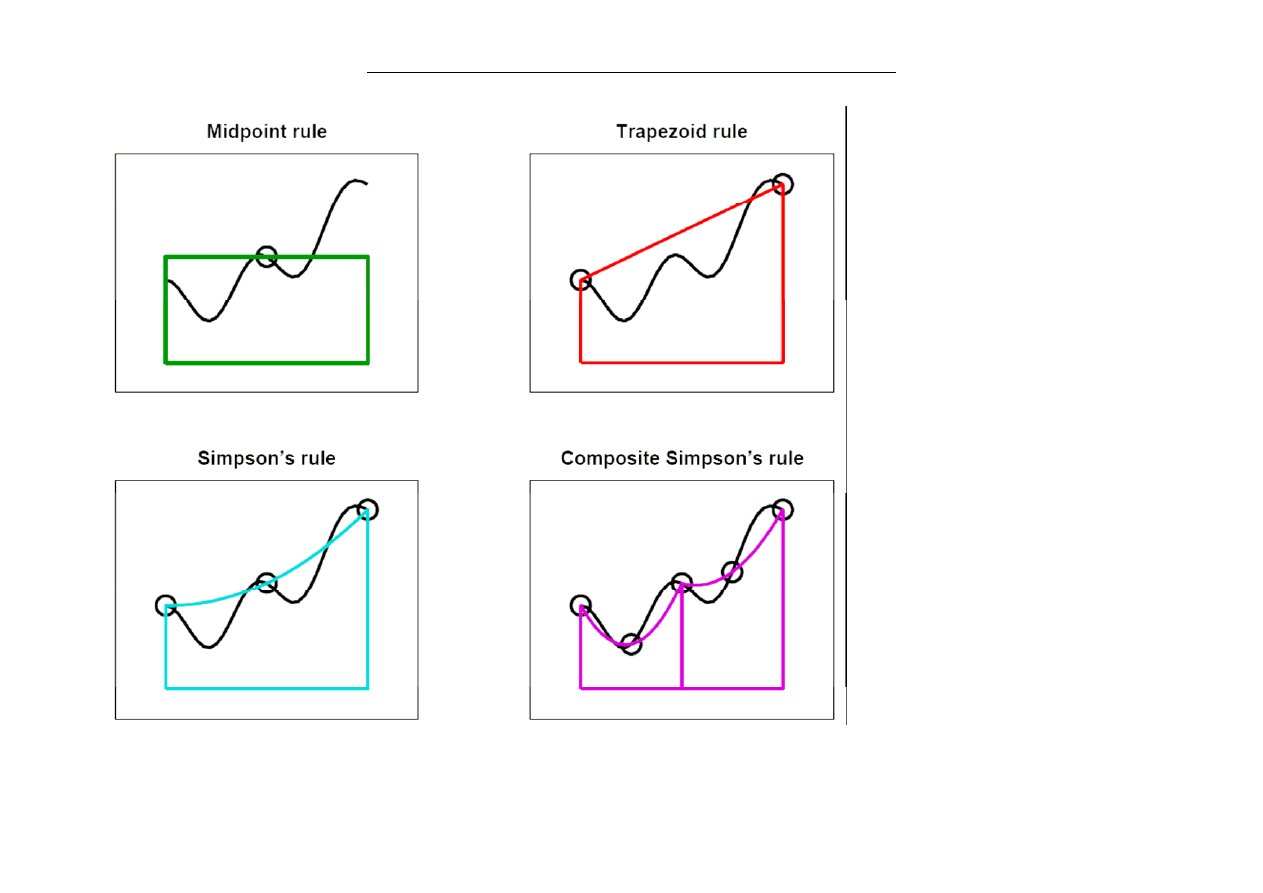
Wzór prostokątów
)
h
(
R
)
h
x
(
f
h
dx
)
x
(
f
n
i
i
b
a
=
+
≈
∑
∫
−
=
1
0
2
Wzór trapezów
[
]
)
h
(
T
)
x
(
f
)
x
(
f
h
dx
)
x
(
f
n
i
i
i
b
a
=
+
≈
∑
∫
−
=
+
1
0
1
2
⎥⎦
⎤
⎢⎣
⎡
+
−
+
+
+
+
=
2
2
)
b
(
f
)
h
b
(
f
)
h
a
(
f
)
a
(
f
h
)
h
(
T
L
Oszacowanie błędu obcięcia:
(
)
)
(
'
'
f
h
a
b
)
h
(
R
dx
)
x
(
f
b
a
ξ
2
24
1
−
≤
−
∫
(
)
)
(
'
'
f
h
a
b
)
h
(
T
dx
)
x
(
f
b
a
ξ
2
12
1
−
≤
−
∫
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 5
W5 - 7
L
+
+
+
+
=
∫
6
3
4
2
2
1
h
a
h
a
h
a
dx
)
x
(
f
)
h
(
T
b
a
Metoda Romberga=
=złożona kwadratura trapezów+ekstrapolacja Richardsona
q=2, p
i
=2i
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 5
W5 - 8
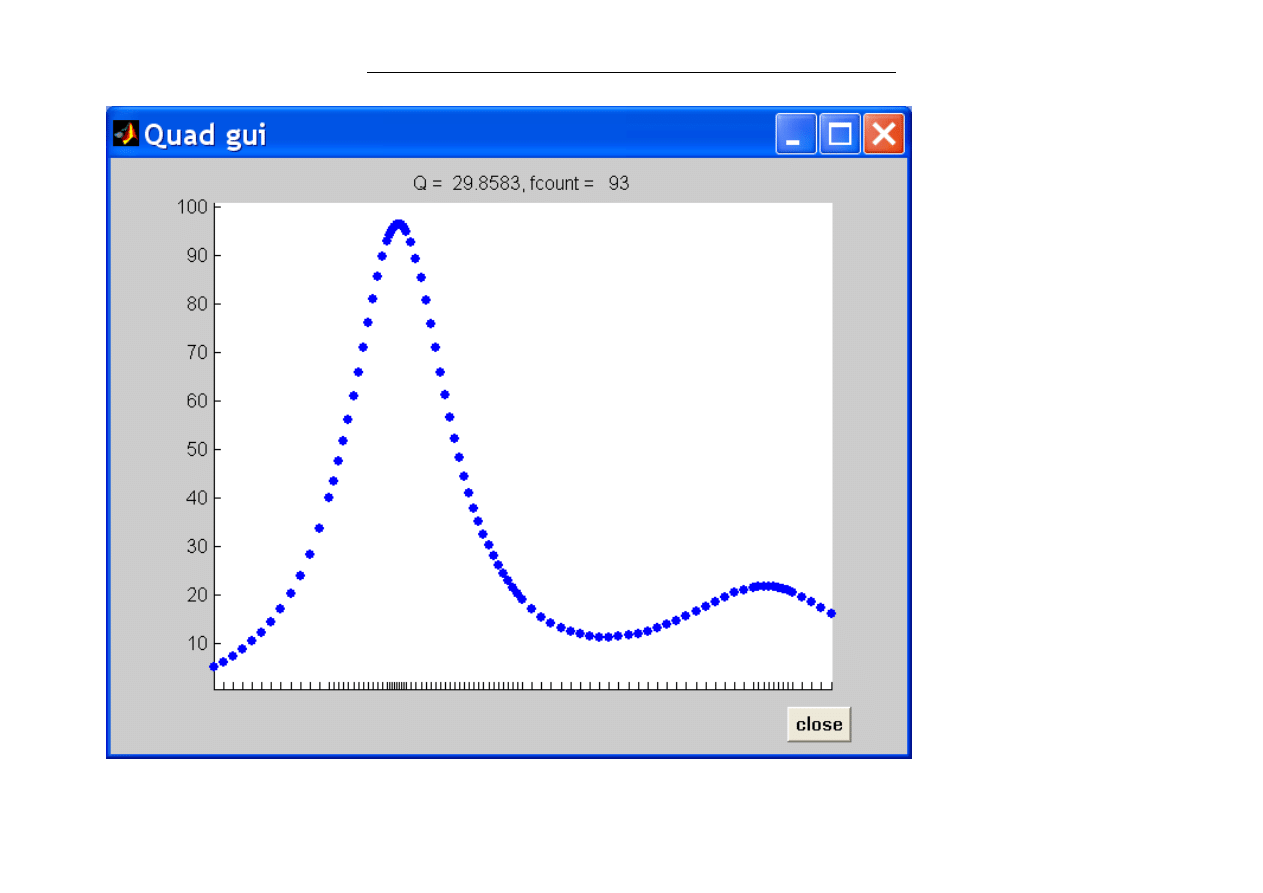
Kwadratury adaptacyjne
Instytut Automatyki Politechniki Łódzkiej - Metody Numeryczne wykład 5
W5 - 9