Prawdopodobieństwo i statystyka

30.11.2009 r.

___________________________________________________________________________

Zadanie 1.

Niech

będzie dwuwymiarową zmienną losową o funkcji gęstości

)

,

(

Y

X

( )

( )

⎪⎩

⎪

⎨

⎧

∈

∈

+

=

przypadku.

przeciwnym

w

0

1

,

0

i

1

,

0

gdy

3

4

2

)

,

(

2

y

x

xy

x

y

x

f

Niech

i

Y

X

S

+

=

X

Y

V

−

=

. Wyznacz

(

)

1

|

=

S

V

E

.

(A)

0

(B)

8

3

(C)

8

3

−

(D)

7

2

(E)

7

2

−

1

Prawdopodobieństwo i statystyka

30.11.2009 r.

___________________________________________________________________________

Zadanie 2.

Załóżmy, że

,

, są niezależnymi zmiennymi losowymi o

jednakowym rozkładzie wykładniczym. Niech

. Oblicz

n

X

X

X

,

,

,

2

1

K

2

>

n

∑

=

=

n

i

i

X

S

1

).

2

/

2

/

2

/

Pr(

2

1

S

X

S

X

S

X

p

n

≤

∧

∧

≤

∧

≤

=

K

(A)

n

n

p

⎟

⎠

⎞

⎜

⎝

⎛ −

=

−1

2

1

1

(B)

0

=

p

(C)

n

n

p

2

2

1 −

=

(D)

1

2

1

−

−

=

n

n

p

(E)

n

n

p

⎟

⎠

⎞

⎜

⎝

⎛ −

=

2

1

1

2

Prawdopodobieństwo i statystyka

30.11.2009 r.

___________________________________________________________________________

Zadanie 3.

Załóżmy, że dysponujemy pojedynczą obserwacją

X z rozkładu normalnego

(

)

2

,

σ

μ

N

. Rozważmy zadanie testowania hipotezy

1

0

:

2

0

=

=

σ

μ

i

H

przeciw alternatywie

.

4

1

:

2

1

=

−

=

σ

μ

i

H

Najmocniejszy test na poziomie istotności

α jest postaci

Odrzuć

, gdy

0

H

)

,

2

(

b

X

−

∉

.

Podaj poziom istotności

α .

(A) 045

,

0

=

α

(B) 027

,

0

=

α

(C) 023

,

0

=

α

(D) 033

,

0

=

α

(E) 114

,

0

=

α

3

Prawdopodobieństwo i statystyka

30.11.2009 r.

___________________________________________________________________________

Zadanie 4.

Niech X i Y będą niezależnymi zmiennymi losowymi o rozkładach normalnych,
przy tym

,

0

]

[

]

=

X

[

=

Y

E

E

3

]

[

=

X

Var

i

1

]

[

=

Y

Var

.

Oblicz

.

]

|

|

|

|

Pr[

Y

X

<

(A)

= 0.3333

]

|

|

|

|

Pr[

Y

X

<

(B)

= 0.7500

]

|

|

|

|

Pr[

Y

X

<

(C)

= 0.5000

]

|

|

|

|

Pr[

Y

X

<

(D)

= 0.6667

]

|

|

|

|

Pr[

Y

X

<

(E)

= 0.8333

]

|

|

|

|

Pr[

Y

X

<

4

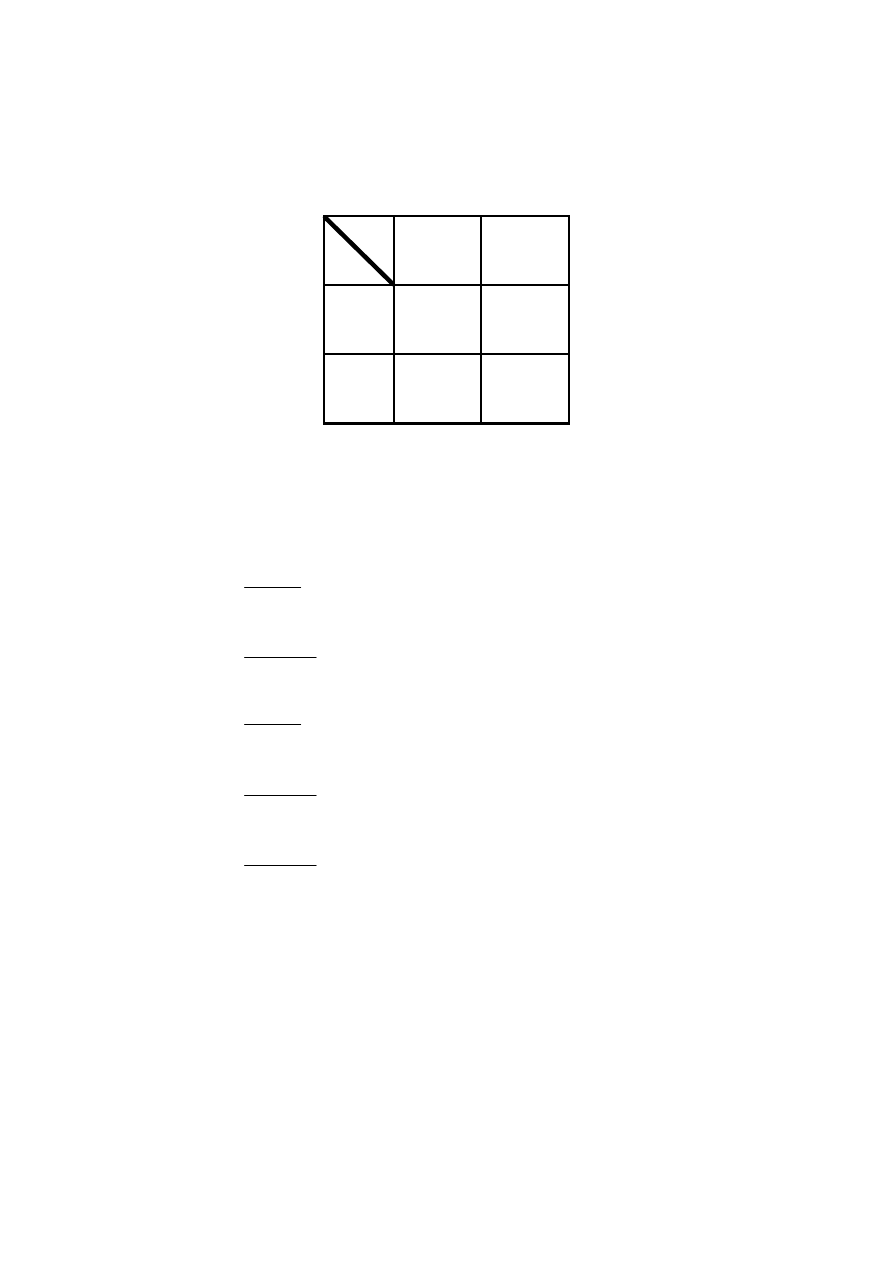
Prawdopodobieństwo i statystyka

30.11.2009 r.

___________________________________________________________________________

Zadanie 5.

Wektor losowy

ma łączny rozkład prawdopodobieństwa dany następującą

tabelką:

)

,

(

Y

X

1

=

Y

2

=

Y

1

=

X

2

θ

(

)

2

1

θ

−

2

=

X

(

)

θ

θ

−

1

)

1

(

θ

θ

−

gdzie )

1

,

0

(

∈

θ

jest nieznanym parametrem. Na podstawie -elementowej próbki z

tego rozkładu, , obliczono estymator największej wiarogodności

. Oblicz wariancję tego estymatora.

n

)

,

(

),...,

,

(

1

1

n

n

Y

X

Y

X

θ

ˆ

(A)

n

Var

2

)

1

(

)

ˆ

(

θ

θ

θ

−

=

(B)

n

Var

2

)

1

(

)

ˆ

(

2

2

θ

θ

θ

−

=

(C)

n

Var

)

1

(

)

ˆ

(

θ

θ

θ

−

=

(D)

n

Var

)

1

(

)

ˆ

(

2

2

θ

θ

θ

−

=

(E)

n

Var

2

)

1

(

)

ˆ

(

2

2

θ

θ

θ

−

=

5

Prawdopodobieństwo i statystyka

30.11.2009 r.

___________________________________________________________________________

Zadanie 6.

Załóżmy, że

są niezależnymi zmiennymi losowymi o jednakowym,

ciągłym rozkładzie prawdopodobieństwa, mającymi momenty rzędu 1, 2 i 3. Znamy

n

X

X

,...,

1

)

(

i

X

E

=

μ

i

.

)

(

2

i

X

Var

=

σ

Niech oznacza gęstość rozkładu pojedynczej zmiennej

. Wiemy, że rozkład

jest symetryczny w tym sensie, że

)

(x

f

i

X

)

(

)

(

x

f

x

f

−

=

+

μ

μ

dla każdego

x

.

Oblicz trzeci moment sumy:

( )

3

n

S

E

, gdzie

n

n

X

X

S

+

+

=

...

1

.

(A)

( )

)

3

2

3

(

2

2

2

2

3

σ

μ

μ

μ

+

−

=

n

n

S

E

n

(B)

( )

)

3

(

2

2

2

3

σ

μ

μ

+

=

n

n

S

E

n

(C)

( )

)

3

(

2

2

2

3

σ

μ

μ

+

=

n

n

S

E

n

(D)

( )

)

(

2

2

2

3

σ

μ

μ

+

=

n

n

S

E

n

(E)

( )

)

)

1

(

3

(

2

2

2

2

3

μ

σ

μ

μ

−

−

+

=

n

n

n

S

E

n

6

Prawdopodobieństwo i statystyka

30.11.2009 r.

___________________________________________________________________________

Zadanie

7.

Załóżmy, że jest ciągiem niezależnych zmiennych losowych o
jednakowym rozkładzie wykładniczym o gęstości

,...

,...,

,

2

1

n

X

X

X

)

exp(

)

(

x

x

f

−

=

dla

.

0

>

x

Zmienna losowa

jest niezależna od

i ma rozkład Poissona o

wartości oczekiwanej

N

,...

,...,

,

2

1

n

X

X

X

λ .

Niech

)

2

,

min(

i

i

X

Y

=

,

i

i

i

Y

X

Z

−

=

,

∑

=

=

N

i

i

Y

Y

S

1

)

(

,

.

∑

=

=

N

i

i

Z

Z

S

1

)

(

Oblicz

(

)

)

(

)

(

,

Z

Y

S

S

Cov

.

(A)

(

)

2

)

(

)

(

2

,

−

=

e

S

S

Cov

Z

Y

λ

(B)

(

)

)

1

(

2

,

2

)

(

)

(

−

−

=

e

S

S

Cov

Z

Y

λ

(C)

(

)

4

)

(

)

(

2

,

−

=

e

S

S

Cov

Z

Y

λ

(D)

(

)

(

)

2

2

)

(

)

(

1

,

−

−

+

=

e

e

S

S

Cov

Z

Y

λ

(E)

(

)

2

)

(

)

(

,

−

= e

S

S

Cov

Z

Y

λ

7

Prawdopodobieństwo i statystyka

30.11.2009 r.

___________________________________________________________________________

Zadanie

8.

Obserwujemy

niezależnych zmiennych losowych o tym samym

rozkładzie Pareto o gęstości

4

3

2

1

,

,

,

X

X

X

X

⎪⎩

⎪

⎨

⎧

≤

>

=

+

1

0

1

)

(

1

1

1

1

x

gdy

x

gdy

x

x

f

θ

θ

θ

i

niezależnych zmiennych losowych o tym samym rozkładzie Pareto o

gęstości

5

2

1

,

,

,

Y

Y

Y

K

⎪⎩

⎪

⎨

⎧

≤

>

=

+

1

0

1

)

(

1

2

2

2

x

gdy

x

gdy

x

x

f

θ

θ

θ

gdzie

1

θ i

2

θ są nieznanymi parametrami dodatnimi.

Wszystkie zmienne losowe są niezależne. Testujemy hipotezę

2

1

0

:

θ

θ

=

H

przy

alternatywie

2

1

1

:

θ

θ

<

H

za pomocą testu o obszarze krytycznym

⎭

⎬

⎫

⎩

⎨

⎧

<

=

t

K

2

1

ˆ

ˆ

θ

θ

gdzie i są estymatorami największej wiarogodności odpowiednio parametrów

1

ˆ

θ

2

ˆ

θ

1

θ i

2

θ wyznaczonymi na podstawie prób losowych

i

.

Dobrać stałą t tak, aby otrzymać test o rozmiarze 0,05.

4

3

2

1

,

,

,

X

X

X

X

5

2

1

,

,

,

Y

Y

Y

K

(A) 0,160

(B) 0,299

(C) 0,326

(D) 0,193

(E) 0,363

8

Prawdopodobieństwo i statystyka

30.11.2009 r.

___________________________________________________________________________

Zadanie

9.

Niech

, będzie próbką z rozkładu Poissona z nieznanym

parametrem

n

X

X

X

,...,

,

2

1

,

1

>

n

λ (parametr jest wartością oczekiwaną pojedynczej obserwacji,

0

)

(

>

=

X

E

i

λ

λ

).

Interesuje nas drugi moment obserwacji, czyli wielkość

.

)

(

)

(

2

2

i

X

E

m

λ

λ

=

Estymator nieobciążony o minimalnej wariancji funkcji

)

(

2

λ

m

jest równy

A)

2

1

1

1

1

⎟

⎠

⎞

⎜

⎝

⎛

+

∑

∑

=

=

n

i

i

n

i

i

X

n

X

n

(B)

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

∑

∑

=

=

n

i

i

n

i

i

X

X

n

1

2

1

2

1

(C)

∑

=

n

i

i

X

n

1

2

1

(D)

∑

=

n

i

i

X

n

1

2

2

1

(E)

(

)

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

−

+

⎟

⎠

⎞

⎜

⎝

⎛

∑

∑

=

=

n

i

i

n

i

i

X

n

X

n

1

2

1

2

1

1

9

Prawdopodobieństwo i statystyka

30.11.2009 r.

___________________________________________________________________________

Zadanie

10.

Pan A przeznaczył 5 zł na pewna grę. W pojedynczej kolejce gry pan A wygrywa 1 zł
z prawdopodobieństwem 1/3 lub przegrywa 1 zł z prawdopodobieństwem 2/3. Pan A
kończy grę, gdy wszystko przegra lub gdy będzie miał 10 zł.
Prawdopodobieństwo, że pan A wszystko przegra jest równe

(A) 0,87

(B) 0,67

(C) 0,50

(D) 0,97

(E) 0,77

10

Prawdopodobieństwo i statystyka

30.11.2009 r.

___________________________________________________________________________

Egzamin dla Aktuariuszy z 30 listopada 2009 r.

Prawdopodobieństwo i statystyka

Arkusz odpowiedzi

*

Imię i nazwisko : ......................... K L U C Z O D P O W I E D Z I ............................
Pesel ...........................................

Zadanie nr

Odpowiedź Punktacja

♦

1 C

2 D

3 B

4 A

5 A

6 C

7 A

8 C

9 E

10 D

*

Oceniane są wyłącznie odpowiedzi umieszczone w Arkuszu odpowiedzi.

♦

Wypełnia Komisja Egzaminacyjna.

11