
1
1. DOBÓR WYMIARÓW KONSTRUKCJI
1.1 SŁUP
Lcol
7.1m
:=
l0
2 Lcol
⋅
14.2 m
=
:=
hs
0.65m
:=
bs
0.65m
:=
l0
hs
21.846
=
l0
bs
21.846
=
20
l0
hs
≤
1
=
warunek spełniony
20
l0
bs
≤
1
=
warunek spełniony
25
l0
hs
≥
1
=
warunek spełniony
25
l0
bs
≥
1
=
warunek spełniony
1.2 RYGIEL
br
bs
:=
a
3.2m
:=
b
2.2m
:=
hr
1
5
a
⋅
0.64 m
=
:=
hr
1
4
a
⋅
0.8 m
=
:=
Przyj
ę
to:
hr
0.65m
:=
1.3 STOPA FUNDAMENTOWA
L
3.5m
:=
B
3.5m
:=
hf
0.25 L
⋅
0.875 m
=
:=
hf
0.5 L
⋅
1.75 m
=
:=
Przyj
ę
to:
hf
1.0m
:=

2
2.ZESTAWIENIE OBCI
Ąś
E
Ń
2.1 WARTO
Ś
CI CHARAKTERYSTYCZNE
2.1.1 CI
Ęś
AR WŁASNY PODPORY
γB
25
kN
m
3
:=
- słup
gs
Lcol
hr
2
−
bs
⋅
hs
⋅
γB
⋅
71.561 kN
⋅
=
:=
- rygiel lewy
d
0.3m
:=
grl
a
d
+
(
) br
⋅
hr
⋅
γB
⋅
36.969 kN
⋅
=
:=
- rygiel prawy
d
0.3m
:=
grp
b
d
+
(
) br
⋅
hr
⋅
γB
⋅
26.406 kN
⋅
=
:=
- stopa fundamentowa
gst
L hf
⋅
B
⋅
γB
⋅
306.25 kN
⋅
=
:=
Gp
gs grl
+
grp
+
gst
+
441.186 kN
⋅
=
:=
2.1.2 OBCI
Ąś
ENIE STAŁE RUROCI
Ą
GÓW
G
60kN
:=
2.1.3 OBCI
Ąś
ENIE ZMIENNE OD TRANSPORTOWANEGO MEDIUM
P
110kN
:=
2.1.4 OBCI
Ąś
ENIE ZMIENNE OD SIŁY POZIOMEJ WYWOŁANEJ TEMPERATUR
Ą
MEDIUM
μ
0.14
:=
H
μ G
P
+
(
)
⋅
23.8 kN
⋅
=
:=

3
2.2 WARTO
Ś
CI OBLICZENIOWE
2.2.1 CI
Ęś
AR WŁASNY PODPORY
γf
1.1
:=
- słup
gsd
gs γf
⋅
78.717 kN
⋅
=
:=
- rygiel lewy
grld
grl γf
⋅
40.666 kN
⋅
=
:=
- rygiel prawy
grpd
grp γf
⋅
29.047 kN
⋅
=
:=
- stopa fundamentowa
gstd
gst γf
⋅
336.875 kN
⋅
=
:=
Gp
gsd grld
+
grpd
+
gstd
+
485.305 kN
⋅
=
:=
2.2.2 OBCI
Ąś
ENIE STAŁE RUROCI
Ą
GÓW
γf
1.1
:=
Gd
G
γf
⋅
66 kN
⋅
=
:=
2.1.3 OBCI
Ąś
ENIE ZMIENNE OD TRANSPORTOWANEGO MEDIUM
γf
1.1
:=
Pd
P
γf
⋅
121 kN
⋅
=
:=
2.1.4 OBCI
Ąś
ENIE ZMIENNE OD SIŁY POZIOMEJ WYWOŁANEJ TEMPERATUR
Ą
MEDIUM
μ
0.14
:=
Hd
μ Gd Pd
+
(
)
⋅
26.18 kN
⋅
=
:=
4
3. STATYKA KONSTRUKCJI
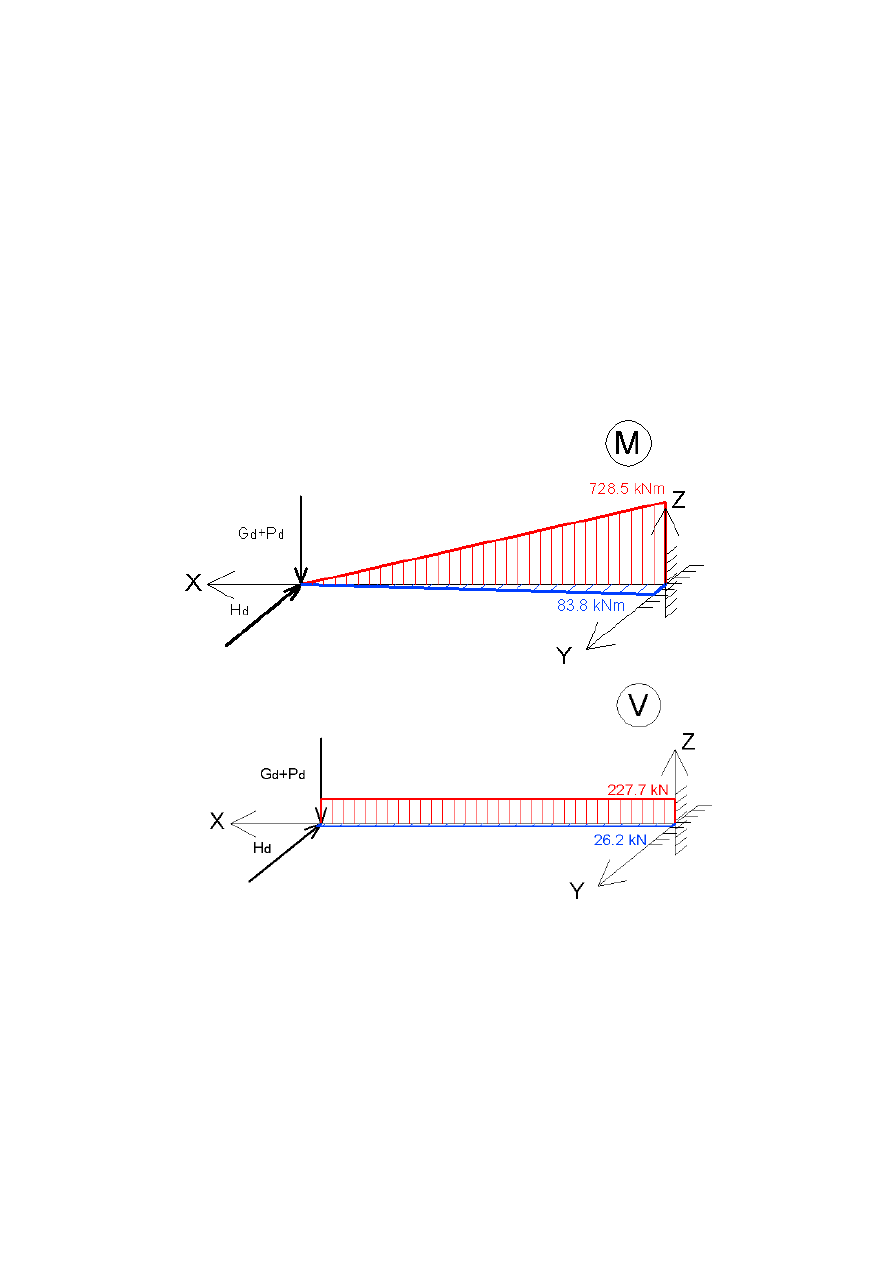
3.1 RYGIEL
-moment
MyR
Gd Pd
+
grld
+
(
)
a
⋅
728.53 kN m
⋅
⋅
=
:=
MzR
Hd a
⋅
83.776 kN m
⋅
⋅
=
:=
- siła tn
ą
ca
VzR
Gd Pd
+
grld
+
227.666 kN
⋅
=
:=
VyR
Hd
26.18 kN
⋅
=
:=

5
3.2 SŁUP
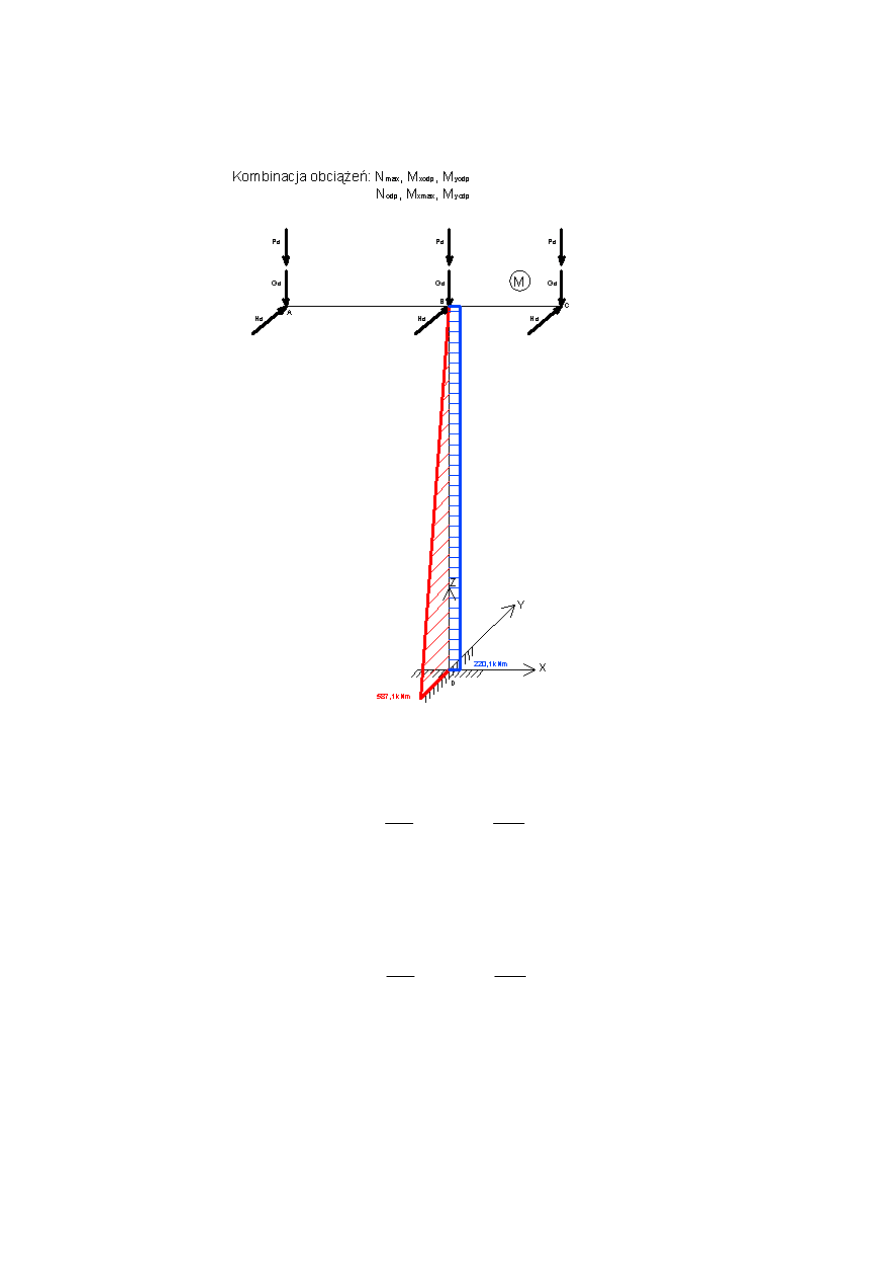
3.2.1 Kombinacja 1: Nmax, Mxodp, Myodp
hł
0.05 m
⋅
:=
Lobl
Lcol
hł
+
hr
2
+
:=
MyB1
Pd
−
a
⋅
Gd
grld
2
+
a
⋅
−
Pd b
⋅
+
Gd
grpd
2
+
b
⋅
+
220.113
−
kN m
⋅
⋅
=
:=
MxB1
Hd 0
⋅
Hd 0
⋅
−
0 kN m
⋅
⋅
=
:=
MzB1
Hd a
⋅
Hd b
⋅
−
26.18 kN m
⋅
⋅
=
:=
MyD1
Pd
−
a
⋅
Gd
grld
2
+
a
⋅
−
Pd b
⋅
+
Gd
grpd
2
+
b
⋅
+
220.113
−
kN m
⋅
⋅
=
:=
MxD1
3 Hd
⋅
Lobl
⋅
587.087 kN m
⋅
⋅
=
:=
MzD1
Hd a
⋅
Hd b
⋅
−
26.18 kN m
⋅
⋅
=
:=
Nmax1
3 Pd
⋅
3 Gd
⋅
+
grld
+
grpd
+
630.712 kN
⋅
=
:=
3.2.2 Kombinacja 2: Nodp, Mxmax, Myodp
MyB2
Pd
−
a
⋅
Gd
grld
2
+
a
⋅
−
Pd b
⋅
+
Gd
grpd
2
+
b
⋅
+
220.113
−
kN m
⋅
⋅
=
:=
MxB2
Hd 0
⋅
Hd 0
⋅
−
0 kN m
⋅
⋅
=
:=
MzB2
Hd a
⋅
Hd b
⋅
−
26.18 kN m
⋅
⋅
=
:=
MyD2
Pd
−
a
⋅
Gd
grld
2
+
a
⋅
−
Pd b
⋅
+
Gd
grpd
2
+
b
⋅
+
220.113
−
kN m
⋅
⋅
=
:=
MxD2
3 Hd
⋅
Lobl
⋅
587.087 kN m
⋅
⋅
=
:=
MzD2
Hd a
⋅
Hd b
⋅
−
26.18 kN m
⋅
⋅
=
:=
Nmax2
3 Pd
⋅
3 Gd
⋅
+
grld
+
grpd
+
630.712 kN
⋅
=
:=
6
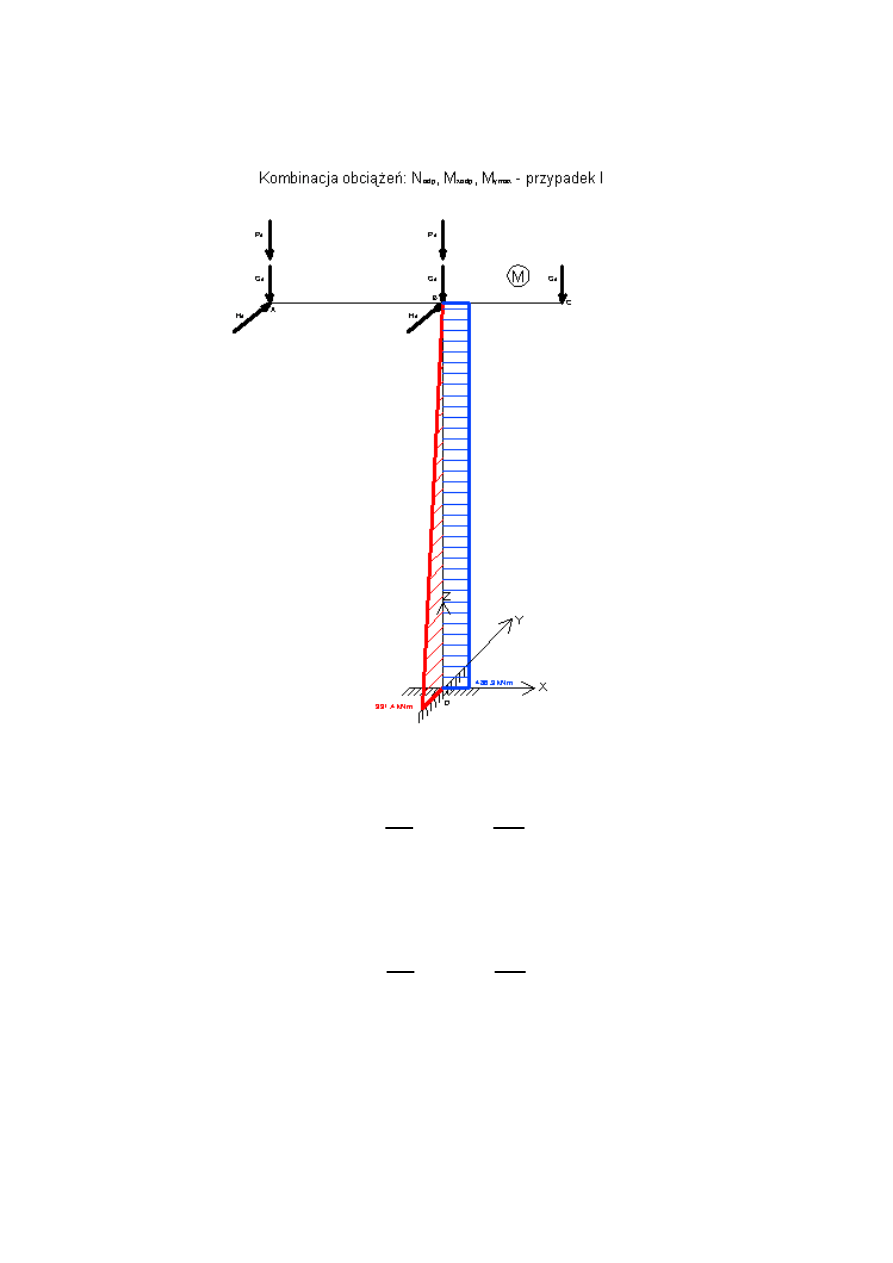
3.2.3 Kombinacja 3: Nodp, Mxodp, Mymax
3.2.3.1 Przypadek I
MyB31
Pd
−
a
⋅
Gd
grld
2
+
a
−
Gd
grpd
2
+
b
⋅
+
486.313
−
kN m
⋅
⋅
=
:=
MxB31
Hd 0
⋅
0 kN m
⋅
⋅
=
:=
MzB31
Hd a
⋅
83.776 kN m
⋅
⋅
=
:=
MyD31
Pd
−
a
⋅
Gd
grld
2
+
a
−
Gd
grpd
2
+
b
⋅
+
486.313
−
kN m
⋅
⋅
=
:=
MxD31
2Hd Lobl
⋅
391.391 kN m
⋅
⋅
=
:=
MzD31
Hd a
⋅
83.776 kN m
⋅
⋅
=
:=
Nmax31
2 Pd
⋅
3 Gd
⋅
+
grld
+
grpd
+
509.712 kN
⋅
=
:=
7
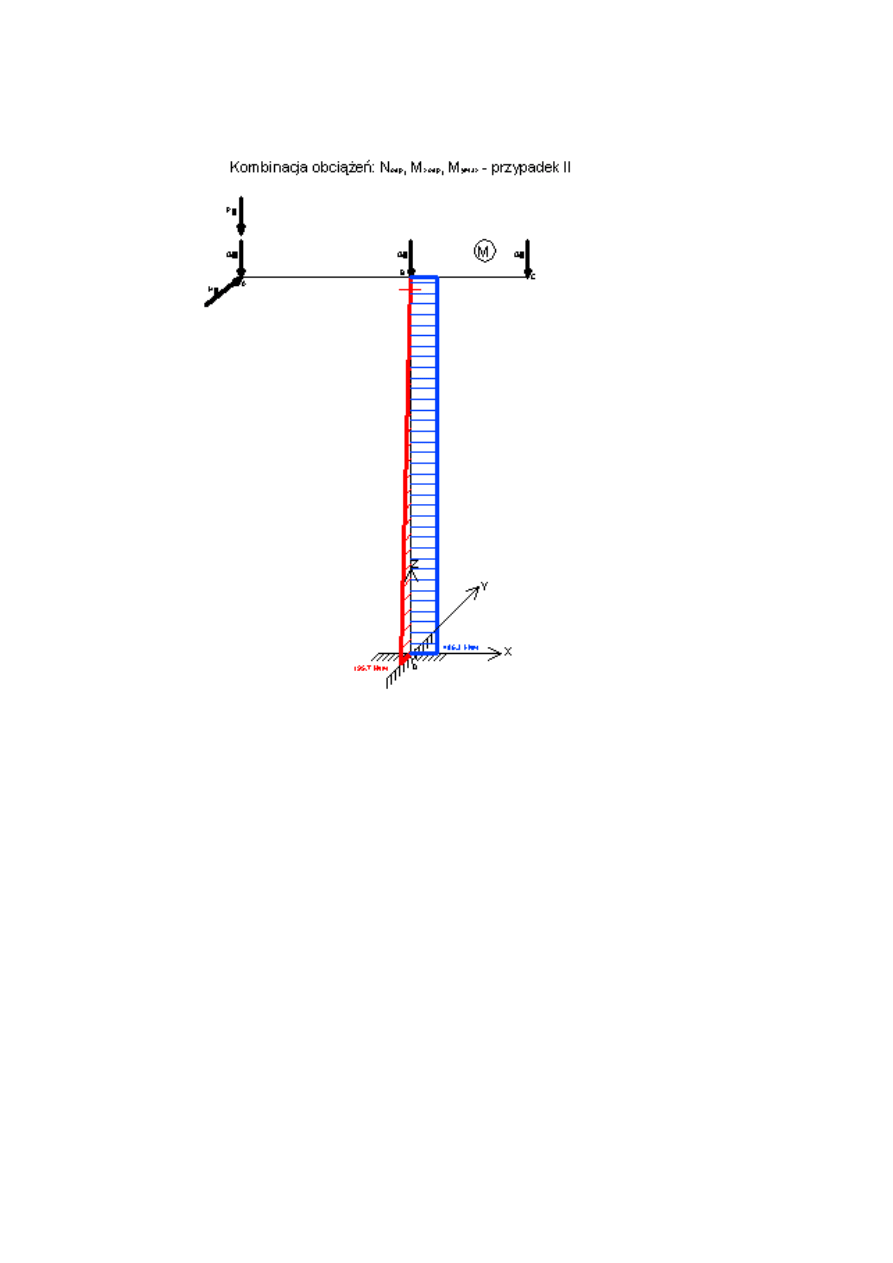
3.2.3.2 Przypadek II
MyB32
Pd
−
a
⋅
Gd
grld
2
+
a
−
Gd
grpd
2
+
b
⋅
+
486.313
−
kN m
⋅
⋅
=
:=
MxB32
Hd 0
⋅
0 kN m
⋅
⋅
=
:=
MzB32
Hd a
⋅
83.776 kN m
⋅
⋅
=
:=
MyD32
Pd
−
a
⋅
Gd
grld
2
+
a
−
Gd
grpd
2
+
b
⋅
+
486.313
−
kN m
⋅
⋅
=
:=
MxD32
Hd Lobl
⋅
195.696 kN m
⋅
⋅
=
:=
MzD32
Hd a
⋅
83.776 kN m
⋅
⋅
=
:=
Nmax32
Pd 3 Gd
⋅
+
grld
+
grpd
+
388.712 kN
⋅
=
:=
8
9
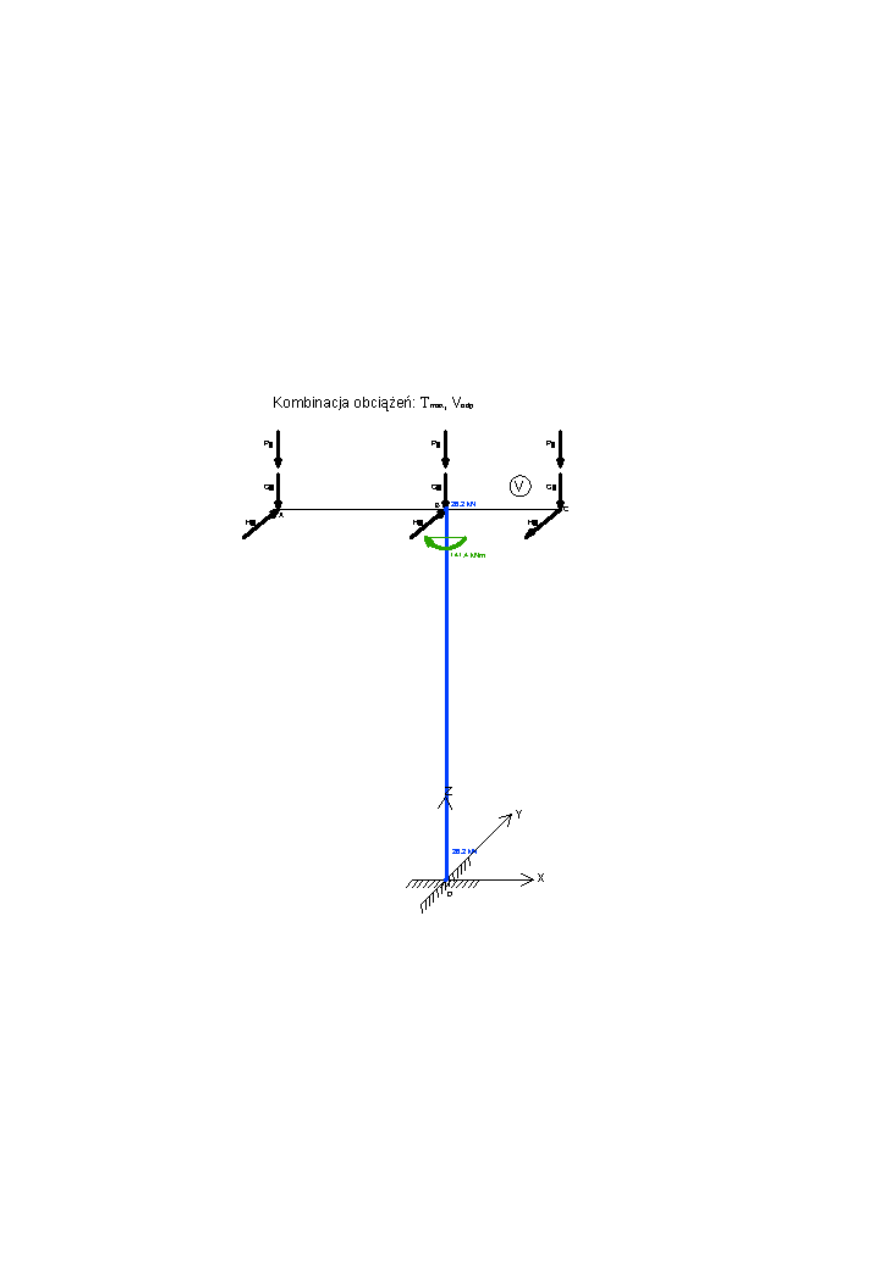
3.2.2 Kombinacja 4: Tmax, Vodp
VyB4
Hd
26.18 kN
⋅
=
:=
VyD4
Hd
26.18 kN
⋅
=
:=
Mzmax4
Hd a
⋅
Hd b
⋅
+
141.372 kN m
⋅
⋅
=
:=
10
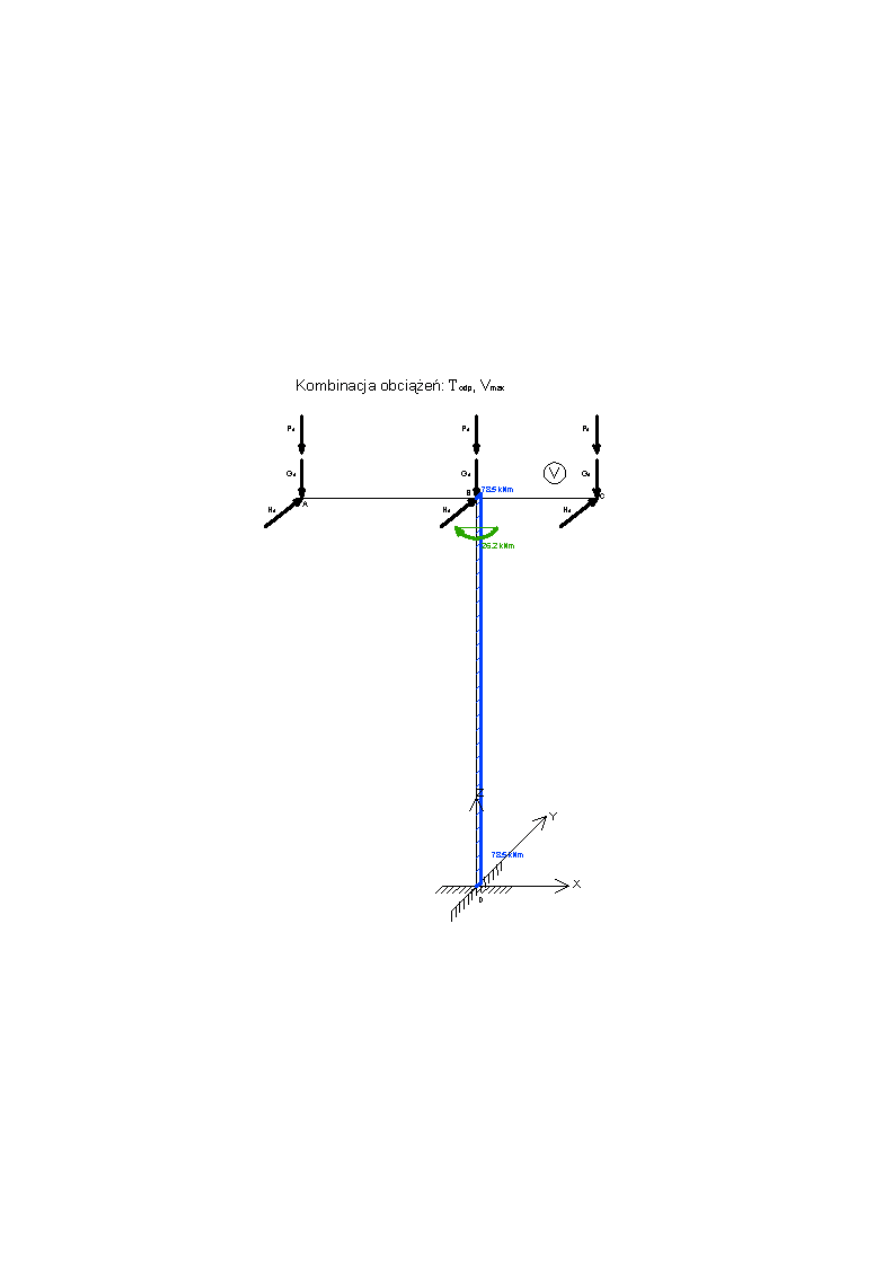
3.2.3 Kombinacja 5: Todp, Vmax
VyB5
3Hd
78.54 kN
⋅
=
:=
VyD5
3Hd
78.54 kN
⋅
=
:=
Mzodp5
Hd a
⋅
Hd b
⋅
−
26.18 kN m
⋅
⋅
=
:=

11
4. DANE DO WYMIAROWANIA
BETON C30/37
•
wytrzymało
ść
charakterystyczna na
ś
ciskanie
fck
30MPa
:=
wytrzymało
ść
obliczeniowa na
ś
ciskanie
fcd
20MPa
:=
wytrzymało
ść
ś
rednia na rozci
ą
ganie
fctm
2.9MPa
:=
wytrzymało
ść
obliczeniowa na rozci
ą
ganie
fctd
1.33MPa
:=
moduł spr
ęż
ysto
ś
ci
Ecm
32GPa
:=
STAL A - IIIN (RB 500 W)
•
charakterystyczna granica plastycznosci stali
fyk
500MPa
:=
obliczeniowa granica plastyczno
ś
ci stali
fyd
420MPa
:=
moduł spr
ęż
ysto
ś
ci stali
Es
200GPa
:=
graniczna warto
ść
wzgl
ę
dnej wysoko
ś
ci
strefy
ś
ciskanej dla stali A-III
ξeff.lim
0.5
:=
STAL A - I
•
charakterystyczna granica plastycznosci stali
fyks
240MPa
:=
obliczeniowa granica plastyczno
ś
ci stali
fyds
210MPa
:=
moduł spr
ęż
ysto
ś
ci stali
Es
200GPa
:=
graniczna warto
ść
wzgl
ę
dnej wysoko
ś
ci
strefy
ś
ciskanej dla stali A-III
ξeff.lims
0.62
:=
Klasa ekspozycji w zale
ż
no
ś
ci od warunków
ś
rodowiska
•
ś
rodowisko cyklicznie mokre i suche CX4
Grubo
ść
otulenia
•
ϕ
28mm
:=
< 32 mm
Cmin
ϕ
≥
- z warunku przekazania sił przyczepno
ś
ci oraz nale
ż
ytego
uło
ż
enia i zag
ę
szczenia betonu
12
Cmin
25mm
:=
- z warunku ochrony przed korozj
ą
∆C
10mm
:=
- odchyłka dopuszczalna
Cnom
Cmin ∆C
+
0.035 m
=
:=
5. WYMIAROWANIE RYGLA
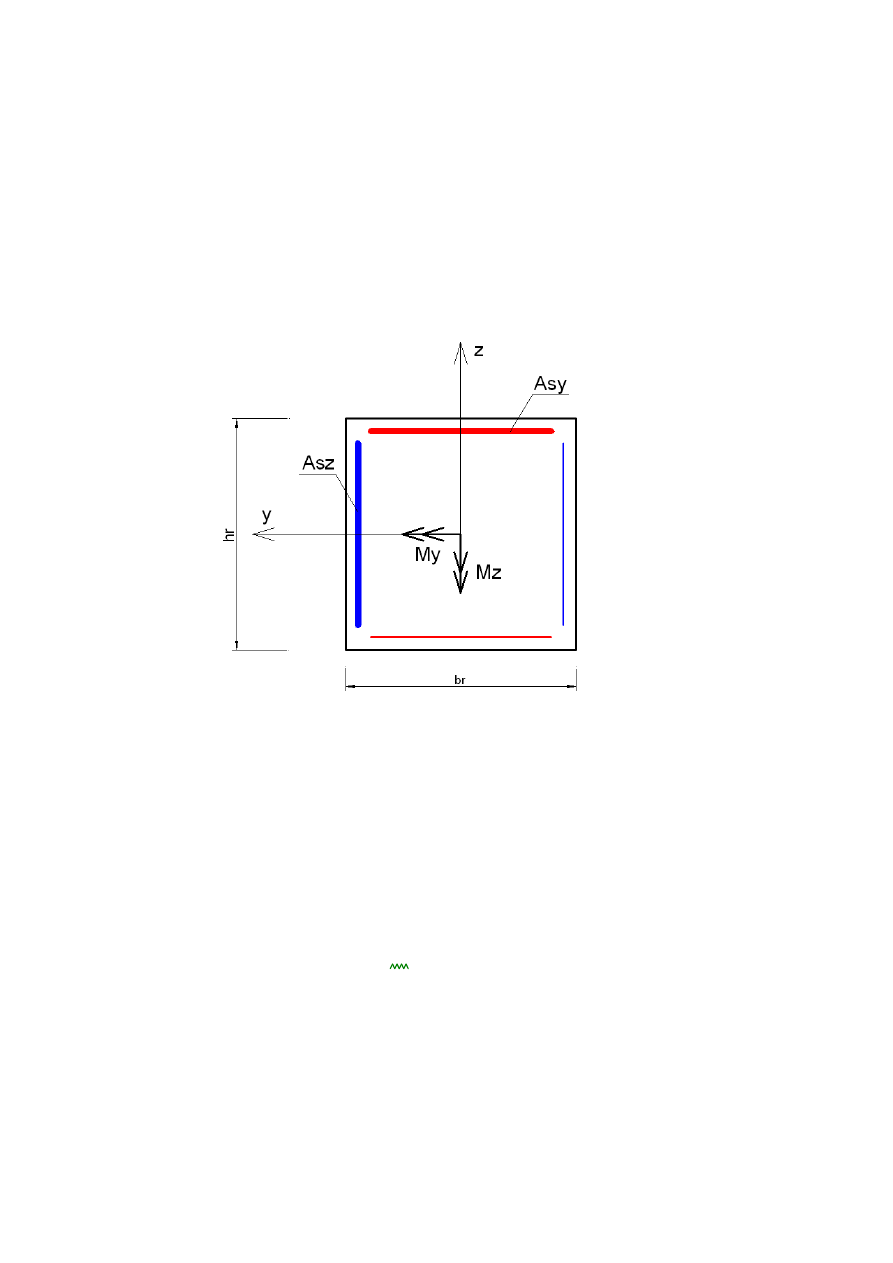
5.1 WYMIARY PRZEKROJU RYGLA
br
0.65 m
=
hr
0.65 m
=
Ac
br hr
⋅
4.225
10
3
×
cm
2
⋅
=
:=
5.2
Ś
REDNICA PR
Ę
TÓW ZBROJENIA
ś
rednica pr
ę
tów głównych
ϕ
28mm
:=
ś
rednica strzemion
ϕs
10mm
:=
warunek
Cnom
ϕ
≥
1
=

13
5.3 WYMIAROWANIE RYGLA "a" NA ZGINANIE
5.3.1 Pole przekroju zbrojenia na zginanie
5.3.1.1 W płaszczy
ż
nie x-z
wysoko
ść
u
ż
yteczna przekroju w płaszczy
ź
nie x-z
•
dz
hr Cnom
−
ϕs
−
ϕ
2
−
59.1 cm
⋅
=
:=
moment statyczny
•
Sc.eff
MyR
fcd br
⋅
dz
2
⋅
0.16
=
:=
wzgl
ę
dna wysoko
ść
strefy sciskanej przekroju
•
ξeff
1
1
2 Sc.eff
⋅
−
−
0.176
=
:=
graniczna warto
ść
wzgl
ę
dnej wysoko
ś
ci strefy
ś
ciskanej
•
ξeff.lim
0.5
:=
sprawdzenie warunku
•
ξeff
ξeff.lim
≤
1
=
przekrój jest pojedy
ń
czo zbrojony
efektywna wysok
ść
strefy
ś
ciskanej
•
xeff
ξeff dz
⋅
0.104 m
=
:=
obliczeniowe pole zbrojenia
•
As1y
fcd br
⋅
xeff
⋅
fyd
32.181 cm
2
⋅
=
:=
przyj
ę
cie powierzchni zbrojenia
•
As1y.prov
49.26 cm
2
⋅
:=
zbrojenie minimalne
•
As.min1
0.26 br
⋅
dz
⋅
fctm
fyk
⋅
5.793 cm
2
⋅
=
:=
As.min2
0.0013 br
⋅
dz
⋅
4.994 cm
2
⋅
=
:=
- współczynnik przy zginaniu
kc
0.4
:=
- współczynnik od wymuszenia
k
1.0
:=
14
- pole rozci
ą
ganej strefy przy zginaniu
Act
0.5 br
⋅
hr
⋅
0.211 m
2
⋅
=
:=
-
ś
rednia wytrzymało
ść
betonu na rozci
ą
ganie w chwili zarysowania
fct.eff
fctm
:=
- napr
ęż
enie w zbrojeniu rozci
ą
ganym natychamiast po zarysowaniu
σs.lim
200MPa
:=
As.min3
kc k
⋅
fct.eff
⋅
Act
σs.lim
⋅
12.253 cm
2
⋅
=
:=
As.min
max As.min1 As.min2
,
As.min3
,
(
)
12.253 cm
2
⋅
=
:=
As1y.prov As.min
≥
1
=
warunek jest spełniony
5.3.1.2 W płaszczy
ź
nie x-y
wysoko
ść
u
ż
yteczna przekroju w płaszczy
ź
nie x-z
•
dy
br Cnom
−
ϕs
−
ϕ
2
−
59.1 cm
⋅
=
:=
moment statyczny
•
Sc.eff
MzR
fcd hr
⋅
dy
2
⋅
0.018
=
:=
wzgl
ę
dna wysoko
ść
strefy sciskanej przekroju
•
ξeff
1
1
2 Sc.eff
⋅
−
−
0.019
=
:=
graniczna warto
ść
wzgl
ę
dnej wysoko
ś
ci strefy
ś
ciskanej
•
ξeff.lim
0.53
:=
sprawdzenie warunku
•
ξeff
ξeff.lim
≤
1
=
przekrój jest pojedy
ń
czo zbrojony
efektywna wysok
ść
strefy
ś
ciskanej
•
xeff
ξeff dy
⋅
1.101 cm
⋅
=
:=
obliczeniowe pole zbrojenia
•
As1z
fcd hr
⋅
xeff
⋅
fyd
3.407 cm
2
⋅
=
:=
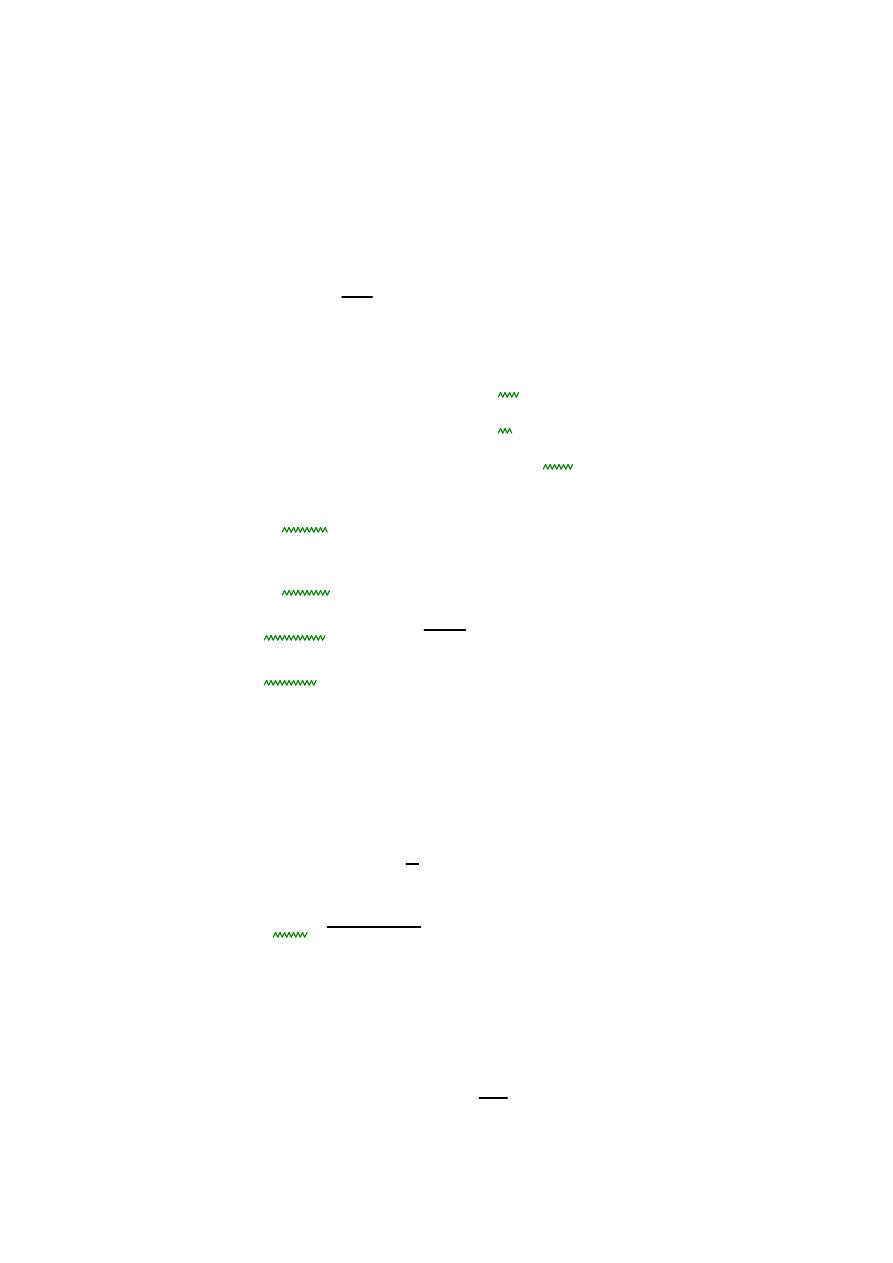
15
przyj
ę
cie powierzchni zbrojenia
•
As1z.prov
12.32cm
2
:=
zbrojenie minimalne
•
0.26 hr
⋅
dy
⋅
fctm
fyk
⋅
5.793 cm
2
⋅
=
0.0013 hr
⋅
dy
⋅
4.994 cm
2
⋅
=
- współczynnik przy zginaniu
kc
0.4
:=
- współczynnik od wymuszenia
k
1.0
:=
- pole rozci
ą
ganej strefy przy zginaniu
Act
0.5 br
⋅
hr
⋅
0.211 m
2
⋅
=
:=
-
ś
rednia wytrzymało
ść
betonu na rozci
ą
ganie w chwili zarysowania
fct.eff
fctm
:=
- napr
ęż
enie w zbrojeniu rozci
ą
ganym natychamiast po zarysowaniu
σs.lim
200MPa
:=
As.min3
kc k
⋅
fct.eff
⋅
Act
σs.lim
⋅
12.253 cm
2
⋅
=
:=
As.min
max As.min1 As.min2
,
As.min3
,
(
)
12.253 cm
2
⋅
=
:=
As1z.prov
As.min
≥
1
=
warunek jest spełniony
5.3.2 No
ś
no
ść
obliczeniowa przekroju na zginanie
5.3.2.1 W płaszczy
ż
nie x-z
a1
Cnom ϕs
+
ϕ
2
+
0.059 m
=
:=
ξeff
As1y.prov fyd
⋅
br dz
⋅
fcd
⋅
0.269
=
:=
ξeff
ξeff.lim
≤
1
=
warunek jest spełniony
σs
fyd
420 MPa
⋅
=
:=
MRdy
dz
2
br
⋅
fcd
⋅
ξeff
⋅
1
ξeff
2
−
⋅
1.058
10
3
×
kNm
⋅
=
:=

16
5.3.2.2 W płaszczy
ż
nie x-y
a1
Cnom ϕs
+
ϕ
2
+
0.059 m
=
:=
ξeff
As1z.prov fyd
⋅
hr dy
⋅
fcd
⋅
0.067
=
:=
ξeff
ξeff.lim
≤
1
=
warunek jest spełniony
σs
fyd
420 MPa
⋅
=
:=
MRdz
dy
2
hr
⋅
fcd
⋅
ξeff
⋅
1
ξeff
2
−
⋅
295.509 kNm
⋅
=
:=
5.3.2.3 Sprawdzenie warunku no
ś
no
ś
ci
MyR
MRdy
MzR
MRdz
+
0.972
=
MyR
MRdy
MzR
MRdz
+
1
≤
1
=
warunek jest spełniony
5.4. WYMIAROWANIA RYGLA"a" NA
Ś
CINANIE
5.4.1 W płaszczy
ż
nie x-z
siła
ś
cinaj
ą
ca
•
VzR
227.666 kN
⋅
=
ś
rednica strzemienia
•
ϕs
10mm
:=
pole strzemion czteroci
ę
tych
•
Asw1
4
π
ϕs
2
4
⋅
3.142 cm
2
⋅
=
:=
obliczeniowa granica plastyczno
ś
ci stali
•
fyds
2.1
10
8
×
Pa
⋅
=
pole przekroju rygla
•
Ac
br hr
⋅
0.423 m
2
=
:=
ramie sił wewn
ę
trzych
•
z
0.9 dz
⋅
:=
współczynnik
•
υ
0.6 1
fck
250 MPa
⋅
−
⋅
0.528
=
:=

17
współczynnik
•
k
1.6m
dz
−
1m
1.009
=
:=
k
max k 1
,
(
)
1.009
=
:=
stopie
ń
zbrojenia podłu
ż
nego
•
ρL
As1y.prov
br dz
⋅
0.013
=
:=
stopie
ń
zbrojenia podłu
ż
nego
•
ρL
min
ρL 0.01
,
(
)
0.01
=
:=
5.4.1.1 No
ś
no
ść
odcinków pierwszego rodzaju
VSd
VzR
227.666 kN
⋅
=
:=
No
ś
no
ść
V Rd1
•
VRd1
0.35k fctd
⋅
1.2
40
ρL
+
(
)
⋅
br
⋅
dz
⋅
288.69 kN
⋅
=
:=
VSd
VRd1
<
1
=
warunek spełniony
No
ś
no
ść
V Rd2
•
VRd2
υ fcd
⋅
br
⋅
z
⋅
3.651
10
3
×
kN
⋅
=
:=
VSd
VRd2
<
1
=
warunek jest spełniony
5.4.1.2 Przyj
ę
cie rozstawu strzemion
Maksymalny rozstaw strzemion przyj
ę
to z warunków konstrukcyjnych
•
smax
min 0.75dz 400mm
,
(
)
40 cm
⋅
=
:=
Przyj
ę
to roztaw strzemion
•
odcinki I-ego rodzaju -
s1
25cm
:=
Stopie
ń
zbrojenia strzemionami
•
ρw
Asw1
s1 br
⋅
1.933
10
3
−
×
=
:=
ρw.min
0.08
fck
MPa
fyks
MPa
1.826
10
3
−
×
=
:=

18
ρw.min ρw
<
1
=
warunek jest spełniony - strzemiona nie maja wpływu na
nosno
ś
c na
ś
cinanie
5.4.2 W płaszczy
ż
nie x-y
siła
ś
cinaj
ą
ca
•
VyR
26.18 kN
⋅
=
ś
rednica strzemienia
•
ϕs 10 mm
⋅
=
pole strzemion czteroci
ę
tych
•
Asw1
4
π
ϕs
2
4
⋅
3.142 cm
2
⋅
=
:=
obliczeniowa granica plastyczno
ś
ci stali
•
fyds
210 MPa
⋅
=
pole przekroju rygla
•
Ac
br hr
⋅
0.423 m
2
=
:=
ramie sił wewn
ę
trzych
•
z
0.9 dy
⋅
:=
współczynnik
•
υ
0.6 1
fck
250 MPa
⋅
−
⋅
0.528
=
:=
współczynnik
•
k
1.6m
dy
−
1m
1.009
=
:=
k
max k 1
,
(
)
1.009
=
:=
ρL
As1z.prov
hr dy
⋅
3.207
10
3
−
×
=
:=
stopie
ń
zbrojenia podłu
ż
nego
•
stopie
ń
zbrojenia podłu
ż
nego
•
ρL
min
ρL 0.01
,
(
)
3.207
10
3
−
×
=
:=
5.4.2.1 No
ś
no
ść
odcinków pierwszego rodzaju
VSd
VyR
26.18 kN
⋅
=
:=
No
ś
no
ść
V Rd1
•
VRd1
0.35k fctd
⋅
1.2
40
ρL
+
(
)
⋅
hr
⋅
dy
⋅
239.664 kN
⋅
=
:=
VSd
VRd1
<
1
=
warunek spełniony
No
ś
no
ść
V Rd2
•
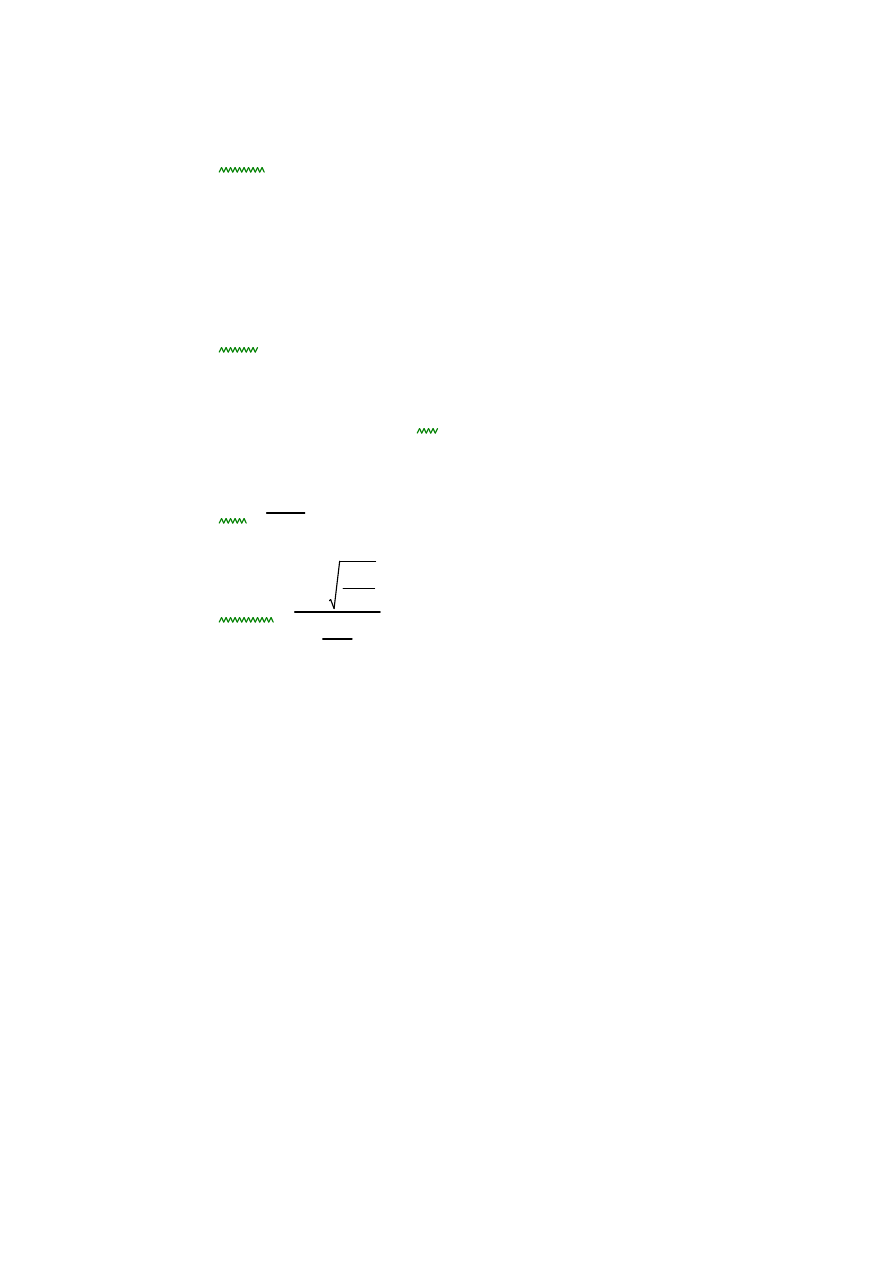
19
VRd2
υ fcd
⋅
hr
⋅
z
⋅
3.651
10
3
×
kN
⋅
=
:=
VSd
VRd2
<
1
=
warunek jest spełniony
5.4.2.2 Przyj
ę
cie rozstawu strzemion
Maksymalny rozstaw strzemion przyjeto z warunków konstrukcyjnych
•
smax
min 0.75dy 400mm
,
(
)
40 cm
⋅
=
:=
Przyj
ę
to roztaw strzemion
•
odcinki I-ego rodzaju -
s1
25cm
:=
Stopie
ń
zbrojenia strzemionami
•
ρw
Asw1
s1 hr
⋅
1.933
10
3
−
×
=
:=
ρw.min
0.08
fck
MPa
fyks
MPa
1.826
10
3
−
×
=
:=
ρw.min ρw
<
1
=
warunek jest spełniony - strzemiona nie maja wpływu na
nosno
ś
c na
ś
cinanie
20
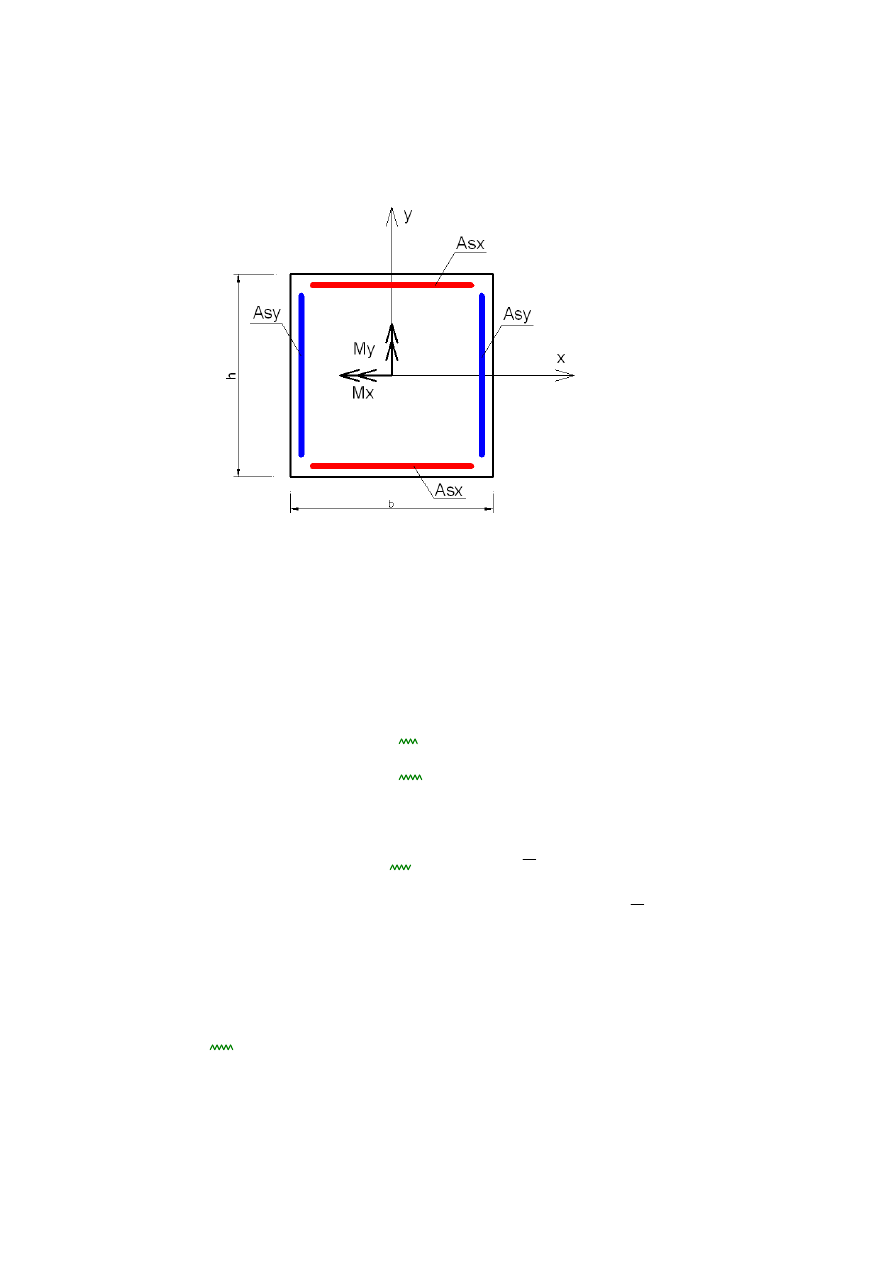
6. WYMIAROWANIE SŁUPA
6.1 WYMIARY PRZEKROJU SŁUPA
hs
0.65 m
=
bs
0.65 m
=
Acs
bs hs
⋅
4.225
10
3
×
cm
2
⋅
=
:=
6.2
Ś
REDNICA PR
Ę
TÓW ZBROJENIA
ś
rednica pr
ę
tów głównych
ϕ
28mm
:=
ś
rednica strzemion
ϕs
10mm
:=
6.3 ODLEGŁO
ŚĆ
Ś
RODKA CI
Ęś
KO
Ś
CI ZBROJENIA
od kraw
ę
dzi rozci
ą
ganej
a1
Cnom ϕs
+
ϕ
2
+
0.059 m
=
:=
a2
Cnom ϕs
+
ϕ
2
+
0.059 m
=
:=
od kraw
ę
dzi mniej rozci
ą
ganej (
ś
ciskanej)
6.4 WYSOKO
ŚĆ
U
ś
YTECZNA PRZEKROJU
dx
bs a1
−
0.591 m
=
:=
w płaszczy
ź
nie z-x
dy
hs a1
−
0.591 m
=
:=
w płaszczy
ź
nie z-y
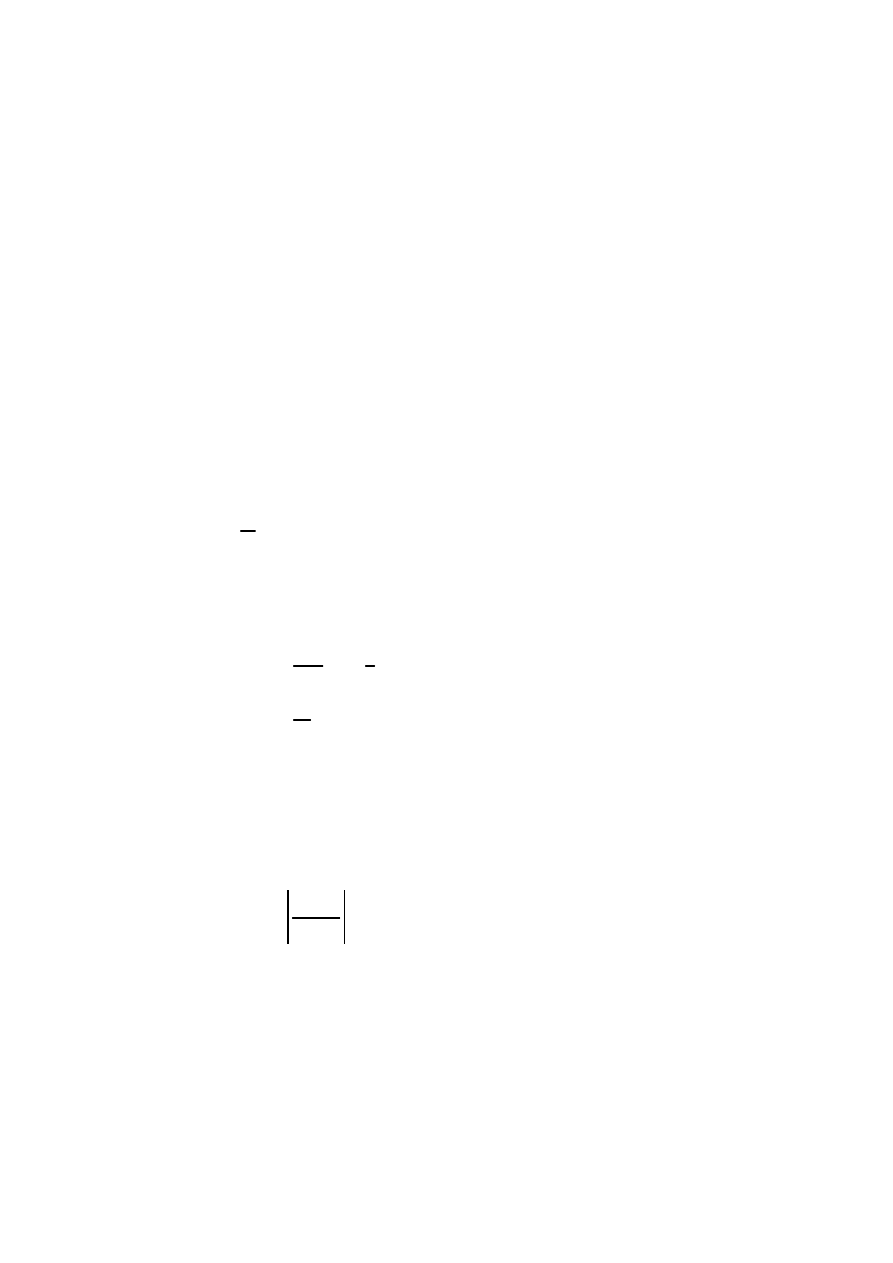
21
6.5 WYMIAROWANIE SŁUPA
6.5.1 Kombinacja 1 i 2
6.5.1.1 Zbrojenie na
ś
ciskanie
6.5.1.1.1 W płaszczy
ź
nie z-y
Wyznaczenie długo
ś
ci obliczeniowej słupa
•
Lcol
7.1m
:=
β
2
:=
lo
β Lcol
⋅
14.2 m
=
:=
Warunek smukło
ś
ci
•
lo
hs
21.846
=
> 7 - słup smukły
Mimo
ś
rod niezamierzony
•
n
1
:=
eay1
Lcol
600
1
1
n
+
⋅
0.024 m
=
:=
eay2
hs
30
0.022 m
=
:=
eay3
0.01m
:=
eay
max eay1 eay2
,
eay3
,
(
)
0.024 m
=
:=
Mimo
ś
rod konstrukcyjny
•
eey
MxD1
Nmax1
0.931 m
⋅
=
:=
Mimo
ś
rod pocz
ą
tkowy
•
eoy
eay eey
+
0.954 m
=
:=
Uwzglednienie smukło
ś
ci
•
wiek betonu w chwili obci
ąż
enia
t0
28
:=

22
wilgotno
ść
wzgl
ę
dna powietrza
RH
80%
:=
pole przekroju elementu
Acs
0.423 m
2
⋅
=
obwód przekroju poddany działaniu powietrza
u
2 bs
⋅
2 hs
⋅
+
2.6 m
⋅
=
:=
miarodajny wymiar przekroju elementu
ho
2
Acs
u
⋅
325 mm
⋅
=
:=
ko
ń
cowy współczynnik pełzania
ϕ ∞ t0
,
(
)
1.77
:=
siła podłu
ż
na wywołana działaniem długotrwałej cz
ęś
ci obcia
ż
e
ń
Nsd.lt
Nmax1
630.712 kN
⋅
=
:=
klt
1
0.5
Nsd.lt
Nmax1
⋅
ϕ ∞ t0
,
(
)
⋅
+
1.885
=
:=
przyj
ę
to powierzchnie zbrojenia
As1p
28 10
4
−
m
2
(
)
⋅
:=
moment bezwładno
ś
ci przyj
ę
tego zbrojenia
Is
0.5 hs
⋅
a1
−
(
)
2
As1p
⋅
1.981
10
4
−
×
m
4
=
:=
ey
max
eoy
hs
0.5
0.01
lo
hs
⋅
−
0.01 fcd
⋅
1
1MPa
⋅
−
,
0.05
,
1.468
=
:=
moment bezwładno
ś
ci przekroju betonowego
Ic
bs hs
3
⋅
12
0.015 m
4
=
:=
Ncrit
9
lo
2
Ecm Ic
⋅
2 klt
⋅
0.11
0.1
ey
+
0.1
+
Es Is
⋅
+
⋅
2.727
10
3
×
kN
⋅
=
:=
η
1
1
Nmax1
Ncrit
−
1.301
=
:=

23
Mimo
ś
ród całkowity
•
etoty
η eoy
⋅
1.242 m
=
:=
Obliczenie pola przekroju zbrojenia
•
ξeff
Nmax1
fcd bs
⋅
dy
⋅
0.082
=
:=
ξeff
ξeff.lim
≤
1
=
warunek spełniony
ξeff
2 a2
⋅
dy
≥
0
=
warunek niespełniony
wysoko
ść
strefy
ś
ciskanej
xeff
2 a2
⋅
0.118 m
=
:=
ramie siły
ś
ciskaj
ą
cej
es1y
dy 0.5 hs
⋅
−
etoty
+
1.508 m
=
:=
Obliczeniowe pole zbrojenia rozci
ą
ganego
•
As1x
Nmax1 es1y dy
−
0.5 xeff
⋅
+
(
)
⋅
fyd dy a2
−
(
)
⋅
27.539 cm
2
⋅
=
:=
pole zbrojenia obliczeniowe mniej rozci
ą
ganego
As2x
As1x
27.539 cm
2
⋅
=
:=
całkowite pole zbrojenia słupa
Asx
As1x As2x
+
55.079 cm
2
⋅
=
:=
Zbrojenie minimalne
•
Asmin
max 0.15
Nmax1
fyd
⋅
0.003 Ac
⋅
,
12.675 cm
2
⋅
=
:=
Zbrojenie maksymalne
•
As.max
4% bs
⋅
hs
⋅
169 cm
2
⋅
=
:=
Zbrojenie zało
ż
one
•
As.zał
56 cm
2
⋅
:=
Sprawdzenie warunków
•
Asx Asmin
≥
1
=
warunek spełniony
≤
=
24
Asx As.max
≤
1
=
warunek spełniony
Asx As.zał
−
Asx
1.672 %
⋅
=
Asx As.zał
−
Asx
20%
≤
1
=
warunek spełniony
Przyj
ę
te zbrojenie
•
zbrojenie rozci
ą
gane
As1x
28 10
4
−
m
2
(
)
⋅
:=
zbrojenie mniej rozci
ą
gane (
ś
ciskane)
As2x
28 10
4
−
m
2
(
)
⋅
:=
pole przekroju zbrojenia
As.yx
As1x As2x
+
56 cm
2
⋅
=
:=
6.5.1.1.2 W płaszczy
ź
nie z-x
Wyznaczenie długo
ś
ci obliczeniowej słupa
•
Lcol
7.1m
:=
β
2
:=
lo
β Lcol
⋅
14.2 m
=
:=
Warunek smukło
ś
ci
•
lo
bs
21.846
=
> 7 - słup smukły
Mimo
ś
rod niezamierzony
•
n
1
:=
eax1
Lcol
600
1
1
n
+
⋅
0.024 m
=
:=
eax2
bs
30
0.022 m
=
:=
eax3
0.01m
:=
eax
max eax1 eax2
,
eax3
,
(
)
0.024 m
=
:=

25
Mimo
ś
rod konstrukcyjny
•
eex
MyD1
Nmax1
0.349 m
⋅
=
:=
Mimo
ś
rod pocz
ą
tkowy
•
eox
eax eex
+
0.373 m
=
:=
Uwzglednienie smukło
ś
ci
•
wiek betonu w chwili obci
ąż
enia
t0
28
:=
wilgotno
ść
wzgl
ę
dna powietrza
RH
80%
:=
pole przekroju elementu
Acs
0.423 m
2
⋅
=
obwód przekroju poddany działaniu powietrza
u
2 bs
⋅
2 hs
⋅
+
2.6 m
⋅
=
:=
miarodajny wymiar przekroju elementu
ho
2
Acs
u
⋅
325 mm
⋅
=
:=
ko
ń
cowy współczynnik pełzania
ϕ ∞ t0
,
(
)
1.77
:=
siła podłu
ż
na wywołana działaniem długotrwałej cz
ęś
ci obcia
ż
e
ń
Nsd.lt
Nmax1
630.712 kN
⋅
=
:=
klt
1
0.5
Nsd.lt
Nmax1
⋅
ϕ ∞ t0
,
(
)
⋅
+
1.885
=
:=
przyj
ę
to powierzchnie zbrojenia
As1p
14cm
2
:=
moment bezwładno
ś
ci przyj
ę
tego zbrojenia
Is
0.5 bs
⋅
a1
−
(
)
2
As1p
⋅
9.906
10
5
−
×
m
4
=
:=
ex
max
eox
bs
0.5
0.01
lo
bs
⋅
−
0.01 fcd
⋅
1
1MPa
⋅
−
,
0.05
,
0.573
=
:=
moment bezwładno
ś
ci przekroju betonowego

26
Ic
hs bs
3
⋅
12
0.015 m
4
=
:=
Ncrit
9
lo
2
Ecm Ic
⋅
2 klt
⋅
0.11
0.1
ex
+
0.1
+
Es Is
⋅
+
⋅
2.369
10
3
×
kN
⋅
=
:=
η
1
1
Nmax1
Ncrit
−
1.363
=
:=
Mimo
ś
ród całkowity
•
etotx
η eox
⋅
0.508 m
=
:=
Obliczenie pola przekroju zbrojenia
•
ξeff
Nmax1
fcd hs
⋅
dx
⋅
0.082
=
:=
ξeff
ξeff.lim
≤
1
=
warunek spełniony
ξeff
2 a2
⋅
dx
≥
0
=
warunek niespełniony
wysoko
ść
strefy
ś
ciskanej
xeff
2 a2
⋅
0.118 m
=
:=
ramie siły
ś
ciskaj
ą
cej
es1x
dx 0.5 bs
⋅
−
etotx
+
0.774 m
=
:=
Obliczeniowe pole zbrojenia rozci
ą
ganego
•
As1y
Nmax1 es1x dx
−
0.5 xeff
⋅
+
(
)
⋅
fyd dx a2
−
(
)
⋅
6.828 cm
2
⋅
=
:=
pole zbrojenia obliczeniowe mniej rozci
ą
ganego
As2y
As1y 6.828 cm
2
⋅
=
:=
Asy
As1y As2y
+
13.657 cm
2
⋅
=
:=
całkowite pole zbrojenia słupa
Zbrojenie minimalne
•
Asmin
max 0.15
Nmax1
fyd
⋅
0.003 Ac
⋅
,
12.675 cm
2
⋅
=
:=

27
Zbrojenie maksymalne
•
As.max
4% bs
⋅
hs
⋅
169 cm
2
⋅
=
:=
Zbrojenie zało
ż
one
•
As.zał
15 cm
2
⋅
:=
Sprawdzenie warunków
•
Asy Asmin
≥
1
=
warunek niespełniony
Asy As.max
≤
1
=
warunek spełniony
Asy As.zał
−
Asy
9.835 %
⋅
=
Asy As.zał
−
Asy
20%
≤
1
=
warunek spełniony
Przyj
ę
te zbrojenie
•
As1y
7.5 10
4
−
m
2
(
)
⋅
:=
zbrojenie rozci
ą
gane
zbrojenie mniej rozci
ą
gane (
ś
ciskane)
As2y
7.5 10
4
−
m
2
(
)
⋅
:=
pole przekroju zbrojenia
As.y
As1y As2y
+
15 cm
2
⋅
=
:=
6.5.1.2 No
ś
no
ść
6.5.1.2.1 W płaszczy
ź
nie z-y
Zakładamy no
ś
no
ść
słupa
•
NRdyz
1.2 10
3
⋅
kN
:=
Obliczenie rzeczywistej no
ś
no
ś
ci słupa
•
przyj
ę
to powierzchnie zbrojenia
As1px
96cm
2
:=
As1x
As1px
2
48 cm
2
⋅
=
:=
As2x
As1px
2
48 cm
2
⋅
=
:=
28
moment bezwładno
ś
ci rzeczywistego zbrojenia
Is
0.5 hs
⋅
a1
−
(
)
2
As1px
⋅
6.793
10
4
×
cm
4
⋅
=
:=
ey
max
eoy
hs
0.5
0.01
lo
hs
⋅
−
0.01 fcd
⋅
1MPa
−
,
0.05
,
1.468
=
:=
moment bezwładno
ś
ci przekroju betonowego
Ic
bs hs
3
⋅
12
0.015 m
4
=
:=
Ncrit
9
lo
2
Ecm Ic
⋅
2 klt
⋅
0.11
0.1
ey
+
0.1
+
Es Is
⋅
+
⋅
7.022
10
3
×
kN
⋅
=
:=
η
1
1
NRdyz
Ncrit
−
1.206
=
:=
Mimo
ś
ród całkowity
•
etoty
η eoy
⋅
1.151 m
=
:=
Obliczenie warto
ś
ci N.Rdy
•
es1y
etoty 0.5 hs
⋅
+
a1
−
1.417 m
=
:=
es2y
etoty 0.5 hs
⋅
−
a2
+
0.885 m
=
:=
- współczynniki pomocnicze
B
1
es1y
dy
−
1.398
−
=
:=
μs1
As1x es1y
⋅
fyd
⋅
bs dy
2
⋅
fcd
⋅
0.629
=
:=
μs2
As2x es2y
⋅
fyd
⋅
bs dy
2
⋅
fcd
⋅
0.393
=
:=

29
- sprawdzenie warunku
es1y dy a2
−
>
1
=
warunek spełniony
ξeff
B
B
2
2
μs1 μs2
−
(
)
⋅
+
+
0.16
=
:=
- sprawdzenie warunku
ξeff
ξeff.lim
<
1
=
warunek spełniony
ξeff
2 a2
⋅
dy
<
1
=
warunek spełniony
No
ś
no
ść
słupa w płaszczy
ź
nie z-y
•
NRdy
fyd As1x
⋅
dy a2
−
(
)
⋅
es2y
1.212
10
3
×
kN
⋅
=
:=
NRdy NRdyz
−
NRdyz
0.965 %
⋅
=
6.5.1.2.1 W płaszczy
ź
nie z-x
Zakładamy no
ś
no
ść
słupa
•
NRdxz
1.28 10
3
⋅
kN
:=
Obliczenie rzeczywistej no
ś
no
ś
ci słupa
•
przyj
ę
to powierzchnie zbrojenia
As1py
36cm
2
:=
As1y
As1py
2
18 cm
2
⋅
=
:=
As2y
As1py
2
18 cm
2
⋅
=
:=
moment bezwładno
ś
ci rzeczywistego zbrojenia
Is
0.5 bs
⋅
a1
−
(
)
2
As1py
⋅
2.547
10
4
×
cm
4
⋅
=
:=
e
max
eox
bs
0.5
0.01
lo
bs
⋅
−
0.01 fcd
⋅
1MPa
−
,
0.05
,
0.573
=
:=
30
moment bezwładno
ś
ci przekroju betonowego
Ic
hs bs
3
⋅
12
0.015 m
4
=
:=
Ncrit
9
lo
2
Ecm Ic
⋅
2 klt
⋅
0.11
0.1
e
+
0.1
+
Es Is
⋅
+
⋅
3.758
10
3
×
kN
⋅
=
:=
η
1
1
NRdxz
Ncrit
−
1.517
=
:=
Mimo
ś
ród całkowity
•
etotx
η eox
⋅
0.565 m
=
:=
Obliczenie warto
ś
ci N.Rdy
•
es1x
etotx 0.5 bs
⋅
+
a1
−
0.831 m
=
:=
es2x
etotx 0.5 bs
⋅
−
a2
+
0.299 m
=
:=
- współczynniki pomocnicze
B
1
es1x
dx
−
0.406
−
=
:=
μs1
As1y es1x
⋅
fyd
⋅
hs dx
2
⋅
fcd
⋅
0.138
=
:=
μs2
As2y es2x
⋅
fyd
⋅
hs dx
2
⋅
fcd
⋅
0.05
=
:=
- sprawdzenie warunku
es1x
dx a2
−
>
1
=
warunek spełniony
ξeff
B
B
2
2
μs1 μs2
−
(
)
⋅
+
+
0.179
=
:=
- sprawdzenie warunku
31
ξeff
ξeff.lim
<
1
=
warunek spełniony
ξeff
2 a2
⋅
dx
<
1
=
warunek spełniony
No
ś
no
ść
słupa w płaszczy
ź
nie z-x
•
NRdx
fyd As1y
⋅
dx a2
−
(
)
⋅
es2x
1.344
10
3
×
kN
⋅
=
:=
NRdx NRdxz
−
NRdxz
5.037 %
⋅
=
6.5.1.2.3 No
ś
no
ść
NRd0
No
ś
no
ść
obliczeniowa przekroju
ś
ciskanego
•
NRdo
fcd bs
⋅
hs
⋅
2 As1x
⋅
2 As1y 4 π
⋅
ϕ
2
4
⋅
−
⋅
+
fyd
⋅
+
1.193
10
4
×
kN
⋅
=
:=
1
1
NRdx
1
NRdy
+
1
NRdo
−
673.265 kN
⋅
=
Okre
ś
lenie współczynnika m
n
•
0.5
ex
ey
bs
hs
⋅
<
2
<
0
=
warunek niespełniony
0.15
Nmax1
fcd bs
⋅
hs
⋅
<
0.5
<
0
=
warunek niespełniony
mn
1
:=
mn Nmax1
⋅
630.712 kN
⋅
=
Sprawdzenie warunku no
ś
no
ś
ci
•

32
mn Nmax1
⋅
1
1
NRdx
1
NRdy
+
1
NRdo
−
<
1
=
warunek został spełniony
Sprawdzenie stopnia zbrojenia
•
ρs
As1x 2
⋅
As1y 2
⋅
+
4
π
⋅
ϕ
2
4
⋅
−
bs hs
⋅
2.541 %
⋅
=
:=
mn Nmax1
⋅
1
1
NRdy
1
NRdx
+
1
NRdo
−
0.937
=
Wykorzystano 93,7% no
ś
no
ś
ci słupa.
6.5.2 Kombinacja 3 - przypadek 1
6.5.2.1 Zbrojenie na
ś
ciskanie
6.5.2.1.1 W płaszczy
ź
nie z-y
Wyznaczenie długo
ś
ci obliczeniowej słupa
•
Lcol
7.1m
:=
β
2
:=
lo
β Lcol
⋅
14.2 m
=
:=
Warunek smukło
ś
ci
•
lo
hs
21.846
=
> 7 - słup smukły
Mimo
ś
rod niezamierzony
•
n
1
:=
eay1
Lcol
600
1
1
n
+
⋅
0.024 m
=
:=
eay2
hs
30
0.022 m
=
:=
eay3
0.01m
:=
33
eay
max eay1 eay2
,
eay3
,
(
)
0.024 m
=
:=
Mimo
ś
rod konstrukcyjny
•
eey
MxD31
Nmax31
0.768 m
⋅
=
:=
Mimo
ś
rod pocz
ą
tkowy
•
eoy
eay eey
+
0.792 m
=
:=
Uwzglednienie smukło
ś
ci
•
wiek betonu w chwili obci
ąż
enia
t0
28
:=
wilgotno
ść
wzgl
ę
dna powietrza
RH
80%
:=
pole przekroju elementu
Acs
0.423 m
2
⋅
=
obwód przekroju poddany działaniu powietrza
u
2 bs
⋅
2 hs
⋅
+
2.6 m
⋅
=
:=
miarodajny wymiar przekroju elementu
ho
2
Acs
u
⋅
325 mm
⋅
=
:=
ko
ń
cowy współczynnik pełzania
ϕ ∞ t0
,
(
)
1.77
:=
siła podłu
ż
na wywołana działaniem długotrwałej cz
ęś
ci obcia
ż
e
ń
Nsd.lt
Nmax31
509.712 kN
⋅
=
:=
klt
1
0.5
Nsd.lt
Nmax31
⋅
ϕ ∞ t0
,
(
)
⋅
+
1.885
=
:=
przyj
ę
to powierzchnie zbrojenia
As1p
20 10
4
−
m
2
(
)
⋅
:=
moment bezwładno
ś
ci przyj
ę
tego zbrojenia
Is
0.5 hs
⋅
a1
−
(
)
2
As1p
⋅
1.415
10
4
−
×
m
4
=
:=
ey
max
eoy
hs
0.5
0.01
lo
hs
⋅
−
0.01 fcd
⋅
1
1MPa
⋅
−
,
0.05
,
1.218
=
:=

34
moment bezwładno
ś
ci przekroju betonowego
Ic
bs hs
3
⋅
12
0.015 m
4
=
:=
Ncrit
9
lo
2
Ecm Ic
⋅
2 klt
⋅
0.11
0.1
ey
+
0.1
+
Es Is
⋅
+
⋅
2.297
10
3
×
kN
⋅
=
:=
η
1
1
Nmax31
Ncrit
−
1.285
=
:=
Mimo
ś
ród całkowity
•
etoty
η eoy
⋅
1.017 m
=
:=
Obliczenie pola przekroju zbrojenia
•
ξeff
Nmax31
fcd bs
⋅
dy
⋅
0.066
=
:=
ξeff
ξeff.lim
≤
1
=
warunek spełniony
ξeff
2 a2
⋅
dy
≥
0
=
warunek niespełniony
wysoko
ść
strefy
ś
ciskanej
xeff
2 a2
⋅
0.118 m
=
:=
ramie siły
ś
ciskaj
ą
cej
es1y
dy 0.5 hs
⋅
−
etoty
+
1.283 m
=
:=
Obliczeniowe pole zbrojenia rozci
ą
ganego
•
As1x
Nmax31 es1y dy
−
0.5 xeff
⋅
+
(
)
⋅
fyd dy a2
−
(
)
⋅
17.137 cm
2
⋅
=
:=
pole zbrojenia obliczeniowe mniej rozci
ą
ganego
As2x
As1x
17.137 cm
2
⋅
=
:=
całkowite pole zbrojenia słupa
Asx
As1x As2x
+
34.274 cm
2
⋅
=
:=
Zbrojenie minimalne
•
Asmin
max 0.15
Nmax31
fyd
⋅
0.003 Ac
⋅
,
12.675 cm
2
⋅
=
:=
35
Zbrojenie maksymalne
•
As.max
4% bs
⋅
hs
⋅
169 cm
2
⋅
=
:=
Zbrojenie zało
ż
one
•
As.zał
36 cm
2
⋅
:=
Sprawdzenie warunków
•
Asx Asmin
≥
1
=
warunek spełniony
Asx As.max
≤
1
=
warunek spełniony
Asx As.zał
−
Asx
5.035 %
⋅
=
Asx As.zał
−
Asx
20%
≤
1
=
warunek spełniony
Przyj
ę
te zbrojenie
•
zbrojenie rozci
ą
gane
As1x
18 10
4
−
m
2
(
)
⋅
:=
zbrojenie mniej rozci
ą
gane (
ś
ciskane)
As2x
18 10
4
−
m
2
(
)
⋅
:=
pole przekroju zbrojenia
As.yx
As1x As2x
+
36 cm
2
⋅
=
:=
6.5.2.1.2 W płaszczy
ź
nie z-x
Wyznaczenie długo
ś
ci obliczeniowej słupa
•
Lcol
7.1m
:=
β
2
:=
lo
β Lcol
⋅
14.2 m
=
:=
Warunek smukło
ś
ci
•
lo
bs
21.846
=
> 7 - słup smukły
36
Mimo
ś
rod niezamierzony
•
n
1
:=
eax1
Lcol
600
1
1
n
+
⋅
0.024 m
=
:=
eax2
bs
30
0.022 m
=
:=
eax3
0.01m
:=
eax
max eax1 eax2
,
eax3
,
(
)
0.024 m
=
:=
Mimo
ś
rod konstrukcyjny
•
eex
MyD31
Nmax31
0.954 m
⋅
=
:=
Mimo
ś
rod pocz
ą
tkowy
•
eox
eax eex
+
0.978 m
=
:=
Uwzglednienie smukło
ś
ci
•
wiek betonu w chwili obci
ąż
enia
t0
28
:=
wilgotno
ść
wzgl
ę
dna powietrza
RH
80%
:=
pole przekroju elementu
Acs
0.423 m
2
⋅
=
obwód przekroju poddany działaniu powietrza
u
2 bs
⋅
2 hs
⋅
+
2.6 m
⋅
=
:=
miarodajny wymiar przekroju elementu
ho
2
Acs
u
⋅
325 mm
⋅
=
:=
ko
ń
cowy współczynnik pełzania
ϕ ∞ t0
,
(
)
1.77
:=
siła podłu
ż
na wywołana działaniem długotrwałej cz
ęś
ci obcia
ż
e
ń
Nsd.lt
Nmax31
509.712 kN
⋅
=
:=
klt
1
0.5
Nsd.lt
Nmax31
⋅
ϕ ∞ t0
,
(
)
⋅
+
1.885
=
:=

37
przyj
ę
to powierzchnie zbrojenia
As1p
35cm
2
:=
moment bezwładno
ś
ci przyj
ę
tego zbrojenia
Is
0.5 bs
⋅
a1
−
(
)
2
As1p
⋅
2.476
10
4
−
×
m
4
=
:=
ex
max
eox
bs
0.5
0.01
lo
bs
⋅
−
0.01 fcd
⋅
1
1MPa
⋅
−
,
0.05
,
1.504
=
:=
moment bezwładno
ś
ci przekroju betonowego
Ic
hs bs
3
⋅
12
0.015 m
4
=
:=
Ncrit
9
lo
2
Ecm Ic
⋅
2 klt
⋅
0.11
0.1
ex
+
0.1
+
Es Is
⋅
+
⋅
3.161
10
3
×
kN
⋅
=
:=
η
1
1
Nmax31
Ncrit
−
1.192
=
:=
Mimo
ś
ród całkowity
•
etotx
η eox
⋅
1.166 m
=
:=
Obliczenie pola przekroju zbrojenia
•
ξeff
Nmax31
fcd hs
⋅
dx
⋅
0.066
=
:=
ξeff
ξeff.lim
≤
1
=
warunek spełniony
ξeff
2 a2
⋅
dx
≥
0
=
warunek niespełniony
wysoko
ść
strefy
ś
ciskanej
xeff
2 a2
⋅
0.118 m
=
:=
ramie siły
ś
ciskaj
ą
cej
es1x
dx 0.5 bs
⋅
−
etotx
+
1.432 m
=
:=
Obliczeniowe pole zbrojenia rozci
ą
ganego
•

38
As1y
Nmax31 es1x dx
−
0.5 xeff
⋅
+
(
)
⋅
fyd dx a2
−
(
)
⋅
20.525 cm
2
⋅
=
:=
pole zbrojenia obliczeniowe mniej rozci
ą
ganego
As2y
As1y 20.525 cm
2
⋅
=
:=
Asy
As1y As2y
+
41.051 cm
2
⋅
=
:=
całkowite pole zbrojenia słupa
Zbrojenie minimalne
•
Asmin
max 0.15
Nmax31
fyd
⋅
0.003 Ac
⋅
,
12.675 cm
2
⋅
=
:=
Zbrojenie maksymalne
•
As.max
4% bs
⋅
hs
⋅
169 cm
2
⋅
=
:=
Zbrojenie zało
ż
one
•
As.zał
43 cm
2
⋅
:=
Sprawdzenie warunków
•
Asy Asmin
≥
1
=
warunek niespełniony
Asy As.max
≤
1
=
warunek spełniony
Asy As.zał
−
Asy
4.749 %
⋅
=
Asy As.zał
−
Asy
20%
≤
1
=
warunek spełniony
Przyj
ę
te zbrojenie
•
As1y
21.5 10
4
−
m
2
(
)
⋅
:=
zbrojenie rozci
ą
gane
zbrojenie mniej rozci
ą
gane (
ś
ciskane)
As2y
21.5 10
4
−
m
2
(
)
⋅
:=
pole przekroju zbrojenia
As.y
As1y As2y
+
43 cm
2
⋅
=
:=
39
6.5.2.2 No
ś
no
ść
6.5.2.2.1 W płaszczy
ź
nie z-y
Zakładamy no
ś
no
ść
słupa
•
NRdyz
1.1 10
3
⋅
kN
:=
Obliczenie rzeczywistej no
ś
no
ś
ci słupa
•
przyj
ę
to powierzchnie zbrojenia
As1px
66cm
2
:=
As1x
As1px
2
33 cm
2
⋅
=
:=
As2x
As1px
2
33 cm
2
⋅
=
:=
moment bezwładno
ś
ci rzeczywistego zbrojenia
Is
0.5 hs
⋅
a1
−
(
)
2
As1px
⋅
4.67
10
4
×
cm
4
⋅
=
:=
ey
max
eoy
hs
0.5
0.01
lo
hs
⋅
−
0.01 fcd
⋅
1MPa
−
,
0.05
,
1.218
=
:=
moment bezwładno
ś
ci przekroju betonowego
Ic
bs hs
3
⋅
12
0.015 m
4
=
:=
Ncrit
9
lo
2
Ecm Ic
⋅
2 klt
⋅
0.11
0.1
ey
+
0.1
+
Es Is
⋅
+
⋅
5.203
10
3
×
kN
⋅
=
:=
η
1
1
NRdyz
Ncrit
−
1.268
=
:=
Mimo
ś
ród całkowity
•
etoty
η eoy
⋅
1.004 m
=
:=
40
Obliczenie warto
ś
ci N.Rdy
•
es1y
etoty 0.5 hs
⋅
+
a1
−
1.27 m
=
:=
es2y
etoty 0.5 hs
⋅
−
a2
+
0.738 m
=
:=
- współczynniki pomocnicze
B
1
es1y
dy
−
1.148
−
=
:=
μs1
As1x es1y
⋅
fyd
⋅
bs dy
2
⋅
fcd
⋅
0.388
=
:=
μs2
As2x es2y
⋅
fyd
⋅
bs dy
2
⋅
fcd
⋅
0.225
=
:=
- sprawdzenie warunku
es1y dy a2
−
>
1
=
warunek spełniony
ξeff
B
B
2
2
μs1 μs2
−
(
)
⋅
+
+
0.134
=
:=
- sprawdzenie warunku
ξeff
ξeff.lim
<
1
=
warunek spełniony
ξeff
2 a2
⋅
dy
<
1
=
warunek spełniony
No
ś
no
ść
słupa w płaszczy
ź
nie z-y
•
NRdy
fyd As1x
⋅
dy a2
−
(
)
⋅
es2y
999.455 kN
⋅
=
:=
NRdy NRdyz
−
NRdyz
9.14 %
⋅
=
41
6.5.2.2.1 W płaszczy
ź
nie z-x
Zakładamy no
ś
no
ść
słupa
•
NRdxz
1.1 10
3
⋅
kN
:=
Obliczenie rzeczywistej no
ś
no
ś
ci słupa
•
przyj
ę
to powierzchnie zbrojenia
As1py
84cm
2
:=
As1y
As1py
2
42 cm
2
⋅
=
:=
As2y
As1py
2
42 cm
2
⋅
=
:=
moment bezwładno
ś
ci rzeczywistego zbrojenia
Is
0.5 bs
⋅
a1
−
(
)
2
As1py
⋅
5.944
10
4
×
cm
4
⋅
=
:=
e
max
eox
bs
0.5
0.01
lo
bs
⋅
−
0.01 fcd
⋅
1MPa
−
,
0.05
,
1.504
=
:=
moment bezwładno
ś
ci przekroju betonowego
Ic
hs bs
3
⋅
12
0.015 m
4
=
:=
Ncrit
9
lo
2
Ecm Ic
⋅
2 klt
⋅
0.11
0.1
e
+
0.1
+
Es Is
⋅
+
⋅
6.256
10
3
×
kN
⋅
=
:=
η
1
1
NRdxz
Ncrit
−
1.213
=
:=
Mimo
ś
ród całkowity
•
etotx
η eox
⋅
1.186 m
=
:=
42
Obliczenie warto
ś
ci N.Rdy
•
es1x
etotx 0.5 bs
⋅
+
a1
−
1.452 m
=
:=
es2x
etotx 0.5 bs
⋅
−
a2
+
0.92 m
=
:=
- współczynniki pomocnicze
B
1
es1x
dx
−
1.457
−
=
:=
μs1
As1y es1x
⋅
fyd
⋅
hs dx
2
⋅
fcd
⋅
0.564
=
:=
μs2
As2y es2x
⋅
fyd
⋅
hs dx
2
⋅
fcd
⋅
0.358
=
:=
- sprawdzenie warunku
es1x
dx a2
−
>
1
=
warunek spełniony
ξeff
B
B
2
2
μs1 μs2
−
(
)
⋅
+
+
0.136
=
:=
- sprawdzenie warunku
ξeff
ξeff.lim
<
1
=
warunek spełniony
ξeff
2 a2
⋅
dx
<
1
=
warunek spełniony
No
ś
no
ść
słupa w płaszczy
ź
nie z-x
•
NRdx
fyd As1y
⋅
dx a2
−
(
)
⋅
es2x
1.02
10
3
×
kN
⋅
=
:=
NRdx NRdxz
−
NRdxz
7.306 %
⋅
=

43
6.5.2.2.3 No
ś
no
ść
NRd0
No
ś
no
ść
obliczeniowa przekroju
ś
ciskanego
•
NRdo
fcd bs
⋅
hs
⋅
2 As1x
⋅
2 As1y 4 π
⋅
ϕ
2
4
⋅
−
⋅
+
fyd
⋅
+
1.268
10
4
×
kN
⋅
=
:=
1
1
NRdx
1
NRdy
+
1
NRdo
−
525.644 kN
⋅
=
Okre
ś
lenie współczynnika m
n
•
0.5
ex
ey
bs
hs
⋅
<
2
<
1
=
warunek spełniony
0.15
Nmax31
fcd bs
⋅
hs
⋅
<
0.5
<
0
=
warunek niespełniony
mn
1
:=
mn Nmax31
⋅
509.712 kN
⋅
=
Sprawdzenie warunku no
ś
no
ś
ci
•
mn Nmax31
⋅
1
1
NRdx
1
NRdy
+
1
NRdo
−
<
1
=
warunek został spełniony
Sprawdzenie stopnia zbrojenia
•
ρs
As1x 2
⋅
As1y 2
⋅
+
4
π
⋅
ϕ
2
4
⋅
−
bs hs
⋅
2.967 %
⋅
=
:=
mn Nmax31
⋅
1
1
NRdy
1
NRdx
+
1
NRdo
−
0.97
=
Wykorzystano 97,0% no
ś
no
ś
ci słupa.
44
6.5.3 Kombinacja 3 -przypadek 2
6.5.3.1 Zbrojenie na
ś
ciskanie
6.5.3.1.1 W płaszczy
ź
nie z-y
Wyznaczenie długo
ś
ci obliczeniowej słupa
•
Lcol
7.1m
:=
β
2
:=
lo
β Lcol
⋅
14.2 m
=
:=
Warunek smukło
ś
ci
•
lo
hs
21.846
=
> 7 - słup smukły
Mimo
ś
rod niezamierzony
•
n
1
:=
eay1
Lcol
600
1
1
n
+
⋅
0.024 m
=
:=
eay2
hs
30
0.022 m
=
:=
eay3
0.01m
:=
eay
max eay1 eay2
,
eay3
,
(
)
0.024 m
=
:=
Mimo
ś
rod konstrukcyjny
•
eey
MxD32
Nmax32
0.503 m
⋅
=
:=
Mimo
ś
rod pocz
ą
tkowy
•
eoy
eay eey
+
0.527 m
=
:=
Uwzglednienie smukło
ś
ci
•
wiek betonu w chwili obci
ąż
enia
t0
28
:=
wilgotno
ść
wzgl
ę
dna powietrza
RH
80%
:=

45
pole przekroju elementu
Acs
0.423 m
2
⋅
=
obwód przekroju poddany działaniu powietrza
u
2 bs
⋅
2 hs
⋅
+
2.6 m
⋅
=
:=
miarodajny wymiar przekroju elementu
ho
2
Acs
u
⋅
325 mm
⋅
=
:=
ko
ń
cowy współczynnik pełzania
ϕ ∞ t0
,
(
)
1.77
:=
siła podłu
ż
na wywołana działaniem długotrwałej cz
ęś
ci obcia
ż
e
ń
Nsd.lt
Nmax32
388.712 kN
⋅
=
:=
klt
1
0.5
Nsd.lt
Nmax32
⋅
ϕ ∞ t0
,
(
)
⋅
+
1.885
=
:=
przyj
ę
to powierzchnie zbrojenia
As1p
18 10
4
−
m
2
(
)
⋅
:=
moment bezwładno
ś
ci przyj
ę
tego zbrojenia
Is
0.5 hs
⋅
a1
−
(
)
2
As1p
⋅
1.274
10
4
−
×
m
4
=
:=
ey
max
eoy
hs
0.5
0.01
lo
hs
⋅
−
0.01 fcd
⋅
1
1MPa
⋅
−
,
0.05
,
0.811
=
:=
moment bezwładno
ś
ci przekroju betonowego
Ic
bs hs
3
⋅
12
0.015 m
4
=
:=
Ncrit
9
lo
2
Ecm Ic
⋅
2 klt
⋅
0.11
0.1
ey
+
0.1
+
Es Is
⋅
+
⋅
2.381
10
3
×
kN
⋅
=
:=
η
1
1
Nmax32
Ncrit
−
1.195
=
:=
Mimo
ś
ród całkowity
•
etoty
η eoy
⋅
0.63 m
=
:=

46
Obliczenie pola przekroju zbrojenia
•
ξeff
Nmax32
fcd bs
⋅
dy
⋅
0.051
=
:=
ξeff
ξeff.lim
≤
1
=
warunek spełniony
ξeff
2 a2
⋅
dy
≥
0
=
warunek niespełniony
wysoko
ść
strefy
ś
ciskanej
xeff
2 a2
⋅
0.118 m
=
:=
ramie siły
ś
ciskaj
ą
cej
es1y
dy 0.5 hs
⋅
−
etoty
+
0.896 m
=
:=
Obliczeniowe pole zbrojenia rozci
ą
ganego
•
As1x
Nmax32 es1y dy
−
0.5 xeff
⋅
+
(
)
⋅
fyd dy a2
−
(
)
⋅
6.332 cm
2
⋅
=
:=
pole zbrojenia obliczeniowe mniej rozci
ą
ganego
As2x
As1x
6.332 cm
2
⋅
=
:=
całkowite pole zbrojenia słupa
Asx
As1x As2x
+
12.663 cm
2
⋅
=
:=
Zbrojenie minimalne
•
Asmin
max 0.15
Nmax32
fyd
⋅
0.003 Ac
⋅
,
12.675 cm
2
⋅
=
:=
Zbrojenie maksymalne
•
As.max
4% bs
⋅
hs
⋅
169 cm
2
⋅
=
:=
Zbrojenie zało
ż
one
•
As.zał
14 cm
2
⋅
:=
Sprawdzenie warunków
•
Asx Asmin
≥
0
=
warunek spełniony
Asx As.max
≤
1
=
warunek spełniony
Asx As.zał
−
Asx
10.556 %
⋅
=

47
Asx As.zał
−
Asx
20%
≤
1
=
warunek spełniony
Przyj
ę
te zbrojenie
•
zbrojenie rozci
ą
gane
As1x
7 10
4
−
m
2
(
)
⋅
:=
zbrojenie mniej rozci
ą
gane (
ś
ciskane)
As2x
7 10
4
−
m
2
(
)
⋅
:=
pole przekroju zbrojenia
As.yx
As1x As2x
+
14 cm
2
⋅
=
:=
6.5.3.1.2 W płaszczy
ź
nie z-x
Wyznaczenie długo
ś
ci obliczeniowej słupa
•
Lcol
7.1m
:=
β
2
:=
lo
β Lcol
⋅
14.2 m
=
:=
Warunek smukło
ś
ci
•
lo
bs
21.846
=
> 7 - słup smukły
Mimo
ś
rod niezamierzony
•
n
1
:=
eax1
Lcol
600
1
1
n
+
⋅
0.024 m
=
:=
eax2
bs
30
0.022 m
=
:=
eax3
0.01m
:=
eax
max eax1 eax2
,
eax3
,
(
)
0.024 m
=
:=
Mimo
ś
rod konstrukcyjny
•
eex
MyD32
Nmax32
1.251 m
⋅
=
:=

48
Mimo
ś
rod pocz
ą
tkowy
•
eox
eax eex
+
1.275 m
=
:=
Uwzglednienie smukło
ś
ci
•
wiek betonu w chwili obci
ąż
enia
t0
28
:=
wilgotno
ść
wzgl
ę
dna powietrza
RH
80%
:=
pole przekroju elementu
Acs
0.423 m
2
⋅
=
obwód przekroju poddany działaniu powietrza
u
2 bs
⋅
2 hs
⋅
+
2.6 m
⋅
=
:=
miarodajny wymiar przekroju elementu
ho
2
Acs
u
⋅
325 mm
⋅
=
:=
ko
ń
cowy współczynnik pełzania
ϕ ∞ t0
,
(
)
1.77
:=
siła podłu
ż
na wywołana działaniem długotrwałej cz
ęś
ci obcia
ż
e
ń
Nsd.lt
Nmax32
388.712 kN
⋅
=
:=
klt
1
0.5
Nsd.lt
Nmax32
⋅
ϕ ∞ t0
,
(
)
⋅
+
1.885
=
:=
przyj
ę
to powierzchnie zbrojenia
As1p
25cm
2
:=
moment bezwładno
ś
ci przyj
ę
tego zbrojenia
Is
0.5 bs
⋅
a1
−
(
)
2
As1p
⋅
1.769
10
4
−
×
m
4
=
:=
ex
max
eox
bs
0.5
0.01
lo
bs
⋅
−
0.01 fcd
⋅
1
1MPa
⋅
−
,
0.05
,
1.961
=
:=
moment bezwładno
ś
ci przekroju betonowego
Ic
hs bs
3
⋅
12
0.015 m
4
=
:=
Ncrit
9
lo
2
Ecm Ic
⋅
2 klt
⋅
0.11
0.1
ex
+
0.1
+
Es Is
⋅
+
⋅
2.443
10
3
×
kN
⋅
=
:=

49
η
1
1
Nmax32
Ncrit
−
1.189
=
:=
Mimo
ś
ród całkowity
•
etotx
η eox
⋅
1.516 m
=
:=
Obliczenie pola przekroju zbrojenia
•
ξeff
Nmax32
fcd hs
⋅
dx
⋅
0.051
=
:=
ξeff
ξeff.lim
≤
1
=
warunek spełniony
ξeff
2 a2
⋅
dx
≥
0
=
warunek niespełniony
wysoko
ść
strefy
ś
ciskanej
xeff
2 a2
⋅
0.118 m
=
:=
ramie siły
ś
ciskaj
ą
cej
es1x
dx 0.5 bs
⋅
−
etotx
+
1.782 m
=
:=
Obliczeniowe pole zbrojenia rozci
ą
ganego
•
As1y
Nmax32 es1x dx
−
0.5 xeff
⋅
+
(
)
⋅
fyd dx a2
−
(
)
⋅
21.744 cm
2
⋅
=
:=
pole zbrojenia obliczeniowe mniej rozci
ą
ganego
As2y
As1y 21.744 cm
2
⋅
=
:=
Asy
As1y As2y
+
43.489 cm
2
⋅
=
:=
całkowite pole zbrojenia słupa
Zbrojenie minimalne
•
Asmin
max 0.15
Nmax32
fyd
⋅
0.003 Ac
⋅
,
12.675 cm
2
⋅
=
:=
Zbrojenie maksymalne
•
As.max
4% bs
⋅
hs
⋅
169 cm
2
⋅
=
:=
Zbrojenie zało
ż
one
•
As.zał
44 cm
2
⋅
:=
50
Sprawdzenie warunków
•
Asy Asmin
≥
1
=
warunek niespełniony
Asy As.max
≤
1
=
warunek spełniony
Asy As.zał
−
Asy
1.175 %
⋅
=
Asy As.zał
−
Asy
20%
≤
1
=
warunek spełniony
Przyj
ę
te zbrojenie
•
As1y
22 10
4
−
m
2
(
)
⋅
:=
zbrojenie rozci
ą
gane
zbrojenie mniej rozci
ą
gane (
ś
ciskane)
As2y
22 10
4
−
m
2
(
)
⋅
:=
pole przekroju zbrojenia
As.y
As1y As2y
+
44 cm
2
⋅
=
:=
6.5.3.2 No
ś
no
ść
6.5.3.2.1 W płaszczy
ź
nie z-y
Zakładamy no
ś
no
ść
słupa
•
NRdyz
0.9 10
3
⋅
kN
:=
Obliczenie rzeczywistej no
ś
no
ś
ci słupa
•
przyj
ę
to powierzchnie zbrojenia
As1px
36cm
2
:=
As1x
As1px
2
18 cm
2
⋅
=
:=
As2x
As1px
2
18 cm
2
⋅
=
:=
moment bezwładno
ś
ci rzeczywistego zbrojenia
Is
0.5 hs
⋅
a1
−
(
)
2
As1px
⋅
2.547
10
4
×
cm
4
⋅
=
:=
ey
max
eoy
hs
0.5
0.01
lo
hs
⋅
−
0.01 fcd
⋅
1MPa
−
,
0.05
,
0.811
=
:=

51
moment bezwładno
ś
ci przekroju betonowego
Ic
bs hs
3
⋅
12
0.015 m
4
=
:=
Ncrit
9
lo
2
Ecm Ic
⋅
2 klt
⋅
0.11
0.1
ey
+
0.1
+
Es Is
⋅
+
⋅
3.518
10
3
×
kN
⋅
=
:=
η
1
1
NRdyz
Ncrit
−
1.344
=
:=
Mimo
ś
ród całkowity
•
etoty
η eoy
⋅
0.708 m
=
:=
Obliczenie warto
ś
ci N.Rdy
•
es1y
etoty 0.5 hs
⋅
+
a1
−
0.974 m
=
:=
es2y
etoty 0.5 hs
⋅
−
a2
+
0.442 m
=
:=
- współczynniki pomocnicze
B
1
es1y
dy
−
0.649
−
=
:=
μs1
As1x es1y
⋅
fyd
⋅
bs dy
2
⋅
fcd
⋅
0.162
=
:=
μs2
As2x es2y
⋅
fyd
⋅
bs dy
2
⋅
fcd
⋅
0.074
=
:=
- sprawdzenie warunku
es1y dy a2
−
>
1
=
warunek spełniony
ξeff
B
B
2
2
μs1 μs2
−
(
)
⋅
+
+
0.125
=
:=

52
- sprawdzenie warunku
ξeff
ξeff.lim
<
1
=
warunek spełniony
ξeff
2 a2
⋅
dy
<
1
=
warunek spełniony
No
ś
no
ść
słupa w płaszczy
ź
nie z-y
•
NRdy
fyd As1x
⋅
dy a2
−
(
)
⋅
es2y
909.273 kN
⋅
=
:=
NRdy NRdyz
−
NRdyz
1.03 %
⋅
=
6.5.3.2.1 W płaszczy
ź
nie z-x
Zakładamy no
ś
no
ść
słupa
•
NRdxz
0.8 10
3
⋅
kN
:=
Obliczenie rzeczywistej no
ś
no
ś
ci słupa
•
przyj
ę
to powierzchnie zbrojenia
As1py
84cm
2
:=
As1y
As1py
2
cm
2
⋅
=
:=
As2y
As1py
2
cm
2
⋅
=
:=
moment bezwładno
ś
ci rzeczywistego zbrojenia
Is
0.5 bs
⋅
a1
−
(
)
2
As1py
⋅
5.944
10
4
×
cm
4
⋅
=
:=
e
max
eox
bs
0.5
0.01
lo
bs
⋅
−
0.01 fcd
⋅
1MPa
−
,
0.05
,
1.961
=
:=
moment bezwładno
ś
ci przekroju betonowego
Ic
hs bs
3
⋅
12
0.015 m
4
=
:=
53
Ncrit
9
lo
2
Ecm Ic
⋅
2 klt
⋅
0.11
0.1
e
+
0.1
+
Es Is
⋅
+
⋅
6.17
10
3
×
kN
⋅
=
:=
η
1
1
NRdxz
Ncrit
−
1.149
=
:=
Mimo
ś
ród całkowity
•
etotx
η eox
⋅
1.465 m
=
:=
Obliczenie warto
ś
ci N.Rdy
•
es1x
etotx 0.5 bs
⋅
+
a1
−
1.731 m
=
:=
es2x
etotx 0.5 bs
⋅
−
a2
+
1.199 m
=
:=
- współczynniki pomocnicze
B
1
es1x
dx
−
1.928
−
=
:=
μs1
As1y es1x
⋅
fyd
⋅
hs dx
2
⋅
fcd
⋅
0.672
=
:=
μs2
As2y es2x
⋅
fyd
⋅
hs dx
2
⋅
fcd
⋅
0.466
=
:=
- sprawdzenie warunku
es1x
dx a2
−
>
1
=
warunek spełniony
ξeff
B
B
2
2
μs1 μs2
−
(
)
⋅
+
+
0.104
=
:=
- sprawdzenie warunku
ξeff
ξeff.lim
<
1
=
warunek spełniony
⋅
54
ξeff
2 a2
⋅
dx
<
1
=
warunek spełniony
No
ś
no
ść
słupa w płaszczy
ź
nie z-x
•
NRdx
fyd As1y
⋅
dx a2
−
(
)
⋅
es2x
782.913 kN
⋅
=
:=
NRdx NRdxz
−
NRdxz
2.136 %
⋅
=
6.5.3.2.3 No
ś
no
ść
NRd0
No
ś
no
ść
obliczeniowa przekroju
ś
ciskanego
•
NRdo
fcd bs
⋅
hs
⋅
2 As1x
⋅
2 As1y 4 π
⋅
ϕ
2
4
⋅
−
⋅
+
fyd
⋅
+
1.142
10
4
×
kN
⋅
=
:=
1
1
NRdx
1
NRdy
+
1
NRdo
−
436.776 kN
⋅
=
Okre
ś
lenie współczynnika m
n
•
0.5
ex
ey
bs
hs
⋅
<
2
<
0
=
warunek niespełniony
0.15
Nmax32
fcd bs
⋅
hs
⋅
<
0.5
<
0
=
warunek niespełniony
mn
1
:=
mn Nmax32
⋅
388.712 kN
⋅
=
Sprawdzenie warunku no
ś
no
ś
ci
•
mn Nmax32
⋅
1
1
NRdx
1
NRdy
+
1
NRdo
−
<
1
=
warunek został spełniony

55
Sprawdzenie stopnia zbrojenia
•
ρs
As1x 2
⋅
As1y 2
⋅
+
4
π
⋅
ϕ
2
4
⋅
−
bs hs
⋅
2.257 %
⋅
=
:=
mn Nmax32
⋅
1
1
NRdy
1
NRdx
+
1
NRdo
−
0.89
=
Wykorzystano 89,0% no
ś
no
ś
ci słupa.
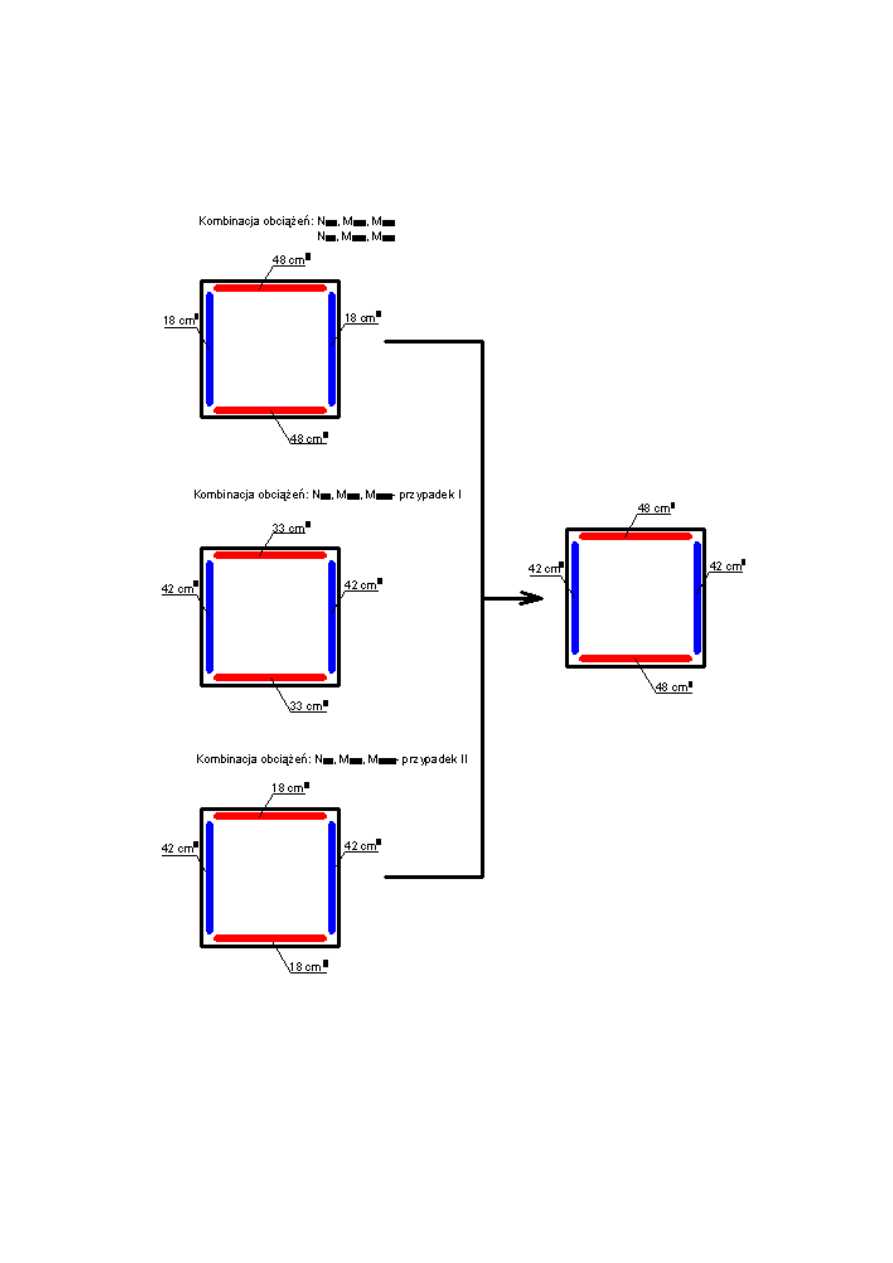
56

57
6.5.4 Kombinacja 4
6.5.1.1 Zbrojenie na
ś
ciskanie przy jednoczesnym skr
ę
caniu
- moment sk
ę
caj
ą
cy słup
Mzmax4
141.372 kNm
⋅
=
- siła poprzeczna słupa
VyD4
26.18 kN
⋅
=
- siła
ś
ciskaj
ą
ca słup
Nmax1
630.712 kN
⋅
=
No
ś
no
ść
V Rd2
•
-
ś
rednie napr
ęż
enie
ś
ciskaj
ą
ce w betonie
σcp
Nmax1
Ac
1.493 MPa
⋅
=
:=
σcp 0.25fcd
≤
1
=
- współczynnik
αc
1
σcp
fcd
+
1.075
=
:=
- k
ą
t nachylenia krzy
ż
ulców betonowych
θ
26.6deg
:=
cot
θ
( )
1.997
=
1
cot
θ
( )
≤
2
≤
1
=
warunek spełniony
- ramie sił wewn
ę
trzych
z
0.9dy
0.532 m
=
:=
- współczynnik
υ
0.6 1
fck
250 MPa
⋅
−
⋅
0.528
=
:=
- no
ś
no
ść
obliczeniowa na
ś
cinanie ze wzgl
ę
gu na
ś
ciskanie betonu
zbrojenie na
ś
cinanie wył
ą
cznie ze strzemion prostopadłych do osi elementu
VRd2
υ fcd
⋅
bs
⋅
z
⋅
cot
θ
( )
1
cot
θ
( )
2
+
⋅
1.462
10
3
×
kN
⋅
=
:=
VRd2.r
αc VRd2
⋅
1.571
10
6
×
N
=
:=

58
No
ś
no
ść
T Rd1
•
- całkowita powierzchnia przekroju elementu zawartego wewn
ą
trz obwodu u
A
bs hs
⋅
0.423 m
2
=
:=
- obwód zewn
ę
trzny przekroju
u
2 bs hs
+
(
)
⋅
2.6 m
=
:=
- grubo
ść
zast
ę
pcza
ś
cianki przekroju
tzas
A
u
0.163 m
=
:=
- minimalna grubo
ść
zast
ę
pcza
ś
cianki przekroju
t
2 Cnom
⋅
0.07 m
=
:=
A
u
tzas
≥
t
>
1
=
warunek spełniony
- pole przekroju dla t
.zas
Ak
bs tzas
−
(
)
hs tzas
−
(
)
⋅
0.238 m
2
=
:=
- obwód rdzenia
uk
2
bs tzas
−
(
)
hs tzas
−
(
)
+
⋅
1.95 m
=
:=
- no
ś
no
ść
obliczeniowa na skr
ę
canie
TRd1
2
υ
⋅
fcd
⋅
tzas
⋅
Ak
⋅
cot
θ
( )
cot 90deg
(
)
+
1
cot
θ
( )
2
+
⋅
326.553 kNm
⋅
=
:=
Warunek ograniczaj
ą
cy
•
Mzmax4
TRd1
2
VyD4
VRd2.r
2
+
1
≤
1
=
warunek spełniony
Obliczenie roztawu strzemion na skr
ę
canie
•
- pole przekroju jednej gał
ę
zi strzemienia 2 ramiennego
asg
π
ϕs
2
4
⋅
0.785 cm
2
⋅
=
:=
fywd
fyds
210 MPa
⋅
=
:=
59
- roztaw sztrzemion przy skr
ę
caniu
st
2 Ak
⋅
asg fywd
⋅
Mzmax4
⋅
cot
θ
( )
⋅
0.111 m
=
:=
- przyj
ę
ty roztaw strzemion - zbrojenie konstrukcyjne
s1
min 10
ϕ
⋅
40 cm
⋅
,
bs
,
hs
,
(
)
28 cm
⋅
=
:=
- pole przekroju strzemion
Asw
2
π
ϕs
2
4
⋅
1.571 cm
2
⋅
=
:=
przyj
ę
to roztaw strzemion
•
sV
11 cm
⋅
:=
sV
st
<
1
=
ρw
Asw
sV hs
⋅
sin 90
(
)
⋅
2.457
10
3
−
×
=
:=
ρw ρw.min
>
1
=
ρw.min
0.08
fck MPa
⋅
⋅
fyks
1.826
10
3
−
×
=
:=
warunek spełniony
Obliczenie zbrojenia podłu
ż
nego na skr
ę
canie
•
- no
ś
no
ść
obliczeniowa na skr
ę
canie z uwagi na zbrojenie
TRd2
Mzmax4
141.372 kNm
⋅
=
:=
- pole zbrojenia podłuznego na skr
ę
canie
Asl
TRd2 uk
⋅
2 Ak
⋅
fyd
⋅
cot
θ
( )
⋅
27.576 cm
2
⋅
=
:=
Przyj
ę
to 28 cm
2
rozmieszczone równomiernie po obwodzie słupa.
pole zbrojenia podłuznego słupa na skr
ę
canie
Asl.prov
28cm
2
:=
Asmin
Asl.prov
≤
Asl
≥
1
=
warunek spełniony

60
6.5.5 Kombinacja 5
6.5.5.1 Zbrojenie na
ś
ciskanie przy jednoczesnym skr
ę
caniu
- moment sk
ę
caj
ą
cy słup
Mzodp5
26.18 kNm
⋅
=
- siła poprzeczna słupa
VyD5
78.54 kN
⋅
=
- siła
ś
ciskaj
ą
ca słup
Nmax1
630.712 kN
⋅
=
No
ś
no
ść
V Rd2
•
-
ś
rednie napr
ęż
enie
ś
ciskaj
ą
ce w betonie
σcp
Nmax1
Ac
1.493 MPa
⋅
=
:=
σcp 0.25fcd
≤
1
=
- współczynnik
αc
1
σcp
fcd
+
1.075
=
:=
- k
ą
t nachylenia krzy
ż
ulców betonowych
θ
26.6deg
:=
cot
θ
( )
1.997
=
1
cot
θ
( )
≤
2
≤
1
=
warunek spełniony
- ramie sił wewn
ę
trzych
z
0.9dy
0.532 m
=
:=
- współczynnik
υ
0.6 1
fck
250 MPa
⋅
−
⋅
0.528
=
:=
- no
ś
no
ść
obliczeniowa na
ś
cinanie ze wzgl
ę
gu na
ś
ciskanie betonu
zbrojenie na
ś
cinanie wył
ą
cznie ze strzemion prostopadłych do osi elementu
VRd2
υ fcd
⋅
bs
⋅
z
⋅
cot
θ
( )
1
cot
θ
( )
2
+
⋅
1.462
10
3
×
kN
⋅
=
:=
VRd2.r
αc VRd2
⋅
1.571
10
6
×
N
=
:=

61
No
ś
no
ść
T Rd1
•
- całkowita powierzchnia przekroju elementu zawartego wewn
ą
trz obwodu u
A
bs hs
⋅
0.423 m
2
=
:=
- obwód zewn
ę
trzny przekroju
u
2 bs hs
+
(
)
⋅
2.6 m
=
:=
- grubo
ść
zast
ę
pcza
ś
cianki przekroju
tzas
A
u
0.163 m
=
:=
- minimalna grubo
ść
zast
ę
pcza
ś
cianki przekroju
t
2 Cnom
⋅
0.07 m
=
:=
A
u
tzas
≥
t
>
1
=
warunek spełniony
- pole przekroju dla t
.zas
Ak
bs tzas
−
(
)
hs tzas
−
(
)
⋅
0.238 m
2
=
:=
- obwód rdzenia
uk
2
bs tzas
−
(
)
hs tzas
−
(
)
+
⋅
1.95 m
=
:=
- no
ś
no
ść
obliczeniowa na skr
ę
canie
TRd1
2
υ
⋅
fcd
⋅
tzas
⋅
Ak
⋅
cot
θ
( )
cot 90deg
(
)
+
1
cot
θ
( )
2
+
⋅
326.553 kNm
⋅
=
:=
Warunek ograniczaj
ą
cy
•
Mzodp5
TRd1
2
VyD5
VRd2.r
2
+
1
≤
1
=
warunek spełniony
Obliczenie roztawu strzemion na skr
ę
canie
•
- pole przekroju jednej gał
ę
zi strzemienia 2 ramiennego
asg
π
ϕs
2
4
⋅
0.785 cm
2
⋅
=
:=
fywd
fyds
210 MPa
⋅
=
:=

62
- roztaw sztrzemion przy skr
ę
caniu
st
2 Ak
⋅
asg fywd
⋅
Mzodp5
⋅
cot
θ
( )
⋅
0.598 m
=
:=
- przyj
ę
ty roztaw strzemion - zbrojenie konstrukcyjne
s1
min 10
ϕ
⋅
40 cm
⋅
,
bs
,
hs
,
(
)
28 cm
⋅
=
:=
- pole przekroju strzemion
Asw
2
π
ϕs
2
4
⋅
1.571 cm
2
⋅
=
:=
sV
11 cm
⋅
:=
przyj
ę
to roztaw strzemion
•
sV
st
<
1
=
ρw
Asw
sV hs
⋅
sin 90
(
)
⋅
2.457
10
3
−
×
=
:=
ρw.min
0.08
fck MPa
⋅
⋅
fyks
1.826
10
3
−
×
=
:=
ρw ρw.min
>
1
=
warunek spełniony
Obliczenie zbrojenia podłu
ż
nego na skr
ę
canie
•
- no
ś
no
ść
obliczeniowa na skr
ę
canie z uwagi na zbrojenie
TRd2
Mzodp5
26.18 kNm
⋅
=
:=
- pole zbrojenia podłuznego na skr
ę
canie
Asl
TRd2 uk
⋅
2 Ak
⋅
fyd
⋅
cot
θ
( )
⋅
5.107 cm
2
⋅
=
:=
Przyj
ę
to 16 cm
2
rozmieszczone równomiernie po obwodzie słupa.
pole zbrojenia podłuznego słupa na skr
ę
canie
Asl.prov
16 cm
2
⋅
:=
≤
≥
=
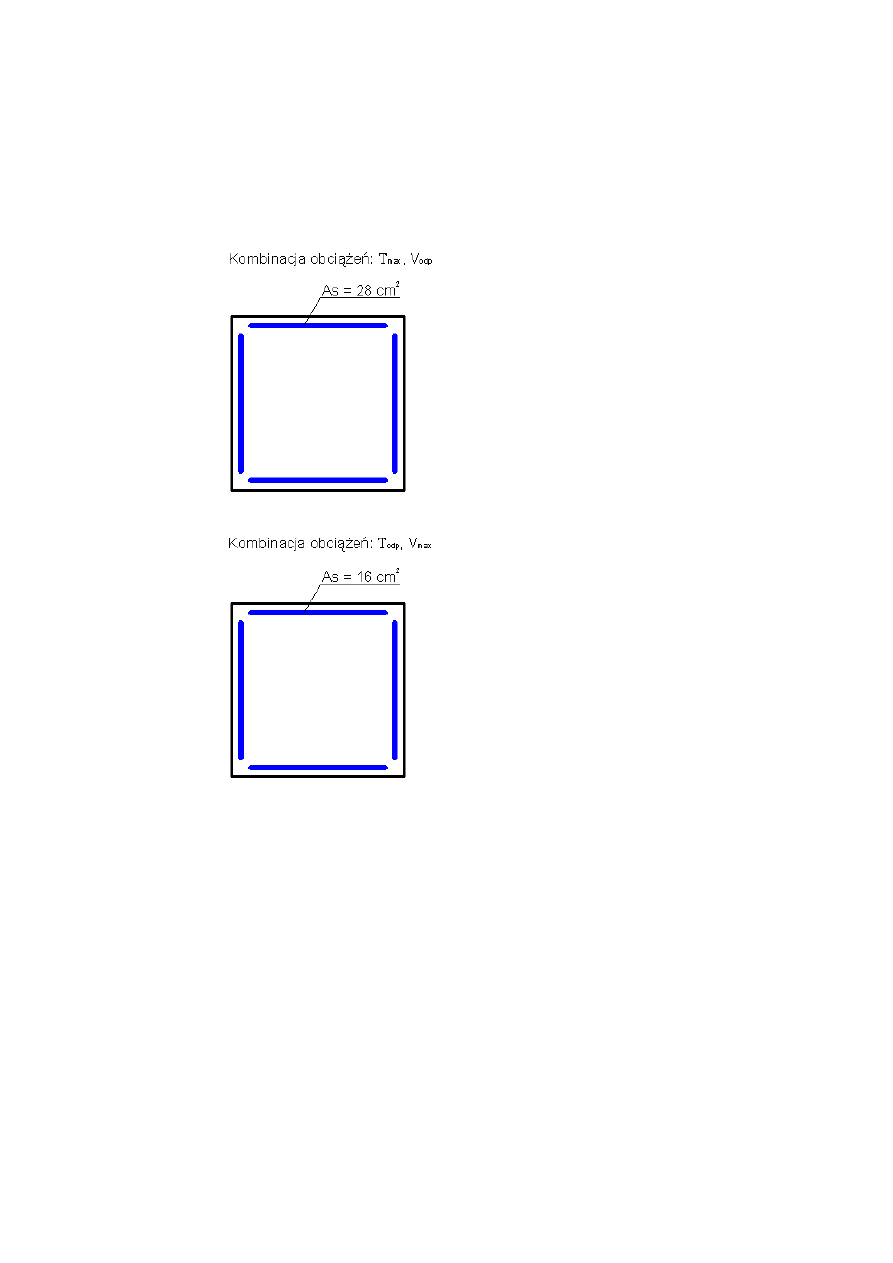
63
Asmin
Asl.prov
≤
Asl
≥
1
=
warunek spełniony
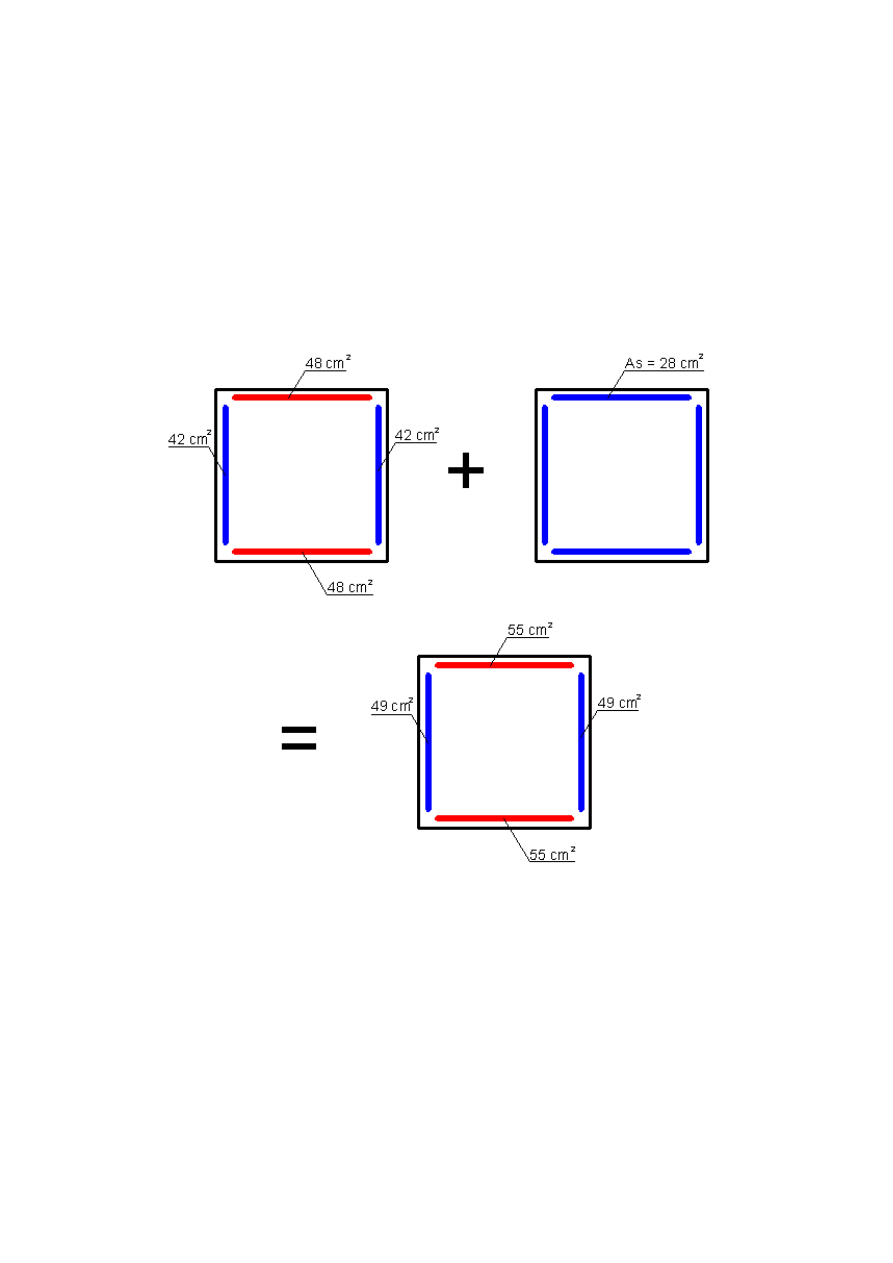
64
OSTATECZNIE PRZYJ
Ę
TO ZBROJENIE POPRZECZNE W SŁUPIE
A.
sx
= 55,42 cm
2 _
9 fi 28
A.
sy
= 49,26 cm
2 _
8 fi 28
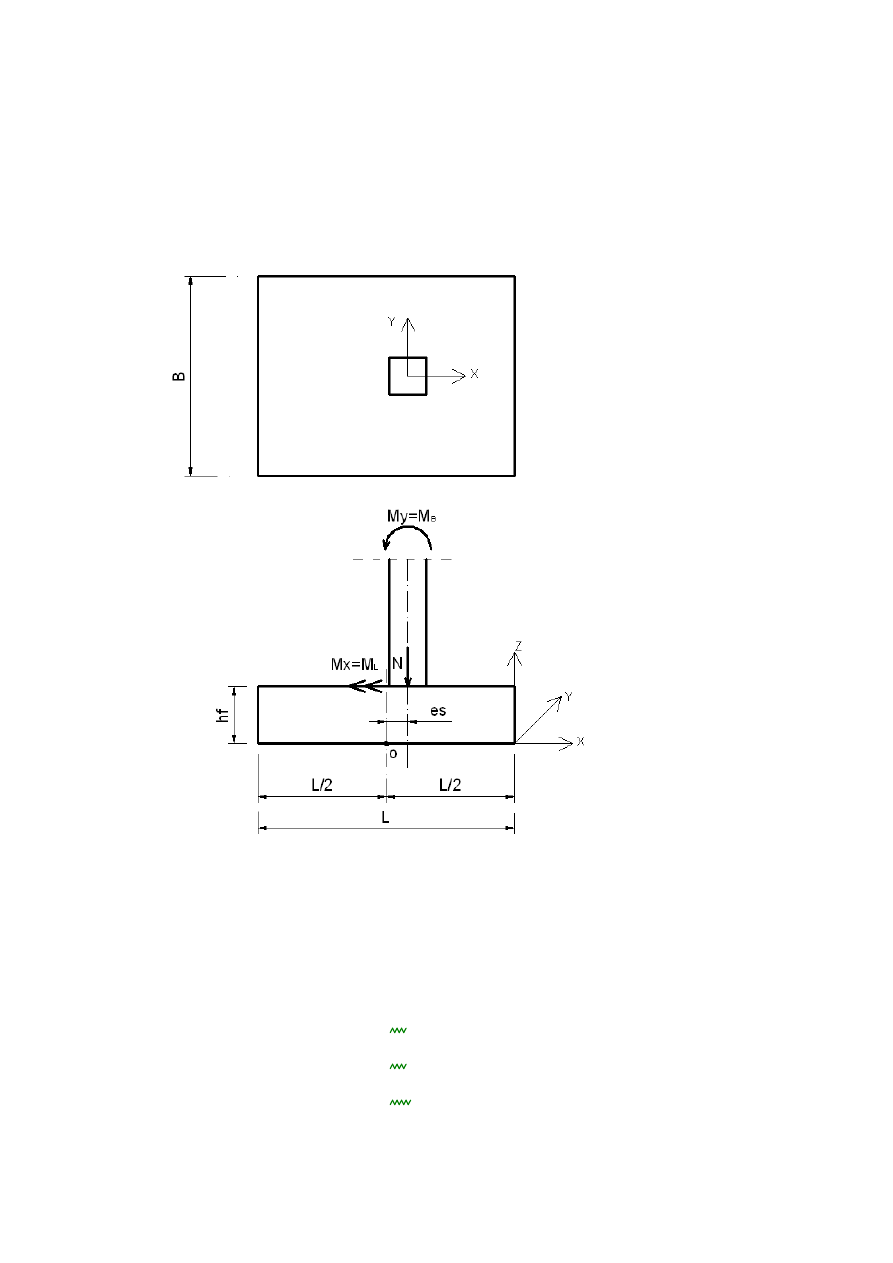
65
7.WYMIAROWANIE STOPY FUNDAMENTOWEJ
7.1 ZAŁO
ś
ENIA
Gł
ę
boko
ść
posadowienia
•
D
1.5 m
⋅
:=
Wymiary przekroju
•
- szeroko
ść
stopy
B
4.0 m
⋅
:=
- długo
ść
stopy
L
5.2 m
⋅
:=
- wysoko
ść
stopy
hf
1 m
⋅
:=

66
Przyj
ę
ta
ś
rednica zbrojenia
•
ϕ
28 mm
⋅
:=
Grubo
ść
otulenia
•
cmin
40 mm
⋅
:=
∆c
10 mm
⋅
:=
cnom
cmin ∆c
+
50 mm
⋅
=
:=
Długo
ść
zakotwienia i zakładu pr
ę
tów w stopie
•
- powierzchnia zbrojenia obliczona
Asreq
208 cm
2
⋅
:=
- powierzchnia zbrojenia przyj
ę
ta
Asprov
209.36 cm
2
⋅
:=
- współczynnik uwzgl
ę
dniaj
ą
cy efektywno
ść
zakotwienia
αa
1.0
:=
fbd
3.0MPa
:=
- granica przyczepno
ś
ci
- podstawowa długo
ść
zakotwienia
lb
ϕ
4
fyd
fbd
⋅
0.98 m
=
:=
- minimalna długo
ść
zakotwienia
lbmin1
0.6lb
0.588 m
=
:=
lbmin2
10
ϕ
⋅
0.28 m
=
:=
lbmin3
100 mm
⋅
:=
lbmin
max lbmin1 lbmin2
,
lbmin3
,
(
)
0.588 m
=
:=
lbd
αa lb
⋅
Asreq
Asprov
⋅
0.974 m
=
:=
lbd
lbmin
>
1
=
warunek spełniony
- współczynnik
α1
1.0
:=
- długo
ść
zakładu pretów
ls
lbd α1
⋅
0.974 m
=
:=
⋅ ⋅ =
:=

67
- minimalna długo
ść
zakładu
lsmin
0.3
αa α1
⋅
lb
⋅
0.294 m
=
:=
lsmin
200 mm
⋅
≥
1
=
warunek spełniony
- przyj
ę
ta długo
ść
zakładu
ls
100 cm
⋅
:=
ls lsmin
≥
1
=
warunek spełniony
7.2 Zestawienie obci
ąż
e
ń
warto
ść
charakterystyczna
warto
ść
obliczeniowa
cie
ż
ar własny stopy
g1k
25
kN
m
3
B L
⋅
hf
⋅
:=
g1d
1.1 g1k
⋅
572 kN
⋅
=
:=
ci
ęż
ar gruntu nad stop
ą
g2k
18
kN
m
3
D
hf
−
(
)
L B
⋅
hs bs
⋅
−
(
)
⋅
:=
g2d
1.2 g2k
⋅
220.077 kN
⋅
=
:=
gk
g1k g2k
+
703.398 kN
⋅
=
:=
gd
g1d g2d
+
792.077 kN
⋅
=
:=
RAZEM
7.3 SPRAWDZENIE WARUNKU NO
Ś
NO
Ś
CI PODŁO
ś
A
7.3.1 Mimo
ś
ród poło
ż
enia
ś
rodka ci
ęż
ko
ś
ci słupa wzgl
ę
dem
ś
rodka ci
ęż
ko
ś
ci stopy
Me1
Pd a
⋅
Gd
grld
2
+
a
⋅
+
grpd
2
b
⋅
−
631.513 kN m
⋅
⋅
=
:=
Me2
Pd
−
b
⋅
Gd
grpd
2
+
b
⋅
−
grld
2
a
⋅
+
378.287
−
kN m
⋅
⋅
=
:=
Ne
Pd Gd
+
grld
+
grpd
+
gsd
+
335.43 kN
⋅
=
:=

68
e1
Me1
Ne
1.883 m
=
:=
e2
Me2
Ne
1.128
−
m
=
:=
es
e1
e2
−
2
0.377 m
=
:=
7.3.2 Obci
ąż
enia
7.3.2.1 Kombinacja I
- siła pionowa w dolnej powierzchni stopy fundamenowej
N1g
Nmax1 gsd
+
g2d
+
929.507 kN
⋅
=
:=
N1d
Nmax1 gd
+
gsd
+
1.502
10
3
×
kN
⋅
=
:=
- siła pozioma na kierunku L, na górnej powierzchni stopy fundamenowej
HL1
0kN
:=
- siła pozioma na kierunku B, na górnej powierzchni stopy fundamenowej
HB1
VyD5
78.54 kN
⋅
=
:=
- moment na kierunku L, na górnej powierzchni stopy fundamenowej
−
⋅
=
:=

69
MB1
MyD1
−
220.113 kNm
⋅
=
:=
- moment na kierunku B, na górnej powierzchni stopy fundamenowej
ML1
MxD1
587.087 kNm
⋅
=
:=
7.3.2.2 Kombinacja II
- siła pionowa w dolnej powierzchni stopy fundamenowej
N2g
2 Gd
⋅
2 Pd
⋅
+
grld
+
grpd
+
gsd
+
g2d
+
742.507 kN
⋅
=
:=
N2d
2 Gd
⋅
2 Pd
⋅
+
grld
+
grpd
+
gsd
+
gd
+
1.315
10
3
×
kN
⋅
=
:=
- siła pozioma na kierunku L, na górnej powierzchni stopy fundamenowej
HL2
0kN
:=
- siła pozioma na kierunku B, na górnej powierzchni stopy fundamenowej
HB2
2 Hd
⋅
52.36 kN
⋅
=
:=
- moment na kierunku L, na górnej powierzchni stopy fundamenowej
MB2
Pd a
⋅
Gd
grld
2
+
a
⋅
+
grpd
2
b
⋅
−
631.513 kNm
⋅
=
:=
- moment na kierunku B, na górnej powierzchni stopy fundamenowej
ML2
MxD31
391.391 kN m
⋅
⋅
=
:=
7.3.2.3 Kombinacja III
- siła pionowa w dolnej powierzchni stopy fundamenowej
N3g
N2g
742.507 kN
⋅
=
:=
N3d
N2d
1.315
10
3
×
kN
⋅
=
:=
- siła pozioma na kierunku L, na górnej powierzchni stopy fundamenowej
HL3
0kN
:=
- siła pozioma na kierunku B, na górnej powierzchni stopy fundamenowej
HB3
2 Hd
⋅
52.36 kN
⋅
=
:=

70
- moment na kierunku L, na górnej powierzchni stopy fundamenowej
MB3
Pd
−
b
⋅
Gd
grpd
2
+
b
⋅
−
grld
2
a
⋅
+
378.287
−
kNm
⋅
=
:=
- moment na kierunku B, na górnej powierzchni stopy fundamenowej
ML3
2 Hd
⋅
Lobl
⋅
391.391 kN m
⋅
⋅
=
:=
7.3.3 Sprawdzenie czy wypadkowa obci
ąż
e
ń
znajduje si
ę
w rdzeniu podstawy
7.3.3.1 Kombinacja I
- wymiary przekroju
- szeroko
ść
stopy
B1
4.0 m
⋅
:=
- długo
ść
stopy
L1
5.2 m
⋅
:=
- wysoko
ść
stopy
hf.1
1 m
⋅
:=
- mimo
ś
ród siły na kierunku B
eB1
ML1 HB1 hf.1
⋅
+
N1d
0.443 m
=
:=
B1
6
0.667 m
=
eB1
B1
6
<
1
=
warunek spełniony
- mimo
ś
ród siły na kierunku L
eL1
MB1 HL1 hf.1
⋅
+
(
)
N1g es
⋅
−
N1d
0.087
−
m
⋅
=
:=
L1
6
0.867 m
⋅
=
eL1
L1
6
<
1
=
warunek spełniony
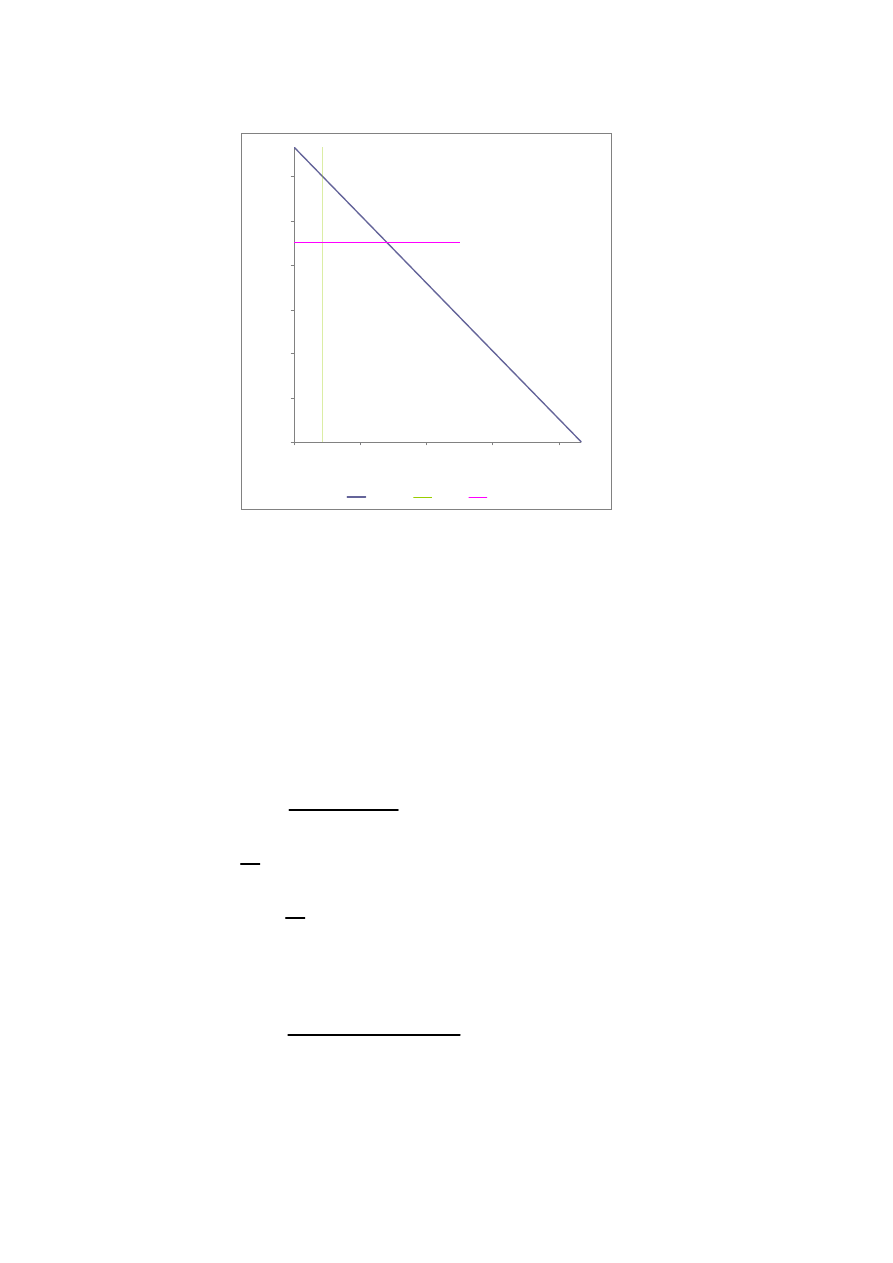
71
0
0,1
0,2
0,3
0,4
0,5
0,6
0
0,2
0,4
0,6
0,8
e.L
e
.B
rdzeń
e.L
e.B
L/6
7.3.3.2 Kombinacja II
- wymiary przekroju
- szeroko
ść
stopy
B2
4.0 m
⋅
:=
- długo
ść
stopy
L2
5.2 m
⋅
:=
- wysoko
ść
stopy
hf.2
1 m
⋅
:=
- mimo
ś
ród siły na kierunku B
eB2
ML2 HB2 hf.2
⋅
+
N2d
0.338 m
=
:=
B2
6
0.667 m
=
eB2
B2
6
<
1
=
warunek spełniony
- mimo
ś
ród siły na kierunku L
eL2
MB2 HL2 hf.2
⋅
+
N2g es
⋅
−
N2d
0.267 m
=
:=
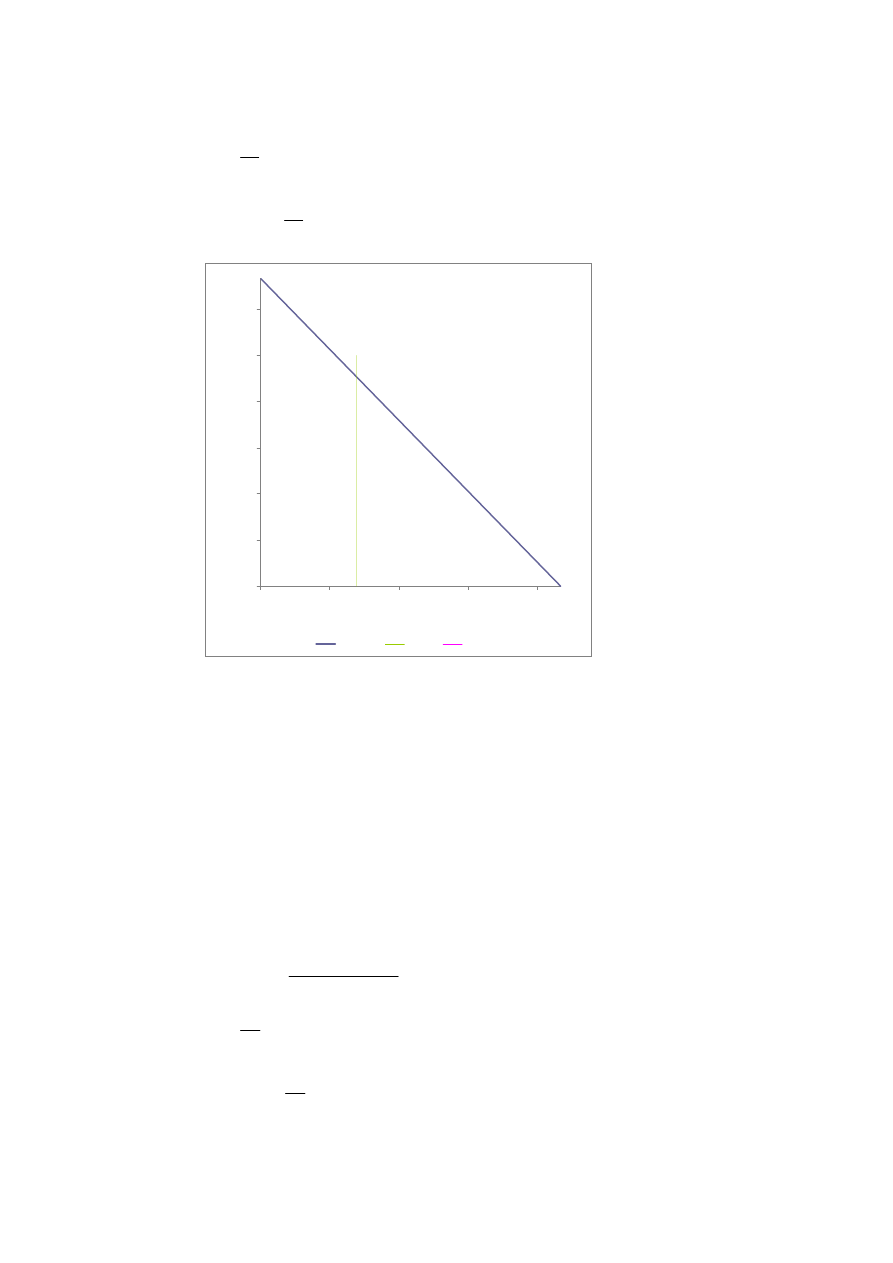
72
L2
6
0.867 m
⋅
=
eL2
L2
6
<
1
=
warunek spełniony
0
0,1
0,2
0,3
0,4
0,5
0,6
0
0,2
0,4
0,6
0,8
e.L
e
.B
rdzeń
e.L
e.B
L/6
7.3.3.3 Kombinacja III
- wymiary przekroju
- szeroko
ść
stopy
B3
4.0 m
⋅
:=
- długo
ść
stopy
L3
5.2 m
⋅
:=
- wysoko
ść
stopy
hf.3
1 m
⋅
:=
- mimo
ś
ród siły na kierunku B
eB3
ML3 HB3 hf.3
⋅
+
N3d
0.338 m
=
:=
B3
6
0.667 m
=
eB3
B3
6
<
1
=
warunek spełniony
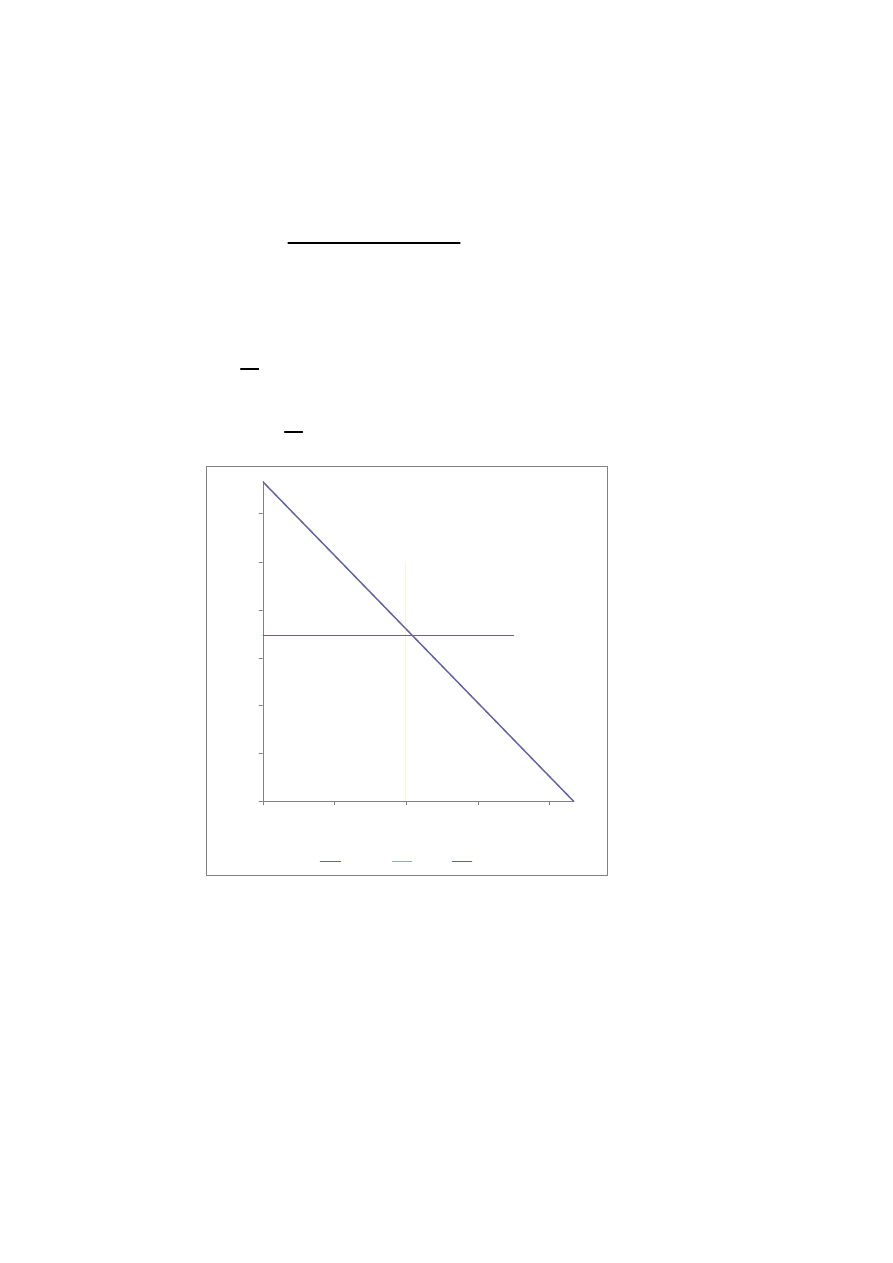
73
- mimo
ś
ród siły na kierunku L
eL3
MB3 HL3 hf.3
⋅
+
N3g es
⋅
−
N3d
0.389
−
m
=
:=
- mimo
ś
ród siły pionowej w płaszczy
ź
nie podstawy stopy wzgl
ę
dem
ś
rodka
cie
ż
ko
ś
ci stopy
L3
6
0.867 m
⋅
=
eL3
L3
6
<
1
=
warunek spełniony
0
0,1
0,2
0,3
0,4
0,5
0,6
0
0,2
0,4
0,6
0,8
e.L
e
.B
rdzeń
e.L
e.B
L/6
7.3.4 Obliczanie napr
ę
ze
ń
kraw
ę
dziowych
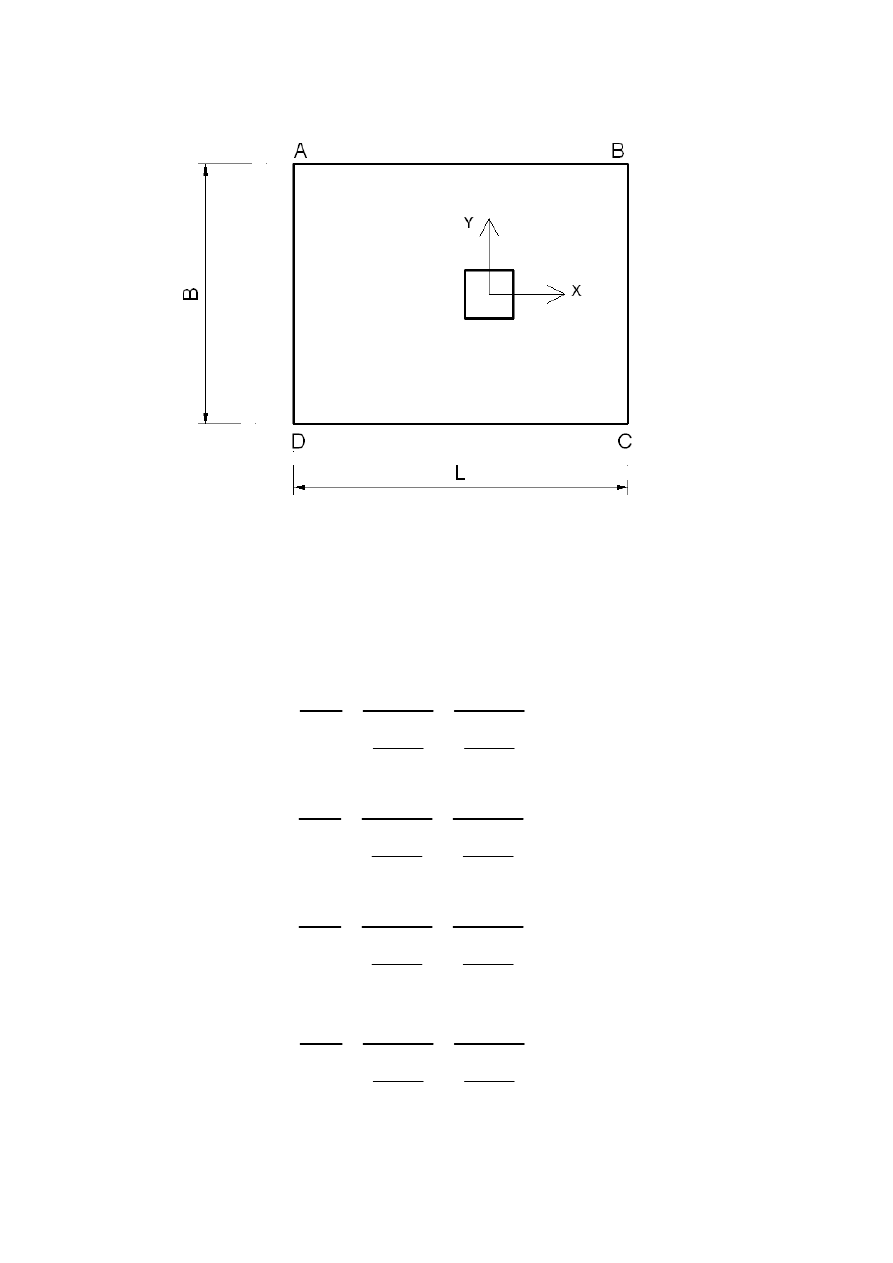
74
7.3.4.1 Kombinacja I
MfL1
ML1 HB1 hf.1
⋅
+
665.627 kN m
⋅
⋅
=
:=
MfB1
MB1 es N1g
⋅
−
130.744
−
kN m
⋅
⋅
=
:=
qA1
N1d
B1 L1
⋅
MfL1
B1
2
L1
⋅
6
+
MfB1
B1 L1
2
⋅
6
+
112.937 kPa
⋅
=
:=
qB1
N1d
B1 L1
⋅
MfL1
B1
2
L1
⋅
6
+
MfB1
B1 L1
2
⋅
6
−
127.443 kPa
⋅
=
:=
qC1
N1d
B1 L1
⋅
MfL1
B1
2
L1
⋅
6
−
MfB1
B1 L1
2
⋅
6
−
31.439 kPa
⋅
=
:=
qD1
N1d
B1 L1
⋅
MfL1
B1
2
L1
⋅
6
−
MfB1
B1 L1
2
⋅
6
+
16.933 kPa
⋅
=
:=
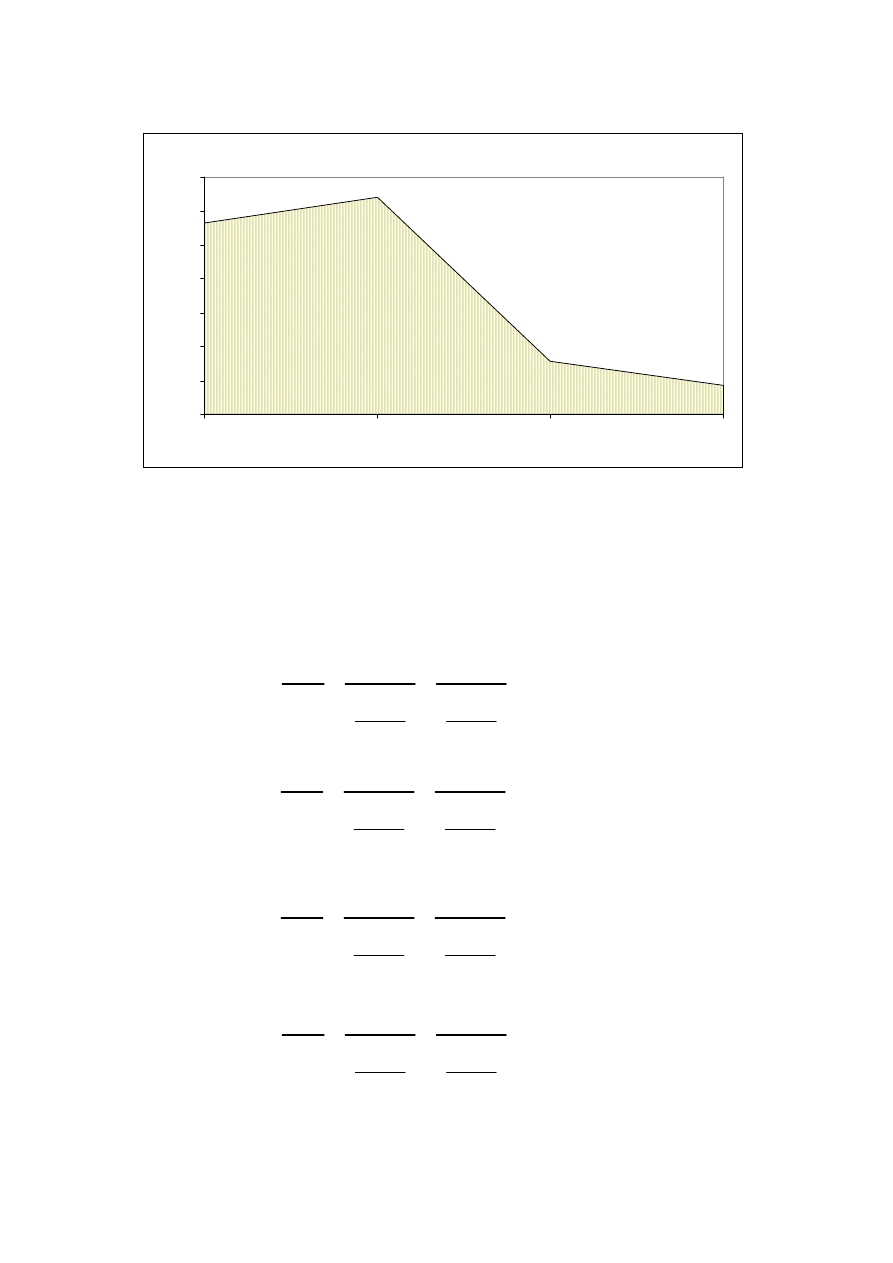
75
NAPR
Ęś
ENIA KRAW
Ę
DZIOWE
16,9
31,4
127,9
112,9
0
20
40
60
80
100
120
140
A
B
C
D
q
[
k
P
a
]
7.3.4.2 Kombinacja II
MfL2
ML2 HB2 hf.2
⋅
+
443.751 kN m
⋅
⋅
=
:=
MfB2
MB2 es N2g
⋅
−
351.242 kN m
⋅
⋅
=
:=
qA2
N2d
B2 L2
⋅
MfL2
B2
2
L2
⋅
6
+
MfB2
B2 L2
2
⋅
6
+
114.683 kPa
⋅
=
:=
qB2
N2d
B2 L2
⋅
MfL2
B2
2
L2
⋅
6
+
MfB2
B2 L2
2
⋅
6
−
75.714 kPa
⋅
=
:=
qC2
N2d
B2 L2
⋅
MfL2
B2
2
L2
⋅
6
−
MfB2
B2 L2
2
⋅
6
−
11.712 kPa
⋅
=
:=
qD2
N2d
B2 L2
⋅
MfL2
B2
2
L2
⋅
6
−
MfB2
B2 L2
2
⋅
6
+
50.681 kPa
⋅
=
:=
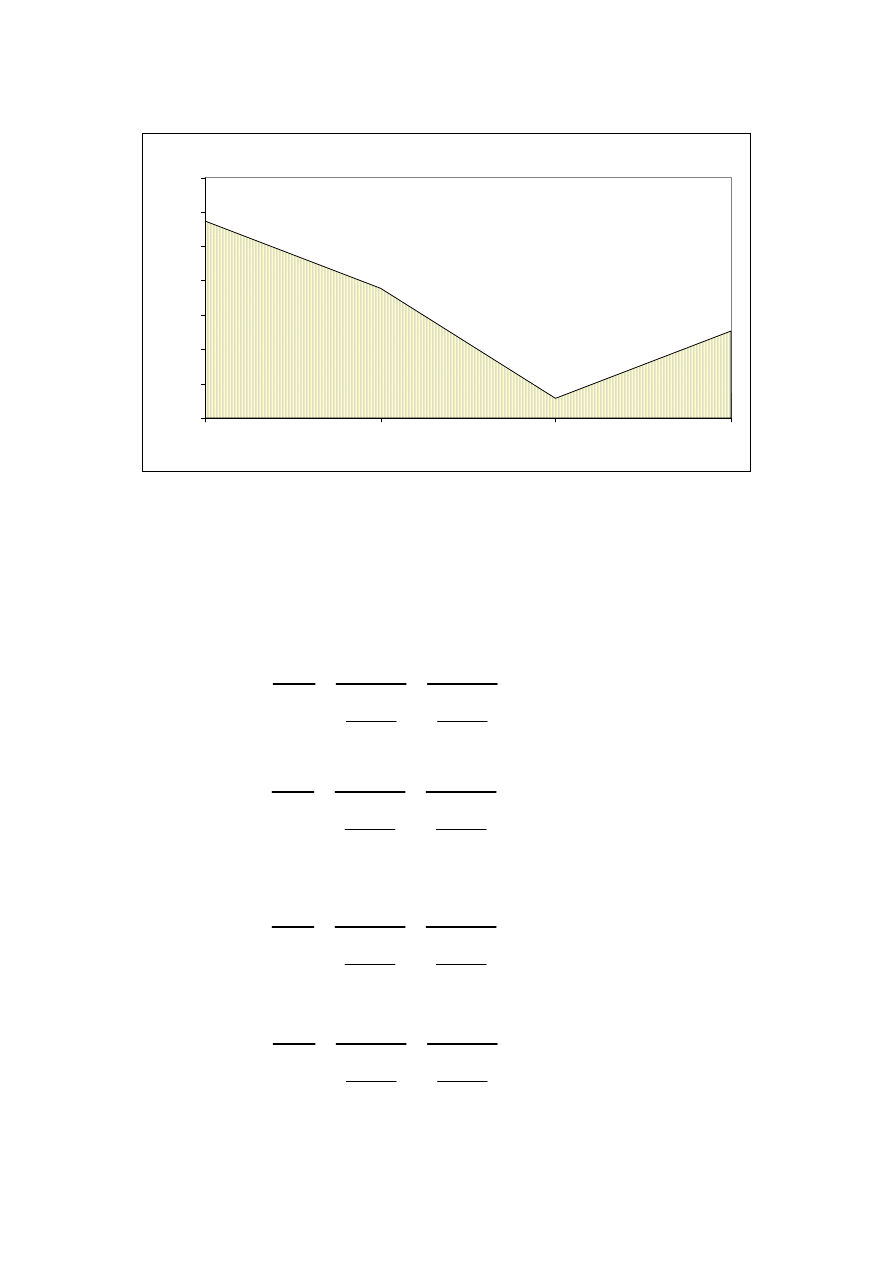
76
NAPR
Ęś
ENIA KRAW
Ę
DZIOWE
50,7
11,7
75,7
114,7
0
20
40
60
80
100
120
140
A
B
C
D
q
[
k
P
a
]
7.3.4.3 Kombinacja III
MfL3
ML3 HB3 hf.3
⋅
+
443.751 kN m
⋅
⋅
=
:=
MfB3
MB3 es N3g
⋅
−
658.558
−
kN m
⋅
⋅
=
:=
qA3
N3d
B3 L3
⋅
MfL3
B3
2
L3
⋅
6
+
MfB3
B3 L3
2
⋅
6
+
58.666 kPa
⋅
=
:=
qB3
N3d
B3 L3
⋅
MfL3
B3
2
L3
⋅
6
+
MfB3
B3 L3
2
⋅
6
−
131.731 kPa
⋅
=
:=
qC3
N3d
B3 L3
⋅
MfL3
B3
2
L3
⋅
6
−
MfB3
B3 L3
2
⋅
6
−
67.729 kPa
⋅
=
:=
qD3
N3d
B3 L3
⋅
MfL3
B3
2
L3
⋅
6
−
MfB3
B3 L3
2
⋅
6
+
5.336
−
kPa
⋅
=
:=
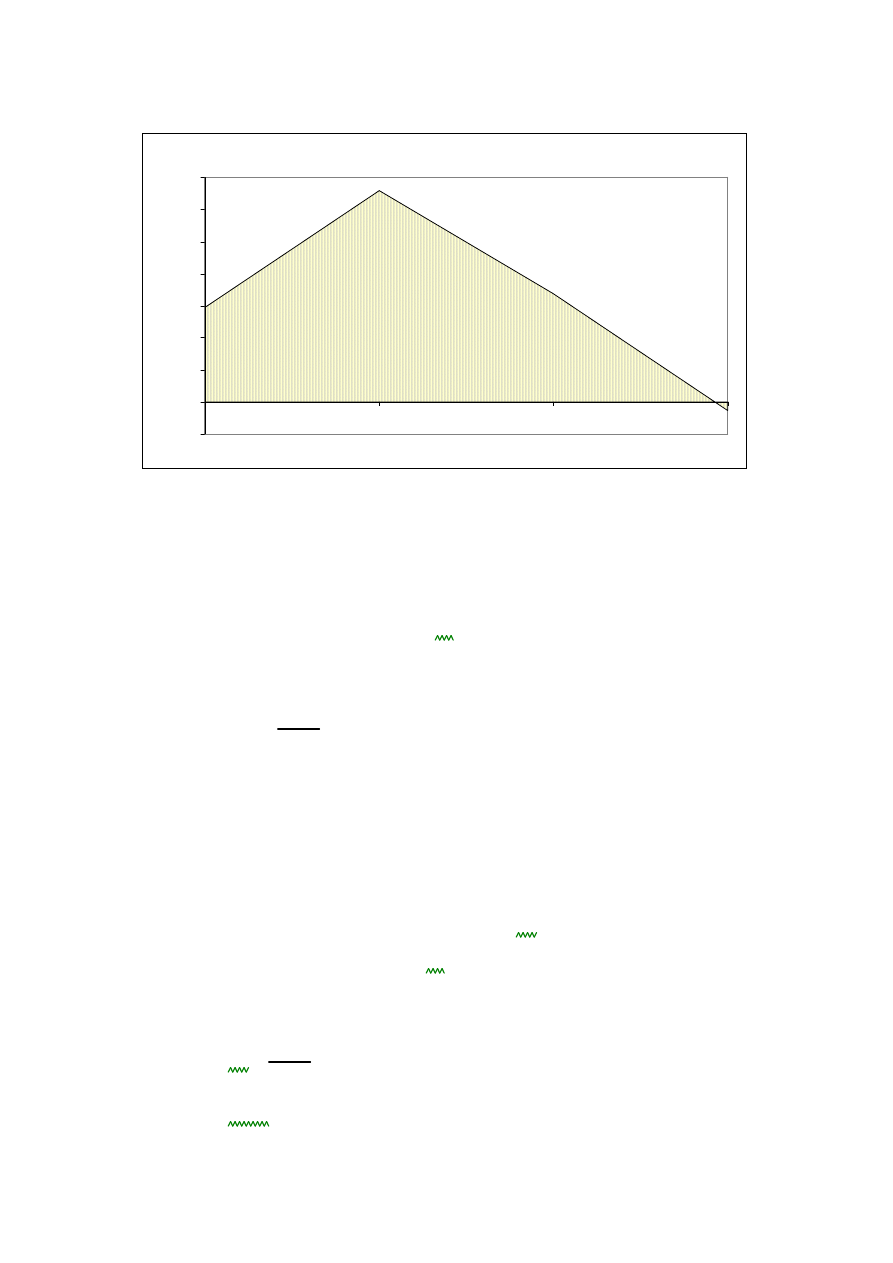
77
NAPR
Ęś
ENIA KRAW
Ę
DZIOWE
-5,3
67,7
131,7
58,7
-20
0
20
40
60
80
100
120
140
A
B
C
D
q
[
k
P
a
]
7.3.5 Sprawdzenie I stanu granicznego
7.3.5.1 Kombinacja I
- napr
ęż
enie maksymalne dopuszczalne
qf
190 kPa
⋅
:=
- współczynnik korekcyjny
m
0.9
:=
- jednostkowy opór podło
ż
a
qs
N1d
B1 L1
⋅
m qf
⋅
≤
1
=
:=
qmax
max qA1 qB1
,
qC1
,
qD1
,
(
)
127.443 kPa
⋅
=
:=
qmax
1.2 m
⋅
qf
⋅
≤
1
=
7.3.5.2 Kombinacja II
- napr
ęż
enie maksymalne dopuszczalne
qf
190 kPa
⋅
:=
- współczynnik korekcyjny
m
0.9
:=
- jednostkowy opór podło
ż
a
qs
N2d
B2 L2
⋅
m qf
⋅
≤
1
=
:=
qmax
max qA2 qB2
,
qC2
,
qD2
,
(
)
114.683 kPa
⋅
=
:=
78
qmax
1.2 m
⋅
qf
⋅
≤
1
=
7.3.5.3 Kombinacja III
- napr
ęż
enie maksymalne dopuszczalne
qf
190 kPa
⋅
:=
- współczynnik korekcyjny
m
0.9
:=
- jednostkowy opór podło
ż
a
qs
N3d
B3 L3
⋅
m qf
⋅
≤
1
=
:=
qmax
max qA3 qB3
,
qC3
,
qD3
,
(
)
131.731 kPa
⋅
=
:=
qmax
1.2 m
⋅
qf
⋅
≤
1
=
7.4 WYMIAROWANIE STOPY FUNDAMENTOWEJ NA ZGINANIE
- metod
ą
wsporników prostok
ą
tnych
Przyj
ę
to zbrojenie:
ϕ
16mm
:=
Aϕ
π ϕ
2
4
:=
Aϕ
2.011 cm
2
⋅
=
dx
hf cnom
−
ϕ
2
−
:=
dx
94.2 cm
⋅
=
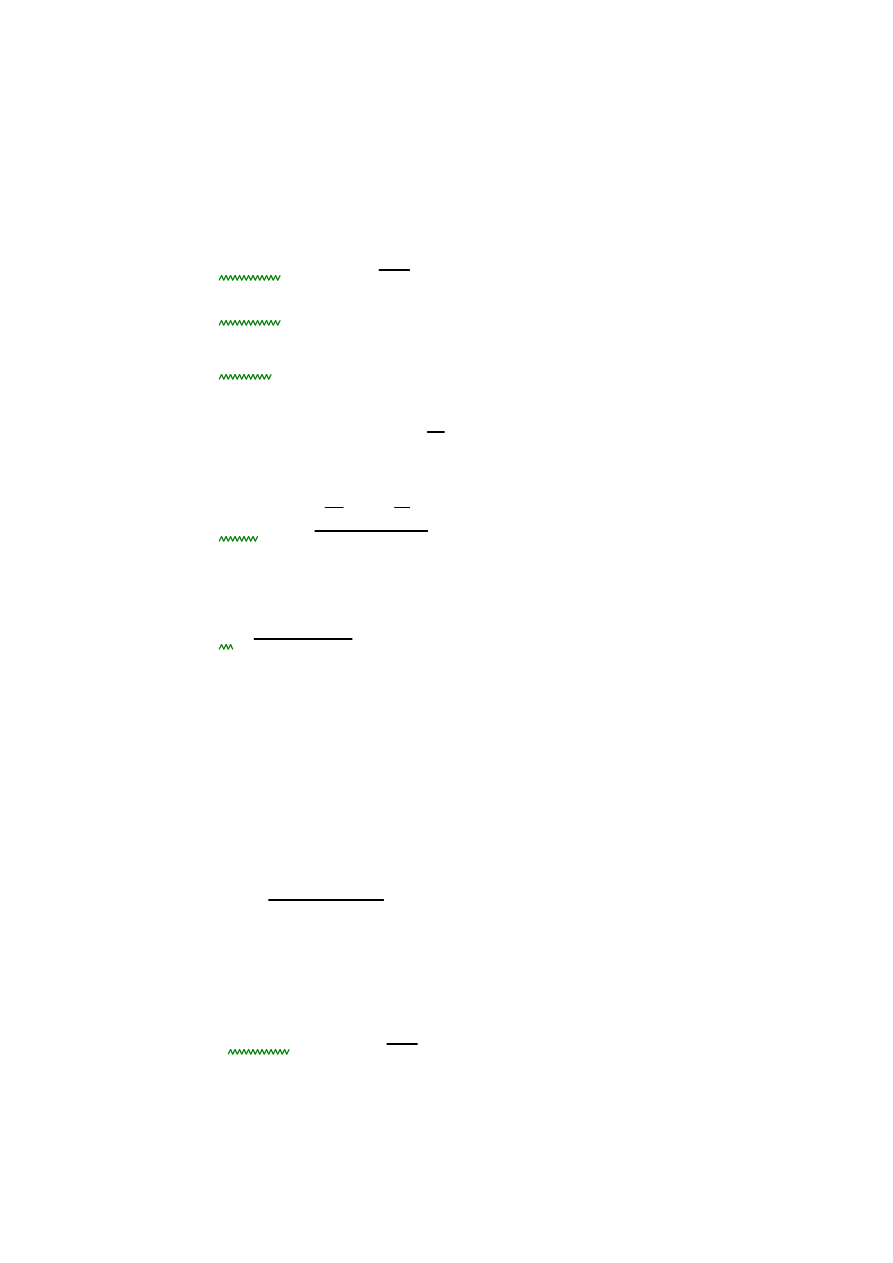
79
7.4.1 Kombinacja I
zbrojenie na kierunek L
•
- Zbrojenie minimalne
As.min1
0.26 B1
⋅
dx
⋅
fctm
fyk
⋅
56.821 cm
2
⋅
=
:=
As.min2
0.0013 B1
⋅
dx
⋅
48.984 cm
2
⋅
=
:=
As.min
max As.min1 As.min2
,
(
)
56.821 cm
2
⋅
=
:=
qsL1
qA1 B1
⋅
4.517
10
5
×
kg
s
2
=
:=
MB1
qsL1
L1
2
es
+
bs
2
−
2
2
⋅
1.589
10
3
×
m kN
⋅
=
:=
- potrzebna liczba pr
ę
tów:
Wst
ę
pnie przyj
ę
to :
n
MB1
0.9 dx
⋅
fyd
⋅
Aϕ
⋅
:=
n
22.197
=
n1
30
:=
- przyj
ę
to zbrojenie
AsL
n1 Aϕ
⋅
60.319 cm
2
⋅
=
:=
AsL
As.min
>
1
=
- rozstaw wynikaj
ą
cy z liczby przyj
ę
tych pr
ę
tów:
r1
B1 2 cnom
⋅
−
ϕ
−
n1
12.947 cm
⋅
=
:=
zbrojenie na kierunek B
•
- Zbrojenie minimalne
As.min1
0.26 L1
⋅
dx
⋅
fctm
fyk
⋅
73.868 cm
2
⋅
=
:=

80
As.min2
0.0013 L1
⋅
dx
⋅
63.679 cm
2
⋅
=
:=
As.min
max As.min1 As.min2
,
(
)
73.868 cm
2
⋅
=
:=
qsB1
qA1 qB1
+
2
L1
⋅
6.25
10
5
×
kg
s
2
=
:=
ML1
B1
2
hs
2
−
2
2
qsB1
⋅
876.739 m kN
⋅
=
:=
- potrzebna liczba pr
ę
tów:
Wst
ę
pnie przyj
ę
to :
n
ML1
0.9 dx
⋅
fyd
⋅
Aϕ
⋅
:=
n
12.246
=
n1
38
:=
- przyj
ę
to zbrojenie
AsB
n1 Aϕ
⋅
76.404 cm
2
⋅
=
:=
AsB
As.min
>
1
=
- rozstaw wynikaj
ą
cy z liczby przyj
ę
tych pr
ę
tów:
r1
L1 2 cnom
⋅
−
n1
0.134 m
=
:=
7.4.2 Kombinacja II
- Zbrojenie minimalne
As.min1
0.26 B2
⋅
dx
⋅
fctm
fyk
⋅
56.821 cm
2
⋅
=
:=
As.min2
0.0013 B2
⋅
dx
⋅
48.984 cm
2
⋅
=
:=
As.min
max As.min1 As.min2
,
(
)
56.821 cm
2
⋅
=
:=
qsL2
qA2 B2
⋅
4.587
10
5
×
kg
s
2
=
:=
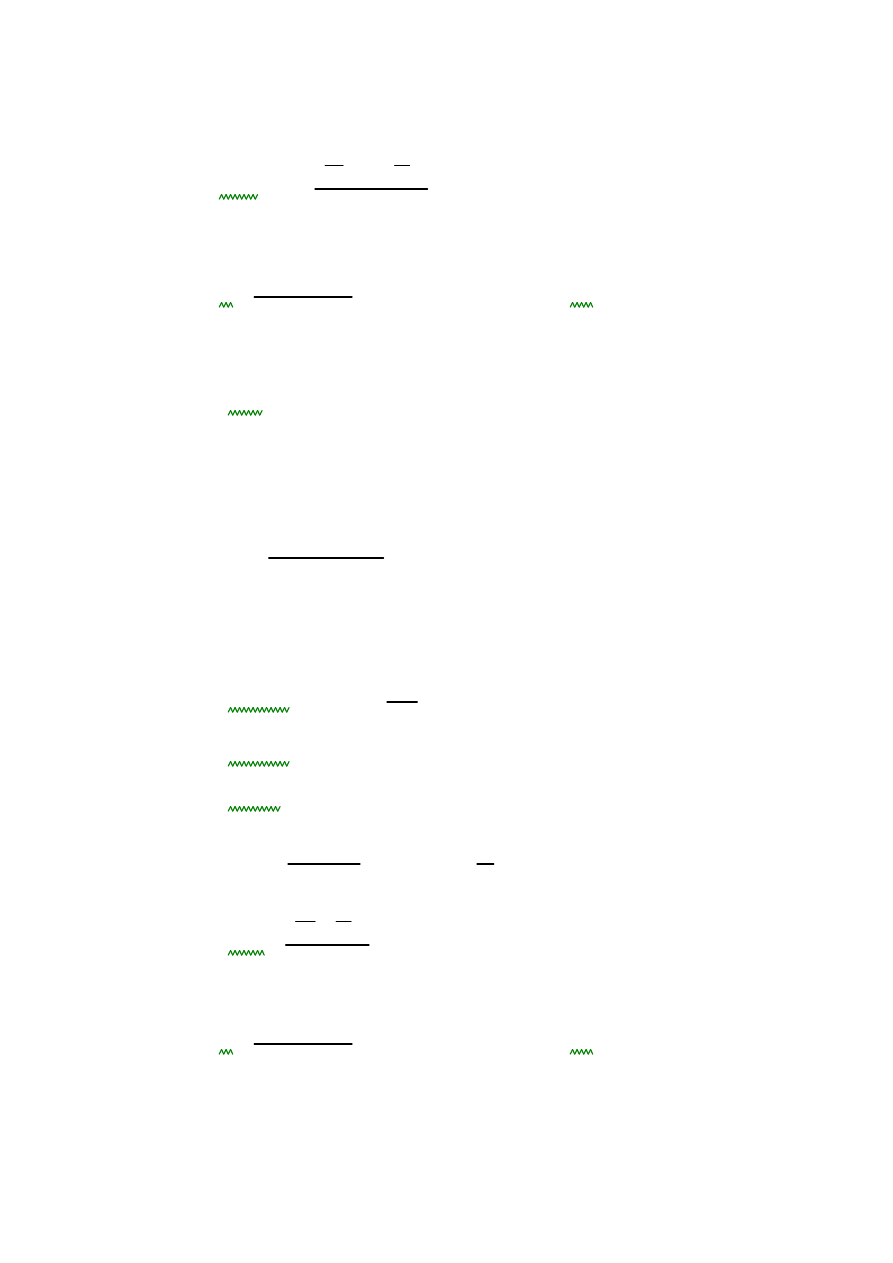
81
MB2
qsL2
L2
2
es
+
bs
2
−
2
2
⋅
1.614
10
3
×
m kN
⋅
=
:=
- potrzebna liczba pr
ę
tów:
Wst
ę
pnie przyj
ę
to :
n
MB2
0.9 dx
⋅
fyd
⋅
Aϕ
⋅
:=
n
22.54
=
n1
30
:=
- przyj
ę
to zbrojenie
AsL
n1 Aϕ
⋅
60.319 cm
2
⋅
=
:=
AsL
As.min
>
1
=
- rozstaw wynikaj
ą
cy z liczby przyj
ę
tych pr
ę
tów:
r2
B2 2 cnom
⋅
−
ϕ
−
n1
12.947 cm
⋅
=
:=
zbrojenie na kierunek B
•
- Zbrojenie minimalne
As.min1
0.26 L2
⋅
dx
⋅
fctm
fyk
⋅
73.868 cm
2
⋅
=
:=
As.min2
0.0013 L2
⋅
dx
⋅
63.679 cm
2
⋅
=
:=
As.min
max As.min1 As.min2
,
(
)
73.868 cm
2
⋅
=
:=
qsB2
qA2 qB2
+
2
L2
⋅
4.95
10
5
×
kg
s
2
=
:=
ML2
B2
2
hs
2
−
2
2
qsB2
⋅
694.439 m kN
⋅
=
:=
- potrzebna liczba pr
ę
tów:
Wst
ę
pnie przyj
ę
to :
n
ML2
0.9 dx
⋅
fyd
⋅
Aϕ
⋅
:=
n
9.7
=
n1
38
:=
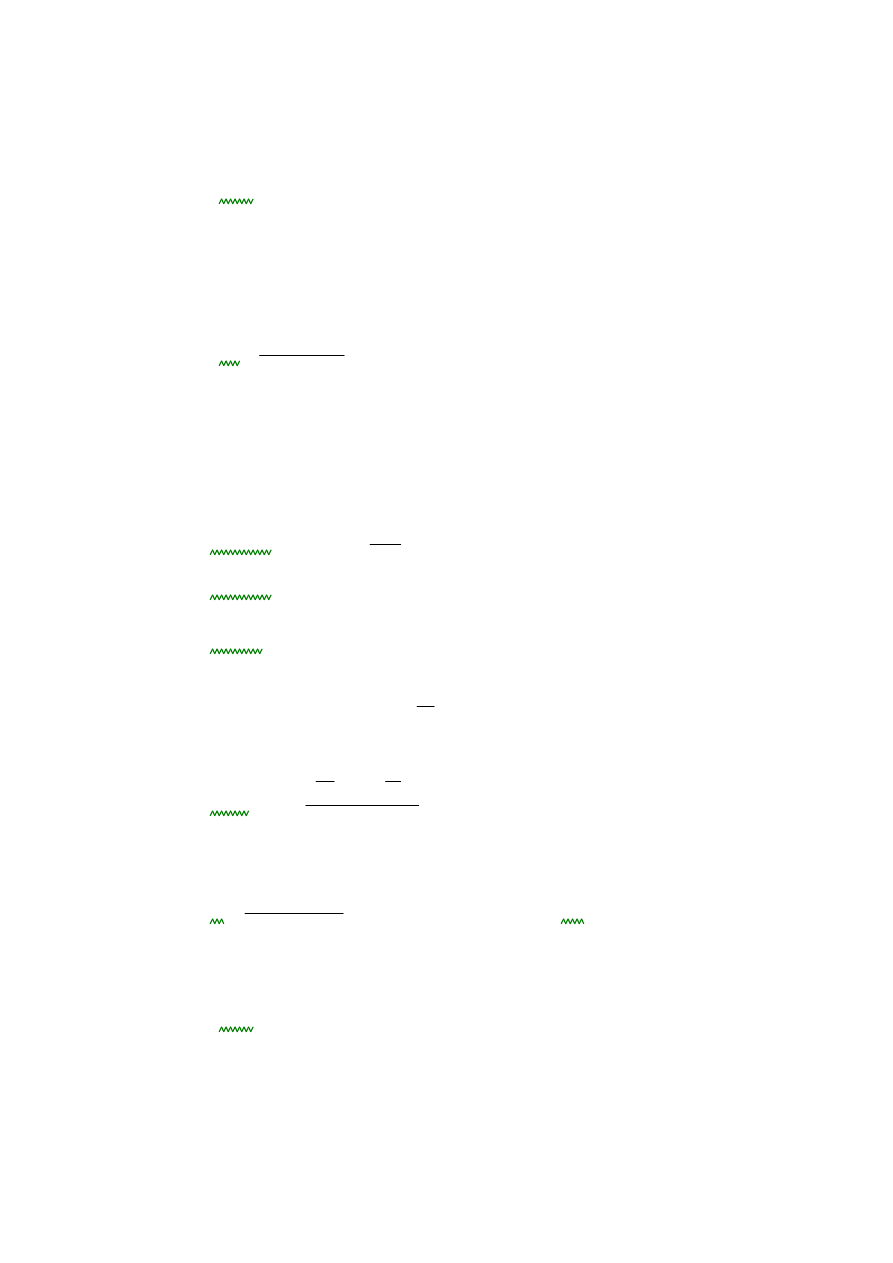
82
- przyj
ę
to zbrojenie
AsB
n1 Aϕ
⋅
76.404 cm
2
⋅
=
:=
AsB
As.min
>
1
=
- rozstaw wynikaj
ą
cy z liczby przyj
ę
tych pr
ę
tów:
r2
L2 2 cnom
⋅
−
n1
0.134 m
=
:=
7.4.3 Kombinacja III
zbrojenie na kierunek L
•
- Zbrojenie minimalne
As.min1
0.26 B3
⋅
dx
⋅
fctm
fyk
⋅
56.821 cm
2
⋅
=
:=
As.min2
0.0013 B3
⋅
dx
⋅
48.984 cm
2
⋅
=
:=
As.min
max As.min1 As.min2
,
(
)
56.821 cm
2
⋅
=
:=
qsL3
qB3 B3
⋅
5.269
10
5
×
kg
s
2
=
:=
MB3
qsL3
L3
2
es
+
bs
2
−
2
2
⋅
1.854
10
3
×
m kN
⋅
=
:=
- potrzebna liczba pr
ę
tów:
Wst
ę
pnie przyj
ę
to :
n
MB3
0.9 dx
⋅
fyd
⋅
Aϕ
⋅
:=
n
25.891
=
n1
30
:=
- przyj
ę
to zbrojenie
AsL
n1 Aϕ
⋅
60.319 cm
2
⋅
=
:=
AsL
As.min
>
1
=
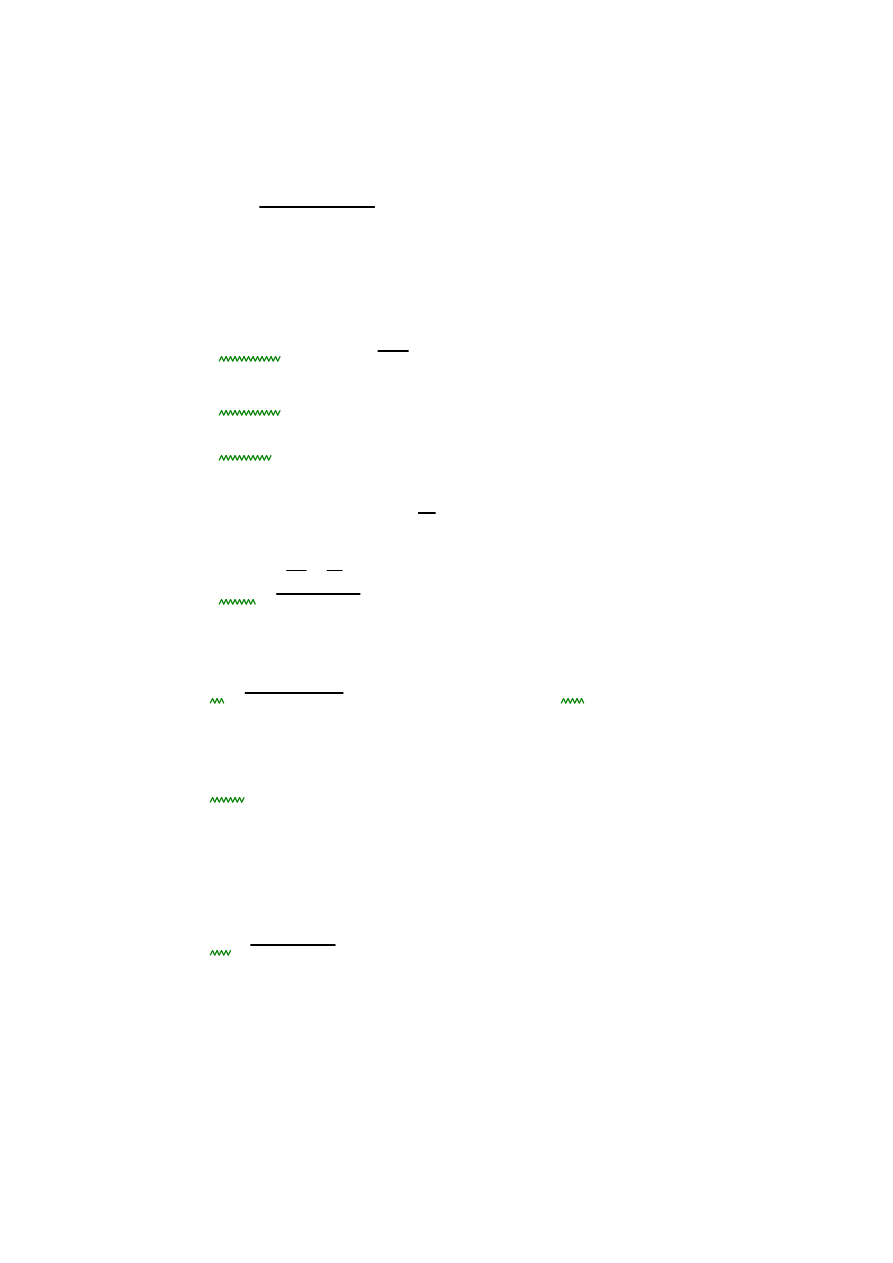
83
- rozstaw wynikaj
ą
cy z liczby przyj
ę
tych pr
ę
tów:
r3
B3 2 cnom
⋅
−
ϕ
−
n1
12.947 cm
⋅
=
:=
zbrojenie na kierunek B
•
- Zbrojenie minimalne
As.min1
0.26 L3
⋅
dx
⋅
fctm
fyk
⋅
73.868 cm
2
⋅
=
:=
As.min2
0.0013 L3
⋅
dx
⋅
63.679 cm
2
⋅
=
:=
As.min
max As.min1 As.min2
,
(
)
73.868 cm
2
⋅
=
:=
qsB3
qB3 L3
⋅
6.85
10
5
×
kg
s
2
=
:=
ML3
B3
2
hs
2
−
2
2
qsB3
⋅
960.929 m kN
⋅
=
:=
- potrzebna liczba pr
ę
tów:
Wst
ę
pnie przyj
ę
to :
n
ML3
0.9 dx
⋅
fyd
⋅
Aϕ
⋅
:=
n
13.422
=
n1
38
:=
- przyj
ę
to zbrojenie
AsB
n1 Aϕ
⋅
76.404 cm
2
⋅
=
:=
AsB
As.min
>
1
=
- rozstaw wynikaj
ą
cy z liczby przyj
ę
tych pr
ę
tów:
r3
L3 2 cnom
⋅
−
n1
0.134 m
=
:=
OSTATECZNIE PRZYJ
Ę
TO:
- na kierunku L:
AsL
30
ϕ
⋅
16
⋅
co 13 cm
- na kierunku B:
AsB
38
ϕ
⋅
16
⋅
co 13 cm

84
7.5.SPRAWDZENIE STOPY NA PRZEBICIE
L
5.2 m
=
- długo
ść
stopy fundamentowej
B
4 m
=
- szeroko
ść
stopy fundamnetowej
hf
1 m
=
- wysoko
ść
stopy
hs
0.65 m
=
- wysoko
ść
słupa
bs
0.65 m
=
- szeroko
ść
słupa
d
hf cnom
−
ϕ
−
0.5
ϕ
⋅
−
0.926 m
=
:=
- wysoko
ść
u
ż
yteczna stopy
- pole powierzchni wielok
ą
ta
A
B 0.5
⋅
L
hs
−
2 d
⋅
−
(
)
⋅
0.5 B
bs
−
2 d
⋅
−
(
)
2
⋅
−
4.274 m
2
=
:=
b1
hs
0.65 m
=
:=
- minimalny zasi
ę
g strefy przebicia
b2
bs 2 d
⋅
+
2.502 m
=
:=
- maksymalny zasi
ę
g strefy przebicia
-
ś
rednia arytmetycza zasiegów strefy przebicia
bm
b1 b2
+
2
1.576 m
=
:=
- maksymalny kraw
ę
dziowy odpór podło
ż
a
pod fundamentem
qfmax
N1d
B L
⋅
1
6 e1
⋅
L
+
⋅
229.005 kPa
⋅
=
:=
qfmax A
⋅
fctd bm
⋅
d
⋅
≤
1
=
warunek spełniony
KONIEC OBLICZE
Ń

85
N
newton
:=
kN
10
3
N
:=
kNm
kN m
⋅
:=
MPa
10
6
Pa
⋅
:=
kN
10
3
N
⋅
:=
MN
10
6
N
:=
kN
10
3
N
:=
MPa
10
6
Pa
:=
fck
:=
mb
m
:=
Dane do projektu:
E
1.5 10
7
⋅
kN
m
:=
MN
10
6
N
:=
MPa
1 10
6
Pa
⋅
:=
g
9.807
m
s
2
=
t
10
3
kg
⋅
:=
kPa
10
3
Pa
:=
kPa
10
3
Pa
⋅
:=
kN
1000N
:=
m
4
1 m
4
=
N
1N
:=
m
2
1 m
2
=
MPa
10
6
N
⋅
m
2
:=
m
1 m
=
N
kg
m
s
2
⋅
:=
cm
0.01 m
⋅
:=
GPa
10
9
Pa
:=
cm
4
1
10
8
−
×
m
4
=
kNm
kN m
⋅
:=
kPa
kN
m
2
:=
Pa
N
m
2
:=
Pa
kg m
⋅
s
2
m
2
:=

86

87

88

89

90
NRdi
ξeff hs
⋅
dy
⋅
fcd
⋅
As2 fyd
⋅
+
As1 fyd
⋅
−
kN
⋅
=
:=
As2

91

92

93

94
NRdi
ξeff hs
⋅
dy
⋅
fcd
⋅
As2 fyd
⋅
+
As1 fyd
⋅
−
kN
⋅
=
:=
As2

95

96

97

98

99

100

101

102

103
MB3
231
−
kN
⋅
m
⋅
:=
MB3
378.287
−
kN
⋅
m
⋅
:=

104
kN
m
2
Wyszukiwarka
Podobne podstrony:
Mathcad SŁUP PROJEKT swieta kopia1
Mathcad SŁUP PROJEKT swieta kopia
Mathcad SŁUP PROJEKT 23 05
Mathcad SŁUP PROJEKT 07 06
Mathcad SŁUP PROJEKT 23 05
Mathcad SŁUP PROJEKT 23 05
Mathcad SŁUP PROJEKT 07 06
Mathcad grunt projekt RŁ
Mathcad Slup
Mathcad Fundamentowanie projekt I
Mathcad, grunt projekt RŁ
Mathcad, 1 podejscie projektowe 2 kombinacja
Mathcad OZE projekt 1 kolektor
Mathcad, 1 podejscie projektowe 1 kombinacja
Mathcad stal projekt 2 RŁ
więcej podobnych podstron