Wyznaczanie współczynników oporu ciał osiowo-symetrycznych

1

WYZNACZANIE WSPÓŁCZYNNIKÓW OPORU CIAŁ

OSIOWO-SYMETRYCZNYCH

6.1. Cel ćwiczenia

Celem ćwiczenia jest określenie wpływu kształtu ciała osiowo-symetrycznego na jego

opór oraz obliczenie współczynników oporu badanych ciał osiowo-symetrycznych.

6.2. Określenia

Podczas ruchu w powietrzu ciała mające oś symetrii lub płaszczyznę symetrii

równoległą do kierunku ruchu nie występuje na tych ciałach składowa reakcji prostopadła do
kierunku ruchu nazywana siłą nośną. Występuje jedynie składowa równoległa do kierunku
ruchu znana jako siła oporu. W przypadku, gdy kierunek strumienia opływającego ciało
osiowo-symetryczne nie będzie równoległy do osi symetrii opływanego ciała, wtedy
powstanie siła nośna.
Wiadomo, że siła oporu jest wprost proporcjonalna do ciśnienia dynamicznego oraz
powierzchni czołowej opływanego ciała oraz od pewnej bezwymiarowej liczby zależącej od
kształtu opływanego ciała, jego usytuowania względem kierunku ruchu, liczby Reynoldsa i
przy dużych prędkościach od liczby Macha. Liczba ta nosi nazwę współczynnika oporu i jest
oznaczana jako c

x.

Ogólny wzór na siłę oporu ma postać:

S

V

c

P

x

x

2

2

∞

=

ρ

Podczas, gdy ciało jest opływane z małymi prędkościami, możemy zaniedbać ściśliwość.
Wtedy opór opływanego ciała osiowo-symetrycznego będzie składał się z oporu tarcia c

xt

i

oporu ciśnieniowego c

xp

(obejmuje opór oderwania i opór wirowy)

Opór tarcia zależy od charakteru przepływu w warstwie przyściennej, natomiast opór

ciśnieniowy zależy od kształtu ciała oraz od położenia obszaru oderwania warstwy
przyściennej od powierzchni opływanego ciała.

Zjawisko oderwania praktycznie nie występuje przy opływie ciał opływowych (np.:

kształt kroplowy). Dlatego też decydującym składnikiem oporu jest opór tarcia. Dla tego
rodzaju ciał współczynnik oporu zmienia się nieznacznie z liczbą Reynoldsa.

Na półkuli, czaszy kulistej, stożku kołowym ustawionym płaską powierzchnią

(ewentualnie wklęsłością) w kierunku napływającego strumienia oderwanie musi wystąpić na
ostrych krawędziach i opór tych ciał praktycznie nie zależy od liczby Reynoldsa ( z
wyłączeniem przepływów przy bardzo małych liczbach Reynoldsa

1

Re

≤

).

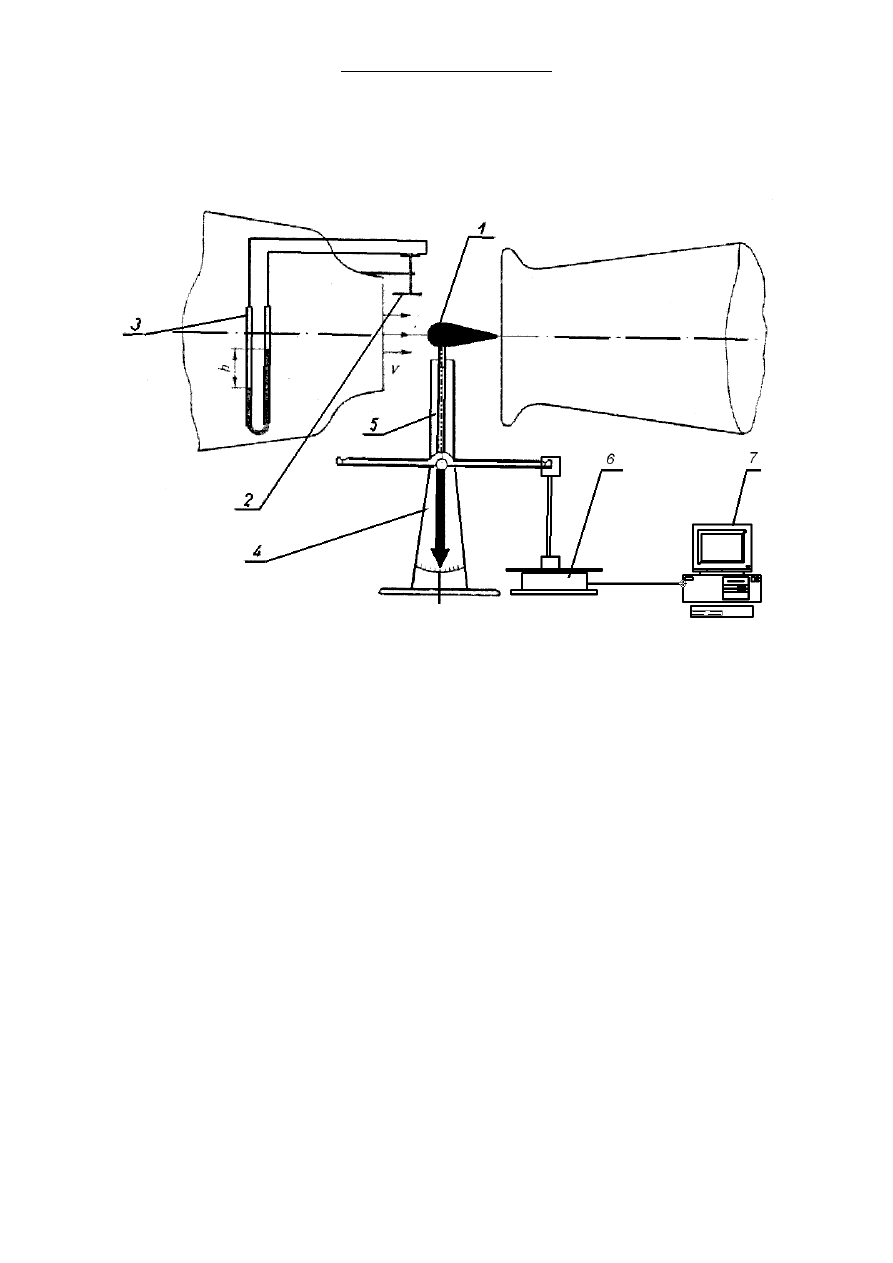
6.3. Stanowisko pomiarowe

Pomiary przeprowadza się w przestrzeni pomiarowej tunelu aerodynamicznego, w

której na wysięgniku (5) jednoskładowej wagi aerodynamicznej(4) umieszcza się modele(1)
różnych ciał osiowo-symetrycznych. Wszystkie badane ciała mają jednakową powierzchnię
czołową, którą jest koło. W celu uniknięcia oddziaływania powietrza na wysięgnik wagi
obudowano go profilowaną osłoną związaną nieruchomo z podstawą wagi.

Za pomocą rurki Prandtla(2) i manometru różnicowego(3) mierząc ciśnienie

dynamiczne można określić prędkość strumienia w przestrzeni pomiarowej. Natomiast
parametry powietrza atmosferycznego należy odczytać z barometru oraz termometru
znajdujących się w pomieszczeniu laboratorium.

Ć

wiczenie laboratoryjne nr 6

2

Siła, z jaką strumień oddziałuje na model jest przekazywana poprzez ramię wagi na wagę
komputerową Mensor (6). Odczyt wartości siły przeprowadza się na przyłączonym do wagi
komputerze PC (7).

Rys. 6.1 Schemat stanowiska pomiarowego

6.4. Metodyka pomiaru

1. Odczytać wartość ciśnienia atmosferycznego i temperatury powietrza wewnątrz

laboratorium i wpisać do protokołu pomiarowego

2. Uruchomić program obsługujący wagę elektroniczną.

•

Otworzyć folder

Advantech Genie znajdujący się na Pulpicie. Uruchomić

program

Genie Runtime

•

Z belki narzędziowej wybrać polecenie

File i uruchomić plik waga6kg.gni

•

Po uruchomieniu się programu nacisnąć przycisk

start znajdujący się na belce

narzędziowej programu. Po pojawieniu się napisu „Waga działa poprawnie”
można wytarować wagę poprzez naciśnięcie przycisku

tara.

3. Zakładając po kolei wszystkie badane modele ciał osiowo-symetrycznych na

wysięgnik wagi pomiarowej dokonać pomiaru tary modeli T

x

.

Po każdym pomiarze

wytarować wagę. Wartości odczytane z programu obsługującego wagę elektroniczną
umieścić w odpowiedniej rubryce protokołu pomiarowego. Przy zakładaniu modelu
zwrócić szczególną uwagę na poprawność jego zamocowania oraz, by oś symetrii
modelu była równoległa do osi tunelu.

4. Po sprawdzeniu tary badanych modeli, jeden z nich pozostawić na wysięgniku, a

następnie uruchomić silnik napędzający wentylator tunelu za pomocą układu Ward-
Leonarda. Przy ustalonej wartości różnicy ciśnień

p

∆

mierzonej rurką Prandtla

dokonać pomiaru całkowitej siły oporu G

x

. Do protokołu pomiarowego wpisać

Wyznaczanie współczynników oporu ciał osiowo-symetrycznych

3

zmierzoną wartość G

x

i wartość

p

∆

przy której było to mierzone. Starać się, by przy

wszystkich pomiarach

p

∆

było w przybliżeniu stałe.

5. Zmniejszyć obrotu wentylatora do minimum, zdjąć model i założyć nowy. Powtarzać

czynności z pkt. 4.

6. Po zmierzeniu siły oporu modeli dokonać pomiar siły oporu trzpienia D

x

przy takim

p

∆

, przy jakim były badane modele. Wartość zanotować w protokole pomiarowym.

7. Po zakończeniu pomiarów ponownie odczytać wartość temperatury powietrza i

ciśnienia atmosferycznego.

8. Nacisnąć przycisk

stop a następnie wyłączyć program obsługujący wagę.

9. Uruchomić pakiet Excell. Otworzyć plik CX.xls i wpisać odczytane wielkości do

arkusza kalkulacyjnego. Arkusz sam obliczy wartości współczynników oporu
poszczególnych ciał osiowo-symetrycznych i innych potrzebnych wielkości.
Słuchacze przepisują obliczone przez arkusz wartości do swojego protokołu
pomiarowego.

6.5. Oznaczenia i wzory obliczeniowe

Współczynnik oporu

qS

P

c

x

x

=

gdzie:

]

[

10

807

,

9

)

(

3

N

D

T

G

P

x

x

x

x

−

⋅

⋅

−

−

=

- siła oporu ciała osiowo-symetrycznego

]

[G

G

x

-całkowita siła oporu ( razem z tarą i oporem trzpienia)

]

[G

T

x

-tara modelu (siła potrzebna do zrównoważenia wagi przy

niepracującym tunelu)

]

[G

D

x

-opór trzpienia









∆

=

2

2

m

N

p

k

q

p

-ciśnienie dynamiczne

p

k -współczynnik poprawkowy dla rurki Prandtla (równy 1.03)

∆

p[N/m

2

]- różnica ciśnień na rurce Prandtla

]

[

2

m

S

- powierzchnia czołowa badanych modeli (koło o średnicy d=0.1 [m])

Liczba Reynoldsa

gdzie:









∆

=

s

m

p

k

V

t

p

ρ

2

-prędkość przepływu w przestrzeni pomiarowej









+

⋅

=

−

3

3

273

10

483

.

3

m

kg

t

p

a

t

ρ

-gęstość powietrza przy ciśnieniu









2

m

N

p

a

i

temperaturze

[ ]

C

t

o













=

s

m

v

t

t

t

2

ρ

µ

-kinematyczny współczynnik lepkości przy danej temperaturze

t

v

Vd

=

Re

Ć

wiczenie laboratoryjne nr 6

4





















+

=

2

75

,

0

0

273

273

m

Ns

t

t

µ

µ

-dynamiczny współczynnik lepkości powietrza przy

danej temperaturze









⋅

=

−

2

6

0

10

064

.

17

m

Ns

µ

-dynamiczny współczynnik lepkości dla powietrza w

temperaturze

C

o

0

i ciśnieniu atmosferycznym









2

72

.

101324

m

N

(wg „Tablic

cieplnych” Kuzmana Raznievica )

6.6. Opracowanie wyników pomiarów

Wyniki pomiarów oraz wartości obliczone przez formułę umieszczoną w Microsoft Excell

należy zamieścić w protokole pomiarowym otrzymanym od prowadzącego zajęcia.
W sprawozdaniu z ćwiczenia laboratoryjnego należy umieścić:

1. Schemat stanowiska pomiarowego
2. Stosowane wzory
3. Protokół pomiarowy
4. Spostrzeżenia, uwagi i wnioski z przeprowadzonego ćwiczenia laboratoryjnego.