1

16. Ruch cząstek naładowanych w polu elektrycznym i magnetycznym

Ładunek punktowy w polu elektrycznym

Pole elektryczne działa na cząstkę naładowaną z siłą wytwarzającą przyspieszenie

(16-1)

gdzie m jest masą cząstki. Rozważmy dwa przykłady przyspieszenia cząstki naładowanej w
jednorodnym polu elektrycznym. Takie pole można wytworzyć łącząc dwie końcówki baterii z
dwiema równoległymi płytkami metalowymi, odizolowanymi od siebie. Jeżeli odległość pomiędzy
płytkami jest mała w porównaniu z rozmiarami płytek, to pole pomiędzy nimi będzie
wystarczająco jednorodne z wyjątkiem obszaru położonego blisko brzegów. Zauważmy, że
rozważając ruch cząstki w polu wytworzonym przez ładunki zewnętrzne, pomijamy pole
wytworzone przez samą cząstkę. Podobnie pole grawitacyjne Ziemi nie wywiera żadnej siły na
samą Ziemię, a tylko na inne przedmioty, powiedzmy kamień, umieszczone w tym polu.
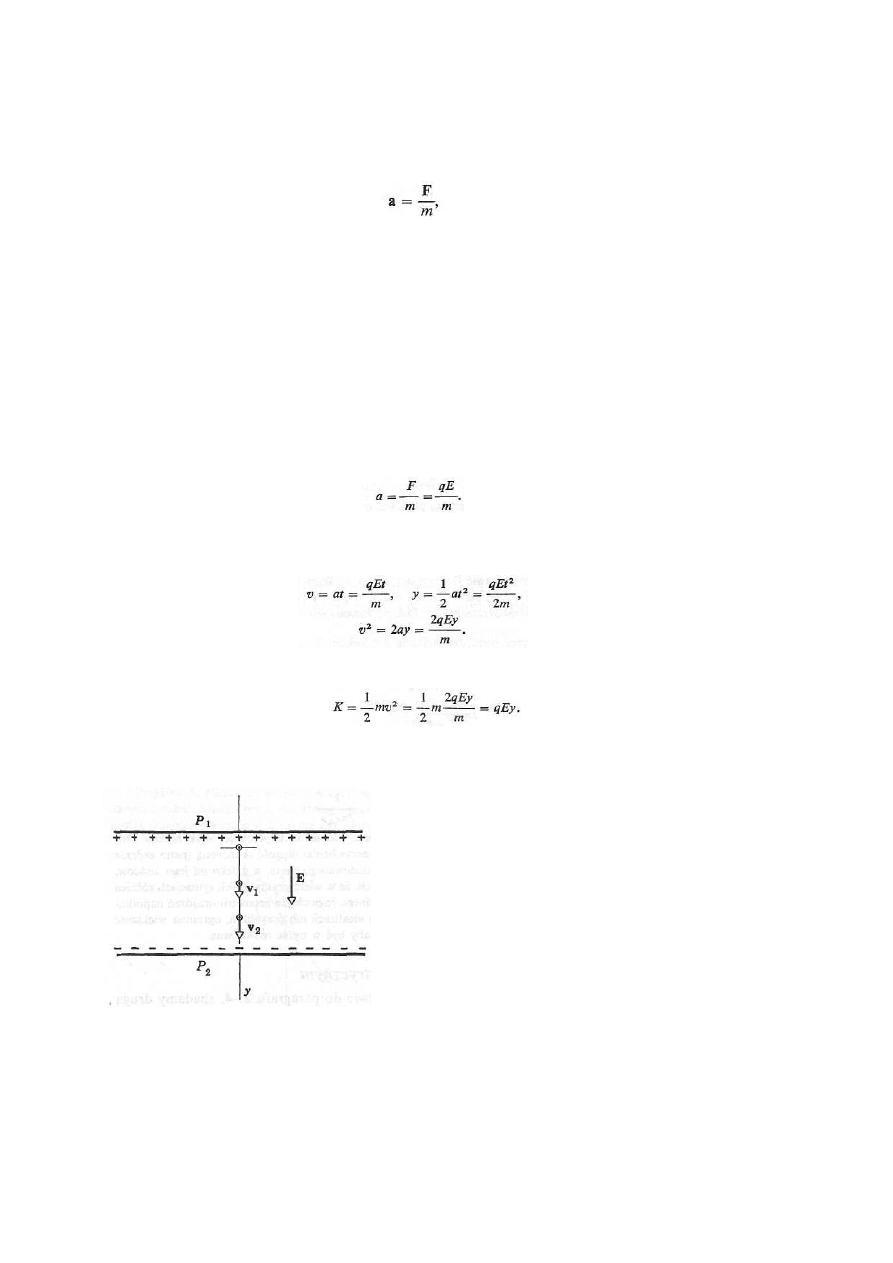
Przykład 1. Wprowadzamy cząstkę o masie m i ładunku q do jednorodnego pola elektrycznego i
puszczamy ją swobodnie (rys. 16-1). Opisać jej ruch.
Ruch ten jest podobny do ruchu ciała spadającego w ziemskim polu grawitacyjnym. Przyspieszenie
dane jest przez

(16-1)

Stosujemy więc równanie ruchu jednostajnie przyspieszonego. Przyjmując v

0

= 0 mamy

(16-2)

Energię kinetyczną osiągniętą po przebyciu odległości y znajdujemy z zależności

(16-3)

Ten wynik można również otrzymać bezpośrednio z twierdzenia o zamianie pracy na energię, gdyż
stała siła qE działa na drodze y.

Przykład 2. Odchylanie wiązki elektronów. Rysunek 16-2 przedstawia elektron o masie m i ładunku q
= e, wpadający do jednorodnego pola elektrycznego z prędkością początkową v

0

, prostopadłą do kie-

runku wektora natężenia pola E. Opisać ruch tego elektronu.

Rys. 16-1. Ruch ładunku w jednorodnym polu elek-
trycznym wytworzonym przez dwie przeciwnie nałado-
wane płyty P

1

i P

2

2

Ruch elektronu będzie podobny do ruchu pocisku wystrzelonego poziomo w polu grawitacyjnym Zie-
mi. Otrzymujemy następujące wyrażenia na składową poziomą (x) i pionową (y) ruchu

(16-4)

Eliminując t otrzymujemy równanie toru

(16-5)

Elektron opuszczając obszar zawarty pomiędzy płytkami (rys. 27-13) porusza się (zaniedbujemy siły
ciążenia) po linii prostej, stycznej do paraboli z równ. (27-9) w punkcie wyjścia. Na jego drodze, w
pewnej odległości przed płytkami, możemy ustawić fluoryzujący ekran S. Wówczas rozważany
elektron razem z innymi elektronami biegnącymi po tej samej drodze będzie widoczny jako mała
plamka świetlna; na tym polega zasada działania elektrostatycznego oscyloskopu katodowego.

Przykład 3. Dodatni, punktowy ładunek próbny q

0

znajduje się w połowie drogi pomiędzy dwoma

równymi umieszczonymi na stałe ładunkami dodatnimi q. Jaka siła działa na niego w punkcie P i w
pobliżu punktu P?

Ze względu na symetrię siła w punkcie P równa się zeru; cząstka znajduje się w równowadze.

Należ) znaleźć rodzaj tej równowagi. Na rysunku 27-14 (porównaj rys. 27-4) pokazane są wektory E
dla czterech punktów w sąsiedztwie punktu P. Jeżeli ładunek próbny porusza się wzdłuż osi z, to
występuje siła przywracająca równowagę; jednakże równowaga jest nietrwała dla ruchu po osiach x i y.
Jest to zatem trójwymiarowy równoważnik siodłowego punktu równowagi (patrz rys. 14-8). Jaki byłby
rodzaj równowagi dla ujemnego ładunku próbnego?

Dipol w polu elektrycznym

Elektryczny moment dipolowy może być traktowany jako wektor p, którego wielkość p dla

dipola, takiego jak opisany w przykładzie 3, jest iloczynem 2aq, tj. wielkości ładunku q i
odległości 2a pomiędzy ładunkami, a kierunek p jest zgodny z kierunkiem od ładunku ujemnego
do dodatniego. Wektorowa natura elektrycznego momentu dipolowego pozwala nam, jak
zobaczymy, sprowadzić wiele wyrażeń do bardziej zwartej postaci poprzez wprowadzenie dipoli
elektrycznych.

Rysunek 16-4a przedstawia dipol elektryczny utworzony przez umieszczenie dwóch ładunków

+q i -q w stałej wzajemnej odległości 2a. Układ jest umieszczony w jednorodnym zewnętrznym
polu elektrycznym E, z którym moment dipolowy p tworzy kąt θ. Na dipol, jak pokazano,
działają dwie równe i przeciwnie skierowane siły F i -F, gdzie F = qE. Wypadkowa siła jest

Rys. 16-2. Przykład 2. Elektron o prędkości po-
czątkowej v

0

wchodzi w obszar pola elektrycznego

wytworzonego przez dwie płytki naładowanego
kondensatora. Kierunek prędkości jest prostopadły do
kierunku pola

Rys. 16-3. Przykład 3. Pole elektryczne w czterech
punktach w pobliżu punktu P, leżącego w środku
odległości między dwoma dodatnimi ładunkami q.

3

oczywiście równa zeru, lecz istnieje wypadkowy moment obracający dipol wokół osi
przechodzącej przez punkt O dany przez

(16-6)

Łącząc te dwa równania i biorąc pod uwagę, że p = 2aq, otrzymujemy

(16-7)

Widzimy, że na dipol elektryczny umieszczony w zewnętrznym polu E działa moment skręcający,
dążący do ułożenia go wzdłuż linii pola. Równanie (16-7) można przepisać w postaci
wektorowej

(16-8)

Odpowiednie wektory pokazane są na rys. 27-15b.

Rys. 16-4. (a) Dipol elektryczny w jednorodnym polu zewnętrznym, (b) Ilustracja zależności τ= p

x

E

Ażeby zmienić położenie dipola elektrycznego w zewnętrznym polu elektrycznym, musi być
wykonana pewna praca (dodatnia lub ujemna) przez czynnik zewnętrzny. Praca ta zostaje
zmagazynowana jako energia potencjalna U układu składającego się z dipola i urządzenia
wytwarzającego pole zewnętrzne. Jeżeli θ na rys. 16-4a ma wartość początkową θ

0

, to praca

potrzebna do obrócenia dipola do kąta θ dana jest równaniem (16-9), czyli

(16-9)

gdzie τ jest momentem skręcającym, wywieranym przez czynnik, który wykonuje pracę. Z tego
równania oraz z zależności (16-7) otrzymujemy

(16-10)

Ponieważ interesują nas tylko zmiany energii potencjalnej, orientację punktu odniesienia, θ

0

możemy dobrać tak, aby miała wygodną wartość, w tym przypadku 90°. Stąd mamy

(16-11)

Ładunki krążące po orbitach

Rysunek 16-5 przedstawia ujemnie naładowaną cząstkę o prędkości v, wprowadzoną do

jednorodnego pola magnetycznego o indukcji B. Zakładamy, że v jest prostopadłe do B, czyli
leży dokładnie w płaszczyźnie rysunku. Z zależności F = qυ

x

B wynika, że na cząstkę działa siła

odchylająca o wartości bezwzględnej qvB. Siła ta leży w płaszczyźnie rysunku, wobec czego
cząstka nie może opuścić tej płaszczyzny.

Przypomina nam to kamień przytrzymywany linką i obracający się w płaszczyźnie poziomej

po okręgu koła. Tutaj również na kamień działa siła o stałej wartości bezwzględnej — napięcie
linki, leżąca stale w jednej płaszczyźnie i prostopadła do prędkości. Naładowana cząstka,
podobnie jak kamień, porusza się ze stałą prędkością po torze kołowym.

(16-12)

4

gdzie r jest promieniem toru. Na rysunku 16-6 pokazany jest spiralny tor (trzy spirale) elektronu o
niskiej energii w komorze pęcherzykowej. Tutaj tor nie jest kołem, ponieważ elektron w czasie
ruchu traci energię wskutek zderzeń.

Prędkość kątowa ω równa jest v/r, czyli

(16-13)

Częstość v dana jest wzorem

(16-14)

Zauważmy, że v nie zależy od prędkości cząstki. Szybkie cząstki poruszają się po dużych kołach,
wolne po małych, ale każda z nich potrzebuje tego samego czasu T, aby wykonać jeden obrót w
polu.

Częstość v jest częstością charakterystyczną dla naładowanej cząstki w polu magnetycznym i

można ją porównać z częstością charakterystyczną wahadła w ziemskim polu grawitacyjnym oraz
z częstością charakterystyczną układu drgającego masa-sprężynka. Częstość ta jest czasami
nazywana częstością cyklotronową cząstki w polu, ponieważ z taką częstością krąży cząstka
w cyklotronie.

Akceleratory cząstek

Cyklotron, uruchomiony po raz pierwszy na Uniwersytecie Kalifornijskim w Berkeley przez

Ernesta Lawrance'a (1902-1958) w roku 1932, jest przyrządem służącym do przyspieszania
naładowanych cząstek, takich jak jądra wodoru (protony) i deuterony, czyli jądra ciężkiego
wodoru do wysokich energii, takich aby cząstki te można było używać w doświadczeniach nad

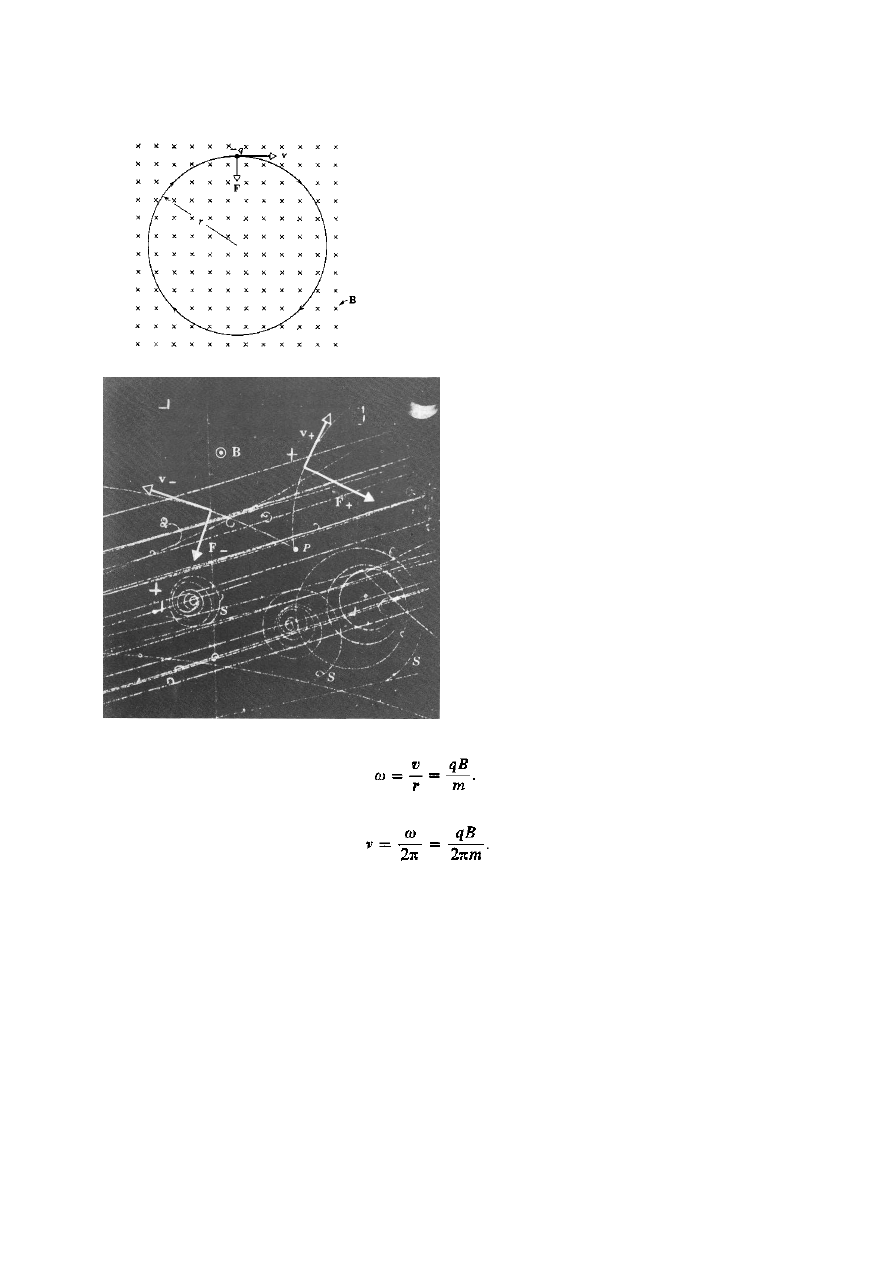
Rys. 16-5. Ładunek -q krąży po torze
kołowym leżącym w płaszczyźnie
prostopadłej do jednorodnego pola
magnetycznego

Rys. 16-6. Komora pęcherzykowa jest urządzeniem
pozwalającym oglądać, dzięki powstającym w nią
małym pęcherzykom, tory cząstek naładowanych,
przechodzących poprzez komorę. Rysunek
przedstawi* fotografię wykonaną przy użyciu takiej
komory umieszczonej w polu magnetycznym o
indukcji B i naświes-lanej promieniowaniem z
wielkiego cyklotronu. Krzywa o kształcie litery V
przechodząca przez punkt F jest utworzona przez
tory dodatniego i ujemnego elektronu, które w polu
magnetycznym są odchylone w przeciwne strony.
Spirale S są śladami trzech niskoenergetycznych
elektronów. (Dzięki uprzejmości E. O. Lawrence'a,
Radiation Laboratory, Uniyersity of California)

5

rozbijaniem atomów. Na rysunku 16-7 przedstawiony jest cyklotron pracujący dawniej na
uniwersytecie w Pittsburghu. Chociaż konwencjonalne cyklotrony tego typu nie są już używane,
przedyskutujemy je z dwóch powodów: (a) dostarczają one doskonałych ram do dyskusji
oddziaływania pól elektrycznego i magnetycznego na cząstki naładowane; (b) od nich wywodzi się
kilka generacji usprawnionych akceleratorów — chociażby synchrotron protonowy. Ten ostatni
dostarcza nawet więcej możliwości badania oddziaływania pól elektrycznych i magnetycznych z
cząstkami naładowanymi. Oczywiście nie jest to jego główne zadanie.

W środku cyklotronu znajduje się źródło jonów, w którym cząsteczki deuteru (ciężkiego

wodoru) bombardowane są elektronami o dosyć wysokiej energii (np. 100 eV), dzięki czemu
podczas zderzeń wytwarza się duża liczba dodatnich jonów. Wiele z tych jonów są to po prostu
swobodne deuterony, które przedostają się przez mały otwór w ściance źródła- jonów do
właściwego cyklotronu i tam mogą być przyspieszane.

W cyklotronie do przyspieszania stosuje się różnicę potencjałów średniej wielkości (np. 10

5

V), ale jony przebywają tę różnicę wielokrotnie. Aby osiągnąć energię 10 MeV, przy różnicy
potencjałów przyspieszających 10

5

V, jony muszą przebyć tę różnicę 100 razy. Do zakrzywiania

toru jonów, tak aby mogły one wielokrotnie przebyć tę samą drogę, stosuje się pole magnetyczne.

Rysunek 16-7 przedstawia widzianą z góry część cyklotronu, która znajduje się wewnątrz

opróżnionego z powietrza zbiornika, oznaczonego na rys. 33-12 literą V. Dwa pierścienie w
kształcie litery D (nazywane duantami), z blachy miedzianej, tworzą część

elektrycznego oscylatora. W przerwie pomiędzy pierścieniami panuje określona różnica
potencjałów przyspieszająca cząstki. Znak tej różnicy potencjałów zmienia się milion razy na
sekundę.

Pierścienie umieszcza się w polu magnetycznym (BS 1,6 T) skierowanym za płaszczyznę

rys. 16-7. Pole wytworzone jest przez ogromny elektromagnes, którego część oznaczono na rys.
16-7 literą R. Ponadto przestrzeń, w której poruszają się jony, opróżniona jest z powietrza do
ciśnienia 10

-6

mmHg. Gdyby tego nie zrobiono, jony zderzałyby się ciągle z cząsteczkami

powietrza.

Przypuśćmy, że deuteron wybiegający ze źródła jonów napotyka na pierścień o potencjale

ujemnym; zostanie on przyspieszony w kierunku tego pierścienia i wejdzie do niego. Wewnątrz
pierścienia jon (deuteron) jest ekranowany od sił elektrycznych przez jego metalowe ścianki.
Pole magnetyczne natomiast swobodnie przechodzi przez te ścianki, wobec czego tor jonu
zostaje zakrzywiony, staje się kołem o promieniu zależnym od prędkości i jest dany równaniem r
= mv/qB. Po czasie t

0

jon wylatuje z pierścienia w kierunku przeciwnym niż początkowo ze

źródła jonów. Załóżmy, że w tym momencie potencjał zmienia znak. Wobec tego jon ma teraz
przed sobą drugi pierścień o potencjale ujemnym, w dalszym ciągu jest przyspieszany i znowu
opisuje półokrąg, ale już w drugim pierścieniu o nieco większym promieniu. Jednakże czas
przejścia przez drugi pierścień znowu jest równy t

0

, ponieważ okres obrotu jonu krążącego w polu

magnetycznym nie zależy od jego prędkości. Ten proces powtarza się aż do chwili, gdy jon zbliży
się do zewnętrznej krawędzi jednego z pierścieni, gdyż wówczas jest on wyrzucony z układu przez
ujemnie naładowaną płytkę odchylającą.

Rys. 16-7. Część cyklotronu przedstawiająca
źródło Z jonów i duanty. Płytka
odchylająca o odpowiednim ujemnym
potencjale skierowuje wiązkę na zewnątrz

6

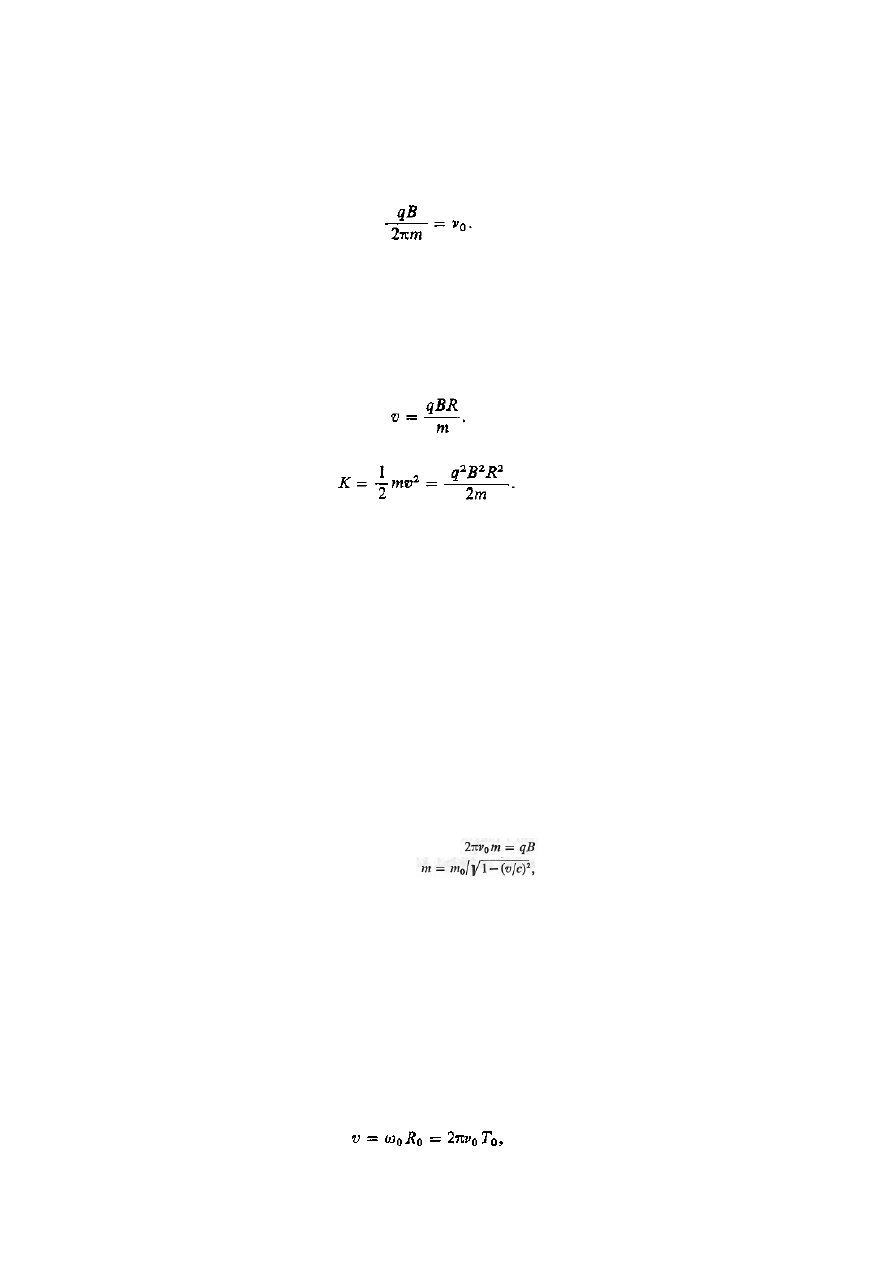
Aby cyklotron działał, częstość charakterystyczna v, z którą jon krąży w polu, musi być

równa ustalonej części v

0

oscylatora elektrycznego, czyli v = v

0

. Jest to warunek rezonansowy. Z

warunku tego wynika, że jeżeli energia krążącego jonu ma wzrastać, trzeba mu dostarczać energię
z częstością v

0

równą jego częstości własnej, z jaką krąży w polu. W ten sposób dostarczamy

energię huśtawce, popychając ją z częstością równą częstości własnej wahań huśtawki.
Korzystając z równania (y = qB/2

π

m) możemy warunek rezonansowy przepisać w postaci

(16-15)

Jeżeli wybraliśmy rodzaj cząstek, które mają być przyspieszane, stosunek q/m jest wielkością

ustaloną. Zwykle oscylatory pracują tylko przy określonej częstości v

0

. Zmieniając B dotąd, aż

równanie (33-17) będzie spełnione, „dostrajamy" cyklotron tak, aby otrzymać na wyjściu
wiązkę cząstek przyspieszonych.

Energia cząstek wytwarzanych w cyklotronie zależy od promienia R pierścienia. Z równania

(33-15) (r = mv\qS) otrzymujemy na prędkość cząstki krążącej po okręgu o danym promieniu
wyrażenie

(16-16)

Energia kinetyczna jest więc równa

(16-17)

Istnieją dwa powody, dla których opisany przez nas klasyczny cyklotron zawodzi przy wysokich
energiach. Jeden z nich wiąże się z fizyką, drugi z kosztami. Omówimy oba. Przy wysokich
energiach działanie cyklotronu, zawodzi, ponieważ w jednym z założeń przyjęliśmy, że częstość
obrotów jonu krążącego w polu magnetycznym nie zależy od jego prędkości, co jest słuszne jedynie
dla prędkości dużo mniejszych od prędkości światła. Gdy prędkość cząstek wzrasta, w równaniu (16-
15) musimy brać pod uwagę masę relatywistyczną m. Ponieważ masa relatywistyczna rośnie wraz z
prędkością, więc przy dostatecznie dużych prędkościach częstość v maleje ze wzrostem prędkości.
Wskutek tego jony krążące w oscylatorze elektrycznym zbaczają z torów i w końcu energia ich
przestaje wzrastać. Drugą trudnością związaną z przyspieszaniem cząstek naładowanych do wysokich
energii jest to,
że wymiary magnesu potrzebnego do prowadzenia takich cząstek po orbitach kołowych muszą być
bardzo duże. Dla protonów o energii — na przykład —30

.

10

9

eV, w polu o indukcji 1,5 T promień

krzywizny wynosi 65 m. Magnes dla takiego cyklotronu (o średnicy około 17 m) byłby niezwykle
kosztowny. Nawiasem mówiąc, protony o energii 30 • 10

9

eV mają prędkość równą 0,99998

prędkości światła.

Oba te ograniczenia, relatywistyczne i ekonomiczne można zlikwidować w sposób, który okaże

się zrozumiały, jeżeli rozpatrzymy równanie (33-17)

podstawiając tam na miejsce m masę

relatywistyczną, daną równaniem (8-20), czyli

gdzie v jest prędkością cząstki, c —

prędkością światła.

Gdy prędkość cząstki rośnie, masa relatywistyczna również rośnie. Aby równość (16-15)

pozostała słuszna i spełniony był warunek rezonansowy, częstość oscylatora v

0

, w miarę jak cząstka

(niech będzie to np. proton) jest przyspieszana, można zmniejszyć w taki sposób, aby iloczyn v

Q

m

pozostawał stały. Akceleratory, w których stosuje się ten sposób, nazywamy synchrocyklotronami.

Aby zlikwidować ograniczenie spowodowane kosztami magnesu, można zmienić zarówno B, jak i

v

0

w sposób cykliczny, tak aby nie tylko przez cały czas spełnione było równanie (33-17), ale również,

aby promień orbity pozostawał nie zmieniony podczas procesu przyspieszenia. Pozwala to na użycie
magnesu pierścieniowego (w kształcie obrączki) zamiast magnesów zwykle stosowanych w
cyklotronach, co znacznie zmniejsza koszty. Mając do dyspozycji dwie zmienne wielkości B i v

0

,

możemy w czasie trwania procesu zachowywać dwie równości, jedną — równanie (16-51) i drugą,
daną zależnością

(16-17)

7

gdzie R

o

jest ustalonym promieniem orbity. Akceleratory, w których stosowana jest tego rodzaju

technika, nazywane są synchrotronami. Tablica 33-2 podaje pewne parametry charakteryzujące
synchrotron zbudowany w Brookhaven National Laboratory w Brookhaven.

Zwracamy uwagę, że nawet energie protonów wstrzykiwanych (50 MeV) do tego akceleratora

daleko przewyższają możliwości cyklotronu konwencjonalnego.

W czasie pisania tego podręcznika (1977) największy synchrotron protonowy (z energią 500 GeV

mającą wzrosnąć do docelowej 1000 GeV) znajdował się w Batavii k. Chicago w stanie Illinois.

System wstrzykujący protony do pierścienia przyspieszającego tego akceleratora jest sam w sobie

imponujący. Protony są początkowo przyspieszane do 750 keV przez układ transformator-prostownik.
Następnie przechodzą przez mający 145 m długości akcelerator liniowy i opuszczają go z energią 200
MeV, która jest energią wejściową do pośredniej wielkości synchrotronu dającego energię 80 GeV.
Dopiero z tą energią wstrzykiwane są do głównego przyspieszającego pierścienia.

We wszystkich tych procesach pola elektryczne i magnetyczne nie tylko przyspieszają protony,

lecz również kierują je w pożądanych kierunkach potrzebnych do przeprowadzanych eksperymentów,
a przede wszystkim ogniskują dobrze zdefiniowaną wiązkę protonową na drodze jej przebiegu
wynoszącej około 1,6

.

10

5

km. Chociaż nie to było głównym celem, nie zbudowano lepszego

„laboratorium" dla zademonstrowania oddziaływania pól elektrycznego i magnetycznego na cząstki
naładowane. Dla ilustracji wielkości i zakresu tej inwestycji podajemy tylko jej roczny budżet za
zużytą energię elektryczną, który wyniósł w 1976 r. kilka milionów dolarów.