1 |

S t r o n a

Lidia Chomicz i Marcin Woźniak, gr.1

Uniwersytet Gdański

Pracownia Chemii Fizycznej

Ćwiczenie 2

Polaryzowalność cząsteczki. Moment dipolowy.

Prowadząca zajęcia:

dr Agnieszka

Wróblewska

Data wykonania:

Ocena:

30.11.2006 r.

1) Wyznaczenie pojemności czynnej i biernej kondensatora.

Zmierzyliśmy pojemność pustego kondensatora i kondensatora wypełnionego rozpuszczalnikiem:

C

0

=44 pF - pojemność pustego kondensatora

C=75 pF - pojemność kondensatora wypełnionego cykloheksanem

Znając dodatkowo względną stałą dielektryczną cykloheksanu (ε

r

=2,023), wyznaczyliśmy

pojemność czynną (C

c

) oraz bierną (C

b

) kondensatora:

]

[

3

,

30

1

0

pF

C

C

C

r

c











]

[

7

,

13

0

pF

C

C

C

c

b







2) Wyznaczenie stałych dielektrycznych poszczególnych roztworów nitrobenzenu w

cykloheksanie.

Zmierzyliśmy pojemność elektryczną kondensatora po napełnieniu go badanymi roztworami.
(Dane dotyczące tych roztworów i pojemności C

x

zamieściliśmy w tabeli 1.)

Na podstawie tych danych obliczyliśmy stałe dielektryczne (ε

x

) badanych roztworów w oparciu o

poniższy wzór:

1







c

x

x

C

C

C



Otrzymane wyniki opisuje tabela 1.

3) Obliczenia dotyczące polaryzacji właściwej.

Aby wyznaczyć polaryzację właściwą poszczególnych roztworów, obliczyliśmy kolejno (wszystkie
wyniki obliczeń – tabela 1):

a) Ułamki molowe nitrobenzenu i cykloheksanu, korzystając ze wzoru (np. dla nitrobenzenu):

c

n

n

n

n

n

n

X





, gdzie:

X

n

– ułamek molowy nitrobenzenu

n

n

– liczba moli nitrobenzenu w badanym roztworze

n

c

– liczba moli cykloheksanu w badanym roztworze

2 |

S t r o n a

b) Gęstość poszczególnych roztworów – w oparciu o zasadę addytywności gęstości:

c

c

n

n

X

d

X

d

d





, gdzie:

d – gęstość roztworu
d

n

=1203,3 [kg/m

3

] – gęstość nitrobenzenu

d

c

=778,6 [kg/m

3

] – gęstość cykloheksanu

c) Wtedy polaryzację właściwą p – ze wzoru:





















kg

m

d

p

x

x

3

1

2

1





4) Wyznaczenie całkowitej polaryzacji molowej P.

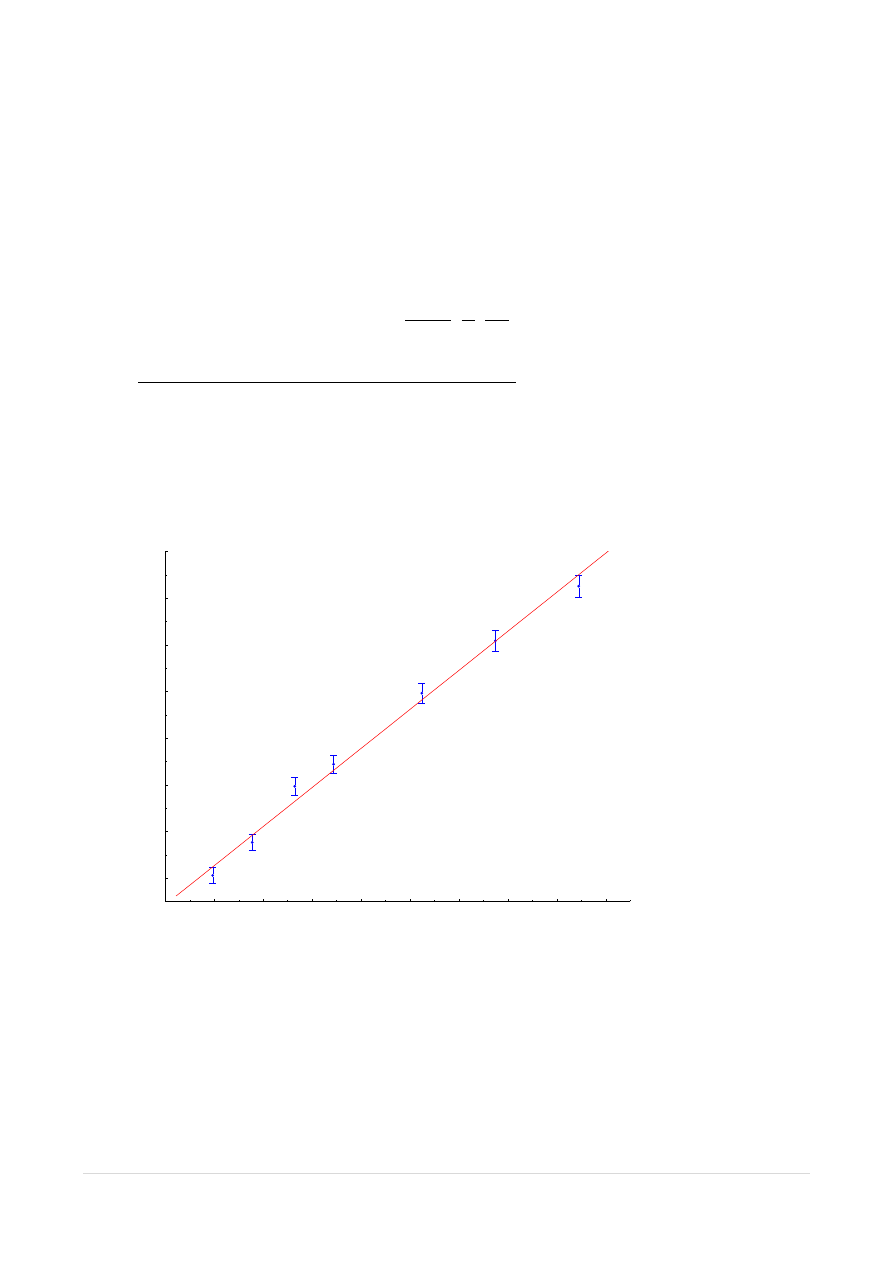
Sporządziliśmy wykres zależności polaryzacji właściwej od ułamka molowego nitrobenzenu
(wykres 1).

0,000

0,005

0,010

0,015

0,020

0,025

0,030

0,035

0,040

0,045

0,00034

0,00036

0,00038

0,00040

0,00042

0,00044

0,00046

0,00048

Regresja liniowa
Y = A*X+B
Parametr

Błąd

A

0,00335

1,43514E-4

B

3,28623E-4

3,1551E-6

R

0,99544

Wykres 1. Zależność polaryzacji p od ułamka molowego X

p

[

m

3

/k

g

]

X

3 |

S t r o n a

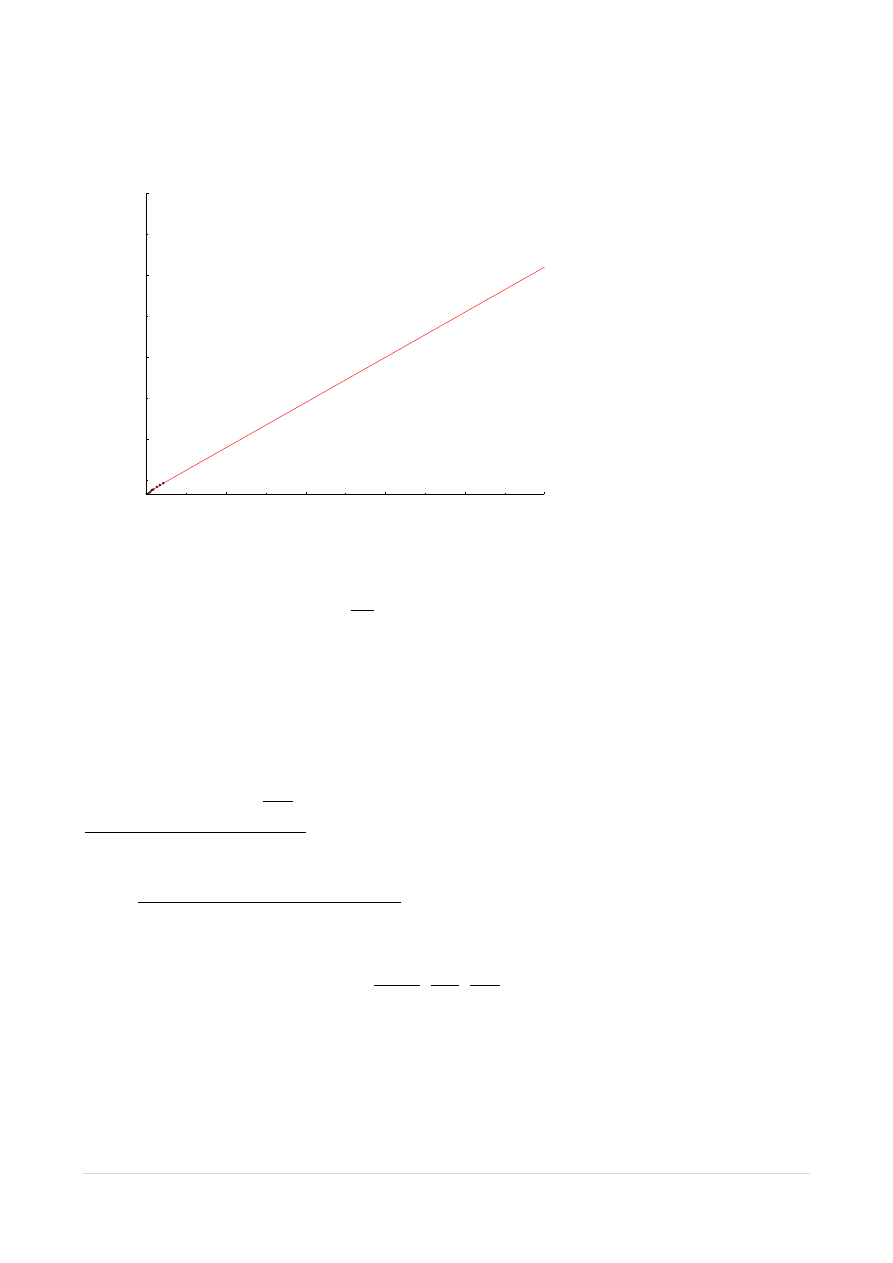
Następnie ekstrapolowaliśmy go do wartości X

n

=1, co pokazuje wykres 2.

0,0

0,2

0,4

0,6

0,8

1,0

0,001

0,002

0,003

0,004

Wykres 2. Zależność polaryzacji p od ułamka molowego X - ekstrapolacja do X=1

p

[

m

3

/k

g

]

X

Z wykresu 2 odczytaliśmy wartość polaryzacji właściwej czystego nitrobenzenu:



















kg

m

X

p

n

3

)

000100

,

0

003094

,

0

(

)

1

(

Dzięki temu mogliśmy obliczyć wartość całkowitej polaryzacji molowej, korzystając ze wzoru:
P=p*M

n

, gdzie M

n

=0,123113 [kg/mol] – masa molowa nitrobenzenu,

Stąd P=38,09*10

-5

[m

3

/mol]

Natomiast niepewność

)

1

(











n

n

X

p

M

P

; zatem





mol

m

P

/

10

23

,

1

3

5









Ostatecznie:

























mol

m

P

3

5

10

23

,

1

09

.

38

5) Refrakcja molowa nitrobenzenu.

Refrakcję molową R

D

obliczyliśmy ze wzoru:





















mol

m

d

M

n

n

R

n

n

D

3

2

2

2

1

, gdzie:

n=1,552 – współczynnik załamania światła dla nitrobenzenu (zbadany przy
pomocy refraktometru)
Stąd:
R

D

=3,269*10

-5

[m

3

/mol]

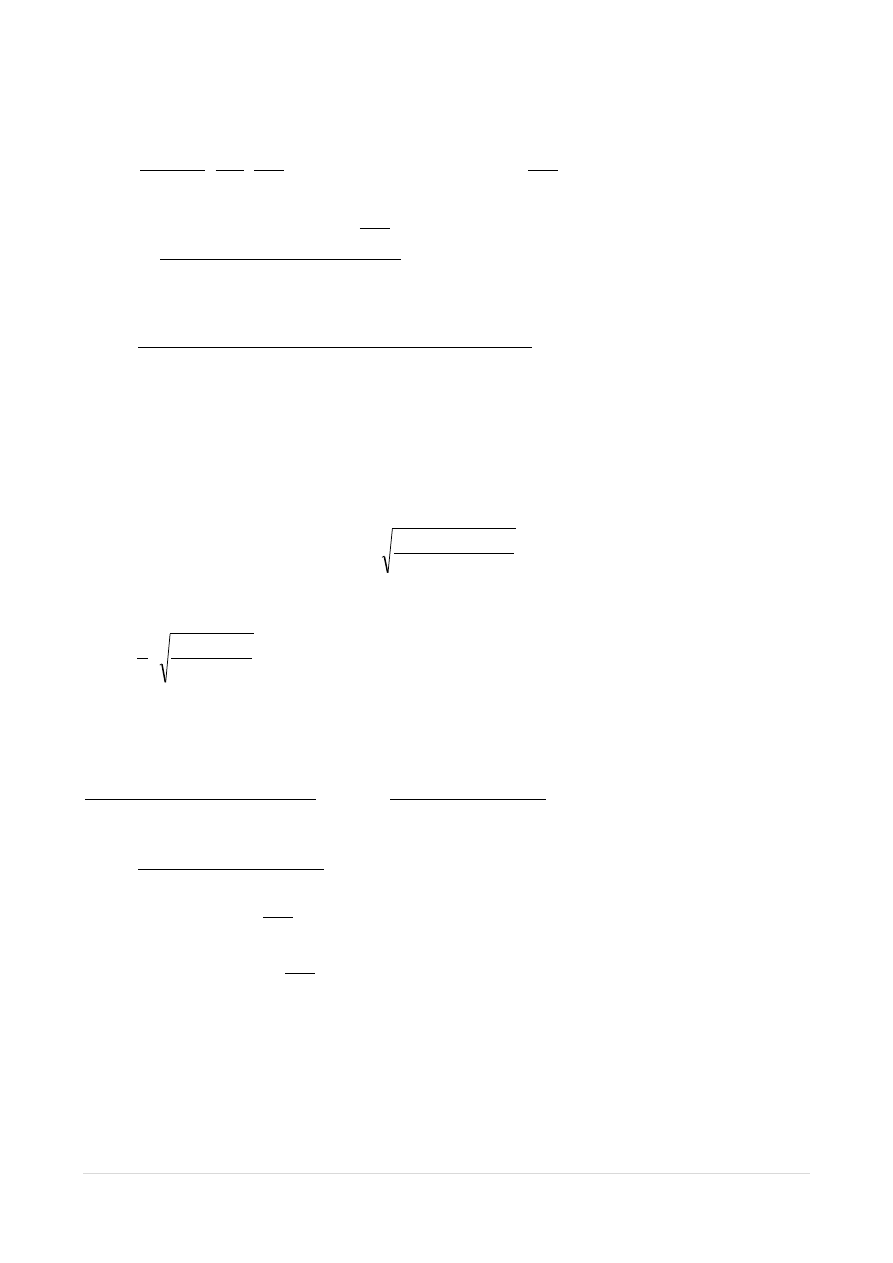
4 |

S t r o n a

Natomiast niepewność obliczyliśmy metodą różniczki zupełnej i otrzymaliśmy, że:

























mol

m

d

M

n

n

R

n

n

D

3

2

2

2

6

, a stąd:





















mol

m

R

D

3

5

10

005

,

0

Zatem:

























mol

m

R

D

3

5

10

005

,

0

269

,

3

6) Wyznaczenie momentu dipolowego nitrobenzenu.

Na podstawie obliczonych dotąd wartości R

D

, P, przyjmując temperaturę otoczenia T=293 K, oraz

znając wartości stałych:

N=6,0238*10

23

[1/mol] – stała Avogadro

ε

0

=8,854*10

-12

[F/m] – bezwzględna stała dielektryczna próżni

k=1,38*10

-23

[J/K] – stała Boltzmanna

mogliśmy obliczyć wartość momentu dipolowego:

 

Cm

N

kT

R

P

D

0

0

9

)

(











Stąd μ

0

=13,65*10

-30

[Cm]=4,09[D].

Natomiast niepewność liczyliśmy znaną już metodą, otrzymując wzór:









m

C

R

P

R

P

N

kT

D

D



















)

(

9

2

1

0

0





Zgodnie z tym:





 

D

m

C

01

,

0

10

02

,

0

30

0















Zatem ostatecznie:









m

C











30

0

10

02

,

0

65

,

13



oraz





 

D

01

,

0

09

,

4

0







7) Zestawienie wyników:

























mol

m

P

3

5

10

23

,

1

09

.

38

























mol

m

R

D

3

5

10

005

,

0

269

,

3









m

C











30

0

10

02

,

0

65

,

13



oraz





 

D

01

,

0

09

,

4

0







5 |

S t r o n a

8) Wnioski:

Celem doświadczenia było wyznaczenie momentu dipolowego nitrobenzenu. Porównując
otrzymaną wartość momentu dipolowego z wartością tablicową, która wynosi 4,3D, widzimy, że
obie wartości nie odbiegają znacząco od siebie (4,88% błędu względnego). Zatem nasz wynik
możemy uznać za wysoce prawdopodobny. Te niewielkie różnice można tłumaczyć m.in.:



tzw. błędem eksperymentatora – czyli niewykluczonym brakiem odpowiedniej precyzji przy
wykonywaniu doświadczenia, np. przy sporządzaniu badanych później roztworów



dokładności pomiarowej użytej aparatury (zarówno szkła laboratoryjnego, jak i
kondensatora i refraktometru)



możliwymi zanieczyszczeniami używanych odczynników i sprzętu pomiarowego



nieco inną, niż tablicowa, temperaturą pomiaru.