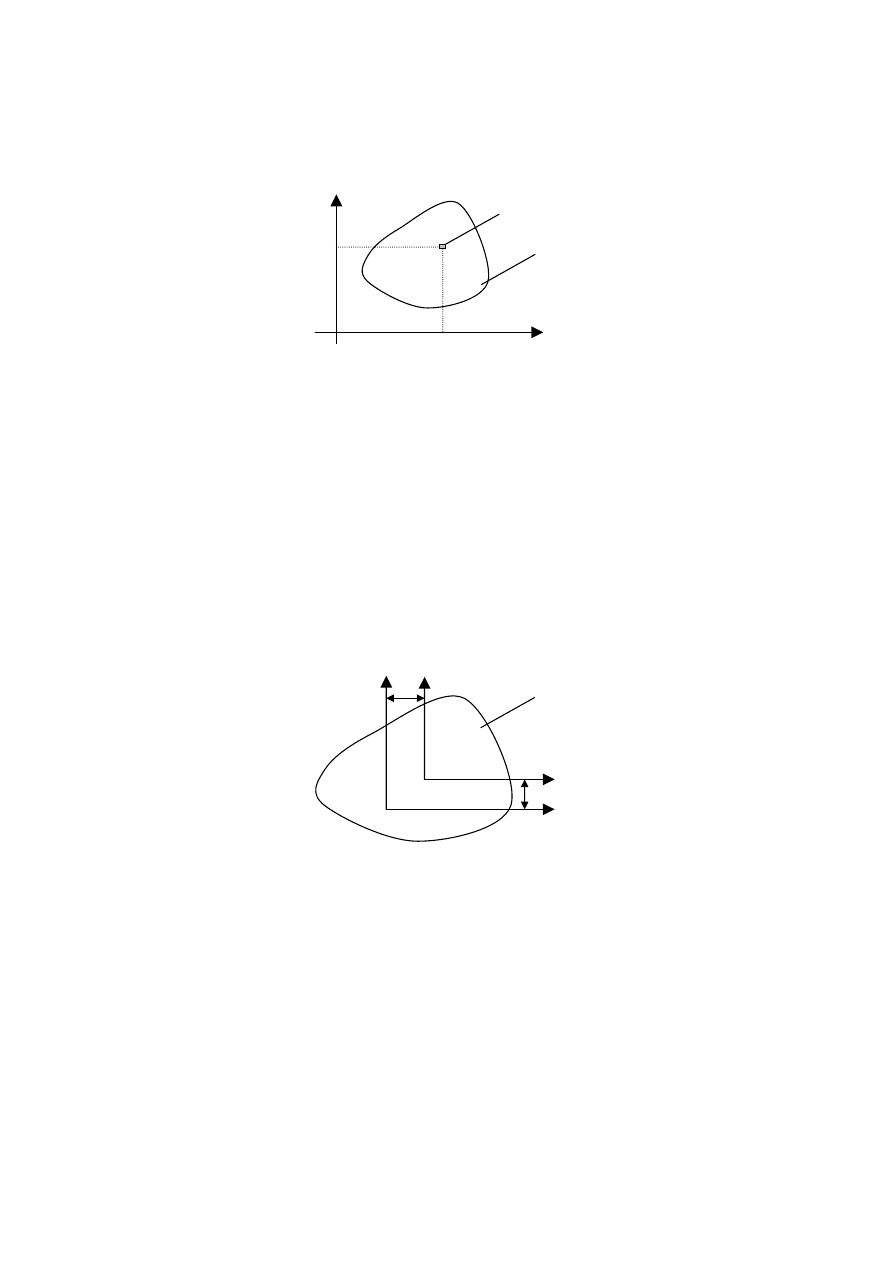
Momenty bezwładności figur płaskich - definicje i wzory 

 
Dana jest figura płaska o polu A oraz prostokątny układ współrzędnych Oxy. 
 

 
 
 
 
 
 
 

 
 
 
 
 
 
 

 

 
 
Momentem bezwładności figury względem osi x jest 

dA

y

I

A

x

∫

=

2

. 

Momentem bezwładności figury względem osi y jest 

dA

x

I

A

y

∫

=

2

. 

Momentem dewiacyjnym figury względem prostokątnego układu osi x i y jest 

∫

=

A

xy

xydA

I

. 

 

Z definicji momentów bezwładności wynika, że mogą być one tylko dodatnie. 

Natomiast moment dewiacyjny może być dodatni, ujemny lub równy zero. 
 

W przypadku równoległego przesunięcia osi układu korzystamy z twierdzenia 

Steinera, wyrażonego poniższymi wzorami: 
 

 
 
 
 
 
 
 

 
 
 
 
 
 
 

 

y 

y 

x

x

O 

A

dA

a

b

x

c 

y

c 

y

x

A

C(b, a)

O

 
 

2

a

A

I

I

c

x

x

⋅

+

=

 

2

b

A

I

I

c

y

y

⋅

+

=

 

b

a

A

I

I

c

c

y

x

xy

⋅

⋅

+

=

 

gdzie osie 

x

c

 i 

y

c

  są osiami centralnymi, natomiast 

b i a  są współrzędnymi punktu C w 

układzie 

Oxy. Z rysunku wynika, że są to odległości między osiami. 

 

Osiowe momenty bezwładności oraz dewiacyjny moment figury względem osi 

centralnych można wyznaczyć korzystając z przekształconych wzorów Steinera:  

2

a

A

I

I

x

x

c

⋅

−

=

 

2

b

A

I

I

y

y

c

⋅

−

=

 

b

a

A

I

I

xy

y

x

c

c

⋅

⋅

−

=

. 

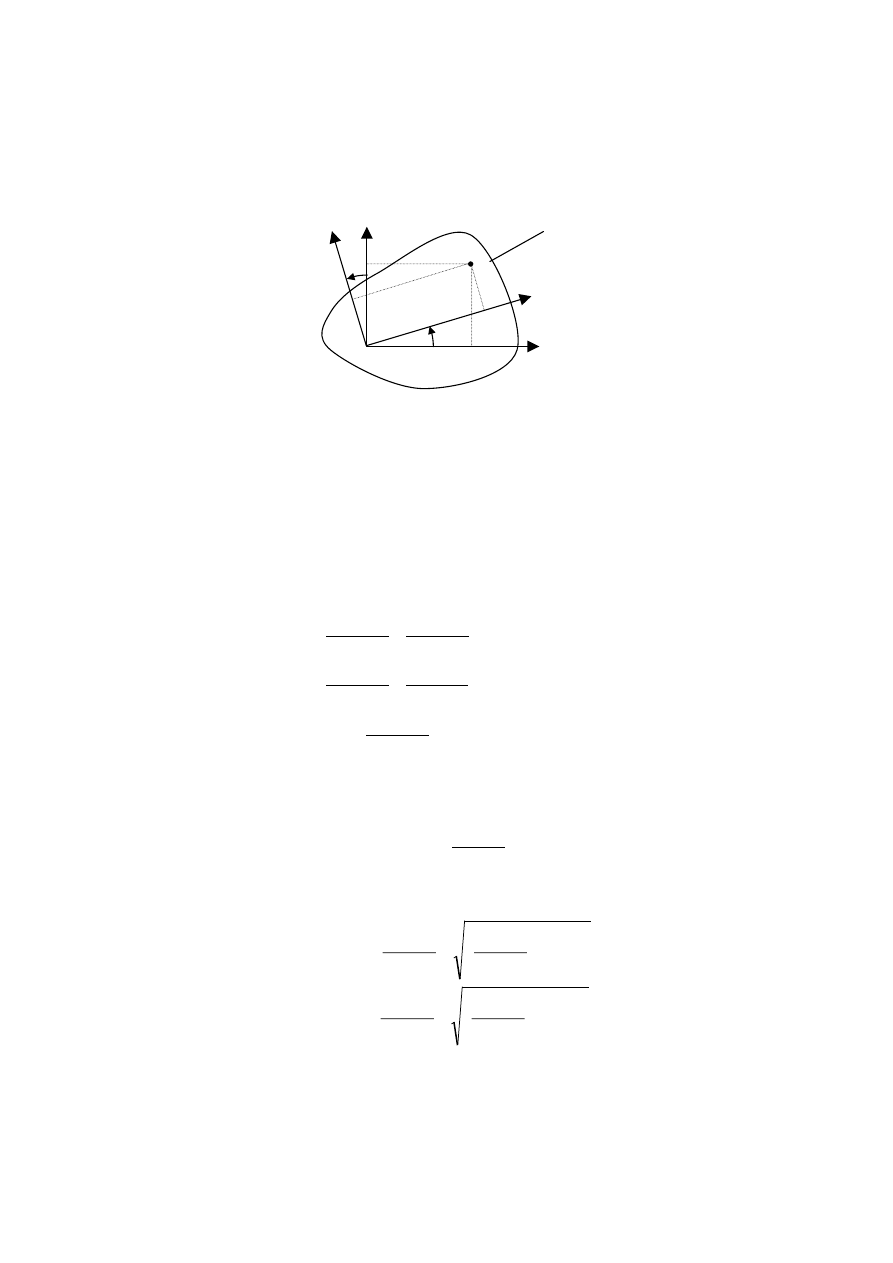
 Przyjmijmy 

prostokątny układ współrzędnych 

Oξη obrócony o kąt φ względem układu 

Oxy. Współrzędne dowolnego punktu figury płaskiej spełniają zależności: 

ξ = x cos φ + y sin φ 

η = y cos φ − x sin φ. 

 

 

ξ

x

O 

y

η 

φ

A

φ 

y

η 

ξ

x

 
 
 
 
 
 
 
 
 
 
 Wykorzystując te zależności wyznaczamy momenty bezwładności i moment 
dewiacyjny w obróconym układzie

 Oξη: 

ϕ

ϕ

−

ϕ

+

ϕ

=

=

∫

cos

sin

I

sin

I

cos

I

dA

η

I

xy

y

x

A

ξ

2

2

2

2

 

ϕ

ϕ

+

ϕ

+

ϕ

=

=

∫

cos

sin

I

sin

I

cos

I

dA

ξ

I

xy

x

y

A

η

2

2

2

2

 

(

)

(

)

ϕ

−

ϕ

+

ϕ

ϕ

−

=

=

∫

2

2

sin

cos

I

cos

sin

I

I

ξηdA

I

xy

y

x

A

ξη

 

lub 

(

) (

)

ϕ

−

ϕ

−

+

+

=

2

2

2

2

sin

I

cos

I

I

I

I

I

xy

y

x

y

x

ξ

 

(

) (

)

ϕ

+

ϕ

−

−

+

=

2

2

2

2

sin

I

cos

I

I

I

I

I

xy

y

x

y

x

η

 

(

)

ϕ

+

ϕ

−

=

2

2

2

cos

I

sin

I

I

I

xy

y

x

ξη

. 

Osie układu prostokątnego, w którym moment dewiacyjny 

I

ξη

 = 0 nazywamy 

głównymi osiami bezwładności. Kąt  φ

o

 między osiami prostokątnego układu 

Oxy  i układu 

głównych osi bezwładności spełnia równanie: 

y

x

xy

I

I

I

tg

−

−

=

ϕ

2

2

o

 

Momenty bezwładności względem głównych osi bezwładności osiągają wartości 

ekstremalne: 

2

2

1

2

2

xy

y

x

y

x

max

I

I

I

I

I

I

I

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

+

+

=

=

 

2

2

2

2

2

xy

y

x

y

x

min

I

I

I

I

I

I

I

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

−

+

=

=

. 

 

Z powyższych wzorów wynika, że 

2

1

I

I

I

I

I

I

η

ξ

y

x

+

=

+

=

+

 

 

Główna oś bezwładności, względem której moment bezwładności ma wartość 

 tworzy z osią  x    kąt 

, natomiast główna oś bezwładności, względem której 

max

I

I

=

1

1

ϕ

 

2

moment bezwładności ma wartość 

min

I

I

=

2

 tworzy z osią  x    kąt 

2

ϕ

. Kierunki główne 

minimalnego i maksymalnego momentów bezwładności wyznaczamy następująco: 

1.  I

x

 > I

y 

 to 

, natomiast 

o

1

ϕ

=

ϕ

2

o

2

π

+

ϕ

=

ϕ

  

2.  I

x

 < I

y 

 to 

2

o

1

π

+

ϕ

=

ϕ

, natomiast 

o

2

ϕ

=

ϕ

 

3.  I

x

 = I

y 

, I

xy

 > 0 to 

4

1

π

−

=

ϕ

, natomiast 

4

2

π

=

ϕ

 

4.  I

x

 = I

y 

, I

xy

 < 0 to 

4

1

π

=

ϕ

, natomiast 

4

2

π

−

=

ϕ

. 

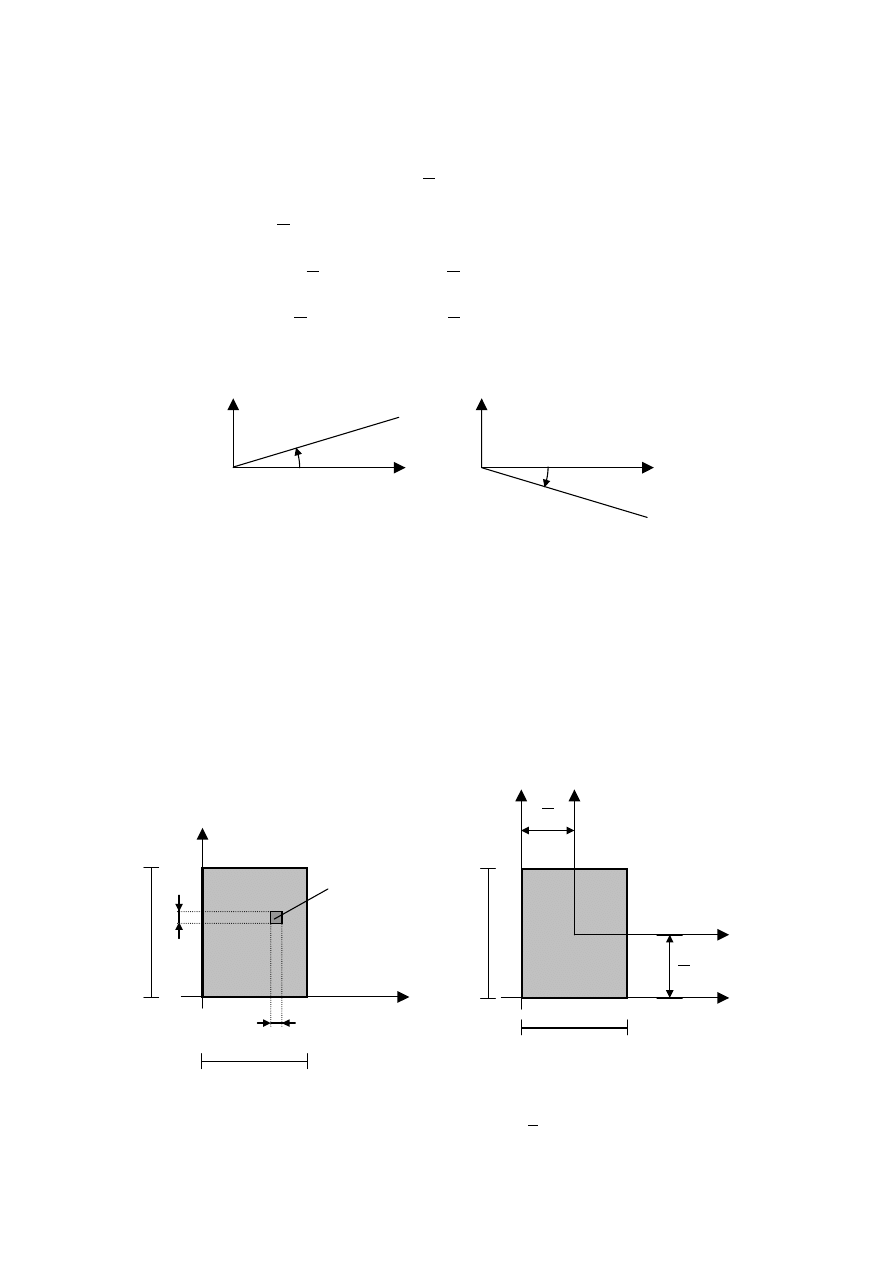
Znak dodatni bądź ujemny kąta φ ilustruje poniższy rysunek. 

 

y

y

x

O 

φ > 0 

O

φ < 0 

x

 

O głównych centralnych osiach bezwładności mówimy wówczas, gdy układ osi 

głównych ma początek w środku ciężkości rozpatrywanej figury płaskiej. Momenty 
bezwładności względem tych osi nazywamy głównymi centralnymi momentami 
bezwładności. 

Jeżeli jedna z osi układu współrzędnych jest osią symetrii figury płaskiej, to moment 

dewiacyjny figury w takim układzie współrzędnych jest równy zero. 

W przypadku wyznaczania momentów bezwładności i momentu dewiacyjnego figury 

złożonej będziemy stosować metodę superpozycji, traktując rozpatrywaną figurę jako sumę 
figur elementarnych, takich jak np. prostokąt, trójkąt i fragment koła. Korzystać będziemy z 
wartości momentów bezwładności i momentu dewiacyjnego dla wymienionych figur. 
1. Prostokąt 

 

 

y

O

b

y

c 

C

2

b

2

h

h

y 

b 

dA

=dxdy

y 

O 

x

dx 

dy 

h 

x

c 

x

x

3

0 0

2

2

3

1

bh

dxdy

y

dA

y

I

b h

A

x

∫∫

∫

=

=

=

 

 

3

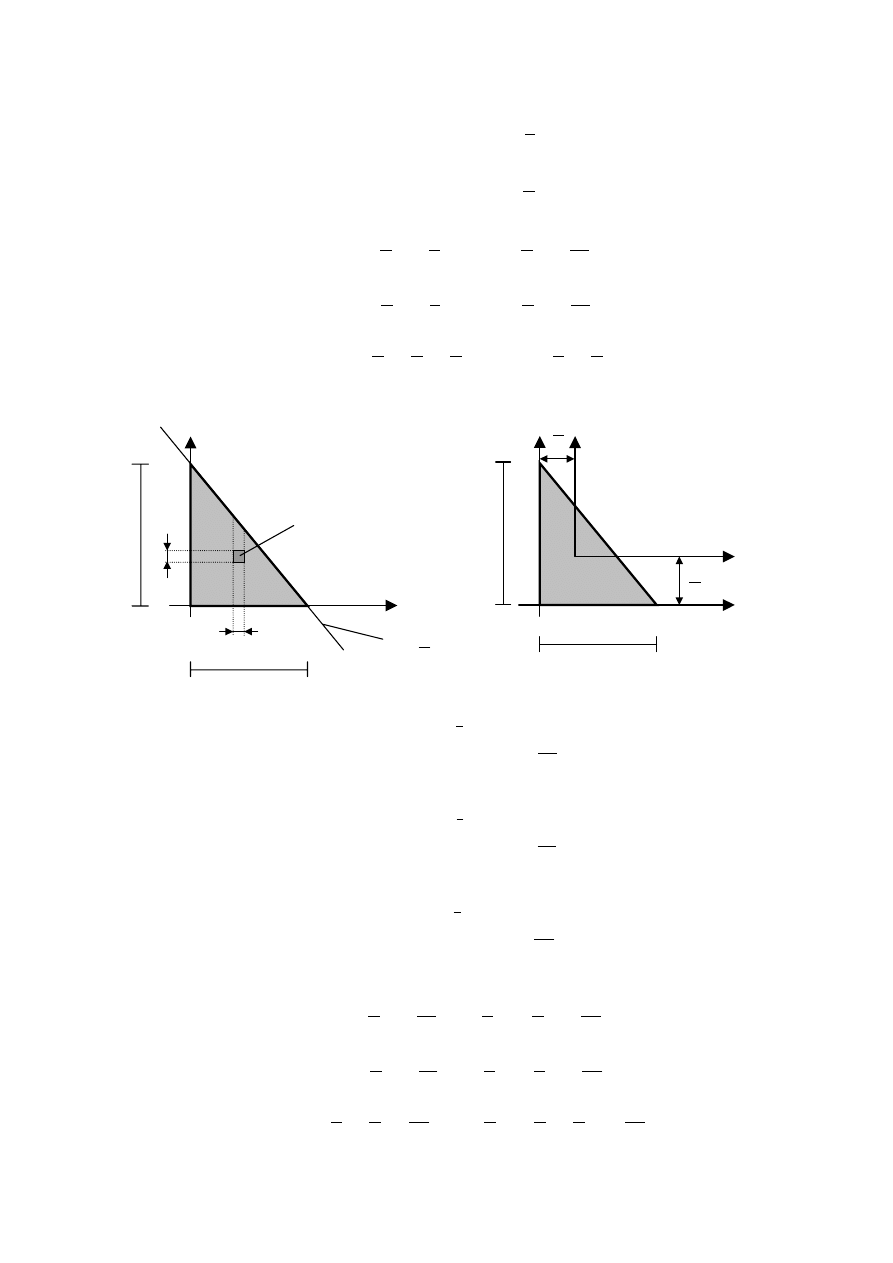
3

0 0

2

2

3

1

hb

dxdy

x

dA

x

I

b h

A

y

=

=

=

∫∫

∫

 

2

2

0 0

4

1

h

b

xydxdy

xydA

I

b h

A

xy

∫∫

∫

=

=

=

 

3

2

3

2

12

1

2

3

1

2

bh

h

bh

bh

h

A

I

I

x

x

c

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

 

3

2

3

2

12

1

2

3

1

2

hb

b

bh

hb

b

A

I

I

y

y

c

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

 

0

2

2

4

1

2

2

2

2

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

h

b

bh

h

b

h

b

A

I

I

xy

y

x

c

c

 

2. Trójkąt 

 

 

b

y

O

C

y

c 

3

h

3

b

h

b

dA=dxdy 

y 

x

O 

x 

dx 

y 

dy 

y=−

h

x

b

h

+

⋅

h 

x

c 

x

3

0

0

2

2

12

1

bh

dx

dy

y

dA

y

I

b

b

x

1

h

A

x

∫ ∫

∫

=

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

=

=

⎟

⎠

⎞

⎜

⎝

⎛ −

 

3

0

0

2

2

12

1

hb

dx

dy

x

dA

x

I

b

b

x

1

h

A

y

∫ ∫

∫

=

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

=

=

⎟

⎠

⎞

⎜

⎝

⎛ −

 

2

2

0

0

24

1

b

h

dx

dy

xy

dA

xy

I

b

b

x

1

h

A

xy

∫ ∫

∫

=

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

=

=

⎟

⎠

⎞

⎜

⎝

⎛ −

 

3

2

3

2

36

1

3

2

1

12

1

3

bh

h

bh

bh

h

A

I

I

x

x

c

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

 

3

2

3

2

36

1

3

2

1

12

1

3

hb

b

bh

hb

b

A

I

I

y

y

c

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

 

2

2

2

2

72

1

3

3

2

1

24

1

3

3

h

b

h

b

bh

h

b

h

b

A

I

I

xy

y

x

c

c

−

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

=

 

 

4

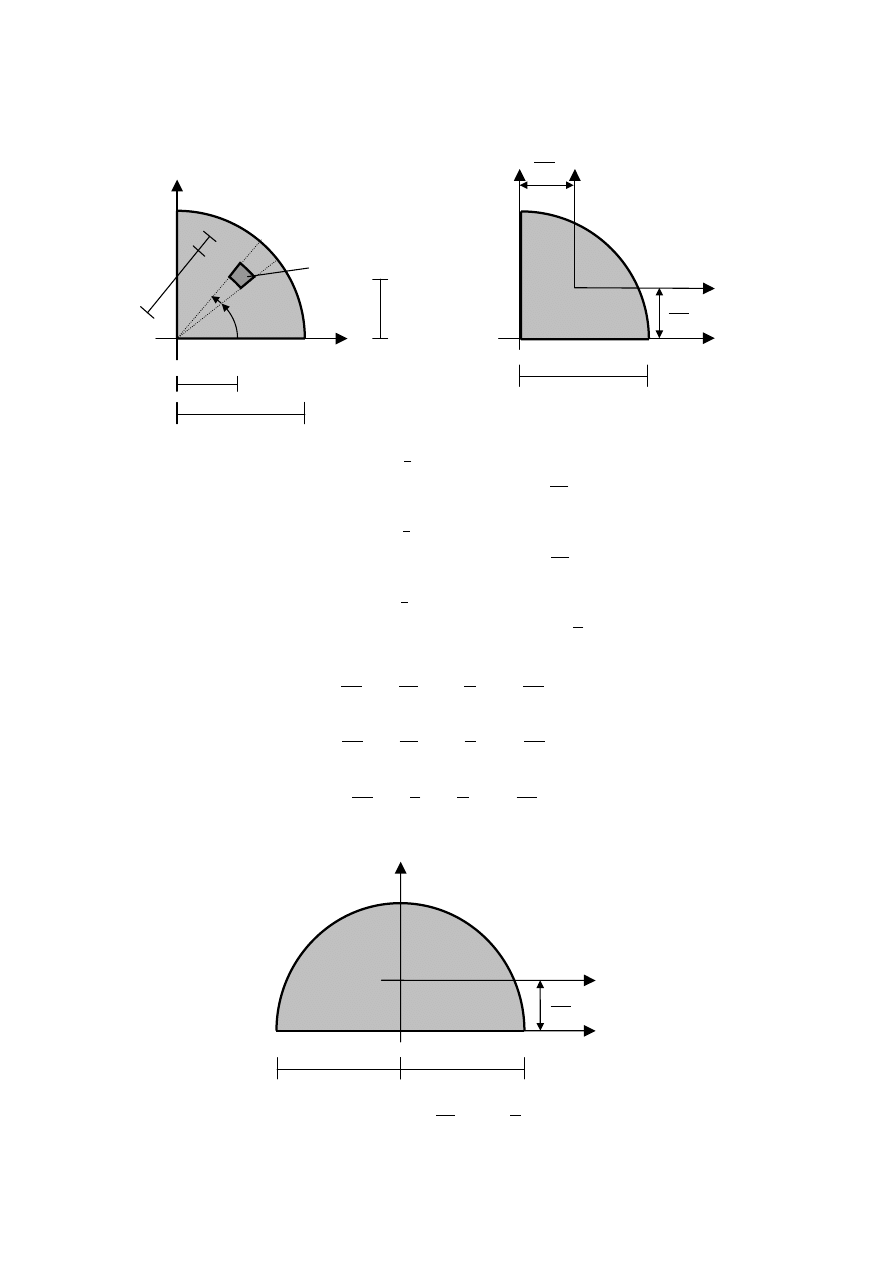
3.  Ćwiartka koła 

 

y

O

C

y

c 

r

π

r

3

4

π

r

3

4

r 

dA=ρdφdρ 

x 

O 

 ρ 

y=ρsinφ

x=ρcosφ 

 dρ 

φ 

dφ 

y 

x

c 

x 

4

0 0

2

2

2

16

1

r

d

d

sin

dA

y

I

2 r

A

x

π

=

ρ

ϕ

ϕρ

ρ

=

=

∫∫

∫

π

 

4

0 0

2

2

2

16

1

os

r

d

d

c

dA

x

I

2 r

A

y

π

=

ρ

ϕ

ϕρ

ρ

=

=

∫∫

∫

π

 

4

0 0

2

8

1

os

r

d

d

c

sin

dA

xy

I

2 r

A

xy

∫∫

∫

π

=

ρ

ϕ

ϕρ

ϕ

ρ

=

=

 

4

2

2

4

2

05488

0

3

4

4

1

16

1

3

4

r

.

r

r

r

r

A

I

I

x

x

c

≅

⎟

⎠

⎞

⎜

⎝

⎛

π

⋅

π

−

π

=

⎟

⎠

⎞

⎜

⎝

⎛

π

⋅

−

=

 

4

2

2

4

2

05488

0

3

4

4

1

16

1

3

4

r

.

r

r

r

r

A

I

I

y

y

c

≅

⎟

⎠

⎞

⎜

⎝

⎛

π

⋅

π

−

π

=

⎟

⎠

⎞

⎜

⎝

⎛

π

⋅

−

=

 

4

2

2

4

2

01647

0

3

4

4

1

8

1

3

4

r

.

r

r

r

r

A

I

I

xy

y

x

c

c

−

≅

⎟

⎠

⎞

⎜

⎝

⎛

π

⋅

π

−

=

⎟

⎠

⎞

⎜

⎝

⎛

π

⋅

−

=

 

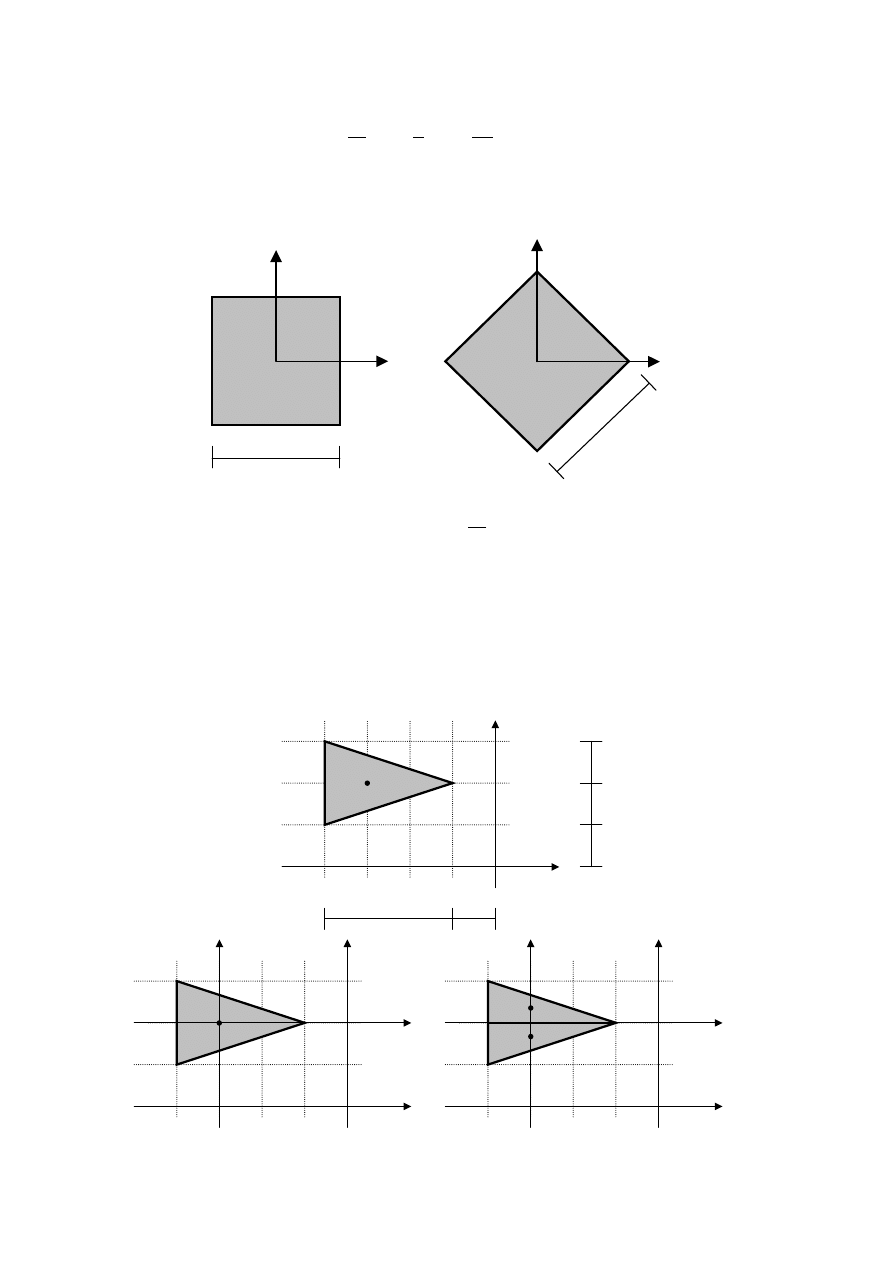
4. Półkole 
 
 
 
 
 
 
 
 
 
 
 
 

 

O

C

r

r 

π

r

3

4

y

c

=y

x

c

x

4

4

8

1

16

1

2

πr

πr

I

I

y

x

=

⋅

⋅

=

=

 

 

5

4

2

2

4

10976

0

3

4

4

1

16

1

2

r

.

r

r

r

I

c

x

≅

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

π

⋅

π

−

π

⋅

=

 

0

=

=

xy

y

x

I

I

c

c

 

5. Kwadrat 

 

 

y

c 

C

y

c 

C

a

x

c 

x

c 

a 

4

12

1

a

I

I

c

c

y

x

=

=

    

0

=

c

c

y

x

I

 

W przypadku kwadratu momenty bezwładności i moment dewiacyjny w dowolnym 

układzie osi centralnych przyjmują podane powyżej wartości. 
 
Przykład I 

Wyznaczyć momenty bezwładności i moment dewiacyjny dla poniższego trójkąta 

równoramiennego w układzie Oxy. 

 

C 

x

y 

y

c 

x

c

C 

O 

O 

C

1

C

2

y

c

a 

a 

a 

x

y 

O

a

x~

c

3

−

=

a

y~

c

2

=

C 

a 

3a

y 

x

c

x 

 

6

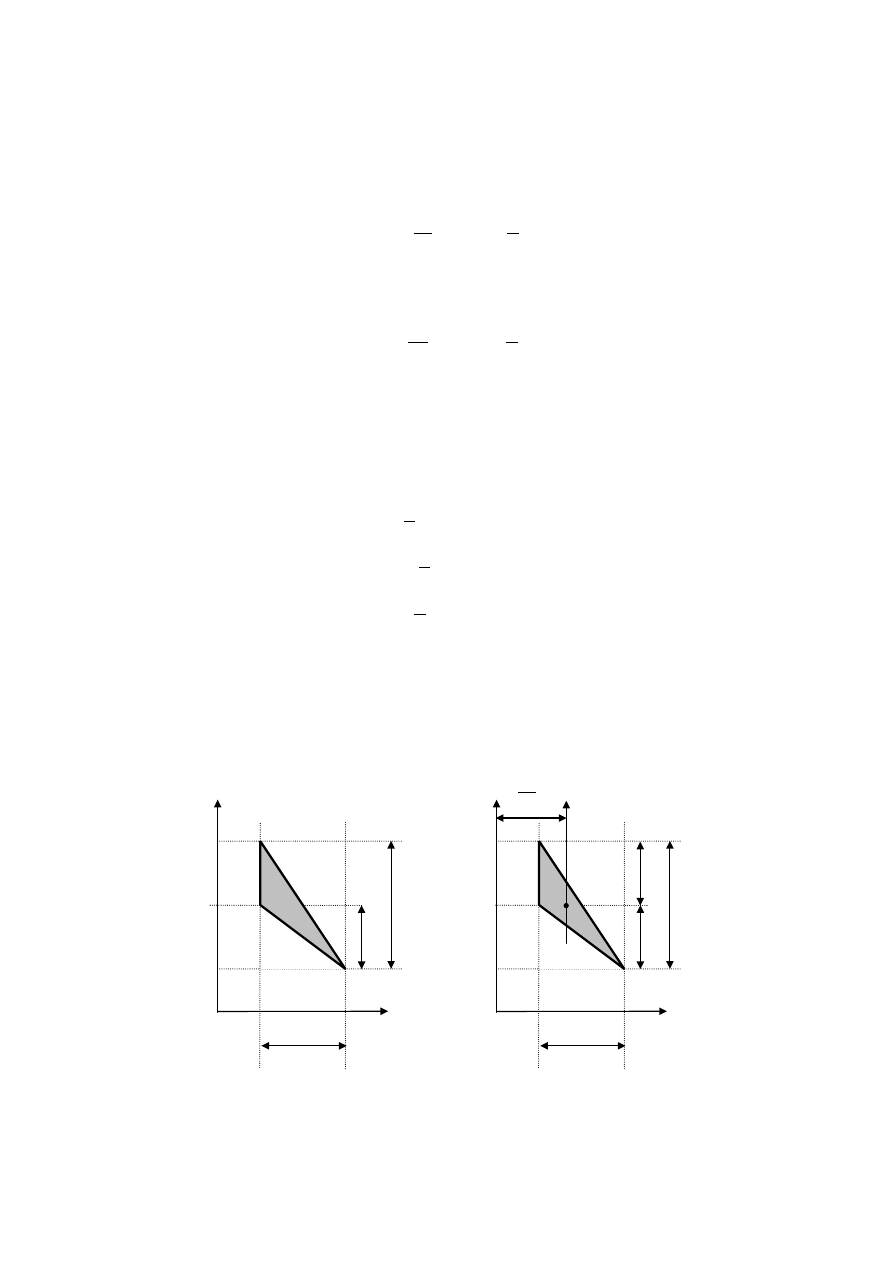
 Wprowadzamy 

układ osi centralnych dla trójkąta. Oś  x

c

 jest osią symetrii figury. 

Następnie dzielimy trójkąt równoramienny na dwa trójkąty prostokątne.  

Moment bezwładności trójkąta równoramiennego względem osi x

c

 jest sumą 

momentów bezwładności względem tej osi dwu jednakowych trójkątów prostokątnych, 
stykających się podstawą z osią x

c

. 

4

3

2

1

3

12

1

2

a

a

a

I

c

x

=

⋅

⋅

⋅

=

 

Moment bezwładności trójkąta równoramiennego względem osi y

c

 jest sumą 

momentów bezwładności względem tej osi dwu jednakowych trójkątów prostokątnych. Na 
osi y

c

 leżą środki ciężkości obu trójkątów, a więc 

( )

4

3

2

3

3

36

1

2

a

a

a

I

c

y

⋅

=

⋅

⋅

=

 

Moment dewiacyjny trójkąta równoramiennego względem układu osi x

c

y

c

 jest równy 

zero, gdyż oś x

c

 jest osią symetrii rozpatrywanej figury. 

0

=

c

c

y

x

I

 

Aby wyznaczyć momenty bezwładności i moment dewiacyjny dla trójkąta 

równoramiennego w układzie Oxy należy skorzystać z twierdzenia Steinera. Pole powierzchni 
trójkąta wynosi 

2

3

2

3

2

1

a

a

a

A

=

⋅

⋅

=

. 

( )

4

2

2

4

2

5

12

2

3

2

1

a

.

a

a

a

y~

A

I

I

c

x

x

=

⋅

+

=

⋅

+

=

 

(

)

4

2

2

4

2

5

28

3

3

2

3

a

.

a

a

a

x~

A

I

I

c

y

y

c

=

−

⋅

+

=

⋅

+

=

 

(

)

4

2

18

2

3

3

0

a

a

a

a

y~

x~

A

I

I

c

c

y

x

xy

c

c

−

=

⋅

−

⋅

+

=

⋅

⋅

+

=

 

 

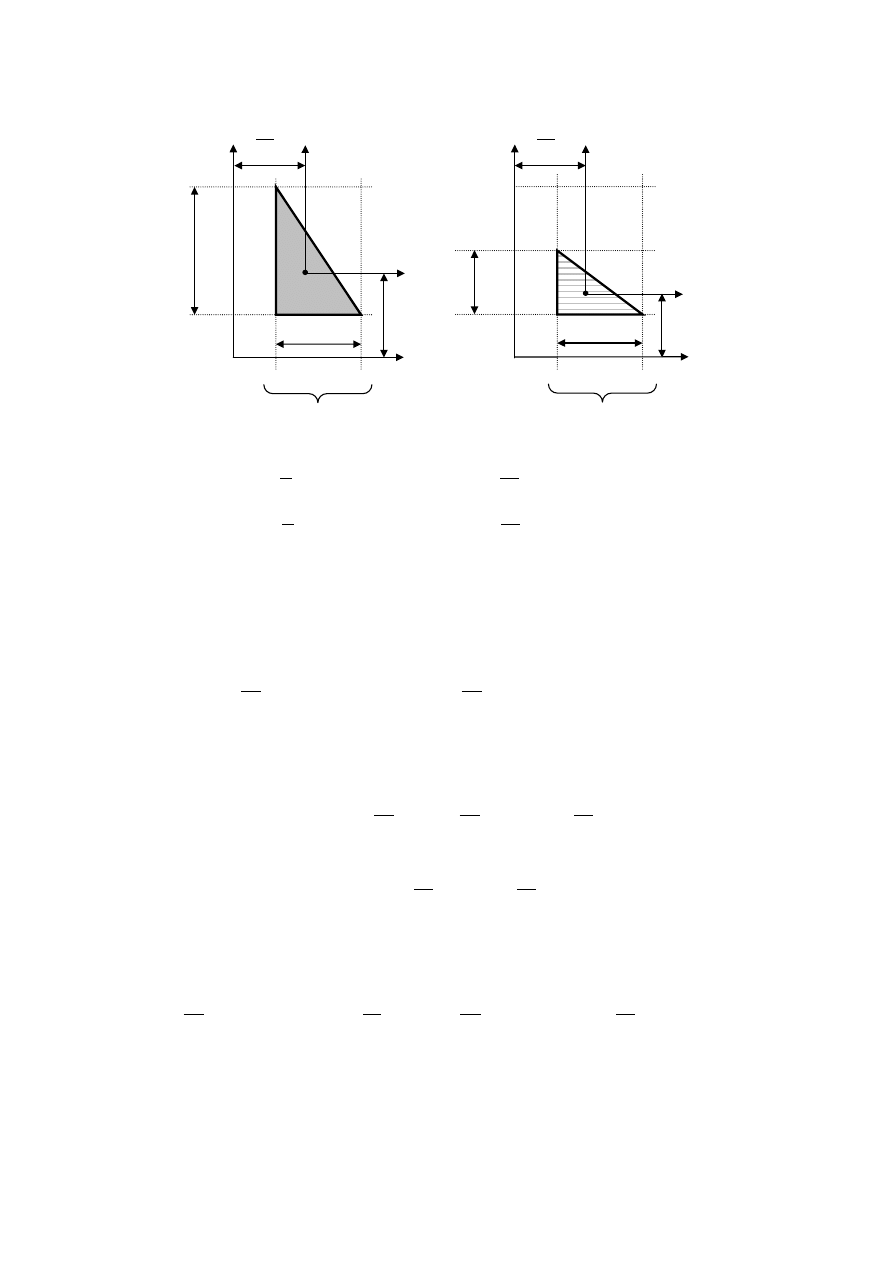
Przykład II 

Wyznaczyć momenty bezwładności i moment dewiacyjny dla poniższego trójkąta w 

układzie współrzędnych Oxy. 

 

c

y

A 

B

3a 

6a 

8a

5a

2a

3a 

C

D

a

3

10

4a

x 

6a 

2a

6a

3a

O 

y 

x 

8a 

5a 

6a 

2a 

4a 

2a 

y

O

 

Rozpatrywaną figurę otrzymamy odejmując figurę II od figury I.  

 

 

7

 

4a

O 

2a 

2a

6a

8a 

C

1 

x 

y 

1

c

y

1

c

x

figura I 

4a 

6a 

a

3

10

2a

5a

3a 

3a

y 

2a

6a  x 

2

c

y

2

c

x

figura II 

4a

C

2

a

3

10

O

 

2

I

12

6

4

2

1

a

a

a

A

=

⋅

⋅

=

,           

a

x~

c

3

10

1

=

,          

a

y~

c

4

1

=

, 

2

II

6

3

4

2

1

a

a

a

A

=

⋅

⋅

=

,            

a

x~

c

3

10

2

=

,          

a

y~

c

3

2

=

. 

2

2

2

II

I

6

6

12

a

a

a

A

A

A

=

−

=

−

=

 

Moment bezwładności względem osi x  wyznaczymy jako różnicę momentu 

bezwładności względem osi x figury I i figury II. 

 

(

)

( )

( )

( )

( )

4

2

2

2

2

2

3

2

2

II

II

2

1

I

I

II

I

159

3

6

3

4

36

1

4

12

6

4

36

1

2

1

a

a

a

a

a

a

a

a

a

y~

A

I

y~

A

I

I

I

I

c

x

c

x

x

x

x

c

c

=

⎥⎦

⎤

⎢⎣

⎡

⋅

+

⋅

⋅

−

⋅

+

⋅

⋅

=

=

⋅

+

−

⋅

+

=

−

=

 

W przypadku wyznaczania momentu bezwładności względem osi y nie musimy 

dzielić figury. Bok BD trójkąta jest równoległy do osi y i do osi 

. Moment bezwładności 

względem osi 

 obliczymy korzystając ze wzoru 

c

y

c

y

( )

4

3

3

3

16

4

3

36

1

36

1

a

a

a

h

b

I

c

y

=

⋅

⋅

=

⋅

⋅

=

 

Moment bezwładności względem osi y wyznaczymy z wykorzystaniem wzoru Steinera 

4

2

2

4

2

a

72

3

10

6

3

16

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

+

=

⋅

+

=

a

a

a

x~

A

I

I

c

y

y

c

 

 

W celu obliczenia momentu dewiacyjnego traktujemy rozpatrywany trójkąt jako 

różnicę figury I i figury II. 

(

)

( ) ( )

( ) ( )

4

2

2

2

2

2

2

2

2

II

II

1

1

I

II

I

94

3

3

10

6

3

4

72

1

4

3

10

12

6

4

72

1

2

1

1

a

a

a

a

a

a

a

a

a

a

a

y~

x~

A

I

y~

x~

A

I

I

I

I

c

c

y

x

c

c

y

x

xy

xy

xy

c2

c

c

c

=

⎥⎦

⎤

⎢⎣

⎡

⋅

+

⋅

−

−

⋅

⋅

+

⋅

⋅

−

=

=

⋅

⋅

+

−

⋅

⋅

+

=

−

=

 

 

Przykład III 

Wyznaczyć momenty bezwładności i moment dewiacyjny dla poniższej figury w 

układzie współrzędnych Oxy. 

 

8

 

 

 

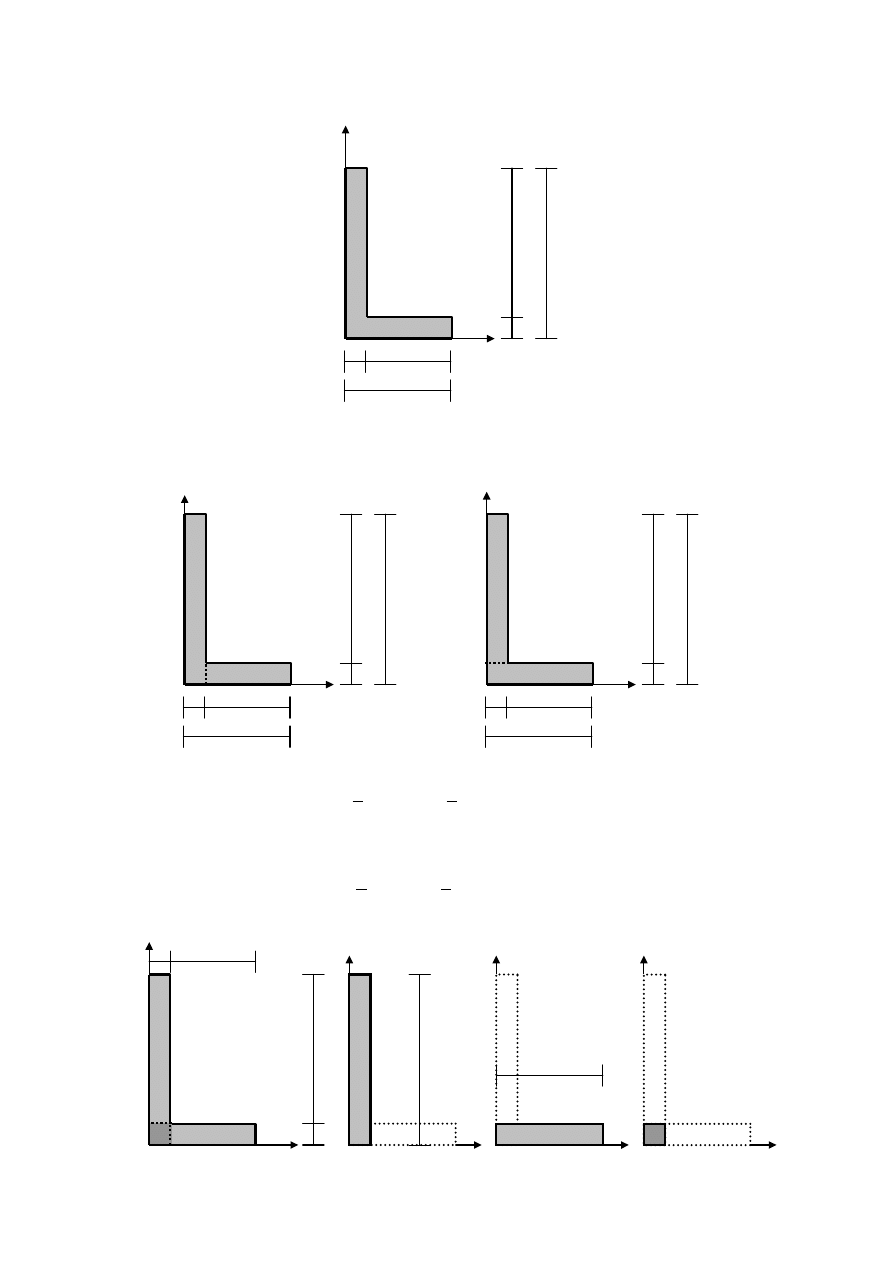
O 

x

5a 

a 

4a

 y 

 

a

7a 8a

 
 
 
 
 
 

 

 
 
 
 
 
 

Przed wyznaczeniem momentu bezwładności rozpatrywanej figury względem osi x 

dokonamy jej podziału na dwa prostokąty, tak żeby każdy prostokąt jednym bokiem stykał się 
z osią x. 

a

7a

4a 

a 

5a 

8a

x 

 y 

 y

x 

5a 

a

4a

a 

7a  8a 

 

 

( )

4

3

3

172

4

3

1

8

3

1

a

a

a

a

a

I

x

=

⋅

⋅

+

⋅

⋅

=

 

W celu obliczenia momentu bezwładności figury względem osi y  dokonamy jej 

podziału na dwa prostokąty, z których każdy jednym bokiem styka się z osią y. 

( )

4

3

3

44

5

3

1

7

3

1

a

a

a

a

a

I

y

=

⋅

⋅

+

⋅

⋅

=

 

Dla wyznaczenia momentu dewiacyjnego zastosujemy jeszcze  inny podział. 

 

a 

7a 

x

 y

x 

 y

 y 

5a

4a 

a 

x 

 y 

8a

x

 

9

Do obliczeń przyjmujemy figury składowe, zgodne z powyższym rysunkiem. Dwa 

prostokąty o wymiarach 8a x a i a x 5a mają część wspólną w postaci kwadratu o boku a, dla 
którego moment dewiacyjny będzie uwzględniony dwukrotnie. Należy więc w obliczeniach 
moment dewiacyjny dla tego kwadratu, traktowanego jako trzecia figura, przyjąć ze znakiem 
minus. 

( )

( )

4

2

2

2

2

2

2

22

4

1

5

4

1

8

4

1

a

a

a

a

a

a

a

I

xy

=

⋅

⋅

−

⋅

⋅

+

⋅

⋅

=

. 

 
 
 
 
 
 
 

 

10