Wyznaczanie momentu bezwładności metodą nawrotu.

1) Podstawowe pojęcia mechaniczne

Momentem bezwładności ciała materialnego nazywamy sumę iloczynów elementarnych mas ciała przez

kwadraty ich odległości od płaszczyzn, osi lub punktu względem, których te momenty obliczamy:

i

i

i

m

r

I

2

,

(1)

gdzie: i = (1, 2,... n),

r

i

- odległość masy elementarnej m

i

,

m

i

- masa elementarna.

Miarą momentu bezwładności jest 1m

2

*kg. Rozwinięcie powyższej zależności w kartezjańskim układzie

współrzędnych pozwala wyznaczyć moment bezwładności względem jednej z trzech osi:

,

d

,

d

,

d

2

2

2

m

z

z

m

y

y

m

x

x

m

r

I

m

r

I

m

r

I

(2)

gdzie: m - masa ciała materialnego,

przy czym w wypadku maszyny elektrycznej gdy założymy idealną sztywność wału mamy do czynienia tylko z
jednym stopniem swobody związanym z obrotem wirnika względem arbitralnie przyjętej osi x będącej jedną z
głównych osi bezwładności.

Zależność (2), w wypadku regularnych ciał jednorodnych, które można podzielić na bryły elementarne,

pozwala w prosty sposób analitycznie wyznaczyć ich moment bezwładności. Skomplikowana struktura wirnika
maszyny elektrycznej sprawia, że nie może być on traktowany jako ciało jednorodne i proste obliczenia
analityczne dają jedynie wynik przybliżony. Dlatego też moment bezwładności wirników maszyn elektrycznych
wyznacza się na drodze pomiarowej, przy czym sposób pomiaru uzależniony jest od wielkości badanej maszyny.

2) Wyznaczanie momentu bezwładności metodą nawrotu

Nieustalony stan elektromechaniczny sztywnego wału maszyny elektrycznej opisuje równanie momentów

obrotowych:

m

e

m

w

m

w

m

w

T

T

t

I

t

I

I

t

d

d

d

d

)

(

d

d

(3)

gdzie: I

w

- wartość chwilowa momentu bezwładności mas wirujących,

m

- prędkość kątowa wirowania wału maszyny,

T

e

- moment elektromagnetyczny,

T

m

- moment mechaniczny,

I

w

m

- moment pędu mas wirujących.

Gdy moment bezwładności ma wartość stałą, równanie (3) upraszcza się do postaci:

m

e

m

w

T

T

t

I

d

d

.

(4)

Moment elektromagnetyczny T

e

jest wynikiem wzajemnego oddziaływania strumienia sprzężonego i

prądów w uzwojeniu stojana i wirnika. W stanie statycznym moment elektromagnetyczny jest równy średniemu
momentowi początkowemu:

r

t

r

p

r

e

t

T

t

T

0

d

1

(5)

gdzie: t

r

- podziałka żłobkowa wirnika.

Moment mechaniczny T

m

w wypadku biegu jałowego reprezentuje moment obciążenia maszyny związany z

tarciem w łożyskach, tarciem szczotek o komutator, stratami wentylacyjnymi:

o

m

T

T

,

(6)

gdzie: T

o

- moment obciążenia,

w ogólnym przypadku zależny od prędkości obrotowej. Moc mechaniczna na wale maszyny jest równa
iloczynowi sumy momentów i prędkości obrotowej:

o

e

o

e

m

P

P

T

T

P

)

(

.

(7)

Po przekształceniach otrzymujemy:

t

P

P

I

o

e

w

d

d

.

(8)

Praktyczne wykorzystanie zależności (8) do wyznaczenia momentu bezwładności polegać będzie na

znalezieniu takiego stanu pracy maszyny elektrycznej, dla którego w prosty sposób można wyznaczyć T

e

, T

o

lub

P

e

, P

o

oraz d /dt.

3) Algorytm pomiaru

Obiektem badanym jest indukcyjny silnik łukowy. Uzwojenia silnika zasilane są z regulatora indukcyjnego

napięciem znamionowym. Dodatkowo w torze zasilania należy umieścić układ styczników umożliwiający
dokonanie zmiany napięcia dwóch pasm fazowych (rewers). W celu wyznaczenia momentu bezwładności
metodą nawrotu należy wyznaczyć początkowy moment rozruchowy silnika dla wybranego położenia wirnika
(mechanicznie zablokowanego), przy czym wartość prądu zasilania nie powinna przekroczyć 1,2I

zn

.

Ułożyskowany wzbudnik połączony jest z ramieniem pomiarowym współpracującym z wagą. Na podstawie
trzech wyznaczonych wartości należy obliczyć moment średni. Wynik pomiaru zapisujemy w Tabeli1.

Tabela 1

długość ramienia [m] =

Pomiar

Wskazania wagi

Moment rozruchowy

Średni moment rozruchowy

[kg]

[Nm]

[Nm]

1

2

3

Pomiaru prędkości obrotowej wirnika podczas rewersu dokonujemy w układzie pomiarowym: prądniczka

tachometryczna prądu stałego (czujnik prędkości obrotowej), przetwornik A/C, komputer, pod nadzorem
oprogramowania VisiDAQ. W opcji „File” programu VisiDAQ wybieramy konfigurację „strtgy3.gni” -
dostosowaną do pomiarów realizowanych za pomocą czujnika prędkości. Pomiary dokonywane SA w kanale 3 z
częstotliwością 50 ms w czasie 22 sekund (440 próbek pomiarowych). Do prezentacji graficznej
wykorzystanych jest tylko 400 próbek. Czas pomiaru jest tak dobrany, aby umożliwiał dokonanie dwóch
kolejnych rewersów.

W celu realizacji pomiaru należy:

- uruchomić silnik,

- uruchomić rejestrację (wybierając przycisk oznaczony symbolem > na pasku narzędziowym,

- dokonać rewersu kierunku obrotów silnika,

- po osiągnięciu przez silnik ustalonej prędkości liniowej dokonać ponownego rewersu,

- zakończyć rejestrację (wybierając przycisk □ na pasku narzędziowym).

Dane pomiarowe zapisywane są w pliku T3.m znajdującym się w katalogu C:/ADAM. Plik ten jest bezpośrednio
czytany przez program MATLAB. W celu uzyskania wykresów ilustrujących przebieg prędkości i
przyspieszenia wirnika oraz trajektorię przyspieszenia w funkcji prędkości, należy otworzyć program
narzędziowy Matlab i wywołać program „dyn”. W oknie graficznym (po każdorazowym przyciśnięciu klawisza
„spacja”) kolejno ukażą się wymienione wyżej przebiegi. Sygnał napięciowy czujnika prędkości został
przetworzony w sygnał prędkości obrotowej wyrażony w [rad/s] dzięki wprowadzeniu odpowiedniego
współczynnika.

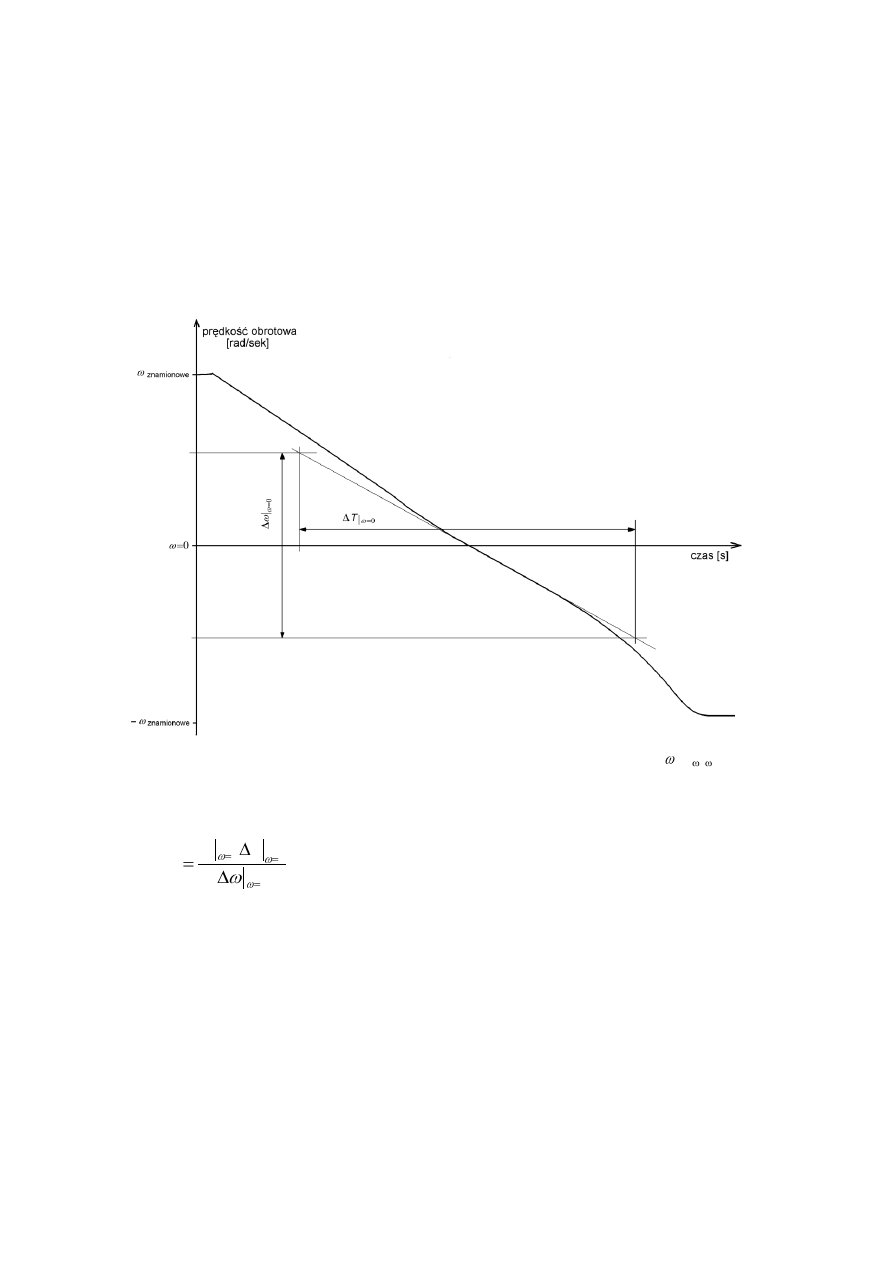
Na podstawie przebiegu prędkości obrotowej w funkcji czasu należy z uwagi na duże tętnienia sygnału

przyspieszenia, metodą graficzną (przez znalezienie stycznej do krzywej w punkcie ω = ω

0

= 0) wyznaczyć

przyspieszenie dω/dt|

ω=ω0

= Δω|

ω=0

/ΔT|

ω=0

. Przedział Δω najlepiej jest dobrać tak, aby Δω = ω

1

, co gwarantuje

dostateczną dokładność wyznaczenia przedziału ΔT (Rys.1).

Rys.1. Krzywa wybiegu maszyny elektrycznej. Metoda graficzna wyznaczenia d /dt|

= 1

.

Moment bezwładności wirnika z zależności:

0

0

0

T

T

I

e

w

Rezultat graficznego wyznaczania wartości Δω/ΔT należy dołączyć do sprawozdania.

Instrukcję opracował Adam Biernat