Klasyczna metoda simplex'ów
●
Problem mający rozwiązanie bez uciekania się do sztucznej bazy
max ( 3⋅x
1
5⋅x
2
)
gdzie:
x
1
– x
2
≤
3
x
1
≤
5
2⋅x
1
5⋅x
2
≤
25
x
i
≥
0
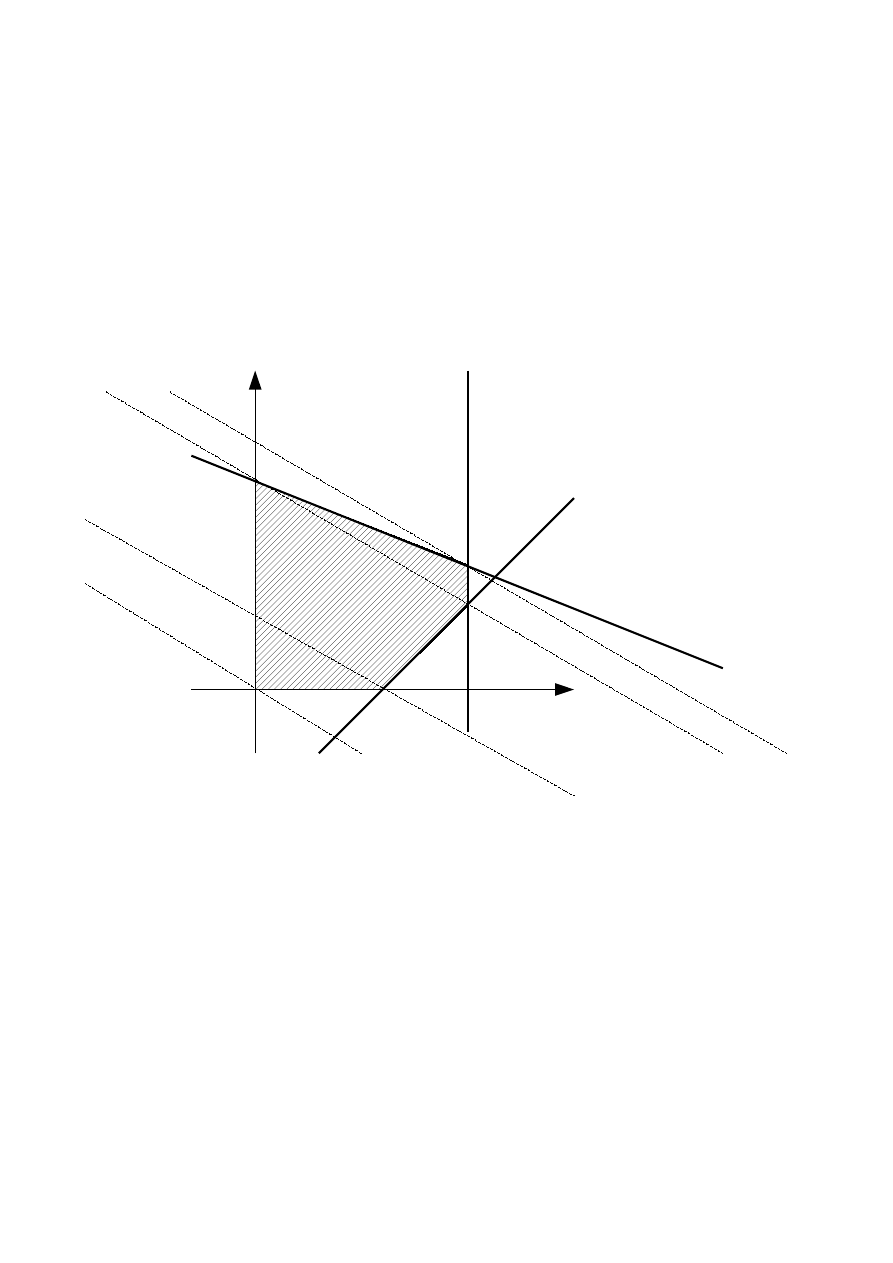
Oto wykres sympleku:
Rozwiązanie zadania programowania liniowego zawsze jest w wierzchołku sympleksu. Oryginalna
metoda Dantziga polega na przeszukiwaniu kolejnych wierzchołków w taki sposób, aby
jednocześnie następował wzrost wartości funkcji celu (gdy wyznaczamy maksimium). Na wykresie
pokazano proste równoległe do prostej funkcji celu przechodzące przez wierzchołki sympleksu.
Swoje optimum zadanie przyjmuje w punkcie (5, 3). Do tego punktu wychodząc z początkowego
rozwiązania bazowego (0, 0) można dojść dwiema trasami:
1. (0, 0) (3, 0) (5, 2) (5,3)
2. (0, 0) (0, 5) (5, 3)
Dla pierwszego zadania przerobimy osobno oba sposoby osiągania wierzchołka optymalnego.
Problem w postaci kanonicznej po dodaniu zmiennych osłabiających:
max ( 3⋅x
1
5⋅x
2
)
gdzie:
x
1
– x
2
x
3
=
3
x
1
x
4
=
5
2⋅x
1
5⋅x
2
x
5
=
25
x
i
≥
0
x1
–
x2
≤
3
x1
x2
0
1
2x1 +
5x2 ≤
25
x1
≤
5
3x1 +
5x2
= 0
5
3
1
5
6
Zmienne osłabiające tworzą jednocześnie początkową bazę. Dowolna transformacje nie może
zmienić kanoniczności postaci – wyrazy wolne nie mogą stać się ujemne.
Całe zadanie umieścimy w następującej tabelce, gdzie kolejne wyróżnione grupy kolumn
oznaczają: zmienne, zmienne osłabiające, zmienne sztucznej bazy, kolumnę wyrazów wolnych;
proszę zwrócić uwagę, że zmienne osłabiające stworzyły pierwszą bazę naszego zadania.
x
1
x
2
x
3
x
4
x
5
x
6
x
7
b
j
1
−
1
1
0
0
3
1
0
0
1
0
5
2
5
0
0
1
25
−
3
−
5
0
0
0
0
Początkowe rozwiązanie bazowe: (0, 0, 3, 5, 25)
Sposób 1 osiągnięcia wierzchołka
Ujemne wartości w wydzielonym ostatnim wierszu tabeli rokują, że można znaleźć korzystniejszy
wierzchołek, taki, że funkcja celu będzie miała większą wartość. Spełniony jest także inny
niezbędny warunek: dodatnie wartości obecne w kolumnach, gdzie w ostatnim wierszu są wartości
ujemne.
Do bazy wprowadzimy zmienną x
1
; pytanie jest o zmienną jaka opuści bazę. Pytanie jest
uzasadnione, bo wszystkie wartości w tej kolumnie są dodatnie. Która jest ta właściwa? Ano należy
kierować się koniecznością zachowania postaci kanonicznej zadania. W tym przypadku elementem
centralnym będzie a
11
. Wybór innego elementu spowodowałby pojawienie się liczb ujemnych
w kolumnie wyrazów wolnych (np. wybór elementu a
21
spowodowałby konieczność odjęcia od
całego pierwszego wiersza wiersza drugiego – bo tylko wtedy a
11
stanie się zerem, ale niejako
przy okazji na pozycji pierwszej kolumny wyrazów wolnych pojawiłaby się zakazana wartość
ujemna: −2 . W przypadku wyboru a
31
jako elementu centralnego jest podobnie.
Przy wyznaczaniu elementu centralnego, jeżeli elementów dodatnich w kolumnie k jest więcej
niż jeden wybieramy ten, który spełnia warunek:
min
b
j
x
jk
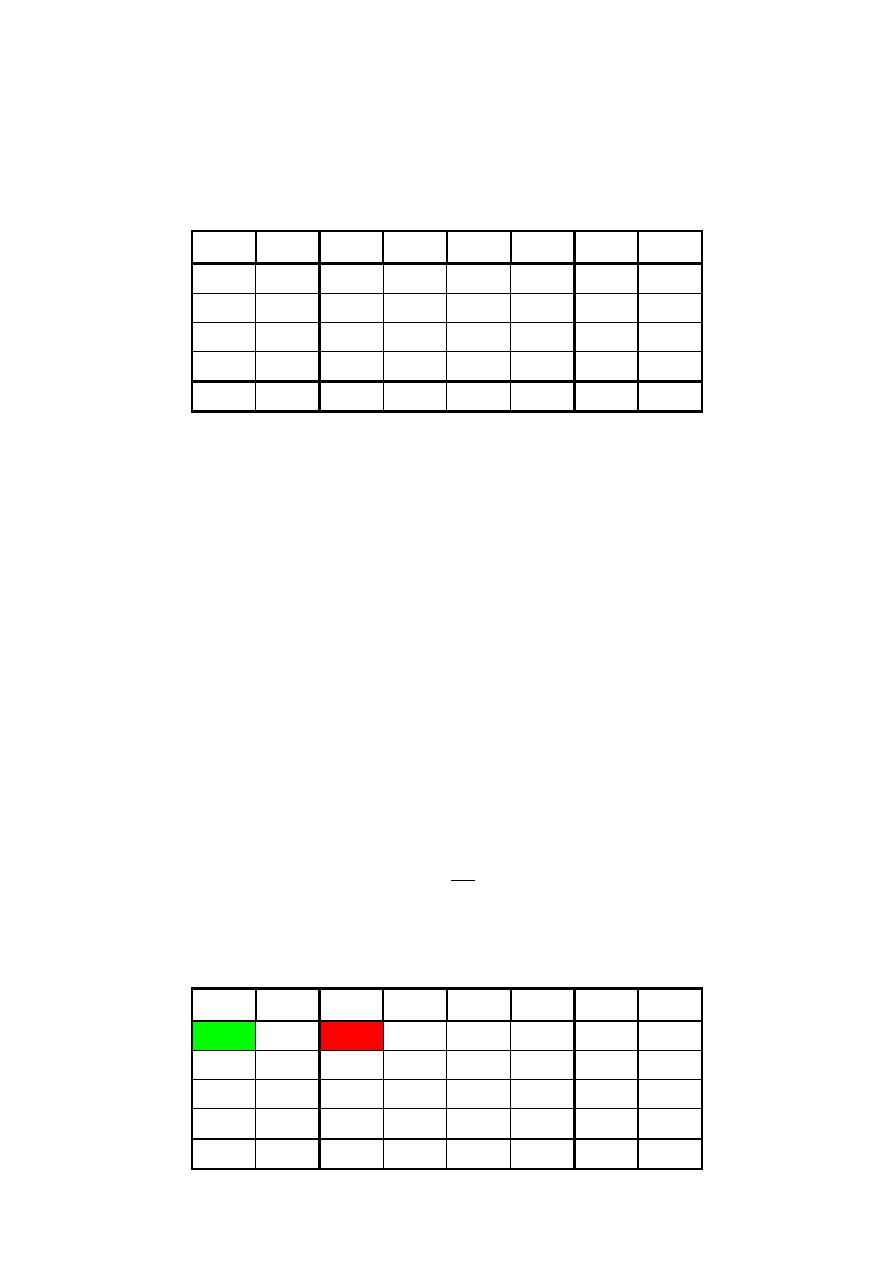
W tabeli czerwonym kolorem oznaczono element, który opuści bazę, na zielono element, który
wchodzi do bazy:
x
1
x
2
x
3
x
4
x
5
x
6
x
7
b
j
1
−
1
1
0
0
3
1
0
0
1
0
5
2
5
0
0
1
25
−
3
−
5
0
0
0
0
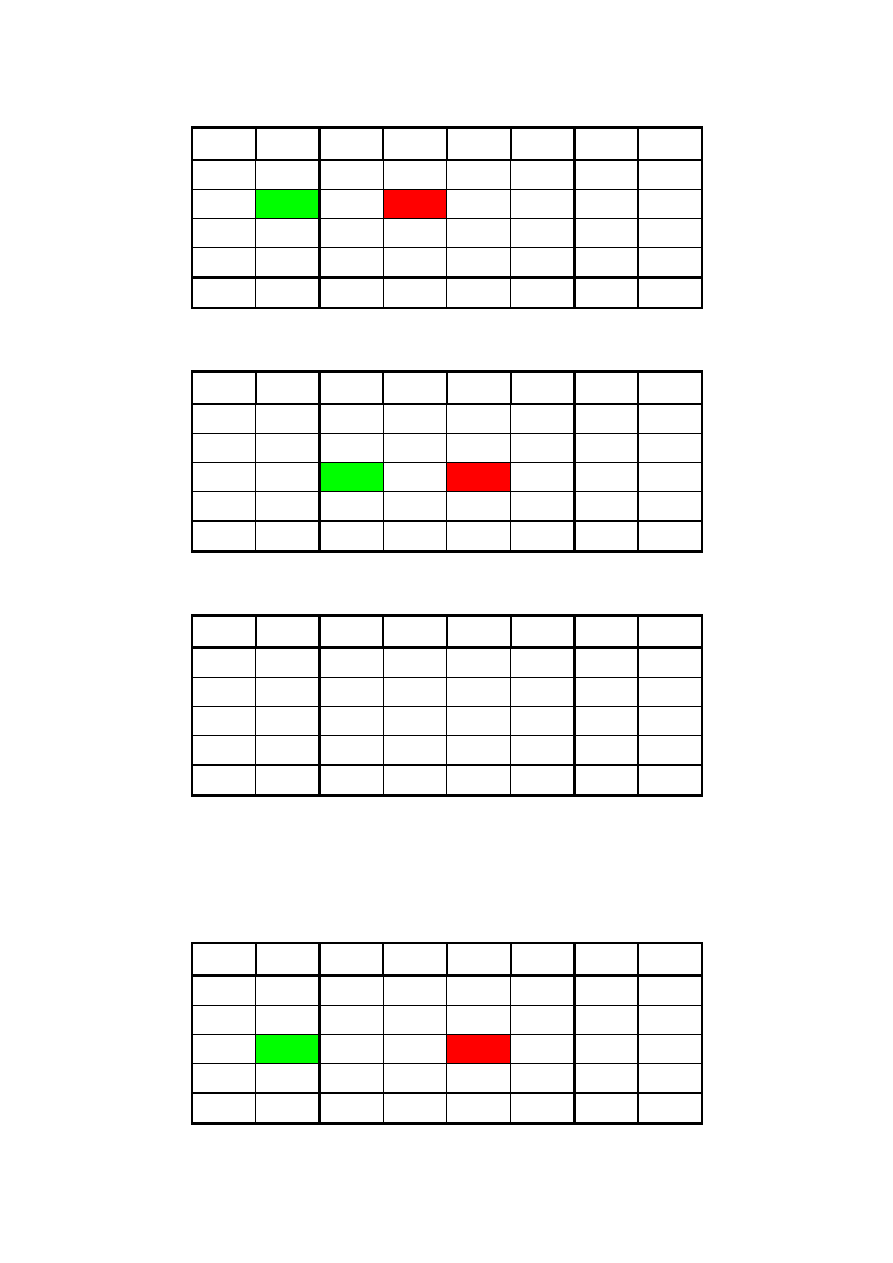
Kolejne etapy transformacji już bez zbędnego komentarza:
x
1
x
2
x
3
x
4
x
5
x
6
x
7
b
1
−
1
1
0
0
3
0
1
−
1
1
0
2
0
7
−
2
0
1
19
0
−
8
3
0
0
9
rozwiązanie bazowe: (3, 0, 0, 2, 19)
x
1
x
2
x
3
x
4
x
5
x
6
x
7
b
1
0
0
1
0
5
0
1
−
1
1
0
2
0
0
5
−
7
1
5
0
0
−
5
8
1
25
rozwiązanie bazowe: (5, 2, 0, 0, 5)
x
1
x
2
x
3
x
4
x
5
x
6
x
7
b
1
0
0
1
0
5
0
1
0
−
0.4
0.2
3
0
0
1
−
1.4
0.2
1
0
0
0
1
1
30
Końcowe rozwiązanie bazowe: (5, 3, 1, 0, 0) – i jednocześnie rozwiązanie zadania.
Sposób 2 osiągnięcia wierzchołka
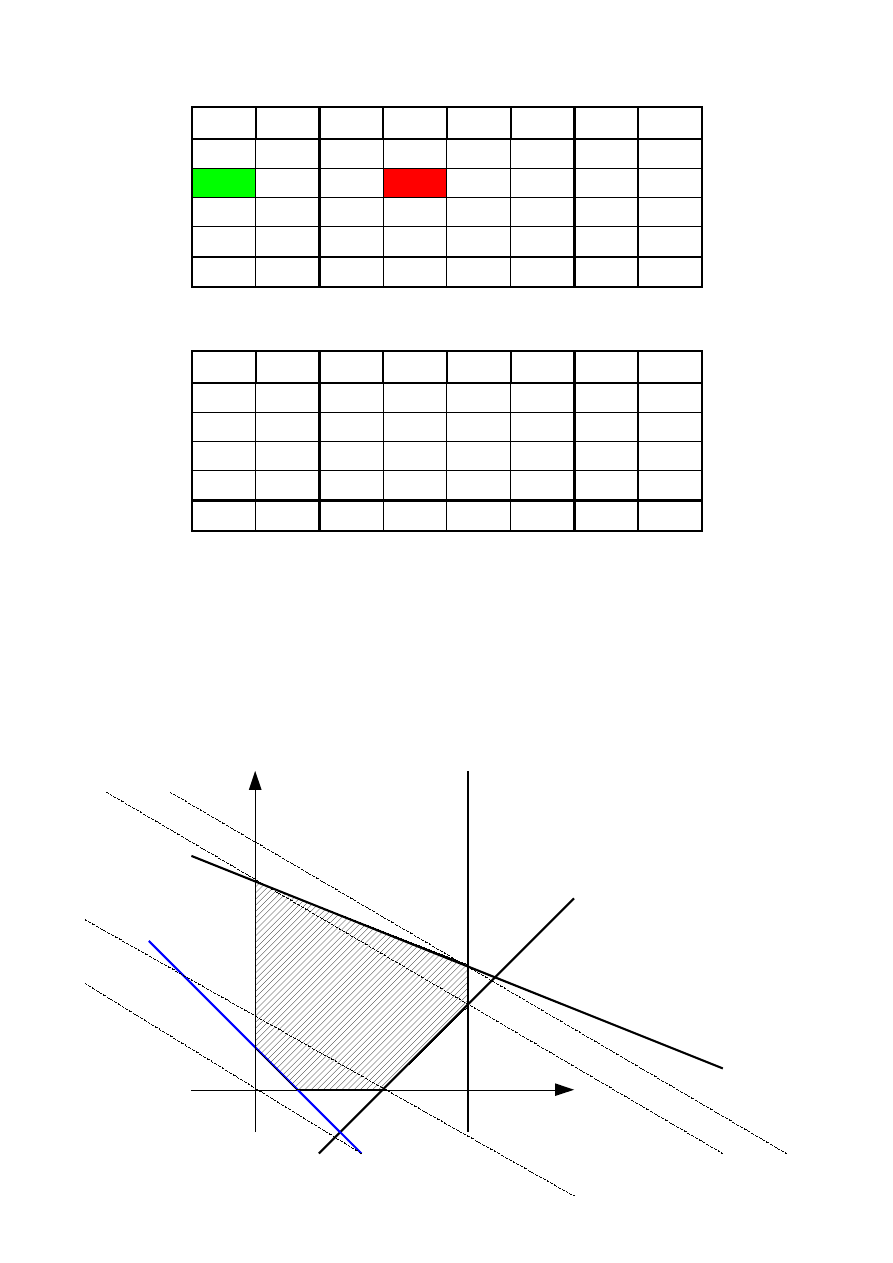
Tym razem kandydat w drugiej kolumnie jest tylko jeden:
x
1
x
2
x
3
x
4
x
5
x
6
x
7
b
j
1
−
1
1
0
0
3
1
0
0
1
0
5
2
5
0
0
1
25
−
3
−
5
0
0
0
0
Początkowe rozwiązanie bazowe: (0, 0, 3, 5, 25)
x
1
x
2
x
3
x
4
x
5
x
6
x
7
b
1.4
0
1
0
0.2
8
1
0
0
1
0
5
0.4
1
0
0
0.2
5
−
1
0
0
0
1
25
rozwiązanie bazowe: (0, 5, 8, 5, 0)
x
1
x
2
x
3
x
4
x
5
x
6
x
7
b
0
0
1
−
1.4
0.2
1
1
0
0
1
0
5
0
1
0
−
0.4
0.2
3
0
0
0
1
1
30
Końcowe rozwiązanie bazowe: (5, 3, 1, 0, 0) – i jednocześnie rozwiązanie zadania.
●
Problem mający rozwiązanie z zastosowaniem sztucznej bazy
Jeżeli do poprzedniego zadania dodamy jedno ograniczenie:
x
1
x
2
≥
1
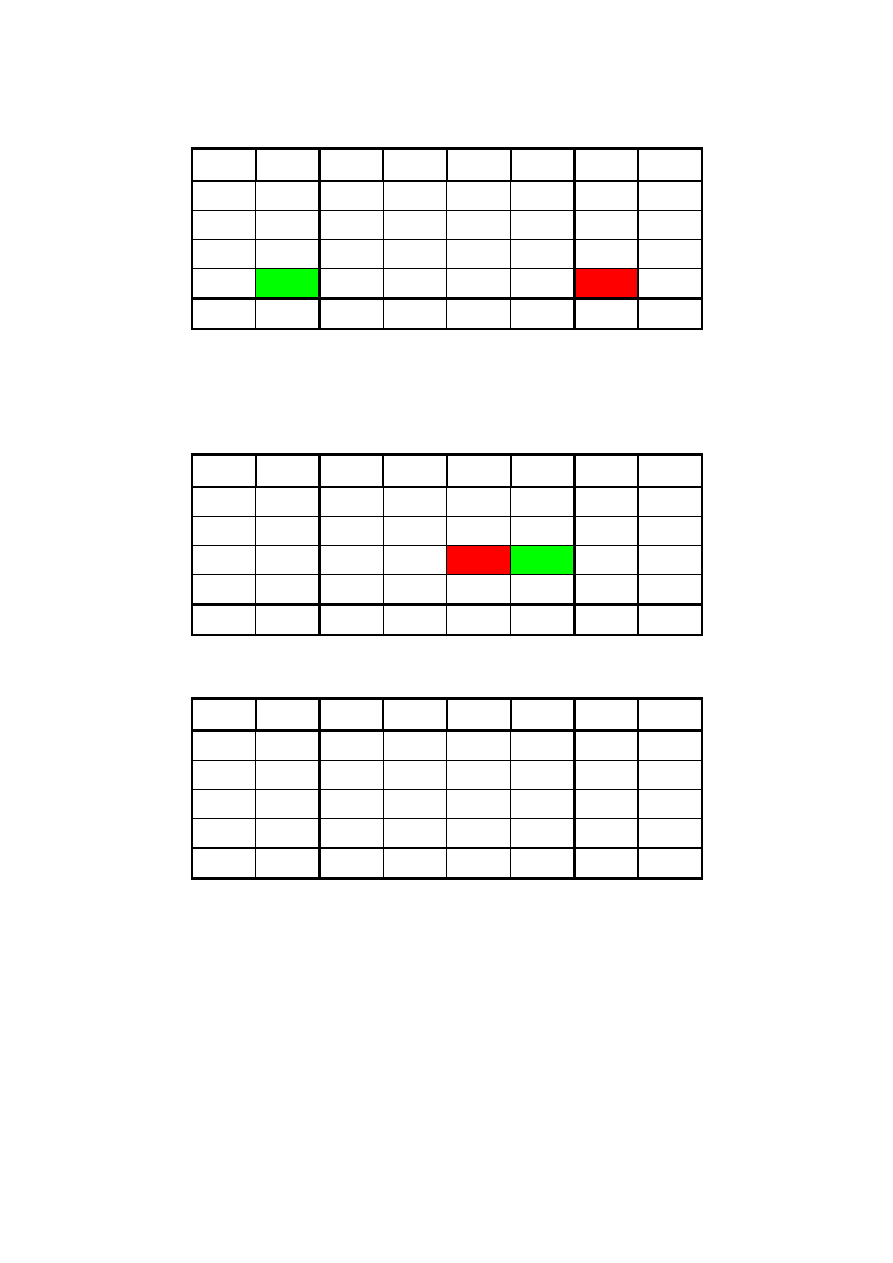
to nasz sympleks będzie wyglądać jak poniżej – proszę zwrócić uwagę, że punkt (0, 0) już nie
należy do rozwiązania:
x1
+ x
2 ≥
1
x1
–
x2
≤
3
x1
x2
0
1
2x1 +
5x2 ≤
25
x1
≤
5
3x1 +
5x2
= 0
5
3
1
5
6
Po doprowadzeniu do postaci kanonicznej (dodany warunek zyskał ujemna zmienną osłabiającą)
i uzupełnienie rozwiązania o jedną sztuczną zmienną bazową nasza tabelka przybrała postać:
x
1
x
2
x
3
x
4
x
5
x
6
x
7
b
j
1
−
1
1
0
0
0
0
3
1
0
0
1
0
0
0
5
2
5
0
0
1
0
0
25
1
1
0
0
0
−
1
1
1
−
3
−
5
0
0
0
0
M
−M+0
Początkowe rozwiązanie dla sztucznej bazy: ( 0, 0, 3, 5, 25, 0, 1)
Proszę zwrócić uwagę, że po wymianie bazy, rozwiązanie związane ze sztuczną bazą znika
a początkowe sześć kolumn daje pierwsze rozwiązanie bazowe problemu.
x
1
x
2
x
3
x
4
x
5
x
6
x
7
b
2
0
1
0
0
−
1
4
1
0
0
1
0
0
5
−
3
0
0
0
1
5
20
1
1
0
0
0
−
1
1
2
0
0
0
0
−
5
5
Rozwiązanie bazowe: ( 0, 1, 4, 5, 20, 0)
x
1
x
2
x
3
x
4
x
5
x
6
x
7
b
1.4
0
1
0
0.2
0
8
1
0
0
1
0
0
5
−
0.6
0
0
0
0.2
1
4
0.4
1
0
0
0.2
0
5
−
1
0
0
0
1
0
25
Rozwiązanie bazowe: ( 0, 5, 8, 5, 0, 4)
Kolejne kroki przećwicz sam, zwłaszcza, że coś bardzo podobnego już było.
●
Problem nie mający rozwiązania (sympleks pusty)
max ( 3⋅x
1
5⋅x
2
)
gdzie:
x
1
– x
2
≤
3
x
1
≤
5
2⋅x
1
5⋅x
2
≤
25
x
1
– 5⋅x
2
≥
30
x
i
≥
0
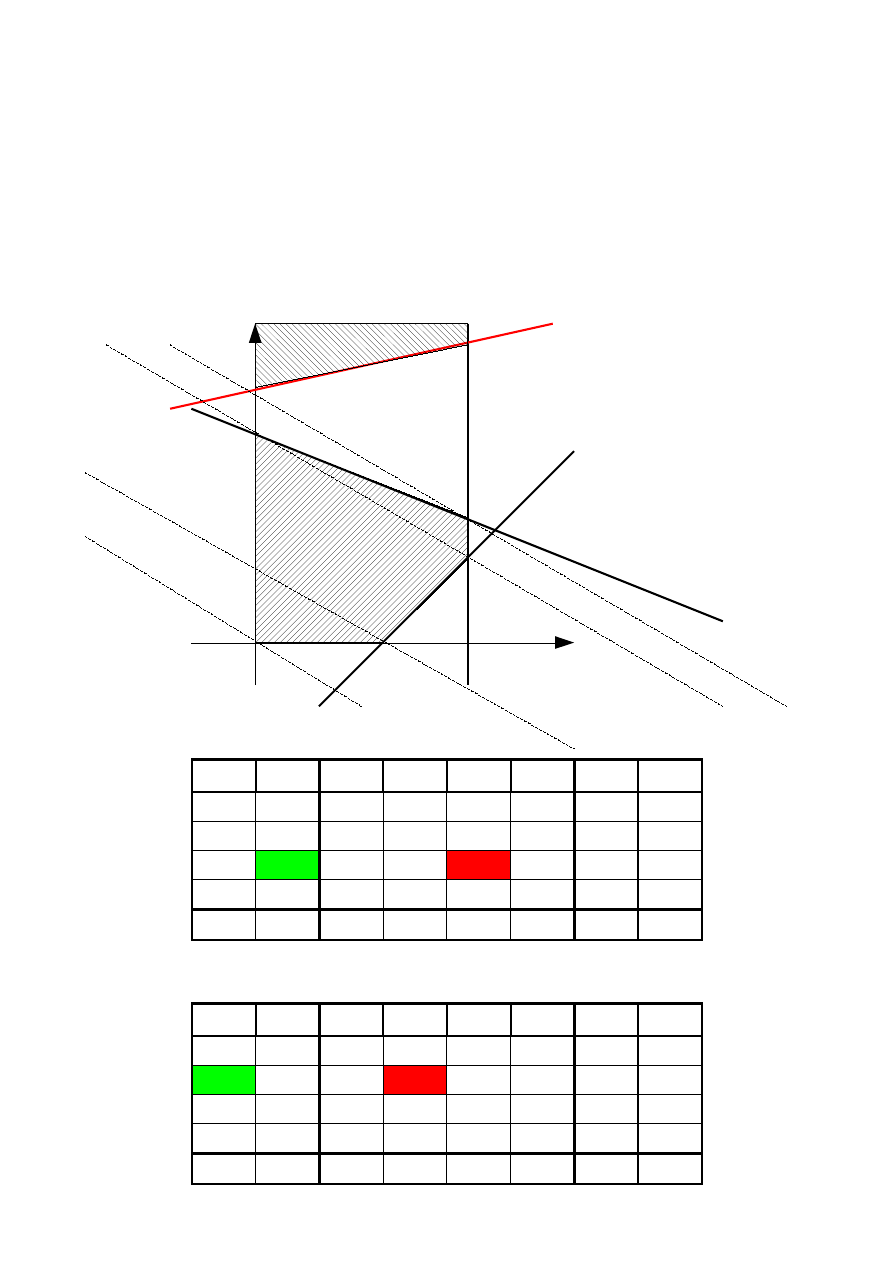
Poniżej graficzna postać sympleksu:
Zadanie ewidentnie nie może mieć rozwiązania; zobaczymy jak to objawia się w trakcie obliczeń.
x
1
x
2
x
3
x
4
x
5
x
6
x
7
b
j
1
−
1
1
0
0
0
0
3
1
0
0
1
0
0
0
5
2
5
0
0
1
0
0
25
1
-5
0
0
0
−
1
1
30
−
3
−
5
0
0
0
0
M
−M+0
Początkowe rozwiązanie dla sztucznej bazy: ( 0, 0, 3, 5, 25, 0, 30)
x
1
x
2
x
3
x
4
x
5
x
6
x
7
b
1.4
0
1
0
0.2
0
0
8
1
0
0
1
0
0
0
5
0.4
1
0
0
0.2
0
0
5
3
0
0
0
1
−
1
1
55
−
1
0
0
0
1
0
M
−M+25
x1
–
x2
≤
3
x1
x2
0
1
2x1 +
5x2 ≤
25
x1
≤
5
x1 – 5x
2 ≥ 30
3x1 +
5x2
= 0
5
3
1
5
6
Rozwiązanie dla sztucznej bazy: ( 0, 5, 8, 5, 0, 0, 55)
x
1
x
2
x
3
x
4
x
5
x
6
x
7
b
0
0
1
−
1.4
0.2
0
0
1
1
0
0
1
0
0
0
5
0
1
0
−
0.4
0.2
0
0
7
0
0
0
−
3
1
−
1
1
50
0
0
0
1
1
1
M
−M+30
Rozwiązanie dla sztucznej bazy: ( 5, 7, 1, 0, 0, 0, 50)
Nic więcej nie jesteśmy w stanie wykonać a nadal istnieje zmienna sztucznej bazy, która nie może
w żaden sposób być usunięta. Zadanie nie ma rozwiązania.
●
Problem nie mający rozwiązania (sympleks nieograniczony)
max ( 3⋅x
1
5⋅x
2
)
gdzie:
x
1
– x
2
≤
3
x
1
≤
5
x
i
≥
0
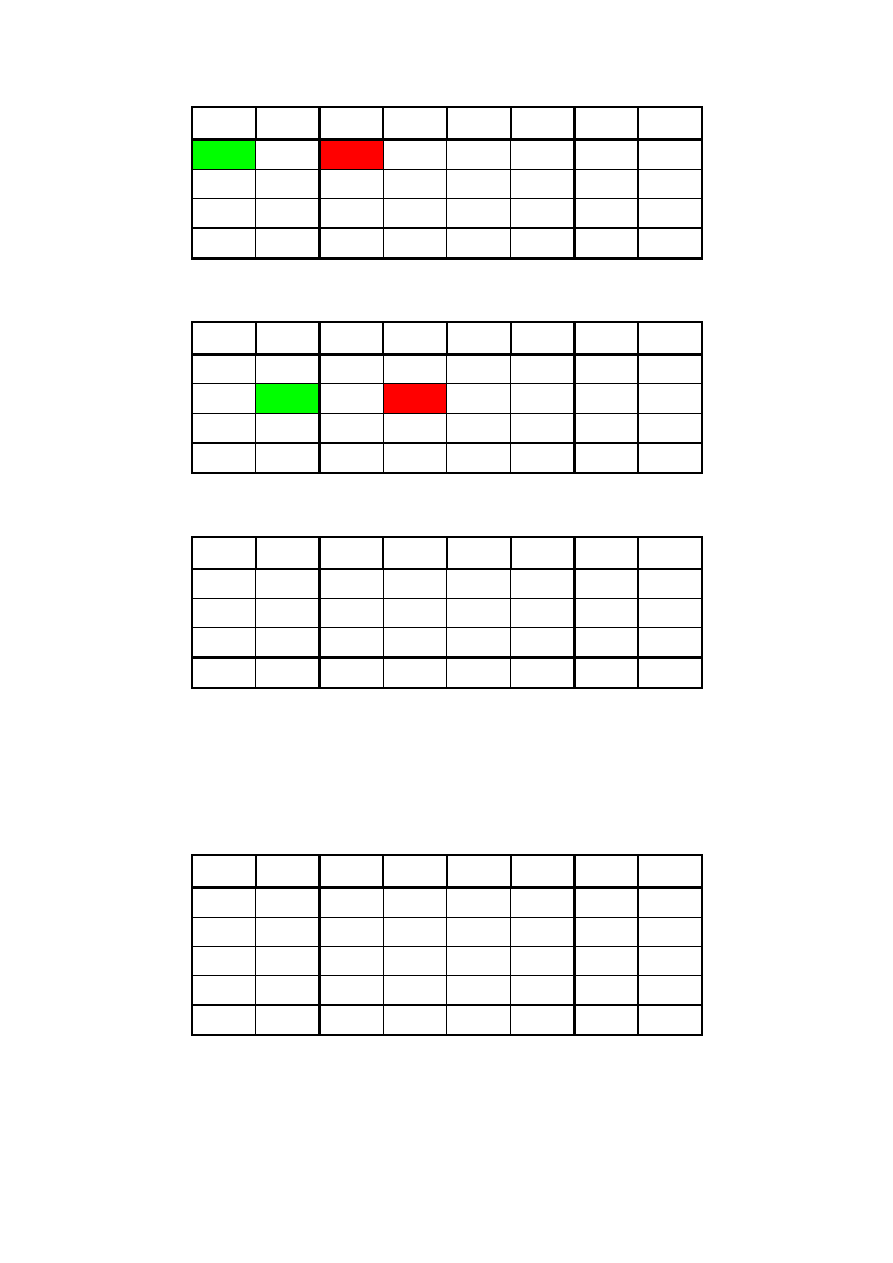
Oto graficzny obraz sympleksu:
x1
–
x2
≤
3
x1
x2
0
1
x1
≤
5
3x1 +
5x2
= 0
5
3
1
5
6
x
1
x
2
x
3
x
4
x
5
x
6
x
7
b
j
1
−
1
1
0
3
1
0
0
1
5
−
3
−
5
0
0
0
0
Początkowe rozwiązanie bazowe ( 0, 0, 3, 5)
x
1
x
2
x
3
x
4
x
5
x
6
x
7
b
1
−
1
1
0
3
0
1
−
1
1
2
0
-8
3
0
9
Kolejne rozwiązanie bazowe ( 3, 0, 0, 2)
x
1
x
2
x
3
x
4
x
5
x
6
x
7
b
1
0
0
1
5
0
1
−
1
1
2
0
0
−
5
8
19
Kolejne rozwiązanie bazowe ( 5, 2, 0, 0)
Jest obiecujący kierunek zmian, ale nie można ustalić elementu centralnego. Zresztą znamiona tego
widoczne był już na pierwszym diagramie: kolumna druga wyglądała obiecująco ale nie można
było tam ustalić elementu centralnego.
x
1
x
2
x
3
x
4
x
5
x
6
x
7
b
Wyszukiwarka
Podobne podstrony:
Yutang Lin Przekroczyć próg wyzwolenia
Próg rentowności
PRTL pl wyniki europejskich lin Nieznany
al lin zad3 rozw
Prog wyk TMM AiR 2010
debussy La fille aux cheveux de lin
Przepisy na zanęty Karp Leszcz Płoć Lin Karaś z obrazkami, Wędkarstwo
Lin
techniki manipulacji politycznych prog 14
cg100 prog iii airbag restore devices support list
prog lidkakor
Prog lab TMM 2006 2007
5ZF Prezentacja5 prog rent
prog w asm podstawy
al lin zad5 rozw
µprog V1 2 bottom
Ansys LAB 6 Tutorial Excel prog Nieznany (2)
Program lin
więcej podobnych podstron