SEDYMENTOLOGIA – W4 – 2015 J. Rotnicka

1. Gęstość (masa właściwa) – stosunek masy do objętości (m / V)





wody morskiej: ~1,03 g/cm

3





wody słodkiej: ~1,00 g/cm

3





lodu lodowcowego: ~0,90 g/cm

3





powietrza: ~0,001 g/cm

3

(0,1% gęstości wody)

Dla porównania:



kwarcu: ~2,63 g/cm

3



minerałów ciężkich > 2,9 g/cm

3

2. Lepkość – miara oporu wewnętrznego, jaki stawia płyn poddawany naprężeniom ścinającym

zmuszającym go do przepływu

Ciecze

Lepkość
(Pa•s)

Gazy

Lepkość

(Pa•s)

Aceton

0.032

Powietrze

0. 0018

Alcohol(etyl)

0. 12

Hel

0. 0019

Benzyna

0.06

Metan

0. 0020

Gliceryna

149

Azot

0. 0018

Olej (lekki)

11

Tlen

0. 0020

Oleje (ciężkie)

66

Para wodna*

0. 0013

Woda

0. 1

Miód

176

Dane w temp. 20

0

C, za wyjątkiem: * dane w temp. 100

0

C

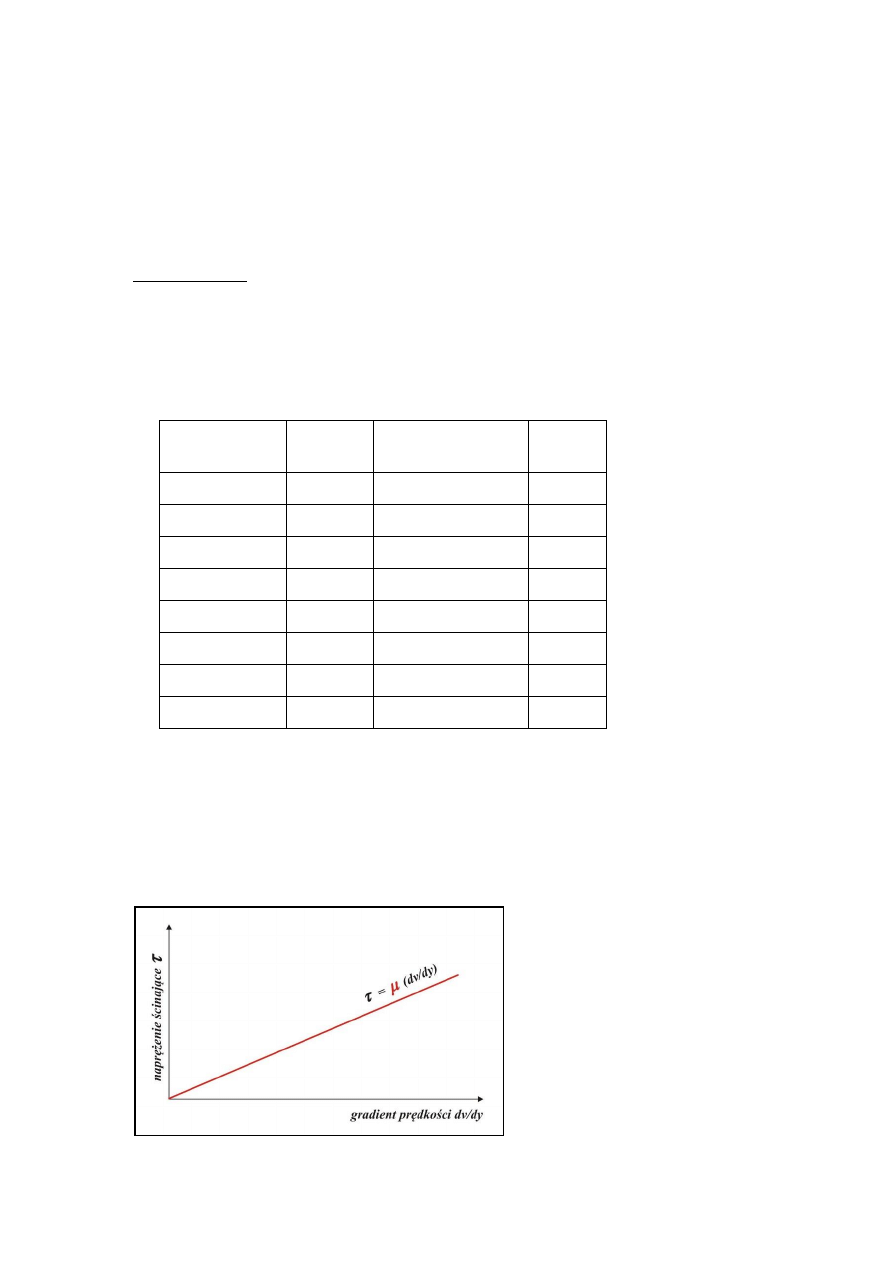
3. Płyny newtonowskie (rzeczywiste)

Wyrazem odkształcenia płynu rzeczywistego jest powstający w nim gradient prędkości dv/dy
określany jako zmiana prędkości na jednostkę długości.

τ = μ (dv/dy) gdzie: μ – lepkość dynamiczna, dv/dy – gradient prędkości

Jeżeli zależność między tempem odkształcenia
(dv/dy) i siłą ścinającą przypadającą na
jednostkową powierzchnię (



) jest liniowa



płyny newtonowskie

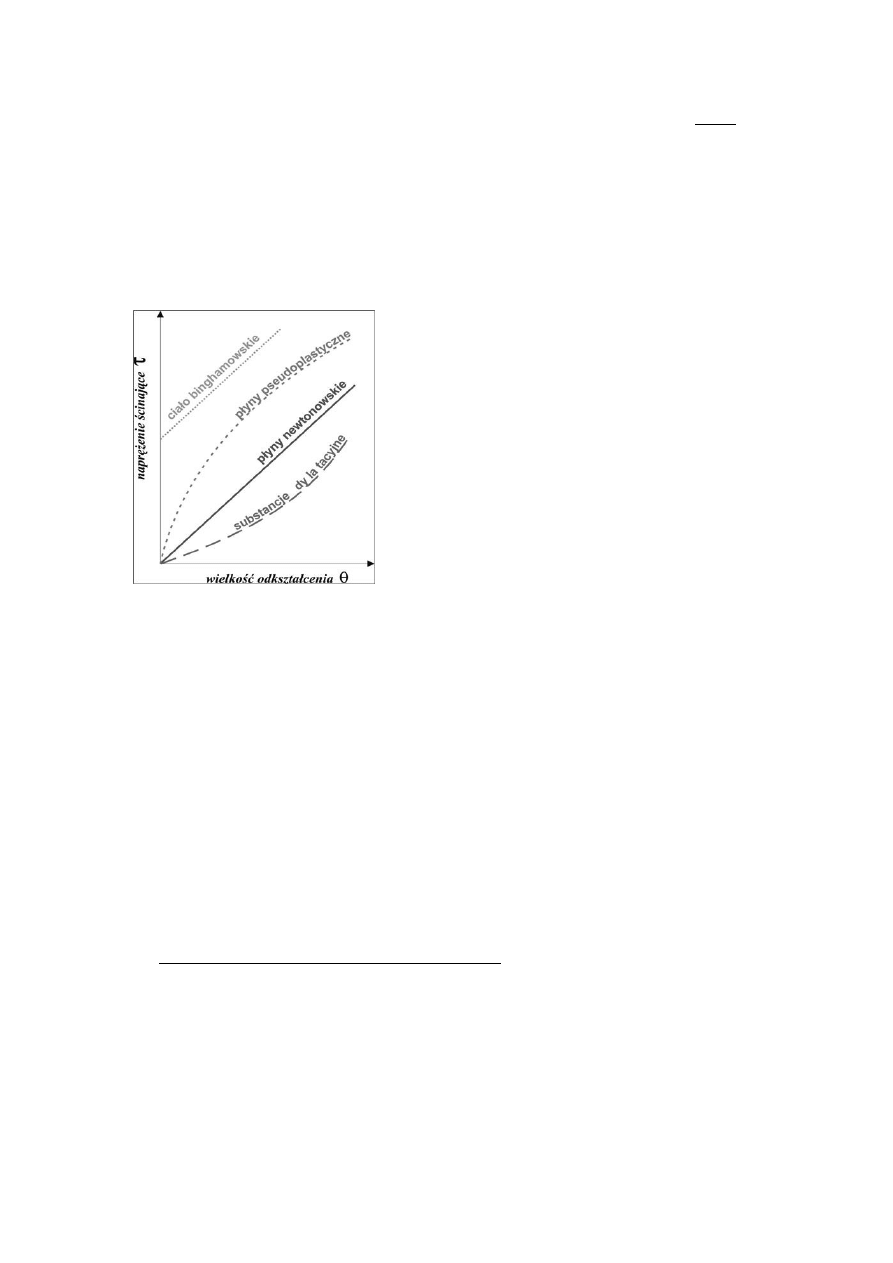
4. Płyny nienewtonowskie (nierzeczywiste) - płyny, w których lepkość dynamiczna μ zależy od:

a) gradientu prędkości ruchu dv/dy:

τ = μ (dv/dy)

n



płyny pseudoplastyczne (n<1): dv/dy 



μ



substancje dylatacyjne (n>1): dv/dy 



μ 

b) długości czasu trwania ścinania t:



substancje tiksotropowe: t 



μ



substancje zagęszczane ścinaniem: t 



μ 

5. Transport hydrauliczny

a) naprężenia ścinające



ruch laminarny:



=



dv/dy



ruch turbulentny:



turb.

= (



+



) dv

śr

/dy gdzie:



- lepkość wirowa i



>>



b) Liczba Reynoldsa: Re = siła bezwładności / siła lepkości

Re = v l / υ
gdzie: υ – lepkość kinematyczna: υ =



/



v – prędkość przepływu
l – charakterystyczny wymiar liniowy



– lepkość dynamiczna



– gęstość

Charakterystyczny parametr liniowy l – przykłady:



Koryta otwarte: l – promień hydrauliczny koryta R = A / P gdzie:
A – powierzchnia poprzecznego przekroju koryta zajętego przez przepływ, P –
obwód zwilżony



Rura o Ø = d całkowicie wypełniona wodą: l = R, gdzie: R = ¼ d (tj. pole przekroju
poprzecznego przez rurę / obwód rury)

c) Liczba Froud’a: Fr = siła bezwładności / siła grawitacji

𝑭 = 𝒗/√𝒈𝒉

gdzie: √𝒈𝒉 – prędkość rozchodzenia się fal grawitacyjnych na powierzchni płynu

g – przyspieszenie ziemskie

h – głębokość przepływu

v – prędkość przepływu

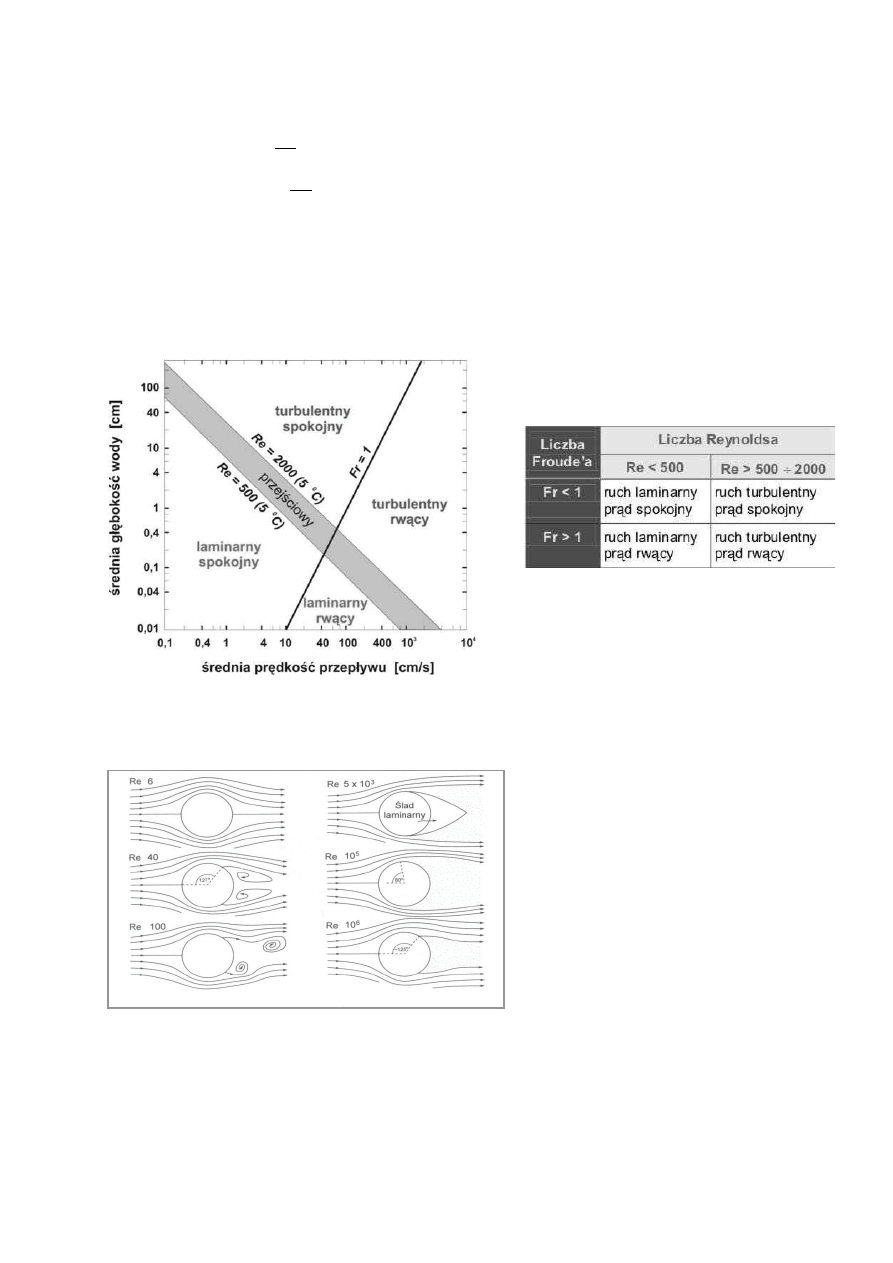
6. Typy przepływów (Sundborg, 1956)

7. Separacja strumienia w zależności od liczby Reynoldsa

8. Ruch materiału ziarnowego

Krytyczna prędkość ścinająca v



kr

– tj. prędkość, przy której naprężenie ścinające osiąga wartość

progową (graniczną)



ruch ziaren





/

0





kr

v

gdzie:



0

– graniczne naprężenie ścinające,



– gęstość płynu

Zapoczątkowanie ruchu ziaren zależy od (Shields, lata 30-te):

 cech teksturalnych ziarna
 kohezji osadu
 ciężaru właściwego ziarna zanurzonego
 lepkości płynu
 ciężaru właściwego płynu

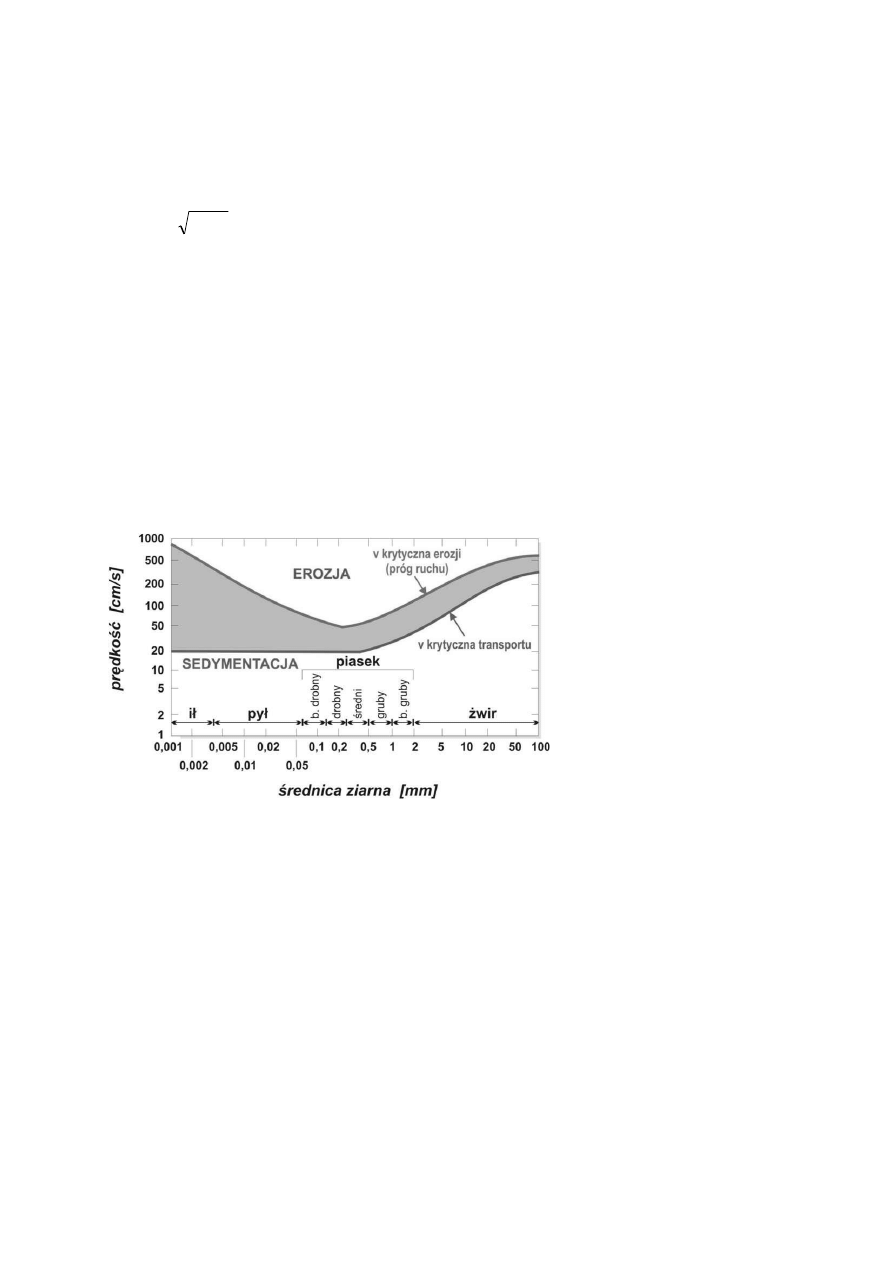
Uproszczone podejście  diagram Hjulstroma- Sundborga (1956): V przepływu ↔ Ø ziarna

Diagram Hjulstroma-Sundborga 1956

9. Prawo Bernoullie’go - wzdłuż linii prądu suma ciśnienia, energii potencjalnej i energii kinetycznej

jest stała

p +



v

2

/2 +



gy = const = p + E

kinetyczna

+ E

potencjalna

gdzie: p – ciśnienie,



– gęstość płynu, v – prędkość przepływu, g – przyspieszenie ziemskie, y –

wysokość położenia