CIEPŁO WŁAŚCIWE

Na pewno wielu z Was, spojrzawszy na tytuł tego artykułu, tylko wzruszy ramionami: 

a co w tym ciekawego? Tak, jest taka wielkość, potrzebna do obliczenia ciepła potrzebnego 

do nagrzania takiego czy innego ciała. W technice jest to oczywiście ważne i dlatego znaleźli 
się   ludzie,   którzy   potracili   mnóstwo   czasu   mierząc   ciepło   właściwe   najróżniejszych 

materiałów (pomiary takie nie są w zasadzie takie trudne – również w szkolnym gabinecie 
fizycznym   istnieją   kalorymetry   i   rozwiązuje   się   zadania   dotyczące   obliczania   ciepła 

właściwego). Następnie zestawiono tablice, w których wartości ciepła właściwego zawsze 
można odnaleźć i nic więcej nie można tu wymyślić.

A jednak…
Jeśli przejrzymy najpoważniejsze naukowe czasopisma, to wciąż będziemy spotykać 

prace, w których bada się ciepło właściwe i niekoniecznie nowych syntetyków, ale zupełnie 
zwykłych materiałów, tylko że w niezwykłych warunkach. O co tu chodzi? Dlaczego w epoce 

laserów, fizyki cząstek elementarnych, mikroelektroniki, syntezy termojądrowej, itp., fizycy 
nie przestają interesować się takim, wydawałoby się, rutynowym pomiarem?

Rzecz w tym, że ciepło właściwe jest mocno związane z budową materii i dynamiką 

ruchu cząstek. Nierzadko pomiary ciepła właściwego pozwalają coś niecoś wnioskować o 

budowie substancji i naturze zjawiska, podczas gdy najbardziej wyrafinowane współczesne 
metody są bezradne.

Aby przekonać się naocznie o takim związku, nie trzeba daleko szukać przykładów. 

Popatrzcie na rysunek 1:

rys. 1

0

1

2

3

4

­250

­200

­150

­100

­50

0

50

100

t [

o

C]

c [

J

/

g*K

]

4,1

4,2

4,3

0

50

100

t [

o

C]

c 

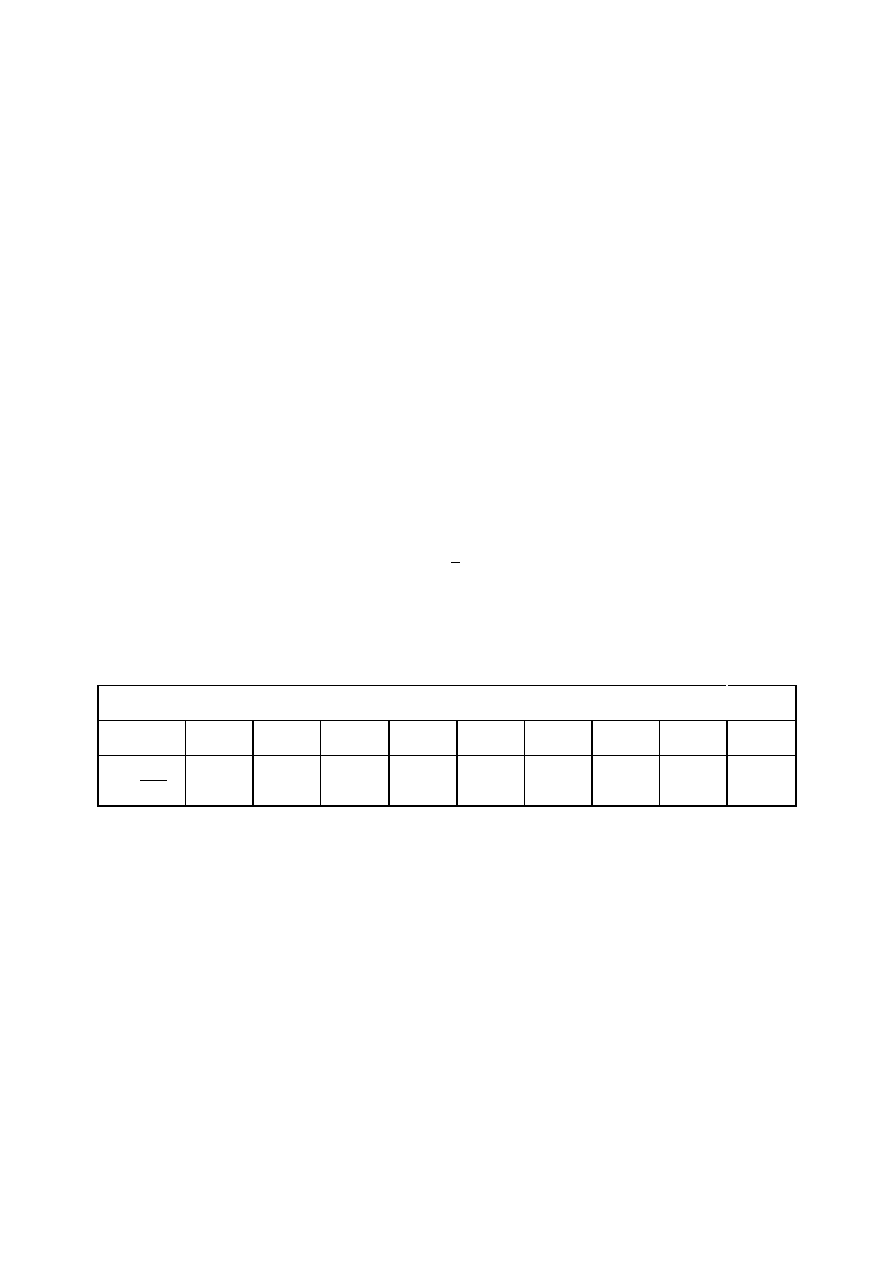
tak   zmienia   się   ciepło   właściwe   zwykłej   wody   przy   zmianach   temperatury.   Na   pewno 
pierwsza sprawa, jaka rzuca się tu w oczy, to skok przy 0°C tj. przy temperaturze przejścia 

wody z jednego stanu skupienia w drugi. Ale to nie wszystko: i w fazie stałej i w ciekłej 
ciepło właściwe w skomplikowany sposób zależy od temperatury. I to dla wody, która jeszcze 

nie tak dawno służyła za wzorzec ciepła właściwego!

Współczesna nauka potrafi wyjaśnić, co się dzieje z wodą, ale my sobie na razie 

możemy to podarować. Lepiej zacząć od przypadku najprostszego – od gazu doskonałego.

GAZ DOSKONAŁY

Ściśle   mówiąc,   nagłówek   nie   jest   zupełnie   właściwy,   ponieważ   chodzi   tu  o   gazy 

realnie istniejące, a doskonałe tylko w jednym sensie: spełniają w temp. pokojowej równanie:

pV

NkT



i energia ruchu postępowego cząsteczki gazu wynosi:

3

2

p

E

kT



(oznaczenia podstawowe)

Wypiszmy   z   tablic   wartości   ciepła   właściwego   dla   stałej   objętości   (c

V

)   zmierzone   dla 

niektórych gazów (tab. 1).

c

V

   gazów w temperaturze pokojowej

tab. 1

gaz

He

Ar

Xe

H

2

N

2

O

2

CO

2

NH

3

CH

4













gK

J

C

V

3,15

0,31

0,096

10,26

0,74

0,66

0,65

1,62

1,68

na pierwszy rzut oka trudno jest dostrzec w tych liczbach jakąś prawidłowość. Nie będziemy 

się tym przejmować, ale postaramy się przedstawić te liczby w nieco innej postaci. Istotne jest 
to, że jeden gram różnych gazów zawiera różną liczbę cząsteczek. A podana wyżej zależność 

na E

p

 podpowiada, że należałoby porównywać wartości w odniesieniu do jednej cząsteczki. 

Nietrudno przeliczyć wartości z tabelki. Przypomnijmy, że mol dowolnej substancji zawiera 
tę samą liczbę cząsteczek – 

23

10

02

,

6

x

 (jest to N

A

 – stała Avogadra).

Ciepło właściwe odniesione do jednego mola – czyli tzw. ciepło molowe – można łatwo 

obliczyć

µ

µ

V

C

C

=

     

(μ – masa molowa)

Wynika stąd, że ciepło właściwe przepadające na jedną cząsteczkę wynosi:

A

V

cz

N

C

C

µ

=

Wielkość ta jest bardzo mała i dlatego wygodniej będzie nam porównywać między sobą 
wartości

cz

cz

c

c

k

8



(łatwo zauważyć, że wielkości c′

cz

 są bezwymiarowe)

Wyznaczamy wartości c′

cz

 dla gazów z tabelki 1. i popatrzmy co otrzymaliśmy (tab.2):

c′

cz

   gazów 

tab. 2

gaz

He

Ar

Xe

H

2

N

2

O

2

CO

2

NH

3

CH

4

cz

c

1,50

1,50

1,50

2,45

2,49

2,53

3,42

3,30

3,23

Od razu daje się zauważyć, że dla wszystkich gazów 1­atomowych c′

cz 

jest takie samo 

i równe 

3

2

 (inaczej: 

3

2

cz

c

k



).

Ale przecież czynnik 

3

2

 figuruje już w zależności na E

p

. Ponieważ ciepło właściwe

E

T

c







,

więc otrzymamy:

3

3

2

2

T

cz

T

k

k c









.

Otrzymujemy   więc   ważny   wniosek:   w   przypadku   helu,   argonu   i   neonu,   całe 

dostarczone ciepło bez reszty przekształca się w energię ruchu postępowego atomów.

Można sobie wyobrazić, że atomy mogą się jeszcze obracać, ale, jak widać, na energię 

tego ruchu nie starcza dostarczanego ciepła, i żadnego ciepła właściwego związanego z tym 

ruchem nie ma.

Przypomnijmy   jeszcze,   że   wniosek   ten   słuszny   jest   tylko   dla   temperaturach 

pokojowych (tab. 1 i 2).

W   bardzo   wysokich   temperaturach   (tysiące   stopni)   to   wszystko   nie   jest   już   takie 

proste, i, jak pokazują doświadczenia oraz teoria, takie obroty mogą się wzbudzić. Ale na 
razie nie będziemy sobie tym utrudniać życia.

I bez tego powstają pytania co do ciepła właściwego gazów 2­ i 3­atomowych. Dla 

tych gazów ciepło właściwe jest wyższe niż w 1­atomowych. Jest interesujące, że nadwyżka 

ciepła właściwego w przypadku gazów 2­atomowych przypadająca na 1 atom wynosi ½ k. W 
przypadku   wieloatomowych   gazów   sytuacja   jest   bardziej   złożona:   odpowiednie   udziału 

wynoszą ~0,65k/atom dla CO

2

 i ~0,34k/atom dla CH

4

. A więc, jak widać, sprawa nie jest taka 

prosta.

Podejdźmy do tego problemu z innej strony – popatrzmy, jakie różne typy ruchu mogą 

wykonywać cząsteczki. Cząsteczkę dwuatomową można przedstawić jak na rys. 2a – atomy 

połączone sprężynką.

                             

 

 

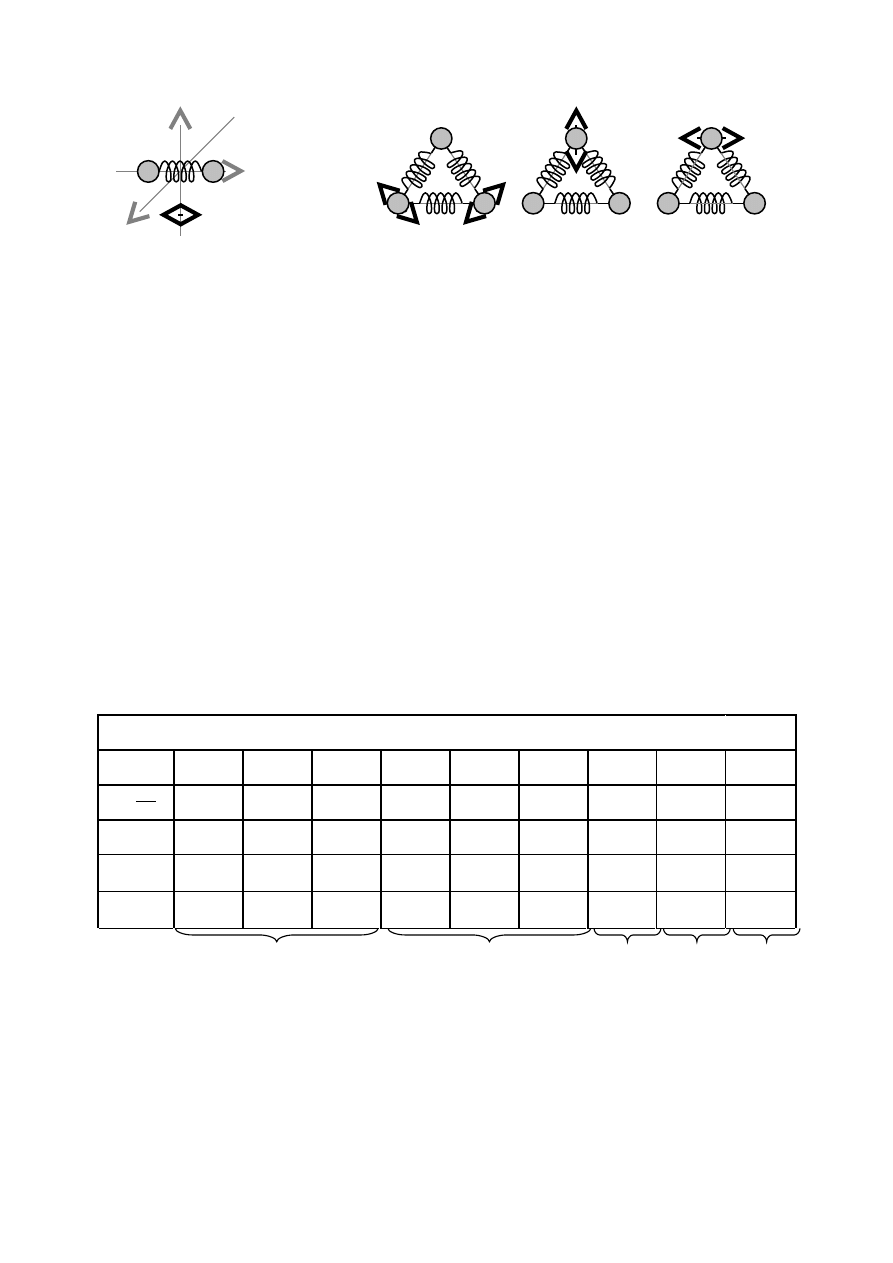
rys. 2a

rys. 2b

Ruch postępowy cząsteczki może być opisany jako uch jej środka masy w układzie 

trzech wzajemnie prostopadłych osi X, Y i Z.

Cząsteczkę   można   obracać   wokół   osi   Y   i   Z,   prostopadłych   do   sprężynki.   Obrót 

cząsteczki wokół osi X, przechodzącej wzdłuż sprężynki, należy prawdopodobnie wyłączyć – 
jest to w istocie to samo, co obrót każdego z atomów wokół własnej osi, a jak to już przed 

chwilą   widzieliśmy   na   przykładzie   gazów   jednoatomowych,   ciepło   nie   jest   w   to 
zaangażowane. I, w końcu, same atomy mogą drgać naprzeciw siebie.

I tak, dla cząsteczek dwuatomowych, możliwych typów ruchu (tzw. stopni swobody), 

łącznie z ruchem postępowym wzdłuż osi X, Y i Z, jest sześć.

Dla   cząsteczek   trzyatomowych   istnieje   dziewięć,   ponieważ   można   ją   już   obracać 

wokół trzech osi oraz istnieją trzy możliwe typy drgań (rys. 2b).

Jeśli cząsteczka zbudowana jest z  n  atomów (

3

n

 ) to rozrysowanie tego jest już 

trudne, ale istnieje prosta reguła, pozwalająca określić liczbę stopni swobody: całkowita ich 

liczba,   włączając   ruch   postępowy   i   obrotowy,   jest   równa   ilości   współrzędnych   atomów 
tworzących cząsteczkę, czyli 3n.

Posługując   się   tą   regułą,   wyliczmy   ilość   możliwych   typów   ruchu   dla   różnych 

cząsteczek gazu i, pamiętając o trzech stopniach swobody przypadających na ruch postępowy, 

dołączmy do tabeli 2. jeszcze dwie rubryki (tab. 3):

tab. 3

gaz

He

Ar

Xe

H

2

N

2

O

2

CO

2

NH

3

CH

4

J

g K

V

c � �

� �

g

3,15

0,31

0,096

10,26

0,74

0,66

0,65

1,62

1,68

cz

cp

1,50

1,50

1,50

2,45

2,49

2,53

3,42

3,30

3,23

Ilość 

obrotów

0

0

0

2

2

2

3

3

3

Ilość 

drgań

0

0

0

1

1

1

3

6

9

1 at.

2 at.

3 at.

4 at.

5 at.

Przypatrzmy   się   teraz   gazom   wieloatomowym:   CO

2

,   NH

3

  i   CH

4

.   Każdą   z   tych 

cząsteczek można obracać wokół 3 osi, ale liczba możliwych typów drgań jest zróżnicowana: 

dla CO

2

  – trzy, dla NH

3

  – sześć, a dla CH

4

  – aż dziewięć. A ciepło właściwe tych gazów 

prawie jednakowe!

Mądrze byłoby założyć, że przy cieplnym ruchu, energia przekazywana cząsteczce, 

zużywana jest na ruch postępowy i obrotowy, a drgania nie są wzbudzane przez ciepło. 

Inaczej mówiąc, drgania nie dają wkładu do ciepła właściwego. Ale wtedy, konsekwentnie, 

H

H

Y

Z

X

O

O

C

O

O

C

O

O

C

należałoby zaniedbać drgania również cząsteczek dwuatomowych i założyć, że nadwyżka (w 

porównaniu do gazów 1­atomowych) ciepła właściwego związana jest wyłącznie z obrotami. 
Dla cząsteczek 2­atomowych, jak widać z tablicy 3, w temperaturze pokojowej jest prawie 
dokładnie równa 

1

2

k  na każdy obrót. Jeśli przyjmiemy tę regułę dla gazów wieloatomowych, 

to ich całkowite ciepło właściwe powinno być równe 3k. W rzeczywistości jest ono nieco 
większe, ale na razie nie będziemy na to zwracać uwagi.

Doszliśmy   tu   do   interesującego   wniosku:   na   każdy   z   możliwych   typów   ruchu 

cząsteczki jako całości (postępowego i obrotowego) przypada takie samo ciepło właściwe, 
równe 

1

2

k .

[jest to tzw. zasada „ekwipartycji energii”]

DRGANIA – POZA REGUŁĄ?

Jeśli to ma być prawo, to dlaczego nie jest ono uniwersalne, dlaczego nie dotyczy 

drgań?   Sytuacja   staje   się   jeszcze   bardziej   skomplikowana   jeśli   popatrzymy   na   grupową 

„supercząsteczkę”   –   cząsteczkę   ciała   stałego.   W   ciałach   stałych   wszystkie   tworzące   je 
cząsteczki znajdują się w węzłach sieci krystalicznej i nie mogą poruszać się ani postępowo, 

ani obrotowo. Jedyny możliwy typ ruchu cząsteczki, jeśli pominiemy ruch całego ciała, to jej 
drgania wokół położenia równowagi. Dlatego też całe ciepło właściwe ciał stałych związane 

jest z drganiami. Tak, prawie wszystkie kryształy, zbudowane z atomów, mają w warunkach 
normalnych ciepło molowe prawie jednakowe i równe 

J

mol K

25

g

. Jest to tzw. prawo Dulonga i 

Petita [1819]. Np. dla aluminium –  

J

mol K

24, 4

g

, srebra – 25,2, miedzi – 24,6, złota – 26,5, 

ołowiu   –   26,6.   Łatwo   wyliczyć,   że   na   każdy   atom   w   ciele   stałym   przypada   3k  ciepła 
właściwego, tj. na każde drganie (dla 1 cząsteczki – trzy rodzaje drgań) przypada nie 

1

2

k , ale 

dwa razy więcej!

Spróbujcie   dla   każdego   typu   drgań   w   cząsteczce   CH

4

  przypisać   wkład   w   ciepło 

właściwe równy k, a otrzymacie ogromną rozbieżność z doświadczeniem.

Aby to rozwiązać, musimy popatrzeć na wyniki doświadczeń. Po pierwsze: niegłupio 

byłoby się przekonać, czy ciepło właściwe gazów zależy od temperatury, a jeśli zależy, to 
jak? Pokażemy taką zależność dla trzech gazów (rys. 3):

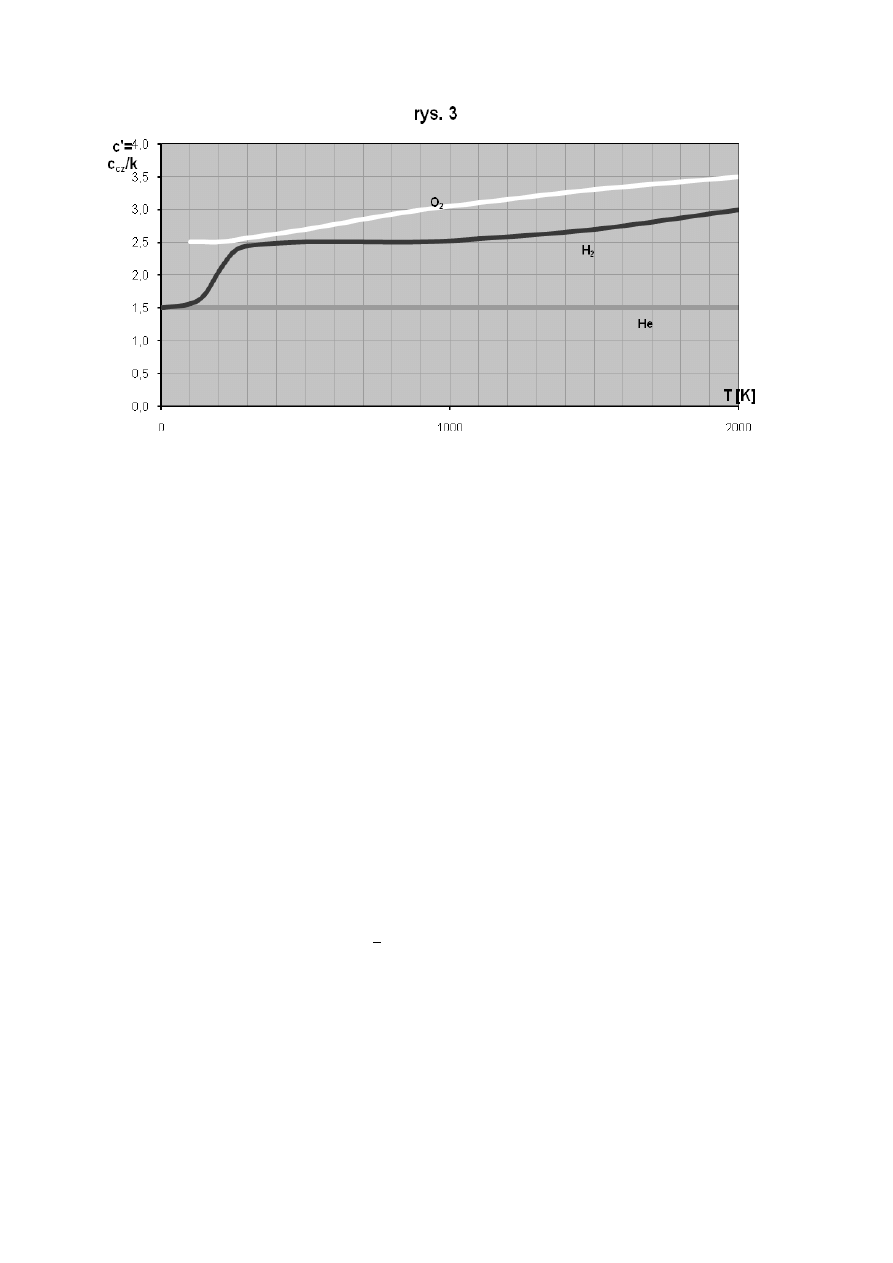
Od razu widać – w gazie jednoatomowym [He], w przedziale temperatur od bliskich 

4,2K (temp. skraplania helu) i do tysięcy stopni Kelvina ciepło właściwe jest niezmienne. Ale 
zależność dla wodoru jest zupełnie inna. W niskich temperaturach, podobnie jak dla helu, 

ciepło właściwe jest dokładnie równe 1,5k – w tym zakresie temperatur wodór zachowuje się 
jak gaz jednoatomowy. W temp. T   70K zaczyna się wzrost ciepła właściwego, i przy 250K

≈

 

osiąga ono nową, prawie stałą wartość 2,5k. Następnie gdzieś ok. 1000K zaczyna się nowy 
wzrost, i przy 2000K ciepło właściwe osiąga wartość 3k. Przy dalszym wzroście temperatury, 

ciepło właściwe nadal się zwiększa, ale nie będziemy zapuszczać się w te obszary, ponieważ 
zbyt dużo zjawisk zachodzi w gazie, gdy jest on silnie nagrzany.

Popatrzmy   lepiej   jak   zachowuje   się   tlen.   Dla   niego   pomiar   ciepła   właściwego   w 

temperaturach znacząco mniejszych od 100K nie jest możliwy, ponieważ tlen przestaje być 

gazem. Gdyby jednak tak nie było, to w niskich temperaturach ciepło właściwe także byłoby 
równe 1,5k, a tak krzywa zaczyna się na poziomie 2,5k, ale w T = 2000K zwiększa się do 

3,5k.

Jakie wnioski możemy z tego wyciągnąć?

1. Ruch postępowy cząsteczek gazu istnieje zawsze i związane z nim ciepło właściwe nie 

zależy od temperatury.

2. Obroty i drgania w niskich temperaturach zanikają (ulegają tzw. „zamrożeniu”), Przy 

tym temperatura pokojowa przypada na obszar, gdy obroty jeszcze są (np. dla wodoru 
„zamarzają” one w temp. T   100K); a drgania są już „zamrożone”.

≈

I, na koniec,

3. W  cząsteczce  tlenu   istnieje  tylko  jeden   typ  drgania,  a  ciepło   właściwe   przy  jego 

„rozmrażaniu” wzrasta nie o 

1

2

k , ale o 1k.

Liczbę tę my już spotkaliśmy – przy ciele stałym! Jak to można wytłumaczyć?

NA POMOC PRZYCHODZI KWANTOWANIE 

Okazuje się, że spawa dotyczy kwantowania. Pokażemy to przy pomocy analogii do 

jednego z najstarszych zjawisk kwantowych – emisji elektronów  z metalu.  Fotoemisja  – 

wyrzut elektronu z metalu pod wpływem światła – zachodzi tylko wtedy, gdy energia kwantu 

światła  hν  jest   większa   od   pracy   wyjścia   elektronu   z   metalu.   Ale   istnieje   również   inne 

zjawisko – termoemisja, szeroko wykorzystywana w technice (np. w kineskopie TV). W tym 
przypadku   elektrony   opuszczają   metal,   kiedy   jest   on   nagrzany   do   wysokiej   temperatury, 

takiej,   że   energia   ruchu   cieplnego   ~kT  staje   się   porównywalna   z   pracą   wyjścia.   Można 
stwierdzić,   że   emisja   jest   „zamrożona”   w   niskich   temperaturach   i   „rozmraża   się”   przy 

nagrzewaniu. Inaczej mówiąc, „zamrażanie” ruchu zachodzi wtedy, gdy do jego wzbudzenia 
należy   przekazać   jakiś   określony   kwant   energii.   I   to   jest   słuszne   zawsze,   nie   tylko   w 

przypadku emisji elektronu.

Wynika stąd: ponieważ drgania i obroty „zamrażają się” to znaczy, że ruchy te są 

skwantowane! Taki wniosek wydaje się szczególnie nieoczekiwany, gdy odniesiemy go do 
obrotów – trudno wyobrazić sobie, że cząsteczki nie mogą obracać się z dowolną (dowolnie 

małą) szybkością. Ale w mechanice kwantowej to niezaprzeczalny (niepodważalny) fakt, i 
cząsteczka albo nie obraca się wcale, albo od razu tak, że jej energia kinetyczna podzielona 

przez   stałą   Boltzmanna  k,   osiągnęła   przykładowo   wartości   dziesięciu   –   stu   kelwinów 
(dokładne liczby zależą od charakterystyk fizycznych cząsteczek konkretnej substancji).

Ale gdy chodzi o gaz zawierający dużą liczbę cząsteczek, to w nim zawsze znajdą się 

takie, które nie obracają się – ich część jest przeważająca w niskich temperaturach: istnieją 

jednak takie, które obracają się i ich udział wzrasta przy wzroście temperatury.

I tak, czysto kwantowe zjawisko wpływa na tak, wydawałoby się, typowo klasyczną 

wielkość jak ciepło właściwe gazu doskonałego.

To samo, co o obrotach, można powiedzieć o drganiach. I teraz jasne jest, że różnica 

między wkładem drgań w ciepło właściwe ciał stałych i gazów w temperaturach pokojowych 
nie ma istoty jakościowej, a ma związek z liczbowymi różnicami między substancjami. Dla 

cząsteczki   wodoru   lub   tlenu   kwant   drgania   w   skali   temperatury   równy   jest   tysiącom 
kelwinów,   a   dla   ciał   stałych   –   tylko   setkom.   I   rzeczywiście,   przy   takich   właśnie 

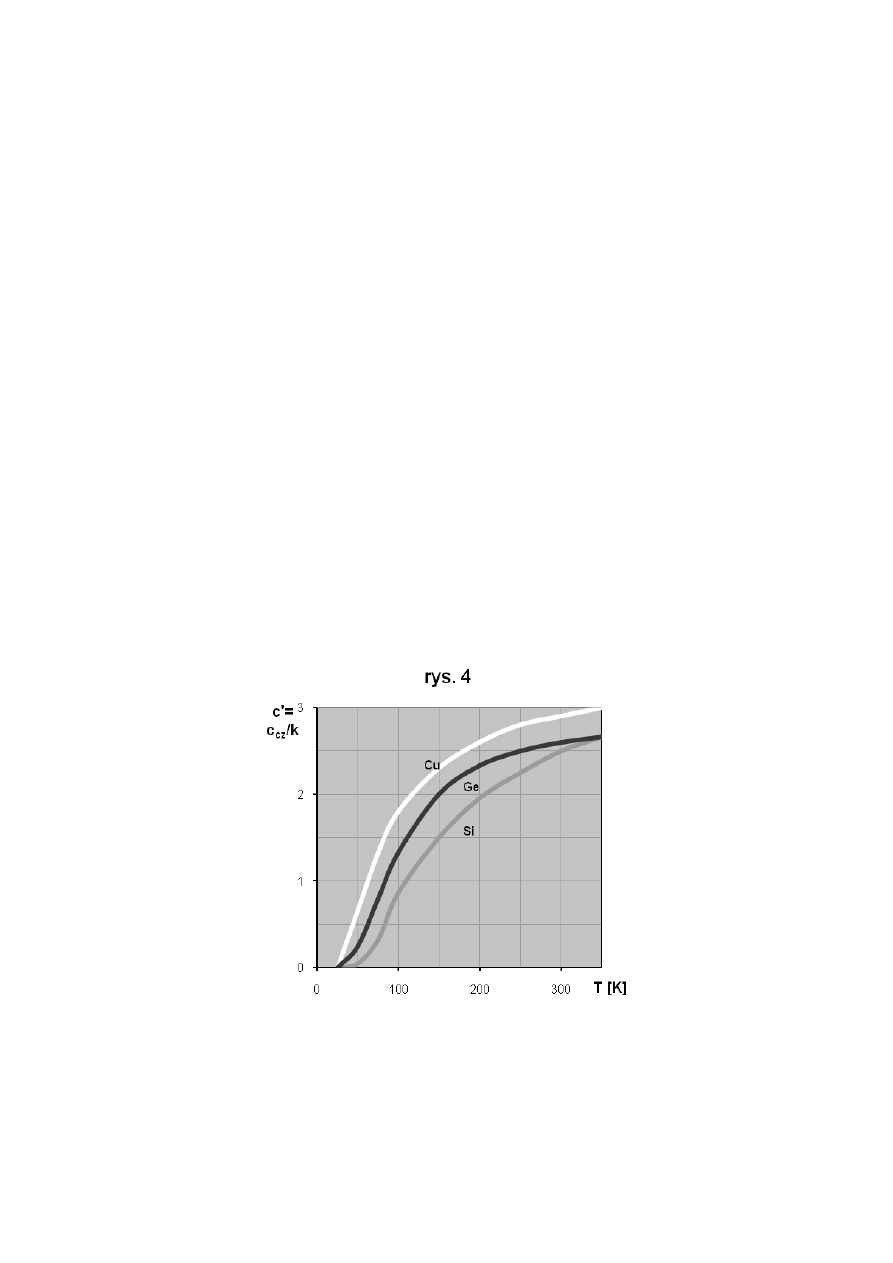
temperaturach ciepło właściwe zaczyna się szybko zmieniać (rys. 4):

I ta zbieżność liczb jest mocno związana z tym, że topnienie ciał stałych zachodzi przy 

temperaturach rzędu tysięcy stopni, a zauważalna dysocjacja cząsteczek tlenu i wodoru – przy 

dziesiątkach  tysięcy stopni. A przecież  mechanizm  obu procesów jest taki sam – jest to 
cieplne rozbudzenie drgań do takiej amplitudy, przy której „rozrywają się” wiązania, i im 

niższa   temperatura,   przy   której   następują   drgania   tym   mniejsza   również   temperatura 
rozerwania wiązania.

Oto   co   można   wywnioskować   z   analizy   ciepła   właściwego!   Do   pełnej   harmonii 

brakuje   jednego   wyjaśnienia:   jak   ułożyć   w   jeden   schemat  

1

2

k   dla   ciepła   właściwego 

związanego z ruchem postępowym i obrotowym, a 1k – dla ruchu drgającego. Okazuje się, że 
jest przepiękne wytłumaczenie. W istocie, zwróćcie uwagę, że  

1

2

k   pojawia się tam, gdzie 

ruch charakteryzuje się tylko energią kinetyczną. Ale przy drganiach istnieje jeszcze energia 

potencjalna, i jeśli pełna energia drgania jest równa kT (tj. ciepło właściwe 1k), a to znaczy, że 
układ oscylatora przechodzi ze stanu z zerową energią kinetyczną i z maksymalną energią 

potencjalną równą kT, w stan z zerową energią potencjalną i maksymalną energią kinetyczną 
także równą  kT. A średnio, w czasie, energia kinetyczna równa jest energii potencjalnej, i, 
oczywiście, obie energie mają średnią wartość 

1

2

kT  – i wróciliśmy do połówki.

I oto końcowe wnioski: w danej temperaturze wzbudzają się te typy ruchu, których 

energia kwantu równa jest kT lub od tej wartości mniejsza. Przy tym i kinetyczna energia i 
potencjalna (o ile ona jest!), przypadająca na 1 stopień swobody jest taka sama i wynosi 

1

2

kT . 

Wnioski   te   doskonale   zgadzają   się   z   wieloma   eksperymentami   i   z   teorią   wynikającą   z 
mechaniki kwantowej.

Oczywiście, że rozpatrywaliśmy przykłady najprostsze z możliwych. Możemy jednak 

zajrzeć głębiej: wyliczając stopnie swobody, rozpatrywaliśmy atomy jako proste cząsteczki, 

ale nie zawsze jest to słuszne. W każdym atomie istnieją własne wewnętrzne stopnie swobody 
ruchu elektronów w powłokach względem jąder. Jednak do ich rozmrożenia potrzeba już 

dziesiątek i setek tysięcy stopni. Fizyka plazmy bada właśnie gazy, w których „rozmrożono” 
ruch elektronów. Można pójść i dalej – również jądra zbudowane z oddzielnych cząstek 

elementarnych, a także same te cząstki niezupełnie elementarne. Ale żeby wzbudzić takie 
cieplne ruchy, potrzebne są już miliony i miliardy stopni (i jeszcze więcej), i tu zaczyna się 

ścieżka wiodąca do historii narodzin gwiazd, galaktyk i samego Wszechświata. A pierwszy 
krok na tej ścieżce – gaz doskonały ze swoimi prawami.