Ciepło właściwe gazów 

doskonałych

 

Opracowanie: dr inż. Ewa Fudalej-Kostrzewa 

1 

CIEPŁO WŁAŚCIWE GAZÓW DOSKONAŁYCH 

 

W kinetycznej teorii gazów udowodniono, że pojemność cieplna gazów doskonałych przy 

stałej objętości 

K

kmol

J

c

 

jest wielkością stałą, proporcjonalną do liczby stopni swobody 

cząsteczki gazu, a nie zależy od rodzaju gazu – a więc zależy od ilości atomów składających 

się na cząsteczkę. Na jeden stopień swobody przypada pojemność cieplna 

R

5

,

0

, czyli: 

K

kmol

J

R

f

c

5

,

0

 

gdzie: 

R

- 

uniwersalna stała gazowa, 

f 

– liczba stopni swobody cząsteczki. 

Liczba stopni swobody ruchu postępowego cząsteczek nie zależy od rodzaju cząsteczki 

i 

wynosi trzy. Cząsteczka może poruszać się w przestrzeni w trzech prostopadłych do siebie 

kierunkach. 

Liczba stopni ruchu obrotowego cząstek zależy od ilości atomów w cząstce. Cząstki 

jednoatomowe nie mają energii kinetycznej ruchu obrotowego w związku z założeniem 

nieskończenie małych rozmiarów (moment bezwładności cząsteczki względem dowolnej osi 

przechodzącej przez nią jest równy zeru).Cząsteczki dwuatomowe mają budowę liniową i mogą 

obracać się dookoła dwóch osi prostopadłych do linii łączącej atomy, przechodzących przez 

każdy z atomów. Moment bezwładności względem osi przechodzącej przez oba atomy jest 

równy zeru. Mają więc dwa stopnie swobody ruchu obrotowego. 

Cząstki trój i więcej atomowe mają trzy stopnie swobody ruchu obrotowego.  

KIlom

olowa pojemność cieplna gazów doskonałych przy stałej objętości wynosi więc: 

Gazy jednoatomowe: 

Liczba stopni swobody f 

: 3 (ruch postępowy - 3, ruch obrotowy – 0) 

K

kmol

kJ

R

R

f

c

47

,

12

7

,

8314

2

3

2

3

2

1

 

Gazy dwuatomowe: 

Liczba stopni swobody f 

: 5 (ruch postępowy - 3, ruch obrotowy – 2) 

K

kmol

kJ

R

R

f

c

787

,

20

7

,

8314

2

5

2

5

2

1

 

Gazy 

trój i wieloatomowe: 

Liczba stopni swobody f 

: 6 (ruch postępowy - 3, ruch obrotowy – 3) 

K

kmol

kJ

R

R

f

c

94

,

24

7

,

8314

2

6

2

6

2

1

 

Ciepło właściwe gazów 

doskonałych

 

Opracowanie: dr inż. Ewa Fudalej-Kostrzewa 

2 

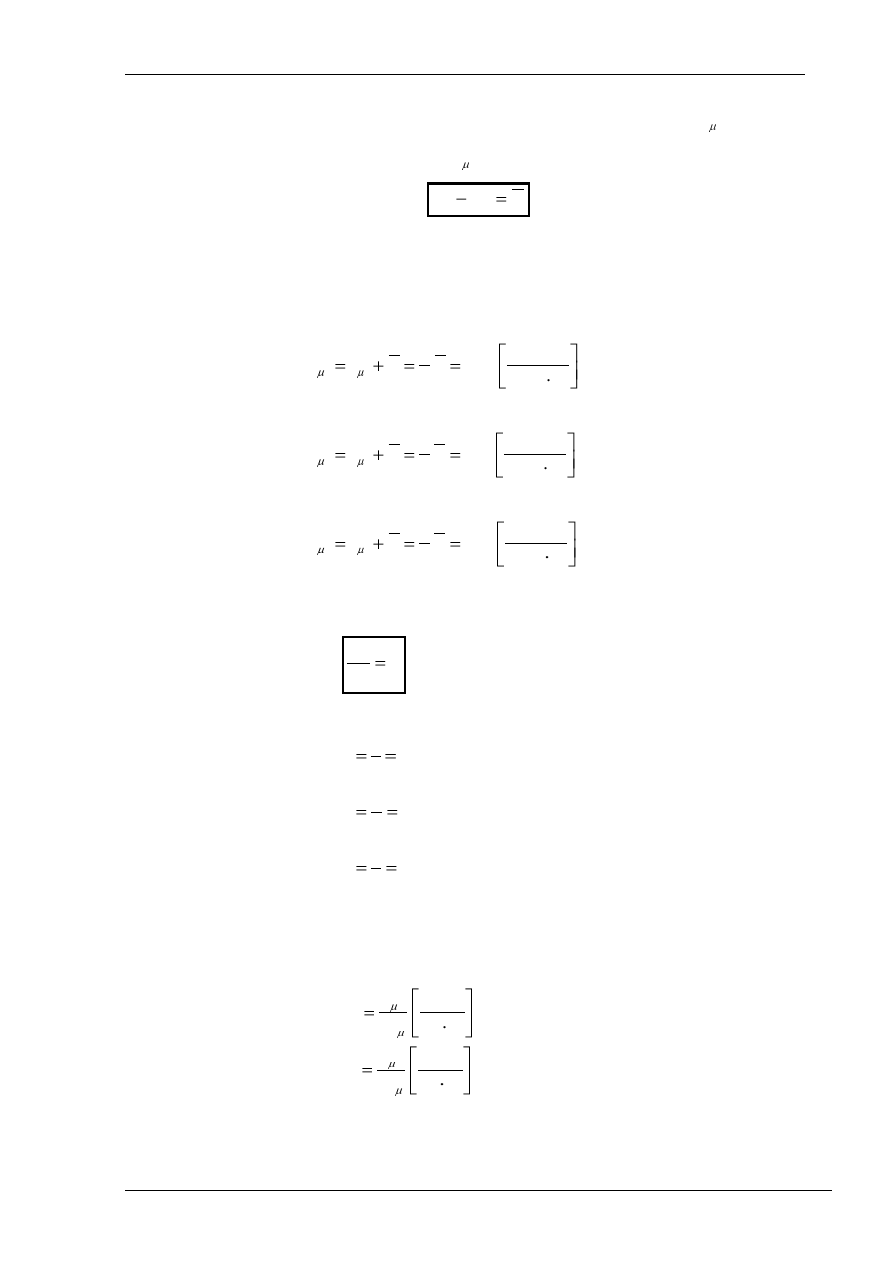
Udowodniono również, że pomiędzy pojemnością cieplną przy stałej objętości 

v

c

 

a 

pojemnością cieplną przy stałym ciśnieniu 

p

c

 

zachodzi następująca zależność: 

R

c

c

μv

μp

 

 

zwana 

równaniem Mayera. 

A zatem kilo

molowa pojemność cieplna gazów doskonałych przy stałym ciśnieniu wynosi: 

- gazy jednoatomowe: 

K

kmol

kJ

,

R

R

c

c

v

p

8

20

2

5

 

- gazy dwuatomowe: 

K

kmol

kJ

,

R

R

c

c

v

p

1

29

2

7

 

- 

gazy trój i wieloatomowe: 

K

kmol

kJ

,

R

R

c

c

v

p

3

33

2

8

 

Ciepło właściwe przy stałym ciśnieniu jest zawsze większe od ciepła właściwego przy stałej 

objętości, a ich stosunek: 

k

c

c

μv

μp

  

jest ważną wielkością w wielu zastosowaniach. I tak dla gazów: 

- jednoatomowych :    

...

,

k

666

1

3

5

 

- dwuatomowych:  

 

4

1

5

7

,

k

 

- 

trój i wieloatomowych :  

...

,

k

333

1

6

8

 

 

Znając masę kilomolową danego gazu można z ciepła kilomolowego obliczyć ciepło właściwe 

odniesione do 1 kg materii: 

K

kg

J

M

c

c

K

kg

J

M

c

c

v

v

p

p

 

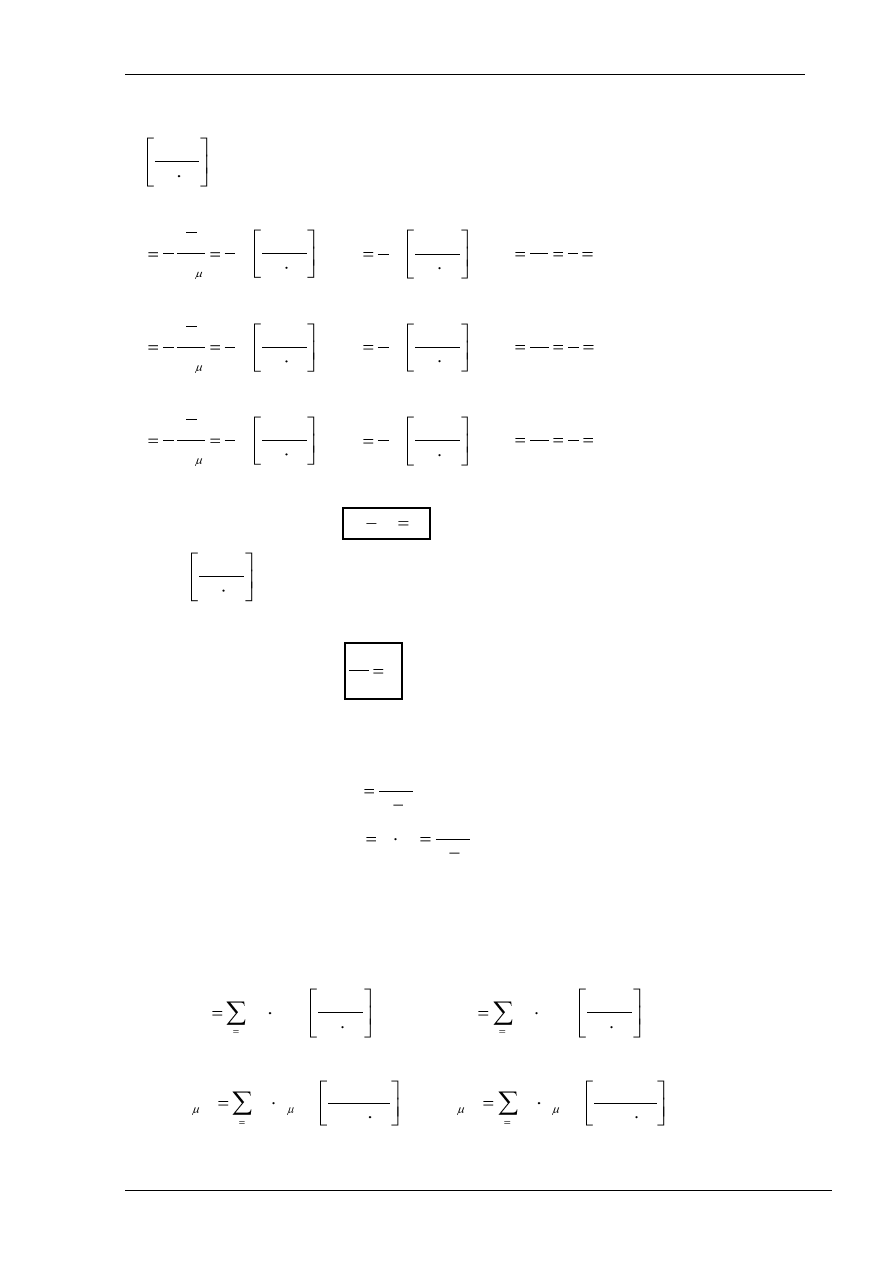
Ciepło właściwe gazów 

doskonałych

 

Opracowanie: dr inż. Ewa Fudalej-Kostrzewa 

3 

Ciepło właściwe gazów doskonałych przy stałej objętości i stałym ciśnieniu, wyrażone 

w 

K

kg

J

, wynosi więc: 

- gazy jednoatomowe: 

K

kg

J

R

M

R

c

v

2

3

2

3

 

K

kg

J

R

c

p

2

5

 

...

,

c

c

k

v

p

66

1

3

5

 

-gazy dwuatomowe: 

K

kg

J

R

M

R

c

v

2

5

2

5

 

K

kg

J

R

c

p

2

7

 

4

1

5

7

,

c

c

k

v

p

 

-

gazy trój i wieloatomowe: 

K

kg

J

R

M

R

c

v

2

6

2

6

 

K

kg

J

R

c

p

2

8

 

...

,

c

c

k

v

p

33

1

6

8

 

Równanie Mayera przyjmuje postać: 

R

c

c

v

p

   

 

 

(1) 

gdzie: 

K

kg

J

R

 - indywidualna s

tała gazowa, 

a  

k

c

c

v

p

 

 

 

 

(2) 

Zależności (1) i (2) pozwalają określić pojemność cieplną przy stałym ciśnieniu i stałej objętości 

w zależności od k i R: 

R

k

k

c

k

c

k

R

c

v

p

v

1

1

 

 

 

CIEPŁO WŁAŚCIWE ROZTWORÓW GAZÓW DOSKONAŁYCH 

Dla 1 [kg] materii: 

K

kg

J

c

g

c

vi

k

i

i

vm

1

   

K

kg

J

c

g

c

pi

k

i

i

pm

1

   

 

(3) 

Dla 1 [kmol] materii: 

K

kmol

J

c

z

c

vi

k

i

i

vm

1

 

K

kmol

J

c

z

c

pi

k

i

i

pm

1

 

 

(4) 

Ciepło właściwe gazów 

doskonałych

 

Opracowanie: dr inż. Ewa Fudalej-Kostrzewa 

4 

Wyprowadzenie zależności (3) i (4) jest przedstawione dalej. 

 

CIEPŁO WŁAŚCIWE PRZEMIAN POLITROPOWYCH 

Wykładnik przemiany politropowej m: 

 

 
 
ILOŚĆ CIEPŁA 

I

lość ciepła pochłoniętego przez czynnik można ogólnie zapisać wzorem: 

)

T

T

(

c

M

Q

1

2

2

1

 

 

jednostki: Q [J], 

c[J/(kg∙K)], T[K] 

(5) 

lub w odniesieniu do 1 kg czynnika: 

)

T

T

(

c

q

1

2

2

1

   

jednostki: q[J/kg], 

c[J/(kg∙K)], T[K]   

(6) 

gdzie: c 

– pojemność cieplna właściwa (ciepło właściwe). 

 

WYPROWA

DZENIE ZALEŻNOŚCI (3) i (4) 

Ilość ciepła pochłoniętą przez mieszaninę gazów można obliczyć jako sumę ciepeł 

pochłoniętych przez tworzące ją gazy: 

2

1

2

1

2

1

2

1

C

B

A

m

Q

Q

Q

Q

 

Załóżmy, że pochłanianie ciepła odbywa się przy stałej objętości. Zapiszemy to następująco: 

)

(

)

(

)

(

)

(

)

(

1

2

1

2

1

2

1

2

2

1

2

1

2

1

2

1

T

T

c

M

c

M

c

M

T

T

c

M

T

T

c

M

T

T

c

M

Q

Q

Q

Q

vC

C

vB

B

vA

A

vC

C

vB

B

vA

A

vC

vB

vA

vm

   

(7) 

Ciepło pochłonięte przez mieszaninę gazów można zapisać, wykorzystując (5), następująco: 

)

(

1

2

2

1

T

T

c

M

Q

vm

m

vm

 

 

 

 

 

 

 

 

 

(8) 

gdzie: M

m

 

– masa mieszaniny, 

K

kg

J

c

m

k

m

c

y

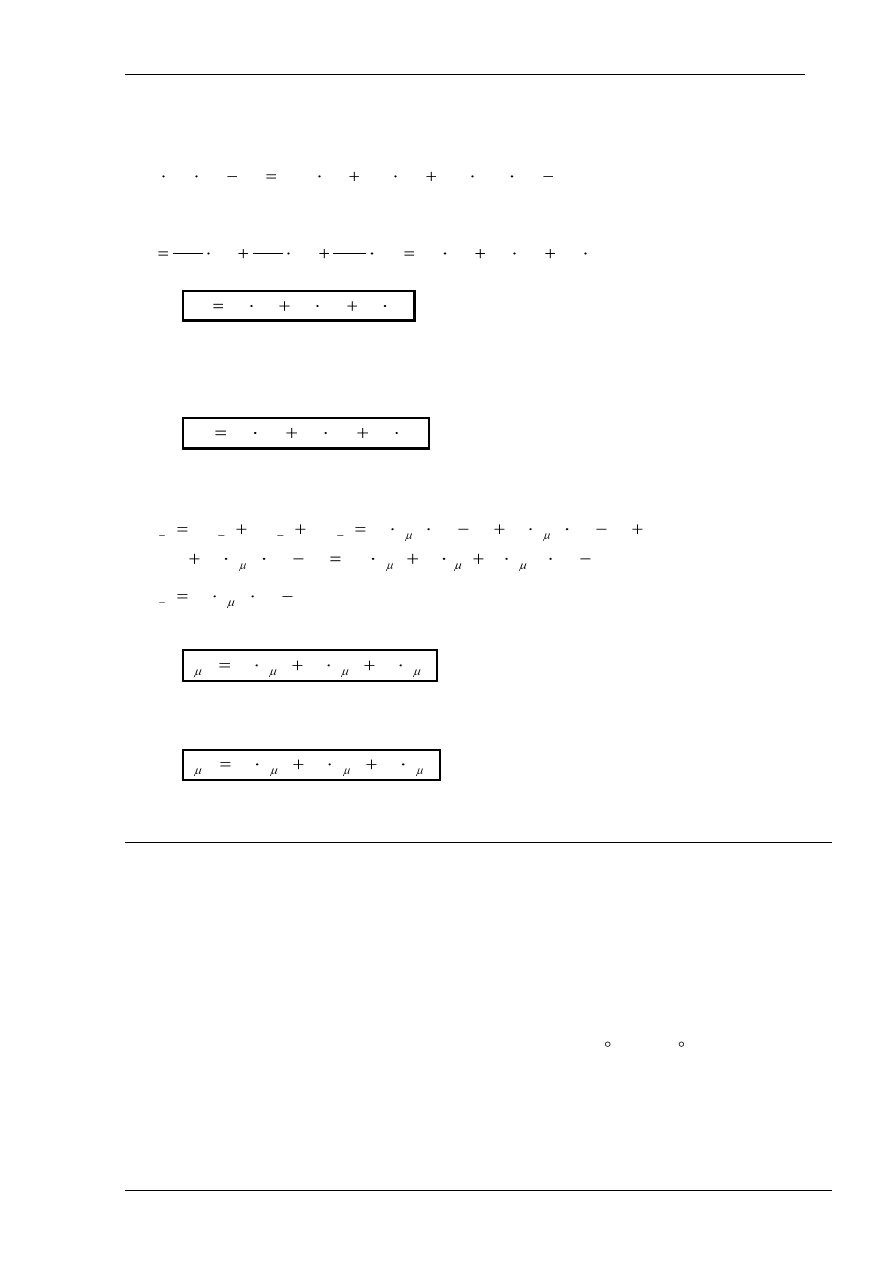
otrzymujem

k

c

c

iu

podstawien

i

c

c

m

c

c

mc

m

c

c

c

c

c

m

ceniu

przeksztal

po

c

c

c

c

m

v

v

p

v

p

v

p

v

p

v

v

p

1

:

:

)

(

)

1

(

)

(

:

Ciepło właściwe gazów 

doskonałych

 

Opracowanie: dr inż. Ewa Fudalej-Kostrzewa 

5 

c

vm

 

– ciepło właściwe mieszaniny przy stałej objętości. 

Porównując prawe strony równań (7) i (8) otrzymamy: 

)

(

)

(

)

(

1

2

1

2

T

T

c

M

c

M

c

M

T

T

c

M

vC

C

vB

B

vA

A

vm

m

 

 

 

 

(9) 

Równanie (9) można przekształcić do następującej postaci: 

vC

C

vB

B

vA

A

vC

M

C

vB

m

B

vA

m

A

vm

c

g

c

g

c

g

c

M

M

c

M

M

c

M

M

c

 

vC

C

vB

B

vA

A

vm

c

g

c

g

c

g

c

 

ciepło właściwe mieszaniny przy stałej objętości 

 

Zakładając, że pochłanianie ciepła odbywa się przy stałym ciśnieniu i dokonując takich 

samych przekształceń otrzymuje się zależność: 

pC

C

pB

B

pA

A

pm

c

g

c

g

c

g

c

 

ciepło właściwe mieszaniny przy stałym ciśnieniu 

 

Stosując zapis molowy ciepła pochłanianego przy stałej objętości: 

)

(

)

(

)

(

)

(

)

(

1

2

1

2

1

2

1

2

2

1

2

1

2

1

2

1

T

T

c

n

c

n

c

n

T

T

c

n

T

T

c

n

T

T

c

n

Q

Q

Q

Q

vC

C

vB

B

vA

A

vC

C

vB

B

vA

A

vC

vB

vA

vm

 

)

(

1

2

2

1

T

T

c

n

Q

vm

m

vm

 

i dokonując przekształceń otrzymuje się: 

vC

C

vB

B

vA

A

vm

c

z

c

z

c

z

c

  

ciepło kilomolowe mieszaniny przy stałej objętości 

 

W przypadku 

pochłaniania ciepła przy stałym ciśnieniu otrzymuje się: 

pC

C

pB

B

pA

A

pm

c

z

c

z

c

z

c

 

ciepło kilomolowe mieszaniny przy stałym ciśnieniu 

 

 
 

ZADANIA 

Zadanie 1 

Obliczyć ciepło właściwe izochoryczne i izobaryczne azotu N

2

. 

Odp.: c

p

 = 1050 J/(kg

∙K), c

v

 = 750 J/(kg

∙K) 

 

Zadanie 2 

Podczas pewnej przemiany gaz d

oskonały został ogrzany od 100 C do 200 C, pobierając 

130 

kJ ciepła. Obliczyć ciepło właściwe gazu podczas tej przemiany, jeśli wiadomo, że ilość 

gazu wynosi 1,5 kg. 

Odp.: c = 867 J/(kg

∙K) 

Ciepło właściwe gazów 

doskonałych

 

Opracowanie: dr inż. Ewa Fudalej-Kostrzewa 

6 

 

Zadanie 3 

W pewnej przemianie 1 kg gazu oddał do otoczenia Q = 37 kJ ciepła. Wiadomo, że cały proces 

odbywał się przy stałym cieple właściwym c = 650 J/(kg∙K). Obliczyć spadek temperatury gazu. 

Odp.:  T = 57 K. 

 

Zadanie 4 

Obliczyć ciepło właściwe jednoatomowego gazu doskonałego w przemianie politropowej 

o 

wykładniku n = 2,1. Stała gazowa R = 208 J/(kg∙K). 

Odp.: c = 122,9 J/(kg

∙K) 

 

Zadanie 5 

Ile ciepła wymienia z otoczeniem wodór w przemianie politropowej o wykładniku m = 1,7 

realizowanej w zakresie temperatur od 300K do 500K. Potraktować wodór jako gaz doskonały. 

Odp.: q = 890,8 kJ/kg 

 

Zadanie 6 

Obliczyć ciepło właściwe tlenu przy stałym ciśnieniu i przy stałej objętości oraz przy przemianie 

politropowej o wykładniku 2. Potraktować tlen jako gaz doskonały. 

Odp.: c

p

 = 918,8 J/(kg

∙K), c

v

 = 656,3 J/(kg

∙K), c = 393,8 J/(kg∙K) 

 

Zadanie 7 

Wyznaczyć ciepło właściwe izochoryczne jednoatomowego gazu doskonałego o masie 

kilomolowej M  

= 40 kg/kmol. Na podstawie wyznaczonej wartości ciepła właściwego obliczyć 

stałą gazową tego gazu. 

Odp.: c

v

 = 315 J/(kg

∙K), R = 210 J/(kg∙K)