Geodezja i Geoinformatyka Grupa IV para VI	Nr ćwiczenia 27
Marta Piotrowska	Temat ćwiczenia: WYZNACZANIE STOSUNKU MOLOWEGO CIEPŁA WŁAŚCIWEGO GAZU PRZY STAŁYM CIŚNIENIU DO MOLOWEGO CIEPŁA WŁAŚCIWEGO TEGO GAZU PRZY STAŁEJ OBJĘTOŚCI (Cp/Cv)
Piotr Łukaszczuk

1. WPROWADZENIE TEORETYCZNE.

Gaz jest to stan skupienia materii, w którym ciało fizyczne łatwo zmienia kształt i zajmuje całą dostępną mu przestrzeń co wynika z własności cząsteczek, które w fazie gazowej mają pełną swobodę ruchu. Wszystkie one cały czas przemieszczają się w przestrzeni zajmowanej przez gaz i nigdy nie zatrzymują się w jednym miejscu. Między cząsteczkami nie występują żadne oddziaływania dalekozasięgowe, a jeśli, to bardzo słabe. Jedyny sposób, w jaki cząsteczki na siebie oddziałują, to zderzenia. Jeśli gaz jest zamknięty w naczyniu, to jego cząsteczki stale zderzają się ze ściankami tego naczynia, wywierając na nie określone i stałe ciśnienie. Przy zderzeniach sprężystych ze ścianką naczynia zachodzi zmiana pędu cząsteczek gazu. Zgodnie z II zasadą dynamiki zmiana pędu ciała równa się popędowi siły. Cząsteczki gazu przemieszczają się z różną szybkością. Średnia szybkość poruszania się cząsteczek w gazie jest zależna wyłącznie od ich masy molowej i temperatury. Podczas obniżania temperatury gazu maleje średnia szybkość cząsteczek, zaś zwiększanie ciśnienia powoduje zmniejszenie średniej odległości między nimi. W fizyce przyjmuje się często prosty model gazu doskonałego, w którym cząsteczki gazu nie przyciągają się i nie mają objętości własnej. Gaz doskonały jest to gaz spełniający następujące warunki:

1. brak oddziaływań międzycząsteczkowych w gazie, z wyjątkiem odpychania w momencie zderzeń cząsteczek;

2. objętość cząsteczek jest znikoma w stosunku do objętości gazu;

3. zderzenia cząsteczek są doskonale sprężyste.

Termodynamika to dział fizyki zajmujący się badaniem energetycznych efektów wszelkich przemian fizycznych i chemicznych, które wpływają na zmiany energii analizowanych układów. Wbrew rozpowszechnionym sądom termodynamika nie zajmuje się wyłącznie przemianami cieplnymi, lecz także efektami energetycznymi reakcji chemicznych, przemian z udziałem jonów, przemianami fazowymi, a nawet przemianami jądrowymi. Termodynamika klasyczna zajmuje się badaniem wcześniej wspomnianych zjawisk, tylko z punktu widzenia energetycznych efektów makroskopowych, nie wnikając w naturę tych przemian na poziomie pojedynczych cząsteczek. Termodynamika statystyczna próbuje wyjaśniać prawa i zjawiska badane przez termodynamikę klasyczną na poziomie rozważań cząsteczkowych.

Energia wewnętrzna w termodynamice (oznaczana zwykle jako U, lub E_p) to część energii układu zależna tylko od jego stanu wewnętrznego, stanowi ona sumę energii oddziaływań międzycząsteczkowych i wewnątrzcząsteczkowych układu, energii potencjalnych wynikających z oddziaływań międzycząsteczkowych oraz energie kinetyczne ruchu postępowego, drgającego, obrotowego (temperatura wiąże się tylko z energią kinetyczną)

Jest jednym z parametrów (potencjałów) termodynamicznych. Według I zasady termodynamiki energia wewnętrzna stanowi jednoznaczną funkcje stanu (funkcje zależną wyłącznie od stanu układu, która nie zależy od stanu poprzedniego), którą dla gazu można wyrazić przez dowolne dwa z trzech parametrów; ciśnienie, temperaturę, objętość.

Energia termiczna, zwana też energią cieplną to ta część energii wewnętrznej układu, która może być przekazywana innemu układowi w formie ciepła.

Ciepło w termodynamice to forma przekazywania energii termicznej. Relacja między energią termiczną a ciepłem jest taka sama jak między pracą i energią w mechanice. Cieplnym odpowiednikiem określenia "wykonanie pracy na układzie" jest określenie "wystąpienie przepływu ciepła". Ciepło przepływa między ciałami, które znajdują się w stosunku do siebie w nierównowadze termicznej, zwykle wtedy, gdy posiadają one różną temperaturę. W niektórych, szczególnych przypadkach może ono jednak także przepływać między ciałami o tej samej temperaturze.

Pierwsza zasada termodynamiki to prosta zasada zachowania energii, czyli ogólna reguła głosząca, że energia w żadnym procesie nie może pojawić się "znikąd".

gdzie:

ΔU - zmiana energii wewnętrznej

W - praca

Q - ciepło

Praca i ciepło są formami przekazywania energii i są wyrażane w dżulach (1J = 1N ∙ 1m). Przy czym praca jest w gruncie rzeczy ilością pracy, a ciepło - ilością ciepła (praca i ciepło to ilości energii dostarczanej do układu). Przyczyną przekazywania energii w postaci ciepła jest różnica temperatur miedzy dwoma układami lub między częściami jednego układu. Praca W jest dodatnia, gdy wykonywana jest nad układem. Ujemna zaś, gdy układ wykonuje prace. Wielkość w jest dodatnia, gdy ciepło jest dostarczane do układu. Ujemna zaś, gdy układ oddaje ciepło.

Temperatura istnieje tylko jako pojecie, nie posiada cech substancjalnych. Temperatura to funkcja stanu w termodynamice, która podobnie jak ciepło jest związana z sumaryczną energią kinetyczną ruchu i drgań wszystkich cząsteczek tworzących dany układ. Wprowadzono to pojęcie w celu określenia stanu chaotycznego ruchu cząsteczek danego ciała, a dokładnie w celu określenia wspomnianej wcześniej energii kinetycznej związanej z chaotycznym ruchem cząsteczek.

Temperatura jest miarą "chęci" do dzielenia się ciepłem. Jeśli dwa ciała mają tę samą temperaturę, to w bezpośrednim kontakcie nie przekazują sobie ciepła, gdy zaś mają różną temperaturę, to następuje przekazywanie ciepła z ciała o wyższej temperaturze do ciała o niższej - aż do wyrównania się temperatur obu ciał. W technice jednostką najczęściej używaną jest Kelwin [K] (T[K] = t[°C] + 273.15 ).W USA natomiast najczęściej spotykamy się z temperaturą wyrażoną w stopniach Fahrenheit'a (t[°C] = (5/9) · (t_F[°F] - 32))

gdzie:

- średnia energia kinetyczna cząsteczek danego układu, przeliczona na jedną cząsteczkę tego układu

k - stała Boltzmana dla gazu doskonałego (1,380658(12) ∙ 10^-23 J/K)

Jest to wzór Boltzmana dla gazu doskonałego

gdzie:

R - stała gazowa

N - stała Avogarda (6,0221367(36) × 10²³ 1/mol)

T - temperatura mierzona w skali bezwzględnej (Kelwina)

Powyższy zapis jest wprawdzie praktyczny, gdyż łatwiej jest mierzyć temperaturę niż wartość energii ruchu cząsteczek ciała, w rzeczywistości jednak to nie energia zależy od temperatury, lecz odwrotnie - temperatura jest funkcją energii.

Wzór na średnią energię kinetyczną (zamieszczony wcześniej) jest słuszny tylko dla jednej cząsteczki układu, o trzech stopniach swobody (trzy niezależne zmienne opisujące jednoznacznie stan układu fizycznego). Dla n - liczby cząstek wzór będzie wyglądał następująco:

a dla dowolnej liczby stopni:

gdzie i oznacza liczbę stopni swobody

T nie zależy od n, gdyż E jest wprost proporcjonalne do n, czyli w danych warunkach

Jeden mol jest to liczność materii, mającej taką samą liczbę cząstek ile jest atomów zawartych w 12 gramach izotopu węgla ¹²C

Ciepłem właściwym c jakiejś substancji nazywamy wielkość fizyczną, liczbowo równą ilości ciepła, jaką należy doprowadzić do kg masy tej substancji, aby podwyższyć jej temperaturę o 1 K. Jednostką ciepła właściwego jest J/(kg ⋅ K). Ciepło właściwe jest współczynnikiem określającym skłonność ciała do łatwiejszej lub trudniejszej zmiany temperatury pod wpływem dostarczonej energii cieplnej

Molowym ciepłem właściwym nazywamy ilość energii cieplnej jaka musimy dostarczyć do układu aby podnieść temperaturę jednego mola substancji o jeden Kelwin. Jednostką molowego ciepła właściwego jest J/(mol ⋅ K)

W przypadku gazów ciepło właściwe zależy od rodzaju przemiany gazu, dlatego dla gazów wprowadzono pojęcie ciepła właściwego przy stałym ciśnieniu (C_p) i przy stałej objętości (C_v),

Dla gazu doskonałego, którego cząsteczki mają trzy stopnie swobody, ciśnienie p wyraża się wzorem:

gdzie:

n₀ - liczba cząsteczek gazu w jednostce objętości

m - masa jednej cząsteczki

V - średnia prędkość cząsteczek

Powyższy wzór jest podstawowym równaniem teorii kinetyczno-molekularnej. Jeżeli do tego wzoru wprowadzimy gęstość ρ, równą liczbowo masie jednostkowej (n₀m), to wyrażenie na ciśnienie p przyjmie postać:

Z tego wynika, że ciśnienie jakie wywiera gaz na ścianki naczynia, jest proporcjonalne do kwadratu średniej prędkości chaotycznego ruchu cząsteczek tego gazu.

Gaz doskonały opisuje równanie Clapeyrona, przedstawiające zależność między ciśnieniem gazu, jego objętością i temperaturą.

gdzie:

V_μ - objętość jednego mola gazu

R - stała gazowa (8,32 J/(K ⋅ mol))

T - temperatura w skali bezwzględnej

Zgodnie z kinetyczno - molekularną teorią gazu doskonałego definicję temperatury T można zapisać następująco:

gdzie E jest średnią energią kinetyczną chaotycznego ruchu cząsteczek gazu.

Z powyższego wynika, że temperatura gazu jest proporcjonalna do średniej energii kinetycznej chaotycznego ruchu cząsteczek tego gazu.

Związek średniej energii kinetycznej ruchu postępowego cząsteczek gazu z temperaturą można otrzymać z równania:

Jeśli pomnożymy obustronnie powyższe równanie przez objętość jednego mola V_μ otrzymamy:

Liczba n₀ V_μ określa liczbę cząsteczek gazu w objętości jednego mola, jest zatem równa liczbie Avogadra N. Wobec tego można zapisać:

Tworzymy układ równań, w których lewe strony są sobie równe:

Zatem:

stąd:

Przy czym R/N = k to wspomniana wcześniej stała Boltzmanna. Ostatecznie otrzymujemy wyrażenie na średnią energię kinetyczną cząsteczek gazu w funkcji temperatury, które ma postać:

Cząsteczki gazu mają trzy stopnie swobody. Na każdy stopień swobody cząsteczki przypada średnio taka sama energia kinetyczna, równa ½ kT. Jest to tzw. prawo ekwipartycji energii.

Procesy adiabatyczne są to takie przemiany gazowe, które zachodzą bez wymiany ciepła z otoczeniem, czyli Q = 0

I zasada termodynamiki przyjmuje postać:

gdzie:

∆U - wzrost lub ubytek energii wewnętrznej, zależnie od znaku W.

Energia wewnętrzna 1 mola gazu doskonałego jako funkcja temperatury ma postać:

Przyrost energii wewnętrznej na skutek zmiany temperatury oblicza się przez zróżniczkowanie powyższego równania względem temperatury:

Praca, jaką wykonuje gaz przy adiabatycznym zwiększeniu objętości o dowolnie małą wartość dV, równa się:

Dla dowolnie małych zmian energii wewnętrznej dU pierwszą zasadę termodynamiki dla procesów adiabatycznych można zapisać w postaci:

Wartość ciśnienia, jakie wywiera gaz na ścianki naczynia, wynika z równania Clapeyrona:

Podstawiając tę wielkość do równania
i przekształcając je otrzymamy:

Całkując powyższe równanie w granicach zmian objętości i temperatury

Otrzymujemy równanie Poissona

lub

gdzie:

Z równania tego wynika, że przy adiabatycznej zmianie objętości gazu następuje zmiana jego temperatury. Wartość C_p jest większa od C_V o wartość pracy, jaką gaz wykonuje przy zwiększeniu objętości dla zachowania stałego ciśnienia podczas ogrzewania i jeden stopień.

Obliczamy wartość pracy W, zakładając że gaz jest zamknięty w naczyniu z ruchomym tłokiem.

Ogrzewając gaz objętość jego wzrośnie o ΔV_μ , czyli tłok przesuwa się o Δh. Praca jaką wykonał gaz przesuwając tłok o powierzchni S na odcinku Δh, obliczymy ze wzoru:

gdzie V'_μ jest objętością gazu po rozprężeniu, więc:

Jeżeli gaz ogrzejemy o jeden stopień, to podstawiając do powyższego równania

otrzymujemy z układu:

czyli:

Stała gazowa R jest równa liczbowo pracy wykonanej przez jeden mol gazu doskonałego pod stałym ciśnieniem przy rozprężeniu podczas ogrzewania go o jeden stopień.

W tym ćwiczeniu do obliczania stosunku C_p / C_V posługujemy się dużym naczyniem szklanym wypełnionym powietrzem pod ciśnieniem nieco wyższym od atmosferycznego.

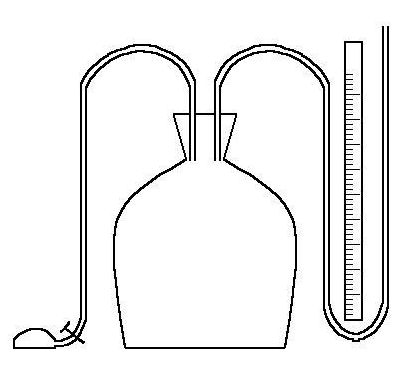
Otwierając korek K i po chwili zamykając ciśnienie gazu w naczyniu zrówna się z ciśnieniem atmosferycznym. Proces ten zachodzi bardzo szybko więc możemy uważać z dobrym przybliżeniem, że przy przejściu ze stanu I do stanu II nastąpiło adiabatyczne rozprężenie gazu.

gdzie:

p - ciśnienie atmosferyczne

V₁ - objętość gazu przed rozprężeniem

V₂ - objętość gazu po rozprężeniu

Przy adiabatycznym rozprężeniu gaz ulega oziębieniu. Po pewnym czasie, na skutek wymiany ciepła z otoczeniem, temperatura gazu w naczyniu zrówna się z temperaturą otoczenia i wytworzy się nadwyżka ciśnienia p₂. Objętość nie ulega zmianie, a więc przy przejściu ze stanu II do stanu III mamy przemianę izochoryczną. Przejście ze stanu I do III jest procesem izotermicznym, ponieważ w obu stanach temperatura gazu równa się temperaturze otoczenia. Słuszne jest tu równanie Boyle'a i Mariotte'a.

tak więc:

rozwijając ln(p +p₁) na szereg mamy:

Podobnie rozwijamy ln(p +p₂). W związku z tym, że p >> p₁ oraz p >> p₂, wyrazy drugiego i wyższych rzędów opuszczamy, a więc

Nadciśnienia p₁ i p₂ można wyrazić za pomocą różnicy poziomów cieczy w h₁ i h₂ nanometrze

gdzie:

ρ - gęstość cieczy

g - przyspieszenie ziemskie.

II. WYKONANIE DOŚWIADCZENIA.

Nr. pomiaru	t°C	h1 [m]	h2 [m]	h1 - h2 [m]	ℵ

ΔV_μ

T, V_μ

Δh

K

B

P

Z

M

P - pompka

Z - zaworek

K - korek

B - pojemnik

M - manometr

---