
Matematyka dyskretna (tryb zaoczny) – cz. I
Wy sza Szkoła Komunikacji i Zarz dzania w Poznaniu
1
TEORIA GRAFÓW
Z
- zbiór liczb całkowitych
{
}
,...
2
,
1
,
0
,
1
,
2
...,
−
−
=
Z
+
Z - zbiór liczb całkowitych dodatnich
{
}
,...
2
,
1
−
Z - zbiór liczb całkowitych ujemnych
{
}
1
,
2
...,
−
−
R
- zbiór liczb rzeczywistych
Funkcje całkowitoliczbowe
Z
R
f
→
:
1)
Funkcja podłoga („floor”)
{
}
x
n
Z
n
n
x
≤
∧
∈
=
:
max
2
2
=
1
75
.
1
=
3
75
.
2
−
=
−
2
=
e
4
−
=
−
π
2)
Funkcja sufit („ceiling”)
{
}
x
n
Z
n
n
x
≥
∧
∈
=
:
min
Najmniejsza liczba całkowita, która jest wi ksza b d równa x
1
5
.
0
=
2
75
.
2
−
=
−
4
=
π
je eli
N
n
∈ , to
n
n
=
je eli
N
n
∉ , to
1
=
= n
n
[ ]
x - cz
całkowita x
[ ]
x
x
=
x
x
−
≠
−
Własno ci:
1.
x
x
−
=
−
2.
1
1
+
<
≤
≤
<
−
x
x
x
x
x
3.
R
x
∈ ,
Z
n
∈
1
+
<
≤
⇔
=
n
x
n
n
x
4.
x
n
x
n
x
<
<
−
⇔
=
1
5.
n
x
n
n
x
≤
<
−
⇔
=
1
6.
1
+
<
≤
⇔
=
x
n
x
n
x
7.
n
x
n
x
+
=
+
Z
n
∈
8.
n
x
n
x
+
=
+
Z
n
∈
5
3
2
3
3
=
+
=
+
=
+
e
e
1
3
2
2
2
−
=
−
=
−
+
=
−
π
π
3
−
=
−
π
Matematyka dyskretna (tryb zaoczny) – cz. I
Wy sza Szkoła Komunikacji i Zarz dzania w Poznaniu
2
Niech
R
y
x
∈
,
y
x
+
y
x
+
3
40
.
3
95
.
1
45
.
1
=
=
+
2
1
1
95
.
1
45
.
1
=
+
=
+
--
Mantysa liczby, cz
ułamkowa
{ } ( )
x
x
x
m
x
−
=
=
{ }
{ }
x
x
x
x
+
=
<
≤
1
0
np.
{ }
25
.
0
3
25
.
3
25
.
3
25
.
3
25
.
3
=
−
=
−
=
{
}
( )
75
.
0
4
25
.
3
25
.
3
25
.
3
25
.
3
=
−
−
−
=
−
−
−
=
−
Przykłady zastosowa :
+
∈ N
n
m - długo słowa w zapisie dwójkowym
10
2
1
1
m
= 1
2
10
m
= 2
3
11
m
= 3
(
)
1
log
1
log
2
2
+
=
+
=
n
n
m
4
100
m
= 3
8
=
n
4
?
=
=
m
5
101
m
= 3
4
1
3
1
8
log
2
=
+
=
+
6
110
m
= 3
2
log
3
2
log
8
log
2
3
2
2
=
=
7
111
m
= 3
( )
4
1699
.
3
1
8
log
2
=
=
+
32000
=
n
?
=
m
15
1
14
1
...
9658
.
14
1
32000
log
2
=
+
=
+
=
+
R
R
f
→
:
funkcja rosn ca okre lona na liczbach rzeczywistych
( ) ( )
2
1
2
1
x
f
x
f
x
x
<
<
( )
( )
x
f
x
f
=
( )
( )
x
f
x
f
=
np.
0
>
x
( )
x
x
f
=
2
2
4
75
.
4
75
.
4
=
=
=
=
4
4
16
99
.
15
99
.
15
=
=
=
=
3
10
24
.
10
24
.
10
=
=
=
--
Liczby Kuuth’a
Liczby zdefiniowane wzorem rekurencyjnym
1
0
=
k

Matematyka dyskretna (tryb zaoczny) – cz. I
Wy sza Szkoła Komunikacji i Zarz dzania w Poznaniu
3
⋅
⋅
+
=
+
3
2
1
3
,
2
min
1
n
n
n
k
k
k
(
)
3
2
1
3
,
2
min
1
3
,
2
min
1
0
0
3
1
2
1
1
1
2
=
+
=
⋅
⋅
+
=
⋅
⋅
+
=
=
+
k
k
k
k
k
k
(
)
4
3
1
3
,
2
min
1
3
,
2
min
1
0
1
3
2
2
2
1
2
3
=
+
=
⋅
⋅
+
=
⋅
⋅
+
=
=
+
k
k
k
k
k
k
(
)
3
2
1
3
,
2
min
1
3
,
2
min
1
0
0
3
0
2
0
1
0
1
=
+
=
⋅
⋅
+
=
⋅
⋅
+
=
=
+
k
k
k
k
k
k
Z
m
n
∈
,
n
m
m
n
m
n
m
n
m
n
=
−
−
+
+
−
+
−
+
)
1
(
...
2
1
np. n = 18 m = 4
m składników
18
4
4
5
5
75
.
3
4
25
.
4
5
4
4
3
18
4
2
18
4
1
18
4
18
=
+
+
+
=
+
+
+
⋅
=
−
+
−
+
−
+
--
S – zbiór liczbowy
S
S
× - produkt kartezja ski dwóch zbiorów
A
,
B
- zbiory
( )
{
}
B
b
A
a
b
a
B
A
∈
∈
=
×
,
:
,
( )
{
}
S
b
S
a
b
a
S
S
∈
∈
=
×
,
:
,
S
S
R
×
⊂
Relacja binarna = dowolny podzbiór produktu kartezja skiego
( )
R
b
a
∈
,
= aRb
element a jest w relacji binarnej R z elementem b
--
Relacja kongruencji (relacja przystawania)
p
mod
, gdzie
Z
p
∈
)
(
n
m
−
jest wielokrotno ci liczby p, tzn. e istnieje liczba k taka, e
p
k
n
m
⋅
=
− )
(
(
)
p
n
m
mod
≡
6
=
p
33
=
m
15
=
n
(
)
?
6
mod
15
33
≡
6
3
18
⋅
=
k p
(
)
p
k
n
m
⋅
=
−
(
)
6
15
33
⋅
=
−
k
6
18
⋅
= k

Matematyka dyskretna (tryb zaoczny) – cz. I
Wy sza Szkoła Komunikacji i Zarz dzania w Poznaniu
4
3
6
18 =
=
k
Te dwie liczby (33, 15) przystaj do siebie
6
mod
(
)
?
7
mod
12
33
≡
tak
(
)
?
7
mod
40
33
≡
tak
(
)
?
7
mod
19
33
≡
tak
Dwie liczby przystaj do siebie, je eli istnieje takie k, e
p
k
n
m
⋅
=
− )
(
(
)
(
)
p
n
m
mod
≡
Liczba m przystaje do liczby n
p
mod
, je eli obie te liczby s podzielne przez p (maj tak
sam reszt z dzielenia)
r
– reszta z dzielenia
r
p
k
m
+
⋅
=
0
≥
> r
p
p
r
<
≤
0
17
=
m
3
=
p
2
3
5
17
+
⋅
=
17
−
=
m
3
=
p
1
3
6
17
+
⋅
−
=
−
r
p
j
n
+
⋅
=
(
)
(
)
p
j
k
p
j
p
k
r
p
j
r
p
k
n
m
⋅
−
=
⋅
+
⋅
=
+
⋅
−
+
⋅
=
−
(
)
p
k
n
m
⋅
=
−
załó my, e
1
r
p
l
m
+
⋅
=
2
r
p
j
n
+
⋅
=
(
)
(
)
2
1
r
r
p
j
l
n
m
−
+
⋅
−
=
−
0
2
1
=
− r
r
2
1
r
r
=
p
r
<
≤
1
0
p
r
<
≤
2
0
p
r
r
p
<
−
<
−
2
1
Podstawowe własno ci relacji przystawania
1.
m
jest w relacji przystawania z samym sob
2.
Je eli
(
)
p
n
m
mod
≡
, to
(
)
p
m
n
mod
≡
-
własno symetrii
)
6
(mod
15
33
≡
6
15
33
⋅
=
−
k
6
18
⋅
= k
k
=
6
18
3
=
k
6
33
13
⋅
=
−
k
6
18
⋅
=
−
k
k
=
−
6
18
3
−
=
k
3.
Je eli
(
)
p
n
m
mod
≡
oraz
(
)
p
s
n
mod
≡
, to wówczas
(
)
p
s
m
mod
≡
-
własno
przechodnio ci
Z
m
∈
Z
p
∈
1
>
p
(
)
p
m
m
mod
≡
własno ci zwrotno ci

Matematyka dyskretna (tryb zaoczny) – cz. I
Wy sza Szkoła Komunikacji i Zarz dzania w Poznaniu
5
np.
Ka da relacja, która jest zwrotna, symetryczna i przechodnia jest relacj
równowa no ci.
--
S
x
∈
[ ]
x
- zbiór wszystkich elementów zbioru S, które s w relacji R z elementem x.
(R – relacja równowa no ci)
S
y
x
∈
,
[ ]
x
[ ]
y
albo
[ ] [ ]
y
x
=
albo
[ ] [ ]
0
=
∧ y
x
[ ]
(
)
{
}
p
n
x
m
x
p
mod
:
≡
=
p
– ilo klas
1
0
≤
≤ r
np.
2
=
p
2
2
4
)
4
(
0
⋅
=
=
−
−
[ ]
{
}
,...
4
,
2
,
0
,
2
,
4
...,
0
2
−
−
=
2
3
6
)
4
(
2
⋅
=
=
−
−
[ ]
{
}
,...
6
,
4
,
0
,
2
,
4
...,
2
2
−
−
=
[ ]
{
}
,...
6
,
4
,
0
,
2
,
4
...,
4
2
−
−
=
[ ]
2
4 - klasa wyznaczona przez 4, gdzie
2
=
p
[ ] [ ] [ ]
...
4
2
0
2
2
2
=
=
=
- zbiór liczb parzystych
[ ] [ ] [ ]
...
5
3
1
2
2
2
=
=
=
- zbiór liczb rzeczywistych
3
=
p
[ ]
3
0
=
r
{
}
,...
9
,
6
,
3
,
0
,
3
,
6
,
9
...,
−
−
−
1
=
r
{
}
,...
10
,
7
,
4
,
1
,
2
,
5
,
8
...,
−
−
−
2
=
r
{
}
,...
11
,
8
,
5
,
2
,
1
,
4
,
7
...,
−
−
−
[…]
( )
( )
(
)
⇔
=
n
g
O
n
f
istnieje
0
>
C
takie, e
( )
( )
n
g
C
n
f
⋅
=
dla dost. du ych warto ci n
3)
Je eli
( )
( )
( )
n
a
O
n
f
=
i
( )
( )
( )
( ) ( )
( ) ( )
(
)
n
b
n
a
O
n
g
n
f
n
b
O
n
g
⋅
=
⋅
=
(
)
6
mod
15
33
≡
(
)
6
mod
9
15
≡
(
)
6
mod
9
33
≡
6
15
33
⋅
=
−
k
6
9
15
⋅
=
−
k
6
9
33
⋅
=
−
k
6
18
⋅
= k
6
6
⋅
= k
6
24
⋅
= k
k
=
6
18
k
=
6
6
k
=
6
24
3
=
k
1
=
k
4
=
k

Matematyka dyskretna (tryb zaoczny) – cz. I
Wy sza Szkoła Komunikacji i Zarz dzania w Poznaniu
6
Istnieje takie C, e
( )
( )
n
a
C
n
f
⋅
≤
Istnieje takie D, e
( )
( )
n
a
D
n
g
⋅
≤
( ) ( )
( ) ( )
( )
( )
( ) ( )
( ) ( )
n
b
n
a
E
n
b
n
a
D
C
n
b
D
n
a
C
n
g
n
f
n
g
n
f
⋅
⋅
=
⋅
⋅
⋅
=
⋅
⋅
⋅
≤
⋅
=
⋅
( ) ( )
( ) ( )
n
b
n
a
E
n
g
n
f
⋅
⋅
≤
⋅
( ) ( )
( ) ( )
(
)
n
b
n
a
O
n
g
n
f
⋅
=
⋅
4)
Je eli
( )
( )
( )
( )
( ) ( )
(
)
(
)
n
b
n
a
O
n
b
O
n
a
O
,
max
=
+
( )
( )
( )
n
a
O
n
f
=
to znaczy, e istnieje takie C, e
( )
( )
n
a
C
n
f
⋅
≤
( )
( )
( )
n
b
O
n
g
=
to znaczy, e istnieje takie D, e
( )
( )
n
a
D
n
g
⋅
≤
( ) ( )
( )
( )
( )
( )
( ) ( )
{
}
( ) ( )
{
}
(
)
( ) ( )
{
}
n
b
n
a
D
C
n
b
n
a
D
n
b
n
a
C
n
g
D
n
a
C
n
g
n
f
n
g
n
f
,
max
,
max
,
max
⋅
+
=
⋅
+
⋅
≤
≤
⋅
+
⋅
≤
+
≤
+
( )
( ) ( )
{
}
n
b
n
a
n
a
,
max
≤
( )
( ) ( )
( )
{
}
n
b
n
a
n
b
,
max
≤
( ) ( )
( ) ( )
{
}
(
)
n
b
n
a
O
n
g
n
f
,
max
=
+
( )
( )
( )
n
a
O
n
f
=
( )
( )
( )
n
b
O
n
g
=
5)
( )
( )
( )
( )
( ) ( )
(
)
n
b
n
a
O
n
b
O
n
a
O
⋅
=
=
Je eli
( ) ( )
n
b
n
a
=
to
( )
( )
[
]
( )
[ ]
(
)
2
2
n
a
O
n
a
O
=
np.
( )
( )
[
]
2
2
n
O
n
O
=
--
Notacja
Ω
( )
( )
(
)
⇔
Ω
=
n
g
n
f
gdy istnieje takie C, e
( )
( )
n
g
C
n
f
⋅
≥
dla dostatecznie du ych n
( )
( )
n
g
C
n
f
⋅
≤
2
1
:
( )
( )
( )
n
f
D
n
f
C
n
g
⋅
=
⋅
≤ 1
( )
( )
( )
( )
(
)
n
f
O
n
g
n
f
D
n
g
=
⋅
≤
( )
( )
(
)
( )
( )
(
)
n
f
O
n
g
n
g
n
f
=
⇔
Ω
=
--
Notacja
Θ (teta)
( )
( )
(
)
( )
( )
(
)
n
g
O
n
f
n
g
n
f
=
⇔
Θ
=
oraz
( )
( )
(
)
n
g
n
f
Ω
=
Je eli np.
( )
1
=
n
g
to istnieje
0
>
C
takie, e
( )
( )
C
n
g
C
n
f
=
⋅
≤

Matematyka dyskretna (tryb zaoczny) – cz. I
Wy sza Szkoła Komunikacji i Zarz dzania w Poznaniu
7
Istnieje
0
>
D
takie, e
( )
( )
D
n
g
D
n
f
=
⋅
≥
--
Własno o
( )
( )
(
)
⇔
=
n
g
o
n
f
dla ka dego
0
>
ε
istnieje
0
n zale ne od
ε
takie, e dla ka dego
0
n
n
>
( )
( )
n
g
n
f
⋅
≤
ε
( )
n
f
0
, gdy
∞
→
n
(
( )
n
f
d y do 0, gdy n d y do
∞
)
10
1
=
ε
4
1
100
1
10
2
⋅
≤
n
2
100n
⋅
--
Liczby pierwsze
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41
∏
=
k
n
k
k
P
n
...
7
5
3
2
2
0
0
0
1
⋅
⋅
⋅
⋅
=
...
7
5
3
2
4
0
0
0
2
⋅
⋅
⋅
⋅
=
...
7
5
3
2
6
0
0
1
1
⋅
⋅
⋅
⋅
=
Ka d liczb mo na tak przedstawi
∏
=
k
n
m
k
k
k
P
n
m
NWD
)
,
min(
)
,
(
najwi kszy wspólny dzielnik
Ile jest liczb pierwszych?
Dowód: załó my, e jest sko czona ilo liczb pierwszych (k)
k
P
,...,
5
,
3
,
2
1
...
3
2
+
⋅
⋅
⋅
=
k
P
M
M nie dzieli si przez 2
M nie dzieli si przez 3
…
M nie dzieli si przez
k
P
Co to znaczy? Albo M jest liczb pierwsz (wi ksz od
k
P ), czyli nieprawda, e
k
P jest
ostatni liczb pierwsz , albo istnieje liczba
k
P
P
>
, która jest liczb pierwsz i jest
dzielnikiem liczby M.

Matematyka dyskretna (tryb zaoczny) – cz. I
Wy sza Szkoła Komunikacji i Zarz dzania w Poznaniu
8
--
Liczby Euklidesa
( )
e
2
1
1
1
=
+
=
e
- liczba pierwsza
3
1
2
2
=
+
=
e
- liczba pierwsza
(5 nie jest liczb Euklidesa)
7
1
2
1
3
=
+
⋅
=
e
e
e
- liczba pierwsza
43
1
3
2
1
4
=
+
⋅
⋅
=
e
e
e
e
- liczba pierwsza
1807
1
43
7
3
2
1
4
3
2
1
5
=
+
⋅
⋅
⋅
=
+
⋅
⋅
⋅
=
e
e
e
e
e
- nie liczba pierwsza
139
13
1807
⋅
=
(13 i 139 to liczby pierwsze)
3263443
1
5
4
3
2
1
6
=
+
⋅
⋅
⋅
⋅
=
e
e
e
e
e
e
- liczba pierwsza
31051
1033
607
547
0807
1065005695
7
⋅
⋅
⋅
=
=
e
(547, 607, 1033 i 31051 to liczby
pierwsze)
Zbadano dotychczas do
17
e (wszystkie do
17
e s liczbami pierwszymi)
264
.
1
=
E
n
a
E
n
=
+
2
1
2
1
=
n
1
2
2
2
097696
.
2
5
.
0
5977696
.
1
10
5
264
.
1
10
5
1
a
E
=
=
=
+
=
+
=
+
2
=
n
2
4
2
3
...
0526
.
3
5
.
0
264
.
1
5
.
0
264
.
1
2
a
=
=
=
+
=
+
Istnieje P takie, e n-ta liczba pierwsza jest postaci
n
P
P
n
2
=
P – n-ta liczba pierwsza
1)
1
ln
lim
=
⋅
∞
→
n
n
P
n
x
2)
( )
x
π
- ilo liczb pierwszych nieprzekraczaj cych liczby x
( )
1
ln
lim
=
∞
→
x
x
x
x
π
3)
( )
2
1
ln
2
3
ln
−
<
<
−
x
x
x
x
π
( )
x
π
⋅
67
≥
x
( )
( )
x
x
x
x
x
π
π
⋅
−
<
<
⋅
−
2
1
ln
2
3
ln
( )
2
3
ln
2
1
ln
−
<
<
−
x
x
x
x
x
π
np.
67
=
x
ile jest liczb pierwszych < 67?
( )
2
1
67
ln
67
67
2
3
67
ln
−
<
<
−
π

Matematyka dyskretna (tryb zaoczny) – cz. I
Wy sza Szkoła Komunikacji i Zarz dzania w Poznaniu
9
( )
705
.
3
67
67
705
.
2
<
<
π
67
1
⋅
( )
769
.
24
67
705
.
2
67
<
<
π
( )
19
67
=
π
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71
19 20
80
=
x
ile jest liczb pierwszych < 80?
( )
22
80
=
π
( )
2
3
80
ln
80
2
1
80
ln
80
−
<
<
−
x
π
( )
759
.
27
618
.
20
<
< x
π
759
.
27
22
618
.
20
<
<
n-ta liczba pierwsza:
( )
( )
(
)
( )
( )
(
)
−
+
⋅
<
<
−
+
⋅
2
1
ln
ln
ln
2
3
ln
ln
ln
n
n
n
P
n
n
n
n
20
>
n
np. dla
20
=
n
:
( )
( )
(
)
( )
( )
(
)
−
+
<
<
−
+
⋅
2
1
20
ln
ln
20
ln
2
3
20
ln
ln
20
ln
20
20
P
( )
( )
−
+
⋅
<
<
−
+
≈
⋅
2
1
3
ln
3
20
2
3
3
ln
3
20
20
P
1
.
1
0986
.
1
)
3
ln(
≈
≈
−
⋅
<
<
−
⋅
2
1
1
.
4
20
2
3
1
.
4
20
20
P
6
.
3
20
6
.
2
20
20
⋅
<
<
⋅
P
72
32
20
<
< P
Setna liczba pierwsza:
( )
( )
(
)
( )
( )
(
)
−
+
⋅
<
<
−
+
⋅
2
1
100
ln
ln
100
ln
100
2
3
100
ln
ln
100
ln
100
100
P
23
.
563
236
.
463
100
<
< P
--
Liczby wzgl dnie pierwsze:
m n = m jest wzgl dnie pierwsze w stosunku do n
Je eli
1
)
,
(
=
n
m
NWD
∏
=
k
m
k
k
P
m
∏
=
k
n
k
k
P
n
dla ka dego k
0
)
,
min(
=
k
k
n
m
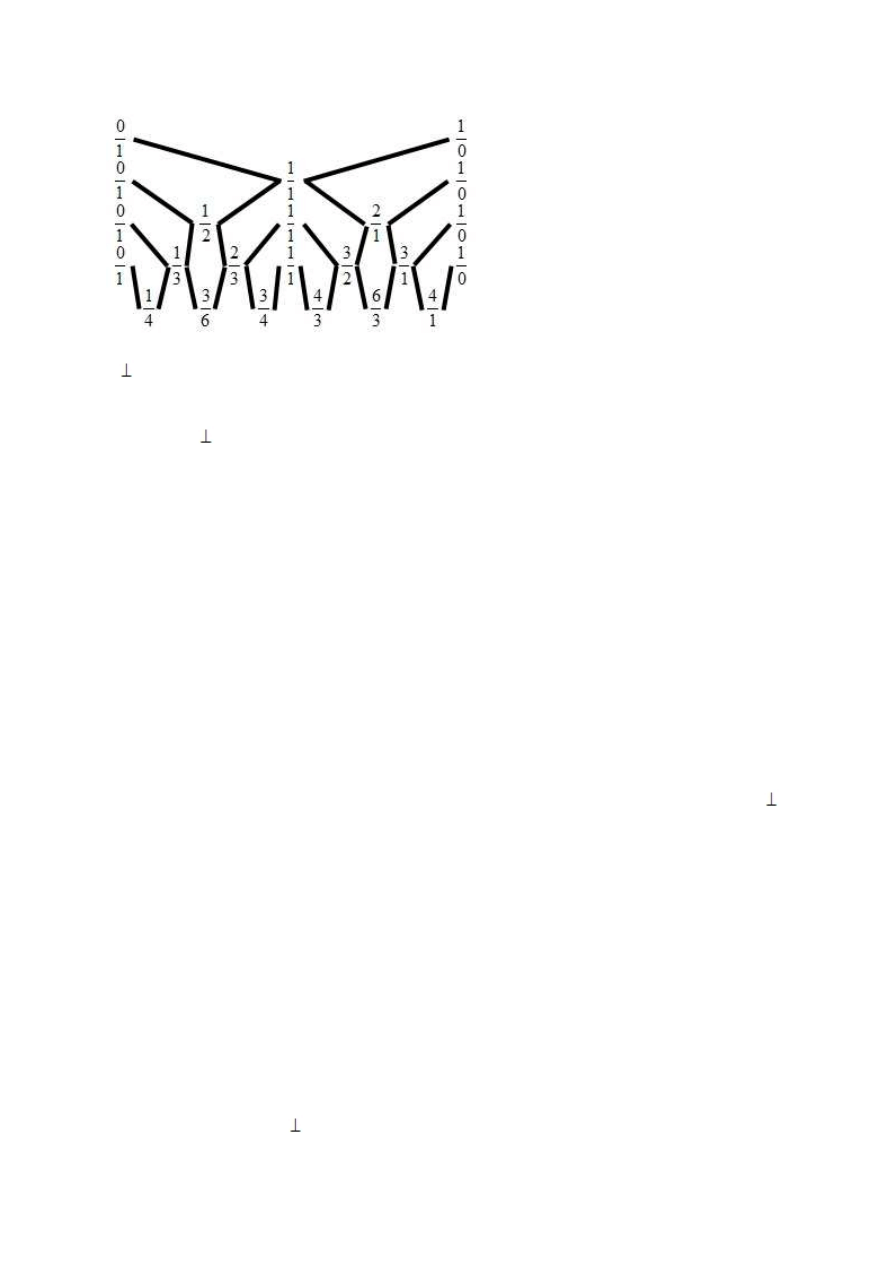
Drzewo liczb wzgl dnie pierwszych
Mediant ułamków, np.
n
m
n
m
′
′
,
mediantem tych ułamków nazywamy
n
n
m
m
′
+
′
+
(mediant
≠ suma ułamków)
Matematyka dyskretna (tryb zaoczny) – cz. I
Wy sza Szkoła Komunikacji i Zarz dzania w Poznaniu
10
Je eli dwie liczby s wzgl dnie pierwsze to…
m n
( )
n
m
n
m
NWW
⋅
=
,
NWW – najwi ksza wspólna wielokrotno
Własno ci m n:
(
)
(
)
m
b
a
n
m
b
a
mod
[
mod
≡
⇔
⋅
≡
oraz
(
)
]
mod n
b
a
≡
(
)
n
b
a
mod
≡
- istnieje k takie, e
(
)
n
k
b
a
⋅
=
−
(
) (
)
n
b
n
a
m
b
a
mod
mod
)
(mod
=
⇔
≡
mod = reszta z dzielenia
np.
1
4
mod
101
=
1
4
mod
201
=
1
25
mod
101
=
1
25
mod
201
=
)
4
(mod
201
101
≡
)
25
(mod
201
101
≡
(
)
(
)
25
4
mod
201
101
⋅
≡
(
)
100
mod
201
101
≡
(
)
(
)
(
)
[
]
n
b
a
m
b
a
n
m
b
a
mod
mod
mod
≡
∧
≡
⇔
⋅
≡
Mamy liczb m. Ile jest liczb n, które s mniejsze od m oraz s wzgl dnie pierwsze od n (m
n) (ile jest ułamków nieskracalnych)?
Tocjent
( )
n
ϕ
( )
n
f
= liczba Eulera
-
( )
1
1
=
f
- je eli p jest liczb rzeczywist , to
( )
1
−
= p
p
f
- je eli m nie jest liczb pierwsz (jest liczb zło on ), to
( )
1
−
< m
m
f
--
Własno ci funkcji Eulera
1.
Je eli P jest liczb pierwsz , a
1
>
k
, to
( )
1
−
−
=
k
k
k
P
P
P
f
2.
Je eli m da si przedstawi w postaci
2
1
m
m
⋅
, przy czym
1
m jest wzgl dnie pierwsze
w stosunku do
2
m , to
( ) ( ) ( )
2
1
m
f
m
f
m
f
⋅
=
2
1
m
m
m
⋅
=
1
m
2
m
( ) ( ) ( )
2
1
m
f
m
f
m
f
⋅
=

Matematyka dyskretna (tryb zaoczny) – cz. I
Wy sza Szkoła Komunikacji i Zarz dzania w Poznaniu
11
( )
m
f
jest odpowiedzi na postawione wcze niej pytanie.
np.
( )
1
1
2
2
=
−
=
f
2
1
<
( )
2
1
3
3
=
−
=
f
3
2
,
1
<
3
2
,
3
1
- nieskracalne ułamki
( )
( )
2
2
4
2
2
2
4
1
2
2
=
−
=
−
=
= f
f
4
3
,
4
1
( )
4
1
5
5
=
−
=
f
( ) ( ) ( ) ( )
2
2
1
3
2
3
2
6
=
⋅
=
⋅
=
⋅
=
f
f
f
f
6
5
,
6
1
( ) ( ) ( ) ( )
( )
( )
8
4
2
5
2
5
4
5
4
20
2
=
⋅
=
⋅
=
⋅
=
⋅
=
f
f
f
f
f
f
( )
=
n
d
d
f
n
n=12
Dzielniki:
12
,
6
,
4
,
3
,
2
,
1
=
d
1
=
d
( )
1
=
d
f
2
=
d
( )
1
2
=
f
3
=
d
( )
2
3
=
f
2 z 3 w mianowniku
4
=
d
2
)
4
(
=
f
2 z 4 w mianowniku
6
=
d
( )
2
6
=
f
12
=
d
( )
( )
( ) ( )
4
3
4
3
2
12
2
=
⋅
=
⋅
=
f
f
f
f
1+1+2+2+2+4=12
Spr.:
12
11
6
5
4
3
3
2
12
7
2
1
12
5
3
1
4
1
6
1
12
1
12
0
12
11
12
10
12
9
12
8
12
7
12
6
12
5
12
4
12
3
12
2
12
1
12
0
1
=
d
2
=
d
--
Liczby Fibonacci’ego
0
.
0
def
F
=
1
1
=
F
2
1
−
−
+
=
n
n
n
F
F
F
2
≥
n
1
0
1
0
1
2
=
+
=
+
=
F
F
F
2
1
1
3
=
+
=
F
3
1
2
4
=
+
=
F
5
2
3
5
=
+
=
F
8
3
5
6
=
+
=
F
13
5
8
7
=
+
=
F

Matematyka dyskretna (tryb zaoczny) – cz. I
Wy sza Szkoła Komunikacji i Zarz dzania w Poznaniu
12
21
8
13
8
=
+
=
F
34
13
21
9
=
+
=
F
Własno ci:
1.
Je eli
0
>
n
, to
( )
n
n
n
n
F
F
F
1
2
1
1
−
=
−
⋅
−
+
( ) ( )
n
n
n
n
F
F
F
1
2
1
1
−
=
−
⋅
−
+
Dowodzenie metod indukcji matematycznej
1.
sprawdzenie wzoru dla najmniejszej warto ci n
2.
zakładaj c prawdziwo wzoru dla
k
n
= nale y pokaza , e wzór jest prawdziwy dla
wzoru
1
+
= k
n
1
=
n
( ) ( )
1
2
1
0
2
1
−
=
−
⋅
F
F
F
1
1
0
1
2
−
=
−
⋅
1
1
−
=
−
P
L
=
Zało enie:
( ) ( )
n
n
n
n
F
F
F
1
2
1
1
−
=
−
⋅
−
+
Musimy pokaza , e
( ) ( )
1
2
1
2
1
+
+
+
−
=
−
⋅
k
k
k
k
F
F
F
( ) ( )
1
2
1
2
1
+
+
+
−
=
−
−
k
k
k
k
F
F
F
( )
(
)
( )
( )
(
)
( )
(
)
(
)
( )
( ) ( )
( ) ( )
( ) ( )
(
) ( )
(
)
[
]
( )
( ) ( )
P
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
L
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
=
−
=
−
−
=
−
−
+
−
⋅
=
−
−
−
−
⋅
=
=
−
−
−
⋅
−
−
+
⋅
=
−
−
−
⋅
−
−
⋅
+
=
=
−
+
−
⋅
−
−
⋅
=
⋅
+
−
⋅
−
−
⋅
=
=
−
⋅
−
−
⋅
=
+
−
⋅
=
−
⋅
=
+
−
+
−
+
−
+
−
+
−
+
−
−
−
+
−
−
+
−
+
+
+
1
1
1
1
1
2
1
2
2
1
2
1
2
1
2
1
2
2
1
1
1
2
2
2
1
1
2
2
2
1
2
2
1
2
1
1
1
1
1
1
1
2
P
L
=
6
=
n
7
=
n
( ) ( )
6
2
6
1
6
1
6
1
−
=
−
⋅
−
+
F
F
F
( ) ( )
7
2
7
6
8
1
−
=
−
⋅
F
F
F
1
8
2
5
7
=
−
⋅ F
F
1
13
8
21
2
−
=
−
⋅
1
64
5
13
=
−
⋅
1
169
168
−
=
−
1
64
65
=
−
1
1
−
=
−
1
1
=
P
L
=
P
L
=
Kolejne własno ci:
2.
Dla ka dego n i ka dego
0
>
k
,
n
k
n
k
k
n
F
F
F
F
F
⋅
+
⋅
=
−
+
+
1
1
n
k
=
(
)
1
1
1
2
−
+
−
+
⋅
=
⋅
−
=
n
n
n
n
n
n
n
F
F
F
F
F
F
F
4
=
n
3
5
4
8
F
F
F
F
+
⋅
=
(
)
2
5
3
21
+
⋅
=
4
8
7 F
F
⋅
=
(
)
(
)
[
]
1
2
1
1
1
1
2
1
1
1
1
2
1
2
2
3
−
+
−
+
−
+
−
+
−
+
+
+
⋅
+
=
−
+
⋅
+
⋅
=
⋅
+
⋅
=
=
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
n
k
F
⋅
jest wielokrotno ci
n
F
--
Matematyka dyskretna (tryb zaoczny) – cz. I
Wy sza Szkoła Komunikacji i Zarz dzania w Poznaniu
13
Funkcja tworz ca dla ci gów liczbowych
n
a
a
a
a
,...,
,
,
2
1
0
- ci g liczbowy
( )
i
i
i
Z
z
a
F
⋅
=
∞
=0
tzw. funkcje tworz ce dla ci gów liczbowych
Dla jakich z, dla których suma istnieje
1
=
i
a
,...
1
,
1
,
1
Jak wygl da funkcja tworz ca dla tego ci gu?
q
a
S
S
−
=
=
∞
1
1
1
<
q
( )
z
z
F
i
i
z
−
=
+
+
+
+
=
⋅
=
∞
=
1
1
...
2
2
2
1
1
3
2
0
przy zało eniu, e
1
<
z
( )
!
)
(
i
z
F
a
i
i
−
=
0
=
z
Jak wygl da taki szereg dla ci gu Fibonacci’ego?
0
0
=
F
0
Z
⋅
0
0
=
F
1
1
=
F
1
Z
⋅
Z
Z
F
=
⋅
1
1
0
1
2
=
+
=
F
F
F
2
Z
⋅
2
0
2
1
2
2
Z
F
Z
F
Z
F
⋅
+
⋅
=
⋅
2
1
2
3
=
+
=
F
F
F
3
Z
⋅
2
1
3
2
3
3
Z
F
Z
F
Z
F
⋅
+
⋅
=
⋅
3
2
3
4
=
+
=
F
F
F
4
Z
⋅
4
2
4
3
4
4
Z
F
Z
F
Z
F
⋅
+
⋅
=
⋅
5
3
4
5
=
+
=
F
F
F
5
Z
⋅
5
3
5
4
5
5
Z
F
Z
F
Z
F
⋅
+
⋅
=
⋅
(
) (
)
...
...
1
...
2
2
1
0
2
3
3
2
2
1
4
4
3
3
2
2
1
0
+
⋅
+
⋅
+
+
+
⋅
+
⋅
+
⋅
+
=
+
⋅
+
⋅
+
⋅
+
⋅
+
Z
F
Z
F
F
Z
Z
F
Z
F
Z
F
Z
Z
F
Z
F
Z
F
Z
F
F
( )
(
)
( )
2
2
2
2
1
0
0
...
1
F
Z
Z
F
Z
F
F
F
F
Z
F
⋅
+
+
⋅
+
⋅
+
+
−
=
( )
( )
( )
Z
F
Z
Z
F
Z
Z
Z
F
⋅
+
⋅
+
=
2
( )
2
1
1
Z
Z
Z
F
−
−
=
dla z takich, e
0
1
2
≠
−
−
Z
Z
0
1
2
=
−
−
Z
Z
0
1
2
=
−
+ Z
Z
( )
5
1
4
1
=
−
⋅
−
=
∆
5
=
∆
2
5
1
1
−
=
Z
2
5
1
2
−
=
Z
Ta funkcja jest dla
2
5
1
+
≠
Z
i dla
2
5
1
−
≠
Z
Liczba
Φ - liczba „złotego podziału”
( )
(
)
n
n
n
F
Φ
−
Φ
=
ˆ
5
1

Matematyka dyskretna (tryb zaoczny) – cz. I
Wy sza Szkoła Komunikacji i Zarz dzania w Poznaniu
14
(
) (
)
(
) (
)
−
−
+
⋅
⋅
=
−
−
+
=
5
5
5
5
5
5
5
5
1
5
1
32
5
1
2
5
1
2
5
1
5
1
F
--
Dwumian Newtona (pozwala wyliczy
(
)
n
b
a
+
)
(
)
=
−
⋅
⋅
=
+
n
k
k
n
k
n
b
a
k
n
b
a
0
Symbol Newtona -
(
)
!
!
!
.
k
n
k
n
k
n
def
−
⋅
=
1
!
0
.
def
=
(
)
0
2
1
0
...
2
1
0
b
a
n
n
b
a
n
b
a
n
b
a
n
b
a
k
n
b
a
k
n
k
n
k
n
k
k
n
k
n
k
n
⋅
⋅
+
+
⋅
⋅
+
⋅
⋅
+
⋅
⋅
=
⋅
⋅
=
+
−
−
−
=
(
)
2
2
0
2
1
1
2
2
2
0
2
2
2
2
1
2
0
2
a
ab
b
b
a
b
a
b
a
b
a
k
n
b
a
k
k
n
k
+
+
=
⋅
⋅
+
⋅
⋅
+
⋅
⋅
=
⋅
⋅
=
+
=
−
(
)
(
)
( )
(
)
(
)
3
2
2
3
3
2
2
3
0
3
1
2
2
1
3
0
3
3
3
2
3
2
1
3
1
0
3
0
3
0
3
3
0
3
3
3
1
!
3
!
3
1
!
2
!
3
!
2
1
!
3
!
3
1
!
3
!
3
3
!
3
!
3
!
2
3
!
2
!
3
!
1
3
!
1
!
3
!
0
3
!
0
!
3
3
3
2
3
1
3
0
3
3
a
b
a
ab
b
a
b
a
b
a
b
b
a
b
a
b
a
b
a
b
a
b
a
b
a
b
a
b
a
k
b
a
k
n
b
a
k
k
k
k
n
k
k
+
+
+
=
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
=
⋅
⋅
−
+
⋅
⋅
−
+
⋅
⋅
−
+
⋅
⋅
−
⋅
=
=
⋅
⋅
+
⋅
⋅
+
⋅
⋅
+
⋅
⋅
=
=
⋅
⋅
=
⋅
⋅
=
+
−
−
−
−
=
−
−
=
(
) (
)
(
) (
)
( )
( )
( )
( )
( )
( )
( )
( )
( )
[
]
5
16
80
5
80
5
16
1
5
5
5
50
5
25
5
16
1
5
1
4
5
2
5
1
2
5
2
5
0
5
2
32
5
1
5
1
5
5
5
1
4
5
5
1
3
5
5
1
2
5
5
1
1
5
5
1
0
5
32
5
1
5
1
5
1
32
5
1
2
5
1
2
5
1
5
1
4
3
2
5
0
5
1
4
2
3
3
2
4
1
5
0
5
5
5
5
5
5
5
=
=
⋅
=
=
+
+
⋅
=
⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
=
=
−
⋅
⋅
+
−
⋅
⋅
+
−
⋅
⋅
+
−
⋅
⋅
+
−
⋅
⋅
+
−
⋅
⋅
⋅
⋅
⋅
=
=
−
−
+
⋅
⋅
=
−
−
+
⋅
=
F
( )
5
5
5
3
=
!
5
!
0
!
5
0
5
⋅
=
5
16
80
5
2
=
=
!
1
!
4
!
5
4
5
⋅
=
(
)
6765
ˆ
5
1
20
20
20
=
Φ
−
Φ
⋅
=
F
1134903170
45
=
F
Dowolna liczba n daje si przedstawi w postaci pewnej sumy liczb Fibonacci’ego

Matematyka dyskretna (tryb zaoczny) – cz. I
Wy sza Szkoła Komunikacji i Zarz dzania w Poznaniu
15
r
k
k
k
F
F
F
n
+
+
+
=
...
2
1
r
k
k
k
>
>
>
...
2
1
55
144
46368
121393
832040
1000000
10
12
24
26
30
+
+
+
+
=
+
+
+
+
=
F
F
F
F
F
=
⋅
=
0
10
k
k
k
b
n
( )
=
⋅
=
0
2
2
k
k
k
b
n
0
(
=
k
b
lub
)
1
n – liczba dziesi tna
2
n - liczba w systemie dwójkowym
( )
=
⋅
=
m
k
k
k
F
F
b
n
2
0
=
k
b
lub
1
n
F
n
F
m
m
>
∧
<
+1
( )
1
1
=
F
( )
10
2
=
F
( )
100
3
=
F
( )
2
5
1
1
6
F
F
F
⋅
+
⋅
=
5
(
=
m
, bo
1001
)
6
6
6
5
=
>
∧
<
F
F
10010
1
1
)
10
(
3
6
=
⋅
+
⋅
=
F
F
F
6
=
m
2
3
4
5
6
F
F
F
F
F
2
1
...
)
(
b
b
b
n
m
m
F
⋅
⋅
⋅
=
−
--
Elementy kombinatoryki (podstawy kombinatoryki):
Mamy n elementów. Permutacja – ka de ustawienie n elementów.
1
=
n
a
2
=
n
ab
ba
3
=
n
abc acb bac bca cab cba
Ilo permutacji - !
n
Permutacje z powtórzeniami (pewne elementy mog si powtarza ).
3
=
n
aab aba baa
1
n - ilo powtórze 1 elementu;
2
n - ilo powtórze 2 elementu;
…
k
n - ilo powtórze n-tego elementu.
n – ilo elementów
Kombinacj n elementów po k elementów nazywamy ka dy k-elementowy podzbiór, przy
czym dwie kombinacje s sobie równe je eli zło one s z tych samych elementów, chocia
umieszczonych nie na tych samych miejscach.
k
n
- ilo wszystkich kombinacji
(
)
!
!
!
k
n
k
n
k
n
−
⋅
=

Matematyka dyskretna (tryb zaoczny) – cz. I
Wy sza Szkoła Komunikacji i Zarz dzania w Poznaniu
16
6 z 49 (Du y Lotek)
13983816
6
49
=
Szansa trafienia „trójki”?
246820
3
49
=
Podstawowe własno ci symbolu Newtona:
1.
(
)
(
)
[
]
(
)
!
!
!
!
!
!
k
k
n
n
k
n
n
k
n
n
k
n
n
k
n
⋅
−
=
−
−
⋅
−
=
−
=
2.
=
−
−
+
−
k
n
k
n
k
n
1
1
1
(
)
(
)
(
)
(
)
(
)
[
]
(
)
(
)
(
)
(
) (
)
(
)
(
) (
)
(
)
(
) (
)
(
)
(
)
=
−
⋅
=
−
⋅
/
+
/
−
⋅
−
−
⋅
−
−
=
=
−
+
⋅
−
−
⋅
−
−
=
−
⋅
−
−
+
−
−
⋅
−
=
−
−
−
⋅
−
−
+
−
−
⋅
−
k
n
k
n
k
n
k
n
k
k
k
n
k
n
k
n
k
n
k
k
n
k
n
k
n
k
n
k
n
k
n
k
n
k
n
k
n
k
n
!
!
!
!
1
!
1
!
1
1
1
!
1
!
1
!
1
!
!
1
!
1
!
1
!
!
1
!
1
1
!
1
!
1
!
1
!
!
1
3
3
2
3
1
3
0
3
2
2
2
2
0
2
1
1
0
1
0
0
-
−
−
⋅
=
⋅
1
1
k
n
n
n
m
k
Ile wynosi
=
=
n
k
n
k
n
0
2 ?
-
(
)
−
⋅
=
⋅
−
k
n
n
k
n
k
n
1
(
)
=
−
⋅
⋅
=
+
n
k
k
n
k
n
b
a
k
n
b
a
0
-
−
−
⋅
=
1
1
k
n
k
n
k
n
1
=
a
1
=
b
-
−
−
⋅
=
⋅
k
m
k
n
k
n
k
m
m
n
( )
⋅
−
=
k
n
k
n
k 0
1
- przy co drugim zmienia si znak
Wyszukiwarka
Podobne podstrony:
mat dys lista zadan zbiorek zadań
Wyklad2 mat
Mat 10 Ceramika
Mat dla stud 2
Wyklad7 mat
mat skale pomiarowe
logika mat
Magn mat
7Komunikacja org mat
mat bud 006 (Kopiowanie) (Kopiowanie)
Materialy do seminarium inz mat 09 10 czesc III
mat 2013 k11
więcej podobnych podstron