1

2

Setelah menyaksikan

tayangan ini anda dapat

Menarik kesimpulan

dengan silogisme, modus

ponens,

dan modus tollens

UN’O
6

3

Logika Matematika

Logika merupakan alat untuk

menarik kesimpulan yang

sahih (sah)

UN’O
6

4

Pernyataan/Proposisi

Kalimat yang mempunyai salah satu

dari nilai benar atau salah

disebut proposisi atau pernyataan.

Pernyataan ditulis dengan

huruf kecil p, q, r dan seterusnya

UN’O
6

5

Ingkaran Pernyataan

Negasi atau ingkaran dari

pernyataan p, ditulis ~p

adalah pernyataan lain yang

menyangkal pernyataan yang

diberikan

UN’O
6

6

Tabel Kebenaran Ingkaran

Contoh:
p : hari ini hujan
~p : hari ini

tidak

hujan

atau

tidak benar

hari ini hujan

p

~p

B

S

S

B

UN’O
6

7

Pernyataan Majemuk

adalah pernyataan baru yang

dibentuk dari beberapa

pernyataan

tunggal (komponen) dengan

menggunakan kata hubung logika

Seperti: ‘dan

dan

’, ‘

’, ‘atau

atau

’, ‘

’, ‘jika…

jika…

maka…

maka…

’,

’,

atau

atau

‘

‘…jika dan hanya jika…

…jika dan hanya jika…

’

’

UN’O
6

8

Nilai Kebenaran

Pernyataan Majemuk

tergantung:

▪ nilai kebenaran dari pernyataan

tunggalnya (komponennya)

▪ kata hubung logika yang

digunakan

UN’O
6

9

Konjungsi

Pernyataan majemuk yang dibentuk

dari pernyataan-pernyataan p dan q

dengan menggunakan

kata hubung logika ‘

dan

’.

Konjungsi “

p dan q

”

dilambangkan “

p Λ q

”

UN’O
6

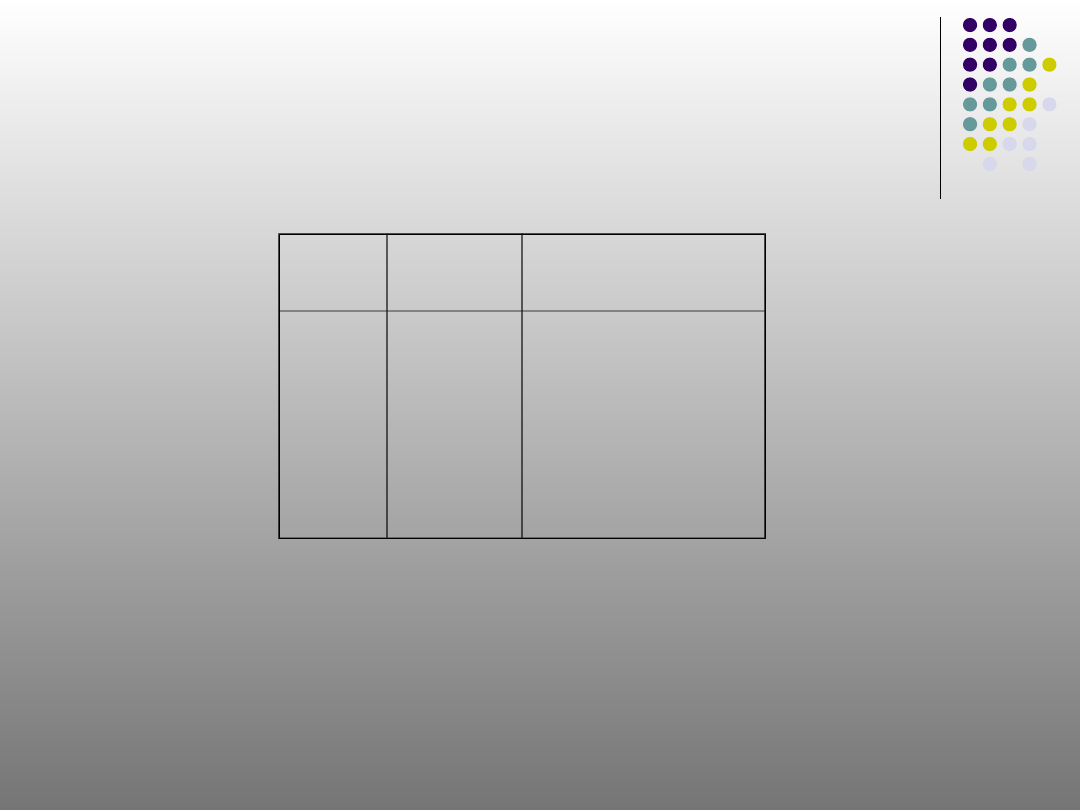
10

Tabel Kebenaran Konjungsi

‘p Λ q’ bernilai benar hanya

apabila

p dan q sama-sama bernilai benar

p

q

p Λ q

B

B

S
S

B

S

B

S

B

S
S
S

UN’O
6

11

Disjungsi

Pernyataan majemuk yang dibentuk

dari pernyataan-pernyataan p dan q

dengan menggunakan

kata hubung logika ‘

atau

’.

Disjungsi “

p atau q

”

dilambangkan “

p V q

”

UN’O
6

12

Tabel Kebenaran Disjungsi

‘p V q’ bernilai salah hanya

apabila

p dan q sama-sama bernilai salah

p

q

p V q

B
B

S

S

B

S

B

S

B
B
B

S

UN’O
6

13

Implikasi

Pernyataan majemuk yang disusun

dari pernyataan-pernyataan p dan

q

dalam bentuk ‘jika p maka q’

Implikasi “

Jika p maka q

”

dilambangkan “

p → q

”

UN’O
6

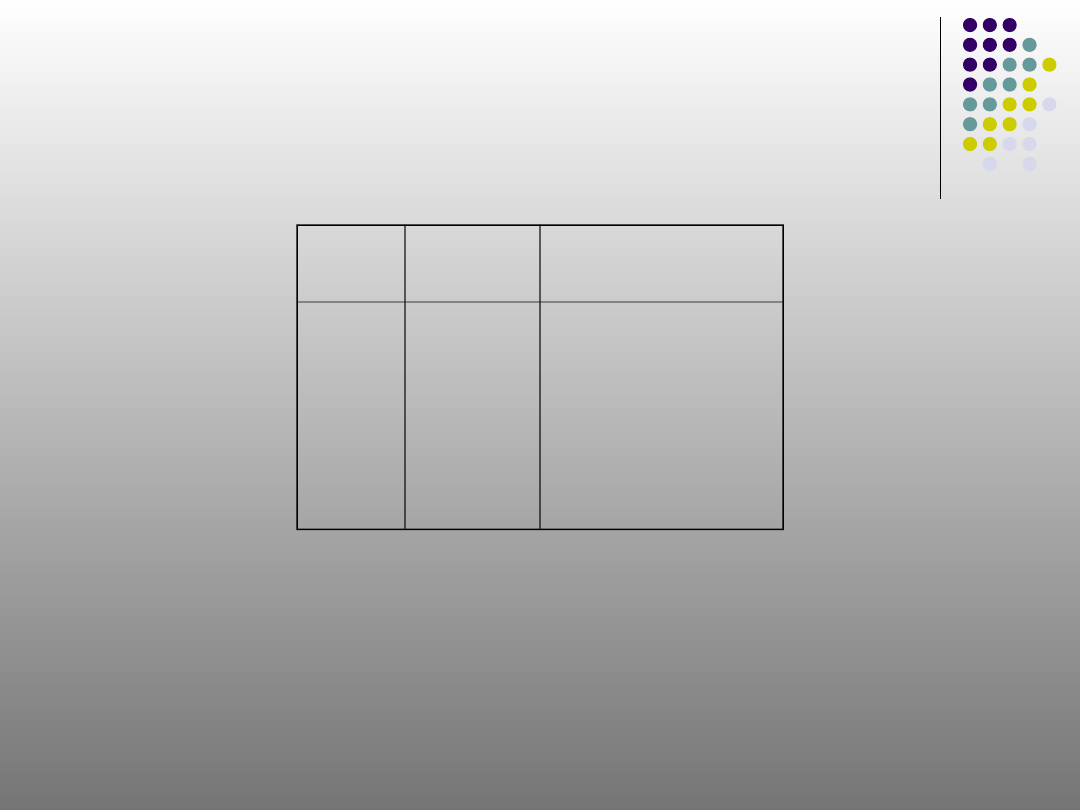
14

Tabel Kebenaran Implikasi

‘p → q’ bernilai salah apabila

p bernilai benar dan q bernilai

salah

p

q

p → q

B

B

S
S

B

S

B

S

B

S

B
B

UN’O
6

15

Biimplikasi

Pernyataan majemuk yang disusun

dari pernyataan-pernyataan p dan

q

dengan kata hubung

‘

jika dan hanya jika

’

Biimplikasi “

p jika dan hanya jika q

”

dilambangkan “

p ↔ q

”

UN’O
6

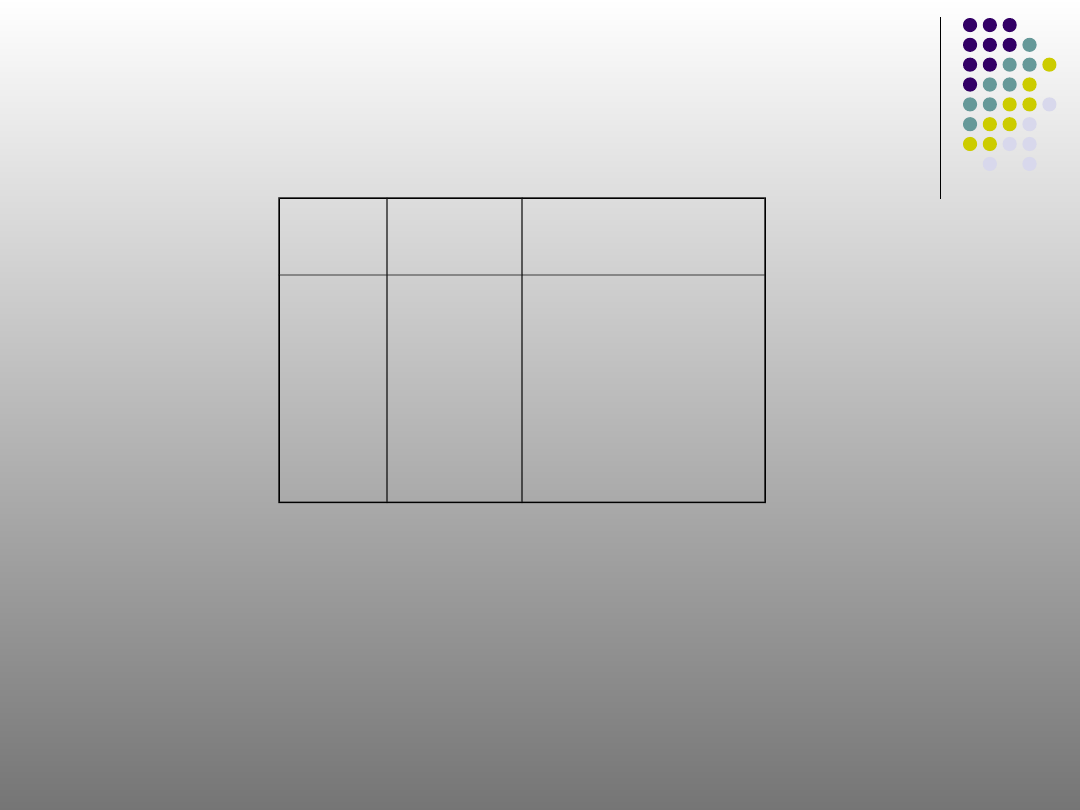
16

Tabel Kebenaran Biimplikasi

‘p ↔ q’ bernilai benar apabila

p dan q

keduanya

bernilai

benar atau salah

p

q

p ↔ q

B

B

S

S

B

S

B

S

B

S
S

B

UN’O
6

17

Contoh 1

Kalimat (p → q) → r bernilai

benar

Jika
(1) p benar, q salah, r salah
(2) p salah, q benar, r salah
(3) p salah, q salah, r benar
(4) p salah, q salah, r salah

UN’O
6

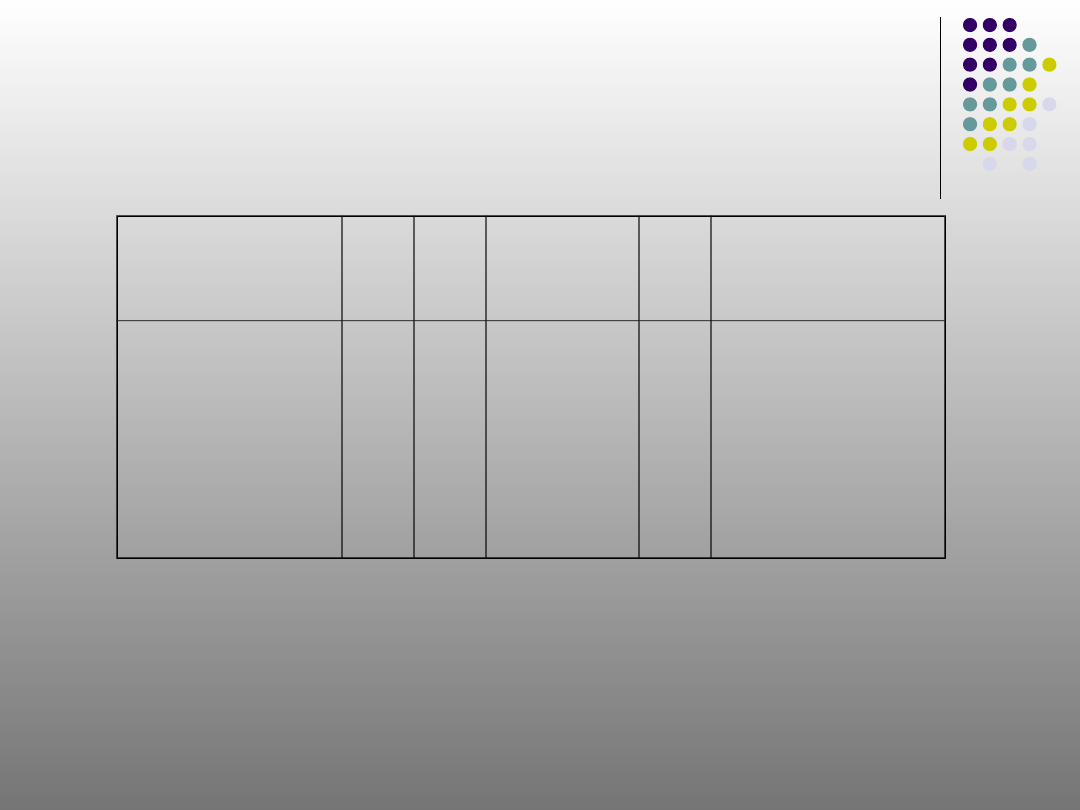
18

Jawab

Jadi, pernyataan yang benar
adalah pernyataan (1) dan
(3)

S
B
B
B

B

S

B

S

Pernyataa

n ke

p

q

(p

q )

r (p  q)  r

1
2
3
4

B

S
S
S

S

B

S
S

S
S
B
S

UN’O
6

19

Contoh 2

Diberikan empat pernyataan p, q, r,
dan s. Jika pernyataan berikut
benar

p ↔ q, q → r, r → s

dan s pernyataan yang salah,
maka di antara pernyataan berikut
yang salah adalah….
a. ~p b. ~r c. ~q
d. p Λ r e. p V ~r

UN’O
6

20

Jawab

s pernyataan yang salah
r → s benar; berarti r salah
q → r benar; berarti q salah
p ↔ q benar; berarti p salah
Jadi, ~p benar; ~r benar; ~q benar
p Λ r salah;  jawaban d
p V ~r benar

UN’O
6

21

Ekivalensi

Pernyataan Majemuk

Dua pernyataan majemuk

yang ekivalen

adalah dua pernyataan majemuk

yang mempunyai nilai kebenaran

yang sama

UN’O
6

22

Pernyataan Ekivalen

1. ~(p Λ q) ≡ ~p V ~q

2. ~(p V q) ≡ ~p Λ ~q

3. p Λ (q V r) ≡ (p Λ q) V (p Λ r)

4. p V (q Λ r) ≡ (p V q) Λ (p V r)

UN’O
6

23

Pernyataan Ekivalen

5. p → q ≡ ~p V q

6. ~(p → q) ≡ p Λ ~q

7. p↔q ≡ (p → q) Λ (q → p)

≡ (~p V q) Λ (~q V p)

8. ~(p ↔ q) ≡ (p Λ ~q) V (q Λ

~p)

UN’O
6

24

Contoh 1:

Ingkaran yang benar dari

pernyataan

“Saya lulus Ujian Nasional dan saya
senang”
adalah….

UN’O
6

25

(1). Saya tidak lulus Ujian Nasional
dan saya tidak senang
(2). Tidak benar bahwa saya lulus

Ujian

Nasional dan saya senang
(3). Saya lulus Ujian Nasional dan
saya tidak senang
(4) Saya tidak lulus Ujian Nasional
atau saya tidak senang

UN’O
6

26

Jawab:

Ingkaran p Λ q adalah
~(p Λ q) ≡ ~p V ~q
Jadi pernyataan yang benar
adalah
(2) Tidak benar saya lulus Ujian
nasional dan saya senang
(4) Saya tidak lulus Ujian

Nasional

atau saya tidak senang

UN’O
6

27

Contoh 2:

Ingkaran dari (p Λ q) → r adalah….
a. ~p V ~q V r b. (~p Λ ~q) V r
c. p Λ q Λ ~r d. ~p Λ ~q Λ r
e. (~p V q) Λ r

Jawab:

ingat bahwa: ~(p→q) ≡ p

Λ ~q

~[(p Λ q) → r] ≡ (p Λ q) Λ

~r

≡ p Λ q Λ ~r
Jadi, jawabannya adalah c

UN’O
6

28

Contoh 3:

Ingkaran pernyataan:
“Jika guru tidak hadir maka semua
murid senang” adalah….
a. Guru hadir dan semua murid

tidak

senang
b. Guru hadir dan ada beberapa

murid

senang
c. Guru hadir dan semua murid

senang

UN’O
6

29

d. Guru tidak hadir dan ada

beberapa

murid tidak senang
e. Guru tidak hadir dan semua

murid

tidak senang

Jawab:

Ingat bahwa: ~(p → q) ≡ p Λ ~q
Jadi ingkaran dari “Jika guru tidak

hadir

maka semua murid senang” adalah
“guru tidak hadir dan ada beberapa
murid tidak senang”  jawaban d

UN’O
6

30

Konvers, Invers, dan

Kontraposisi

Jika diketahui implikasi

p → q

maka:

Konversnya adalah q → p

q → p

Inversnya adalah ~p → ~q

~p → ~q

Kontraposisinya adalah

~q → ~p

Catatan:

p → q

≡

~q → ~p

UN’O
6

31

Contoh 1:

~p → q mempunyai nilai kebenaran
sama dengan….
(1). p V q (2). p Λ q
(3). ~q → p (4). ~q Λ ~p

Jawab:

ingat bahwa: p → q ≡ ~p V ~q
≡ ~q → ~p
~p → q ≡ ~q → p… (3)
≡ p V q … (1)

UN’O
6

32

Contoh 2:

Pernyataan berikut yang ekivalen
dengan:
“Jika p benar maka q salah”

adalah….

a. p benar atau q salah
b. Jika q salah maka p benar
c. Jika p salah maka q benar
d. Jika q benar maka p salah
e. Jika q benar maka p benar

UN’O
6

33

Jawab:

Implikasi p → q ekivalen dengan
Kontraposisi ~q → ~p dan ~p V

q

Jadi “Jika p benar maka q salah”
ekivalen dengan
“Jika q benar maka p salah”
atau
“p salah atau q salah”

UN’O
6

34

Penarikan Kesimpulan

menentukan pernyataan nilai

(konklusi) dari pernyataan-

pernyataan (premis) melalui

aturan tertentu

UN’O
6

35

Suatu kesimpulan (konklusi)

dianggap sah jika:

▪ implikasi dari konjungsi

premisnya

dengan konklusinya adalah

tautologi

(selalu benar untuk semua

kondisi)

▪ Konjungsi semua premisnya

benar maka konklusinya benar

UN’O
6

36

Penarikan Kesimpulan

yang sah

Di dalam logika matematika ada

beberapa penarikan kesimpulan

yang sah, di antaranya adalah

UN’O
6

37

1. Modus Ponens:

p → q (premis 1

= benar)

p (premis 2

=

benar)

q (konklusi benar)

Contoh:
Jika hujan lebat maka terjadi

banjir

Hari ini hujan lebat
Terjadi banjir





UN’O
6

38

2. Modus Tollens:

p → q (premis 1

=

benar)

~q (premis 2

=

benar)

~p (konklusi

benar)

Contoh:
Jika BBM naik maka ongkos bis

naik

Ongkos bis tidak naik
BBM tidak naik





UN’O
6

39

3. Silogisme:

p → q (premis 1

= benar)

q  r (premis 2

=

benar)

p  r (konklusi benar)
Contoh:
Jika Budi rajin belajar maka lulus

UN

Jika lulus UN maka orangtua

senang

Jika Budi rajin belajar maka
orangtua senang





UN’O
6

40

Soal 1:

Diketahui pernyataan p dan q
Argumenatsi: ~p  q
~r  ~q
r  p

disebut….

a. Implikasi b.

Kontraposisi

c. Modus ponens d. Modus

tollens

e. silogisme



UN’O
6

41

Bahasan

Argumentasi:
~p  q ~p  q
~r  ~q ≡ q  r

(kontraposisi)

~r  p ~p  r
≡ ~r  p

(kontraposisi)

Jadi, disebut silogisme
jawaban e





UN’O
6

42

Soal 1:

Diketahui pernyataan p dan q
Argumenatsi: ~p  q
~r  ~q
r  p

disebut….

a. Implikasi b.

Kontraposisi

c. Modus ponens d. Modus

tollens

e. silogisme



UN’O
6

43

Soal 2

Penarikan kesimpulan dari premis-
premis: p V q
~q
….

a. p

b. ~p

c. q

d. ~(p V q)

e. ~ q



UN’O
6

44

Bahasan

p V q ≡ ~p  q

(ekivalensi)

~p  q ≡ ~q  p

(kontraposisi)

dengan demikian
p V q
~q
berarti: ~q  p
~q
p
Jawabannya a

Modus
ponens



UN’O
6

45

Soal 2

Penarikan kesimpulan dari premis-
premis: p V q
~q
….

a. p

b. ~p

c. q

d. ~(p V q)

e. ~ q



UN’O
6

46

Soal 3

Penarikan kesimpulan dari
1. p V q
~p
q
yang sah adalah….
a. hanya 1 b. hanya 1 dan 2
c. hanya 3 d. hanya 1 dan 3
e. hanya 2 dan 3



2. p  q

q  ~r

~r  ~p



3. p  ~q

q V r
p  r



UN’O
6

47

Bahasan

1. p V q
~p
q

argumenatsi nomor 1 di atas sah
karena merupakan modus ponens





~p  q (ekivalen)

~p



q

UN’O
6

48

Bahasan

2. p  q
q  ~r
~r  ~p


argumenatsi nomor 2 di atas
tidak sah karena bukan silogisme





p 

q

q

~r



p

~r

p

~r

r ~p

(kontraposisi)

UN’O
6

49

Bahasan

3. p  ~q
q V r
p  r

argumentasi nomor 3 di atas
sah karena merupakan silogisme
Jadi, jawabannya hanya 1 dan 3  d





p  ~q

~q  r



p  r

(ekivalensi)

UN’O
6

50

Soal 3

Penarikan kesimpulan dari
1. p V q
~p
q
yang sah adalah….
a. hanya 1 b. hanya 1 dan 2
c. hanya 3 d. hanya 1 dan 3
e. hanya 2 dan 3



2. p  q

q  ~r

~r  ~p



3. p  ~q

q V r
p  r



UN’O
6

51

SELAMAT BELAJAR