PRZEPŁYW PŁYNÓW (podstawowe pojęcia)
Ilościowe określanie przepływu:
Masowe natężenie przepływu: [ G ] = [kg/s]
&
Objętościowe natężenie przepływu: [V ] = [m
&
3
/s]
ρ
G
V
&
& =
Prędkość masowa: [W] = [kg/(m
2
⋅s)]
S
G
W
&
=
Średnia liniowa prędkość przepływu: [
w] = [m/s]
S
V
w
&
=
Bilans materiałowy strumienia płynu
Równania ciągłości strumienia
const
w
S
.........
w
S
w
S
ρ
.........
ρ
ρ
const.
ρ
w
S
.........
ρ
w
S
ρ
w
S
const.
ρ
V
..........
ρ
V
ρ
V
const.
G
......
..........
G
G
n
n
2
2
1
1
n
2
1
n
n
n
2
2
2
1
1
1
n
n
2
2
1
1
n
2
1
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
Bilans energetyczny strumienia płynu (równanie Bernoullego)
Przepływ izotermiczny cieczy doskonałej (bez tarcia)
g
2
w
g
p
z
g
2
w
g
p
z
2
2
2
2
2
1
1
1
+
⋅
+
=
+
⋅
+
ρ
ρ
Przepływ cieczy doskonałej z tarciem
)
u
u
(
g
2
w
g
p
z
g
2
w
g
p
z
1
2
2
2
2
2
2
1
1
1
−
+
+
⋅
+
=
+
⋅
+
ρ
ρ
str
2
2
2
2
2
1
1
1
h
g
2
w
g
p
z
g
2
w
g
p
z
+
+
⋅
+
=
+
⋅
+
ρ
ρ
g
u
u
h
1
2
str
−
=
UOGÓLNIONE RÓWNANIE BERNOULLEGO
2
2
2
2
2
2
1
2
1
1
1
1
u
2
w
v
p
gz
q
l
u
2
w
v
p
gz
+
+
+
=
+
+
+
+
+
2
w
i
gz
q
l
2
w
i
gz
2
2
2
2
2
1
1
1
+
+
=
+
+
+
+
Czas opróżniania zbiorników
Zbiornik cylindryczny
(
)
2
1
o
h
h
g
2
2
S
S
−
⋅
⋅
⋅
=
φ
τ
Zbiornik kulisty
g
2
d
D
15
16
2
o
2
/
5
⋅
⋅
=
τ
Zbiornik stożkowy
D – średnica. H – wysokość stożka
1
2
/
5
2
o
2
2
h
g
2
d
H
D
5
2
⋅
⋅
⋅
⋅
⋅
=
φ
τ
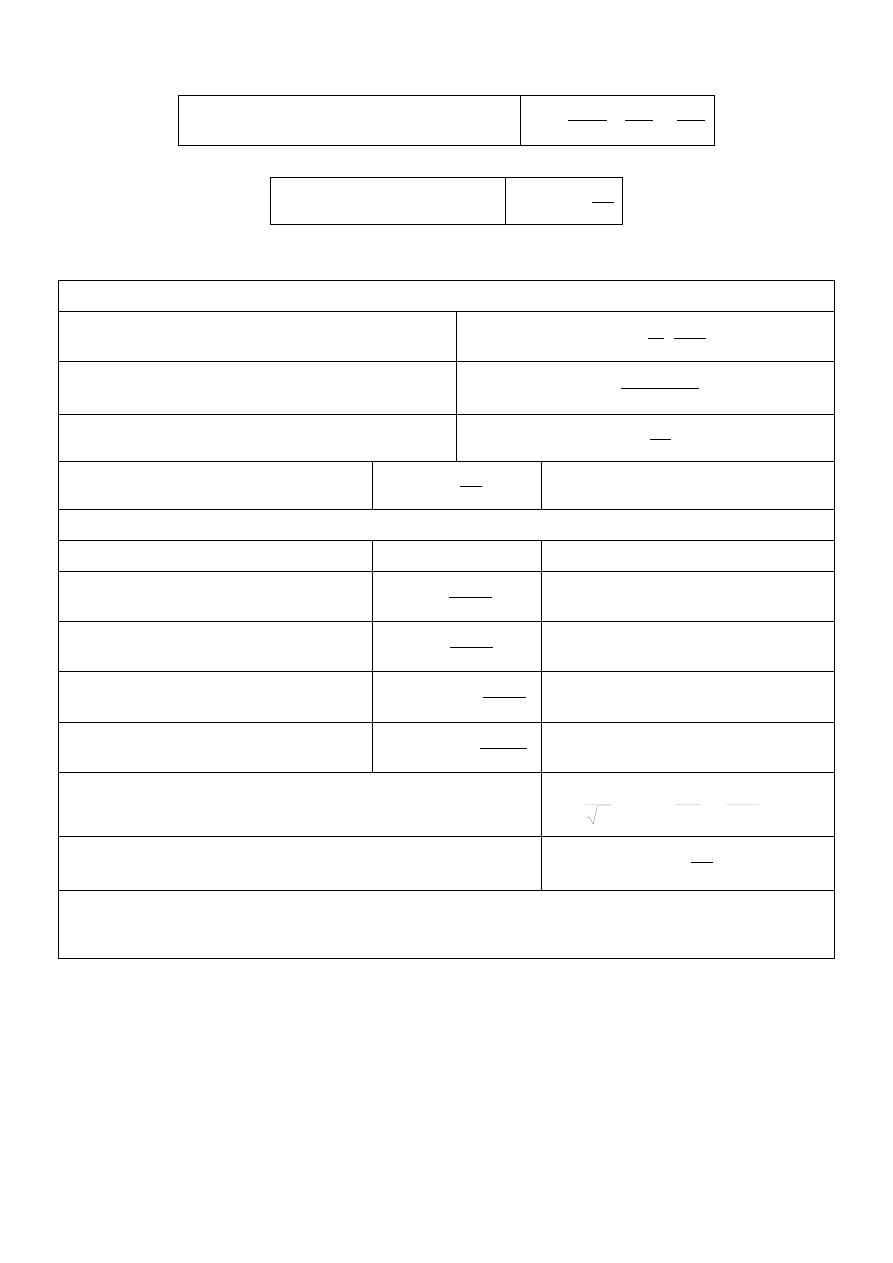
Liczba Reynoldsa jako kryterium ruchu płynu
η
ν
η
ρ
WD
wD
wD
=
Re
=
=
Średnica zastępcza przewodów
B
S
4
r
4
D
h
e
=
=
OPORY PODCZAS PRZEPŁYWU PŁYNÓW PRZEZ PRZEWODY
Równanie Darcy – Weisbacha
2
w
D
L
P
2
t
ρ
λ
Δ
⋅
⋅
=
Ruch laminarny (równanie Poiseuille’a)
L
128
D
P
V
4
t
η
Δ
π
⋅
⋅
=
&
Współczynnik oporu
λ
dla ruchu laminarnego
Re
64
=
λ
Dla przekrojów niekołowych
Re
k
=
λ
Kwadrat: k = 57; pierścień k = 96
Współczynnik oporu
λ
dla ruchu burzliwego w rurach gładkich
Autor wzoru
Wzór
Zakres Re
Blausius
25
.
0
Re
316
.
0
=
λ
4
3
10
5
10
3
⋅
−
⋅
Generaux
16
.
0
Re
16
.
0
=
λ
7
3
10
2
10
4
⋅
−
⋅
Herman
3
.
0
Re
396
.
0
0054
.
0
+
=
λ
6
3
10
2
10
5
.
2
⋅
−
⋅
Nikuradze
237
.
0
Re
221
.
0
0032
.
0
+
=
λ
8
5
10
1
10
1
⋅
−
⋅
Współczynnik oporu
λ
dla ruchu burzliwego w rurach szorstkich
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
+
−
=
9
.
0
Re
81
.
6
7
.
3
lg
2
1
ε
λ
Chropowatość względna
e
D
e
=
ε
Chropowatość bezwzględna: średnia wysokość garbów chropowatości na ściankach rury e [mm]
(np. nowe rury stalowe: 0.06-0.1 mm; rury stalowe nieznacznie skorodowane: 0.1-0.2 mm; rury
betonowe: 3-9 mm)
2
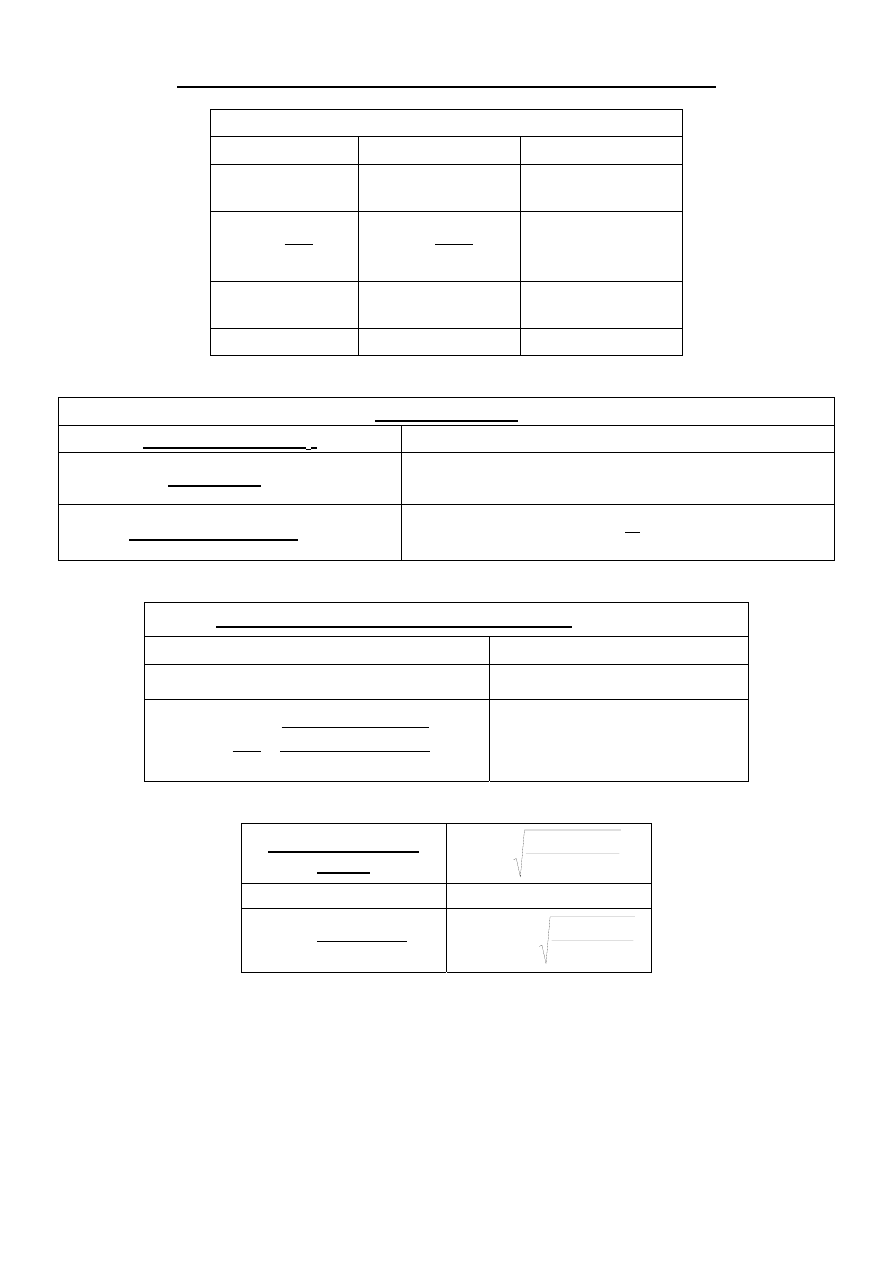
RUCH CZĄSTEK STAŁYCH W POLU SIŁ MASOWYCH
Siła oporu ośrodka dla różnych obszarów opadania
Laminarny Przejściowy Burzliwy
4
.
0
Re
10
1
o
4
<
<
⋅
−
3
o
10
1
Re
4
.
0
⋅
<
<
5
o
3
10
2
Re
10
1
⋅
<
<
⋅
o
Re
24
=
λ
6
.
0
o
Re
5
.
18
=
λ
44
.
0
=
λ
o
w
d
3
R
η
π
=
o
4
,
0
6
,
0
4
,
1
w
d
3
,
2
R
ρ
η
≈
2
o
2
w
d
17
,
0
R
ρ
≈
Stokes Allen Newton
Cząstki niekuliste:
średnica zastępcza (d
z
)
Średnica kuli o takiej samej objętości jak dana cząstka
sferyczność (
ψ
)
Stosunek powierzchni kuli o objętości cząstki
rzeczywistej do powierzchni tej cząstki,
1
<
ψ
współczynnik kształtu (
ϕ
)
ψ
ϕ
1
=
Współczynnik oporu dla cząstek niekulistych:
)
,
(Re
f
o
λ
ψ
=
Ruch laminarny
Ruch burzliwy
05
,
0
Re
o
<
5
o
3
10
2
Re
10
1
⋅
<
<
⋅
o
o
Re
)
065
,
0
/
log(
843
,
0
24
Re
a
ψ
λ
=
=
ψ
λ
87
,
4
31
,
5
−
=
Prędkość opadania
cząstki
λρ
ρ
ρ
3
)
(
dg
4
w
s
o
−
=
Ruch laminarny
Ruch burzliwy
(
)
η
ρ
ρ
18
g
d
w
s
2
o
−
=
(
)
ρ
ρ
ρ
g
d
74
.
1
w
s
o
−
⋅
≈
3
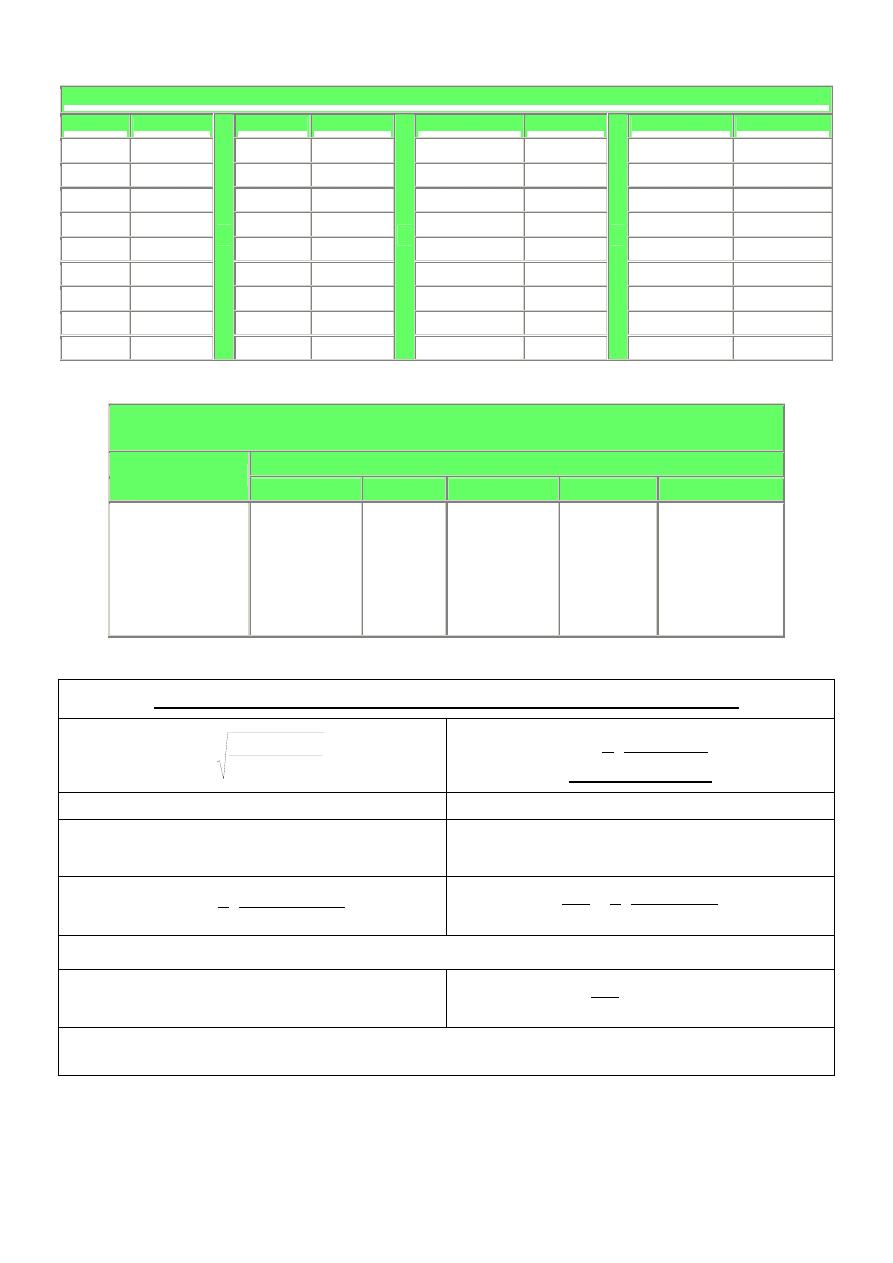
Współczynnik oporu ośrodka
λ
jako funkcja liczby Reynoldsa Re dla cząstek kulistych
Re
λ
Re
λ
Re
λ
Re
λ
0 1
240
10
4 10
700
0 5
5×10
4
0 49
0 3
80
20
2 55
1000
0 46
7×10
4
0 50
0 5
49 5
30
2 00
2000
0 42
10
5
0 48
0 7
36 5
50
1 50
3000
0 40
2×10
5
0 42
1 0
26 5
70
1 25
5000
0 38
3×10
5
0 20
2 0
14 4
100
1 07
7000
0 39
4×10
5
0 084
3 0
10 4
200
0 77
10000
0 40
6×10
5
0 10
5 0
6 9
300
0 65
20000
0 45
10
6
0 13
7 0
5 4
500
0 55
30000
0 47
3×10
6
0 20
Zależność współczynnika oporu
λ
od liczby Reynoldsa Re i sferyczności
ψ
dla ciał
niekulistych izometrycznych
Re
ψ
1
10
100
400
1000
0,670
0,806
0,846
0,946
1,000
28
27
27
27
26,5
6
5
4,5
4,5
4,1
2,2
1,3
1,2
1,1
1,07
2,0
1,0
0,9
0,8
0,6
2,0
1,1
1,0
0,8
0,46
Uproszczona metoda obliczania prędkości opadania cząstek lub ich średnicy
λρ
ρ
ρ
3
)
(
dg
4
w
s
o
−
=
2
o
s
w
)
(
dg
3
4
ρ
ρ
ρ
λ
−
⋅
=
Prędkość opadającej cząstki
Średnica opadającej cząstki
Z równania na
λ
eliminujemy nieznaną wielkość
mnożąc obustronnie przez
2
o
w
2
o
Re
Z równania na
λ
eliminujemy nieznaną wielkość
dzieląc obustronnie przez
d
o
Re
2
s
3
2
o
g
)
(
d
3
4
Re
η
ρ
ρ
ρ
λ
−
⋅
=
3
o
2
s
o
w
g
)
(
3
4
Re
ρ
ρ
ρ
η
λ
−
⋅
=
W oparciu o wykres
)
(Re
f
o
=
λ
konstruujemy zmodyfikowane wykresy oporów ośrodka:
)
(Re
f
Re
o
2
o
=
λ
)
(Re
f
Re
o
o
=
λ
Znając wartość prawej strony równań można odczytać wielkość liczby Reynoldsa, co następnie pozwala
obliczyć szukaną wartość prędkości opadania lub średnicy opadającej cząstki
4
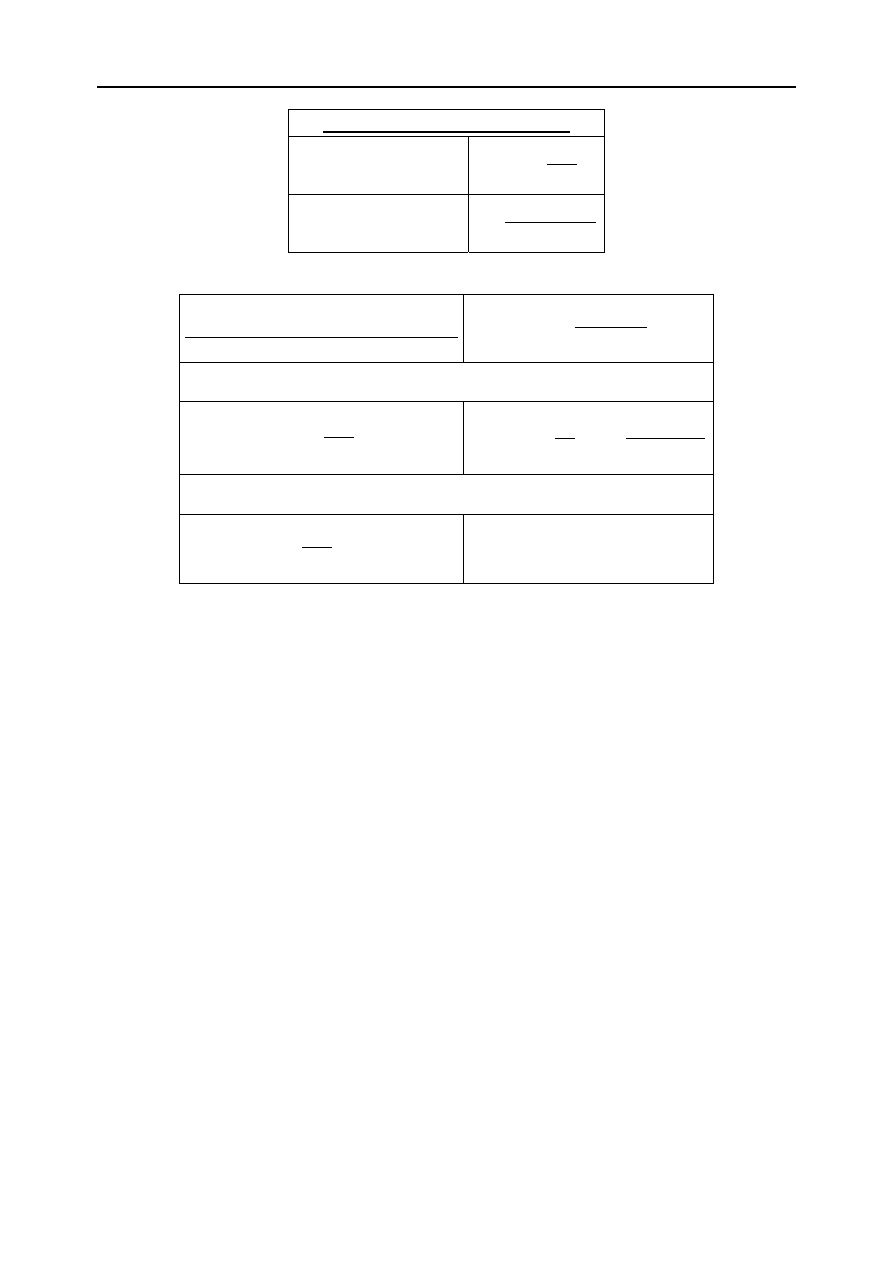
PRZEPŁYW PŁYNU PRZEZ ZŁOŻE ROZDROBNIONEGO MATERIAŁU
Liczbowa charakterystyka złoża
Porowatość
s
nas
1
ρ
ρ
ε
−
=
Powierzchnia właściwa
z
d
)
1
(
6
a
ϕ
ε
⋅
−
⋅
=
Opory przepływu płynu przez złoże
ϕη
ε
ρ
)
1
(
d
w
Re
z
R
−
=
Ruch laminarny (Re
R
<10) (wzór Leva)
R
R
Re
400
=
λ
3
2
2
2
z
R
)
1
(
w
d
L
200
P
ε
ϕ
ε
η
Δ
−
⋅
⋅
⋅
⋅
=
Ruch burzliwy (wzór Erguna)
75
,
1
Re
150
R
R
+
=
λ
65
,
0
40
,
0
3000
Re
1
R
<
<
<
<
ε
5
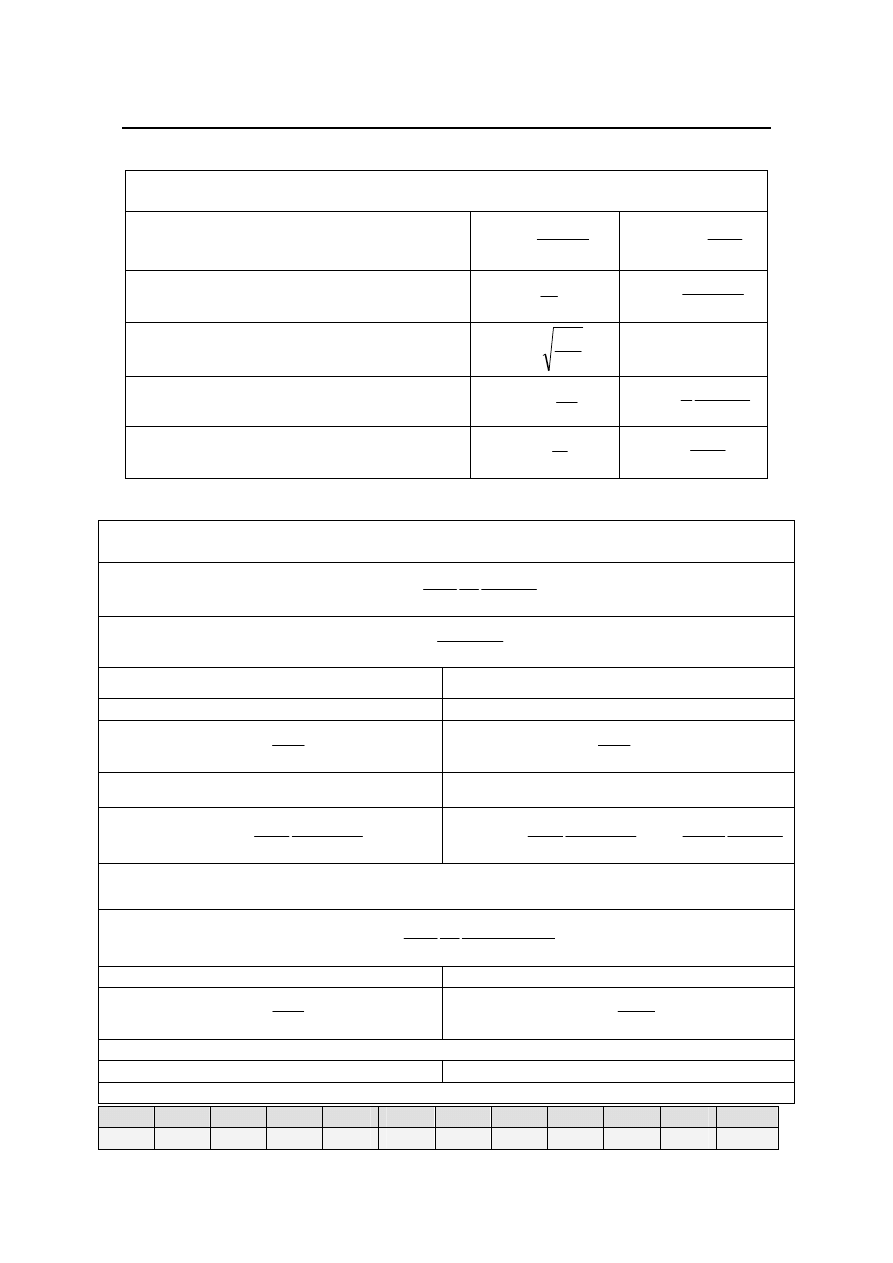
PRZEPŁYW PŁYNU PRZEZ ZŁOŻE ROZDROBNIONEGO MATERIAŁU
Liczbowa charakterystyka złoża i elementów złoża
Porowatość
warstwy
kapilar
V
V
=
0
ε
s
nas
ρ
ρ
ε
−
= 1
0
Powierzchnia właściwa
el
A
V
N
a
=
(
)
z
d
a
ϕ
ε
0
1
6
−
=
Średnica zastępcza elementów wypełnienia
3
6
Π
=
s
z
V
d
Średnica zastępcza kapilar
a
d
zK
ε
4
=
( )
ϕ
ε
ε
−
=
1
3
2
z
zK
d
d
Współczynnik kształtu
ψ
ϕ
1
=
2
e
el
d
A
Π
=
ϕ
Opory przepływu przez złoże
( )
3
2
1
2
ε
ϕ
ε
ρ
ω
λ
−
=
∆
z
R
R
d
L
P
( )
ϕη
ε
ρ
ω
−
=
1
Re
z
R
d
Ruch laminarny
Ruch burzliwy
10
Re
<
100
Re
>
R
R
Re
400
=
λ
50
,
3
Re
300 +
=
R
R
λ
Wzór Leva
Wzór Erguna
( )
3
2
2
2
1
200
ε
ϕ
ε
ωη
−
=
∆
z
R
d
L
P
( )
( )
3
2
3
2
2
2
1
75
,
1
1
150
ε
ϕ
ε
ρ
ω
ε
ϕ
ε
ωη
−
+
−
=
∆
z
z
R
d
L
d
L
P
Uogólnione równanie Leva
( )
3
3
3
2
1
2
ε
ϕ
ε
ρ
ω
λ
n
n
z
L
R
d
L
P
−
−
−
=
∆
Ruch laminarny n = 1
Ruch burzliwy n = f(Re)
L
L
Re
400
=
λ
1
,
0
Re
L
L
b
=
λ
Współczynnik
b
zależy od szorstkości materiału, z którego wykonane jest wypełnienie.
Wypełnienie ceramiczne b = 10,5 – 14
Wypełnienie szklane b = 7
Współczynnik
n
zależy od wartości liczby Reynoldsa.
Re
10
20
40
80
100
200
400
1000 2000 4000 10000
n
1,0
1,15
1,3
1,45
1,55
1,7
1,8
1,85
1,9
1,93
1,96
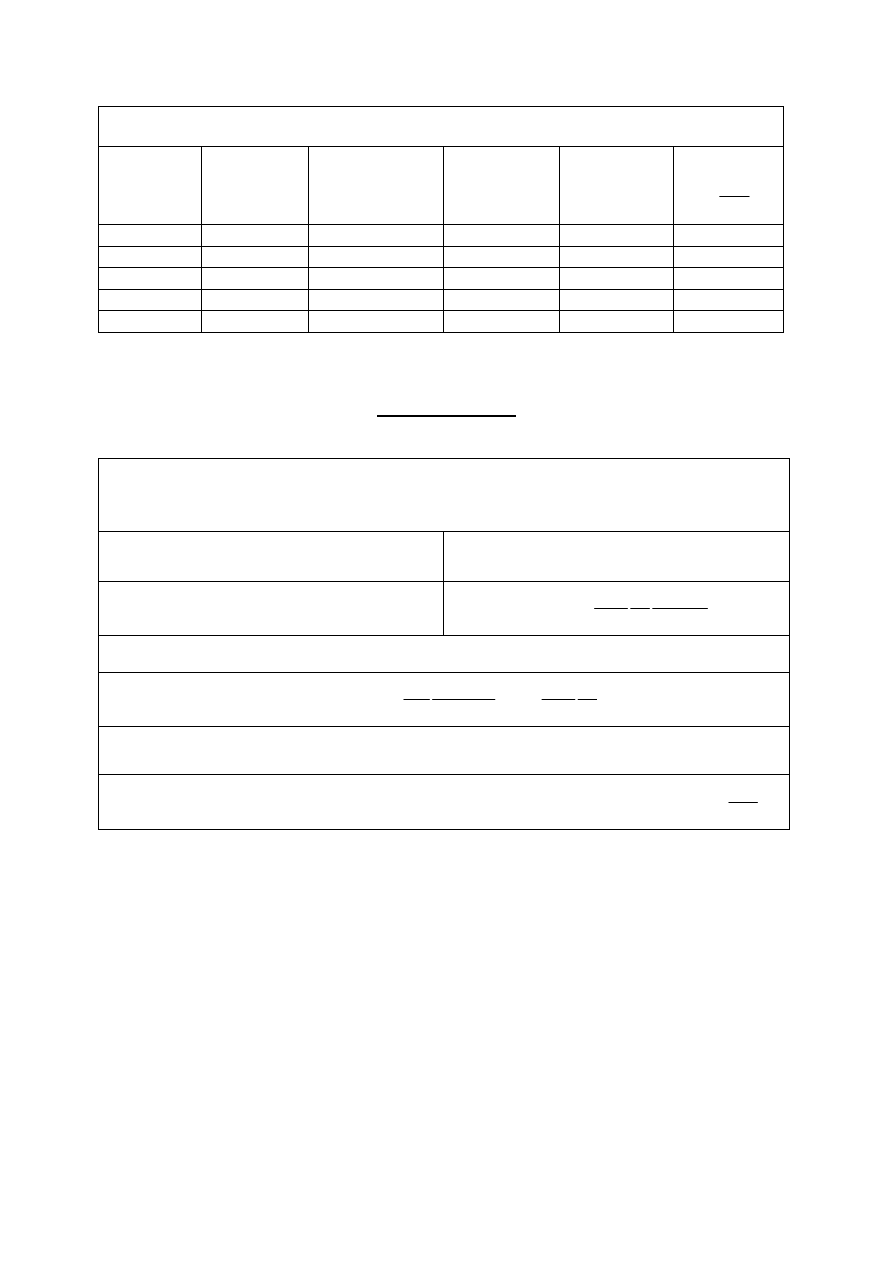
Parametry charakterystyczne dla wypełnień z pierścieni Raschiga
Średnica
zewnętrzna
[mm]
Grubość
ścianki
[mm]
Liczba
elementów1m
3
Porowatość
Powierzchnia
właściwa
[m
2
/m
3
]
Parametr
kg
s
m
2
β
16
2,0
192500
0,73
300
0,0533
25
2,4
43000
0,81
174
0,0512
38
4,4
12700
0,76
115
0,0471
50
4,4
6000
0,79
95
0,0348
75
9,5
1900
0,71
69
-
FLUIDYZACJA
Minimalna prędkość fluidyzacji –
-
siła pozornego ciężaru złoża zostaje zrównoważona siłą spadku ciśnienia na złożu
2
1
F
F
=
Siła pozornego ciężaru złoża F
1
(
) ( )
ε
ρ
ρ
−
−
=
1
1
gL
A
F
s
Siła oporu przepływu płynu przez złoże F
2
( )
3
2
2
1
2
ε
ϕ
ε
ρ
ω
λ
−
=
z
R
d
L
A
F
Zastosowawszy wzór Erguna na spadek ciśnienia na złożu otrzymano:
(
)
( )
3
2
3
2
2
75
,
1
1
150
ε
ϕ
ρ
ω
ε
ϕ
ε
ωη
ρ
ρ
z
z
s
d
d
g
+
−
=
−
Maksymalna prędkości fluidyzacji
odpowiada prędkości opadania cząstki.
Kryterium występowania fluidyzacji jednorodnej jest liczba Frouda:
1
<
Fr
z
gd
Fr
2
ω
=
PRZEPŁYWY W UKŁADACH WIELOFAZOWYCH - UKŁAD GAZ – CIECZ
Ruch gazu
Ruch cieczy
g
g
zK
I
g
g
d
η
ρ
ω
=
Re
L
L
zK
I
L
d
L
η
ρ
ω
=
Re
ε
ω
ω
g
I
g
=
a
d
zK
ε
4
=
δ
ω
ω
a
L
I
L
=
δ
4
=
zK
d
δ
Sa
S
L
=
δ
ω
ω
ω
Sa
S
S
V
I
L
L
I
L
L
=
=
=
•
g
mg
g
g
g
g
a
g
a
η
η
ρ
ω
4
4
Re
=
=
L
mL
L
L
L
L
a
g
a
η
η
ρ
ω
4
4
Re
=
=
Przepływ laminarny
40
Re
<
g
Przepływ burzliwy
150
Re
>
g
2300
Re
≈
KR
L
Strata ciśnienia przy przepływie gazu przez zraszane wypełnienie (∆P
ZR
)
mL
ZR
g
P
P
β
=
∆
∆
log
Maksymalna dozwolona prędkość przepływu fazy ciekłej
Obliczenia w oparciu o bezwymiarowe kompleksy X i Y
16
,
0
3
2
=
O
L
L
g
g
g
a
X
η
η
ρ
ρ
ε
ω
g
L
g
L
m
m
Y
ρ
ρ
=
•
•
η
o
- lepkość wody w temperaturze 20ºC
g
L
g
L
g
L
m
m
ρ
ρ
ω
ω
=
•
•
Równanie Baina i Hougena
25
,
0
75
,
1
022
,
0
log
X
Y
−
=
Stopień użyteczności powierzchni wypełnienia
−
=
D
L
L
e
08
,
0
exp
39
,
3
187
,
0
ω
ϕ
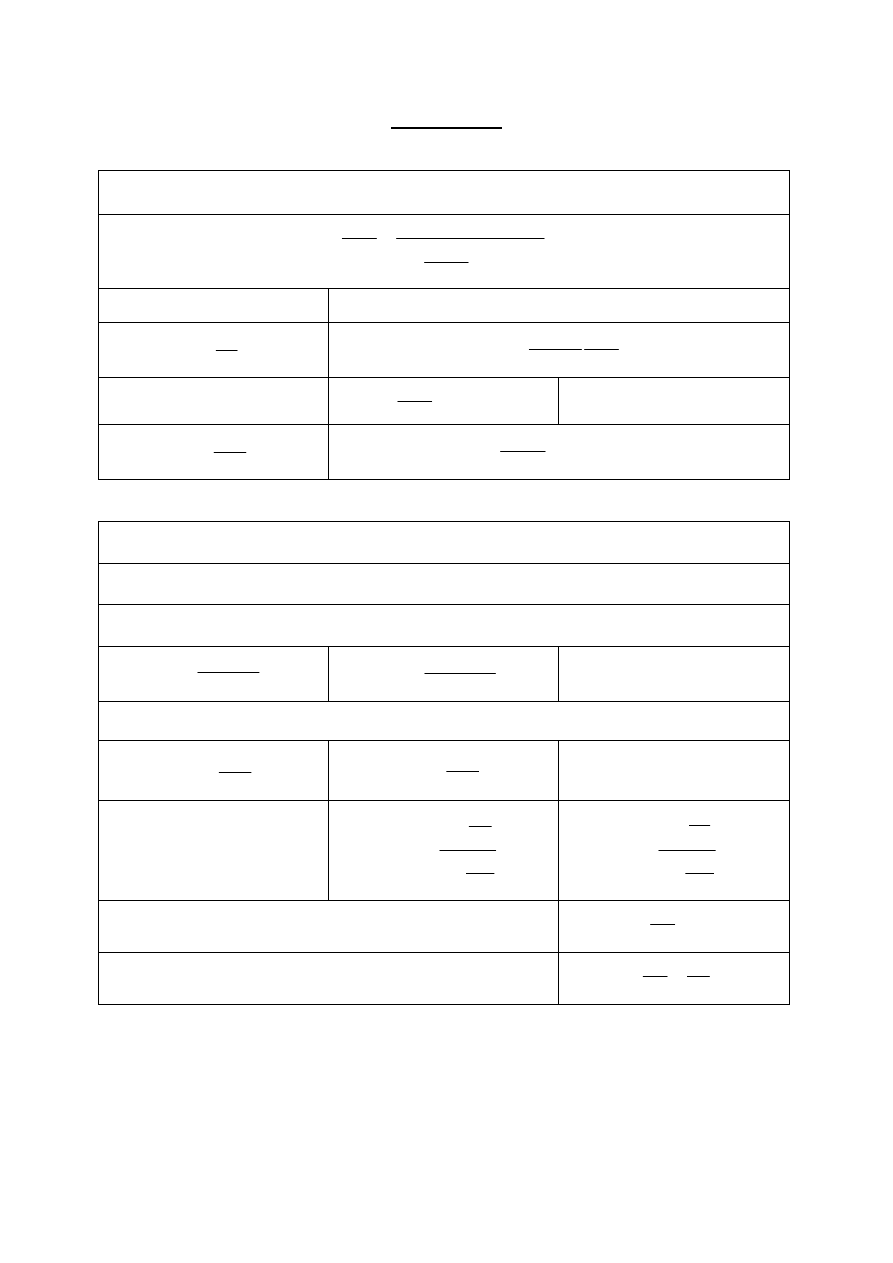
FILTRACJA
Podstawowe równanie filtracji
+
∆
∆
=
t
S
O
L
R
P
A
xV
P
Ad
dV
α
η
τ
Gęstość osadu[kg/m
3
]
Opór właściwy osadu [m/kg]
V
m
x
s
=
3
2
2
1
ε
ε
ρ
ϕ
α
−
=
s
I
a
k
Opór właściwy przegrody
[1/m]
S
P
b
∆
=
−
3
1
ε
ε
b
k
k
I
=
A
axC
R
t
=
S
O
S
s
P
P
ka
∆
=
∆
=
α
ρ
ϕ
α
2
2
Równanie filtracji izobarycznej (Równanie Rutha)
τ
K
CV
V
=
+ 2
2
Stałe filtracji dla danego filtru i osadu
S
O
t
P
x
A
R
C
∆
=
α
η
α
x
P
A
K
O
S
−
∆
=
1
2
2
Stałe filtracji dla tego samego układu filtracyjnego i innego ciśnienia
S
I
I
P
P
C
C
∆
∆
=
S
I
I
P
P
K
K
−
∆
∆
=
1
Ściśliwość osadu
1
2
1
2
log
log
1
P
P
K
K
s
∆
∆
−
=
1
2
2
1
log
log
P
P
C
C
s
∆
∆
=
Filtracja przez warstwę o stałej grubości
τ
k
H
H
=
2
1
ln
Filtracja zawiesiny o dużych cząstkach
τ
1
1
2
1
ln
H
k
H
H
=
Document Outline