Podstawowe liniowe człony dynamiczne
automatyki. Równania różniczkowe,
transmitancje operatorowe,
charakterystyki czasowe
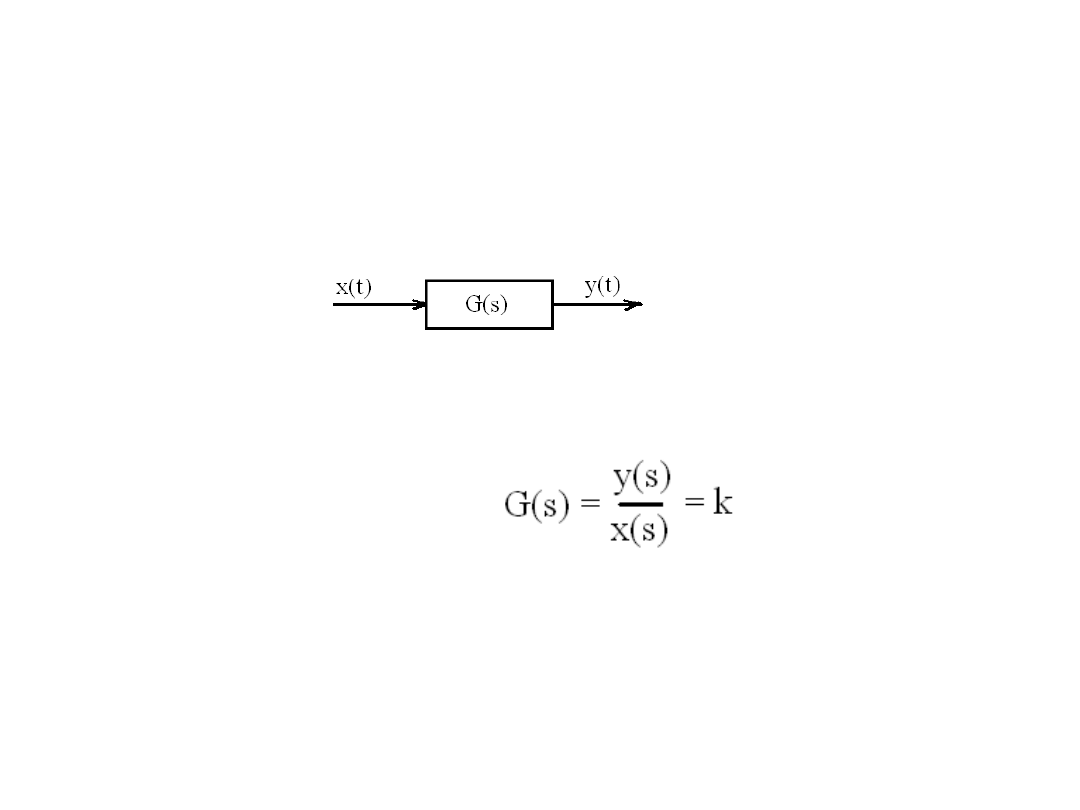
1. Element proporcjonalny:
-Równanie różniczkowe: y(t) = k x(t) (rzędu
zerowego)
-Równanie po transformacji Laplace’a: y(s) = k x(s)
-Transmitancja operatorowa:
-„k” – współczynnik wzmocnienia elementu proporcjonalnego
(proporcjonalności)
jeśli „k” > 1 to element jest wzmacniaczem sygnału;
jeśli „k” < 1 to element jest dzielnikiem sygnału
-
element proporcjonalny c.d.
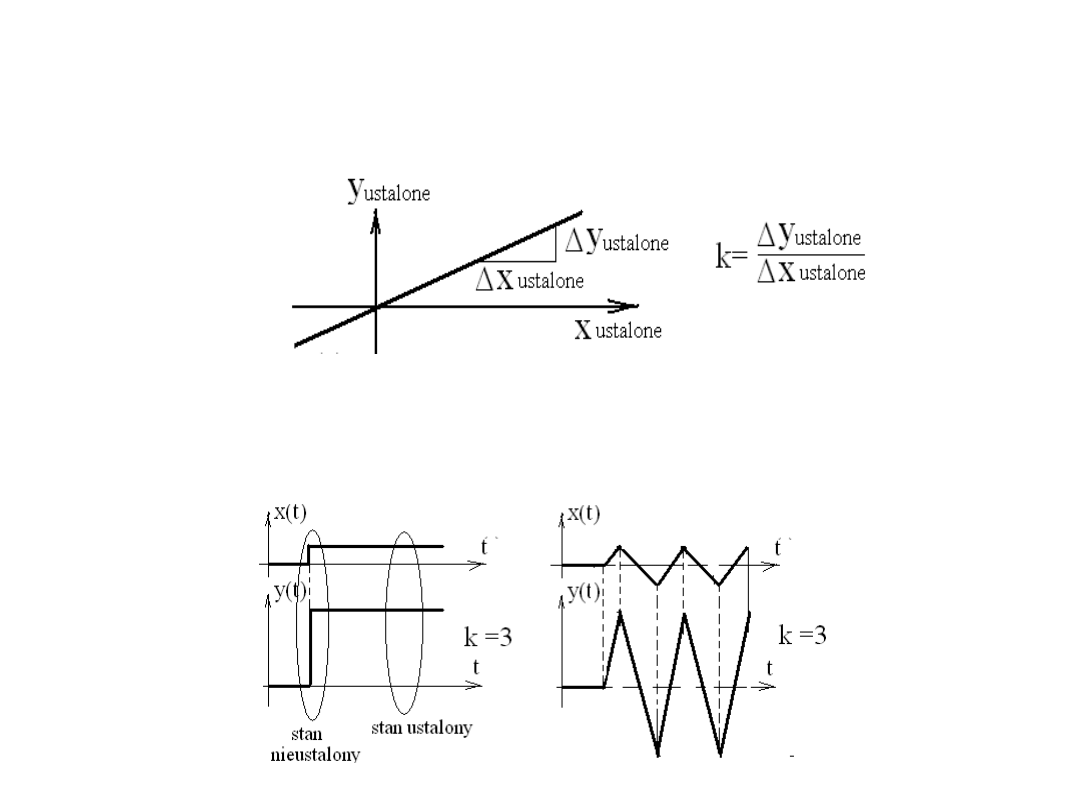
- Charakterystyka statyczna (zależność funkcyjna pomiędzy
ustalonym sygnałem wejściowym i ustalonym sygnałem
wyjściowym):
-Stany nieustalone:
( można analizować przebieg zmian w czasie sygnału
wyjściowego jako odpowiedź na wybrany sygnał wyjściowy np.
skok jednostkowy, liniowy itp..
- odpowiedź na skok jednostkowy i sygnał liniowy dla „k” =3
y(t)=3x(t)
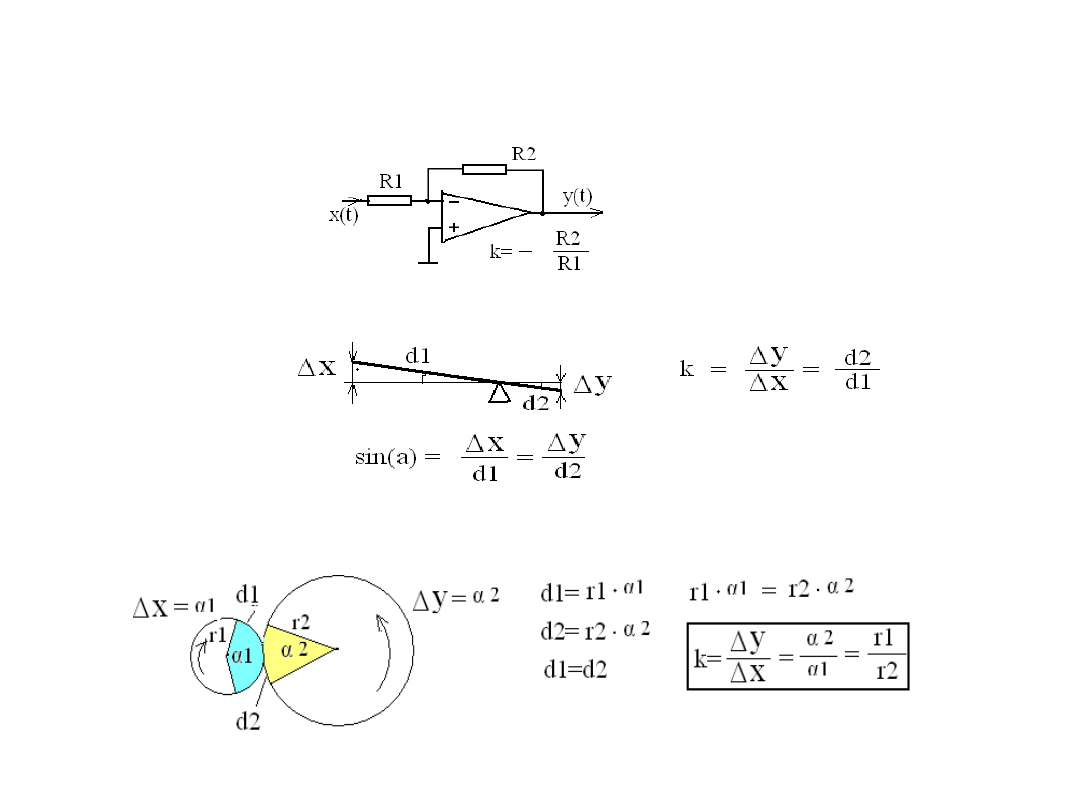
- Element proporcjonalny c.d.
Przykłady urządzeń technicznych będących elementami
proporcjonalnymi
-Elektroniczny wzmacniacz operacyjny:
- Sztywna równoważnia ( np. w regulatorach pneumatycznych):
- Przekładnia mechaniczna: (np. w kole sterowym):
2. Element inercyjny I rzędu
-równanie różniczkowe
:
-równanie po transformacie Laplace’a:
-transmitancja operatorowa:
)
(
)
(
)
(
t
x
k
t
y
dt
t
dy
T
)
(
)
(
)
(
s
x
k
s
y
s
y
s
T
sT
k
s
x
s
y
s
G
1
)
(
)
(
)
(
element inercyjny c.d.
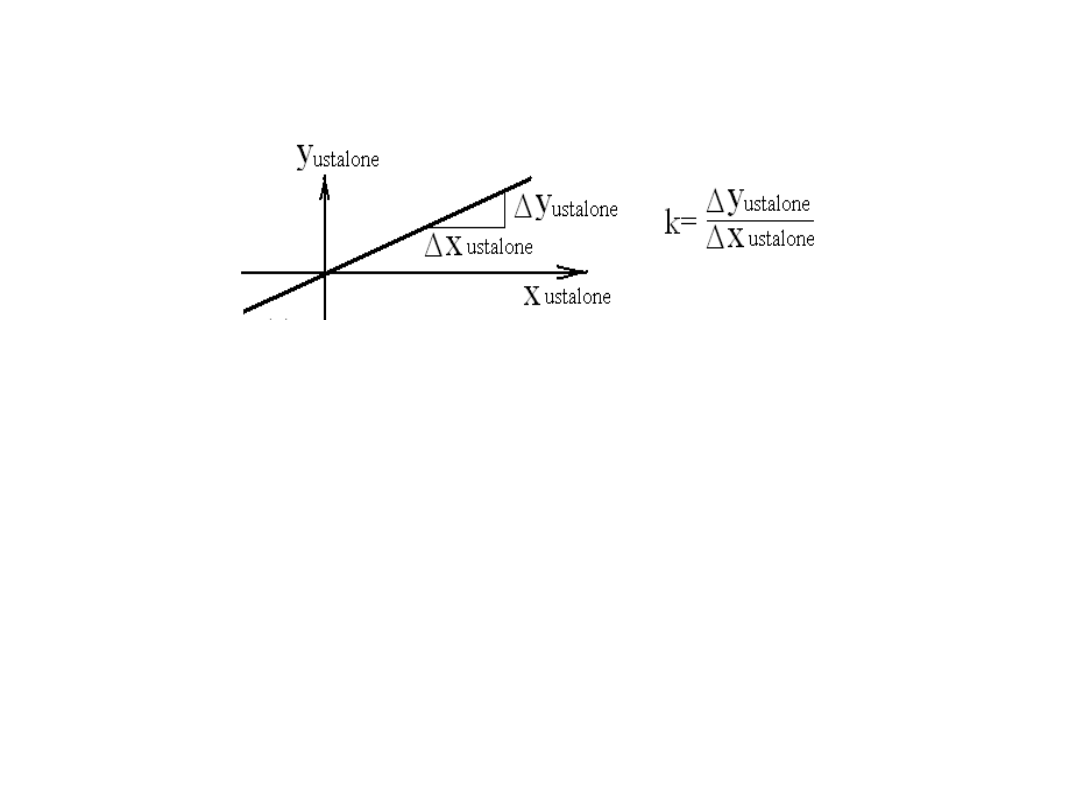
- Charakterystyka statyczna (zależność funkcyjna pomiędzy
ustalonym sygnałem wejściowym i ustalonym sygnałem
wyjściowym):
Stany nieustalone:
(odpowiedź na skok jednostkowy)
Definicja stałej czasowej elementu inercyjnego I rzędu
Stała czasowa elementu inercyjnego I rzędu to czas,
po którym sygnał wyjściowy y(t) osiąga wartość
równą 63.2% swojej wartości ustalonej po
pobudzeniu go skokiem jednostkowym
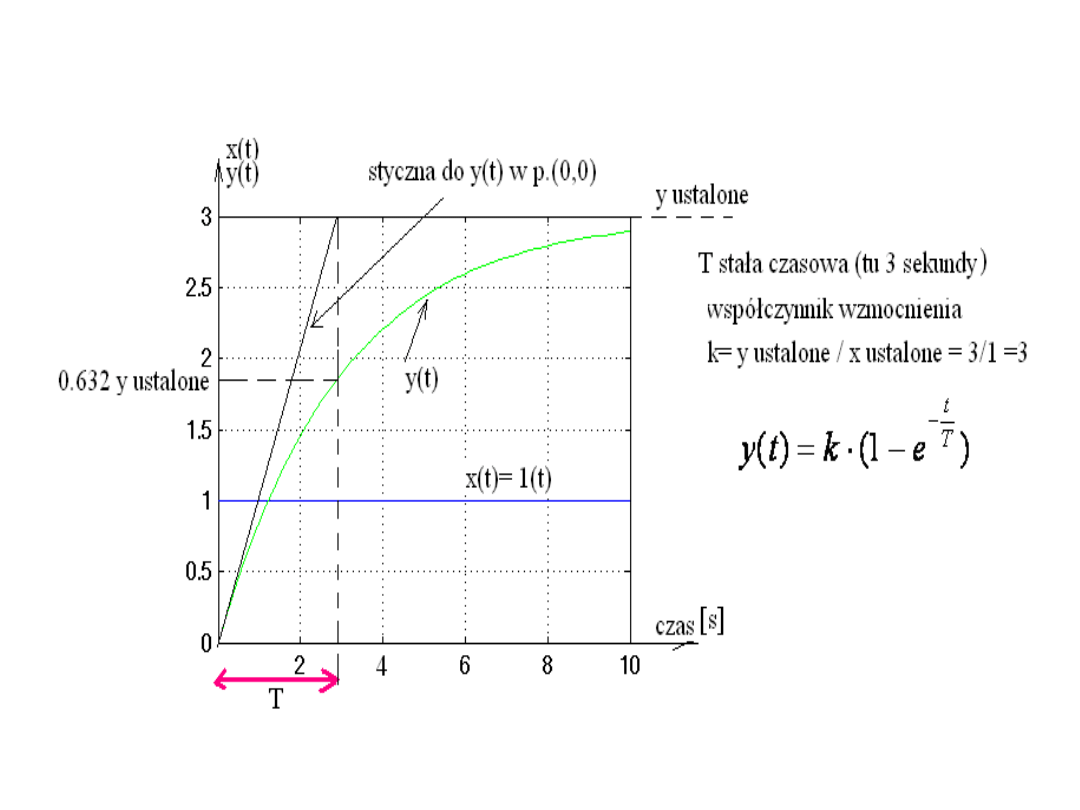
Odpowiedź elementu inercyjnego I rzędu na skok jednostkowy
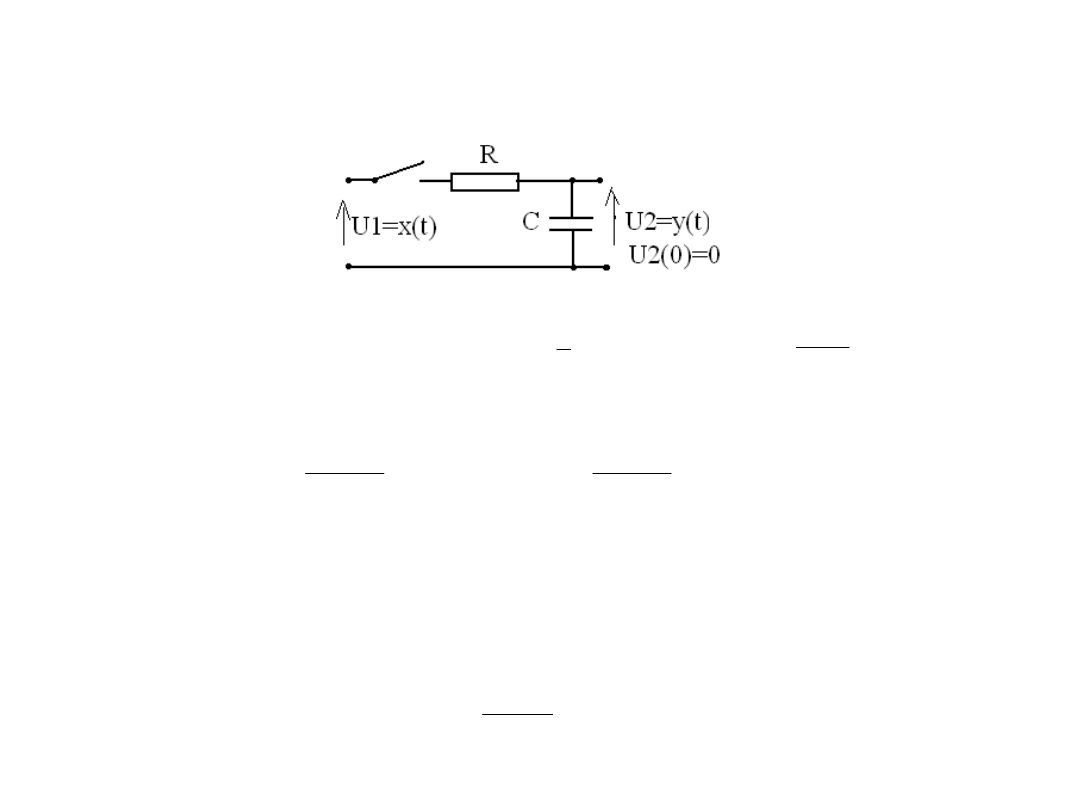
• Przykłady elementów inercyjnych I rzędu
-elektryczny układ RC ( filtr
dolnoprzepustowy)
Równanie oczka elektrycznego
Równanie różniczkowe wiążące U2(t) z U1(t)
Równanie po transformacji Laplace’a:
Transmitancja operatorowa:
R
i
t
U
t
U
)
(
2
)
(
1
t
dt
i
c
t
U
0
1
)
(
2
C
dt
dU
t
i
2
)
(
R
C
dt
t
dU
t
U
t
U
)
(
2
)
(
2
)
(
1
)
(
1
)
(
2
)
(
2
t
U
t
U
dt
t
dU
C
R
T
C
R
sT
s
G
1
1
)
(
)
(
1
)
(
2
)
(
2
s
U
s
U
s
U
s
T
Odpowiedź na skok jednostkowy
- Statek jako obiekt sterowania prędkością kątową
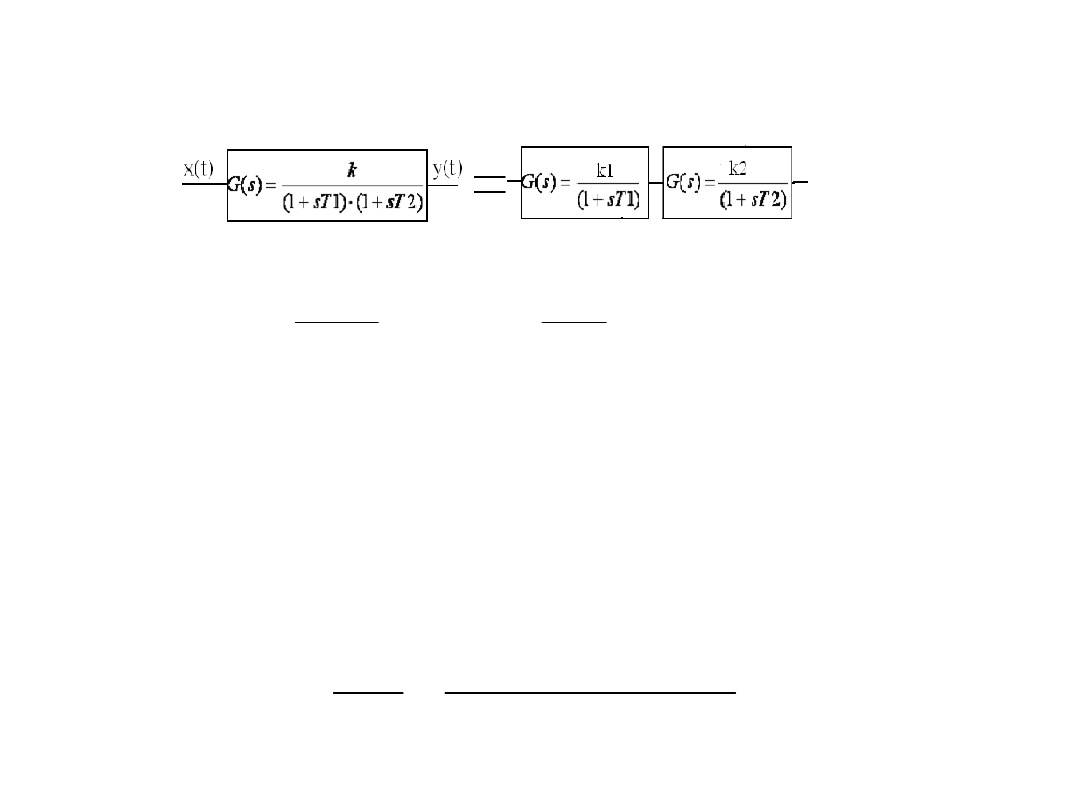
3. Elementy inercyjne wyższych rzędów
- Element inercyjny II rzędu
- Równanie różniczkowe:
- Równanie po transformacji Laplace’a:
- Transmitancja operatorowa:
)
(
)
(
)
(
)
2
1
(
)
(
2
1
2
2
t
x
k
t
y
dt
t
dy
T
T
dt
t
y
d
T
T
)
(
)
(
)
(
)
2
1
(
)
(
2
1
2
s
x
k
s
y
s
y
s
T
T
s
y
s
T
T
)
(
]
1
)
2
1
(
2
1
[
)
(
2
s
x
k
s
T
T
s
T
T
s
y
)
(
)]
2
1
(
)
1
1
[(
)
(
s
x
k
T
s
T
s
s
y
)
(
)]
2
1
(
)
1
1
[(
)
(
s
x
k
T
s
T
s
s
y
)
2
1
(
)
1
1
(
)
(
)
(
)
(
sT
sT
k
s
x
s
y
s
G
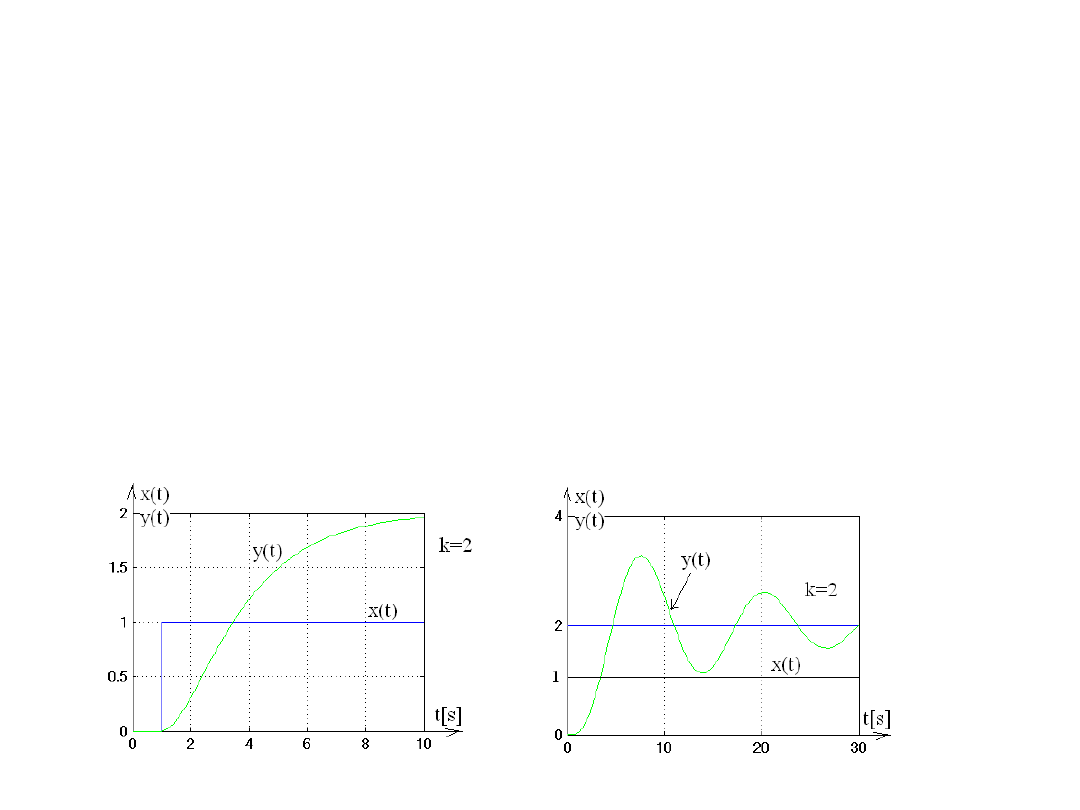
Uwagi:
- element inercyjny II rzędu charakteryzuje się dwiema stałymi
czasowymi
T1 i T2 oraz wzmocnieniem „k”;
- związek pomiędzy sygnałem wejściowym x(t)i sygnałem
wyjściowym y(t) opisuje liniowe równanie różniczkowe drugiego
stopnia;
- transmitancja takiego elementu może być przedstawiona jako
iloczyn transmitancji dwóch elementów inercyjnych I rzędu;
- własności dynamiczne zależą od wartości T1 i T2: element może
odpowiedzieć na skok jednostkowy aperiodycznie lub oscylacyjnie.
Własności dynamiczne (odpowiedź na skok jednostkowy)
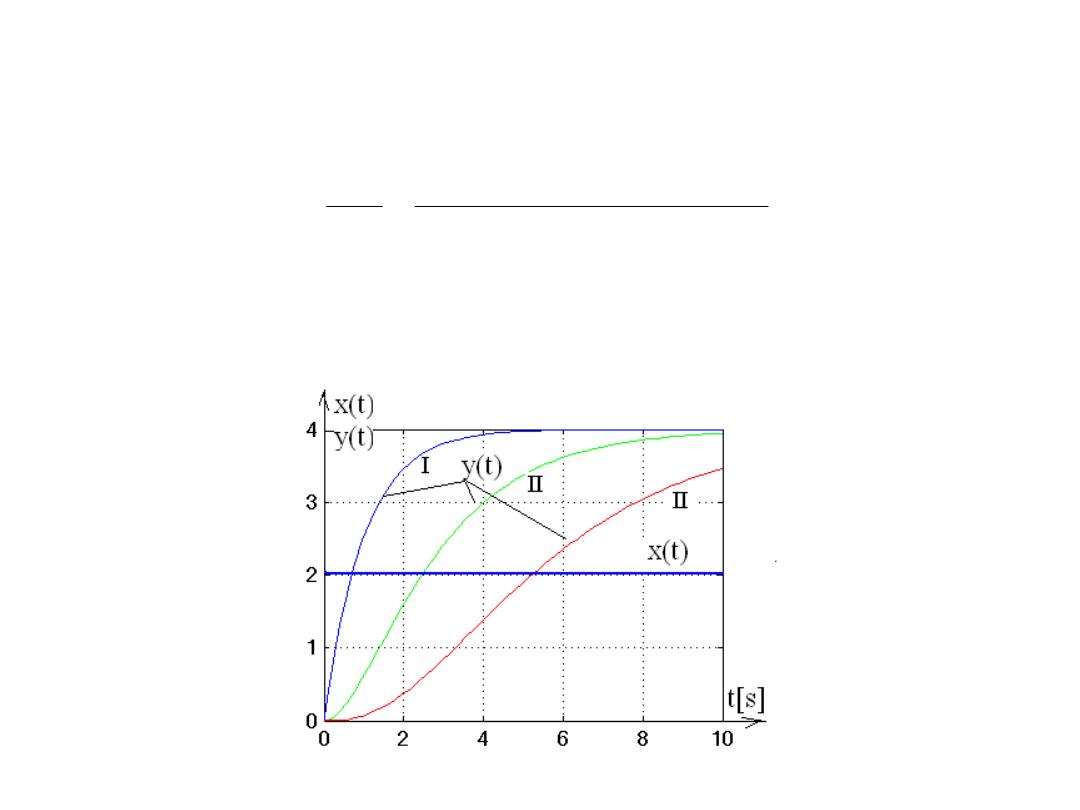
- Elementy inercyjne wyższych rzędów
- Elementy te można opisywać transmitancjami będącymi
iloczynami transmitancji I rzędu np.: transmitancja elementu III
rzędu ma postać:
- doświadczalne wyznaczenie stałych czasowych T1, T2, T3 jest
trudne
( z reguły nie wiemy którego rzędu jest element inercyjny)
- odpowiedzi na skok jednostkowy elementów wyższych rzędów:
)
3
1
(
)
2
1
(
)
1
1
(
)
(
)
(
)
(
sT
sT
sT
k
s
x
s
y
s
G
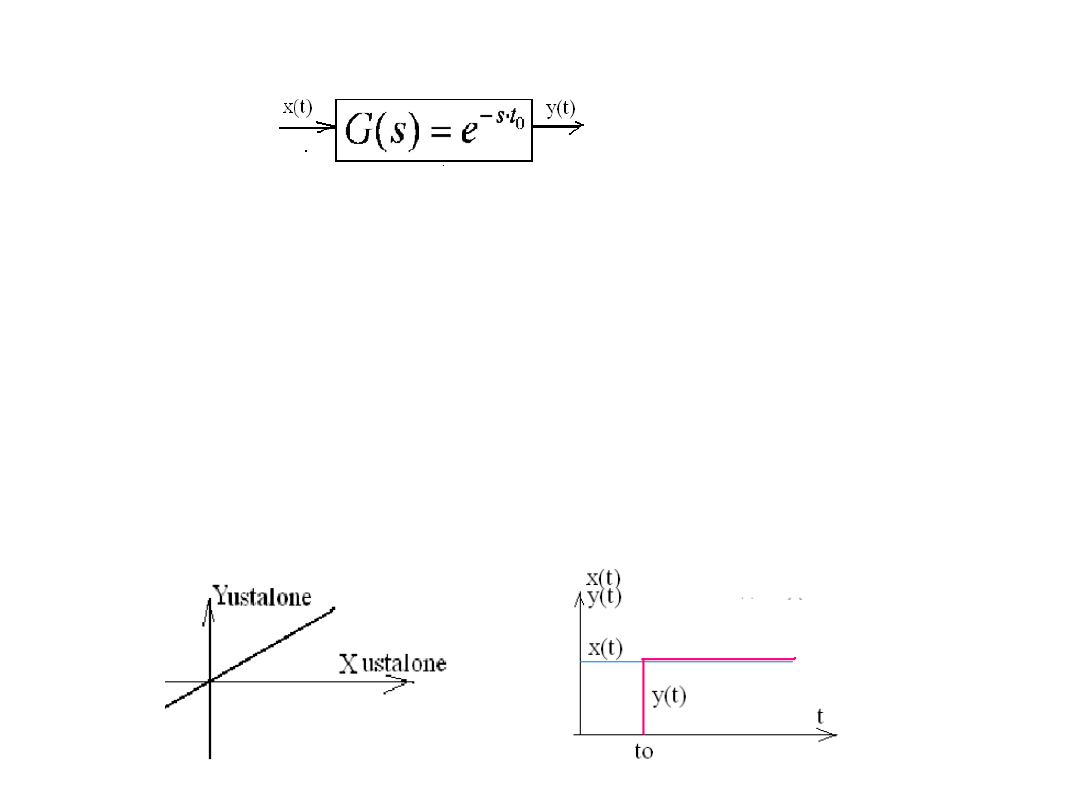
4. Element opóźniający:
- Równanie różniczkowe ( zerowego rządu):
- Równanie po transformacji Laplace;a:
- Transmitancja operatorowa:
- Charakterystyki (statyczna, odpowiedź na skok jednostkowy):
)
(
)
(
0
t
t
x
t
y
0
)
(
)
(
t
s
e
s
x
s
y
0
)
(
t
s
e
s
G
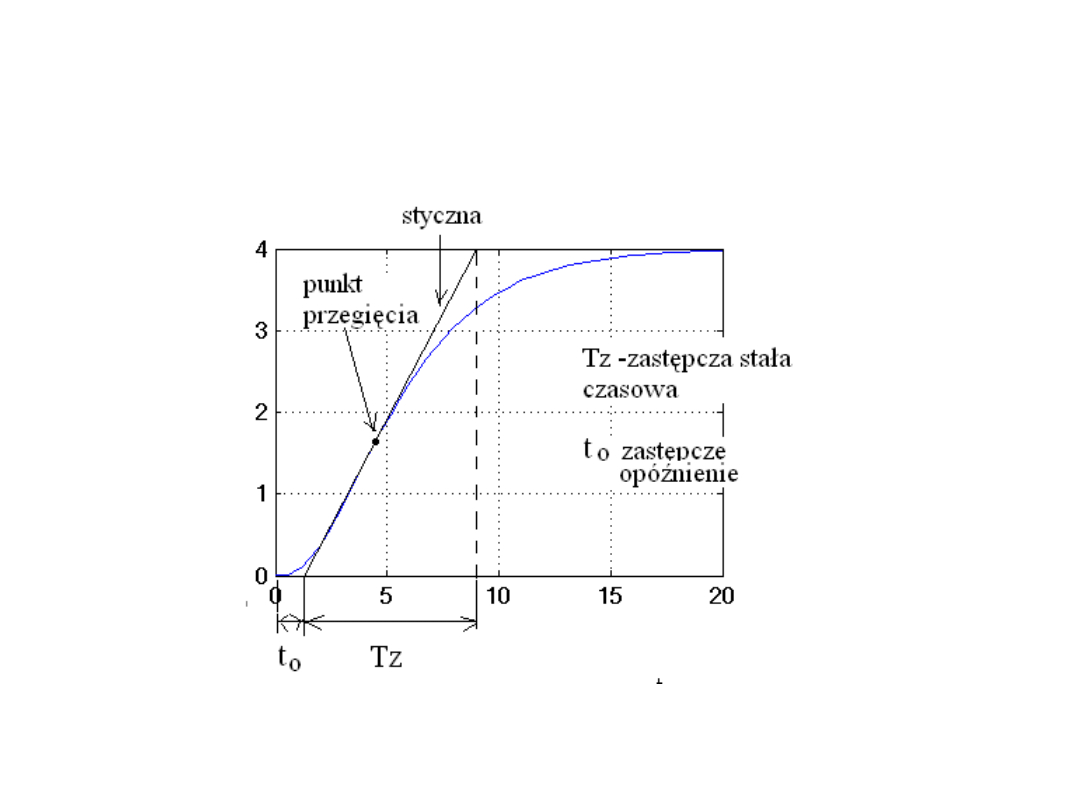
Aproksymacja elementu inercyjnego wyższego rzędu elementem inercyjnym
I rzędu z opóźnieniem
- W opisie matematycznym elementów inercyjnych stosuje się uproszczenia zastępując złożone
transmitancje z wieloma stałymi czasowymi elementem inercyjnym I rzędu z opóźnieniem
- Procedura określenia Tz i to:
- 1. określićpunk przegięcia krzywej,
- 2. poprowadzic styczną w punkcie przegięcia,
- 3. poprowadzić styczną poziomą do krzywej dla nieskończoności,
- 4. odczytać z punktów przecięcia wartości stycznych i osi czasu wartości
„Tz” oraz „to”,
5. przyjąc transmitancję elementu inercyjnego wyższegorzędu jako:
Procedura określenia „Tz” i „to”(zastepczej stałej
czasowej i zastępczego opóźnienia)
- 1. określić punkt przegięcia krzywej,
- 2. poprowadzić styczną w punkcie przegięcia,
- 3. poprowadzić styczną poziomą do krzywej (dla czasu w
nieskończoności),
- 4. odczytać z punktów przecięcia stycznych i osi czasu wartości
„Tz” oraz „to”,
5. przyjąc transmitancję elementu inercyjnego wyższego rzędu
jako:
gdzie:
0
1
)
(
t
s
e
Tz
s
k
s
G
ustalone
ustalone
x
y
k
5. Element inercyjny II rzędu oscylacyjny
Równanie różniczkowe:
- dla przypadku :
- Przy oznaczeniach:
ωo częstotliwość drgań własnych
β współczynnik tłumienia
)
(
)
(
)
(
)
2
1
(
)
(
2
1
2
2
t
x
k
t
y
dt
t
dy
T
T
dt
t
y
d
T
T
0
2
1
4
)
2
1
(
2
T
T
t
T
2
0
1
2
1
T
T
0
2
)
2
1
(
T
T
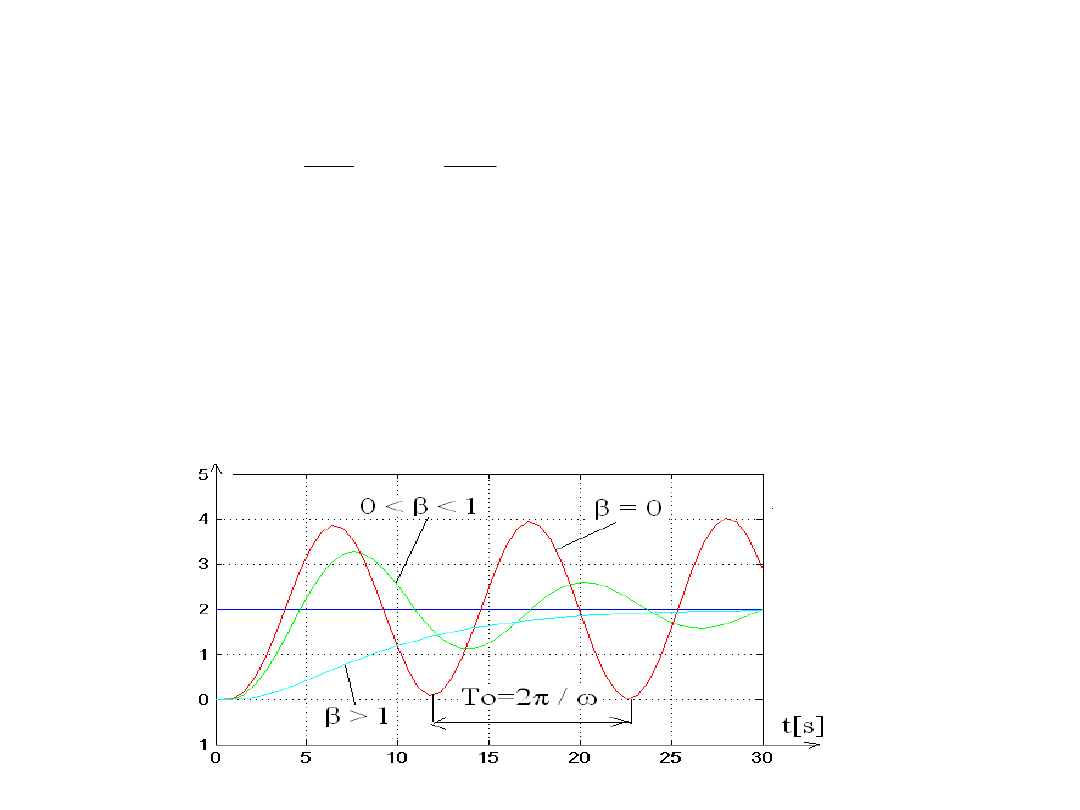
• c.d. element oscylacyjny
- Równanie po transformacji Laplace’a:
- Wyrażenie w nawiasie może mieć pierwiastki:
• dwa pierwiastki rzeczywiste β > 1 (element inert. II rzedu)
• pierwiastek podwójny rzeczywisty β = 1 (element inert. II rzędu)
• dwa pierwiastki zespolone β < 1 (element oscylacyjny )
Odpowiedź elementu oscylacyjnego na skok jednostkowy dla
różnych β)
)
(
]
1
2
1
[
)
(
0
2
2
0
s
x
k
s
s
s
y