Radioactivity

 

 

Radiation

Radiation

: The process of emitting 

energy in the form of waves or 
particles.

Where does radiation come from?

Radiation is generally produced 
when particles interact or decay.

A large contribution of the radiation
on earth is from the sun (solar) or 
from radioactive isotopes of the 
elements  (terrestrial).

Radiation is going through you at
this very moment!

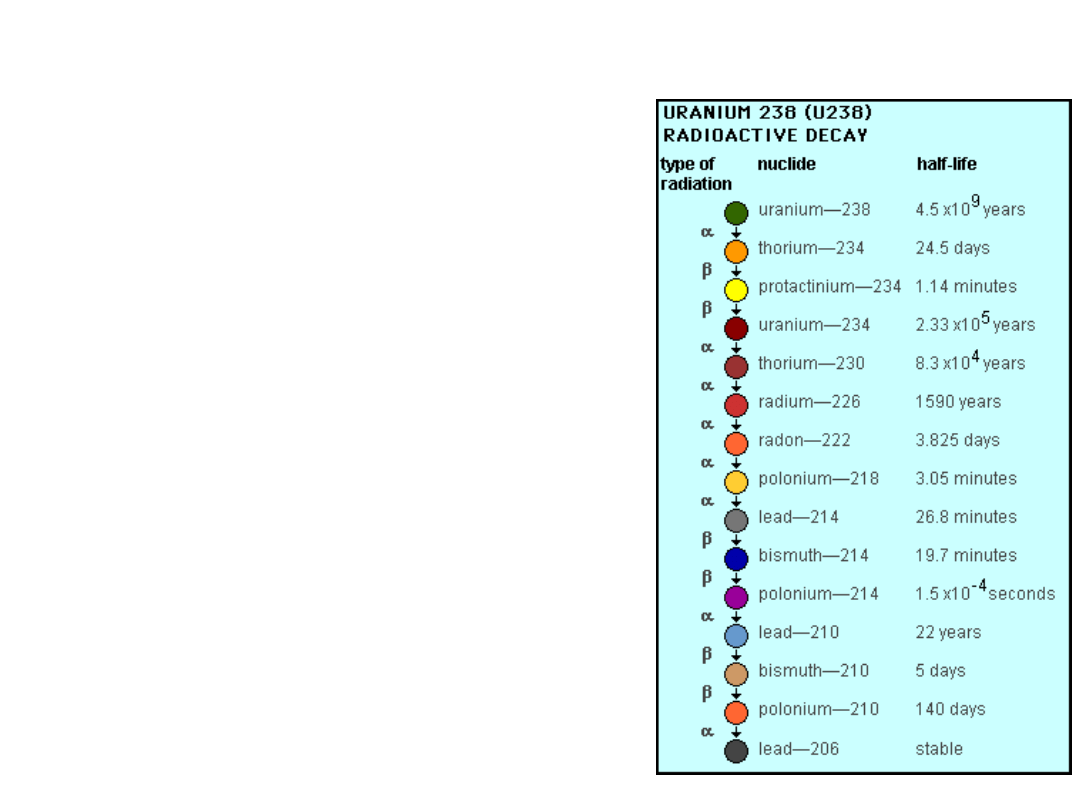
http://www.atral.com/U238.html

 

 

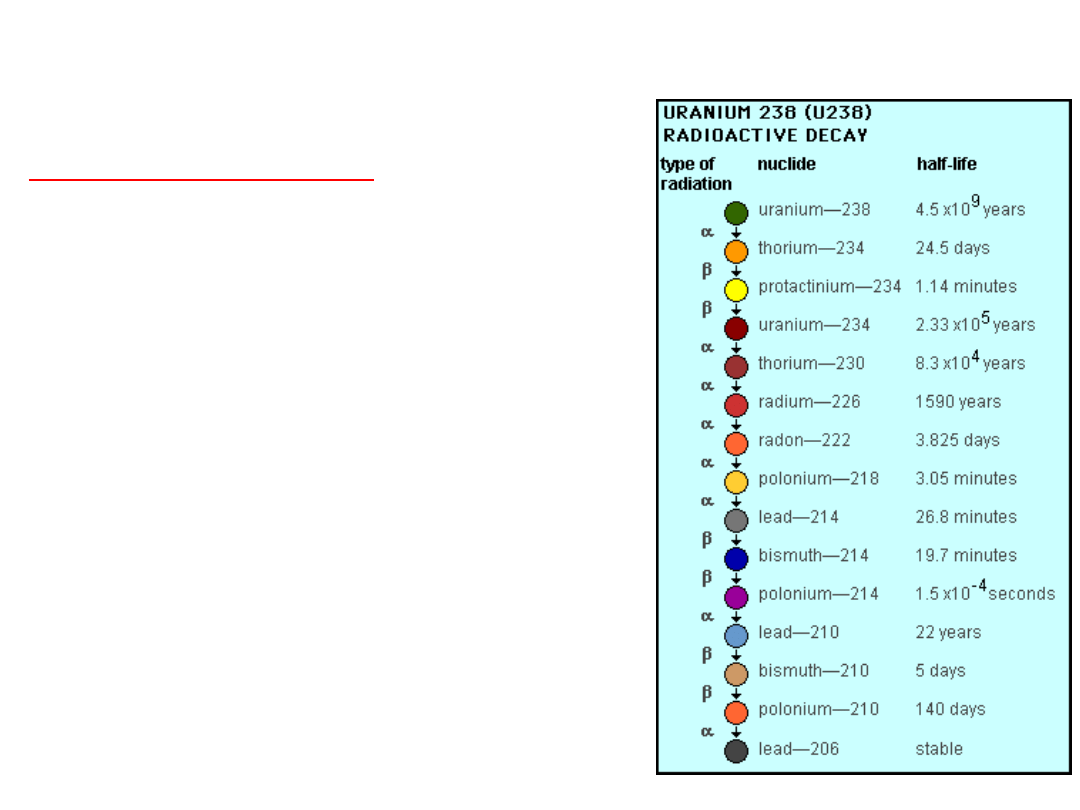
Isotopes

What’s an isotope?

Two or more varieties of an 
element  
having the same number of 
protons but 
different number of neutrons. 
Certain  
isotopes are “unstable” and 
decay to 
lighter isotopes or elements.

Deuterium

 and 

tritium

 are 

isotopes of hydrogen. In 
addition to the 1 proton, they 
have 1 and 2 additional 
neutrons in the nucleus 
respectively*.

Another prime example is 
Uranium 238, or just 

238

U.

 

 

Radioactivity

By the end of the 1800s, it was known that certain 
isotopes emit penetrating rays. Three types of radiation 
were known:

1) Alpha particles  ()

2) Beta particles    ()

3) Gamma-rays       ()

By the end of the 1800s, it was known that certain 
isotopes emit penetrating rays. Three types of radiation 
were known:

1) Alpha particles  

()

2) Beta particles    

()

3) Gamma-rays       

()

 

 

Where do these particles come 

from ?

These particles generally come 
from the 

nuclei of atomic isotopes

 

which are 

not stable

.

 The decay chain of Uranium 
produces all three of these forms
of radiation.

 Let’s look at them in more detail…

 

 

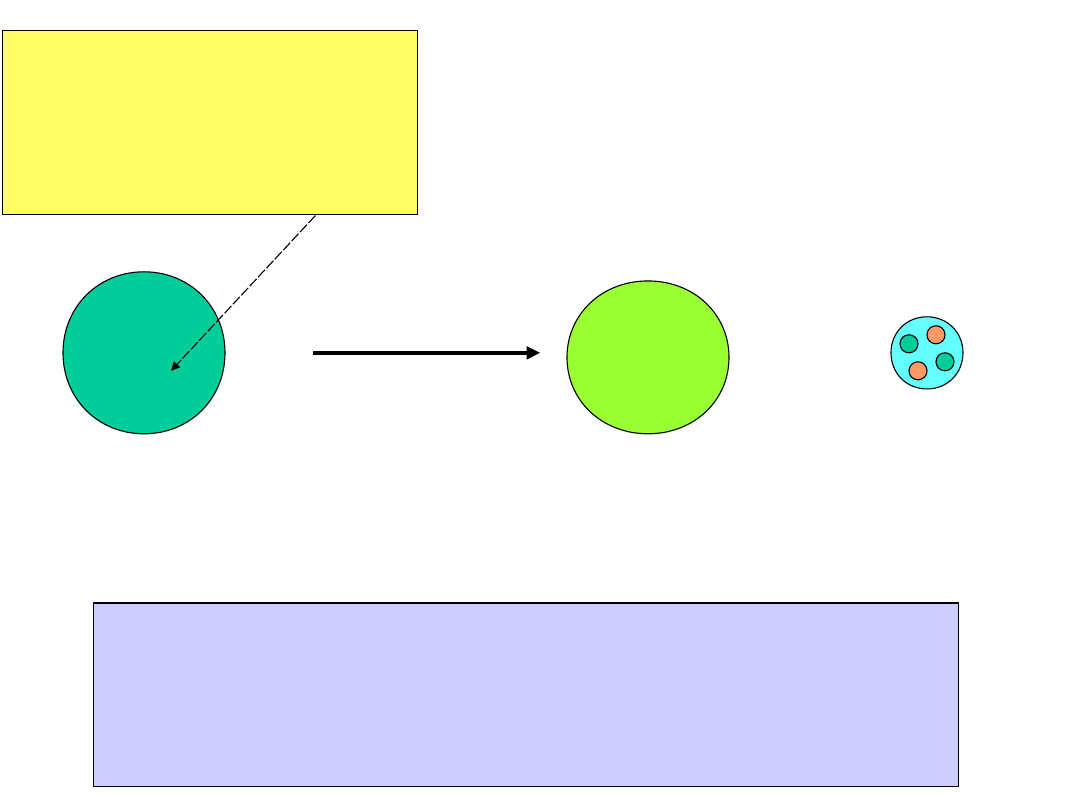
Alpha Particles 

()

Radium

R

226

88   protons
138 neutrons

Radon

Rn

222

Note: This is the
atomic weight, which
is the number of
protons plus neutrons

86   protons
136 neutrons

+

n

n

p

p







He

)

2   protons
2 neutrons

The 

alpha-particle

 



 is a 

Helium nucleus

. 

It’s the same as the element 

Helium

, with the 

electrons stripped of

 !

 

 

Beta Particles ()

Carbon

C

1

6   protons
8   neutrons

Nitrogen

N

1

7   protons
7   neutrons

+

e

-

electron

(beta-particle)

We see that one of the neutrons from the C

1

 nucleus 

“converted” into a proton, and an electron was ejected. 
The remaining nucleus contains 7p and 7n, which is a 

nitrogen

 

nucleus. In symbolic notation, the following process occurred:

n  p + e

   ( + 

Yes, the same 

neutrino we 

saw 

previously

 

 

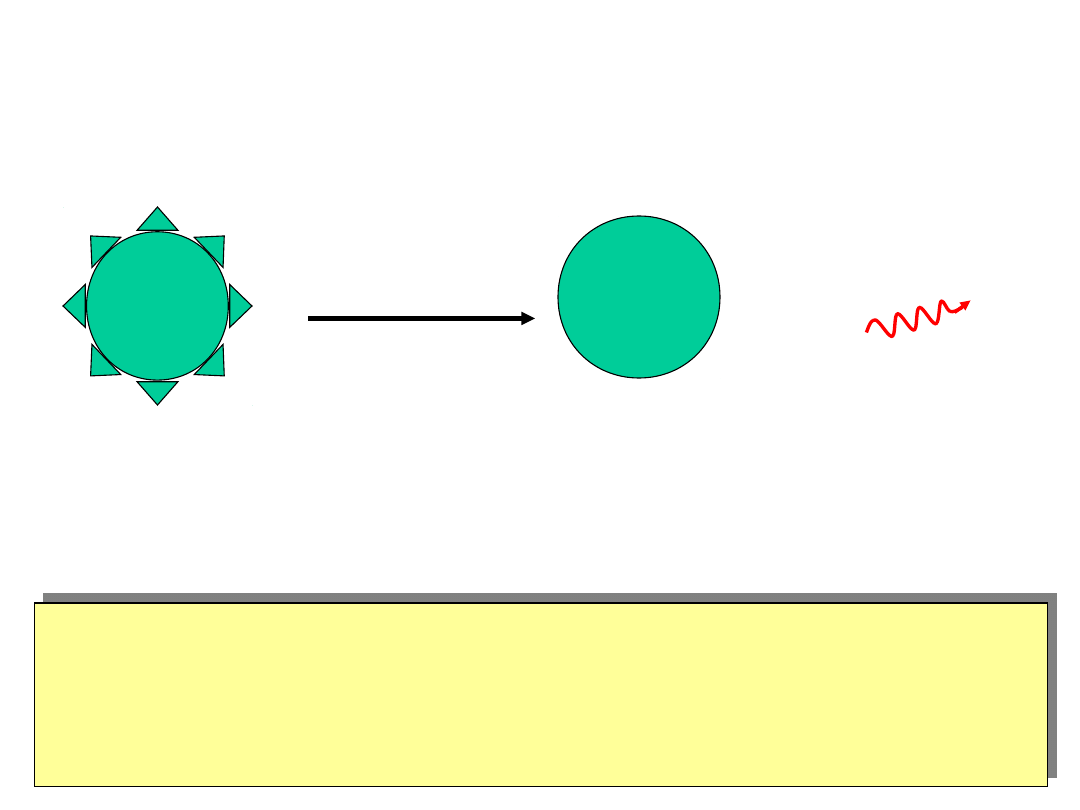
Gamma particles ()

In much the same way that electrons in atoms can be in an 

excited state

, so can a nucleus.

Neon

Ne

20

10   protons

10   neutrons

(in excited state)

10   protons

10   neutrons

(lowest energy state)

+

gamma

Neon

Ne

20

A gamma is a high energy light particle.

It is NOT visible by your naked eye because it is not in 
the visible part of the EM spectrum. 

A 

gamma

 is a high energy 

light particle

.

It is NOT visible by your naked eye because it is not in 
the visible part of the EM spectrum. 

 

 

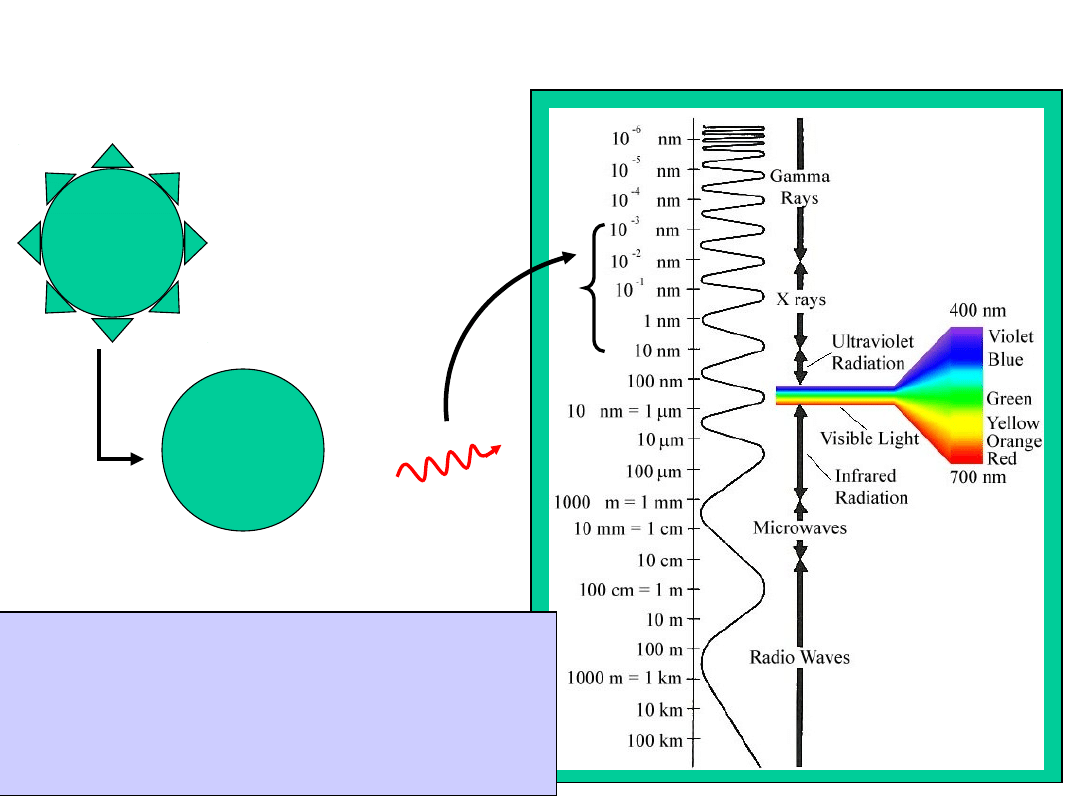
Gamma Rays

Neon

Ne

20

+

The gamma from nuclear decay

is in the X-ray/ Gamma ray 

part of the EM spectrum

(very energetic!)

Neon

Ne

20

 

 

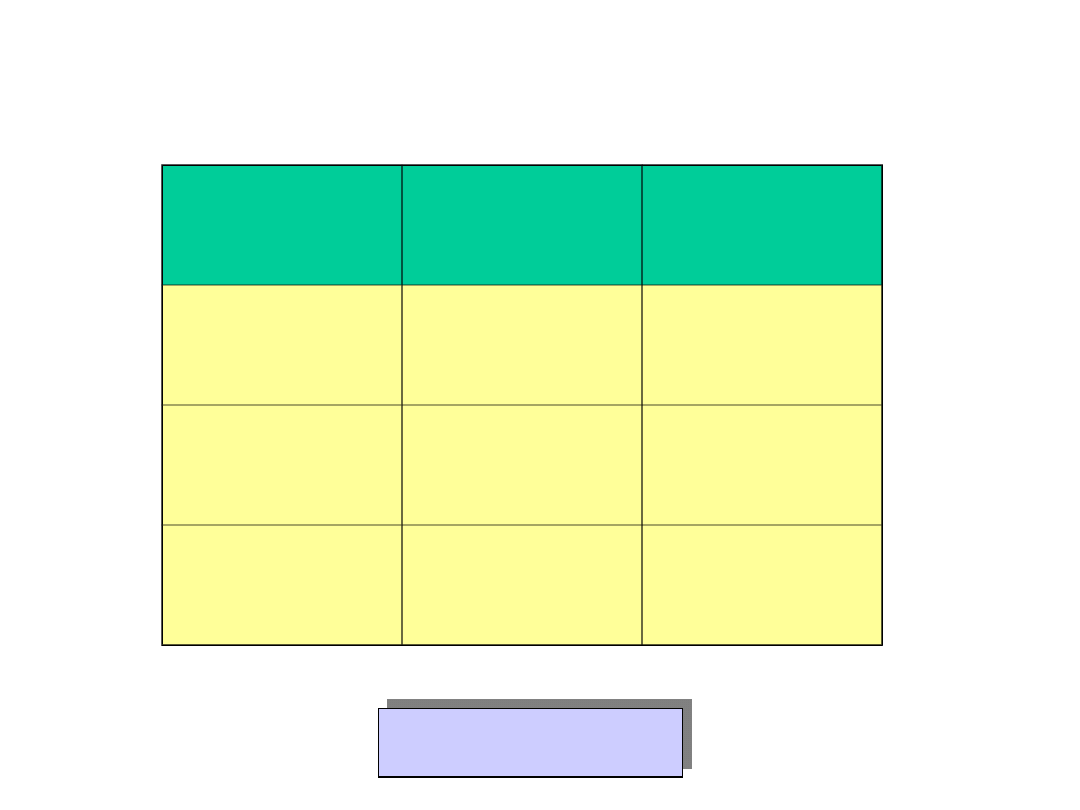
How do these particles 

differ ?

Particle

Mass*

(MeV/c

2

)

Charge

Gamma 

()

0

0

Beta ()

~0.5

-1

Alpha ()

~3752

+2

* m = E / c

2

* m = E / c

2

 

 

Rate of Decay

Beyond knowing the types of particles which are emitted
when an isotope decays, we also are interested in 

how frequently

one of the atoms emits this radiation.

 A very important point here is that we 

cannot predict when a

particular entity will decay

.

 We do know though, that if we had a large sample of a radioactive 
substance, some number will decay after a given amount of time.

 Some radioactive substances have a very high “rate of decay”,
while others have a very low decay rate.

 To differentiate different radioactive substances, we look to

quantify

 this idea of “

decay rate

”

 

 

Half-Life

 The 

“half-life” (h)

 is the time it takes for 

half the atoms

 of a 

radioactive substance to decay.

 For example, suppose we had 20,000 atoms of a radioactive 
substance. If the half-life is 1 hour, how many atoms of that 
substance would be left after:

10,000              (50%)

 5,000                (25%)

 2,500               (12.5%)

1 hour (one lifetime) ?

2 hours (two lifetimes) ?

3 hours (three lifetimes) ?

Time 

#atoms

remaining

% of atoms

remaining

 

 

Lifetime ()

 The “lifetime” of a particle is an alternate definition of
the rate of decay, one which we prefer.

 It is just another way of expressing how fast the substance
decays..

 It is simply: 1.44 x h, and one often associates the 
letter “” to it.

 The lifetime of a “free” neutron is 14.7 minutes 
     {neutron=14.7 min.}

 Let’s use this a bit to become comfortable with it…     

 The 

“lifetime”

 of a particle is an alternate definition of

the 

rate of decay

, one which we prefer.

 It is just another way of expressing how fast the substance
decays..

 It is simply: 

1.44 x h, and one often associates the 

letter 

“”

 to it.

 

The lifetime of a 

“free”

 neutron is 14.7 minutes 

     {neutron=14.7 min.}

 Let’s use this a bit to become comfortable with it…     

 

 

Lifetime (I)

 The lifetime of a free neutron is 1.7 minutes.

 If I had 1000 free neutrons in a box, after 1.7 
minutes some number of them will have decayed.

 The 

number remaining

 after some time is given by the 

radioactive decay law

/

0

t

N N e

t

-

=

/

0

t

N N e

t

-

=

N

0

 = starting 

number of       
particles



 

  = particle’s 

lifetime

This is the “exponential”. It’s 
value is 2.718, and is a very useful
number. Can you find it on your
calculator?

 

 

Lifetime (II)

/

0

t

N N e

t

-

=

Note by slight rearrangement of this formula:

Fraction

 of particles which 

did not decay

:      

N / N

0

 = 

e

-t/



# 

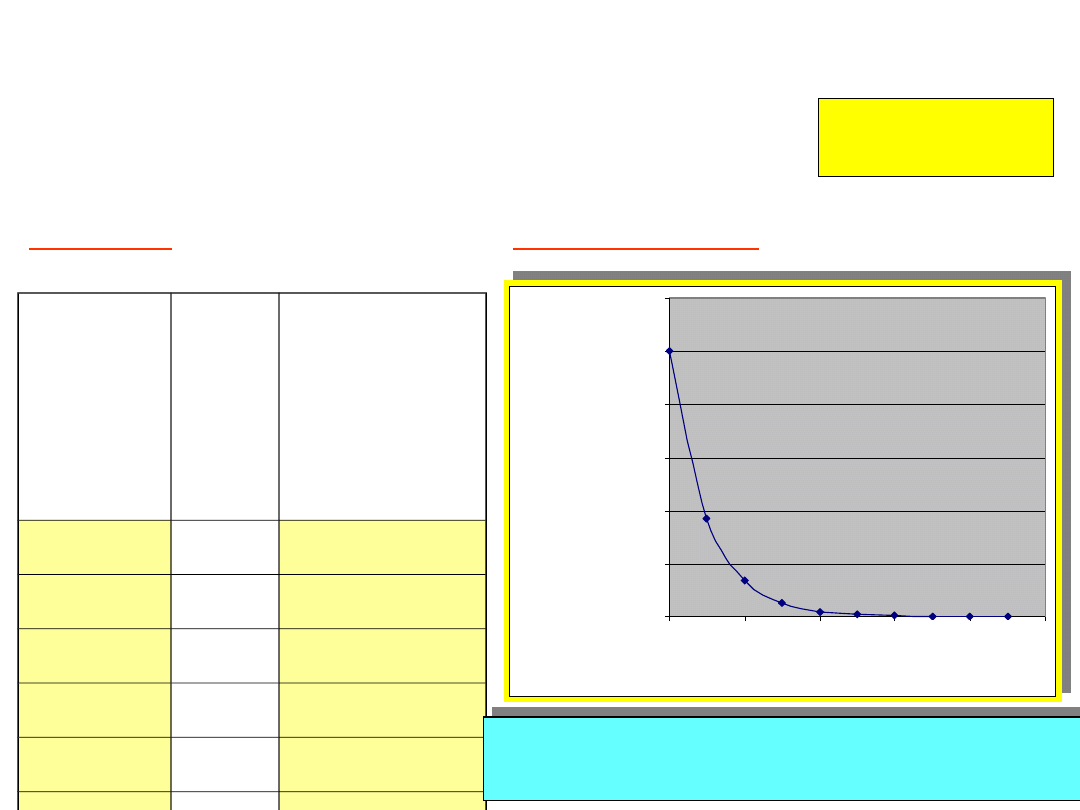
lifetim

es

Tim

e

(min

)

Fraction 

of 

remainin

g

neutrons

0

0

1.0

1

14.7

0.368

2

29.4

0.135

3

44.1

0.050

4

58.8

0.018

5

73.5

0.007

0.00

0.20

0.0

0.60

0.80

1.00

1.20

0

2



6

8

10

Lifetimes

F

ra

ct

io

n

 S

u

rv

iv

ed

0.00

0.20

0.0

0.60

0.80

1.00

1.20

0

2



6

8

10

Lifetimes

F

ra

ct

io

n

 S

u

rv

iv

ed

After -5 lifetimes, almost all of the
unstable particles have decayed away!

After -5 lifetimes, almost all of the
unstable particles have decayed away!

 

 

Lifetime (III)

 Not all particles have the same lifetime.

 Uranium-238 has a lifetime of about 6 billion 
    (6x10

9

) years !

 Some subatomic particles have lifetimes that are 
    less than 1x10

-12

 sec !

 Given a batch of unstable particles, we cannot
say which one will decay.

 The process of decay is statistical. That is, we can 
only talk about either, 

1) the lifetime of a radioactive substance*,     or
2) the “probability” that a given particle will decay.

 Not all particles have the same lifetime.

 Uranium-238 has a lifetime of about 

6 billion 

    (6x10

9

) years

 !

 Some 

subatomic particles

 have lifetimes that are 

    less than 

1x10

-12

 sec

 !

 Given a batch of unstable particles, we 

cannot

say which one will decay

.

 The process of decay is 

statistical

. That is, we can 

only talk about either, 

1) the 

lifetime

 of a radioactive substance*,     or

2) the “

probability

” that 

a given particle will decay

.

 

 

Lifetime (IV)

 Given a batch of 1 species of particles, some will decay 
within 1 lifetime (1, some within 2, some within 3and 

so on…

 We CANNOT say “

Particle 44 will decay at t =22 min

”. 

You just can’t !

 All we can say is that:

 After 

1

 

lifetime

, there will be 

(37%) 

remaining

 After 

2 lifetimes

, there will be 

(1%) 

remaining

 After 

3 lifetimes

, there will be 

(5%) 

remaining

 After 

 lifetimes

, there will be 

(2%) 

remaining

, etc

 

 

Lifetime (V)

 If the particle’s lifetime is very short, the particles 
decay away very quickly. 

 When we get to subatomic particles, the lifetimes
are typically only a small fraction of a second!

 If the lifetime is long (like 

238

U) it will hang around 

for a very long time!

 If the particle’s lifetime is very short, the particles 
decay away very quickly. 

 When we get to subatomic particles, the lifetimes
are typically only a small fraction of a second!

 If the lifetime is long (like 

238

U) it will hang around 

for a very long time!

 

 

Lifetime (IV)

What if we only have 1 particle before us? What can we say
about it? 

  

Survival Probability   =

   

N / N

0

 = e

-t/



           

Decay Probability

 = 1.0 – (Survival Probability)

# 

lifetimes

Survival 

Probability

  

(percent)

Decay Probability

 = 

1.0 – Survival Probability 

(Percent)

1

37%

63%

2

14%

86%

3

5%

95%

4

2%

98%

5

0.7%

99.3%

 

 

Summary

 Certain particles are radioactive and undergo decay. 

 Radiation in nuclear decay consists of , , and  particles

 The rate of decay is give by the radioactive decay law:

Survival Probability = (N/N

0

)e

-t/

 After 5 lifetimes more than 99% of the initial particles 
have decayed away.

 Some elements have lifetimes ~billions of years. 

 Subatomic particles usually have lifetimes which are
    fractions of a second… We’ll come back to this!

 Certain particles are radioactive and undergo decay. 

 Radiation in nuclear decay consists of , , and  particles

 The rate of decay is give by the radioactive decay law:

Survival Probability = (N/N

0

)e

-t/

 After 5 lifetimes more than 99% of the initial particles 
have decayed away.

 Some elements have lifetimes ~billions of years. 

 Subatomic particles usually have lifetimes which are
    fractions of a second… We’ll come back to this!