Twierdzenie Thevenina-

Twierdzenie Thevenina-

Nortona

Nortona

Twierdzenie Thevenina-

Twierdzenie Thevenina-

Nortona

Nortona

u

i

A

B

G

z

i

z

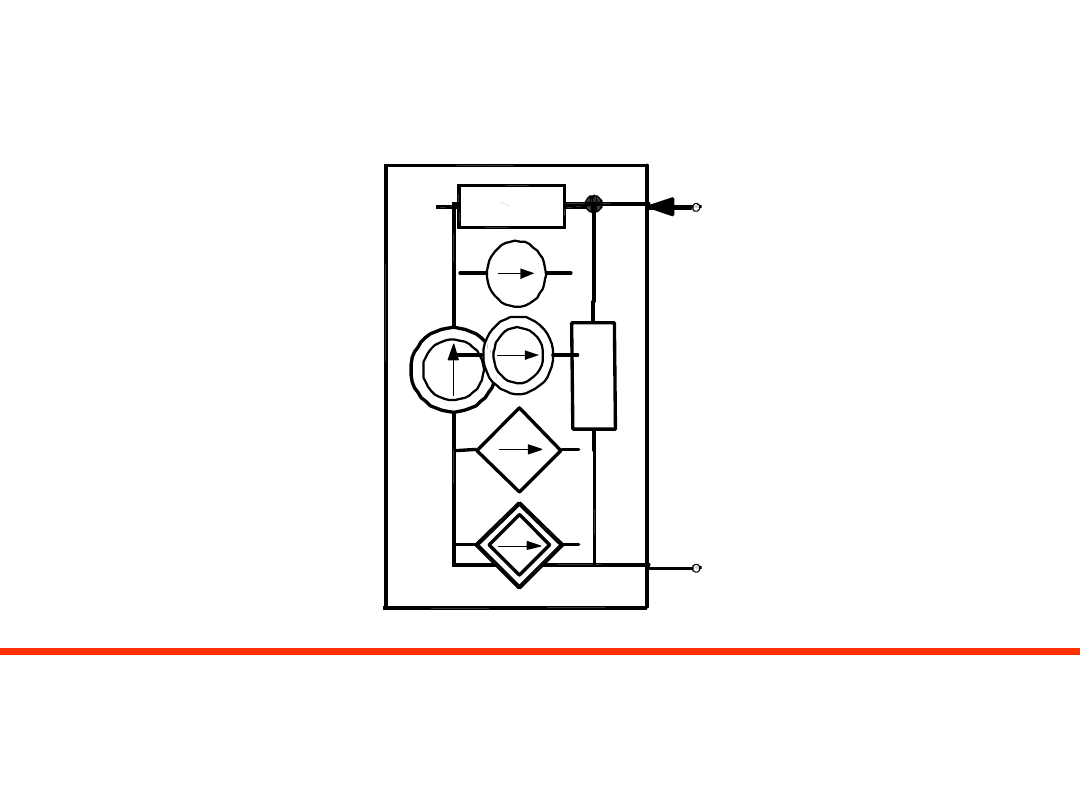
A. Twierdzenie Nortona

Każdy liniowy dwójnik aktywny można zastąpić z wybranej pary zacisków AB
rzeczywistym źródłem prądu o parametrach i

z

i G

z.

Prąd i

z

jest prądem zwarciowym, a konduktancję liczymy z zacisków AB

po usunięciu wszystkich źródeł niezależnych.

u

i

A

B

u

z

R

z

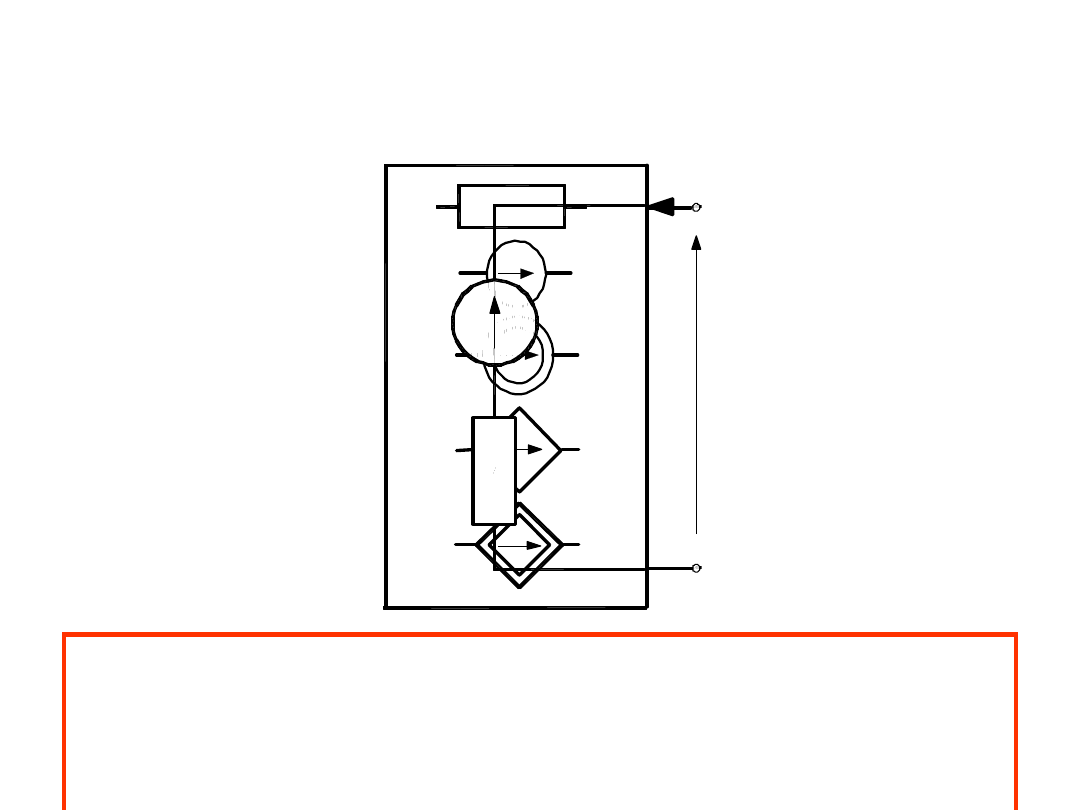
A. Twierdzenie Thevenina

Każdy liniowy dwójnik aktywny można zastąpić z
wybranej pary zacisków AB rzeczywistym źródłem
napięcia o parametrach u

z

i R

z

.

Napięcie u

z

występuje na rozwartych zaciskach AB, a

rezystancję liczymy z zacisków AB po usunięciu
wszystkich źródeł niezależnych.

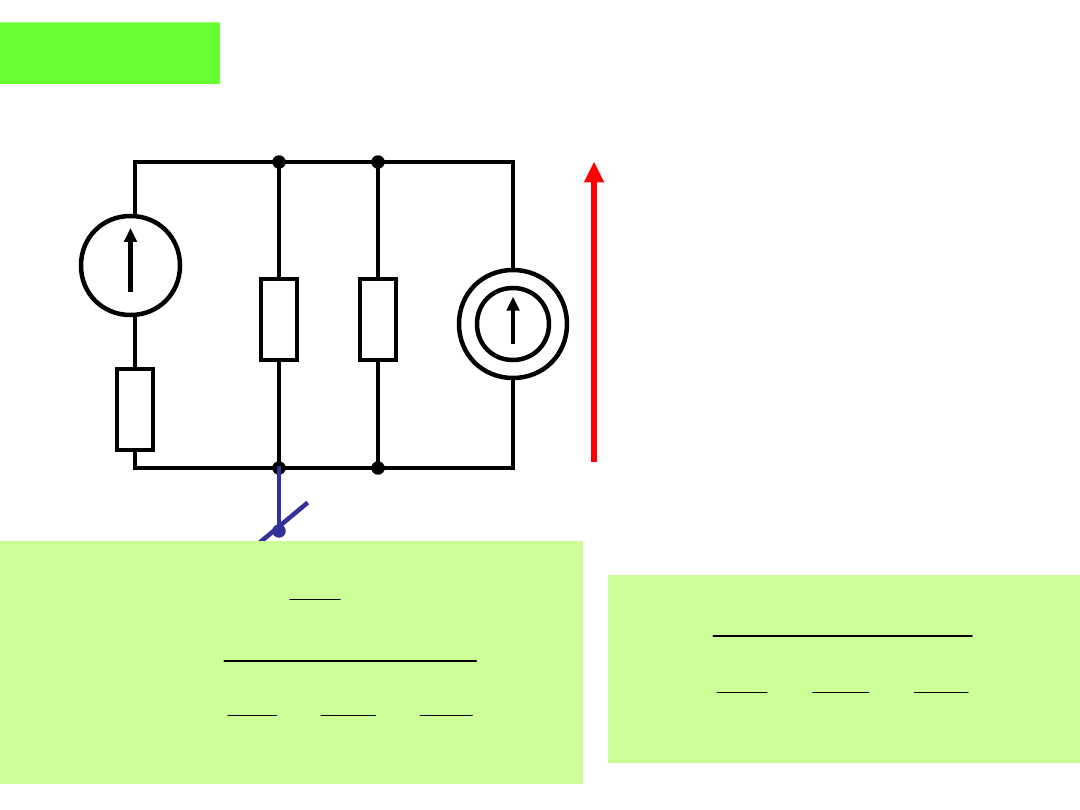
Przykład:

E

1

J

R

1

R

2

R

3

Wyznaczymy parametry dwójnika Thevenina (E

z

i R

z

)

widzianego z zacisków AB.

Dane:

A

J

V

E

R

R

R

2

4

3

6

2

1

3

2

1

















A

B

U

AB

V

R

R

R

J

R

E

V

u

A

AB

4

1

1

1

3

2

1

1

1























1

1

1

1

1

3

2

1

R

R

R

R

z

A

B

E

z

R

z

V

E

Z

4





1

Z

R

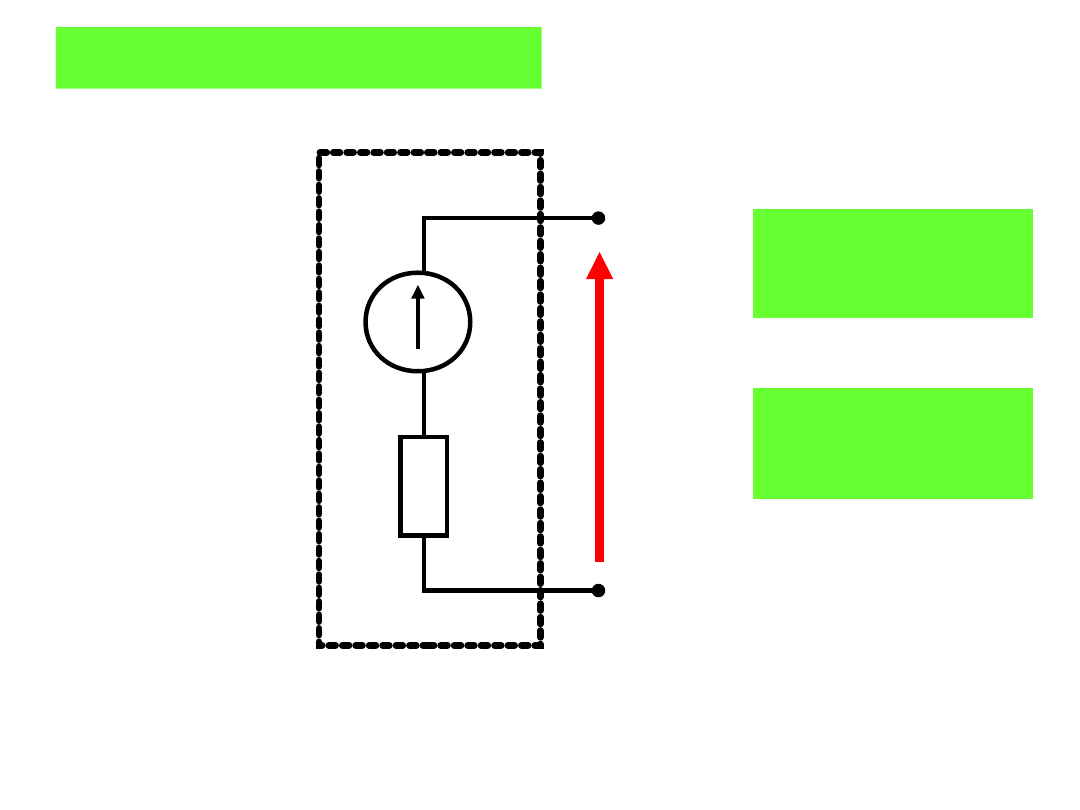
Dwójnik Thevenina:

u

AB

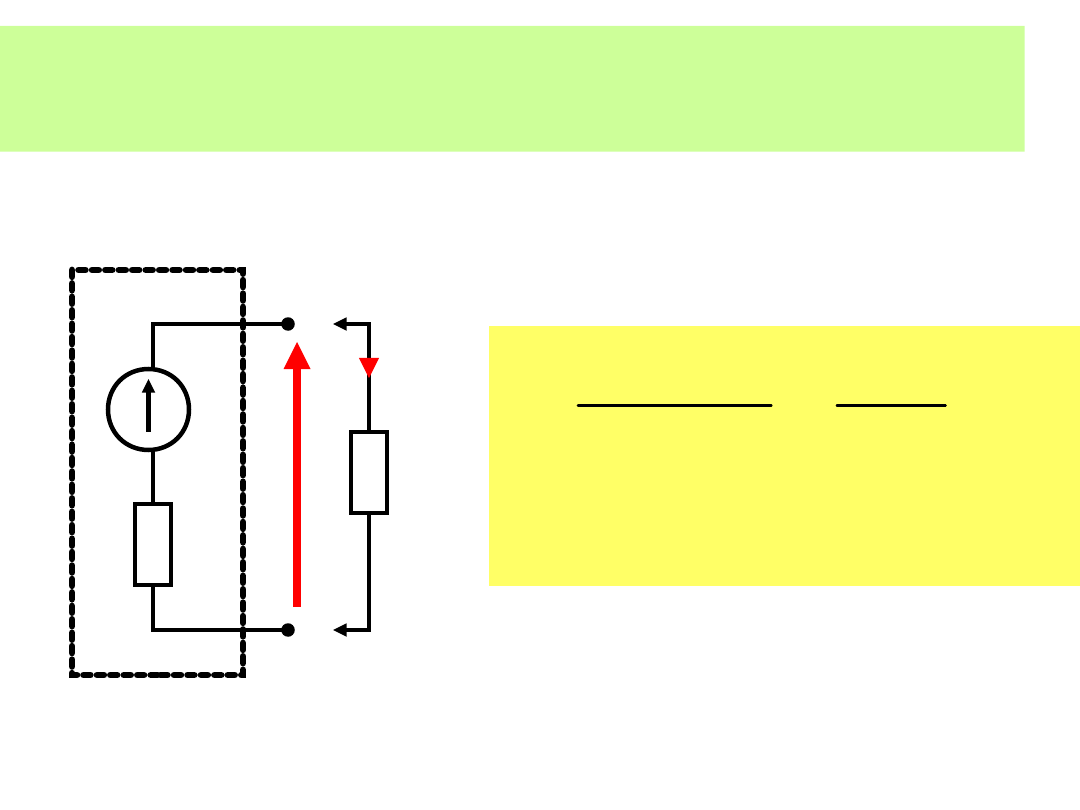
R

0

A

B

E

z

R

z

Jak zmieni się napięcie u

AB,

gdy do dwójnika dołączymy rezystor R

0

=3Ω?

V

iR

u

A

R

R

E

i

AB

z

z

3

3

1

1

3

1

4

0

0



















i

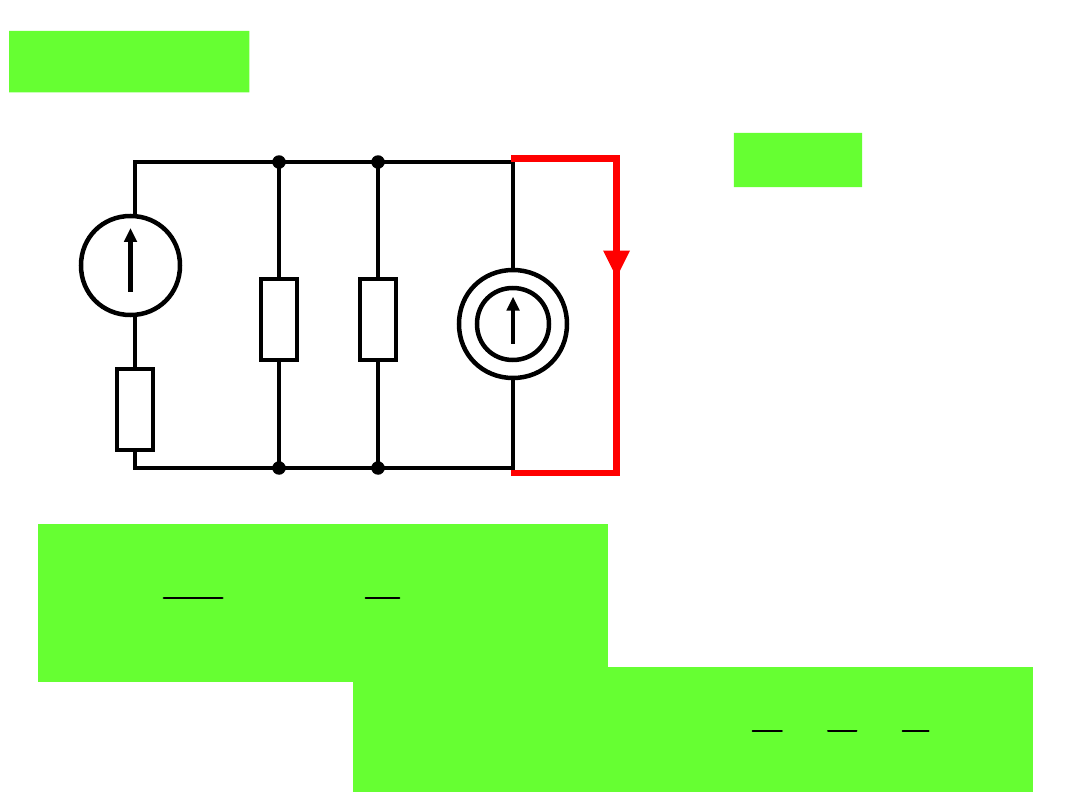
E

1

J

R

1

R

2

R

3

Wyznaczymy parametry dwójnika Nortona (J

z

i G

z

)

widzianego z zacisków AB.

Przykład:

A

J

V

E

R

R

R

2

4

3

6

2

1

3

2

1

















Dane:

A

B

J

Z

A

J

R

E

J

Z

4

2

2

4

1

1











S

G

G

G

G

Z

1

3

1

6

1

2

1

3

2

1















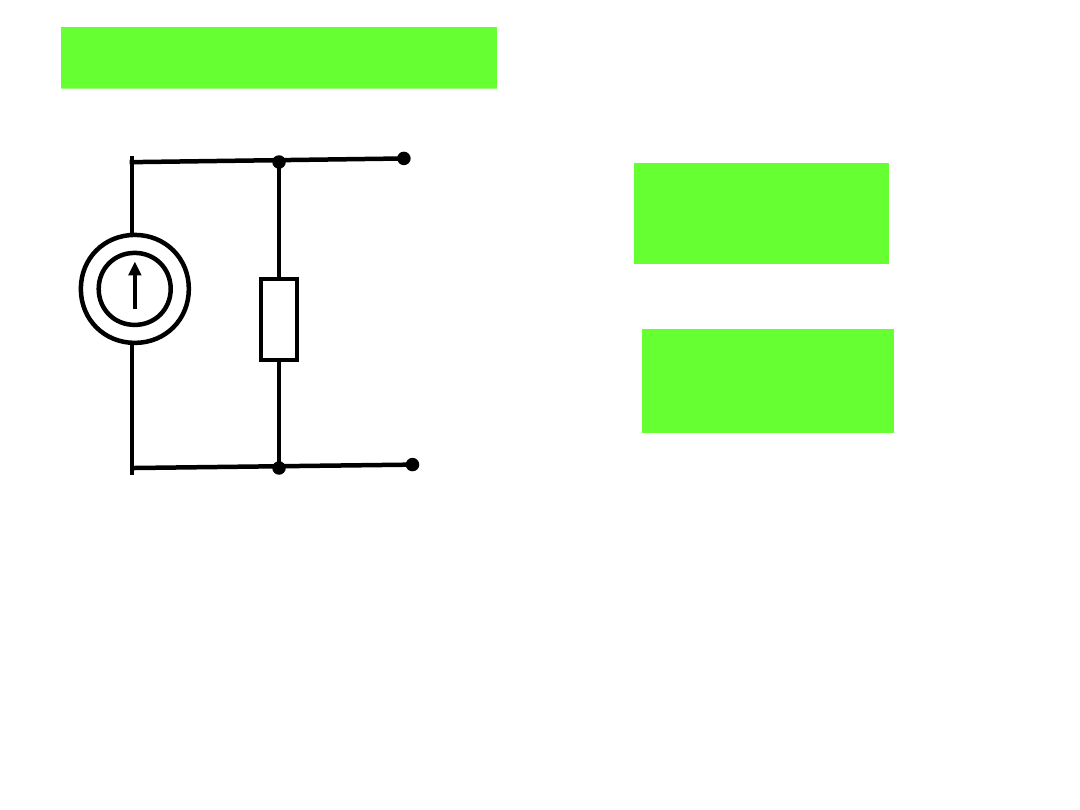
J

G

Z

A

B

Dwójnik Nortona:

A

J

Z

4



S

G

Z

1



Podstawy topologii

obwodów

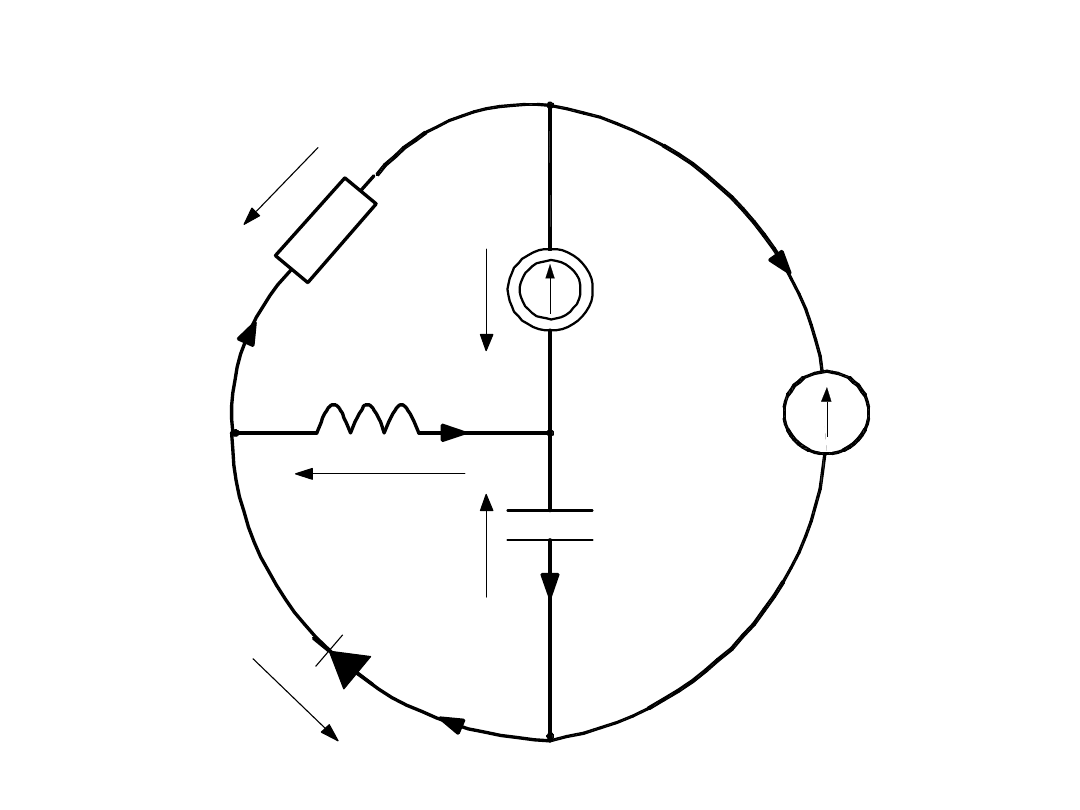
OBWÓD

- GRAF - GRAF ZORIENTOWANY

e

1

j

2

u

2

L

4

i

4

u

4

C

3

i

3

u

3

u

6

i

6

R

5

i

5

u

5

i

1

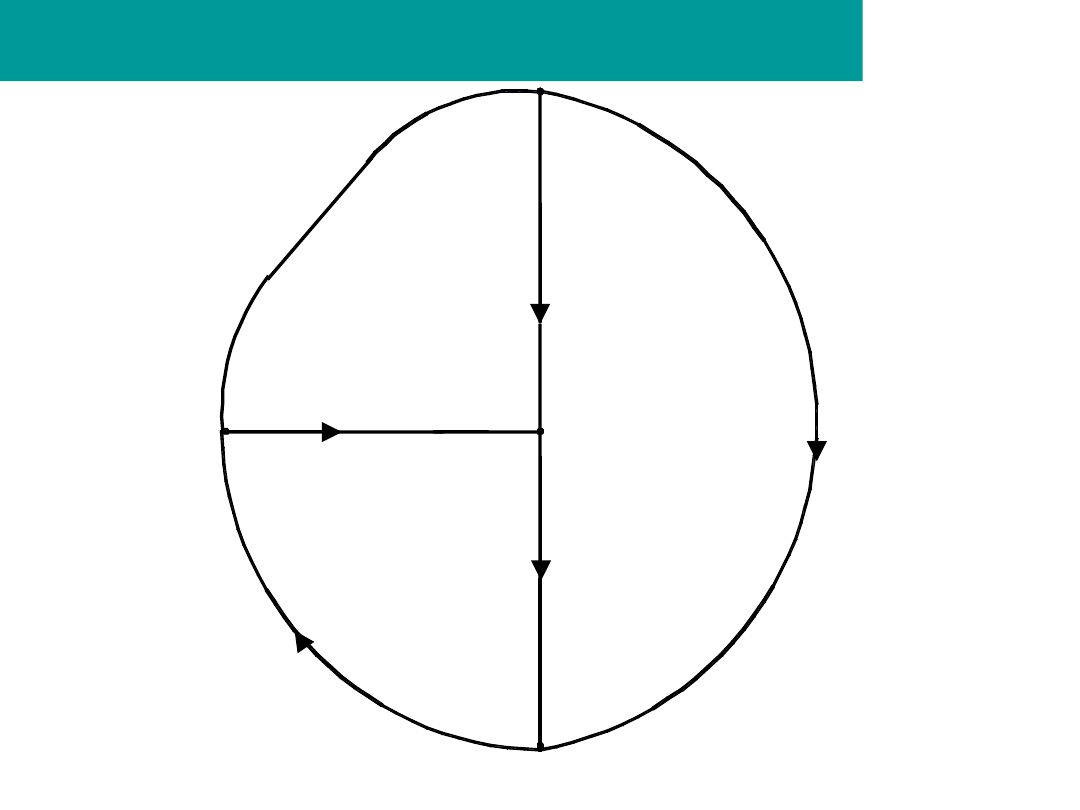
OBWÓD -

GRAF

- GRAF NIEZORIENTOWANY

OBWÓD - GRAF -

GRAF ZORIENTOWANY

2

4

3

6

5

1

Drogą

między węzłami j i k nazywamy zbiór

gałęzi grafu utworzony w ten sposób, że
•kolejne gałęzie mają wspólny węzeł,
•w żadnym węźle nie łączą się więcej niż
dwie gałęzie zbioru,
•z węzłem j oraz z węzłem k łączy się
dokładnie jedna gałąź zbioru

.

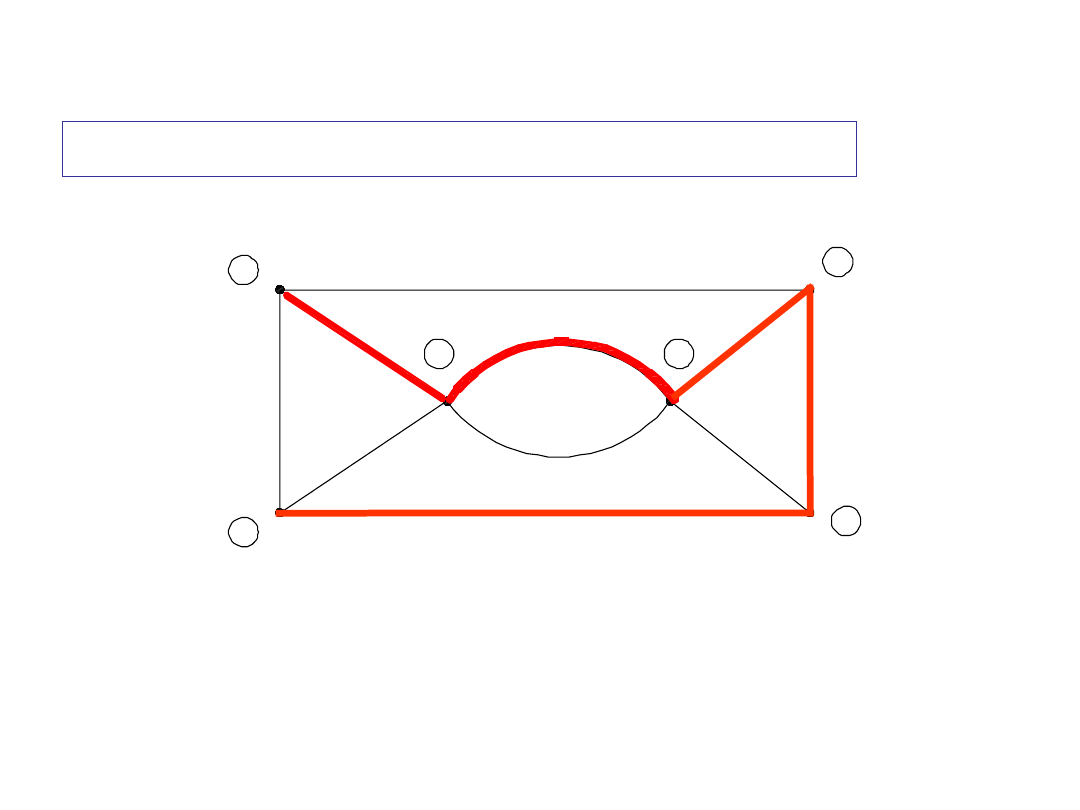
Droga

1

2

3

4

5

6

a

b

c

d

e

f

g

j

i

h

Zbiór gałęzi

e-f-g-c-d

spełnia warunki definicji drogi

Przykład

1

drogi między węzłami 1 i 2

1

2

3

4

5

6

a

b

c

d

e

f

g

j

i

h

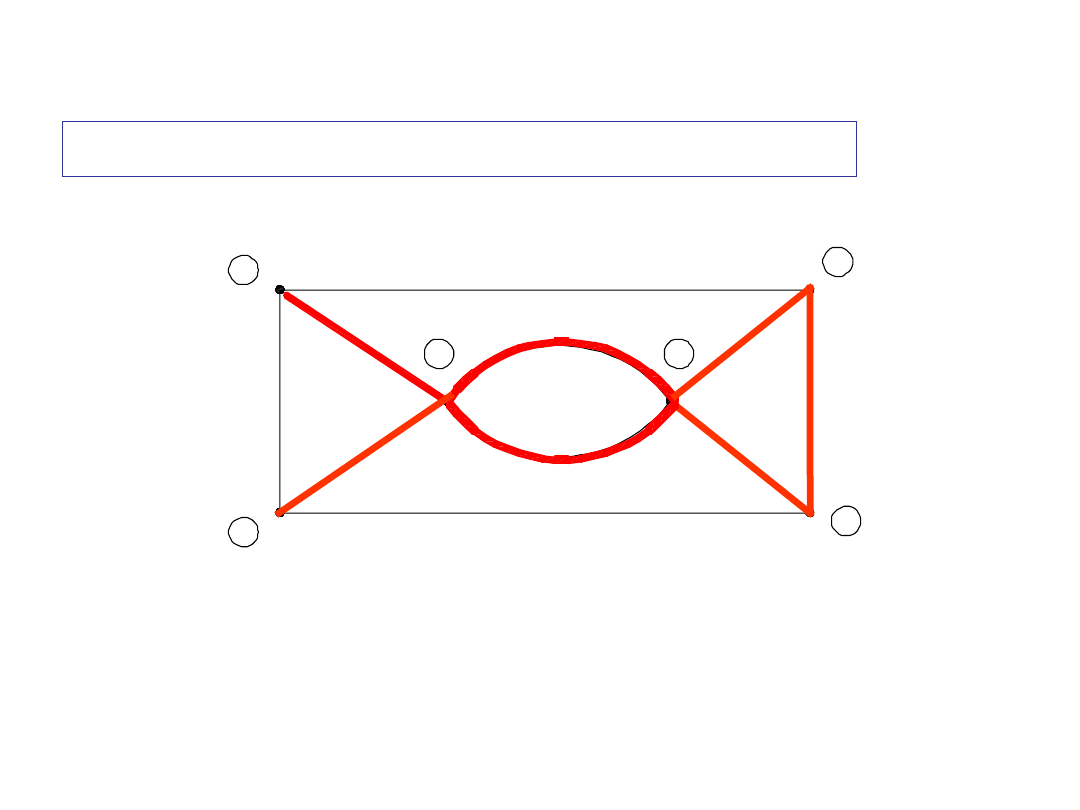
Zbiór gałęzi

e-f-g-c-h-i-j

nie spełnia warunku (2) definicji drogi

Przykład

2

drogi między węzłami 1 i 2

Pętlą

grafu nazywamy podgraf grafu

spełniający następujące warunki
•podgraf jest spójny,
•w każdym węźle podgrafu łączą się
dwie i tylko dwie gałęzie.

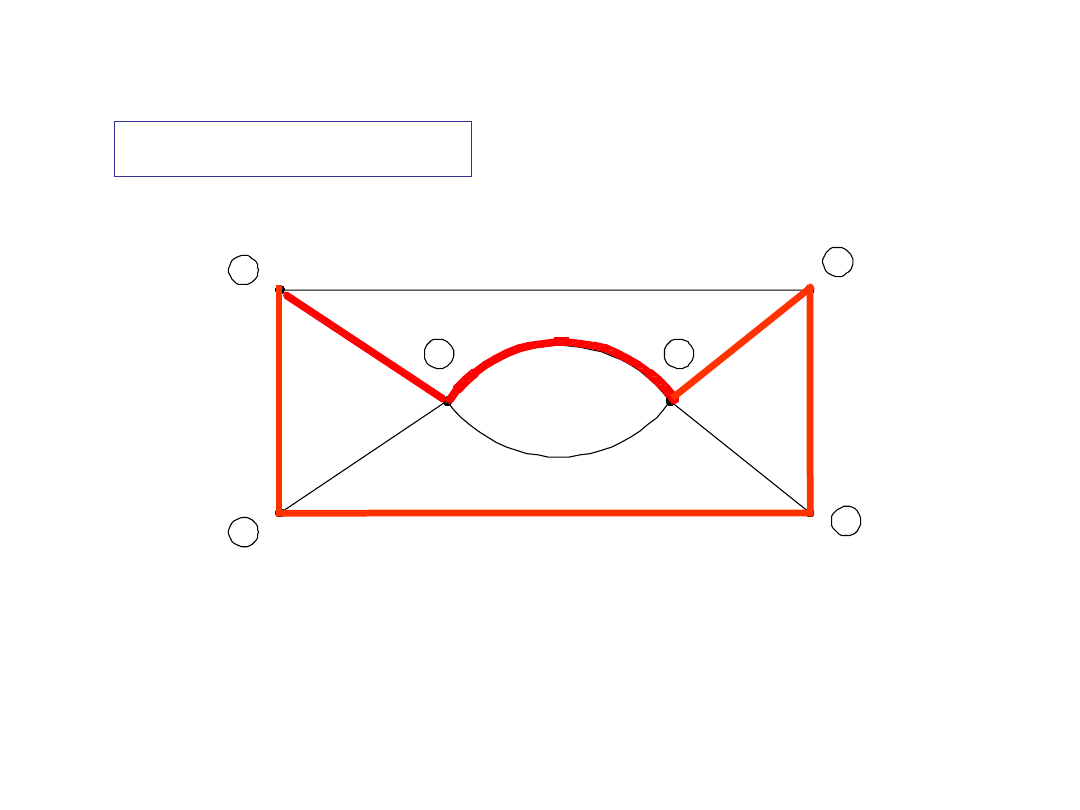
Pętla

1

2

3

4

5

6

a

b

c

d

e

f

g

j

i

h

Zbiór gałęzi

e-f-g-c-d-a

spełnia warunki definicji pętli

Przykład

1

pętla

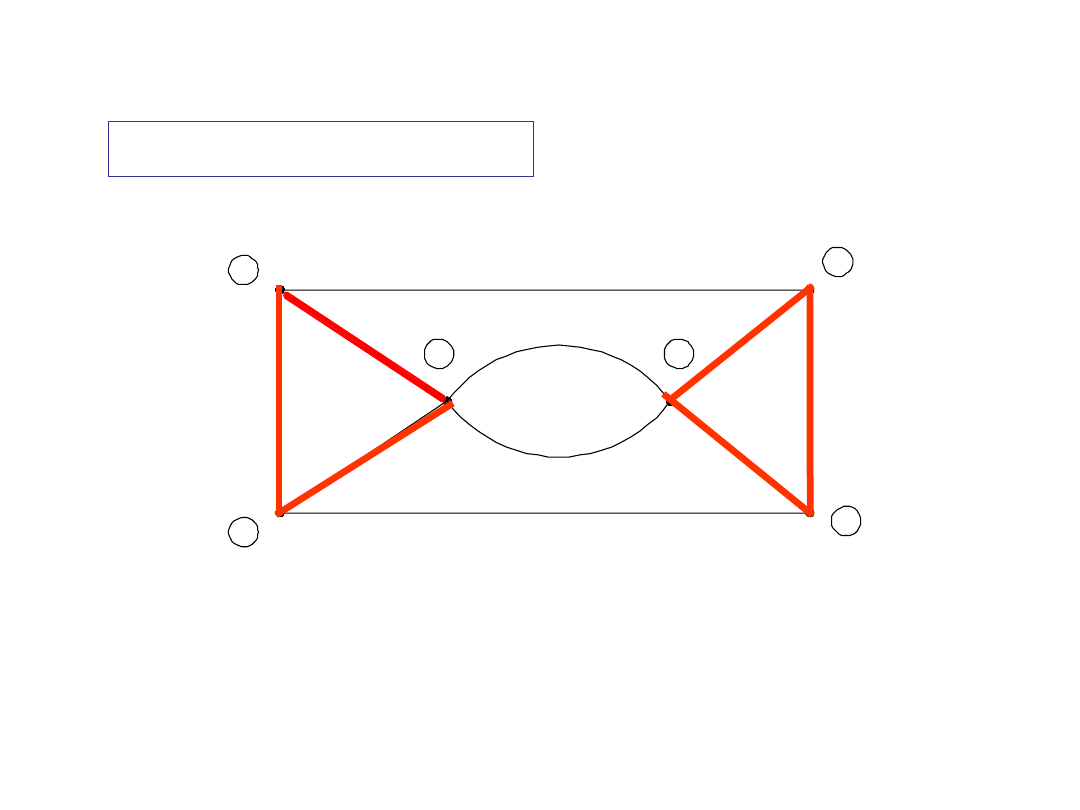
1

2

3

4

5

6

a

b

c

d

e

f

g

j

i

h

Zbiór gałęzi

e-j-a-g-c-h

nie

spełnia warunku 1 definicji pętli

Przykład

2

nie-pętla

Drzewem

grafu spójnego nazywamy

spójny podgraf obejmujący wszystkie
węzły i nie zawierający żadnej pętli.

Pozostałe gałęzie grafu tworzą

przeciwdrzewo

(

DOPEŁNIENIE

)

Drzewo

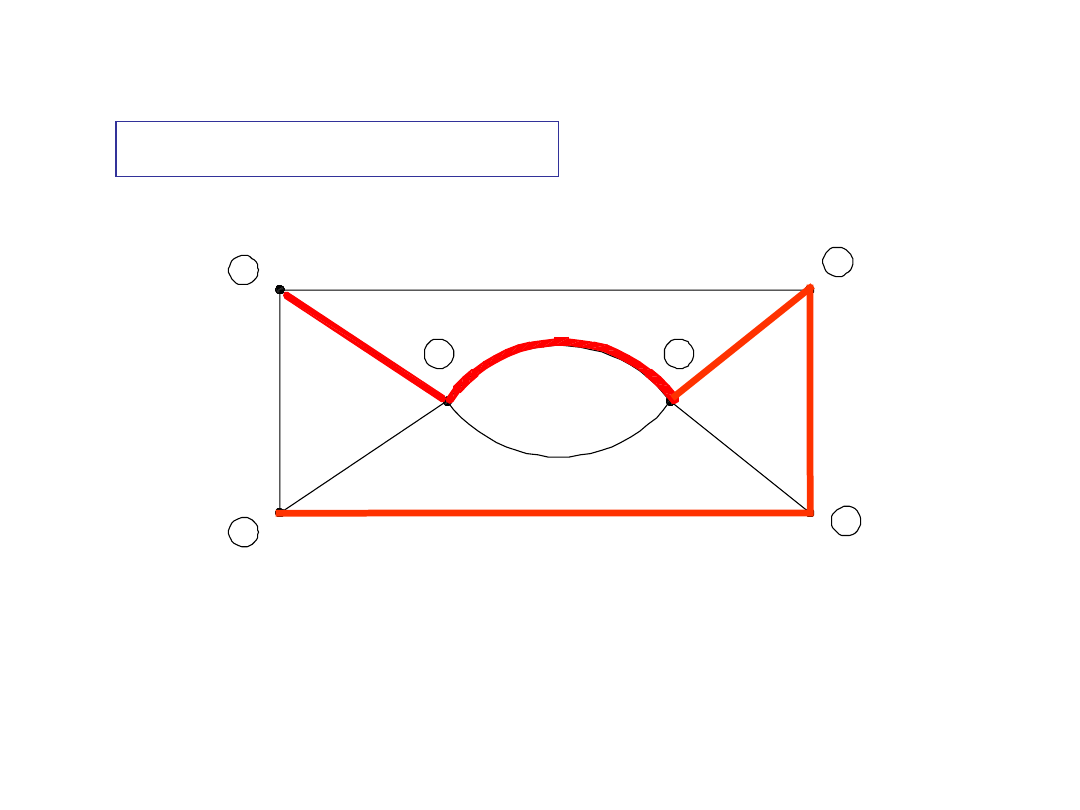
1

2

3

4

5

6

a

b

c

d

e

f

g

j

i

h

Zbiór gałęzi

e-f-g-c-d

spełnia warunki definicji drzewa

Przykład

1

DRZEWO

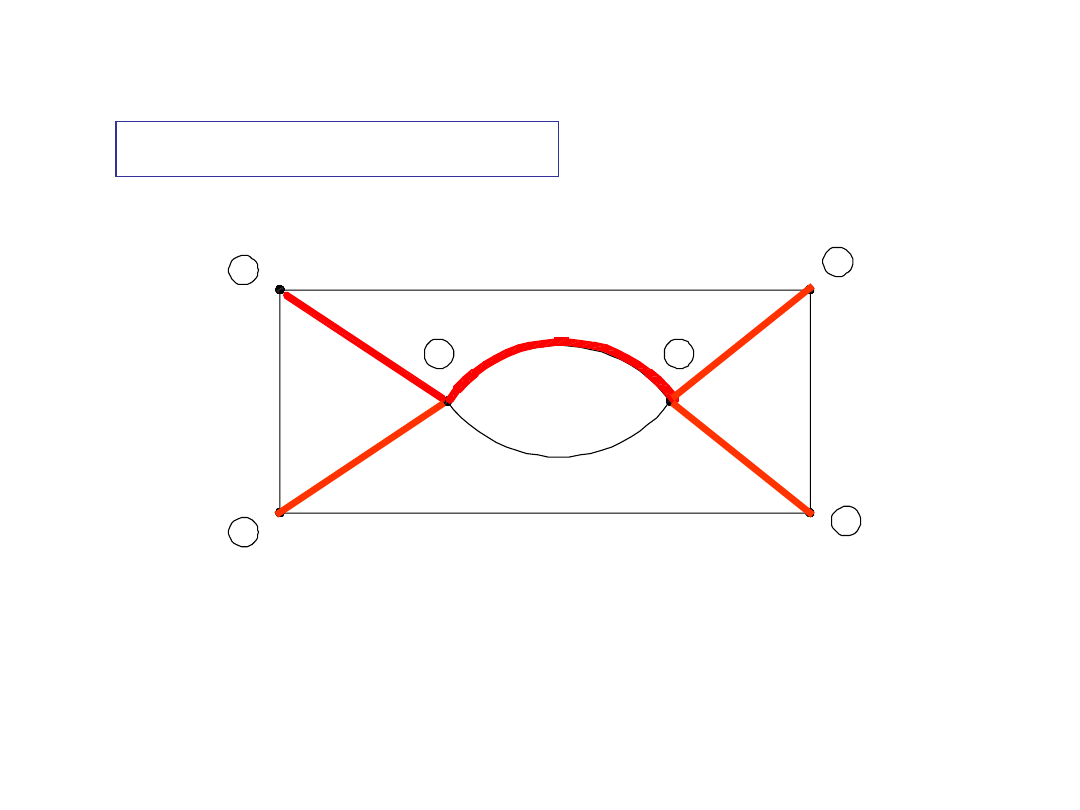
1

2

3

4

5

6

a

b

c

d

e

f

g

j

i

h

Zbiór gałęzi

e-f-g-h-j

spełnia warunki definicji drzewa

Przykład

2

DRZEWO

Dowód
(indukcyjny):

Drzewo

grafu spójnego o  węzłach i

b gałęziach zawiera  - 1 gałęzi.

•Dla n=2, b=1 (n= )
twierdzenie prawdziwe

Twierdzenie

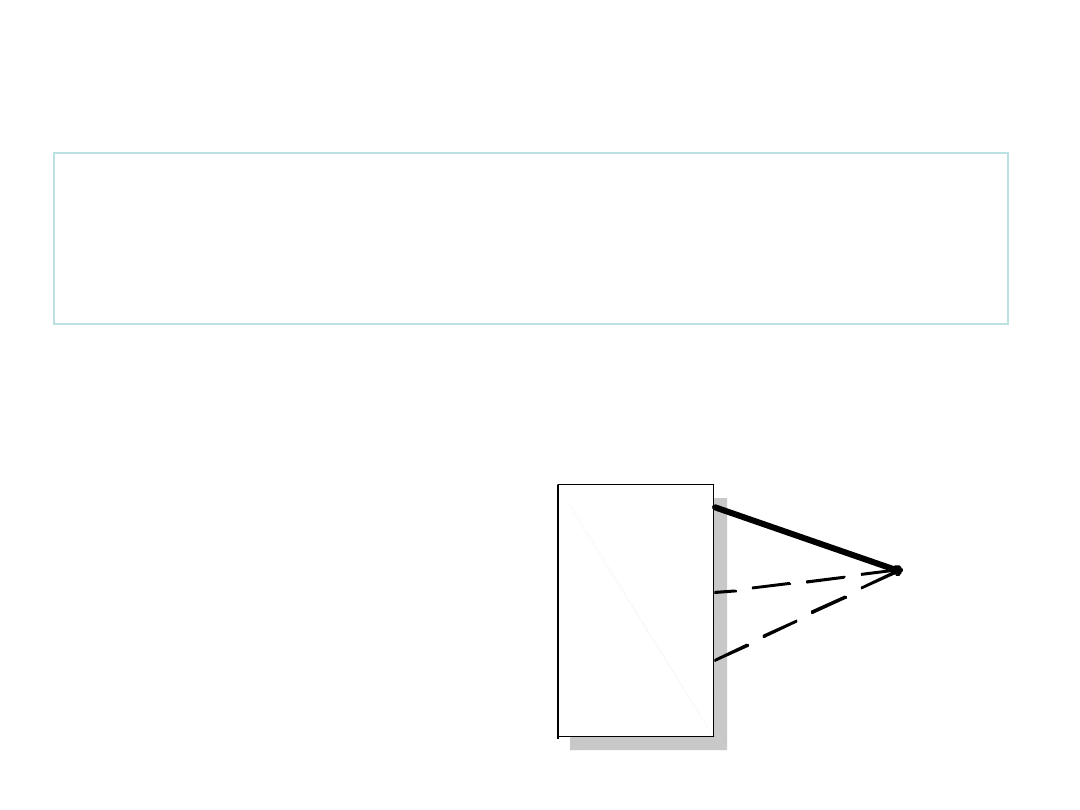
Cd.
Dowód
(indukcyjny)cz.2:

Załóżmy, że twierdzenie jest prawdziwe dla grafu n-węzłowego.
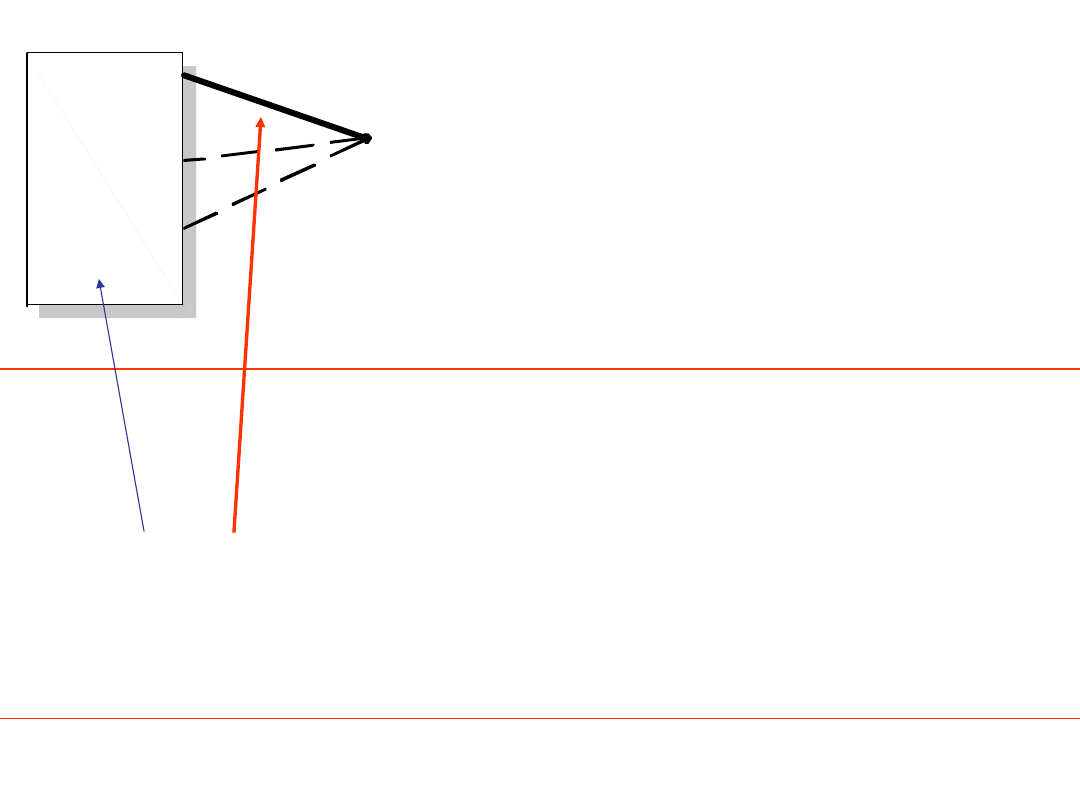
Rozpatrzmy graf o n+1 węzłach, utwórzmy drzewo
i wyodrębnijmy ten węzeł, w którym zbiega się tylko
jedna gałąź drzewa.

d

k

n+1

Graf
o
n węzłach

d

k

n+1

Graf
o
n węzłach

Drzewo rozpatrywanego grafu skład się zatem
z drzewa grafu n-węzłowego oraz gałęzi d

k

.

Uwzględniając założenie indukcyjne otrzymamy:
(

n-1

)+

1

=n

WNIOSEK:
Dopełnienie grafu spójnego  węzłach i b gałęziach

zawiera b -  + 1 gałęzi.

PRZEKRÓJ

Przekrojem

grafu spójnego nazywamy

zbiór
gałęzi spełniający następujące warunki
(1) usunięcie wszystkich gałęzi przekroju
bez węzłów końcowych powoduje podział
grafu na dwa podgrafy
(2) usunięcie wszystkich gałęzi przekroju
poza jedną nie narusza spójności grafu.

1

2

3

4

5

6

a

b

c

d

e

f

g

j

i

h

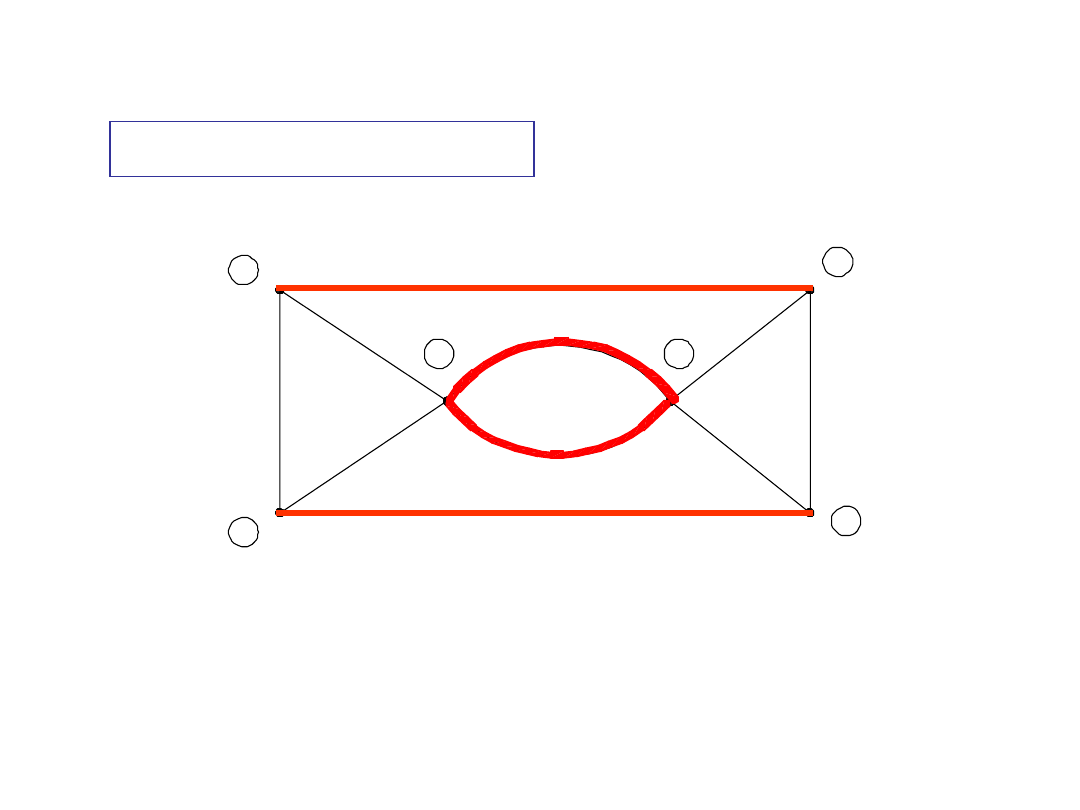
Zbiór gałęzi

b-f-i-d

spełnia warunki definicji przekroju

Przykład

1

przekrój

1

2

3

4

5

6

a

b

c

d

e

f

g

j

i

h

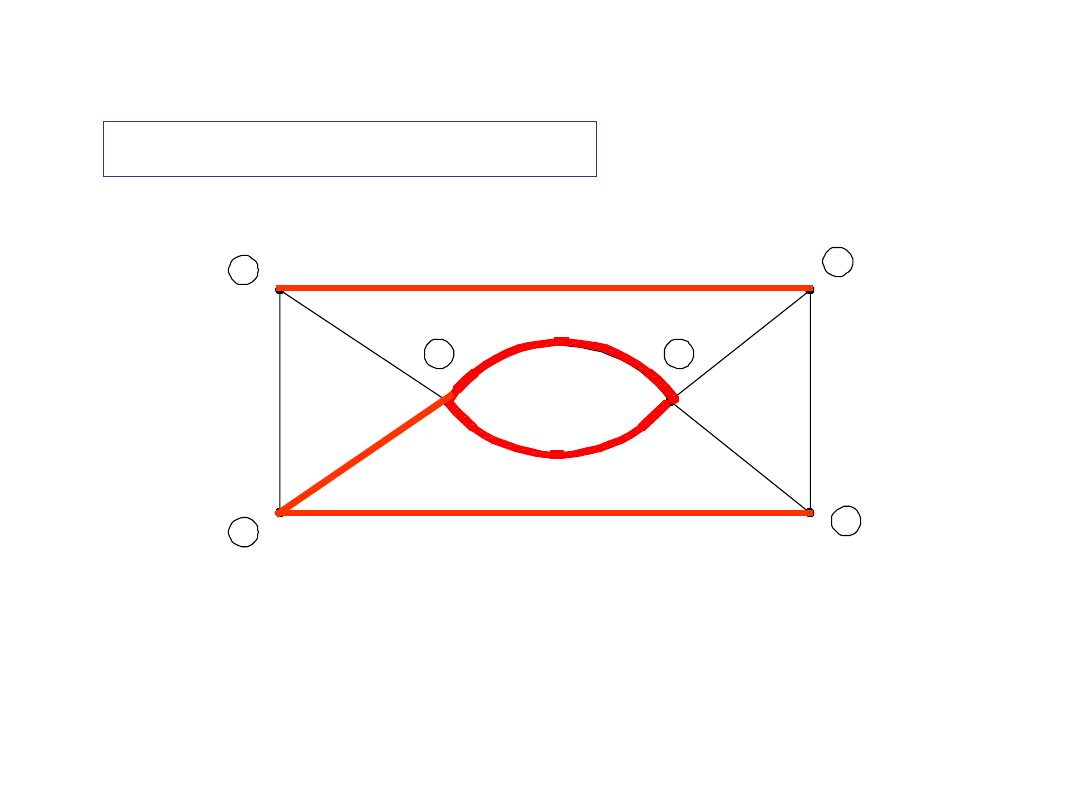
Zbiór gałęzi

b-f-i-d-j

nie spełnia warunków (2) definicji przekroju

Przykład

2

nie- przekrój

PRZEKRÓJ
FUNDAMENTALNY

Przekrój

grafu spójnego nazywamy

fundamentalnym jeżeli jest utworzony
z dokładnie jednej gałęzi drzewa i
gałęzi dopełnienia.
Jest ich w grafie

 - 1

1

2

3

4

5

6

a

b

c

d

e

f

g

j

i

h

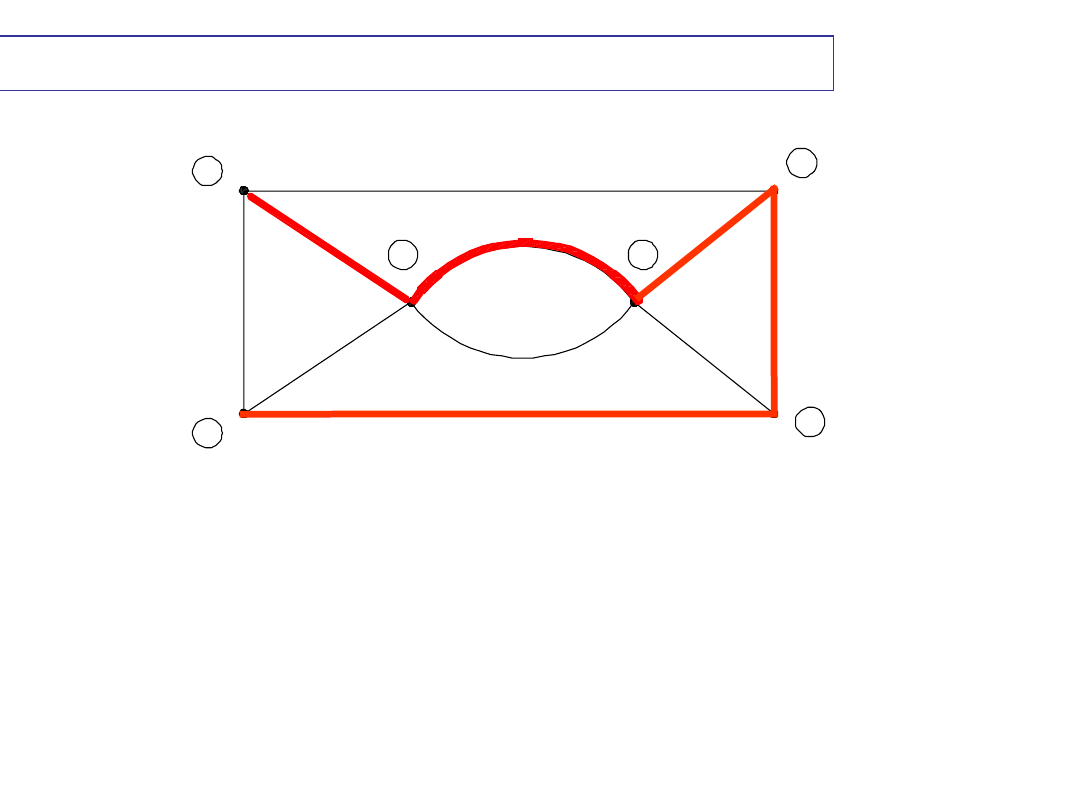
Przekroje fundamentalne dla drzewa

e-f-g-c-d

(1) eab (2) fbija (3) gbhja (4) chja (5) dja

DRZEWO grafu i przekroje fundamentalne

Pętla
FUNDAMENTALNA

Pętlę

nazywamy fundamentalną

jeżeli jest utworzona z dokładnie
jednej gałęzi dopełnienia i gałęzi
drzewa.
Jest ich w grafie

b -  + 1

1

2

3

4

5

6

a

b

c

d

e

f

g

j

i

h

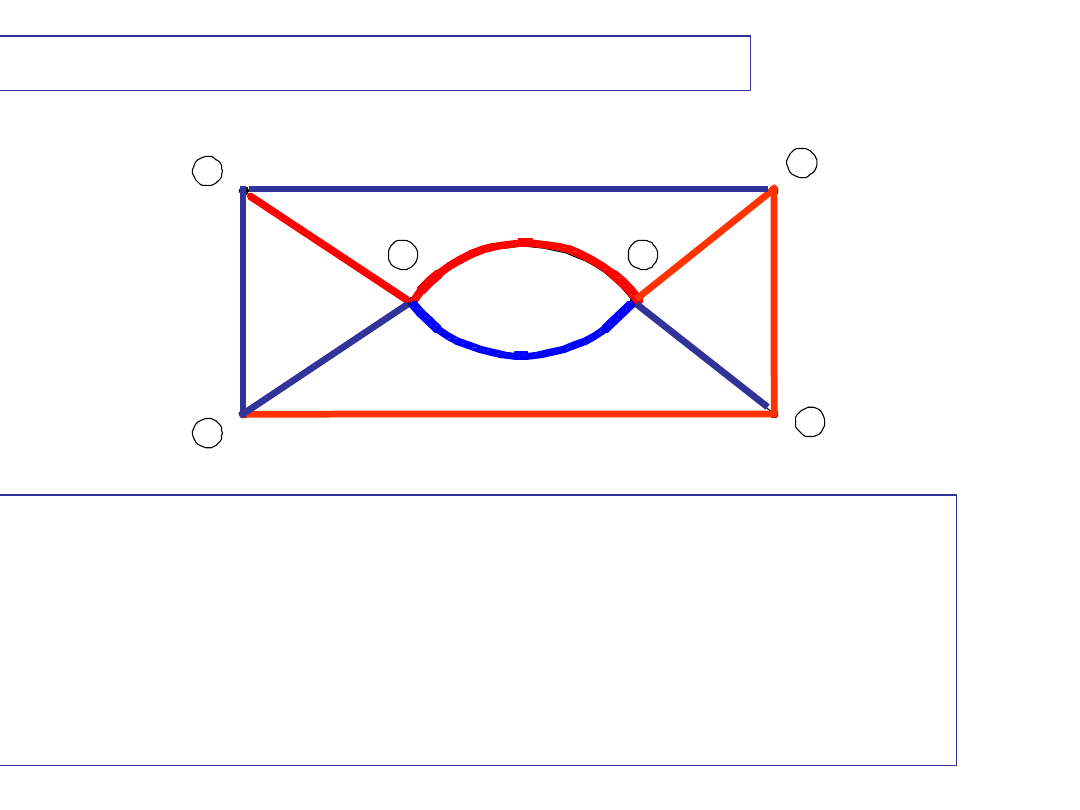
Pętle fundamentalne dla drzewa

e-f-g-c-d

(1)

a

efgcd

(2)

b

gfe

(3)

h

cg

(4)

i

f

(5)

j

fgcd

DRZEWO grafu i

pętle fundamentalne

Twierdzenia dotyczące

PRAW KIRCHHOFFA

(1) Maksymalna liczba równań liniowo niezależnych
otrzymanych z PPK wynosi  -1.

Równania te można napisać stosując PPK do

 -1

fundamentalnych przekrojów.

(2) Maksymalna liczba równań liniowo niezależnych
otrzymanych z NPK wynosi b -  +1 .

Równania te można napisać stosując PPK do b -  +1

fundamentalnych pętli.

DEFINICJA

GRAFU PLANARNEGO:

Graf planarny to taki graf, który może być
narysowany na płaszczyźnie tak aby gałęzie przecinały
się tylko w węzłach.

TWIERDZENIE
Graf planarny zawiera b -  +1 oczek.

Równania NPK napisane dla b -  +1

są liniowo niezależne.

DEFINICJA

OCZKA:

Oczkiem grafu planarnego nazywamy pętlę
nie zawierająca wewnątrz żadnych gałęzi.

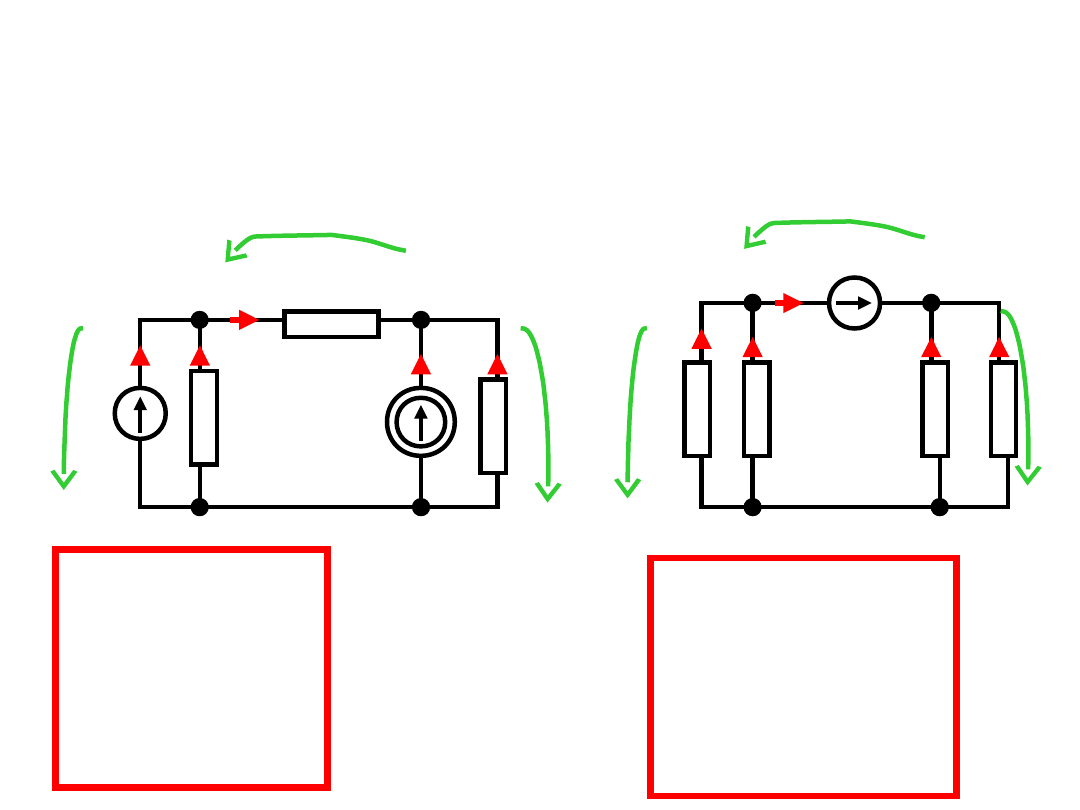
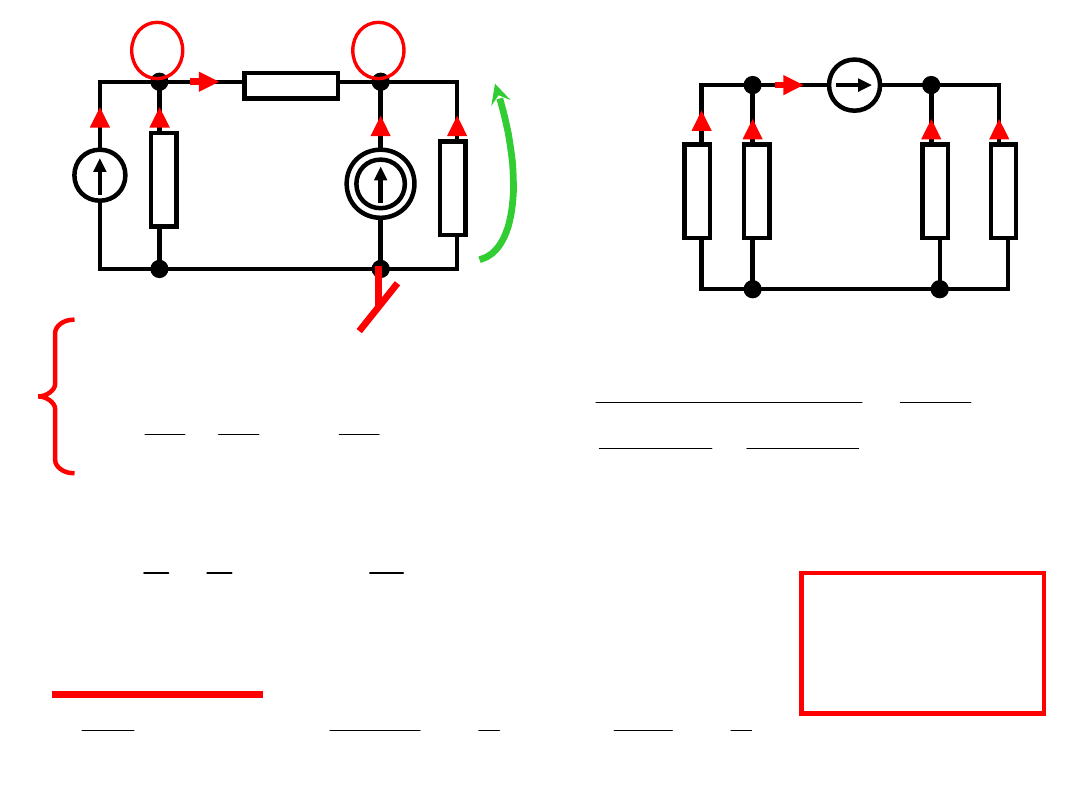
Przykład:

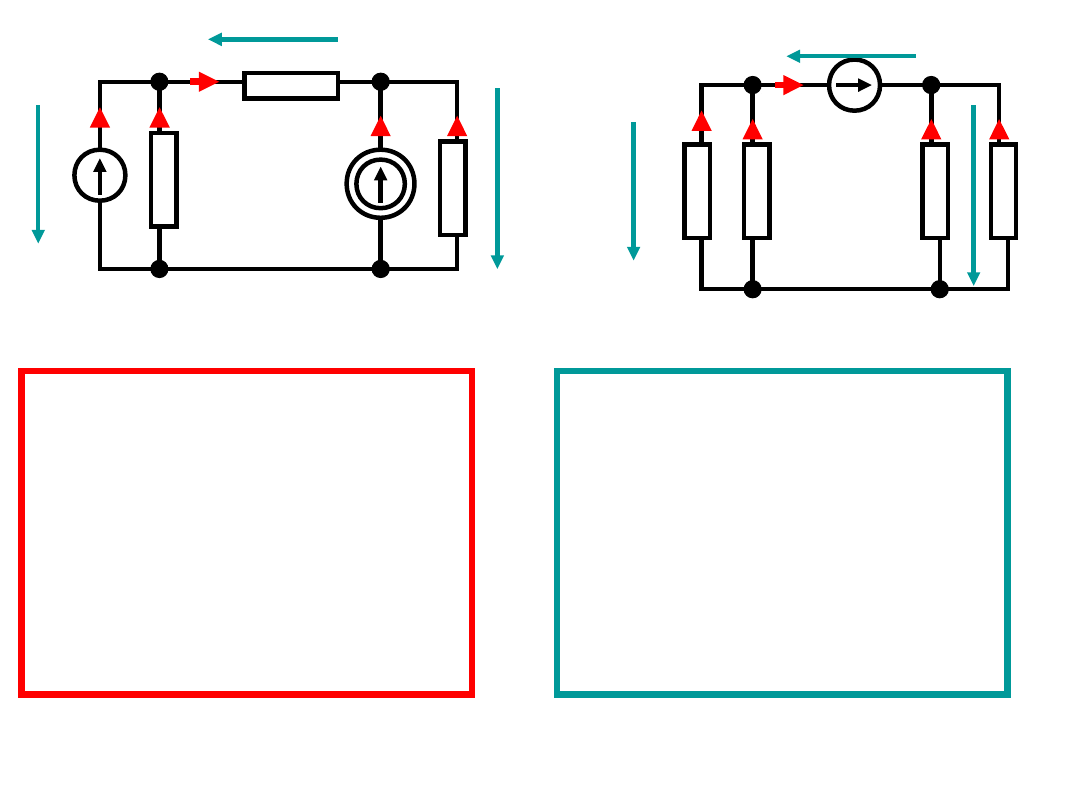
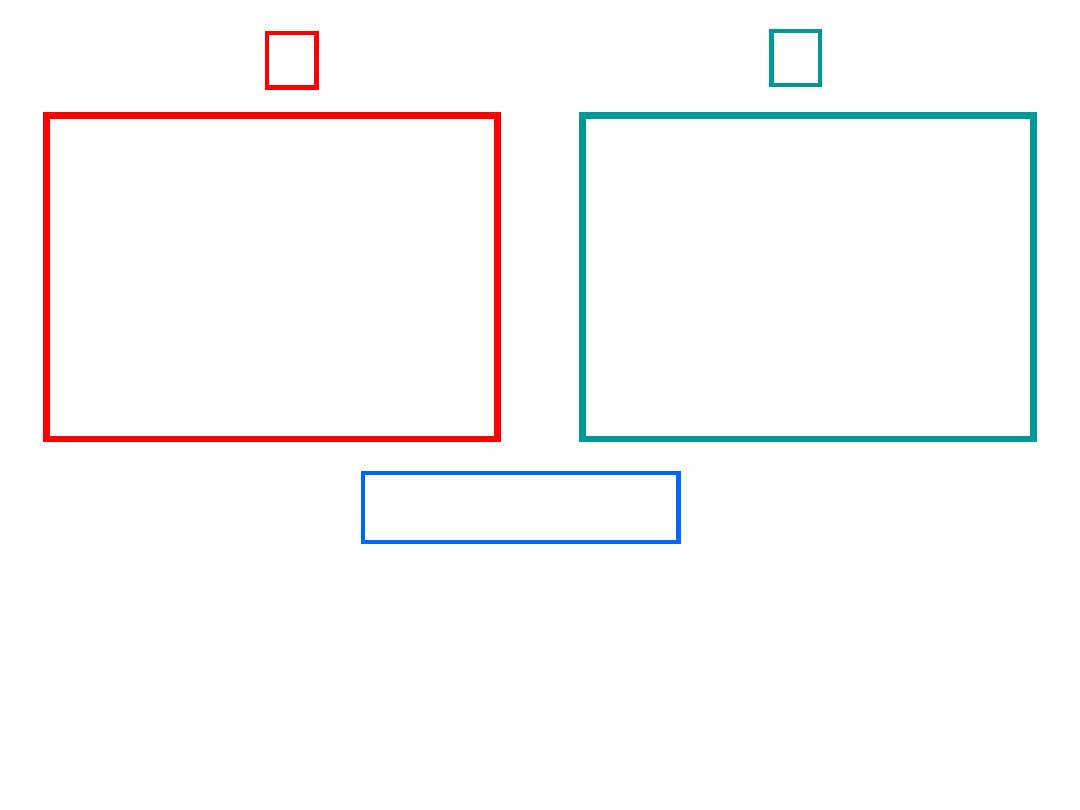
Rozważymy dwa obwody o takiej samej topologii:

R

2

R

3

R

5

e

1

R

4

R

1

R

2

R

5

e

3

Dane:
R

2

=4

R

3

=R

4

=2

J

4

=3A

e

1

=4V





Dane:
R

1

=R

2

=6

R

4

=R

5

=4

E

3

=10V





J

4

i

1

i

2

i

3

i

4

i

5

i

1

i

2

i

3

i

4

i

5

u

4

u

4

u

1

u

1

u

4

u

4

R

2

R

3

R

5

e

1

R

4

R

1

R

2

R

5

e

3

i

1

i

2

i

3

i

4

i

5

i

1

i

2

i

3

i

4

i

5

4

3

1

5

3

2

1

1

1

1

1

4

J

R

e

R

R

V

e

V























V

V

e

J

V

5

2

2

1

2

1

2

1

4

2

















 

1

2

A

R

R

R

R

R

R

R

R

e

i

2

2

3

10

5

4

5

4

2

1

2

1

3

3















A

i

i

A

i

i

1

1

5

4

2

1











A

R

V

i

A

R

V

V

i

A

R

e

i

2

5

2

1

1

5

2

5

3

2

1

3

2

1

2

























R

2

R

3

R

5

e

1

R

4

R

1

R

2

R

5

e

3

A

i

A

i

A

i

A

i

A

i

5

,

2

3

5

,

0

1

5

,

0

5

4

3

2

1

















V

u

V

u

V

u

V

u

V

u

5

5

1

4

4

5

4

3

2

1





















A

i

A

i

A

i

A

i

A

i

1

1

2

1

1

5

4

3

2

1















V

u

V

u

V

u

V

u

V

u

4

4

10

6

6

5

4

3

2

1

















A

i

A

i

A

i

A

i

A

i

5

,

2

3

5

,

0

1

5

,

0

5

4

3

2

1

















V

u

V

u

V

u

V

u

V

u

5

5

1

4

4

5

4

3

2

1





















A

i

A

i

A

i

A

i

A

i

1

1

2

1

1

5

4

3

2

1















V

u

V

u

V

u

V

u

V

u

4

4

10

6

6

5

4

3

2

1

















0

5

1







k

A

k

A

k

i

u

0

5

1







k

B

k

B

k

i

u

0

5

1







k

B

k

A

k

i

u

0

5

1







k

A

k

B

k

i

u

A

B

Bilans mocy