Potencjał normalny i przyśpieszenie normalne siły ciężkości.

Potencjał normalny siły ciężkości, to potencjał elipsoidy obrotowej

uzupełniony potencjałem siły odśrodkowej.

Model potencjału elipsoidy obrotowej musi spełniać następujące

warunki:

1.rozmiar i kształt elipsoidy (a,e) są tak dobrane, aby powierzchnia

elipsoidy była jak najlepszą aproksymacją geoidy,

2. masa elipsoidy jest równa masie Ziemi M
3. prędkość kątowa wirowania elipsoidy wokół małej osi jest równa

prędkości wirowania Ziemi 

4. powierzchnia przyjętej elipsoidy ma być z definicji powierzchnią

ekwipotencjalną o potencjale U

0

równym rzeczywistemu

potencjałowi siły ciężkości geoidy W

0

.

0

0

const

W

U

def





Elipsoidę taką nazywamy elipsoidą ekwipotencjalną albo elipsoidą
poziomową, zaś model pola siły ciężkości reprezentowany przez tę
elipsoidę nazywamy normalnym polem siły ciężkości.

Przyśpieszenie normalne siły ciężkości określa wektor

0

gradU





Przyśpieszenie normalne na elipsoidzie GRS’80





2

2

2

2

sin

00000058

.

0

sin

0053024

.

0

1

780327

.

9









ms







dokładność obliczę tym wzorem 0.1 mgal

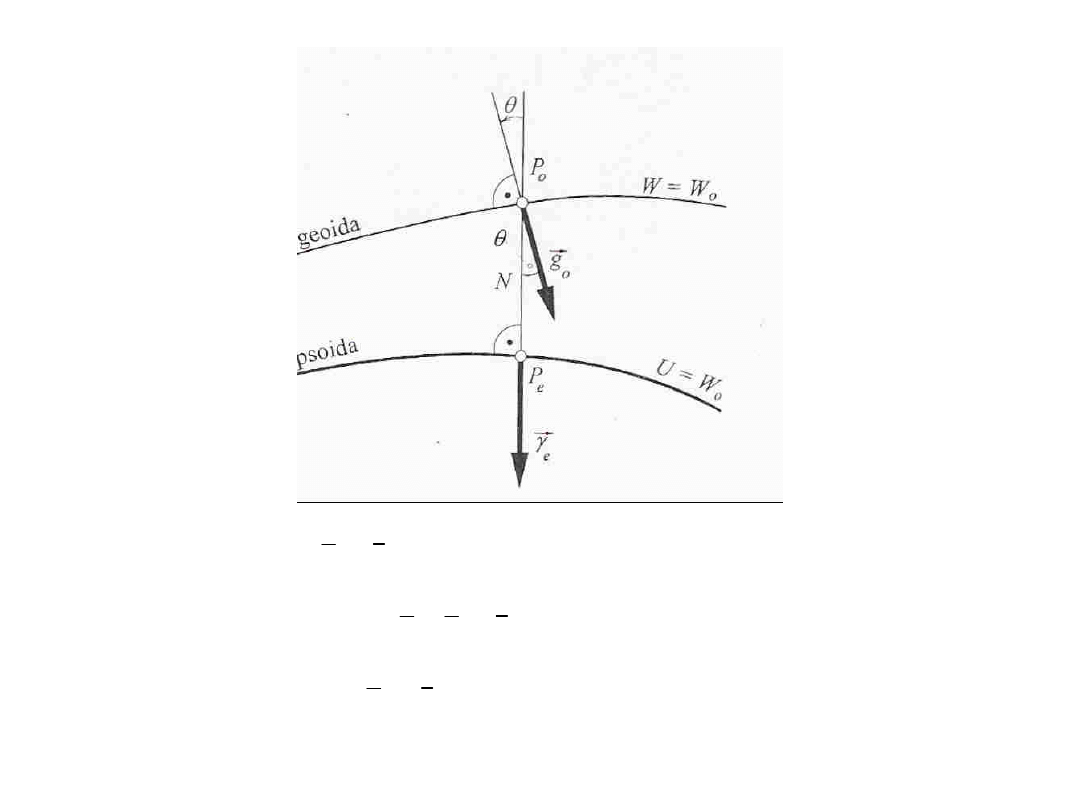
Anomalie grawimetryczne

Wektor będący różnicą nazywamy wektorem anomalii
grawimetrycznej (odniesionej do geoidy)

e

g





0

e

g

g









0

różnicę modułów wektorów i nazywamy anomalią grawimetryczną.

0

g

e



e

g

g









0

Niektóre częściej stosowane redukcje grawimetryczne

Aby obliczyć anomalie grawimetryczne, które potrzebne są między
innymi do badania przebiegu geoidy względem elipsoidy które to
konieczne są do zredukowania wartości przyspieszenia siły ciężkości
pomierzonego na fizycznej powierzchni Ziemi na geoidę

Omówimy kolejno następujące wybrane redukcje grawimetryczne:
1. wolnopowietrzną Faye’a
2. Bougera – Younga
3. Poincare – Praya
4. Terenowa

Redukcja wolnopowietrzna (Faye’a)

Redukcja ta polega jedynie na uwzględnieniu wpływu wysokości stanowiska nad geoidą

h

h

g

g

F











gdzie:

h

h

g

g

F







-redukcja wolnopowietrzna
-pionowy gradient przyspieszenia siły ciężkości

-wysokość punktu (nad geoidą)

lub też wzorem:





mgal

h

g

F

3086

,

0





h – powinna być wyrażona w metrach

Różnice pomiędzy wartością zredukowaną pomierzonego
przyspieszenia siły ciężkości a przyspieszeniem normalnym
nazywamy anomalią grawimetryczną w tym przypadku nazywamy ją
anomalią Faye’a - Δg

F

F

e

F

g

g

g













gdzie: g – wartość przyspieszenia siły ciężkości na fizycznej powierzchni Ziemi

Redukcja Bougera - Younga

Jeżeli teren wokół stanowiska był płaski albo też uwzględniliśmy
poprawkę terenową (o czym dalej), to usuwając wpływ płaskiej płyty
o grubości h możemy otrzymać przyspieszenie w punkcie na
wysokości h nad geoidą. Redukcja usuwa jedynie wpływ mas
pomiędzy fizyczną powierzchnią Ziemi i geoidą (nazywamy ją
niepełną redukcją Bougera).





mgal

h

g

B









0419

,

0

Aby otrzymać zredukowane przyspieszenie na geoidzie musimy
jeszcze wykonać redukcję wolnopowietrzną.
Redukcja Bougera – Younga ma postać:









mgal

h

g

Y

B











0419

,

0

3086

,

0

gdzie: σ – średnia gęstość utworów zalegających pomiędzy fizyczną

powierzchnią Ziemi a geoidą

Anomalię Bougera obliczamy ze wzoru:

Y

B

e

B

g

g

g















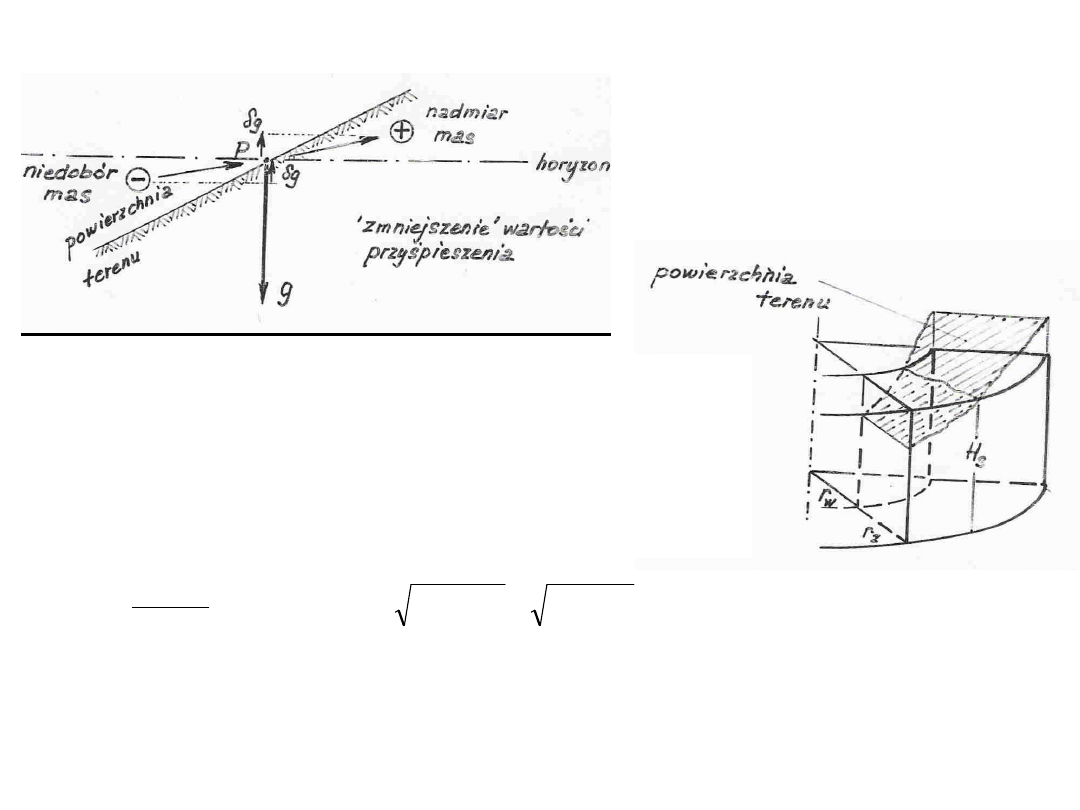
Poprawka terenowa

0419

,

0

2



G

i

w

r

r 

1





i

z

r

r

ij

S

H

H 





























n

j

r

i

ij

i

ij

i

i

i

t

r

H

r

H

r

r

r

n

g

2

2

2

2

1

1

0419

,

0

n – liczba sektorów
r

r

– liczba koncentrycznych stref

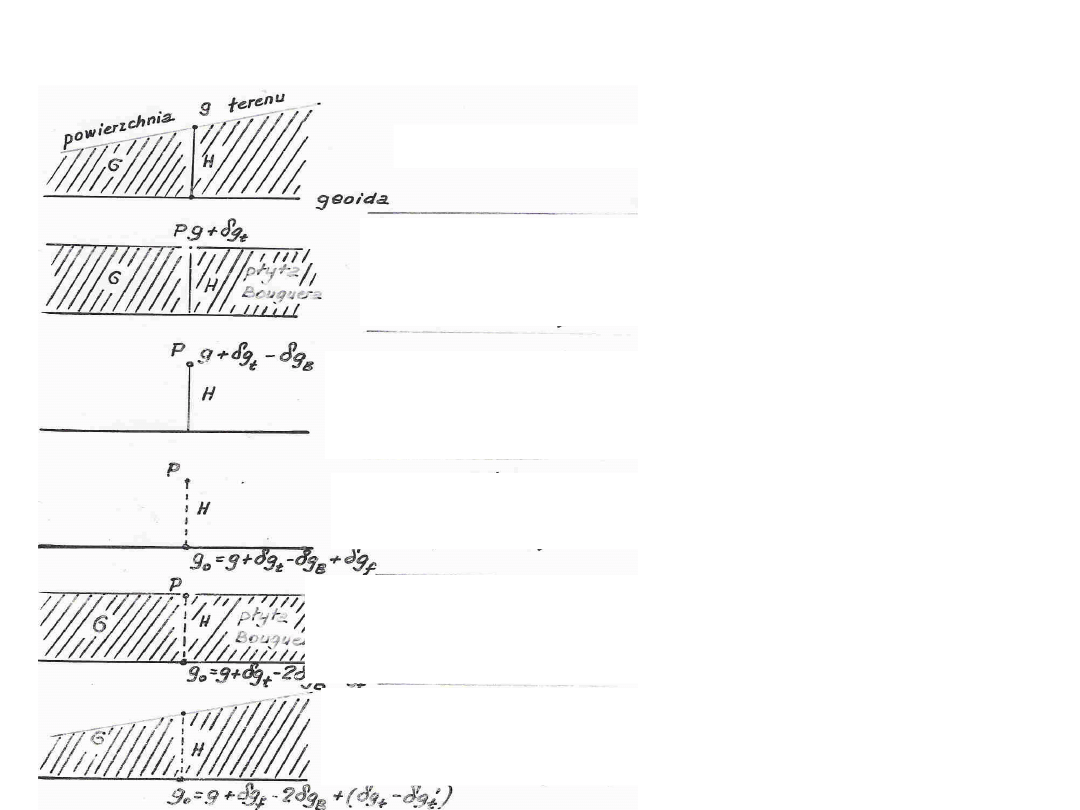
Redukcja Poincare-Prey’a:

cel: rzeczywista wartość przyśpieszenia wewnątrz skorupy ziemskiej

przed redukcją

poprawka terenowa

(dodatnia)

t

g



redukcja Bouguera
(usunięcia płyty)
(ujemna)

B

g



redukcja wolnopowietrzna
(dodatnia)

f

g



redukcja Bouguera
(przywrócenie płyty)
(ujemna – punkt pod płyą)

B

g



poprawka topograficzna (terenowa)
przywrócenie topografii
(ujemna)

t

g'



Suma poprawek terenowych

t

t

T

g

g

g

'











punkt na

fizycznej

powierzc

hni Ziemi

punkt

na

geoidz

ie

(ta różnica w terenach płaskich jest z reguły bardzo mała)

T

B

f

P

P

g

g

g

g

















2

Redukcja Poincare-Prey’a









mgal

g

H

g

T

PP













0838

,

0

03086

,

0

gdy

0





T

g









mgal

H

g

PP









0838

,

0

3086

,

0