OPTYKA

OPTYKA

czyli nauka o świetle

czyli nauka o świetle

Informacje ogólne

Informacje ogólne

Optyka tradycyjnie była nauką o

świetle i budowaniu przyrządów
optycznych. Jednak w miarę rozwoju
fizyki i poznawania natury światła,
okazało się, że do optyki zaczęto
zaliczać szereg zjawisk nie
związanych bezpośrednio z
widzeniem, czy nawet narządem
wzroku jakiegokolwiek zwierzęcia. 

Klasyczną optykę zazwyczaj dzieli się na
dwa działy:



optykę geometryczną



optykę falową

Nowe działy optyki dość luźno odnoszą się do

tego

podziału. W ramach nowoczesnej optyki mieści

się

m.in.: 



spektroskopia



optyka atomowa i jądrowa, 



optyka kwantowa 



i szereg innych poddziedzin wynikających z

istnienia bardzo różnych zjawisk związanych

z emisją fal elektromagnetycznych.

Podział optyki

Podział optyki

Czym jest światło?

Czym jest światło?

Światło jest falą

elektromagnetyczną o

długości od 400 nm do

800 nm. Światło

rozchodzi się w próżni i

ciałach przezroczystych.

Biegnie prostoliniowo i

przenosi energię ze

źródła do ciała na które

pada. Światło rozchodzi

się w próżni z szybkością

300 000 km/s.

Źródła światła

Źródła światła

Źródłami światła są wszystkie ciała

świecące światłem własnym. Najsilniejszymi

źródłami światła docierającymi do Ziemi są

gwiazdy. Źródłami są również inne ciała

wysyłające światło w wyniku:



Podgrzania do wysokiej temperatury

(żarówka),



Pobudzenia do świecenia cząsteczek gazów w

silnym polu elektrycznym (neonówka),



Pochłaniania promieniowania ultrafioletowego

(luminofor),



Reakcji chemicznych (płomień świecy).

Rozchodzenie się światła

Rozchodzenie się światła

W ośrodkach jednorodnych (np. w

próżni) światło porusza się po liniach

prostych. Jeżeli światło na swej

drodze napotyka ciało

nieprzezroczyste, na ekranie

powstaje cień tego ciała.

Optyka

Optyka

geometryczna

geometryczna

Wprowadzenie

Wprowadzenie

Założeniem optyki geometrycznej

jest, że światło rozchodzi się jako strumień

promieni. Przyjmuje się też, że promienie

te biegną prostoliniowo od źródła światła

do momentu w którym napotkają na

przeszkodę, lub zmianę ośrodka.

Jednak w wielu typowych, znanych z

codziennego życia sytuacjach model

optyki geometrycznej całkiem nieźle się

sprawdza – w oparciu o niego świetnie

działają takie przyrządy jak: aparaty

fotograficzne, okulary, lornetki i teleskopy.

Zjawiska optyki

Zjawiska optyki

geometrycznej

geometrycznej

Na wstępie napisano, że bieg promieni

świetlnych jest prostoliniowy. Stwierdzenie
to odnosi się tylko do sytuacji, gdy ośrodek
jest jednolity (jednorodny). W przypadku,
gdy ośrodek się zmienia - np. światło
dochodzi do granicy powietrza i wody,
zachodzi najczęściej zmiana kierunku
rozchodzenia się światła. 

Odpowiadają za to dwa główne zjawiska:



odbicie światła



załamanie światła

Odbicie światła

Odbicie światła

Światło padające na granicę

dwóch ośrodków może ulec odbiciu.

Dzieje się tak bardzo często, przy

czym dodatkowo część wiązki świetlnej

może dodatkowo ulegać załamaniu.

Odbiciem rządzi dość proste prawo

zwane prawem odbicia:

Kąt odbicia równy jest kątowi

padania. 

Kąty -  padania i odbicia leżą w

jednej płaszczyźnie.

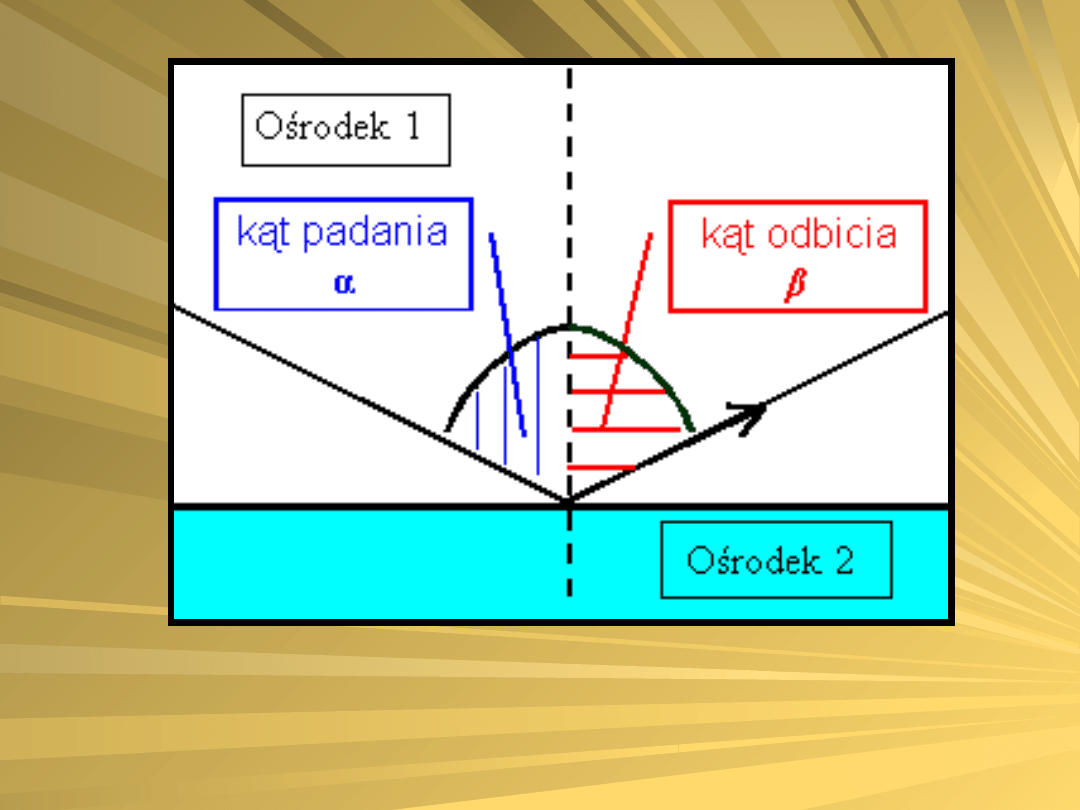
β = α

β = α

Jeżeli światło napotyka na swej drodze gładki

(wypolerowany) przedmiot zwany lustrem lub

zwierciadłem, wówczas odbija się od niego.

Przedmioty, które nie są źródłami światła, widzimy

dlatego, że padające na nie światło zostaje rozproszone

i część promieni świetlnych dociera do naszych oczu.

Załamanie światła

Załamanie światła

Załamanie różni się zdecydowanie od odbicia,

ponieważ w jego wyniku światło zmienia ośrodek

w jakim się rozchodzi. Wraz ze zmianą ośrodka

dochodzi najczęściej do zmiany kierunku

rozchodzenia się światła.

Załamanie światła powoduje szereg ciekawych

efektów - m.in. złudzenie "złamania" łyżeczki od

herbaty umieszczonej w szklance, nieprawidłowej

lokalizacji dna jeziora, gdy patrzymy na nie z

brzegu. Załamanie światła jest wykorzystywane do

budowy soczewek stosowanych w okularach,

obiektywach aparatów, lunetach i innych

przyrządach optycznych.

Zmiana kierunku promieni świetlnych

podczas załamania nie jest
przypadkowa. Opisuje to prawo
załamania światła nazywane niekiedy
prawem Snelliusa

Prawo załamania światła łączy ze sobą

dwa kąty - kąt padania na powierzchnię
rozgraniczającą dwa ośrodki i kąt
załamania powstający gdy promień
przejdzie granicę i zacznie się rozchodzić
w drugim ośrodku (patrz rysunek niżej).

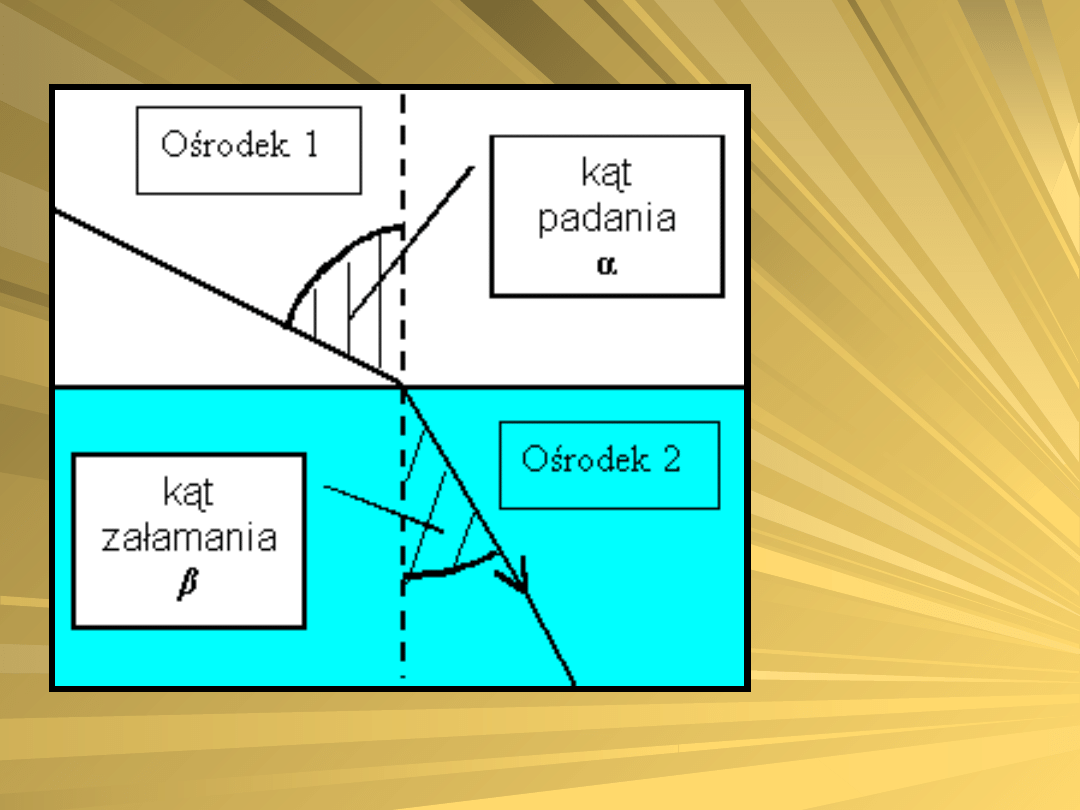
α – kąt
padania
β – kąt
załamani
a

Prawo załamania światła

Prawo załamania światła

α – kąt padania

β – kąt załamania
v1 – prędkość światła w ośrodku 1
v2 – prędkość światła w ośrodku 2

Słownie prawo załamania można sformułować

następująco:

Stosunek sinusa kąta padania, do

sinusa kąta załamania jest dla danych

ośrodków stały i równy stosunkowi

prędkości fali w ośrodku pierwszym, do

prędkości fali w ośrodku drugim. Kąty

padania i załamania leżą w tej samej

płaszczyźnie

.

.

sin α

v1

____

=

____

sin β v

2

Współczynniki załamania

Współczynniki załamania

światła

światła

Bezwzględny współczynnik załamania światła

Bezwzględny współczynnik załamania światła dany

jest wzorem 

v – prędkość światła w danym ośrodku

c – prędkość światła w próżni

(c = 299 792 458 m/s)

n – bezwzględny współczynnik załamania

Znajomość bezwzględnych współczynników

załamania umożliwia szybkie obliczenie prędkości
światła w danych ośrodku, wg wzoru:

 

 

c

n

=

____

v

v

c

=

____

n

Tabela współczynników

Tabela współczynników

załamania światła

załamania światła

Ośrodek

bezwzględny współczynnik

załamania n

prędkość światła w

ośrodku v [m/s]

diament

2,42

ok. 125 000 000

lód

1,31

ok. 229 000 000

sól kamienna

1,54

ok. 194 000 000

szkło (różne rodzaje)

od 1,4 do 1,9 - średnio 1,5 od 1,53 ∙10

8

do 2,15∙10

8

  

woda

1,33

225 000 000

etanol

1,36

220 000 000

powietrze

1,0003

299 706 000

próżnia

1

c = 299 792 458

Rozszczepienie światła

Rozszczepienie światła

Rozszczepienie światła spowodowane jest

różną prędkością rozchodzenia się
promieni świetlnych o różnych barwach.
Różna prędkość rozchodzenia się światła
owocuje oczywiście różnym współczynnikiem
załamania światła i różnym kątem załamania.
Ponieważ zaś światło białe jest mieszaniną
świateł o wielu barwach, to przepuszczenie go
przez pryzmat spowoduje rozdzielenie
poszczególnych składowych na piękną tęczę.

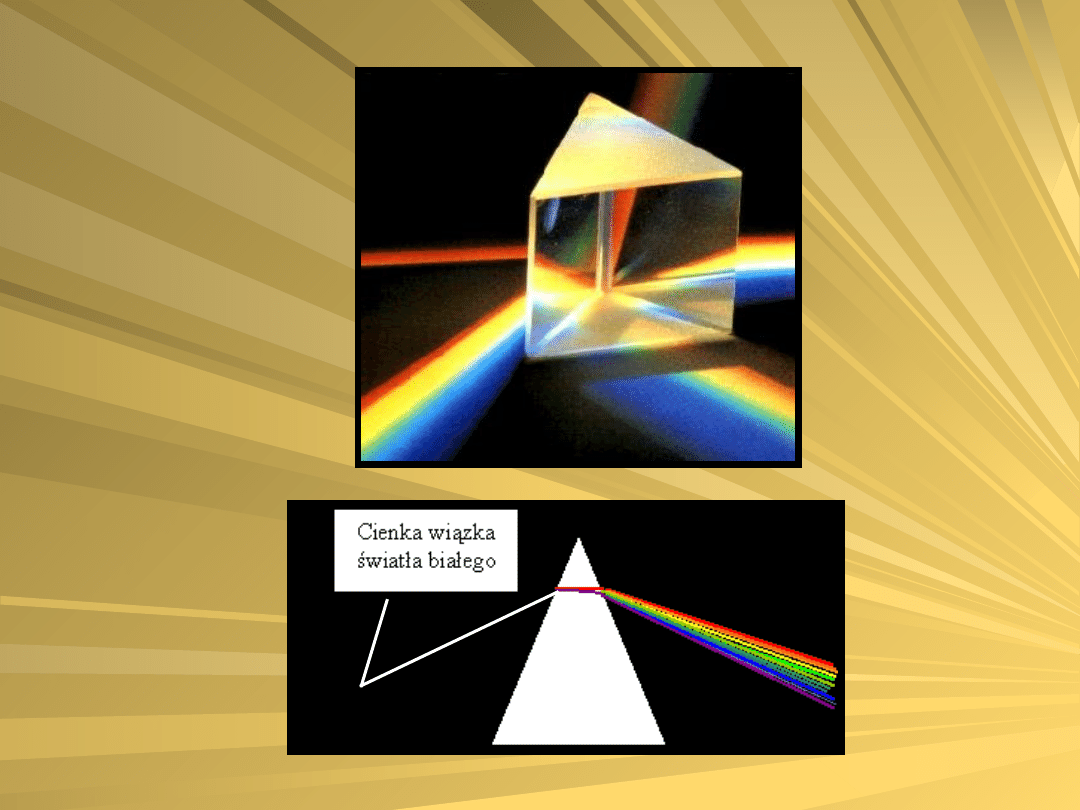
Promienie czerwone rozchodzą się w szkle szybciej

niż promienie fioletowe. Dlatego też promienie

czerwone załamują się słabiej niż fioletowe.

Załamanie i rozszczepienie światła występuje dla

większości materiałów przezroczystych. Ono

nadaje piękny poblask brylantom i kryształom, ono

powoduje powstawanie tęczy (światło jest wtedy

załamywane i rozszczepiane przez miniaturowe

kropelki wody).

Rozszczepienie najłatwiej jest zaobserwować w

pryzmacie (w porównaniu do tego samego efektu

padającego na zwykłą granicę dwóch ośrodków),

ponieważ załamuje on i rozszczepia światło

dwukrotnie dzięki czemu barwne promienie są

silniej rozbieżne niż w przypadku załamania

jednokrotnego.

OPTYKA FALOWA

OPTYKA FALOWA

Wstęp

Wstęp

Zanim odkryto, że światło jest falą, przez długi

czas królował wyłącznie model optyki

geometrycznej - czyli taka wizja rozchodzenia

się światła, w której "cząstki" świetlne poruszają

się od źródła po liniach prostych, odbijając co

najwyżej od niektórych przedmiotów. 

Dziś wiemy, że model optyki geometrycznej jest

niepełny, a w szczególnych sytuacjach w ogóle

się załamuje, dając błędne przewidywania.

Przyczyną tego jest m.in. to, że 

Światło jest falą.
– Odkrycie to zawdzięczamy przede wszystkim

fizykom francuskim, którzy w początkach XIX

wieku tworzyli podwaliny wiedzy o zjawiskach

falowych.

Dyfrakcja

Dyfrakcja

Zjawisko uginania się fal świetlnych na

granicy światła i cienia, polegające na

przenikaniu ruchu falowego w obręb cienia, na

skutek uginania rozchodzącej się fali na

krawędzi przeszkody. W przyrządach

fotooptycznych może powodować nieostrość

obrazów wskutek ugięcia światła na

krawędziach otworów tych przyrządów, np.

przysłony. Skutkiem dyfrakcji są w fotografii

świetliste aureole wokół przedmiotów

fotografowanych pod światło oraz zanik obrazu

przedmiotów o małych wymiarach, np. zbyt

cienkich, fotografowanych pod światło, tzw.

wyżerki świetlne.

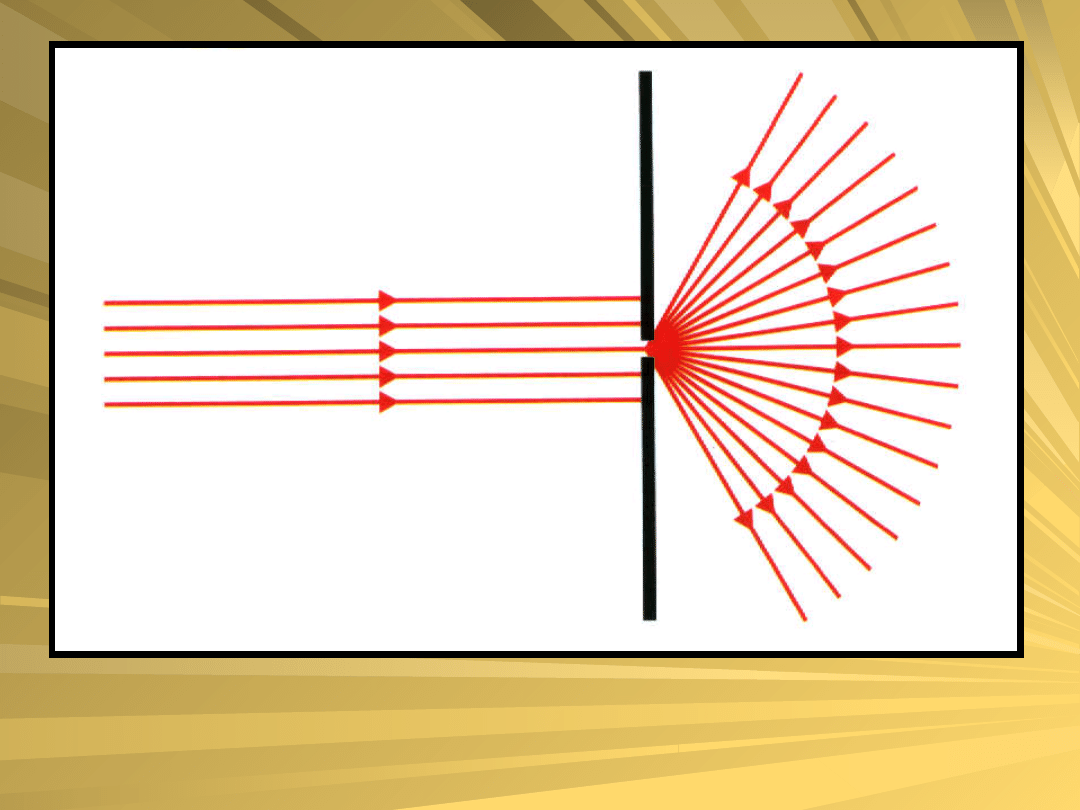
Zjawisko dyfrakcji

Interferencja

Interferencja

Interferencja to zjawisko nakładania

się fal prowadzące do zwiększania lub

zmniejszania amplitudy fali wypadkowej.

Interferencja zachodzi dla wszystkich

rodzajów fal, we wszystkich ośrodkach, w

których mogą rozchodzić się dane fale. W

ośrodkach nieliniowych oprócz interferencji

zachodzą też inne zjawiska wywołane

nakładaniem się fal, w ośrodkach liniowych

fale o jednakowej częstotliwości ulegając

interferencji spełniają zasadę superpozycji.

Interferencja fal
sferycznych
pochodzących z
rozmieszczonych
na różne sposoby
źródeł

SOCZEWKA

SOCZEWKA

I JEJ OGNISKO

I JEJ OGNISKO

Czym jest soczewka?

Czym jest soczewka?

Soczewka to właściwie nic innego tylko

lupa, choć gdy jest wykorzystywana w

przyrządach optycznych, to pozbawiona

jest samodzielnej oprawki. 

Typowa soczewka – tzw. soczewka

sferyczna - powstaje z przecięcia dwóch

sfer i wypełnienia tego przecięcia

materiałem przezroczystym dla światła

– najczęściej szkłem.

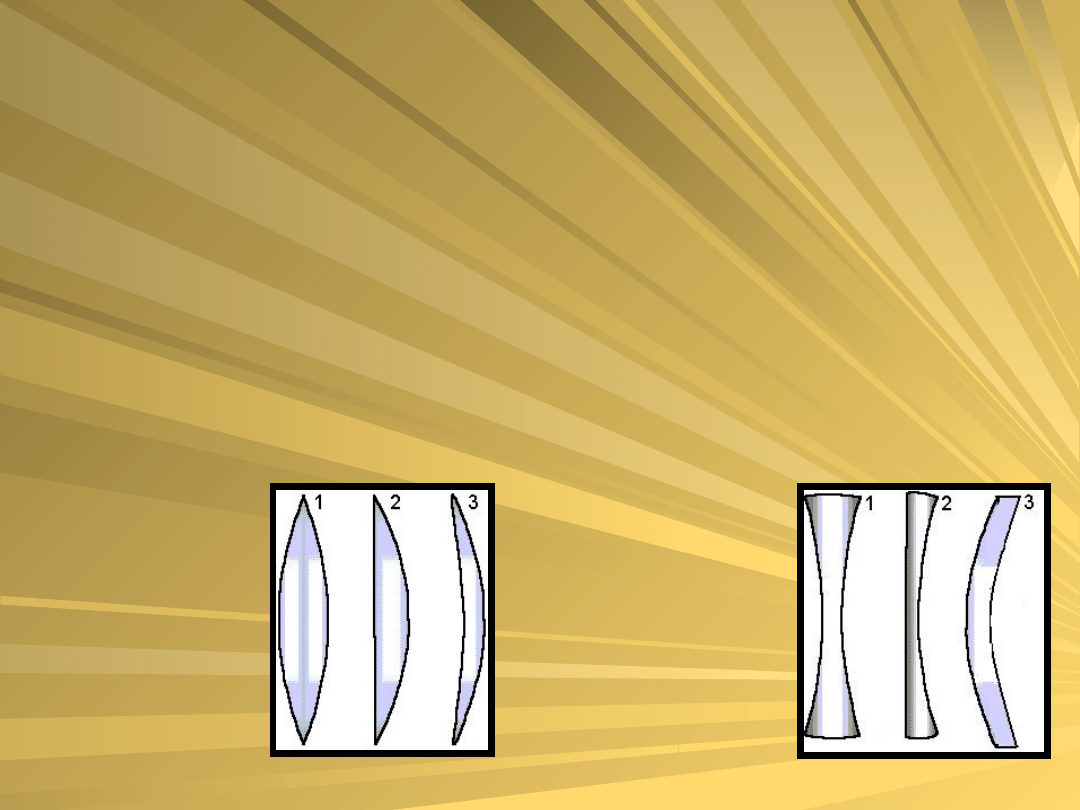
Rodzaje soczewek

Rodzaje soczewek

Soczewki dzielimy na dwie podstawowe

grupy: skupiające i rozpraszające.
Poniżej przedstawiony został podział
soczewek optycznych ze względu na
kształt:

Soczewki wypukłe Soczewki

wklęsłe

1 – dwuwypukła

2 – płasko-wypukła

3 – wklęsło-
wypukła

1 – dwuwklęsła

2 – płasko-wklęsła

3 – wypukło-wklęsła

OTRZYMYWANIE

OTRZYMYWANIE

OBRAZU ZA POMOCĄ

OBRAZU ZA POMOCĄ

SOCZEWEK

SOCZEWEK

Każdy punkt przedmiotu wysyła

światło w różnych kierunkach. Część
promieni tego światła pada na
soczewkę. Aby wyznaczyć położenie
obrazu świecącego punktu, wystarczy
wybrać dwa promienie wychodzące z
niego i padające na powierzchnie
soczewki. Mogą to być dwa promienie
spośród trzech następujących:



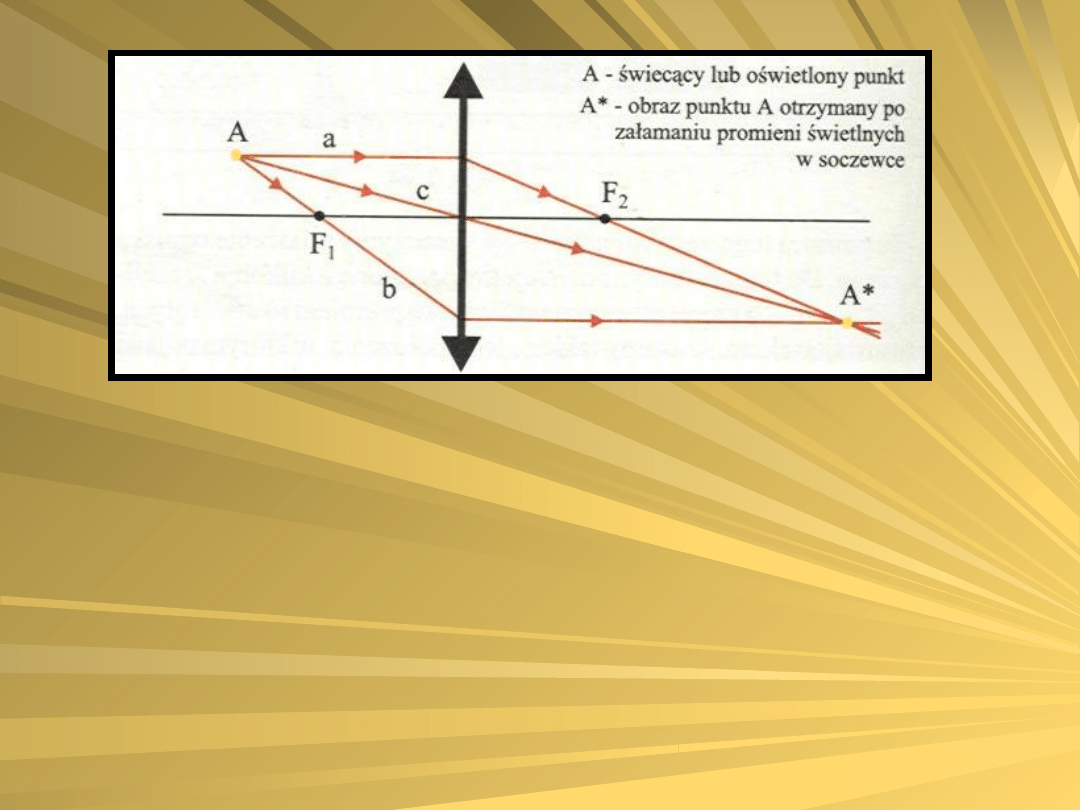
Promień równoległy do osi optycznej – po przejściu przez

soczewkę promień ten przechodzi przez jej ognisko,



Promień przechodzący przez ognisko – po przejściu przez

soczewkę promień ten biegnie równolegle do osi

optycznej,



Promień przechodzący przez środek soczewki – po

przejściu przez soczewkę nie zmienia kierunku

Wielkości opisujące

Wielkości opisujące

soczewki

soczewki

Soczewki można scharakteryzować za

pomocą parametrów stosowanych przy

zwierciadłach. Soczewki posiadają ogniska

(F1; F2), środki krzywizn (O1; O2), ogniskową

(f) oraz promienie krzywizn (r1; r2).

Płaszczyznę, w której przecinają się

promienie tworzące wiązki równoległe,

nazywamy płaszczyzną ogniskową soczewki.

Punkt przecięcia płaszczyzny ogniskowej z

główną osią optyczną soczewki nosi nazwę

ogniska (punkt F). Każda soczewka skupiająca

ma dwa ogniska rzeczywiste. Ogniskowa f to

odległość ogniska od środka soczewki.

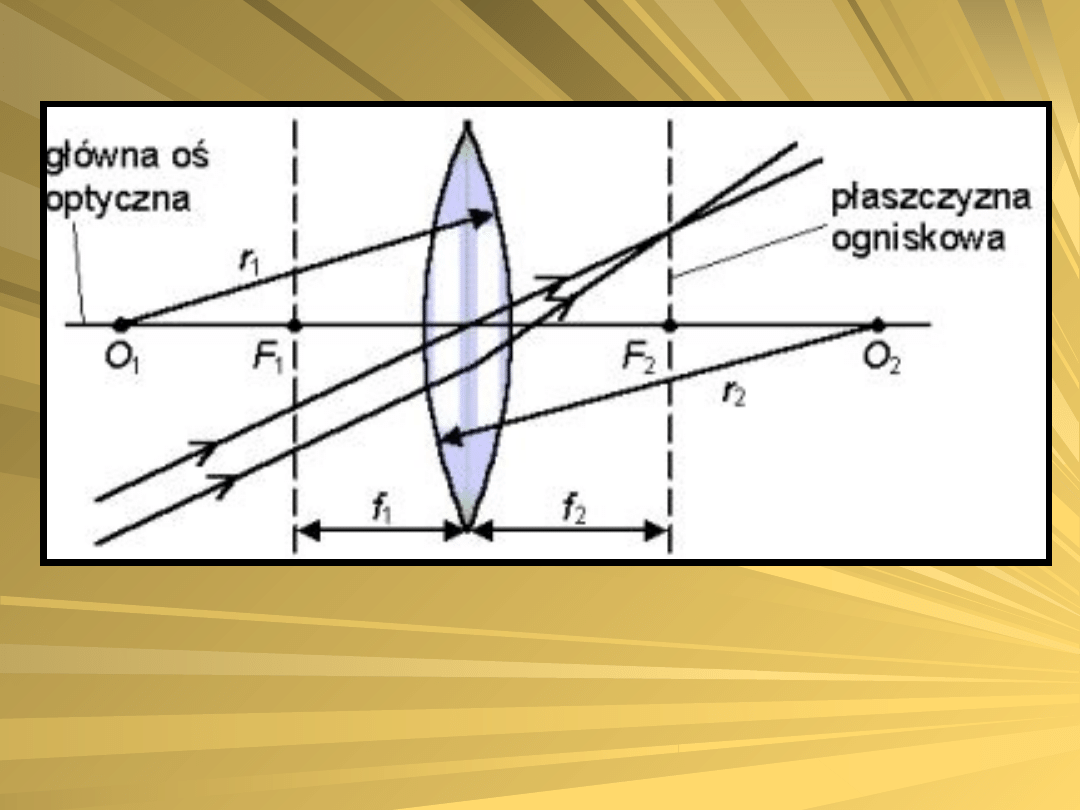
SOCZEWKA

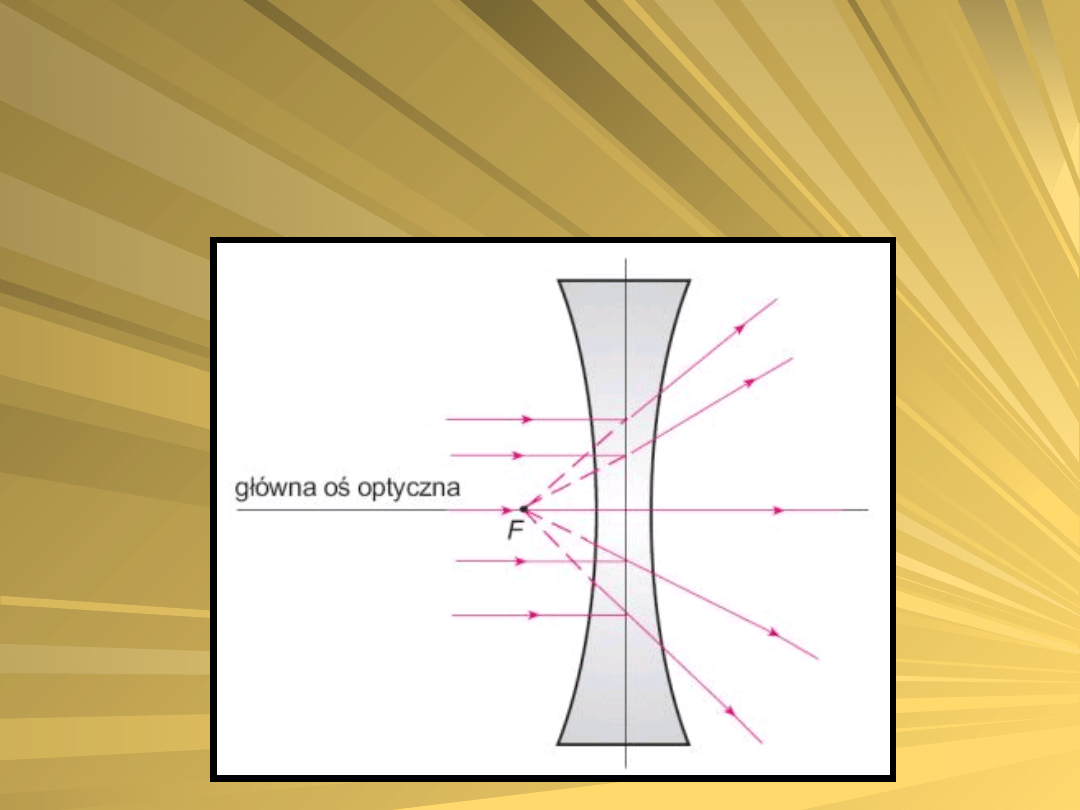
Wiązka światła równoległa do osi optycznej i padająca na

soczewkę rozpraszającą (wklęsłą) staje się rozbieżna.

Przedłużenia promieni wychodzących z soczewki przecinają

się w jednym punkcie F, który nazywamy ogniskiem

pozornym soczewki rozpraszającej.

Zdolność skupiająca soczewki Z to

odwrotność jej ogniskowej wyrażona w

metrach.

Jednostką zdolności skupiającej jest

dioptria (symbol dp lub D).

Mówimy, że soczewka posiada

zdolność skupiającą równą 1 dioptrii,

jeżeli jej ogniskowa wynosi 1 m.

Obrazy w soczewce skupiającej mogą być

rzeczywiste i pozorne, proste i odwrócone,
powiększone i pomniejszone. Charakter
obrazu zależy od odległości x, w jakiej
przedmiot znajduje się przed soczewką.

Na rysunkach poniżej przedstawiono
konstrukcję obrazów w soczewce skupiającej,
przy różnych położeniach przedmiotu.

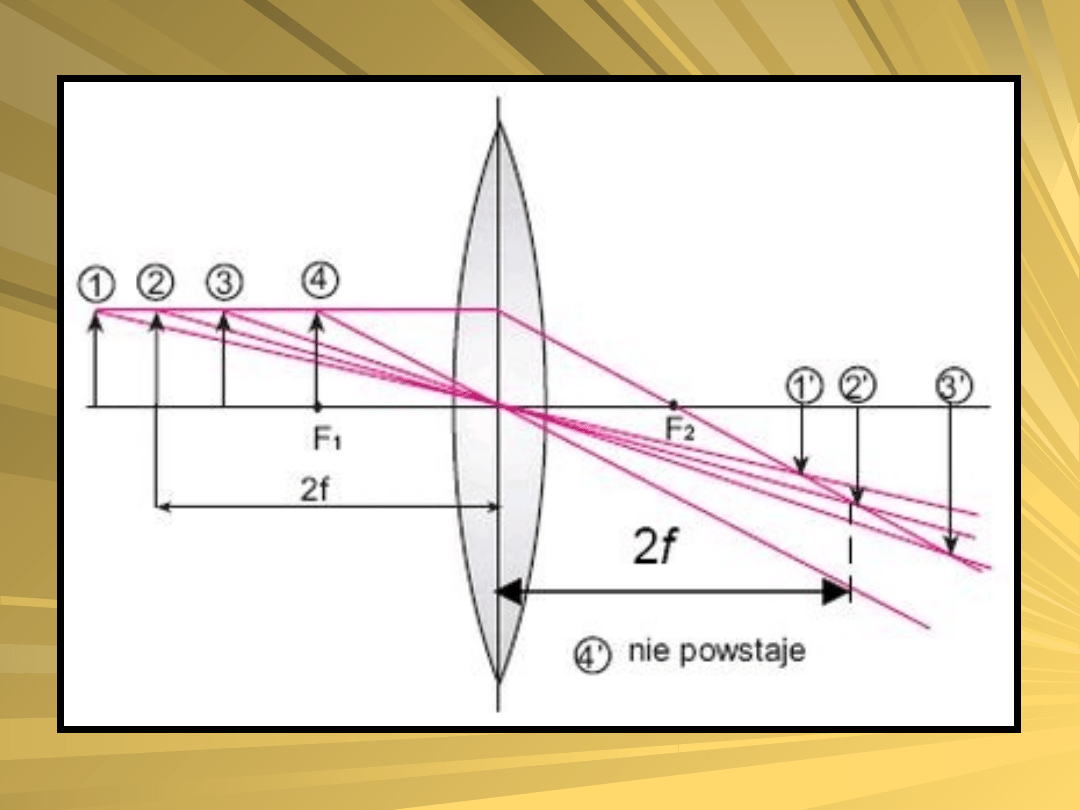
Z rysunków tych wynikają następujące

prawidłowości:

1) Jeżeli przedmiot leży przed soczewką w odległości

x > 2f, to jego obraz jest odwrócony,

pomniejszony i rzeczywisty.

2) Jeżeli przedmiot leży przed soczewką w odległości

x = 2f, to jego obraz jest odwrócony, tej samej

wielkości co przedmiot

i rzeczywisty.

3) Jeżeli przedmiot leży przed soczewką w odległości

f < x < 2f, to jego obraz jest odwrócony,

powiększony i rzeczywisty.

4) Jeżeli przedmiot leży przed soczewką w odległości

x = f, to obraz nie powstaje.

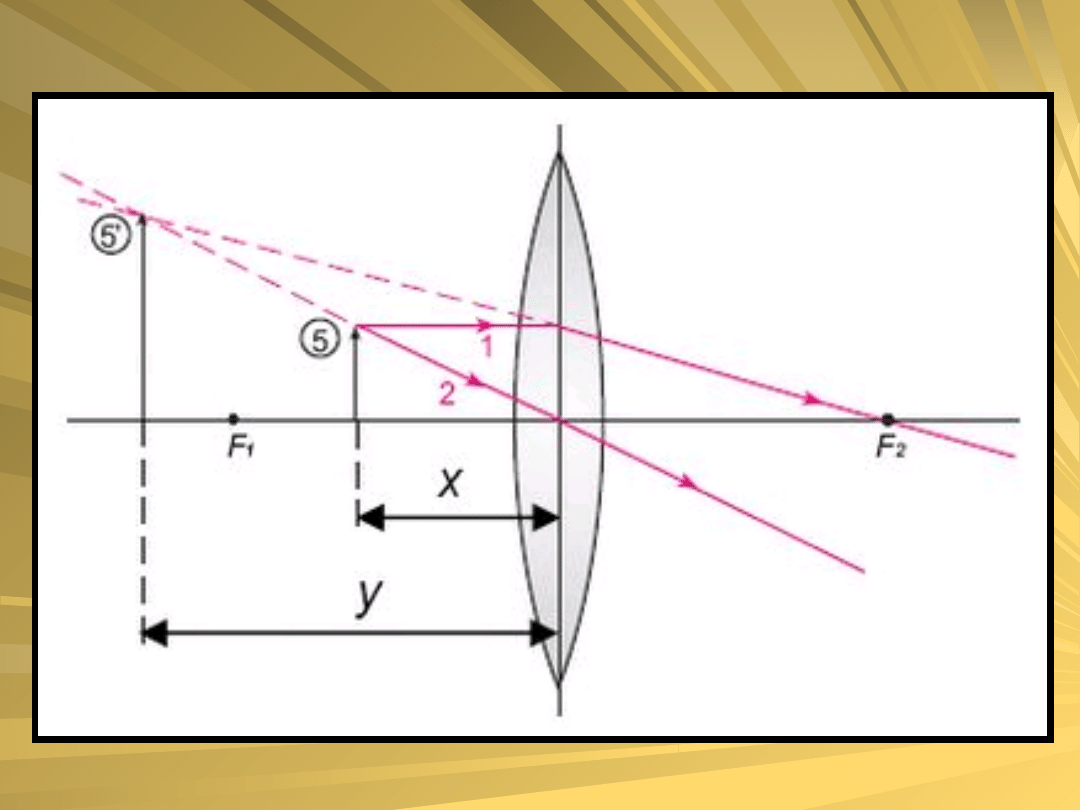
5) Jeżeli przedmiot leży przed soczewką w odległości

x < f, to jego obraz jest prosty, powiększony

i pozorny. Obraz ten leży po tej samej stronie, po

której znajduje się przedmiot.

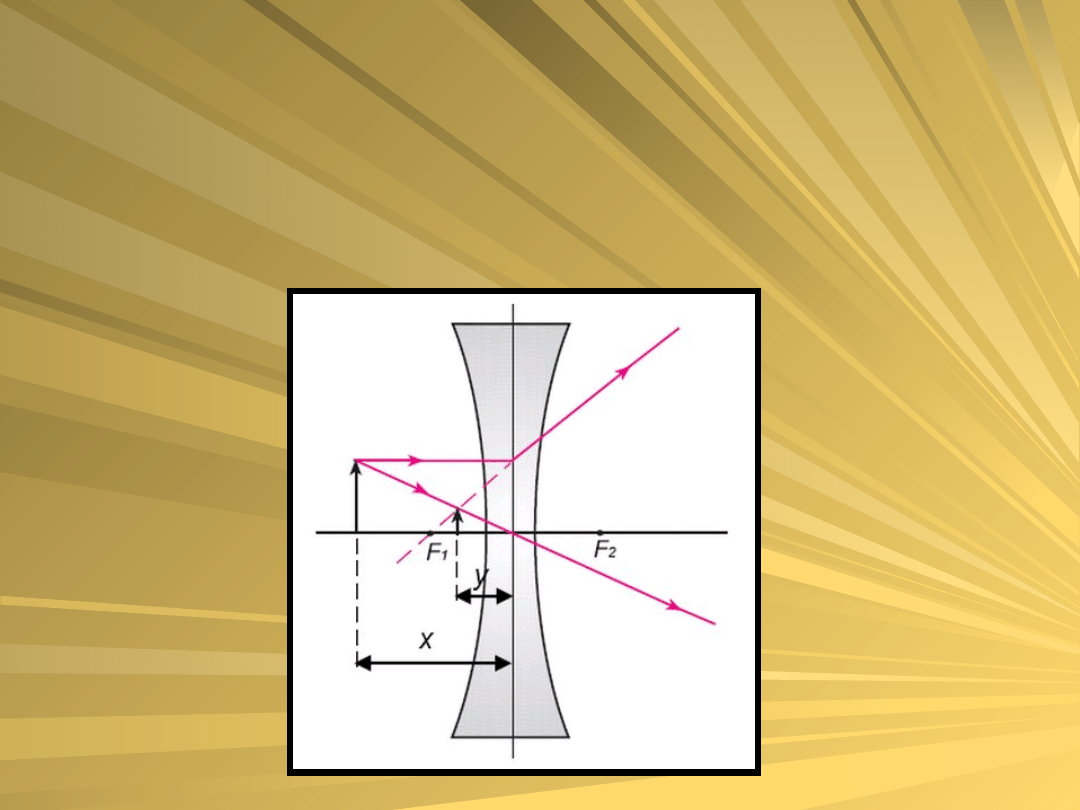
Obrazy w soczewce rozpraszającej są zawsze

pozorne, proste i pomniejszone. Wielkość obrazu
rośnie, gdy przedmiot zbliżamy do soczewki.
Konstrukcję obrazu w takiej soczewce
przedstawiono na rysunku:

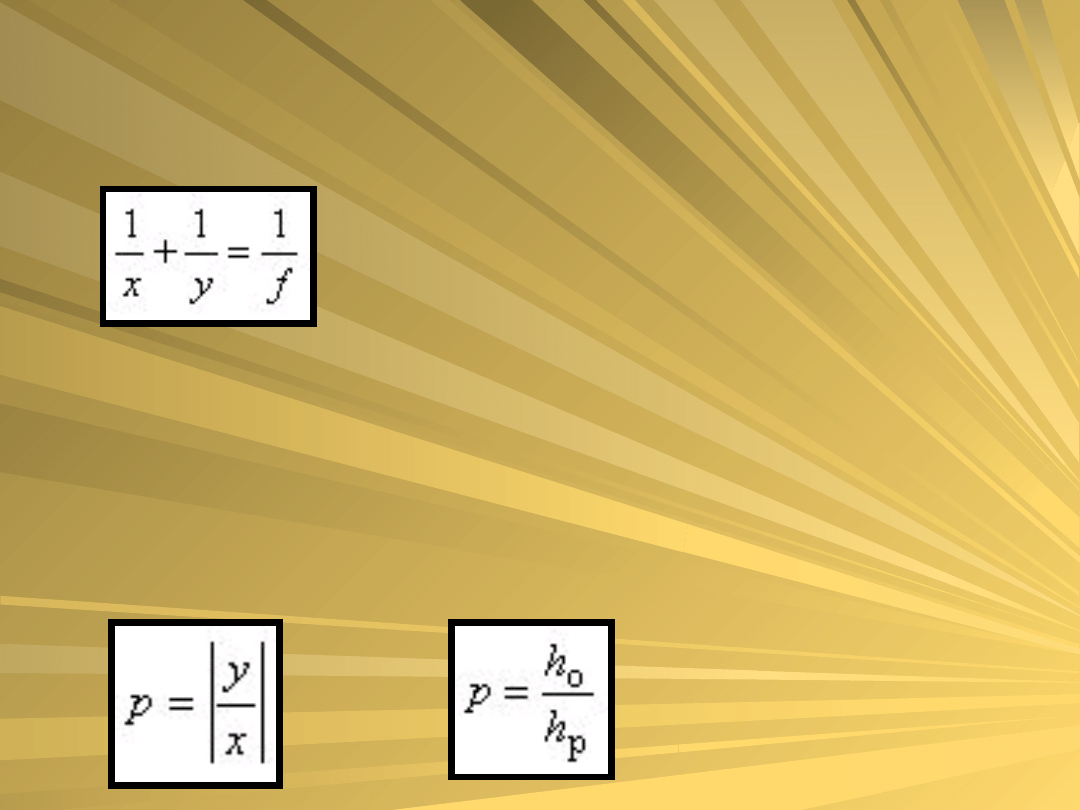
Związek pomiędzy x i y dla soczewki jest

analogiczny jak dla zwierciadeł:

Jeżeli obraz jest pozorny, to przed y wstawiamy
znak minus, a jeżeli soczewka jest
rozpraszająca, to dodatkowo przed f
wstawiamy znak minus.

Powiększenie p obrazu w soczewce
obliczamy ze wzorów:

lub

gdzie:
ho –
wysokość
obrazu, hp –
wysokość
przedmiotu.

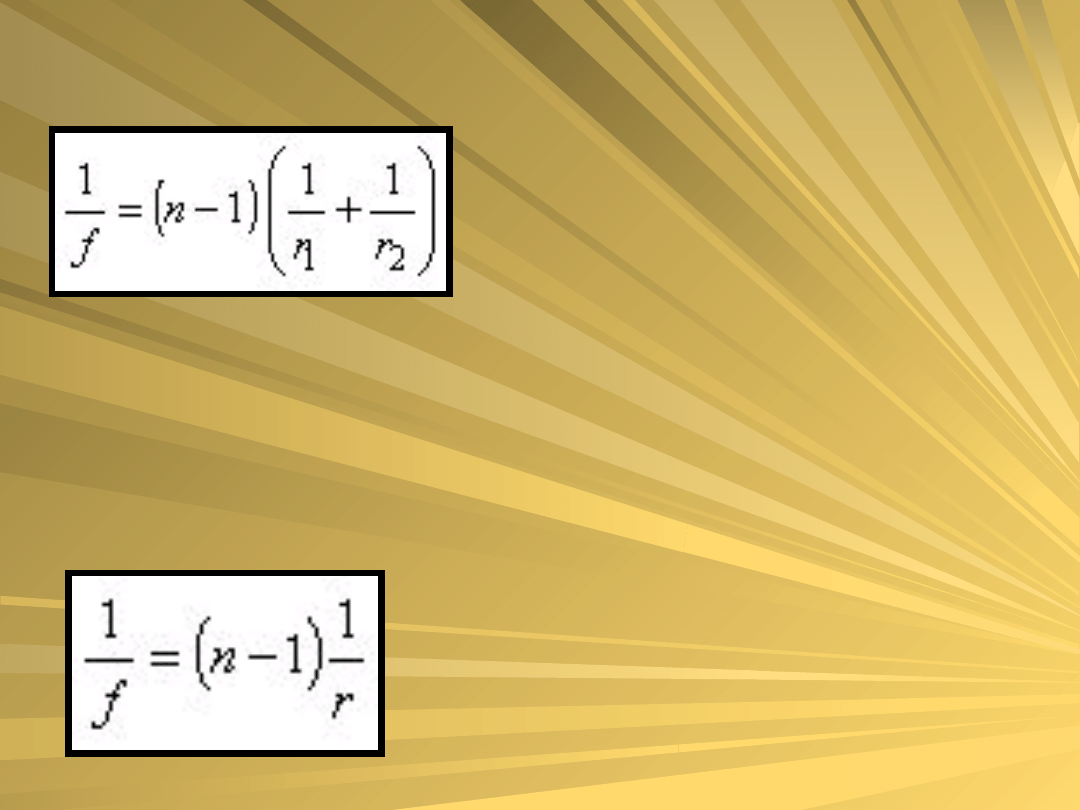
Równanie soczewki ma postać:

gdzie: n – względny
współczynnik załamania
materiału soczewki
względem ośrodka
otaczającego,
r1, r2 – promienie
krzywizny,
f – ogniskowa soczewki.

Dla soczewki płasko-wypukłej (r2 › ∞)
równanie przybiera postać:

Lupa

Lupa

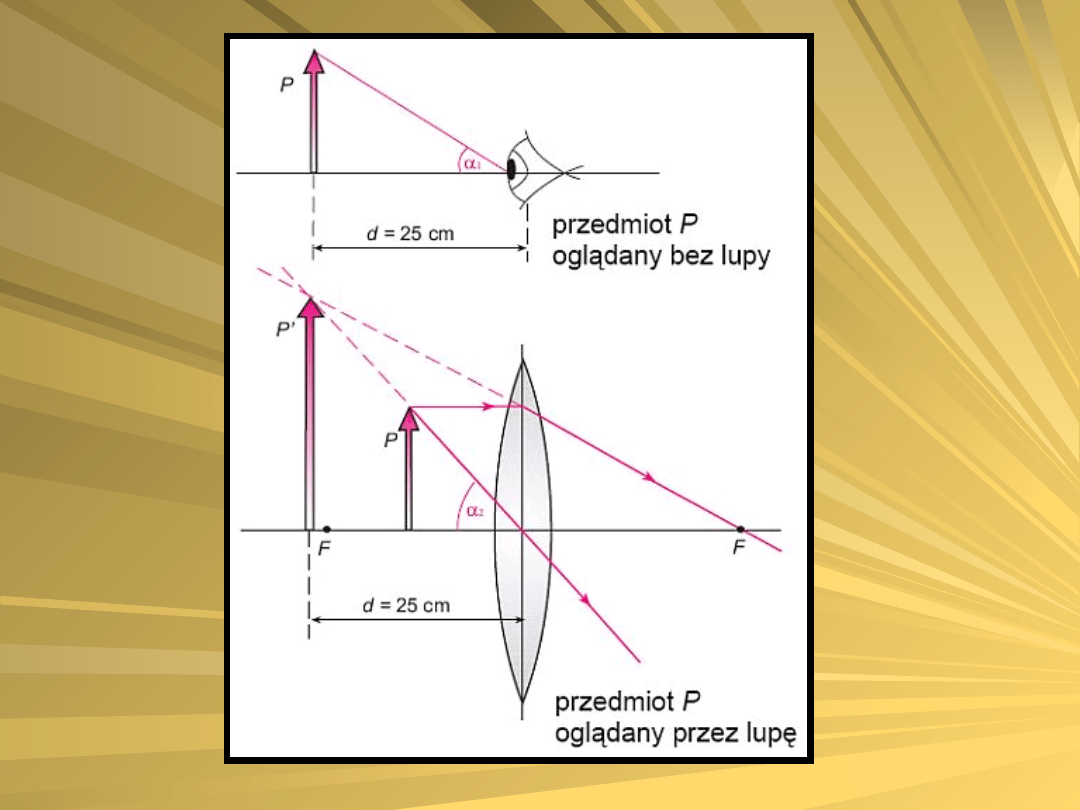
Lupa jest typowym przyrządem

optycznym powiększającym kąt
widzenia. Lupa to w praktyce
oprawiona soczewka skupiająca.
Powstawanie obrazu w lupie i sposób
powiększania kąta widzenia
przedstawiono na rysunku:

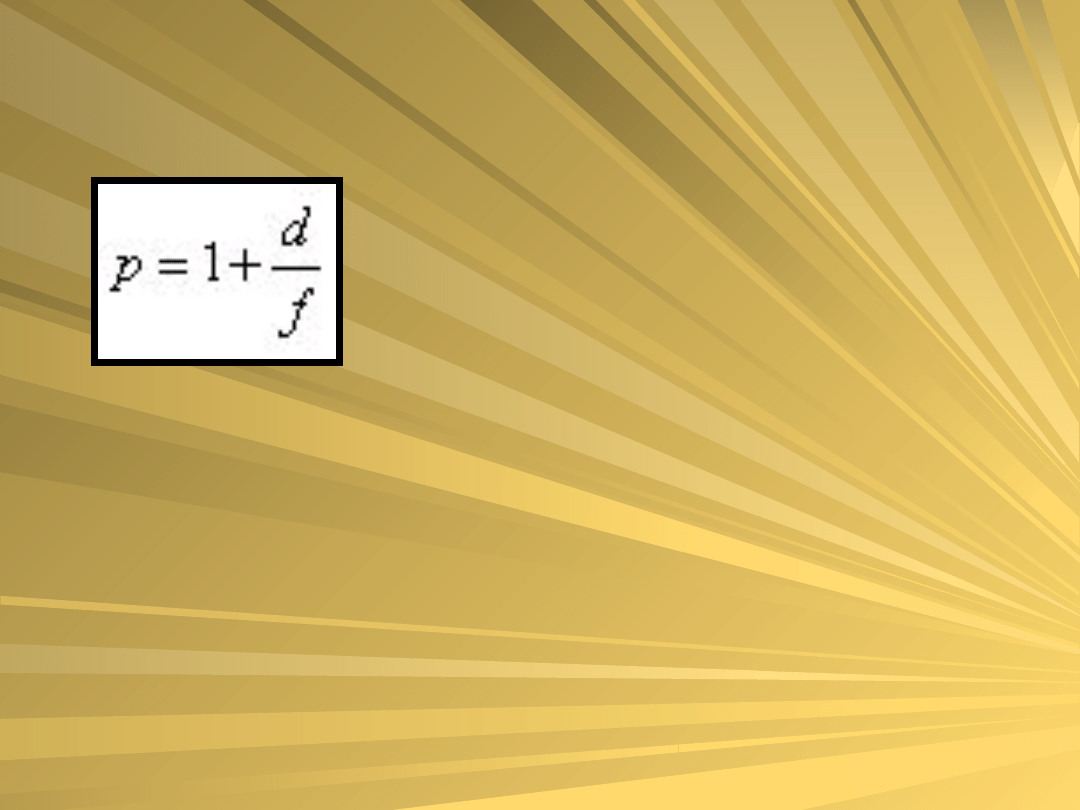
Powiększenie lupy obliczamy ze wzoru:

gdzie: d – odległość
dobrego widzenia
(przyjmuje się: d =
25cm),
f – ogniskowa lupy.

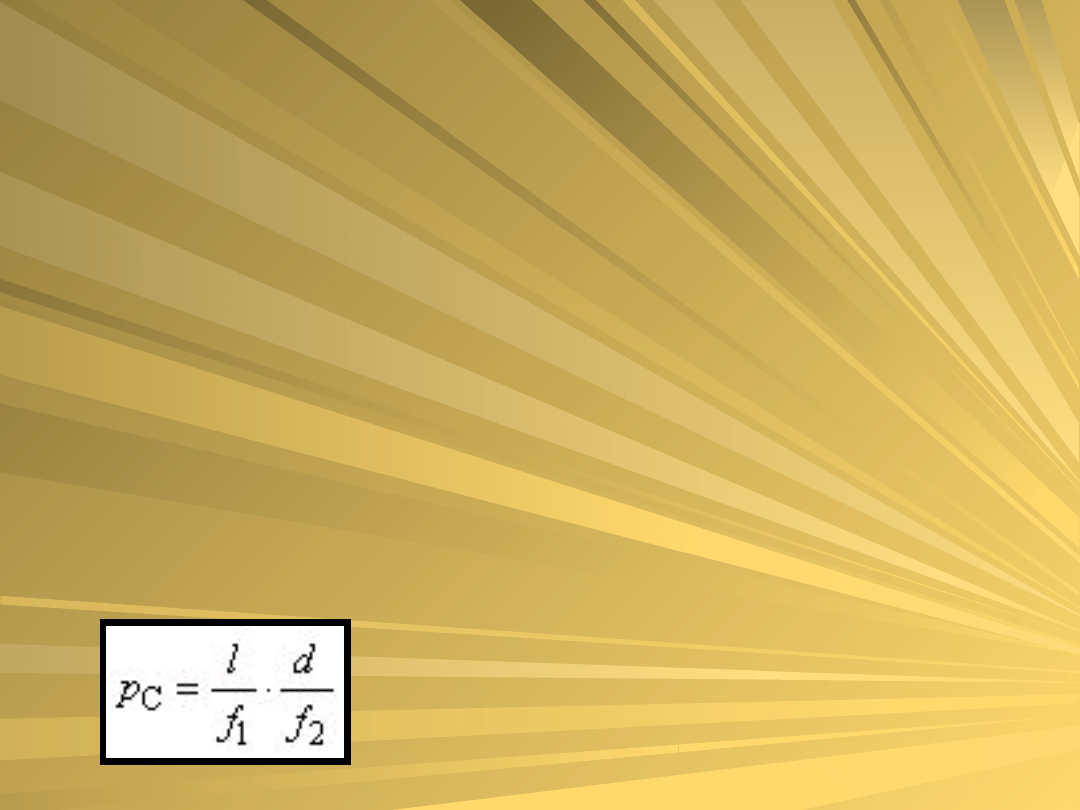
Mikroskop

Mikroskop

Mikroskop umożliwia uzyskiwanie dużych

powiększeń dzięki dwukrotnemu powiększaniu

obrazu: najpierw w obiektywie, a następnie w

okularze. Całkowite powiększenie pC jest iloczynem

powiększeń okularu pok i obiektywu pob:

pC = pob·pok

Powiększenie mikroskopu można również wyrazić

wzorem:

gdzie: f1, f2 – ogniskowe okularu
i obiektywu,
l – długość tubusu mikroskopu
(odległość pomiędzy okularem
i obiektywem).

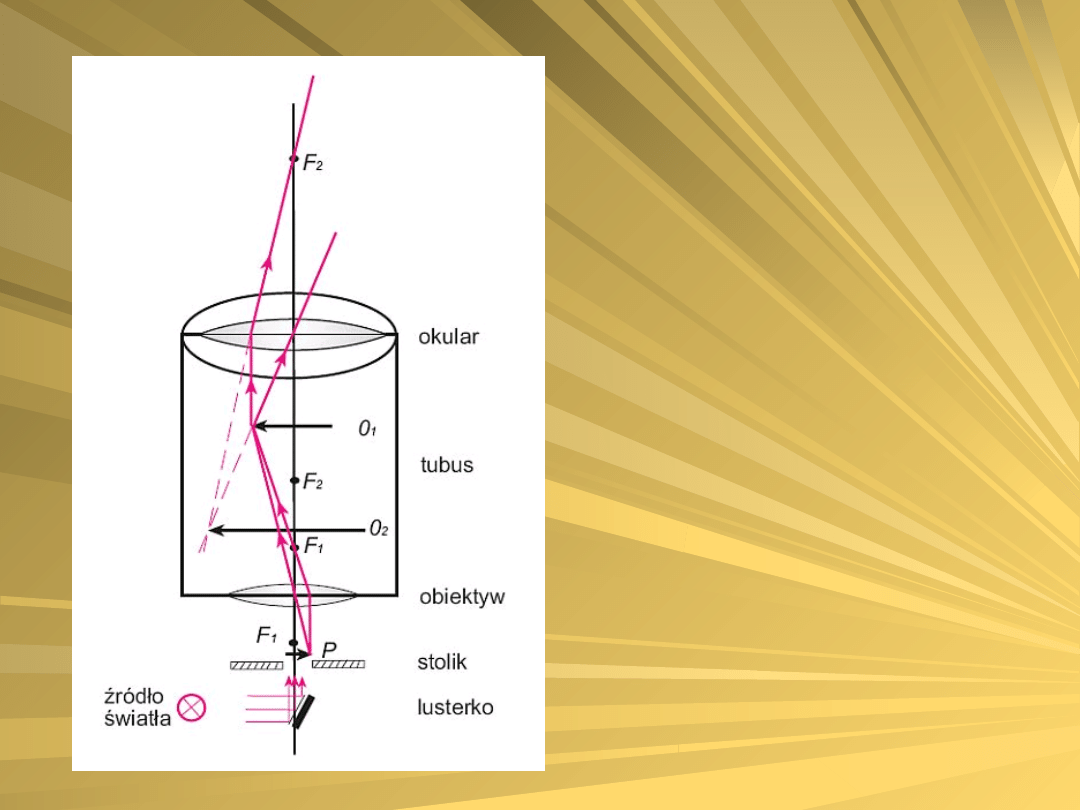
Bieg promieni w

mikroskopie i
schemat
powstawania
obrazu
przedstawiono na
rysunku:

Luneta

Luneta

Luneta astronomiczna składa się, podobnie jak

mikroskop, z okularu

i obiektywu. Obraz odległego przedmiotu

powstaje tuż za ogniskową obiektywu, a

jednocześnie tuż przed ogniskiem okularu F2.

Okular pełni więc rolę lupy. Luneta zwiększa kąt

widzenia. Do oka dociera wiązka światła pod

kątem α1. Kąt ten jest większy od kąta α, pod

jakim widzimy przedmiot bez użycia lunety.

Powiększenie kątowe lunety pK wyraża się

wzorem:

gdzie:
f1, f2 –
ogniskowe
okularu i
obiektywu.

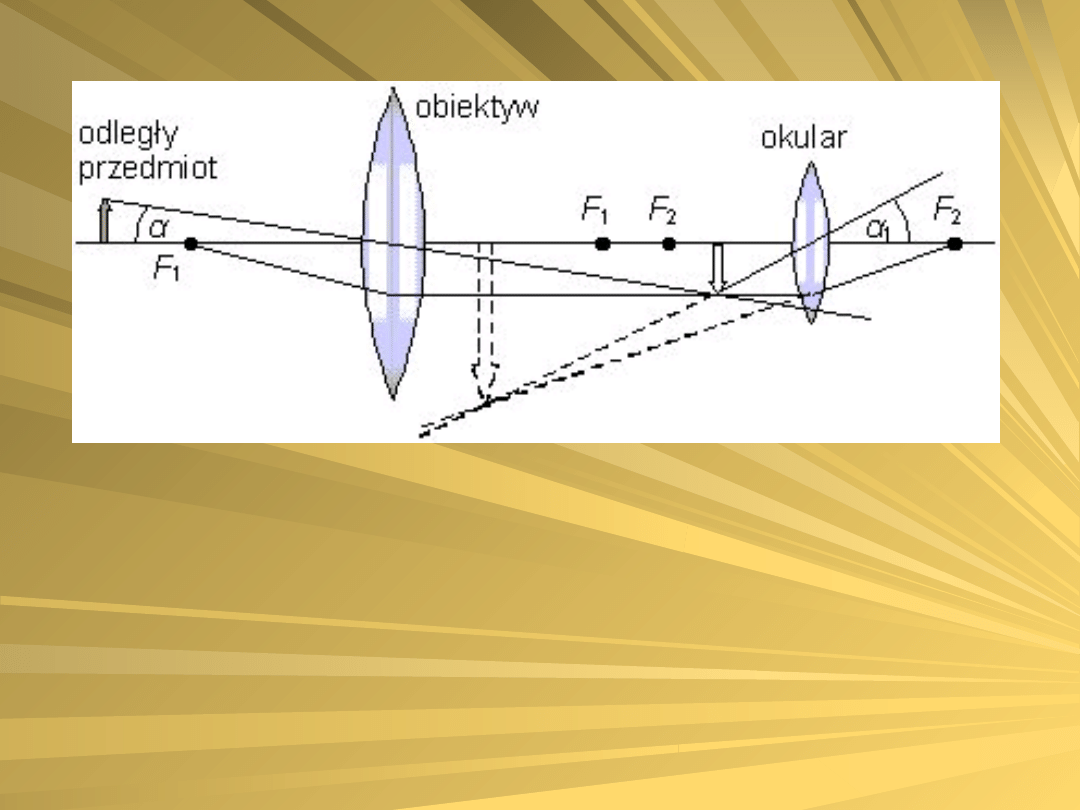
Schemat lunety

Soczewki do korekcji wzroku

stosuje się zarówno u dalekowidzów,

jak i krótkowidzów. W oku krótkowidza

obraz powstaje przed siatkówką,

dlatego stosujemy soczewkę

rozpraszającą (minusową). W oku

dalekowidza obraz powstaje za

siatkówką, więc korekcja tej wady

wymaga zastosowania soczewek

skupiających (plusowych).

Bieg promieni w oku krótkowidza i

dalekowidza przed korekcją i po użyciu

soczewek przedstawiono na rysunkach:

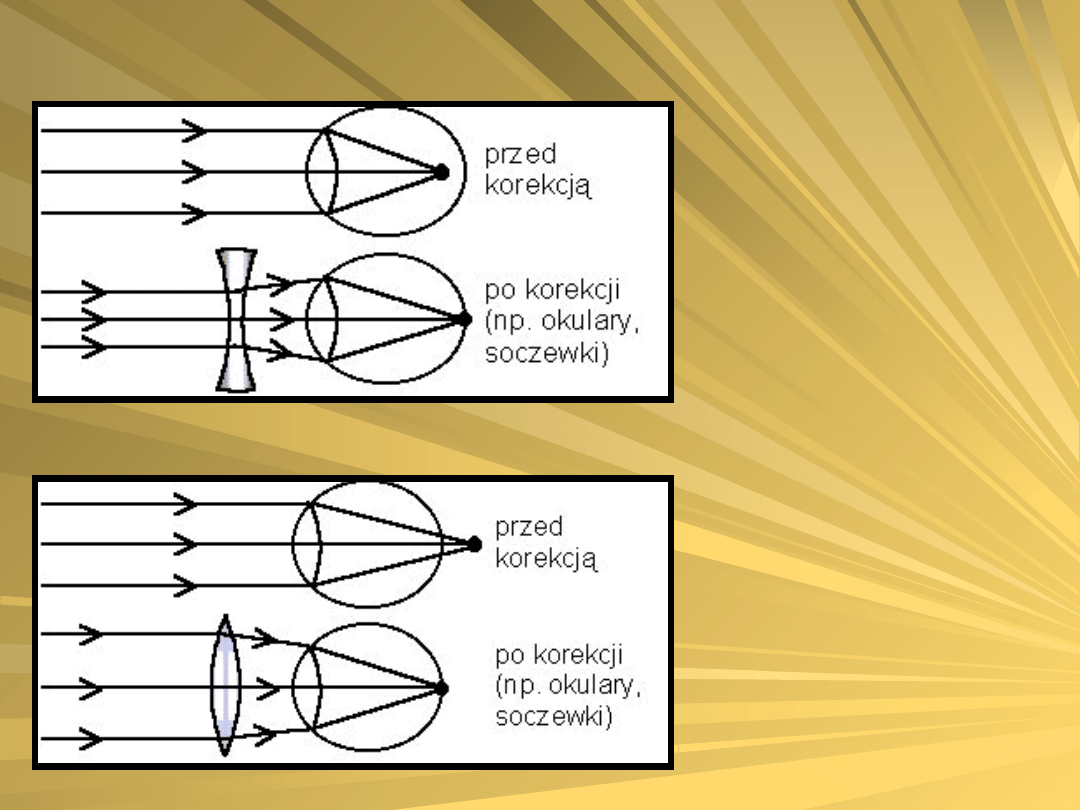
Dla krótkowidza

Dla dalekowidza

Zwierciadła

Zwierciadła

OBRAZY OTRZYMYWANE

OBRAZY OTRZYMYWANE

W ZWIERCIADLE

W ZWIERCIADLE

PŁASKIM

PŁASKIM

Obraz, który można

zobaczyć w lustrze jest
obrazem pozornym. Za
pomocą zwierciadła
płaskiego otrzymujemy
obraz pozorny i
symetryczny
względem powierzchni
zwierciadła.

ZWIERCIADŁA KULISTE

ZWIERCIADŁA KULISTE

Zwierciadło kuliste stanowi

część gładkiej, wypolerowanej części
kuli. W związku z tym wyróżniamy
zwierciadła kuliste:



Wklęsłe – gdy jako zwierciadło
wykorzystujemy wewnętrzną
powierzchnię kuli,



Wypukłe – gdy jako zwierciadło
wykorzystujemy zewnętrzną
powierzchnię kuli.

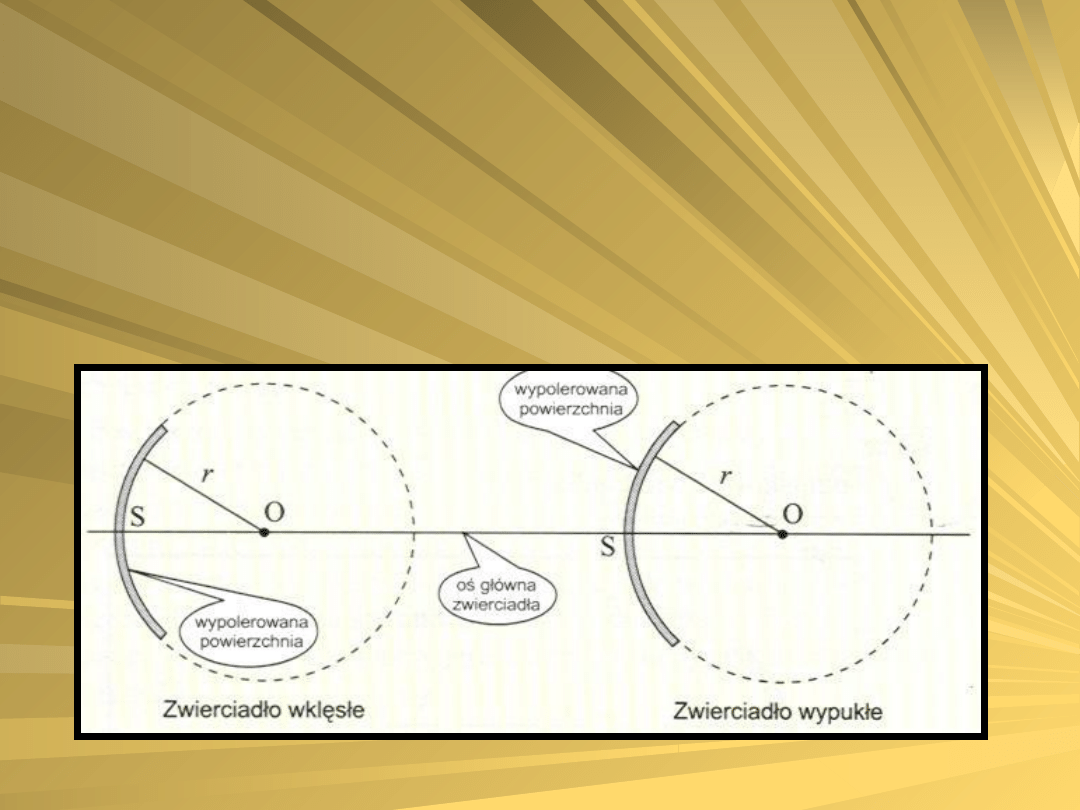
Każde zwierciadło kuliste posiada:



Środek krzywizny,



Promień krzywizny,



Oś główną.

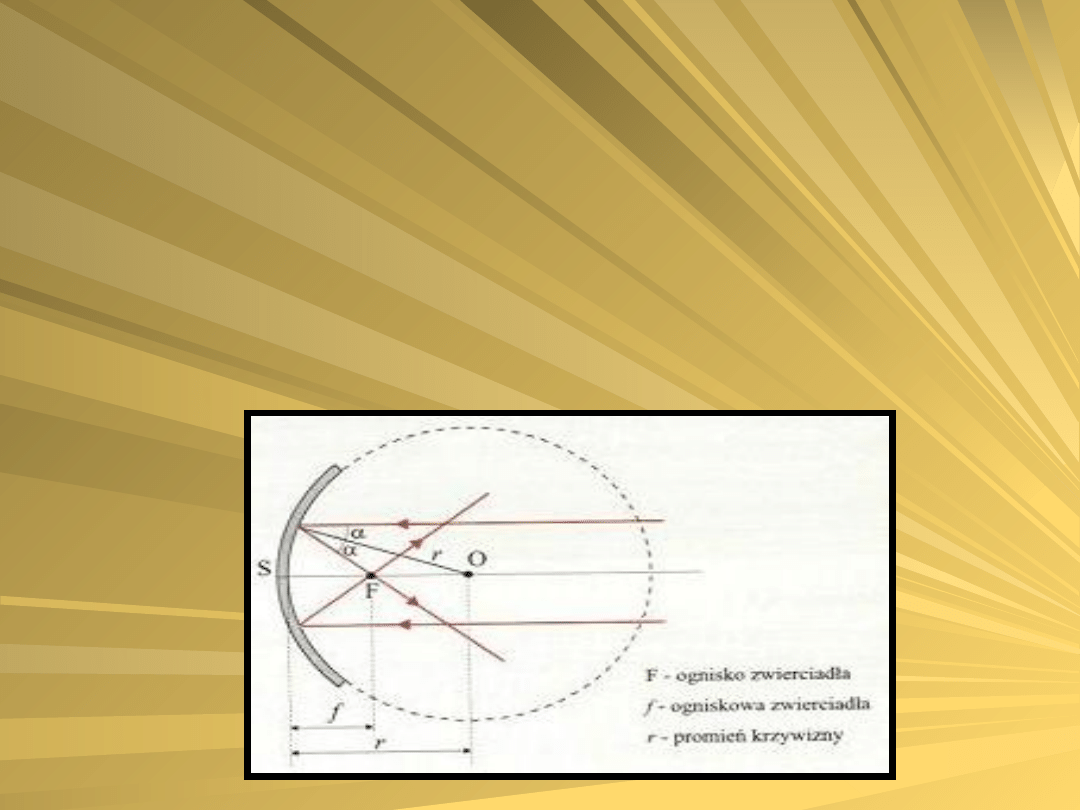
OTRZYMYWANIE OBRAZU W

OTRZYMYWANIE OBRAZU W

ZWIERCIADLE WKLĘSŁYM

ZWIERCIADLE WKLĘSŁYM

Promienie świetlne równoległe do osi głównej po od

biciu od powierzchni zwierciadła kulistego wklęsłego
przechodzą przez jeden punkt zwany ogniskiem
zwierciadła. Ognisko to leży na osi głównej
zwierciadła odległość ogniska od środka czaszy
zwierciadła nazywamy ogniskową.

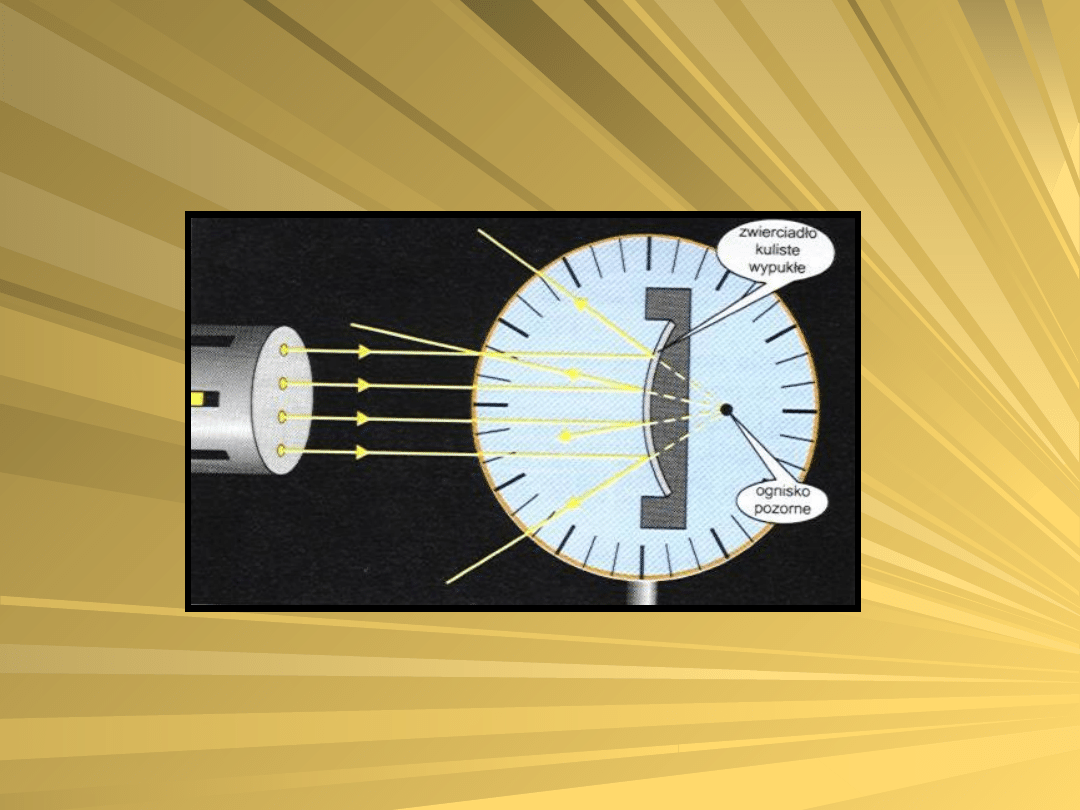
OTRZYMYWANIE OBRAZU

OTRZYMYWANIE OBRAZU

W ZWIERCIADLE

W ZWIERCIADLE

WYPUKŁYM

WYPUKŁYM

Zwierciadło kuliste wypukłe posiada ognisko

pozorne. Wiązka promieni równoległych do osi

głównej po odbiciu od powierzchni zwierciadła

staje się wiązką promieni rozbieżnych.

PRZYKŁADOWE

PRZYKŁADOWE

ZADANIA Z OPTYKI

ZADANIA Z OPTYKI

Zadanie 1

Zadanie 1

Przedmiot o wysokości 2 cm

ustawiono prostopadle do osi
optycznej soczewki, w odległości 15
cm od niej. Zdolność skupiająca
soczewki wynosi 10 D. Znajdź
położenie i wysokość obrazu.

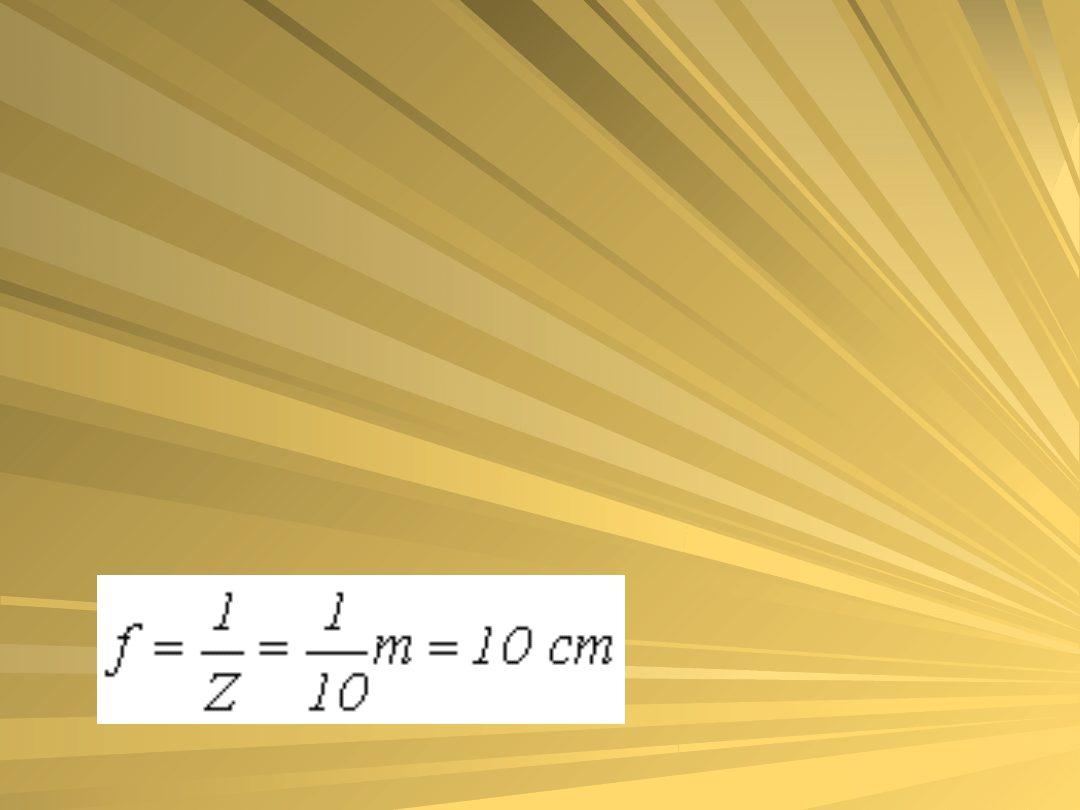
Dane:
X - wysokość przedmiotu - 2 cm

Y - wysokość obrazu -?

Z - zdolność skupiająca soczewki - 10 D

x - odległość przedmiotu - 15 cm

y - odległość obrazu - ?

Zdolność skupiająca to odwrotność

ogniskowej wyrażonej w metrach.

Jeśli więc

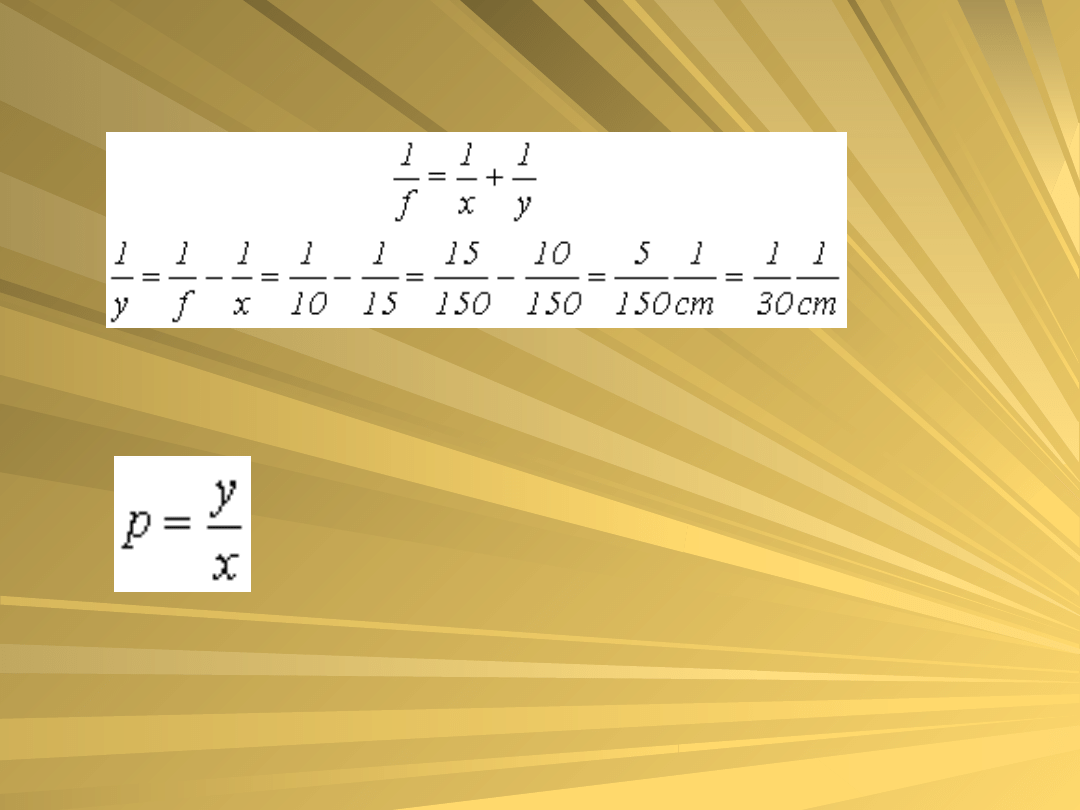
to z równania soczewki otrzymujemy

czyli odległość obrazu y = 30 cm

Jeżeli powiększenie

wyrażamy jako stosunek odległości
obrazu do odległości przedmiotu to
mamy

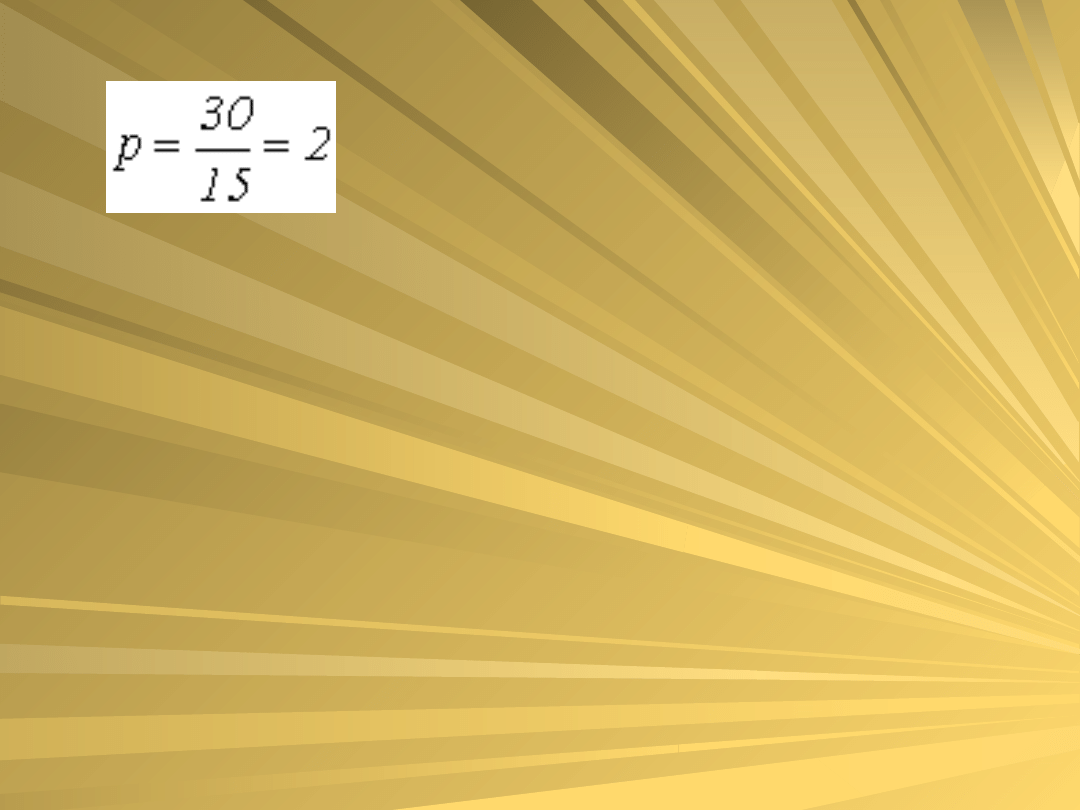
czyli przedmiot został powiększony

dwukrotnie.

Jeśli więc rozmiar przedmiotu

był 2 cm to obraz ma wysokość 4
cm.

Odpowiedź
Rozmiar obrazu ma wysokość 4
cm.

Zadanie 2

Zadanie 2

Pod jakim kątem na płytkę

kwarcową o współczynniku
załamania 1,545 pada z powietrza
promień świetlny, jeśli promień
odbity i promień załamany tworzą
kąt prosty?

n = 1,545

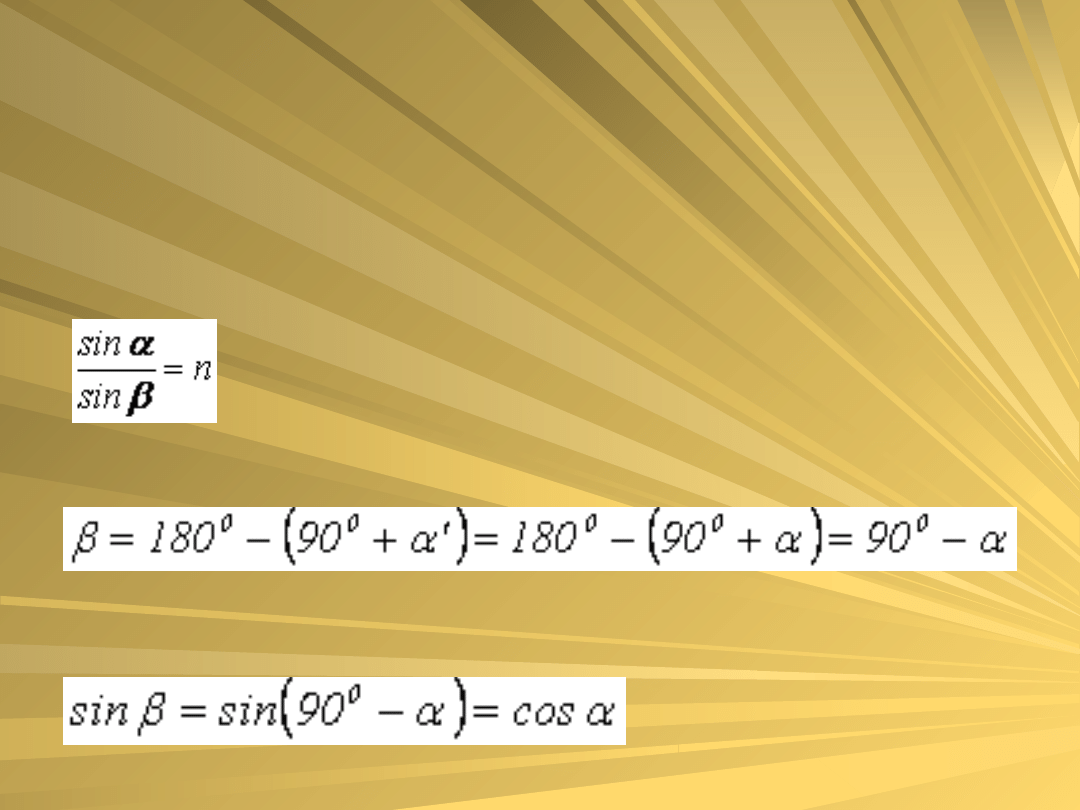
Rozwiązanie
Szukamy a - kąt padania.
Z prawa odbicia i załamania światła
a' =a

więc

skąd mamy

otrzymujemy więc z prawa załamania,

że

w takim razie tga = 1,545, skąd z
tablic odczytujemy a = 57o5'

Odp. Jeśli kąt padania jest równy
57o5' to promień załamany jest
prostopadły do odbitego.

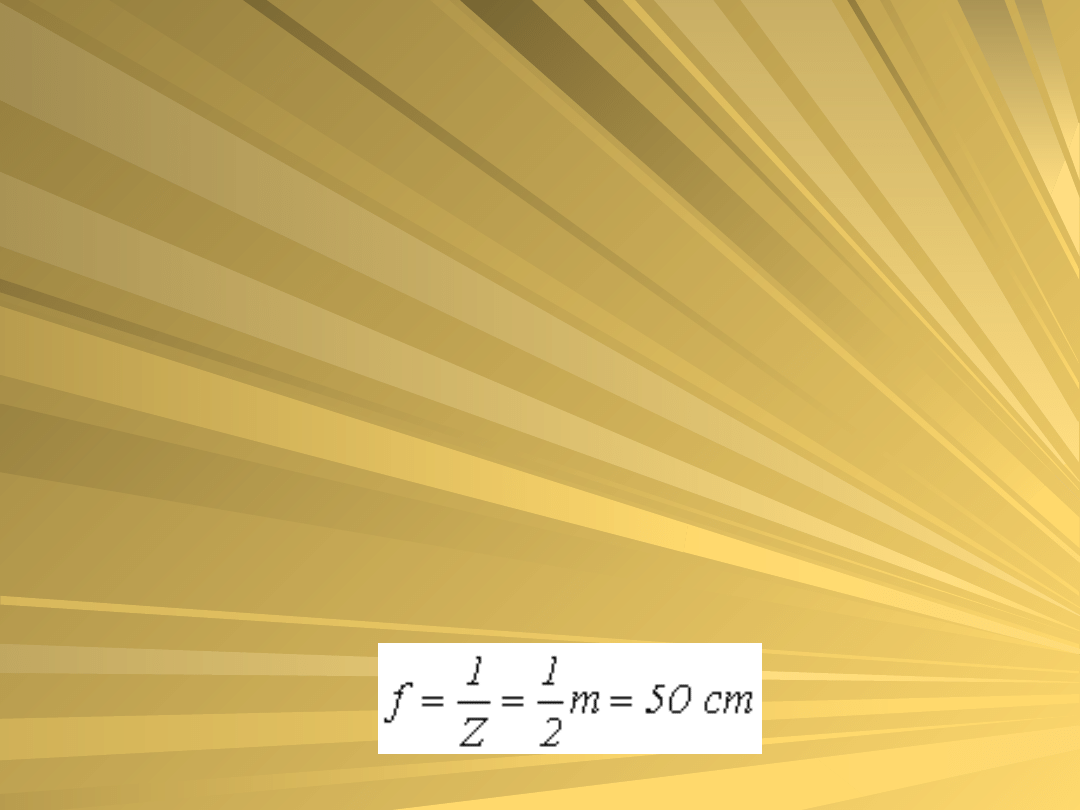
Zadanie 3

Zadanie 3

Gdy krótkowidz używa okularów o

zdolności skupiającej Z = -2D, widzi
dobrze z odległości 25cm. Oblicz
odległość dobrego widzenia tego
krótkowidza.

Rozwiązanie
:Zdolność skupiająca to odwrotność
ogniskowej wyrażonej w metrach.
Jeśli więc

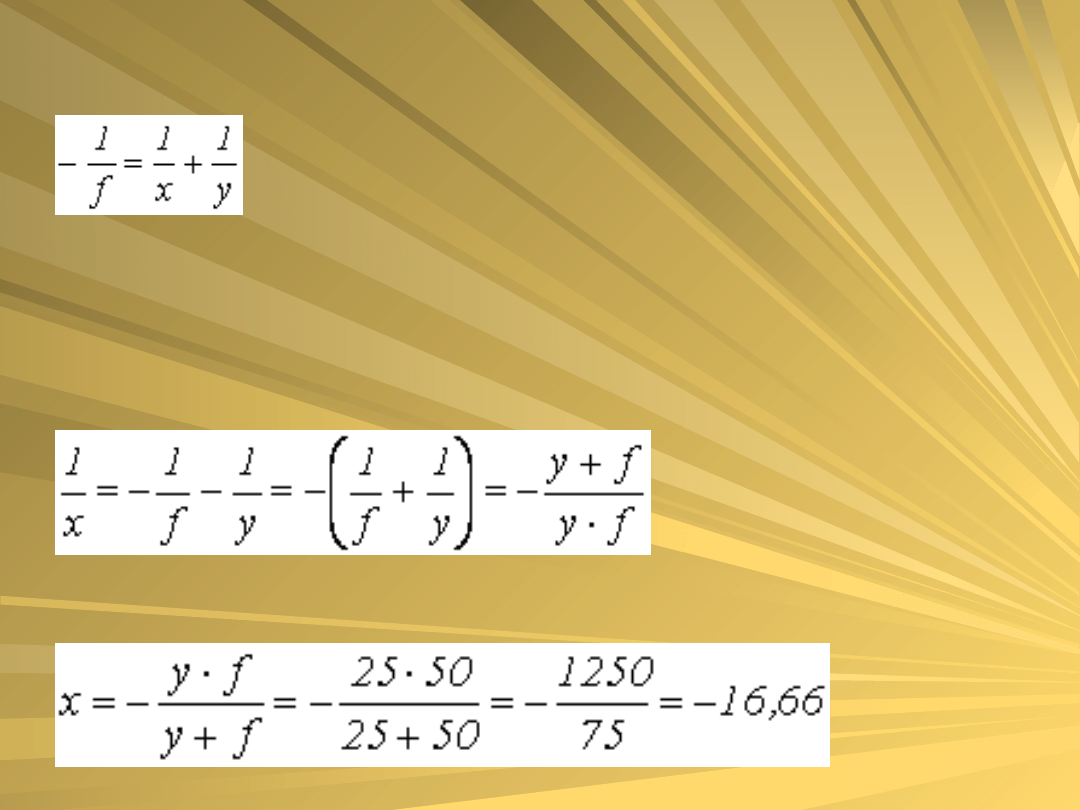
Z równania soczewki mamy:

(gdy człowiek patrzy w okularach to
widzi obraz już "przetworzony" przez
soczewkę.)
Szukamy, więc odległości przedmiotu
x.

wię
c

Minus oznacza, że mówimy o obrazie

pozornym.

Odp. Krótkowidz widzi dobrze bez

okularów w odległości 16,66cm.

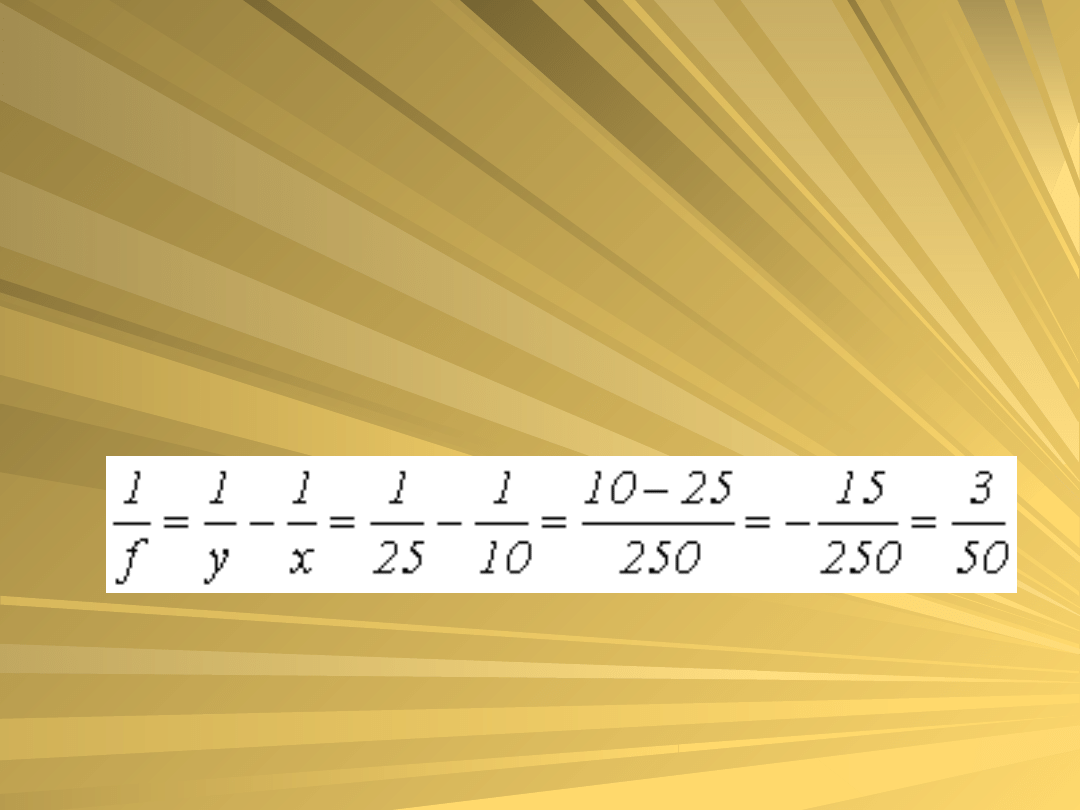
Zadanie 4

Zadanie 4

Krótkowidz widzi dobrze z

odległości 10cm. Jakich okularów
musi używać by widzieć dobrze z
odległości 25cm.

Z równania soczewki wynika, że:

Z = 0.06 dioptrii

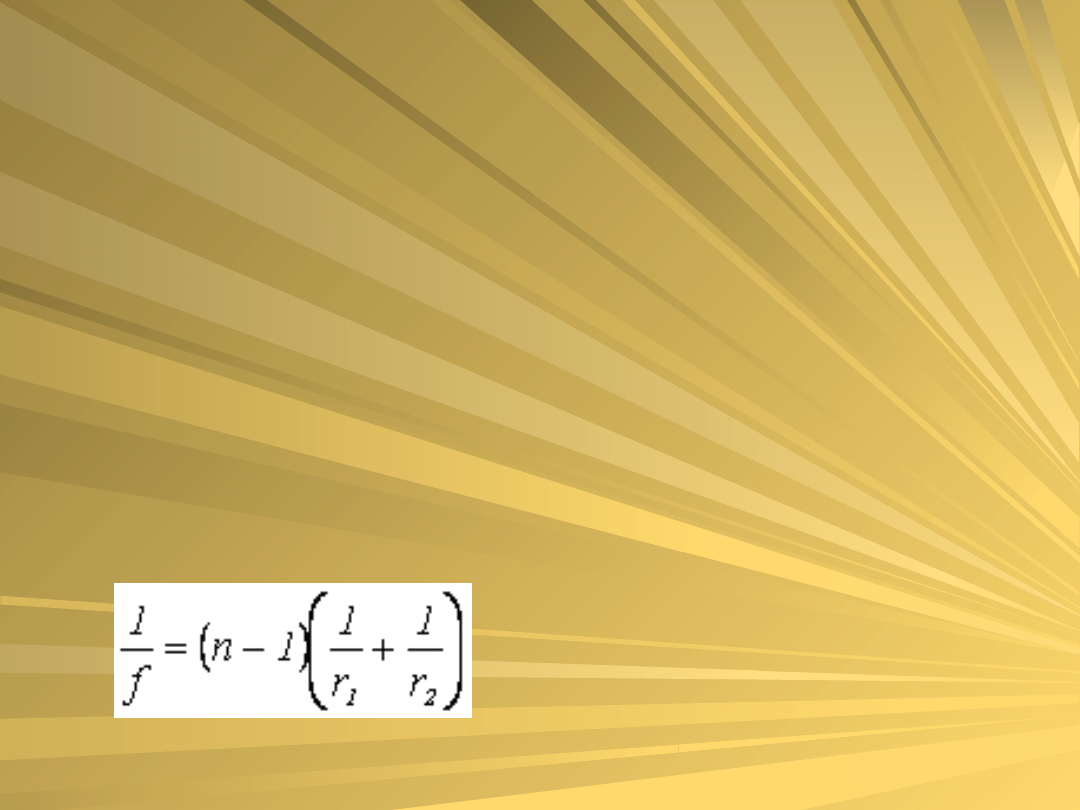
Zadanie 5

Zadanie 5

Oblicz bezwzględny współczynnik

załamania szkła, z którego wykonano
cienką, symetryczną soczewkę
skupiającą o promieniu krzywizn
równym jej ogniskowej w powietrzu.

Rozwiązanie:
Dla soczewek dwuwypukłych mamy

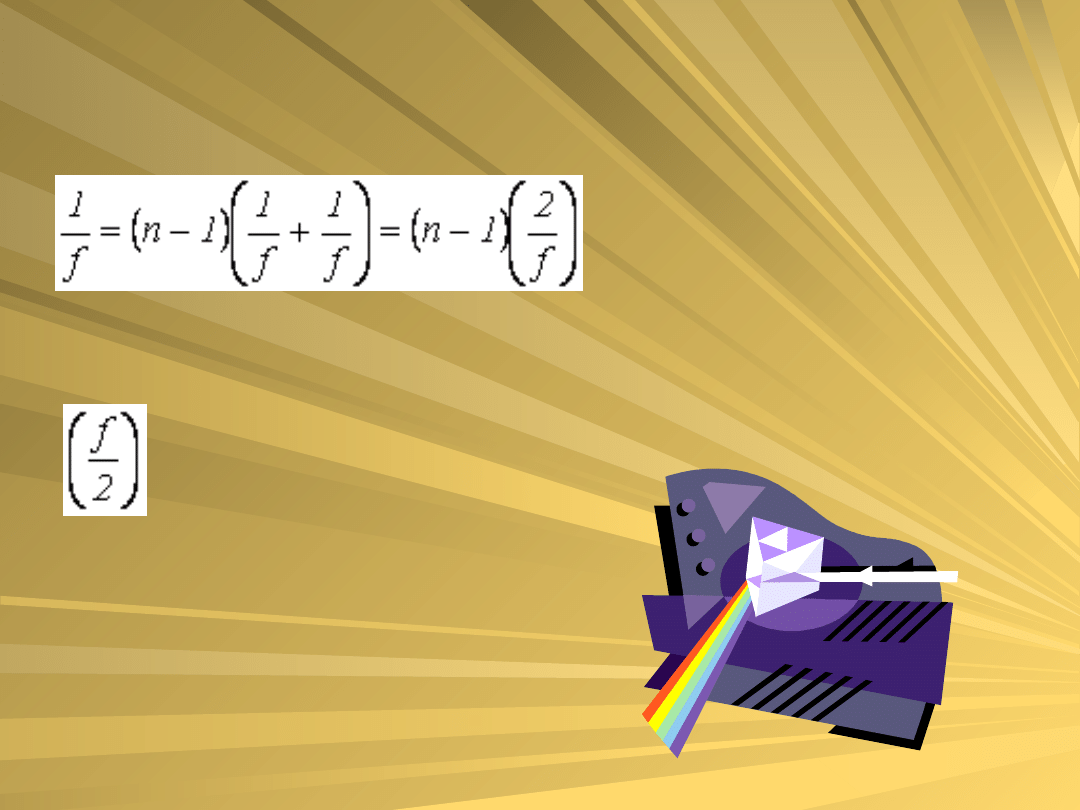
jeśli r1 = r2 = f

to

mnożymy obie strony przez

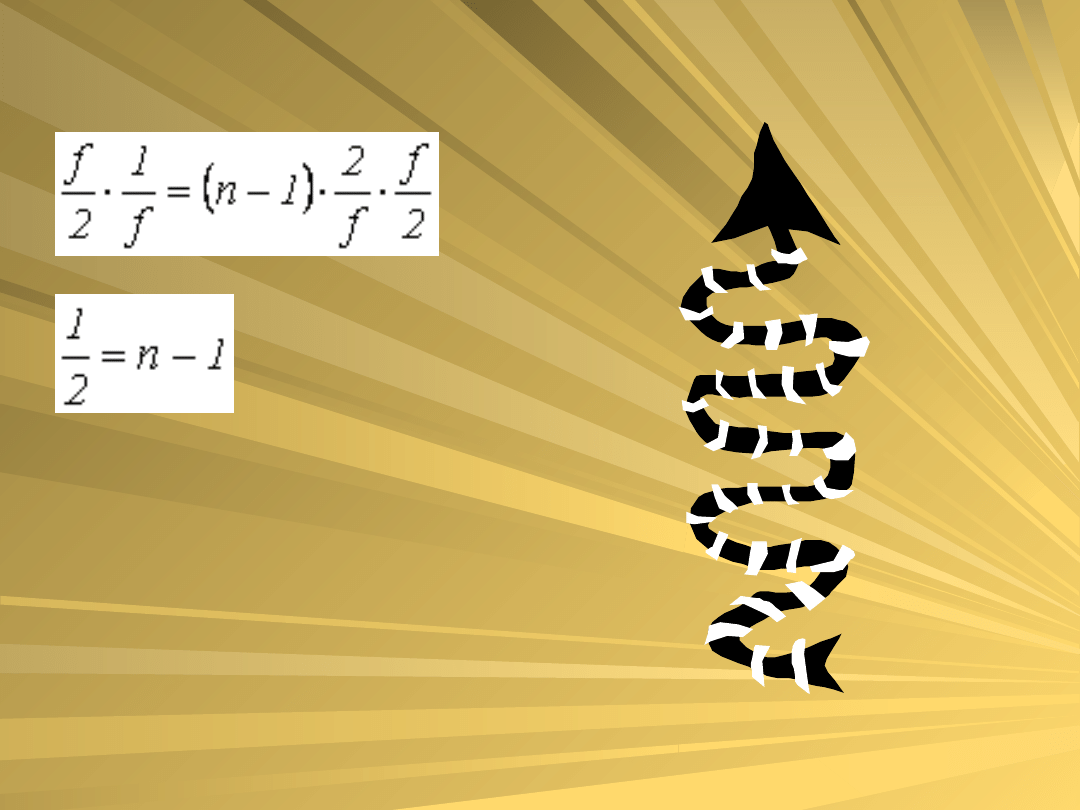
i otrzymujemy

czyli n = 1,5

Zadanie 6

Zadanie 6

Promienie krzywizny dwuwypukłej

soczewki szklanej używanej jako lupy
są równe 3cm i 5cm. Współczynnik
załamania szkła wynosi 1,5.

Oblicz powiększenie tej lupy dla

odległości dobrego widzenia równej
25cm.

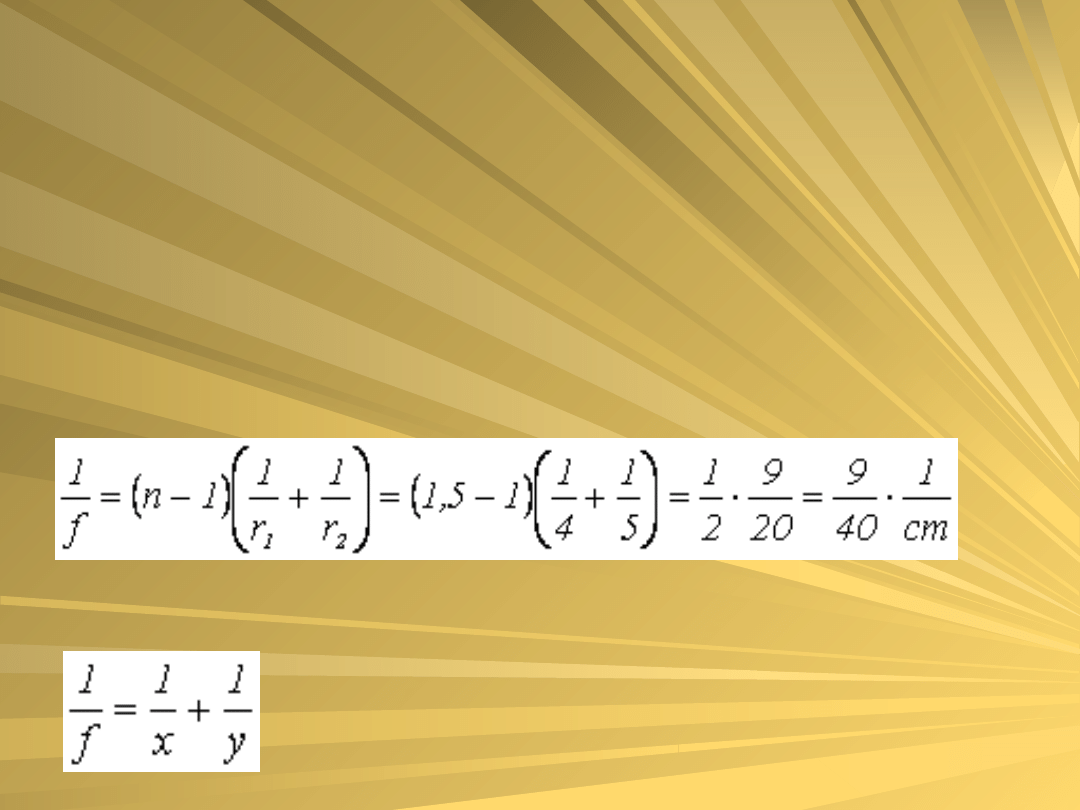
Rozwiązanie:
Dane:
r1 = 4 cm
r2= 5 cm
n = 1,5
y = 25 cm

Szukane:
p=?

z równania soczewki

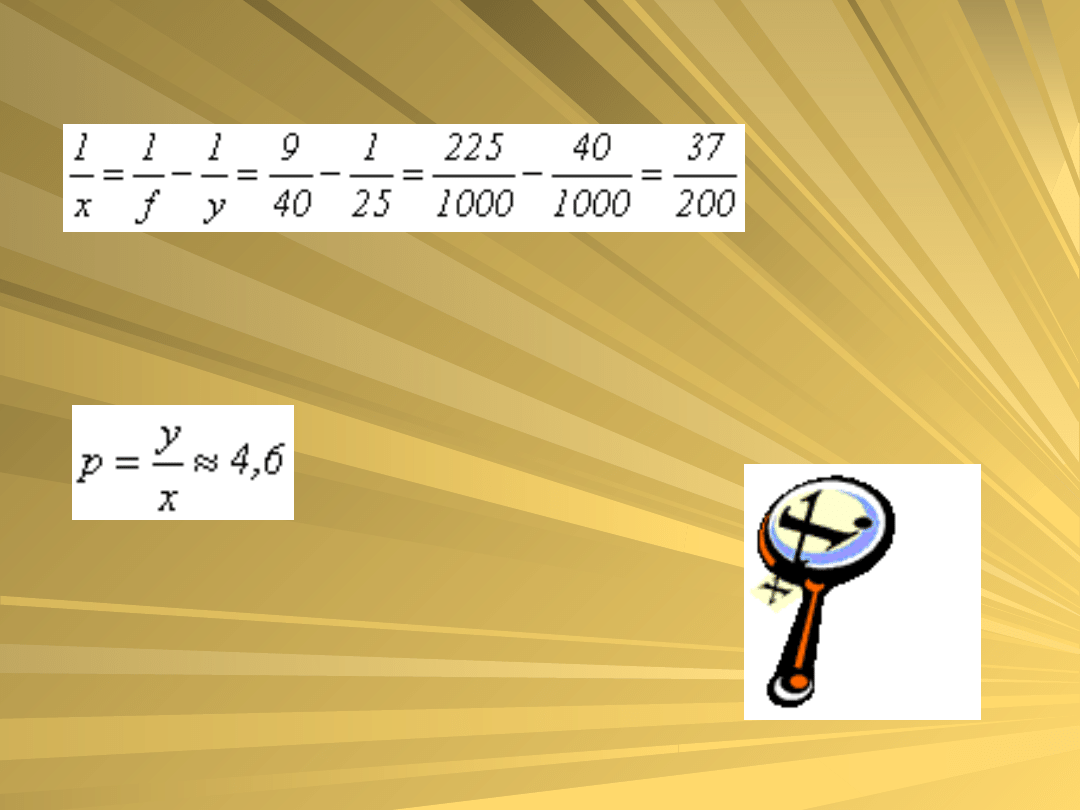
znajdziemy odległość przedmiotu x

czyli x = 5,4
powiększenie to

Zadanie 7

Zadanie 7

Soczewka dwuwypukła o

jednakowych promieniach krzywizn
jest wykonana ze szkła o
współczynniku załamania 1,5.
Soczewka ta użyta jako lupa przez
człowieka, dla którego odległość
dobrego widzenia wynosi 25cm, dała
powiększenie 11 razy.

Oblicz promień krzywizn powierzchni

Dane:
n = 1,5
y = 25 cm
p = 11
Rozwiązanie:

Szukane:
r1 = r2= ? cm

wię
c

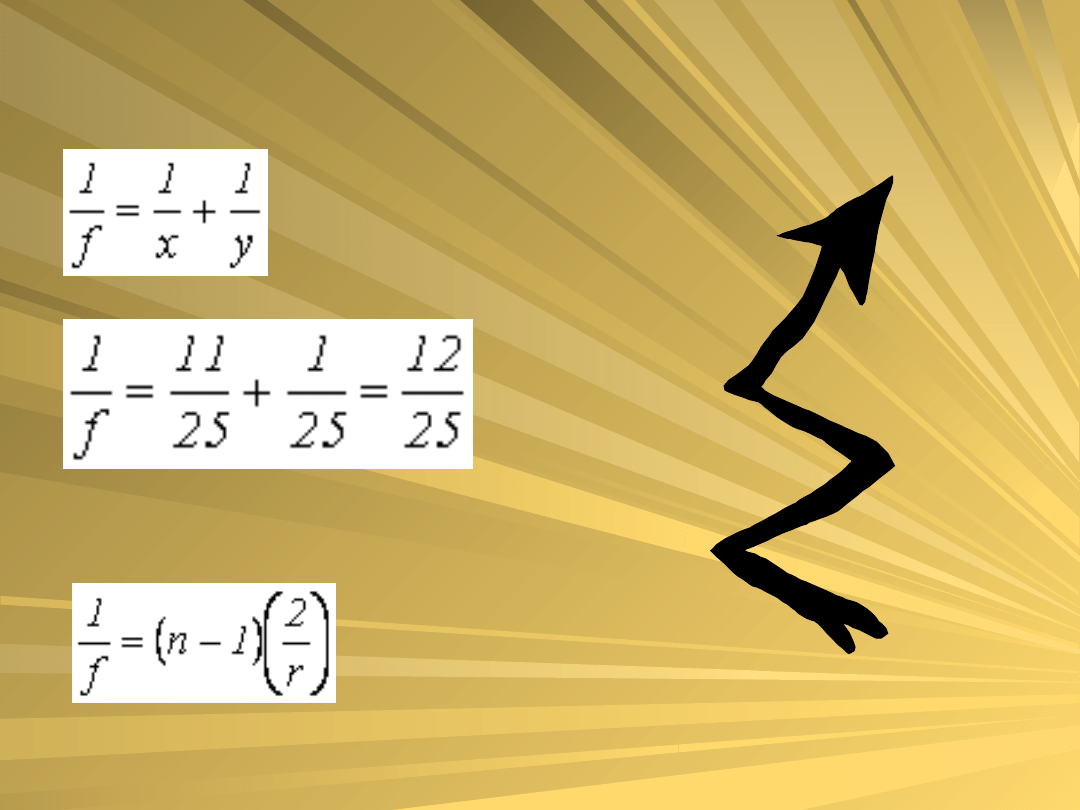
z równania soczewki

więc z równania

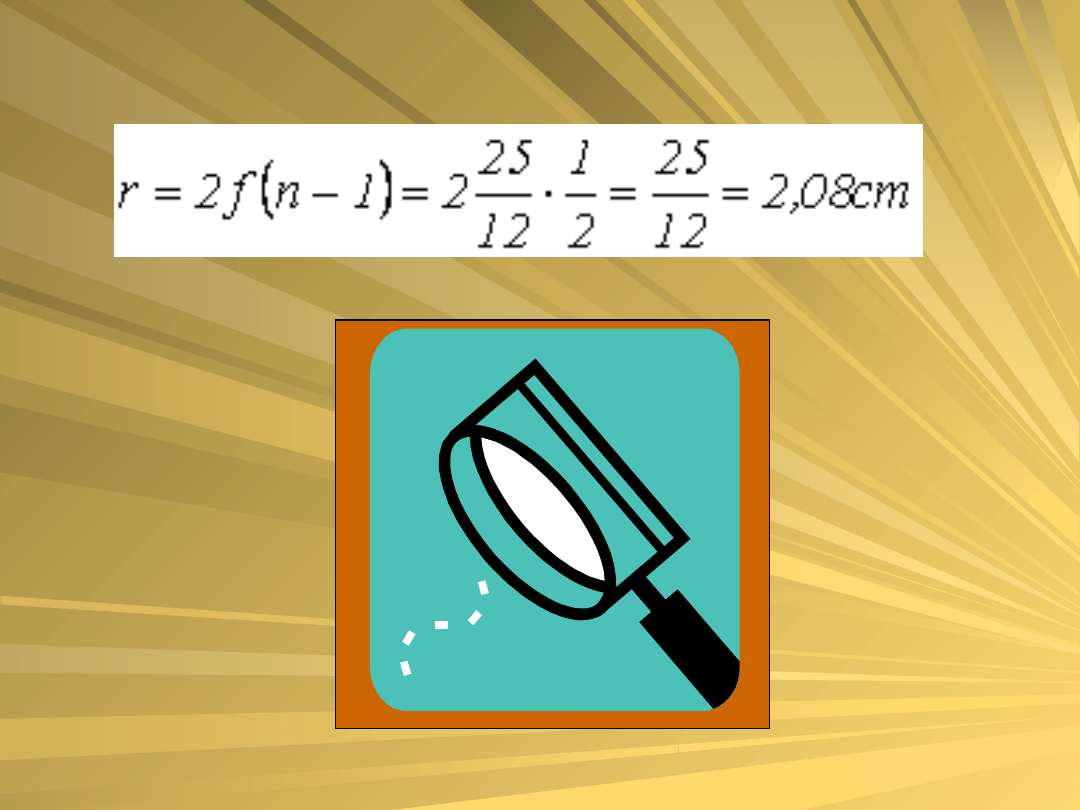
wyliczamy r