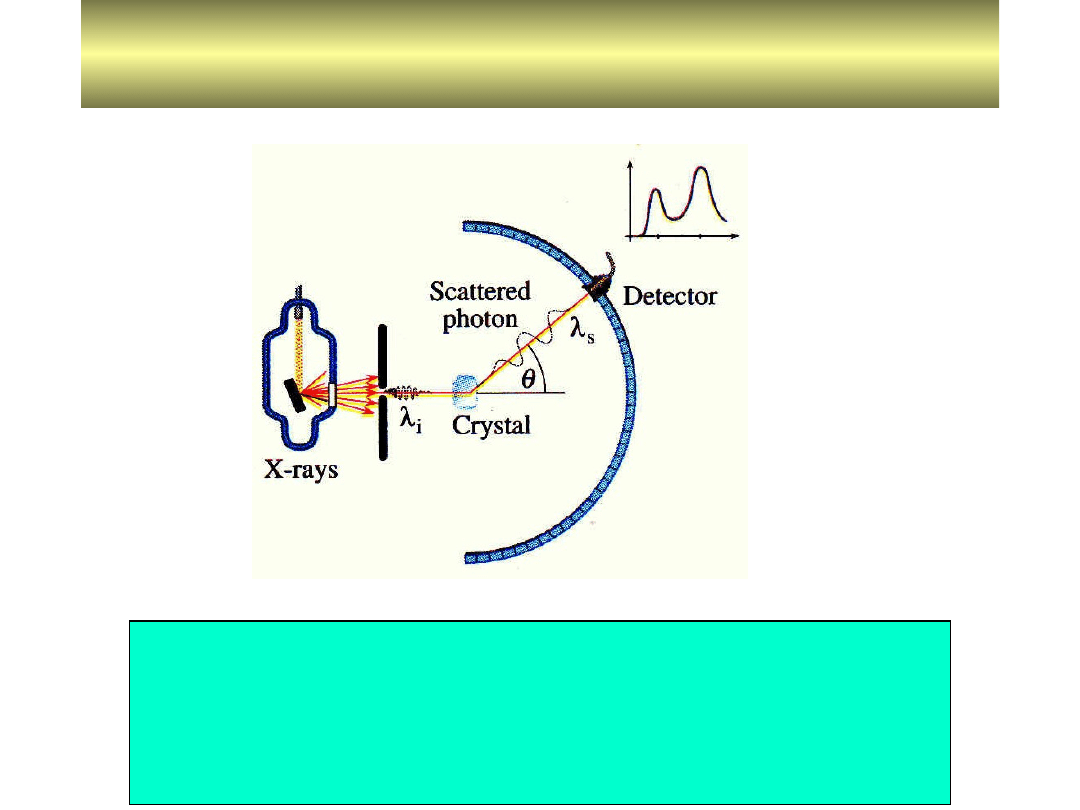
Efekt Comptona.

Efektem Comptona nazywamy zmianę
długości fali elektromagnetycznej w
wyniku rozpraszania jej na swobodnych
elektronach

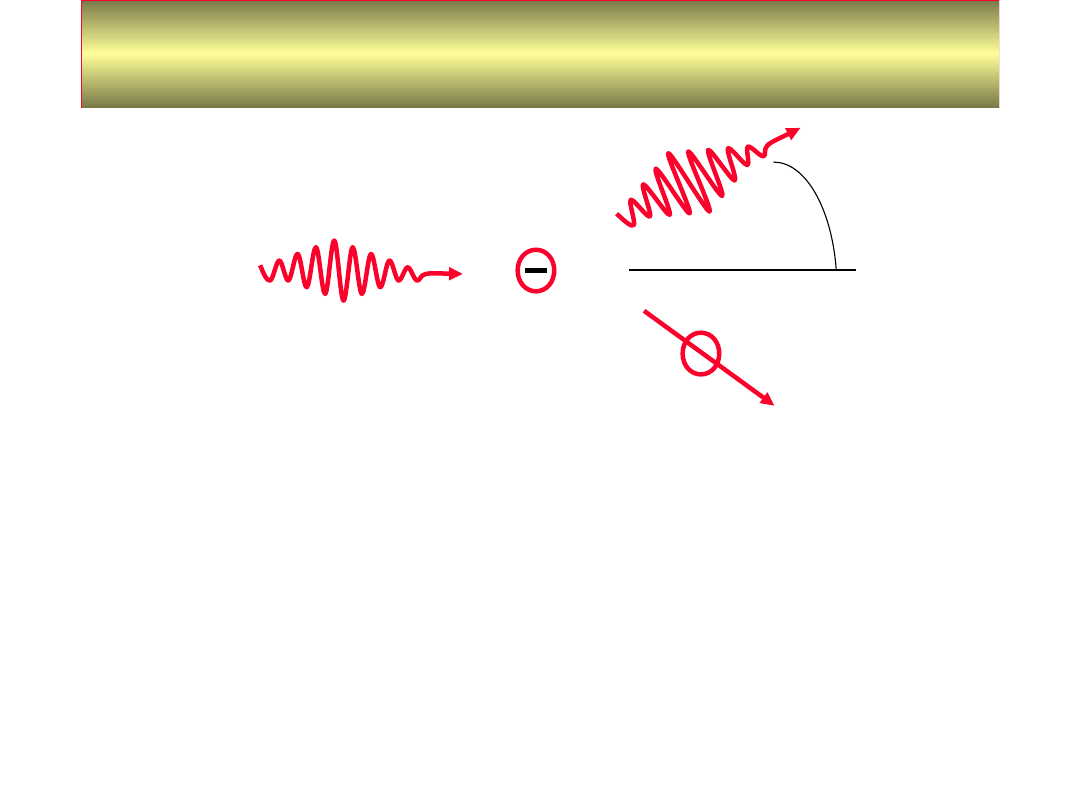
foton

elektron

f

p

0



e

p

f

p



e

p

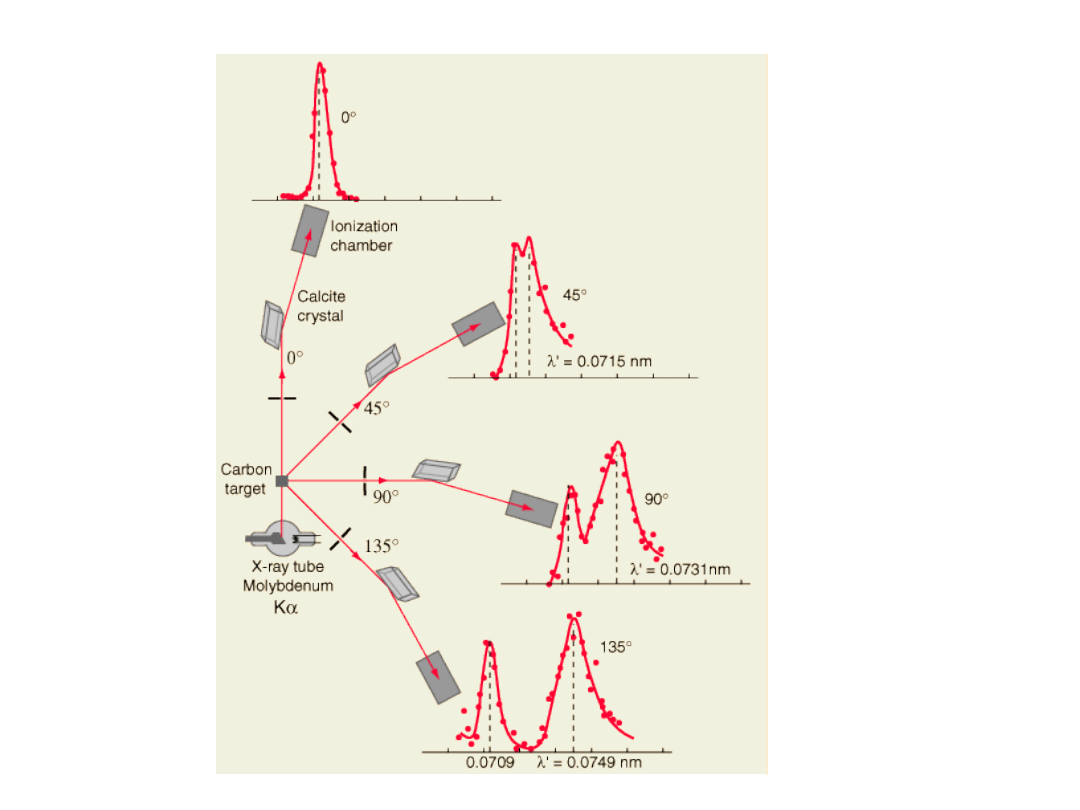
Efekt Comptona.

• Zderzenia fotonów o pędzie p

f

i energii E=hc/ ze

spoczywającymi elektronami.
• Elektron uzyskuje pęd p

e

, a pęd fotonu maleje do wartości p

f

’.

• Długość rozpraszanej fali elektromagnetycznej zwiększa się do
wartości ’=h/p

f

’.

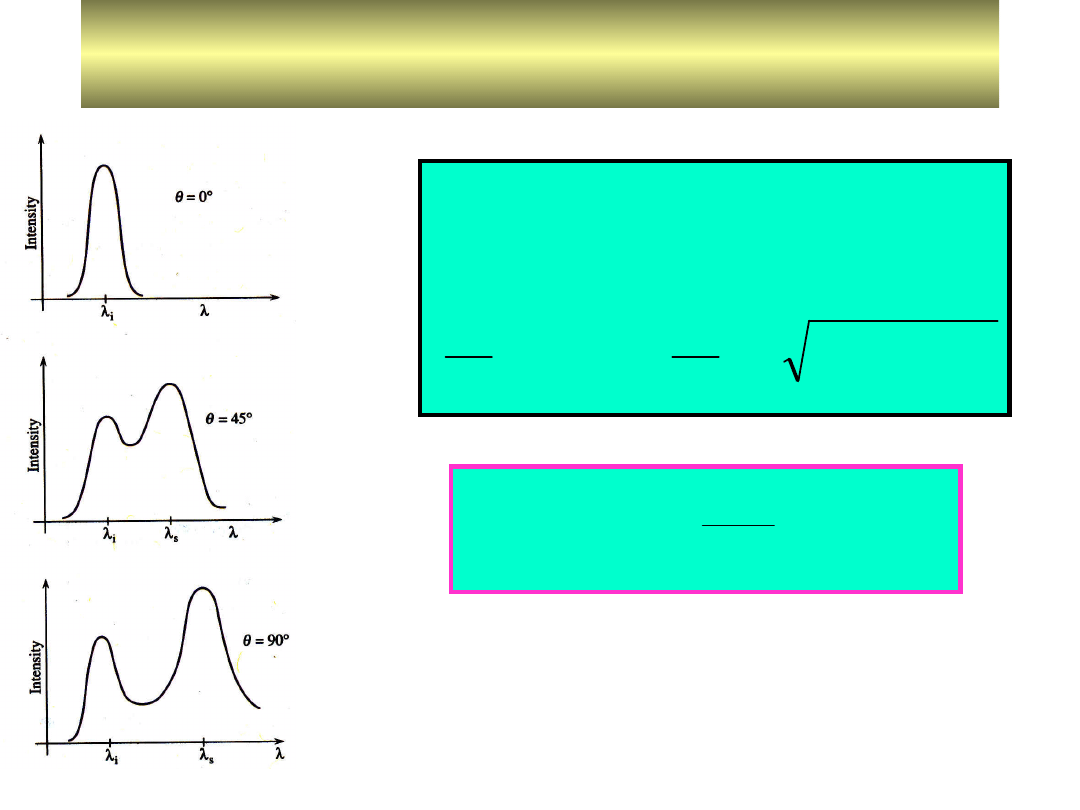
• Kierunek propagacji fali ulega zmianie o kąt



. Zmiana długości

fali jest tym większa , im większy jest kąt rozproszenia. Zależność
zmiany długości fali od kąta rozpraszania wyznaczyć można
wykorzystując prawa zachowania pędu i energii.



Efekt Comptona.





hc

h

E





2

2

2

p

c

m

c

E

o





2

2

2

p

c

m

c

h

o







Jeżeli m

o

= 0, to







h

c

h

p

cp

h









Efekt Comptona.

2

2

2

0

'

2

'

e

o

e

f

f

p

c

m

c

hc

c

m

hc

oraz

p

p

p























)

cos

1

(

0

'



















c

m

h

Efekt Comptona.

)

cos

1

(

0

'



















c

m

h

c

m

h

o

C





Długość fali Comptona dla cząsteczki o masie m

0

m

m

A

p

C

e
C

15

12

10

2

.

1

10

43

.

2

0243

.

0



















Dla elektronu
Dla protonu

Wzór Comptona:

Efekt Comptona.

Wnioski z doświadczenia:

Zmiana długości fali fotonu obliczona teoretycznie
Doskonale zgadza się z doświadczeniem,
Czyli założenia co do masy i pędu fotonu były słuszne:

Doświadczenie potwierdza istnienie fotonu jako skończonej
porcji energii.

Dualizm korpuskularno-

falowy.

 Dualizm falowo-cząstkowy fali elektromagnetycznej.

•

W zjawiskach takich jak dyfrakcja czy interferencja fala

elektromagnetyczna wykazuje typowe własności falowe.

•

W zjawiskach takich jak efekt Comptona czy efekt

fotoelektryczny fala elektromagnetyczna wykazuje naturę
korpuskularną, tzn. jest strumieniem cząstek zwanych

fotonami.

Fale materii.

Hipoteza de Broglie'a

.

•

W 1924 roku L. de Broglie założył, że

dualizm cząstkowo - falowy jest własnością
charakterystyczną nie tylko dla fali
elektromagnetycznej, ale również dla cząstek o
masie spoczynkowej różnej od zera . Oznacza
to,że cząstki takie jak np. elektrony powinny
również wykazywać własności falowe. Fale te
nazwał on

falami materii.

Założył, że długość

fal materii określona jest tym samym
związkiem, który stosuje się do fotonów.

Fale materii.

p

h





długość fal materii

pęd cząstki

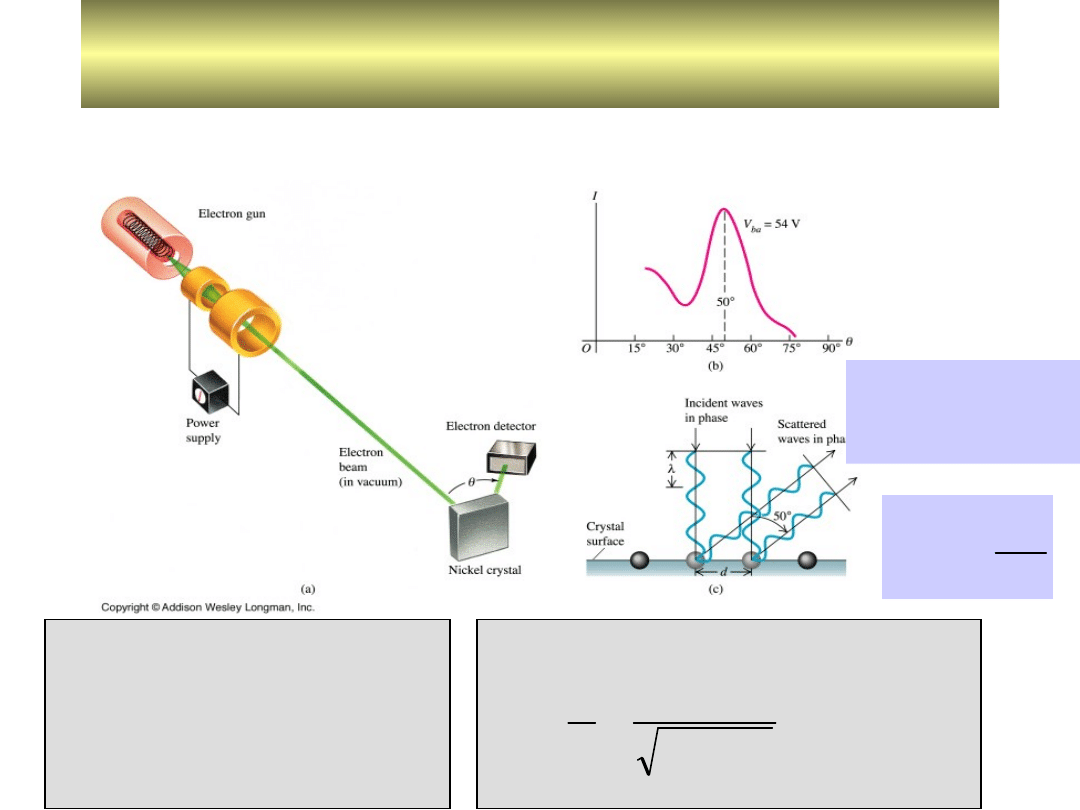
Fale materii.

Doświadczenie C.J.Davissona i L.G.Germera

1927 r.

Z
dyfrakcji

nm

165

.

0

sin 







d

Wzór de Broglie

nm

167

.

0

2







ba

meV

h

p

h



m

p

eV

ba

2

2



d

Ni

=0.915n

m

Dyfrakcja na

polikrystalicznej folii

aluminiowej.

Dyfrakcja
promieniowania
X

Dyfrakcja
elektronów

Fale materii.

Doświadczenia przy użyciu elektronów, neutronów,
cząstek alfa,i innych cząstek wykazały, że:

Każdej poruszającej się cząstce
materialnej
można przypisać falę materii,
której długość
jest określona wzorem de
Broglie’a.

Fale materii.

Długość fal materii jest niewielka, dlatego nie mogą one być
wykrywane w doświadczeniach makroskopowych
(przeprowadzonych z ciałami o dużych rozmiarach). W tych
przypadkach materia wykazuje swoje własności cząsteczkowe.

Fale materii.

Jaka jest długość fali de Broglie’a ziarnka grochu
o wadze 1g toczącego się z prędkością 1 cm/s?

!

!

10

2

.

1

/

100

50

10

62

.

6

33

34

m

s

kgm

Js

















Długość fali elektronu poruszającego się z
prędkością 100 m/s

v  7.1• 10

-6

m

Jaka jest długość fali 50 kg worka poruszającego
się z prędkością 100 m/s?

m

29

10

7

.

6





Odp:
około

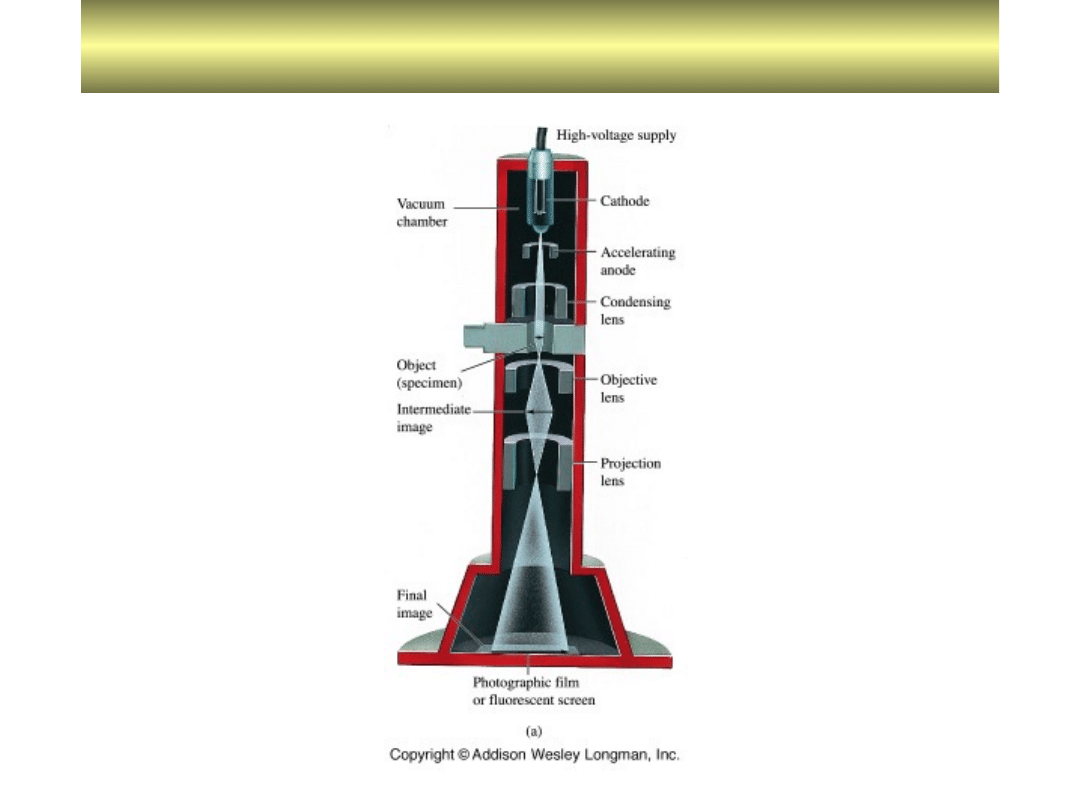
Mikroskop elektronowy

Fale materii.



Zasada komplementarności:

Fotony

czy

też

elektrony

oraz

obiekty

mikroświata w jednych zjawiskach mogą
zachowywać się jak fala, a w innych jak cząstka
tzn. wykazują zarówno własności falowe jak i
korpuskularne. Obie te cechy uzupełniają się
wzajemnie, dając pełny opis danego obiektu.

Mechanika kwantowa.

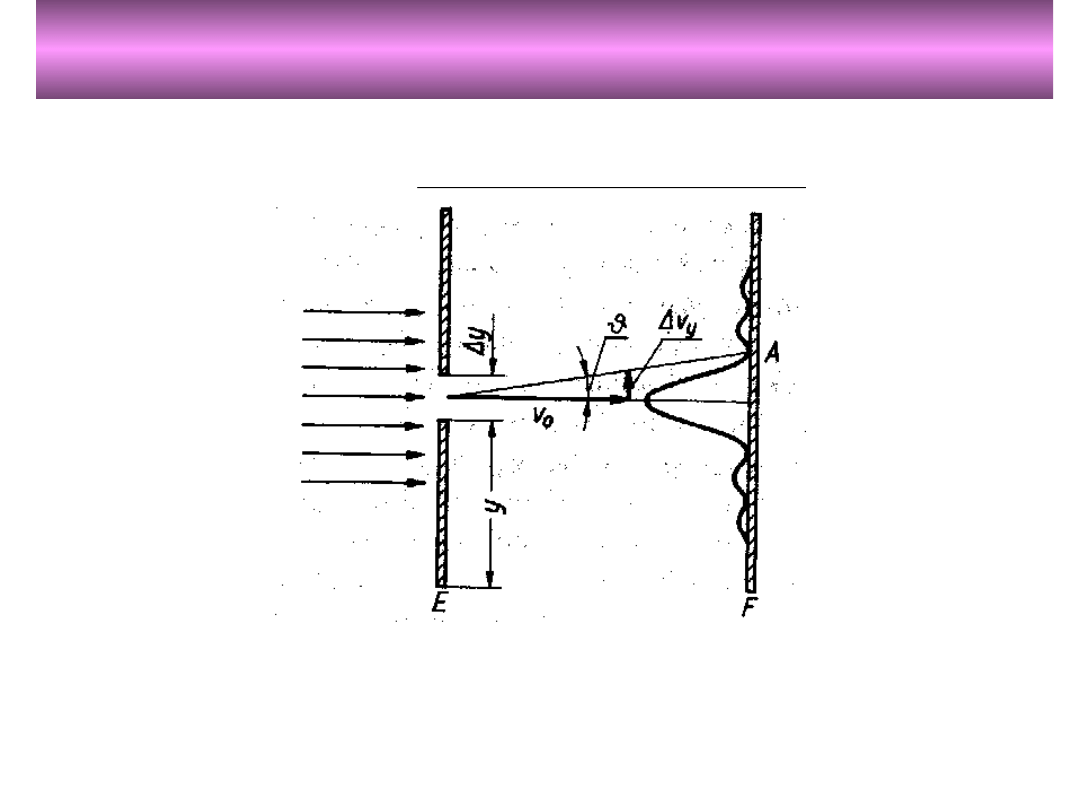
Zasada nieoznaczoności

Heisenberga

dla pędu i położenia

Zasada nieoznaczoności

Heisenberga

dla pędu i położenia

Iloczyn niepewności pomiaru pędu i pomiaru położenia
cząstki jest zawsze nie mniejszy od stałej Plancka.

h

p

x

x







Zasada nieoznaczoności

Heisenberga

dla momentu pędu i położenia kątowego cząstki

Iloczyn niepewności pomiarów momentu pędu cząstki
i pomiaru jej położenia kątowego jest zawsze
nie mniejszy od stałej Plancka.

h

L









Zasada nieoznaczoności

Heisenberga

dla energii i czasu

Jeżeli cząstka ma energię E, to dokładność E

jest zależna od czasu dokonywania pomiaru t

zgodnie z nierównością:

h

t

E 





Tzn. im dłużej cząstka zachowuje energię tym dokładniej
można tę energię wyznaczyć.

Zasada nieoznaczoności

Heisenberga

Pary wielkości kanonicznie sprzężone:



Pęd, położenie



Moment pędu, położenie kątowe



Energia, czas

Zasada nieoznaczoności

Heisenberga

Ogólne sformuowanie:

Iloczyn niepewności pomiaru pary wielkości fizycznych
kanonicznie sprzężonych jest zawsze nie mniejszy
od stałej Plancka.

Zasada nieoznaczoności

Heisenberga

• Fizyka klasyczna

– dokładność pomiaru jest zdeterminowana

jedynie jakością aparatury pomiarowej

– Nie ma teoretycznych ograniczeń na

dokładność z jaką mogą być wykonane

pomiary

• Mechanika kwantowa

– Obowiązuje

zasada nieoznaczoności

:

pewnych wielkości fizycznych nie można

zmierzyć równocześnie z dowolną

dokładnością

Funkcja falowa

Zgodnie z hipotezą de Broglie'a, cząstki takie jak elektron
czy proton, mają własności falowe.

Własności falowe cząstki (lub innego obiektu) w mechanice
kwantowej opisuje tzw.

funkcja falowa

(x,t)

:



zawiera w sobie wszystkie informacje o obiekcie (np.

cząstce)



w ogólnym przypadku jest to funkcja zespolona

współrzędnych
przestrzennych oraz czasu



musi być funkcją ciągłą , a także musi mieć ciągłą pochodną



Kwadrat modułu funkcji falowej

jest gęstością prawdopodobieństwa znalezienia cząstki

w chwili t w pewnym punkcie przestrzeni







*

2

















V

dV

V

p

1

2

2

Funkcję falową,



dla danej cząstki, lub bardziej złożonego

układu fizycznego, otrzymujemy rozwiązując równanie
różniczkowe nazywane równaniem Schroedingera. Jeżeli
energia potencjalna cząstki U nie zależy od czasu, to
równanie Schroedingera jest równaniem niezależnym od
czasu i nazywa się

stacjonarnym równaniem

Schroedingera

.

)

(

)

(

)

(

2

2

2

2

x

E

x

x

U

dx

d

m











 

Równanie Schroedingera

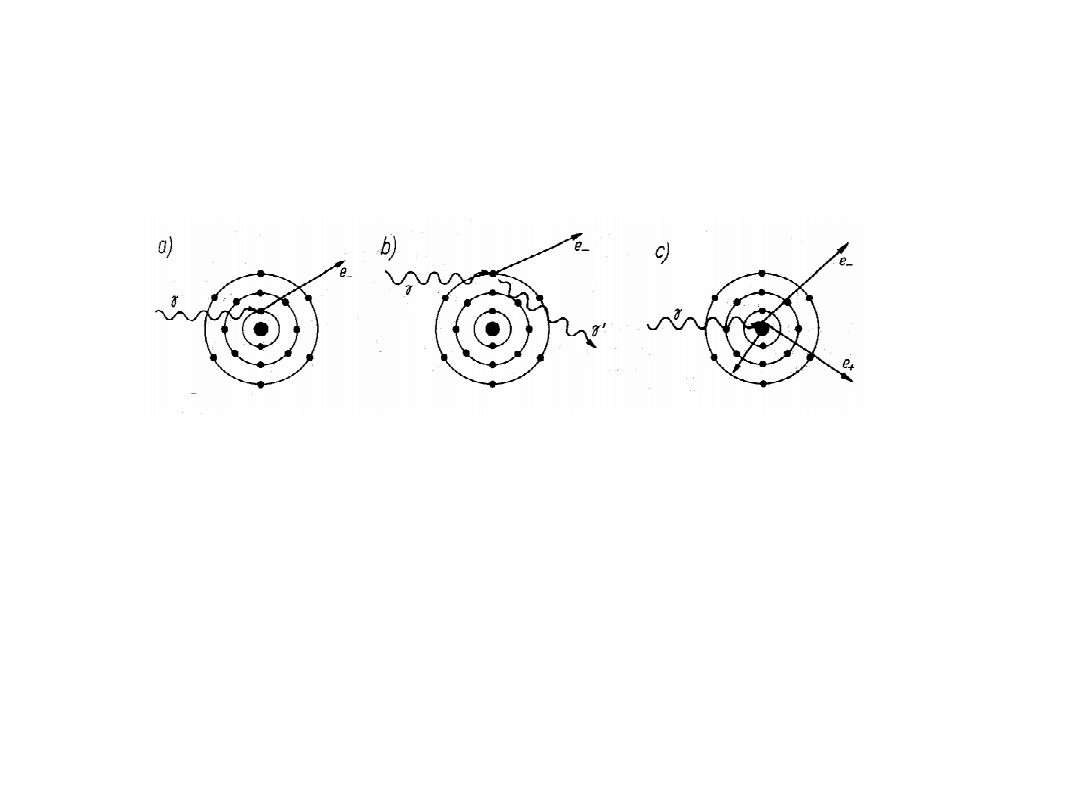
Oddziaływanie kwantów  z materią:

a) Zjawisko fotoelektryczne,
b) Zjawisko Comptona,
c) Zjawisko tworzenia pary :elektron-pozyton,