POSTAĆ

ILOCZYNOWA

FUNKCJI

KWADRATOWEJ

Dany jest wzór funkcji f, przekształćmy go do postaci
ogólnej:

a) f(x)=-4(x+1)(x-5)
f(x)=-4(x

2

-5x+x-5)

f(x)=-4(x

2

-4x-5)

f(x)=-4x

2

+16x+20 -

postać ogólna funkcji

kwadratowej

b) f(x)=2(x-8)x
f(x)=2(x

2

-8x)

f(x)=2x

2

-16x

- postać ogólna funkcji kwadratowej

Funkcje zapisane w postaci iloczynowej przekształciliśmy do
postaci ogólnej.

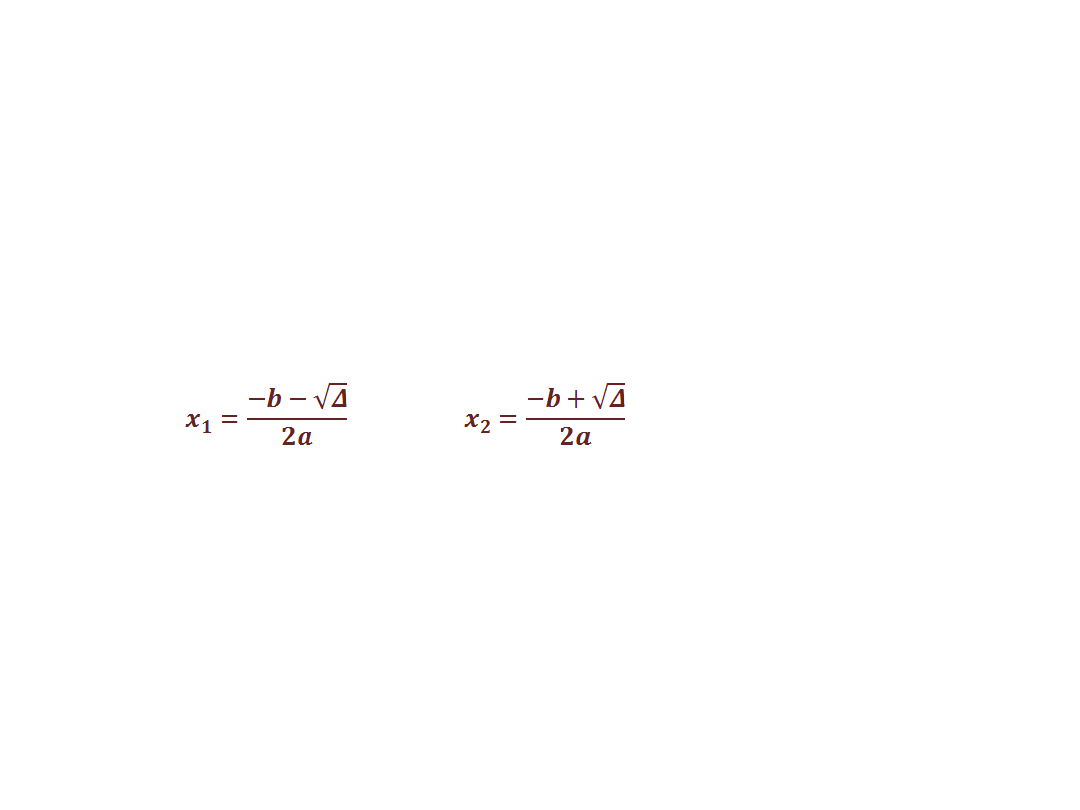
Funkcja kwadratowa zapisana w postaci ogólnej

y=ax

2

+bx+c

może być zapisana w postaci iloczynowej:

1)) Jeżeli Δ>0 to funkcja kwadratowa ma dwa miejsca

zerowe:

wtedy postać iloczynowa wyraża się wzorem:

y=a(x-x

1

)(x-x

2

)

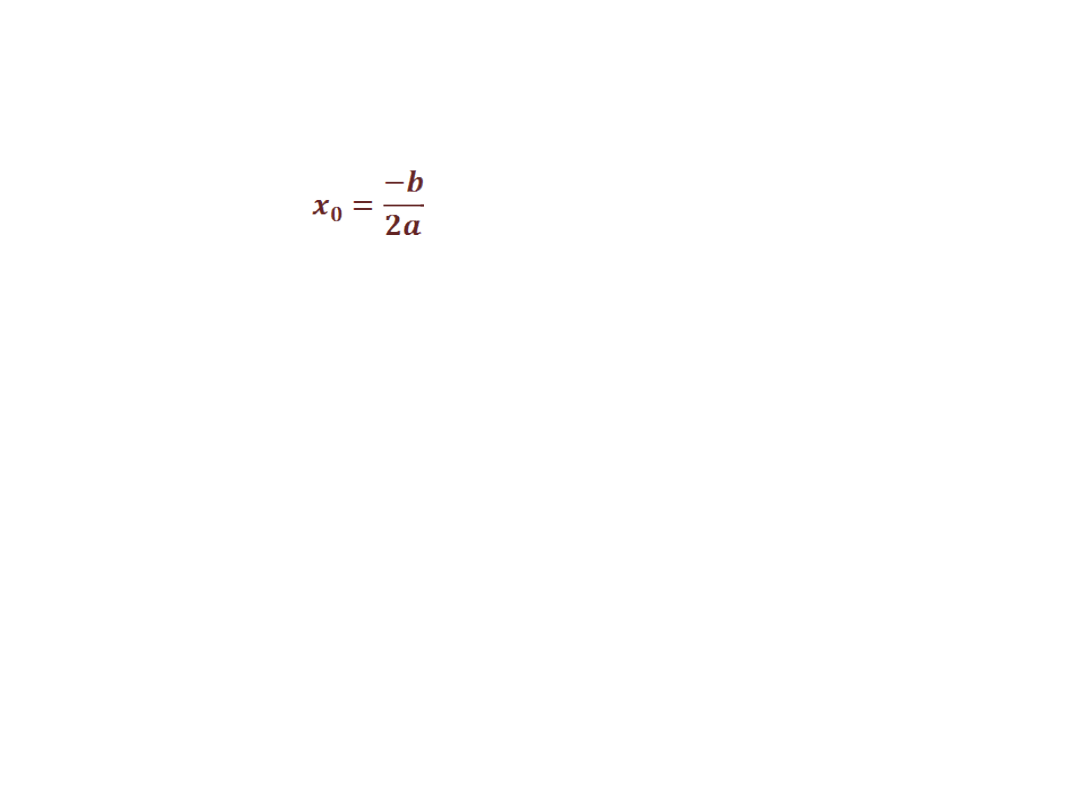
2)) Jeżeli Δ=0 to funkcja ma jedno miejsce zerowe:

wtedy postać iloczynowa wyraża się wzorem:

y=a(x-x

0

)(x-x

0

)

y=a(x-x

0

)

2

3)) Jeżeli Δ<0 to funkcja nie ma miejsc zerowych, nie

można funkcji przedstawić w postaci iloczynowej.

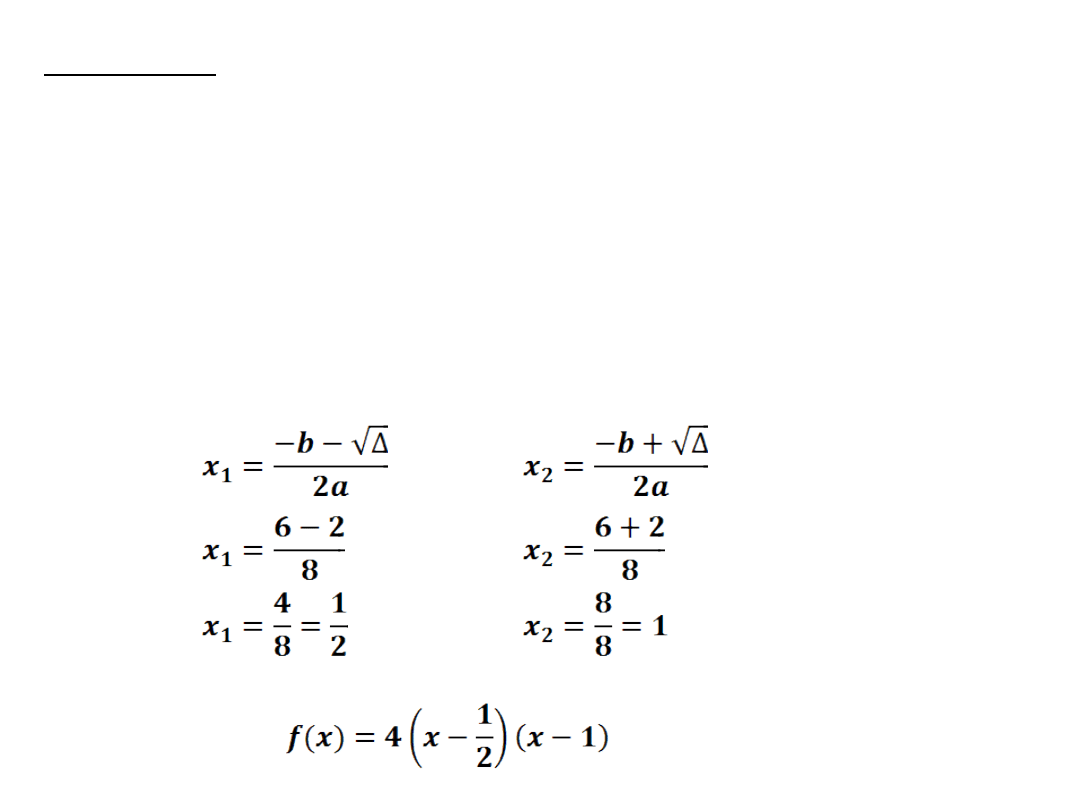
Zadanie1: Przedstaw funkcję w postaci iloczynowej:

a)

f(x)=4x

2

-6x+2

a=4 b=-6 c=2

Δ = b

2

- 4ac

Δ = (-6)

2

- 4·4·2 = 36 - 32 = 4

Δ > 0 funkcja posiada dwa miejsca zerowe

- postać iloczynowa

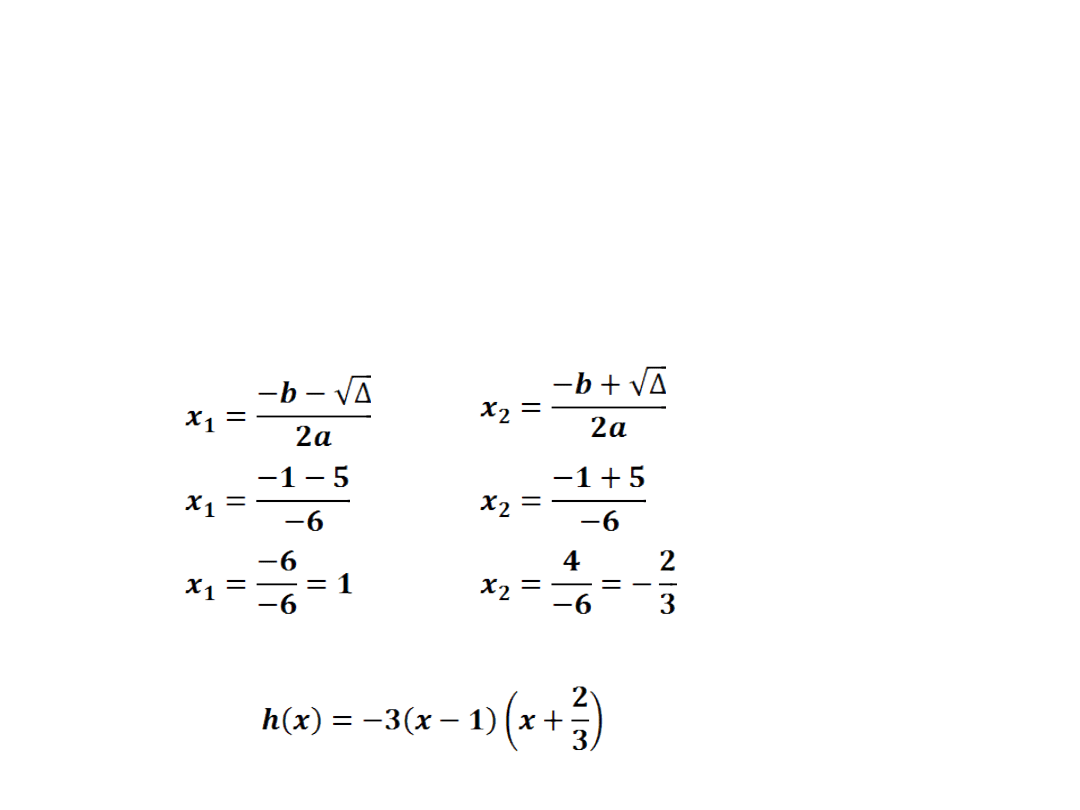
b)

h(x)=-3x

2

+x+2

a=-3 b=1 c=2

Δ = b

2

- 4ac

Δ = 1

2

- 4·(-3)·2 = 1 + 24 = 25

Δ > 0 funkcja posiada dwa miejsca zerowe

c)

g(x)=x

2

+6x+10

a=1 b=6 c=10

Δ = b

2

- 4ac

Δ = 6

2

- 4·1·10 = 36 - 40 = -4

Δ < 0 funkcja nie posiada miejsc zerowych; nie

można jej

przedstawić w postaci iloczynowej

d)

y=x

2

-3x+3

a=1 b=-3 c=3

Δ = b

2

- 4ac

Δ = (-3)

2

- 4·1·3 = 9 - 12 = -3

Δ < 0 funkcja nie posiada miejsc zerowych; nie

można jej

przedstawić w postaci iloczynowej

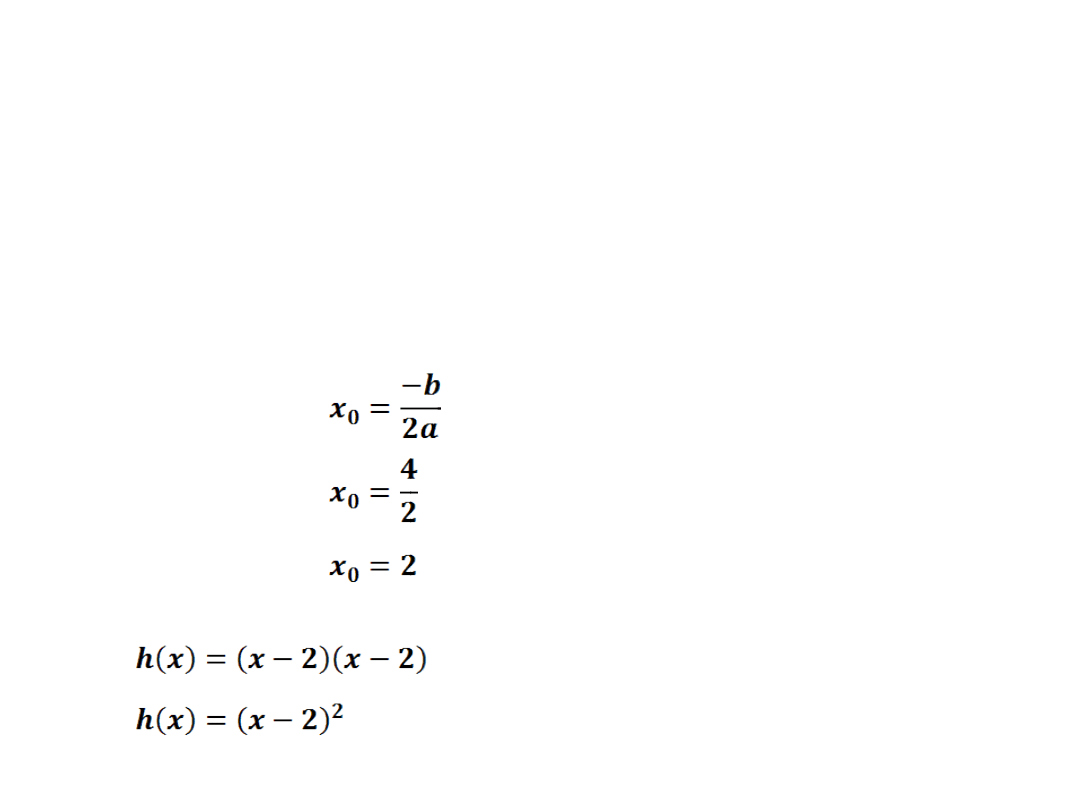
e)

h(x)=x

2

-4x+4

a=1 b=-4 c=4

Δ = b

2

- 4ac

Δ = (-4)

2

- 4·1·4 = 16 - 16 = 0

Δ = 0 funkcja posiada jedno miejsce zerowe

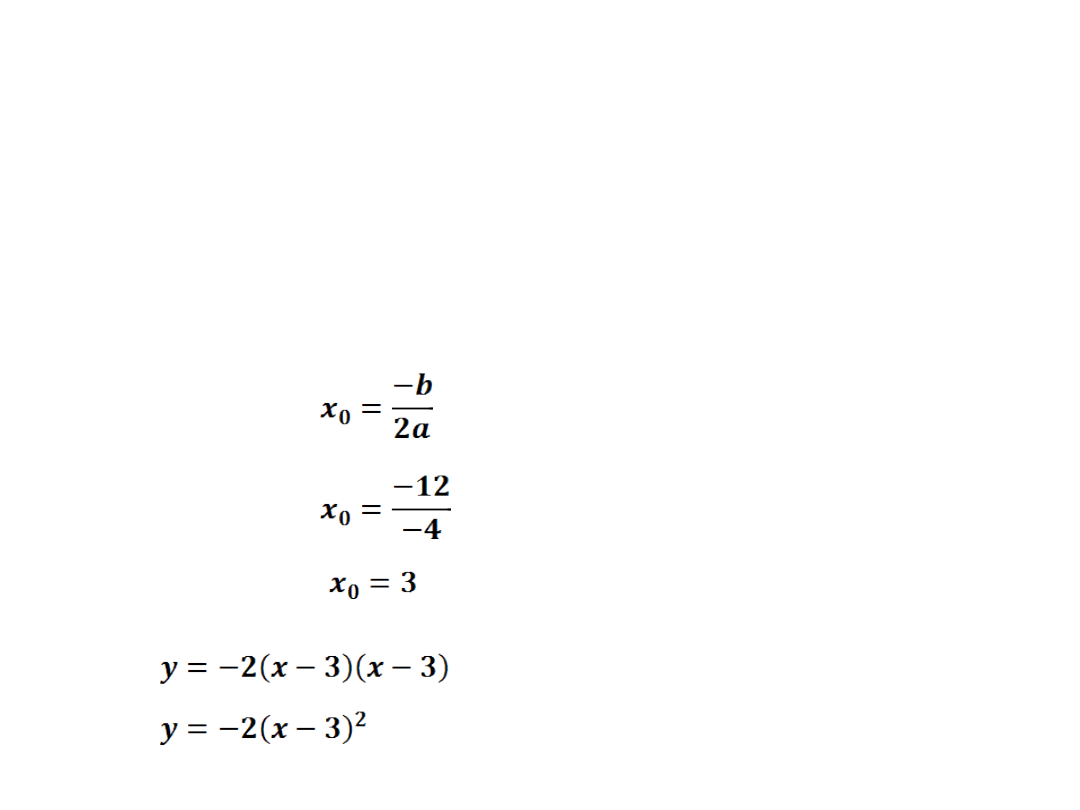
f)

y=-2x

2

+12x-18

a=-2 b=12 c=-18

Δ = b

2

- 4ac

Δ = 12

2

- 4·(-2)·(-18) = 144 - 144 = 0

Δ = 0 funkcja posiada jedno miejsce zerowe

Zadanie2: Podaj pierwiastki trójmianu kwadratowego:

a)

y=(x+3)(x-30)

Miejscami zerowymi (pierwiastkami) są liczby: -3 oraz
30.

b)

y=-2(x+0,4)(x-3,2)

Miejscami zerowymi (pierwiastkami) są liczby: -0,4
oraz 3,2.

c)

y=-4x(x-8)

Miejscami zerowymi (pierwiastkami) są liczby: 0 oraz
8.

Zadanie3: Oblicz współczynniki b i c funkcji
kwadratowej

y=-2x

2

+bx+c

o podanych

pierwiastkach:

a)3 i 5
Przedstawimy najpierw funkcję w postaci
iloczynowej:
y=-2(x-3)(x-5)
y=-2(x

2

-5x-3x+15)

y=-2(x

2

-8x+15)

y=-2x

2

+16x-30

porównując wzory odczytamy że b=16, c=-30

b) 2 i -8

y=-2(x-2)(x+8)
y=-2(x

2

+8x-2x-16)

y=-2(x

2

+6x-16)

y=-2x

2

-12x+32

porównując wzory odczytamy że b=-12, c=32

Zadanie4: Miejscami zerowymi funkcji
kwadratowej są liczby 5 i 10. Napisz wzór funkcji,
wiedząc że punkt P=(2,24) należy do jej wykresu.

Przedstawimy najpierw funkcję w postaci
iloczynowej:
y=a(x-x

1

)(x-x

2

)

y=a(x-5)(x-10)

Punkt P należy do wykresu funkcji
y=a(x-5)(x-10)
24=a(2-5)·(2-10)
24=a(-3)·(-8)
24=a·24
a=1
y=(x-5)(x-10) – postać iloczynowa
y=x

2

-15x+50 – postać ogólna funkcji kwadratowej

Zadanie5: Wyznacz równanie osi symetrii wykresu
funkcji f, której miejscami zerowymi są liczby -2 oraz
8. Wierzchołek paraboli ma współrzędne W=(3,50).
Napisz wzór funkcji f.

Oś symetrii wykresu funkcji to prosta przechodząca
przez
wierzchołek paraboli, dlatego szukana prosta ma
równanie: x=3.
Przedstawimy najpierw funkcję w postaci
iloczynowej:
y=a(x-x

1

)(x-x

2

)

y=a(x+2)(x-8)

Wierzchołek W należy do wykresu funkcji
y=a(3+2)(3-8)
50=a·5·(-5)
50=a·(-25)
a=-2
y=-2(x+2)(x-8) – postać iloczynowa
y=-2x

2

+12x+32 – postać ogólna funkcji kwadratowej

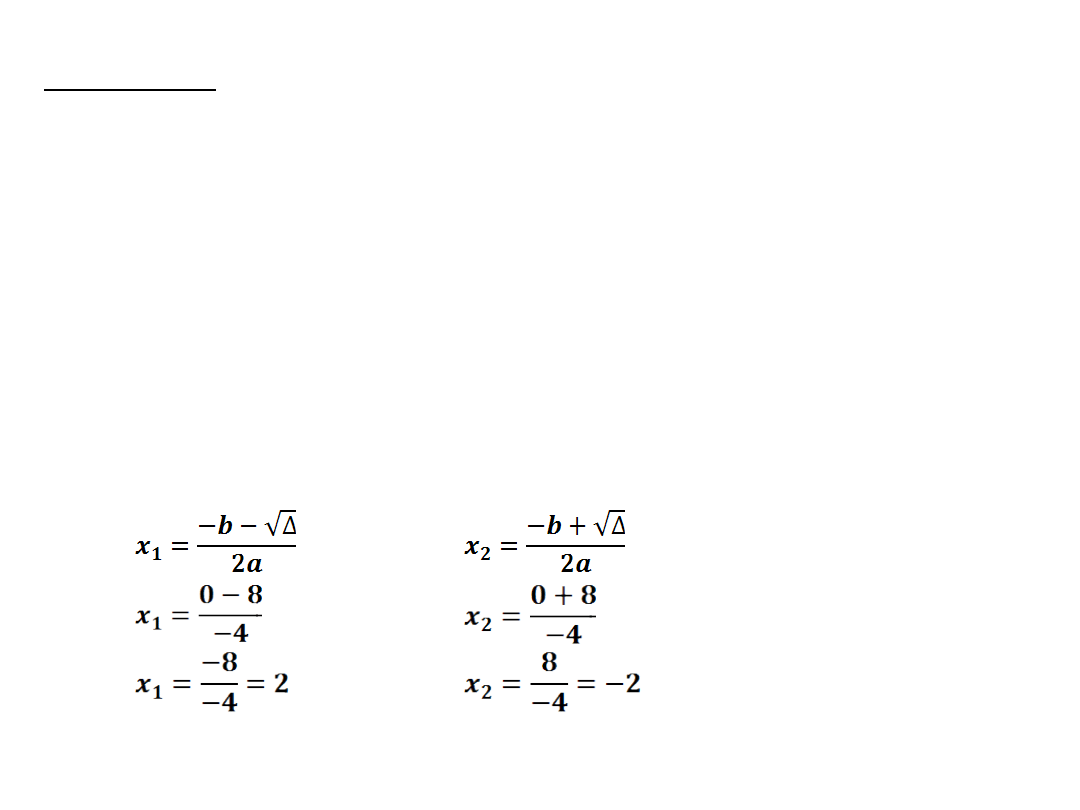
Zadanie6: Mając wzór funkcji kwadratowej

f(x)=-

2x

2

+8

a)przedstaw ją w postaci iloczynowej
b)napisz równanie osi symetrii wykresu
c)oblicz pole trójkąta, którego wierzchołkami są
punkty przecięcia wykresu z osią x oraz wierzchołek
W.

Ad.a)
Obliczamy miejsca zerowe funkcji: a=-2 b=0 c=8

Δ = b

2

- 4ac

Δ = 0

2

- 4·(-2)·8 = 0 + 64 = 64

Δ > 0 funkcja posiada dwa miejsca zerowe

f(x)=-2(x-2)(x+2)

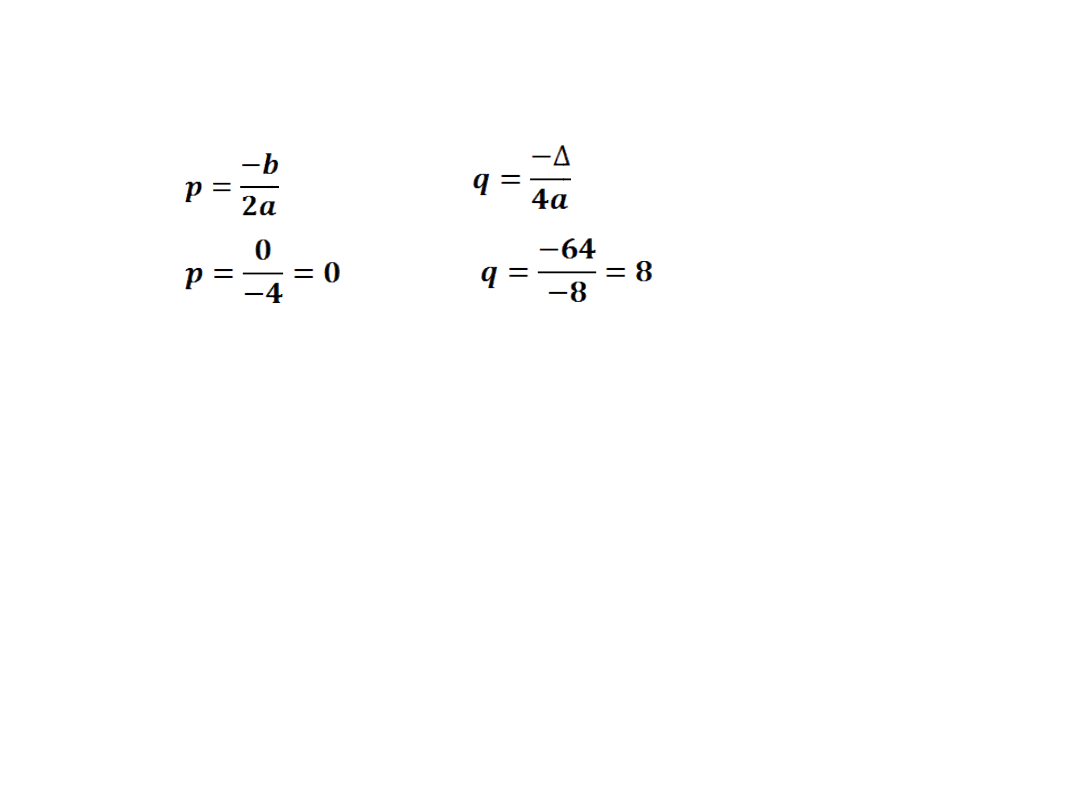
Ad.b)
Obliczamy współrzędne wierzchołka W paraboli:
W=(p,q)

W=(0,8)

Osią symetrii wykresu jest prosta o równaniu x=0

Ad.c)
Szukamy punktów przecięcia wykresu funkcji z

osiami układu

współrzędnych.

Z OSIĄ X: f(x)=0
-2(x-2)(x+2)=0
x=2 lub x=-2

PUNKTY PRZECIĘCIA: A=(2,0) oraz B=(-2,0)

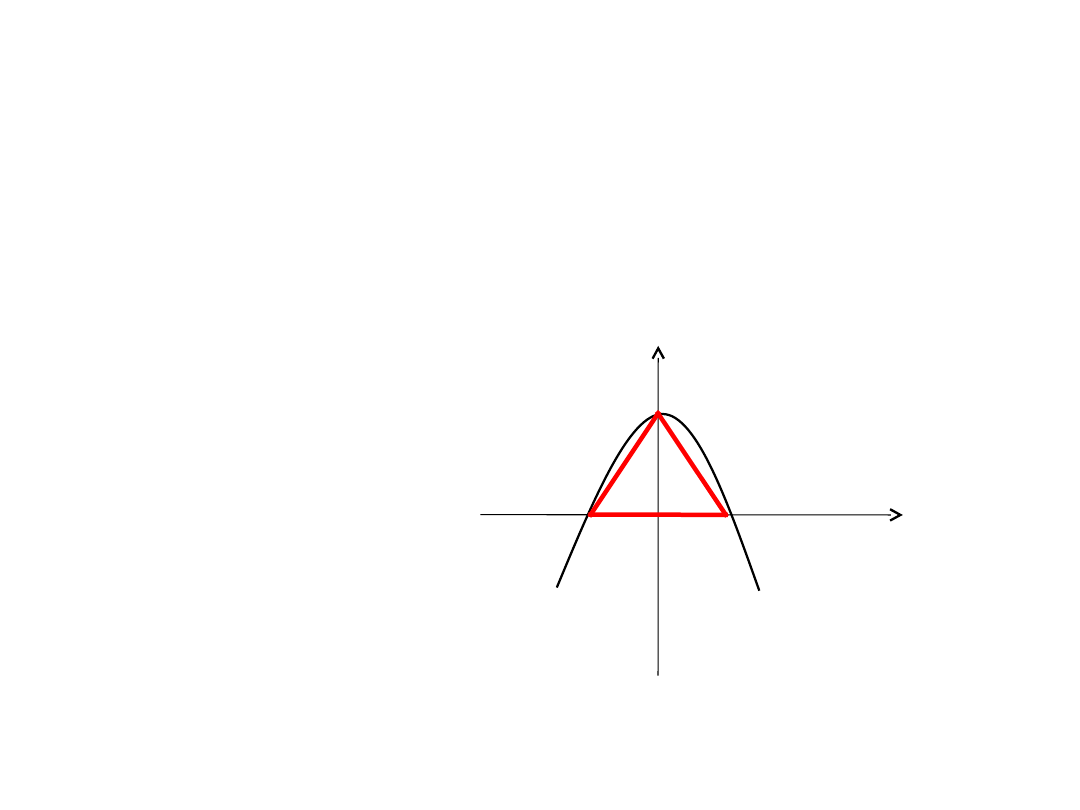
Z OSIĄ Y: f(0) = -2 · 0 + 8 = 8

PUNKT PRZECIĘCIA: C=(0,8)

Wierzchołki trójkąta to punkty A, B, C.

P

Δ

= ½ ·a ·h

P

Δ

= ½ ·|AB| ·h

P

Δ

= ½ ·4 ·8

P

Δ

= 16 j

2

C

B

A

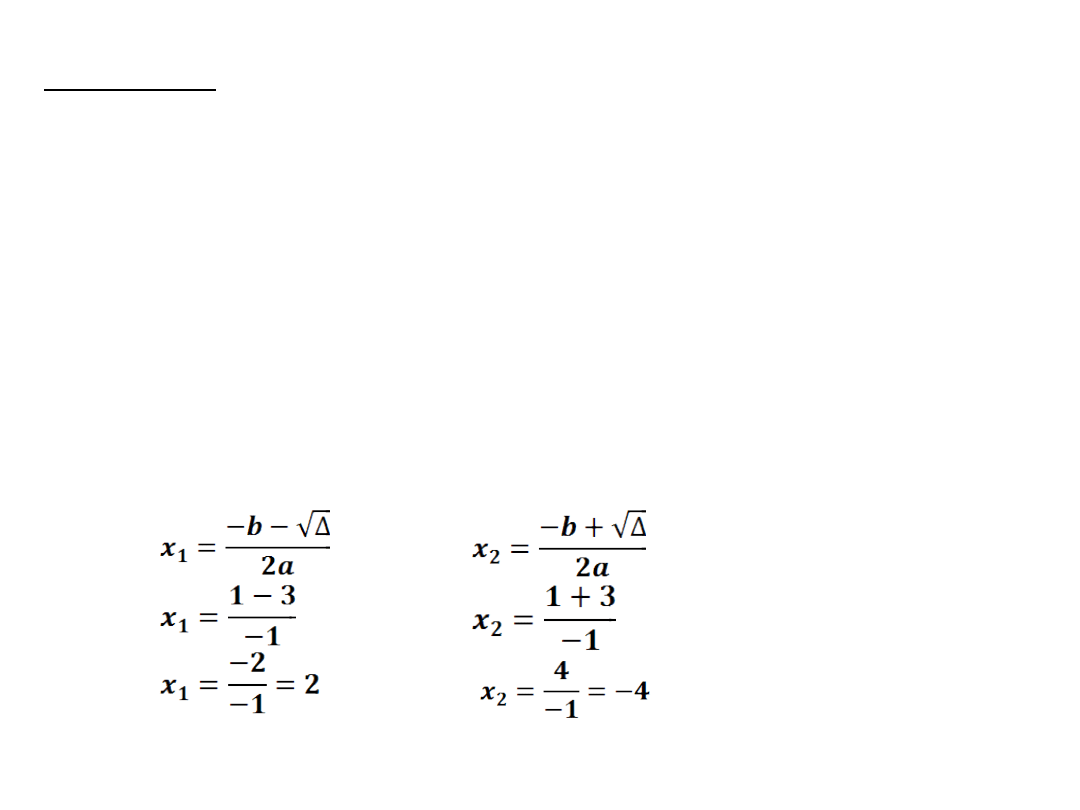
Zadanie7: Dana jest funkcja

g(x)=- ½x

2

-x+4

a)przedstaw ją w postaci iloczynowej
b)napisz równanie osi symetrii wykresu
c)oblicz pole trójkąta, którego wierzchołkami są
punkty przecięcia wykresu z osiami układu
współrzędnych.

Ad.a)
Obliczamy miejsca zerowe funkcji: a=-½ b=-1 c=4

Δ = b

2

- 4ac

Δ = (-1)

2

- 4·(-½)·4 = 1 + 8 = 9

Δ > 0 funkcja posiada dwa miejsca zerowe

g(x)=-½(x-2)(x+4)

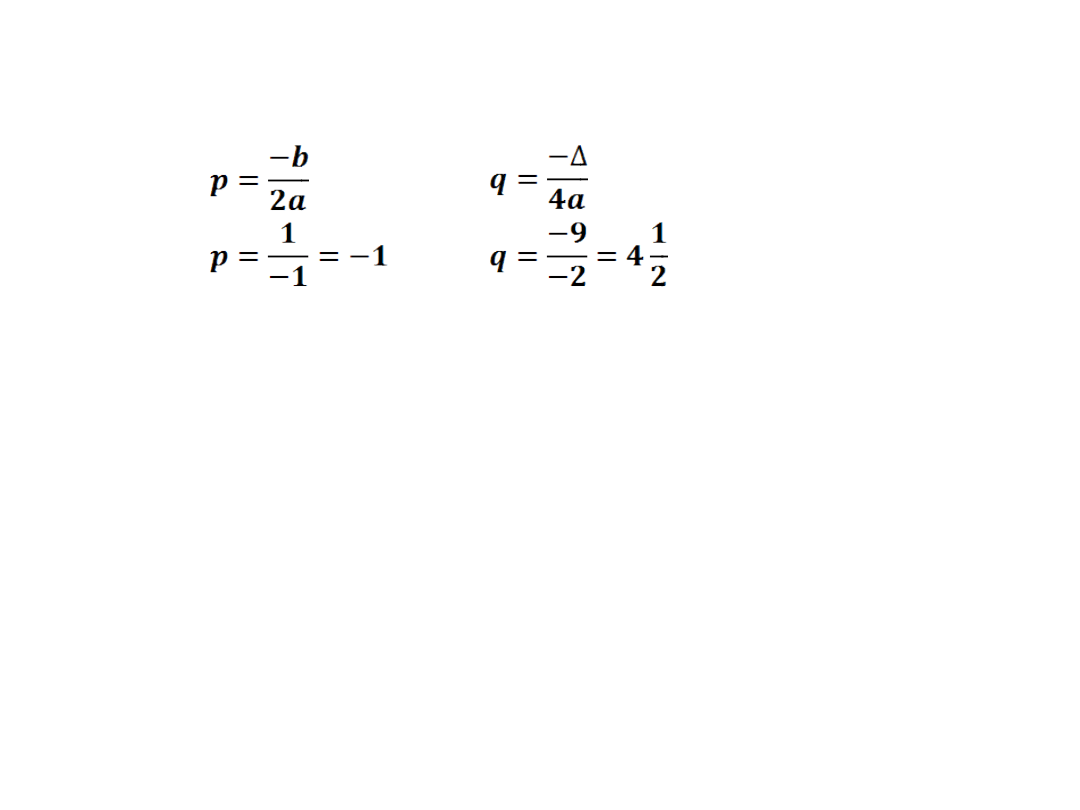
Ad.b)
Obliczamy współrzędne wierzchołka W paraboli:
W=(p,q)

W=(-1,4½)

Osią symetrii wykresu jest prosta o równaniu x=-1

Ad.c)
Szukamy punktów przecięcia wykresu funkcji z

osiami układu

współrzędnych.

Z OSIĄ X: g(x)=0
- ½ (x-2)(x+4)=0
x=2 lub x=-4

PUNKTY PRZECIĘCIA: A=(-4,0) oraz B=(2,0)

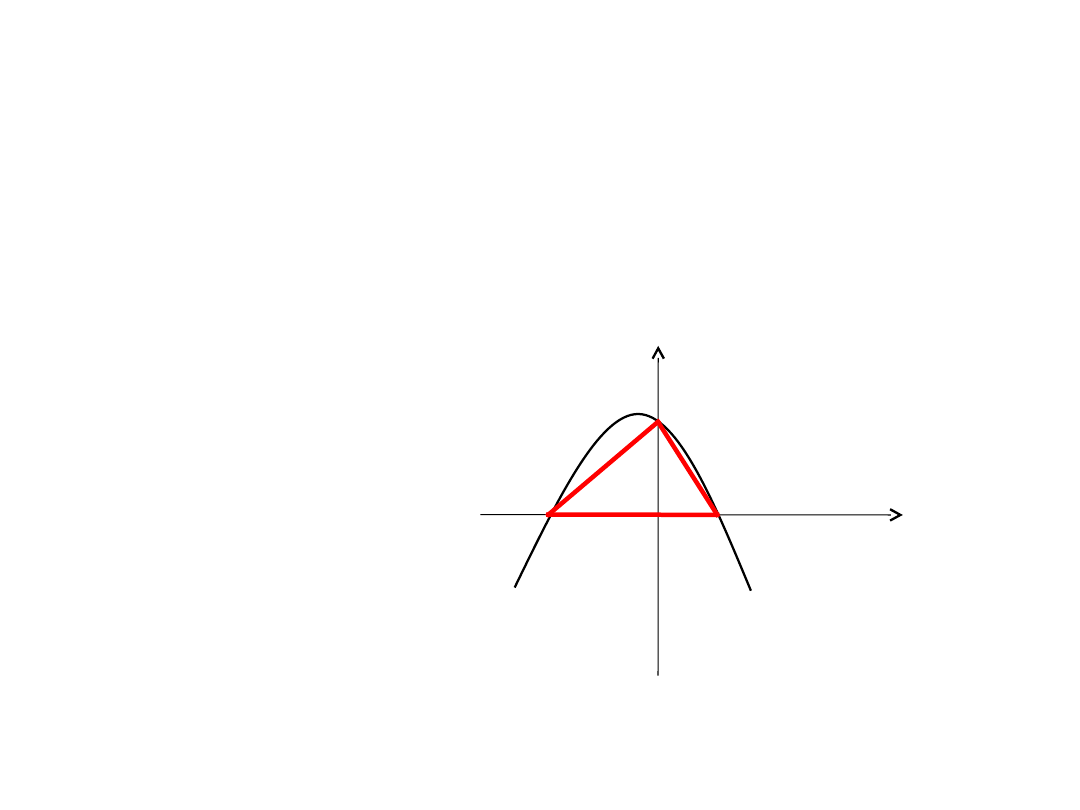
Z OSIĄ Y: g(0) = - ½ · 0 - 0 + 4 = 4

PUNKT PRZECIĘCIA: C=(0,4)

Wierzchołki trójkąta to punkty A, B, C.

P

Δ

= ½ ·a ·h

P

Δ

= ½ ·|AB| ·h

P

Δ

= ½ ·6 ·4

P

Δ

= 12 j

2

B

C

A