POSTAĆ OGÓLNA

FUNKCJI

KWADRATOWEJ

Jeżeli a ≠ 0 to funkcję

f(x)=ax

2

+bx+c

nazywamy

funkcją kwadratową (trójmianem kwadratowym).
Jest to

postać ogólna funkcji

.

Dziedziną funkcji jest zbiór liczb rzeczywistych.
Wykresem funkcji jest parabola.

PRZYKŁADY FUNKCJI:

f(x)=6x

2

-4x+10

g(x)=-2x

2

-10

h(x)=x

2

-x

f(x)=4x

2

+5x

p(x)=7x

2

g(x)=-2x

2

-2x-2

h(x)=x

2

-8

Zadanie1: Przedstaw funkcję w postaci ogólnej:

a) f(x)=x(x-10)+2(x-8)
f(x)=x

2

-10x+2x-16

f(x)=x

2

-8x-16-

postać ogólna funkcji kwadratowej

a=1 b=-8 c=-16

b) f(x)=2(x+4)(x-3)
f(x)=2(x

2

-3x+4x-12)

f(x)=2x

2

-6x+8x-24

f(x)=2x

2

+2x-24

- postać ogólna funkcji

kwadratowej
a=2 b=2 c=-24

c) f(x)=2(x-2)

2

f(x)=2(x

2

-4x+4)

f(x)=2x

2

-8x+8-

postać ogólna funkcji kwadratowej

a=2 b=-8 c=8

d) f(x)=-3(x+4)

2

f(x)=-3(x

2

+8x+16)

f(x)=-3x

2

-24x-48

- postać ogólna funkcji

kwadratowej

a=-3 b=-24 c=-48

e) f(x)=-x(x+4)-4x(x+1)
f(x)=-x

2

-4x-4x

2

-4x

f(x)=-5x

2

-8x

- postać ogólna funkcji kwadratowej

a=-5 b=-8 c=0

Zadanie2: Sprawdź nie rysując, czy do wykresu funkcji

f(x)=3x

2

-x-2 n

ależą punkty: A=(0,4) B=(1,0) C=(-

2,3).

A: f(x)=3x

2

-x-2

4=3·0

2

-0-2

4=-2

- fałsz A∉f

B: f(x)=3x

2

-x-2

0=3·1

2

-1-2

0=0

B

ϵ

f

C: f(x)=3x

2

-x-2

3=3·(-2)

2

-(-2)-2

3=3·4+2-2
3=12

- fałsz C∉f

Do wykresu funkcji należy punkt B.

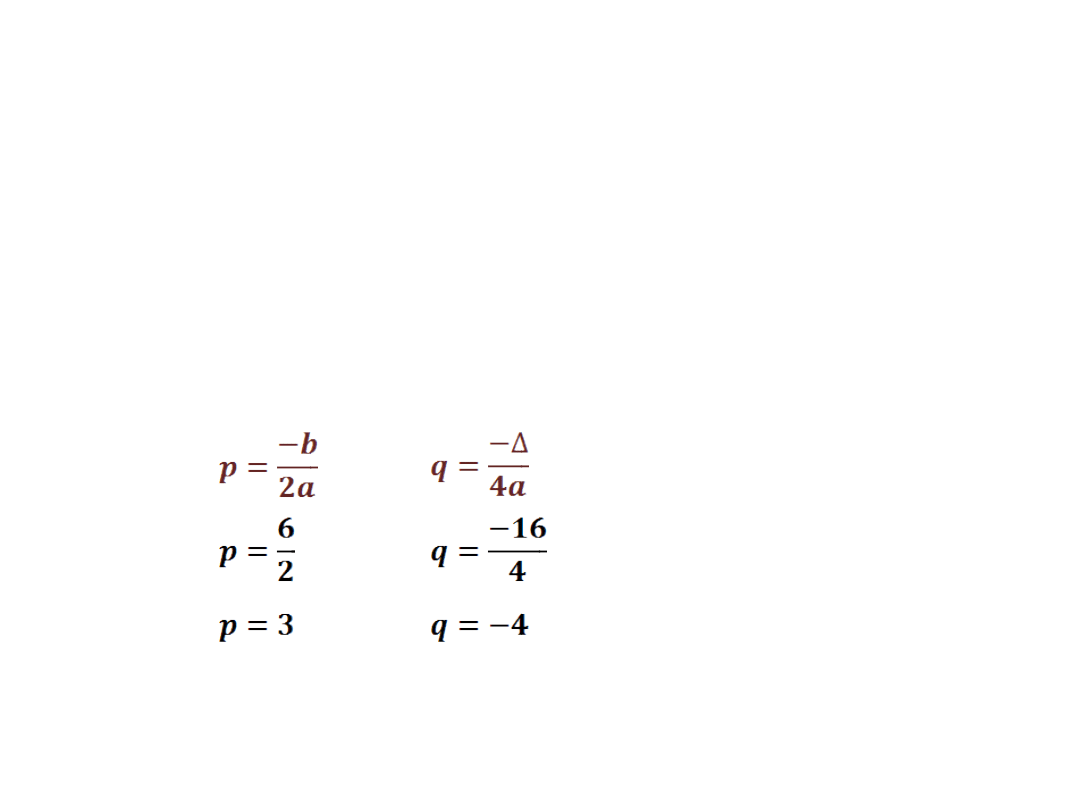
Zadanie3: Funkcję zapisaną w postaci ogólnej,
przedstaw
w postaci kanonicznej i iloczynowej:

a)f(x)=x

2

-6x+5

a=1 b=-6 c=5

Δ = b

2

- 4ac

Δ = (-6)

2

- 4·1·5 = 36 – 20 = 16

Przypominamy postać kanoniczną:

f(x)=a(x-

p)

2

+q

f(x)=(x-3)

2

-4

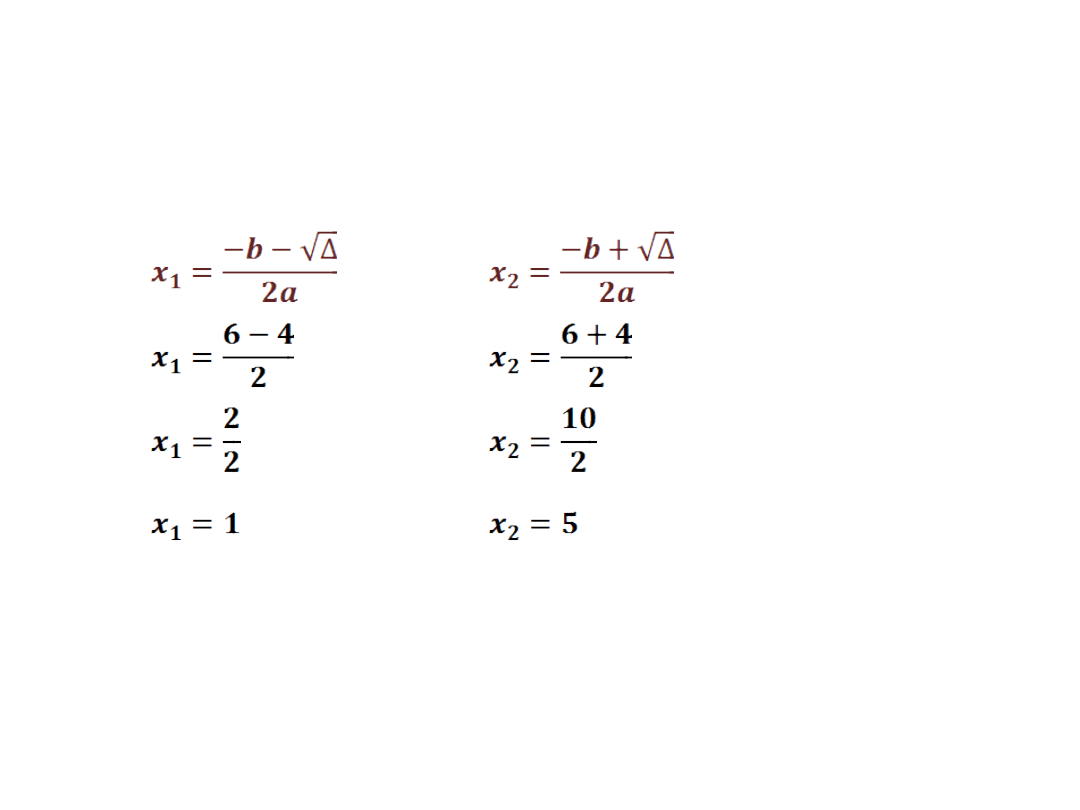
Przypominamy postać iloczynową: f(x)=a(x-x

1

)

(x-x

2

)

Δ > 0 funkcja posiada dwa miejsca zerowe

f(x)=(x-1)(x-5)

Wykresem funkcji jest parabola skierowana

ramionami do góry, ponieważ współczynnik a
jest dodatni. (a=1)

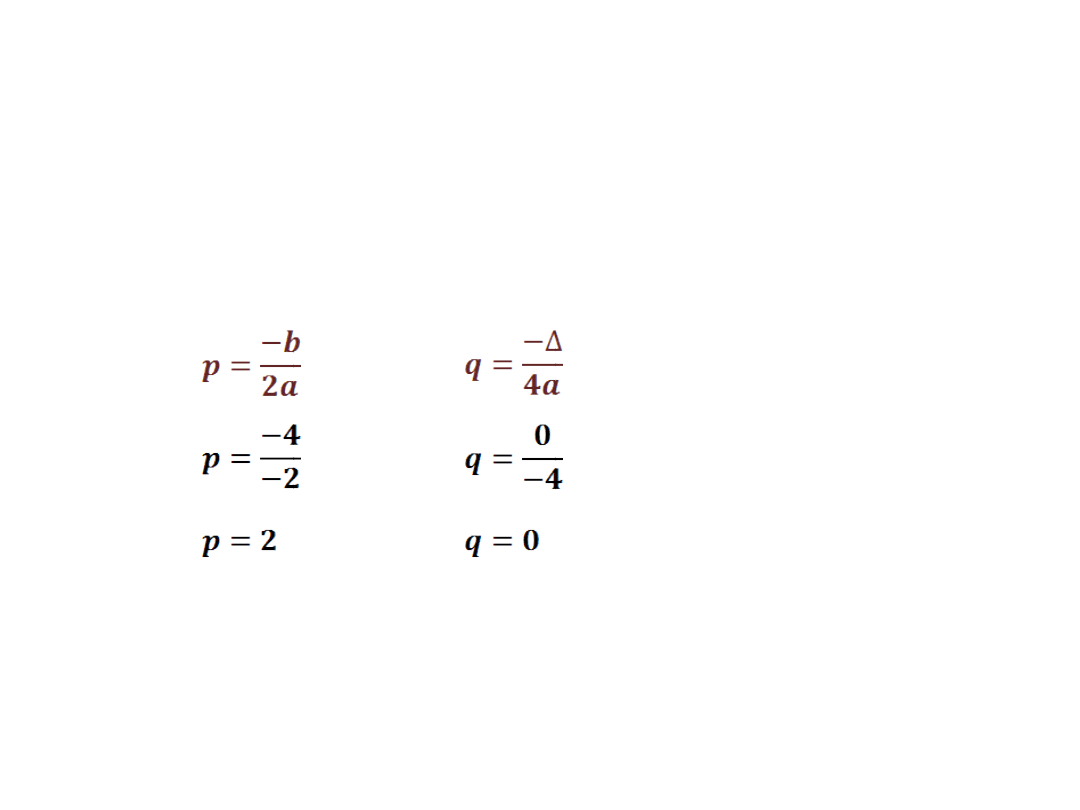
b) f(x)=-x

2

+4x-4

a=-1 b=4 c=-4

Δ = b

2

- 4ac

Δ = 4

2

- 4·(-1)·(-4) = 16 – 16 = 0

f(x)=a(x-p)

2

+q

f(x)=-(x-2)

2

–

postać kanoniczna

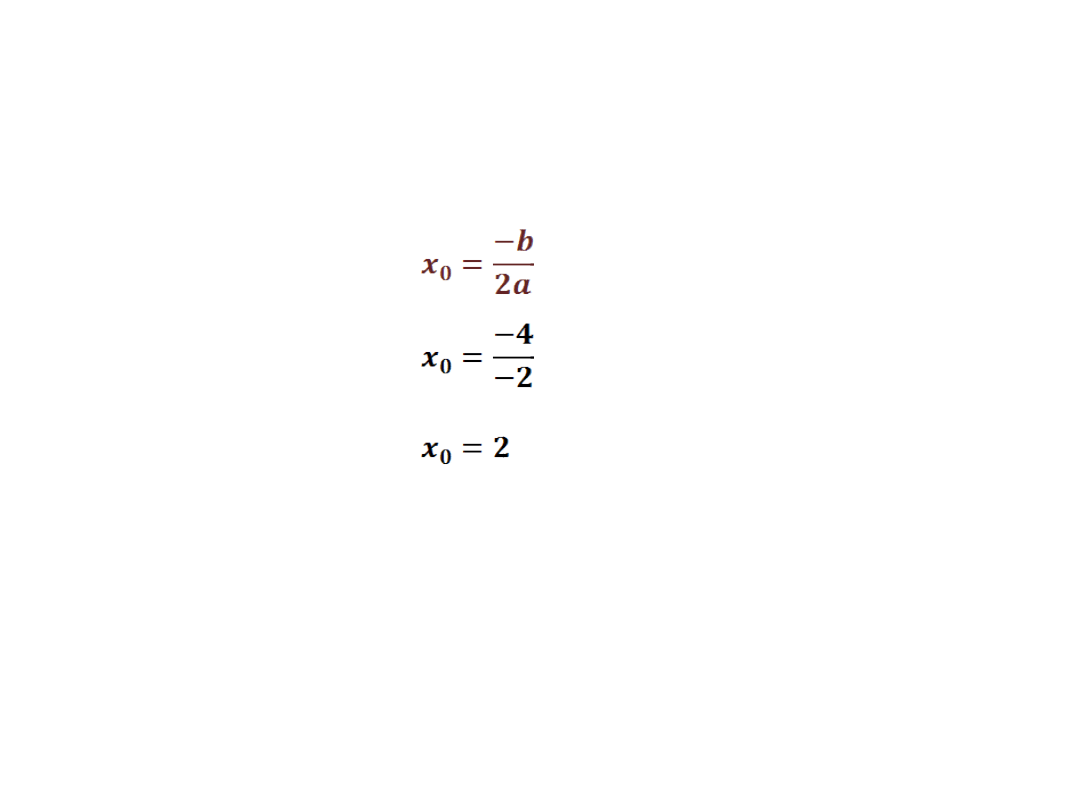
Przypominamy postać iloczynową: f(x)=a(x-x

0

)

2

Δ = 0 funkcja posiada jedno miejsce zerowe

f(x)=-(x-2)

2

Wykresem funkcji jest parabola skierowana

ramionami

w dół, ponieważ współczynnik a jest ujemny. (a=-1)

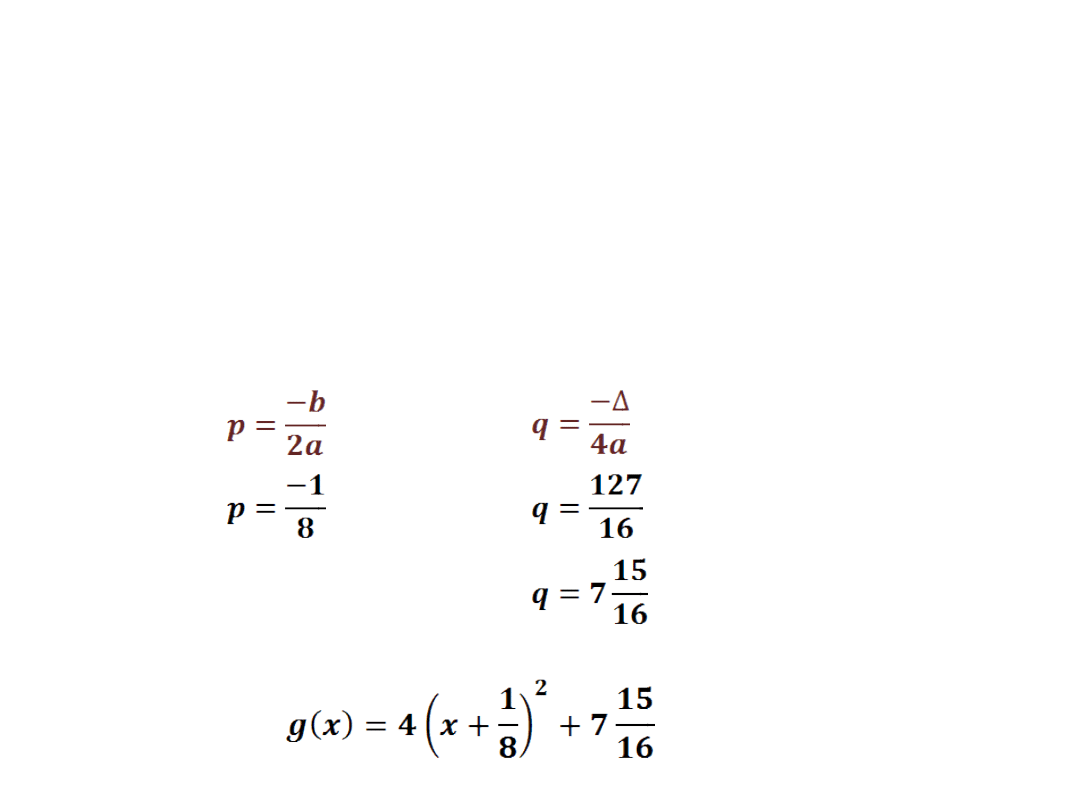
c) g(x)=4x

2

+x+8

a=4 b=1 c=8

Δ = b

2

- 4ac

Δ = 1

2

- 4·4·8 = 1 - 128 = -127

Δ < 0 funkcja nie posiada miejsc zerowych; nie

można jej

przedstawić w postaci iloczynowej

-

postać kanoniczna

Zadanie4: Funkcję zapisaną w postaci kanonicznej
zapisz
w postaci ogólnej. Odczytaj współrzędne wierzchołka
paraboli.

a)f(x)=-2(x+2)

2

+4

f(x)=-2(x

2

+4x+4)+4 W=(-2,4)

f(x)=-2x

2

-8x-8+4

f(x)=-2x

2

-8x-4

b)g(x)=4(x-7)

2

g(x)=4(x

2

-14x+49) W=(7,0)

g(x)=4x

2

-56x+196

c) h(x)=(x+5)

2

-5

h(x)=(x

2

+10x+25)-5 W=(-5,-5)

h(x)=x

2

+10x+20

Zadanie5: Funkcję zapisaną w postaci iloczynowej
przedstaw w postaci ogólnej.

a)h(x)=-3(x+4)(x-5)
h(x)=-3(x

2

+4x-5x-20)

h(x)=-3(x

2

-x-20)

h(x)=-3x

2

+3x+60 a=-3 b=3 c=60

b) p(x)=-4(x-1)x
p(x)=-4(x

2

-x)

p(x)=-4x

2

+4x a=-4 b=4 c=0

c) f(x)=6(x+3)

2

f(x)=6(x

2

+6x+9)

f(x)=6x

2

+36x+54 a=6 b=36 c=54

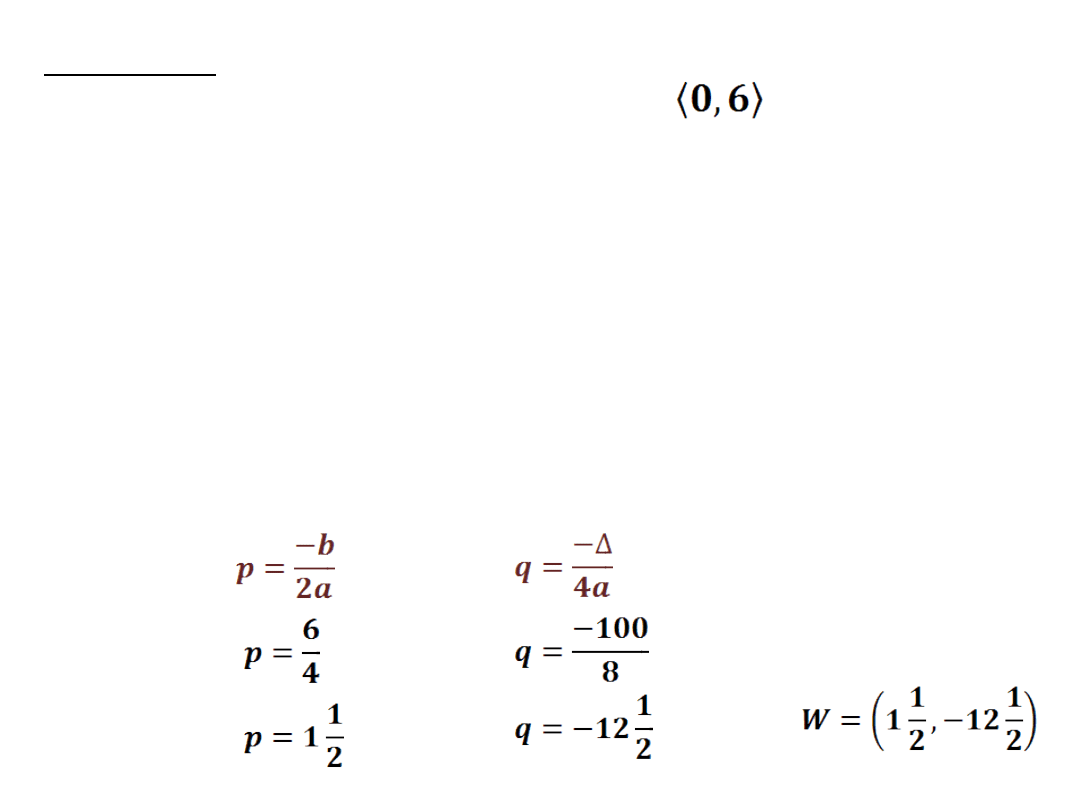
Zadanie6: Wyznacz wartość najmniejszą i największą
funkcji: f(x)=2(x+1)(x-4) w przedziale

Najpierw przekształcimy funkcję do postaci
kanonicznej
f(x)=2(x

2

-4x+x-4)

f(x)=2(x

2

-3x-4)

f(x)=2x

2

-6x-8

a=2 b=-6 c=-8

Δ = b

2

- 4ac

Δ = (-6)

2

- 4·2·(-8) = 36 + 64 = 100

Wyznaczamy współrzędne wierzchołka paraboli, aby
sprawdzić czy odcięta wierzchołka należy do
przedziału.

Odcięta wierzchołka należy do przedziału

Obliczamy wartości funkcji f na końcach przedziału:
f(0)=2·0

2

-6·0-8 = -8

f(6)=2·6

2

-6·6-8 = 72-36-8= 28

Najmniejszą wartością funkcji f w podanym

przedziale jest

wartość -rzędna wierzchołka paraboli,

największą

wartością funkcji jest 28 dla argumentu 6 będącego

końcem

podanego przedziału.

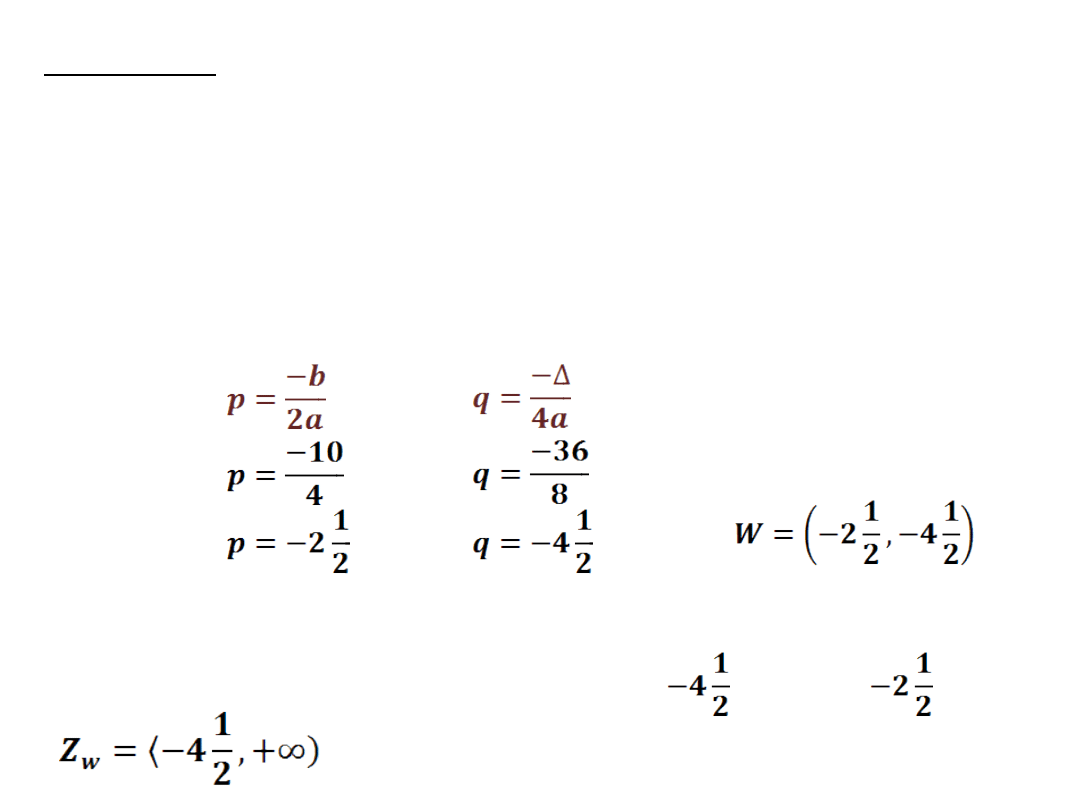
Zadanie7: Wyznacz współrzędne wierzchołka
paraboli, wyznacz wartość najmniejszą oraz zbiór
wartości funkcji: y=2x

2

+10x+8

a=2 b=10 c=8

Δ = b

2

- 4ac

Δ = 10

2

- 4·2·8 = 100 - 64 = 36

Wykresem funkcji jest parabola skierowana
ramionami w

górę. Wartość najmniejsza jest równa dla x=