Próbkowanie sygnału

analogowego

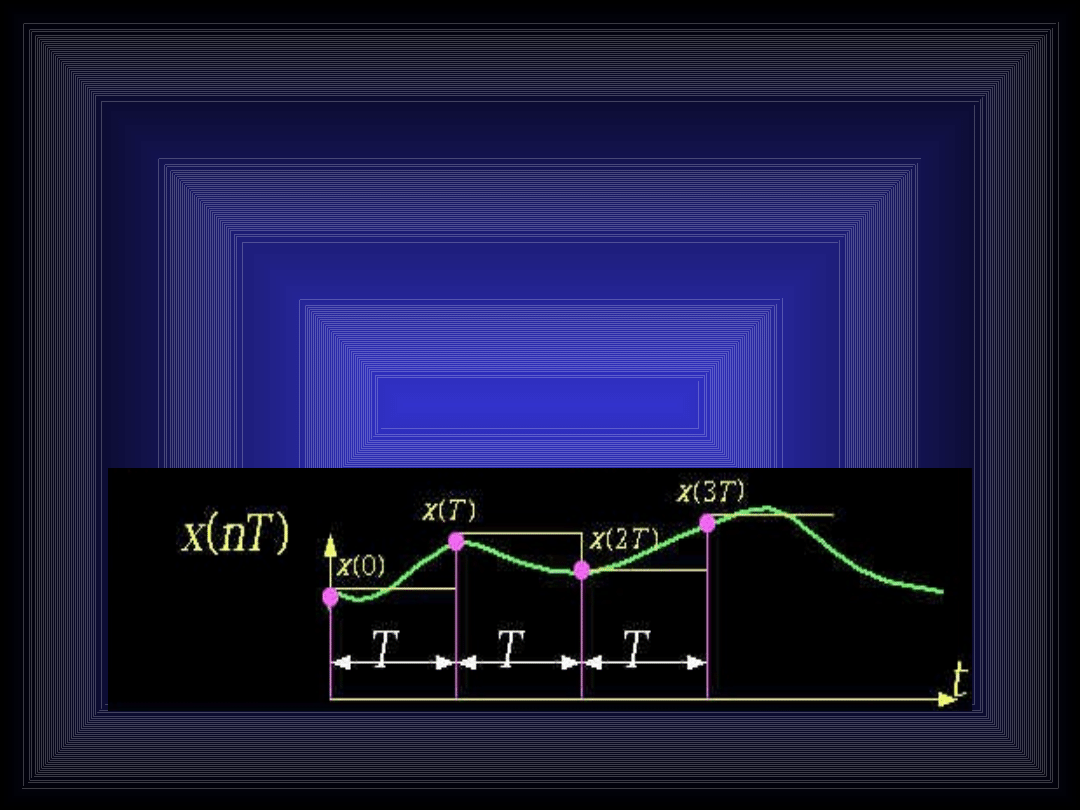
Próbkowanie sygnału (pomiar jego wartości
chwilowej) odbywa się w dyskretnych punktach
oddalonych od siebie o stałą odległość nazywaną
krokiem lub okresem próbkowania.

Tego uczą elektronicy ...

Sinusoida – modelowy

(analogowy) sygnał przemienny

)

2

sin(

)

(









ft

A

t

y

t

Czas, zmienna niezależna, dziedzina sygnału. Jest
wielkością ciągłą (aczkolwiek dziedziną sygnału nie
musi być czas).

A

Amplituda (napięcie V, prąd A, położenie m itd.)

f

Częstotliwość (Hz). Niekiedy używane jest pojęcie
częstotliwość kątowa (pulsacja)

f





2





Kąt przesunięcia fazowego

0

0









t

t

ft









2

Punkt wędrujący po okręgu ze stałą prędkością
kątową

T

T

t









2

4

/

8

/









T

T

t









2

2

/

4

/









oś liczb

rzeczywistych

o

ś l

ic

zb

u

ro

jo

n

y

ch

 

t

j

Z



exp



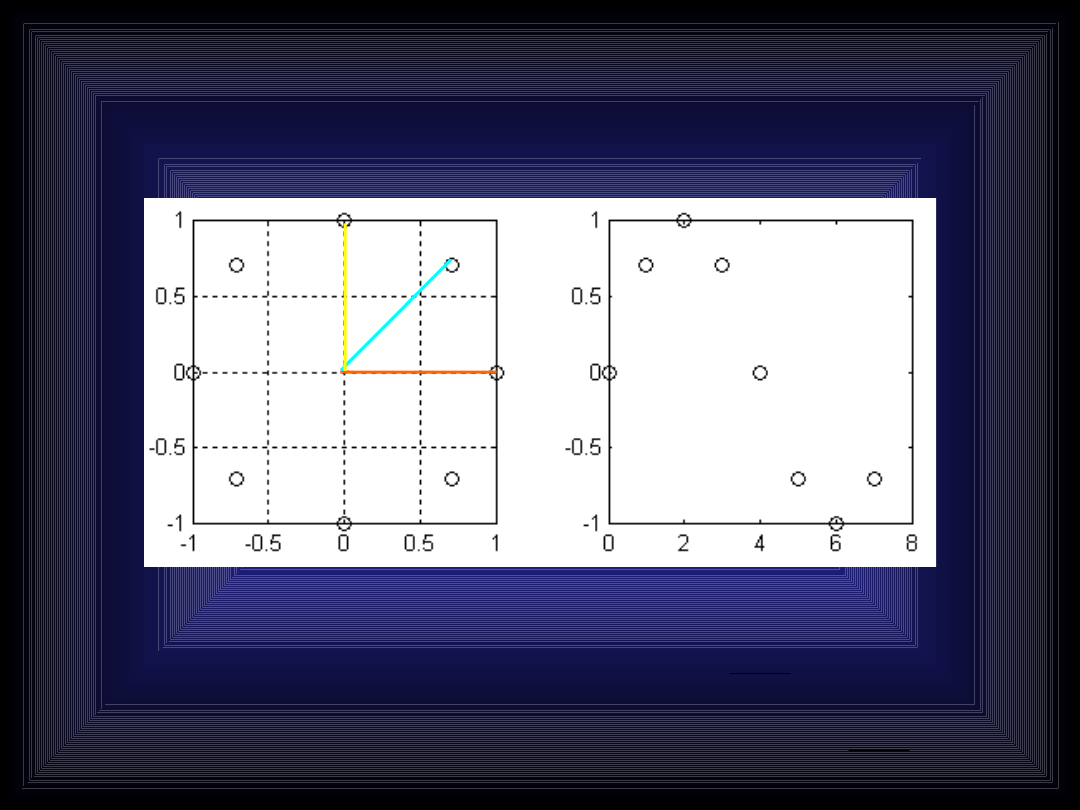
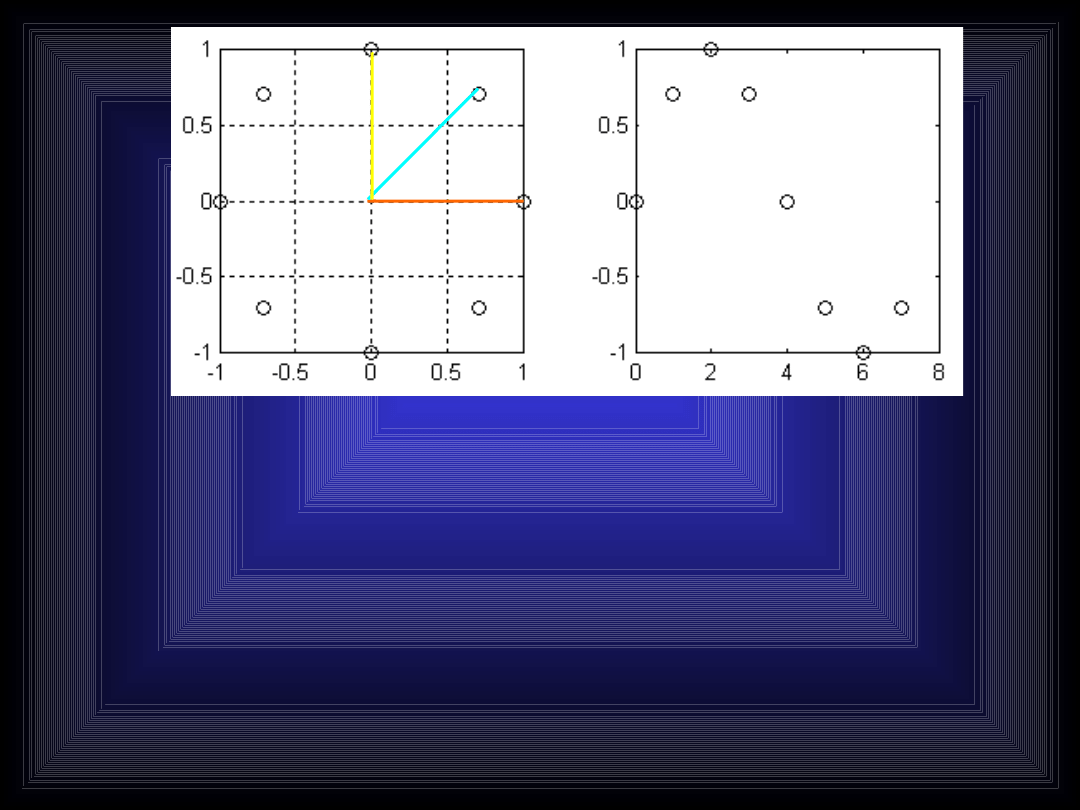
Rzut Z na oś urojoną daje sinus, rzut na oś
rzeczywistą daje cosinus

Rozpoczynamy

od

badania

zachowania

sinusoidy ponieważ za pomocą superpozycji
sinusoid można zbudować prawie wszystkie
interesujące nas sygnały (warunki Dirichleta).

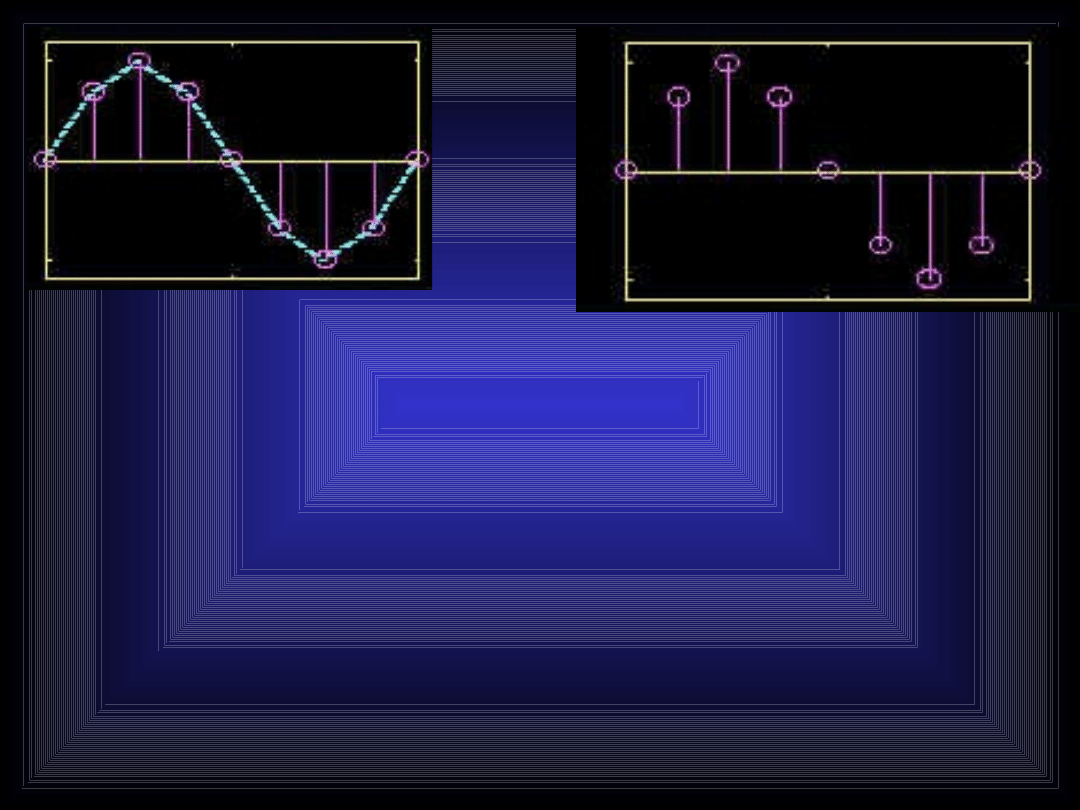
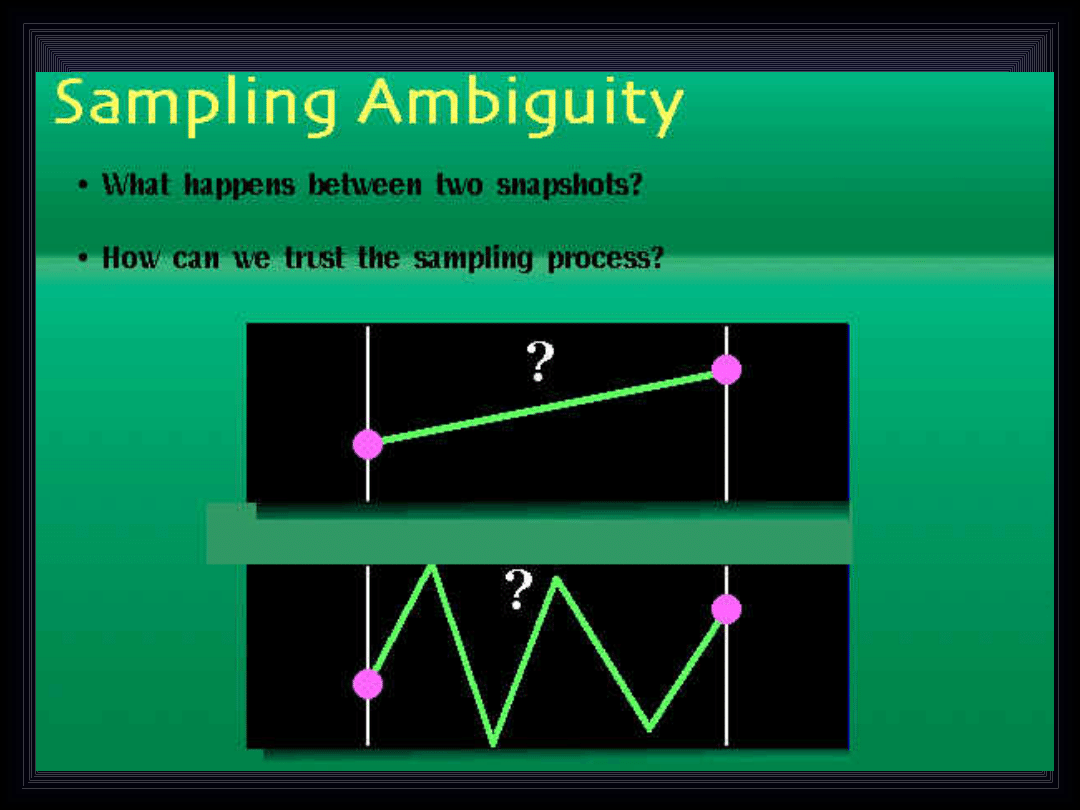
Sygnał dyskretny stanowi zbiór próbek wartości
chwilowej

sygnału

ciągłego.

Nie

można

jednoznacznie określić częstotliwości sygnału
analogowego

na

podstawie

znajomości

jedynie jego próbek.

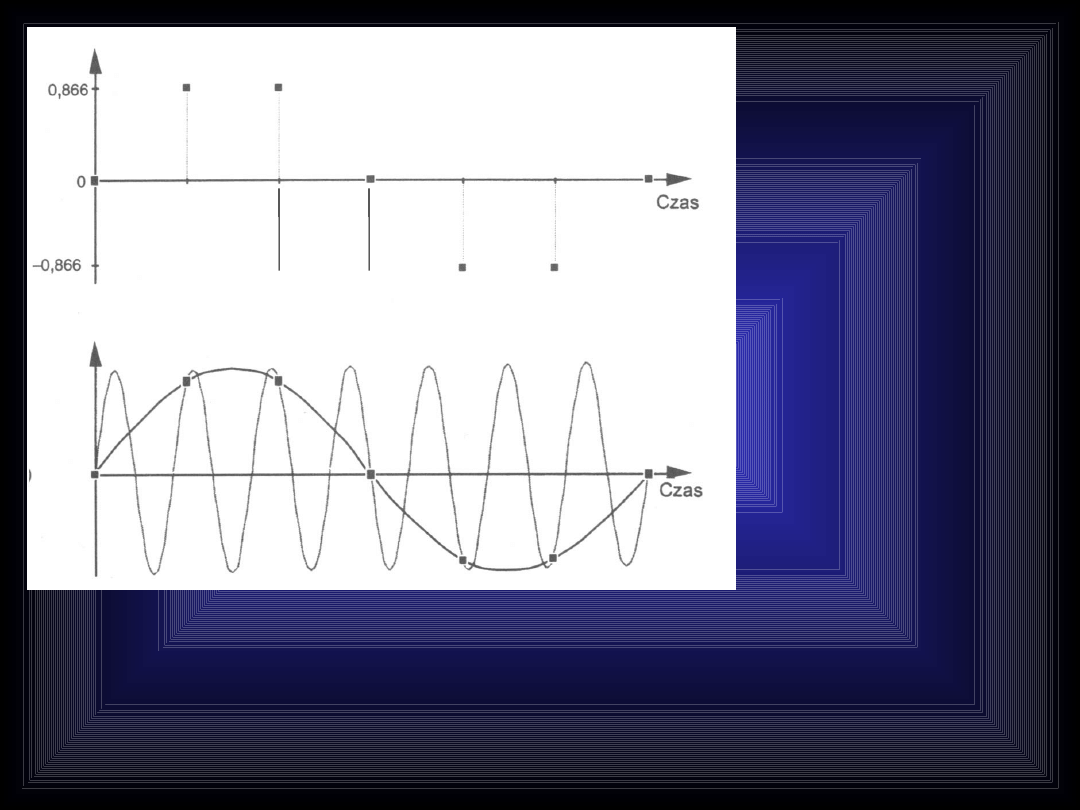
mamy

próbki

sygnału ...

...znamy fs

...ale próbki nie określają

sygnału jednoznacznie

)

2

sin(

)

(

ft

t

s





T

f

1



sygnał ciągły

p

s

p

T

f

f

1





Próbki dyskretne sygnału:

N

k

f

fk

k

s

p



0

)

/

1

2

sin(

]

[









)

2

/

2

sin(

)

4

/

2

sin(

)

2

/

2

sin(

)

/

1

2

sin(

]

[

































m

k

f

f

k

f

f

k

f

f

f

fk

k

s

p

p

p

p

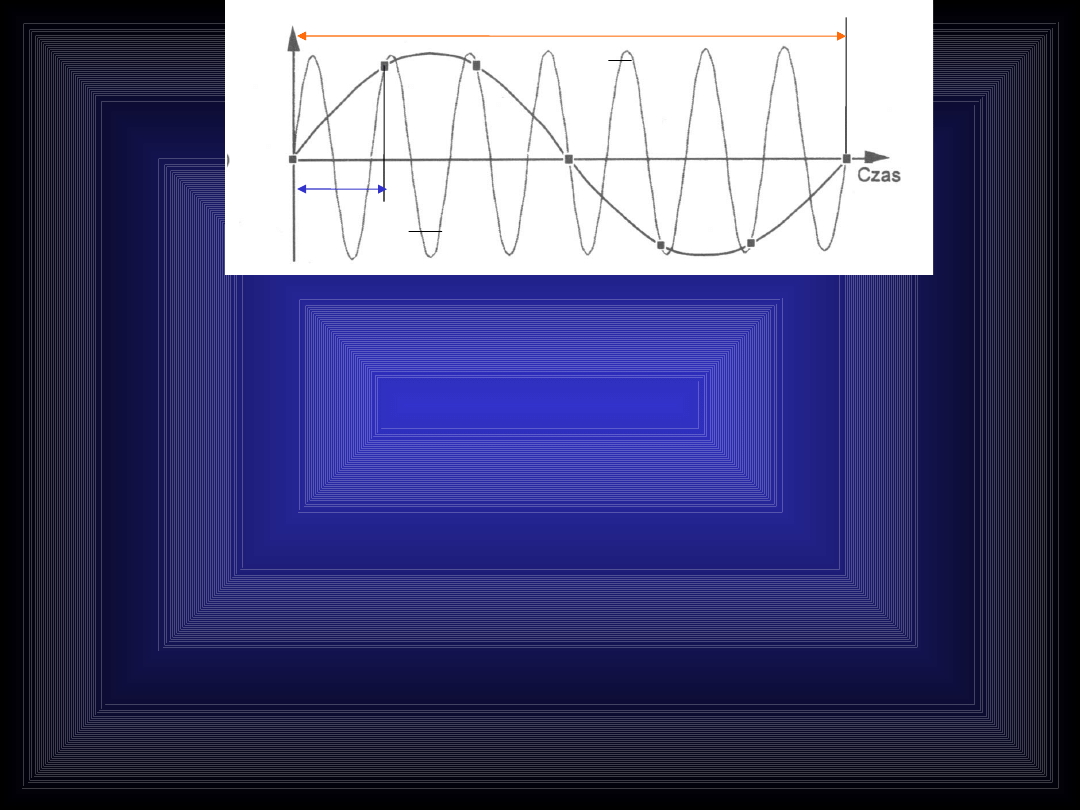
Sygnał dyskretny s[k] powstały przez

próbkowanie z częstotliwością fp sinusoidy s(t) o

częstotliwości f opisuje zbiór sinusoid o

częstotliwościach:

)

2

/

2

sin(

]

[











mk

k

f

f

k

s

p

)]

(

/

2

sin[

]

[

p

p

mf

f

f

k

k

s







czas

częstotliwoś

ć

Wniosek (!!!):

Niech „m” stanowi wielokrotność indeksu „k”

m

f

f

p



gdzie m jest dowolną liczbą całkowitą

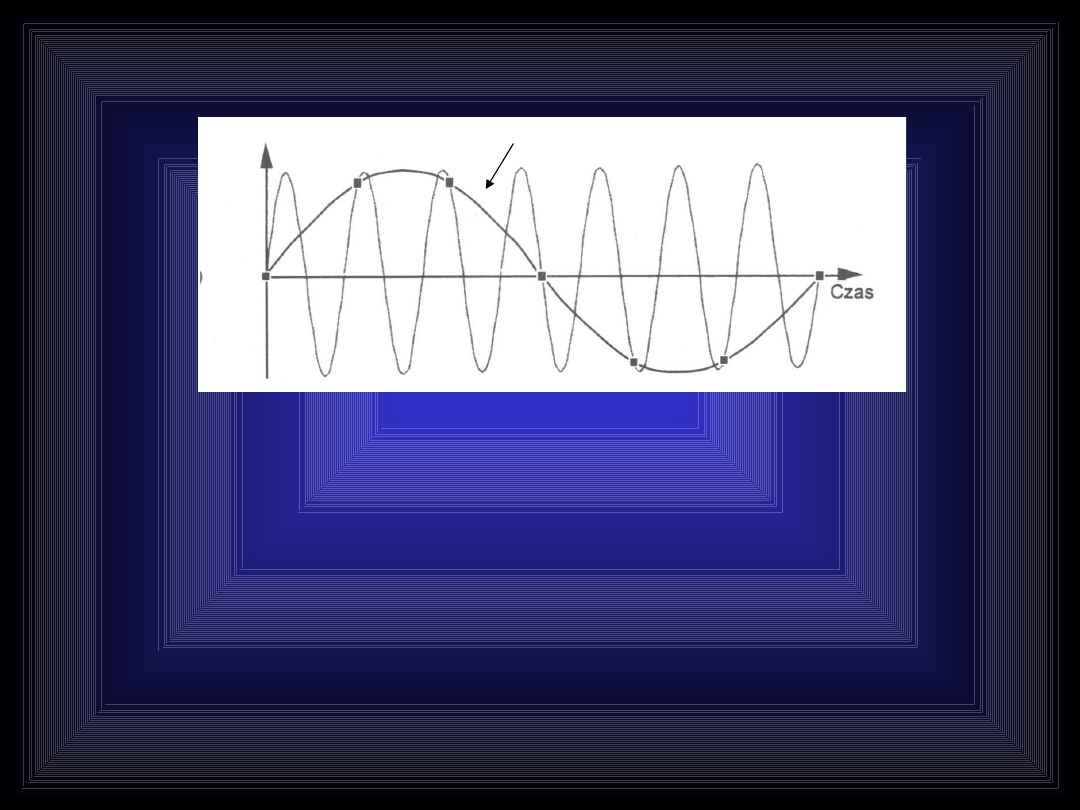
kHz

f 1



Weryfikacja

kHz

f

p

6



Odczytujemy z wykresu

Zatem częstotliwość „szybszej ”

sinusoidy wynosi:

kHz

kHz

kHz

f

7

6

1

1

2









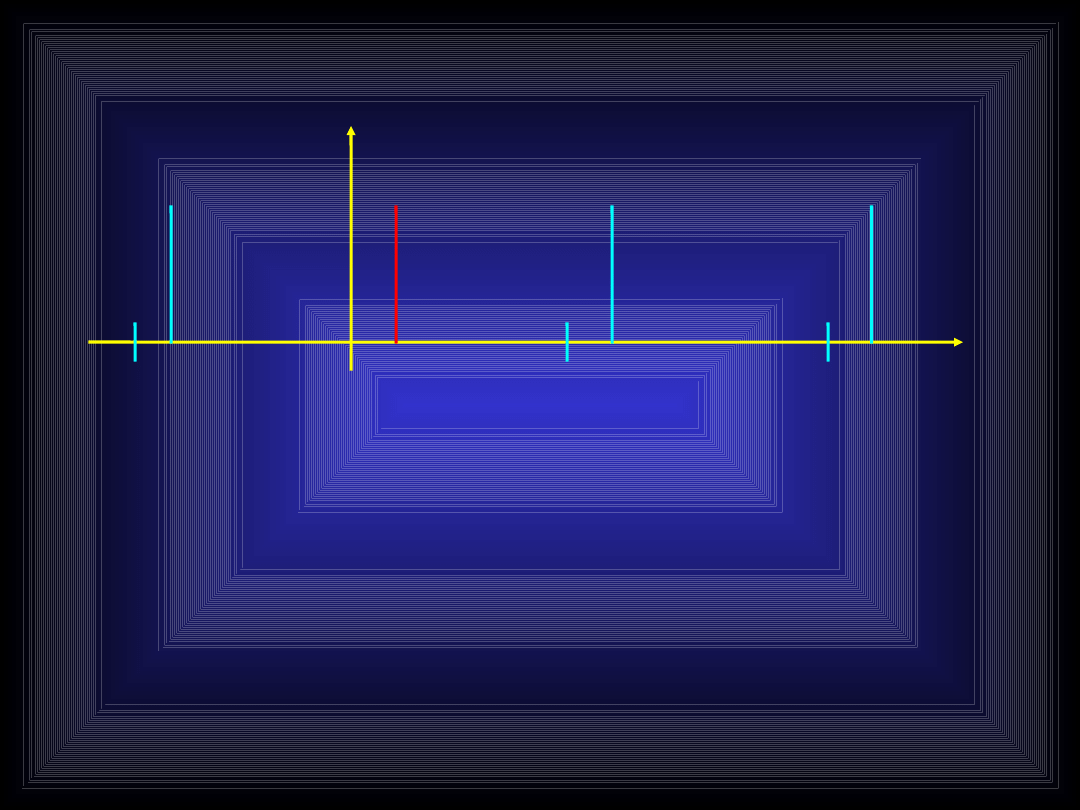
Mroczne widmo sinusoidy

częstotliwoś

ć

„o

b

e

cn

o

ść

sin

u

so

id

y

o

d

a

n

e

j

cz

ę

st

o

tli

w

o

śc

i”

0

kHz

1

kHz

f

p

6



f

f

p



1

p

f

2

f

f

p



2

p

f



f

f

p





Widmo sygnału dyskretnego (czyli

naszych próbek s[k]) jest okresowe

Zjawisko powyższe nazywamy

powieleniem widma

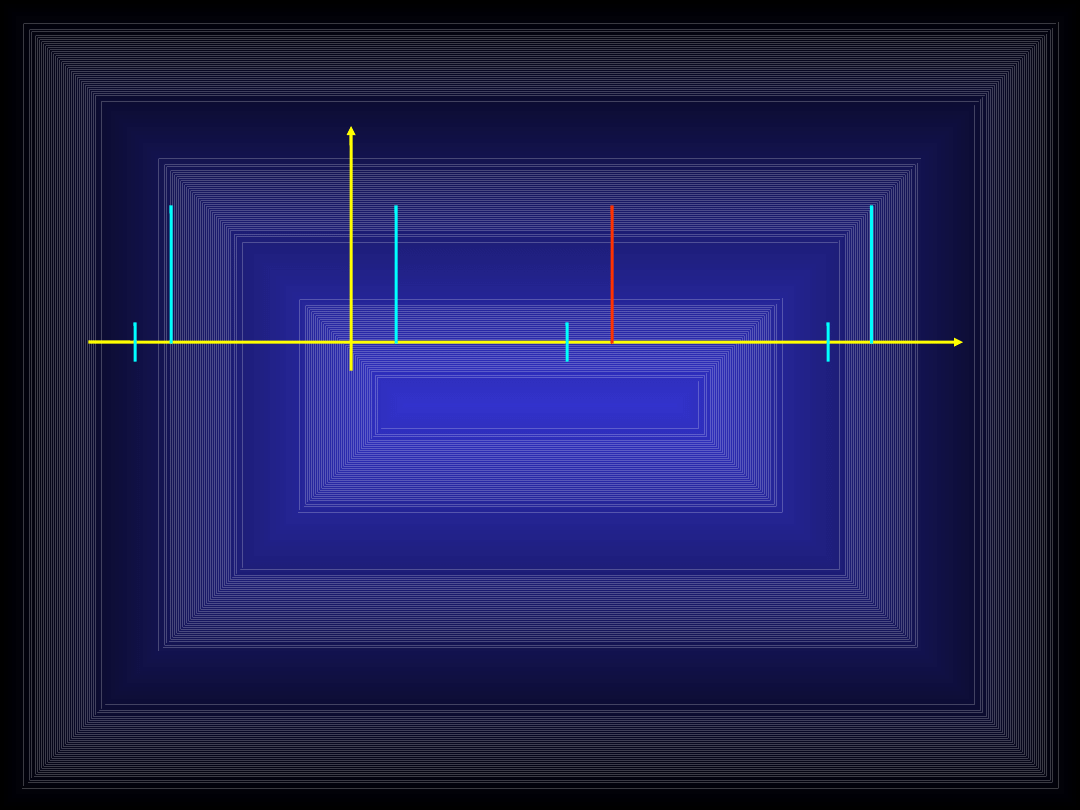
Efekt działa też w drugą stronę

0

f

f

p





kHz

f

p

6



kHz

7

p

f

2

f

f

p



p

f



f

f

p



 2

Próbkujemy ton sinusoidalny (sygnał o

ściśle określonej częstotliwości 7kHz) ale

z częstotliwością 6kHz. Widmo sygnału

cyfrowego zawiera fałszywy prążek

widmowy 1kHz (alias)

Wstępna konkluzja:

Dla uniknięcia maskowania widma

(aliasingu) wskazane jest, żeby

częstotliwość próbkowania była wyższa

od częstotliwości próbkowanego sygnału.

Jednakże podstawowe twierdzenie o

próbkowaniu (Shannon-Kotielnikow)

mówi:

Dla uniknięcia maskowania widma

(aliasingu) wskazane jest, żeby

częstotliwość próbkowania była

przynajmniej dwa razy wyższa od

częstotliwości próbkowanego sygnału.

Gdzie jest błąd?

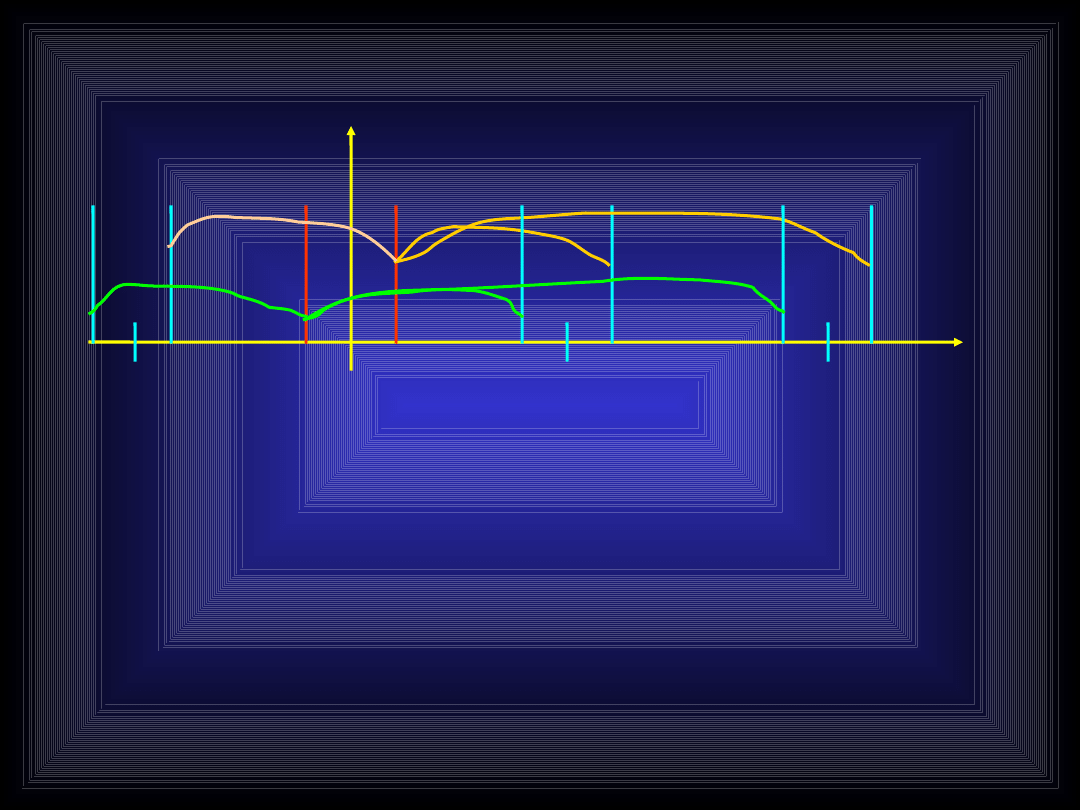
Widmo rzeczywistej sinusoidy

0

f

p

f

p

f

f 

p

f

2

f

f

p



2

p

f



f

f

p



 2

f



prążek –f również się powiela:

p

f

f 



p

f

f 



p

f

f 2





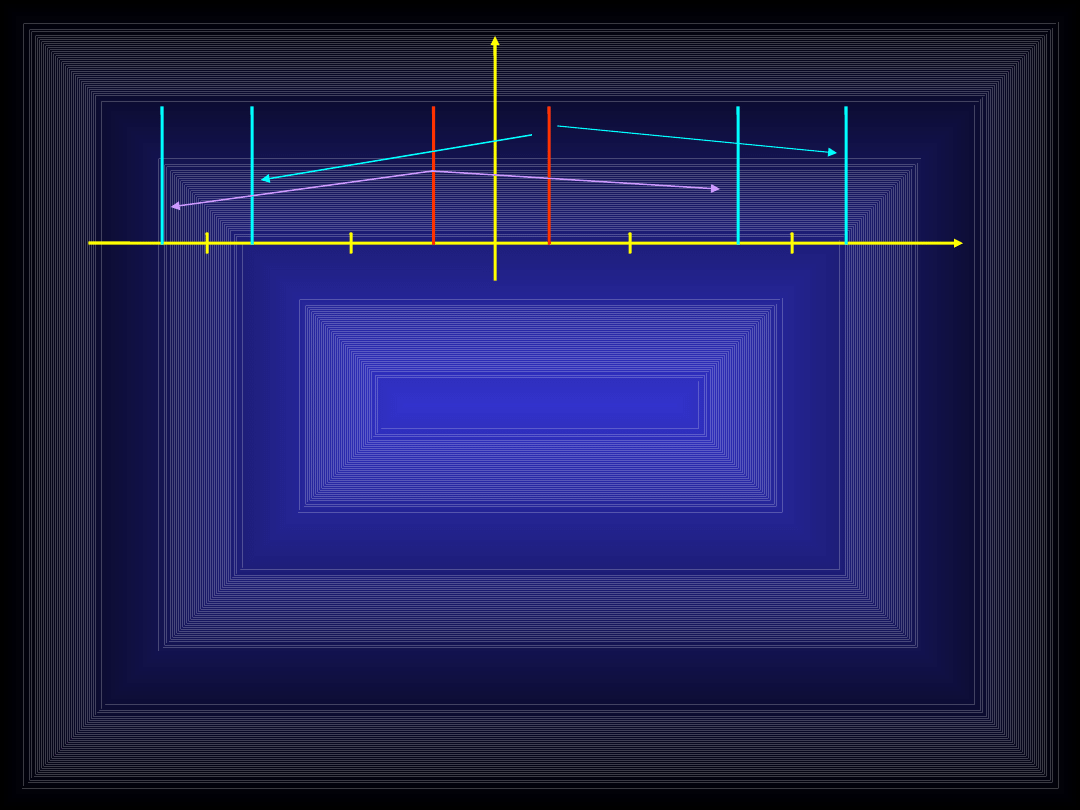
0

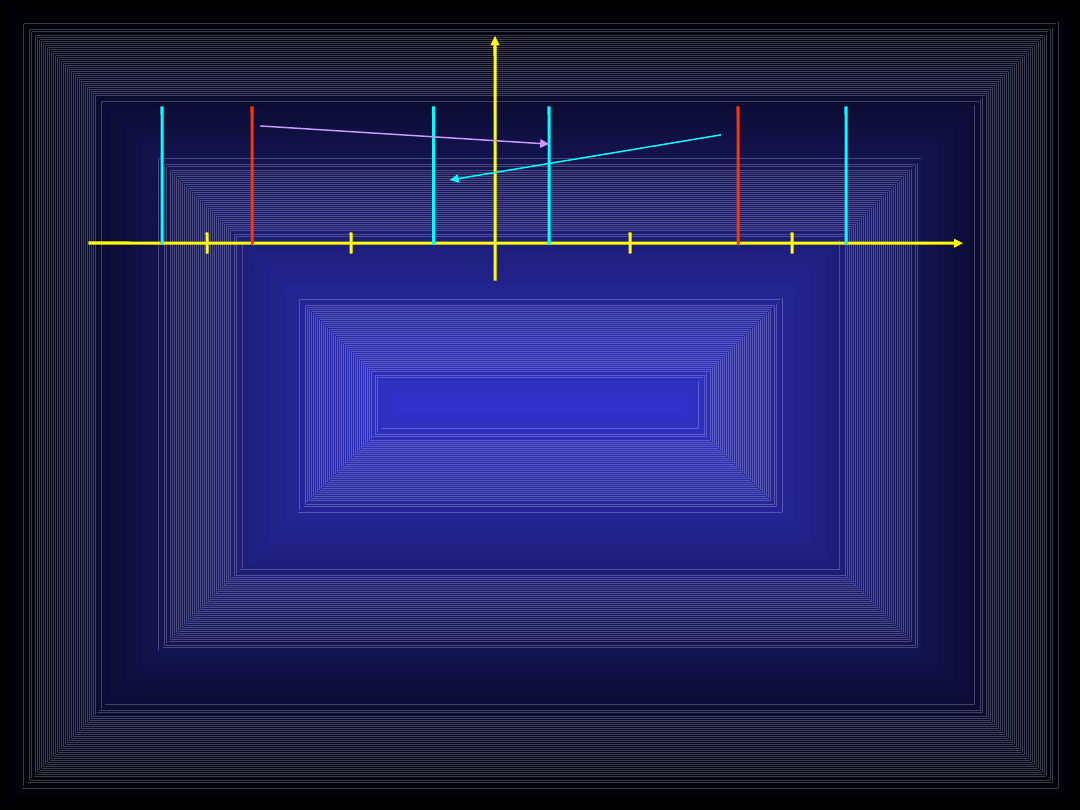
W widmie sinusoidy (ciągłej) oprócz

prążka o częstotliwości f pojawia się

zawsze drugi o częstotliwości -f

2

/

p

f

p

f

2

/

p

f



p

f



f

f



Pomimo, że próbkowanie jest prawidłowe

prążek fp-f pojawia się. Ponieważ jest on

odbiciem można go zignorować

ograniczając badane pasmo do zakresu

0-fp/2. Pod jednym wszakże warunkiem...

0

2

/

p

f

p

f

2

/

p

f



p

f



f

f



Postać widma jest zatem analogiczna i nie można

rozstrzygnąć jaka była częstotliwość sygnału (alias

sygnału f trafia w analizowany obszar widma).

Konieczne jest zapewnienie braku sygnałów w paśmie

powyżej fp/2. Można to osiągnąć przez zastosowanie

analogowego filtru dolnoprzepustowego zwanego

filtrem antyaliasingowym