FUNKCJA

FUNKCJA

JEJ WŁASNOŚCI ORAZ

RODZAJE

FUNKCJ

FUNKCJ

A

A

FUNKC

JA LIN

IOWA

FUNKC

JA LIN

IOWA

I JEJ W

ŁASNO

ŚCI

I JEJ W

ŁASNO

ŚCI

CO TO JEST

CO TO JEST

FUNKCJA

FUNKCJA

?

?

WŁASNOŚC

I

FUNKCJI

FUNKCJI

PR

ZY

KŁ

AD

Y

FU

NK

CJI

PR

ZY

KŁ

AD

Y

FU

NK

CJI

NI

EL

IN

IOW

YC

H

NI

EL

IN

IOW

YC

H

Co to jest funkcja

Co to jest funkcja

?

?

B

A

a

b

c

d

e

1

2

3

4

5

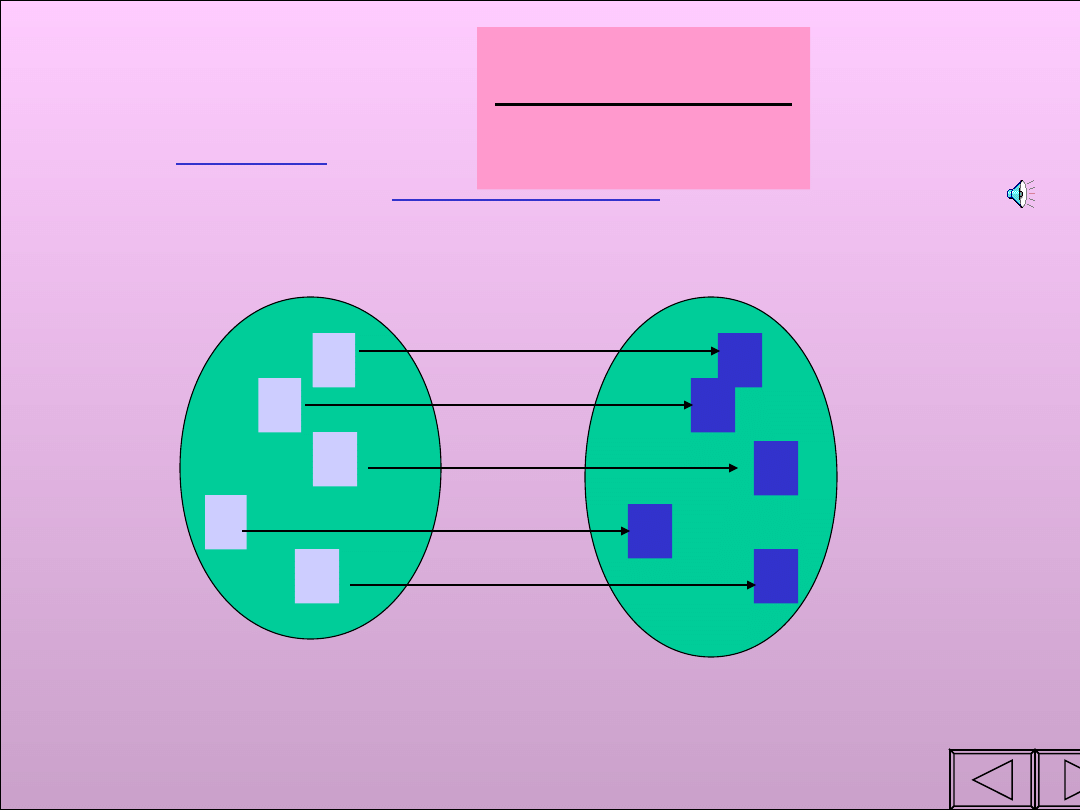
Definicja

:

Jeżeli

każdemu

elementowi zbioru A

przyporządkujemy

dokładnie jeden

element zbioru

B, to takie przyporządkowanie nazywamy funkcją ze
zbioru A do zbioru B.

Dane są dwa zbiory A
i B

A - dziedzina funkcji

elementy zbioru A-
argumenty

B - przeciwdziedzina
funkcji

elementy zbioru B - wartości

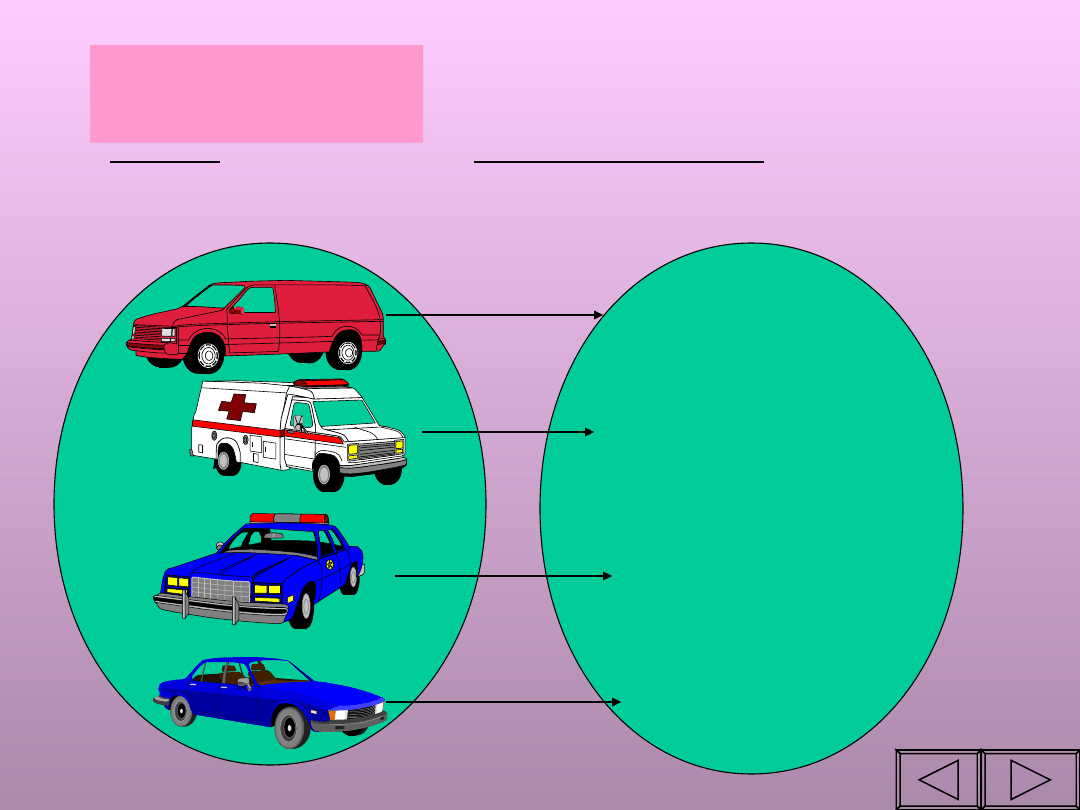
Przykład
funkcji I

Każdy
samochód,

ma dokładnie jeden numer
rejestracyjny.

WRZ 2435

KRB 18003

CEK 2112

CZS 4503

A

dziedzina

B

przeciwdziedzin
a

5

7

12

19

2
1

Przykład funkcji II

Każdy
uczeń

ma dokładnie jeden numer w
dzienniku

Jola K.

Kasia B.

Jacek Z.

Tomek

D

.

Zbyszek

W

.

A

A - DZIEDZINA

B

B - PRZECIWDZIEDZINA

Każdy ma jeden numer

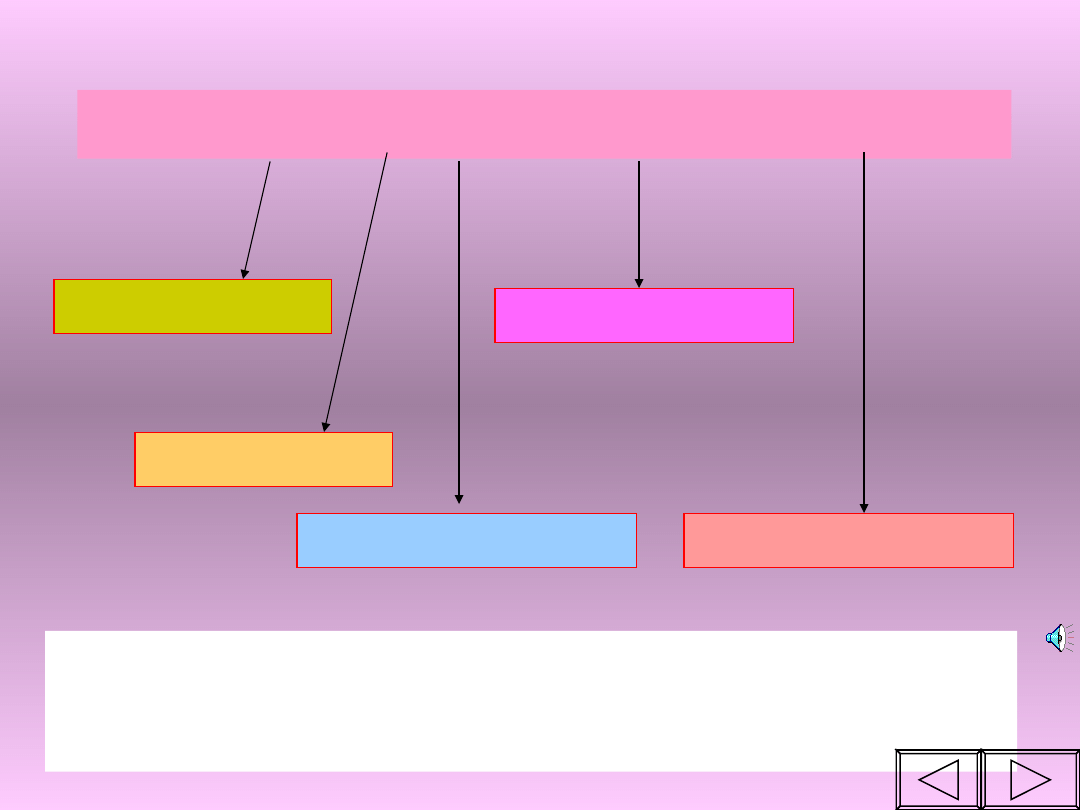
Różne sposoby opisywania funkcji

SŁOWNIE

WZOREM

TABELĄ

GRAFEM

WYKRESEM

Uwaga: Z każdego opisu musi jednoznacznie

wynikać sposób przyporządkowania, dziedzina i

przeciwdziedzina funkcji.

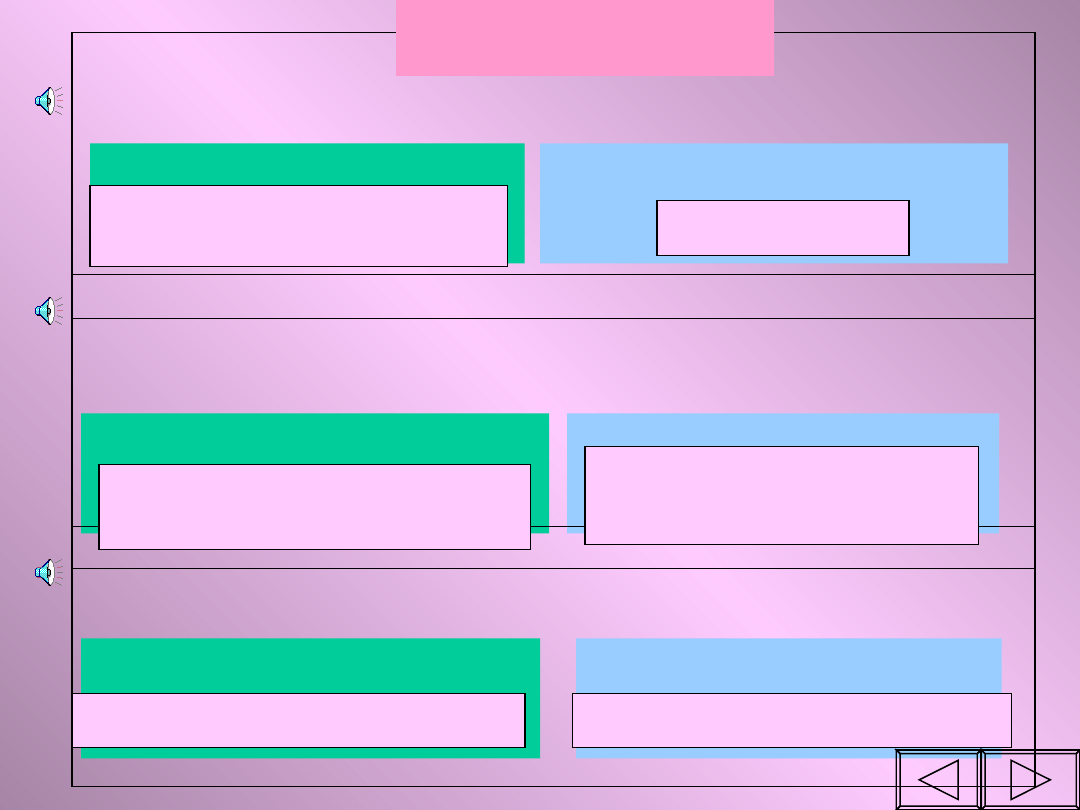
Przeciwdziedzina

Przeciwdziedzina

Przeciwdziedzina

Dziedzina

Dziedzina

Dziedzina

zbiór liczb naturalnych

.

Przykład II -

Każdej liczbie ze zbioru X = {-3,-2,-

1,0,1,2,3} przyporządkowujemy liczbę o 3

większą.

Przykład I

- Każdemu uczniowi w klasie

przyporządkowujemy pierwszą literę

imienia.

O P I S

O P I S

S Ł O W

S Ł O W

N Y

N Y

Przykład III -

Każdej liczbie naturalnej

przyporządkowujemy liczbę do niej

przeciwną.

zbiór uczniów danej

klasy

.

zbiór liter

zbiór Y =

{0,1,2,3,4,5,6}

zbiór X = {-3,-2,-

1,0,1,2,3}

zbiór liczb całkowitych

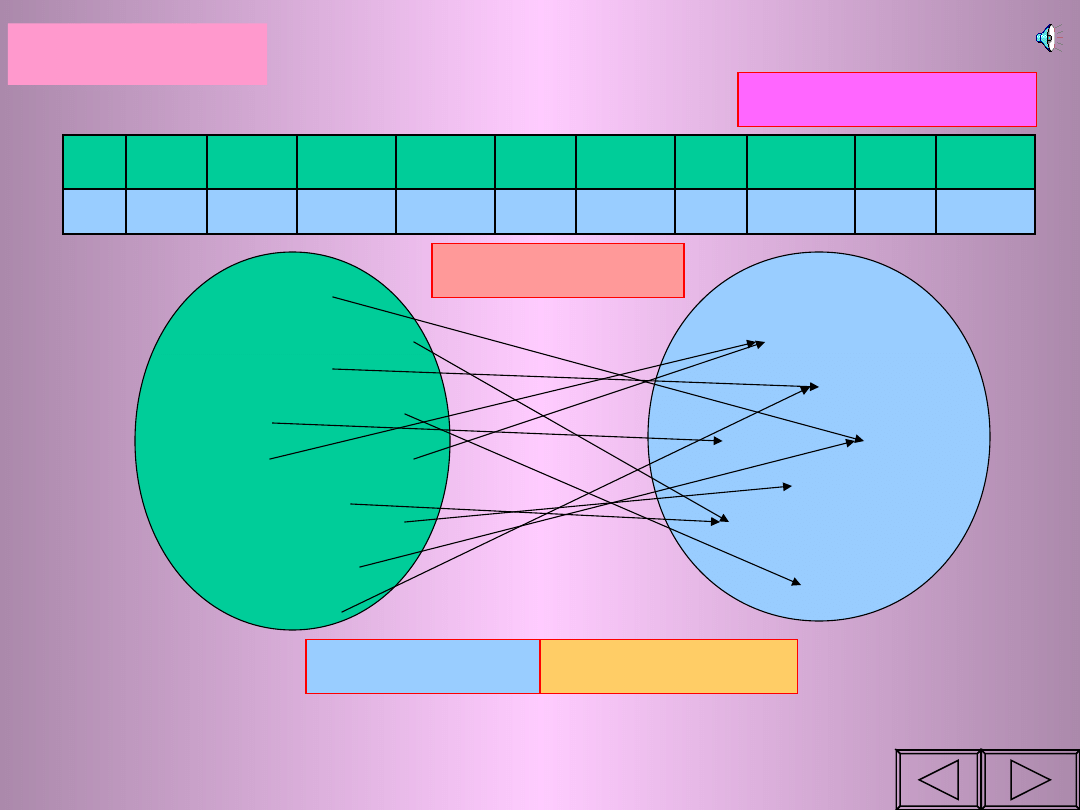
Przykład I

Przykład I

Jola Kasia Tomek Waldek Bogdan Basia Wiesiek Marta Mariusz Paweł Kamil

J K T W B B W M. M. P K

TABELA

WZÓR

GRAF

WYKRES

J

K

T

W

B

M

P

Jola

Kasia

Tomek

Waldek

Bogdan

Basia

Wiesiek

Marta

Mariusz

Paweł

Kamil

Uwaga! Tej funkcji nie da się opisać wzorem ani

wykresem ponieważ nie jest to funkcja liczbowa

Każdemu uczniowi w klasie

Każdemu uczniowi w klasie

przyporządkowujemy pierwszą literę

przyporządkowujemy pierwszą literę

imienia

imienia

.

.

f:x x+3

f(x) =

x+3

y = x+3

lu

b

lu

b

dla x € {-3,-2,-1,0,1,2,3}

Przykład II

Przykład II

TABELĄ

-3 -2 -1 0 1 2 3

0 1 2 3 4 5 6

WZOREM

WYKRESEM

Każdej liczbie ze zbioru X = {-3,-2,-

Każdej liczbie ze zbioru X = {-3,-2,-

1,0,1,2,3} przyporządkowujemy liczbę

1,0,1,2,3} przyporządkowujemy liczbę

o 3 większą.

o 3 większą.

y

(-3;0)

(-2;1)

(-1;2)

(0;3)

(1;4)

(2;5)

(3;6)

0

1

2

3

4

5

6

7

-4

-3

-2

-1

0

1

2

3

4

x

-10

-9

-8

-7

-6

-5

-4

-3

-2

-1

0

1

2

3

4

5

6

7

8

9

10

-1

0

-9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10

x

y

WZÓR

TABELA

WYKRES

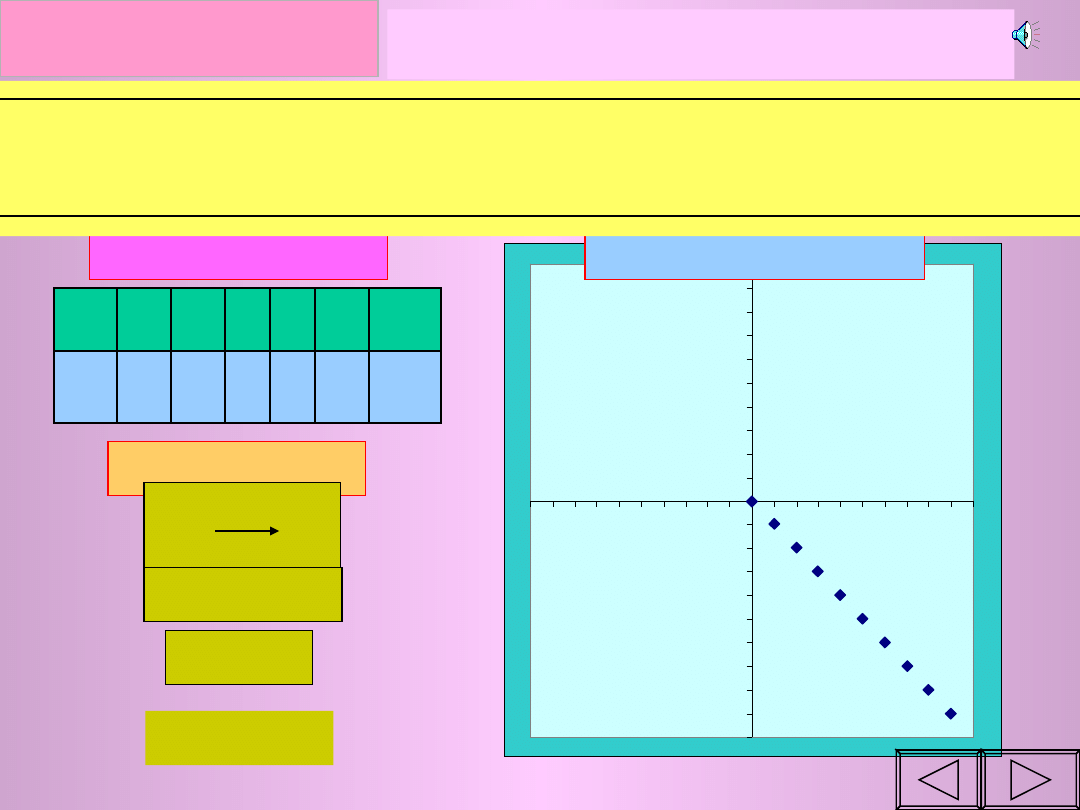
Przykład III

Przykład III

Każdej liczbie naturalnej

przyporządkowujemy liczbę do niej

przeciwną

.

Uwaga! Ponieważ dziedziną tej funkcji jest

nieskończony

zbiór

liczb naturalnych, nie można sporządzić tabeli ani grafu.
Możemy się ograniczyć do

tabeli

częściowej

(tzn. dla

kilku wybranych elementów).

x 0 1 2 3 4 5

y 0 -1 -2 -3 -4 -5

f:x -
x

f(x) = - x

y = - x

dla x € N

-6

-5

-4

-3

-2

-1

0

1

2

3

4

5

6

-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6

WYKRES

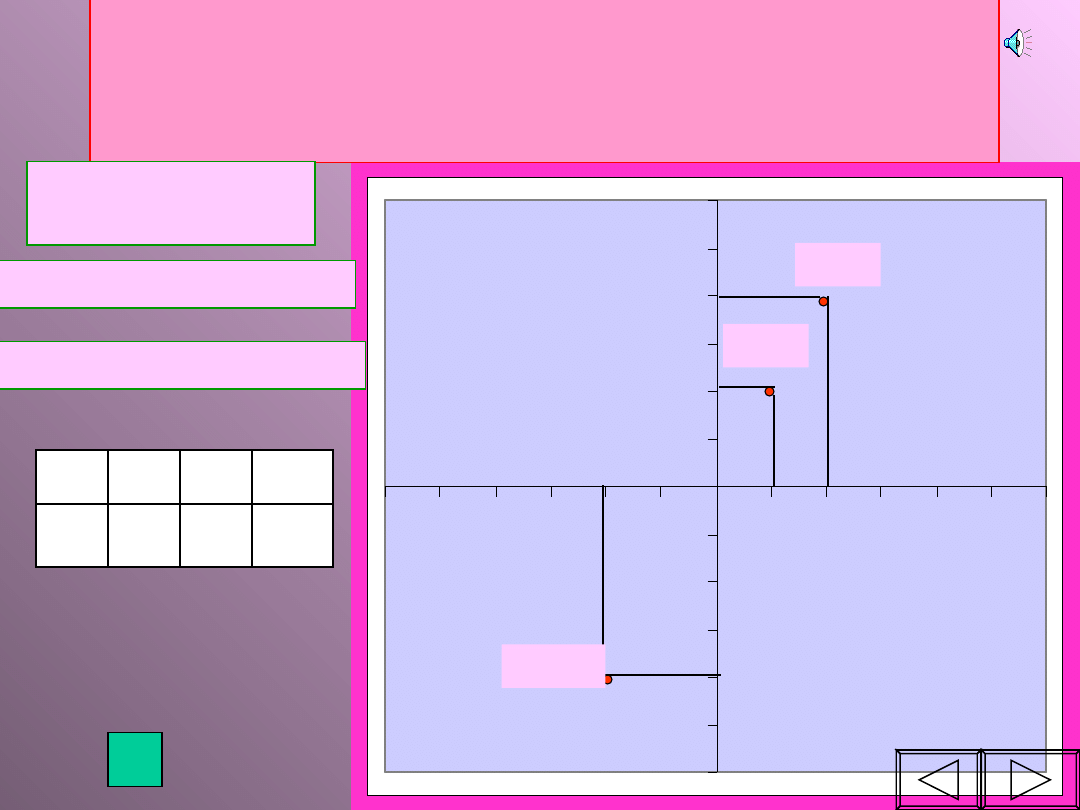
WYKRES -jest to zbiór punktów na
płaszczyźnie, których pierwsza współrzędna jest
argumentem, a druga wartością funkcji dla tego
argumentu.

(x, f(x))

(x, f(x))

y=2x

jeżeli

x = 1,

to

y

= 2

jeżeli

x = 2

,

to

y = 4

jeżeli

x = -2

, to

y = - 4

x

y

1

2

2

4

(1,2)

(2,4)

(-2,-4)

x

y

- 2

- 4

f(x) = y= 2x

wartość jest dwa
razy
większa od
argumentu

*

y=2x+1

-4

-2

0

2

4

6

8

-4

-3

-2

-1

0

1

2

3

4

x

y=2x+1

-10

-8

-6

-4

-2

0

2

4

6

8

10

12

-6 -5 -4 -3 -2 -1

0

1

2

3

4

5

6

x

y

y=2x+1

-10

-8

-6

-4

-2

0

2

4

6

8

10

12

-6

-5

-4

-3

-2

-1

0

1

2

3

4

5

6

x

y

Dziedzina funkcji

x € {1, 2, 3}

Dziedzina funkcji

x € R

Dziedzina Funkcji

x € C

f(x) = y =
2x+1
x-argument
y-wartość

Przykłady wykresów funkcji y = 2x+1 dla różnych dziedzin

WŁASNOŚCI

FUNKCJI

w

a

r

t

o

ś

c

i

a r g u m e n t y

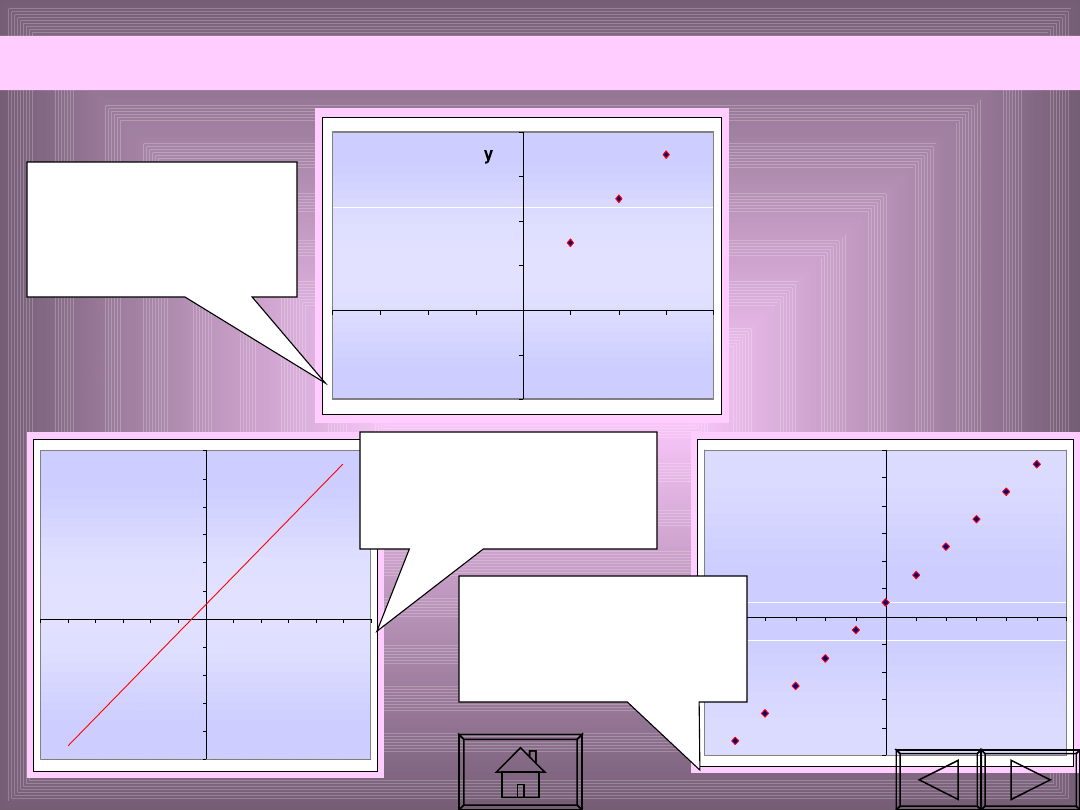
Wraz ze wzrostem
argumentów,

rosną wartości
funkcji.

y

x

X1

X2

X3

X4

X5

Y1

Y2

Y3

Y4

Y5

Jeżeli

X1 < X2

, to

Y1 < Y2.

FUNKCJA jest ROSNĄCA jeżeli wraz ze

wzrostem

argumentów

rosną

jej wartości.

*

Funkcja liniowa jest rosnąca dla a > 0.

ro

sn

ą

rosną

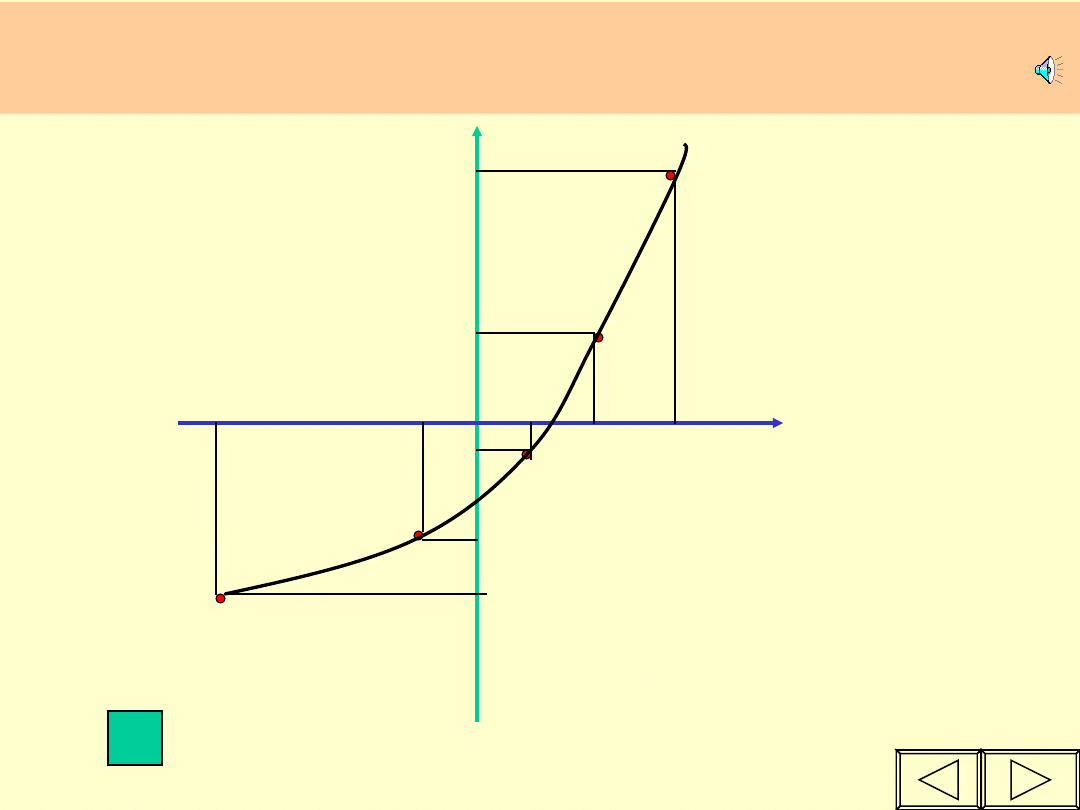
Wraz ze wzrostem
argumentów,

maleją wartości
funkcji.

a r g u m e n t y

w

a

r

t

o

ś

c

i

FUNKCJA jest MALEJĄCA jeżeli wraz ze

wzrostem

argumentów

maleją

jej wartości.

Y

x

0

x1

x2

y1

y2

Jeżeli

x1 < x2,

to

y1 > y2.

*

Funkcja liniowa jest malejąca dla a < 0.

rosną

m

a

le

ją

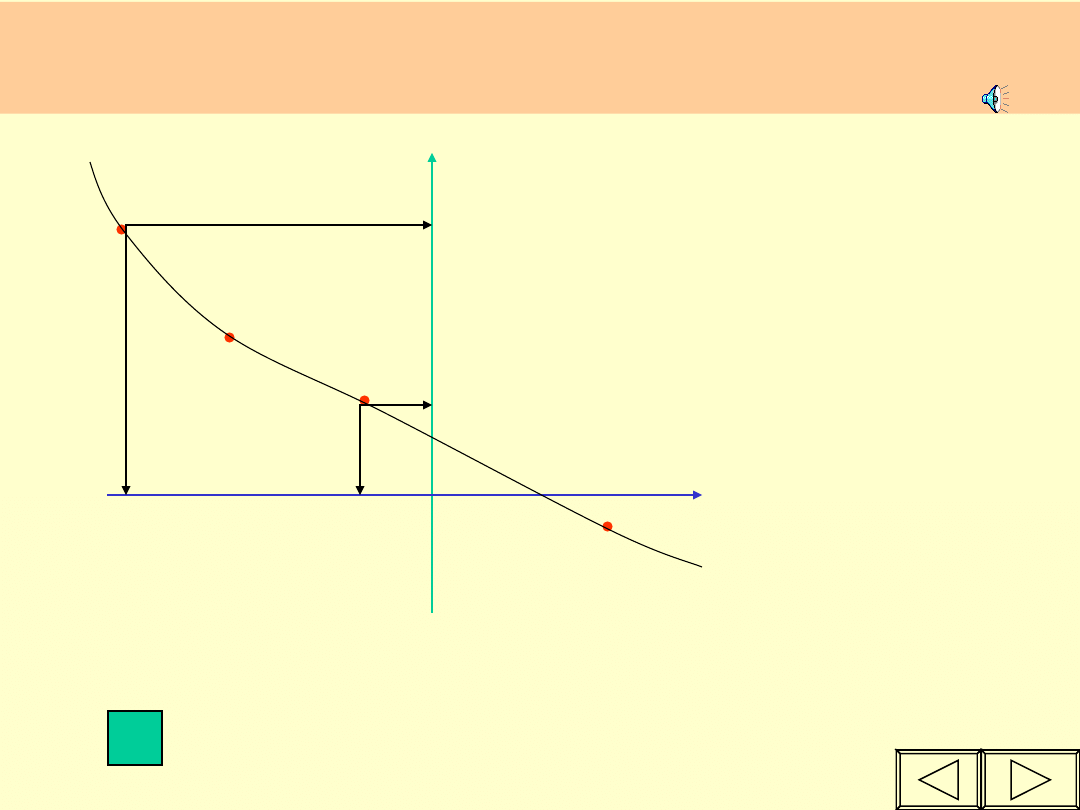
Różne
argumenty,

równe wartości funkcji.

a

r

g

u

m

e

n

t

y

w a r t o ś c i

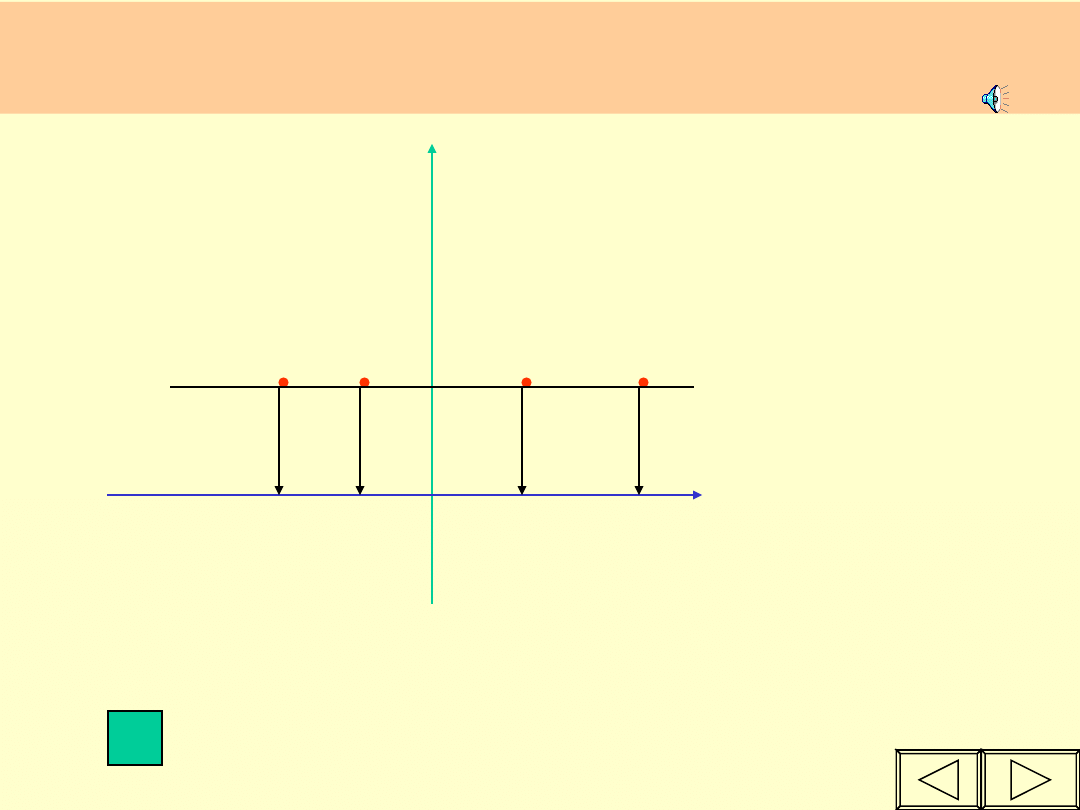
FUNKCJA jest STAŁA jeżeli

wszystkim

argumentom odpowiada

ta sama

wartość.

Y

x

0

x1

x

2

* Funkcja liniowa jest stała dla a =0.

x3

x4

y

y

y

y

y

Jeżeli x1< x2,

to y = y ( jest stały )

różne argumenty

te same wartość

-5

-4

-3

-2

-1

0

1

2

3

4

5

6

7

8

-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7

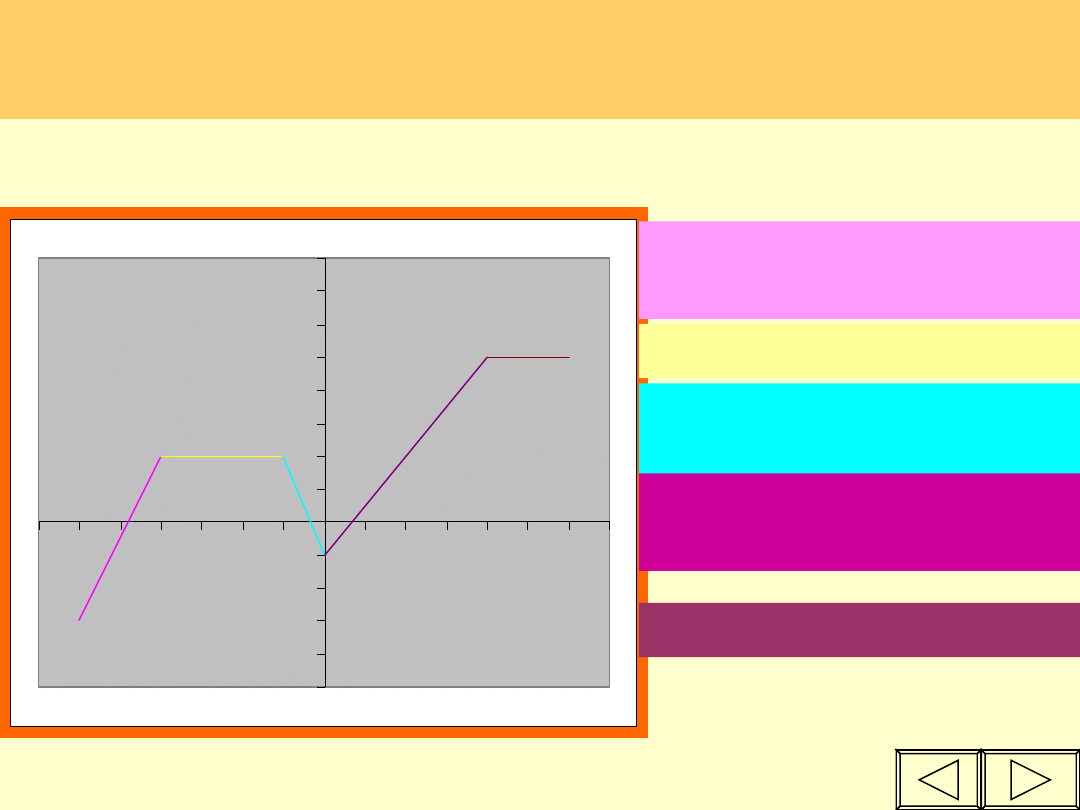
Uwaga ! Nie wszystkie funkcje są monotoniczne

(tzn. rosnące, malejące lub stałe) w całej

dziedzinie.

Ta funkcja jest przedziałami monotoniczna.

Dla x (- 6 ; - 4) -

rosnąca

Dla x (- 4 ; -1) - stała

Dla x (-1 ; 0) -

malejąca

Dla x (4 ;6 ) - stała

Dla x ( 0 ; 4 ) -

rosnąca

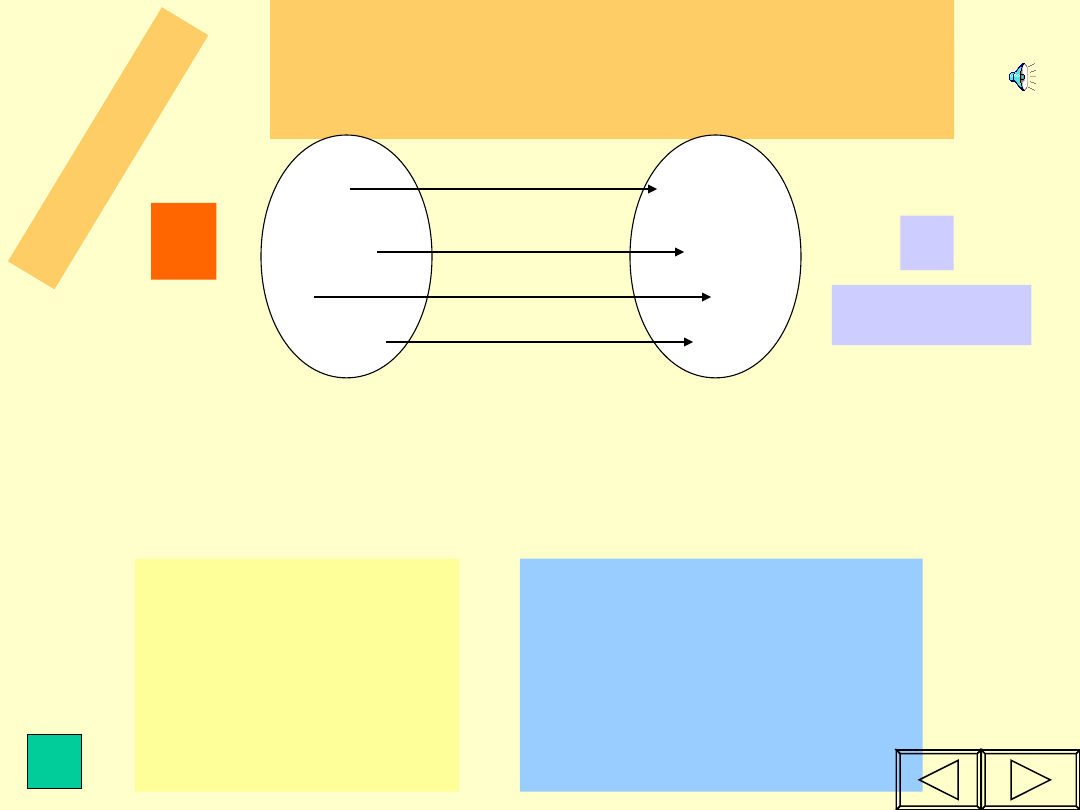
D

E

F

IN

IC

JA

Miejscem zerowym funkcji jest

argument,

dla którego wartość funkcji wynosi

0.

Liczymy

argument

x = ?

Wartość funkcji wynosi 0

y = 0

Przykłady obliczania miejsc zerowych dla funkcji
określonych wzorami:

Funkcja liniowa

y

= 2

x

- 5

0

= 2

x

- 5

2

x

= 5

x

o

= 2,5

Funkcja kwadratowa

y

=

x

2

- 9

0

=

x

2

- 9

x

2

= 9

x

o

= 3 lub

x

o

= - 3

A

B

x

o

0

x

1

x

2

x

3

y

1

y

2

y

3

f(x)

f(x

o

) = 0.

x

o

y

*

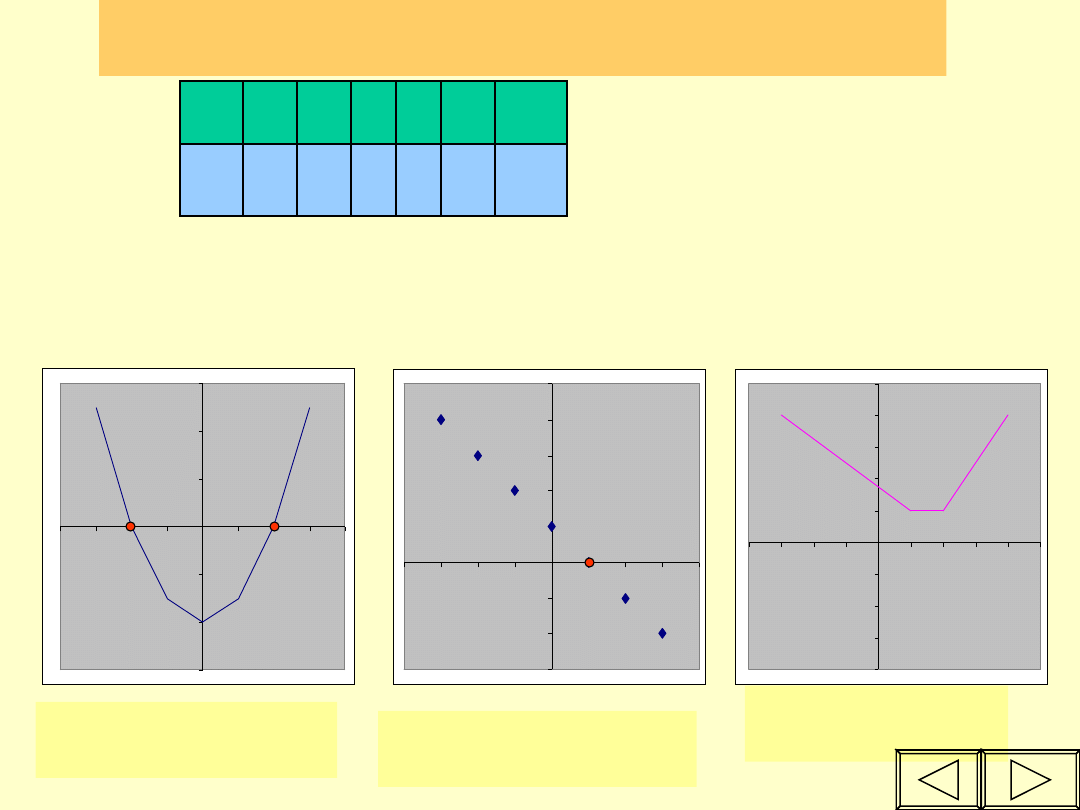
Miejsce zerowe funkcji odczytujemy z wykresu,

określając odciętą punktu przecięcia z osią OX.

-6

-4

-2

0

2

4

6

-4

-3

-2

-1

0

1

2

3

4

x

y

-6

-4

-2

0

2

4

6

8

10

-4

-3

-2

-1

0

1

2

3

4

x

y

-4

-3

-2

-1

0

1

2

3

4

5

-4 -3 -2 -1

0

1

2

3

4

5

x

y

Dwa miejsca zerowe

Xo = - 2 i Xo = 2

Jedno miejsce zerowe

Xo = 1

Brak miejsc

zerowych

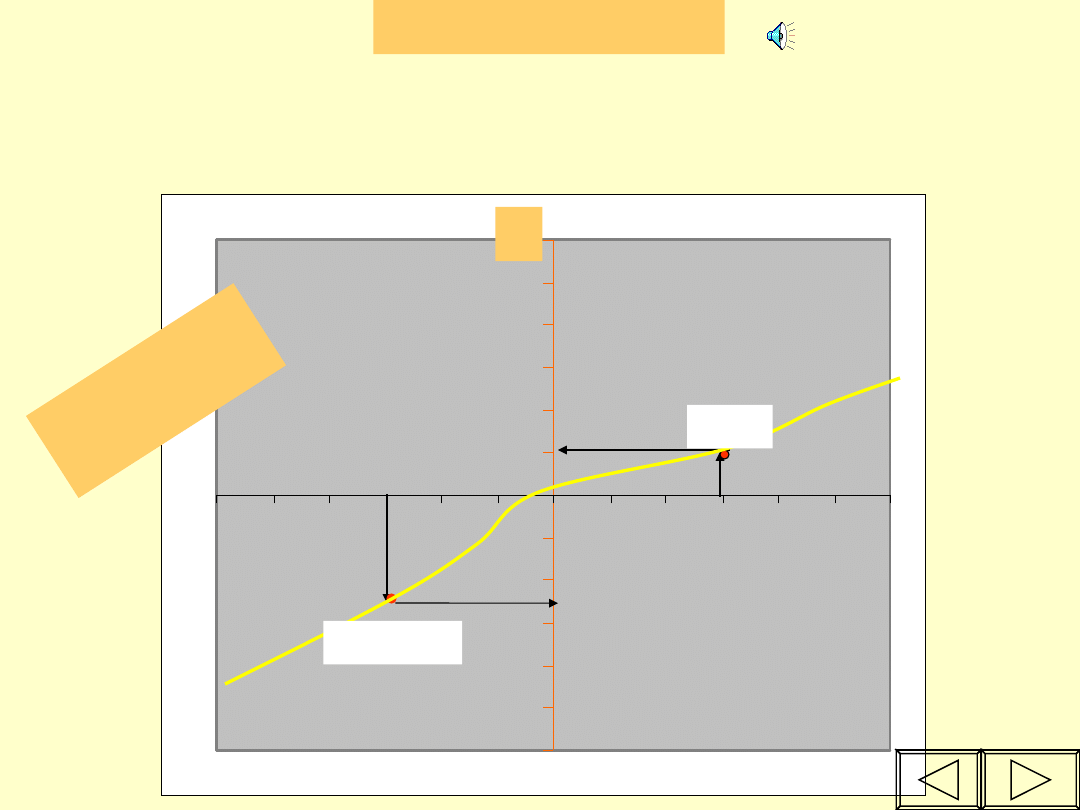
Miejsca zerowe można także odczytać z

tabeli i wykresu.

x -1 1

2

3 4 5

y -3 -1

0

-3 -4 -5

y = 0 dla

x

o

= 2

-6

-5

-4

-3

-2

-1

0

1

2

3

4

5

6

-6 -5 -4 -3 -2 -1 0

1 2

3 4

5 6

DODATNIE

UJEMNE

+

+

+

+

+

+

+

+

+

-

-

-

-

-

-

-

-

-

-

Y

Wartości funkcji

Wartości funkcji odczytujemy na osi Y.
Dla argumentu x = - 3, wartość wynosi y = -2,5,
dla argumentu x = 3, wartość wynosi y = 1.

WA

RT

OŚ

CI

f(x

) =

y

X

(- 3;-2.5)

(3,1)

-6

-5

-4

-3

-2

-1

0

1

2

3

4

5

6

-6 -5 -4 -3 -2 -1 0

1

2

3

4

5

6

DODATNIE

UJEMNE

+

+

+

+

+

+

+

+

+

-

-

-

-

-

-

-

-

-

-

JAK

IE W

AR

TO

ŚC

I ?

JA

KI

E

AR

GU

M

EN

TY

?

Dla x  ( -1.5; 2) wartości funkcji wynoszą 0.

Dla x ( -6; -1,5) wartości funkcji są ujemne.

Dla x  (2; 6) wartości funkcji są dodatnie.

*

FUNKCJA

FUNKCJA

LINIOWA

LINIOWA

I JEJ WŁASNOŚI

I JEJ WŁASNOŚI

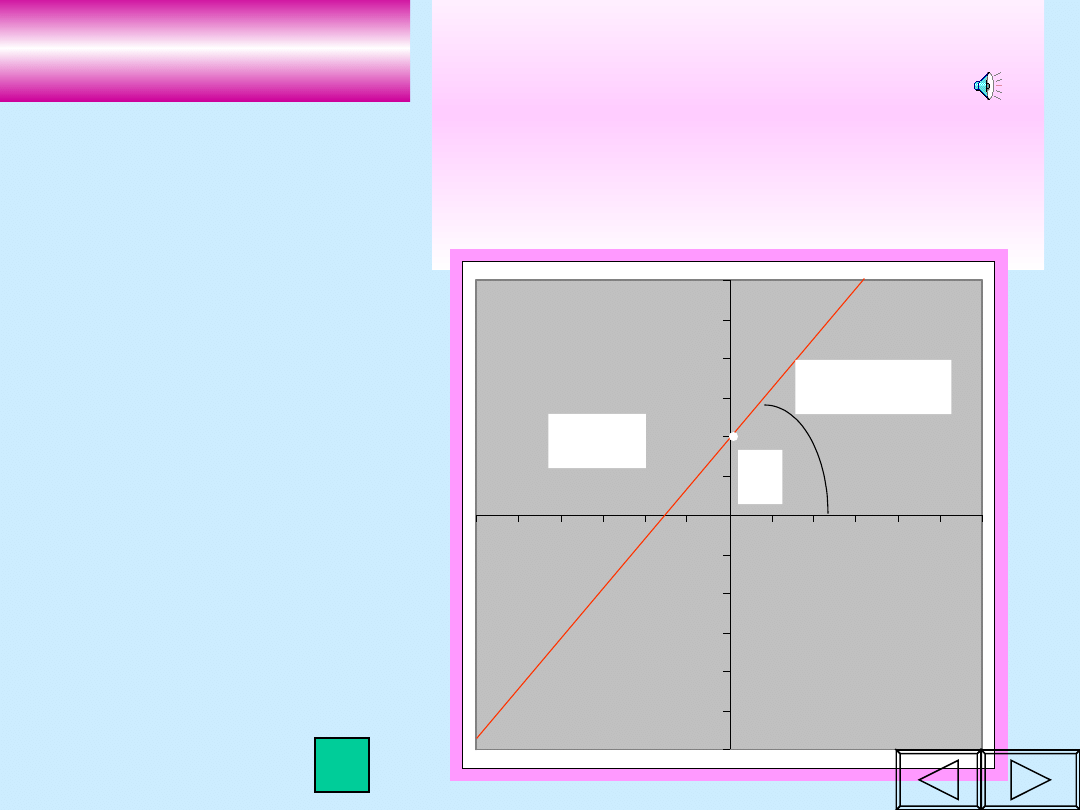
FUNKCJA LINIOWA

y =

a

x+

b

Jest to funkcja opisana
wzorem
y = ax+b, gdzie a i b są
stałymi współczynnikami
liczbowymi.
x jest argumentem, y
wartością funkcji, x R.

-Wykresem
funkcji liniowej
jest linia prosta.

-

a

nazywamy

współczynnikiem
kierunkowym

,

wskazuje on kąt
nachylenia prostej
do osi OX.

-

współczynnik b

określa punkt
przecięcia
prostej z osią OY.

-6

-5

-4

-3

-2

-1

0

1

2

3

4

5

6

-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6

x

y

a = tg

b=2



*

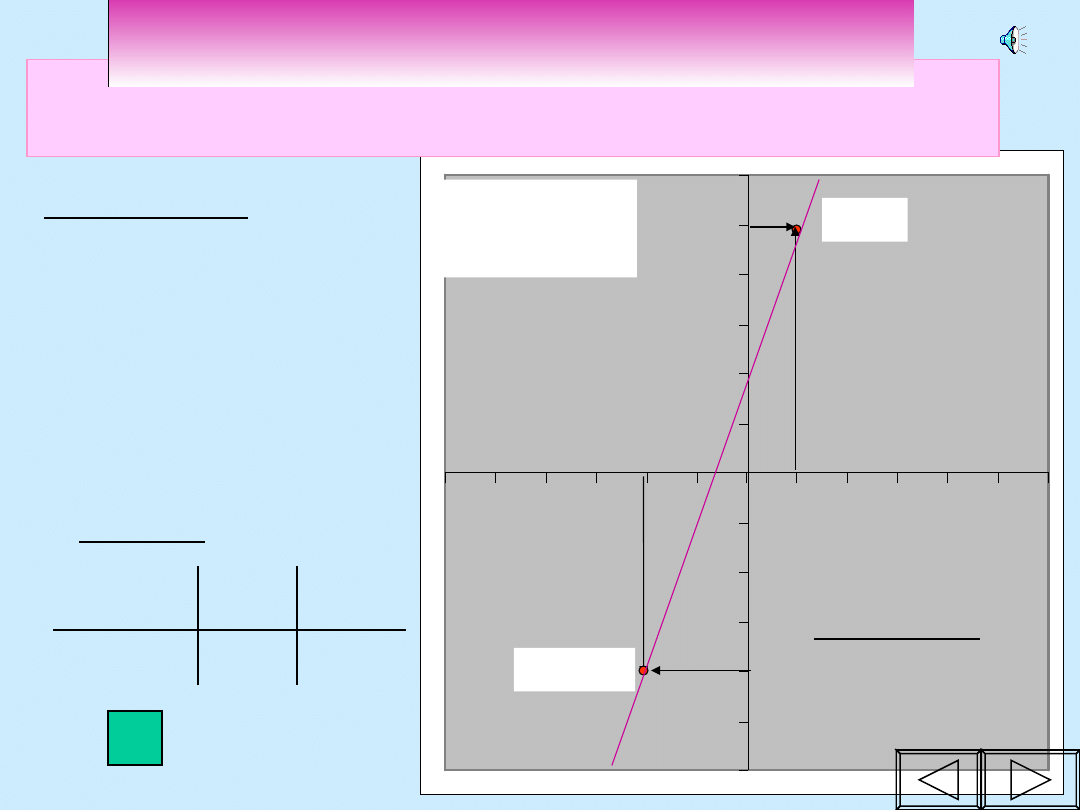
Jak rysujemy

wykres

funkcji liniowej?

-6

-5

-4

-3

-2

-1

0

1

2

3

4

5

6

-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6

Żeby narysować prostą trzeba mieć co najmniej 2

punkty

jeżeli x=1 to

y=3*1+2=5

punkt (

1

,

5

)

(1,5)

x = -2 to

y=3*(-2)+2 = - 4

punkt (

- 2

,

-4

)

y = 3x+2

(-2, -4 )

x

y=3x+2

1

-2

-4

5

OBLICZENIA

TABELA

WYKRES

Wykresem funkcji liniowej jest

linia prosta.

*

-50

-40

-30

-20

-10

0

10

20

30

40

50

-10

-8

-6

-4

-2

0

2

4

6

8

10

x

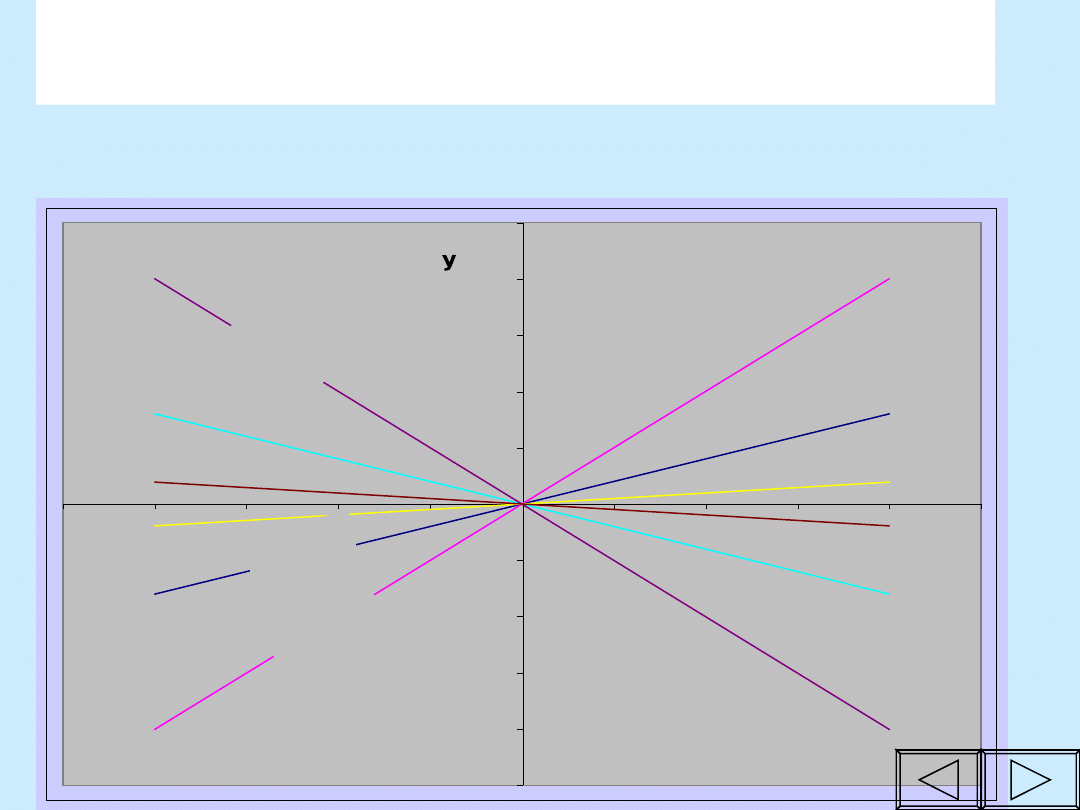
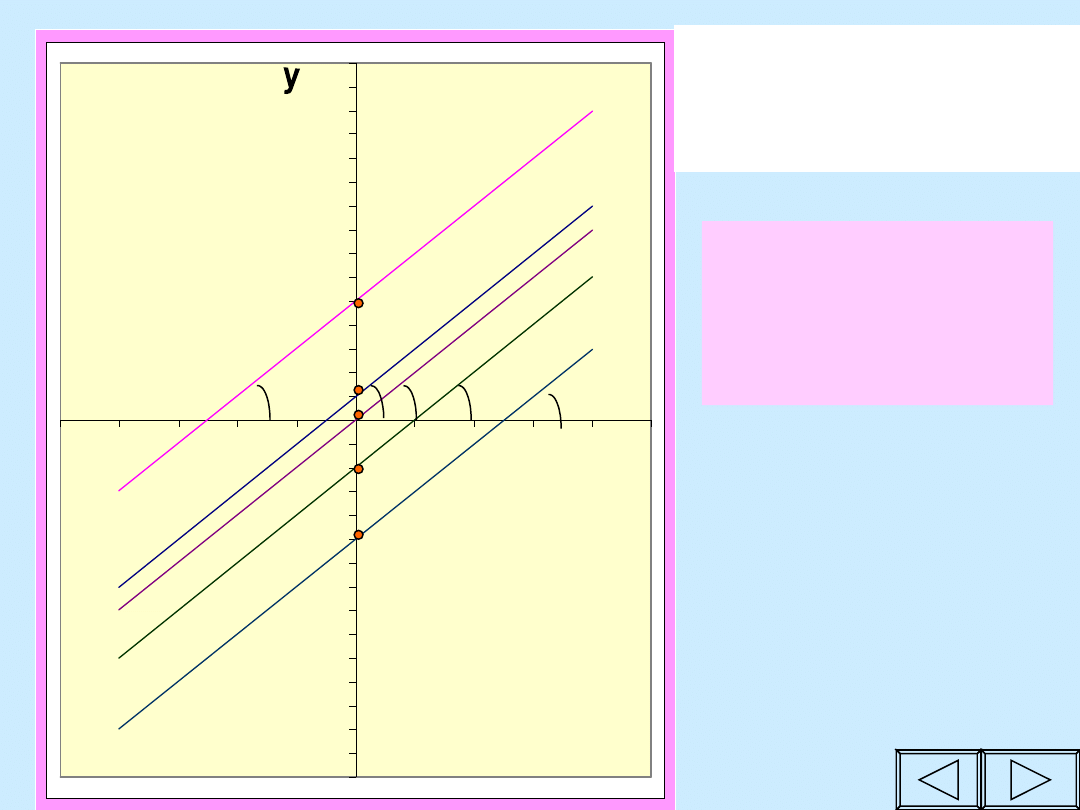
Wykresy funkcji

y = ax

w zależności od

współczynnika kierunkowego

a

. (b=0)

y =

2

x

a=

2

y =

5

x

a=5

a=1/2

y=

-2

x

a= -2

y=

-5

x

a= -5

Różne współczynniki a,

różne kąty nachylenia do osi OX

a > 0

wykres leży w

I i III ćwiartce

a < 0

wykres leży w

II i IV ćwiartce

I

III

II

IV

-30

-28

-26

-24

-22

-20

-18

-16

-14

-12

-10

-8

-6

-4

-2

0

2

4

6

8

10

12

14

16

18

20

22

24

26

28

30

-10

-8

-6

-4

-2

0

2

4

6

8

10

x

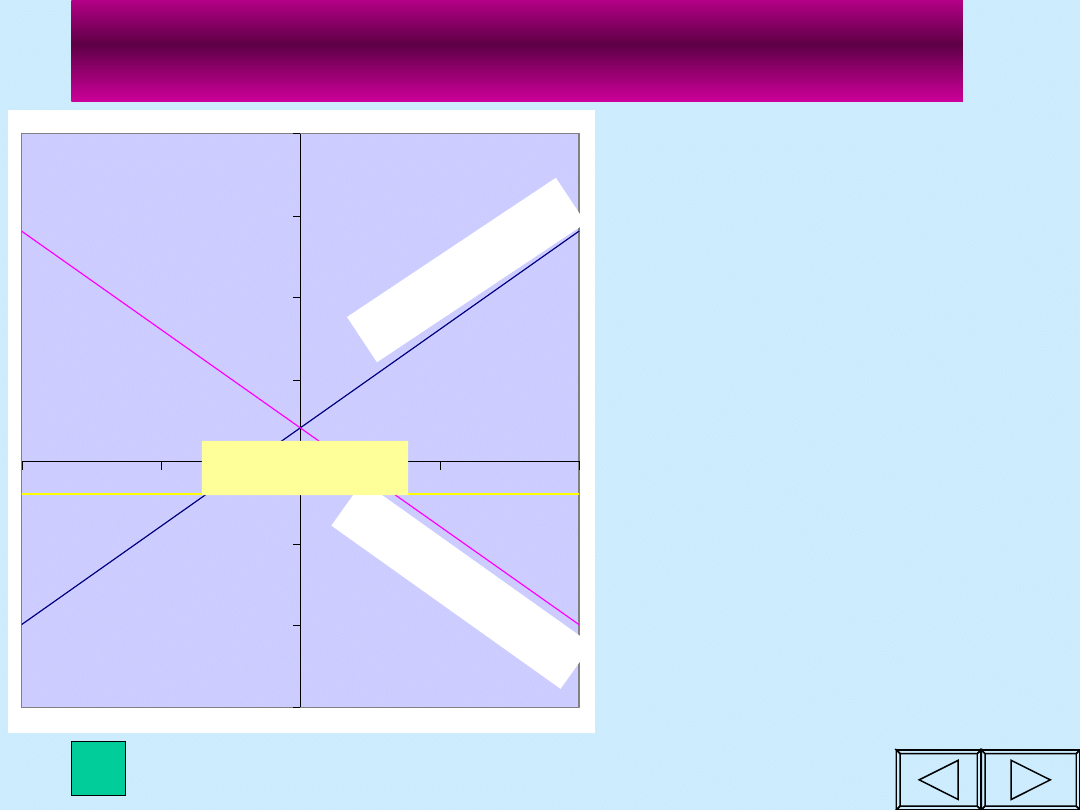
Wykresy funkcji

liniowych

y=ax+b

Współczynnik b -

wskazuje punkt

przecięcia z osią

OY (0,b)

b=10

b=2

b=

-4

b= -10

b=

0

y=

2

x+

10

y=

2

x+

2

y=

2

x

y=

2

x-

4

y=

2

x-

10

Współczynnik

kierunkowy a=2

wskazuje kąt

nachylenia prostej

do osi OX.

(ten sam kąt -

proste są

równoległe)

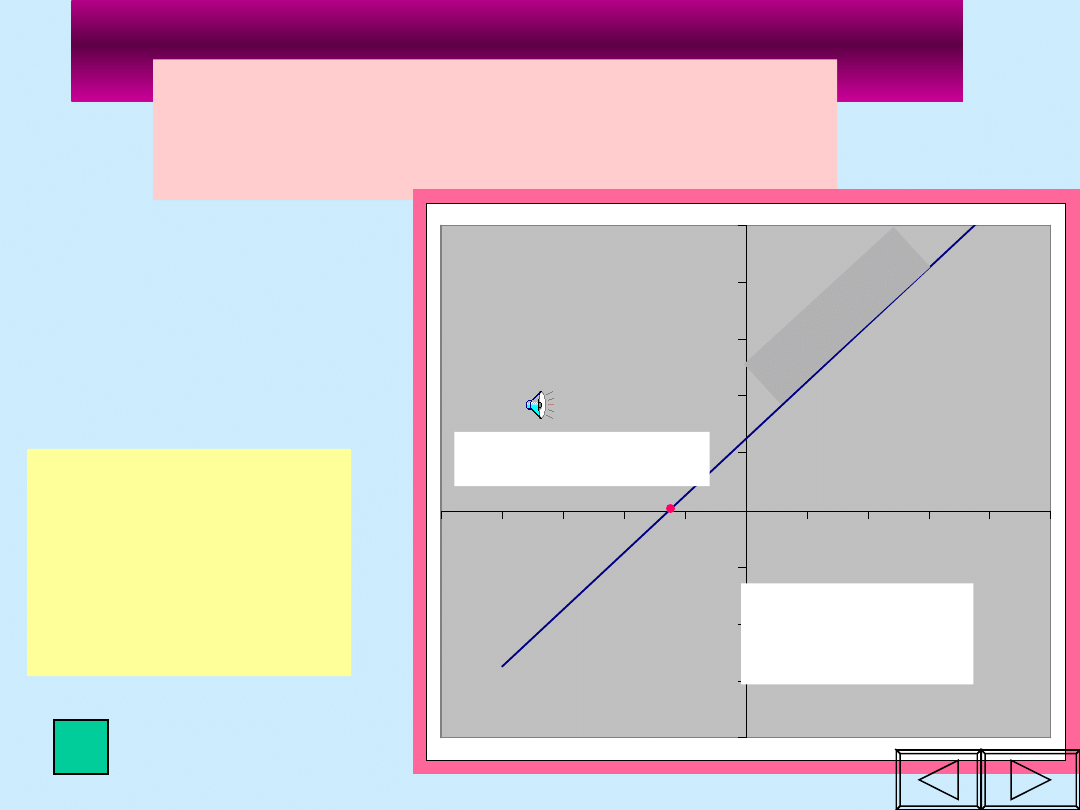
Monotoniczność funkcji liniowej y =

ax+b

-15

-10

-5

0

5

10

15

20

-4

-2

0

2

4

x

y

Funkcja liniowa jest

rosnąca,

gdy

współczynnik
kierunkowy a jest
dodatni.

np. y=

2

x+2

Funkcja liniowa jest

malejąca,

gdy

współczynnik
kierunkowy a jest
ujemny.

np. y=

-2

x+2

Funkcja liniowa jest

stała,

gdy współczynnik
kierunkowy a wynosi 0.

np. y=

0

x -2=-2

y = ax+b

ro

sn

ąc

a a

>0

m

ale

jąc

a a

<0

stała a=0

*

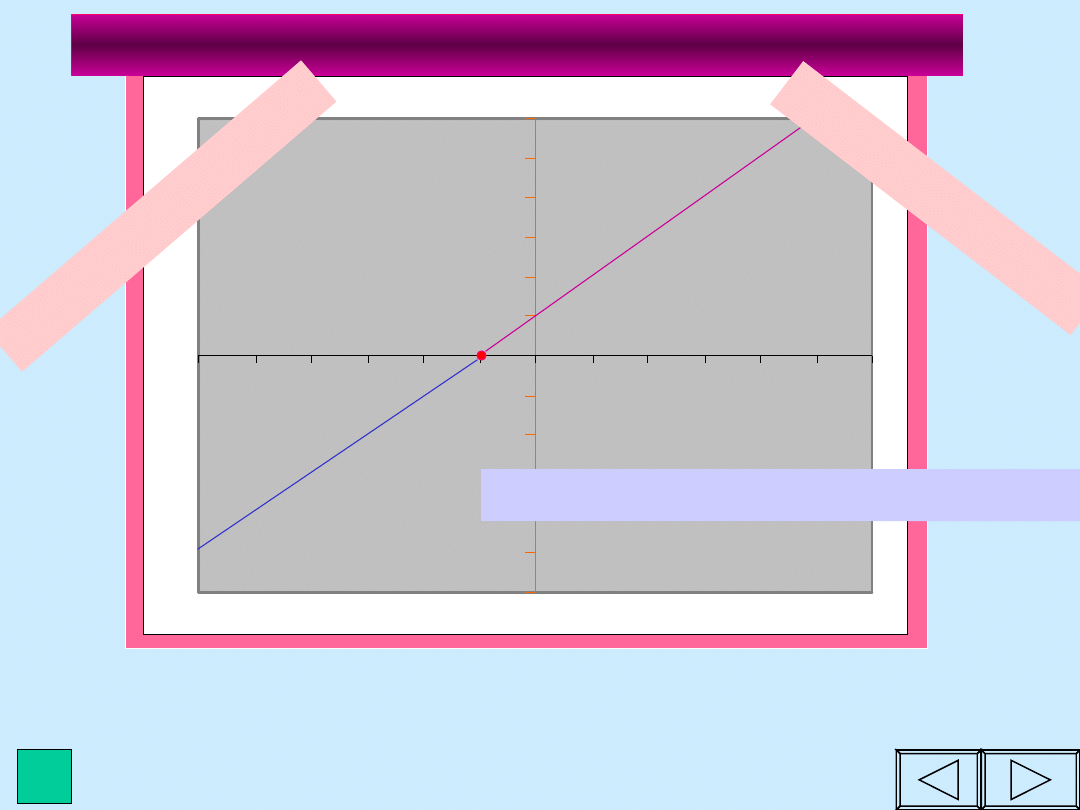
Miejsce zerowe funkcji liniowej y =

ax+b

Miejscem zerowym funkcji jest

argument, dla którego wartość

funkcji wynosi 0.

Liczymy

argument

x

o

= ?

Wartość funkcji wynosi 0

y = 0

y

= 4

x

- 5

0

= 4

x

- 5

4

x

= 5

x

= 5/4

x

= 1,25

-16

-12

-8

-4

0

4

8

12

16

20

-5

-4

-3

-2

-1

0

1

2

3

4

5

x

y

y

=

4x

+

5

A= ( 1,25; 0)

1,25

X

0

= 1,25

miejsce zerowe

*

-6

-5

-4

-3

-2

-1

0

1

2

3

4

5

6

-6 -5 -4 -3 -2 -1 0

1

2

3

4

5

6

DODATNIE

UJEMNE

Wartości funkcji liniowej y = ax+b

+

+

+

+

+

+

+ +

+

-

-

- -
- -

JAK

IE W

AR

TO

ŚC

I ?

JA

KI

E

AR

GU

M

EN

TY

?

Dla x< -1 wartości funkcji są ujemne.

Dla x > -1 wartości

funkcji

są dodatnie.

y

=

x +

1

x

o

= -1 jest miejscem zerowym funkcji.

*

Przykłady wielkości wprost proporcjonalnych

• y=4x, x-długość boku y-obwód kwadratu

• y=¶x, x-średnica okręgu y-długość okręgu

• y=nx, x-długość boku wielokąta foremnego
y-obwód wielokąta
n- liczba boków

• y=kx, x-ilość towaru y- wartość towaru
k- cena towaru

• s=vt, t-czas, s-droga,
v prędkość w ruchu jednostajnym

Wielkości x i y nazywamy wprost

proporcjonalnymi

Przykładem funkcji liniowej jest

proporcjonalność prosta

y = ax, b=0

Wykres jest prostą

przechodzącą przez

początek układu

współrzędnych

*

PRZYKŁADY

PRZYKŁADY

FUNKCJI

FUNKCJI

nieliniowych

nieliniowych

FUNKCJA KWADRATOWA

FUNKCJA KWADRATOWA

Jest to funkcja opisana wzorem y = ax

y = ax

2

2

+ b

+ b

,

,

gdzie a i b są dowolnymi liczbami

rzeczywistymi i ao.

PROPORCJONALNOŚĆ ODWROTNA

PROPORCJONALNOŚĆ ODWROTNA

Jest to funkcja opisana wzorem y = a /x

y = a /x

gdzie a jest dowolną liczbą rzeczywistą różną od 0.

MODUŁ LICZBY

MODUŁ LICZBY

Jest to funkcja opisana wzorem y = | ax+ b |

y = | ax+ b |

gdzie a i b są dowolnymi liczbami rzeczywistymi.

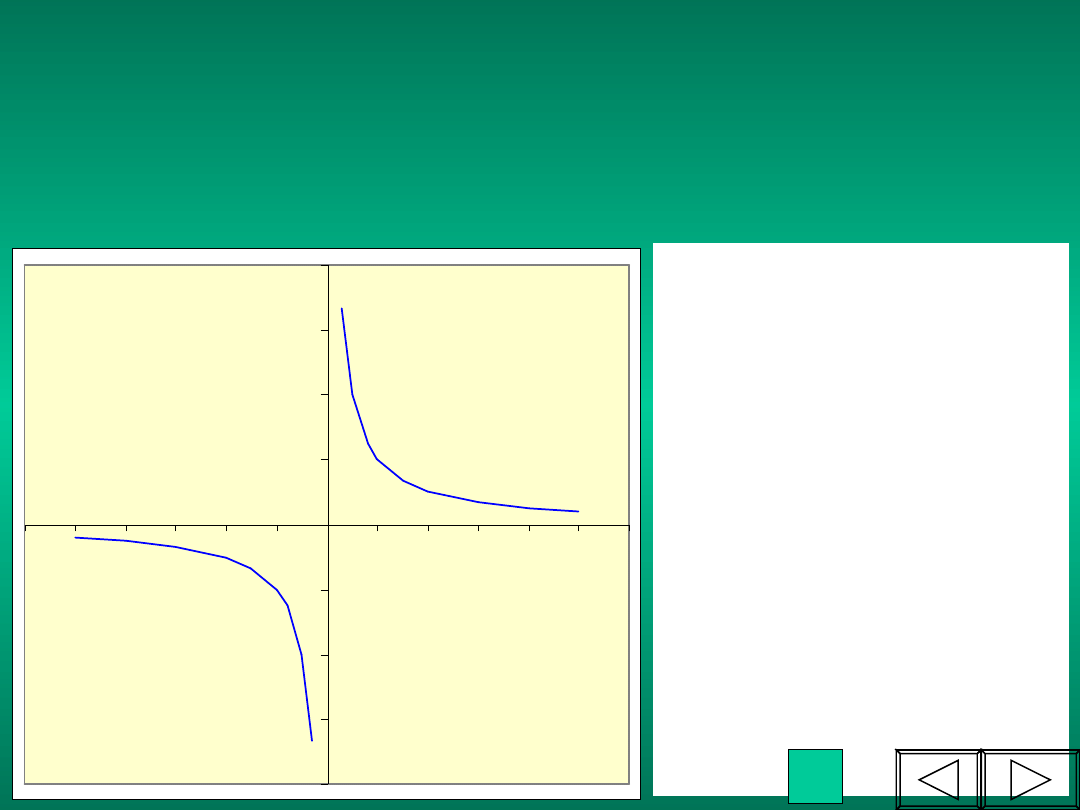
Wykresem proporcjonalności odwrotnej jest hiperbola

Wykresem proporcjonalności odwrotnej jest hiperbola

y = —

y = —

a

a

x

x

a = x•y

a = x•y

współczynnik

współczynnik

proporcjonalności

proporcjonalności

-4

-3

-2

-1

0

1

2

3

4

-6

-5

-4

-3

-2

-1

0

1

2

3

4

5

6

x

x

y

y

a

a





0

0

x i y nazywamy

x i y nazywamy

wielkościami

wielkościami

odwrotnie

odwrotnie

proporcjonalnymi.

proporcjonalnymi.

Przykładem wielkości

Przykładem wielkości

odwrotnie

odwrotnie

proporcjonalnych

proporcjonalnych

są długości

są długości

zmieniających się

zmieniających się

boków prostokąta przy

boków prostokąta przy

stałym polu.

stałym polu.

P =x•y

P =x•y

x,y -długości boków.

x,y -długości boków.

*

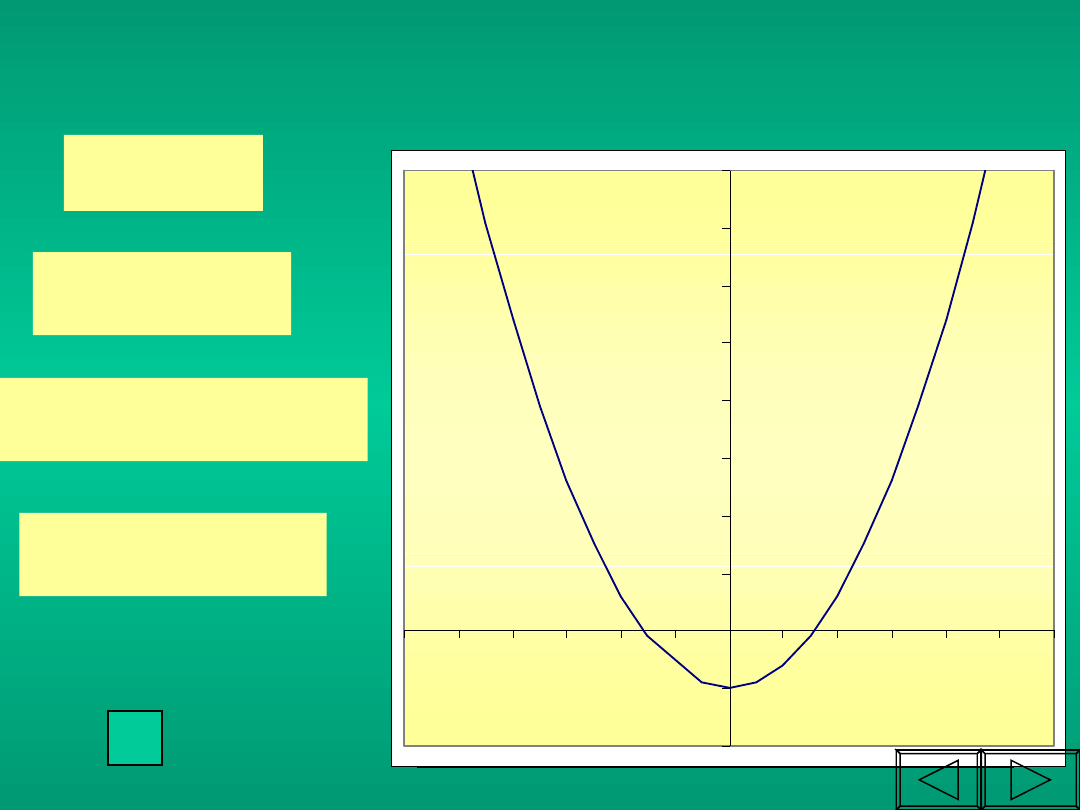
Wykresem funkcji kwadratowej jest parabola

Wykresem funkcji kwadratowej jest parabola

y= 2x

2

y = -2x

y = -2x

2

2

y = 2x

y = 2x

2

2

+10

+10

y = 2x

y = 2x

2

2

-5

-5

0

10

20

30

40

50

60

-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6

a>0

a>0

1

1

-60

-50

-40

-30

-20

-10

0

10

20

30

40

-6

-5

-4 -3

-2

-1

0

1

2

3

4

5

6

2

2

a<0

a<0

0

5

10

15

20

25

30

35

40

-6

-5

-4 -3

-2

-1

0

1

2

3

4

5

6

3

3

b=10

b=10

-10

-5

0

5

10

15

20

25

30

35

40

-6

-5

-4

-3

-2

-1

0

1

2

3

4

5

6

b=-5

b=-5

4

4

*

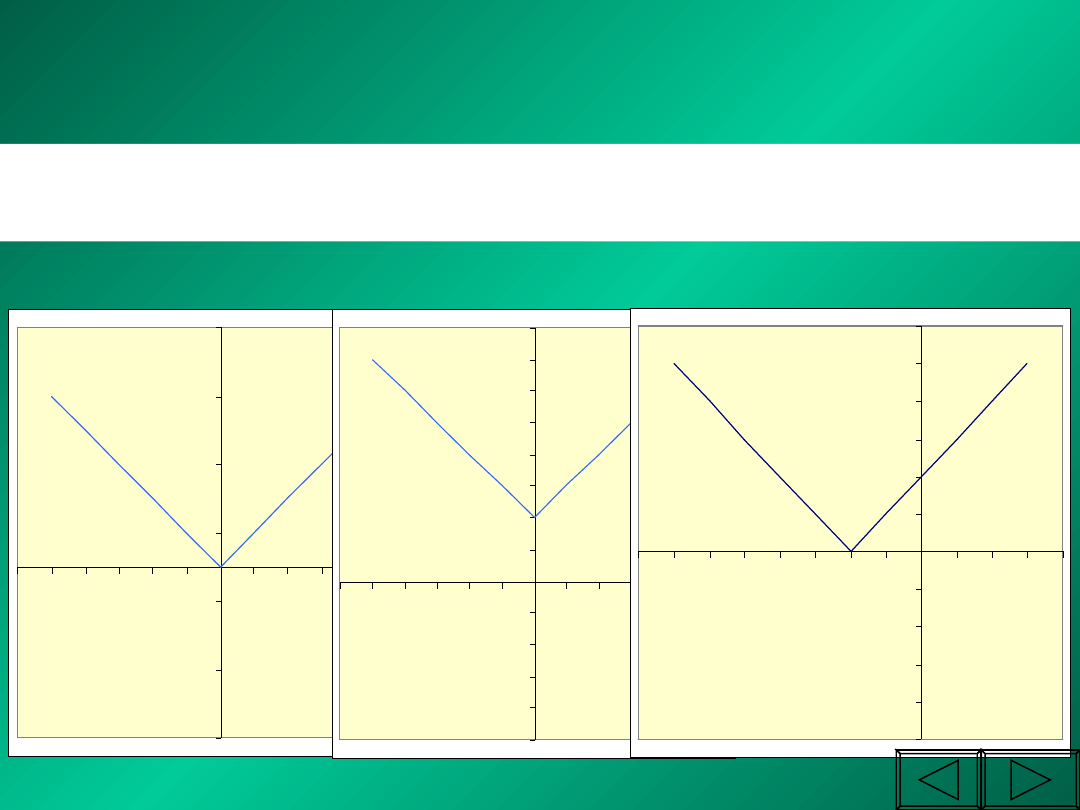
Moduł liczby to inaczej jej wartość bezwzględna.

Moduł liczby to inaczej jej wartość bezwzględna.

Moduł liczby jest zawsze liczbą nieujemną

Moduł liczby jest zawsze liczbą nieujemną

.

.

Jeżeli każdej liczbie rzeczywistej przyporządkujemy jej moduł,

Jeżeli każdej liczbie rzeczywistej przyporządkujemy jej moduł,

to otrzymujemy funkcję

to otrzymujemy funkcję y =

y =





x

x





-5

-3

-1

1

3

5

7

-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6

y =

y =





x

x





-5

-4

-3

-2

-1

0

1

2

3

4

5

6

7

8

-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6

y =

y =





x

x





+2

+2

-5

-4

-3

-2

-1

0

1

2

3

4

5

6

-8 -7 -6 -5 -4 -3 -2 -1 0

1

2 3

4

y =

y =





x+2

x+2





Dziękuję za uwagę

Koniec pokazu

D o w ie d z ie liś m y s ię

c o to je s t fu n k c ja .

U trw a liliś m y

w ła s n o ś c i fu n k c ji

P rz yp o m n ie liś m y w ia d o m o ś c i

o fu n k c ji lin io w e j

i in n yc h fu n k c ja c h

P o w tó rz yliś m y w ia d o m o ś c i

o fo n k c ji