Rachunek

prawdopodobieństwa 1

uczelnia: PJWSTK
przedmiot: Matematyka Dyskretna 2
wykładowca: dr Magdalena Kacprzak
data: grudzień 2008

Materiały pomocnicze do wykładu

Przestrzeń zdarzeń

elementarnych

Definicje

Pojedyncze wyniki doświadczenia losowego
nazywamy

zdarzeniami elementarnymi

.

Zbiór wszystkich zdarzeń elementarnych
odpowiadających pewnemu doświadczeniu
tworzy

przestrzeń zdarzeń elementarnych

,

którą oznaczamy symbolem





Przykład

Ustal przestrzeń zdarzeń elementarnych i jej

moc

1)

Zdarzenie polega na rzucie dwiema
kostkami do gry

2)

Zdarzenie polega na rzucie trzema
monetami

            

1 1

1 2

1 

2 1

2 2

2 

  





 = {(o,o,o), (o,o,r), (o,r,o),...,(r,r,r) }

|  | = 66=36

Przykład c.d.

Ocena końcowa pewnego przedmiotu zależy od
liczby punktów uzyskanych na dwóch
sprawdzianach i na egzaminie. Na każdym
sprawdzianie można uzyskać co najwyżej 20
punktów, a na egzaminie co najwyżej 60.



={(x,y,z) N

3

: x  20, y  20, z  60}.

|



 =2121 61

Zdarzenia

Definicja

Niech  będzie przestrzenią zdarzeń
elementarnych. Dowolny podzbiór A przestrzeni
zdarzeń elementarnych nazywamy

zdarzeniem

.

Powiemy, że zaszło zdarzenie A, jeśli wynikiem
doświadczenia jest zdarzenie elementarne
należące do A.

Przykład 1

Doświadczenie polega na rzucie dwiema
rozróżnialnymi kostkami sześciennymi do gry.
Wówczas  = {(i,j) : i, j = 1, 2, ...6}. Wypisz
wszystkie wyniki sprzyjające każdemu z
poniższych zdarzeń

(a) Zdarzenie A = "suma oczek na obu kostkach

wynosi 7".

A={(1,6), (2,5), (3,4), (4,3), (5,2), (6,1)}

|A|=6

Przykład 1

(b) Zdarzenie B = "suma oczek na obu

kostkach wynosi nie więcej niż 12".

(c) Zdarzenie C = "suma oczek na obu

kostkach wynosi 1".

Jest to zdarzeniem pewnym, bo każde zdarzenie
elementarne ma tę własność.

Jest to zdarzeniem niemożliwe, bo na każdej kostce
musimy wyrzucić co najmniej jedno oczko, co w sumie
daje co najmniej dwa oczka.

Przykład 2

Rozważmy doświadczenie z przykładu 1. Ile
zdarzeń elementarnych sprzyja zdarzeniu F-"liczba
oczek na pierwszej kostce jest dzielnikiem liczby
oczek na drugiej kostce"?

F={(1,1), (1,2), (1,3), (1,4), (1,5), (1,6),

(2,2), (2,4), (2,6), (3,3), (3,6), (4,4), (5,5), (6,6)}

|F|=14

Operacje na zdarzeniach

Zdarzenia identyczne

Na zdarzeniach wykonujemy takie same
operacje jak na zbiorach.

Powiemy, że dwa zdarzenia w pewnej
przestrzeni zdarzeń elementarnych



są

identyczne

, jeśli mają te same zbiory

sprzyjających zdarzeń elementarnych.

Suma zdarzeń

Sumą zdarzeń

A i B nazywamy

zdarzenie AB, któremu sprzyjają
wszystkie zdarzenia elementarne
sprzyjające zdarzeniu A lub zdarzeniu B.

Iloczyn zdarzeń

Iloczynem zdarzeń

A i B nazywamy

zdarzenie A



B, któremu sprzyjają

zdarzenia elementarne sprzyjające
zdarzeniu A i zdarzeniu B.

Zdarzenia przeciwne i

wykluczające się

Zdarzenie A'=\A nazywamy

zdarzeniem

przeciwnym

do zdarzenia A. Zdarzeniu A'

sprzyjają tylko te zdarzenia elementarne
rozważanej przestrzeni, które nie należą do A.

Powiemy, że dwa

zdarzenia

A i B

wykluczają

się

(albo są rozłączne) wtedy i tylko wtedy,

gdy AB=.

Przykład 1

Doświadczenie polega na rzucie dwiema
rozróżnialnymi kostkami sześciennymi do gry.
Zdarzenie A - "suma oczek na obu kostkach
wynosi 7". Zdarzenie D –"co najmniej raz
wyrzucono 5". Wyznacz Iloczyn zdarzeń A i
D oraz zdarzenie przeciwne do zdarzenia D.

A={(1,6), (2,5), (3,4), (4,3), (5,2), (6,1)},

D={(5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (1,5), (2,5), (3,5), (4,5), (6,5)}

AD={(2,5), (5,2)}, |AD|=2

D’={(1,1), (1,2),...,(1,4), (1,6),...(6,6)}, |D’|=25

Przykład 2

Niech będzie urna z 52 kartami. Rozważamy doświadczenie
polegające na wylosowaniu kolejno 2 kart, z tym, że po
wylosowaniu karty wkładamy ją znów do urny (losowanie ze
zwracaniem). Zdarzenia
A - "wylosowano za każdym razem asa" i
B = "za drugim razem wylosowano dziesiątkę"
są zdarzeniami

wyłączającymi się

. Nie ma takich zdarzeń

elementarnych, które sprzyjają równocześnie obu
zdarzeniom. Natomiast zdarzenie, które jest sumą zdarzeń
A i B ma

?????????

zdarzeń sprzyjających.

Przykład 2

Niech będzie urna z 52 kartami. Rozważamy doświadczenie
polegające na wylosowaniu kolejno 2 kart, z tym, że po
wylosowaniu karty wkładamy ją znów do urny (losowanie ze
zwracaniem). Zdarzenia
A - "wylosowano za każdym razem asa" i
B = "za drugim razem wylosowano dziesiątkę"
są zdarzeniami

wyłączającymi się

. Nie ma takich zdarzeń

elementarnych, które sprzyjają równocześnie obu
zdarzeniom. Natomiast zdarzenie, które jest sumą zdarzeń
A i B ma

44+524

zdarzeń sprzyjających.

Prawdopodobieństwo

Definicja (Kołmogorow 19)

Niech  oznacza skończoną przestrzeń zdarzeń
elementarnych.

Prawdopodobieństwem

nazywamy

funkcję P określoną na zdarzeniach taką, że

(1) P(A)  0 dla dowolnego zdarzenia A,
(2) P(AB) = P(A) + P(B) dla dowolnych,

wykluczających się zdarzeń A, B
(3) P() = 1.

Wniosek: 0P(A)1

Lemat

Jeżeli zdarzenia A

1

, A

2

, ..., A

n

, określone w

pewnej przestrzeni zdarzeń elementarnych

,

wykluczają się parami, to

P(A

1

...A

n

)=P(A

1

)+P(A

2

)+...+P(A

n

).

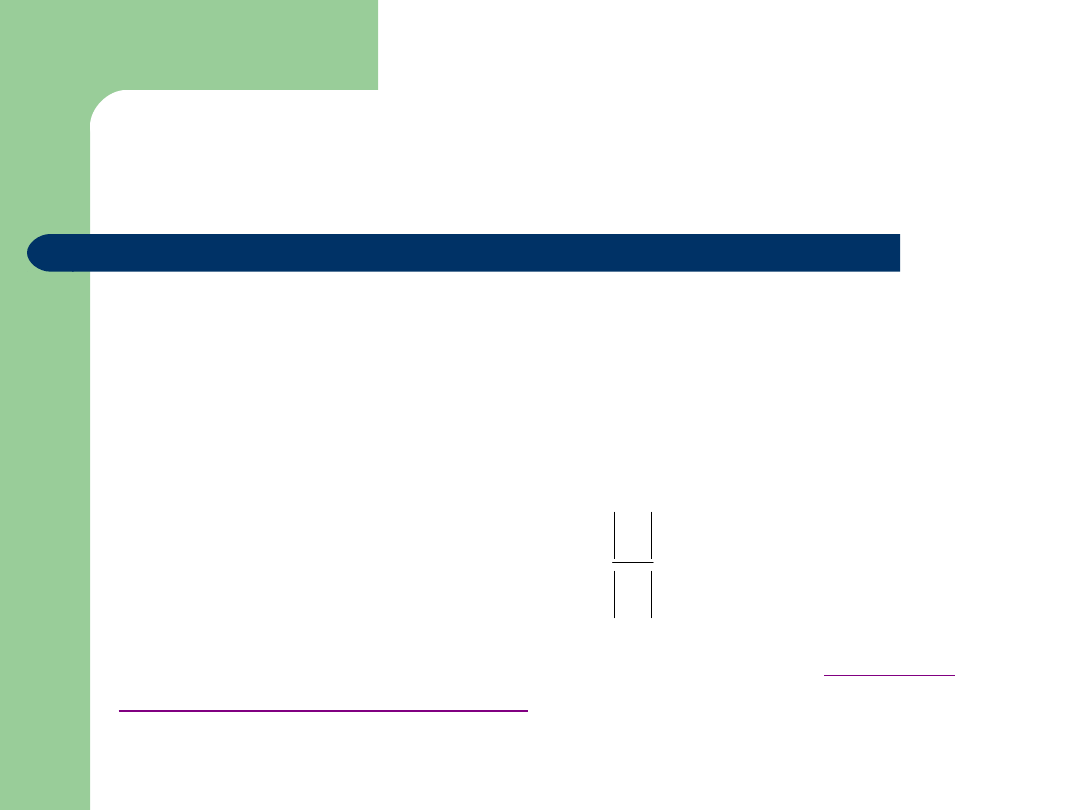
Twierdzenie

Prawdopodobieństwo zdarzenia A   jest ilorazem
liczby zdarzeń elementarnych sprzyjających zdarzeniu A

i

liczby zdarzeń elementarnych rozważanej skończonej
przestrzeni , o ile zdarzenia elementarne są tak samo
prawdopodobne, tzn.

Wzór zawarty w powyższym twierdzeniu nazywa się

klasyczną

definicją prawdopodobieństwa

, a został on sformułowany przez

Laplace'a.

Ω

A

P(A)

Przykład 1

Rzucamy 10 razy monetą. Jakie jest
prawdopodobieństwo, że w dziesięciu
rzutach dokładnie 4 razy pojawi się orzeł?

Przykład 1

Rzucamy 10 razy monetą. Jakie jest
prawdopodobieństwo, że w dziesięciu
rzutach dokładnie 4 razy pojawi się orzeł?

|| = 2

10

=1024

|A| = = 210

P(A) = 210/1024

4

10

C

Własności

prawdopodobieństwa

Niech  będzie przestrzenią zdarzeń
elementarnych, a A i B dowolnymi zdarzeniami.
Wtedy

–

P() = 0,

–

jeżeli A  B, to P(A)  P(B),

–

dla każdego A  , P(A)  1,

–

P(A') =1 - P(A),

–

P(A  B) = P(A) + P(B) - P(A  B).

Dowód

(a) Ponieważ prawdopodobieństwo zdarzenia pewnego wynosi

1, a zdarzenie puste wyklucza się ze zdarzeniem

pewnym, zatem P() + P() = P(  ) = P() = 1. Czyli

musi być P() = 0.

(b) Jeżeli A  B, to B = (B\A)  A oraz (B\A)  A = 

W konsekwencji definicji prawdopodobieństwa mamy P(B)

= P((B\A)  A ) = P(B\A) + P(A). Ponieważ
P(A)  0 i P(B\A)  0, zatem P(A)  P(B).

(c) Natychmiastowa konsekwencja punktu (b) i definicji

prawdopodobieństwa.

Dowód c.d.

(d) Ponieważ 1 = P() = P(A  A') = P(A) + P(A'),

więc P(A') =1 - P(A).

(e) Z praw teorii mnogości, dla dowolnych zbiorów

A i B mamy A  B = A  B\A = B\A  A\B oraz

A  B\A =  , B\A  A\B = . Wynika stąd, na

mocy definicji prawdopodobieństwa, że

P(AB)=P(A)+P(B\A), P(B)=P(B\A)+P(AB).

Stąd P(AB)=P(A)+P(B)- P(AB).

Przykład 1

Rozpatrzymy ilość (dm

3

) wody jaką może mieć do

przeprowadzenia w ciągu sekundy betonowy przepust.
Dotychczasowe obserwacje pozwalają przyjąć, że

(1)

maksymalna możliwa ilośc wody wynosi 300 dm

3

/s.

(2)

P(A) – prawdopodobieństwo, że ilość wody (na sekundę)

przyjmie wartość z przedziału (125,250] wynosi 0,6,

(3)

P(B) - prawdopodobieństwo, że ilość wody (na sekundę)

przyjmie wartość z przedziału (200,300] wynosi 0,7 oraz

(4)

P(AB)=0,8.

Obliczyć P(A’), P(AB), P(A’B’), P(A’B).

Przykład 1

(a)

P(A’)=1-0,6=0,4

(b)

P(AB)=P(A)+P(B)-P(AB)=0,6+0,7-0,8=0,5

(c)

P(A’B’)=P((AB)’)=1-P(AB)=1-0,8=0,2

(d)

P(A’B)=P(A\B)=P(A)-P(AB)=0,7-0,5=0,2

Przykład 2

Udowodnij, że P(A\B)P(A)-P(B).

Dowód: Najpierw zauważmy, że ABB. Zatem

P(AB)P(B). Stąd -P(AB)  -P(B).

Teraz mamy:
P(A\B)=P(A-(AB))=P(A)-P(AB)  P(A)-P(B).

Prawdopodobieństwo

warunkowe

Definicja

Prawdopodobieństwo zajścia zdarzenia A

pod warunkiem, że

zaszło zdarzenie B,

oznaczane

P(A|B)

, wyraża się wzorem:

P(A|B) = P(AB)/P(B) o ile P(B)>0.

Przykład

Z talii 52 kart losujemy 5 kart. Oblicz
prawdopodobieństwo wylosowania 2 kierów, jeżeli
wiadomo, że wśród wylosowanych kart nie ma

kolorów

pik i trefl.

A - zdarzenie polegające na wylosowaniu 2 kierów,
B - zdarzenie polegające na wylosowaniu kart wśród

których nie ma kolorów pik i trefl

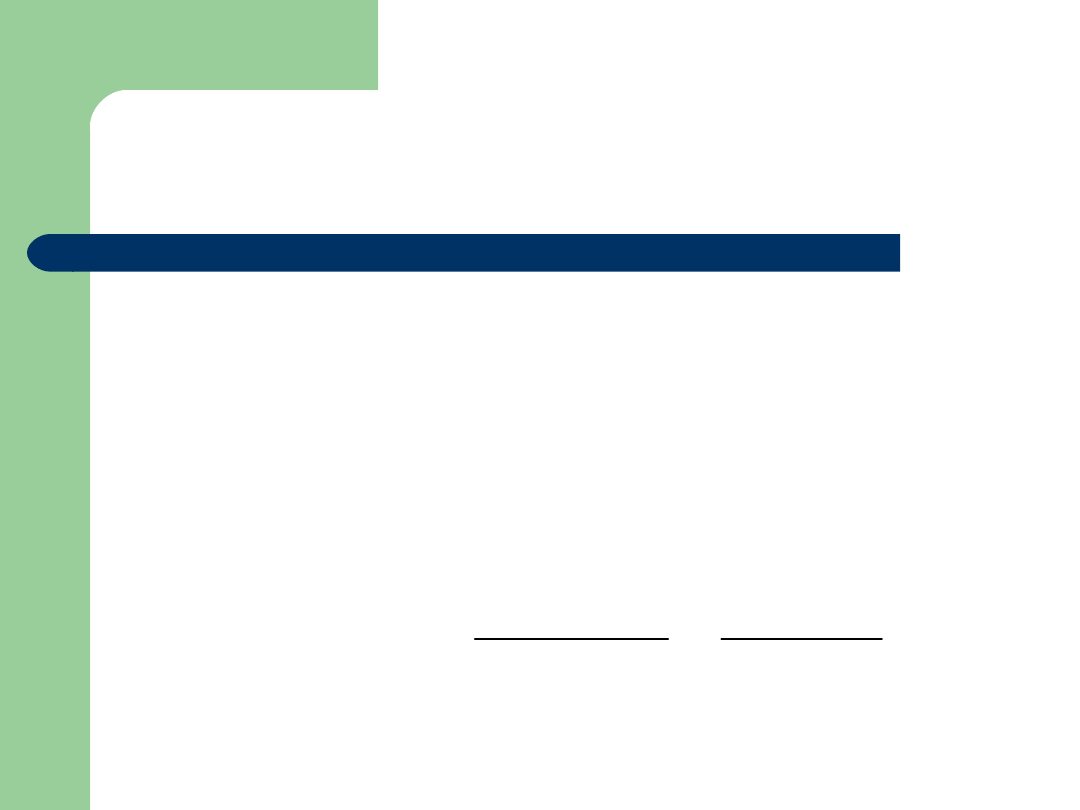
Przykład

5

26

3

13

2

13

3

13

2

13

5

26

5
52

C

C

C

)

B

(

P

)

B

A

(

P

)

B

/

A

(

P

C

C

|

B

A

|

C

|

B

|

C

|

|





















Niezależność zdarzeń

Definicja

Zdarzenia A i B nazywamy

niezależnymi

,

jeśli prawdopodobieństwo iloczynu zdarzeń jest
równe iloczynowi prawdopodobieństw tych
zdarzeń

P(AB) = P(A)P(B).

Definicja

Niech będzie dany ciąg zdarzeń losowych
A

1

,...,A

n

w pewnej przestrzeni . Powiemy, że

zdarzenia te są

niezależne

wtedy i tylko wtedy,

gdy dla dowolnego podciągu i

1

,..., i

k

ciągu 1,...,n,

P(A

i

1

 ...  A

i

k

) = P(A

i

1

)  ... P(A

i

k

).

Lemat

Jeżeli zdarzenia A i B są niezależne, to
zdarzenia A i B' też są niezależne.

Przykład-zadanie Bernsteina

3 ściany czworościanu zostały pomalowane na biało,
czerwono i zielono, zaś czwarta – w pasy biało-czerwono-
zielone. Doświadczenie polega na rzucaniu czworościanu
na płaszczyznę i obserwowaniu koloru ściany, na którą
upadł czworościan. Zdarzenia B, C, Z określone są
następująco:

B – czworościan upadł na ścianę z kolorem białym,

C – czworościan upadł na ścianę z kolorem czerwonym,

Z – czworościan upadł na ścianę z kolorem zielonym.

Zbadać, czy zdarzenia B, C, Z są (a) niezależne parami,
(b) niezależne wzajemnie.

Przykład-zadanie Bernsteina

P(B)=2/4, P(C)=2/4, P(Z)=2/4
P(BC)= P(BZ)=P(CZ)=1/4

(a) P(BC)=1/4, P(B)  P(C) = 2/4  2/4 = 1/4, stąd
P(BC) = P(B)  P(C), czyli zdarzenia B i C są

niezależne. Podobnie dla zdarzeń B i Z oraz C i Z.

(b) P(BCZ) = 1/4, P(B)P(C)P(Z) =1/2  1/2  1/2=1/8,

stąd P(BC)  P(B)  P(C)  P(Z), czyli zdarzenia
B,C i Z nie są niezależne.

Prawdopodobieństwo

całkowite

Twierdzenie

Jeżeli zdarzenia losowe A

1

,..., A

n

stanowią podział

przestrzeni zdarzeń elementarnych , oraz
P(A

i

)>0, dla i =1,2...n to dla dowolnego zdarzenia

B

w tej przestrzeni zachodzi równość:

P(B)=P(A

1

)P(B|A

1

)+P(A

2

)P(B|A

2

)+...+P(A

n

)P(B|A

n

).

Wzór Bayesa

Twierdzenie

Niech zdarzenia losowe A

1

,...A

n

stanowią podział

przestrzeni zdarzeń elementarnych , oraz
P(A

i

)>0 dla i =1,2...n. Wtedy dla dowolnego

zdarzenia B zachodzi wzór, zwany

wzorem

Bayesa

:

P(B|A

i

)P(A

i

)

P(A

i

|B) =

P(A

1

)P(B|A

1

)+P(A

2

)P(B|A

2

)+...+P(A

n

)P(B|A

n

)

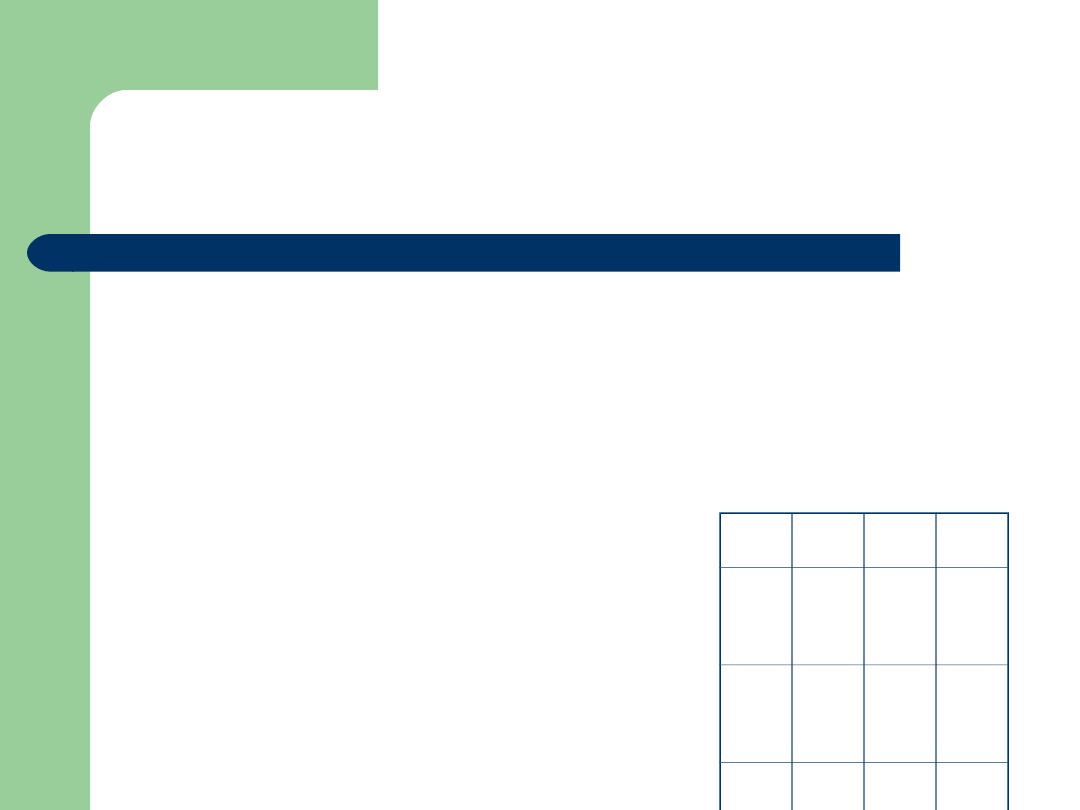
Przykład

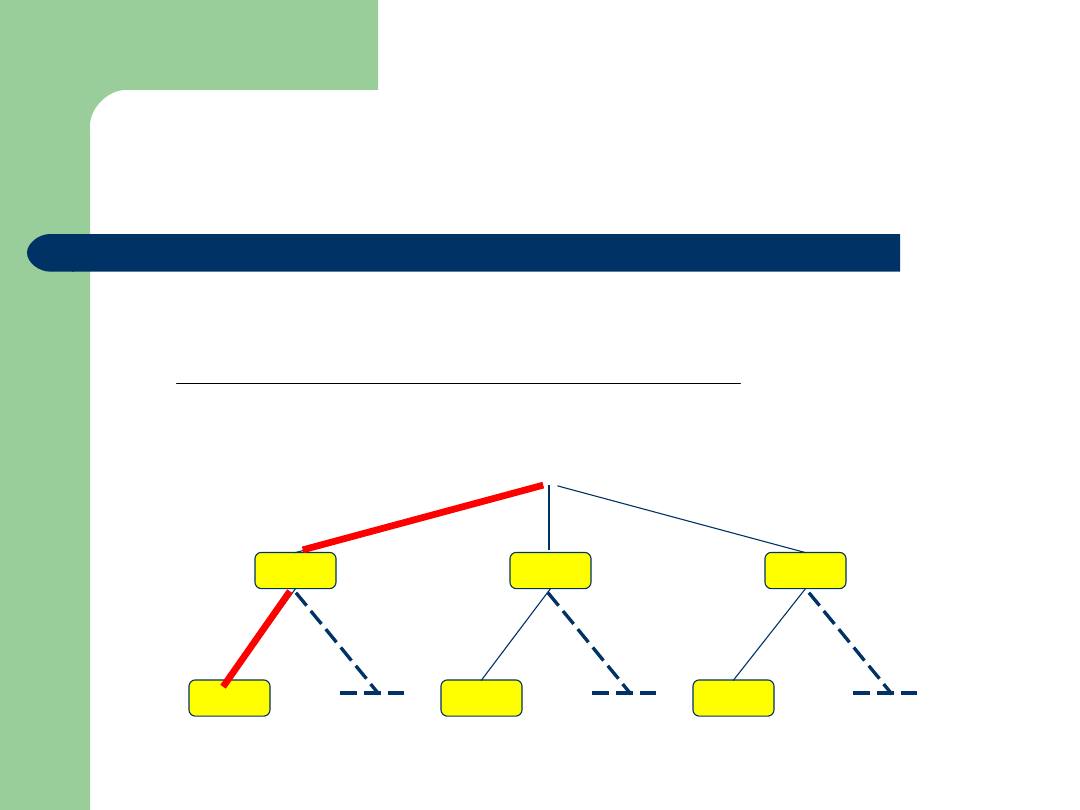
Kanałem łączności nadaje się tylko 3 rodzaje ciągów liter AAAA,

BBBB,

CCCC odpowiednio z prawdopodobieństwami 0,4; 0,3; 0,3. Wysyłane
sygnały kodujące litery podlegają niezależnie losowym zakłóceniom/
Prawdopodobieństwo poprawnego przesłania albo zakłócenia podaje
tabela.
(a) Znaleźć p-d odebrania na wyjściu

sygnału ACAA .

(b) Na wyjściu odebrano sygnał ACAA.

Obliczyć prawdopodobieństwo,
że został on nadany jako AAAA.

A

B

C

A

0,

8

0,

1

0,

1

B

0,

1

0,

8

0,

1

C

0,

1

0,

1

0,

8

S y g n a ł o d e b r a n y

s
y
g
n
a
ł

n
a
d
a
n
y

Przykład

(a)

(b)

8

,

0

)

1

,

0

(

3

,

0

)

1

,

0

(

3

,

0

1

,

0

)

8

,

0

(

4

,

0

3

4

3















987

,

0

8

,

0

)

1

,

0

(

3

,

0

)

1

,

0

(

3

,

0

1

,

0

)

8

,

0

(

4

,

0

1

,

0

)

8

,

0

(

4

,

0

3

4

3

3





















AAAA

BBBB

CCCC

ACAA

ACAA

ACAA

(0,8)

3

0,1 (0,1)

4

0,8



(0,1)

3

0,4 0,3 0,3

Schemat Bernoulliego

Definicja

Niech D będzie pewnym doświadczeniem, w wyniku
którego może zajść zdarzenie A lub zdarzenie przeciwne
A'.

Schematem Bernoulliego

nazywamy serię n

niezależnych powtórzeń tego samego doświadczenia D,
dla pewnego nN.

Wykonanie kolejnego doświadczenia D nazywa się

próbą

. Zajście zdarzenia A nazywa się

sukcesem

, a

zajście zdarzenia A' -

porażką

.

Twierdzenie

W schemacie Bernoulliego o n próbach
prawdopodobieństwo otrzymania dokładnie k sukcesów
jest równe

gdzie k=0,1,2,...,n; n1 oraz p jest

prawdopodobieństwem

sukcesu w jednej próbie.

k

n

k

p)

(1

p

k

n

p)

k,

P(n,



















Przykład

Jeżeli przeciętnie 5 dni w ciągu tygodnia jest deszczowych,

to jak

duże jest p-d, że 2 spośród 3 dni będą pogodne?

Przykład

Jeżeli przeciętnie 5 dni w ciągu tygodnia jest deszczowych,

to jak

duże jest p-d, że 2 spośród 3 dni będą pogodne?

Przyjmijmy , że sukcesem jest wystąpienie pogodnego dnia.
Wówczas mamy:
n=3 (ilość prób), k=2 (ilość sukcesów), p=2/7 (p-d sukcesu)

343

60

7

2

1

7

2

2

3

7

2

3,2,

P

1

2













 









































