Laplace Transform

•Pierre Simon de Laplace

•Oliver Heaviside

•Laplace transform definition

•Convergence region for Laplace
transform

•Laplace transform – analytic function

•Laplace transform examples

•Laplace transform properties

•Time differentiation

•Initial condition and value theorems

•Summary

„Signal Theory” Zdzisław Papir

Pierre Simone de
LAPLACE (



1749

-

†

1827)

Laplace was a mathematician and astronomer. Laplace
initially made an impact by

solving a complex problem of

mutual gravitation

that had eluded both Euler and

Lagrange. Laplace was among the most influential
scientists of his time and was called the Newton of France
for his study of and contributions to the

understanding of

the stability of the solar system

. Laplace generalized the

laws of mechanics for their application to the motion and
properties of the heavenly bodies. He is also famous for
his great treatises entitled

Mécanique céleste

and

Théorie

analytique des probabilités

. They were advanced in large

part by the mathematical techniques that Laplace
developed; most notably among those techniques are

generating functions, differential operators, and definite
integrals

.

„Signal Theory” Zdzisław Papir

Oliver HEAVISIDE

He then conducted private electrical research in a state of
near poverty. His views on

using inductance coils for

improving the performance of long-distance cables

ultimately proved correct. In 1901 he predicted the

existence of the ionosophere

. Heaviside formulated a

basis

for operational calculus

converting linear differential

equations into algebraic ones the solution of which can be
accomplished by relatively simple methods.

The Royal Society refused to publish his paper and Lord
Rayleigh once wrote to him „In the form, as it is, I am
afraid that your paper may not be of use to anyone”.

(



1850

- †

1925)

Oliver Heaviside, English mathematical physicist and
electrical engineer, made important contributions to
electromagnetic theory and measurement and anticipated
several advanced developments in mathematics and
electrical engineering. Heaviside had a brief career as
a telegrapher until growing deafness forced him to retire.

„Signal Theory” Zdzisław Papir

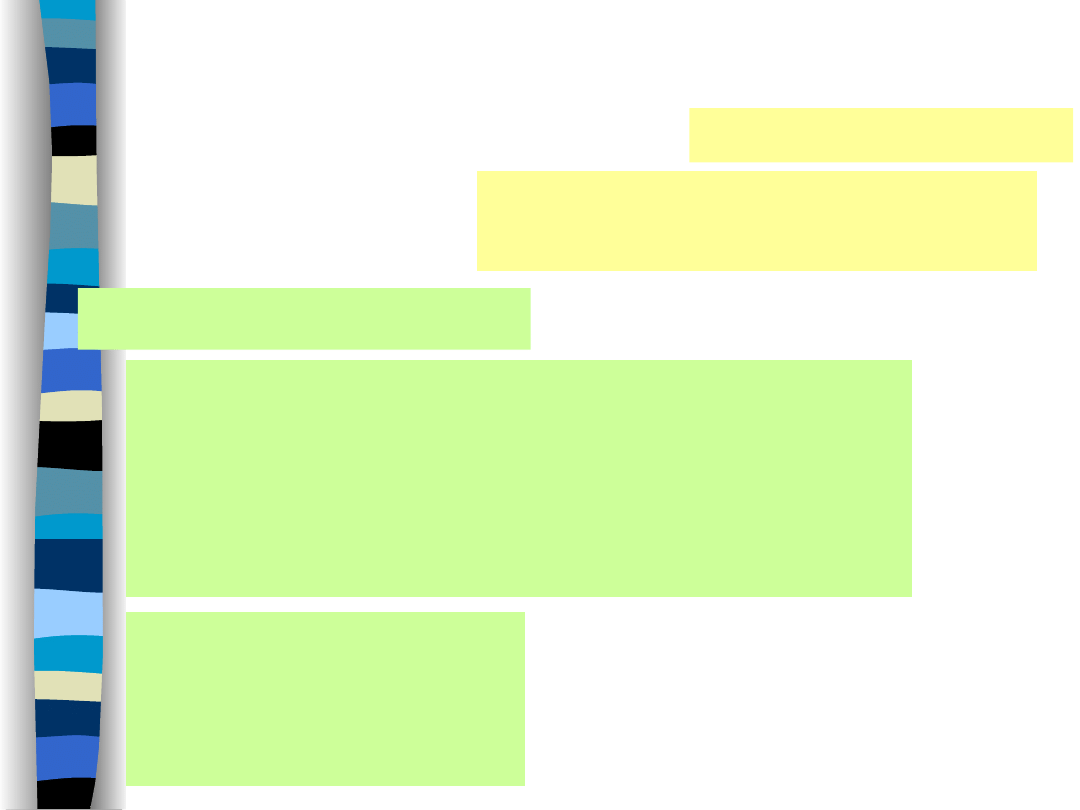
Laplace transform
definition

Fourier transform

 

 













dt

e

t

x

j

X

t

j





Laplace transform

 

 

 



 

































0

0

signal)

(causal

0

for

0

dt

e

e

t

x

dt

e

t

x

s

X

j

s

t

t

x

t

j

t

st









„Signal Theory” Zdzisław Papir

 

 



 

 

 

t

x

s

X

dt

e

t

x

s

X

st

L











0

Laplace transform
definition – comment #1

 

 

 



 

































0

0

signal)

(causal

0

for

0

dt

e

e

t

x

dt

e

t

x

s

X

j

s

t

t

x

t

j

t

st









Laplace transform

„Signal Theory” Zdzisław Papir

 

 





t

j

e

t

x

s

X







F

Laplace transform can be interpreted as a Fourier transform
of an original signal x(t) attenuated by an decaying
exponential term

exp(-j



t),



> 0

. Therefore, one can expect

that a broader class of signals is Laplace-transformable.

Laplace transform
definition – comment #2

 

 

 



 

































0

0

signal)

(causal

0

for

0

dt

e

e

t

x

dt

e

t

x

s

X

j

s

t

t

x

t

j

t

st









Laplace transform

„Signal Theory” Zdzisław Papir

The lower limit in the Laplace integral allows for
inclusion any Dirac pulses



(t)

.

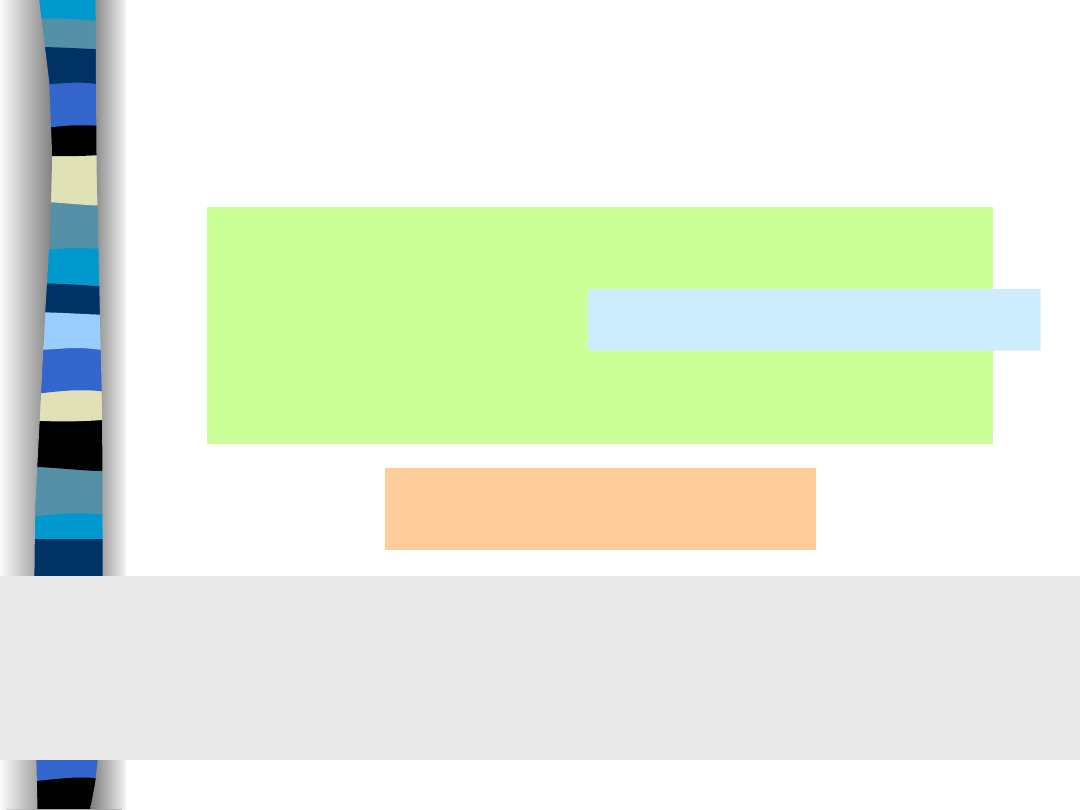
Inverse Laplace transform

 

 

 

 

 





s

X

t

x

ds

e

s

X

j

ds

e

s

X

j

t

x

j

j

st

j

j

st

1

-

L













































lim

2

1

2

1

„Signal Theory” Zdzisław Papir

Laplace transform
definition – comment
#3

• An efficient method for obtaining the inverse Laplace
transform employs the

partial fraction expansion

of a Laplace transform being a

rational function

in s.

• Laplace transform without any

essential singularities

are rational function

in s.

Convergence region for
Laplace transform

 

 

 





 

0

,

1

0

0





























a

a

j

j

X

j

a

e

dt

e

e

j

X

e

t

t

x

t

j

a

t

j

at

at













1

Fourier transform

„Signal Theory” Zdzisław Papir

Fourier transform

(integral) is

convergent for a < 0

only,

moreover, it is convergent on the imaginary

j



axis solely.

 

 

 









 

a

a

s

s

X

s

a

e

e

s

a

e

dt

e

e

s

X

e

t

t

x

t

j

t

a

t

s

a

st

at

at

















































,

1

0

0

0

1

Laplace transform

„Signal Theory” Zdzisław Papir

Convergence region for
Laplace transform

Laplace transform

(integral) is

convergent for any a

in a complex halfplane

Re

(s) =



> a.

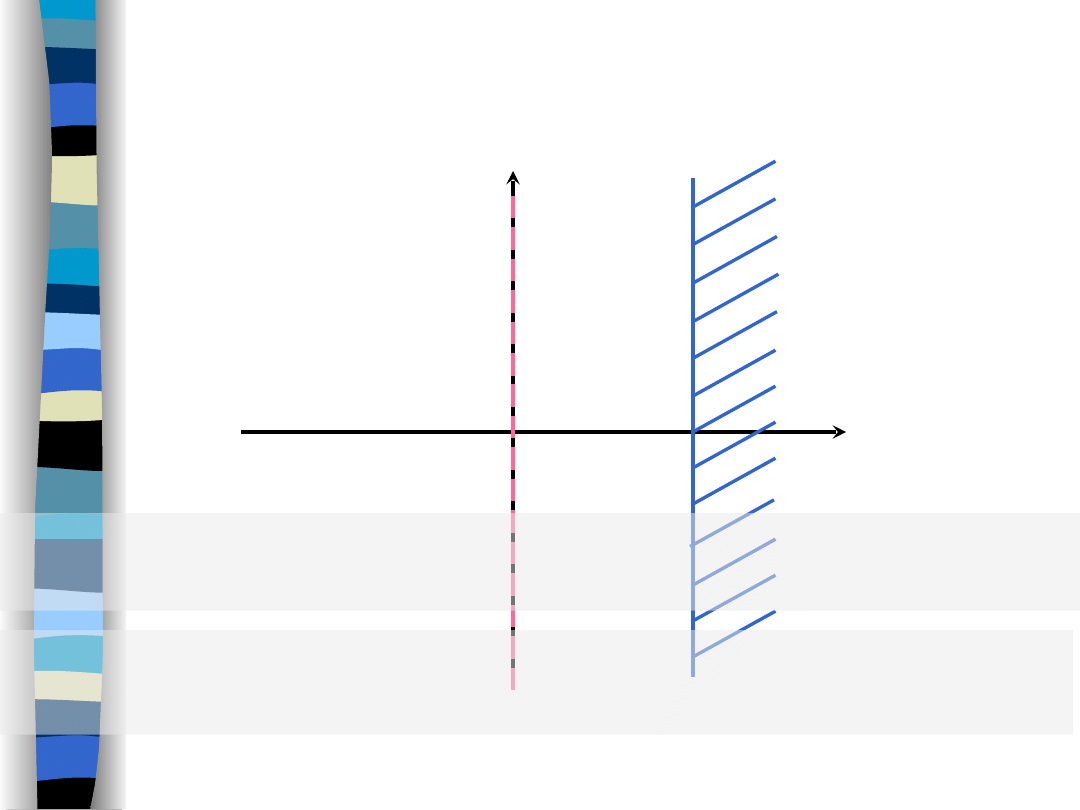
Convergence regions
compared

„Signal Theory” Zdzisław Papir



j







j

s





L



> a

a < 0

F



= 0

a

Fourier transform

(integral) is

convergent for a < 0

only,

moreover, it is convergent on the imaginary

j



axis solely.

Laplace transform

(integral) is

convergent for any a

in a complex halfplane

Re

(s) =



> a.

 

 



 

























0

0

dt

e

e

t

x

dt

e

t

x

s

X

t

j

t

st





„Signal Theory” Zdzisław Papir

Convergence regions
compared



j







j

s





L



> a

a < 0

F



= 0

a

Laplace transform can be interpreted as a Fourier transform
of an original signal x(t) attenuated by an decaying
exponential term

exp(-j



t),



> 0

. As result,

a broader class of signals is Laplace-transformable.

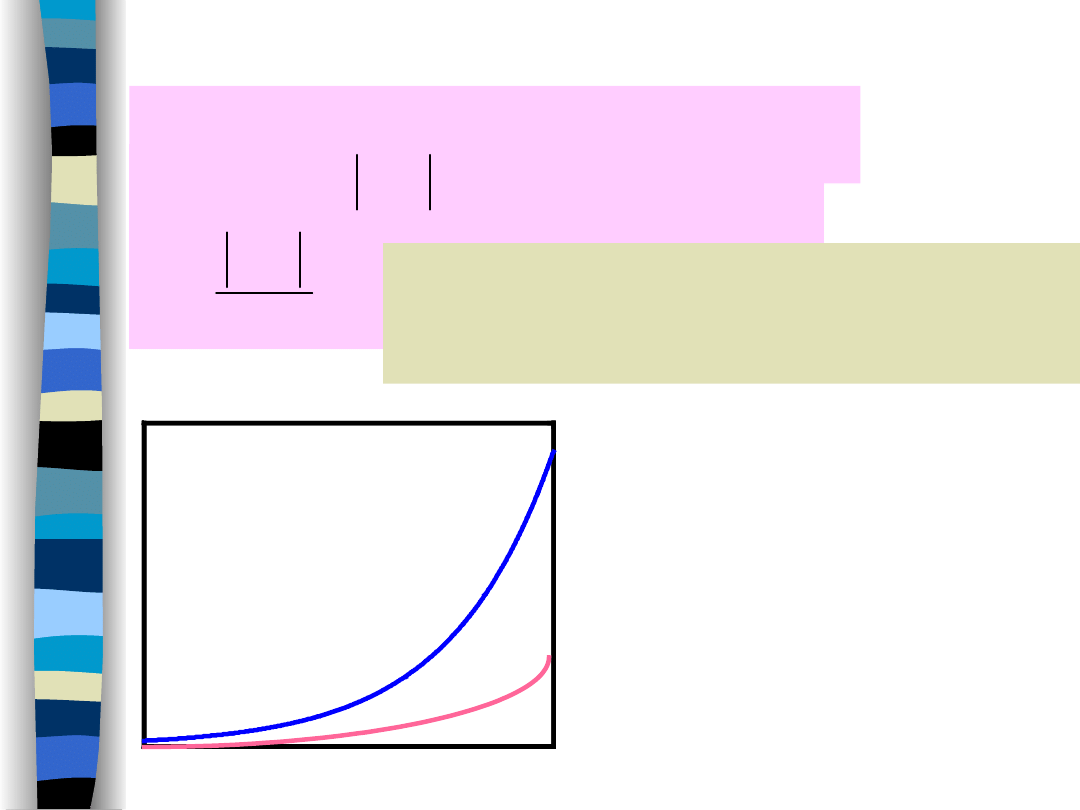
Exponential growth index

Signal x(t) is said to be of
exponential order if:

 

 

.

0

lim

for

:

0

,



















t

t

t

Me

t

x

t

Me

t

x

M







Signal x(t) does not grow faster than
some exponential signal;



is called a

growth index of x(t).

t

Me



 

t

x

„Signal Theory” Zdzisław Papir

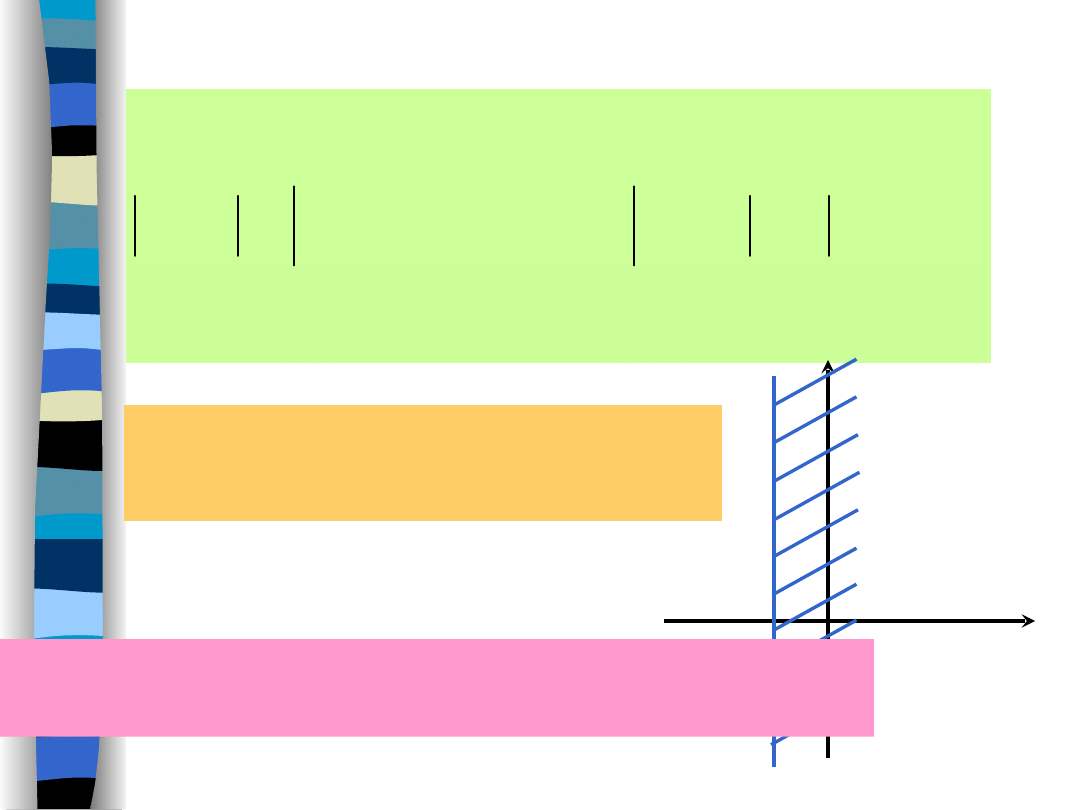
Convergence abscissa

 

 



 



 

 



 



































































0

0

0

0

0

0

dt

Me

dt

e

Me

dt

e

t

x

dt

e

e

t

x

s

X

dt

e

e

t

x

dt

e

t

x

s

X

t

t

t

t

t

j

t

t

j

t

st







































0

a

dt

Me

t









j







j

s





L



>





< 0

Exponential growth index





Convergence abscissa



for Laplace transform.

„Signal Theory” Zdzisław Papir

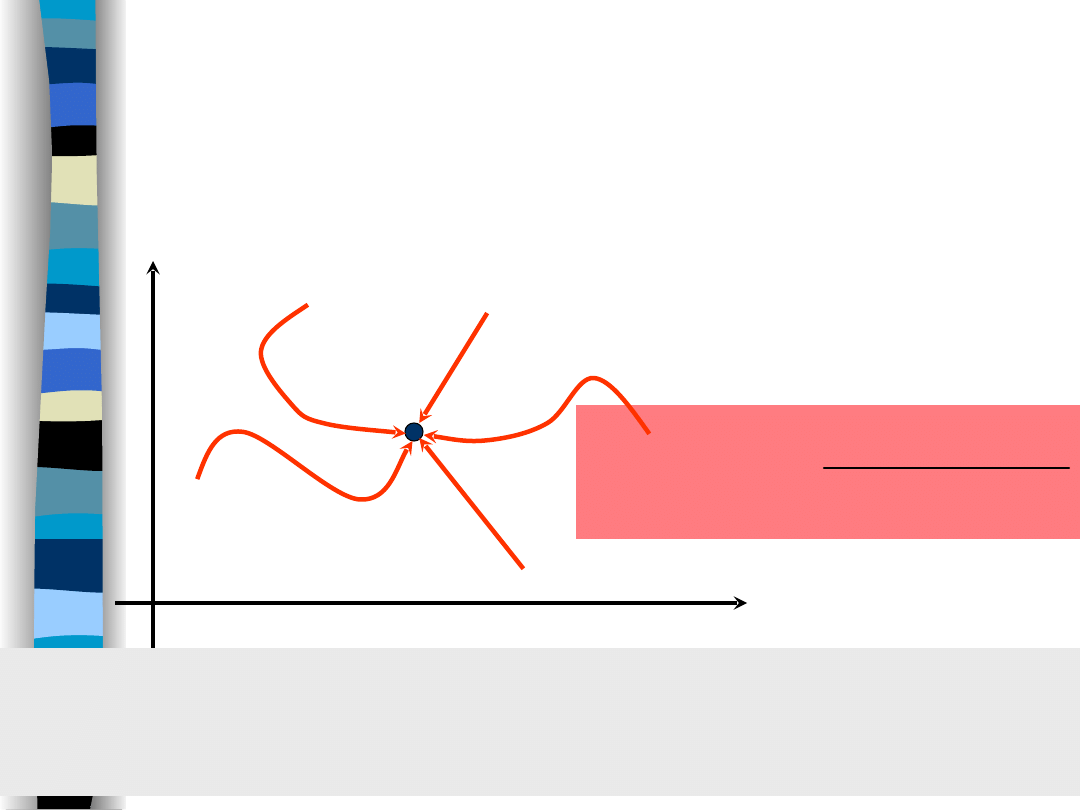
Laplace transform
– analytic function

Function

C

 f(s), s 

C

is analytic if its derivative exists no

matter which path s is approaching s

0

.

 

 

 

0

0

0

0

lim

s

s

s

X

s

X

s

X

s

s













j







j

s





0

s

„Signal Theory” Zdzisław Papir

Laplace transforms

are

analytic functions

(for

Re

s 



) so

important results are valid based on a

complex function

analysis

.

Cauchy integral theorem

 







L

0

ds

s

X



j







j

s





L

L

„Signal Theory” Zdzisław Papir

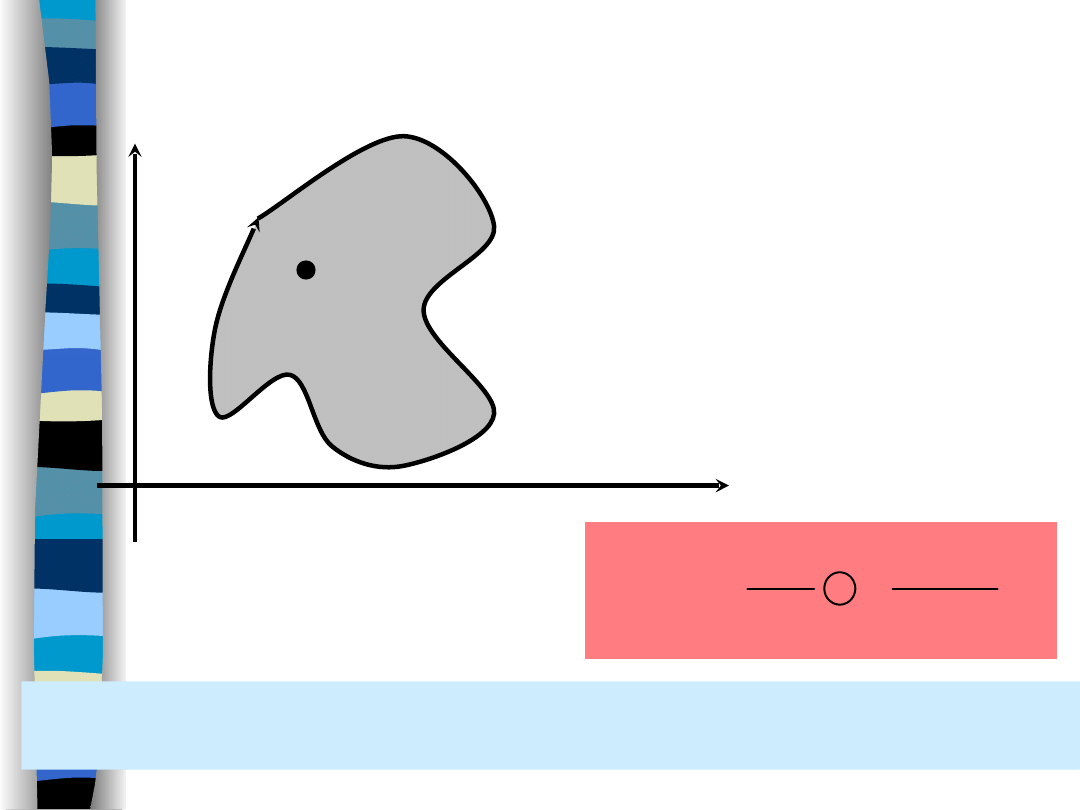
Laplace transform
– analytic function – Cauchy
theorem



j







j

s





L

Cauchy integral formula

 

 









L

ds

s

s

s

X

j

s

X

0

0

2

1



Value of an analytic function in any point s

0

 L can be determined

if its values on an area boundary L are known.

L

0

s

„Signal Theory” Zdzisław Papir

Laplace transform
– analytic function – Cauchy
formula

Laplace transform
examples

 





 





 

 

 

 





a

s

e

s

t

s

n

t

s

t

s

s

t

at

n

n

t

t

t

t

t





















1

1

1

!

sin

cos

1

2

0

2

0

0

2

0

2

0

1

1

1

1

1













„Signal Theory” Zdzisław Papir

Some signals that are not Fourier-transformable
(in an ordinary sense) are Laplace-transformable.

Laplace transform
properties

 

 

 

 

 

 

 



 

 





   

   





 

0

,

0





























a

s

X

e

a

t

x

s

Y

s

X

t

y

t

x

a

s

X

t

x

e

s

s

X

d

x

a

a

s

X

at

x

s

bY

s

aX

t

by

t

ax

as

at

t





„Signal Theory” Zdzisław Papir

Laplace transform properties are similar
to Fourier transform properties; the difference is
in convergence regions.

Time differentiation

 





 



 

 



 

 

 

 

 

s

sX

x

e

x

dt

e

t

x

s

e

t

x

dt

e

t

x

t

x

Me

x

s

s

X

st

st

st













































0

lim

as

,

0

0

0

0

 

 



 

 













L

 





   









0

x

s

sX

t

x

L

„Signal Theory” Zdzisław Papir

Time differentiation is a significant property as it replaces

differentiation in the time domain

to an

ordinary multi-

plication by s

in the complex frequency domain.

Time differentiation

 





   

 





 

   

 





 

 

   















































0

0

0

0

0

0

2

3

2

x

x

s

x

s

s

X

s

t

x

x

x

s

s

X

s

t

x

x

s

sX

t

x

L

L

L

Time differentiation is quite significant property as:

• differential equations can be solved using

algebraic techniques

(d()/dt operator is replaced

by s-operator),

•

initial conditions

are included automatically,

• initial values and initial conditions have not to be
distinguished

(initial/final value theorem)

.

„Signal Theory” Zdzisław Papir

Time differentiation
(Fourier transform)

 





 



 

 



 

 

 

 

 

























j

X

j

x

e

x

dt

e

t

x

j

e

t

x

dt

e

t

x

t

x

x

j

j

X

t

j

t

j

t

j

















































0

lim

0

for

,

0

0

0

0



 



 





 



 



F

Fourier transform

makes

algebraic solving differential

equations possible as well, however:

• assumptions are more restrictive

• is not convenient as consecutive derivative operators are:
(j



, -



2

, -j



3

,



4

...) as opposed to the Laplace transform

(s, s

2

, s

3

, s

4

, s

5

...).

„Signal Theory” Zdzisław Papir

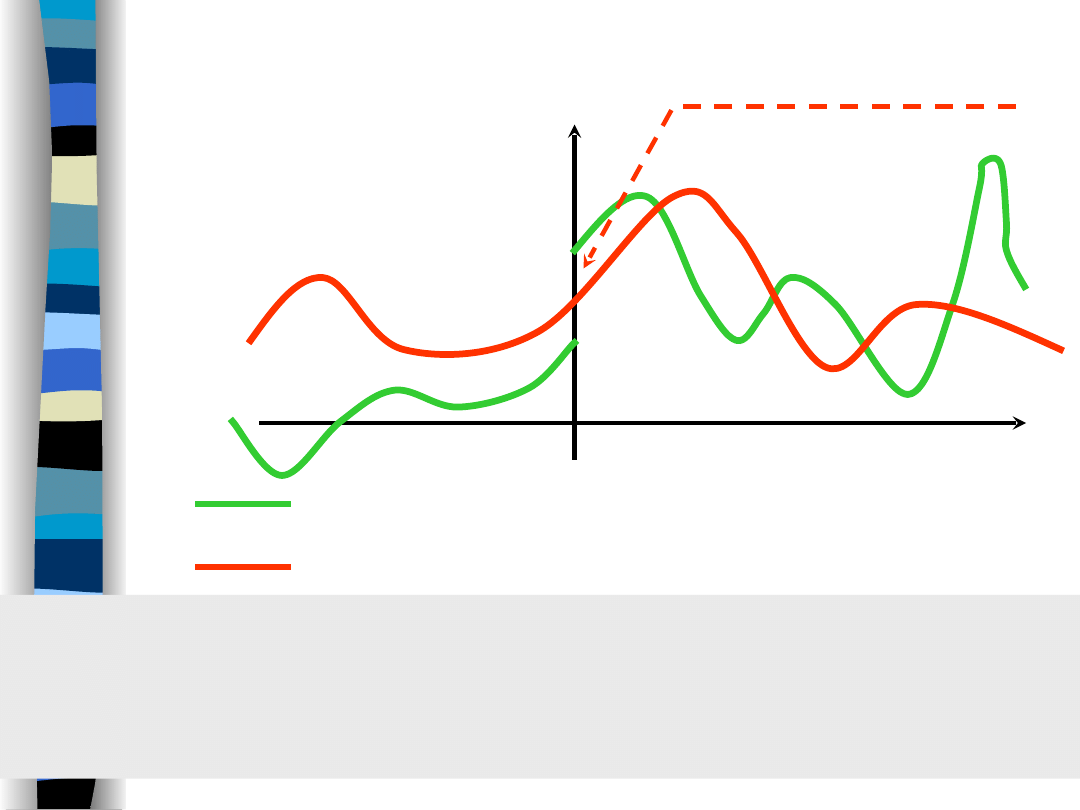
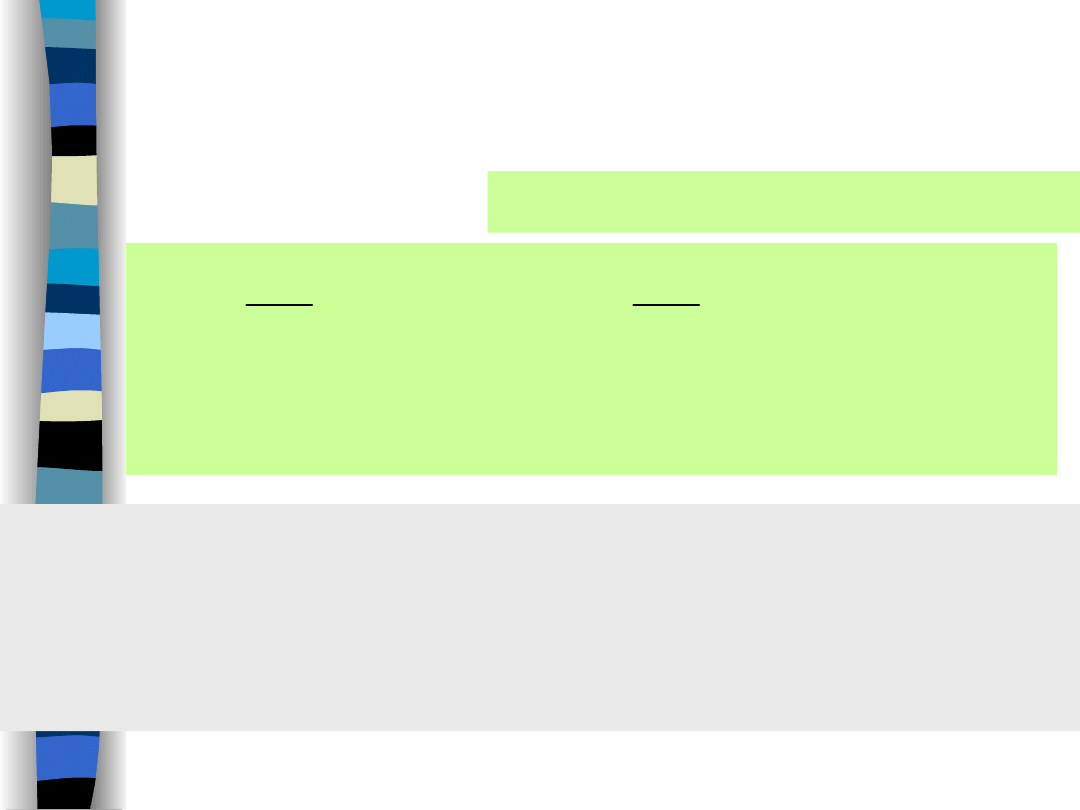
Initial condition
& value theorems

x(t)

t

continuous signal

discontinuous signal

x(0–)

x(0+)

x(0–) = x(0+) = x(0)

x(0–) –

initial

condition

x(0+) –

initial

value

„Signal Theory” Zdzisław Papir

Initial conditions can differ from initial values

when:

• signal driving an electric network changes stepwise

• electric network structure is subjected to a change
of its structure and was not deenergized right before.

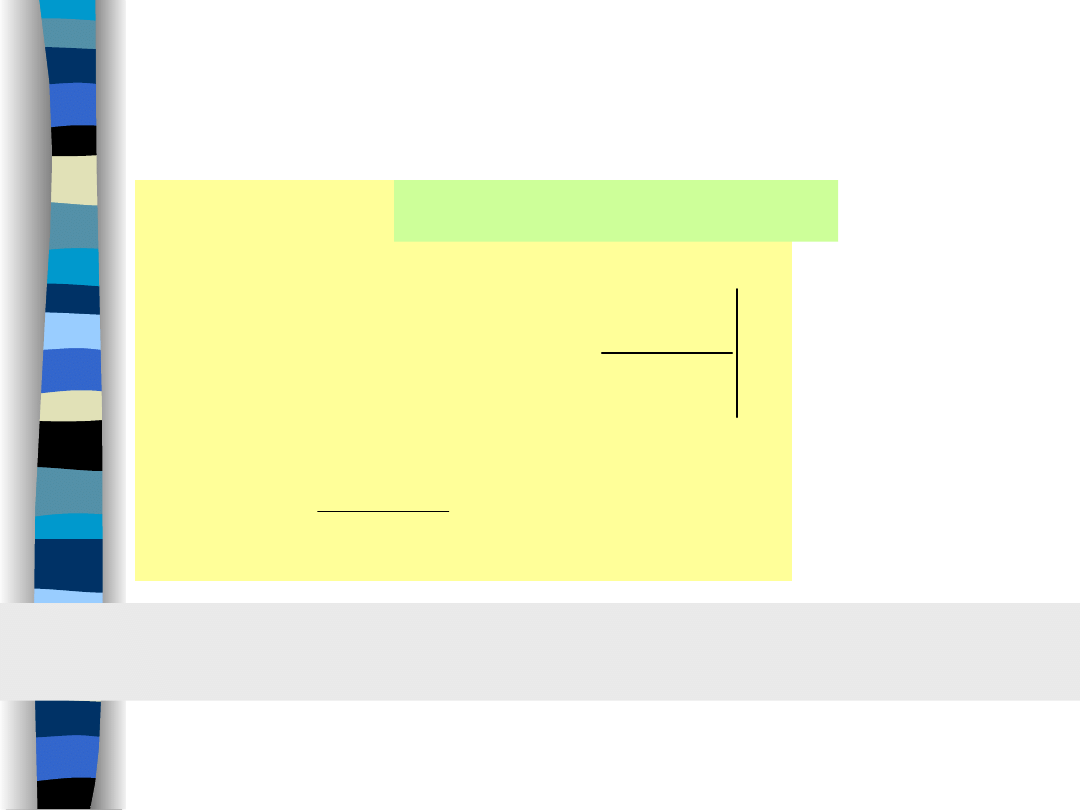
Initial value theorem

„Signal Theory” Zdzisław Papir

Consider a signal x(t) either continuous or

having

a finite discontinuity

at t = 0.

 

 

   

 

s

sX

x

t

x

s

X

t

x

s

t

















lim

0

lim

0

The

initial value theorem

emphasizes the fact

that the

initial value

of a signal is to be determined

from

knowledge of its transform

(no matter if there is

a discontinuity x(0–)  x(0+) at t = 0).

Final value theorem

„Signal Theory” Zdzisław Papir

Let the Laplace transform x(t)  X(s) be analytic
in a right halfplane (

Re

s  0)

 

 

 

 

s

sX

t

x

s

X

t

x

s

t

0

lim

lim











The

final value theorem

emphasizes the fact

that the

steady state value

of a signal is to be determined

from

knowledge of its transform

.

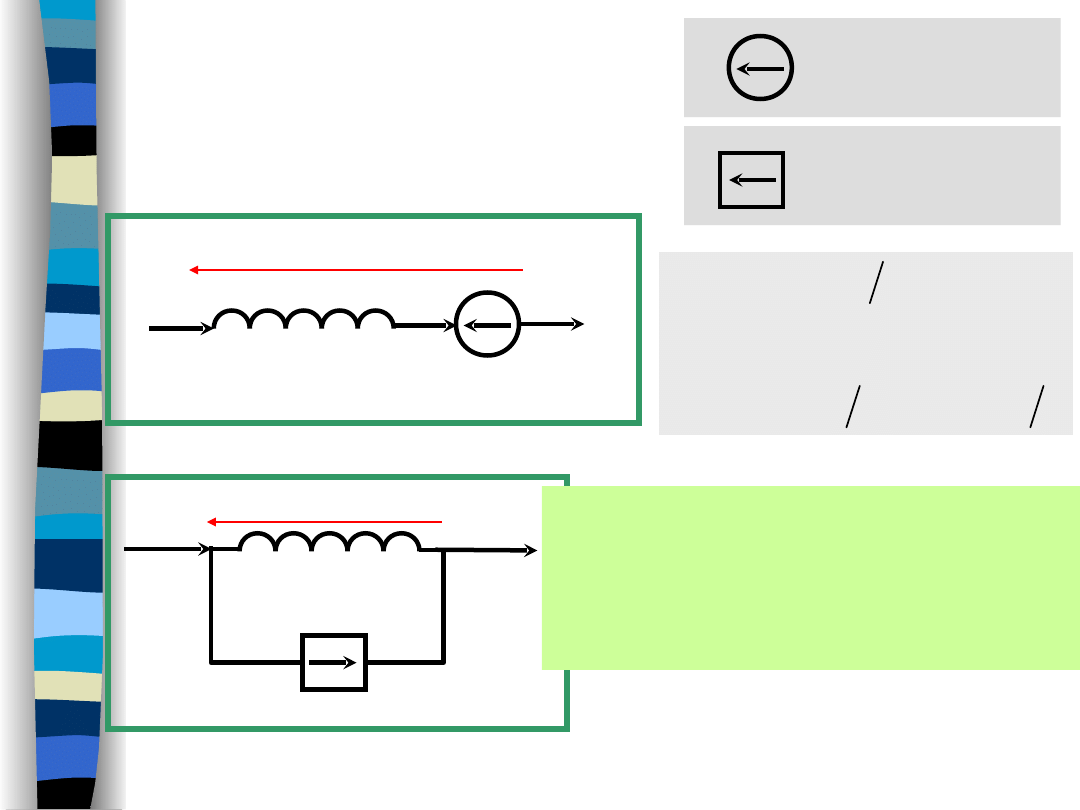
Initial condition
(an inductor)

Voltage source

„Signal Theory” Zdzisław Papir

Current source

 

 

 

 

 

 

 

 

s

i

Ls

s

U

s

I

Li

s

LsI

s

U

dt

t

di

L

t

u















0

0

Li(0–)

Ls

I(s)

U(s)

1/Ls

i(0–)/s

U(s)

I(s)

Initial energy storage in
an inductor is accounted for
by additional equivalent
sources (voltage/current).

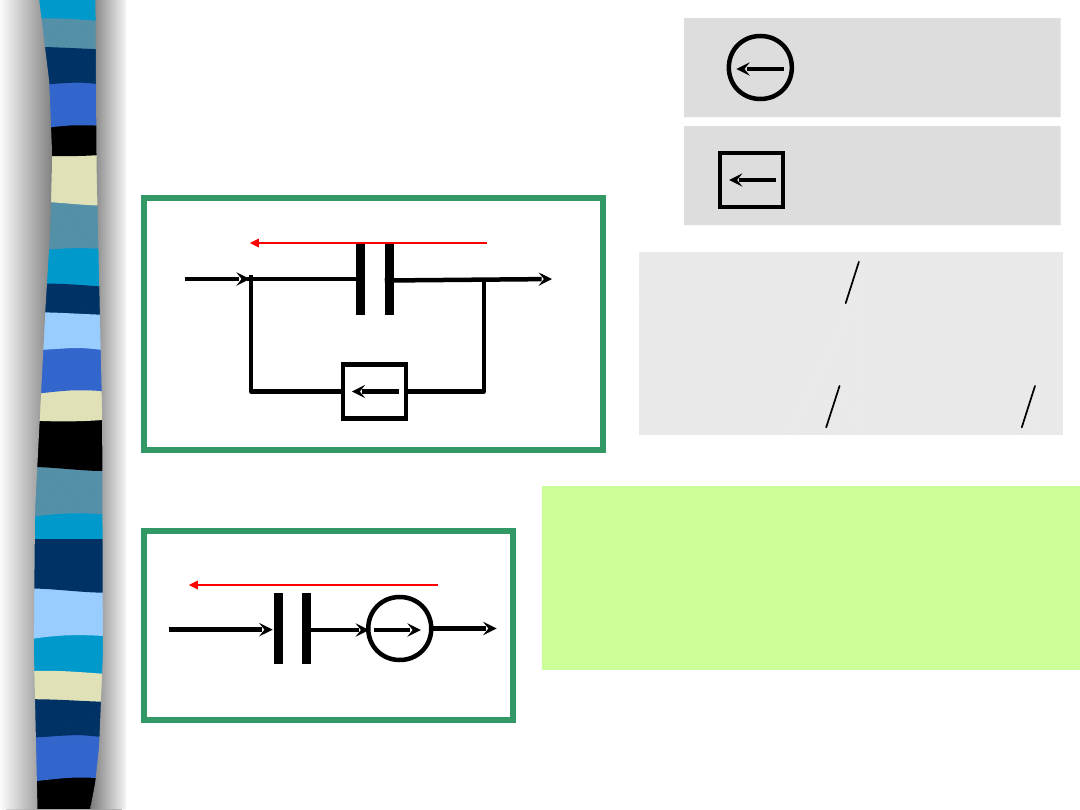
Initial condition
(a capacitor)

„Signal Theory” Zdzisław Papir

Voltage source

Current source

 

 

 

 

 

   

 

s

u

Cs

s

I

s

U

Cu

s

CsU

s

I

dt

t

Cdu

t

i















0

0

Initial energy storage in
an inductor is accounted for
by additional equivalent
sources (voltage/current).

Cs

Cu(0–)

I(s)

U(s)

u(0–)/s

1/Cs

I(s)

U(s)

 

 

 











 





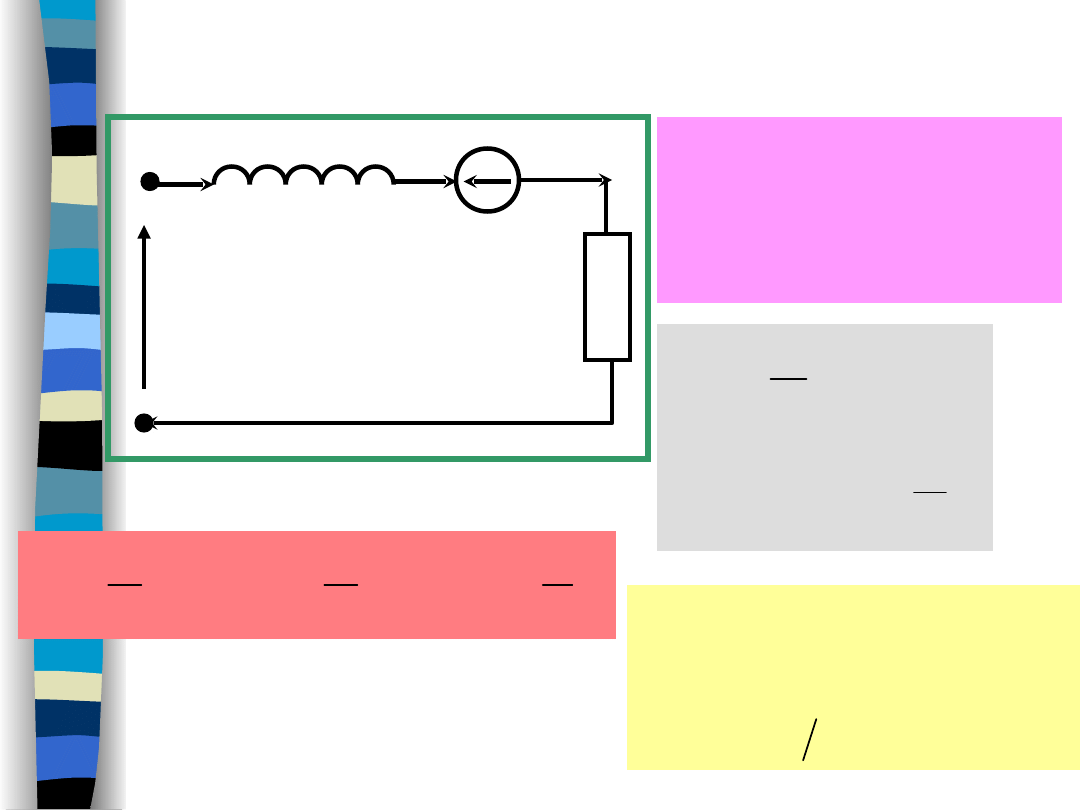
t

L

R

A

t

i

t

R

U

t

i

exp

T

F

1

Example (a classic
approach)

 

   

R

U

I

A

I

i

i

i

i

A

i

























0

0

F

T

)

0

(

)

0

(

0

0

0

 

 

 











 











 





t

L

R

t

R

U

I

t

R

U

t

i

exp

0

1

1

Li(0–) =
LI

0

L

 

t

U

1

R

i(t)

 

 

 

 

 

response

transient

-

response

forced

-

T

F

T

F

t

i

t

i

t

i

t

i

t

i





„Signal Theory” Zdzisław Papir

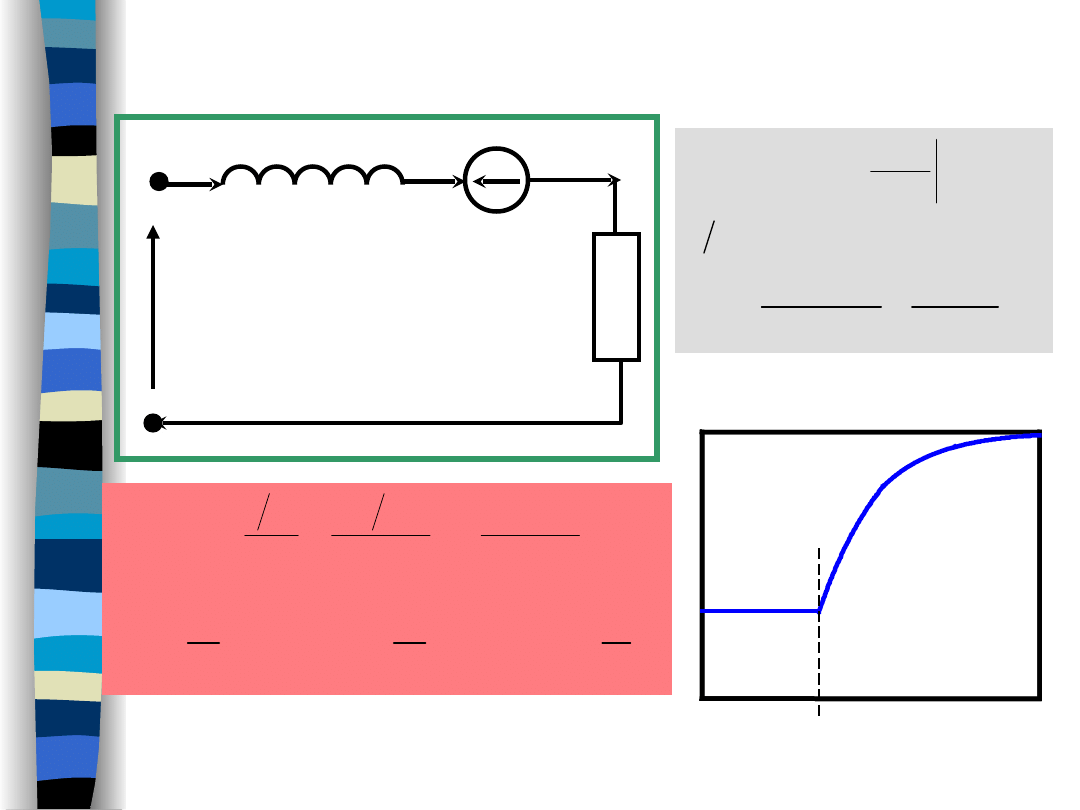
Example (Laplace
transform)

 

 

 

 

 

 

  



Ls

R

LI

Ls

R

s

U

s

I

LI

s

LsI

s

RI

s

U

dt

t

di

L

t

Ri

t

u





















0

0

L

 

 

 

 











 











 



























t

L

R

t

R

U

I

t

R

U

t

i

Ls

R

LI

Ls

R

R

L

s

R

U

s

I

exp

1

0

0

1

1

Li(0–) =
LI

0

L

 

t

U

1

R

i(t)

„Signal Theory” Zdzisław Papir

t = 0

t

I

0

i(t)

U/R

Summary

• Laplace transform is a convenient tool for solving
models of linear,
time-invariant systems (a set of fixed coefficients,
ordinary differential equations) as:
- it replaces the d()/dt operator by an algebraic s-

operator,
- yields a full solution comprising of a decaying
transient response (to initial conditions) and a forced
response (to external excitations).

• Class of Laplace-transformable signals is broader
than a class
Fourier-transformable signals due to a attenuating
term in the Laplace
transform kernel.

• Laplace transform are analytic functions (from
complex function analysis point of view) so we are
supported by a powerful technical apparatus (most
spectacular result are Hilbert relationships).

Telecommunication signals modeling is interested in a steady state in
most cases, therefore, more emphasis has been placed on the Fourier
transform which is more easy for a physical interpretation.

„Signal Theory” Zdzisław Papir