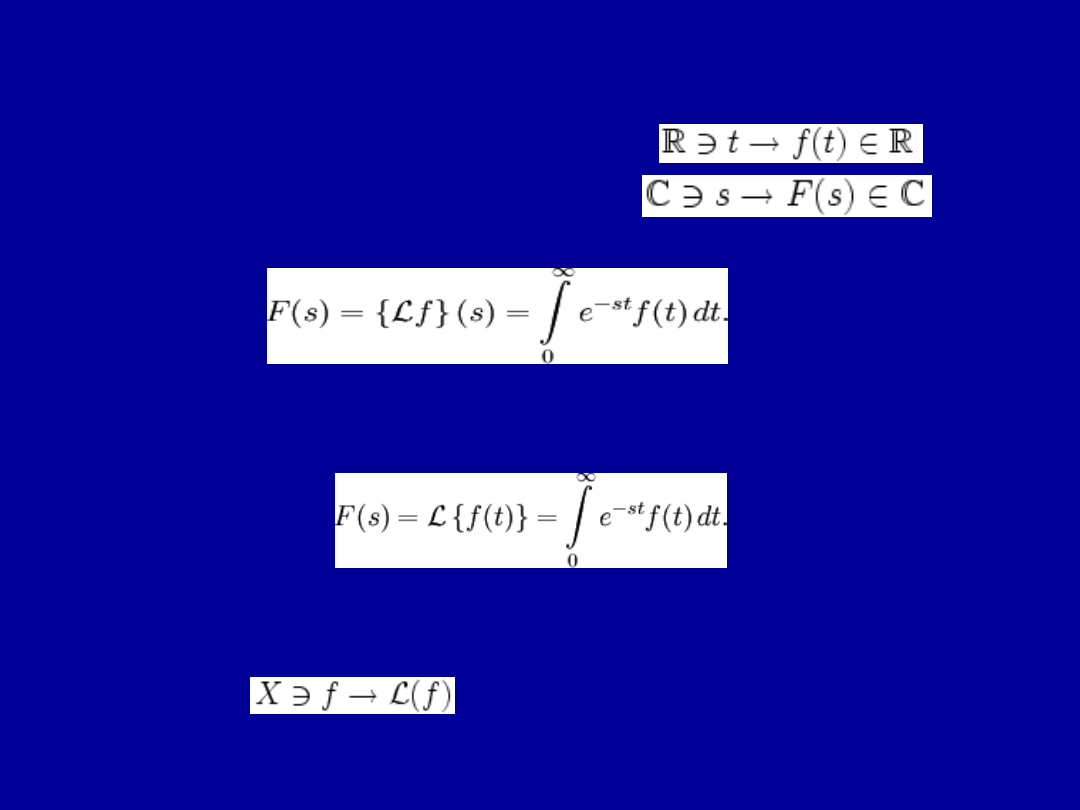
Transformata Laplace'a

Transformatą Laplace'a funkcji

…………………………..

nazywamy następującą funkcję

…………………………….

gdzie :

często zapisywaną, zwłaszcza w środowisku inżynierskim,

w następującej formie:

Niech X oznacza przestrzeń funkcji, dla których powyższa

całka (zwana całką Laplace'a) jest zbieżna.

Funkcję nazywamy transformacją

Laplace'a

Transformata Laplace'a

Należy zwrócić uwagę na rozróżnienie pomiędzy pojęciem
transformaty, a transformacji Laplace'a. Zgodnie z
powyższą definicją transformacja Laplace'a jest
przekształceniem zbioru funkcji, dla których całka
Laplace'a jest zbieżna w zbiór funkcji zespolonych
zmiennej zespolonej. Natomiast transformata Laplace'a
jest jedynie obrazem pewnej funkcji f(t) przez
transformację Laplace'a.
Transformata Laplace'a posiada kilka własności, które
czynią ją szczególnie użyteczną w analizie liniowych
układów dynamicznych.

Warunki zbieżności całki z transformatą Laplace'a
Istnieje zawsze funkcja, która majoryzuje czyli ogranicza
wykładniczo funkcję f(t): dla każdego t > 0 istnieje takie M oraz
d, dla którego zachodzi zależność: |f(t)| < Me

dt

Własności

Liniowość

                                                                                          

Transformata pochodnej                                                   
gdzie f'(0

+

)

oznacza granicę prawostronną funkcji f(t) w punkcie t=0

                                             
                                                                    

Pochodna transformaty                                        

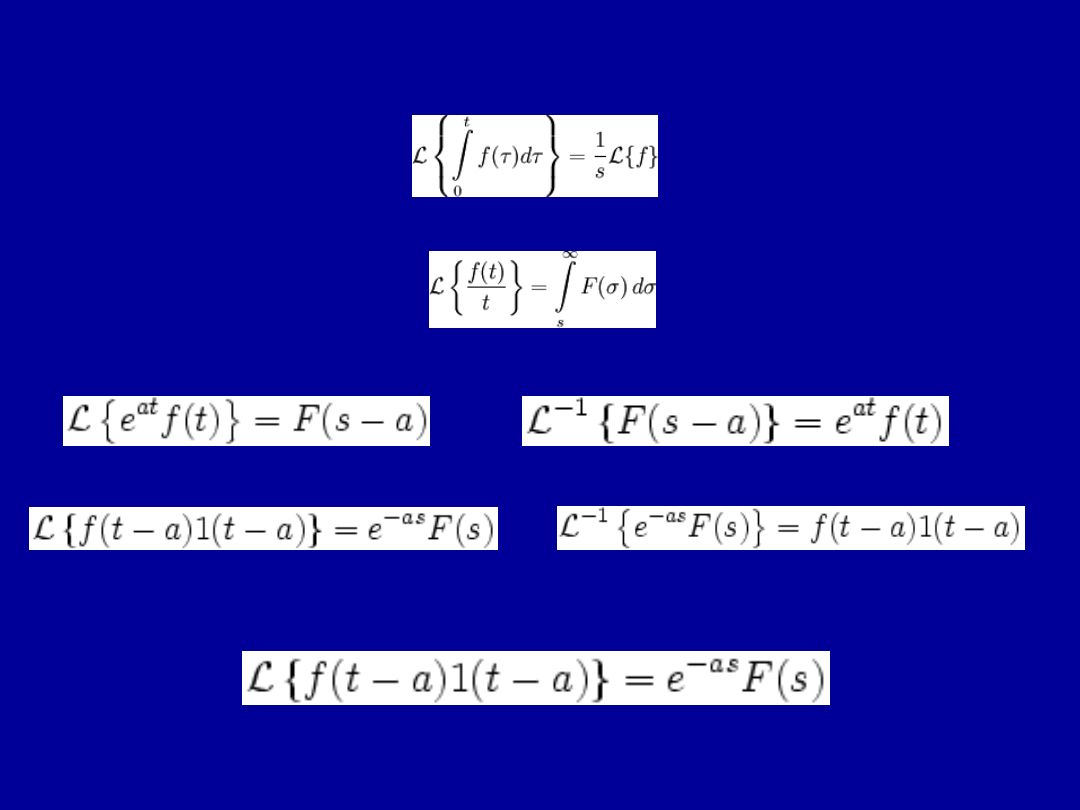
Transformata całki

Całka transformaty

Przesunięcie w dziedzinie transformaty

Transformata funkcji z przesunięciem

gdzie 1(t) oznacza skok jednostkowy

Splot

Jest to tzw. Twierdzenie Borela o splocie.

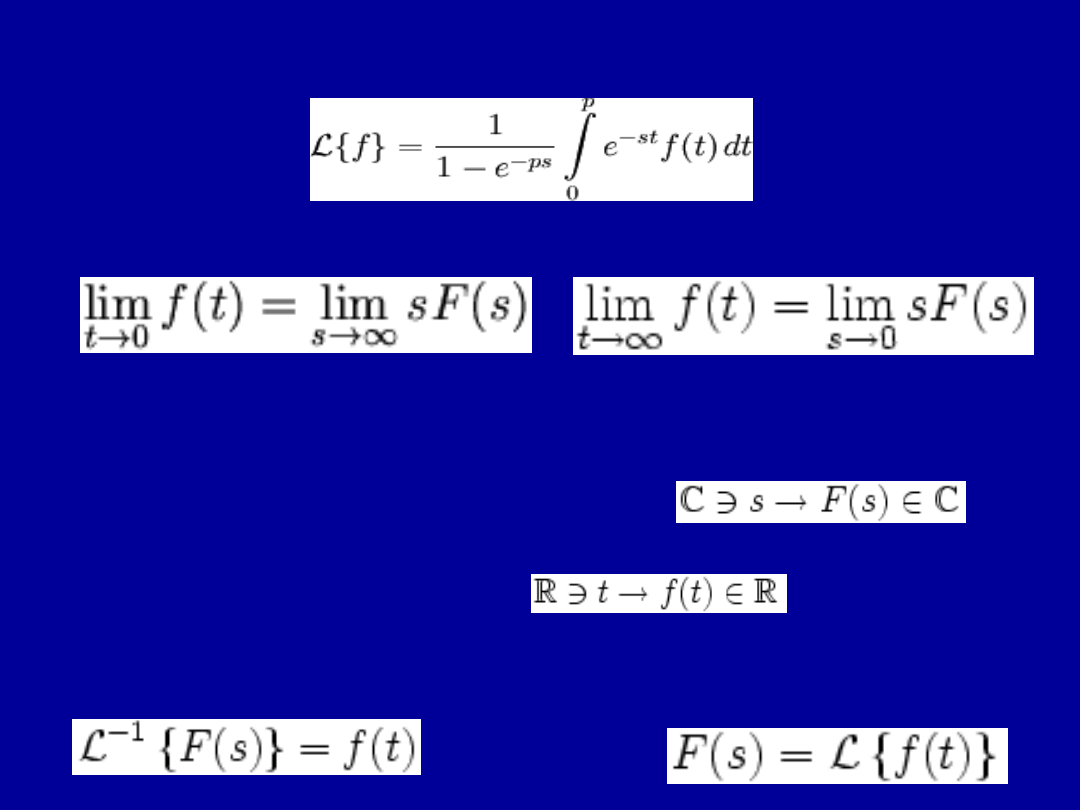
Transformacja funkcji okresowej o okresie p

Własności graniczne

Transformata odwrotna Laplace'a

Transformatą odwrotną

funkcji

……………………

nazywamy taką funkcję ,

która jest

jej transformatą Laplace'a:

jeżeli

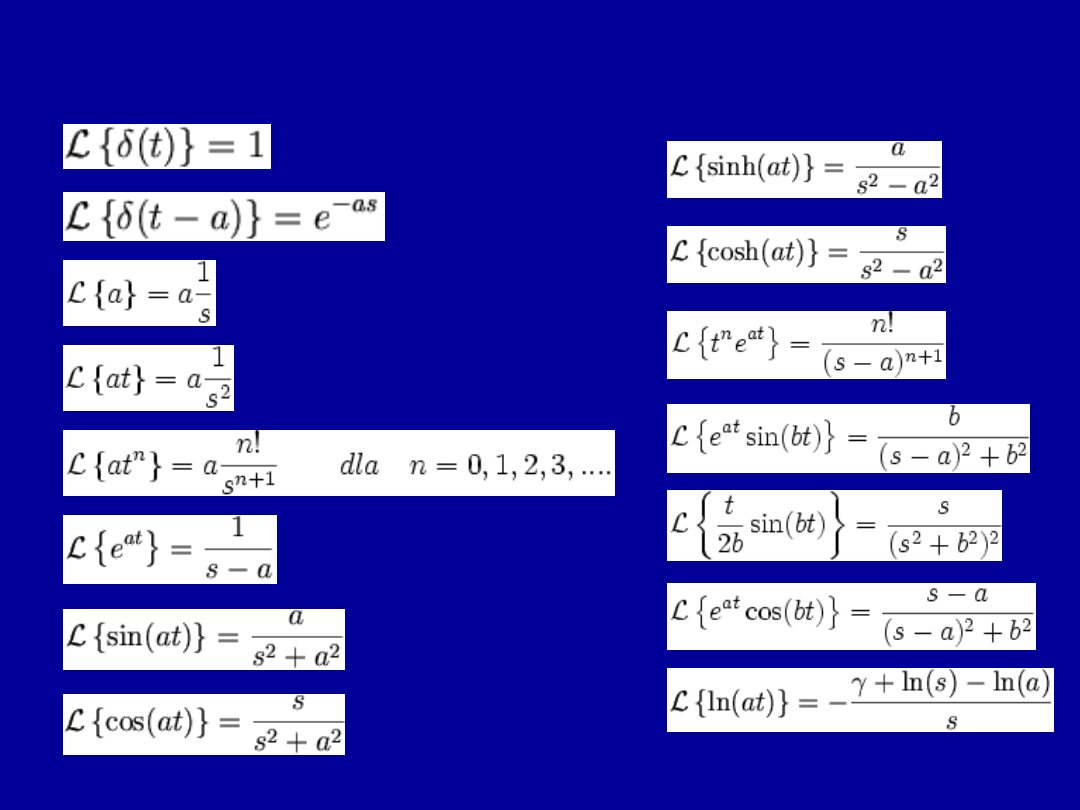
Transformaty Laplace'a częściej

spotykanych funkcji

gdzie γ - stała Eulera

ZADANIE

Wyznaczyć transformatę Laplace’a funkcji

f(t)=tsin(t), =const.

• Z definicji transformaty Laplace’a otrzymujemy:

• F(s)= [f(t)]=

L

[tsin(t)]

Oznaczając:

F(s) =

L

[tsin(t)] = /(s

2

+

2

)

Z twierdzenia o różniczkowaniu

dla n=1 i f1(t)= sin(t) otrzymujemy:

L

[(-1

1

)sin(t)] = (d

(1)/

ds)F

1

(s) = (d/ds)(/s

2

+

2

) =

2s/( s

2

+

2

)

2

A wtedy:

F(s)=

L

[f(t)]=

L

[t

2

] +

L

[sin(t)]

•

Transformaty cząstkowe:

•

L

[t

2

] = n!/s

n+1

= 2/s

3

•

L

[sin(t)] = /( s

2

+

2

)

Czyli poszukiwana transformata:

F(s)= 2/s

3

+ /( s

2

+

2

)

Odpowiedź:

F(s)=

L

[tsin(t)] = 2/s

3

+ /

( s

2

+

2

)