Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

Procesy Mechaniczne.

Przepływ płynów jednorodnych

c.d.

Płyny rzeczywiste c.d.

Opory przepływów

i różne problemy przepływu w

rurach

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

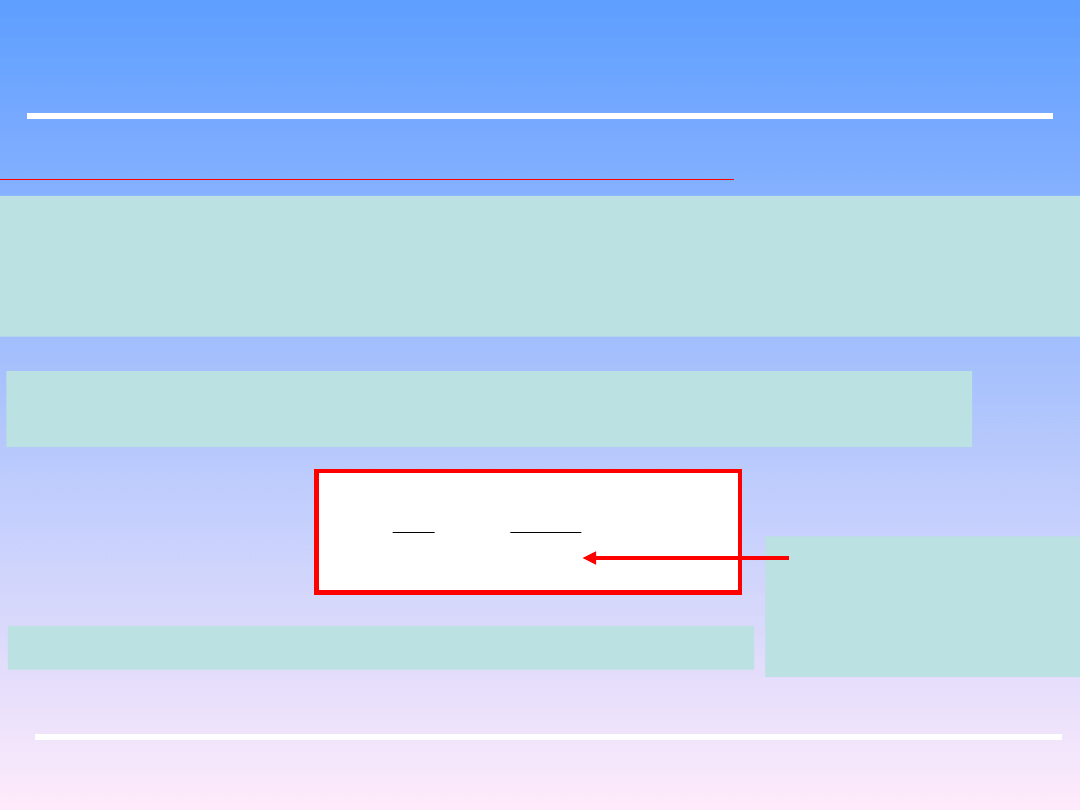
1) Równanie Bernoullego dla płyny rzeczywistego

W przypadku przepływu płynu rzeczywistego, posiadającego lepkość, a więc
wykazującego tarcie wewnętrzne, podczas przepływu, założenia o odwracalności
wprowadzone na wykładzie 2 podczas wyprowadzania bilansu energetycznego
układu przepływowego są nieaktualne

Stosując to równanie należy wprowadzić poprawkę dZ kompensującą
nieodwracalności

0

2

2





















dZ

g

u

d

dp

dz





α nie znika bo
pojawia się rozkład
prędkości w przekroju
strumienia.

Poprawka dZ jest określana jako opór hydrauliczny.

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

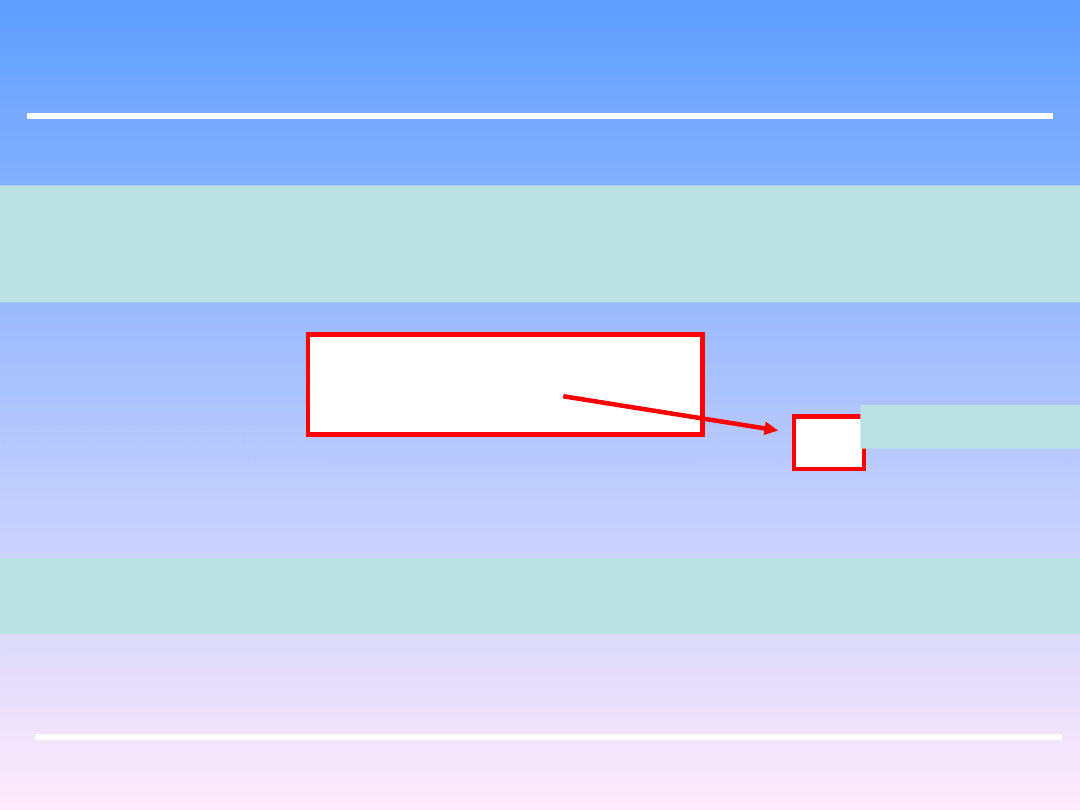
Ponieważ założenie o nieściśliwości cieczy jest spełnione możemy scałkować to
wyrażenie:

2

,

1

2

2

2

2

2

1

2

1

1

1

2

2

Z

g

u

z

p

g

u

z

p





















Z

1,2

– jest to opór hydrauliczny na odcinku strumienia między przekrojami 1 i 2.

Podczas przepływu pojawiać się będą straty ciśnienia ich znajomość jest niezbędna
do doboru odpowiednich urządzeń pompujących i oceny ekonomicznej procesu

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

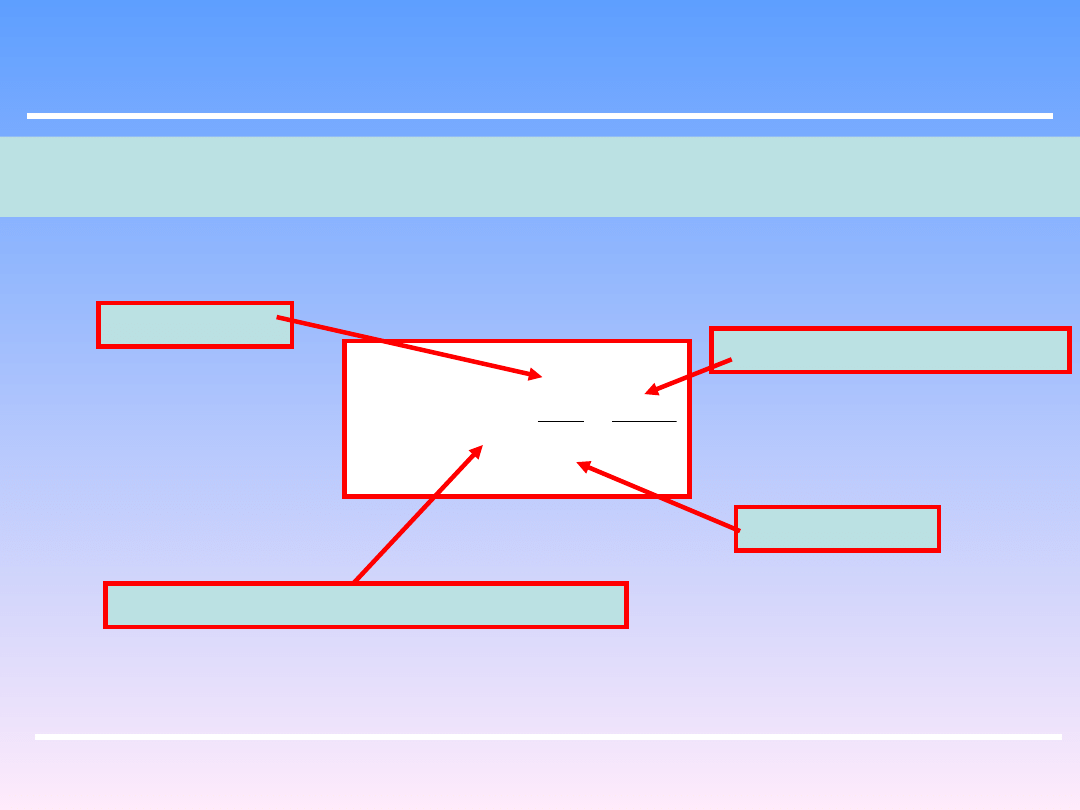
Tylko dla przepływów bez zmiany poziomów wlotu i wylotu (z

1

=z

2

) oraz bez zmiany

prędkości liniowej (u

1

=u

2

) – przepływ w poziomej rurze o stałej średnicy, spadek

ciśnienia jest równy:

2

,

1

2

1

Z

p

p









g



ciężar właściwy

W innych układach spadek ciśnienia będzie zależał nie tylko od oporów, ale też od
zmian prędkości i poziomów  trzeba rozwiązywać pełne rów. Bernoullego

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

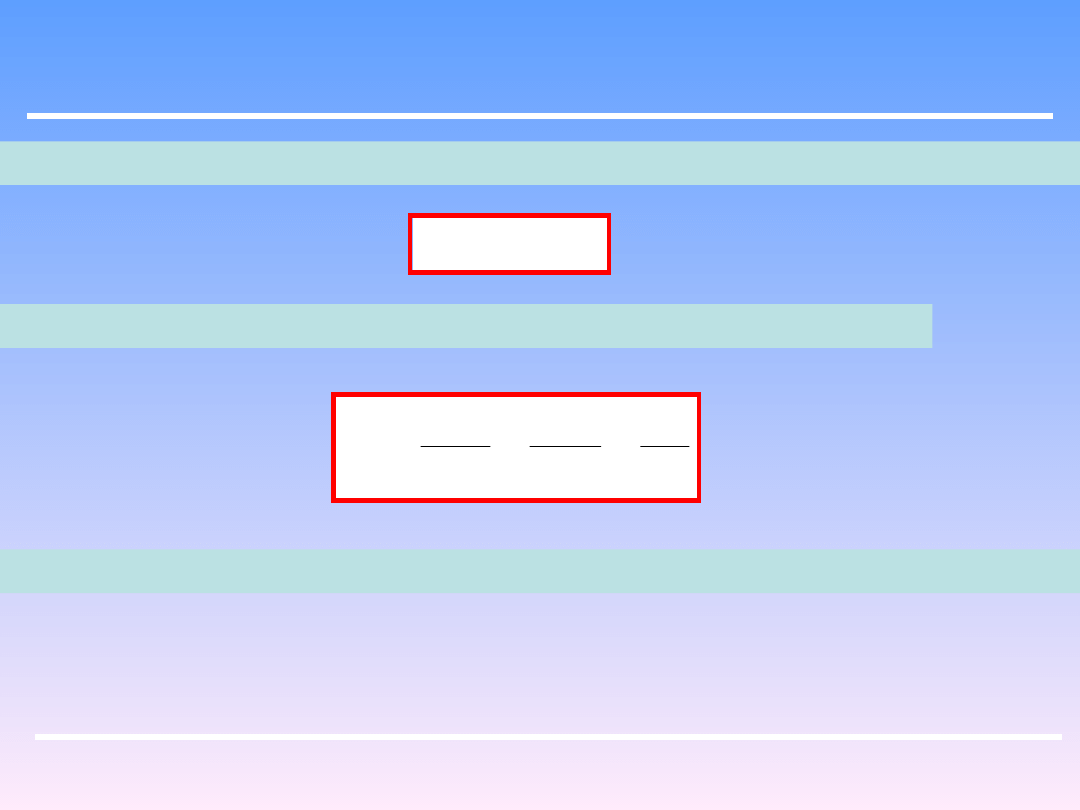
Opór Z

1,2

występujący w równaniu Bernoullego w przypadku przepływu przez rury

określa równanie Darcy – Weisbacha:

Średnia prędkość liniowa

g

u

D

L

Z

2

2

2

,

1









Długość rury

Średnica rury

Bezwymiarowy współczynnik oporów

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

Bezwymiarowy współczynnik oporów jest funkcją liczny Reynoldsa i szorstkości rury









Re,

f



Bezwymiarowa liczba Reynoldsa może być przedstawiona następująco:











uD

uD

g

uD







Re

Jest to jedna z najważniejszych liczb kryterialnych w inżynierii chemicznej

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

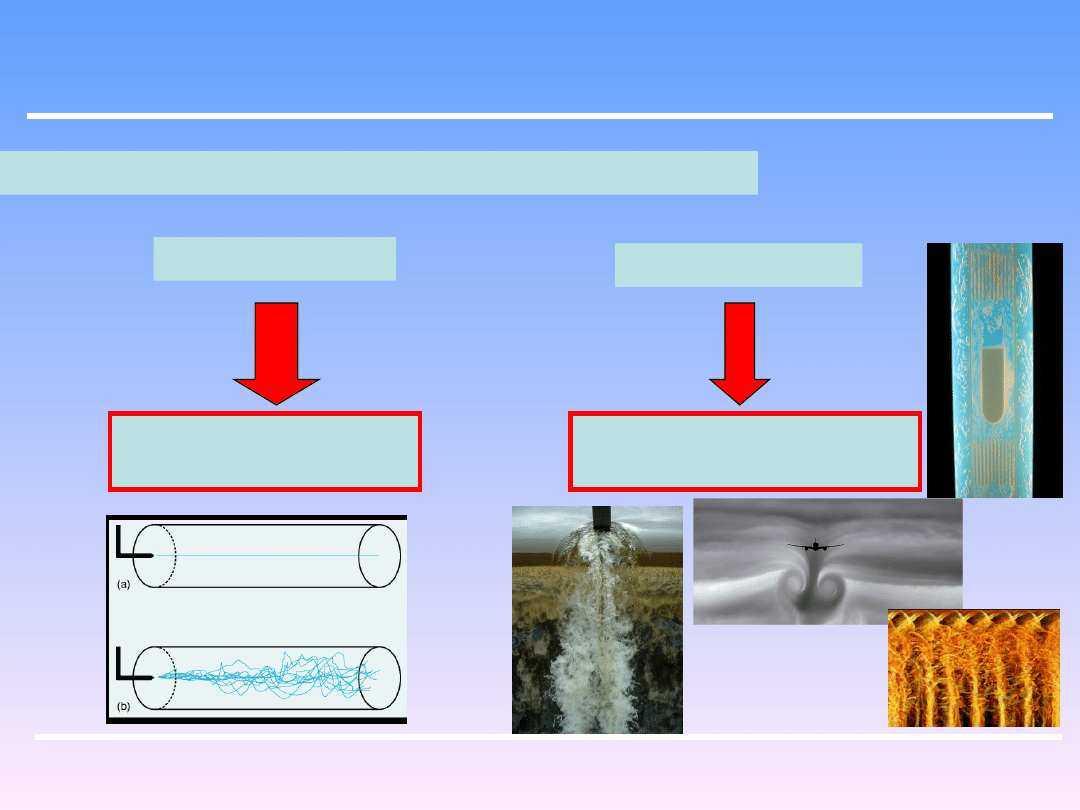
Jej wartość mówi nam o charakterze przepływu płynów

Przepływ LAMINARNY

(UWARSTWIONY)

Przepływ TURBULENTNY

(BURZLIWY)

Mała wartość Re

Duża wartość Re

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

Dla przepływu laminarnego przez gładką rurę szorstkość nie odgrywa roli i zależność
na bezwymiarowy współczynnik oporu przyjmuje postać:

2100

Re

Re

64





Uwzględniając definicję liczby Re w tym równaniu otrzymujemy
bezpośrednią zależność na spadek ciśnienia przy ruchu laminarnym. Jeżeli
możemy zaniedbać różnicę poziomów pomiędzy wlotem a wylotem
otrzymujemy równanie:

2

2

1

32

D

L

u

p

p







Równanie Poiseuilla

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

W przypadku ruchu burzliwego jak też i przejściowego pomiędzy ruchem laminarnym i
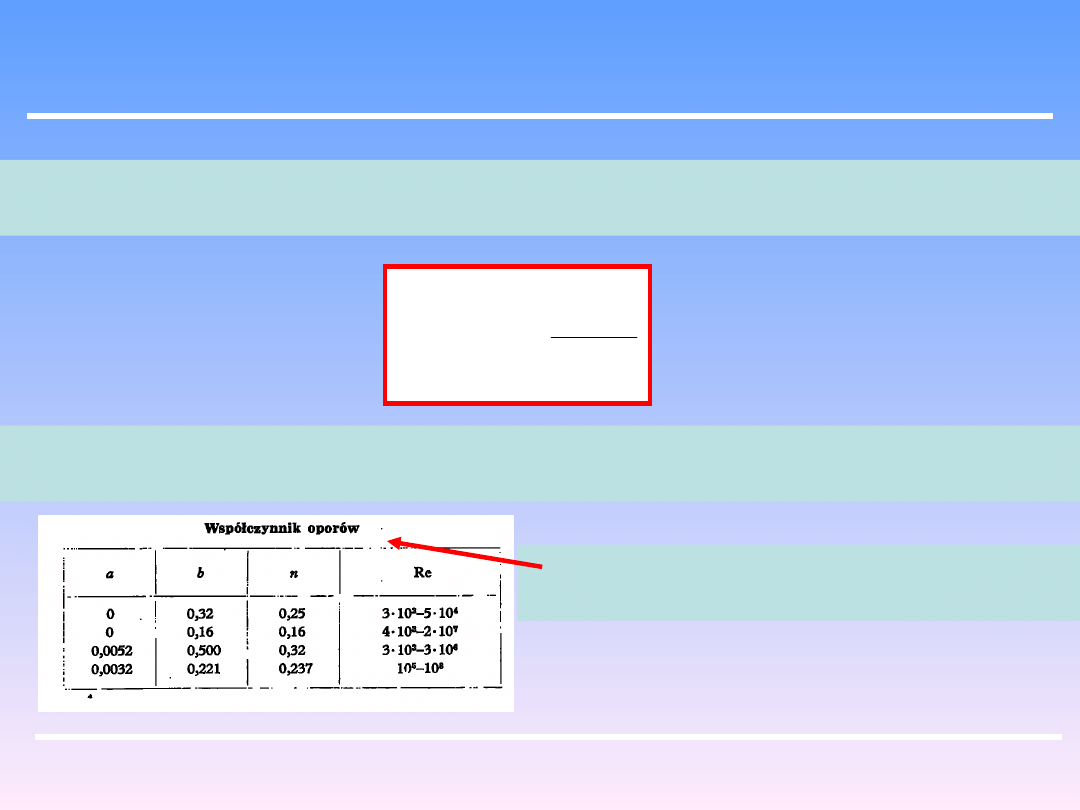
burzliwym dla Re > 2100 stosuje się równanie empiryczne typu:

n

b

a

Re







Współczynniki empiryczne a, b, n zależą od zakresu liczby Re i od rodzaju rury. Ich
wartość można znaleźć w kalendarzach i literaturze.

zestawienie dla rur „gładkich” szklanych
i z metali półszlachetnych

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

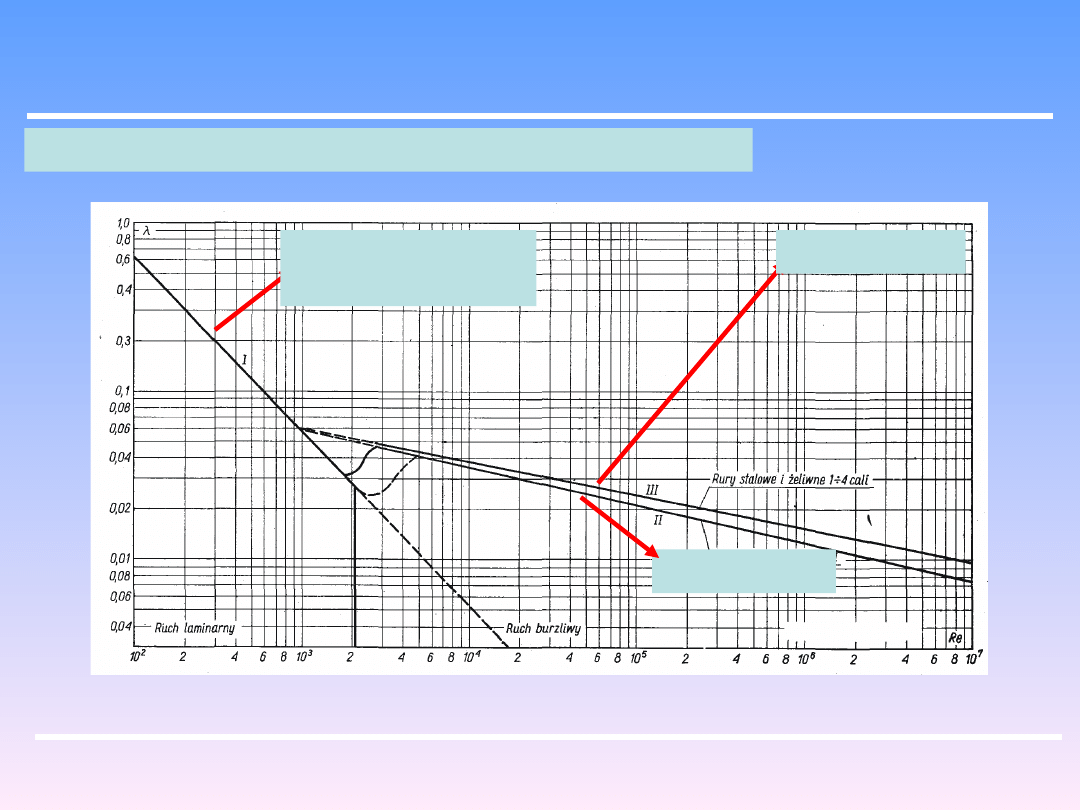
Dla rur stalowych można posługiwać się wykresem :

rury stalowe

ruch laminarny
dowolny materiał

rury gładkie

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

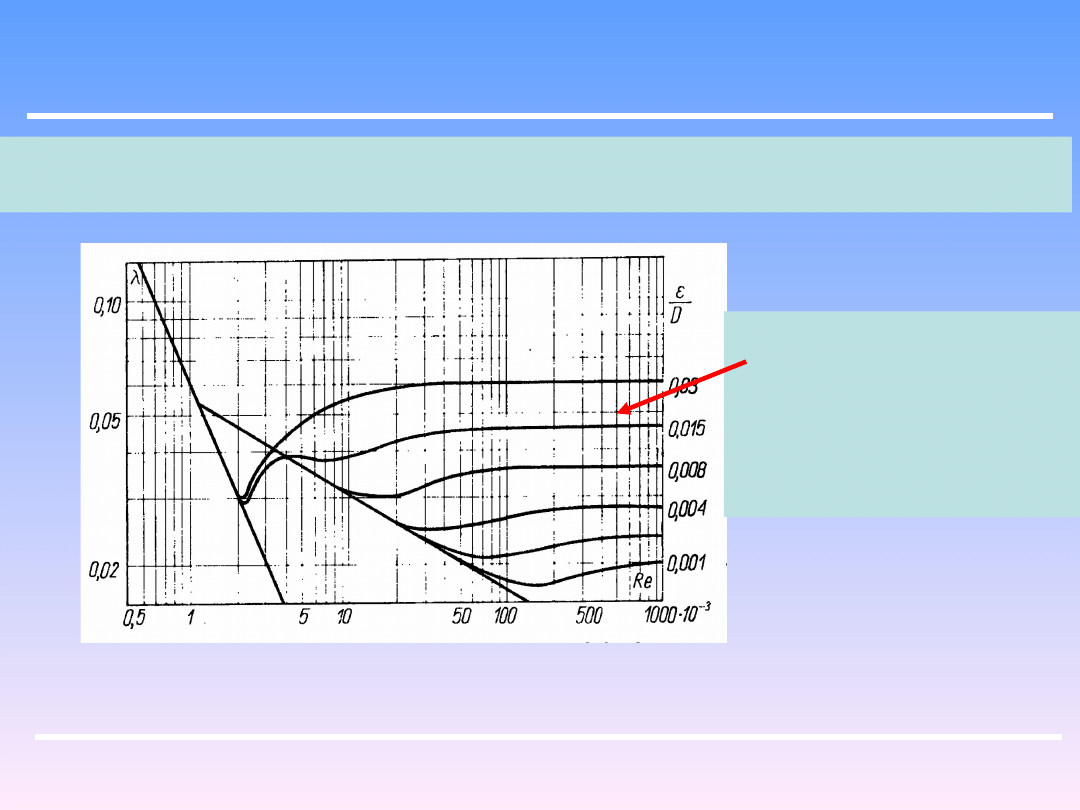
Dla rur z innych tworzyw można stosować wykres uogólniony, operujący miarą
szorstkości ε lub bezwymiarowym stosunkiem ε /D :

Im wyższe ε tym szybciej
przy niższych wartościach
Re nastepuje ustalenie
się wartośći λ , czyli
osiągnięcie pełnej
burzliwości

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

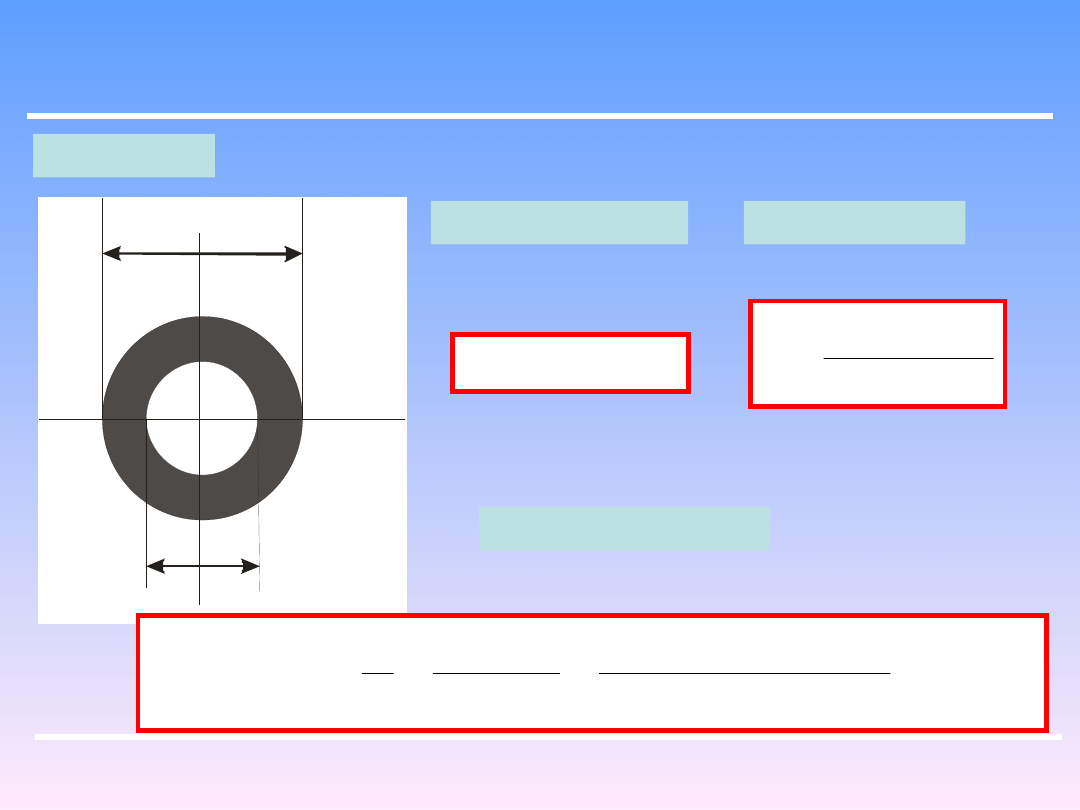
Może mieć miejsce przepływ przewodem nie kołowym. W tym przypadku opory
oblicza się przy pomocy równania Darcy – Weisbacha, gdzie D oznacza teraz tzw.
średnicę zastępczą .

B

F

r

D

h

z









4

4

promień hydrauliczny:

pole przekroju strumienia:

Obwód zwilżony przekroju
strumienia

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

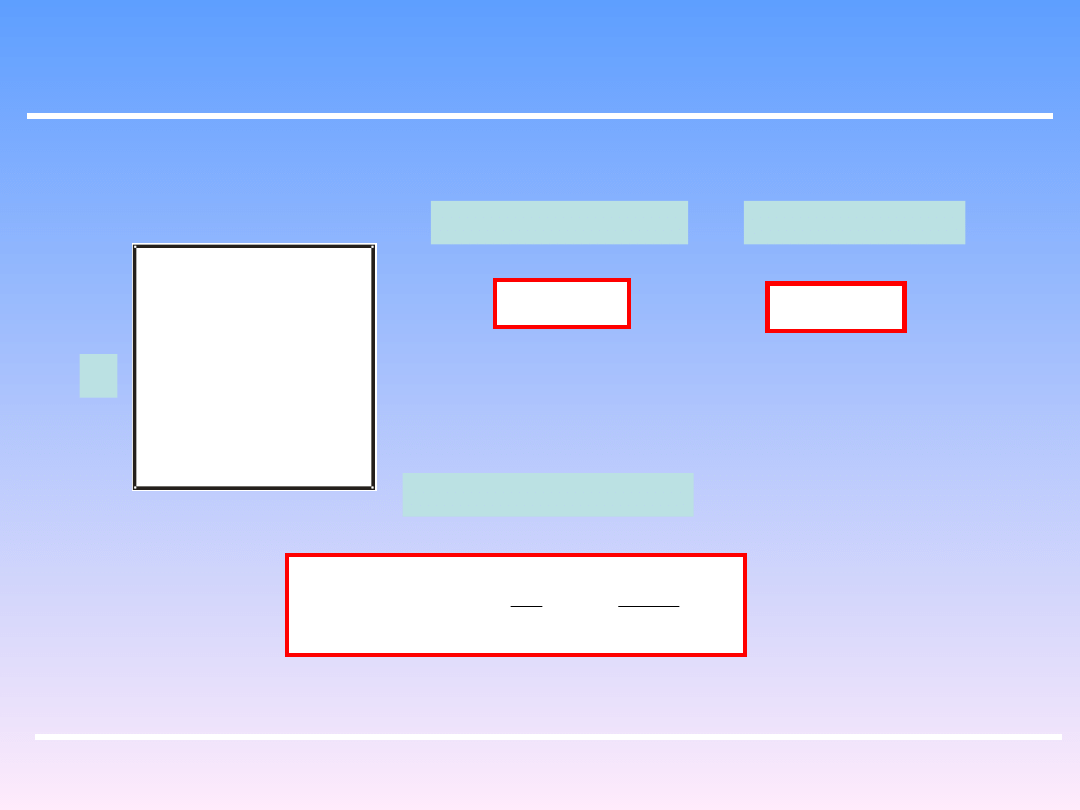
Przykłady:

D

1

D

2

Pole przekroju:





4

2

1

2

2

D

D

F







Obwód zwilżony :





2

1

D

D

B







Średnica zastępcza:



 



1

2

2

1

1

2

1

2

2

1

2

1

2

2

4

4

D

D

D

D

D

D

D

D

D

D

D

D

B

F

r

D

h

z





























Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

a

Pole przekroju:

a

a

F





Obwód zwilżony :

a

B



4

Średnica zastępcza:

a

a

a

a

B

F

r

D

h

z



















4

4

4

4

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

Przy pomocy średnicy zastępczej należy określać wartość liczby Reynoldsa.

Współczynnik oporów λ w przypadku ruchu burzliwego określa się według wzorów
lub wykresów aktualnych dla przewodów kołowych. Dla przepływów laminarnych
wprowadzony jest wzór:

Re

a





Gdzie wartości a mogą być określone teoretycznie, np.. Dla przekroju pierścieniowego
A = 96, dla kwadratowego a = 57

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

Istotnym źródłem oporów w przewodach są zmiany przekroju i kierunku przepływu.

W przypadku znormalizowanych kształtek do rur ( kolanka , redukcje, zawory itp. )
Najlepiej posługiwać się pojęciem długości zastępczej L

z

– przewodu o średnicy D

(pasującej do tej kształtki)

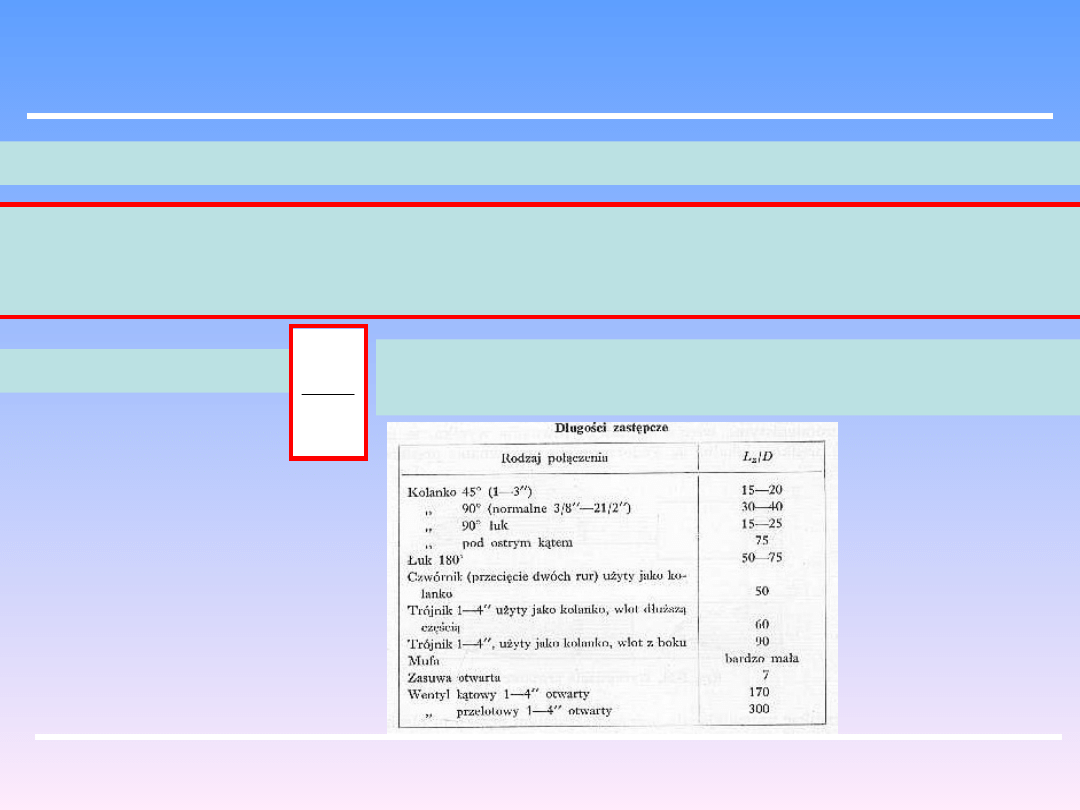
Wartości stosunków

D

L

z

dla ważniejszych kształtek są znormalizowane i
można je znaleźć w tablicach np.:

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

Identyfikujemy w obliczanej instalacji odcinki proste i kształtki. Następnie korzystając
z tablic znajdujemy sumę długości zastępczych dla kształtek i armatury. Dodajemy
to do rzeczywistej długości odcinków prostych. Tak otrzymaną wielkość wstawiamy
do równania Darcy- Weisbacha obliczamy opory na rurociągu.

g

u

D

L

D

L

Z

z

rz

2

2

2

,

1



























2

,

1

2

2

2

2

2

1

2

1

1

1

2

2

Z

g

u

z

p

g

u

z

p





















Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

2

,

1

2

1

Z

p

p







Dla przepływu dla którego z

1

=z

2

i u

1

= u

2

:

g

u

D

L

D

L

p

p

z

rz

2

2

2

1































Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

Często spotykamy się z problemem:
Musimy określić średnicę przewodu, która przy ustalonym przepływie
objętościowym V [m

3

/s] spowoduje dany z góry spadek ciśnienia (np. gdy

występuje w układzie zbiornik ciśnieniowy lub pompa o określonym
ciśnieniu na wylocie)

Zagadnienie ma charakter „uwikłany”. Nie znając średnicy przewodu nie możemy
obliczyć prędkości liniowej płynu a więc nie możemy wyznaczyć wartości liczby
Re i współczynnika oporu.

Należy skorzystać z metody „prób i błędów”

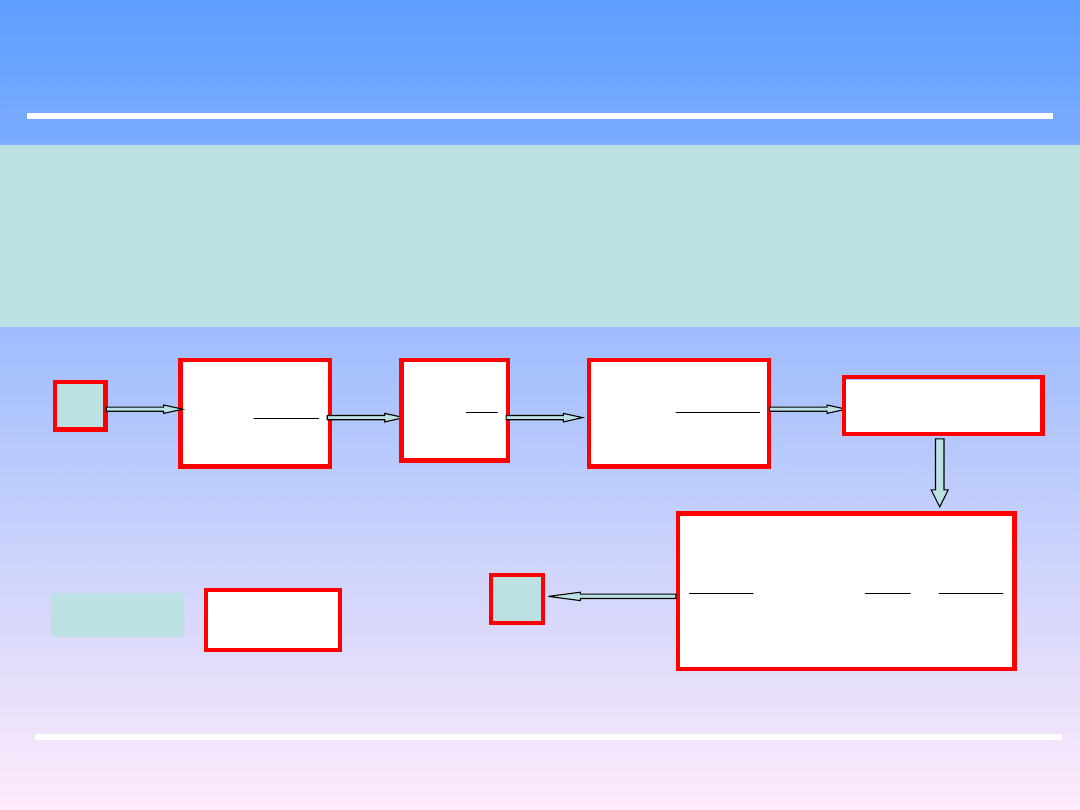
Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

Zakładamy dowolną wartość średnicy

D

z

(szukana), stąd znajdujemy przekrój

przewodu F , a następnie prędkość liniową u. Pozwala to obliczyć liczbę Re , a stąd
odczytać z wykresu wartość λ. Wstawiając jego wartość do równania
Darcy – Weisbacha, a także L i u , znajdujemy z tego równania średnicę D

0

.

Wykonujemy szereg takich przeliczeń.

4

2

z

D

F





D

z

F

V

u 





z

uD



Re









Re,

f



g

u

D

L

p

2

2













D

0

Na ogół

0

D

D

z



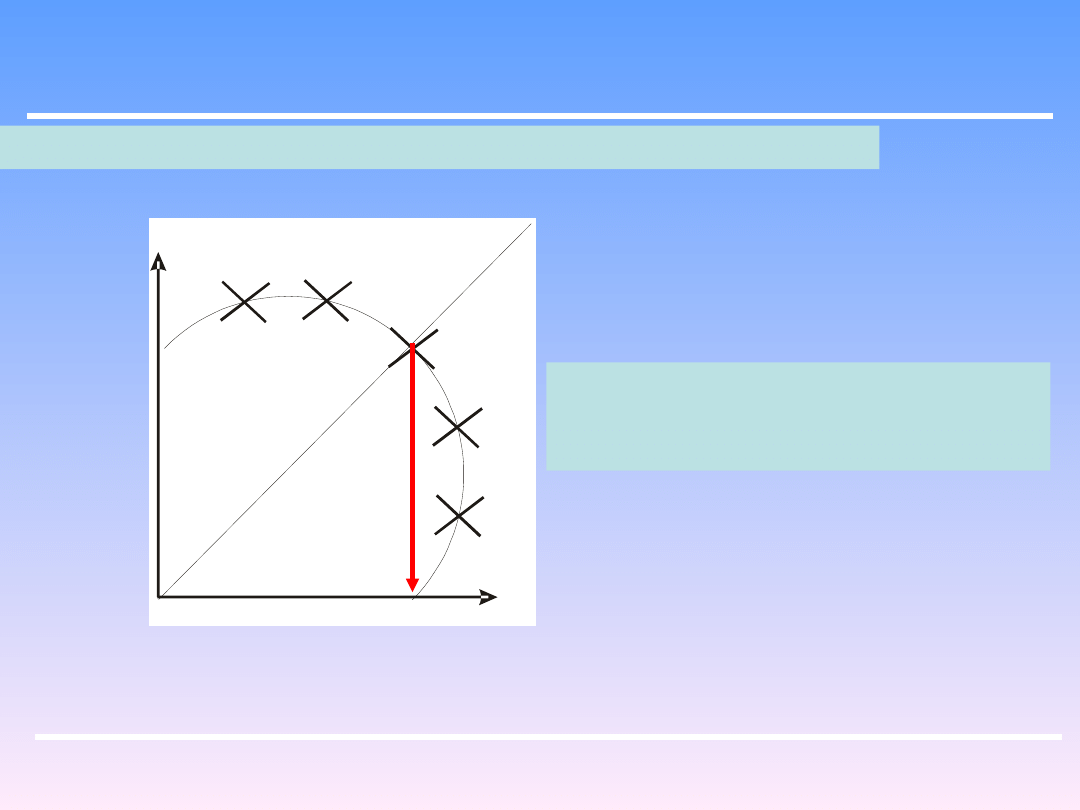
Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

Po wykonaniu szeregu takich przeliczeń, można uzyskać wykres:

D

z

D

0

D

Przecięcie krzywej przedstawiającej
tę zależność z dwusieczną układu
daje właściwe rozwiązanie.

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

Często można wyeliminować metodę „prób i błędów” przez odpowiednią zmianę
układu współrzędnych na wykresie podstawowym danego zagadnienia.
W rozpatrywanym problemie prędkość liniowa u jest funkcją natężenia objętościowego

2

4

D

V

u









po wstawieniu do równania Darcy-Weisbacha

g

D

LV

Z

2

5

2

2

,

1

8







a po w stawieniu do definicji liczby Re

D

V





4

Re

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

g

D

LV

Z

2

5

2

2

,

1

8







rugując z tego wyrażenia D za pomocą

D

V





4

Re

Otrzymamy ostatecznie:

5

5

3

2

,

1

5

3

Re

128











L

g

Z

V

Wartość lewej strony równania możemy wyznaczyć gdyż nie zawiera szukanej średnicy.

Dysponując wykresem współczynników oporu λ od Re, możemy łatwo
skonstruować
nowy wykres zależności λRe

5

od Re. Odczytując na tym wykresie wartość,

odpowiadającą lewej stronie równania, znajdujemy aktualną dla danego
problemu wartość Re a stąd D

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

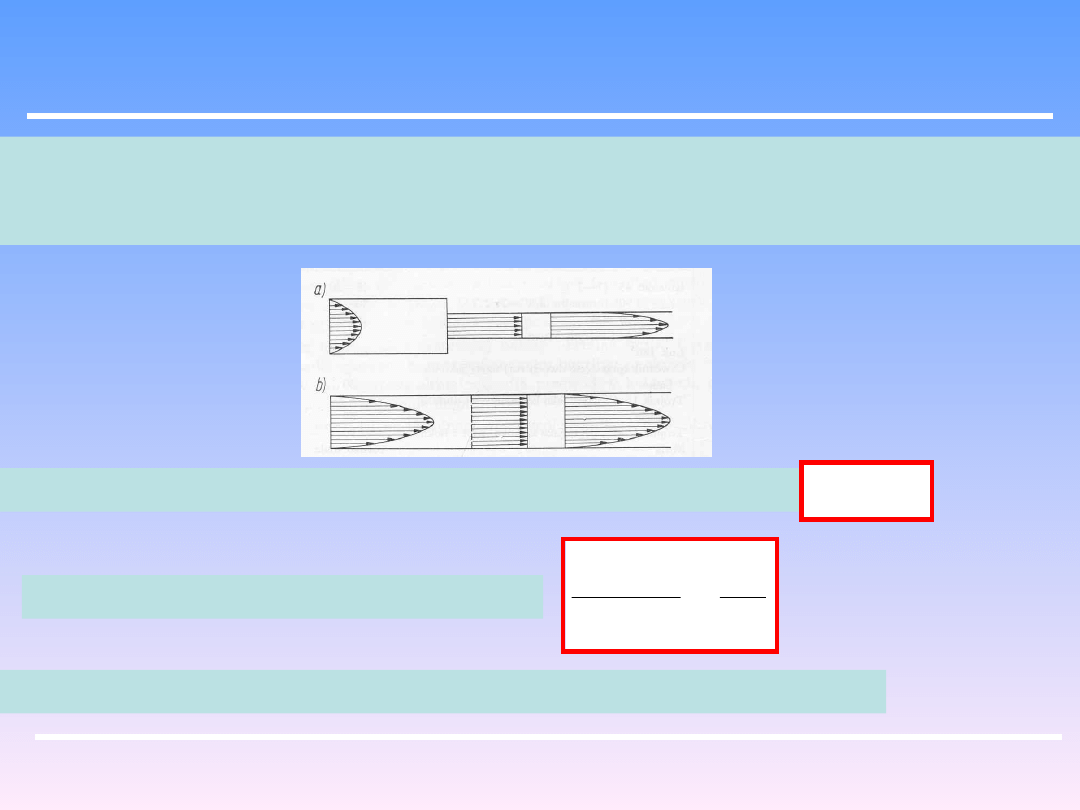
W pewnych problemach technologicznych może zależeć na wyrównaniu lokalnych
prędkości przepływu w danym miejscu przewodu. Stosuje się wtedy zasadę
zwężenia przewodu:

Prędkość u w zwężeniu jest znacznie większa niż przed nim.

1

2

u

u 

u

2

u

1

Stąd z równania Bernoullego wynika:

g

u

p

p

2

2

2

1

2







Ponieważ ciśnienie jest stałe w przekroju to i u musi być stałe !!!

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

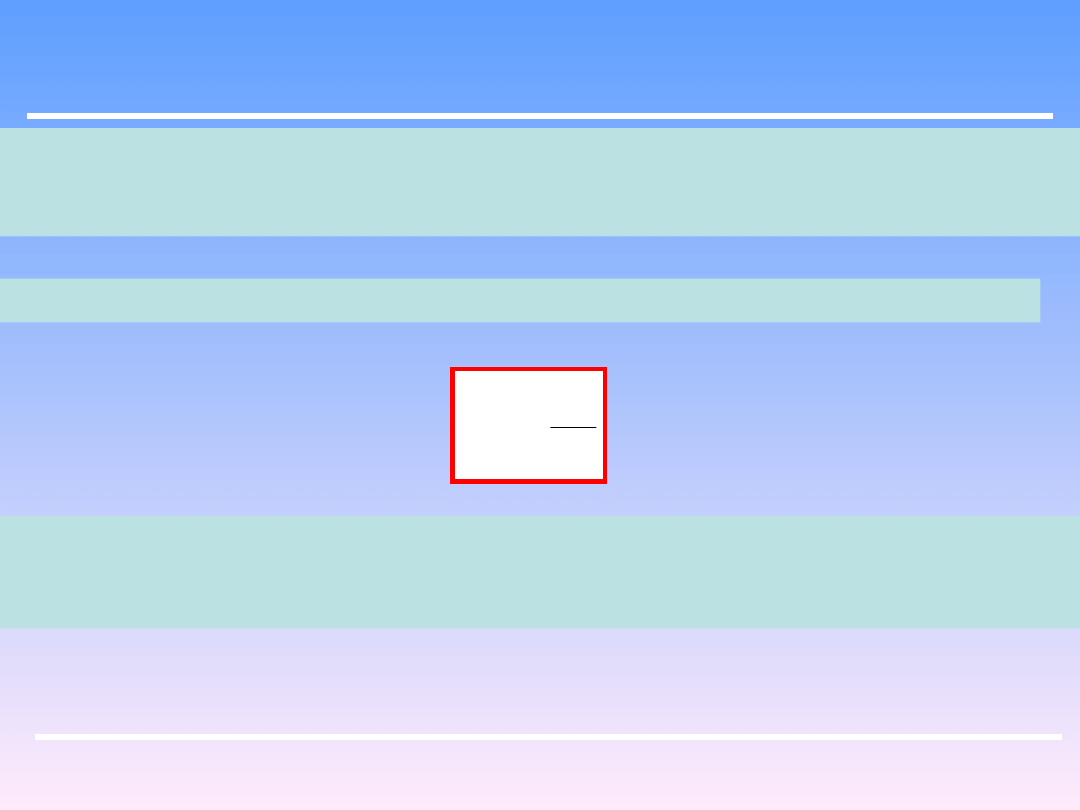
Podobny efekt wyrównania prędkości można też uzyskać wstawiając do przewodu
o stałym przekroju blachę dziurkowaną (b). Każdy otworek odgrywa rolę zwężenia
Stąd w niewielkiej odległości od blachy prędkość jest wyrównana.

Opory przepływu przez blachę dziurkowaną można przedstawić następująco:

g

u

Z

2

2

0





Gdzie u

0

to prędkość w otworkach. Współczynnik φ jest współczynnikiem oporów

dla wlotu, przepływu przez otwór i wylotu. Minimum oporu uzyskuje się dla blachy
o grubości 5 mm.

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

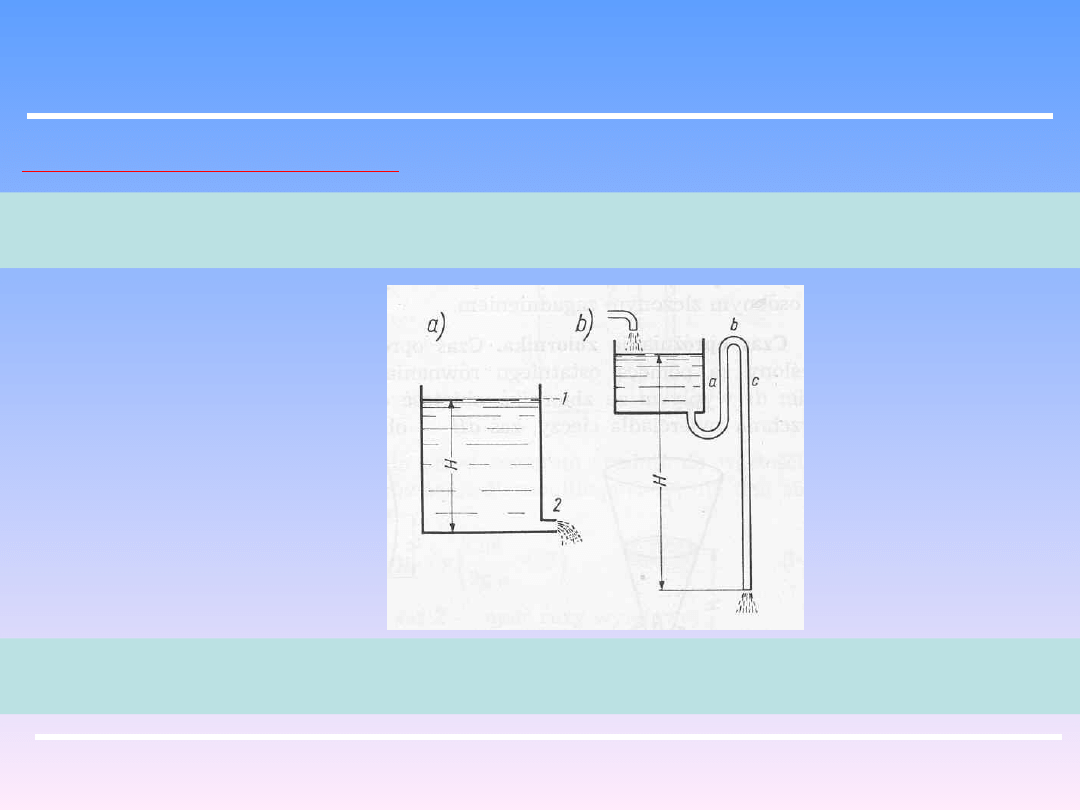
Wypływ cieczy ze zbiornika:

Stosujemy równanie Bernoullego dla zwierciadła cieczy oraz dla przekroju strumienia
w otworze wylotowym.

Zaniedbujemy opory, prędkość obniżania się zwierciadła przyjmujemy jako znikomo
małą, a ciśnienia nad zwierciadłem i u wylotu za jednakowe.

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

g

u

z

z

2

2

2

2

1





Otrzymujemy:

gH

u

2

2



Prędkość wypływu cieczy ze zbiornika

Prędkość ta zależy od H, a nie zależy od kształtu naczynia.

Urządzenie rys. (b) stanowi przykład samoczynnie działającego aparatu pulsacyjnego.
Przy ciągłym dopływie cieczy do pustego zbiornika początkowo ciecz z niego
nie wypływa. Dopiero gdy poziom cieczy sięgnie do kolanka i zaleje rurę spustową
nastąpi opróżnienie zbiornika.

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

gH

u

2

2



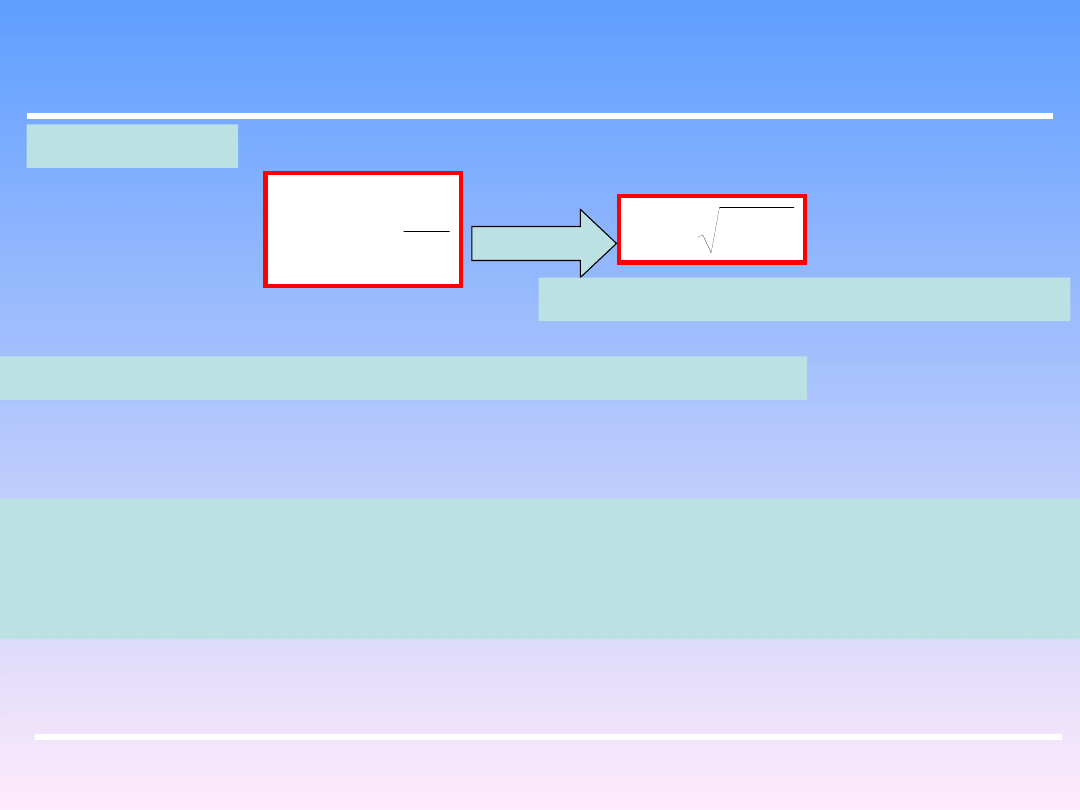
Jeżeli wyrażenie :

Pomnożymy przez powierzchnię otworka
wylotowego f, to nie otrzymamy objętościowego
natężenia wypływu, wskutek zjawiska
zwężenia strumienia tuż za otworem wylotowym.

Wprowadzono współczynnik wypływu:

gH

f

Q

2









Współczynnik φ zależy od rodzaju cieczy i od profilu otworu wylotowego. Dla
wypływu cieczy doskonałej przez ostry otwór w ścianie zbiornika wynosi on
0,611. Dla innych profili wylotowych φ = 0.57 – 1.00

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

Przy pomocy równania:

gH

f

Q

2









można określić czas opróżniania
zbiornika.

Bilans masy:

 

out

m

dt

m

d



dt

dH

F

dt

dV







gH

f

dt

dH

F

2













Q

dt

dV



Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

dt

gH

f

dH

F













2



















k

t

H

dt

g

f

H

dH

F

0

0

2











H

k

dH

H

F

g

f

t

0

2

1



Ogólny wzór na prędkość opróżniania zbiornika.

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

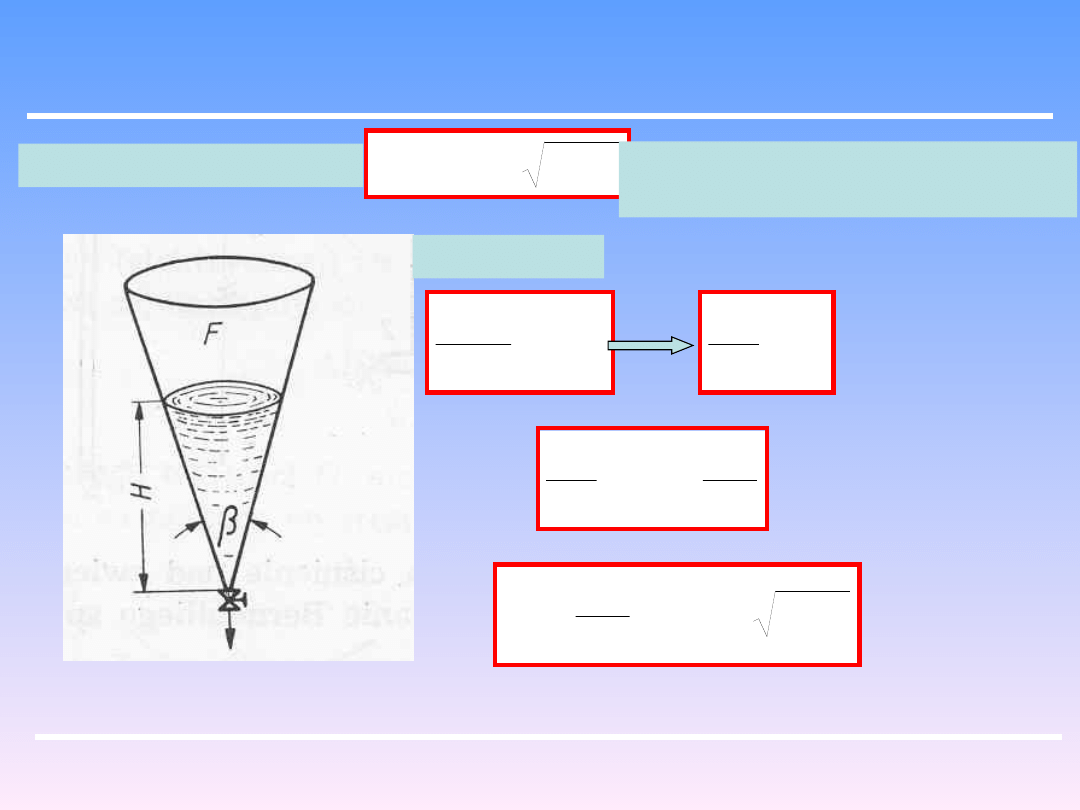
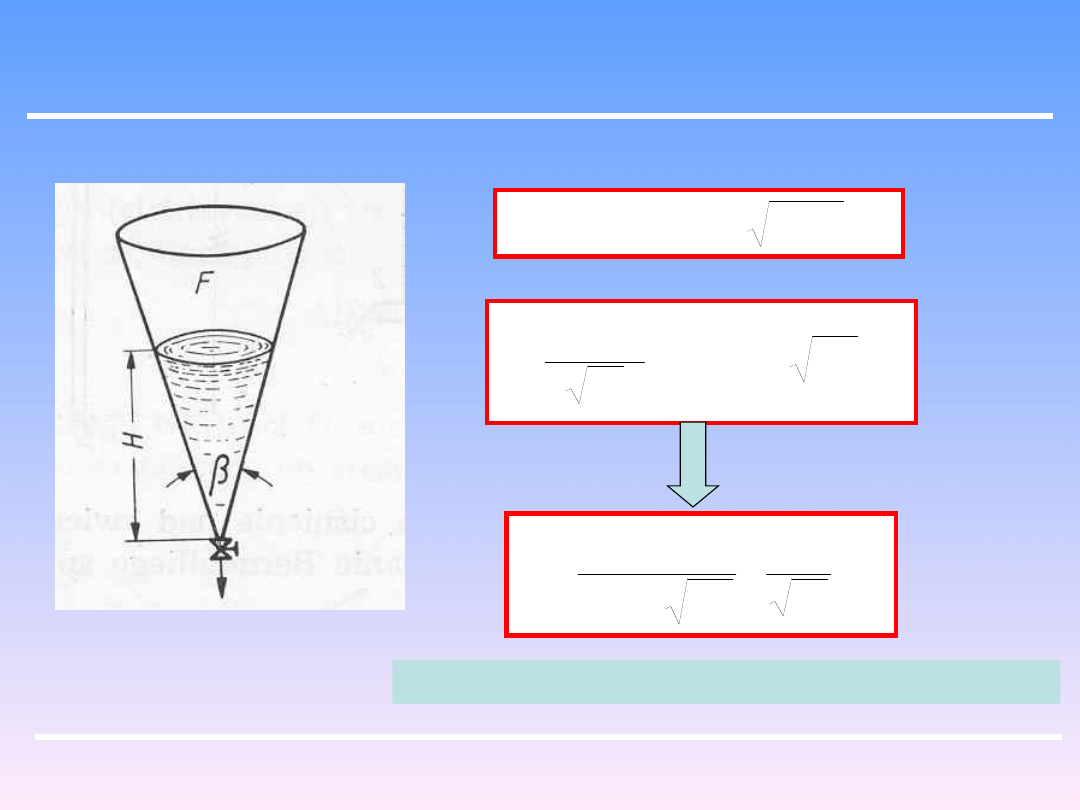
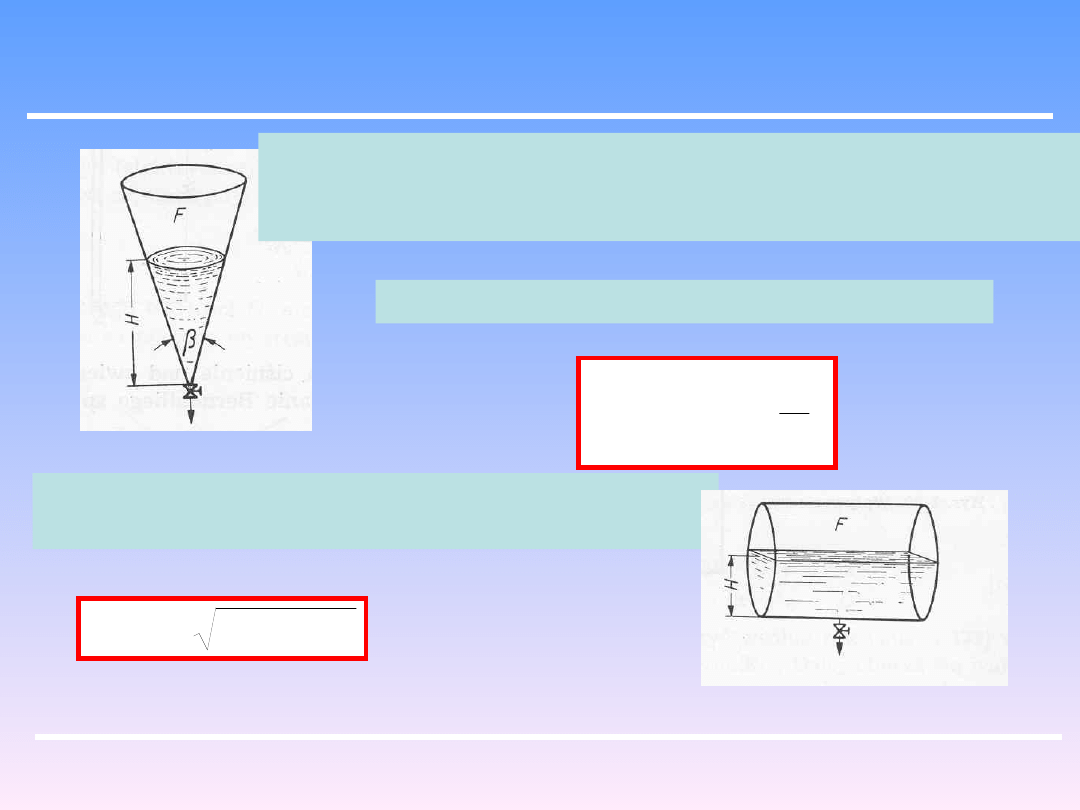
Z kształtu zbiornika wynika zależność powierzchni zwierciadła
cieczy od wysokości H. Dla zbiornika cylindrycznego
F=const.

Dla stożkowego z kątem wierzchołkowym β:















2

2

2





tg

H

F

Dla poziomej cylindrycznej cysterny o długości L
i średnicy D:

2

2

H

HD

L

F





Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

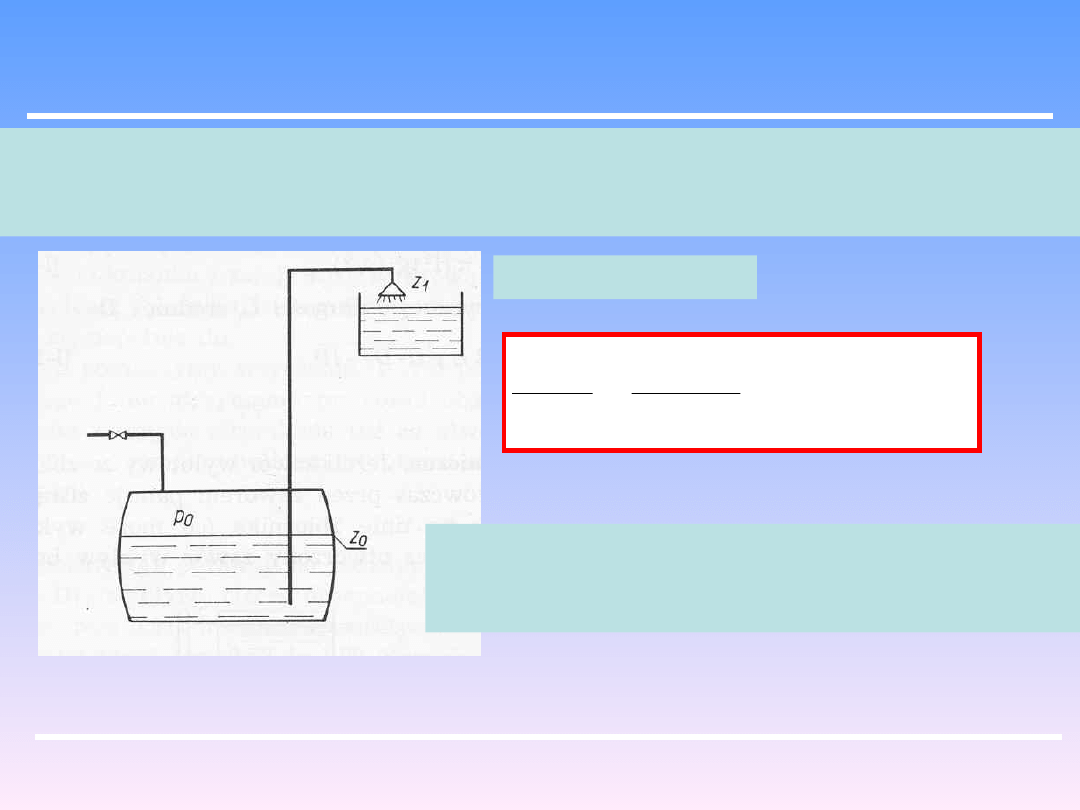
Wypływ ze zbiornika może być też spowodowany ciśnieniem powietrza sprężonego
działającego na powierzchnię cieczy w zamkniętym zbiorniku, jak to ma miejsce w
podnośniku hydraulicznym.

Rów. Bernoullego:





1

,

0

0

1

1

0

1

2

1

2

Z

z

z

p

p

g

u















Prędkość wypływu cieczy zależy więc od:
nadciśnienia w zbiorniku, wysokości podnoszenia
oraz oporów w przewodzie.

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

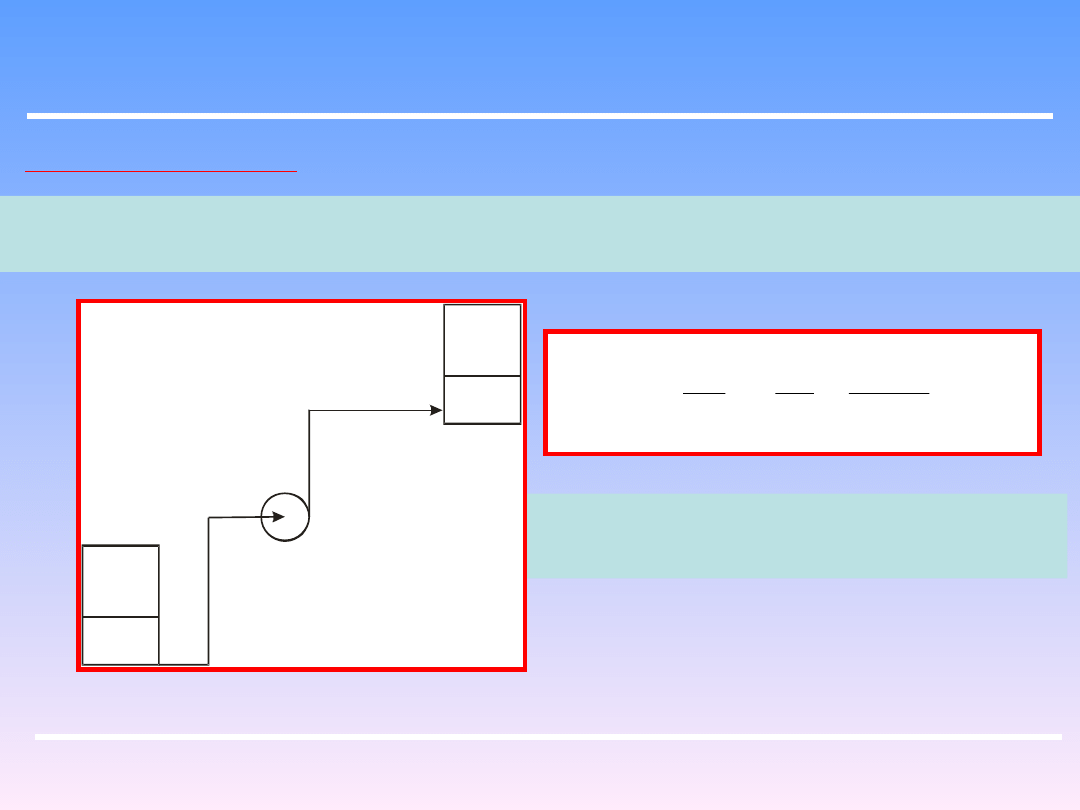
Pompowanie cieczy:

Istnieje granica wysokości ssania dla każdej pompy. Można ją określić stosując
Równanie Bernoullego dla zwierciadła cieczy (0) i dla przekroju (1) przed pompą























1

,

0

1

2

1

1

0

0

1

2

Z

g

u

p

p

z

z







Stąd wynika że z

1

-z

0

musi być mniejsze

Od p

0

/γ. Dla wody jest to około 10 m

z

0

z

1

z

2

z

3

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

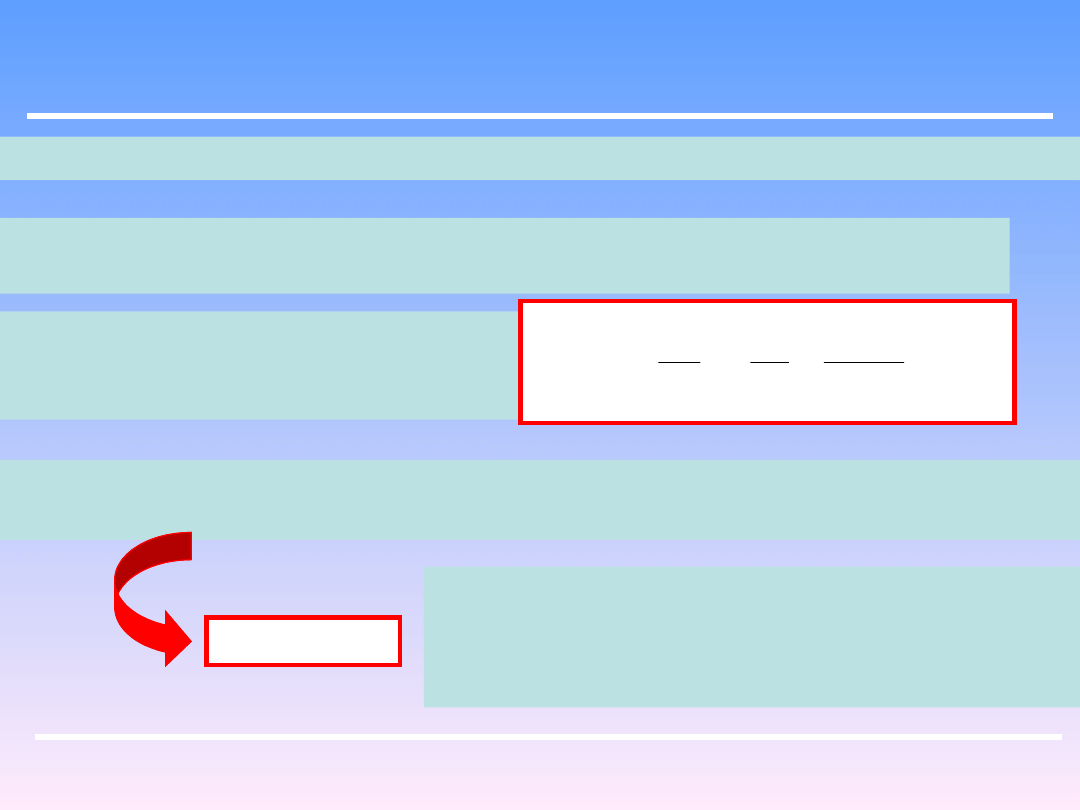
Ta graniczna wartość wysokości ssania ulega zmianie wskutek wielu czynników

Wahania ciśnienia atmosferycznego ( ok. 1 m słupa wody )
Na dużych wysokościach zmienia się wartość ciśnienia atmosferycznego

Wysokość ssania zgodnie z równaniem
maleje też ze wzrostem szybkości
pompowania























1

,

0

1

2

1

1

0

0

1

2

Z

g

u

p

p

z

z







Istotny jest wpływ temperatury cieczy, gdyż ciśnienie przed pompą p

1

nie może spaść

poniżej prężności pary nasyconej

KAWITACJA

Wrzenie cieczy w przewodzie na skutek spadku
ciśnienia, poniżej prężności pary nasyconej
prowadzi to do zakłóceń lub przerwania pracy
pompy.

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

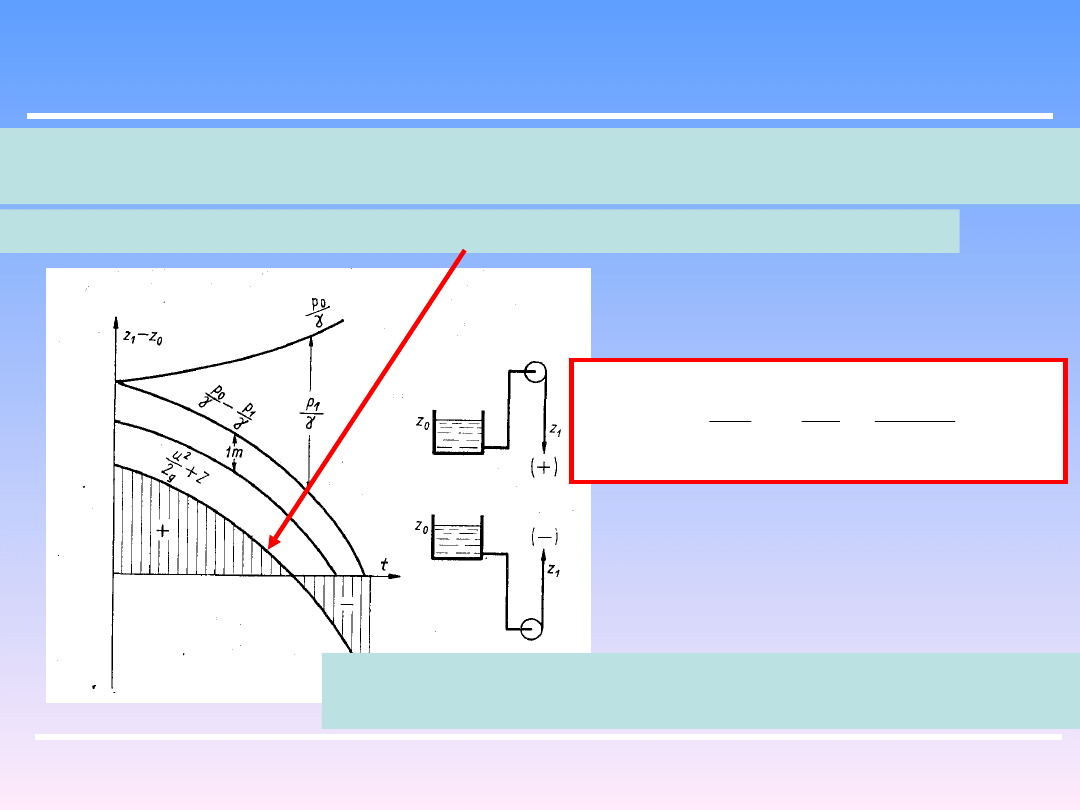
Ze wzrostem temperatury rośnie prężność pary, a ciężar właściwy cieczy γ nieco
maleje.

Można przedstawić krzywą wysokości ssania jako funkcję temperatury:

Wartości ujemne, dla gorących cieczy  pompa musi stać

Poniżej poziomu cieczy.























1

,

0

1

2

1

1

0

0

1

2

Z

g

u

p

p

z

z







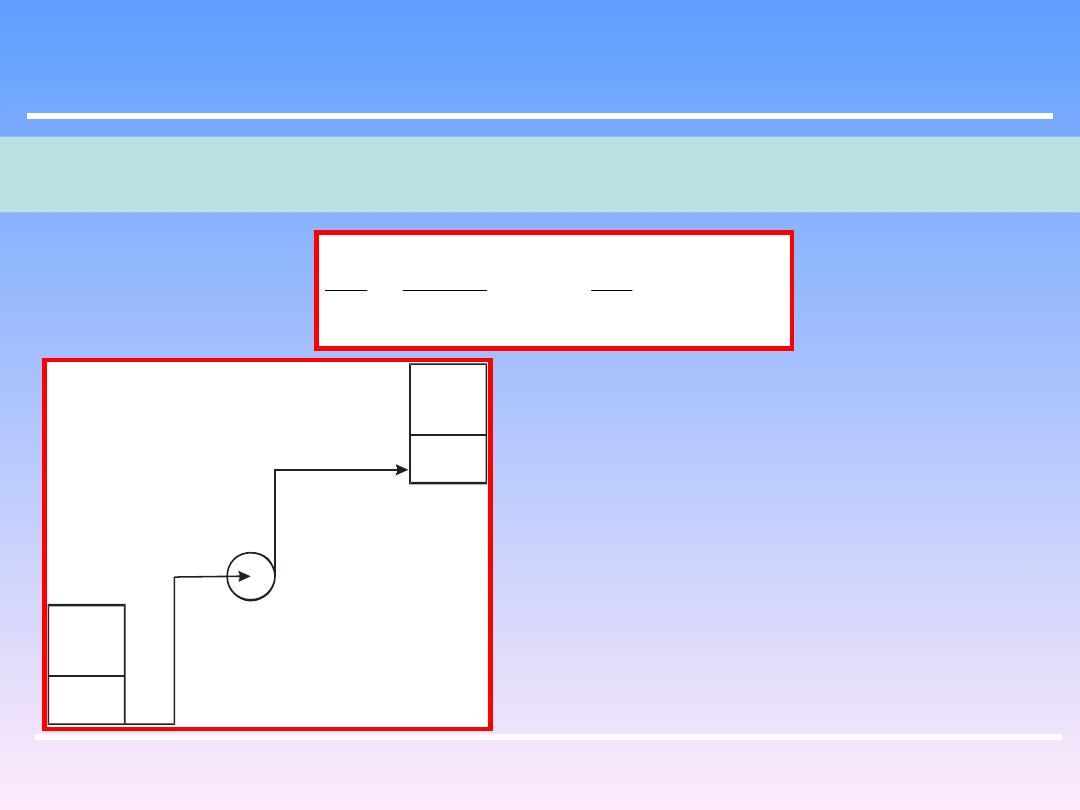
Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

Dla przypadku przedstawionego na schemacie, równanie Bernoullego dla przekroju
za pompą i dla zwierciadła w górnym zbiorniku, przyjmuje postać:

3

,

2

3

3

2

2

2

2

2

2

Z

z

p

z

g

u

p

















z

0

z

1

z

2

z

3

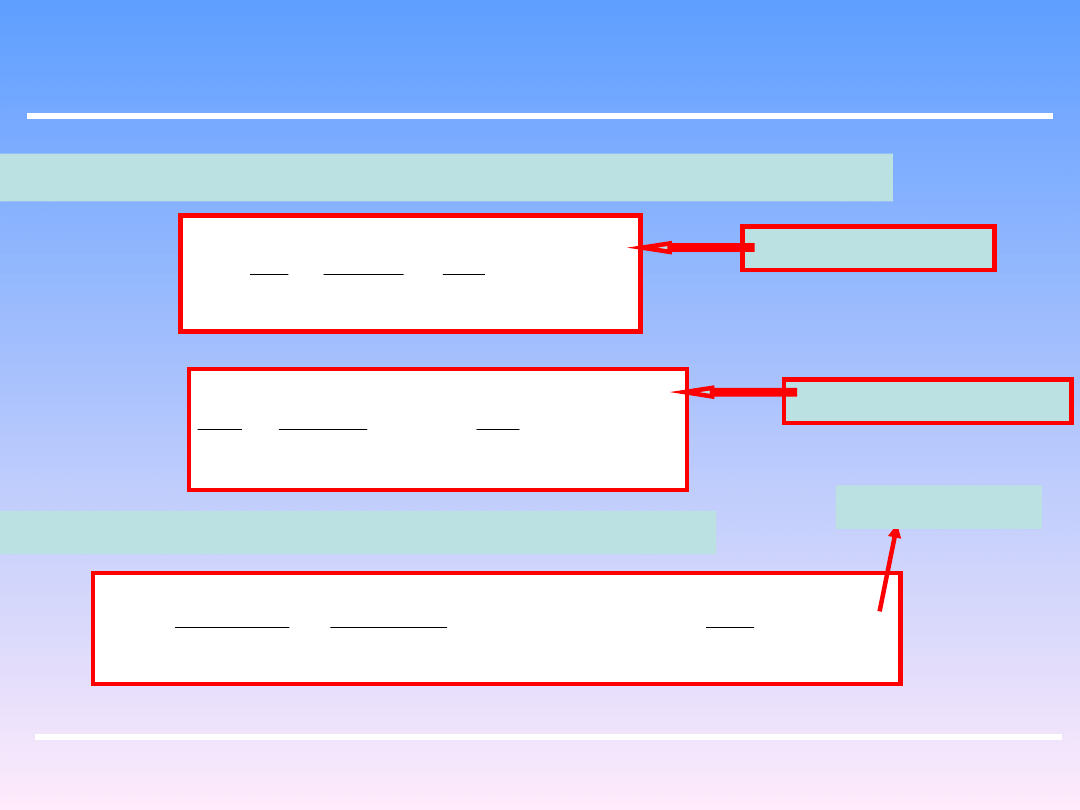
Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

Średnice za i przed pompą są zwykle jednakowe u

2

=u

3

z równań :

3

,

2

3

3

2

2

2

2

2

2

Z

z

p

z

g

u

p

















1

,

0

0

0

1

2

1

1

1

2

Z

z

p

g

u

p

z

















na ssaniu pompy

na tłoczeniu pompy





Z

z

p

Z

z

z

p

p

p

p

H































0

3

0

3

1

2

Otrzymujemy różnicę ciśnień które pokonuje pompa:

Suma oporów

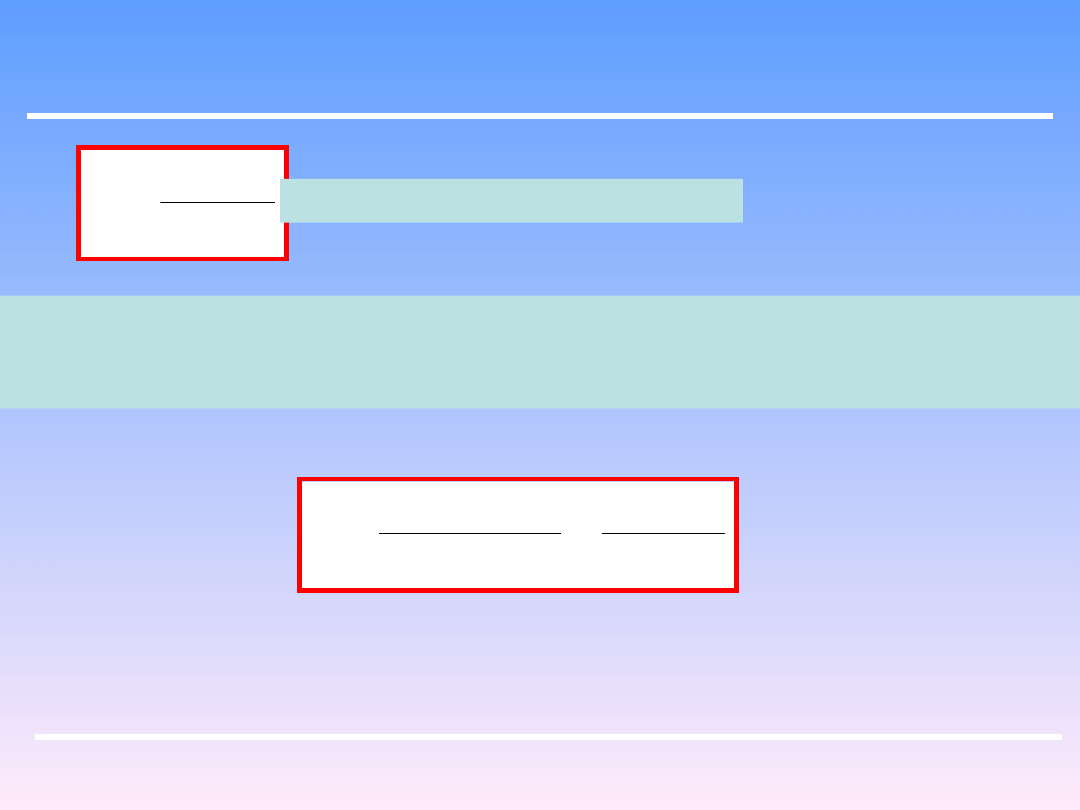
Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów



1

2

p

p

H





Jest to wysokość pompowania

Można wykazać, że iloczyn różnicy ciśnień na pompie (p

2

-p

1

) i natężenia objętościowego

przepływu V oznacza pracę pompy na jednostkę czasu. Uwzględniając sprawność
pompy η otrzymujemy wzór na moc silnika:























V

H

V

p

p

N

1

2

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

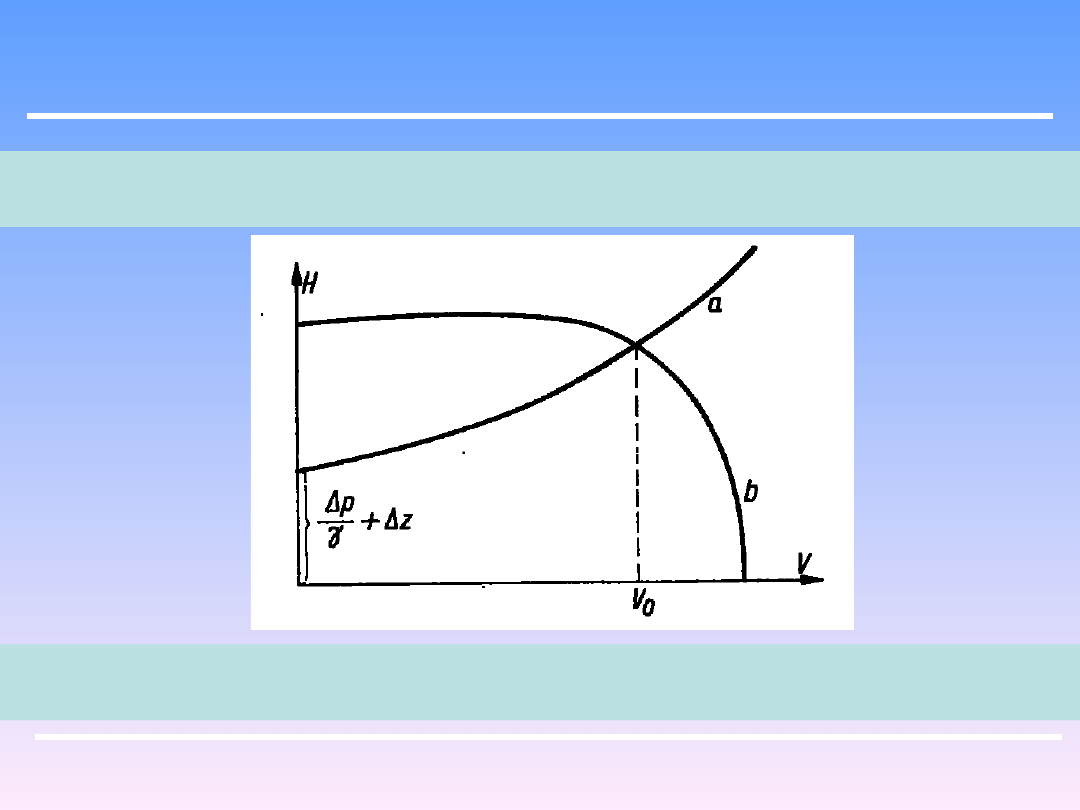
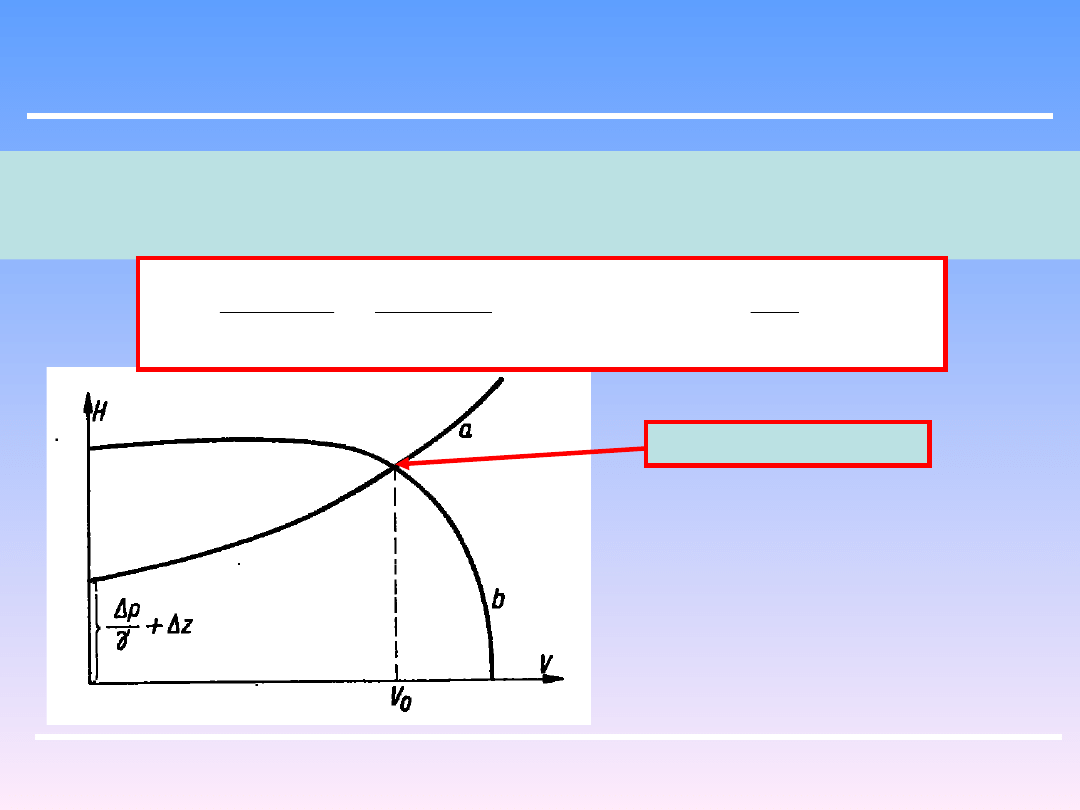
Każda pompa ma własną charakterystykę – zależność między wysokością pompowania
H i wydajnością V krzywa b .

Można za jej pomocą wyznaczyć jaką wydajność uzyska się z danej pompy załączonej
do określonego układu.

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

Uwzględniając zależność oporu Z od prędkości przepływu (np.. rów. Darcy –
Weisbacha) a więc i od natężenia przepływu V , można określić wysokość
pompowania H jako funkcji V ( krzywa a)

Punkt pracy pompy





Z

z

p

Z

z

z

p

p

p

p

H































0

3

0

3

1

2

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

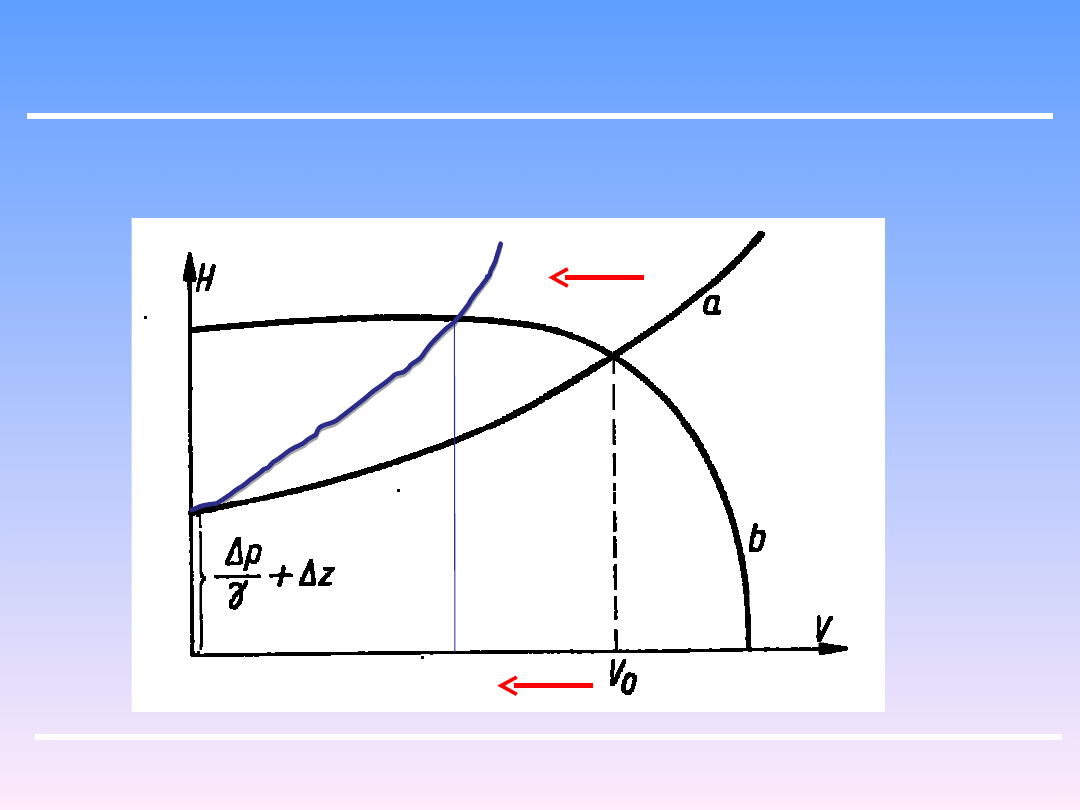
a`

V

0

`

Zwiększenie oporów

Inżynieria Chemiczna i Procesowa

Wykład nr 4 : Procesy mechaniczne. Opory przepływów

Dla szeregowego połączenia dwóch pomp
Dla tej samej wartości Q dodajemy wysokości
podnoszenia H

Dla szeregowego połączenia dwóch pomp
Dla tej samej wartości Q dodajemy wysokości
podnoszenia H

Dla równoległego połączenia dwóch pomp
dla tej samej wartości H dodajemy Q

Dla równoległego połączenia dwóch pomp
dla tej samej wartości H dodajemy Q