Analiza techniczna

Teoria Carolana

Kurs analityka giełdowego

Cz. 4

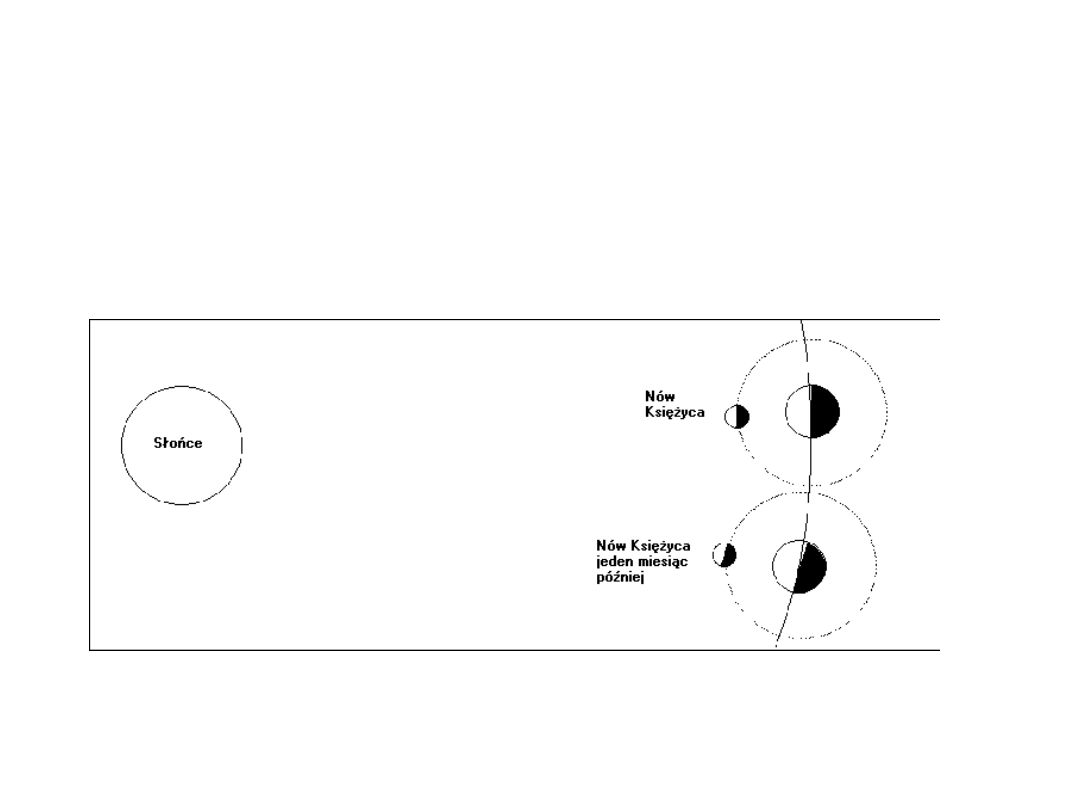
Miesiąc księżycowy

Lunacja

• Odstęp czasu między kolejnymi nowiami

Księżyca, równy 29 dniom 12 godzinom i

44 minutom (29,530589 dnia), =

miesiącem synodycznym lub lunacją.

• Miesiąc synodyczny jest o ponad 2 dni

dłuższy od okresu obiegu Księżyca wokół

Ziemi (po tym czasie Księżyc wraca do

tego samego położenia względem

gwiazd - zwany także miesiącem

syderycznym.







4



Zależności

Co oddziałuje na inwestorów

• Także Carolan w swojej książce

podkreśla wagę związków
zachodzących między zachowaniami
poszczególnych inwestorów a
odpowiednio:

• Oddziaływaniem Księżyca
• Oddziaływaniem Słońca
• Oddziaływaniem innych planet

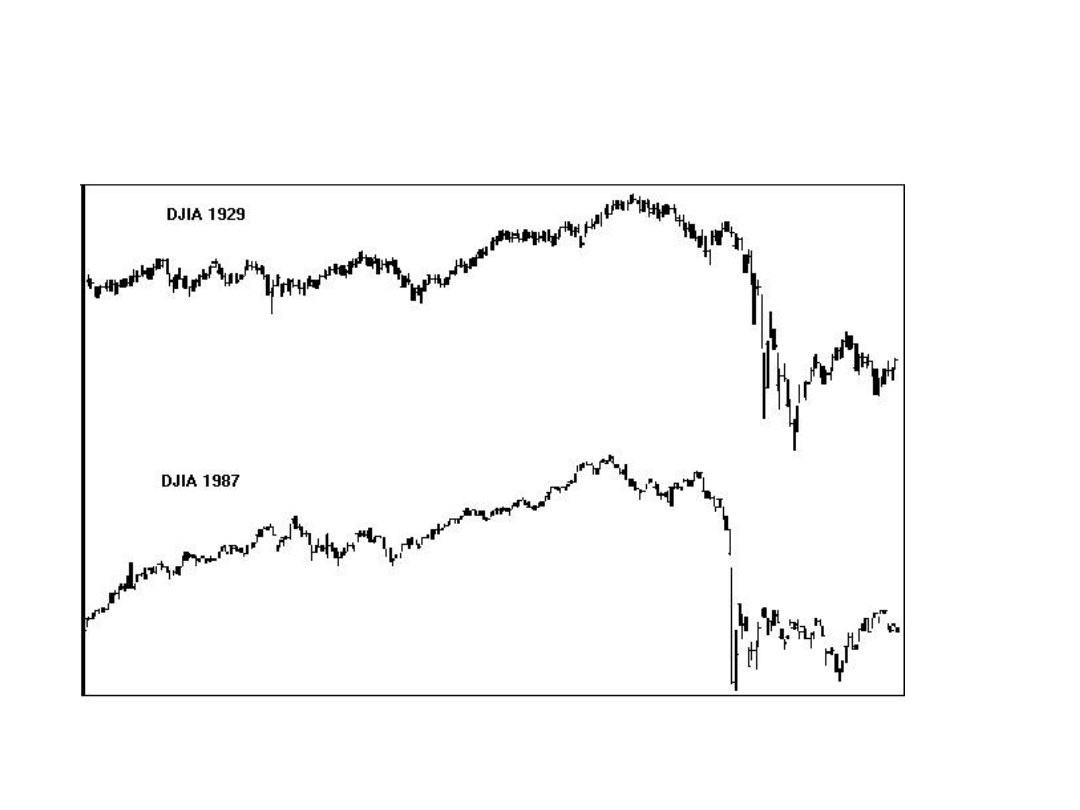
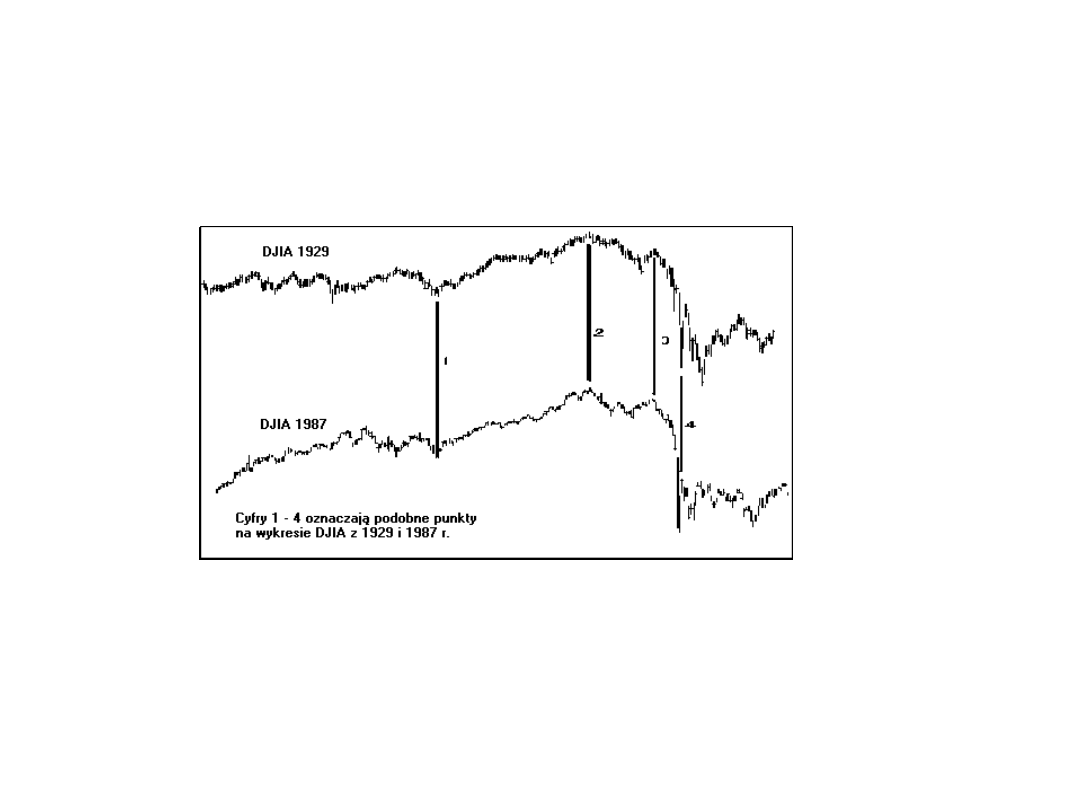
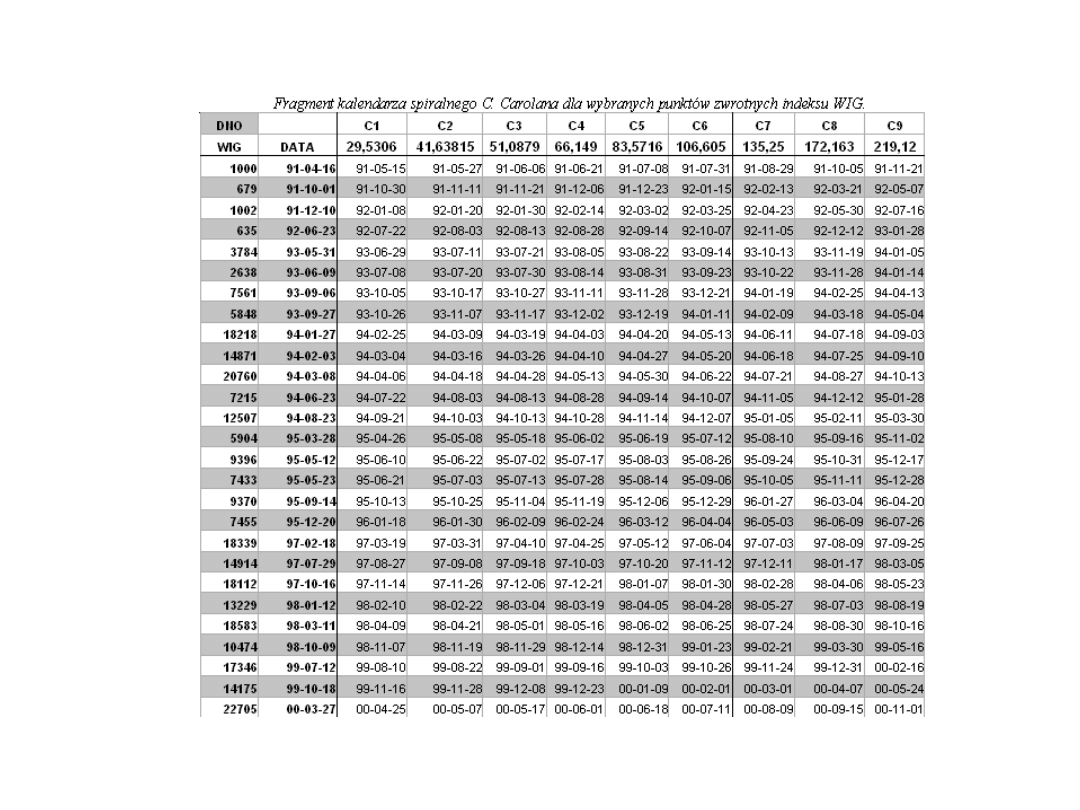
Wg Carolana między datami obu krachów istniał związek opisany za pomocą kalendarza spiralnego

Źródło: opracowanie własne na podstawie strony internetowej:

www.calendarresearch.com

z dnia 15.08.2000

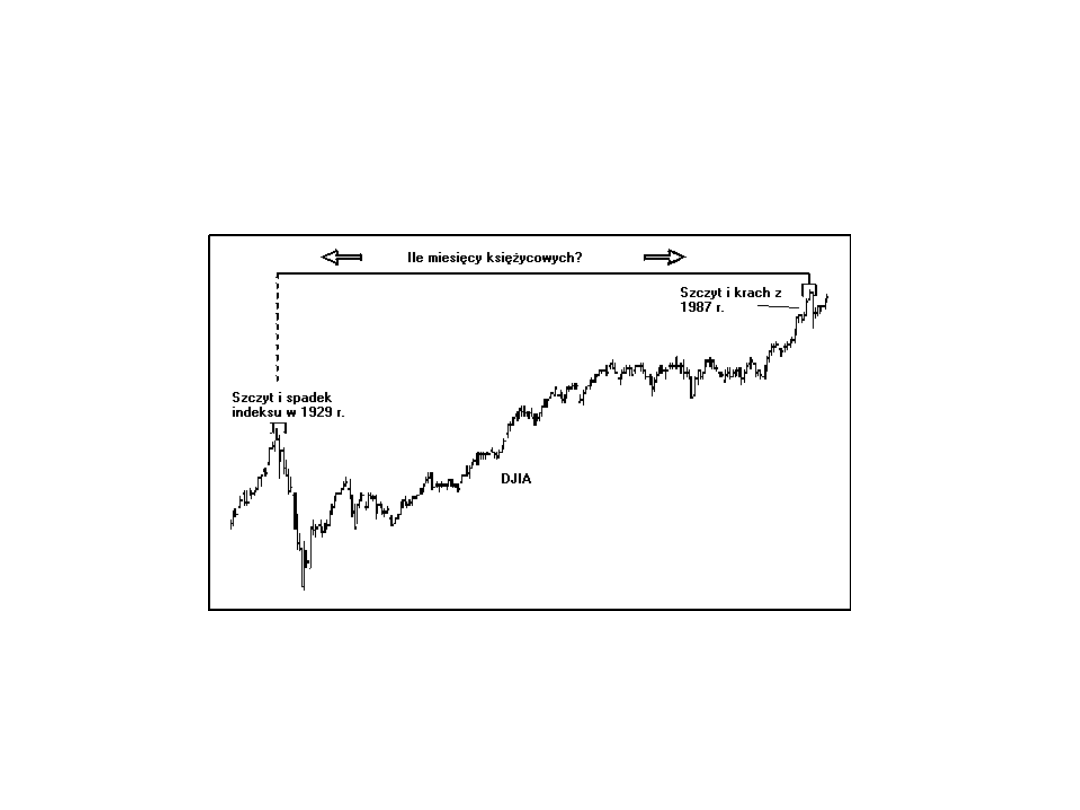
Kluczowym zagadnieniem jest ocena odległości czasowych za pomocą kalendarza spiralnego, którego jednostką jest miesiąc księżycowy.

Źródło: opracowanie własne na podstawie strony internetowej: www.calendarresearch.com z dnia 15.08.2000

Warunki

• Aby wystąpił identyczny wzór zachowań

rynku, konieczne jest, zdaniem C.

Carolana, spełnienie trzech warunków:

1. Okres między analogiami musi odpowiadać

jednostce kalendarza spiralnego lub

stanowić dokładną sumę tych jednostek.

2. Analogie występują w tej samej porze roku

słonecznego (harmonia solarna).

3. Analogie występują w tej samej fazie

Księżyca (harmonia lunarna).

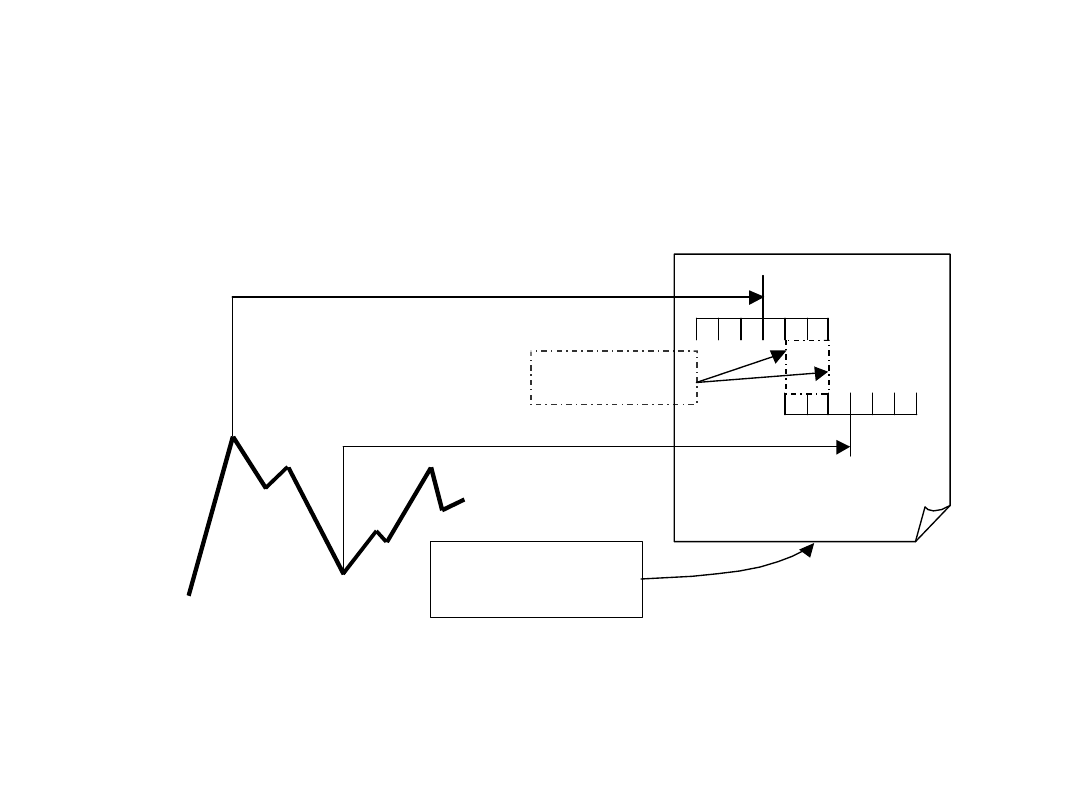
Etapy tworzenia kalendarza spiralnego na przykładzie dwu wybranych punktów zwrotnych D1 i D2.
W rzeczywistości liczba punktów zwrotnych jest znacznie większa.

D1

D2

D1m - m -ty dzień docelowy dla D1

D2n - n -ty dzień dzień docelowy dla D2

Rama czasowa dla D2

<D2n-3; D2n+3>

Rama czasowa dla D1

<D1m -3; D1m+3>

Część wspólna obu ram

to okienko czasowe

Sprawdzenie czy dni docelowe

D1m i D2n

spełniają warunki skupiska dat

Źródło: opracowanie własne

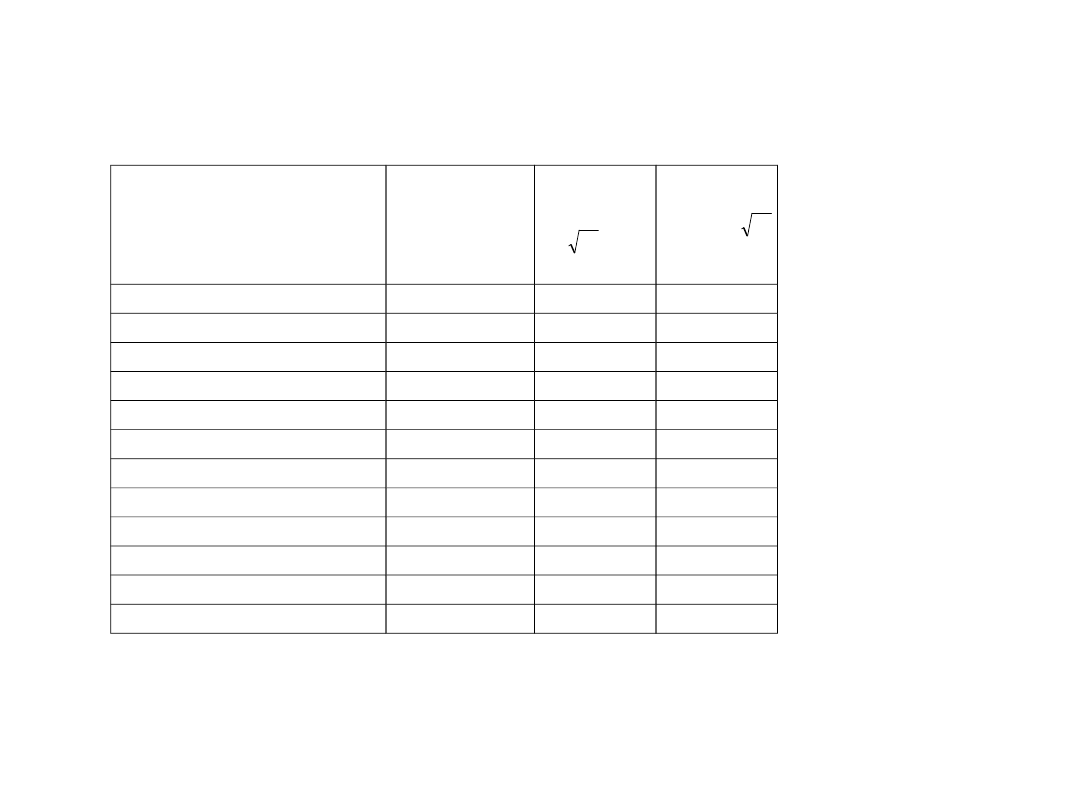
Kalendarz spiralny Carolana

Liczba
księżyców

n

F

Liczba
dni

n

F

*

5306

,

29

Numer kolejny

- indeks

N

A

(dwa podciągi – objaśnienie w

tekście)

Kolejna liczba

ciągu

Fibonacciego

F

n

1

1

1,00

29,53

2

1

1,00

29,53

3

2

1,41

41,8

4

3

1,73

51,1

5

5

2,24

66,0

6

8

2,83

83,5

7

13

3,61

106,5

8

21

4,58

135,3

9

34

5,83

172,2

10

55

7,42

219,0

11

89

9,43

278,6

12

144

12,00

354,4

A

– Ciąg kolejnych indeksów rozbity został na podciągi o jednostkach parzystych i nieparzystych.

Źródło: Carolan C.„Kalendarz spiralny”, WIG – Press, Warszawa 1996

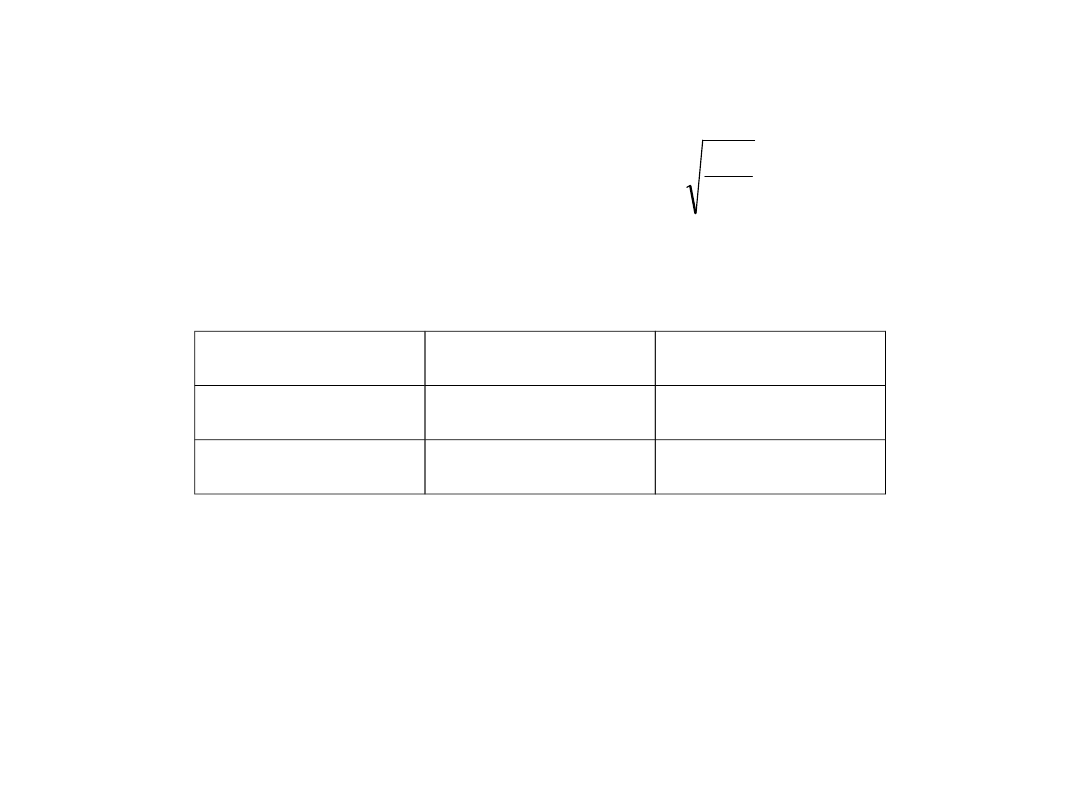
Parametry skupiska wg C. Carolana

Ten sam ciąg

Różne ciągi

Różnica dni
kalendarzowych

6 lub mniej dni

3 lub mniej

Różnica wartości
indeksów

8 lub mniej

5 lub mniej

Źródło: Carolan C. „Kalendarz spiralny”, WIG – Press, Warszawa 1996

...

618

,

1

lim

2













n

n

n

F

F

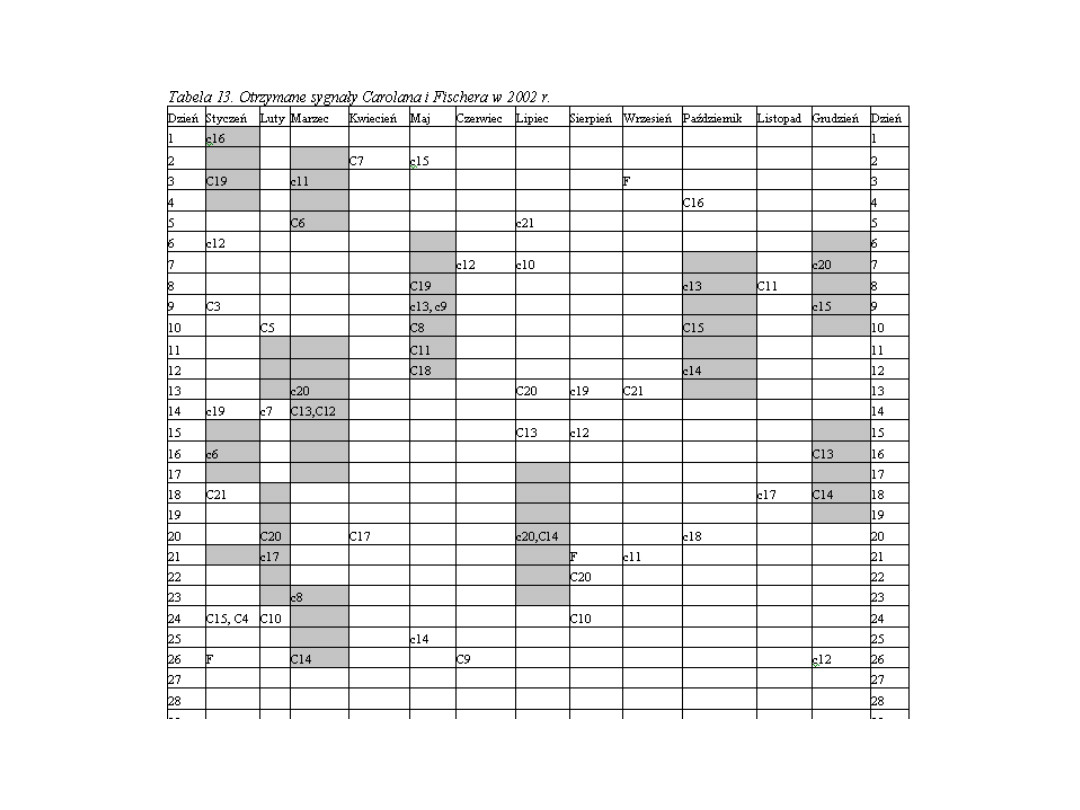
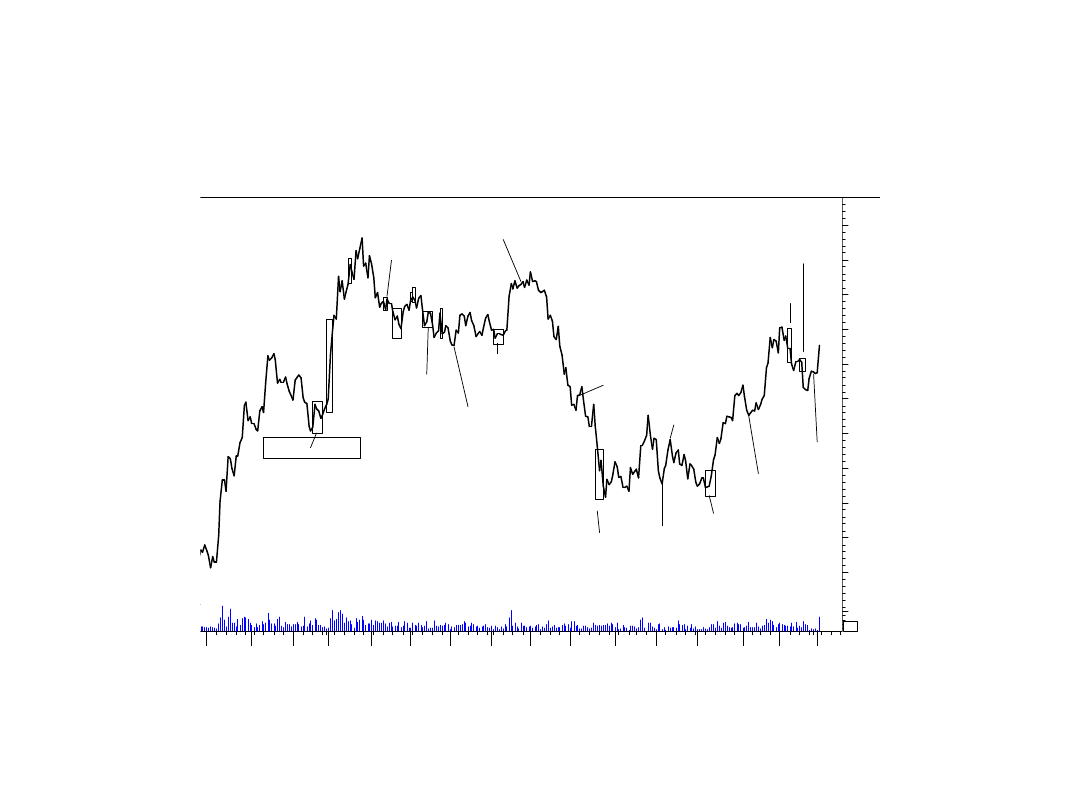
Sygnały Carolana i Fischera w 2002 r.

Oct

Nov

Dec

2002

Feb

Mar

Apr

May

Jun

Jul

Aug

Sep

Oct

Nov

Dec

2003

50000

x10

11500

12000

12500

13000

13500

14000

14500

15000

15500

16000

16500

O

21.01

P

F

26 stycznia

18-22 luty

O

2 - 5 marzec

11 - 17 marca

Wig - w cenach zamknięcia

23 -26 marca

6 - 12 maja

O

15 maj

O

C17 - bez okna

17 - 27 grudnia
3 okienka Carolana

P

c12

7 czerwca

j

C9

26 czerwca

i

C20 i C13

13 - 15 lipca

17 - 23 lipca

O

F

21 sierpnia

+ C20

7 - 13 październik

k

c18

20 paźdz.

h

c17

18 listopad

6-9 grudnia

15-19 grudnia

11-13 luty

h

F

27 grudnia

C7
dołek z początku kwietnia

c14

c21 i c10

C21

C11

c12
26 grudnia

O

F

3 września

WIG (14,584.89, 14,794.97, 14,564.39, 14,770.53, +392.420)

Źródło: opracowanie własne

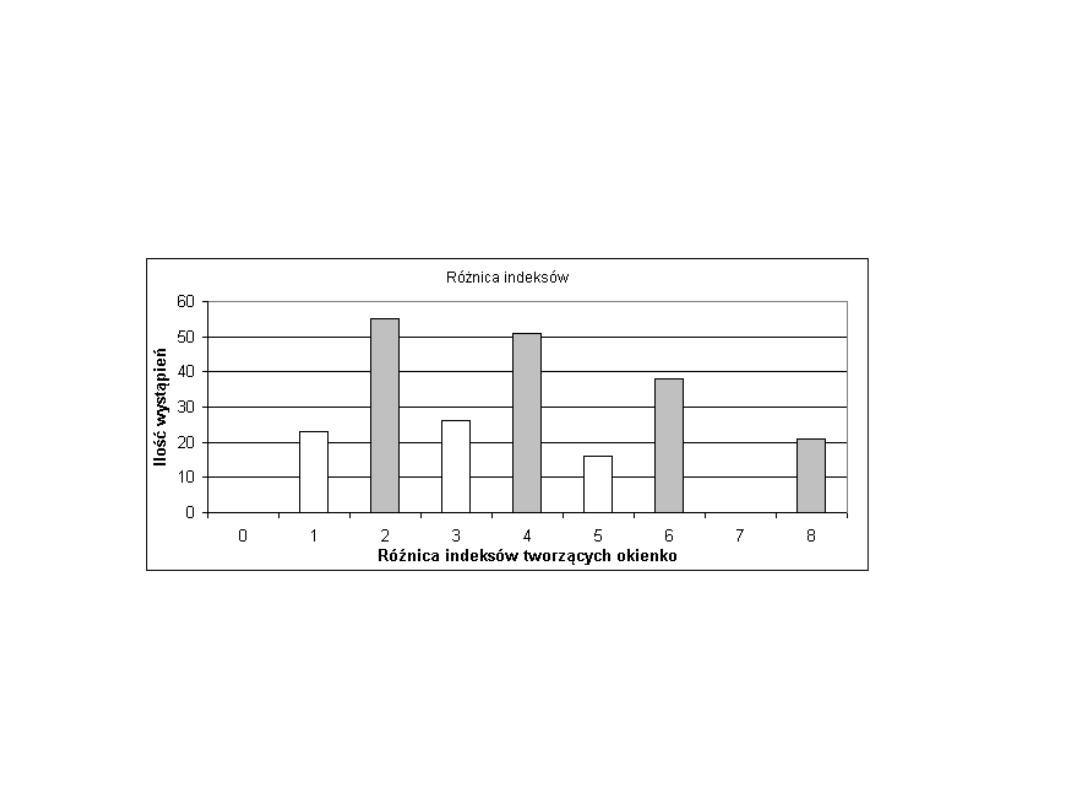
Liczebność różnic indeksów tworzących okienka Carolana

Źródło: opracowanie własne

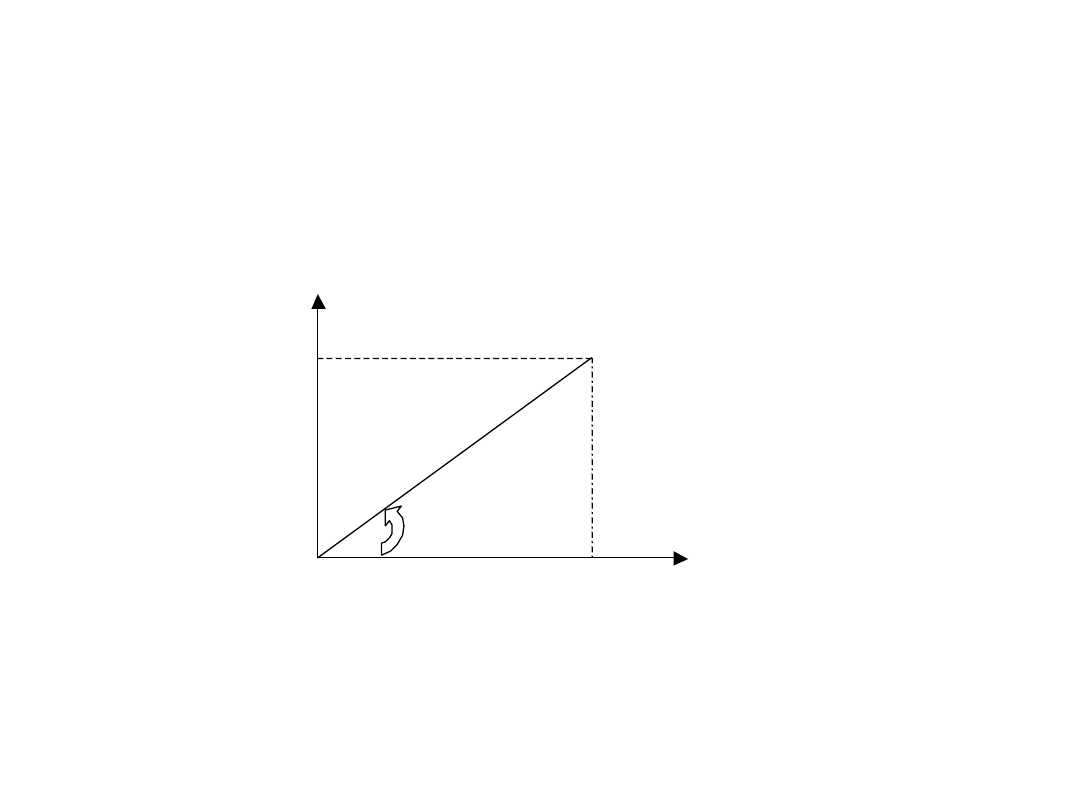
Teoria spiral

Układ biegunowy



r

P

y

x

Źródło: opracowanie własne

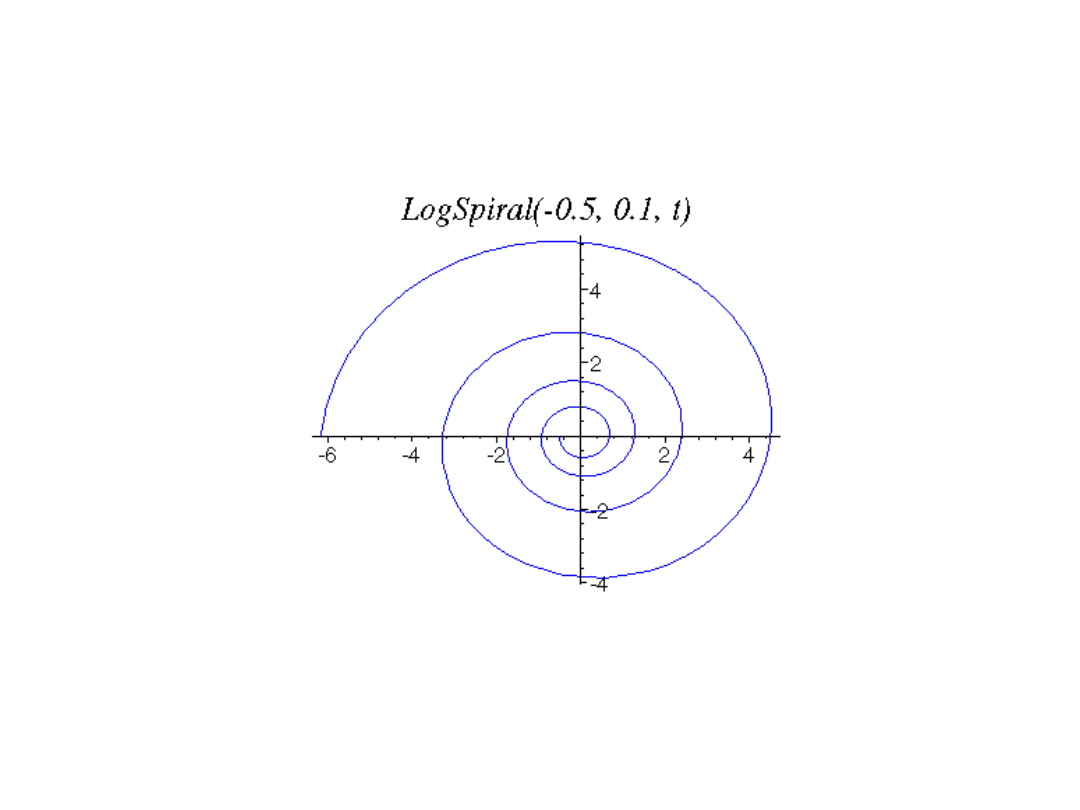
Przykład spirali logarytmicznej o q = 0,1 i początku w punkcie –0,5 dla

 =0.

Źródło: strona internetowa: http://arnold.usno.navy.mil/murison/curves/Maple/curves2D/Curves2D22.html z dnia 22.06.2001

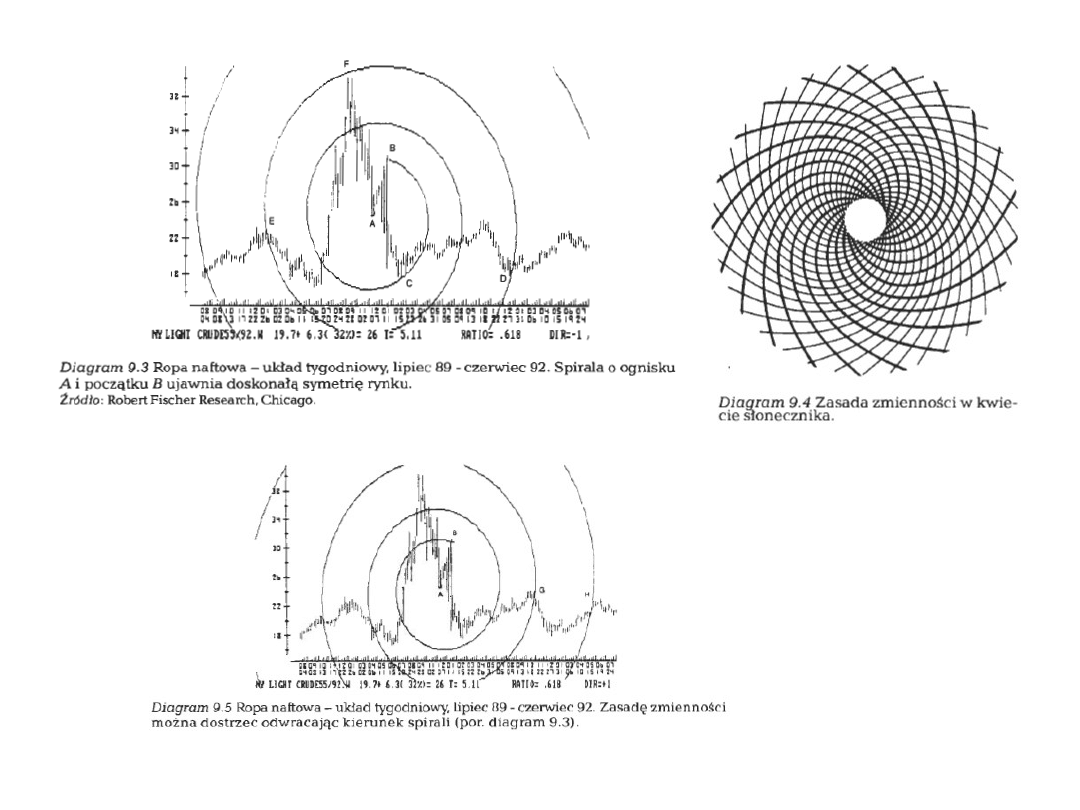
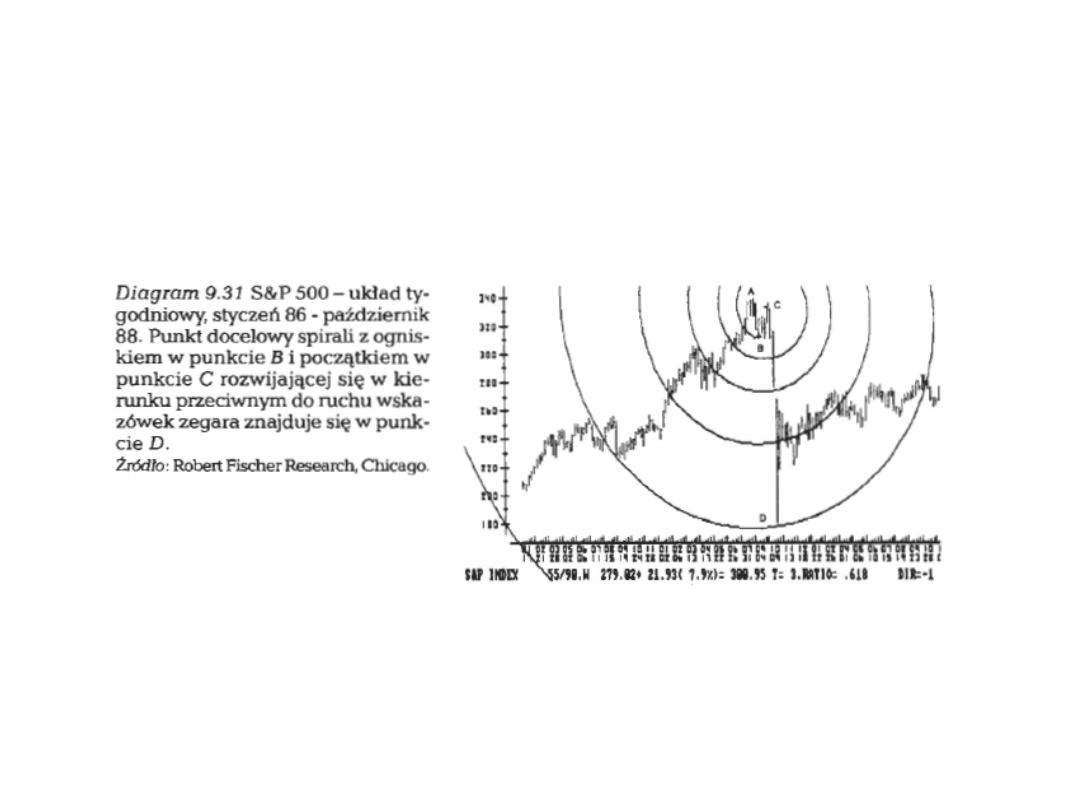
Reguła
zmienności

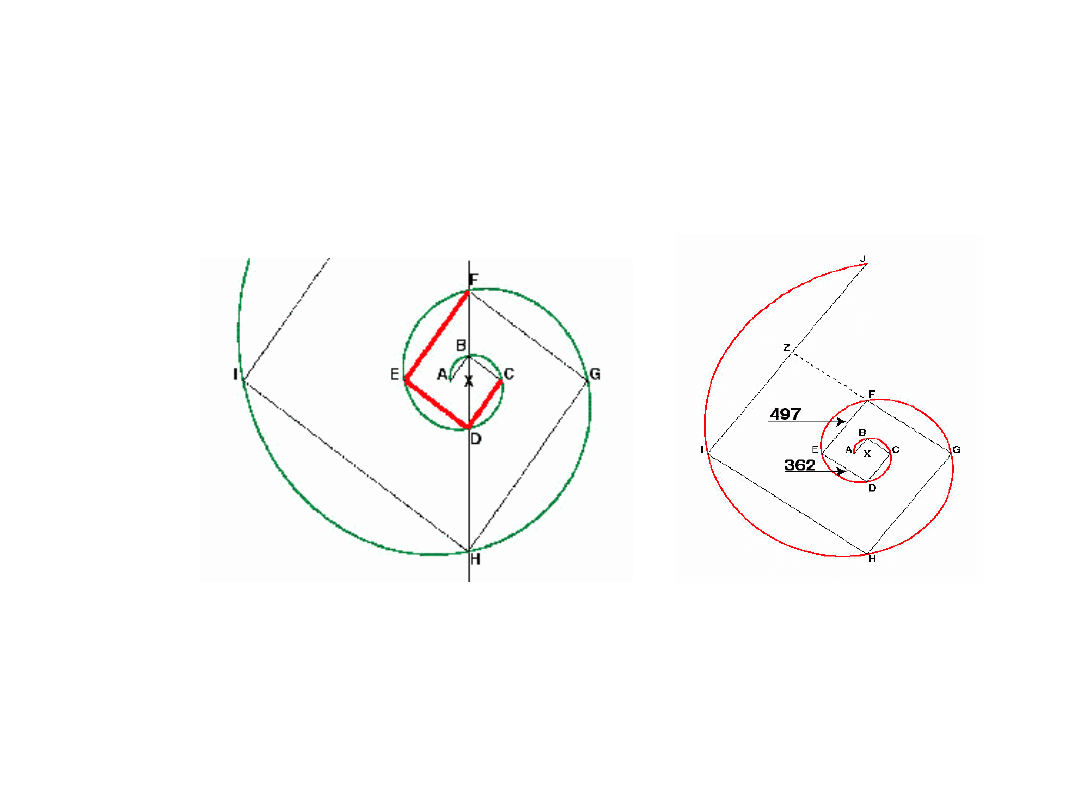
Przykład spirali prostokątnej

Spirala logarytmiczna prostokątna z dniami bazowymi 497
i 362 dni

Źródło: strona internetowa http://www.ermanometry.com/example5.htm z dnia 30.07.2001

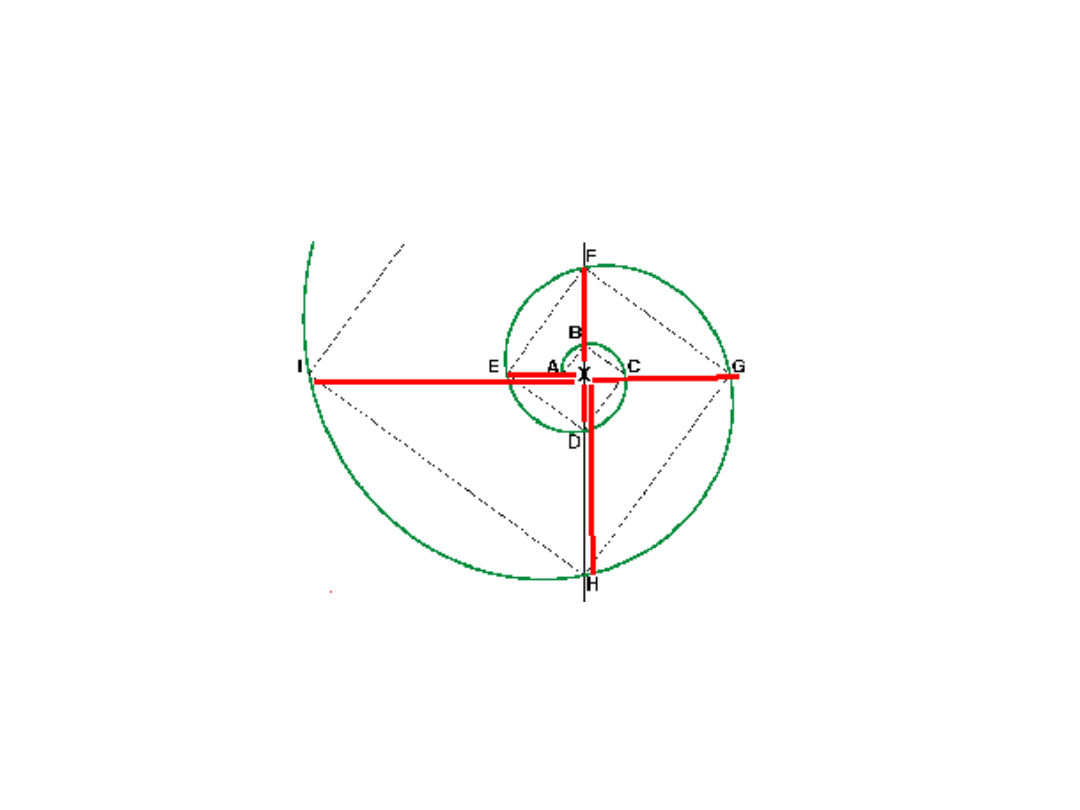
Dodawanie odcinków poziomych i pionowych w prostokątnej spirali logarytmicznej

Źródło: strona internetowa http://www.ermanometry.com/ z dnia 30.07.2001

Ermanometria

Spirala logarytmiczna trójwymiarowa – czas płynie
na osi k

Źródło: opracowanie własne na podstawie strony internetowy http://arnold.usno.navy.mil/murison/ z dnia 22.06.2002

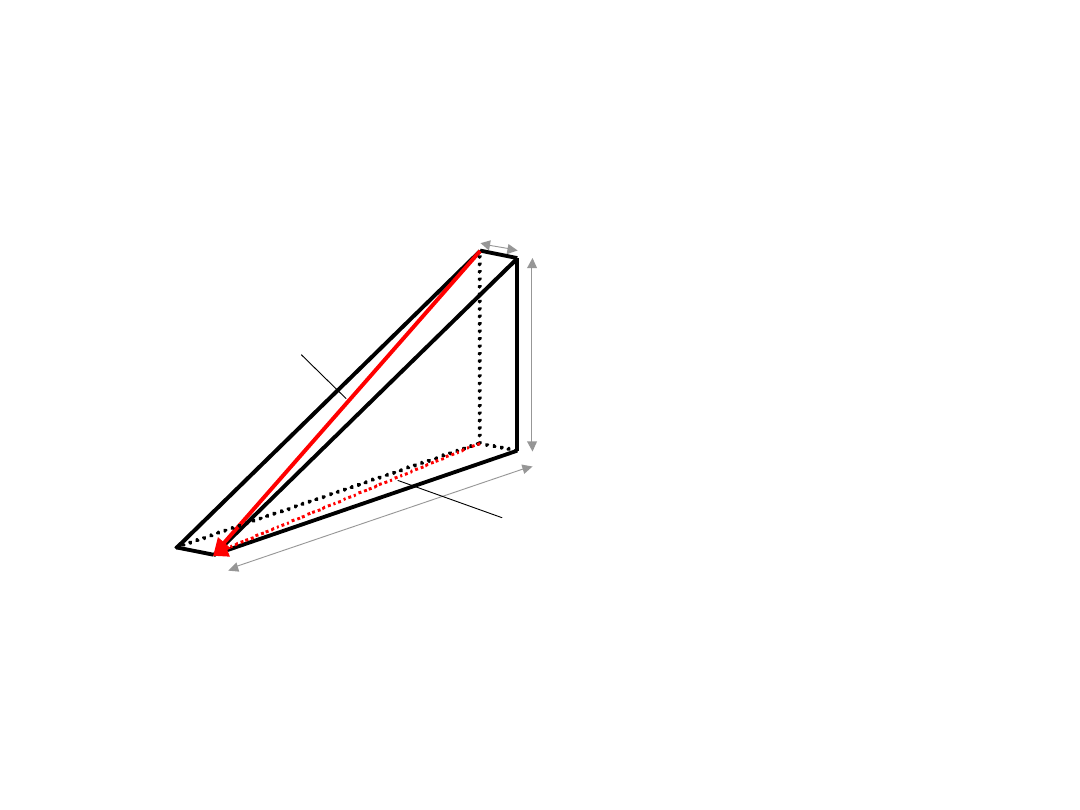
Ruch rynku w przestrzeni wielowymiarowej

A

B

C

D

a

b

c

d

e

Ruch wzdłuż równi

Rzut ruchu wzdłuż równi na
paszczyznę nadłuższego
boku

Źródło: opracowanie własne na podstawie strony internetowy http://arnold.usno.navy.mil/murison/ z dnia 22.06.2002

Ruch rynku zrzutowany na płaszczyznę równi

Źródło: strona internetowa http://www.ermanometry.com/example5.htm z dnia 30.07.2001

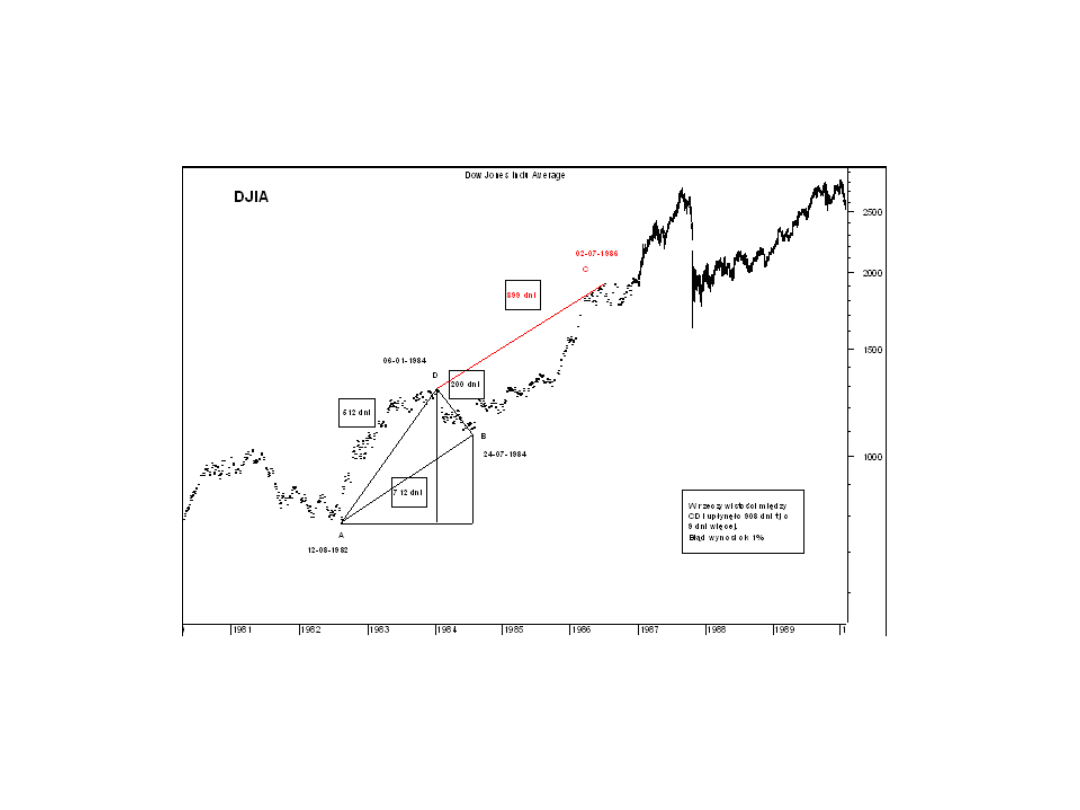
Wyznaczanie punktów zwrotnych w przyszłości na podstawie trzech punktów zwrotnych tj.
dwu odcinków na przykładzie dziennego wykresu Dow Jones Industrial Average (DJIA).

Źródło: strona internetowa http://www.ermanometry.com/example5.htm z dnia 30.07.2001

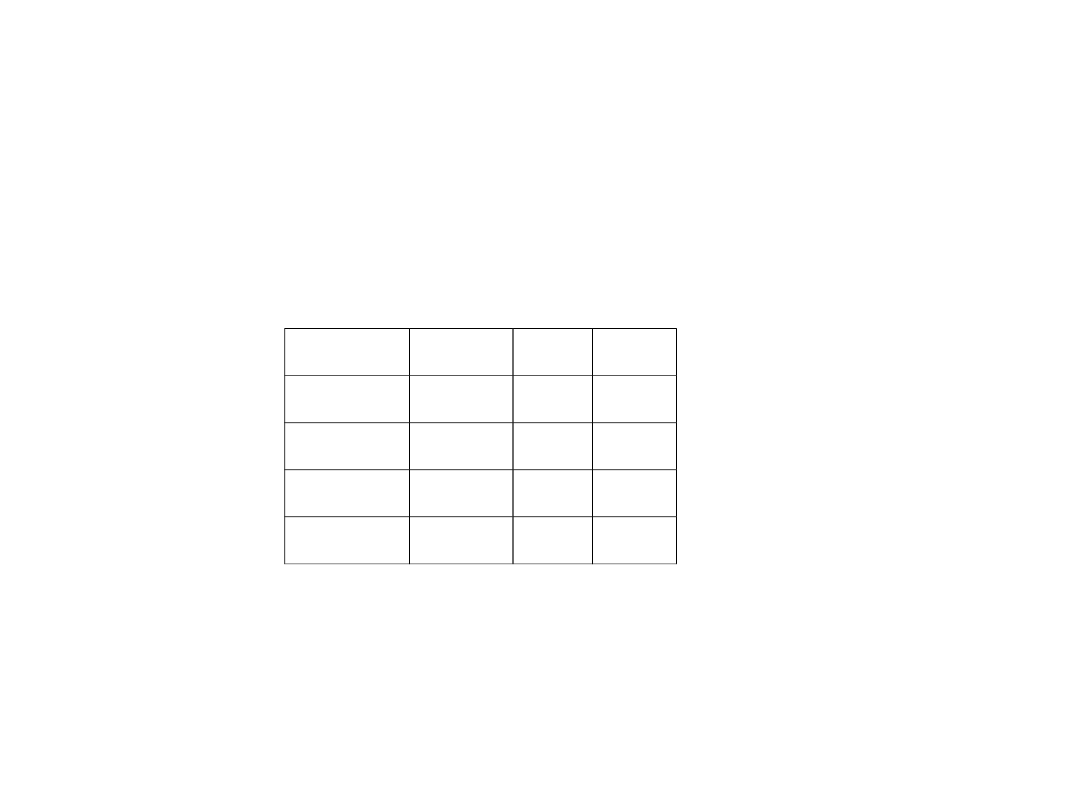
Przykład zastosowania ermanometrii do wyznaczania punktów zwrotnych

Data1

Data2

Liczba

dni

Odcine

k

1982-08-12

1984-01-

06

512

a

1984-01-06

1984-07-

24

200

d

1982-08-12

1984-07-

24

712

b

1984-01-06

1986-07-

02

899

e

Źródło: opracowanie własne

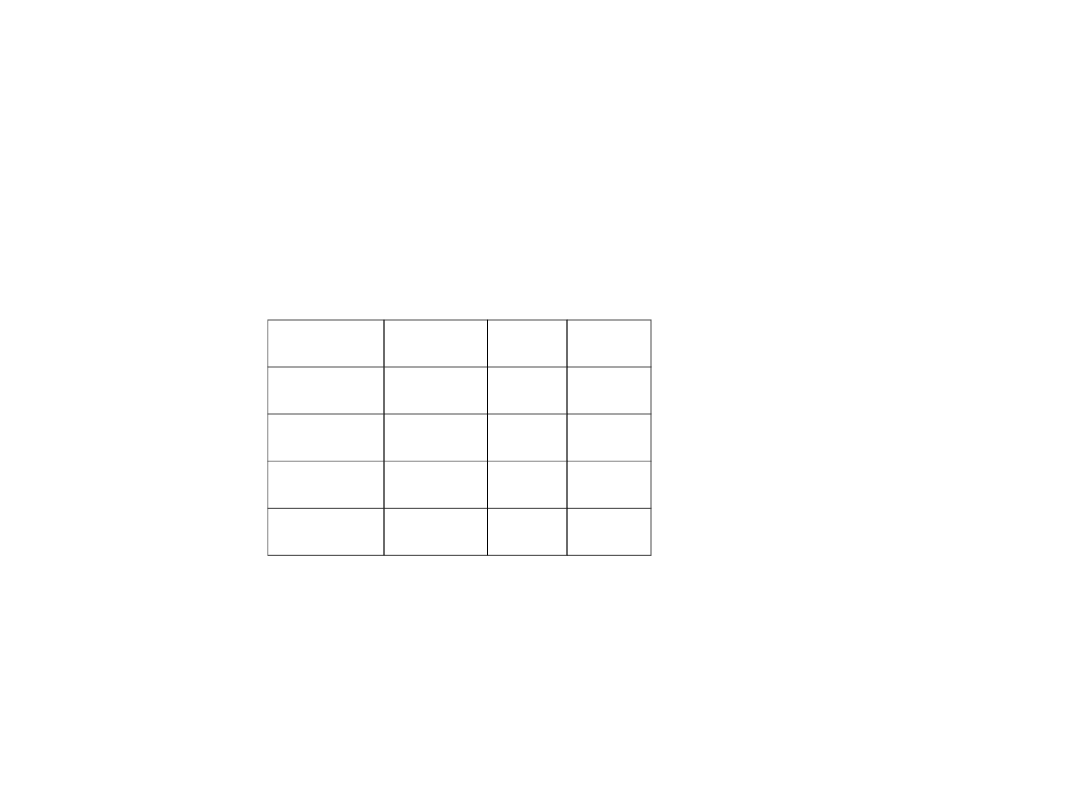
Przykład zastosowania ermanometrii do wyznaczania punktów zwrotnych

Data1

Data2

Liczba

dni

Odcine

k

1982-08-12

1987-08-

25

1839

a

1987-08-25

1990-10-

11

1143

d

1982-08-12

1990-10-

11

2982

b

1987-08-25

1997-09-

26

3685

e

Źródło: opracowanie własne

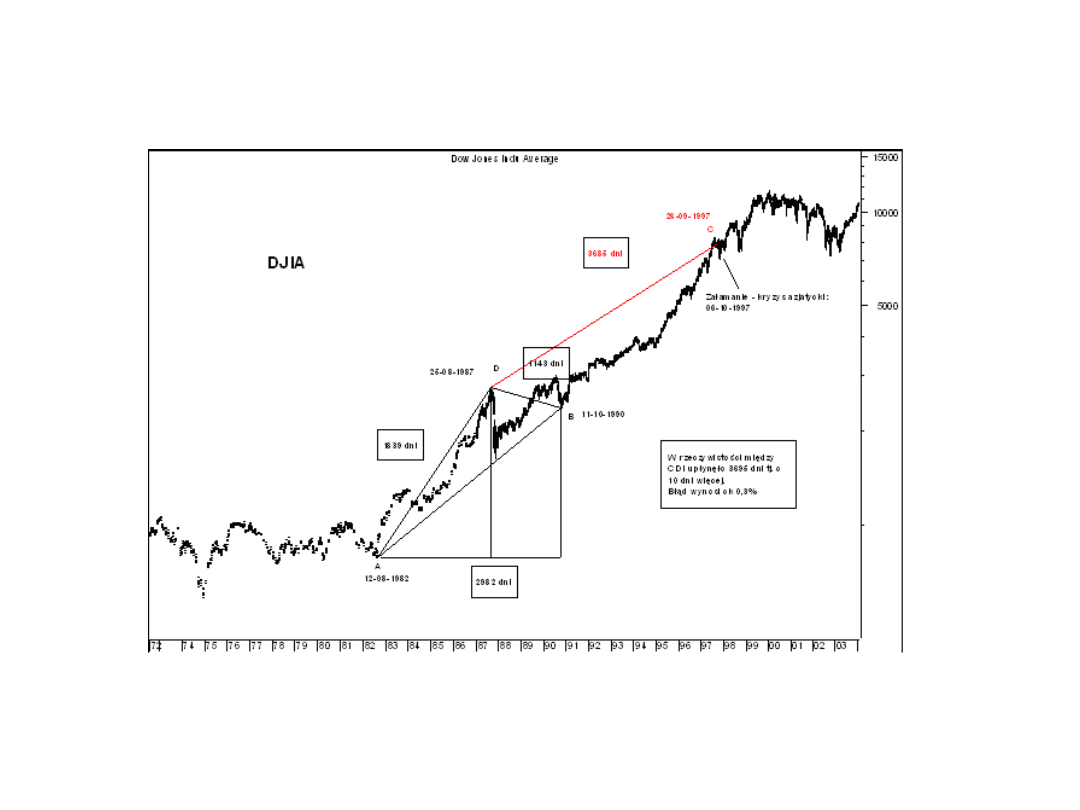
Wyznaczanie punktów zwrotnych w przyszłości na podstawie trzech punktów zwrotnych tj.
dwu odcinków na przykładzie dziennego wykresu Dow Jones Industrial Average (DJIA).

Źródło: opracowanie własne

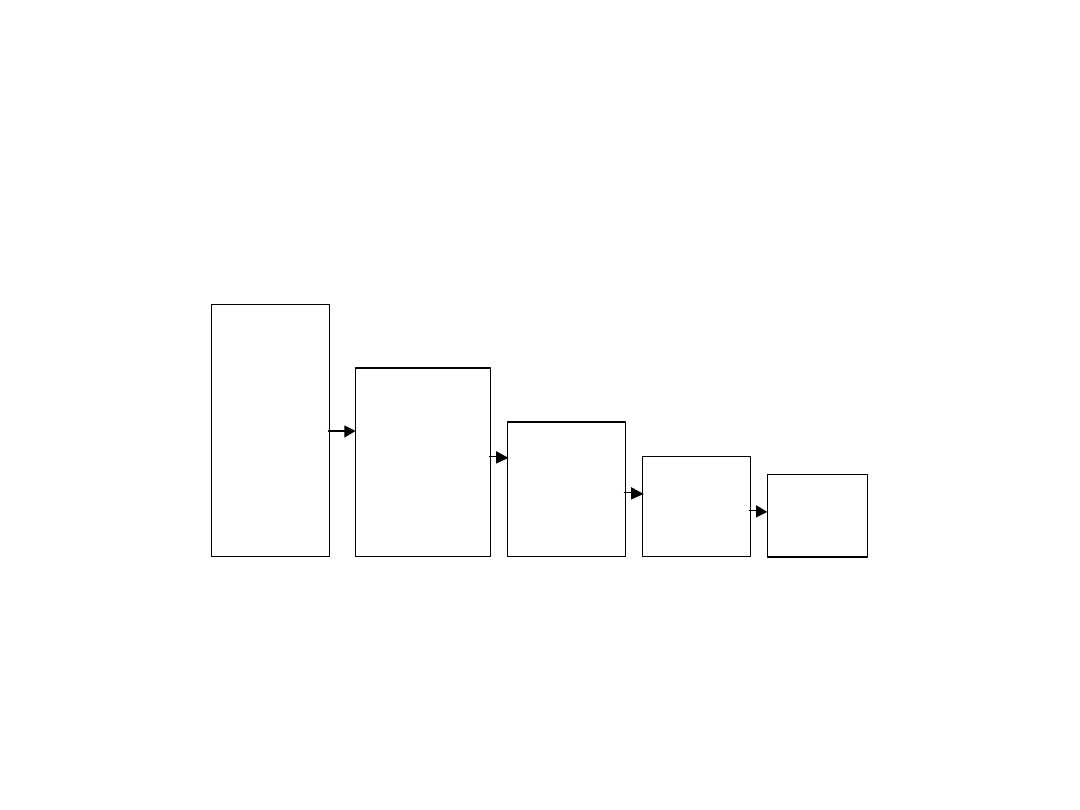
Połączenie poszczególnych teorii z ermanometrią

Ermanometria

Teoria fal

R. Elliotta

Teoria

spirali

logarytmicznych

(zwykłych i

prostokątnych)

Teoria

C. Carolana

Teoria

R. Fischera

Źródło: opracowanie własne

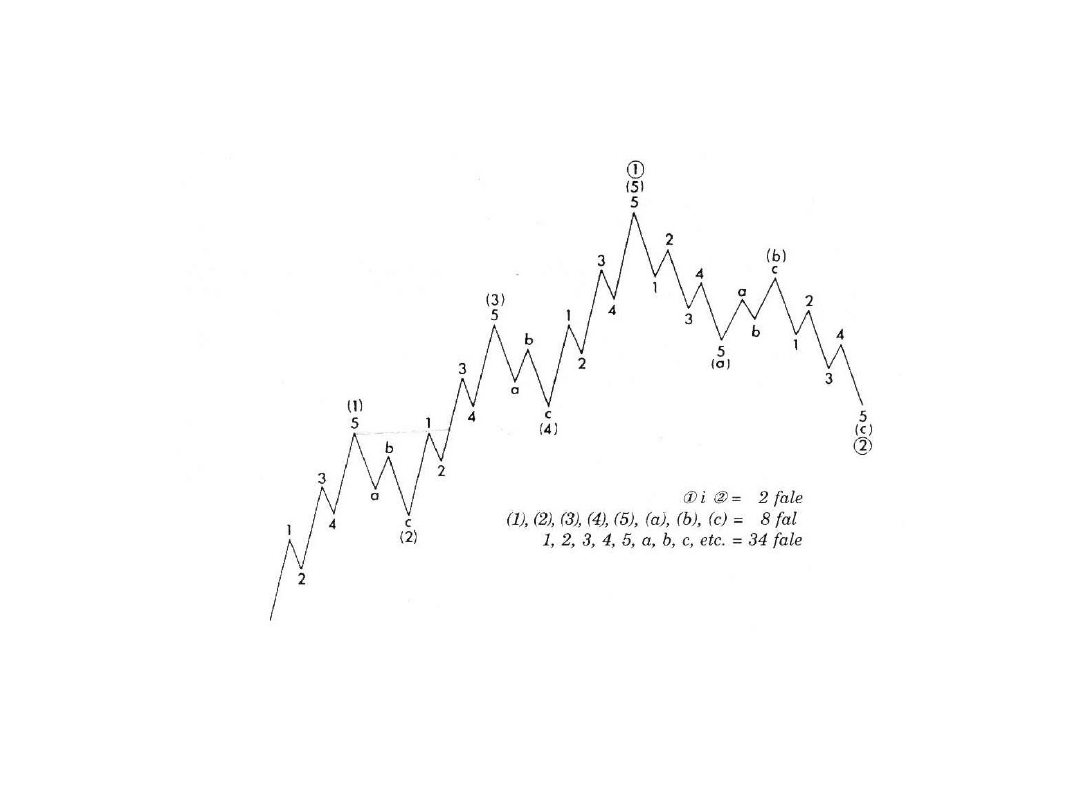
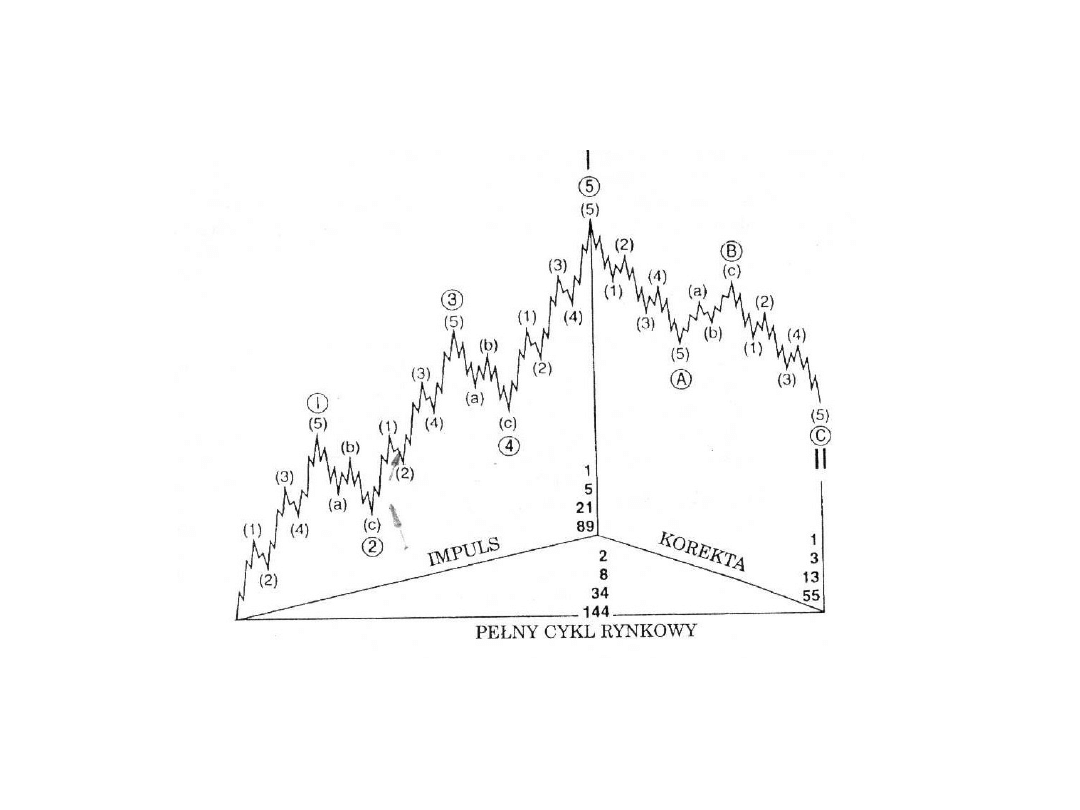
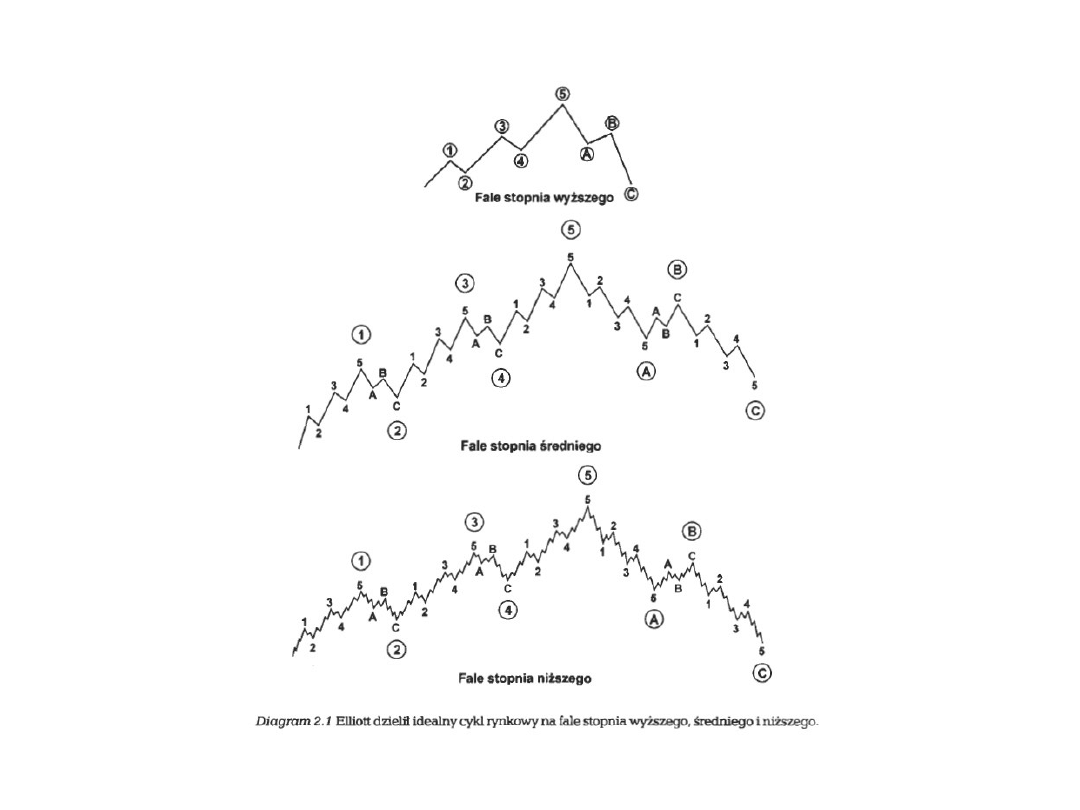
Teoria Fal Elliotta

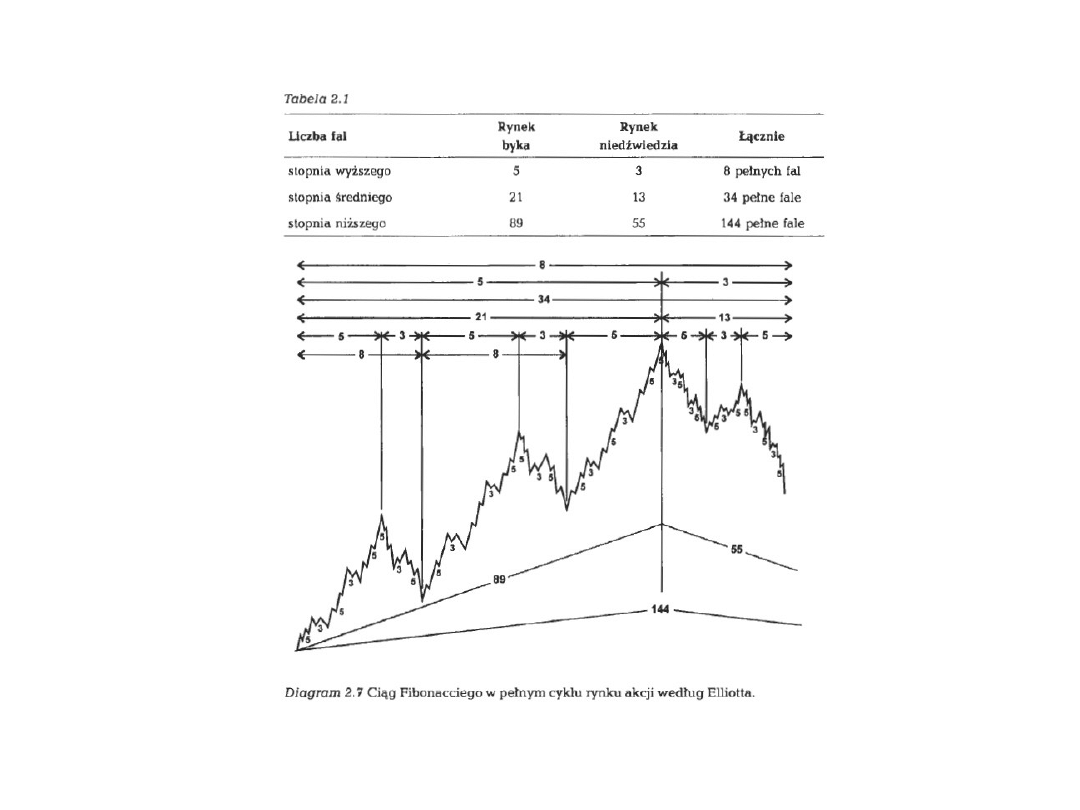
1

2

3

4

5

a

b

c

Ilustracja podstawowej formacji 5-3 w teorii Elliotta
Opracowanie autora

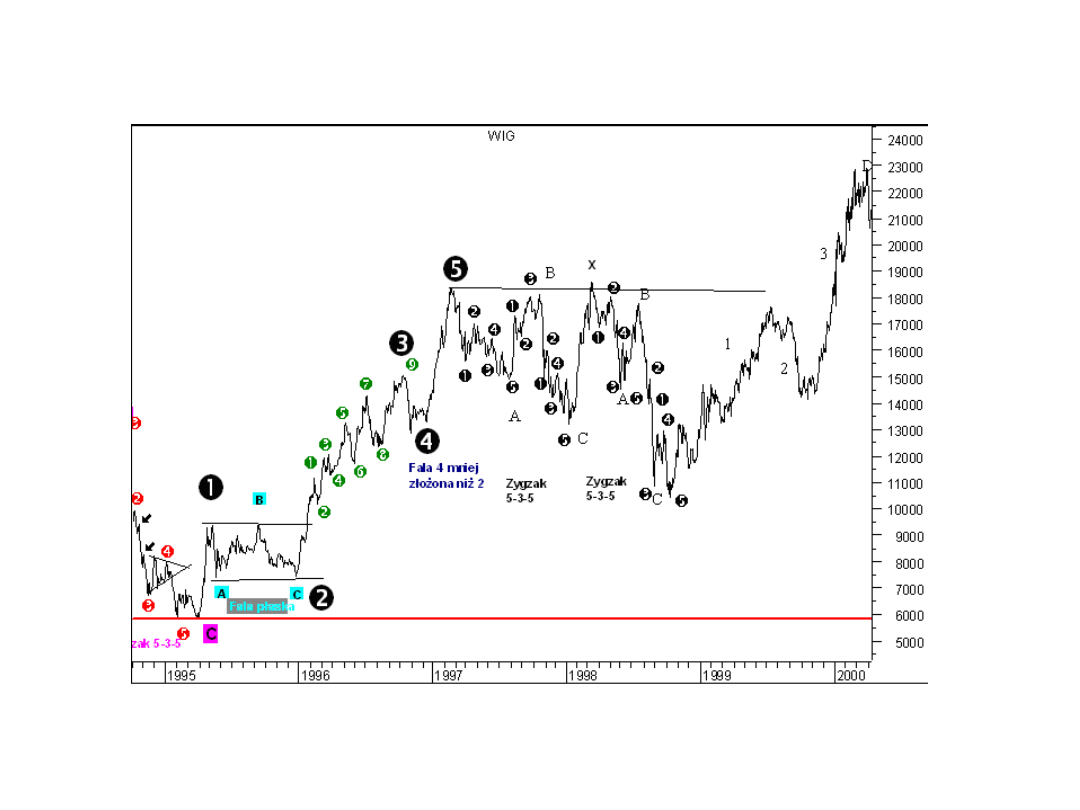
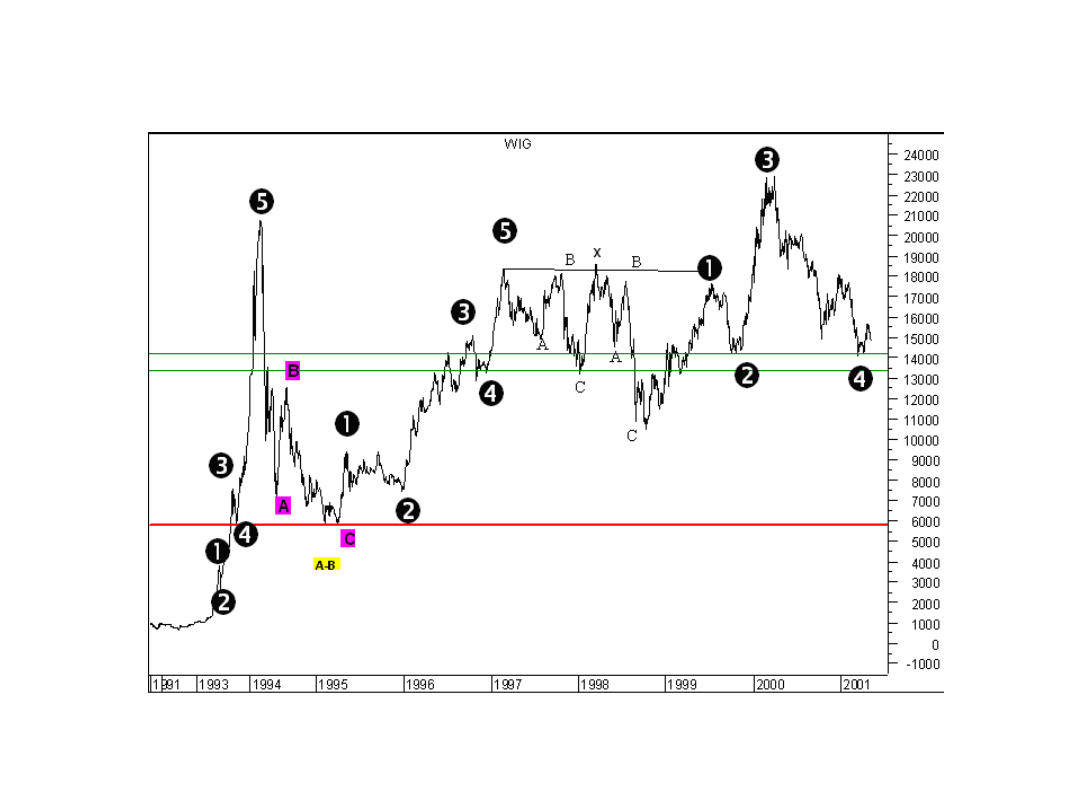
Fale wydłużone

I

II

IV

V

1

2

3

4

5

1+2+3+4+5

= III

T1+T2+T4+T5 =

T3 (= t1+t2+t3+t4+t5)

I+II+III(1+2+3+4+5)+IV+V=9 fal

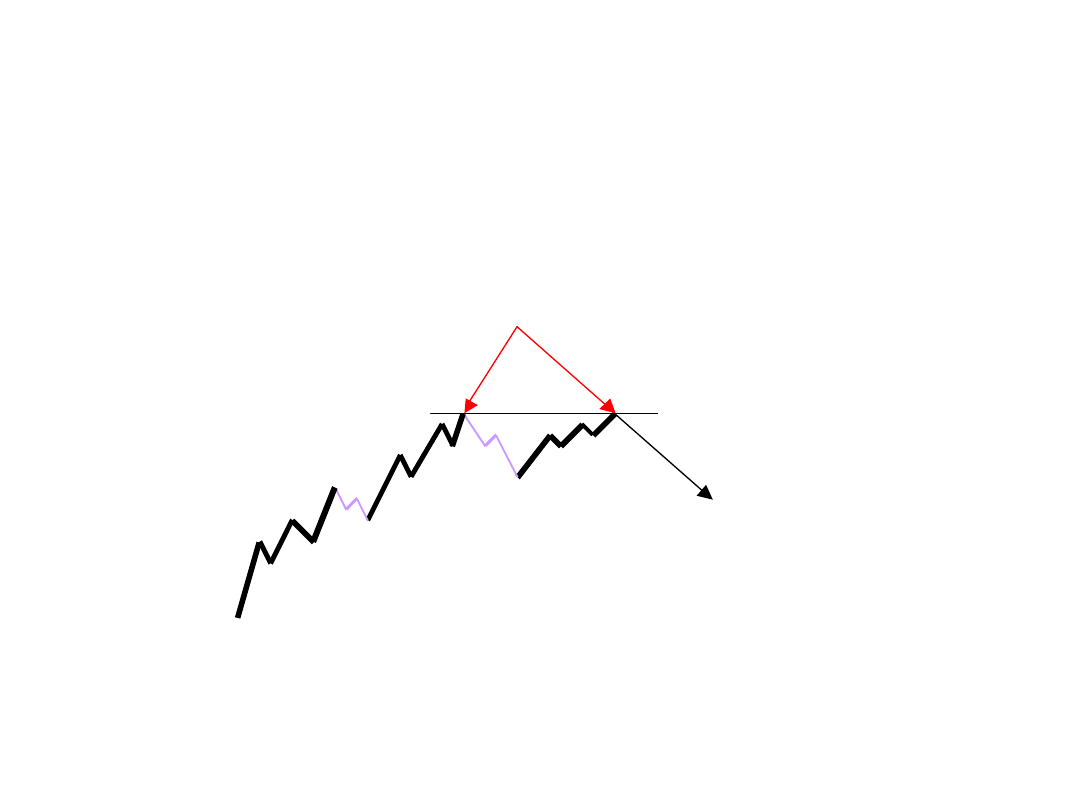
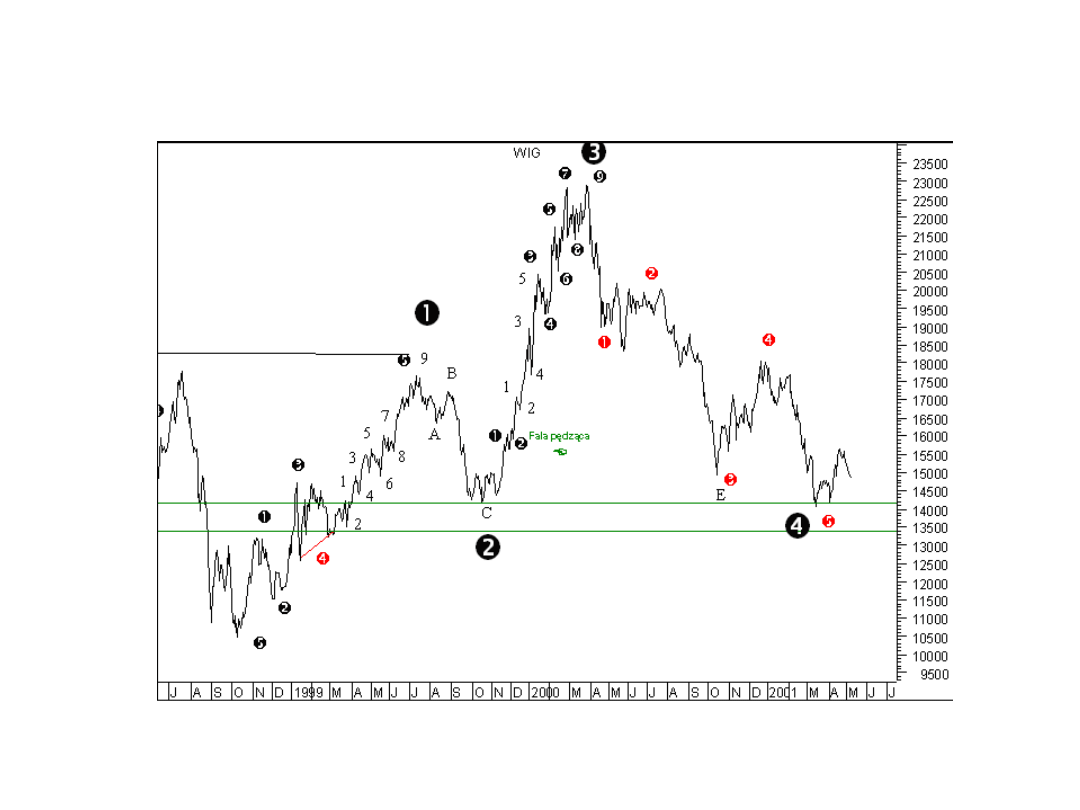
Fala załamana

I

II

III

IV

V

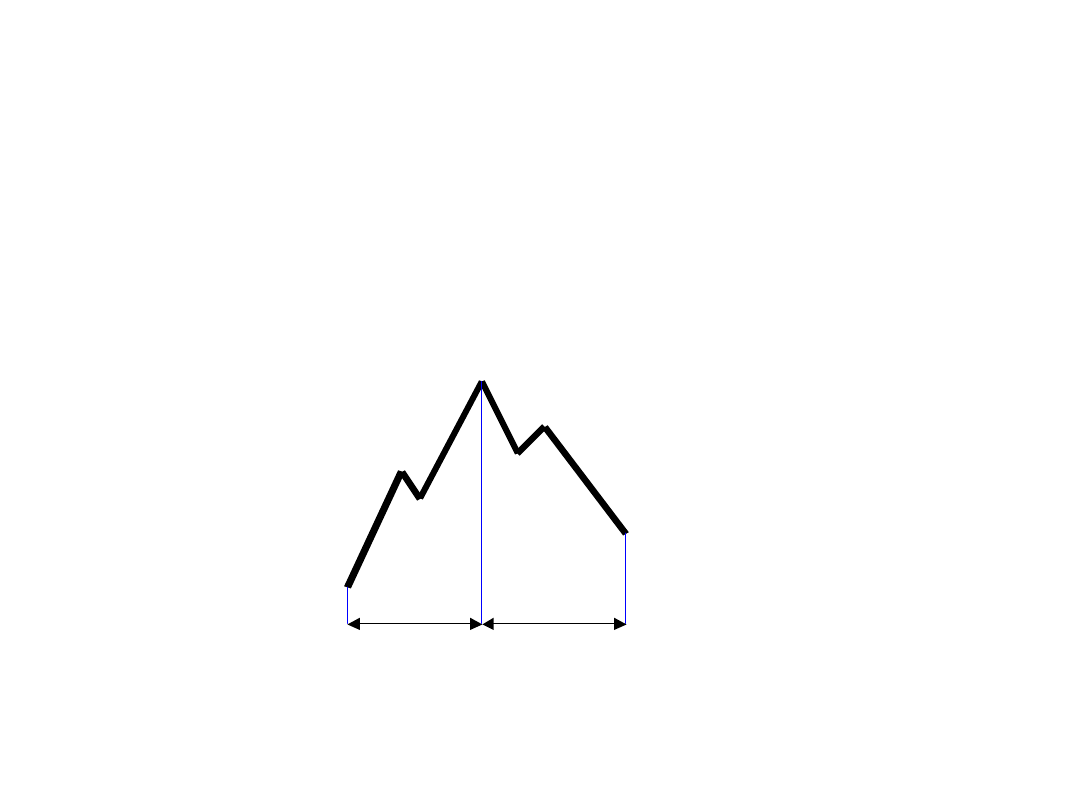
Podwójny szczyt

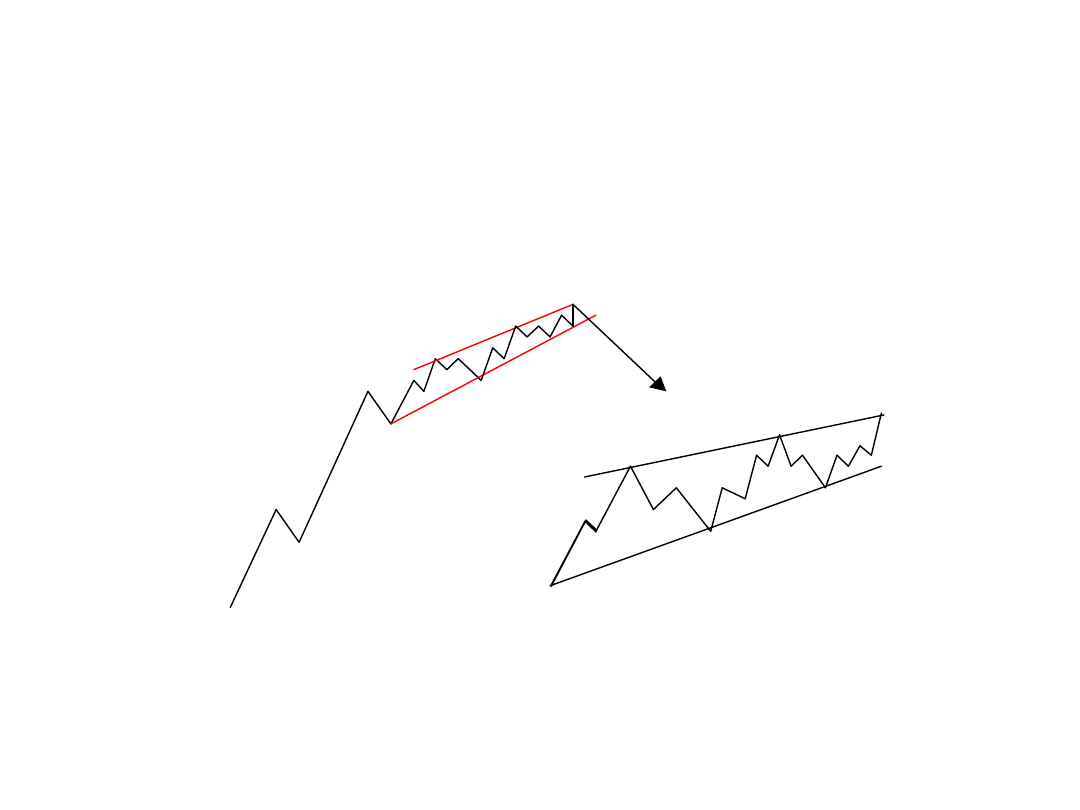
Trójkąty ukośne w fali piątej

I

II

III

IV

1

2

3

4

5

1

2

3

4

5

Klin zwyżkujący

3-3-3-3-3

5-3-3-3-5 (fala początkowa)

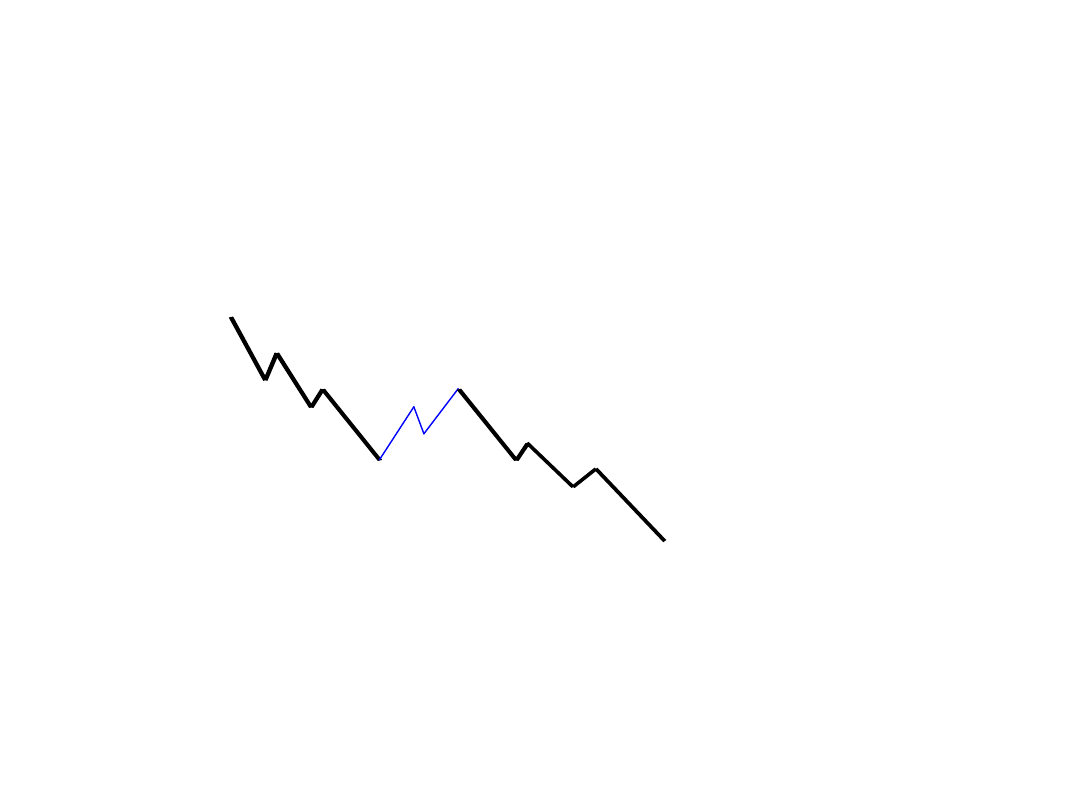
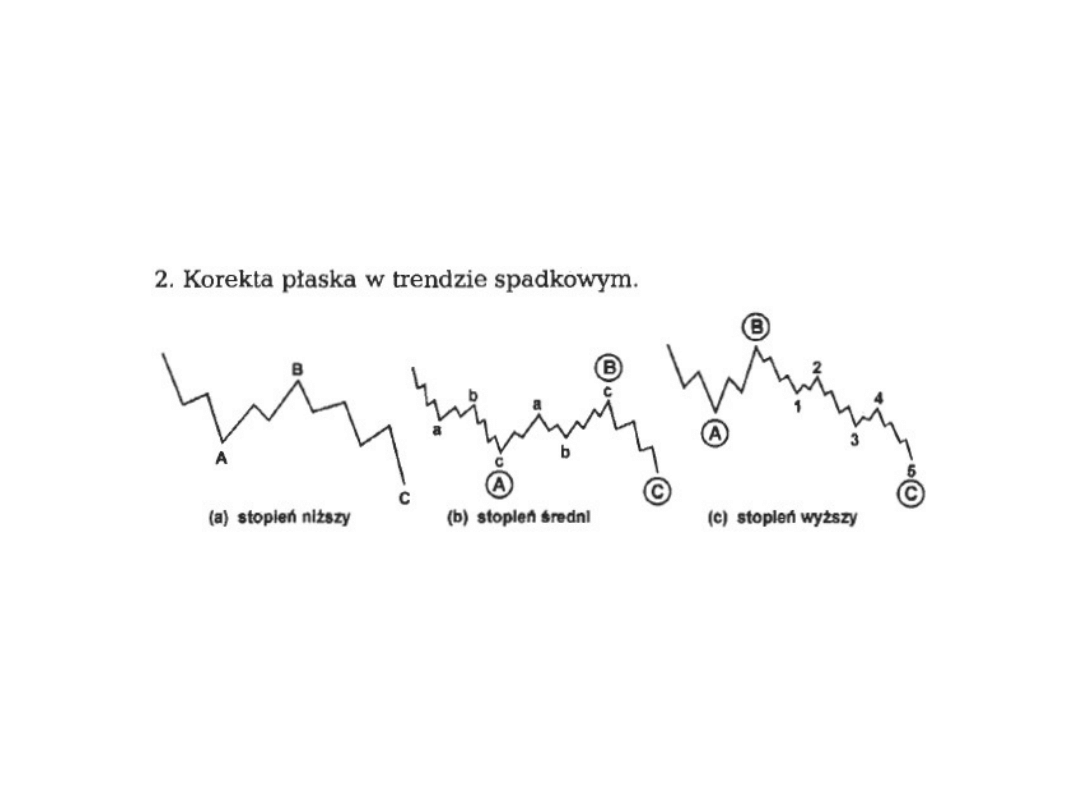
Fale korekty

Fale korekty:

Zygzak 5-3-5

A

B

C

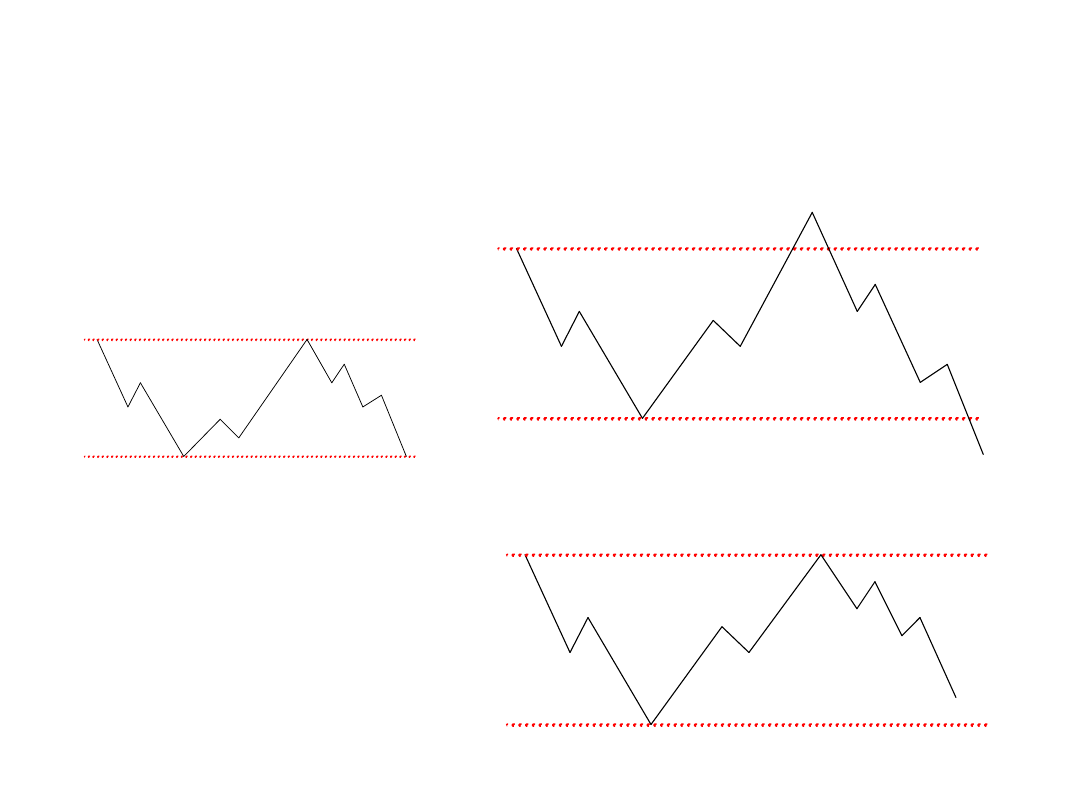
Fale korekty

Fale płaskie

A

B

C

Fala plaska - regularna

3-3-5

A

B

C

Fala plaska - nieregularna I

A

B

C

Fala plaska - nieregularna II

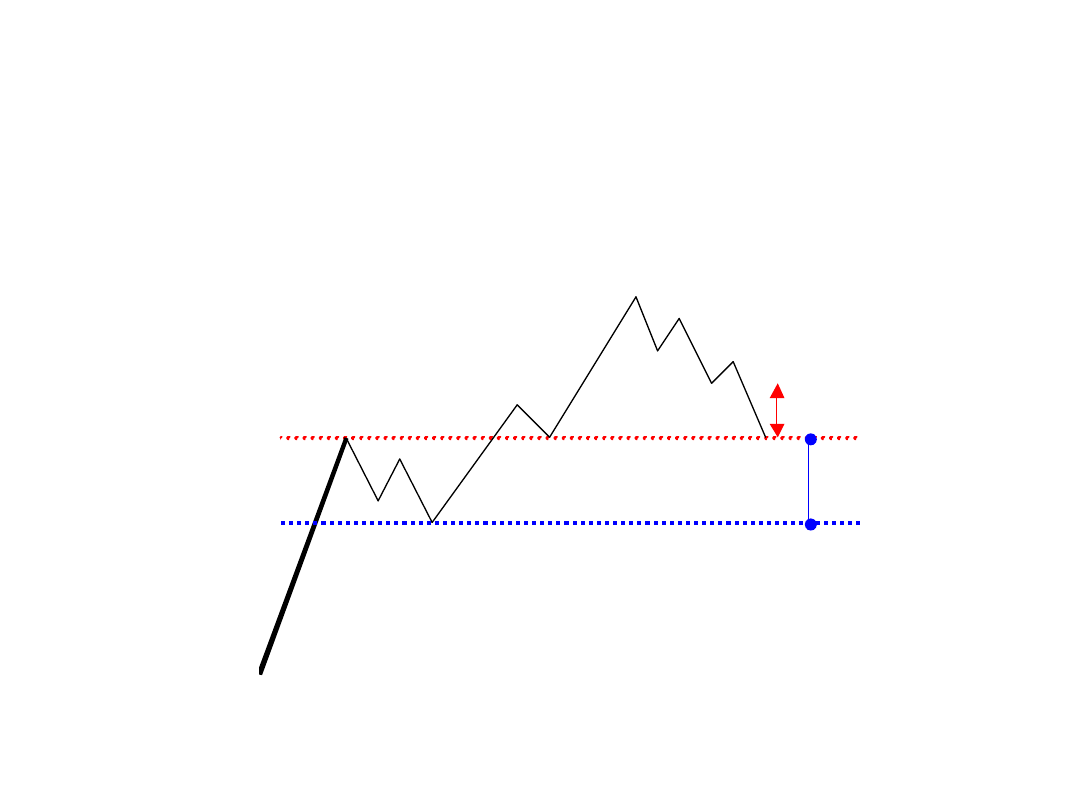
Fale korekty

A

B

C

Fala pędząca

K

3-3-5

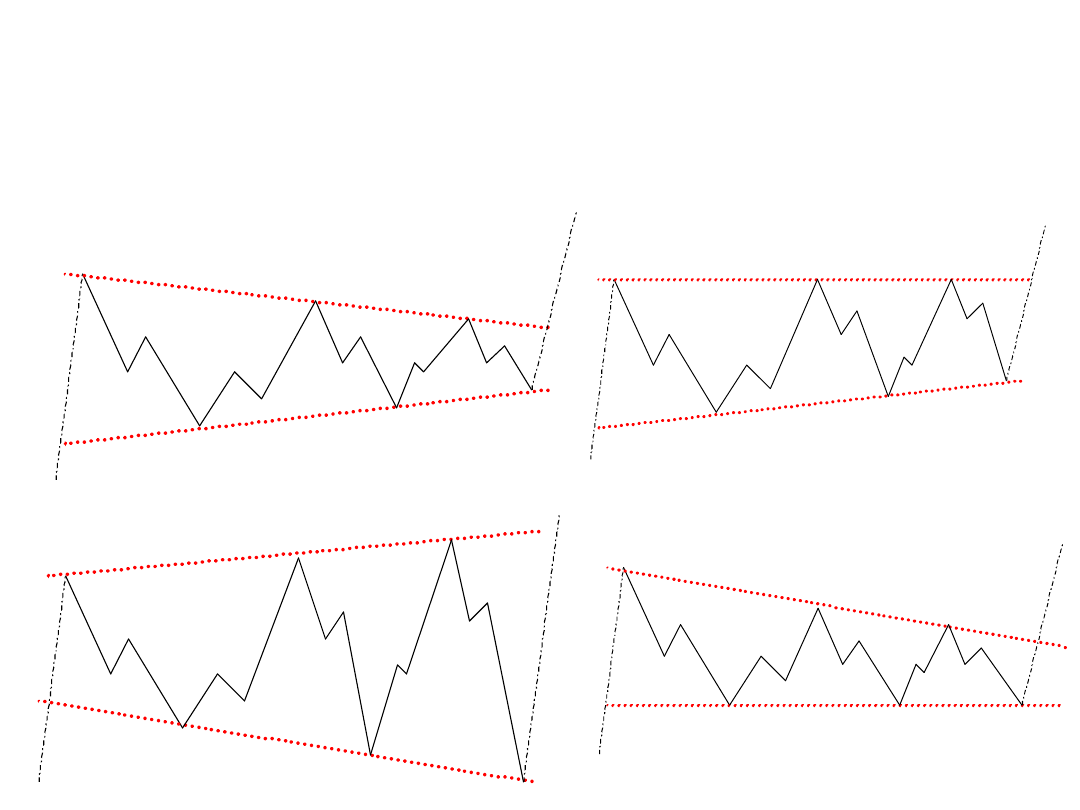
Trójkąty

Trójkąty (3-3-3-3-3)

1

2

3

Trójkąt symetryczny

4

5

1

2

3

Trójkąt zwyżkujący

4

5

1

2

3

Trójkąt symetryczny
rozszerzający się

4

5

1

2

3

Trójkąt zniżkujący

4

5

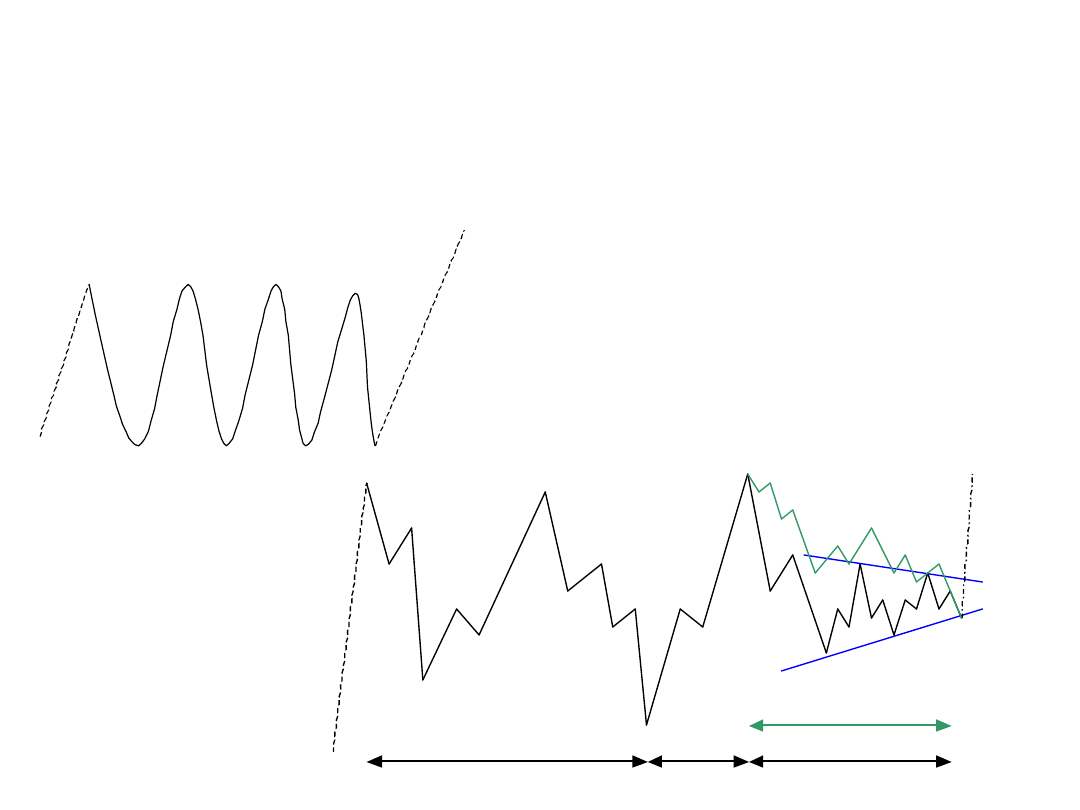
Korekty połączone

A

B

C

A

B

C

X

Podwójna trójka

Potrójna trójka

A

B

C

X

A

B

C

D

E

Plaska

Dowolna trójka

Trójkąt

a

b

c

Zygzak

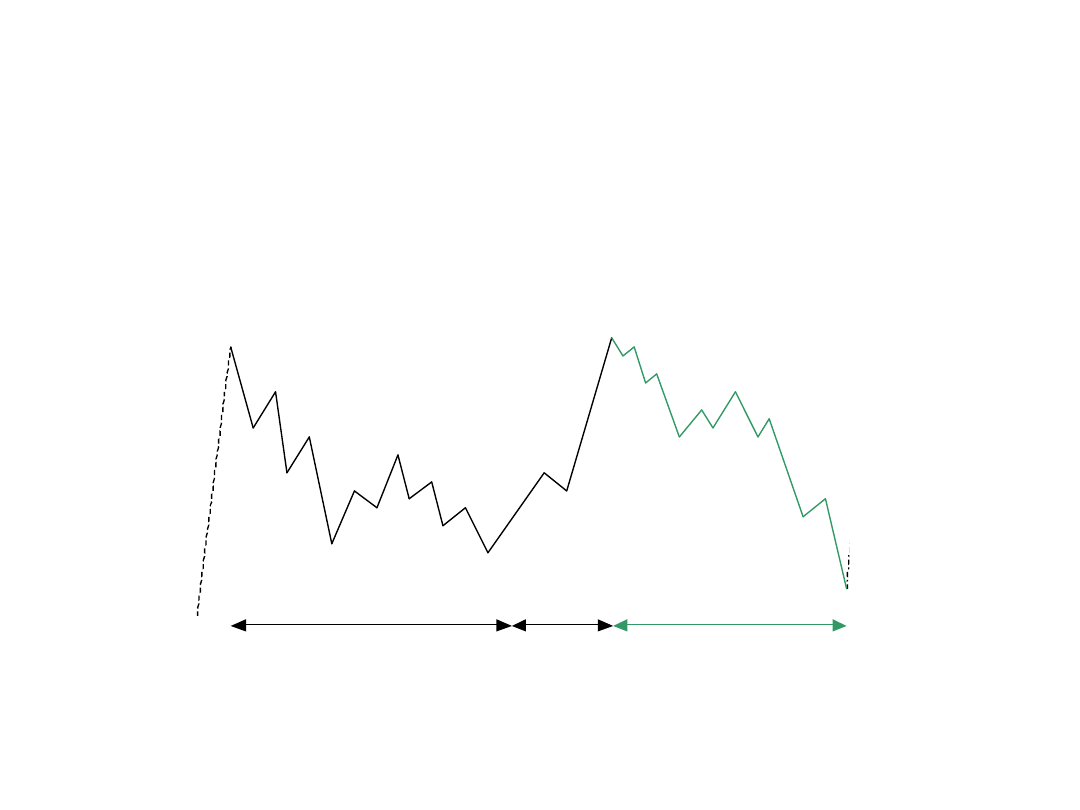
Łączenie korekt

A

B

C

X

A

C

Zygzak

Dowolna trójka

B

Zygzak

Podwójny zygzak

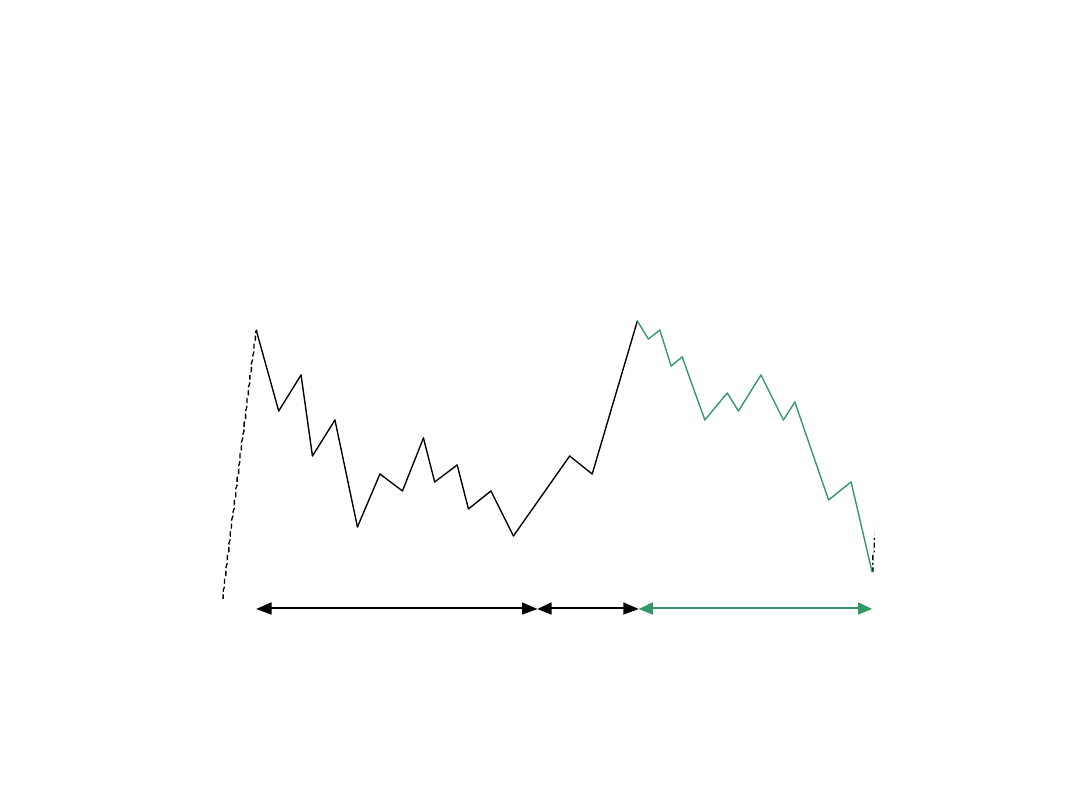
Zasada zmienności

A

B

C

X

A

C

Zygzak

Dowolna trójka

B

Zygzak

Podwójny zygzak

Zasady

• Zmienność:

• czas trwania korekty

• inny rodzaj fali korekty (fala płaska,

zygzaka)

• gwałtowna / powolna

• prosta / złożona

• Ocena siły trendu na podstawie fali korekty:

• Zygzak – normalna siła

• Fale płaskie, nieregularne, podwójne i

potrójne trójki – silniejszy rynek

• Fale pędzące – bardzo silny

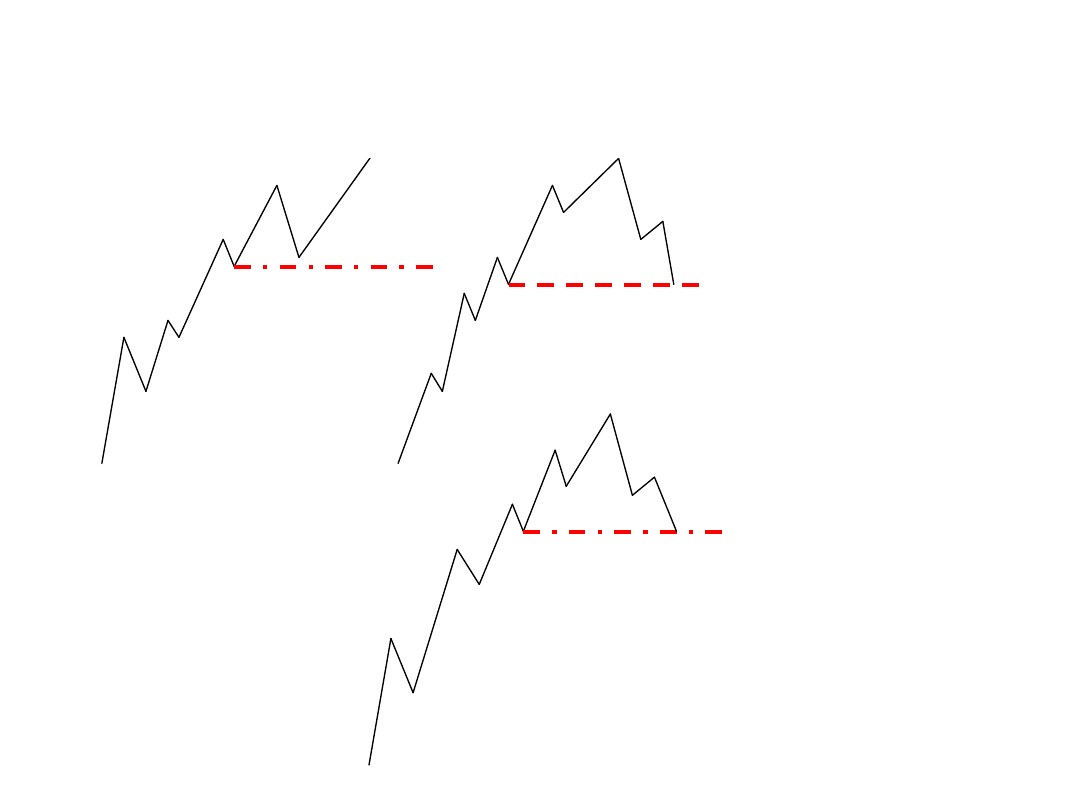
Głębokość fal korygujących

1

I

II

2

3

4

5

IV

V

1

2

3

4

5

II

III

IV

V

A

B

C

1

I

II

2

3

4

5

IV

A

B

C

III

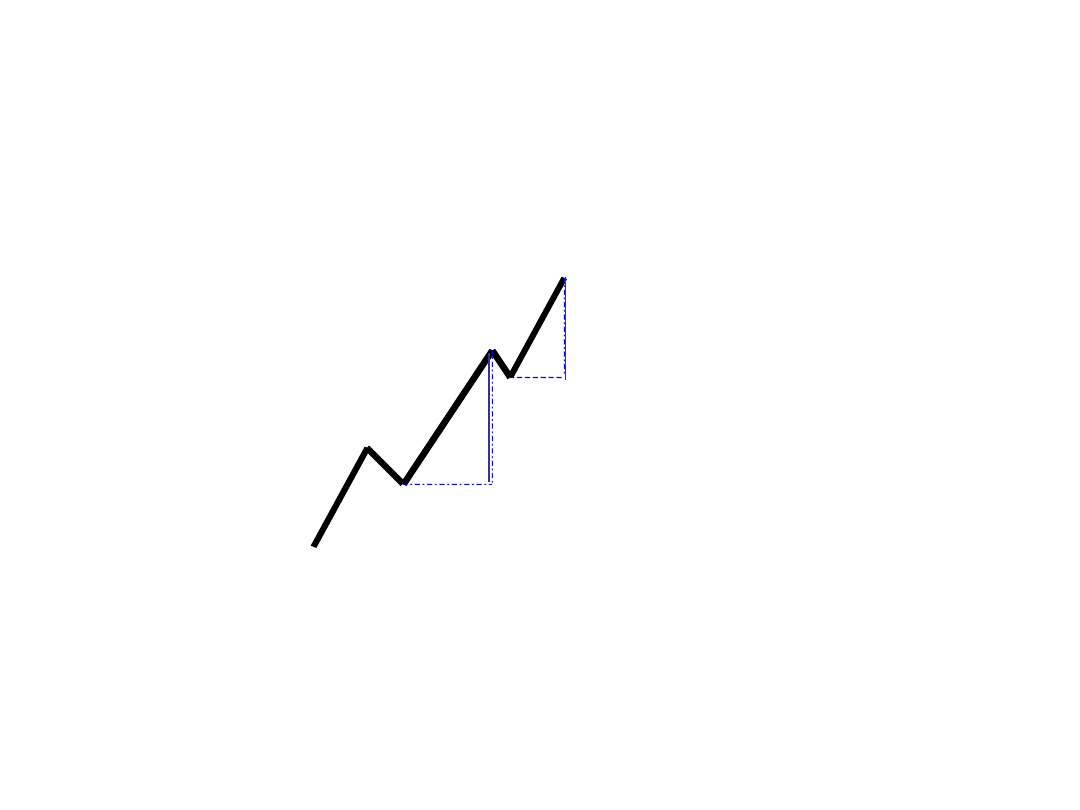
Zależności

Fala 5 = fala 1
Fala 5 = 0,618*fala 3

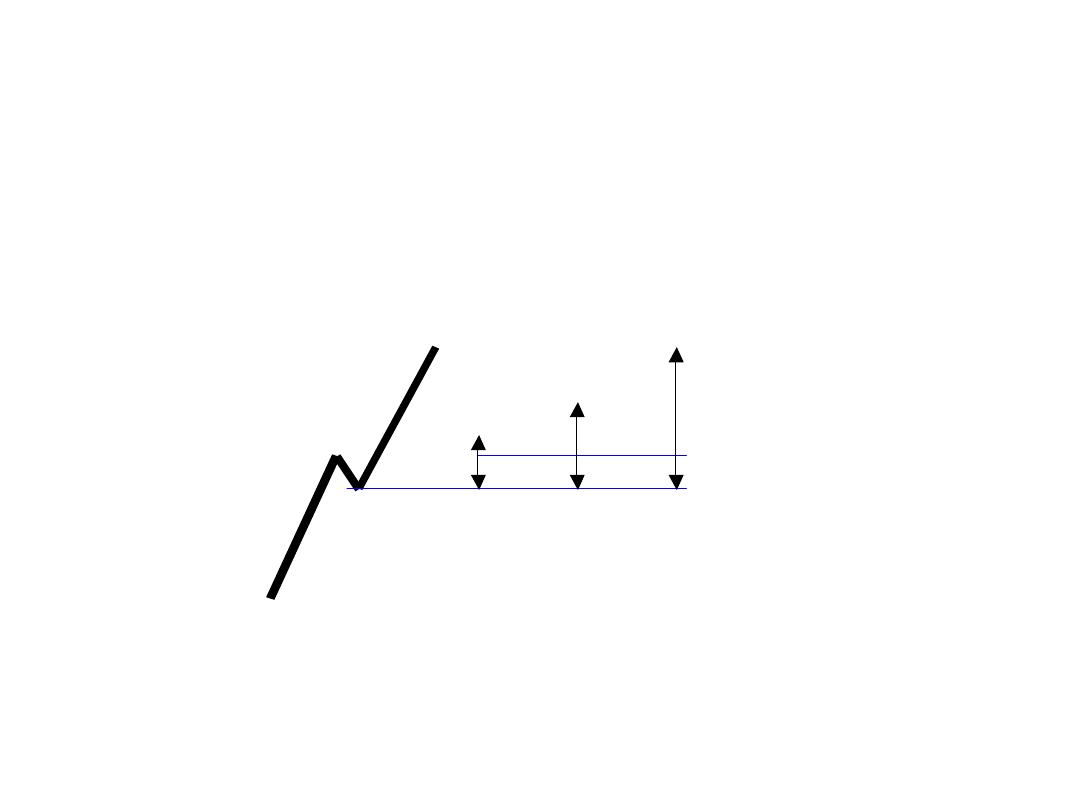
1,618

2,618

4,236

Obliczenie potencjalnych punktów
zwrotnych przy wykorzystaniu
wspólczynników Fibonacciego

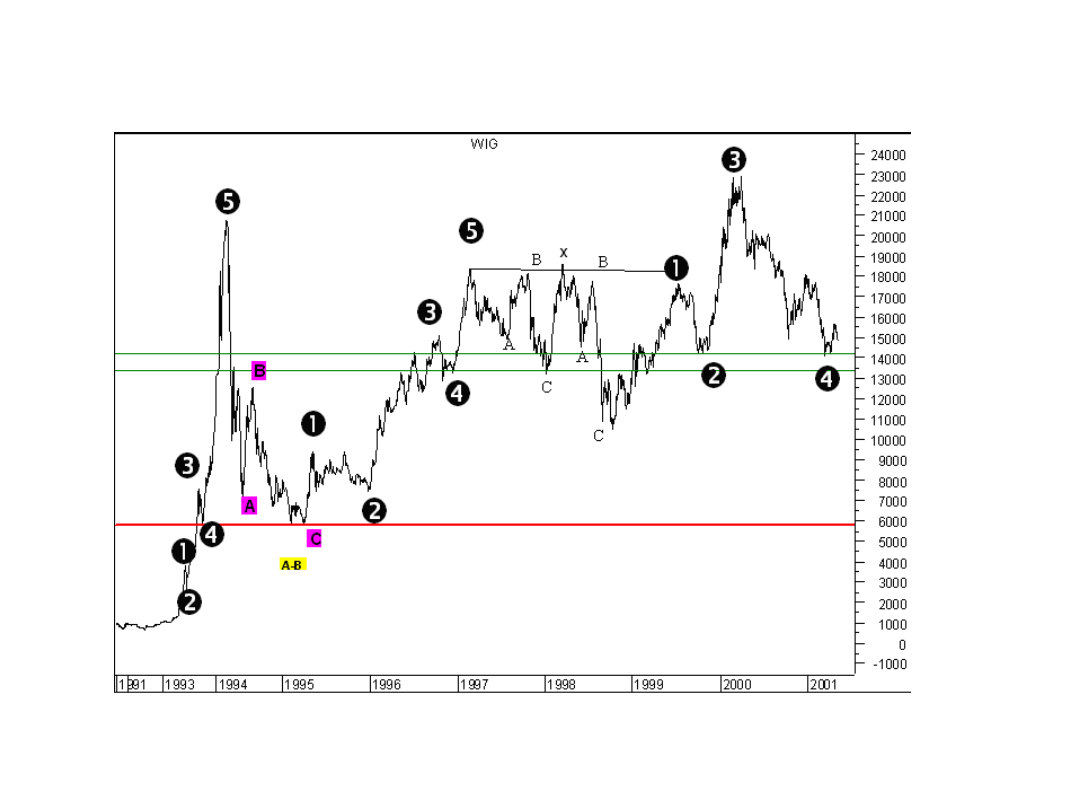
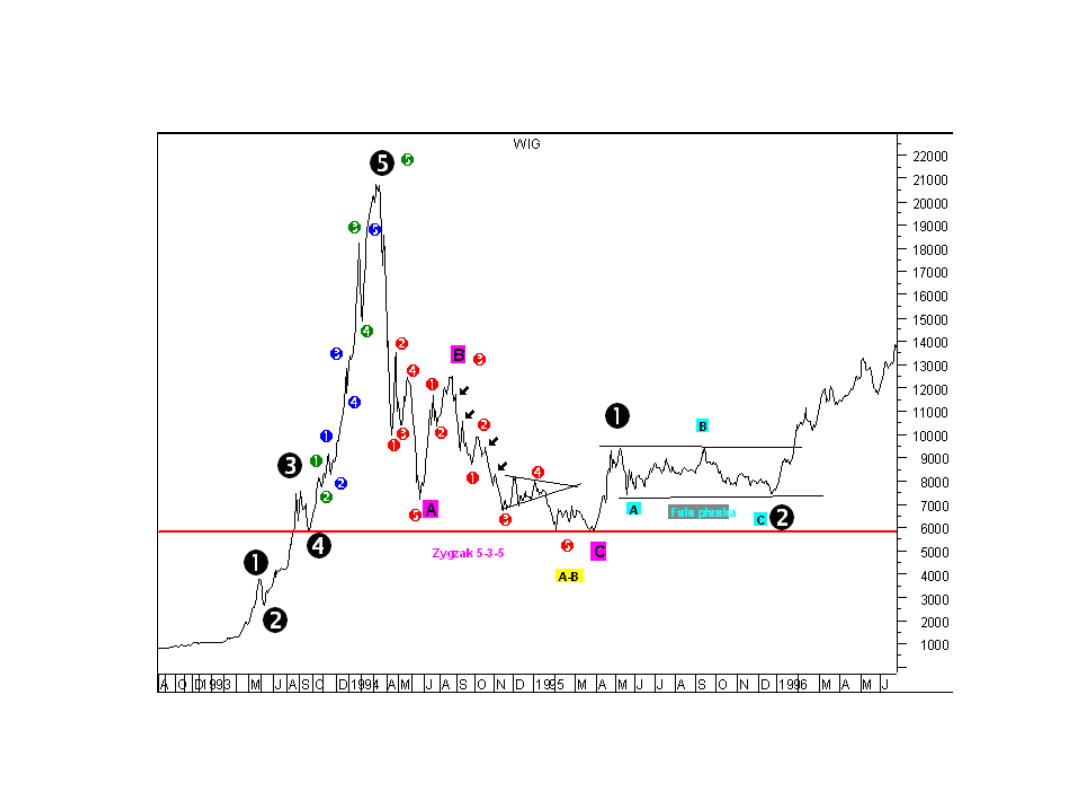
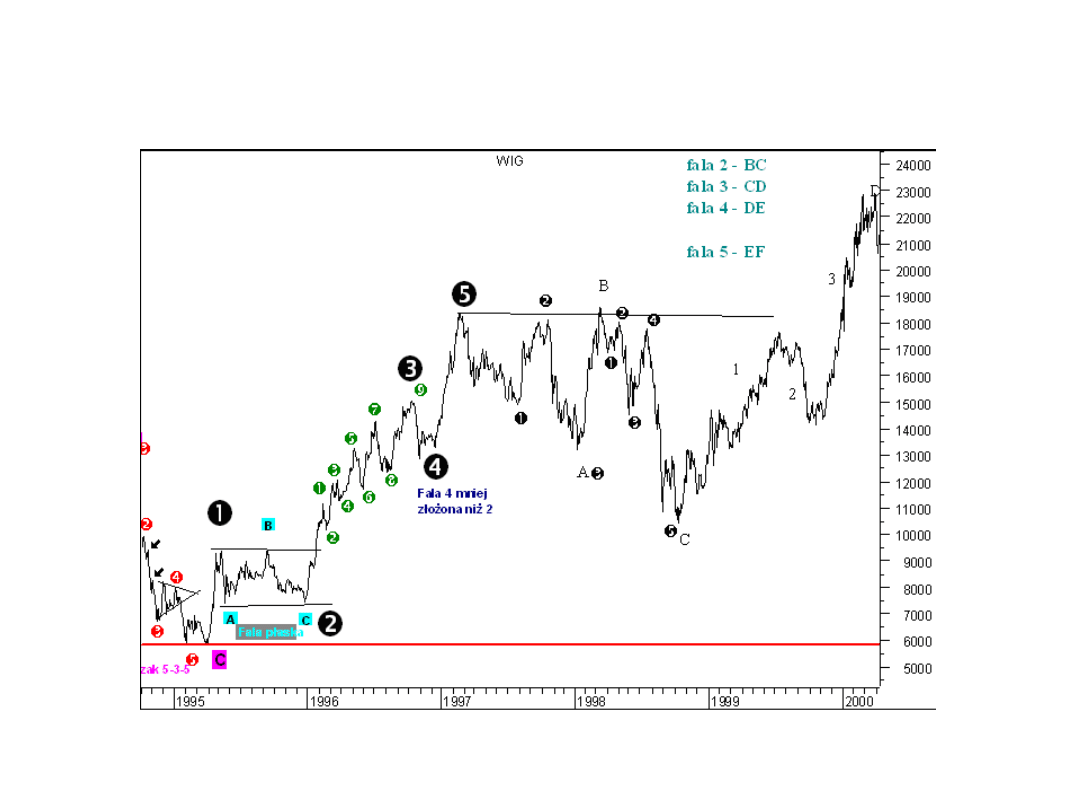
Teoria pulsu cenowego

Etap I

Etap II

a

b

c

x

y

z

AT i Astrologia?

• Współczynniki Fibonacciego występują

także w okresach orbitalnych planet
naszego układu słonecznego.

• Odległość księżyców od planety, wokół

której krążą (dla systemów
planetarnych o więcej niż jednym
księżycu), pozostają w proporcjach
opisanych przez odpowiednie potęgi
liczby .

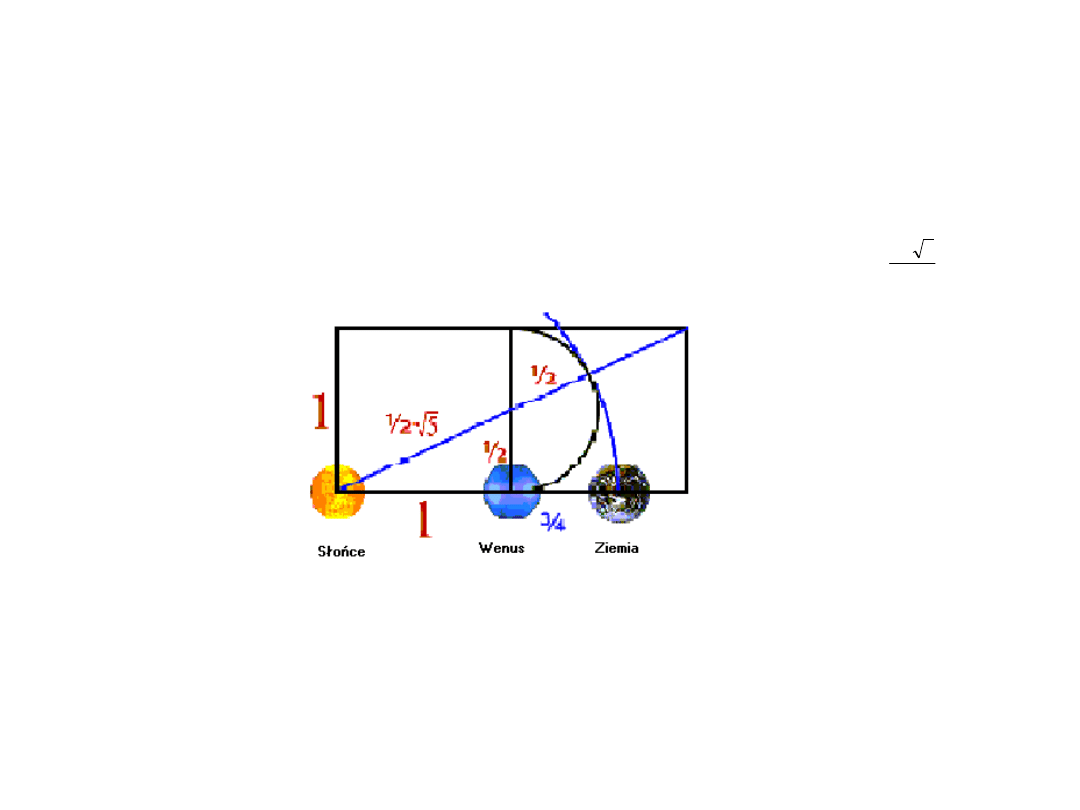
Wzajemna zależność między odległością Wenus i Ziemi od Słońca:

2

5

1





Źródło: opracowanie własne na podstawie strony internetowej: http://www.aeronivest.com z dnia 05.05.2002

Model D. Bradleya

• Model D. Bradleya oparty jest na relacjach kątowych

między planetami (są to tzw. aspekty) a ich wpływem na

zachowanie uczestników rynków kapitałowych, a zwłaszcza

akcji notowanych na Wall Street.

• Autor metody stworzył formułę matematyczną obliczającą

skumulowany potencjał wszystkich aspektów planetarnych

systemu słonecznego z wykorzystaniem wag odległości

planet od ich istotnych aspektów.

• Moment czasu, w którym planety ustawiają się w ściśle

określony sposób charakteryzuje się większym

prawdopodobieństwem wystąpienia zmiany

dotychczasowego trendu.

• Metoda Bradleya znalazła zastosowanie w dwu programach

komputerowych: Quick Harmonic Trader oraz Galactic

Trader.

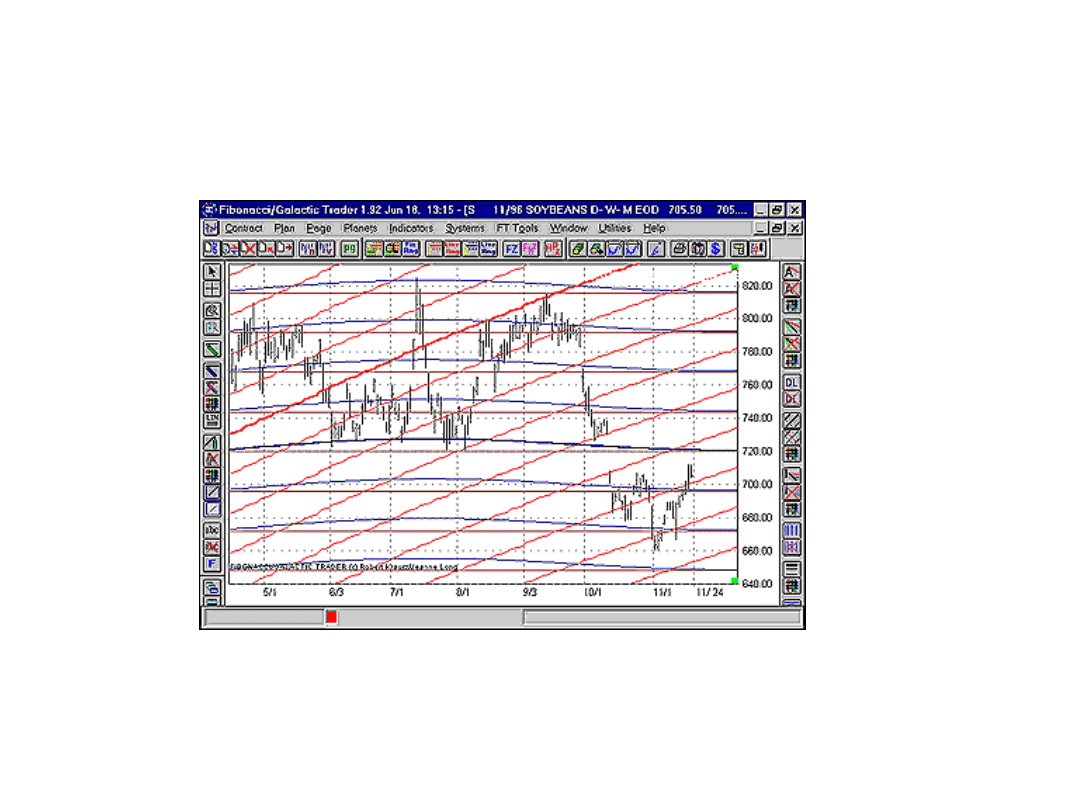
Wykres ceny trzymiesięcznych kontraktów terminowych na dostawę soji z listopada 1996 r.

Źródło: opracowanie własne na podstawie strony internetowej: http://www.galacticinvestor.com/review/Galactic.htm
z dnia 30.09.2002 i programu Galactic Trader v.

Objaśnienia

• Rysunek przedstawia wykres ceny kontraktu terminowego na

dostawę soji z listopada 1996 r. wraz z naniesionymi nań

liniami:

• Liniami wsparcia występującymi co 24 centy z uwagi na fakt, że

podział kąta pełnego tj. 360 stopni przez 15, dokonany po raz

pierwszy przez Ganna daje w rezultacie taki właśnie wynik. Z

zapisków tego legendarnego gracza wiadomo, że taki podział

szczególnie przypadł mu do gustu. Linie wsparcia na rysunku

mają przebieg zbliżony do horyzontalnego.

• Linie cen planet skorelowane wraz długością geocentryczną

Saturna. Z uwagi na fakt, że planeta ta porusza się bardzo

wolno przez Zodiak, tworzy ona na wykresie linie ukośne o

nieznacznym kącie nachylenia w stosunku do osi poziomej.

• Linie ceny planetarnej dla heliocentrycznej długości Marsa.

Planeta ta charakteryzuje się znacznie szybszym ruchem przez

Zodiak, w związku z tym na rysunku utworzy ona linie ukośne o

nieco większym nachyleniu do osi poziomej, które będziemy

nazywać diagonalnymi.

Objaśnienia

• Linie cen planet z punktu 2 i 3 stanowią

poziomy wsparcia i oporu dla ceny kontraktu na
dostawę soji. Już pobieżna analiza tego rysunku
uwidacznia, z jaką precyzją wyznaczają punkty
zatrzymania ruchu ceny kontraktu.

• Linie planet mogą być wykorzystane również do

określenia potencjalnych poziomów wsparcia i
oporu dla głównych indeksów giełdowych.
Rysunek 30 przedstawia linie planet Uran i Mars
wraz z wykresem indeksu S&P.

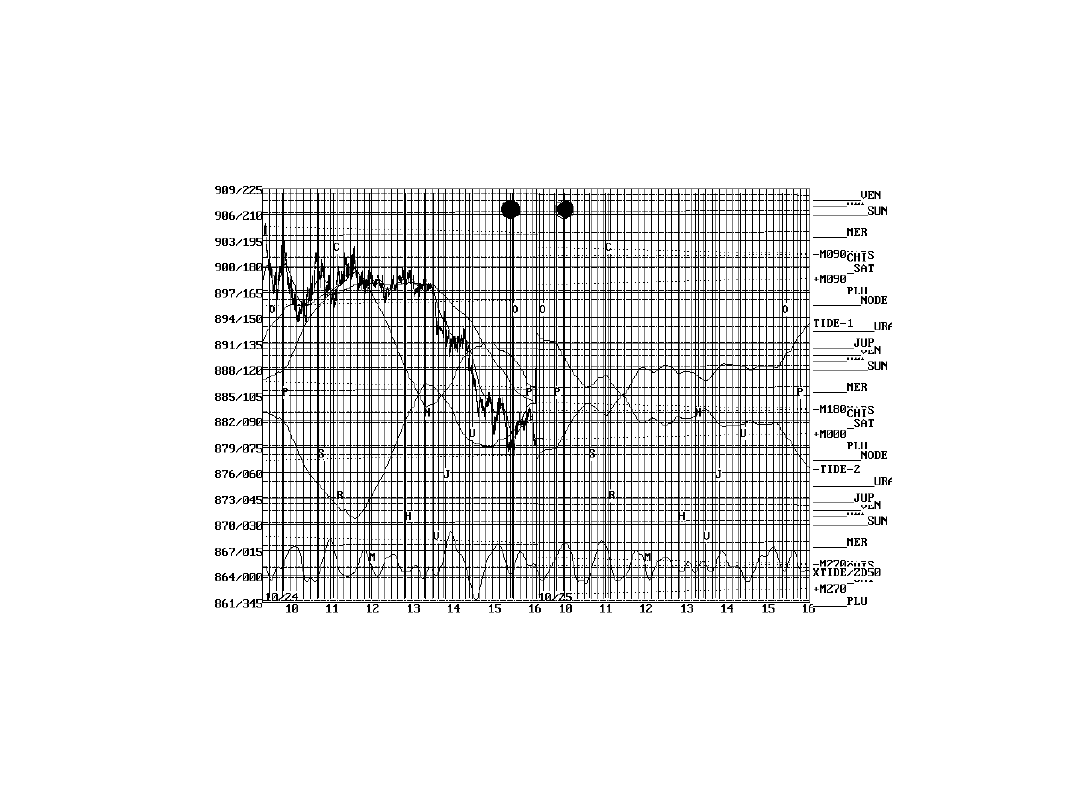
Linie planet na wykresie indeksu S&P. Poziomy wsparcia wyznaczone przez planetę Uran: 857, 875 i 893 i przez planetę Mars: 861, 883, 901.

Źródło: opracowanie własne na podstawie programu: Larson Chaos Trader.

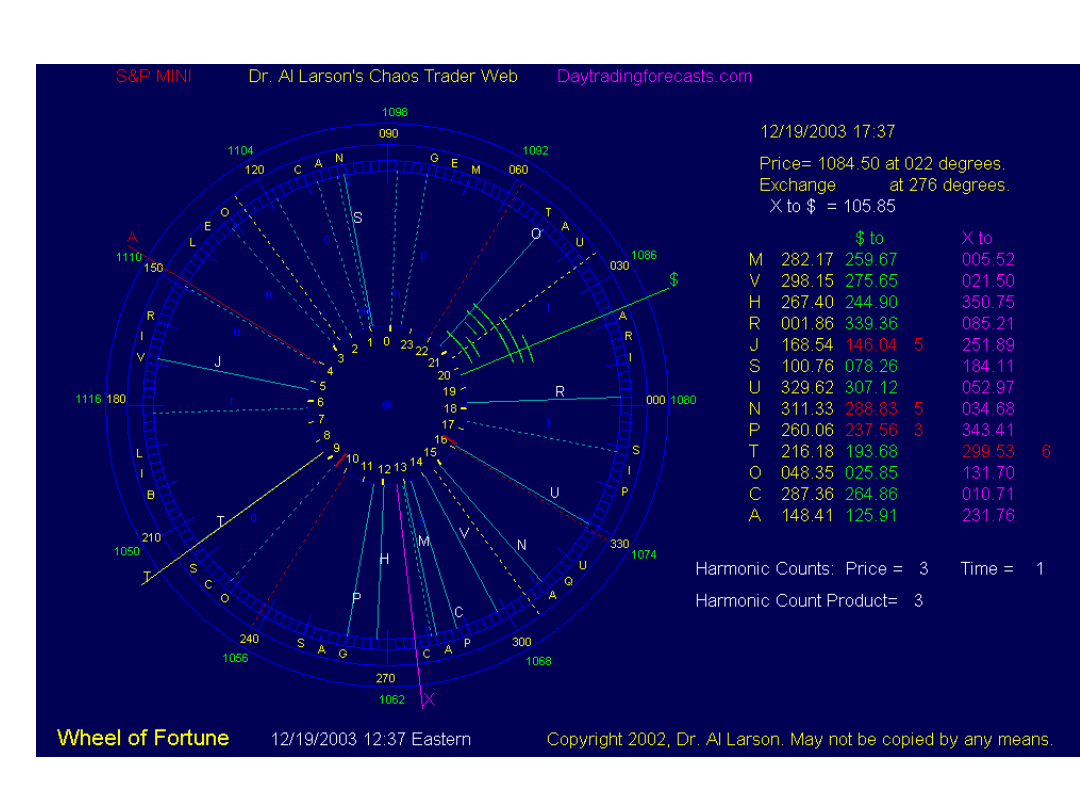
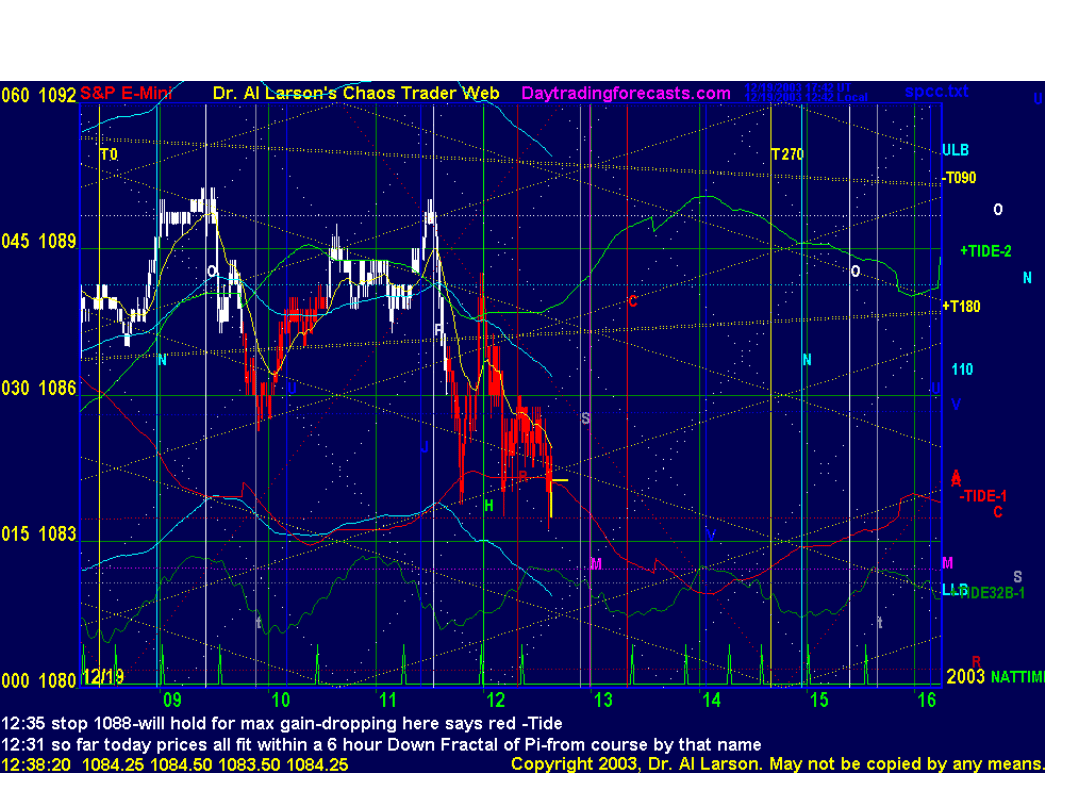
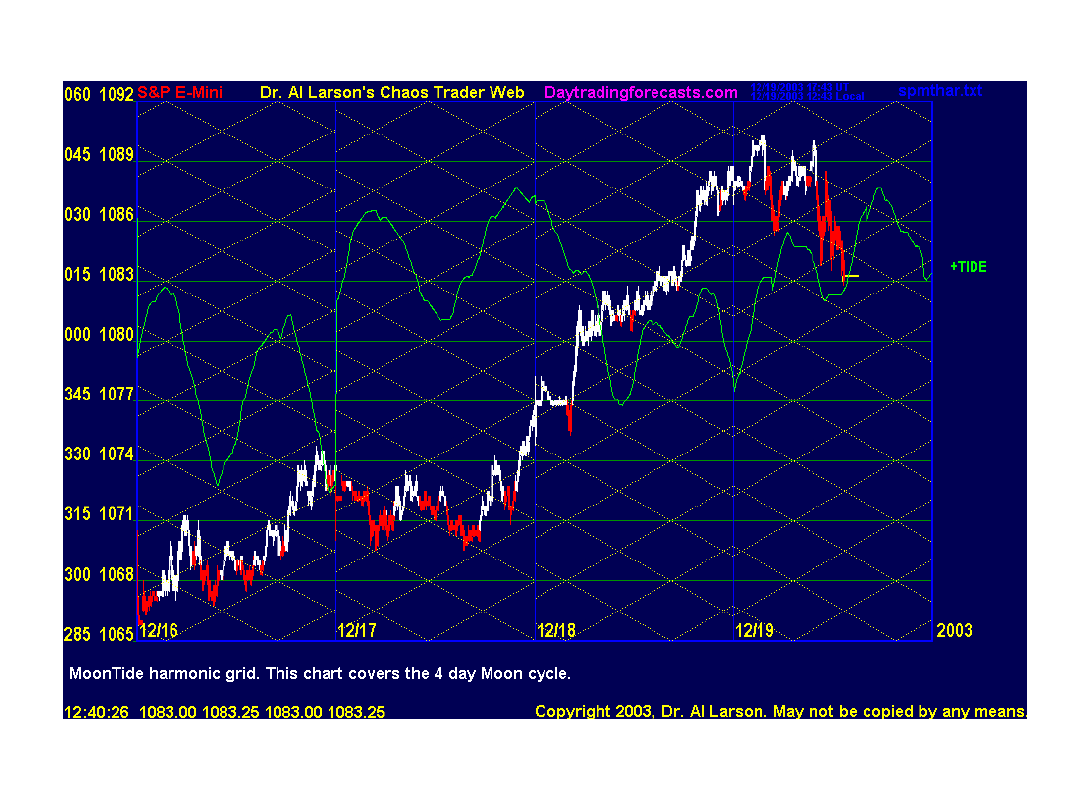
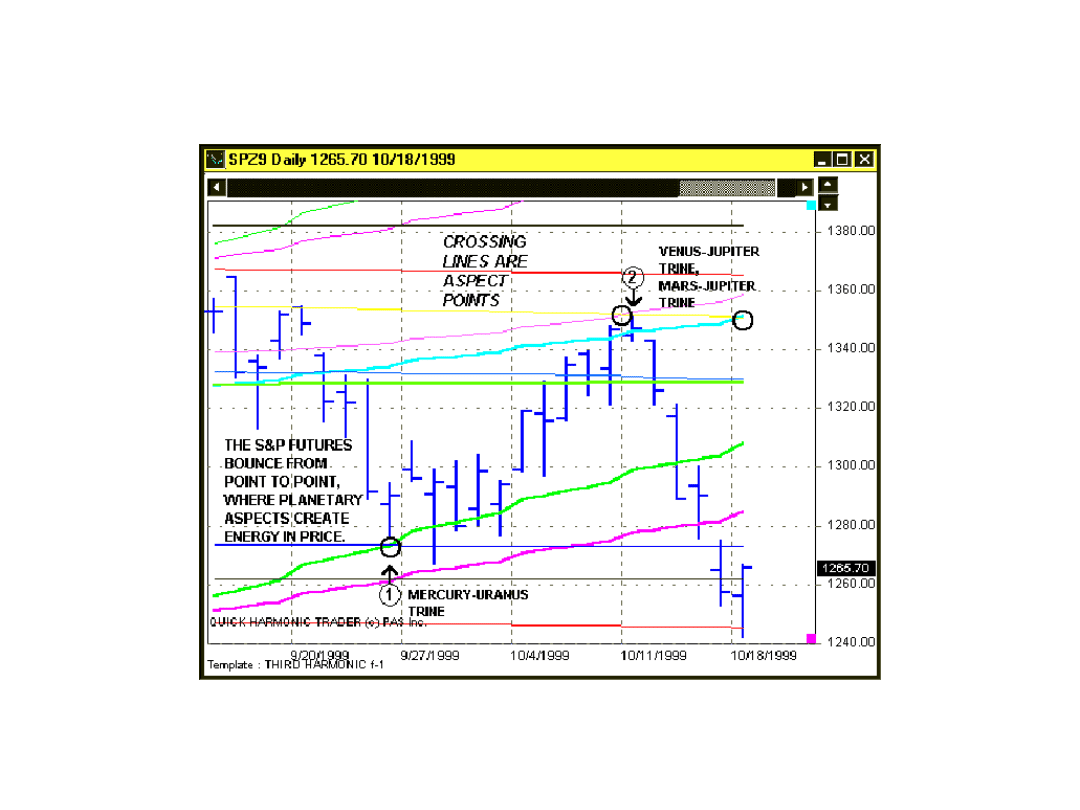
Przykład zastosowania programu Quick Harmonic Trader – indeks S&P

Źródło: opracowanie własne przy wykorzystaniu strony internetowej:
http://www.marketdetective.com/QHT/qhtinfo.htm z dnia 30.06.2001.

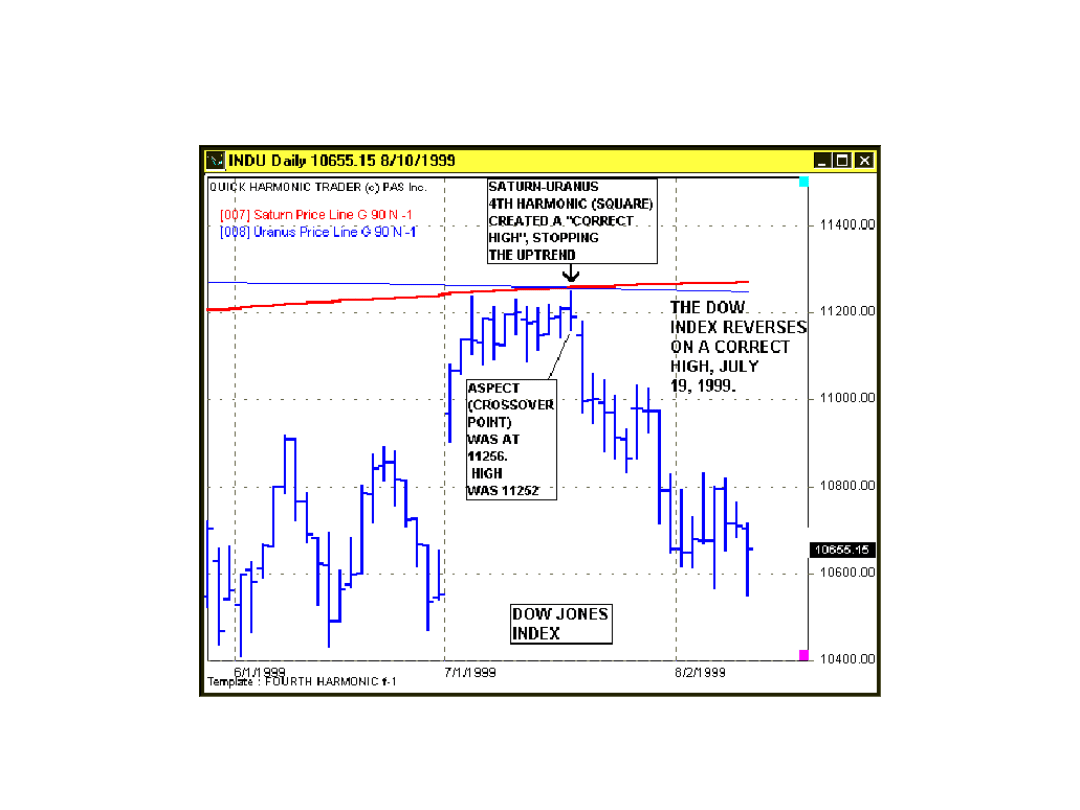
Przykład zastosowania programu Quick Harmonic Trader – indeks DJIA

Źródło: opracowanie własne przy wykorzystaniu strony internetowej:

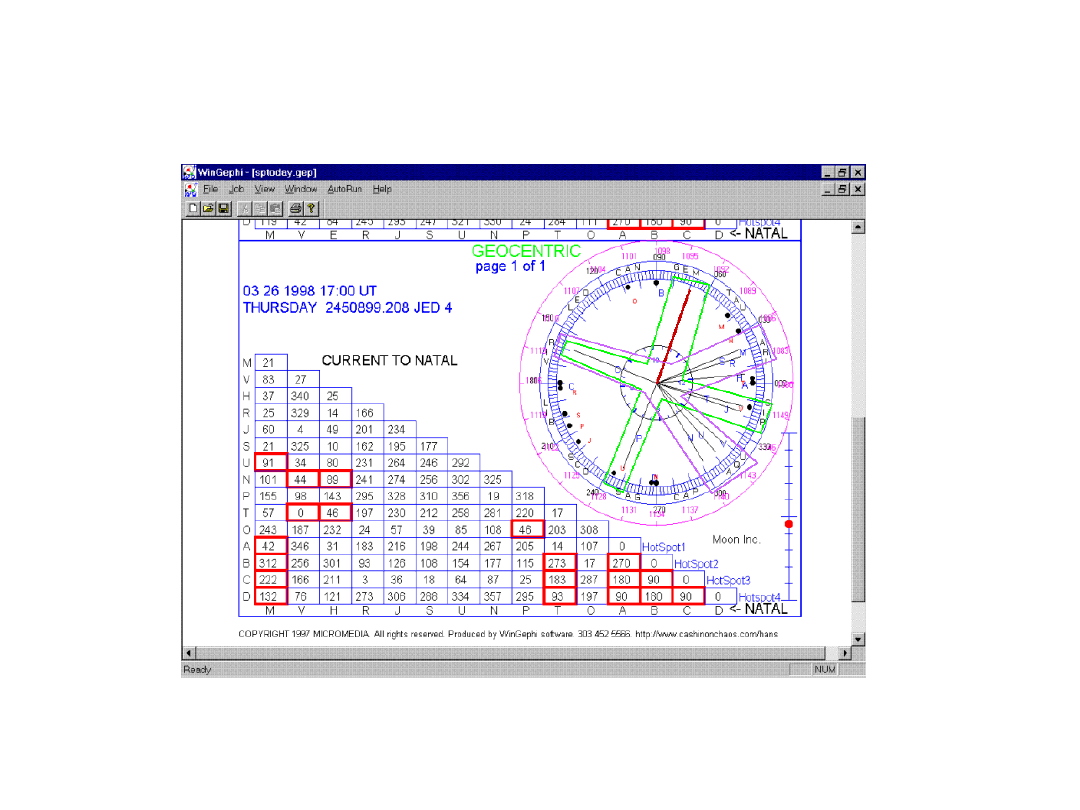
Wyznaczenie punktów zwrotnych indeksu S&P przy pomocy wpływu planet na zachowanie inwestorów.

Źródło: strona internetowa: http://www.marketdetective.com/QHT/qhtinfo.htm z dnia 30.06.2001.

Objaśnienia

• Rysunek przedstawia tzw. geocentryczne koło planetarne

stworzone na dzień 26 marca 1998 r. tj. jedną sesje po silnym

spadku indeksu S&P. W jego środku umieszczona została

Ziemia, a na obrzeżach poszczególne ciała niebieskie naszego

Układu Słonecznego, oznaczone odpowiednimi literami np. M -

Merkury, V – Wenus, R -Mars i T – Księżyc itd. Wewnętrzne

koło reprezentuje zegar ziemski. Linia pogrubiona oznacza

godzinę 16.15 tj. moment zamknięcia notowań indeksu w

Nowym Yorku.

• W kole geocentrycznym wykreśla się takie figury jak: trójkąty,

kwadraty, pentagony i heksagony. Wzorem o kluczowym

znaczeniu w naszym przykładzie jest tzw. wielki krzyż

(prostokąt). W jego wnętrzu znajduje się: linia zamknięcia

sesji w Nowym Jorku, dwie fazy Księżyca oraz planety: Wenus,

Uran, Jupiter i Pluton. Drugi wzór stanowi formacja zwana „Y”

(

yod lub yoda

). Jedno jej ramię zawiera planety: Uran, Neptun

i Wenus. Drugie – Saturna, Marsa, Merkurego i Słońce.

• Kosmologiczna interpretacja położenia planet wskazuje na

istotny punkt zwrotny.

• Wpływowi planet na zachowanie inwestorów

poświęcono stosunkowo dużo pozycji zwracając

uwagę, że oprócz Księżyca także i one silnie

oddziałują na ludzkie emocje[1].

• Ponadto wiele firm korzysta także z usług

astrologów, którzy na podstawie układu planet

prognozują wydarzenia gospodarcze[2]. „Chodzi tu

przede wszystkim o wzajemne położenie Jowisza i

Saturna. Np. razem z koniunkcją obydwu planet w

Strzelcu w 1983 r. rozwój gospodarczy uległ

przyspieszeniu. Od stycznia do sierpnia następnego

roku Jowisz, Saturn, a także Neptun i Mars tworzyły

negatywne aspekty, czego odbiciem był spadek

notowań na giełdach. Kiedy w 1985 r. Jowisz znalazł

się w pozytywnych aspektach z Uranem i Plutonem,

wzrosły również notowania giełdowe.”[3]

• Obecnie wykonuje się także horoskopy dla

poszczególnych giełd światowych, które mają

wychwycić korelację odmienną w stosunku do

światowej.[4]

Gdzie to znaleźć

• [1] Np.

• Meridian B. „Planetary Stock Trading”, Cycles Research,

• Luther J. “Astro – Cycles and Speculative Markets”, Lambert – Gann

Publishing Co.,

• Hanula H. “Market Astro Physics and Chaos”, Micromedia,

• Karklins M. “Planetary Cycles: Advanced Studies”, Planetary Cycles

Publishing.

• Karklins M. “Planetary Cycles: Soybean Calendar”, Planetary Cycles

Publishing,

• [2] Typowym przykładem mogą być prace: Stathis G. „Starcycles

Calendar Appointment Book 2001”, Starcycles, Oakland CA 2000 i

Stathis G. „Business Astrology 101: Weaving to the Web Between

Business and Myth”, Starcycles, Oakland CA 2001 oraz Parker D.,

Paricora J. “The Complete Astrologer”, McGraw – Hill, New York 1971.

• [3] Czerniawski R. „Giełdy”, Wydawnictwo Park, Bielsko – Biała 1992.

• [4] Czerniawski R. „Giełdy”, Wydawnictwo Park, Bielsko – Biała 1992.

Pioruny

• Rynki finansowe poruszają się przechodząc ze wzoru

opisanego za pomocą jednego tzw. dziwnego

atraktora[1] do wzoru opisanego za pomocą innego.

• Jeśli atraktor staje się już nieaktualny wtedy zmienia

się w tzw. atraktor odrzucony. Zmianę atraktora

oznacza się jako SA/SR. Bardzo często wzory SA/SR

na wykresie cen akcji tworzą tzw. pioruny kuliste.

•

[1] Atraktor - obszar lub punkt w pewnej przestrzeni stanów, do którego system

zmierza i wokół którego system pozostaje w dowolnie dużej skali czasu. Do

najprostszych przykładów atraktora należy punkt w przestrzeni fazowej

odpowiadający położeniu spoczynkowemu wahadła (lub ogólniej oscylatora)

Klasycznymi atraktorami są atraktor Płykina, atraktor Henona, atraktor Loziego,

atraktor Lorentza. Peitgen H., Juergens H., Saupe D. „Granice chaosu –

fraktale”, Wydawnictwo Naukowe PWN, Warszawa 1995.

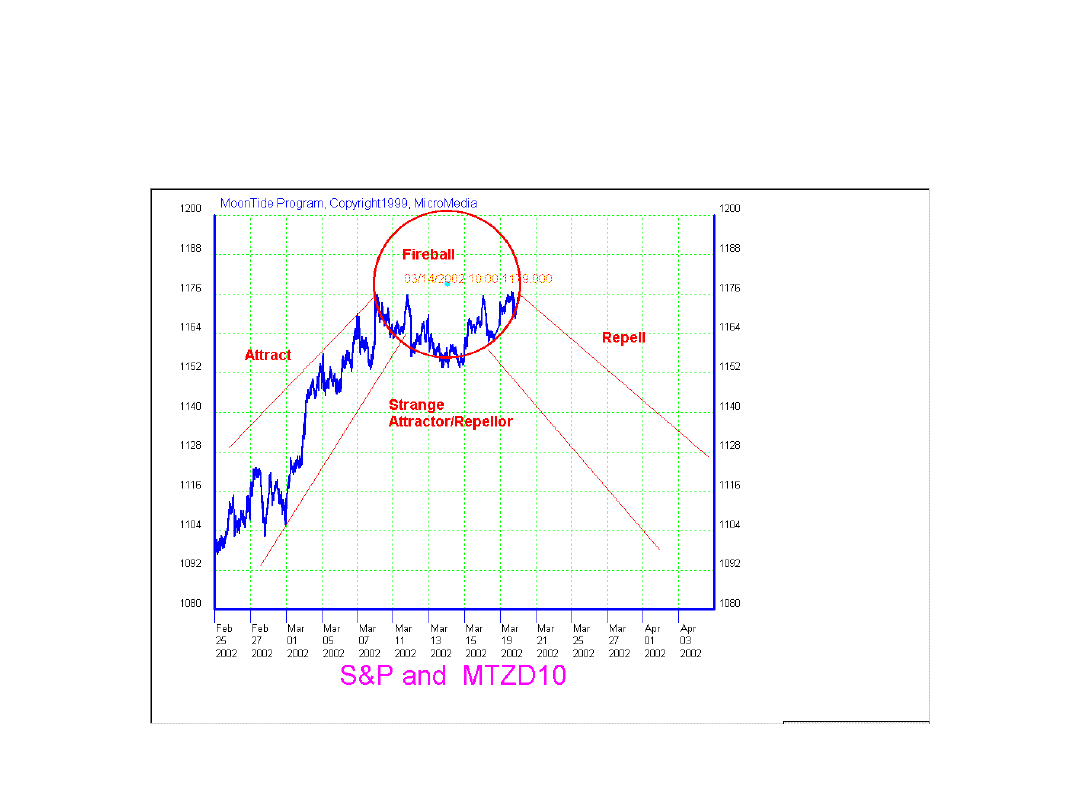
Atraktor

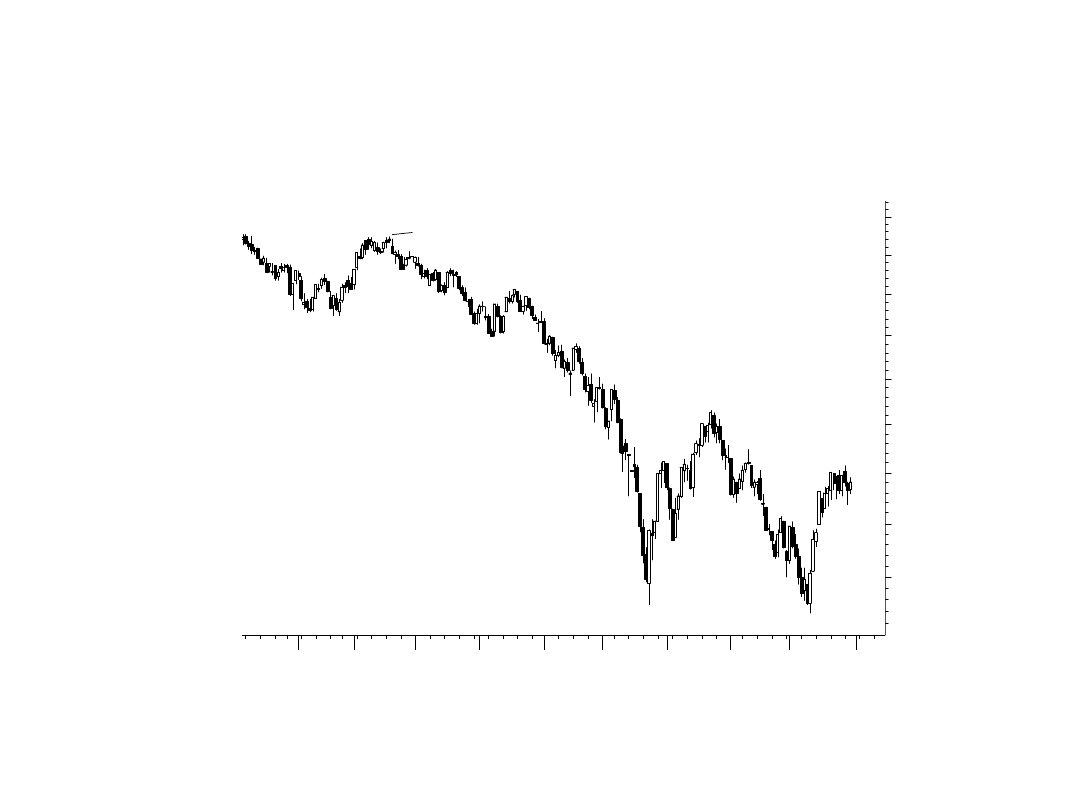
2002

February

March

April

May

June

July

August

September October

November

800

850

900

950

1000

1050

1100

1150

1200

S&P 500

Szczyt formacji wypadł 19.03.2002

S&P 500 (USA)

Objaśnienia

• Piorun kulisty utworzony na wykresie S&P sugeruje szybki

ruch rynku do jakiego niewątpliwie dojdzie po wybiciu z

formacji.

• Koniec formacji pioruna przypada w dniu równo-nocy

wiosennej (co znacznie zwiększa wagę tego sygnału),

będącego jak wiemy początkiem roku w przyrodzie.

• Kierunek wybicia z formacji powinien uwidocznić trend na

najbliższe 365 dni kalendarzowych.

• Przy użyciu specjalnej techniki analitycznej można

oszacować, że większe jest prawdopodobieństwo wybicia

indeksu dołem.

•

• Wybicie z formacji miało miejsce rzeczywiście dołem.

Tendencja zniżkowa jest, jak widać, stosunkowo silna.

• Szczyt indeksu wystąpił w dniu 19.03.2002 r. a więc dwa dni

przed prognozowanym.