Podstawowe pojęcia algebry liniowej

(uzupełnienie):

•

Określenie przestrzeni liniowej nad pewnym ciałem

(niepusty zbiór elementów, w którym zdefiniowano operację
dodawania elementów oraz mnożenia elementów przez skalar).
Jakie warunki muszą spełniać operacje mnożenia i dodawania?
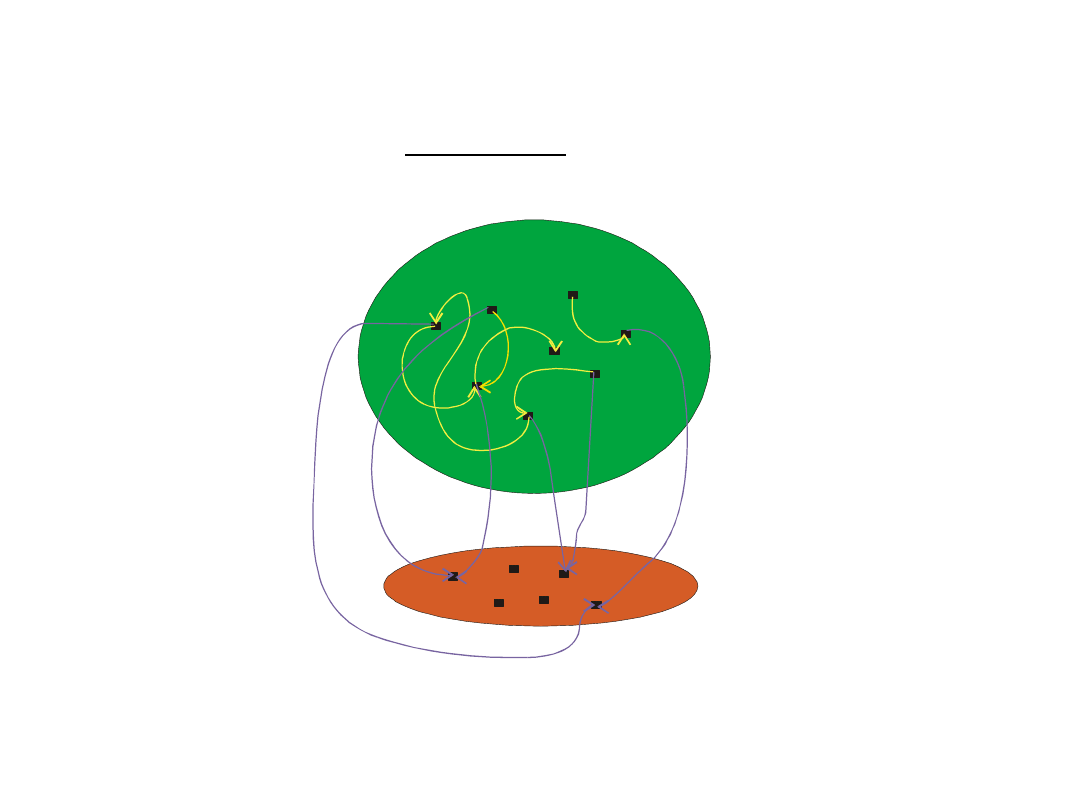
Przestrzeń liniowa rzeczywista i zespolona

φ1

φ3

φ2

φ4

φ5

φ6

L

K

c1

c
2

c3

c4

φ1+ φ2

φ3+ φ5

φ2×c1

φ4×c3

•

Liniowa zależność i liniowa niezależność wektorów

Przyjmijmy, że φ

1

, φ

2

, φ

3

, ... są elementami przestrzeni liniowej

(wektorami), natomiast c

1

, c

2

, c

3

, ... są skalarami.

Jeżeli istnieją liczby c

1

, c

2

, ..., c

n

(z których co najmniej jedna jest

różna od zera) takie, że równość c

1

φ

1

+ c

2

φ

2

+ c

3

φ

3

+...+ c

n

φ

n

=0 jest

spełniona, to wektory φ

1

, φ

2

, ..., φ

n

nazywamy liniowo zależnymi (w

przeciwnym wypadku wektory te nazywamy liniowo niezależnymi).



Przykład:
Jeżeli mamy wektory φ

1

=[2,0], φ

2

=[5,0], to możemy pokazać, że

wektory te są liniowo zależne, gdyż można wybrać c

1

= –2.5 i c

2

= 1

i zapisać, że –2.5×[2,0] + 1×[5,0] = 0
uwaga: [0,0] – wektor zerowy będzie spełniał rolę elementu
zerowego przestrzeni liniowej (czyli będzie spełniona równość c

1

φ

1

+

c

2

φ

2

= 0)



Fakt, że wektory φ

1

i φ

2

są liniowo zależne oznacza, że jeden z nich

można wyrazić za pomocą drugiego. Wynika to z równania:

c

1

φ

1

+ c

2

φ

2

= 0

Jeżeli do naszego zbioru dwóch liniowo zależnych wektorów

(φ

1

=[2,0], φ

2

=[5,0]) dodamy jakikolwiek wektor φ

3

, to taki zbiór

trzech wektorów będzie na pewno liniowo zależny.

/ponieważ współczynnik c

3

występujący w równaniu

c

1

φ

1

+ c

2

φ

2

+ c

3

φ

3

=0 można wziąć jako równy zero i wtedy równanie to

będzie ponownie spełnione/.

To stwierdzenie jest ogólne i można je rozszerzyć na dowolną liczbę

dodawanych wektorów – wynikowy zbiór, uzyskany z połączenia

wektorów liniowo zależnych z dowolnymi wektorami będzie zawsze

liniowo zależny (jako całość).

Uwaga ogólna:
Jeżeli mamy dany zbiór wektorów liniowo zależnych φ

1

,

φ

2

, ..., φ

n

to przynajmniej jeden z nich można wyrazić za

pomocą wektorów pozostałych
/inaczej mówiąc: przynajmniej jeden z nich jest kombinacją
liniową wektorów pozostałych/.
Dla wektorów liniowo niezależnych, równość
c

1

φ

1

+ c

2

φ

2

+ c

3

φ

3

+...+ c

n

φ

n

=0

może być spełniona jedynie wtedy, gdy wszystkie
współczynniki c są równe zero.

Np. wektory φ

1

=[2,0], φ

2

=[0,5] są liniowo niezależne.

•

Kombinacja liniowa
Kombinacją liniową wektorów φ

1

, φ

2

, ..., φ

n

nazywamy wektor

c

1

φ

1

+ c

2

φ

2

+...+ c

n

φ

n

Jeżeli dany wektor, np. wektor Φ, można zapisać jako
Φ= c

1

φ

1

+ c

2

φ

2

+...+ c

n

φ

n

,

to mówimy, że wektor Φ jest kombinacją liniową wektorów φ

1

, φ

2

, ..., φ

n

.

/stwierdzenie, że wektor Φ jest kombinacją liniową wektorów φ

1

, φ

2

, ...,

φ

n

oznacza tyle, że wektor Φ możemy zbudować z elementów φ

1

, φ

2

, ...,

φ

n

, biorąc każdy z tych elementów z odpowiednim wkładem, czyli

współczynnikiem c/

Skalary c

1

, c

2

, c

3

, ..., c

n

nazywamy współczynnikami kombinacji liniowej.

•

Wymiar przestrzeni liniowej
Wymiar przestrzeni to maksymalna liczba liniowo niezależnych

wektorów, które można znaleźć w tej przestrzeni. Wymiar jest zgodny z

intuicją, gdy myślimy o znanych nam przestrzeniach. Np. prosta, którą

można uważać za zbiór odcinków (w tym sensie prosta jest przestrzenią

liniową, a wektorami tej przestrzeni są odcinki leżące na tej prostej) ma

„jeden wymiar”, czyli jej wymiar wynosi 1.

•

Płaszczyzna (przestrzeń liniowa, której wektorami są leżące na

niej odcinki) ma wymiar 2. Znana z geometrii kartezjańska

przestrzeń, której elementami są wektory określane przez trzy

liczby (współrzędne) w prostokątnym układzie współrzędnych,

ma wymiar równy 3.

•

Wymiar przestrzeni a liniowa niezależność wektorów
W przestrzeni o wymiarze równym na przykład 2, której

przykładem jest płaszczyzna będąca zbiorem wektorów [x,y]

można znaleźć co najwyżej dwa wektory liniowo niezależne.

Jeżeli do takiej pary dodamy jakikolwiek trzeci wektor, to mamy

już zbiór trzech wektorów liniowo zależnych. Czyli, że jeden z

wektorów można będzie wyrazić jako kombinację liniową

pozostałych). Inaczej mówiąc, jeden z tych trzech wektorów da

się „zbudować” z dwóch pozostałych wektorów
BAZA:
Określenie bazy: bazą w n-wymiarowej przestrzeni L nazywamy

zbiór n wektorów liniowo niezależnych w tej przestrzeni.
Baza jest jakby fragmentem przestrzeni liniowej (bo jest to po

prostu zbiór kilku wektorów należących do tej przestrzeni).

Uwagi dotyczące bazy:



Liczba wektorów bazy jest zawsze taka, jak wymiar przestrzeni.



W każdej przestrzeni istnieje baza.



Co więcej, w każdej przestrzeni istnieje nieskończenie wiele baz.



Każda baza w danej przestrzeni zawiera tyle samo wektorów
bazy.



Wszystkie bazy, które można znaleźć w danej przestrzeni są
formalnie równoważne (tzn. nie ma baz lepszych i gorszych). Ze
względów technicznych (np. z punktu widzenia wykonywanych
rachunków) niektóre bazy są po prostu wygodniejsze niż inne.



Baza generuje przestrzeń liniową, inaczej mówiąc: przestrzeń
liniowa jest rozpięta na wektorach bazowych, jest liniową
powłoką bazy.



Przykład: baza wersorów w kartezjańskiej przestrzeni 3-
wymiarowej.

•

Iloczyn skalarny (jako przykład funkcjonału)
Iloczyn skalarny jest funkcjonałem dwuargumentowym, czyli

pewną funkcją dwóch argumentów (zmiennych), która każdej

parze wektorów x,y, należących do pewnej przestrzeni

liniowej, przyporządkowuje liczbę (skalar), przy czym to

przyporządkowanie musi spełniać określone aksjomaty

Iloczyn skalarny dwóch wektorów x oraz y zapisuje się

zazwyczaj jako (x,y) lub <x|y>

•

Iloczyn skalarny w przestrzeni funkcyjnej
Elementami (czyli wektorami) przestrzeni liniowej mogą być

również funkcje ciągłe (argumentu t) określone w przedziale

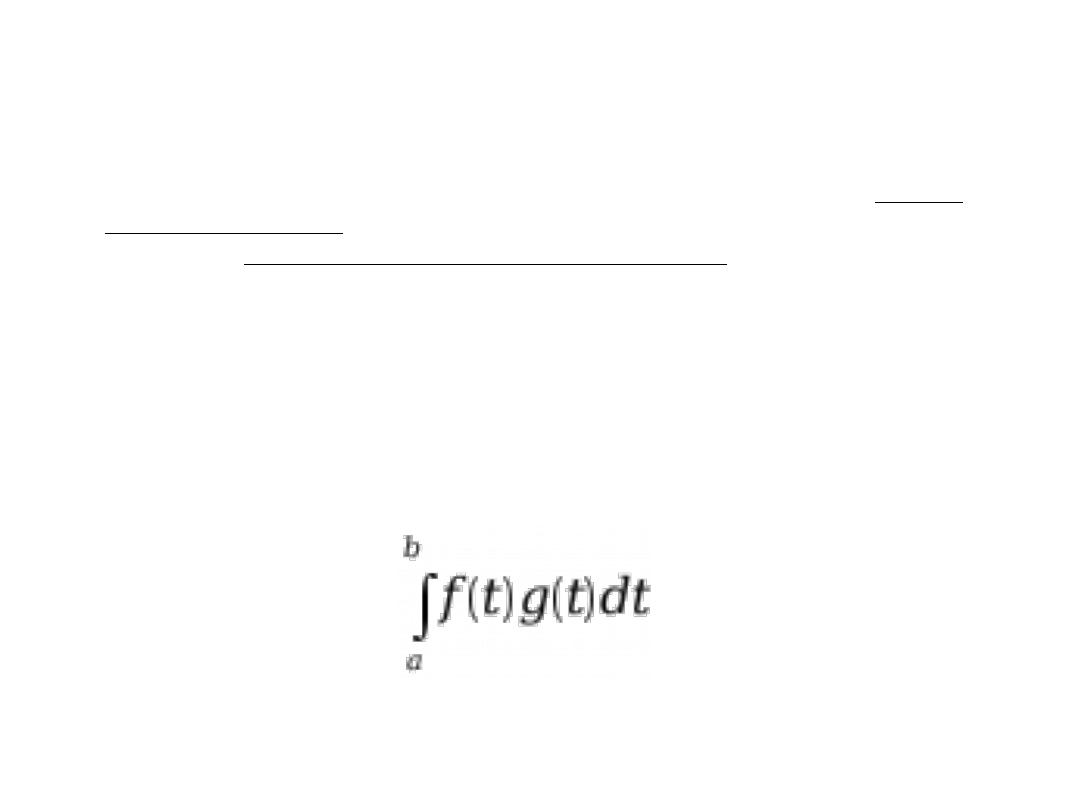
<a,b>. Iloczyn skalarny dwóch dowolnych funkcji f(t) i g(t)

należących do tej przestrzeni, określa się zazwyczaj jako całkę

z ich iloczynu:

•

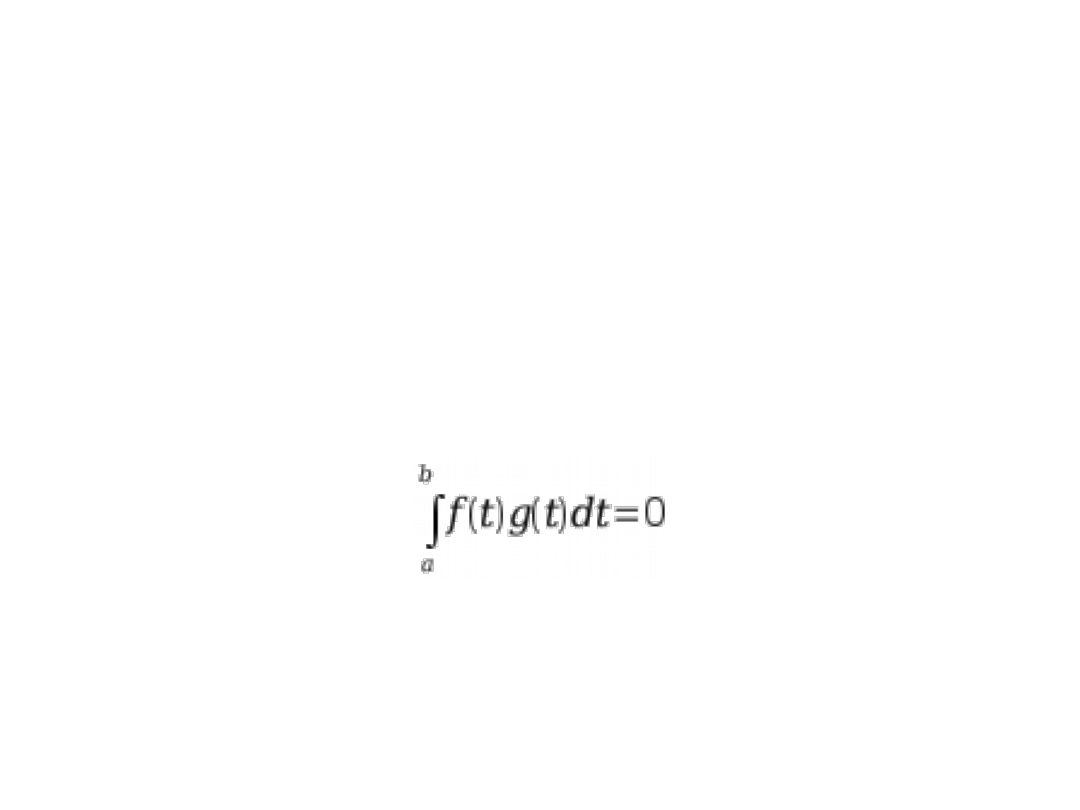
Ortogonalność (dwóch wektorów)

Dwa wektory określamy jako ortogonalne jeżeli ich iloczyn
skalarny znika (czyli jest równy zero).
A zatem, jeżeli (x,y) = 0 to wektory x oraz y są wzajemnie
ortogonalne.
Analogicznie: funkcje f(t) i g(t) są wzajemnie ortogonalne jeżeli
ich iloczyn skalarny znika, czyli:

•

Unormowanie wektora

Wektor x należący do przestrzeni liniowej L nazywamy unormowanym (lub
znormalizowanym), jeżeli iloczyn skalarny tego wektora z sobą samym jest równy 1.
A zatem, jeżeli (x,x)=1 to mówimy, że wektor x jest unormowany.
Jeżeli mamy do czynienia z przestrzeniami funkcyjnymi, których elementami są

funkcje ciągłe (np. ψ

1

, ψ

2

, ψ

3

,...) to o danej funkcji ψ (np. ψ

1

) powiemy, że jest

unormowana, jeżeli:

przy czym całkujemy po całym zakresie zmienności wszystkich

zmiennych.
W sytuacji, gdy elementami przestrzeni liniowej są funkcje zmiennej

zespolonej, powyższy warunek unormowania wygląda następująco:

(również w tym przypadku całkujemy po całym zakresie zmienności

wszystkich zmiennych).

1

*

1

1











d

Przekształcenia przestrzeni liniowej (operatory)
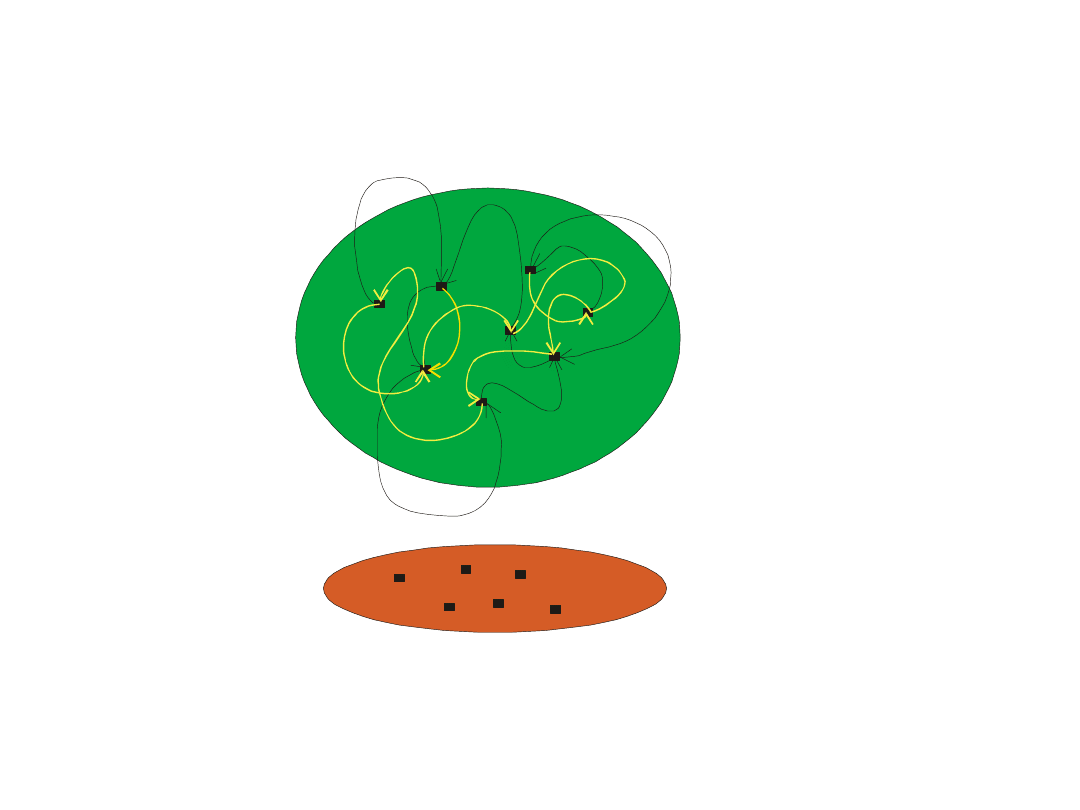
Przekształceniem przestrzeni L nazywamy funkcję, która
każdemu wektorowi x przestrzeni L przyporządkowuje wektor y
tej przestrzeni.

L

K

Kolorem żółtym zdefiniowano przekształcenie A

przestrzeni L

Kolorem czarnym zdefiniowano przekształcenie B

przestrzeni L

Różnica między przekształceniem (operatorem) a iloczynem
skalarnym
Zbiorem wartości dla funkcjonału jest ciało skalarów, czyli liczby.
Zbiorem wartości dla przekształceń jest przestrzeń, czyli wektory.
Dlatego np. iloczyn skalarny jest funkcjonałem, a nie
przekształceniem, bo iloczyn skalarny jest zawsze liczbą.

L

K

Kolorem żółtym zdefiniowano pewne przekształcenie w przestrzeni L

Kolorem granatowym zdefiniowano iloczyn skalarny

Postulaty mechaniki kwantowej:

Postulaty, teoria fizyczna, interpretacja znanych faktów i przewidywanie

nowych.

I postulat mechaniki kwantowej:

Stan układu kwantowochemicznego (posiadającego f stopni swobody)
określa funkcja falowa



, która zależy od zmiennych

q

1

, q

2

, …, q

f

, t , czyli



=



( q

1

, q

2

, …, q

f

, t)

gdzie q

i

to współrzędne, natomiast t oznacza czas.

Funkcja falowa



nazywana jest funkcją stanu

Statystyczna interpretacja funkcji falowej (zaproponowana przez
Borna) mówi, że kwadrat modułu funkcji falowej pomnożony przez
element objętości d określa prawdopodobieństwo P, że w chwili t

wartości współrzędnych zawarte są w przedziałach od q

1

do q

1

+dq

1

,

od q

2

do q

2

+dq

2

, …, i od q

f

do q

f

+dq

f

P = |



( q

1

, q

2

, …, q

f

, t)|

2

d



Dla pojedynczej cząstki (np. dla elektronu), mamy funkcję

 postaci

( x, y, z, t), natomiast P = |(x, y, z, t)|

2

dx∙dy∙dz

gdyż d

=dx∙dy∙dz (w przypadku pojedynczej cząstki)

Uwaga: kwadrat modułu funkcji  zdefiniowany jest jako: |

|

2

=



∙

*

Dla stanów związanych (dla których odległości między cząstkami

tworzącymi układ są skończone) sumaryczne prawdopodobieństwo

znalezienia układu w dowolnym elemencie objętości całej

przestrzeni musi być równe jedności (gdyż jest to zdarzenie pewne),

gdzie całkowanie obejmuje cały zakres zmienności wszystkich

zmiennych.

Powyższy warunek oznacza, że funkcje falowe muszą być
funkcjami znormalizowanymi (unormowanymi).

Funkcje klasy Q:
Funkcje falowe muszą być funkcjami klasy Q (quantum), co

oznacza, że muszą to być funkcje:
(i) ciągłe,
(ii) znormalizowane,
(iii) znikające w nieskończoności

Gęstość prawdopodobieństwa
Ponieważ prawdopodobieństwo P wyraża się przez

P=|



|

2

d



wobec tego gęstość prawdopodobieństwa



(czyli P/d



) będzie

równa kwadratowi modułu funkcji falowej, czyli



= |



|

2

oraz P =



∙d



Funkcja falowa ( ) – opisuje stan układu, zawiera wszystkie

dostępne informacje o układzie (brak interpretacji fizycznej)
Kwadrat modułu funkcji falowej ( ||

2

) – określa gęstość

prawdopodobieństwa (posiada interpretację fizyczną).

•

Interpretacja Schrödingera oraz interpretacja

statystyczna
Schrödinger – uważał, że iloczyn gęstości prawdopodobieństwa i

ładunku (



∙ e) należy interpretować dosłownie jako gęstość

ładunku, czyli uważał, że elektron jest tworem rozmytym a nie

cząstką punktową
Born – uważał, że elektron jest cząstką, przy czym kwadrat

modułu funkcji falowej (czyli gęstość) informuje o gęstości

prawdopodo-bieństwa napotkania cząstki w danym miejscu w

przestrzeni w danej chwili t

•

Nieodróżnialność cząstek identycznych. Bozony i fermiony
Nieodróżnialność oddziałujących ze sobą cząstek identycznych

(np. elektronów) wynika z niemożności określenia ich torów.
Permutacja (przenumerowanie, zamiana) cząstek identycznych

(np.

elektronów)

nie

może

zatem

zmieniać

gęstości

prawdopodobieństwa, czyli np.

|



(q

1

, q

2

, q

3

)|

2

= |



(q

1

, q

3

, q

2

)|

2

(gdzie q

k

oznacza współrzędne k-tej cząstki)

Aby spełniony był warunek niezmienniczości kwadratu modułu
funkcji falowej względem permutacji cząstek, sama funkcja może
wskutek permutacji albo pozostawać bez zmian, albo zmieniać
znak. Czyli,

 (q

1

, q

2

, q

3

) =

 (q

1

, q

3

, q

2

)

lub

 (q

1

, q

2

, q

3

) = –

 (q

1

, q

3

, q

2

)

Jeżeli funkcja

 nie zmienia się wskutek permutacji cząstek,

nazywamy ją symetryczną (względem permutacji);

Jeżeli funkcja

 zmienia znak wskutek permutacji cząstek,

nazywamy ją antysymetryczną (względem permutacji);



Okazuje się, że symetryczność lub antysymetryczność

względem permutacji jest cechą danego rodzaju cząstek



Cząstki, dla których funkcja falowa jest antysymetryczna

względem permutacji nazywamy fermionami



Cząstki, dla których funkcja falowa jest symetryczna

względem permutacji nazywamy bozonami



Przykłady fermionów: elektrony, protony, neutrony,

neutrina, jądra o nieparzystej liczbie nukleonów –

podlegają statystyce Fermiego-Diraca



Przykłady bozonów: mezony, fotony, jądra o parzystej

liczbie nukleonów – podlegają statystyce Bosego-Einsteina

II postulat mechaniki kwantowej

Każdej zmiennej dynamicznej A przyporządkowujemy w mechanice

kwantowej pewien operator posługując się regułami Jordana.
Zmienne dynamiczne, obserwable
mierzalne wielkości fizyczne (współrzędna, pęd, moment pędu,

czas, energia, moment dipolowy, etc.)
Operatory
Operatorami

nazywamy

przekształcenia

zdefiniowane

w

przestrzeni liniowej. Mówimy, że operator „działa” na element

przestrzeni liniowej, produkując (w wyniku tego działania) element

przestrzeni liniowej.

Reguły Jordana
(i)

jeżeli zmienną dynamiczną jest współrzędna (lub czas) to działanie

operatora (współrzędnej lub czasu) na funkcję polega na

pomnożeniu funkcji przez tę zmienną (współrzędną lub czas);

(ii)

jeżeli zmienną dynamiczną jest pęd p

j

, to odpowiadającym jej

operatorem (pędu) jest

lub równoważnie

np. dla składowej x-owej (p

x

) wektora pędu ( ) mamy:

, przy czym



ˆ

j

j

q

i

p











ˆ

j

j

q

i

p









 

ˆ

p



x

i

p

x









 

ˆ



2

h





(i)

jeżeli zmienną dynamiczną jest wielkość inna niż współrzędna,
pęd lub czas,

to odpowiadający jej operator znajdujemy

poprzez wyrażenie zmiennej

dynamicznej za pomocą

współrzędnych, czasu i pędu, a następnie zastąpienie

tych

ostatnich odpowiednimi operatorami (zgodnie z regułami (i)
oraz (ii))

Przykłady:

Energia kinetyczna elektronu (T) i jej operator są następujące:

Energia potencjalna (V) oddziaływania elektronu z jądrem o
ładunku Z·e,
jest wyrażona przez V = –Ze

2

/r

wobec tego operator energii potencjalnej ma postać:

)

(

2

1

2

2

2

z

y

x

p

p

p

m

T







































2

2

2

2

2

2

2

2

ˆ

z

y

x

m

T



r

Ze

V

2

ˆ 



Działanie operatora na funkcję

(1) operator działa na funkcję umieszczoną po jego prawej
stronie,
(2) jeżeli mamy iloczyn (zlożenie) operatorów, to ABψ =
A(Bψ),
(3) potęga operatora polega na wielokrotnym wykonaniu tej
samej operacji (zdefiniowanej przez operator).

Komutator

•

Operatory zazwyczaj nie są przemienne, co oznacza, że
kolejność zapisu operatorów jest istotna.

•

Komutatorem operatorów nazywamy operator postaci:
który oznaczamy przez
Dla operatorów przemiennych komutator znika. Jeżeli
operatory są przemienne (ich komutator znika), to mówimy,
że operatory te komutują.

Operator Hamiltona (hamiltonian)

•

Operator energii całkowitej (E), oznaczany symbolem

B

A ˆ

,

ˆ

A

B

B

A

ˆ

ˆ

ˆ

ˆ 

]

ˆ

,

ˆ

[ B

A

V

T

E





V

T

H

ˆ

ˆ

ˆ





Hˆ

III postulat mechaniki kwantowej

Jeżeli stan układu opisywany jest funkcją ψ(q

1

, q

2

, ..., q

f

, t),

to zmiana funkcji falowej ψ w czasie (ewolucja czasowa

układu) określona jest równaniem:

lub równoważnie

Jest to tzw. równanie Schrödingera zawierające czas

Równanie to jest zarazem równaniem ruchu w mechanice

kwantowej (znajomość operatora Hamiltona oraz funkcji ψ

(czyli stanu układu) w pewnej chwili t

0

, umożliwia

wyznaczenie funkcji ψ w dowolnej chwili t (przeszłej lub

przyszłej).





H

t

i

ˆ

















H

t

i

ˆ











IV postulat mechaniki kwantowej

Wynikiem pomiaru zmiennej dynamicznej A może być tylko wartość

własna odpowiadającego jej operatora ( )
Problem własny

A – zmienna dynamiczna,
– operator odpowiadający zmiennej A
ψ – funkcja własna operatora
a – wartość własna operatora (związana z funkcją własną ψ )

Badany układ może przebywać w różnych stanach, np. w stanie

opisywanym funkcją falową ψ

1

, lub w stanie opisywanym funkcją falową

ψ

4

. Wówczas, zagadnienie własne wyglądałoby następująco

lub

Wniosek: jeżeli układ znajduje się w stanie ψ

k

, przy czym funkcja ψ

k

jest

funkcją własną operatora ,to wynikiem pomiaru zmiennej A będzie

dokładnie wartość a

k

(będąca wartością własną operatora związaną z

funkcją własną ψ

k

.

n

n

n

a









ˆ



ˆ



ˆ



ˆ

1

1

1

ˆ







a



4

4

4

ˆ







a





ˆ



ˆ

ˆ

Konsekwencje IV postulatu mechaniki kwantowej:

1. Ponieważ wynikiem pomiaru zmiennej dynamicznej może być

tylko

liczba

rzeczywista,

to

operatory

odpowiadające

obserwablom muszą być hermitowskie.

Wyjaśnienie: operator

nazywamy hermitowskim, jeżeli dla

dwóch dowolnych funkcji f oraz g klasy Q zachodzi równość:

(gdzie dτ oznacza całkowanie po całym zakresie zmienności

wszystkich zmiennych)

Można udowodnić, że wartości własne operatorów hermitowskich

są rzeczywiste (dowód na ćwiczeniach).

1.

Jeżeli operatory isą przemienne (komutują), to odpowiadające

im obserwable A i B mogą mieć jednocześnie ściśle określone

wartości. Jest tak dlatego, że przemienne operatory mają wspólny

zbiór funkcji własnych (dowód na ćwiczeniach). A zatem:















d

g

f

d

f

g

*

)

ˆ

(

ˆ

*



ˆ



ˆ



ˆ













n

n

n

n

n

n

b

a













ˆ

ˆ

Jeśli układ znajduje się w stanie opisywanym funkcją ψ

n

to

obserwable A i B (odpowiadające operatorom

i ) mają

w tym stanie dokładnie wartości a

n

i b

n

. Obie wielkości można więc

jednocześnie dokładnie zmierzyć.

Wniosek: zasada nieokreśloności Heisenberga nie dotyczy tych
par zmiennych, którym odpowiadają przemienne operatory.

Nieprzemienne operatory mają natomiast różne funkcje własne.

Załóżmy, że układ jest w stanie opisywanym funkcją ψ.

Jeżeli funkcja ψ jest funkcją własną operatora , czyli zachodzi

to zmienną A można dokładnie zmierzyć (uzyskując wynik równy

a). Załóżmy, że chcemy jeszcze zmierzyć wielkość G, której

odpowiada operator

,przy czym operatory

i

nie komutują. W tej sytuacji funkcja ψ (opisująca stan układu w

danej chwili) nie jest funkcją własną operatora , a zatem wynik

pomiaru zmiennej G w tym stanie będzie nieokreślony.

Wniosek: zasada nieokreśloności Heisenberga dotyczy tych par

zmiennych, którym odpowiadają nieprzemienne operatory.



ˆ



ˆ



ˆ







a



ˆ



ˆ



ˆ



ˆ



ˆ

1.

Postulat IV stwierdza (w odniesieniu do energii), że wynikiem

pomiaru energii może być tylko wartość własna operatora

energii (hamiltonianu):

Pamiętamy, że równanie ruchu ma postać:

Podstawiamy prawą stronę równania ruchu do równania

własnego dla operatora Hamiltona i otrzymujemy:

Jeżeli hamiltonian, a więc i energia, nie zależy od czasu, mamy

do czynienia ze stanem stacjonarnym, a rozwiązaniem

powyższego równania jest funkcja:

)

,

,...,

,

(

)

,

,...,

,

(

ˆ

2

1

2

1

t

q

q

q

E

t

q

q

q

H

f

f











H

t

i

ˆ











)

,

,...,

,

(

)

,

,...,

,

(

2

1

2

1

t

q

q

q

E

t

q

q

q

t

i

f

f

























 







iEt

q

q

q

t

q

q

q

f

f

exp

)

,...,

,

(

)

,

,...,

,

(

2

1

2

1





co można sprawdzić przez podstawienie (dowód na
ćwiczeniach).

Wstawiając powyższą funkcję do równania Schrödingera

otrzymujemy:

Dzielimy obie strony przez czynnik wykładniczy (który jest zawsze

różny od zera) i otrzymujemy:

Równanie Schrödingera nie zawierające czasu:

lub krótko:

Równanie to angażuje nie zależącą od czasu funkcję falową i

dotyczy procesów (stanów) stacjonarnych.











 















 







iEt

q

q

q

E

iEt

q

q

q

H

f

f

exp

)

,...,

,

(

exp

)

,...,

,

(

ˆ

2

1

2

1





)

,...,

,

(

)

,...,

,

(

ˆ

2

1

2

1

f

f

q

q

q

E

q

q

q

H











E

H 

ˆ

V postulat mechaniki kwantowej:

Wiadomo, iż pomiar zmiennej dynamicznej A przeprowadzony na

układzie opisywanym funkcją ψ, prowadzi do wartości własnej

operatora (odpowiadającego zmiennej A), o ile funkcja ψ jest

funkcją własną operatora , czyli:

(gdzie liczba a (wartość własna) będzie wynikiem pomiaru zmiennej

A)

Powyższe informacje stanowią treść IV postulatu mechaniki

kwantowej.

Postulat V dotyczy sytuacji, w której funkcja φ opisująca stan układu
nie jest (ściślej: nie musi być) funkcją własną operatora obserwabli,
którą chcemy zmierzyć.
Postulat V stwierdza, że jeżeli układ opisywany jest funkcją φ, która
nie jest funkcją własną operatora , to pomiar zmiennej A może dać
(z określonym prawdopodobieństwem) jedną z wartości własnych
operatora

(np. a

1

, a

2

, a

3

, ...).



ˆ



ˆ







a



ˆ



ˆ



ˆ

Postulat V nazywany jest „postulatem o wartości średniej”, gdyż

precyzuje, iż średnia wartość zmiennej A w stanie opisywanym

funkcją φ wynosi:

Zakładamy, że funkcja jest unormowana, czyli, że: ∫φ*φ dτ = 1
Jeżeli funkcja φ nie jest unormowana, to wyrażenie na wartość
średnią ma postać:

Zauważmy, że jeżeli funkcja φ jest unormowana, oraz jeżeli jest to
funkcja własna operatora , to ponieważ ∫φ*φ dτ = 1 mamy:

















d

a

ˆ

*

























d

d

a

*

ˆ

*



ˆ

a

d

a

d

a

d

































*

*

ˆ

*

Zasada superpozycji stanów:



Zmiennej

dynamicznej

(wielkości

mierzalnej)

przyporządkowujemy operator



Każdy operator posiada pewien zbiór funkcji własnych.



Zbiór funkcji własnych może tworzyć układ zupełny
Układ zupełny funkcji – zbiór funkcji {ψ

i

}, za pomocą

których można przedstawić dowolną funkcję φ w postaci:

Jeżeli zbiór funkcji własnych operatora odpowiadającego
pewnej zmiennej dynamicznej tworzy układ zupełny, to
taką zmienną nazywamy obserwablą
W

mechanice

kwantowej

rozważamy

wyłącznie

obserwable.









1

i

i

i

c





Zasada superpozycji stanów głosi, że jeżeli zbiór {ψ

1

, ψ

2

,

ψ

3

, ...} wszystkich funkcji własnych pewnego operatora

kwantowo-mechanicznego jest zbiorem zupełnym, czyli, że
dowolny stan układu (funkcję φ) można przedstawić w postaci
superpozycji tych funkcji własnych:

to kwadrat modułu współczynnika rozwinięcia | c

i

|

2

jest udziałem

stanu ψ

i

w stanie φ.

Inaczej mówiąc, kwadrat modułu współczynnika rozwinięcia | c

i

|

2

jest prawdopodobieństwem, że jeśli układ jest w stanie φ , to
ma właściwości stanu ψ

i

.









1

i

i

i

c



