Chemia fizyczna w

układach biologicznych

2008

Chemia fizyczna zajmuje się fizycznymi podstawami procesów chemicznych
i usiłuje wyjaśnić strukturę materii i jej zmiany odwołując się do pojęć
podstawowych, takich jak atomy, elektrony, energia.

Najogólniejszy opis materii polega na wyróżnieniu trzech stanów
skupienia:
gazów, cieczy i ciał stałych.

Gaz stanowi stan płynny materii, wypełniającej całą dostępną objętość
zbiornika, w której została zamknięta.

Ciecz jest płynnym stanem materii charakteryzującym się dobrze
zdefiniowaną powierzchnią. W polu grawitacyjnym ciecz wypełnia dolną
część zbiornika, w którym została zamknięta.

Ciało stałe zachowuje kształt niezależny od kształtu zbiornika w
którym się znajduje

.

Znaczenie terminu stan:
a. stan skupienia (gazowy, ciekły, stały)
b. opis pewnej wybranej części materii określający pewne
charakteryzujące ją wartości
objętości, ciśnienia, temperatury i ilości substancji

.

Objętość próbki V jest miarą przestrzeni jaką próbka
zajmuje

.

Ciśnienie p przedstawia siłę działającą na jednostkową
powierzchnię: ciśnienie = siła/powierzchnia;
jednostka paskal [Pa] 1 Pa=1 N.m

-2

; 1 bar = 10

5

Pa

Temperatura jest wielkością, która określa kierunek przepływu
energii, gdy ciało znajduje się w kontakcie z innym: energia
(ciepło) przepływa od ciała o wyższej do ciała o niższej
temperaturze; jednostka T [K] = t [ºC]+273,15

Masa, m, ciała jest miarą ilości materii w tym ciele;

jednostka [kg]

Mol ,n, ilość substancji w próbce n = masa/(masa molowa) =

liczba cząsteczek/ (liczba cząsteczek w molu)= liczba

cząsteczek/ liczba Avogadro; N

A

=6.02214●10

23)

Równanie stanu przedstawia matematyczną zależność między
objętością, ciśnieniem, temperaturą. Te trzy zmienne intensywne
(wielkość ich zależy od ilości) nie są nawzajem niezależne.

/

m

m

pV

RT

V

V n

=

=

Dla gazu doskonałego

:

1

1

1

1

8.3145 [

] lub [

]

-

-

-

-

=

=

pV nRT

R

kPa l K mol

J K mol

gg

g

g

g

1

nRT

p

p

V

V

=

:

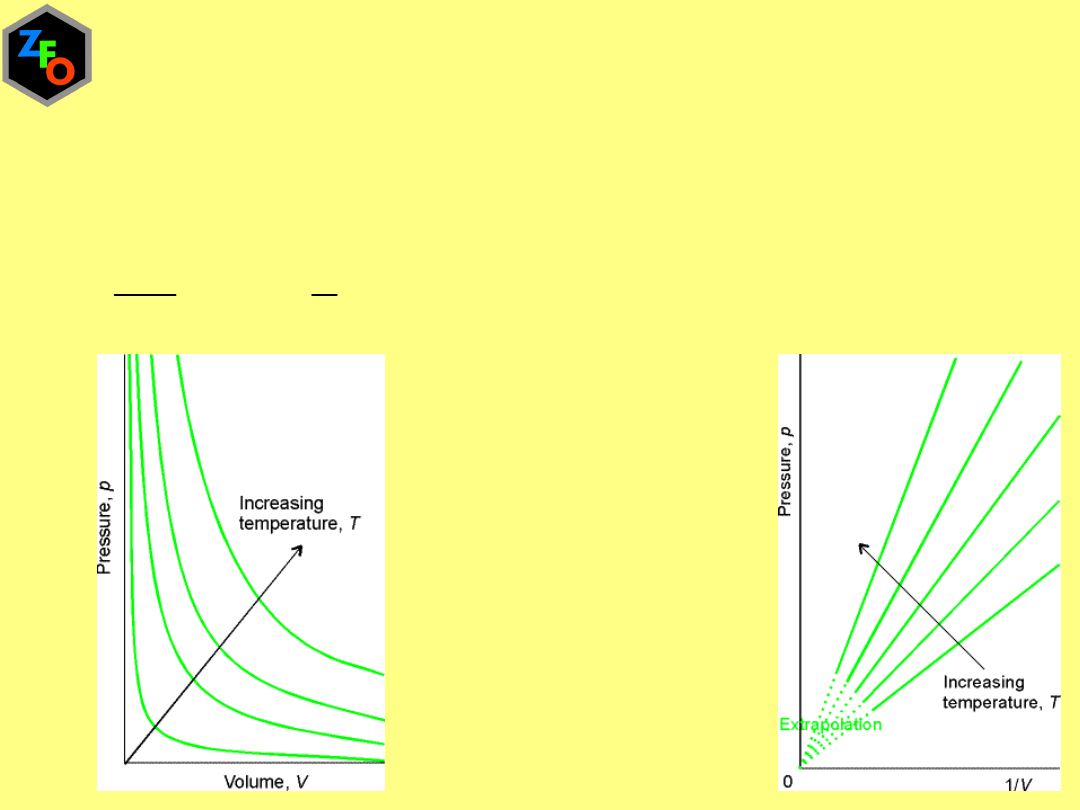
Prawo Boyle`a

Wykres zależności p=f(V)
dlaT=const
nosi nazwę

izotermy

Przemiana izotermiczna T=const

Równanie Clapeyrona

nRT

V

V T

p

=

:

Prawo Gay-Lussaca

Zasada Avogadro:
W danej temperaturze i pod danym ciśnieniem
równe objętości różnych gazów zawierają te same
ilości cząsteczek

V n

:

Przemiana izobaryczna p=const

Przemiana izochoryczna, V=const

Prawo
Charlesa

nRT

p

p T

V

=

:

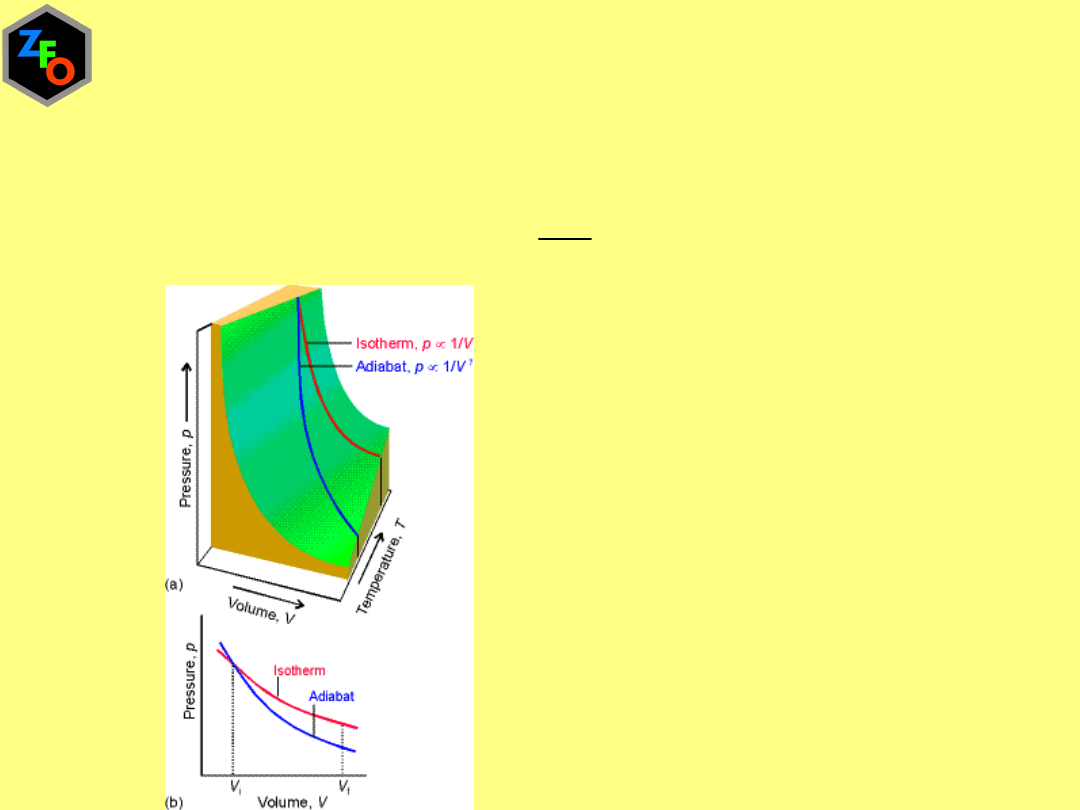
Przemiana adiabatyczna,
bez wymiany ciepła z otoczeniem

p

V

c

pV

const

c

k

k

=

=

Prawo Poissona

1 1

2 2

1 1

2 2

1

2

1

2

pV

pV

pV

pV

n

n

RT

RT

T

T

=

=

�

=

Zastosowania prawa gazu doskonałego

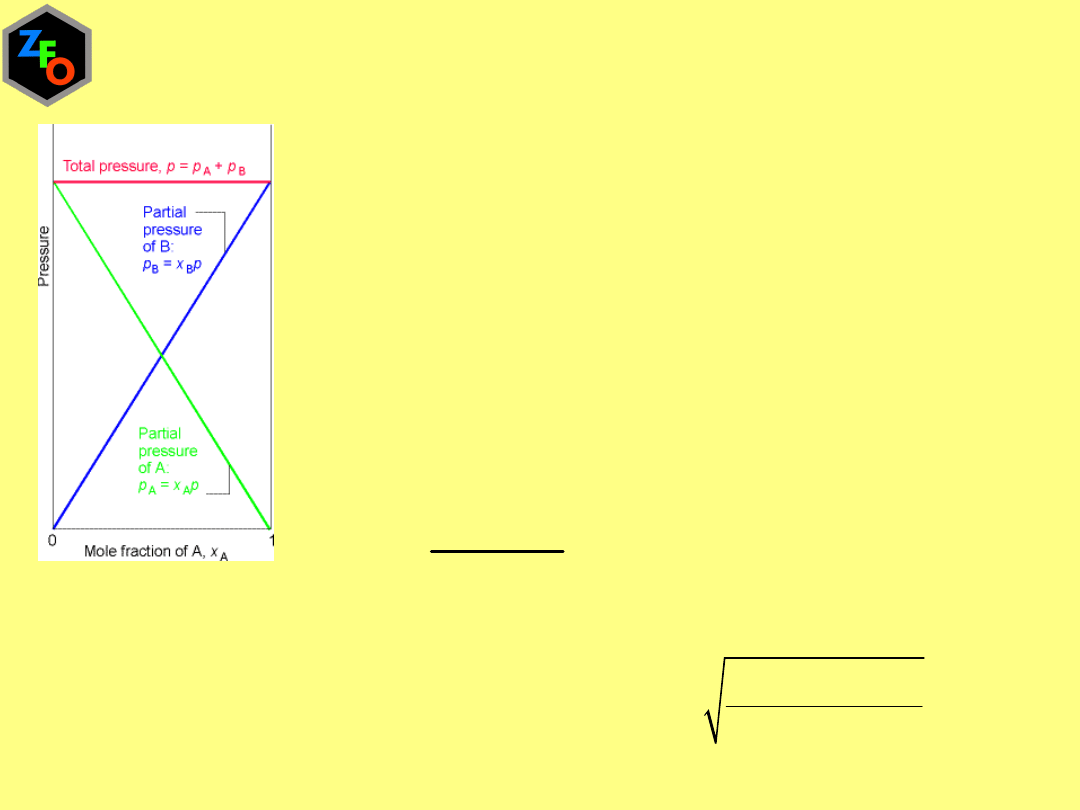
Mieszaniny gazów i ciśnienie cząstkowe

Prawo Daltona: ciśnienie wywierane przez mieszaninę gazów
doskonałych jest sumą ciśnień, jaki wywierałby każdy z gazów z
osobna, gdyby zajmował taką samą objętość jaką zajmuje
mieszanina.

Udział jaki wnosi dany gaz do ciśnienia całkowitego nosi nazwę
ciśnienia cząstkowego albo parcjalnego.

A

B

A

B

A

B

n RT

n RT

p

p

to

p p

p

V

V

=

=

=

+

Ułamek molowy, x

A

przedstawia ilość substancji chemicznej A

wyrażoną jako ułamek całkowitej ilości wszystkich cząsteczek
znajdujących się w próbce

.

1

..

A

A

i

i

A

B

i

n

x

n

n

n

n

=

=

+ + +

�

A

A

p

x p

=

Jest to ogólna definicja ciśnienia cząstkowego,
dla gazów doskonałych równoważna prawu Daltona

Uzasadnienie:

Z prawa Clapeyrona

RT

p

V

n

=

wstawiając do

:

=

=

A

A

A

A

n RT

n

p

otrzymamy

p

p

V

n

g

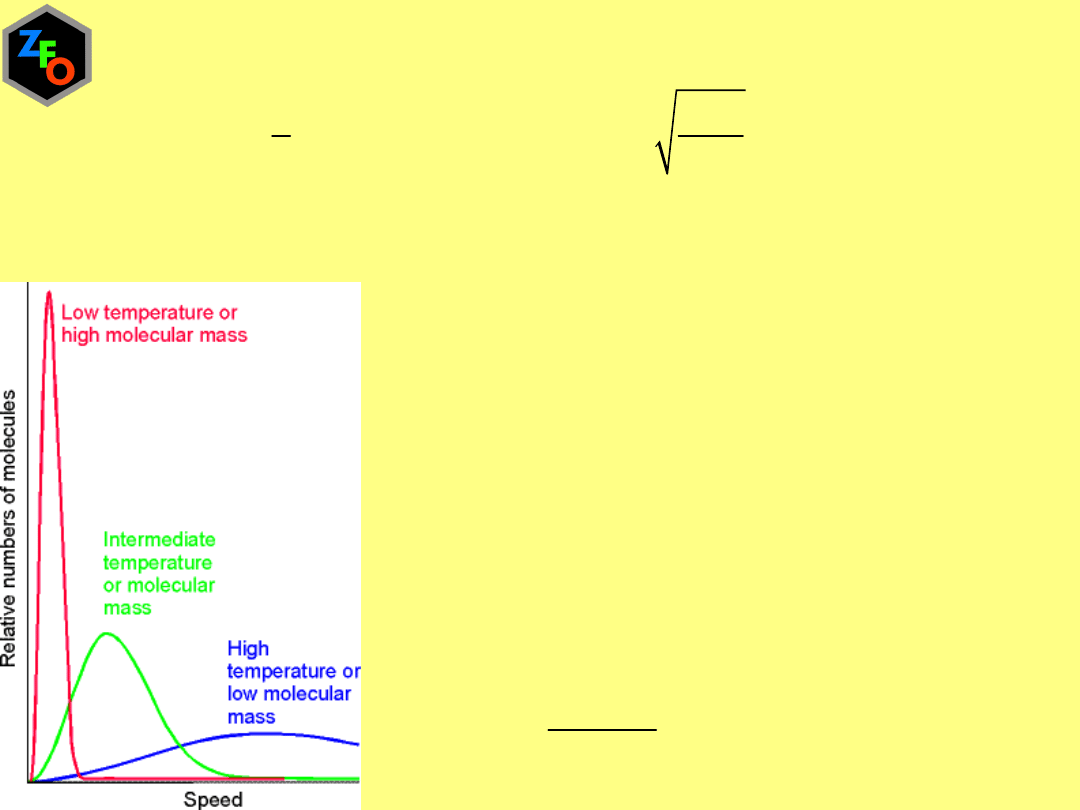
Teoria kinetyczna gazów

Założenia:
gaz składa się z cząstek znajdujących się w nieustannym
przypadkowym ruchu
wymiary cząsteczek są zaniedbywalnie małe,
mniejsze od drogi swobodnej
cząsteczki nie oddziaływują na siebie (poza zderzeniami

)

2

3

nMc

p

V

=

Gdzie c średnia szybkość kwadratowa

2

2

2

1

2

..

N

c

c

c

c

N

+ + +

=

2

1

3

3

RT

pV

nMc

nRT

c

M

=

=

�

=

2

3/2

2

/

4

2

Ms RT

M

f

s e

ds

RT

p

p

-

�

�

=

�

�

�

�

Rozkład szybkości Maxwella

Dyfuzja – proces samorzutnego mieszania się dwóch substancji

Eufuzja – wypływ gazu ze zbiornika
przez mały otwór w ścianie naczynia.

Prawo Grahama.
W danych warunkach ciśnienia i temperatury
szybkość eufuzji gazu jest odwrotnie proporcjonalna
do pierwiastka kwadratowego z jego masy molowej

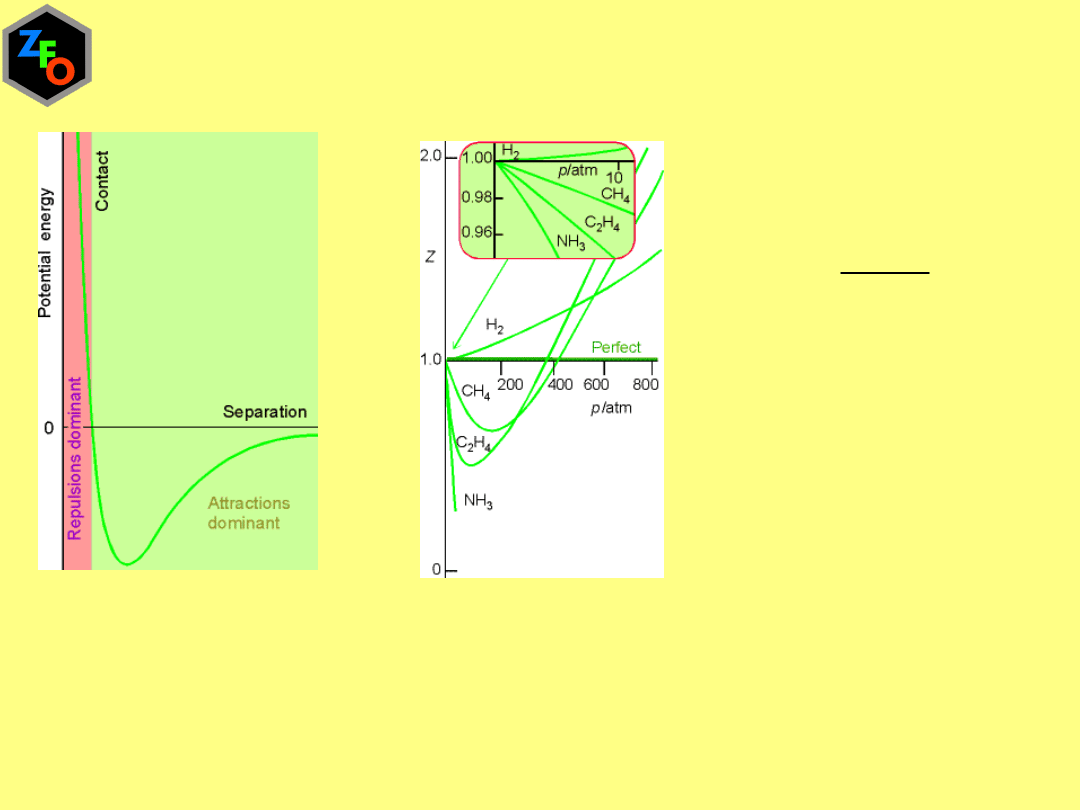
Gazy rzeczywiste

m

pV

Z

RT

=

Współczynnik ściśliwości Z

CO

2

2

1

....

m

m

m

B

C

pV

RT

V

V

�

�

=

+

+

+

�

�

�

�

Wirialne równanie stanu

1

, .

0

m

m

pV

Z

gdy V

tj gdy p

RT

=

�

� �

�

Równanie van der Waalsa

2

`

`

nRT

n

p

a

V nb

V

� �

=

-

� �

-

� �

2

m

m

RT

a

p

V

b V

=

-

-

Termodynamika

nauka o transformacjach energii

Układ jest interesującą nas częścią rzeczywistości, oddzielony od
otoczenia wyraźnymi granicami

Otoczenie jest miejscem, z którego dokonujemy obserwacji,
czyli wszystko to co nie należy do układu

Układ otwarty możliwy jest przepływ materii
i energii do otoczenia

Układ zamknięty możliwy jest przepływ
tylko energii do otoczenia

Układ izolowany albo zamknięty niemożliwy jest
przepływ materii ani energii do otoczenia

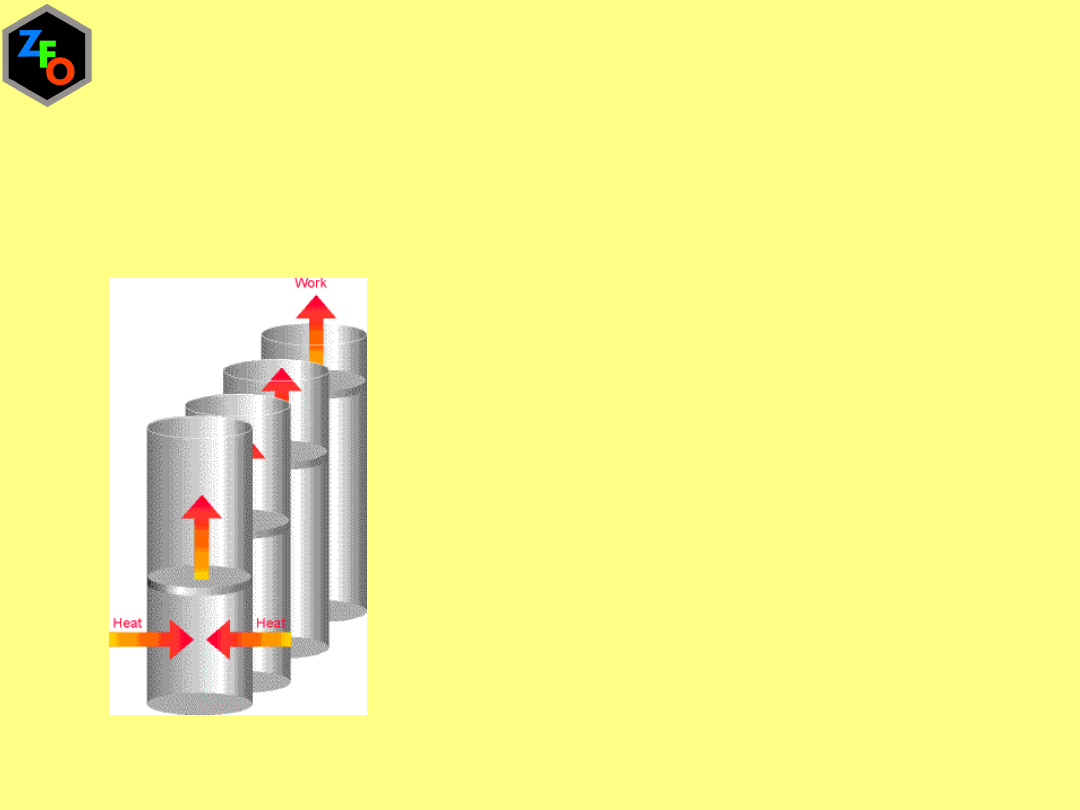
Praca, ciepło i energia

Energia – zdolność do wykonania pracy

Pracą nazywamy przeniesienie energii w taki sposób, że może ona być
użyta do podniesienia w otoczeniu ciężaru na pewną wysokość

Ciepłem nazywamy przeniesienia energii następujące w wyniku różnicy
temperatur pomiędzy układem i otoczeniem.

W ujęciu molekularnym ciepło jest formą przekazywania energii,
które polega na chaotycznym ruch cząsteczek.

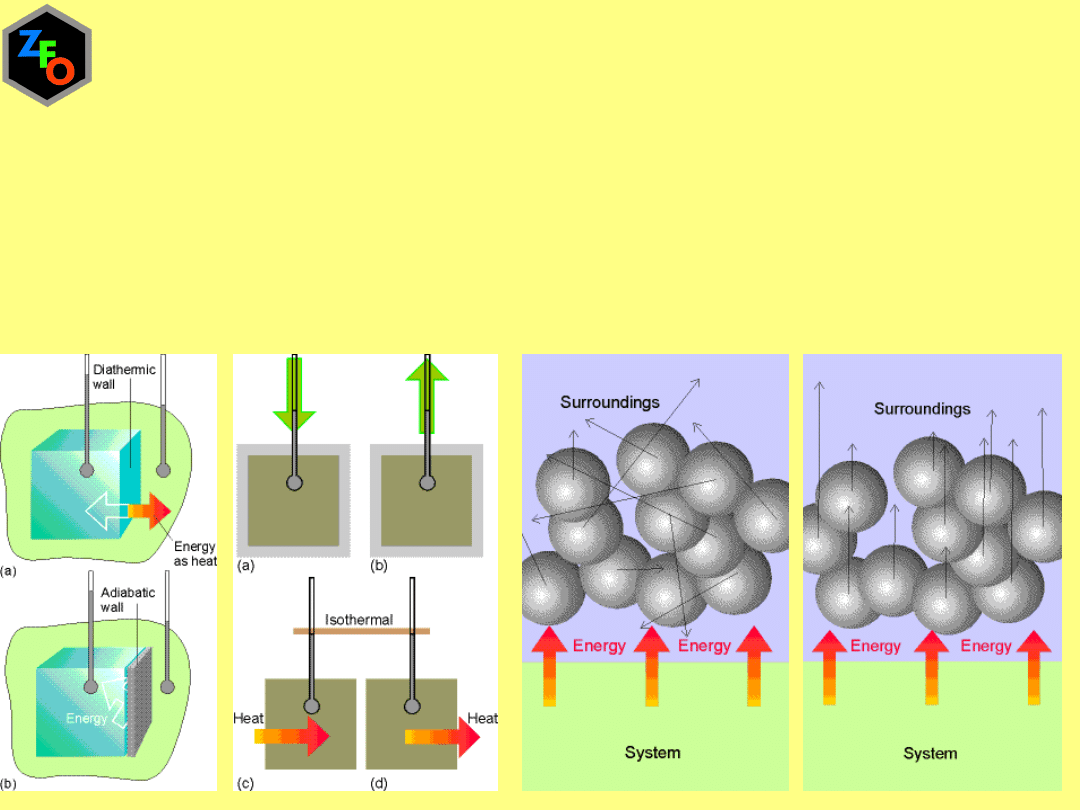
Procesy, które pochłaniają energię jako ciepło nazywamy endotermicznymi

Procesy uwalniające energię jako ciepło nazywamy egzotermicznymi

W termodynamice całkowitą energię układu nazywamy jego
energią wewnętrzną i oznaczamy jako U

k

p

U U U

D =

-

Energia wewnętrzna jest funkcją
stanu

Funkcją stanu nazywamy wielkość fizyczną,
której wartość zależy wyłącznie od stanu,
w jakim układ się znajduje, nie zaś od drogi,
po której do tego stanu doszedł

Parametry stanu układu to wielkości fizyczne
jednoznacznie określające stan układu, np.
ciśnienie (p), temperatura (T), objętość (V),
liczba moli (n

)

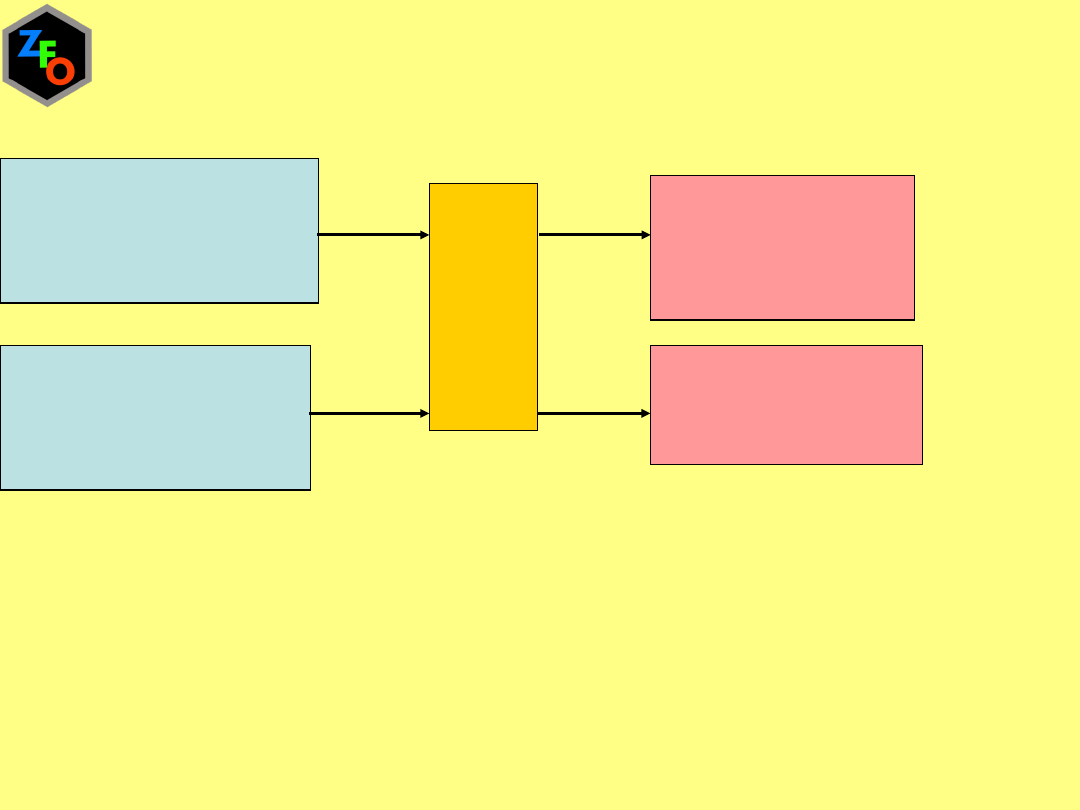
Energia dostarczona

na sposób pracy z

otoczenia

do układu

Energia dostarczona

na sposób ciepła z

Otoczenia do układu

UKŁAD

Energia oddana

na sposób pracy z

układu do otoczenia

Energia oddana

na sposób ciepła z

układu do otoczenia

+w

-w

-q

+q

w – wymiana energii na sposób pracy
q – wymiana energii na sposób ciepła

OTOCZENIE

Zmiana energii wewnętrznej układu otwartego (ΔU)

może nastąpić na sposób ciepła (q) lub na sposób pracy (w)

ΔU = q + w

równanie

Helmholtza

Jest to matematyczna postać pierwszej zasady

termodynamiki

Inna jej postać mówi, że

energia wewnętrzna układu izolowanego jest stała
ΔU = const (q = 0, w = 0)

lub

praca potrzebna do przejścia układu adiabatycznego z
jednego wyróżnionego stanu w drugi jest, bez
względu na jej rodzaj zawsze taka sama

Ogólne wyrażenie na pracę

dw

Fdz

=-

gdzie F – siła, dz - -przesunięcie

Rodzaj pracy

dw

uwagi

jednostk
i

objętościowa

-p

zew

dV -p

zew

ciśnienie zewnętrzne

dV zmiana objętości

Pa
m

3

powierzchnio
wa

γdσ

γ napięcie
powierzchniowe
dσ zmiana pola
powierzchni

N*m

-1

m

2

rozciągania

fdl

f naprężenie
dl zmiana długości

N
m

elektryczna

φdq

φ potencjał elektryczny
dq zmiana ładunku

V
C

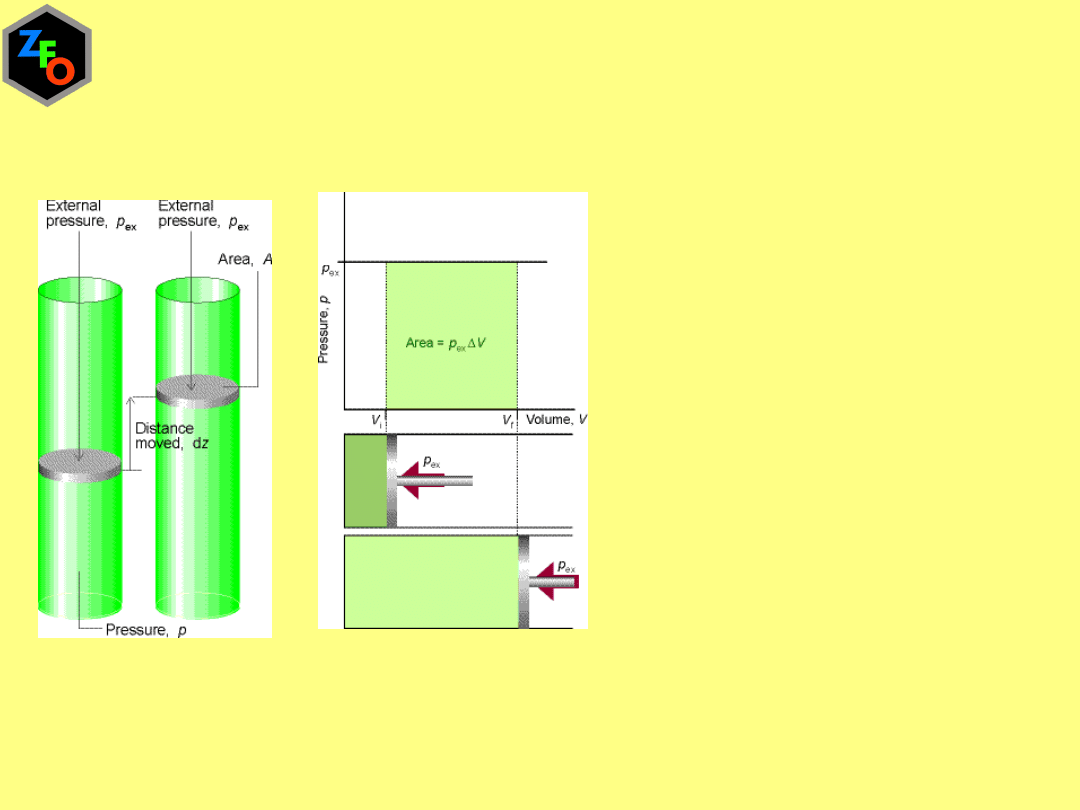
Praca objętościowa

(

)

k

p

zew

V

zew

zew

k

p

V

zew

dw

p dV

w

p

dV

p V V

w

p V

=-

=-

=-

-

=-

D

�

Rozprężanie odwracalne, równowagowe, p

zew

= p

k

p

zew

V

V

dw

p dV

pdV

w

pdV

=-

=-

=-

�

Odwracalne rozprężanie

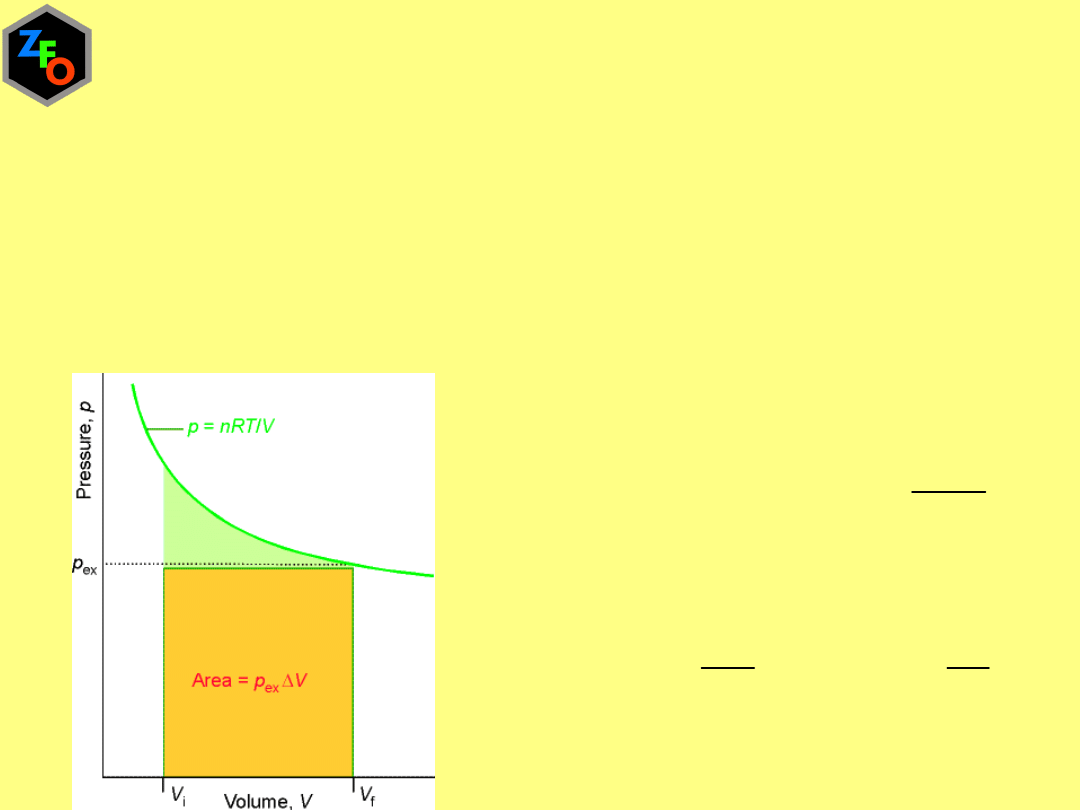
izotermiczne

ln

k

p

V

k

V

p

nRT

pV nRT

p

V

V

dV

w

nRT

nRT

V

V

=

�

=

� �

=-

=-

� �

� �

� �

�

obj

z

dU dq dw

dw

= +

+

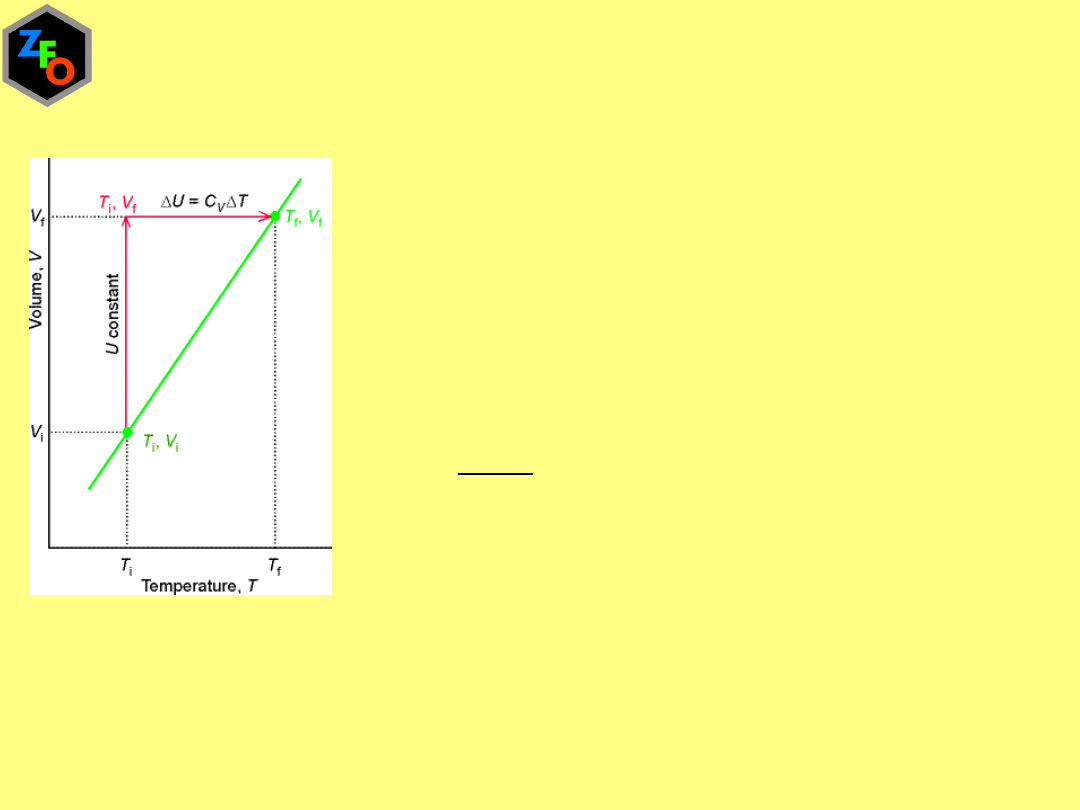
gdy V=const

V

dU dq

=

q C T

= D

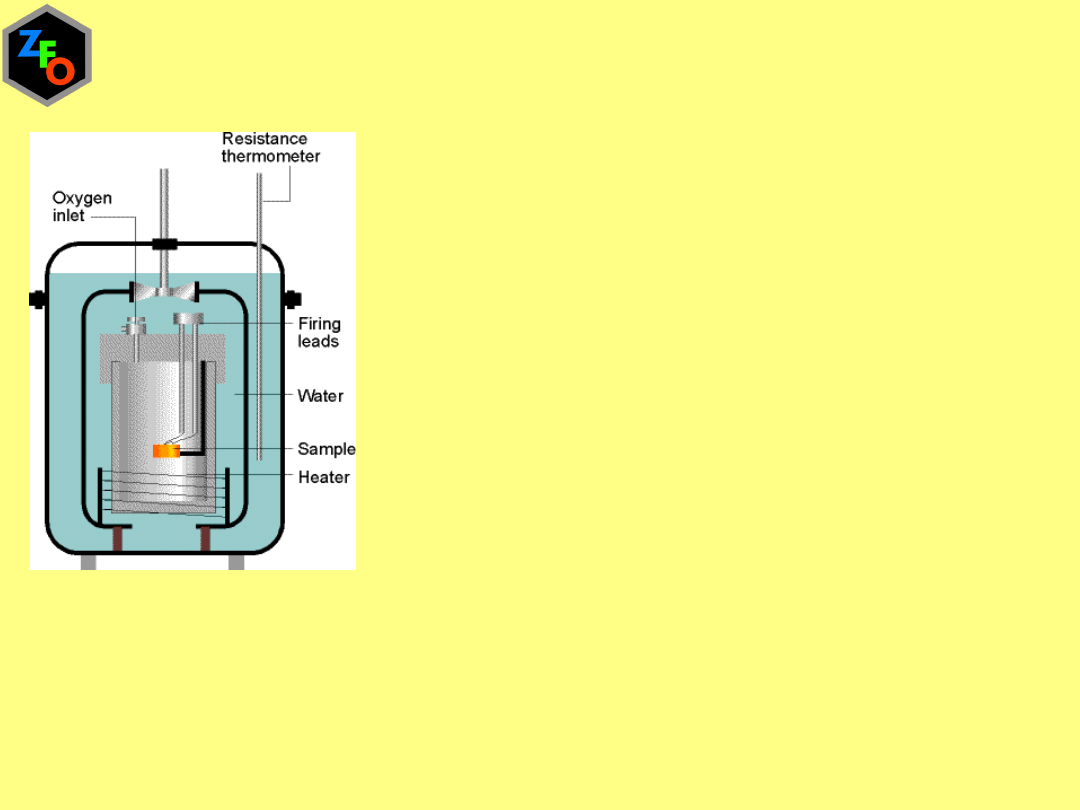
Ciepło wydzielane podczas spalania substancji

w bombie kalorymetrycznej

Wyznaczanie energii wewnętrznej

Pojemność cieplna

1

( , )

0

[

]

-

=

�

�

� �

� �

=

+

� �

� �

�

�

� �

� �

=

=

�

� �

=

=� �

�

� �

�

� �=

� �

�

� �

T

V

V

V

V

U U T V

U

U

dU

dV

dT

V

T

dla

V const

dV

U

dU dQ

dT

T

U

c

J K

T

g

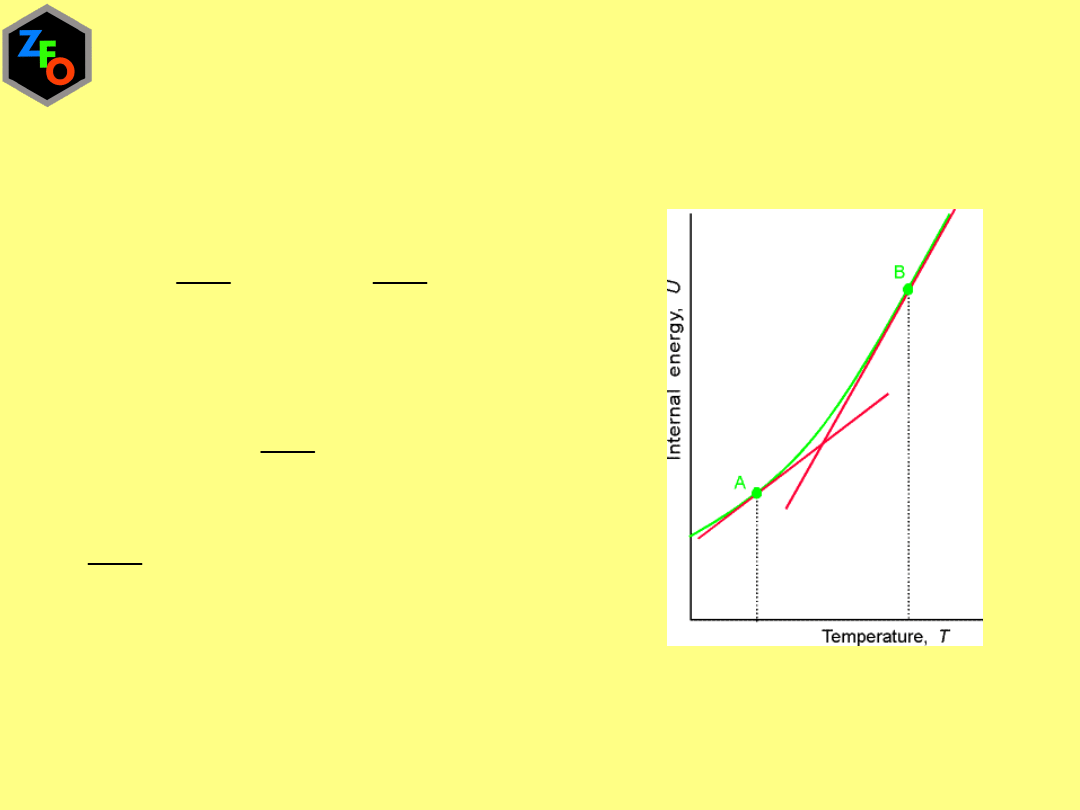
Pojemność cieplna w stałej objętości

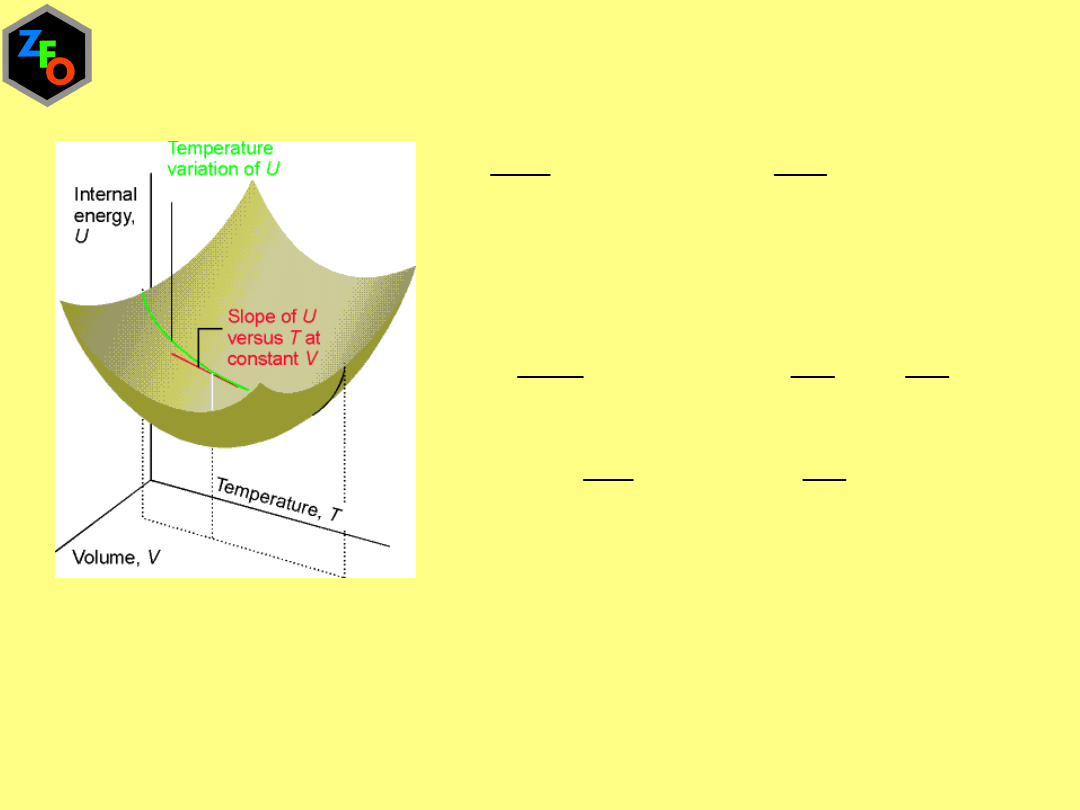
T

V

U

p

p T

V

T

�

�

� �

� �

=- +

� �

� �

�

�

� �

� �

dla gazu

doskonałego

0

V

T

nRT

p

nR

p

i

V

T

V

U

nR

stąd

p T

p p

V

V

�

� �

=

=

� �

�

� �

�

� �=- +

=- + =

� �

�

� �

W stałej temperaturze energia wewnętrzna układu

utworzonego z gazu doskonałego nie zależy od objętości

Dla warunków adiabatycznych q=0

V

ad

dU c dT w

=

=

v

c dT

pdV

=-

Dla gazu doskonałego

nRT

p

V

=

ln

ln

k

k

p

p

v

v

v

T

V

V T

V

k

k

V

p

p

c

c

nR

nR

k k

p p

dT

dV

c

nR

T

V

dT

dV

c

nR

T

V

T

V

c

nR

T

V

V T

V T

=-

=-

� �

� �

=-

� �

� �

� �

� �

� �

� �

=

�

�

inna postać adiabaty

p

V

c
c

pV

const

=

Podczas oddychania wydychamy około V=0,5 litra (5*10

-4

m

3

) powietrza

Przeciwko stałemu ciśnieniu p=1 at (101 kPa)

w=-pΔV=-(.01810

5

Pa)*(0.5*10

-4

m

3)

=-51 Pa*m

3

=-

51

J

w=-m*g*h=(7.0 kg)*(9.81 m*s

-2

)*(0.75 m)=-

52

J

CaCO

3

→CaO+CO

2

Tylko część dostarczonego ciepła
zwiększa energię wewnętrzną a część zostaje
oddana otoczeniu w postaci pracy

2 C

57

H

110

O

6

(s)+163 O

2

→114 CO

2

(g)+110 H

2

O(c)

163-114=49 moli, objętość maleje
i otoczenie wykonuje pracę na układzie,
Jaka jest zmiana energii wewnętrznej?

Entalpia

H U pV

= +

Ponieważ U, p oraz V zależą jedynie od

aktualnego stanu entalpia jest funkcją stanu

dla p=const

(

)

H

U

pV

U p V

D =D +D

=D + D

m

m

m

m

m

H

U

pV

H

U

RT

=

+

=

+

dla gazu doskonałego

H U pV

= +

Ponieważ U, p oraz V zależą jedynie od

aktualnego stanu entalpia jest funkcją stanu

dla p=const

dH dq

dla p const

=

=

Zmiana entalpii jest równa ciepłu
dostarczonemu do układu pod stałym
ciśnieniem

(dopóki

układ

nie

wykonuje

dodatkowej

pracy

objętościowej)

;

zew

zew

zew

zew

zew

H

U p V

U p

V

U q w q p

V w

p

V

H q p

V p

V q

D =D + D =D +

D

D = + = -

D

=-

D

D = -

D +

D =

Układ wykonuje pracę objętościową przeciwko ciśnieniu zewnętrznemu

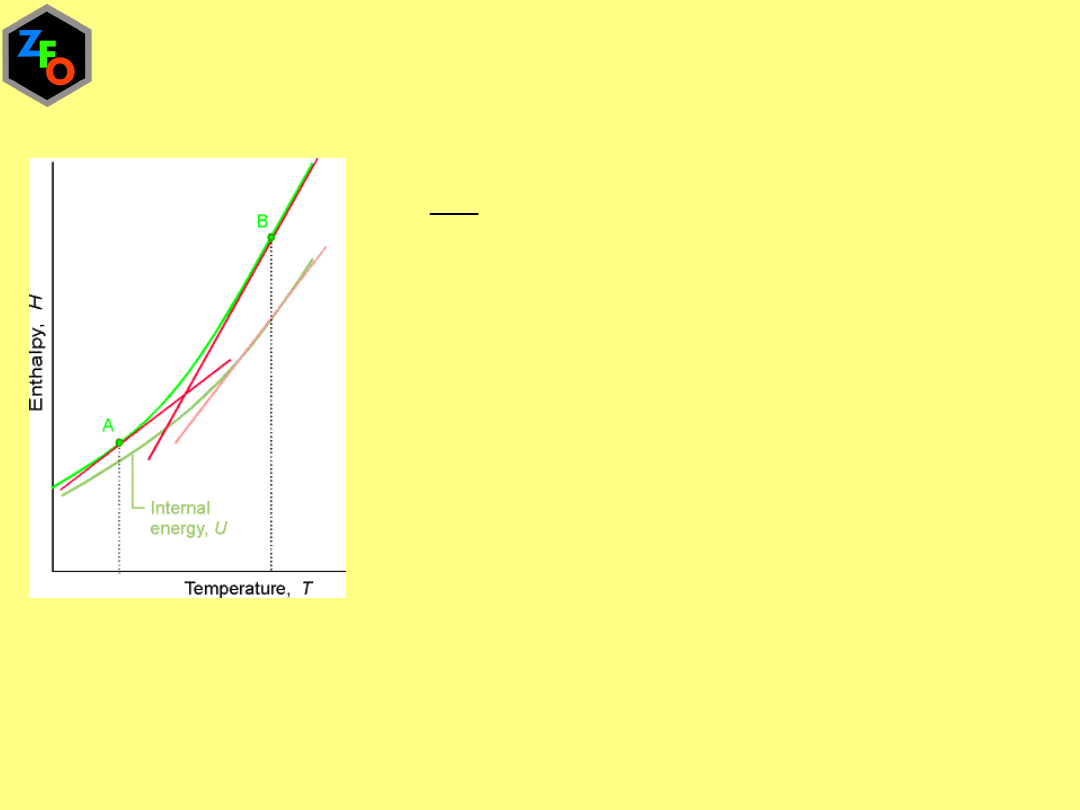
Pojemność cieplna pod stałym ciśnieniem (c

p

)

p

p

H

c

T

�

� �

=� �

�

� �

p

H c T

D = D

p

dH c dT

=

gdy c

p

nie zależy od

temperatury

dla p=const

dla gazy doskonałego c

p,m

=c

v.m

+R

Podsumowanie przemian gazu doskonałego

W przypadku każdej przemiany odwracalnej czy też nieodwracalnej

;

;

v

p

dU c dT dH c dT dU dH RdT

=

=

=

-

Dla przemian odwracalnych gazów doskonałych słuszne są zależności

:

Przemiana izotermiczna

:

2

1

1

2

ln

ln

=

=

=D -

V

p

w RT

RT

V

p

q

U w

0

dU dH

=

=

Przemiana izobaryczna:

=

=D =

= D = D

�

p

p

dH c dT

q

H

c dT

w p V R T

Podsumowanie przemian gazu doskonałego

Przemiana izochoryczna

:

0

=

=D =

=

�

v

V

dU c dT

q

U

c dT

w

Przemiana adiabatyczna

:

2

2

1

1

2

2

1

1

0;

ln

ln

ln

ln

V

V

p

q

dU

dw

c dT

pdV

T

V

c

R

T

V

T

p

c

R

T

p

=

=-

=-

=-

=

Termochemia

zajmuje się analizą wydzielonego i pochłoniętego

ciepła w reakcjach chemicznych

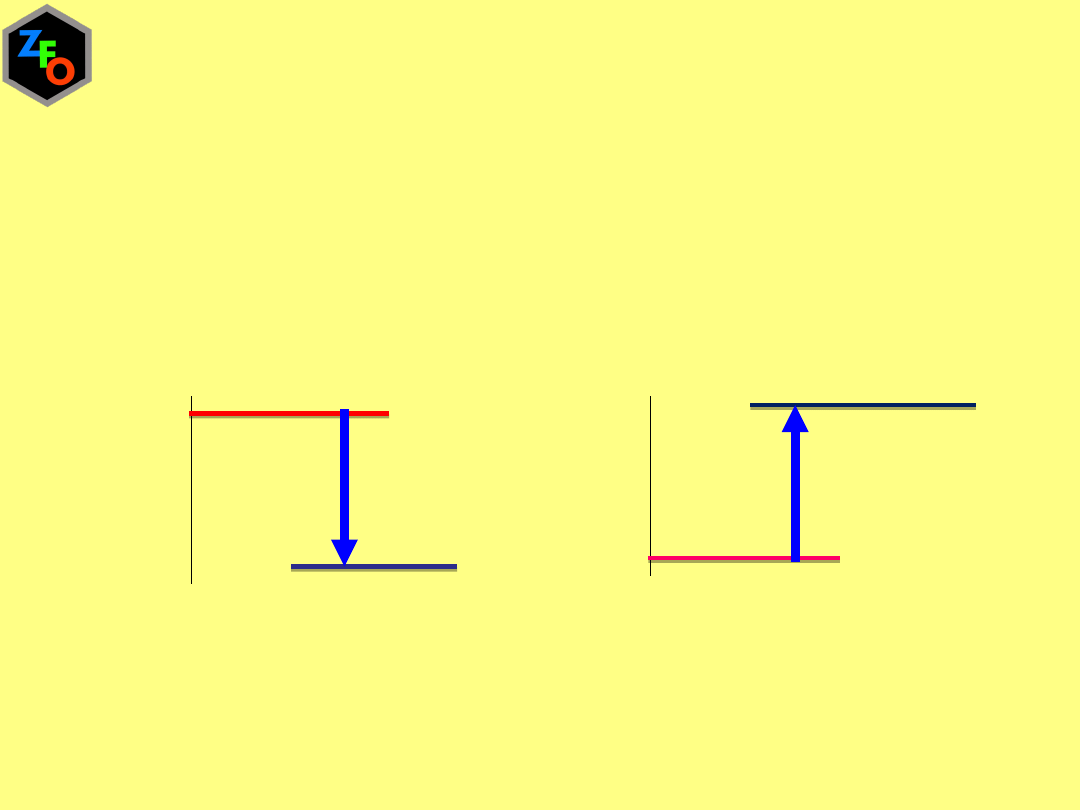
Zmiany entalpii a efekt energetyczny reakcji

substra

ty

produkty

substra

ty

produkty

-ΔH

+ΔH

ΔH

2

ΔH

1

ΔH

1

ΔH

2

r. egzoenergetyczna

r. endoenergetyczna

ΔH

2

-

ΔH

1

<0

ΔH<

0

ΔH

2

- ΔH

1

>0

ΔH>0

ΔH= ΔH(produktów)- ΔH(substratów)

ΔH

0

zmiana

entalpii

standardowej

czyli zmiana entalpii procesu, gdy wszystkie

substraty i produkty są w swoich stanach

standardowych w temperaturze przemiany

Stan standardowy substancji w danej temperaturze

odpowiada

jej czystej postaci pod ciśnieniem 1 bar

Stan standardowy pierwiastka w danej temperaturze i pod

ciśnieniem 1 bar jest stan odpowiadający jego najbardziej

stabilnej postaci w danej temperaturze

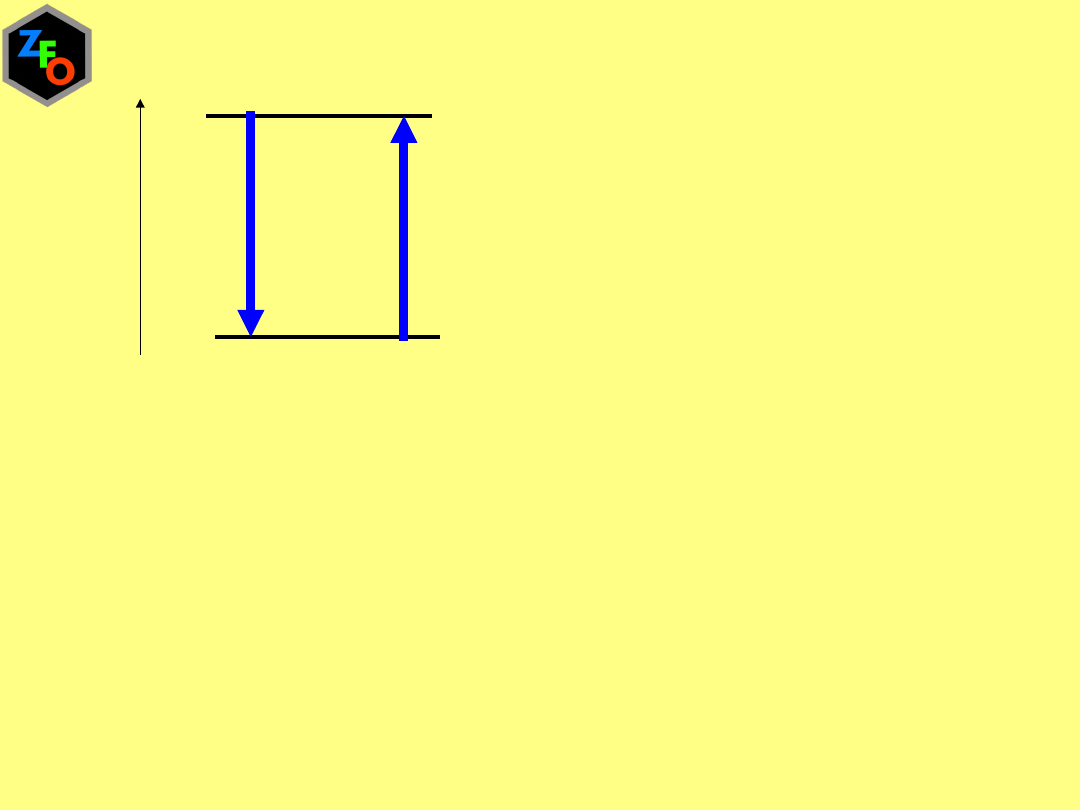
B

A

E

n

ta

lp

ia

,

H

Δ

H

0

(A

→

B

)

-Δ

H

0

(

B

→

A

)

Prawo Lavoisiera-Laplace`a

Efekt cieplny reakcji przebiegającej w danym kierunku jest równy

efektowi cieplnemu reakcji przebiegającej w kierunku odwrotnym

ze znakiem przeciwnym

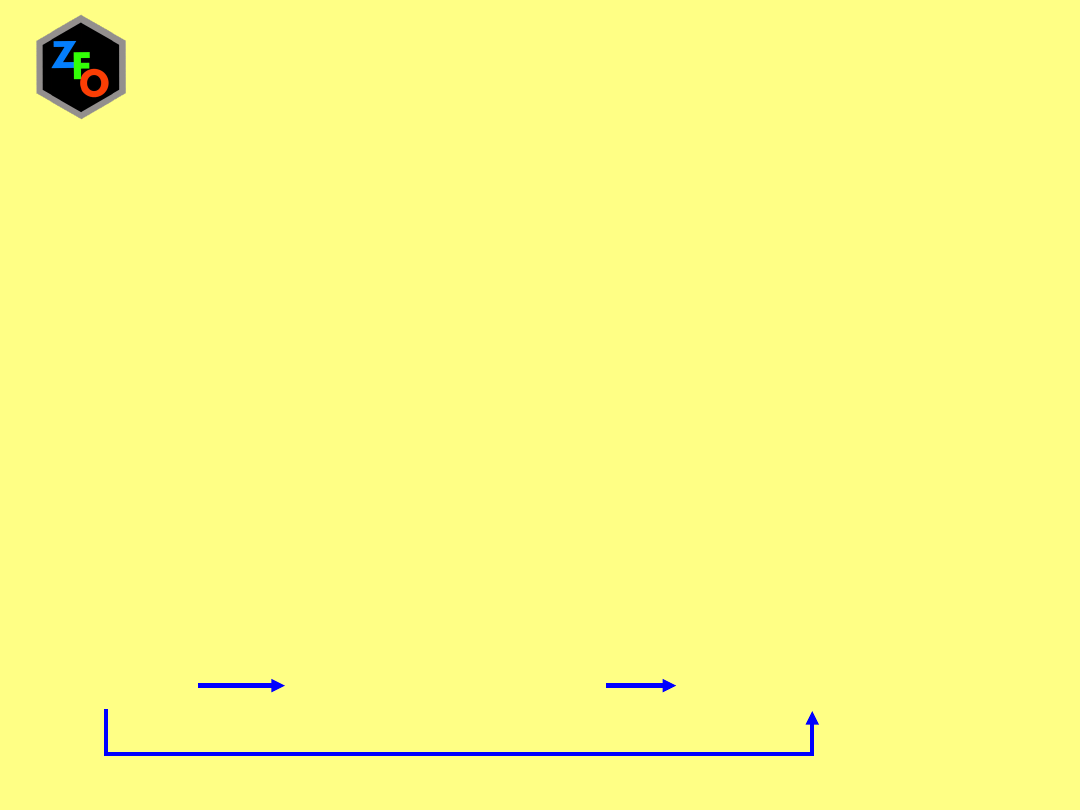
Prawo Hessa

Efekt cieplny reakcji nie zależy od drogi przemiany pod warunkiem,

że wszystkie procesy są izobaryczne lub izochoryczne

lub

standardowa entalpia reakcji całkowitej jest sumą standardowych entalpii

poszczególnych reakcji składowych, na które można daną reakcję rozłożyć

Standardowa entalpia reakcji jest Δ

r

H jest zmianą entalpii reakcji, w której

substraty w swoich stanach standardowych ulegają przemianie w produkty

znajdujące się w stanach standardowych

0

0

0

r

m

m

produkty

substraty

H

H

H

n

n

D

=

-

�

�

ν –współczynniki stechiometryczne w równaniu chemicznym

substraty

produkty pośrednie

produkty

końcowe

ΔH

1

ΔH

2

ΔH

3

przemiana

proces

oznaczeni

e

Przejście fazowe

faza α→faza β

ΔH

pf

Topnienie

s → c

ΔH

top

Parowanie

c → g

ΔH

par

Sublimacja

s → g

ΔH

sub

Mieszanie

sub. pojedyncze →
mieszanina

ΔH

miesz

Rozpuszczanie

sub. rozpuszczana →roztwór

ΔH

roz

Hydratacja

X

±

(g) → X

±

(aq)

ΔH

hyd

Atomizacja

cząsteczka (s,c,g) →atomy(g) ΔH

at

Jonizacja

X(g) → X

+

(g) +e

-

(g)

ΔH

jon

Przyłączanie
elektronu

X(g) +e

-

(g)→ X

-

(g)

ΔH

p.e.

Reakcja

substraty → produkty

ΔH

r

Spalanie

substancja (s,c,g) +O

2

→

CO

2

(g), H

2

O (g,c)

ΔH

s

Tworzenie

pierwiastki → związek
chemiczny

ΔH

tw

Aktywacja

substraty → kompleks

aktywny

ΔH

#

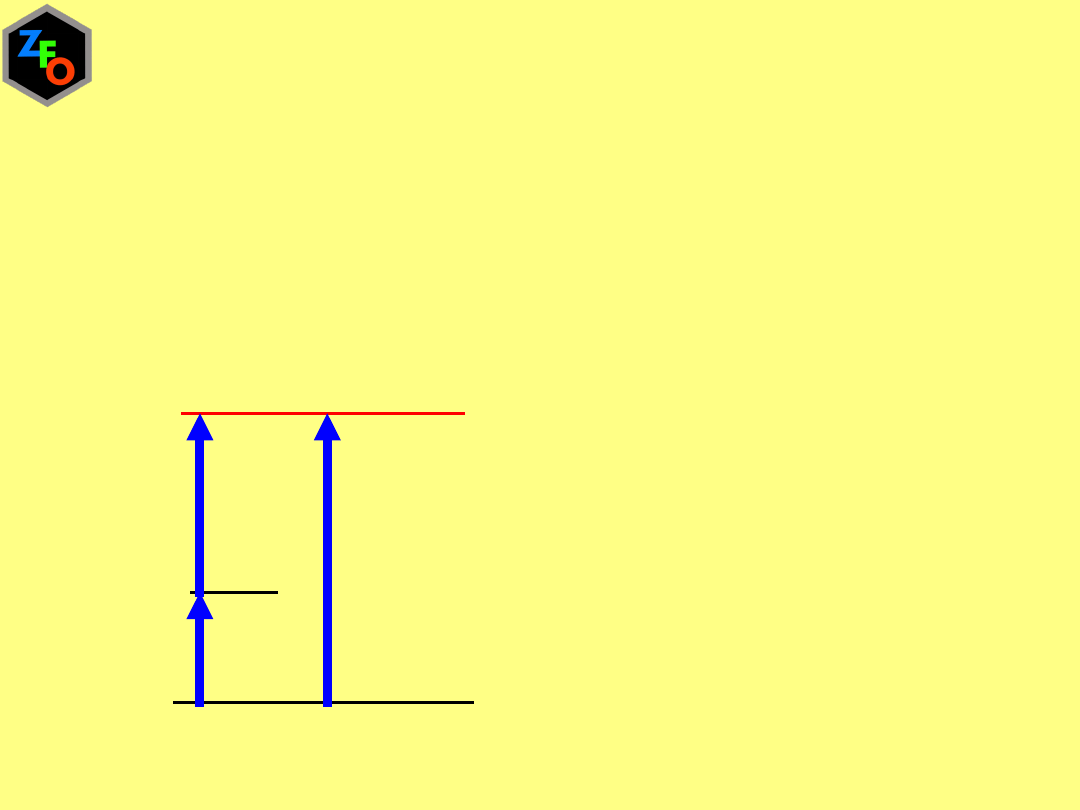
Standardowa entalpia przemiany fazowej ΔH

p.f

przedstawia

entalpię przemiany gdy obie fazy są w stanach standardowych,

tj. jako czyste substancje pod ciśnieniem 1 bara

Gdy przemiana jest złożona to standardowa entalpia przemiany jest

sumą standardowych entalpii procesów na które można rozłożyć

daną przemianę

ΔH

top

ΔH

par

ΔH

sub

ΔH

sub

= ΔH

top

+ ΔH

par

Standardowa entalpia tworzenia substancji przedstawia standardową

entalpię reakcji, w której 1 mol danej substancji tworzy się

z pierwiastków w ich stanach podstawowych

Stan podstawowy pierwiastka – najtrwalsza jego odmianaw

panujących warunkach

H

2

(g) + ½ O

2

(g)

H

2

O (c) ΔH

tw

= -286 kJ

Standardowa entalpia reakcji chemicznej jest równa sumie

standardowych

entalpii tworzenia produktów i substratów, w której każdy wyraz jest

pomnożony przez współczynnik stechiometryczny odpowiedniego

reagenta (dodatni dla produktu, a ujemny dla substratu.

pierwiastki

substraty

produk

ty

ΣΔH

0

tw,sub

ΣΔH

0

tw,prod

ΔH

0

r

0

0

0

.

.

r

tw prod

twsub

H

H

H

u

u

D

=

D

-

D

�

�

2 HN

3

(c) + 2NO(g)→ H

2

O

2

(c) +4N

2

(g)

ΔH

0

r

=ΔH

0

tw

(H

2

O,c) +4 ΔH

0

tw

N

2

(g) – {2 ΔH

0

tw

(NH

3

,c) +2 ΔH

0

tw

(NO,g)}

Standardowe ciepło spalania związku ΔH

0

sp

rozumiemy ciepło

spalania

1 mola cząsteczek tego związku w tlenie , pod ciśnieniem 1 bara,

przy czym powstają CO

2

, H

2

O (ciekła), SO

2

,N

2

0

0

0

,

,

D

=

D

-

D

�

�

r

sp subst

sp prod

H

H

H

u

u

( )

4

2

2

4

2

2

2

2

2

2

2

2

4

2

2

2

2

2

2

2

2

0

0

0

0

1

2

3

4

0

3

2

(4)

2

2 0

(2)

1

(3)

2

1

(4)

2

1* (2) 1* (3) 3* (4)

1

3

2

3

2

3

2

2

3

równanie

CH

H

CO

H

możnaotrzymać przezdodanierównań

CH

O

CO

H

CO

O

CO

H

O

H O

CH

O

CO

O

H

O

CO

H O CO

H O

H

H

H

H

+

=

+

-

+

=

+

+

=

+

=

-

-

+

-

-

-

-

=

+

-

-

D

=D

- D

- D

,

,

r

sp subst

sp prod

H

H

H

u

u

D

=

D

-

D

�

�

można to otrzymać z równania ogólnego

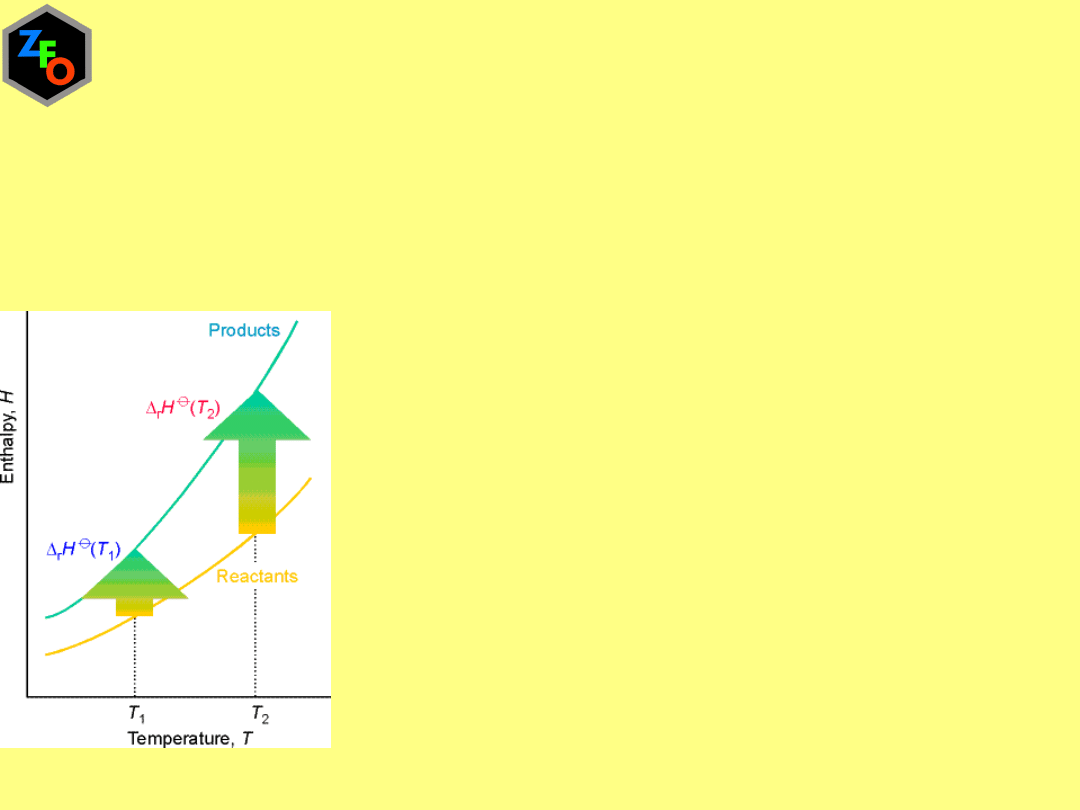
Zależność entalpii od

temperatury

prawo Kirchhoffa

2

1

2

1

,

,

( )

( )

T

r

r

i p prod

i p sub

i

i

T

H T

H T

c

c

dT

u

u

�

�

D

=D

+

-

�

�

�

�

�

�

�

`

1

2

`

2

1

,

,

. .,

,

,

( )

( )

T

r

r

i p prod

i p sub

i

i

T

T

k

p f k

i p prod

i p sub

i

i

T

H T

H T

c

c

dT

H

c

c

dT

u

u

u

u

u

�

�

D

=D

+

-

�

�

�

�

�

�

+ D

+

-

�

�

�

�

�

�

�

�

�

�

często c

p,i

przedstawia się za pomocą szeregu

potęgowego

2

2

,

p i

i

i

i

i

c

a bT cT

dT

-

= +

+

+