CHEMIA KWANTOWA

Zakład Chemii

Kwantowej

Piotr Skurski
(wykład) pok. 302

Iwona Anusiewicz
(ćwiczenia audytoryjne) pok. 325

www.chem.univ.gda.pl/zchk

Chemia teoretyczna –

dział chemii

wyodrębniony ze względu na metodykę
badań.

Działy chemii teoretycznej:

•

termodynamika (badania makroskopowych
właściwości substancji)

•

mechanika i termodynamika statystyczna
(badania wielkich zbiorów cząsteczek poprzez
zastosowanie praw mechaniki klasycznej)

•

chemia kwantowa (badania budowy cząsteczek,
oddziaływań oraz reakcji chemicznych
metodami mechaniki kwantowej).

Zakres wykładu kursowego:

•

Fizyczne podstawy mechaniki kwantowej.

–

dualistyczny charakter promieniowania i materii

–

model atomu według Bohra

–

zasada nieokreśloności Heisenberga

•

Postulaty mechaniki kwantowej.

–

opis stanu układu kwantowomechanicznego

–

równanie ruchu w mechanice kwantowej

–

teoria pomiaru

•

Proste zastosowania mechaniki kwantowej.

–

cząstka swobodna

–

cząstka w pudle (studni) potencjału

–

efekt tunelowy

–

kwantowy oscylator harmoniczny i rotator sztywny

–

atom wodoru

•

Przybliżone metody chemii kwantowej.

–

rachunek zaburzeń (metody perturbacyjne)

–

metody wariacyjne

•

Symetria funkcji falowych. Teoria spinu.

•

Przybliżenie jednoelektronowe.

•

Konfiguracje elektronowe atomów. Termy.

•

Metoda pola samouzgodnionego (SCF).

•

Korelacja elektronów.

–

metoda mieszania (oddziaływania) konfiguracji (CI)

–

wielokonfiguracyjne metody SCF (MCSCF, CASSCF)

–

rachunek zaburzeń Møllera-Plesseta (MP) wyższych rzędów

–

metoda sprzężonych klasterów (coupled-cluster, CC)

Podstawowe narzędzia chemii kwantowej
metoda orbitali molekularnych (MO)
metoda wiązań walencyjnych (VB)
Cząsteczki wieloatomowe
efekt Jahna-Tellera pierwszego i drugiego rzędu
hybrydyzacja orbitali atomowych
Cząsteczki π-elektronowe
Współczesne zastosowania chemii kwantowej.

Podręczniki:
W. Kołos „Chemia kwantowa”
A. Gołębiewski „Elementy mechaniki i chemii kwantowej”

Fizyczne podstawy mechaniki

kwantowej:

I.

Dualistyczny charakter promieniowania

Początek XX wieku:

–

hipoteza Plancka (1900 r.) dotycząca aktu emisji (lub absorpcji)
promieniowania: emisja promieniowania nie zachodzi w sposób
ciągły, ale określonymi porcjami, o energii proporcjonalnej do
częstości: E = h·
(gdzie h jest stałą Plancka, 6.626×10

–34

J·s)

promieniowanie ciała doskonale czarnego = promieniowanie cieplne

(termiczne),

promieniowanie termiczne ciał: „świetlne” (dla dużych T) i podczerwone (dla
małych T); promieniowanie termiczne ciał umożliwia równoważenie temperatury
(wymiana z otoczeniem).

Hipoteza
Plancka

Max Planck
1858-1947

prawo Rayleigha-Jeansa (wyprowadzone z elektrodynamiki klasycznej)
bardzo dobrze opisuje gęstość strumienia promieniowania jedynie dla

niskich

częstości

2

2

P

kT

c

n

=

poprawne tylko

dla

niewielkich

wartości ν

Prawo R-J nie może być prawdziwe dla wysokich częstości

(scałkowanie

wzoru R-J po wszystkich częstościach prowadzi do

nieskończenie dużej

wartości gęstości energii P (tzw. katastrofa w nadfiolecie)

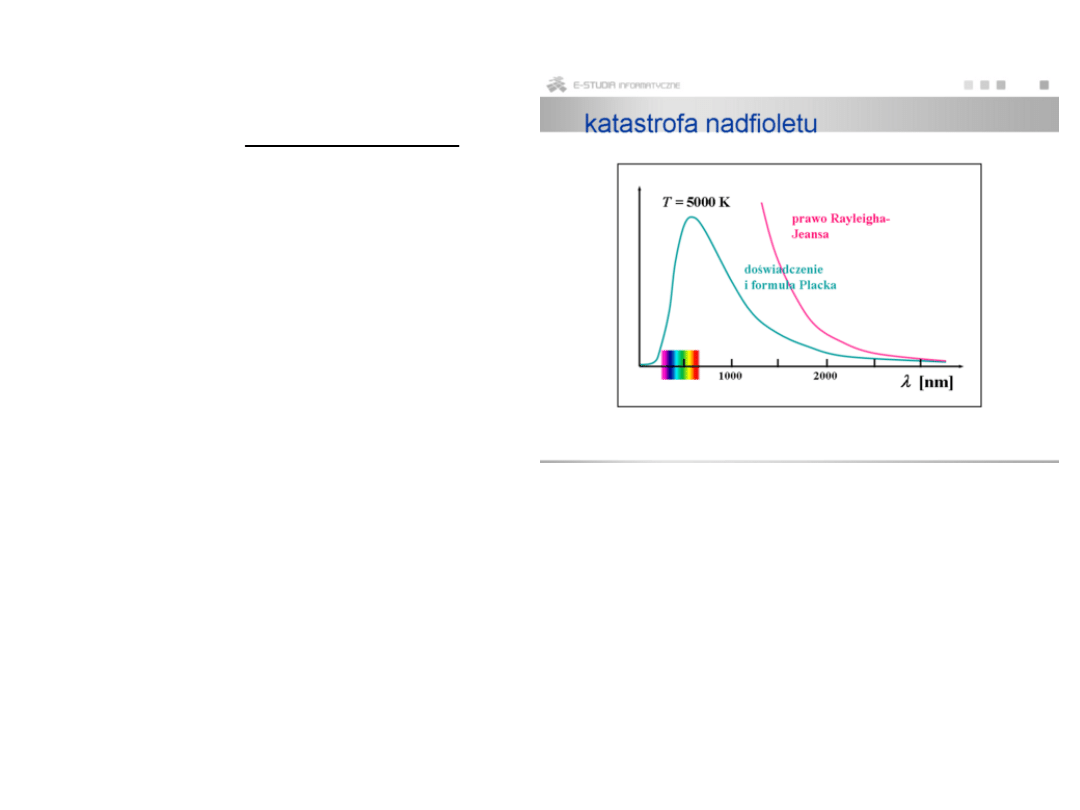
wzór Plancka (wyprowadzony przy założeniu kwantowania energii)

3

2

/

( , )

(

1)

h kT

h

P v T dv

dv

c e

n

n

=

-

poprawny w całym zakresie

częstości ν

Planck potraktował atomy jako niewielkie oscylatory o

częstościach ν

Oscylatory te emitują i absorbują promieniowanie a ich energie

są skwantowane

czyli przyjmują tylko określone wartości zgodnie z E

n

= nhν

Uwaga:
Bardziej precyzyjne byłoby przyjęcie kwantowania E

n

= (n+½)

hν

Fizyczne podstawy mechaniki

kwantowej:

I.

Dualistyczny charakter promieniowania (ciąg
dalszy)

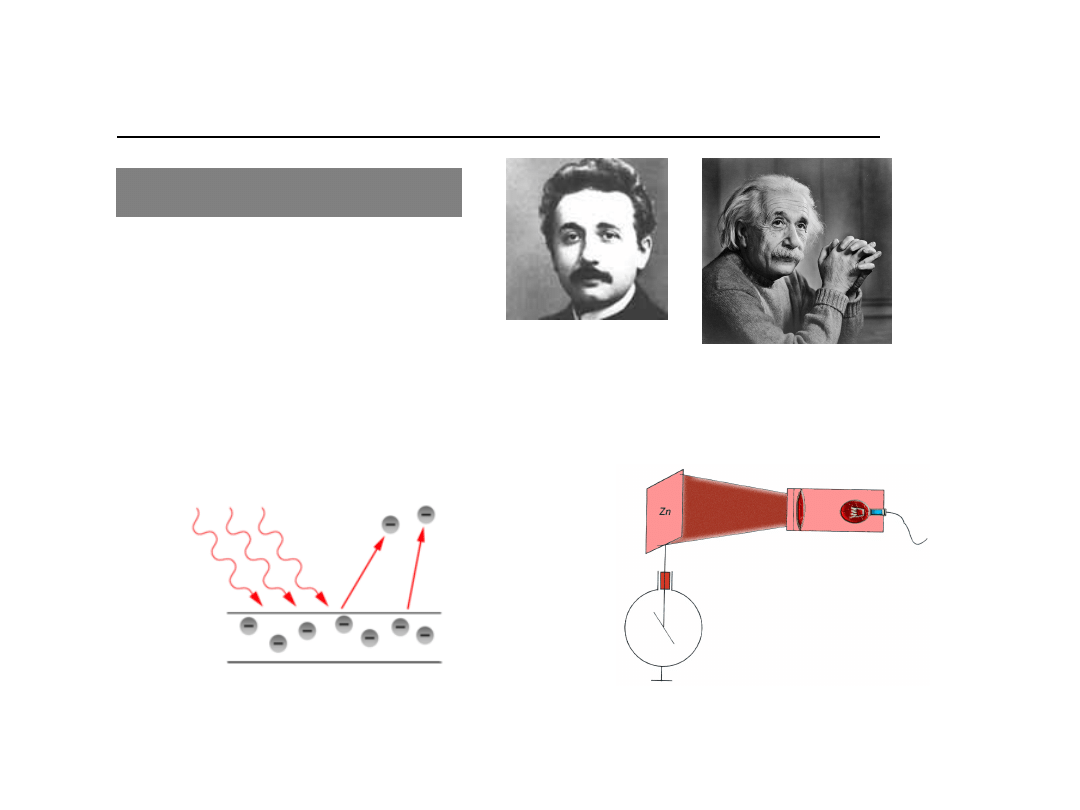
Płytka metalowa (np. cynkowa) zostaje naładowana ujemnie
(ładunki elektryczne) a następnie oświetlona promieniowaniem
nadfioletowym – ulega ona wówczas szybkiemu rozładowaniu.

Uwaga: tej samej płytki ale naładowanej dodatnio nie można
rozładować poprzez oświetlenie nadfioletem.

Eksperyment

demonstrujący

zjawisko

fotoelektryczne:

Efekt
fotoelektryczny

Albert Einstein
1879-1955

Fizyczne podstawy mechaniki

kwantowej:

I.

Dualistyczny charakter promieniowania (ciąg
dalszy)

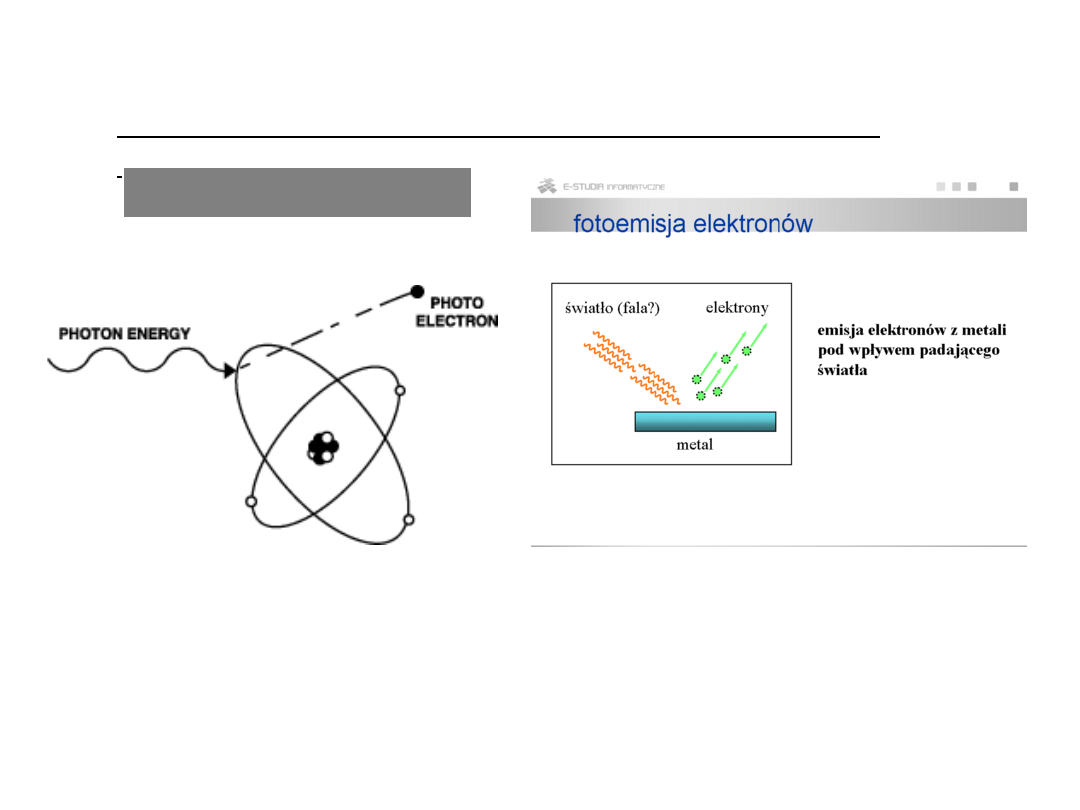
wyjaśnienie efektu fotoelektrycznego przez Einsteina
(1905 r.):
wypromieniowana porcja energii wysyłana jest w określonym
kierunku i może zachowywać się jak cząstka
(dla porcji energii hν przyjęto nazwę kwant promieniowania
lub foton)

Efekt
fotoelektryczny

Fotoelektrony są emitowane jedynie wtedy, gdy częstość światła
jest wyższa niż charakterystyczna wartość ν

g

(zależna od

materiału z którego wykonana jest płytka)

Zjawiska fotoelektrycznego nie można wyjaśnić na gruncie fizyki
klasycznej (czyli bez przyjęcia hipotezy o kwantach światła
(energii) )
Zgodnie z fizyką klasyczną należałoby oczekiwać, że energia
uwalnianych elektronów powinna wzrastać ze wzrostem natężenia
światła. Okazuje się jednak, że energia elektronów nie zależy od
natężenia światła, lecz jedynie od jego częstości.

Część energii światła hν zostaje zużytkowana na uwolnienie
elektronu z metalu (czyli na wykonanie tzw. pracy wyjścia)

Bilans

energii

w

efekcie

fotoelektrycznym:

2

v

2

m

hv W

= -

energia

kwantu

światła

energia
kinetyczna
fotoelektronu

praca
wyjścia
fotoelektro
nu

Fizyczne podstawy mechaniki

kwantowej:

I.

Dualistyczny charakter promieniowania (ciąg
dalszy)

Promieniowanie elektromagnetyczne wzbudza elektrony (np. w
atomach). Wzbudzone elektrony emitują promieniowanie (tzw.
promieniowanie rozproszone) o takiej samej długości fali.

Zjawisko Comptona (efekt Comptona):
rozpraszanie promieniowania elektromagnetycznego

przez elektrony

(zazwyczaj słabo związane lub swobodne)

Zjawisko
Comptona

Compton (w latach 1921-1923) zauważył, że dodatkowo pojawia
się promieniowanie rozproszone o zmienionej długości fali co jest
związane również ze zmianą kąta rozpraszania

Arthur

Compton

(USA),

1892-

1962

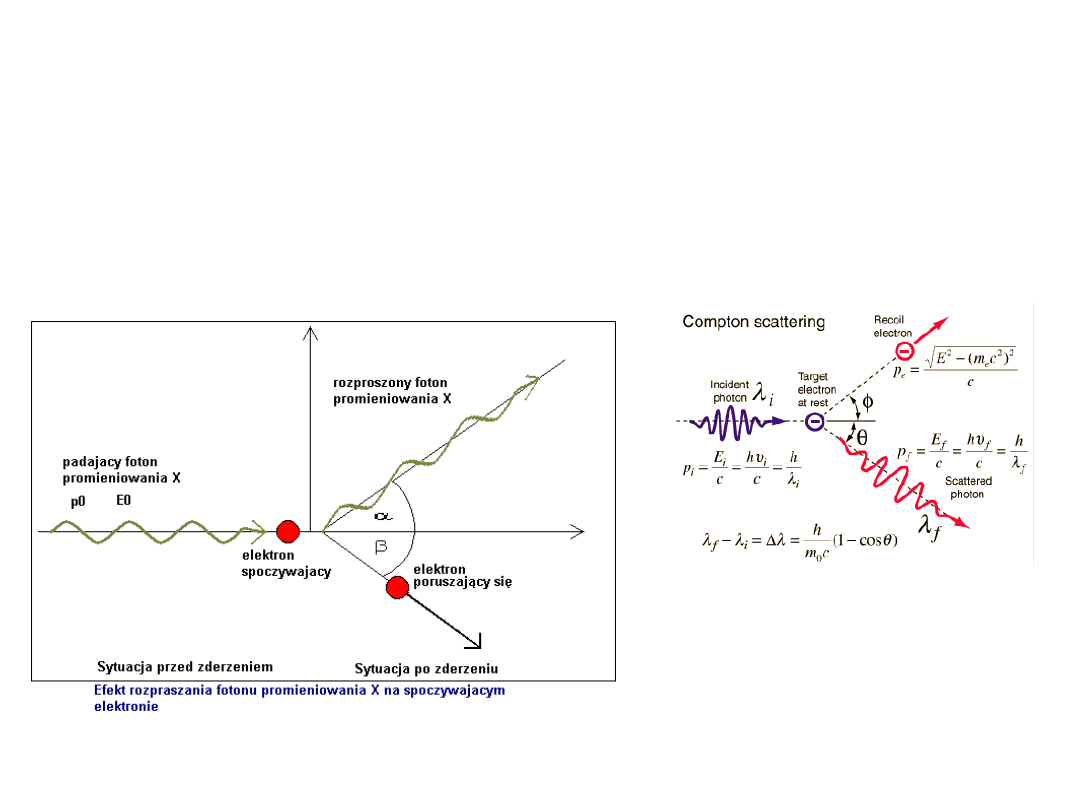
Wyjaśnienie doświadczeń Comptona nie było możliwe w oparciu o
falowy model światła (promieniowania elektromagnetycznego).

Stosując hipotezę o kwantach promieniowania można wyjaśnić
efekt Comptona w sposób następujący:

- dochodzi do zderzenia między dwiema cząstkami: fotonem i
elektronem
- podczas zderzenia przenoszone są pęd i energia

Pęd

i

energia

fotonu

przenoszone są do elektronu,
w wyniku czego rozproszony
kwant promieniowania ma
mniejszą energię i mniejszy
pęd

Opis

dostarczony

przez

Plancka,

wyjaśnienie

efektu

fotoelektrycznego przez Einsteina

oraz doświadczenia Comptona pokazały, że
promieniowanie ma charakter dualistyczny – zachowuje się jak fale

oraz jak cząstki

(tzw. dualizm korpuskularno-falowy)

Konkluzja

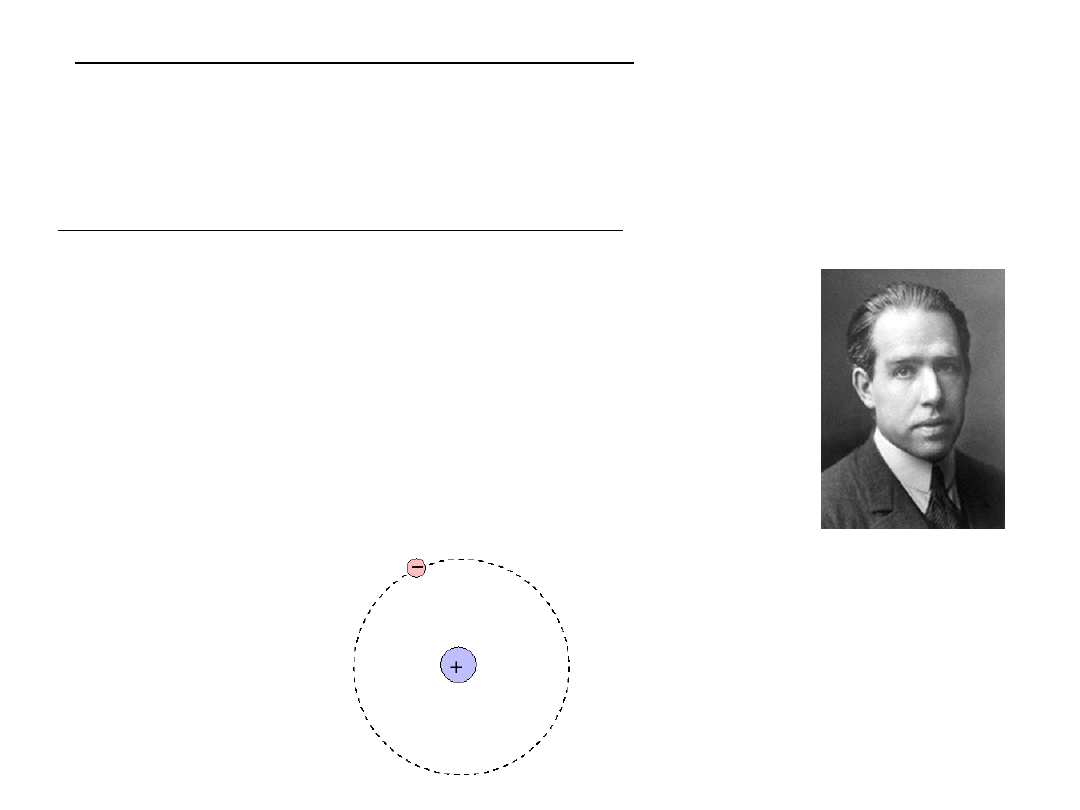
II. Model atomu według Bohra

Planetarny model atomu wodoru, zaproponowany w 1913 r. przez

Nielsa Bohra, był pierwszym poważnym modelem atomu

uwzględniającym dualistyczny charakter promieniowania oraz

kwantowanie energii.

Niels Bohr
(Dania), 1885-

1962

Podstawowe założenia modelu Bohra:

–

elektrony (traktowane jako punktowe
ładunki ujemne) krążą dokoła dodatnio
naładowanego jądra po „orbitach”
(analogia do Układu Słonecznego)

–

w odróżnieniu od systemu planetarnego,
w którym decydującą rolę odgrywają siły
grawitacyjne, w modelu atomu wg Bohra
kluczową rolę w ruchu elektronów wokół
jądra odgrywają siły Coulomba
(oddziaływania elektrostatyczne)

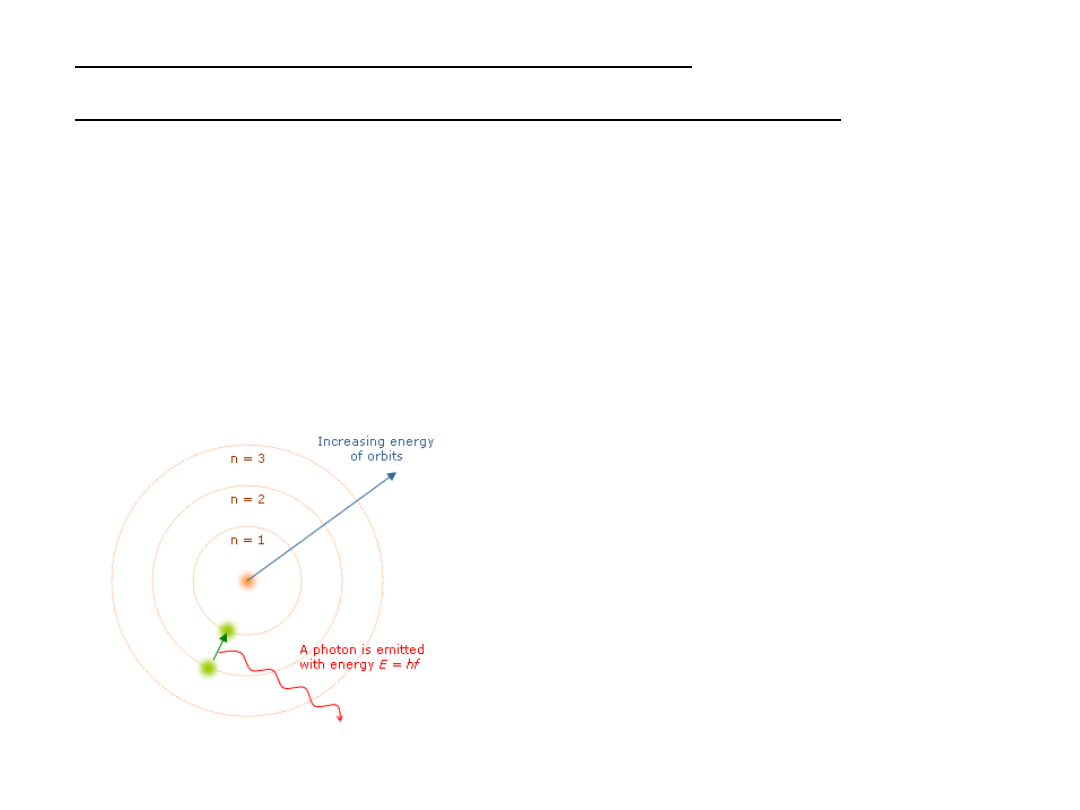
II. Model atomu według Bohra

Podstawowe założenia modelu Bohra (ciąg dalszy):

–

energia atomu może przyjmować tylko pewne
określone wartości, inaczej mówiąc, atom może
istnieć tylko w pewnych stanach stacjonarnych
(założenie sprzeczne z fizyką klasyczną). Przejścia
między stanami będą się zatem wiązały z emisją (lub
absorpcją) promieniowania o określonej wartości
energii (równej różnicy energetycznej między
stanami)

–

energia elektronu w atomie (wodoru) jest
skwantowana

emisja

promiaeniowania

w

modelu Bohra

II. Model atomu według Bohra

2

2

2

v

e

m

Ze

r

r

=

W modelu Bohra elektrony poruszają się wokół jądra po orbitach

kołowych o

promieniu r z prędkością v
Model zakłada istnienie równowagi dynamicznej pomiędzy:

siłą odśrodkową

Zgodnie z postulatem Bohra moment pędu elektronu jest

skwantowany:

i

kulombowską

siłą

przyciągania

elektronów przez jądro

v

e

M m r

n

=

= h

gdzie

n

jest

liczbą

naturalną

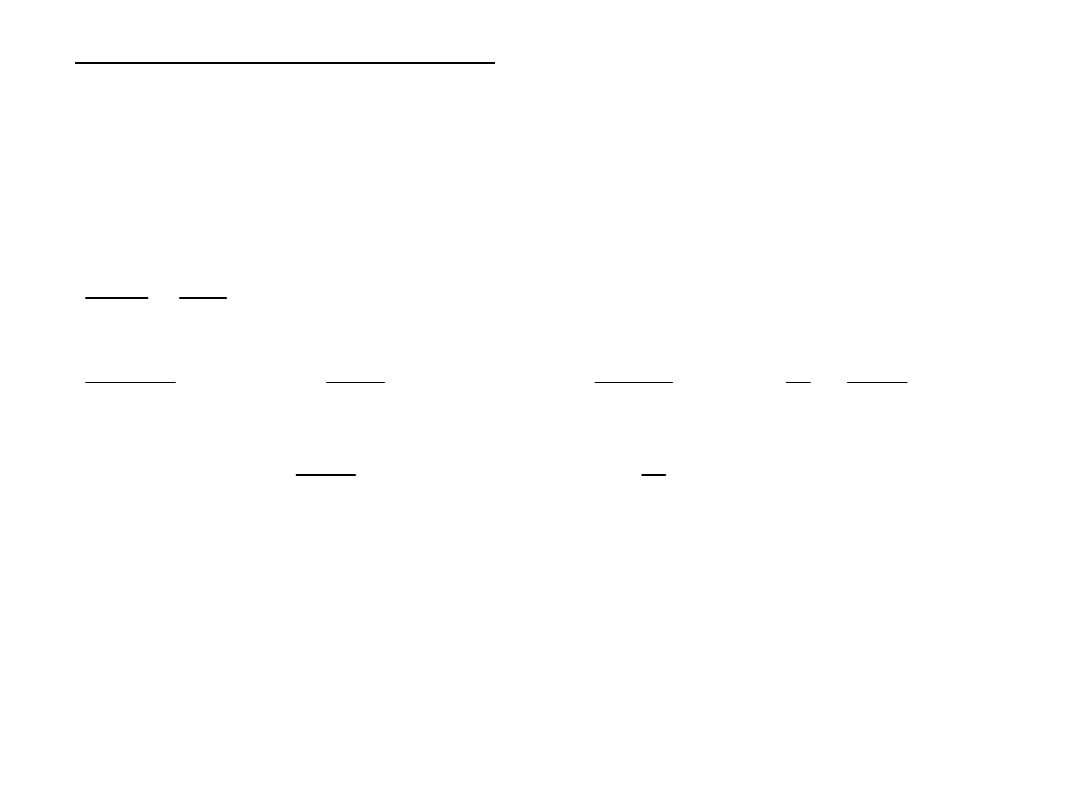
II. Model atomu według Bohra

2

2

2

2

2 2

2 2 2

2

2 2 2

2 2

2 2

2

2

2

2

2

2

2

2

0

0

2

v

,

v

,

v

v

1

,

,

1

,

e

e

e

e

e

e

e

e

e

m

Ze

zatem m r Ze a ponieważ n

m r

r

r

m r

n

n

Ze czyli

Ze więc r

czyli r

n

mr

mr

Ze m

Z

e m

przyjmując a

można zapisać że r

n a

e m

Z

=

=

=

=

=

=

=

=

=

h

h

h

h

h

wyrażenie na promień pierwszej orbity

Bohra:

v

e

M m r

n

=

= h

warunek

kwantowania

momentu pędu:

a

0

= 0,529 × 10

-10

m =

0,529 Å

inaczej a

0

= 1 bohr

(atomowa

jednostka

długości)

II. Model atomu według Bohra

Sukces teorii Bohra:
wyjaśnienie widma atomowego wodoru

Porażka teorii Bohra:
brak stosowalności do atomów wieloelektronowych

Wprowadzenie torów eliptycznych , uwzględnienie ruchów

periodycznych i inne

zabiegi nie pozwoliły ani na opis atomu helu ani też na wyjaśnienie

tworzenia

wiązań chemicznych.

Model Bohra pozostał modelem opisującym tylko atom H oraz jony

wodoropodobne

czyli np. He

+

, Li

2+

, Be

3+

, itd.

III

. Dualistyczny charakter materii

•

Hipoteza Louisa de Broglie’a (1924 r.):

„Dwoisty charakter korpuskularno-falowy
jest ogólną własnością materii, nie tylko promieniowania,
lecz także takich ciał, które uważano dotąd wyłącznie za cząstki”

Równania końcowe, podane przez de Broglie’a, można wyprowadzić

w następujący sposób:

Z równań: E=mc

2

i E=h

mamy: mc

2

=h , więc m=h/c

2

Wykorzystujemy równania: p=mc i c= (v=s/t =>

c=/T, =/T)
Podstawiając m=h/c

2

do p=mc,

mamy p= (h/c

2

)·c, czyli p=h/c

Wstawiamy c= do równania p=h/c
otrzymując: p = h/c = h/ = h/,

a więc: p = h /  (relacja de Broglie’a)

Louis de Broglie
(Francja), 1892-

1987

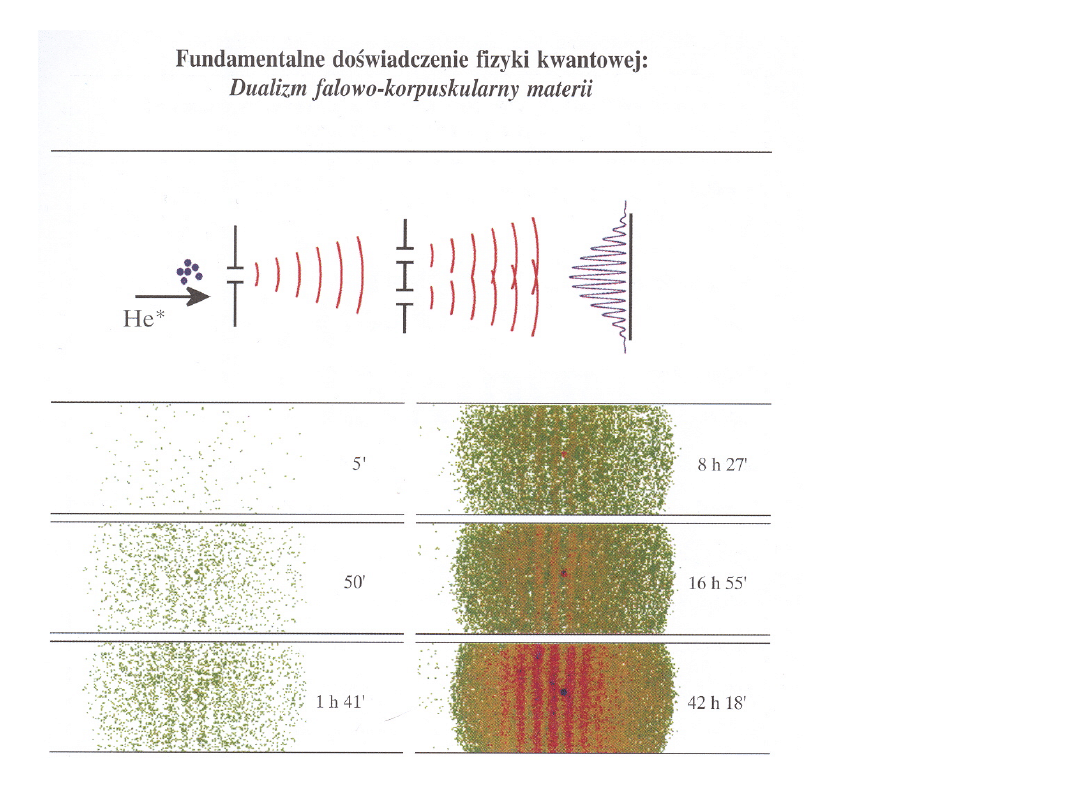
przepuszczanie
wiązki atomów

He

przez

układ

dwóch

szczelin

interferencj

a

fal materii

Hipoteza de Broglie’a zakłada istnienie „fal materii”. Zgodnie z
nią, każdej cząstce jest przypisana fala, przy czym długość tej fali
jest odwrotnie proporcjonalna do pędu cząstki (współczynnikiem
jest stała Plancka, czyli h).

Wzór de Broglie’a:
p = h /  (lub mv = h  )
łączy własności korpuskularne materii (poprzez masę m) z
własnościami falowymi (poprzez długość fali λ)

Relacja de Broglie’a i kwantowanie energii a fizyka klasyczna:

-

W fizyce klasycznej zakładano, że emisja i absorpcja
promieniowania zachodzi w sposób ciągły, co oznacza brak
kwantowania energii.

-

Kwant energii byłby mniejszy w świecie, w którym stała Plancka
(h) byłaby mniejsza od 6.626×10

–34

J·s (gdyż E=h)

-

Zmniejszając wartość stałej Plancka (h→0) mielibyśmy światy, w
których kwanty energii byłyby coraz mniejsze

–

W świecie, w którym stała Plancka byłaby równa zeru, emisja i
absorpcja zachodziłyby w sposób ciągły, czyli zgodnie z prawami
fizyki klasycznej

–

W takim „świecie fizyki klasycznej”, w którym h=0, również
długość fali (de Broglie’a) związanej z cząstką byłaby równa zeru
(ponieważ p = h /  , więc  = h / p , a zatem  = 0 gdy h = 0 ).
Wniosek: w świecie opisywanym prawami fizyki klasycznej,
materia miałaby charakter wyłącznie korpuskularny (a nie
dualistyczny), czyli nie istniałyby fale materii

–

Fala materii związana z cząstką jest tym krótsza, im większa jest
masa cząstki, gdyż:

= h / p, czyli = h / mv , a zatem 0 gdy m∞),

czyli charakter falowy materii zanika, gdy od mikrocząstek o
małej masie (takich jak elektrony) przechodzimy do ciał
makroskopowych (o dużej masie).

•

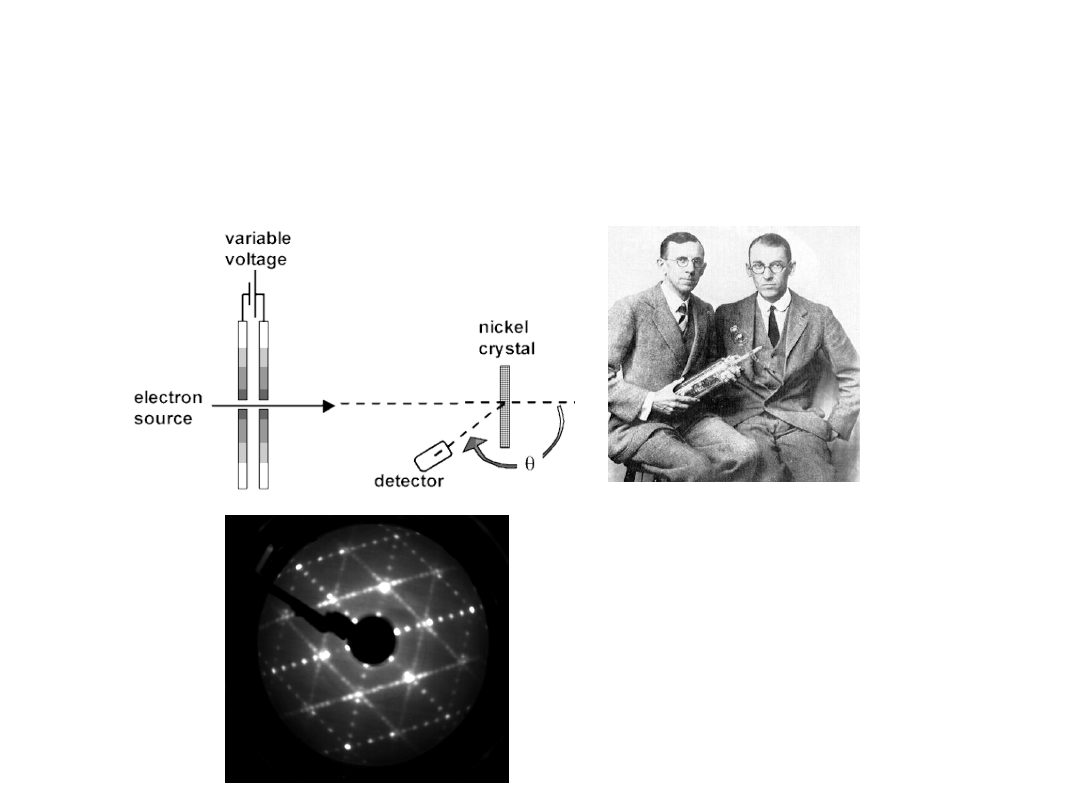
Eksperymentalne potwierdzenie hipotezy de Broglie’a
1927 r. – Davisson i Germer obserwują zjawisko dyfrakcji wiązki
elektronów na krysztale. Elektrony (cząstki) zachowują się więc
jak fale, gdyż dyfrakcja jest zjawiskiem typowym dla fal, np.
analogicznej dyfrakcji na krysztale ulegają promienie X.

Mechanika falowa Schrödingera

W 1926 r. Erwin Schrödinger sformułował zasady tzw.
mechaniki falowej, wprowadzając równanie umożliwiające
znalezienie matematycznej postaci fal materii. Matematyczna
postać fali materii jest dzisiaj nazywana FUNKCJĄ
FALOWĄ.

Erwin

Schrödinger

(Austria),

1887-

1961

„Kot Schrödingera” – eksperyment

myślowy

(kot jednocześnie żywy i martwy)

Zasada nieokreśloności Heisenberga

W latach 1923-1930, Werner Heisenberg przedstawił koncepcję

zasady nieokreśloności (nieoznaczoności), z której wynika, że

takie pojęcia, jak orbita elektronu w atomie, prędkość

elektronu w atomie, tor elektronu, czy pęd elektronu w atomie,

nie mają sensu fizycznego, gdyż nie można ich zmierzyć. Przy

czym niemierzalność nie wynika z niedoskonałości urządzeń

pomiarowych, ale z natury badanych obiektów.

Werner

Heisenberg

(Niemcy), 1901-

1976

Przyczyna nieokreśloności

opisanych przez Heisenberga

wynika też z konieczności

oddziaływania obiektu

mierzonego z układem

(narzędziem) pomiarowym.

Niektóre akty pomiarowe

zmieniają stan cząstki, wobec

czego następujące po nich

kolejne akty pomiarowe dotyczą

już cząstki znajdującej się w

innym stanie.

Relacje nieokreśloności Heisenberga są następujące:

x · p

x

≥ h

y · p

y

≥ h oraz

E · t ≥ h

z · p

z

≥ h

Wniosek: istnieją pary wielkości fizycznych (tzw. wielkości
komplementarne lub wielkości kanonicznie sprzężone), których
nie da się jednocześnie zmierzyć (lub obliczyć) w sposób dokładny.

Np. relacja x · p

x

≥ h wskazuje, że im dokładniej zostanie wyznaczona

wartość p

x

(składowa x-owa pędu cząstki), tym większy błąd będzie

popełniony w określeniu współrzędnej x-owej tej cząstki.
Czyli, im mniejsza wartość p

x

tym większa wartość x (i odwrotnie),

tak, aby relacja x · p

x

≥ h była spełniona.

Jeżeli natomiast zmierzymy jedną z tych wielkości (np. p

x

) dokładnie, czyli

popełniając błąd p

x

=0), to druga z wielkości będzie niemierzalna (tzn.

mierząc ją popełnimy nieskończenie duży błąd p

x

)

Pojęcie toru elektronu w atomie nie ma sensu fizycznego

Ponieważ nie można wyznaczyć dokładnie (jednocześnie) położenia i

pędu

(prędkości) elektronu w atomie, nie można mówić o torze elektronu.

determinizm klasyczny, demon Laplace’a (znający położenia i

pędy

wszystkich cząstek we wszechświecie oraz siły na nie

działające w chwili t

0

),

obalenie determinizmu jednostkowego.

Relacja E · t ≥ h dotyczy energii układu i czasu pomiaru.

Czas pomiaru wiąże się z czasem życia układu (pomiar nie może trwać

dłużej

niż czas życia układu).

•

W stanach podstawowych molekuł czas życia jest bardzo duży, czyli

t∞, więc E0 (energia może być wyznaczona z bardzo dużą

dokładnością)

•

Cząsteczki w stanach wzbudzonych mają natomiast znacznie krótszy

czas życia (t).
[czas życia t zależy od rodzaju stanu wzbudzonego i rodzaju układu].
Wobec tego czas pomiaru nie może być wówczas większy od t, z czego

wynika nieokreśloność energii zgodnie z relacją Heisenberga.

Relacje nieokreśloności Heisenberga a fizyka klasyczna:

W fizyce klasycznej mamy h=0.

W tej sytuacji średnie kwadraty błędów wszystkich

mierzonych wielkości mogą być jednocześnie równe zero,

czyli zasada nieokreśloności Heisenberga nie obowiązuje.

Świat makroskopowy: duże masy ciał, małe prędkości,

dobra stosowalność praw fizyki klasycznej.