Wojciech Piątkowski

Wykład VII

ADSORPCJA I

ADSORPCJA I

CHROMATOGRAFIA

CHROMATOGRAFIA

Katedra Inżynierii Chemicznej i Procesowej

Wydział Chemiczny, Politechnika Rzeszowska

LITERATURA

R. Petrus; G. Aksielrud; J. Gumnicki; W. Piątkowski – „ Wymiana masy w

układzie ciało stałe – ciecz”
N. Kielcew – „Podstawy techniki adsorpcyjnej”

Z. Witkiewicz – „Podstawy chromatografii”

Z. Kembłowski, St. Michałowski, Cz. Strumiłło, R. Zarzycki –„ Podstawy

teoretyczne Inżynierii Chemicznej i Procesowej”
Tadeusz Hobler – „Dyfuzyjny ruch masy i absorbery”

Praca zbiorowa pod red. Z. Ziółkowskiego – „Procesy dyfuzyjne i

termodynamiczne” – skrypt Pol. Wrocławskiej część;1; 2; 3;
K.F.Pawłow; P.G. Romankow; A.A. Noskow – „Przykłady i zadania z zakresu

aparatury i inżynierii chemicznej”
Z. Kawala; M. Pająk; J. Szust – „Zbiór zadań z podstawowych procesów

inżynierii chemicznej”; skrypt Pol. Wrocławskiej cz.: I, II, III
T.Kudra (pod redakcją) – „Zbiór zadań z podstaw teoretycznych inżynierii

chemicznej i procesowej”
R. Zarzycki – „Zadania rachunkowe z inżynierii chemicznej”

Praca zbiorowa pod red. J. Bandrowskiego – „Materiały pomocnicze do

ćwiczeń i projektów z inżynierii chemicznej” – skrypt Pol. Śląskiej

ADSORPCJA

Podstawowe pojęcia

Podział

adsorbentów

adsorbentów

ze względu na porowatość:



Adsorbenty

Adsorbenty

nieporowate - mają one niewielką powierzchnię właściwą,

rzadko przewyższającą 10 m

2

/g. Najczęściej powierzchnia ta wynosi od 0,1

do 1 m

2

/g.

Należą do nich:

 sadza grafitowana,

 BaSO

4

,

 aerożele krzemionkowe.


Adsorbenty

Adsorbenty

porowate - ciała stałe o powierzchniach właściwych od

setek do tysiąca m

2

/g. Adsorbenty takie stosuje się w postaci ziarnistej

(tabletki, granulki, kulki) w celu nadania im odpowiedniej wytrzymałości i
zmniejszenia oporu w stosunku do strumienia gazu lub cieczy. Rozmiary
ziaren wynoszą najczęściej od 0,1 do 15 m.

Wyróżniamy wśród nich:

 żele krzemionkowe,

 uwodniony Al

2

O

3,

 węgle aktywne,

 sita molekularne (zeolity),

 szkła porowate.

Metody otrzymywania

adsorbentów

Adsorbenty nieporowate

otrzymuje się przez:

 strącanie krystalicznych osadów, jak np. BaSO

4

,

 mielenie szklistych lub krystalicznych ciał stałych,
 niepełne spalanie substancji organicznych (tzw. czarne sadze) lub

krzemoorganicznych (tzw. białe sadze),

 hydrolizę chlorowcobezwodników kwasu ortokrzemowego np. SiCl

4

lub SiF

4

w silnie przegrzanej parze wodnej, uzyskując tzw. aerozole

krzemionkowe,

 obróbkę zwykłej sadzy polegającą na ogrzewaniu jej w temperaturze

3000°C pod zmniejszonym ciśnieniem, w atmosferze gazu obojętne-
go lub atmosferze redukującej. W temperaturze 3000°C cząsteczki
sadzy przybierają postać wielościanów, których płaszczyzny
zbudowane są z grafitu. Otrzymujemy tu sadze grafitowane.

ADSORPCJA

Podstawowe pojęcia

ADSORPCJA

Podstawowe pojęcia

Metody otrzymywania

adsorbentów

Wyróżniamy dwie główne metody otrzymywania

adsorbentów porowatych:

1. synteza (aglomeracja) -

która polega na zbudowaniu sztywnego szkieletu

adsorbentu z małych cząstek o rozmiarach koloidalnych; cząstki te
(korpuskuły) zlepiają się lub zrastają w miejscach zetknięcia, tworząc
szkielet o olbrzymiej powierzchni wewnętrznej; w ten sposób otrzymuje się
m.in. żele krzemionkowe, uwodniony Al

2

O

3

;

ADSORPCJA

Podstawowe pojęcia

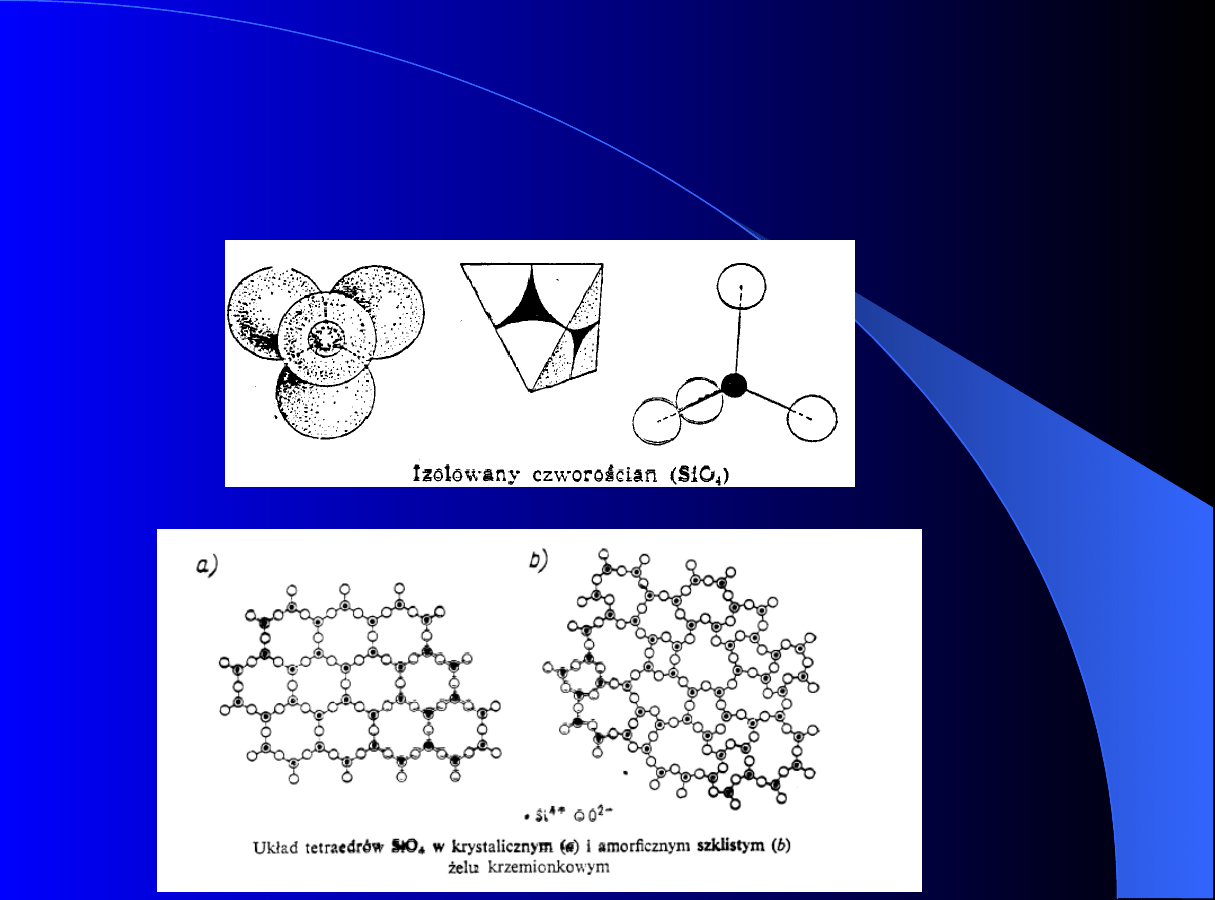
Cząstki żelu krzemionkowego zbudowane są z

Cząstki żelu krzemionkowego zbudowane są z

tetraedrów

SiO

tetraedrów

SiO

4

4

ułożonych

w

postaci

ułożonych

w

postaci

przestrzennej nieuporządkowanej sieci.

przestrzennej nieuporządkowanej sieci.

ADSORPCJA

Podstawowe pojęcia

Metody otrzymywania

adsorbentów

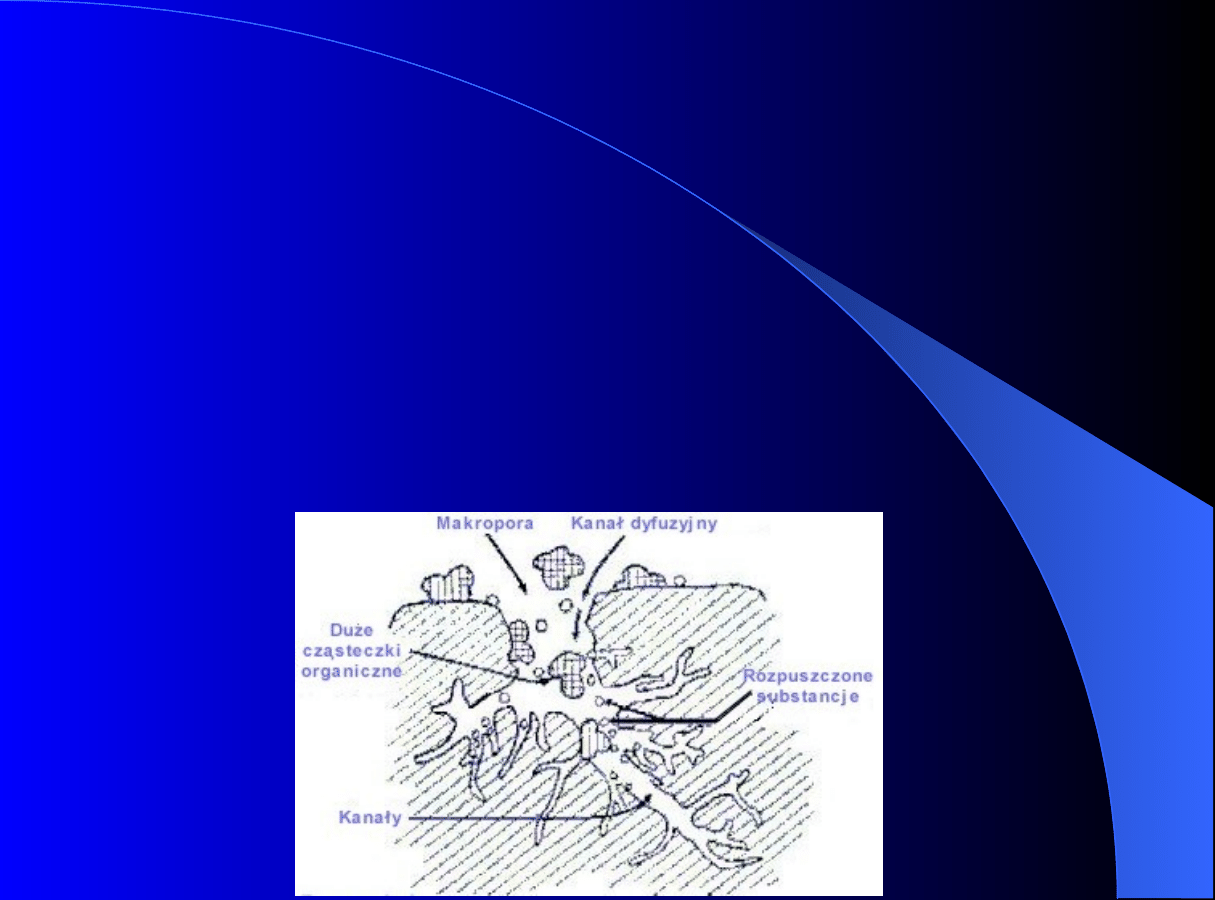
2. wywarzanie porów w litym materiale wyjściowym -

polega na

działaniu na porowate lub nieporowate ciała (koks, szkło),
aktywnymi gazami lub cieczami.

Przykłady:

 węgiel aktywny

z bardzo rozwiniętą powierzchnią (rozmiary porów od

kilku do kilkudziesięciu nm) - powstaje podczas działania na nieaktywny
węgiel gazami utleniającymi w temperaturze od 1123 do 1223 K;
wówczas część węgla ulega spaleniu;

 szkła porowate -

otrzymuje się działając kwasami na szkło sodowo –

borowe. Rozmiary porów zależą od obróbki cieplnej szkła i końcowego
przemywania roztworami NaOH lub KOH;

 metale porowate,

jak np. nikiel Raney’a otrzymuje się poprzez

wyługowanie NaOH stopu Ni z Al; w stopie tym podczas krzepnięcia
wydzielają się obydwa metale jako oddzielne fazy; po rozpuszczeniu
glinu w NaOH pozostaje porowaty szkielet niklowy.

ADSORPCJA

Podstawowe pojęcia

Adsorbenty porowate

Adsorbenty porowate

Klasyfikacja porów wg Dubinina:

Klasyfikacja porów wg Dubinina:





mikropory

mikropory

– pory o promieniach mniejszych od

– pory o promieniach mniejszych od

2 nm,

2 nm,





pory pośrednie (mezopory)

pory pośrednie (mezopory)

– pory o

– pory o

promieniach większych od 2 nm a mniejszych od

promieniach większych od 2 nm a mniejszych od

200 nm,

200 nm,





makropory

makropory

– pory o promieniach większych od

– pory o promieniach większych od

200 nm.

200 nm.

ADSORPCJA

Podstawowe pojęcia

Powierzchnia

Powierzchnia

adsorbentu

adsorbentu

znajduje się w innym stanie

energetycznym niż jego wnętrze, a siły działające na tej
powierzchni są niezrównoważone. Wyeksponowanie ciała stałego w
płynie spowoduje zjawisko gromadzenia się cząstek płynu na
powierzchni tego ciała. Efekt ten będzie tym lepszy, im większa
będzie powierzchnia właściwa (przypadająca na jednostkę masy
ciała stałego). Zdolność pokrywania powierzchni ciała stałego
cząstkami tego samego rodzaju substancji jest charakterystyczna
dla danego układu płyn-ciało stałe. Zatem cząstki płynu będącego
mieszaniną dwu- lub więcej składników mogą mieć różne
powinowactwo do powierzchni ciała stałego. Spowoduje to zmianę
stężenia każdej substancji biorącej udział w

ruchu masy

ruchu masy

: stężenia

objętościowego tej substancji w płynie oraz jej stężenia
powierzchniowego, w warstwie osadzonej na powierzchni ciała
stałego. Opisane zjawisko nosi nazwę

adsorpcji

adsorpcji.

Równowaga termodynamiczna układu dwufazowego płyn-ciało stałe
jest zazwyczaj silnie przesunięta na korzyść stężenia substancji
zaadsorbowanej w warstwie powierzchniowej i przez to

adsorpcja

adsorpcja

jest szczególnie efektywną metodą rozdziału mieszanin, pozwalającą
na zmniejszenie stężenia objętościowego danej substancji w płynie,
nawet do wartości stężenia rzędu ppm.

Charakter sił wiążących

adsorbat

adsorbat

z

powierzchnią adsorbentu

powierzchnią adsorbentu

dzieli

adsorpcję

adsorpcję

na dwa rodzaje: (*)

adsorpcję typu fizycznego

adsorpcję typu fizycznego

oraz (*)

adsorpcję typu chemicznego

adsorpcję typu chemicznego

.

Adsorpcja fizyczna

Adsorpcja fizyczna

jest spowodowana działaniem przyciągających

sił międzycząsteczkowych, w większości przypadków sił typu van der
Waalsa, spotęgowanych niekiedy siłami elektrostatycznymi lub siłami
wiązania wodorowego.

Adsorpcja chemiczna

Adsorpcja chemiczna

- chemisorpcja

- chemisorpcja

,

zwana

adsorpcją aktywowaną

adsorpcją aktywowaną

, jest związana z wytworzeniem

wiązania chemicznego między

adsorbatem

adsorbatem

a

adsorbentem.

adsorbentem.

Następujące kryteria pozwalają rozróżnić

adsorpcję

adsorpcję

fizyczną

fizyczną

od

chemisorpcji:

chemisorpcji:

1. 

ciepło adsorpcji

ciepło adsorpcji

- małe wartości ciepła adsorpcji, rzędu 220

[kJ/mol] dla

adsorpcj

adsorpcj

i

i

fizyczn

fizyczn

ej

ej

, duże dla - zmiana równowagi

procesu jest łatwa w przypadku

adsorpcj

adsorpcj

i

i

fizyczn

fizyczn

ej

ej

, spowodowanie

chemisorpcji

chemisorpcji

, rzędu 20400 [kJ/mol], porównywalne z ciepłem

reakcji;
2.

odwracalność procesu

odwracalność procesu

takiej zmiany dla

chemisorpcji

chemisorpcji

wiąże się

z koniecznością zastosowania bardziej drastycznych warunków, na

przykład zwiększenia temperatury desorpcji,
3.

grubość warstw adsorpcyjnych

grubość warstw adsorpcyjnych

- w przypadku

adsorpcj

adsorpcj

i

i

fizyczn

fizyczn

ej

ej

tworzą się na powierzchni warstewki

adsorba

adsorba

tu

tu

, których

grubość odpowiada kilku średnicom cząstek tego ostatniego; w

przypadku

chemisorpcji

chemisorpcji

powstają warstewki jednocząsteczkowe

warstewki

adsorbatu

adsorbatu

.

ADSORPCJA

Podstawowe pojęcia

Podczas

adsorpcji

adsorpcji

w układzie ciecz-ciało stałe często jest możliwe

wystąpienie obu typów

adsorpcji

adsorpcji

jednocześnie już w temperaturze

otoczenia.

Z termodynamicznego punktu widzenia, w adsorpcji, jak w
każdym procesie równowagowym, obowiązuje równanie Gibbsa:

 



G

=



H

r

-T



S

Ze względu na to, że

adsorpcja

adsorpcja

jest procesem samorzutnym energia

swobodna Gibbsa



G < 0.

Przejście

adsorptywu

adsorptywu

A

z płynu w

adsorbat

adsorbat

zaadsorbowany na powierzchni

adsorbentu

adsorbentu jest związane

z utratą co najmniej jednego stopnia swobody (zahamowany ruch
translacyjny), a więc wystąpi także zmiana entropii układu



S < 0.

Wtedy



H < 0,

ADSORPCJA

ADSORPCJA

JEST WIĘC

PROCESEM

PROCESEM

EGZOTERMICZNYM

EGZOTERMICZNYM

.

W związku z tym, stężenie

adsorbatu

adsorbatu

na powierzchni

adsorbentu

adsorbentu

maleje ze wzrostem temperatury procesu a rośnie ze wzrostem
stężenia

adsorptywu

adsorptywu

w płynie.

ADSORPCJA

Podstawowe pojęcia

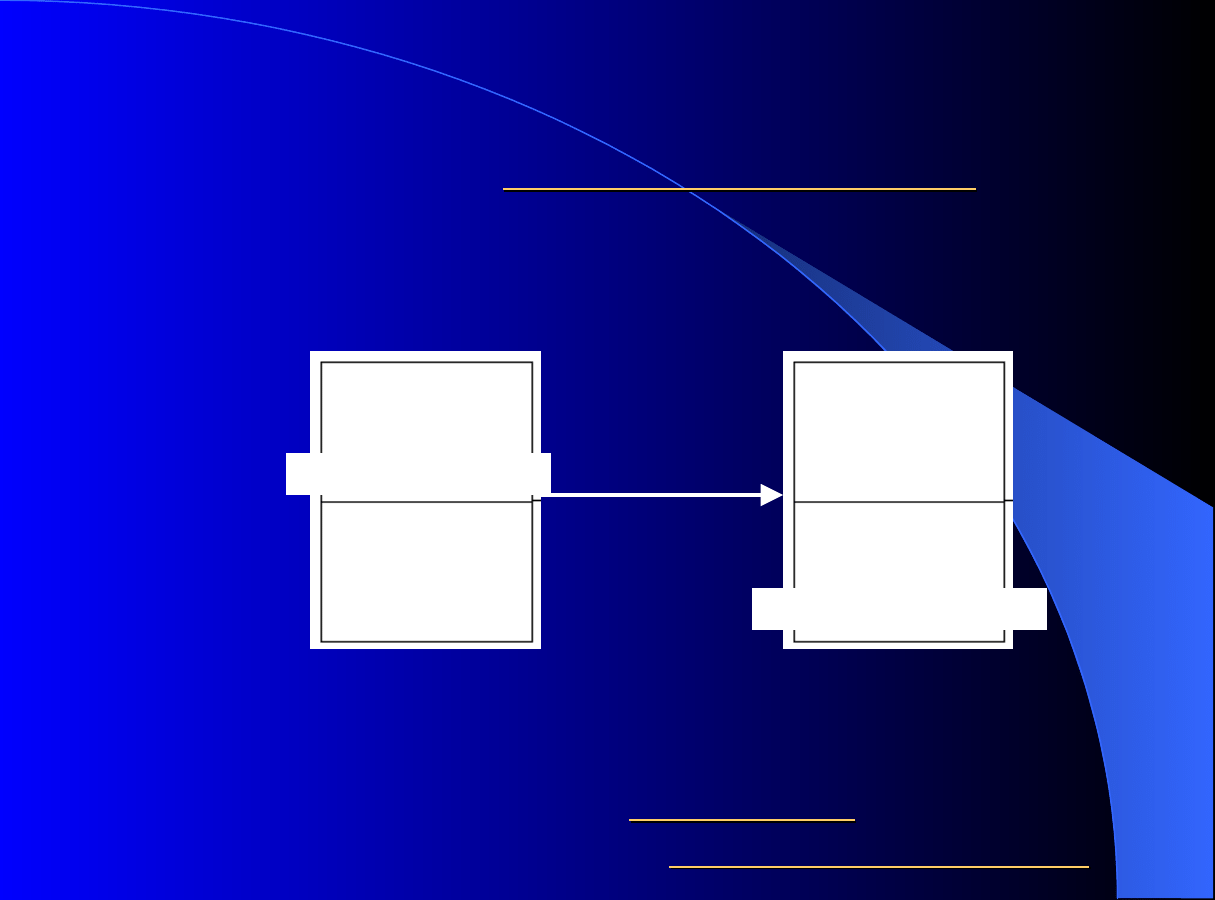
ADSORPCJA

Statyka procesu

O ilości parametrów, jakie możemy przyjmować dowolnie (zmienne

niezależne) w warunkach

równowagi a

równowagi a

d

d

sorpcyjnej

sorpcyjnej

w układzie

gaz(lub ciecz)  płyn-ciało stałe informuje nas reguła faz.

W przypadku najprostszego układu 3-składnikowego:

s = i + 2 - f

-

gdzie:

i

-

ilość

składników

;

f -

ilość faz

; s -

ilość stopni swobody

.

początek

koniec

i = 3; f = 2; s = 3 + 2 - 2 = 3

stopnie swobody

Dwa z nich zajmujemy:

T

oraz

p.

Jeżeli 3-ci stopień swobody zajmiemy

jednym ze stężeń np.

c

A

-

stężeniem składnika kluczowego

(adsortywu)

(adsortywu)

A

w fazie płynu, to

stężenie tego składnika na powierzchni

adsorbentu (adsorbat)

adsorbentu (adsorbat)

po

osiągnięciu stanu równowagi będzie funkcją:

q*

A

= f(c

A

; T; p).

adsorbent

(złoże)

Faza stała

adsorbat+adsorbent

Faza stała

A* S

Faza płynu

A* + B

Faza płynu

A + B

adsorptyw+eluent

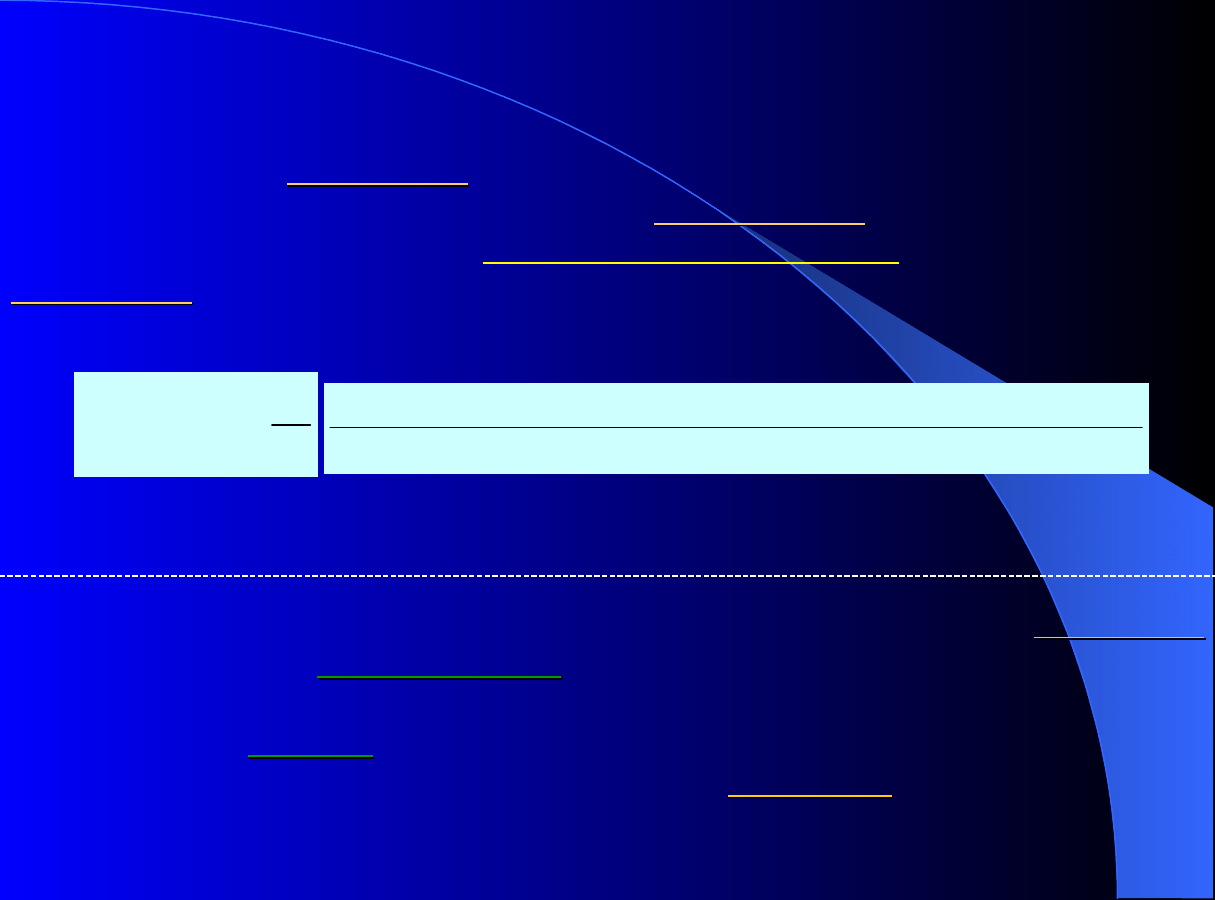
ADSORPCJ
A

Statyka
procesu c.d.

Prawidłowy, szczegółowy rodzaj stężenia użytego w modelu

adsorpcji

adsorpcji

wynika z wymiaru

bilansu masy

bilansu masy

w sześcianie jednostkowym, w którym

każdy człon winien mieć wymiar [kmolA/m

3

s]. Mimo tego, że adsorpcja

to przypadek

dyfuzji

dyfuzji

1)

lub

3)

rodzaju to dogodnym i podstawowym

stężeniem jest

koncentracja

koncentracja

molow

molow

a

a lub

masow

masow

a.

a.

Ze zmianą dwóch, głównych parametrów

T

oraz

p (dla układu gaz-

ciało stałe)

a

a

d

d

sorpcja

sorpcja

przebiega następująco. Ze wzrostem

temperatury stężenie równowagowe

adsorbatu

adsorbatu

się zmniejsza, a ze

wzrostem ciśnienia rośnie (układ gaz-ciało stałe!). Z tego powodu

a

a

d

d

sorpcj

sorpcj

ę

ę

należy prowadzić w jak najniższej temperaturze i jak

najwyższym

ciśnieniu

(zakresy

zmian

tych

parametrów

są

charakterystyczne dla danego układu absorpcyjnego) ponieważ
maksymalizujemy wówczas

si

si

łę

łę

nap

nap

ę

ę

dow

dow

ą

ą

procesu. Każdorazowy stan

równowagi powiązany jest zależnością:

(

)

*

const

K

A

T, p

A

q

c

=

=

lynu

p

fazie

w

skladnika

e

rownowagow

stezenie

adsorbentu

i

powierzchn

na

skladnika

e

rownowagow

stezenie

A

A

gdzie:

K -

stała równowagi adsorpcyjnej.

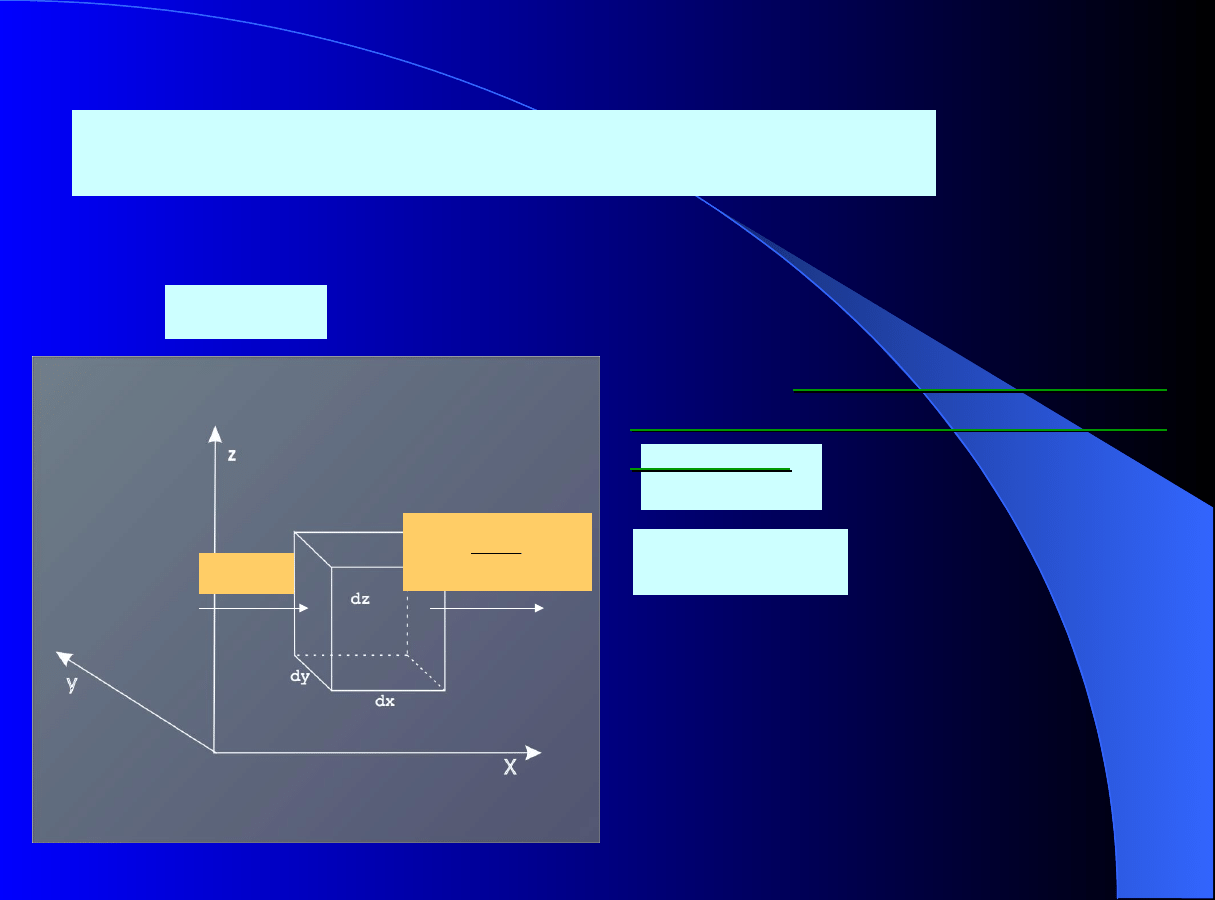
Dynamika adsorpcji























































reakcji

wyniku

w

skl.

ubytek

skl.

akumulacja

skl.

odplywu

natezenie

skl.

doplywu

natezenie

A

A

A

A

Stężeniem najcz

ęś

ciej używanym w modelu adsorpcji jest

koncentracja molowa
– [kmolA/m

3

]

/

A

A

C

n V

=

z

y

x

x

N

N

Ax

Ax

d

d

d





















dz

dy

N

Ax

'

A

A

A

N c u

=

Definicja

g

g

ę

ę

sto

sto

ś

ś

ci strumienia

ci strumienia

masy – miary prędkości

masy – miary prędkości

procesu:

procesu:

[kmolA/m

2

s]

'

'

d

d

A

A

N x

m

=

[kmolA/s]

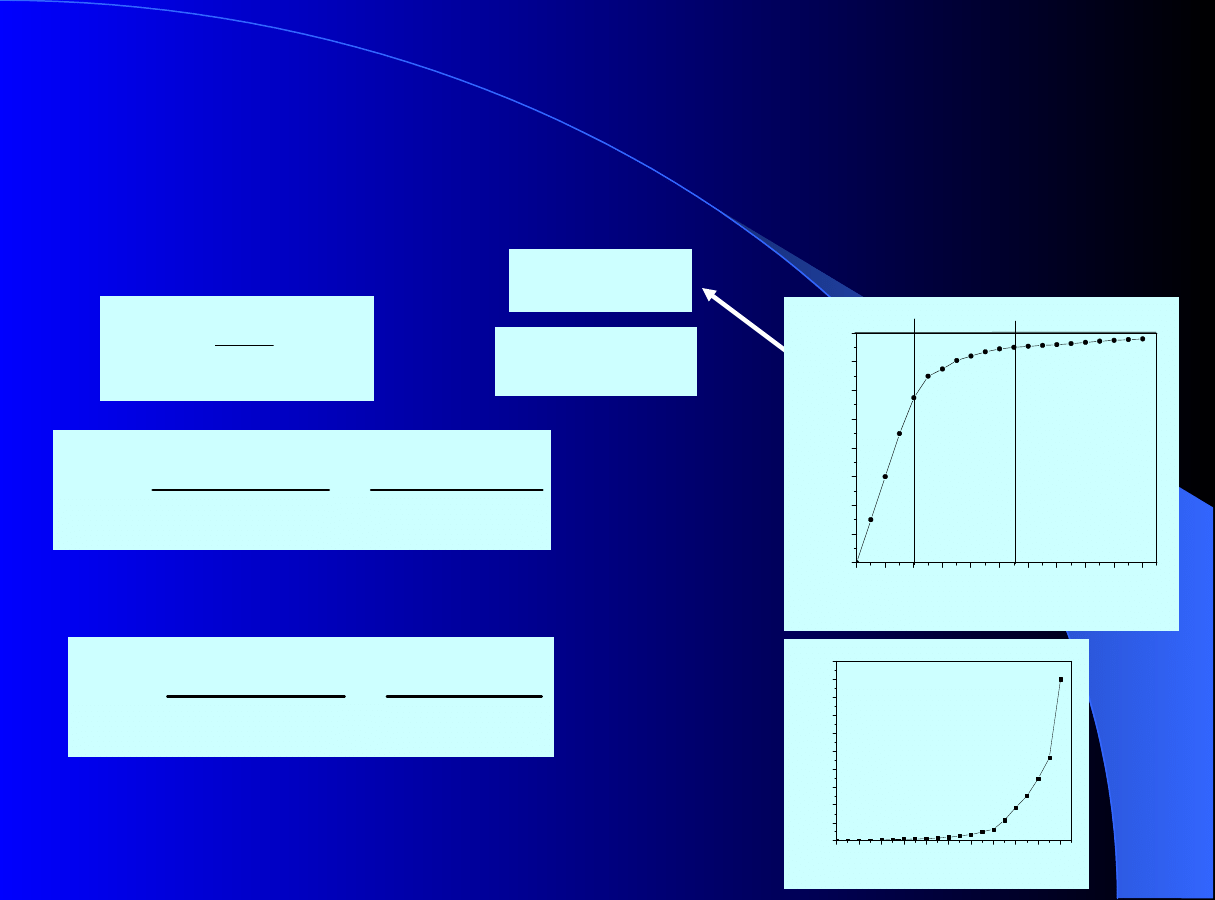
I

I

zotermy pojedyncze

zotermy pojedyncze

-

-

Modele izotermy dla idealnej

Modele izotermy dla idealnej

adsorpcji

adsorpcji

na homogenicznej powierzchni adsorbentu

na homogenicznej powierzchni adsorbentu

*

'

'

1

1

ri

i

i

i

i

ri

i

ri

i

q b c

H c

q

b c

b c

�

=

=

-

-

Izoterma antyLangmuira:

*

1

1

ri

i

i

i

i

ri

i

ri

i

q K c

H c

q

K c

K c

�

=

=

+

+

Izoterma Langmuira:

)

(

1

1

S

A

k

k

S

A

-





*

i

i

i

q

H c

=

Izoterma Henry’ego:

K

q

H

ri

i





gdzie:

0

2

4

6

8

10

12

14

16

18

20

0

2

4

6

8

10

12

14

16

III

II

I



q

C

q

*

Langmuir

0

2

4

6

8

10

12

14

16

18

20

0.0

0.2

0.4

0.6

0.8

1.0

1.2

1.4

1.6

1.8

2.0

C

q

*

q



antyLangmuir

R. Petrus; G. Aksielrud; J. Gumnicki; W.
Piątkowski – „ Wymiana masy w układzie
ciało stałe – ciecz” , podrozdz. 7.2.1.

ADSORPCJ
A

Statyka
procesu c.d.

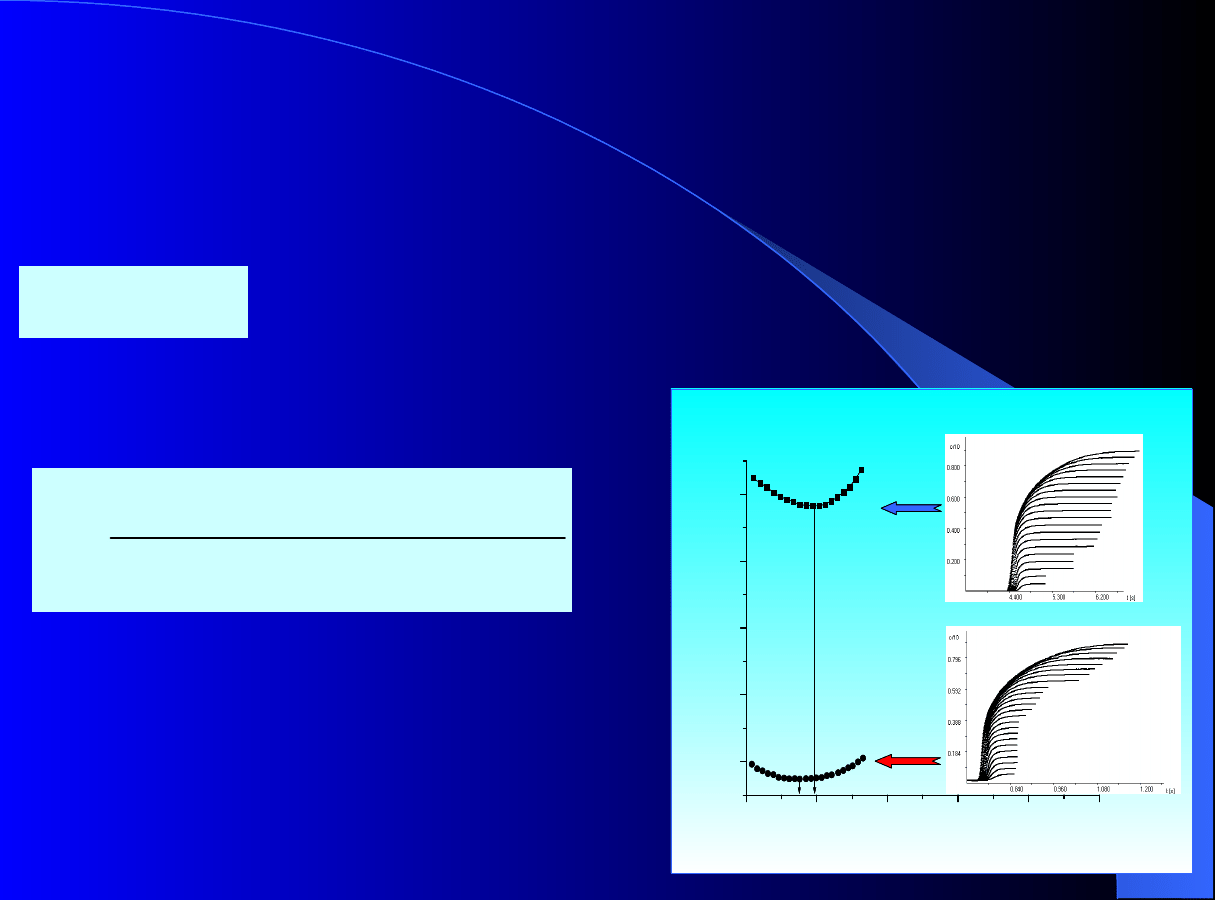
I

I

zotermy pojedyncze

zotermy pojedyncze

-

-

Modele izotermy dla

Modele izotermy dla

nie

nie

idealnej

idealnej

adsorpcji

adsorpcji

na homogenicznej powierzchni adsorbentu

na homogenicznej powierzchni adsorbentu

0

5

10

15

20

25

16

18

20

22

24

Packed

Monolith

MeOH/H

2

O (65/35)

B

re

a

kth

ro

ug

h

cu

rv

es

minimum slope
of chord isotherm

q

*/

c

c [g/dm

3

]

0

5

10

15

20

25

16

18

20

22

24

Packed

Monolith

MeOH/H

2

O (65/35)

B

re

a

kth

ro

ug

h

cu

rv

es

minimum slope
of chord isotherm

q

*/

c

c [g/dm

3

]

Izoterma BET:

(

) (

)

*

1

1

i

ri i

i

L i

L i

ri i

q K c

q

K c

K c K c

�

=

-

-

+

Izoterma BET dla układu ciecz-ciało
stałe. Kształt zależności wartości

q*/c

q*/c

-

-

w funkcji stężenia

w funkcji stężenia

c

c oraz

charakterystyczny kształt krzywych
wyjścia naprowadza na prawidłowy
model izotermy adsorpcji – tutaj BET

*

1/

F

k

n

i

i

q

c

=

Izoterma Freundlicha:

gdzie:

k

F

i

n –

parametry równania

ADSORPCJ
A

Statyka
procesu c.d.

Izoterma
biLangmuira:

I

I

II

II

*

I

II

1

1

A

i

A

i

A

i

i

q K c q K c

q

K c

K c

�

�

=

+

+

+

Izoterma
UNILAN

:

 

 

 























h

C

K

h

C

K

h

2

q

q

i

i

A

*

A

exp

1

exp

1

ln

ADSORPCJ
A

Statyka
procesu c.d.

I

I

zotermy pojedyncze

zotermy pojedyncze

-

-

Modele izotermy dla idealnej

Modele izotermy dla idealnej

adsorpcji

adsorpcji

na h

na h

etero

etero

genicznej powierzchni adsorbentu

genicznej powierzchni adsorbentu

*

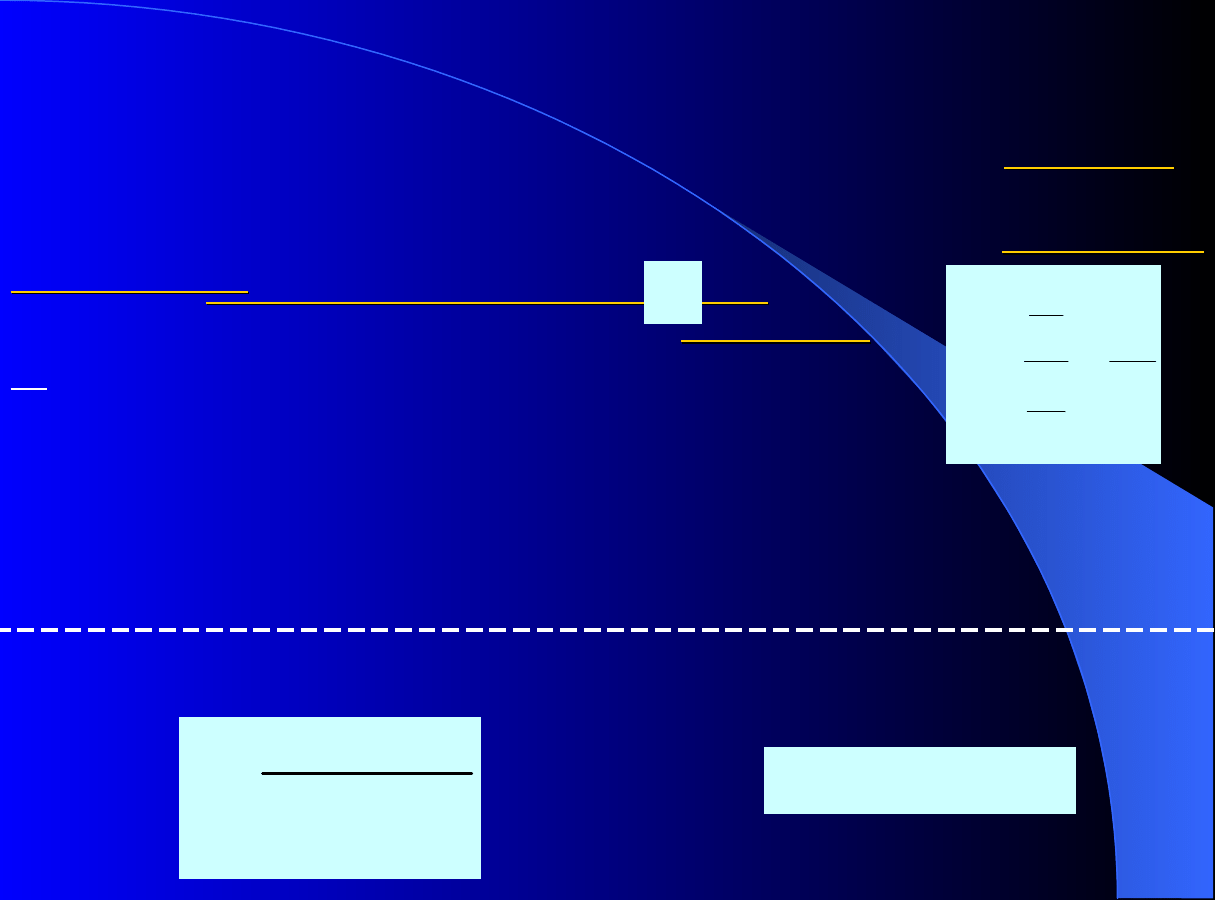
1

*

1

i

i

ri

ij

j

rj

j

q

c

K

S

q

K

c

=

=

IZOTERMY

IZOTERMY

KONKURENCYJNE -

KONKURENCYJNE -

WIELOSK

WIELOSK

Ł

Ł

ADNIKOWE

ADNIKOWE

i nazywany

selektywno

selektywno

ś

ś

ci

ci

ą

ą

równowagow

równowagow

ą

ą

, gdzie

:

q

i j

,

*

Selektywność rozdziału adsorpcyjnego

S

i,j

w przypadku

adsorpcji

adsorpcji

z

płynu więcej niż jednego adsorptywu, jest mierzona analogicznie jak w
przypadku innych metod rozdziału przez stosunek stałych

równowagi

równowagi

adsorpcyjnej

adsorpcyjnej

(analog np. lotności względnej w destylacji), definiowany

jako:

- ilość zaadsor-bowanej substancji

(

adsorbatu

adsorbatu

i/j)

w jednostce masy adsorbentu (stężenie

powierzchniowe adsorbatu) w warunkach równowagi
termodynamicznej; -

c

i,j

-

stężenie adsorptywu w

płynie;

K

ri,j

- stała równowagi adsorpcji dla składnika

kluczowego

i

lub

j.

Rozdział mieszaniny przez adsorpcję jest możliwy,
jeśli równowagowa selektywność substancji

i

od

j

jest

rzędu

S

i,j

= 1.21.5

lub większa.

Izoterma konkurencyjna
Langmuira:

*

2

1

1

i

i

i

i

j

j

j

q K c

q

K c

�

=

=

+

�

założenie:

const









tot

i

q

q

ADSORPCJ
A

Statyka
procesu c.d.

IZOTERMY WIELOSK

IZOTERMY WIELOSK

Ł

Ł

ADNIKOWE

ADNIKOWE









N

i

*

i

tot

q

q

1

jeśli:

wówczas izoterma konkurencyjna
Langmuira zamienia się w izotermę
stechiometryczną

Izoterma stechiometryczna:

B

S

A

k

k

S

B

A

-







)

(

)

(

1

1

(

)

(

)

1

1

1

*

A

rA

A

A

rA

A

A

A

rA

A

rA

A

q K c

q K c

q

C

K c

K

c

�

�

=

=

-

+

+

-

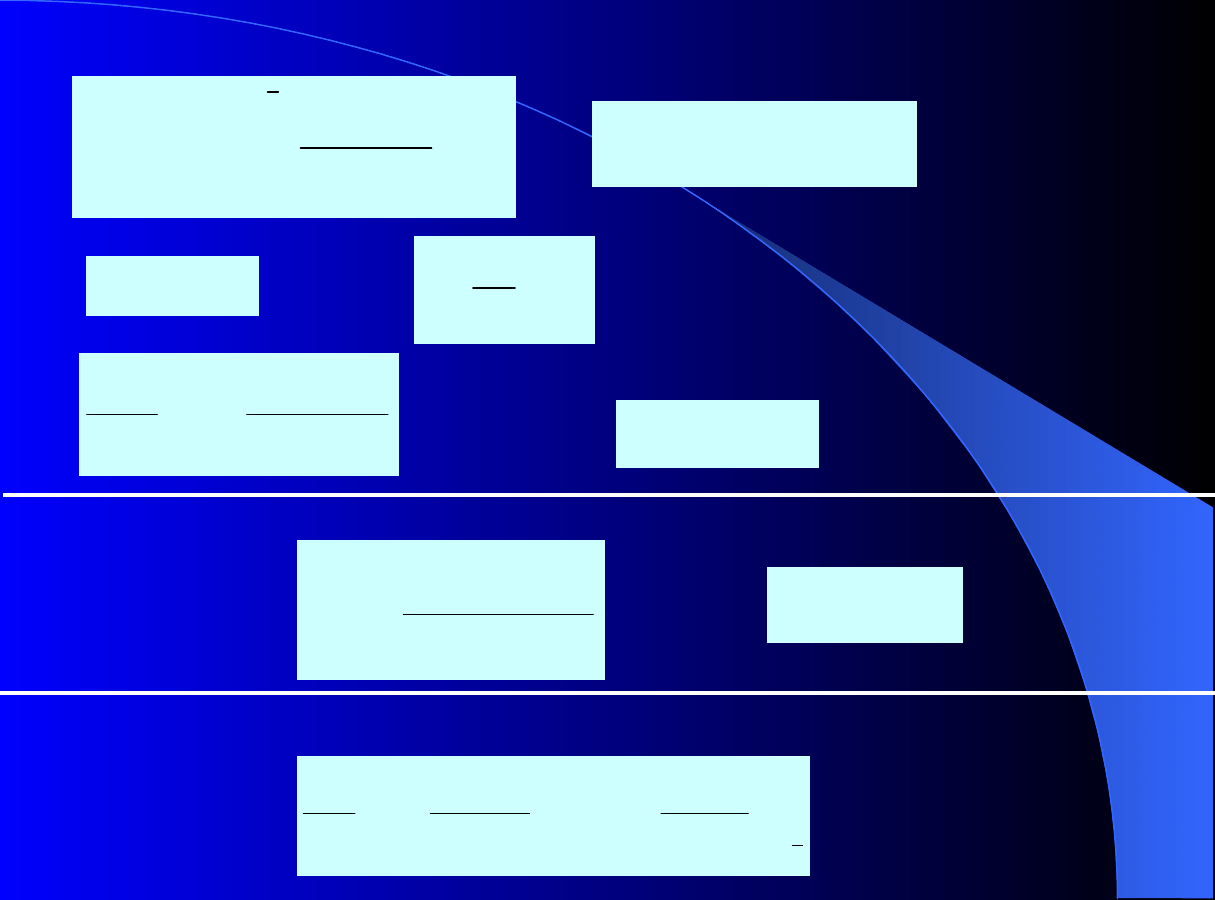
IZOTERMA KONKURENCYJNA - TEORI

IZOTERMA KONKURENCYJNA - TEORI

A

A

IAS

IAS

( )

( )

( )

0

*

0

0

0

0

0

d

i

i

c

i

i

i

i

i

q c

c

c

c

p

=

�

( )

0

i

i

mix

c

p

p

=

0

s

i

i

i

c

x c

=

0

1

1

NC

i

i

i

c

c

=

=

�

 







NC

i

i

*

i

s

i

*

tot

C

q

x

q

1

0

1

prz
y:

*

tot

s

i

*

i

q

x

q 

TEORIA AST

TEORIA AST

a

K

a

K

q

q

i

ri

i

ri

*

i







1

i

i

i

x

a





gdzie:

Na przykładzie
izotermy
Langmuira:

TEORIA RAS

TEORIA RAS

 

x

,

T

NC

i

i

i

s

i

NC

i

i

*

i

s

i

*

tot

ln

x

c

q

x

q





























1

1

0

1





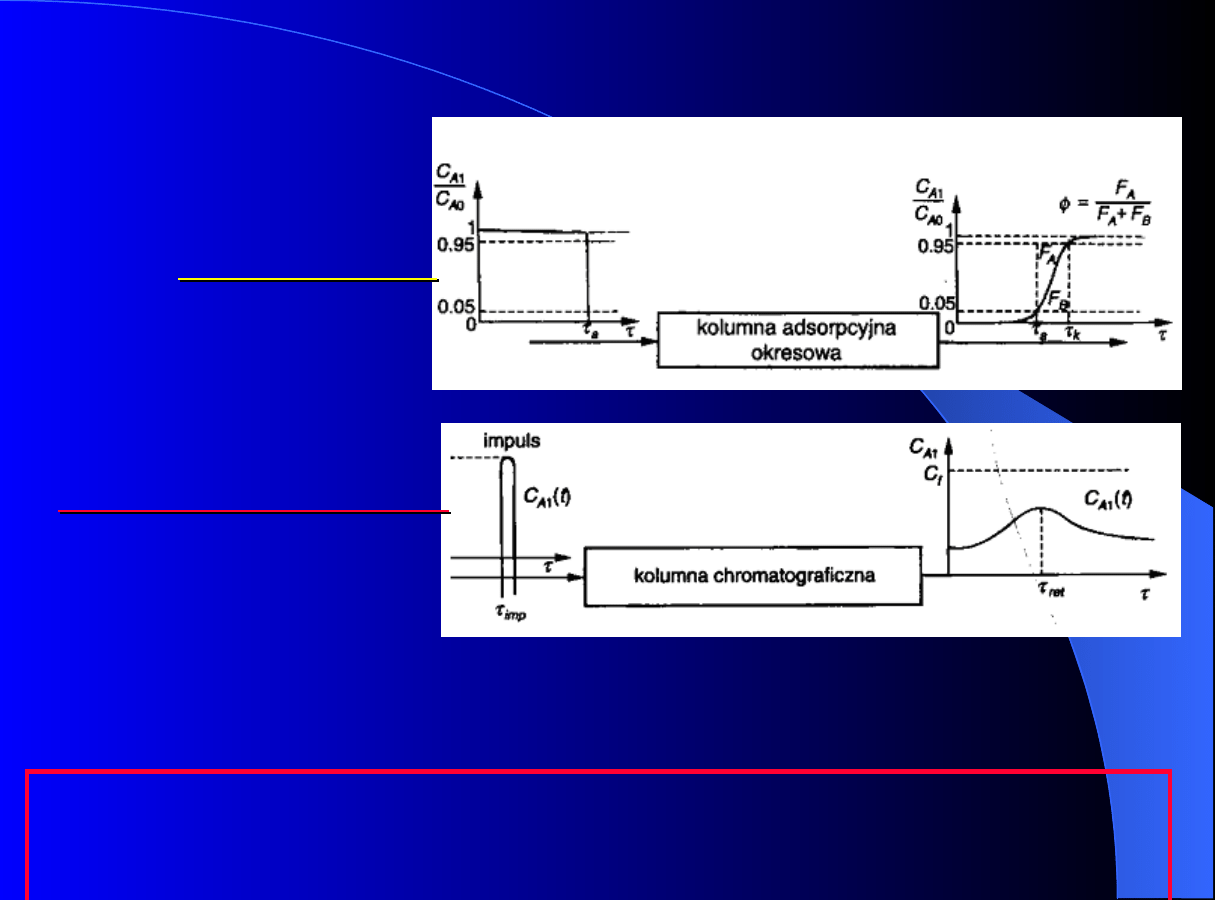
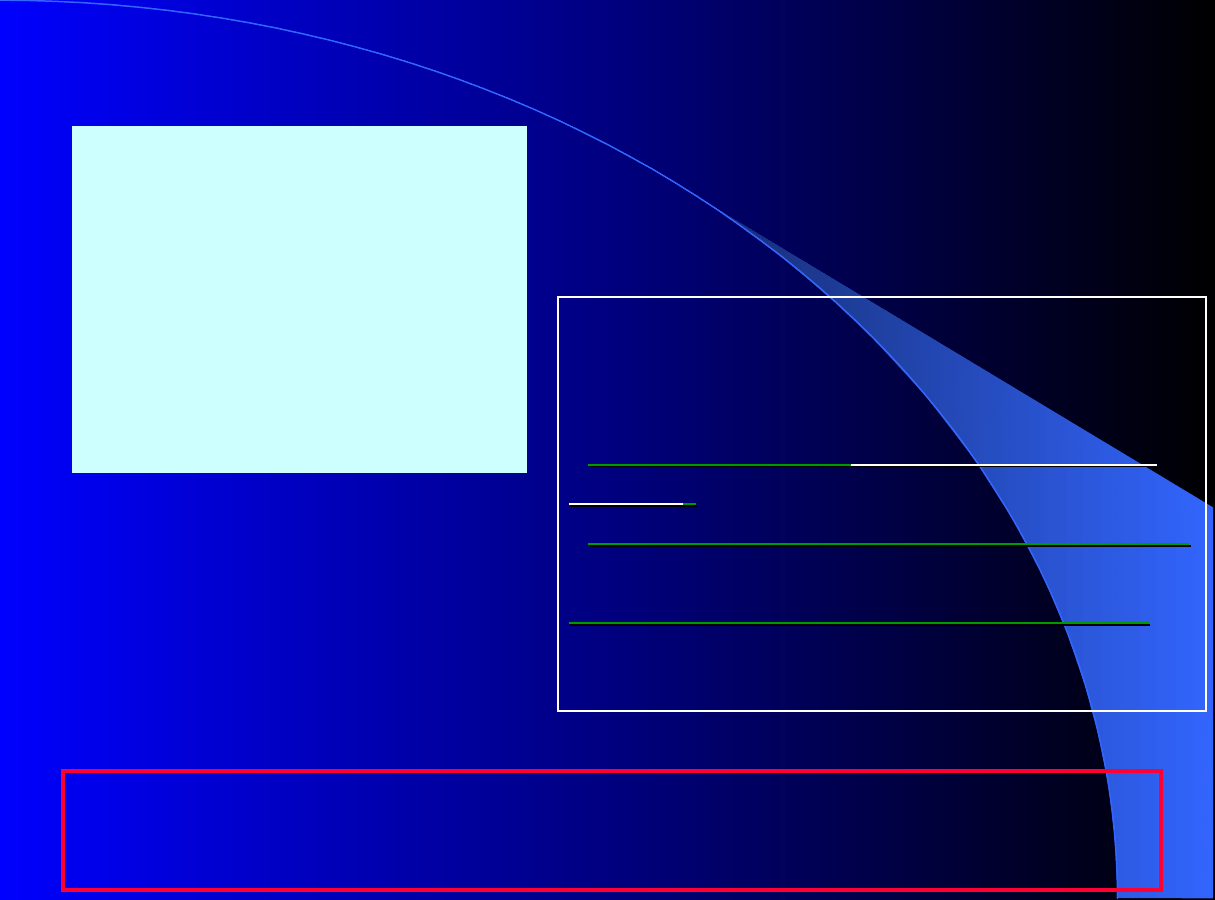
Dynamika adsorpcji i

chromatografii

Proces w kolumnie adsorpcyjnej lub
chromatograficznej z nieruchomym złożem adsorbentu
jest procesem okresowym –

procesem nieustalonym!

Różnice pracy kolumny
okresowej:

oraz
--

chromatograficznej

chromatograficznej

--

adsorpcyjnej

adsorpcyjnej

Dynamika adsorpcji

Matematyczne zależności między istotnymi
dla danego procesu wielkościami nazywa się
modelem dynamiki układu (procesu; aparatu)























pedu

ia

przenoszen

równanie

reakcji

kinetyka

procesu

mika)

(termodyna

statyka

masy

u

transport

kinetyka

masy

(bilanse)

bilans

ciepla

u

transport

kinetyka

ciepla

(bilanse)

bilans

Proces może być ustalony

(1)

lub

nieustalony

(2).

W przypadkach:

•

(2) – procesu

(2) – procesu

nieustalonego w

nieustalonego w

czasie

czasie

;

;

•

–

–

zmiennej powierzchni procesu

zmiennej powierzchni procesu

(

powierzchnia procesu

–

powierzchnia izokoncentryczna

powierzchnia izokoncentryczna

,

to miejsce geometryczne punktów o
jednakowym stężeniu w danej chwili
czasu)

Model

Model

dynamiki procesu

dynamiki procesu

transportu masy

transportu masy

to układ równań

to układ równań

różniczkowych wyrażonych jako

różniczkowych wyrażonych jako

bilanse masy dla sześcianu

bilanse masy dla sześcianu

jednostkowego

jednostkowego

Proces w kolumnie adsorpcyjnej lub chromatograficznej z
nieruchomym złożem adsorbentu jest procesem okresowym –

procesem nieustalonym!

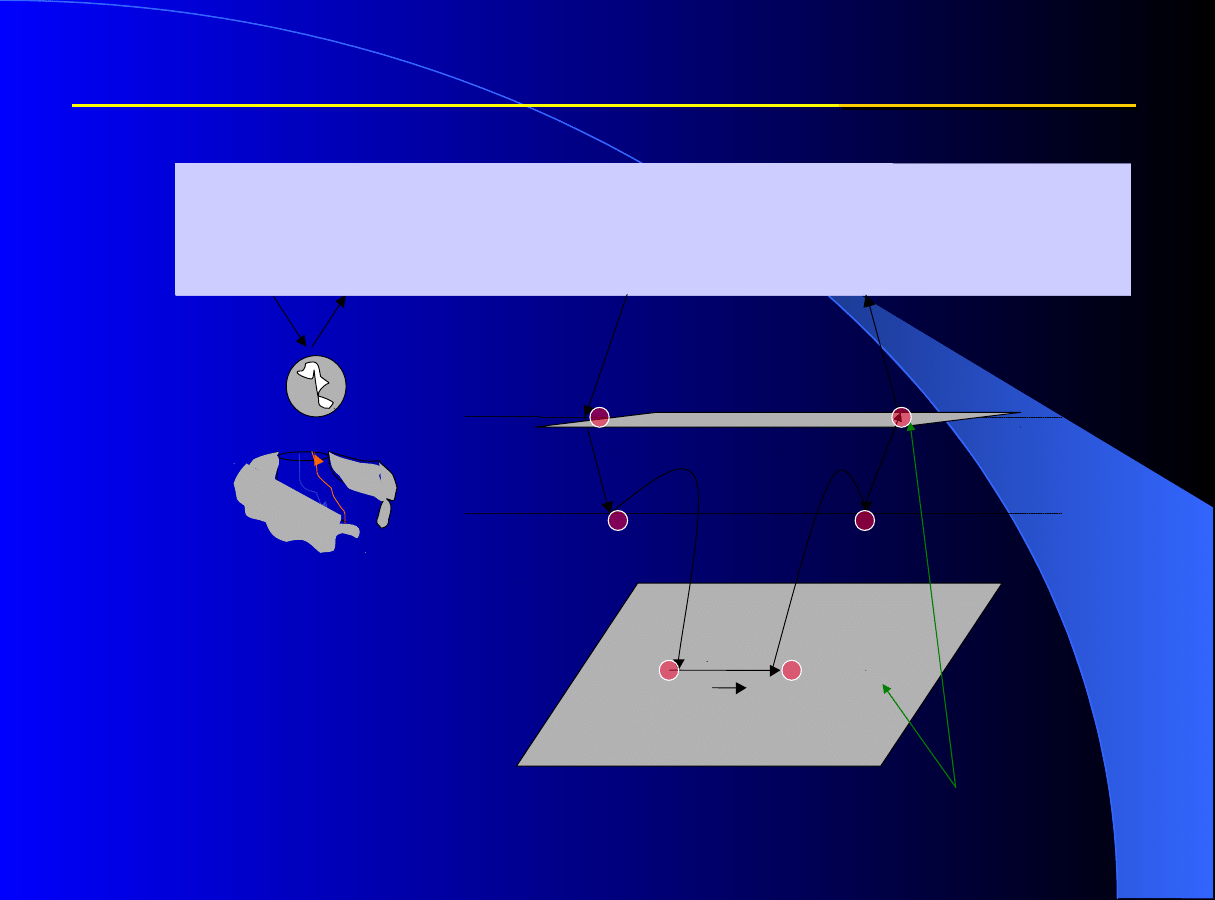
A

B

A

B

A

B

A

B

Powierzchnia

1

2

3

4

5

7

1

7

2,6

Płyn

Konwekcja,
dyspersja

1; 7 dyfuzja zewnętrzna

2; 6 dyfuzja wewnętrzna
3; 5 proces powierzchniowy
adsorpcja- desorpcja
4 dyfuzja powierzchniowa

6

wewnętrzna

zewnętrzna

Proces ogólny nazywany

adsorpcją

adsorpcją

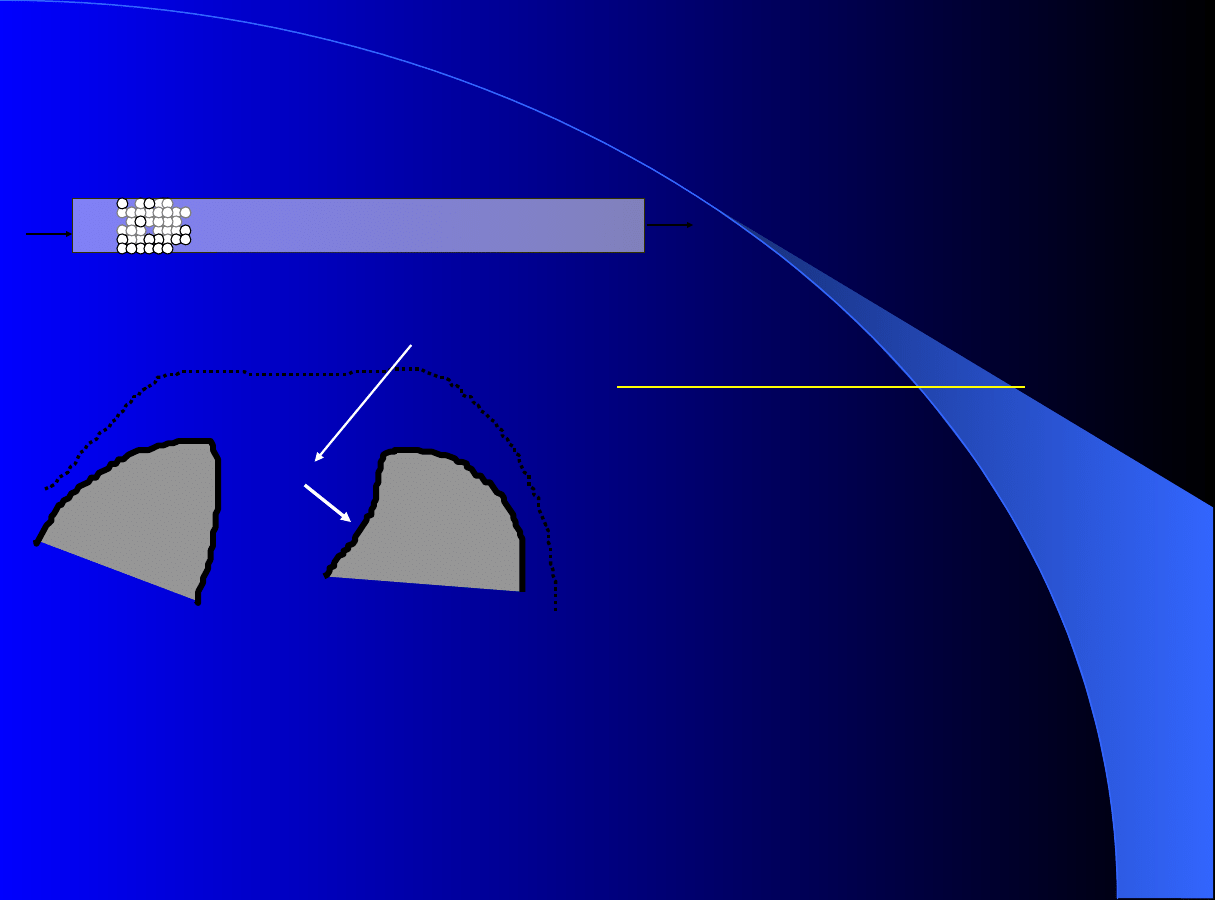
Dynamika adsorpcji

Model ogólny – GR

Model ogólny – GR

(

(

dla Chromatografii

dla Chromatografii

)

)

c

iF

(t)

x = 0

x = L

Założenia upraszczające:
(*) proces jest izotermiczny,
(*) szybkość fazy ruchomej jest stała, jej
ściśliwość jest do pominięcia,
(*) złoże jest upakowane porowatymi
ziarnami

adsorbentu

o

sferycznym

kształcie i ujednoliconej wielkości,
(*)

gradient

stężenia

w

kierunku

promieniowym w aparacie jest do
pominięcia,
(*) dla każdego składnika systemu
istnieje równowaga lokalna pomiędzy
wartością

stężenia

na

powierzchni

adsorbentu a wartością stężenia w
nieruchomym filmie płynu,
(*) wartości współczynników: dyspersji
wzdłużnej oraz przenikania masy w
aparacie są stałe.

Solid phase

Bondary Layer

R

p

c

pi

c

i

q

*

i

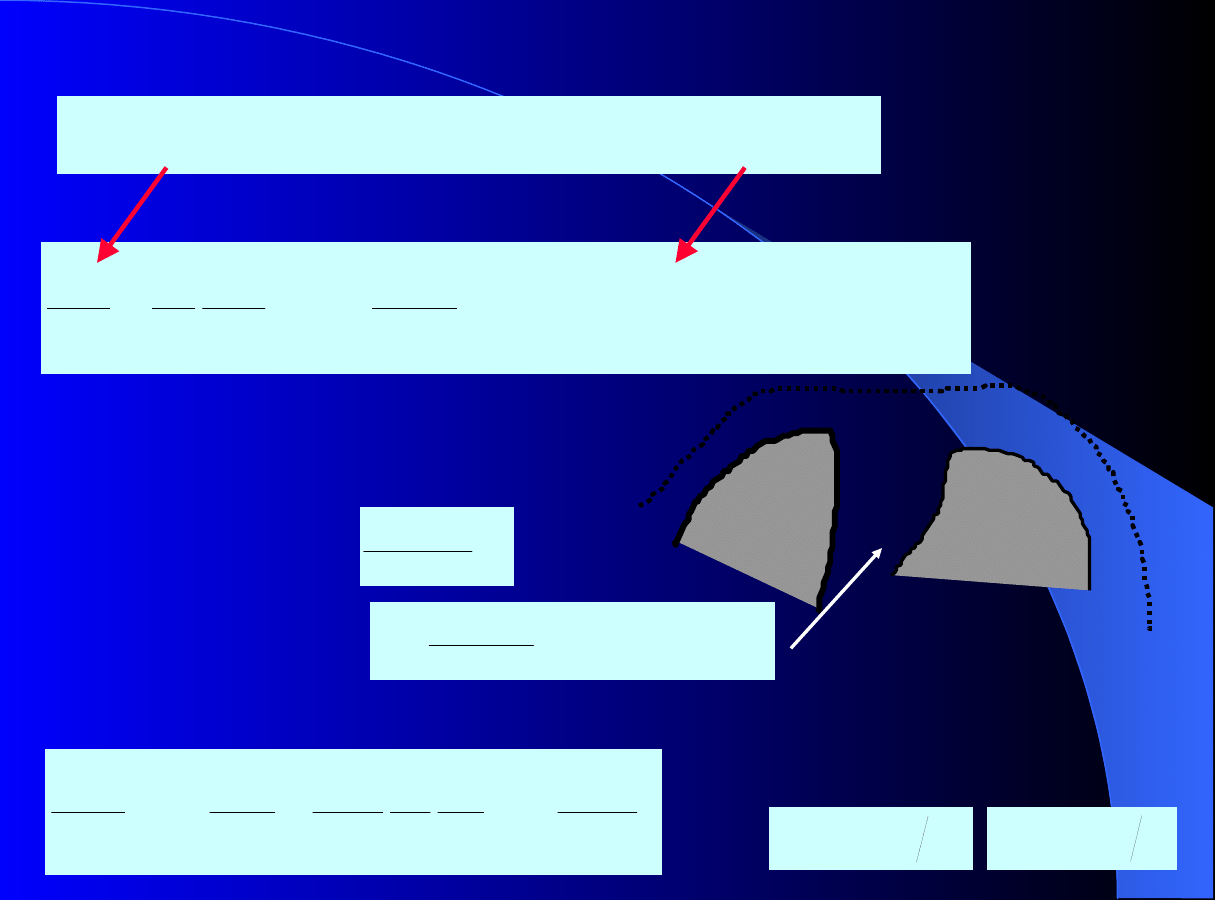
Bilans masy dla

Bilans masy dla

i

i

-tego sk

-tego sk

ł

ł

adnika w fazie ruchomej:

adnika w fazie ruchomej:





)

(

2

2

p

pi

i

p

i,

ext

i

L

i

e

i

R

r

c

c

a

k

'

F

x

c

D

x

c

u

t

c

























Bilans mas

Bilans mas

y

y

w nieruchomym filmie p

w nieruchomym filmie p

łynu w porach:

łynu w porach:



















r

c

r

r

r

D

t

q

"

F

t

c

pi

p

effi

i

pi

















2

2

1

gdzie:

 

;

1

e

e

'

F









 

p

p

''

F







 1

Solid phase

Bondary Layer

D

effi

c

i

( , )

( , )

,

c

t r

pi

D

k

c c

t r

ext i i

pi

eff

r

�

�

�

�

�

�

�

�

=

-

( , )

0

c

t r

pi

r

�

�

=

dla

t > 0; r = 0 oraz

Model ogólny – GR

Model ogólny – GR

(

(

dla Chromatografii

dla Chromatografii

)

)

c.d.

c.d.

ubytekskl.

akumulacja

natezenie

natezenie

doplywu skl.

odplywu skl.

w wyniku reakcji

skl.

A

A

A

A

�

� �

� �

� �

�

+

=

�

� �

� �

� �

�

�

� �

� �

� �

�

-

Zale

Zale

ż

ż

no

no

ść

ść

mi

mi

ę

ę

dzy porowato

dzy porowato

ś

ś

ciami uk

ciami uk

ł

ł

adu

adu





t

t

,

,





e

e

,

,





p

p

:

:

p

e

e

t









)

1

( 





gdzie:



t

,



e

,



p

są odpowiednio porowatością całkowitą, zewnętrzną oraz

wewnętrzną układu;

Dyfuz

Dyfuz

y

y

j

j

ność

ność

wewn

wewn

ę

ę

trzna

trzna

obliczana

obliczana

jest nast

jest nast

ę

ę

puj

puj

ą

ą

co:

co:





mi

p

p

mi

p

pi

D

D

D

2

2

2















D

D

ef

ef

jest

efektywnym

jest

efektywnym

wsp

wsp

ół

ół

czynnikiem dyfuzji

czynnikiem dyfuzji

w porach:

w porach:

























C

pi

*

i

si

p

p

pi

effi

c

d

q

d

D

D

D





1

Do równa

Do równa

ń

ń

bilansów masy w modelu GR nale

bilansów masy w modelu GR nale

ż

ż

y do

y do

łą

łą

czy

czy

ć

ć

równani

równani

a:

a:

- zależności pomiędzy stężeniem powierzchniowym a stężeniem w płynie w
postaci:

równania kinetycznego lub równania izotermy adsorpcji
w przypadku gdy kinetyka jest szybka:
- warunki początkowe oraz warunki brzegowe całkowania dla

chromatografii.

 

;

p

c

f

q

i



 

;

p

c

f

q

*

i



Model ogólny – GR

Model ogólny – GR

(

(

dla Chromatografii

dla Chromatografii

)

)

c.d.

c.d.

Dynamika adsorpcji









R

r

s

c

c

p

c

c

,

p

sc

c

c

c

,

p

k

w

c

*

Lc

c

e

c

T

T

a

c

'

F

T

T

c

d

x

T

D

x

)

T

(

u

t

T





































4

2

2

Model ogólny – GR

Model ogólny – GR

(

(

dla

dla

Adsorpcji

Adsorpcji

)

)

uzupełnienie

uzupełnienie

Bilans

Bilans

ciepła

ciepła

w fazie ruchomej:

w fazie ruchomej:

Bilans

Bilans

ciepła

ciepła

w

w

ziarnie adsorbentu

ziarnie adsorbentu

:

:

gdzie: - współczynnik dyspersji wzdłużnej w aparacie dla
transportu ciepła;

c

p,c

- ciepło właściwe płynu;



c

-

gęstość płynu

;



c

-

współczynnik wnikania ciepła od płynu do powierzchni adsorbentu;



w

-

współczynnik wnikania ciepła od płynu do ściany aparatu

; T

c

-

temperatura cieczy

; T

s

-

temperatura zewnętrznej powierzchni

adsorbentu;

T

sc

- temperatura ściany;

d

k

-

średnica aparatu.

D

Lc

*

t

q

c

H

r

T

r

r

T

c

t

T

s

s

,

p

s

s

s

s

,

p

,

es

s















































2

2

2

0

gdzie:



es0

- efektywny współczynnik przewodzenia ciepła w ziarnie;

c

p,s

-

ciepło właściwe ciała stałego;



s

-

gęstość ziarna

;



H -

ciepło

adsorpcji.

+ warunki początkowe oraz warunki brzegowe całkowania dla adsorpcji.

Dynamika adsorpcji

W rozdz. VII pkt 7.4 cytowanej poniżej książki - podano
rozwiązania analityczne modelu

dynamiki ad

dynamiki ad

sorpcji

sorpcji dla

wybranego aparatu i odpowiednich, założonych uproszczeń
modelu.
Takie analityczne rozwiązania modelu pozwalają poznać jak
zachowa się proces w odpowiedzi na konkretny sygnał wlotowy –

mimo tego, że są to w większości przypadków rozwiązania za
mało dokładne!

Dynamika adsorpcji

Rozwiązania analityczne modelu dynamiki adsorpcji

Rozwiązania analityczne modelu dynamiki adsorpcji

R. Petrus; G. Aksielrud; J. Gumnicki; W. Piątkowski – „ Wymiana masy w układzie ciało
stałe – ciecz” , podrozdz. 7.2.3.

Proces nazywany

adsorpcją

adsorpcją jest procesem złożonym z

szeregowo – równoległych procesów cząstkowych. Należy szukać
i stawiać hipotezę

mechanizmu

mechanizmu tego procesu dla każdego,

badanego przypadku. Jednym z punktów tej hipotezy jest
założenie, który z procesów cząstkowych jest natychmiastowy,
szybki, a który wolny, bardzo wolny – czyli który z procesów jest
„

mechanizmem kontrolującym

mechanizmem kontrolującym” szybkość

procesu ogólnego

procesu ogólnego.

W adsorpcji oraz chromatografii wszystkie kombinacje,

który z procesów cząstkowych kontroluje szybkość ogólną

procesu są możliwe. Za pomocą modelu GR oraz różnych

zakładanych mechanizmów sorpcji można interpretować

dane doświadczalne, weryfikować hipotezę mechanizmu i

oceniać dokładność modelu.

Dynamika adsorpcji

Na

ogólną szybkość procesu adsorpcji

ogólną szybkość procesu adsorpcji mogą mieć wpływ

szybkości następujących etapów:

1. wnikania masy adsorptywu A od płynu do zewnętrznej

powierzchni adsorbentu (

dyfuzji zewnętrznej

dyfuzji zewnętrznej),

2. dyfuzji adsorptywu poprzez porowatą strukturę adsorbentu do

wnętrza ziarna (

dyfuzji wewnętrznej

dyfuzji wewnętrznej),

3. adsorpcji składnika A na powierzchni adsorbentu (

procesu

procesu

powierzchniowego adsorpcja-desorpcja

powierzchniowego adsorpcja-desorpcja).

Kinetyka procesu





)

(

p

pi

i

p

i,

ext

A

R

r

c

c

a

k

'

F

'

N







Szybkość

dyfuzji zewnętrznej

dyfuzji zewnętrznej

–

wnikania masy

w płynie na zewnątrz ziarna

R. Petrus; G. Aksielrud; J. Gumnicki; W. Piątkowski – „ Wymiana masy w układzie ciało
stałe – ciecz” , podrozdz. 7.2.3.

















r

c

r

r

r

D

'

N

pi

p

effi

A









2

2

1

Szybkość

dyfuzji wewnętrznej

dyfuzji wewnętrznej

– dyfuzji w porach ziarna adsorbentu

Szybkość

procesu powierzchniowego

procesu powierzchniowego

adsorpcja- desorpcja

)

(

1

1

S

A

k

k

S

A

-





i

i

i

i

pi

i

A

q

k

)

q

q

(

c

k

'

N

1

1

















i

*

pi

ri

i

q

q

c

K

k

i









)

1

(

1

To są przykłady zapisu równań szybkości poszczególnych

procesów cząstkowych w zapisie z

Modelu ogólnego– GR

Modelu ogólnego– GR

(

(

dla

dla

chromatografii

chromatografii

)

)

Przypadek podany dla Langmuira!

Dynamika adsorpcji

Dynamika adsorpcji

Zaletą modelu GR jest możliwość analizowania na jego
podstawie wpływu prawie wszystkich

oporów transportu

oporów transportu

masy

masy

występujących

w

dynamice

dynamice

adsorpcji

adsorpcji

lub

chromatografii

chromatografii

. Jednocześnie model GR jest relatywnie

skomplikowany

a

rozwiązanie

numeryczne

wymaga

stosunkowo długiego czasu komputerowego obliczeń.
W praktyce, w budowie

modelu dynamiki

modelu dynamiki

adsorpcji

adsorpcji

lub

lub

chromatografii

chromatografii

bardzo często stosuje się uproszczenia

modelu GR, które mają w określonych warunkach podobną
dokładność opisu. Rozwiązania tych uproszczonych modeli są
wystarczające do opisu rzeczywistości

adsorpcji

adsorpcji

lub

chromatografii

chromatografii

, ale otrzymuje się je znacznie szybciej.

Model Równowagowo-

Model Równowagowo-

D

D

yspersyjny

yspersyjny

(ED)

(ED)

Z

Z

a

a

ł

ł

o

o

ż

ż

enia upraszczaj

enia upraszczaj

ą

ą

c

c

e:

e:

(*) wszystkie opory procesów cząstkowych ruchu masy „ukryte” w D

a

,

(*) układ osiąga równowagę termodynamiczną procesu

powierzchniowego praktycznie natychmiast.

R

R

óż

óż

niczkowy bilans masy dla

niczkowy bilans masy dla

i

i

-tego sk

-tego sk

ł

ł

adnika w

adnika w

fazie ruchomej:

fazie ruchomej:

2

2

x

c

D

x

c

w

t

q

F

t

c

m

i

a

m

i

*

i

m

i



























;

1

t

t

F













;

2

N

a

D

L

w

a



(6)

gdzie:

t

u

w





Dynamika chromatografii

Modele uproszczone

Model Kinetyczno-Dyspersyjny

Model Kinetyczno-Dyspersyjny

(

(

TD

TD

)

)

2

2

x

c

D

x

c

w

t

q

F

t

c

i

t

L

e

i

i

i



























R

R

óż

óż

niczkowy bilans masy dla

niczkowy bilans masy dla

i

i

-tego sk

-tego sk

ł

ł

adnika w fazie

adnika w fazie

ruchomej:

ruchomej:

(7)

Kinetyka zewnętrznego i wewnętrznego transportu masy a także kinetyka

procesu powierzchniowego adsorpcja-desorpcja są przedstawione łącznie za
pomocą równania szybkości procesu:

)

(

*

i

i

mi

i

q

q

k

t

q









gdzie:

k

mi

jest zastępczym współczynnikiem przenikania masy

(8)

Model

Model

Reakcyjno-Dyspersyjny

Reakcyjno-Dyspersyjny

(

(

RD

RD

)

)

i

i

i

i

pi

i

i

q

k

q

q

c

k

t

q

1

1

)

(

















(9)

gdzie: jest pojemnością adsorbentu (maksymalnym pokryciem złoża
miejscami aktywnymi);

jest stałą równowagi

adsorpcyjnej:





i

*

pi

ri

i

q

q

c

K

k

i









)

1

(

1

i

i

ri

k

k

K

1

1









i

q

Model

Model

Idealny

Idealny

(I

(I

D

D

)

)

0







x

c

w

t

q

F

t

c

i

*

i

i













(10)

Bilans masowy tego modelu jest

Bilans masowy tego modelu jest

nast

nast

ę

ę

puj

puj

ą

ą

cy:

cy:

MODELE DYSKRETNE

MODELE DYSKRETNE

–

–

Model Craiga

Model Craiga

Równanie bilansu masowego w modelu Craiga dla

Równanie bilansu masowego w modelu Craiga dla

i

i

-

-

tego

tego

sk

sk

ł

ł

adnika w

adnika w

j

j

-

-

tym stopniu teoretycznym oraz w

tym stopniu teoretycznym oraz w

k

k

-

-

tym etapie:

tym etapie:





0

1

1

1



















k

j

,

i

k

j

,

i

k

j

,

i

k

j

,

i

q

q

F

c

c

'

'

a

k

k

0

0

c

1

N

N





Związek pomiędzy ilością stopni
teoretycznych N

c

a sprawnością

kolumny N

a

(model ED):

(11)

(12)

PORÓWNANIE ROZWI

PORÓWNANIE ROZWI

Ą

Ą

ZA

ZA

Ń

Ń

ANALITYCZNYCH

ANALITYCZNYCH

MODELI GR ORAZ ED

MODELI GR ORAZ ED

(13)

































































e

p

p

ex

e

eff

e

p

e

a

k

'

F

u

k

k

k

'

F

d

u

D

'

F

d

u

k

k

u

D

L

t

p

L

w

a

D









1

2

1

1

2

2

1

6

60

1

2

2

N

ED

HETP

GR

HETP

2

2

HETP

p

p

d

u

u

d

c

b

a







Równanie Van

Równanie Van

Deemtera

Deemtera

a = 2



2



e

; b = 2



1



e

D

m

;

































eff

e

'

D

F

k

k



60

1

1

2

2

1

1

c

(14)

gdzie:

PORÓWNANIE ROZWI

PORÓWNANIE ROZWI

Ą

Ą

ZA

ZA

Ń

Ń

ANALITYCZNYCH

ANALITYCZNYCH

MODELI GR

MODELI GR

ORAZ

ORAZ

T

T

D

D

(15)

m

'

t

e

'

'

e

L

k

k

u

k

k

u

D

0

2

0

0

1

2

2

TD

HETP

GR

HETP











































eff

p

'

e

t

m

D

d

F

k

60

1

2

1





A

2

0

0

2

1

1

0

1

1

1































'

'

'

k

k

k

k

k

A

Porównując równania (14) oraz (15) otrzymuje się (16):

(16)

gdzie:

)

(

*

i

i

mi

i

q

q

k

t

q









(8)

PRZYK

PRZYK

Ł

Ł

AD ZASTOSOWANIA ZMODYFIKOWANEGO MODELU GR

AD ZASTOSOWANIA ZMODYFIKOWANEGO MODELU GR

(*) opór wnikania masy na zewnątrz ziarna dąży do 0,

(*) opór dyfuzji powierzchniowej dąży do 0 – r-nie (3) przechodzi w
postać (17),

(*) z uwagi na wielowarstwową adsorpcję porowatość wewnętrzna
złoża 

p

jest

zmienna i zależy od stężenia składnika chromatografowanego
wewnątrz porów.

Równanie na efektywny wspó

Równanie na efektywny wspó

ł

ł

czynnik dyfuzji w porach:

czynnik dyfuzji w porach:

 































r

c

D

c

D

p

p

p

p

eff







(17)

Z

Z

ale

ale

ż

ż

no

no

ść

ść





p

p

od st

od st

ęż

ęż

enia sk

enia sk

ł

ł

adnika chromatografowanego:

adnika chromatografowanego:

 

pi

p

p

p

t

p

p

c

c

a











0

1











(18)

Dodatkowe z

Dodatkowe z

a

a

ł

ł

o

o

ż

ż

enia

enia

mechanizmu sorpcji

mechanizmu sorpcji

upraszczaj

upraszczaj

ą

ą

c

c

e

e

model GR:

model GR:

(*) budowa przestrzenna wypełnienia kolumny monolitycznej składa się
z cylindrycznych porów połączonych ze sobą,

0 . 0 0

0 . 0 5

0 . 1 0

0 . 1 5

0 . 2 0

0 . 2 5

0 . 3 0

0 . 3 5

0 . 0

0 . 2

0 . 4

0 . 6

0 . 8

1 . 0

1 . 2

1 . 4

1 . 6

1 . 8

2 . 0

2 . 2

2 . 4

H

E

P

T

[

c

m

]

*

1

e

-

3

u [c m / s ]

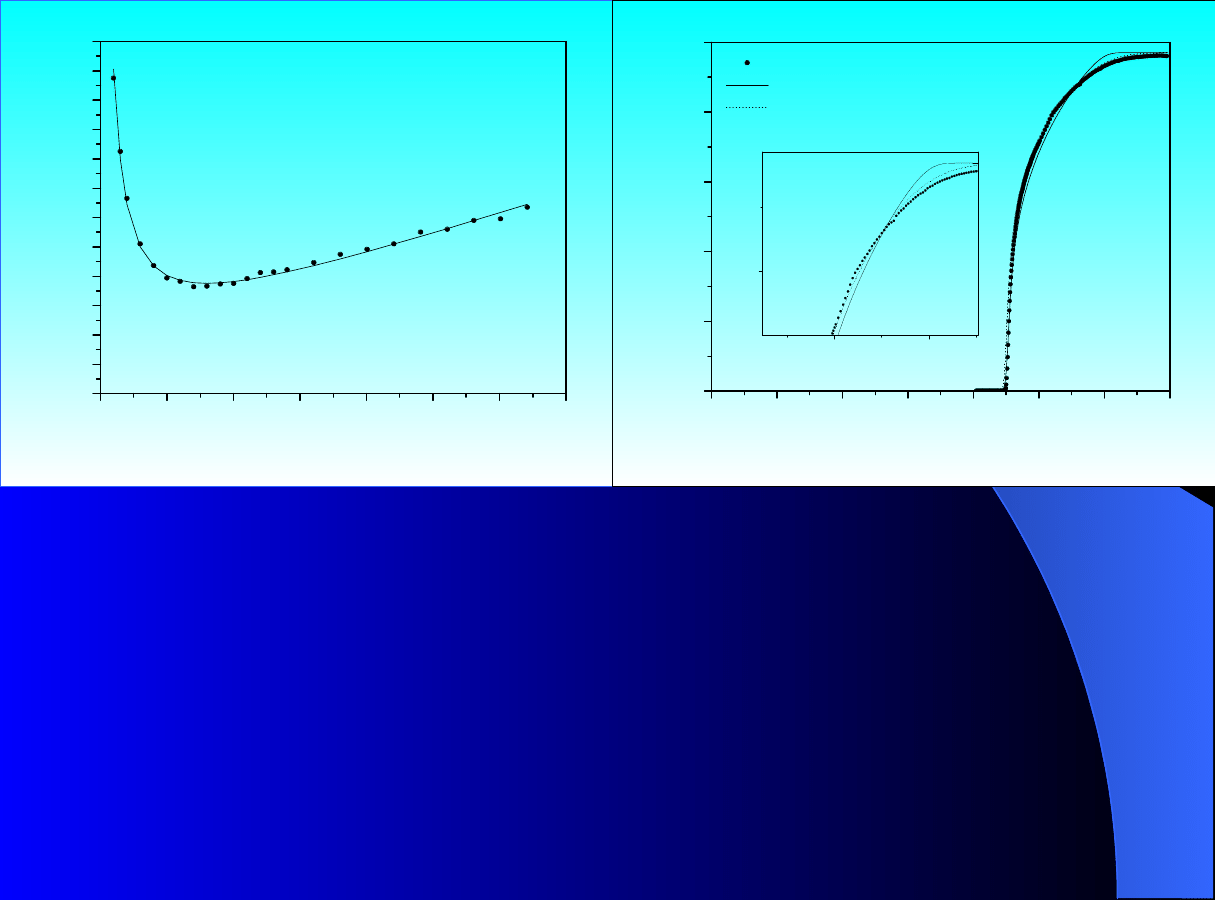
Rys.1.

Porównanie

doświadczalnego

przebiegu

krzywej

Van

Deemtera

oraz

wyników

symulacji

symulacji

modelem

modelem

GR

GR

w przypadku gdy parametry

w przypadku gdy parametry

modelu

zależą

od

zmian

modelu

zależą

od

zmian

porowatości wewnętrznej

porowatości wewnętrznej





p

p

–

linia ciągła. Otrzymano metodą
impulsu przy plateau c = 0
[g/dm

3

] dla benzoesanu butylu,

faza ruchoma 65% vol. roztwór
MeOH w wodzie; punkty –
doświadczenie, linia – symulacja

0

1 0 0

2 0 0

3 0 0

4 0 0

5 0 0

6 0 0

7 0 0

0

2

4

6

8

1 0

5 0 0

6 0 0

8

c

[

g

/d

m

3

]

t [s ]

e x p . d a ta
s i m u la ti o n a )
s i m u la ti o n b )

c

[

g

/d

m

3

]

t [s ]

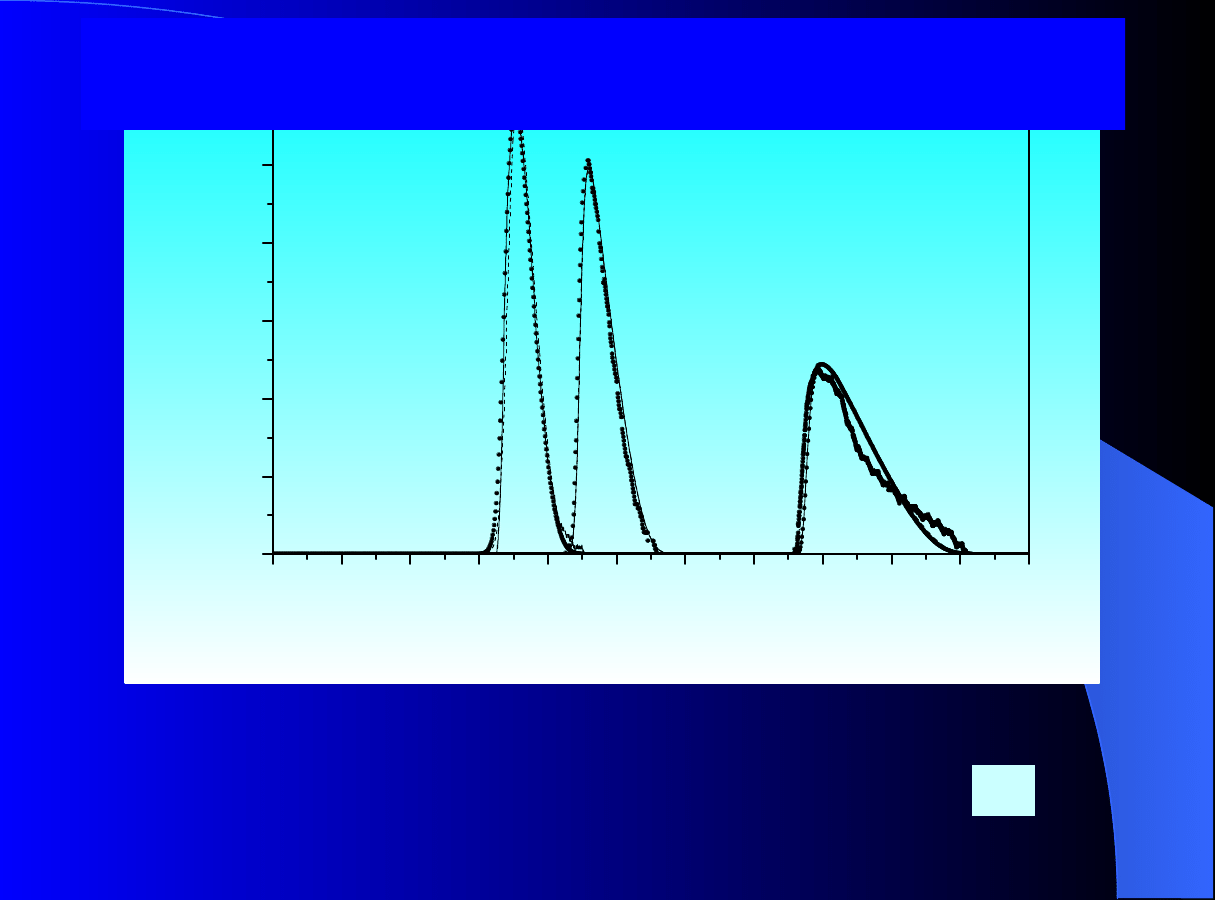
Rys.2.

Porównanie

doświadczalnego

profilu

stężenia (punkty) benzoesanu
butylu oraz wyniku symulacji
modelem

GR

w

dwóch

przypadkach gdy:
a)

parametry modelu nie

parametry modelu nie

zależą od zmian porowatości

zależą od zmian porowatości

wewnętrznej

wewnętrznej





p

p

– linia ciągła;

oraz

b)

b)

parametry modelu zależą

parametry modelu zależą

od

zmian

porowatości

od

zmian

porowatości

wewnętrznej

wewnętrznej





p

p

–

linia

–

linia

przerywana

przerywana

0

mod

c

0

100

200

300

400

500

600

700

800

900

1000

1100

0.0

0.2

0.4

0.6

0.8

1.0

1.2

C

3

2

1

c

[m

ol

/c

m

3

]

1

0

5

t [s]

Rys.3. Porównanie doświadczalnego profilu stężenia (punkty) cholanu metylu
oraz

wyników

symulacji

dla

następujących

stężeń:

składnika

chromatografowanego
c

f

= 1.89*10

-5

[mol/cm

3

], oraz następujących stężeń modyfikatora eluentu:

= 2.83*10

-3

(1); 2.25*10

-3

(2);1.17 *10

-3

[mol/cm

3

] (3); punkty -

doświadczenie; linia ciągła –

symulacje model

symulacje model

a

a

m

m

i

i

TD oraz GR z

TD oraz GR z

estymowaną wartością współczynnika dyfuzji powierzchniowej

estymowaną wartością współczynnika dyfuzji powierzchniowej

D

D

s.

s.

PRZYK

PRZYK

Ł

Ł

AD

AD

(1)

(1)

ZAST

ZAST

ĄPIENIA

ĄPIENIA

MODELU GR

MODELU GR

MODELEM TD

MODELEM TD

PRZYK

PRZYK

Ł

Ł

AD

AD

(2)

(2)

ZAST

ZAST

ĄPIENIA

ĄPIENIA

MODELU GR

MODELU GR

MODELEM TD

MODELEM TD

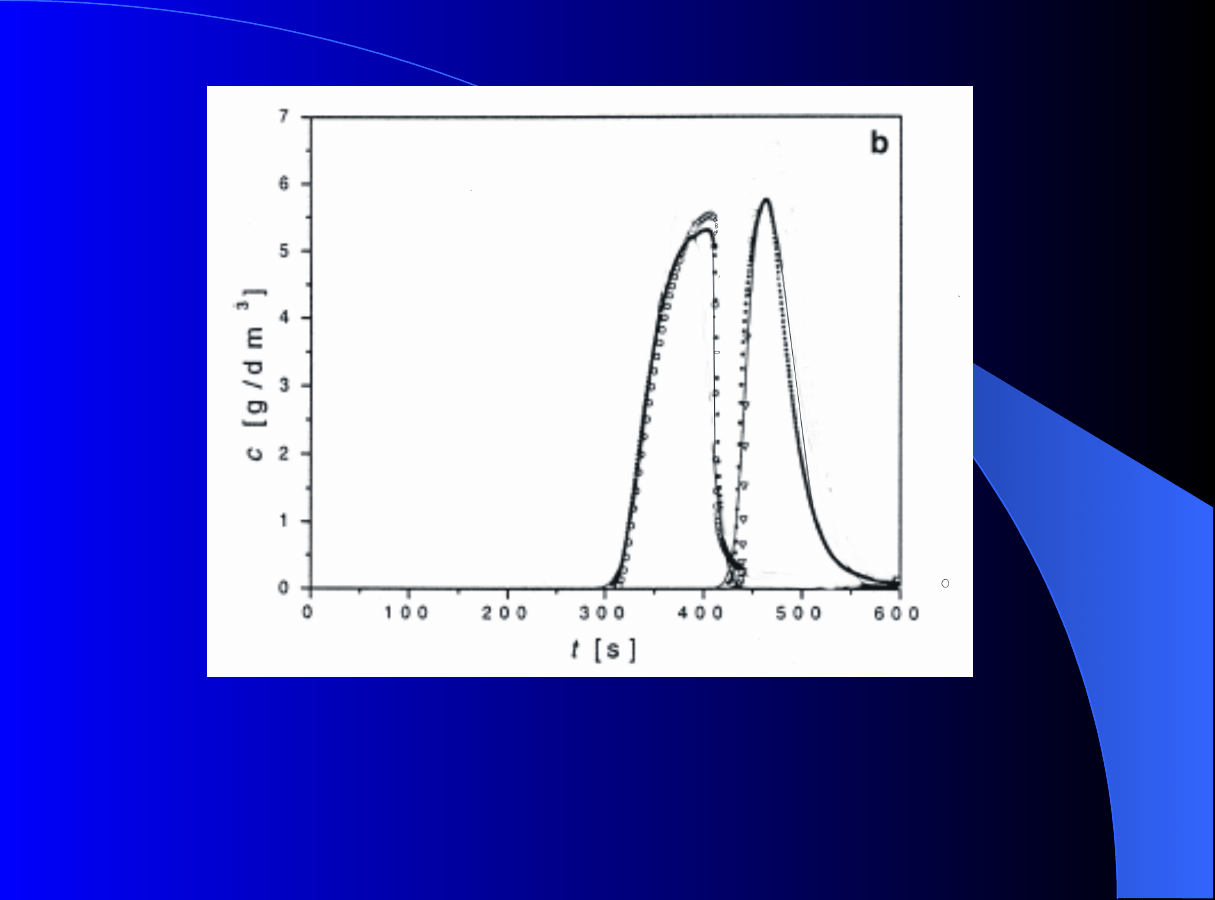
Rys.4. Porównanie pomiędzy danymi doświadczalnymi i symulowanymi
profilami stężenia dla fenetolu oraz benzoesanu propylu. Faza ruchoma:
65%

vol.

roztwór

metanolu

w

wodzie.

D

m

= 4.87 10

-6

[cm

2

/s]; (a) c

0

= 14.496 [g/cm

3

].

Profile stężenia

symulow

symulow

ane za pomocą modeli: GR oraz TD

ane za pomocą modeli: GR oraz TD

z

z

wprowadzoną

wprowadzoną

izotermą konkurencyjną opartą na pojedynczych

izotermą konkurencyjną opartą na pojedynczych

izoterm

izoterm

ach

ach

BET

BET

0

100

200

300

400

500

600

0

200

400

600

800

1000

0

1 0 0

2 0 0

3 0 0

4 0 0

5 0 0

6 0 0

7 0 0

0

2

4

6

8

1 0

1 2

1 4

1 6

1 8

t [s ]

c

[

g

/d

m

3

]

m

A

U

t [s]

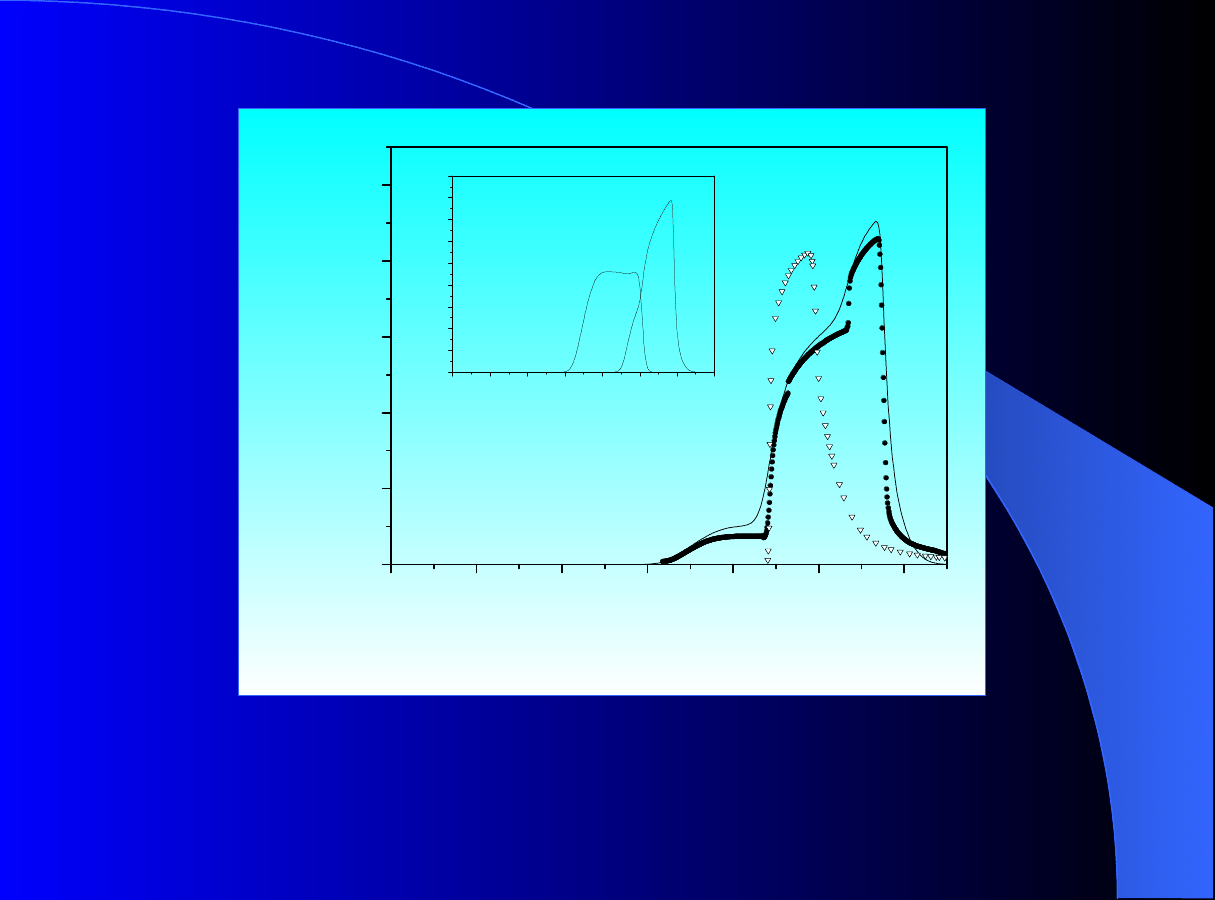
Rys.6. Porównanie danych doświadczalnych z symulowanymi profilami

stężenia dla mieszaniny fenetolu oraz benzoesanu propylu. Profile

symulow

symulow

ane za pomocą

ane za pomocą

modelu TD z wyprowadzoną na podstawie

modelu TD z wyprowadzoną na podstawie

izoterm pojedynczych BET izotermą konkurencyjną

izoterm pojedynczych BET izotermą konkurencyjną

według teorii

według teorii

IAS.

IAS.

C

01

= C

02

= 12.08 [g/cm3];

P

P

RZYKŁAD ZASTOSOWANIA TEORII IAS

RZYKŁAD ZASTOSOWANIA TEORII IAS

P

P

RZYKŁAD ZASTOSOWANIA TEORII AST

RZYKŁAD ZASTOSOWANIA TEORII AST

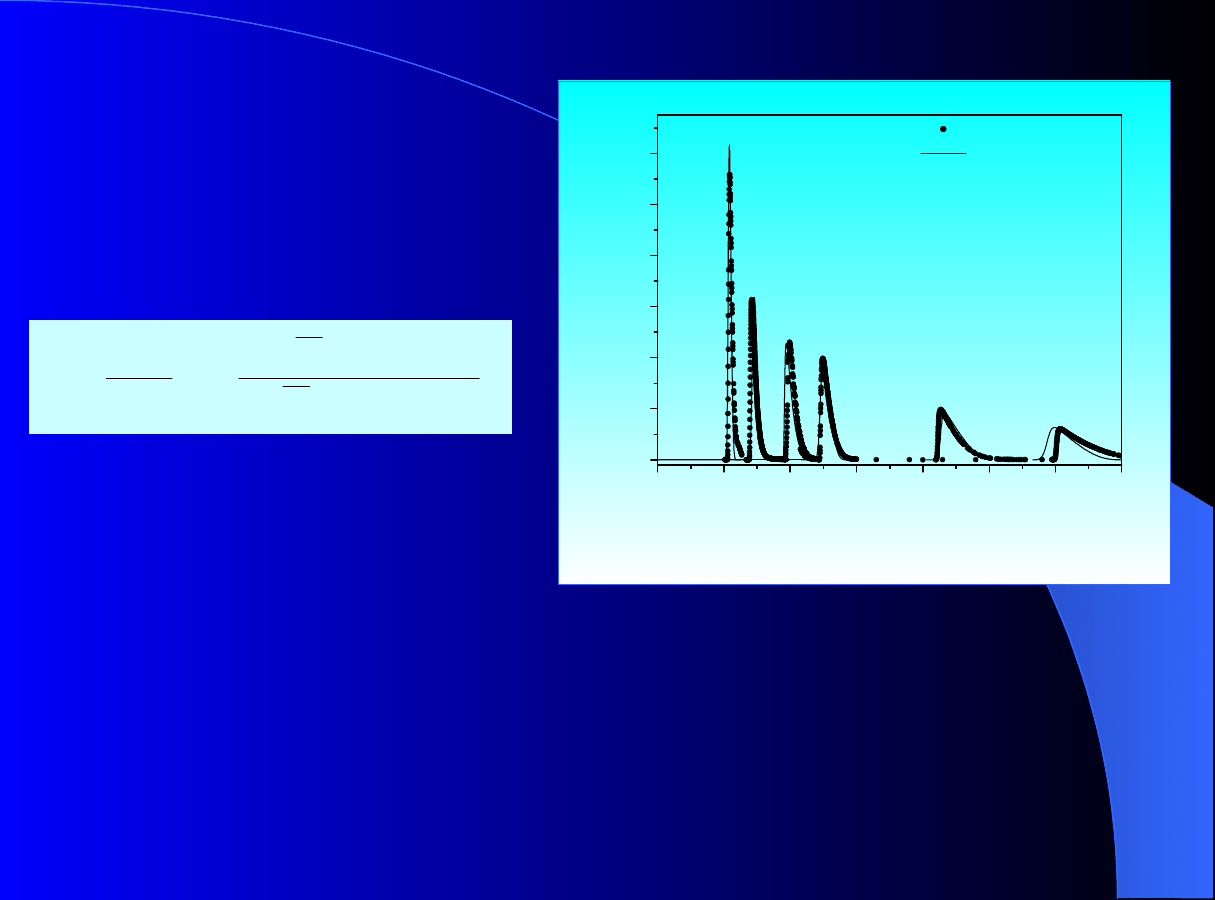
Rys. 7. Porównanie doświadczalnych profili stężenia cyklopentanonu
(C5) rejestrowane przy różnym stężeniu modyfikatora eluentu:
octanu etylu (EA) w fazie ruchomej odpowiednio: x

EA

= 0 (1); 0.066

(2);

0.129

(3);

0.25

(4);

0.364

(5);

1

(6);

eluent EA – n-heksan - z wynikami

symulacji za pomocą

symulacji za pomocą

modelu ED

modelu ED

ze wstawioną izotermą konkurencyjną opartą na

ze wstawioną izotermą konkurencyjną opartą na

teorii AST

teorii AST

otrzymanej

otrzymanej

z

z

nadmiarowych

nadmiarowych

izoterm pojedynczych UNILAN dla

izoterm pojedynczych UNILAN dla

każdego z chromatografowanych składników.

każdego z chromatografowanych składników. Wlotowe stężenie
cyclopentanonu x

C5,F

= 0.053 = const dla wszystkich przebiegów.

0

200

400

600

800

1000

1200

1400

0

1

2

3

4

5

6

C5 - exp.
Unilan isotherm

t [s]

x

A

m

ol

e

ra

tio

*

1e

3

6

4

3

5

2

1

 

 

 























h

a

K

h

a

K

h

2

q

q

i

i

A

*

A

exp

1

exp

1

ln

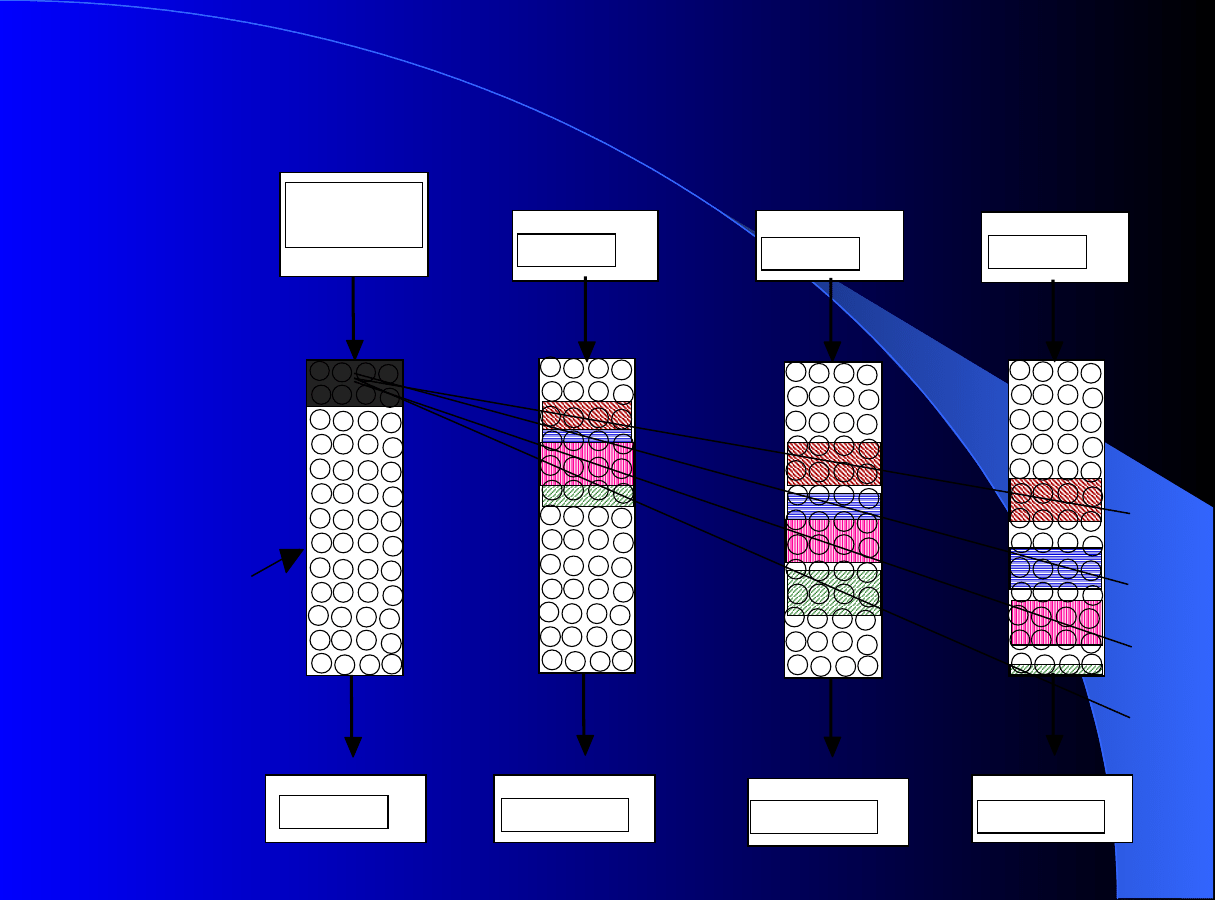
Zasilanie

próbką

Czas: 0

Kolumna

chromatograficzn

a

upakowana

złożem

adsorbentu

Idea chromatografi

Idea chromatografi

i

i

okresow

okresow

e

e

j

j

izokratyczn

izokratyczn

e

e

j

j

Eluent

Czas: 10

Eluent

Czas: 20

Eluent

Czas: 30

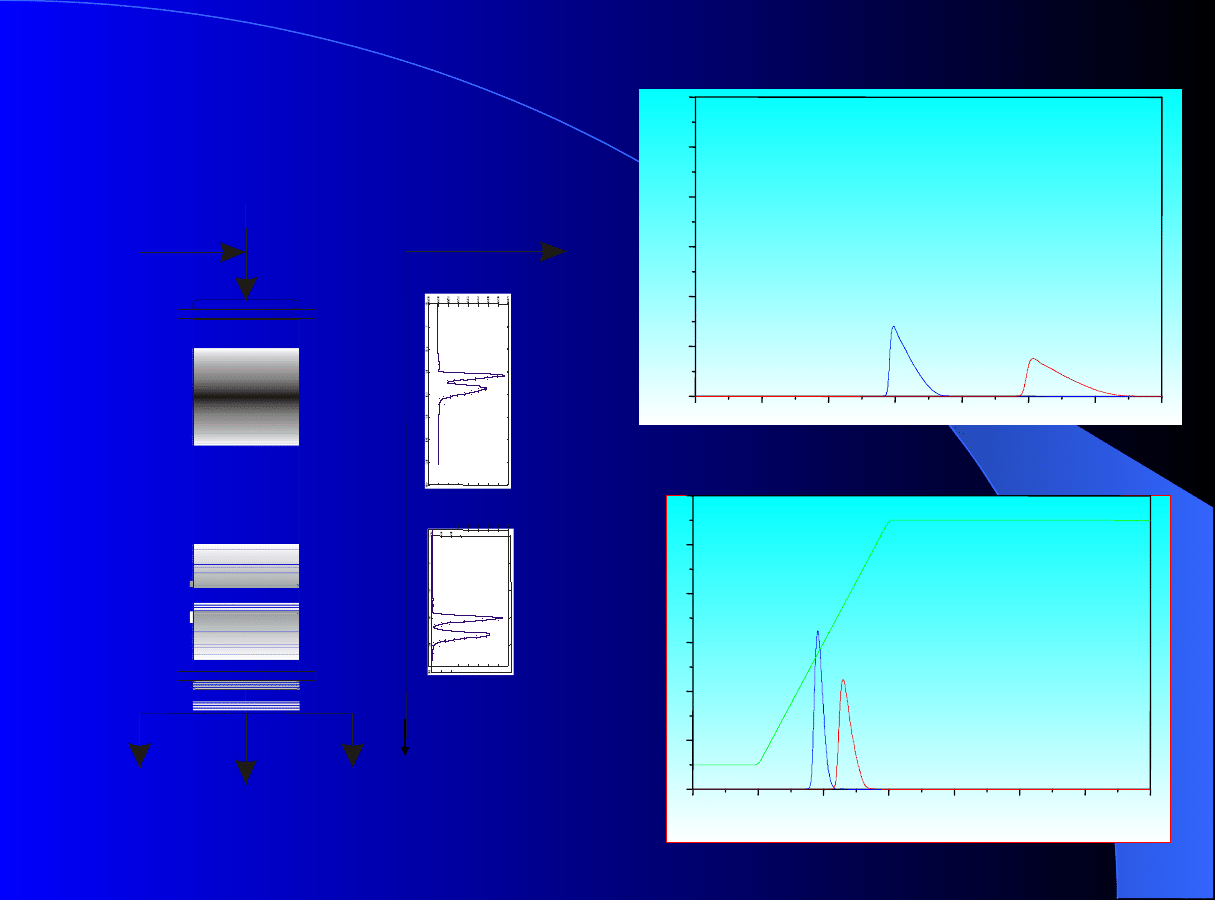
Eluent (E)

(A+E)

(B+E)

,

F

e

e

d

(

A

+

B

)

Efluent

C

H

Chromatografia okresowa

Chromatografia okresowa

0

100

200

300

400

500

600

700

0.0

0.2

0.4

0.6

0.8

1.0

1.2

C

on

ce

nt

ra

tio

n

Isocratic elution

0

100

200

300

400

500

600

700

0.0

0.2

0.4

0.6

0.8

1.0

Time [s]

Gradient elution

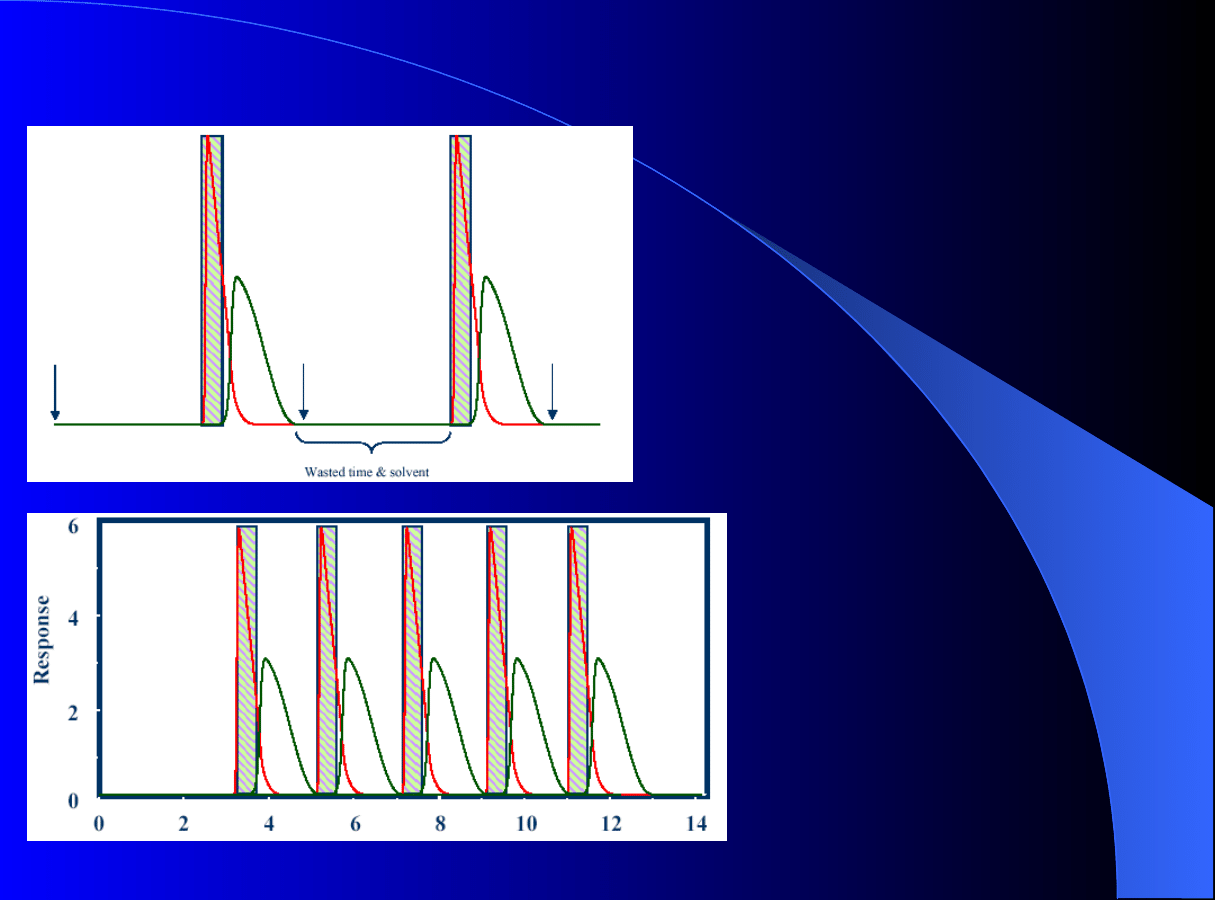
Okresowość a półciągłość procesu chromatografii

Okresowość a półciągłość procesu chromatografii

Chromatografia okresowa

Chromatografia okresowa

Chromatografia cykliczna

Chromatografia cykliczna

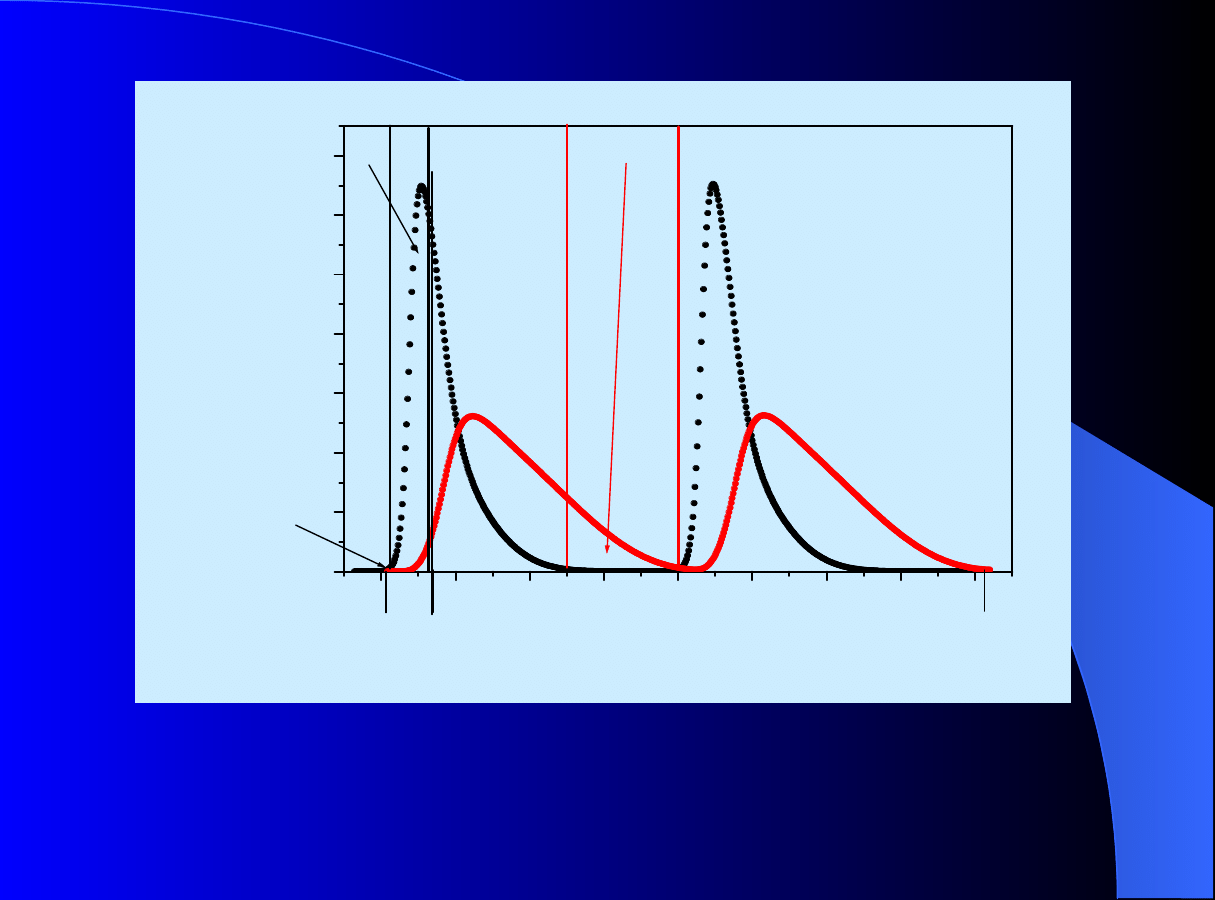
Chromatografia cykliczna

Chromatografia cykliczna

100

120

140

160

180

200

220

240

260

0.0

0.2

0.4

0.6

0.8

1.0

1.2

1.4

t

sII

interfraction

t

eII

II fraction

t

eI

t

end

t

sI

C

treshold

I fraction

C

on

ce

nt

ra

tio

n

[g

/l]

Time [s]

Chromatografia cykliczna

Czas trwania

∆t

c

dla dwóch kolejnych cykli:

∆t

c

= t

end

– t

sI

;

Czas odbioru i-tej frakcji:

∆t

frac

= t

ei

- t

si

ORGANIZACJA PROCEDURY

ORGANIZACJA PROCEDURY

PRZENOSZENIA SKALI

PRZENOSZENIA SKALI

ORAZ

ORAZ

OPTYMALIZACJI

OPTYMALIZACJI

CHROMATOGRAFII

CHROMATOGRAFII

1. Przeprowadzić procedurę budowania modelu dynamiki

chromatografii zaczynając od cyklu badań doświadczalnych na
kolumnie analitycznej:

 Wyznaczyć parametry modelu izotermy.

 Uzyskać wszystkie inne, potrzebne dane fizykochemiczne dla

optymalizowanego, wieloskładnikowego układu
chromatograficznego.

 Wyznaczyć parametry modelu dynamiki procesu. Im bardziej

skomplikowany model dynamiki tym większa ilość parametrów
modelu koniecznych do wyznaczenia.

 Wybrać adekwatny typ modelu dynamiki procesu.

2. Podjąć decyzje dotyczące parametrów optymalizacyjnych. W tym

celu należy:  

 Wybrać funkcję celu oraz składnik kluczowy procesu. Wybrać

ograniczenia i zmienne decyzyjne optymalizacji.

3. Wybrać metodę

optymalizacji

.

c

col

t

i

i

t

F

m







Pr

%

c

V

m

F

,

i

inj

i

i

100

Y 

D

D

efini

efini

cje najczęściej używanych w chromatografii

cje najczęściej używanych w chromatografii

funkcji celu:

funkcji celu:

Pr

EC

elu

V



i

i

i

Y

Pr

Pf 

Zmienne decyzyjne ci

Zmienne decyzyjne ci

ą

ą

g

g

ł

ł

e oraz zmienne decyzyjne

e oraz zmienne decyzyjne

dyskretne optymalizacji

dyskretne optymalizacji

:

:

mod

c











i

col

t

F

,

i

inj

i

,

f

q

V

c

V

L



1

t

wash

parametr

d

p

2

/L

2

0 p

m

max

d

k

L

u

p

p









Ograniczenia procesu

Ograniczenia procesu

optymalizacji

optymalizacji

:

:

min

i

i

Pu

Pu 

2

1

Pu

c

c

c

i

i





produkt

kluczowy

0

200

400

600

800 1000 1200 1400 1600 1800 2000 2200

0.0

0.1

0.2

0.3

0.4

0.5

c

m

[g

/d

m

3

]

t [s]

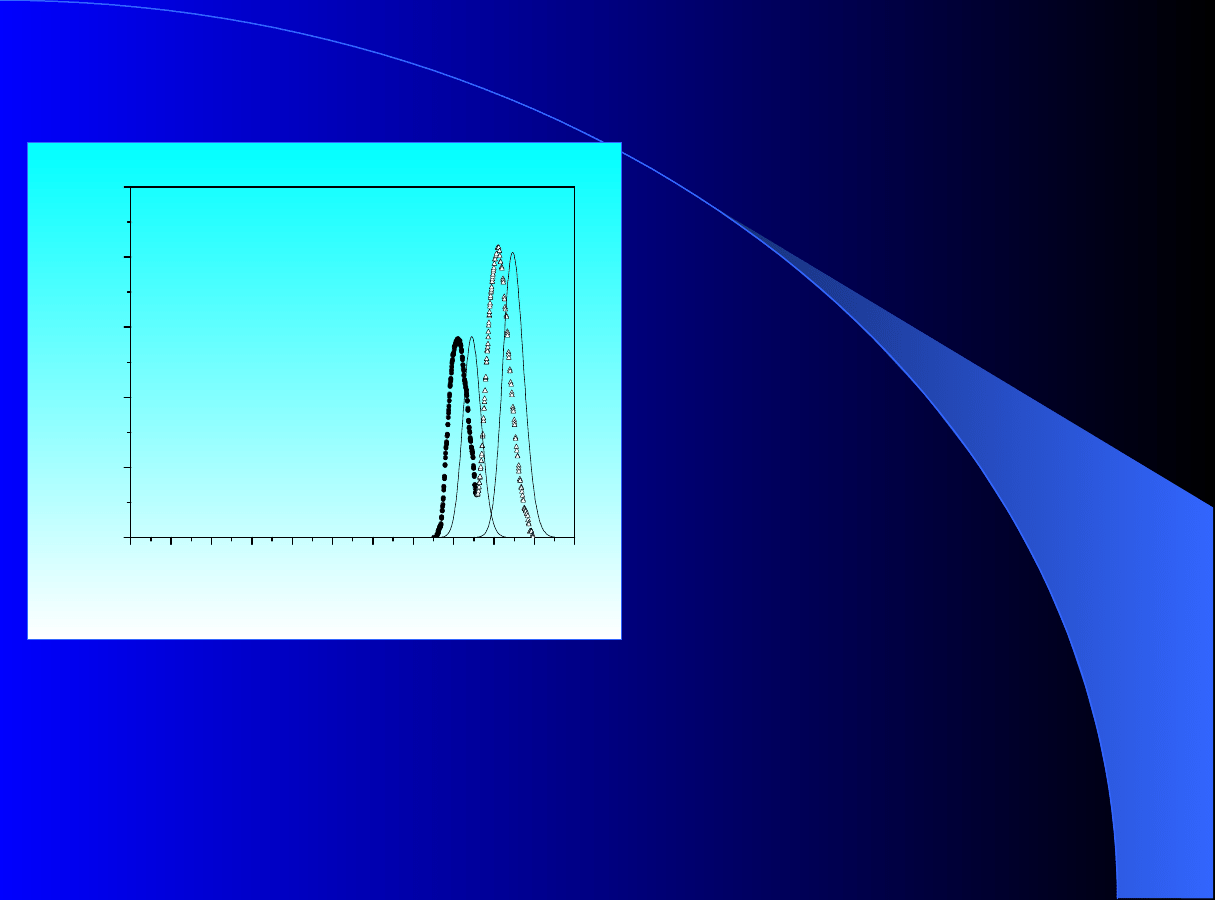
Rys. 11. Przenoszenie skali
chromatografii:

z

z

kolumn

kolumn

y

y





4

4

mm;

mm;

d

d

p

p

=

=

5

5





m

m

na

na

kolumn

kolumn

ę

ę





10

10

mm

mm

;

;

d

d

p

p

=

=

12

12





m

m

.

.

L

L

= 10cm.

= 10cm.

Mieszanina izomerów cis- (C)
oraz
trans- (T) analogów terpenów.

Symulacja modelem ED;

Symulacja modelem ED;

izoterma konkurencyjna

izoterma konkurencyjna

Langmuira

Langmuira

PRZENOSZENIE SKALI CHROMATOGRAFII

PRZENOSZENIE SKALI CHROMATOGRAFII

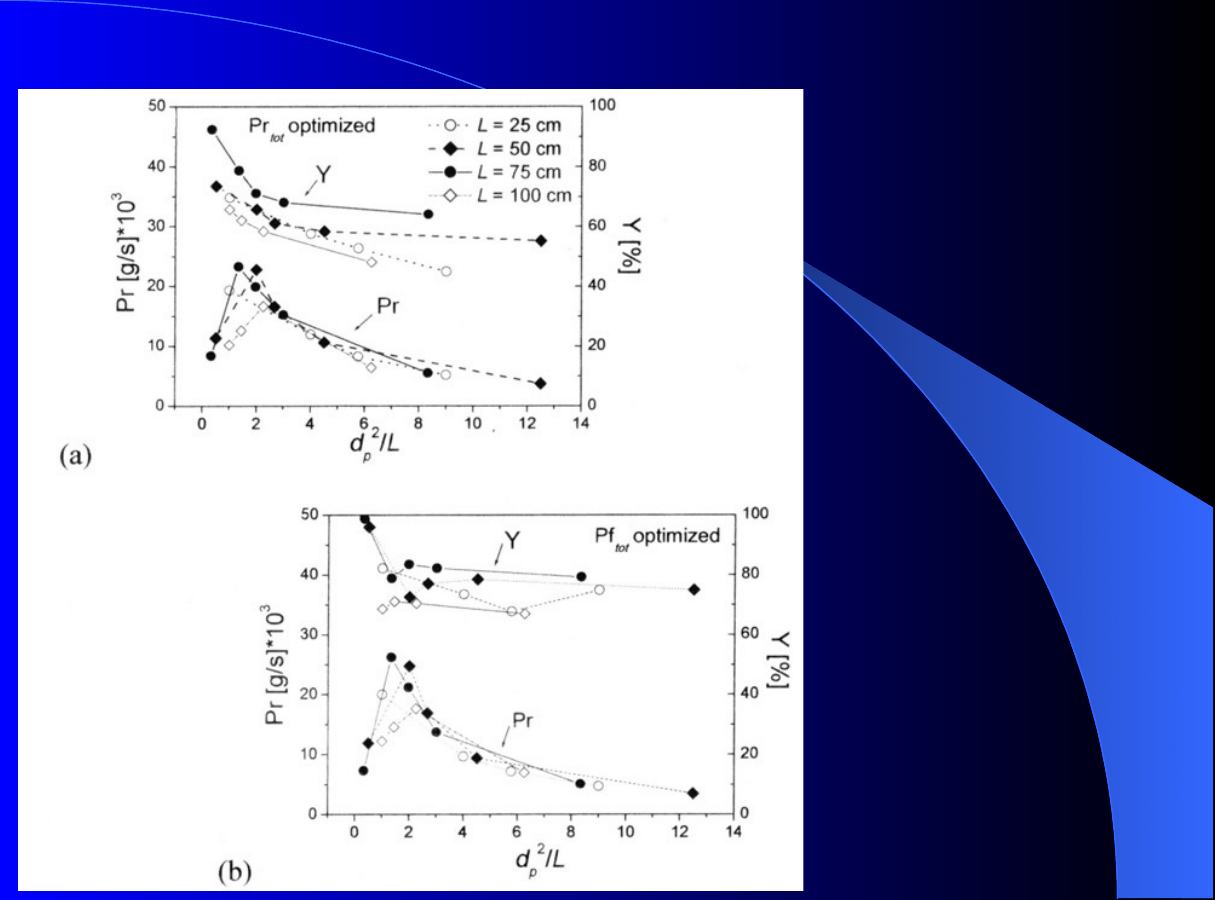
OPTYMALIZACJ

OPTYMALIZACJ

A CHROMATOGRAFII

A CHROMATOGRAFII

Rys. 11. Wyniki
optymalizacji
chromatografii:
Mieszanina izomerów
cis- (C) oraz
trans- (T) analogów
terpenów.

Symulacja modelem

Symulacja modelem

ED; izoterma

ED; izoterma

konkurencyjna

konkurencyjna

Langmuira

Langmuira

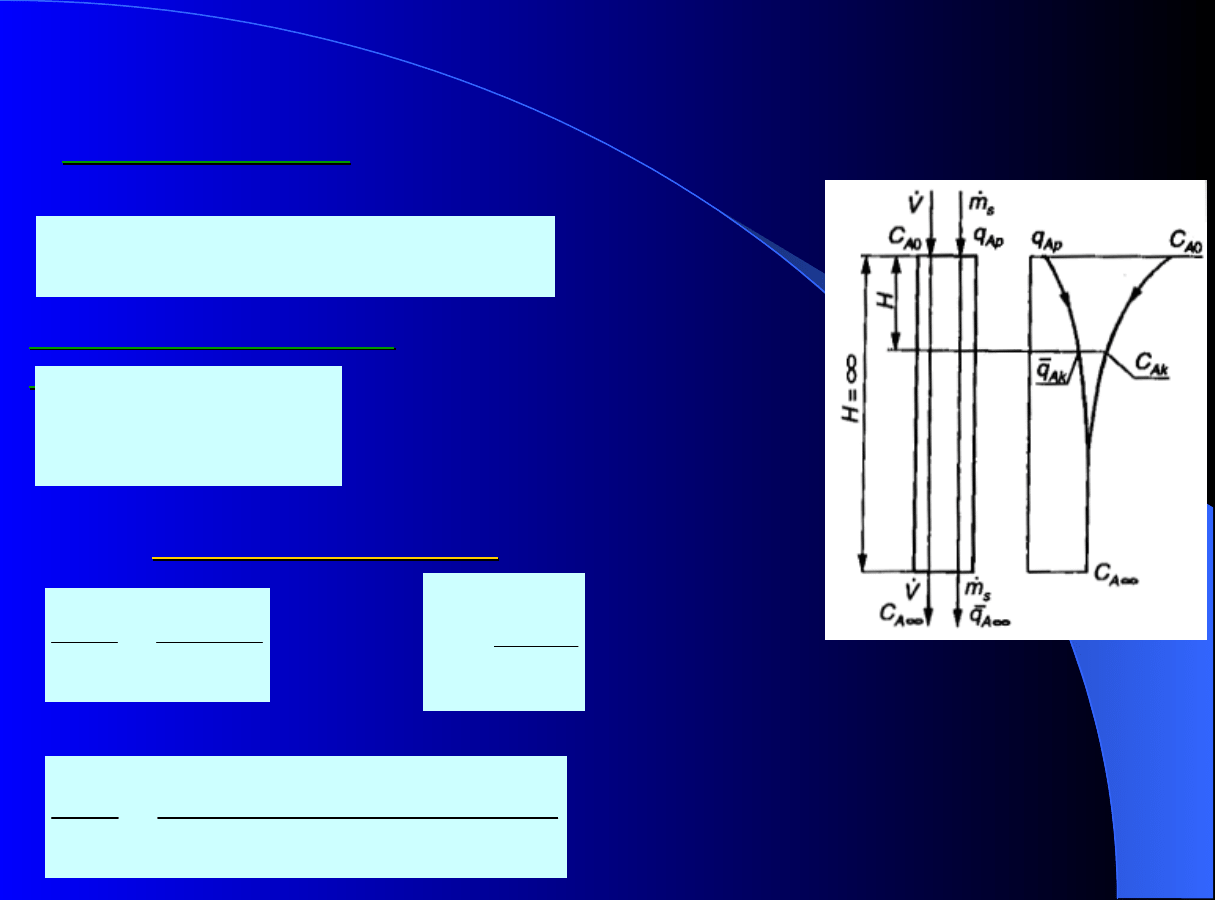
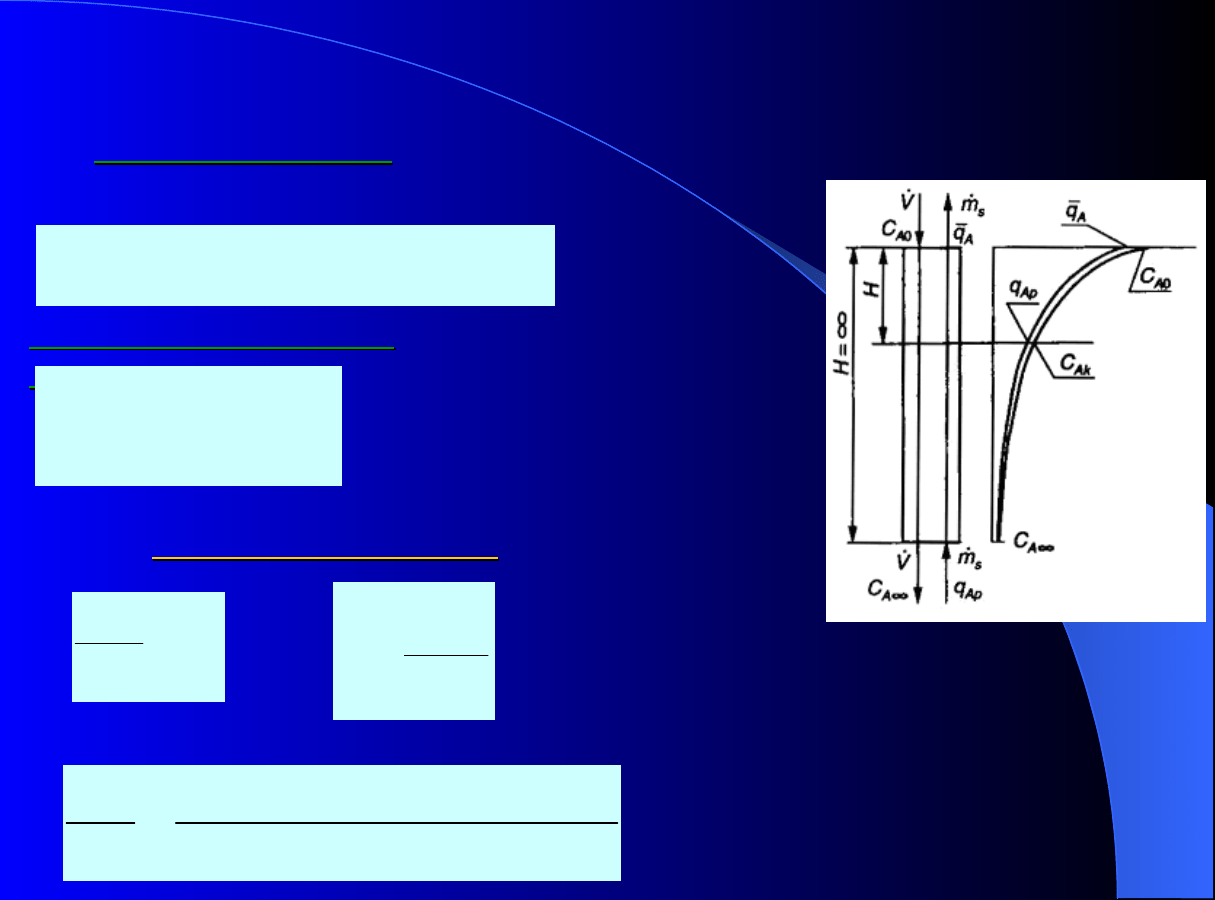
Bila

Bila

ns masowy

ns masowy

dla kolumny od

wlotu do wylotu:

Dynamika adsorpcji ciągłej

Dynamika adsorpcji ciągłej









Ap

Ak

s

Ak

A

A

q

q

m

C

C

V

m















0

S

S

zybko

zybko

ść

ść

transportu

transportu

masy

masy

:

:









A

A

s

z

A

A

A

z

A

*

C

C

A

k

m

*

C

C

k

'

N











Wynik dla

izotermy liniowej

izotermy liniowej

oraz dla



k



C
C

Ak

A0

1

1







'

Adsorber współprądowy







V

H

m

s

'



gdzie:

C
C

Ak

A

k

0

1

31

1













 



'

'

'

exp[ (

) ]

dla



k

rzeczywistego

Dynamika adsorpcji ciągłej

Dynamika adsorpcji ciągłej

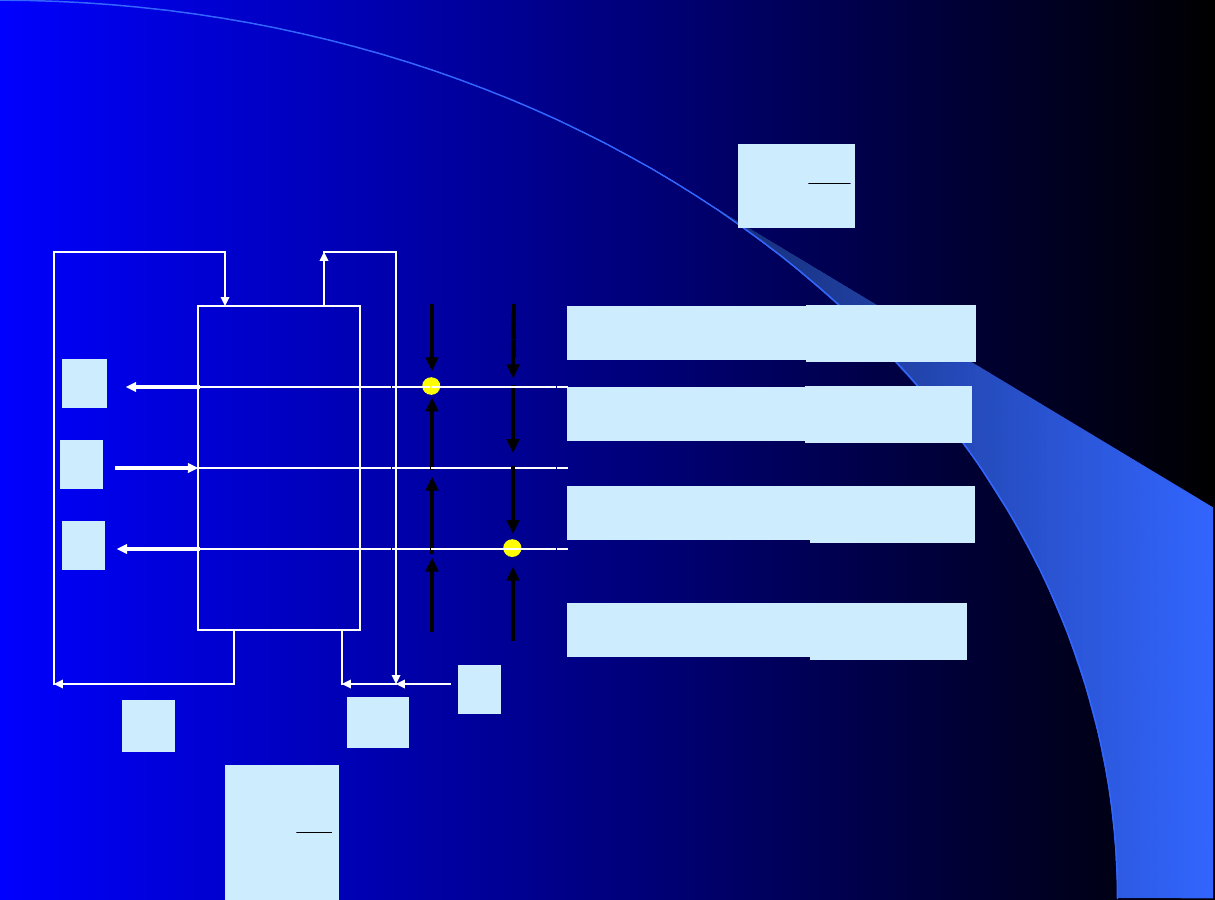
Adsorber przeciwprądowy

Bila

Bila

ns masowy

ns masowy

dla kolumny

od wlotu do wylotu:









Ak

Ap

s

Ak

A

A

q

q

m

C

C

V

m















0

S

S

zybko

zybko

ść

ść

transportu

transportu

masy

masy

:

:







V

H

m

s

'



gdzie:

C

C

Ak

A0

0



C

C

Ak

A

k

k

0

1

3

1

3

1















(

) exp[

(

) ]

exp[

(

) ]

'

'

'

'





















A

A

s

z

A

A

A

z

A

*

C

C

A

k

m

*

C

C

k

'

N











Wynik dla

izotermy liniowej

izotermy liniowej

oraz dla



k



dla



k

rzeczywistego

F

V

D

V

R

V

E

V

S

V

K

V

Zone IV

Zone III

Zone II

Zone I

Rozwiązanie dla izotermy liniowej q* = HC

Jeśli:

1

2

H

H

S

j

,

i



1

1

1

C

V

C

H

V

III

s







2

2

2

C

H

V

C

V

s

II







2

II

H

m 



1

III

H

m 



1

1

1

C

H

V

C

V

S

IV







2

2

2

C

V

C

H

V

I

S







2

I

H

m 



1

IV

H

m 



m

k

to bezwymiarowy stosunek

przepływów faz w danej strefie: k = I - IV

comp. 1

comp. 2

feed

comp. 1 comp. 2

.

.

s

k

k

V

V

m 

Chromatografia ciągła - TMB

Chromatografia ciągła - TMB

M. Mazzotti, G. Storti, M. Morbidelli, AIChE J, 40 (2004), 1825.

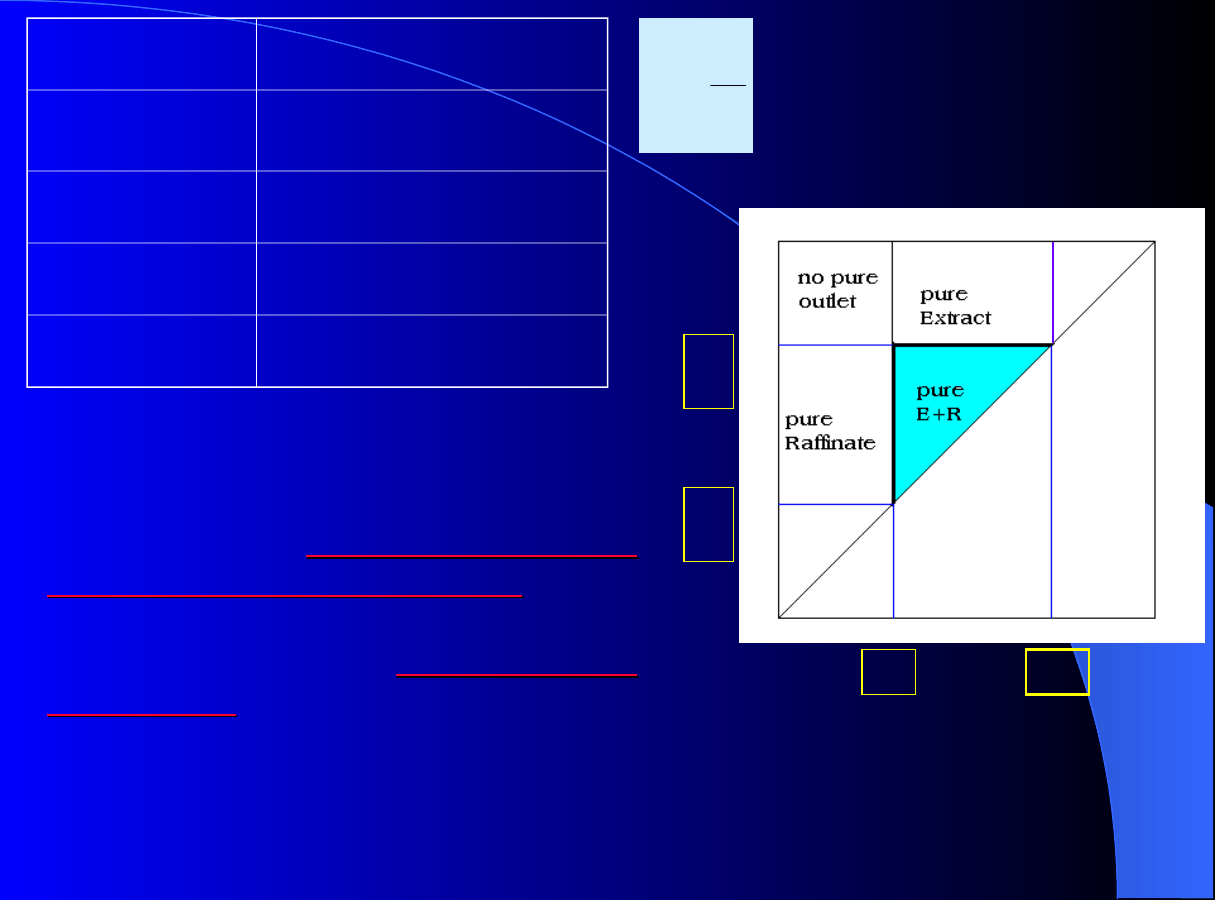
Rys.

pokazuje

graficznie

ograniczenia zred. przepływu m

k

w

strefach II i III a także

rozwiązanie

rozwiązanie

analityczne

analityczne

modelu idealnego

modelu idealnego

dynamiki

chromatografii

dynamiki

chromatografii

w

w

postaci

tzw.

trójkąta

postaci

tzw.

trójkąta

operacyjnego

operacyjnego dla

chromatografii

chromatografii

ciągłej TMB

ciągłej TMB

(SMB).

Trójkąt operacyjny (region pełnego
rozdziału) jest zaznaczony w funkcji
m

k

w

sekcjach II oraz III

Sekcja

m

k

I

m

I

> H

1

; m

I

> H

2

II

H

1

< m

II

< H

2

III

H

1

< m

III

< H

2

IV

m

IV

< H

1

; m

IV

< H

2

H

2

H

1

H

2

m

II

m

III

H

1

.

.

s

k

k

V

V

m 

Solid stream

Feed

(A,B)

Extract

(A)

Raffinate

(B)

I

III

IV

II

B

A

Desorbent

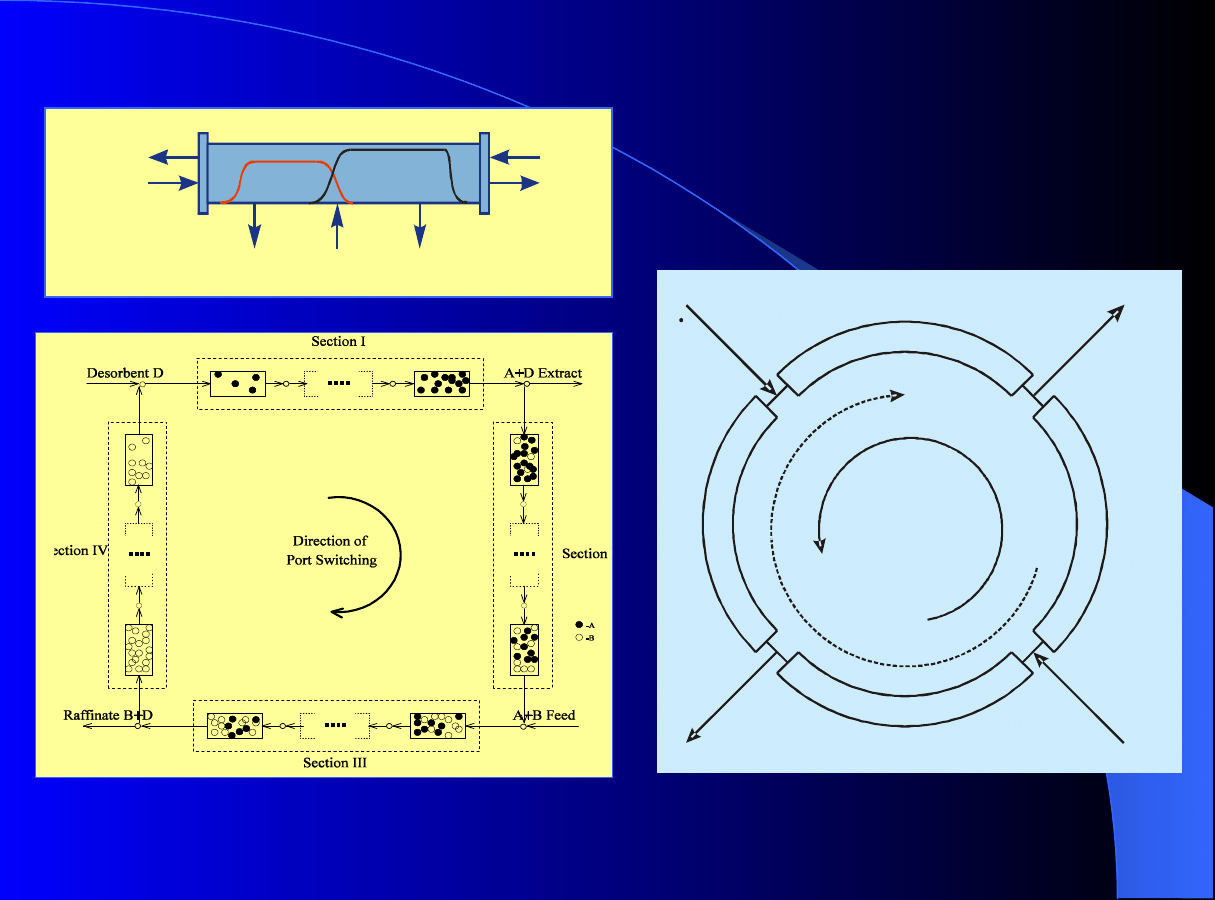
Idea symulowanego ruchu złoża - SMB

Idea symulowanego ruchu złoża - SMB

Z o n e I

Z o n e I I I

Zo

ne

IV

Zo

ne

I

I

F e e d ( 1 + 2 )

F

C

m o d , F

V

R a ff i n a t e ( 1 )

V

R

.

F l u i d fl o w

S o l i d fl o w

D e s o r b e n t

m o d , D

C

V

D

.

E x tr a c t ( 2 )

V

.

E

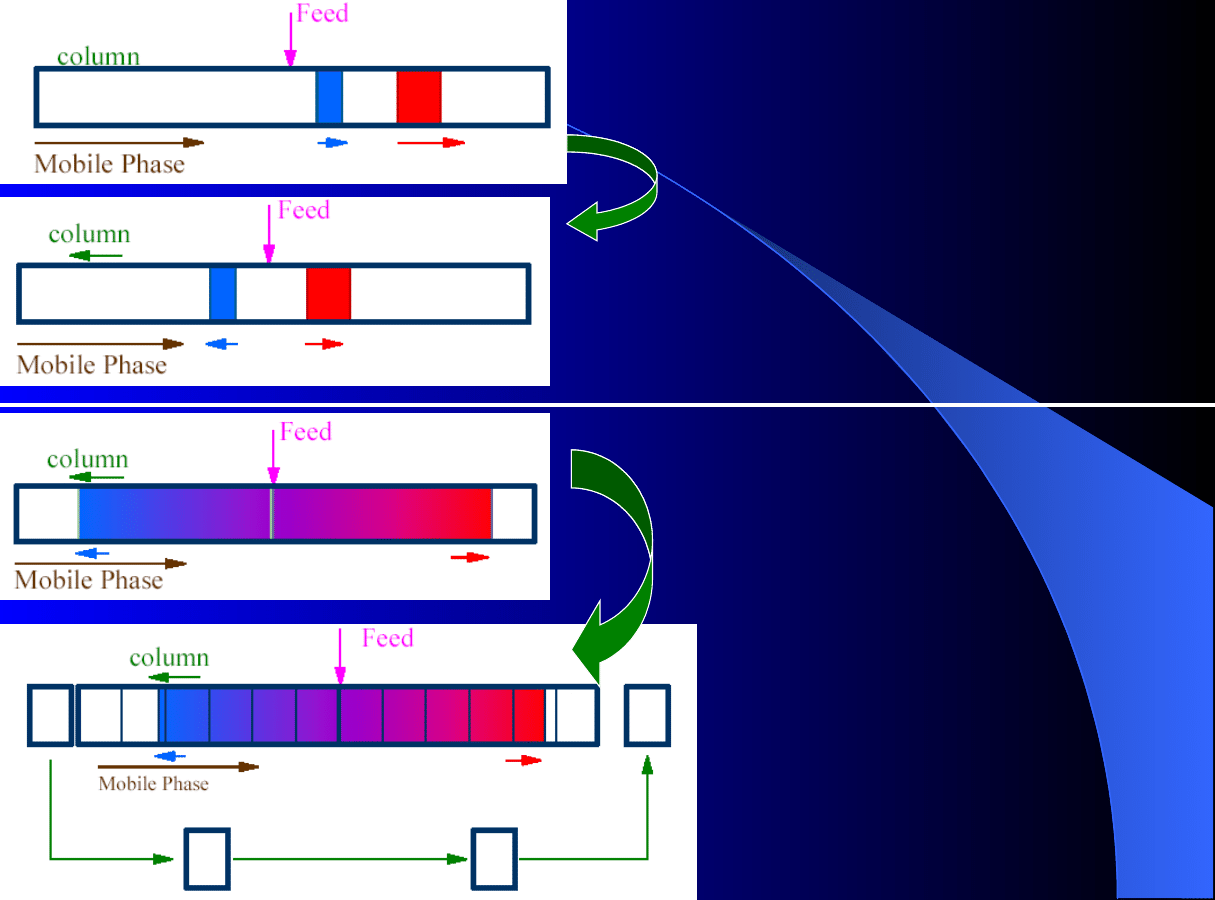
W kolumnie okresowej strumień

zasilający (feed) jest podawany w

centralny punkt kolumny okresowej.

Dwa rozdzielane składniki poruszają

się z różną szybkością i następuje ich

rozdział.

...

względem

nieruchomego

obserwatora.

Jeśli kolumna jest

odpowiednio

długa,

piki

chromatograficzne obu składników

będą rozdzielone.

Ponieważ jest to proces czysto

ciągły,

zaczynają

się

więc

problemy: potrzebuje on kolumny

o nieskończonej długości oraz

dodatkowej

drogi

na

wprowadzenie

oraz

wyprowadzenie

próbki

i

produktów rozdziału.

Modelowanie procesu polega

na podzieleniu kolumny na

małe

segmenty

oraz

symulowaniu

ich

ruchu.

Strumień zasilający (feed) oraz

eluent są teraz wprowadzane

pomiędzy segmenty.

Jeśli teraz nałożymy ruch kolumny

z prawej do lewej, z szybkością

mieszczącą

się

między

szybkościami

poruszania

się

składników,

składniki

zaczną

poruszać

się

w

przeciwnych

kierunkach

...

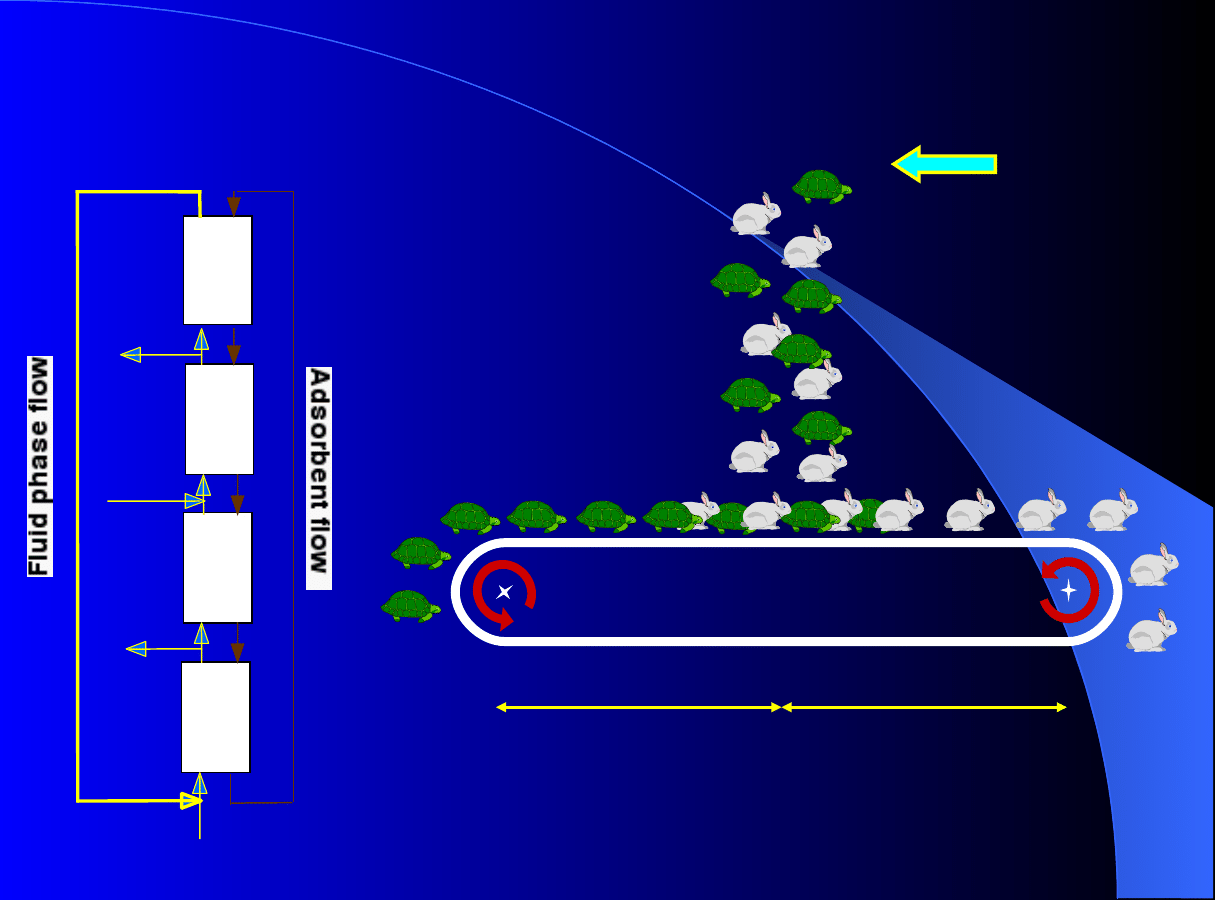
Przeciwprą

Przeciwprą

d

d

owa chromatografia ci

owa chromatografia ci

ą

ą

gła

gła

A+B

A

B

Desorbent

Zone

I

Zone

II

Zone

III

Zone

IV

Zone

II

Zone

III

A

B

A + B

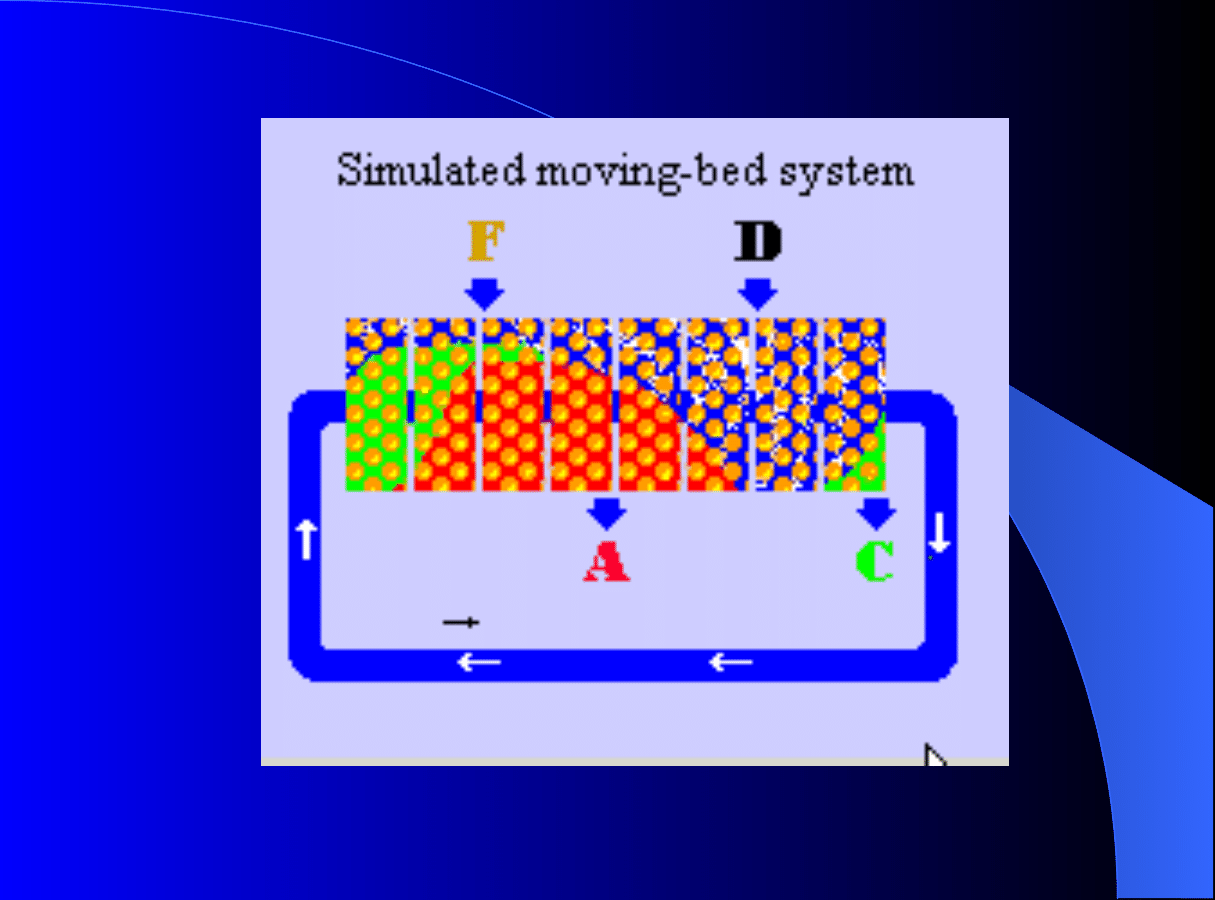
Chromatografia oddziaływań hydrofobowych (HIC)

Podstawowe pojęcia

Jest szeroko wykorzystywana do separacji i oczyszczania
makrocząsteczek białkowych. Białka adsorbowane są na złożu dzięki
występowaniu oddziaływań hydrofobowych fragmentów białka z silnie
hydrofobowymi grupami ligandów, trwale umocowanych na
powierzchni nośnika pozbawionego ładunku elektrycznego. Różne
czynniki mają wpływ na zachowanie się cząsteczek białkowych w
kontakcie z hydrofobowym adsorbentem. Niektóre z nich mają
krytyczny wpływ na rozdzielczość i selektywność metody, a także
zdolność wiązania cząsteczek przez złoże.
Poniżej są wymienione najważniejsze czynniki, jakie mają wpływ na

selektywnośc rozdziału chromatograficznego, takie jak:
- typ liganda oraz jego gęstość na powierzchni nośnika,
- rodzaj nośnika,
- rodzaj i stężenie soli,
- stężenie jonów wodorowych - pH,
- temperatura,
- skład solwentów.

Chromatografia chiralna

Podstawowe pojęcia

Możliwość bezpośredniego
rozdzielenia chiralnych izomerów ma
niezwykle istotne znaczenie w chemii
i to zarówno z analitycznego, jak i
preparatywnego punktu widzenia, a
w szczególnooeci dla preparatów
farmakologicznych oraz w
biotechnologii.

Według najnowszych danych z ponad
200 najczęściej przepisywanych
leków, 114 posiada przynajmniej 1
centrum chiralne, a 25% z nich
sprzedawanych jest w postaci
racemicznej, mimo, że najczęściej
tylko jeden z optycznie czynnych
izomerów wykazuje pożądaną
czynność farmakologiczną, podczas
gdy drugi może być balastem lub
działać wręcz szkodliwie. Klasycznym
przykładem takiego oddziaływania
jest imid kwasu
N-ftaliloglutaminowego znany w
handlu pod nazwą

Talidomid

PREPARATIVE

SEPARATION

METHODS

Preferential Crystallization

Chromatograp

hic methods

Membrane

technologie

s

Other e.g.,

chiral

extraction

Przemysłowy rozdział mieszanin

racemicznych jest bardzo

opłacalny z poniższych powodów::

• rozdział mieszanin enancjomerów
jest
bardzo ważnym procesem w
przemysłach:
farmaceutycznym,
biotechnologicznym czy
agrochemicznym

• ceny chiralnych sustancji czynnych w
farmacji
rosną w stosunku powyżej 13%
rocznie
i obecnie osiągają wartość 200 mld $.

Przewidywania na rok 2009 mówią o
sprzedaży rzędu 300 mld $.

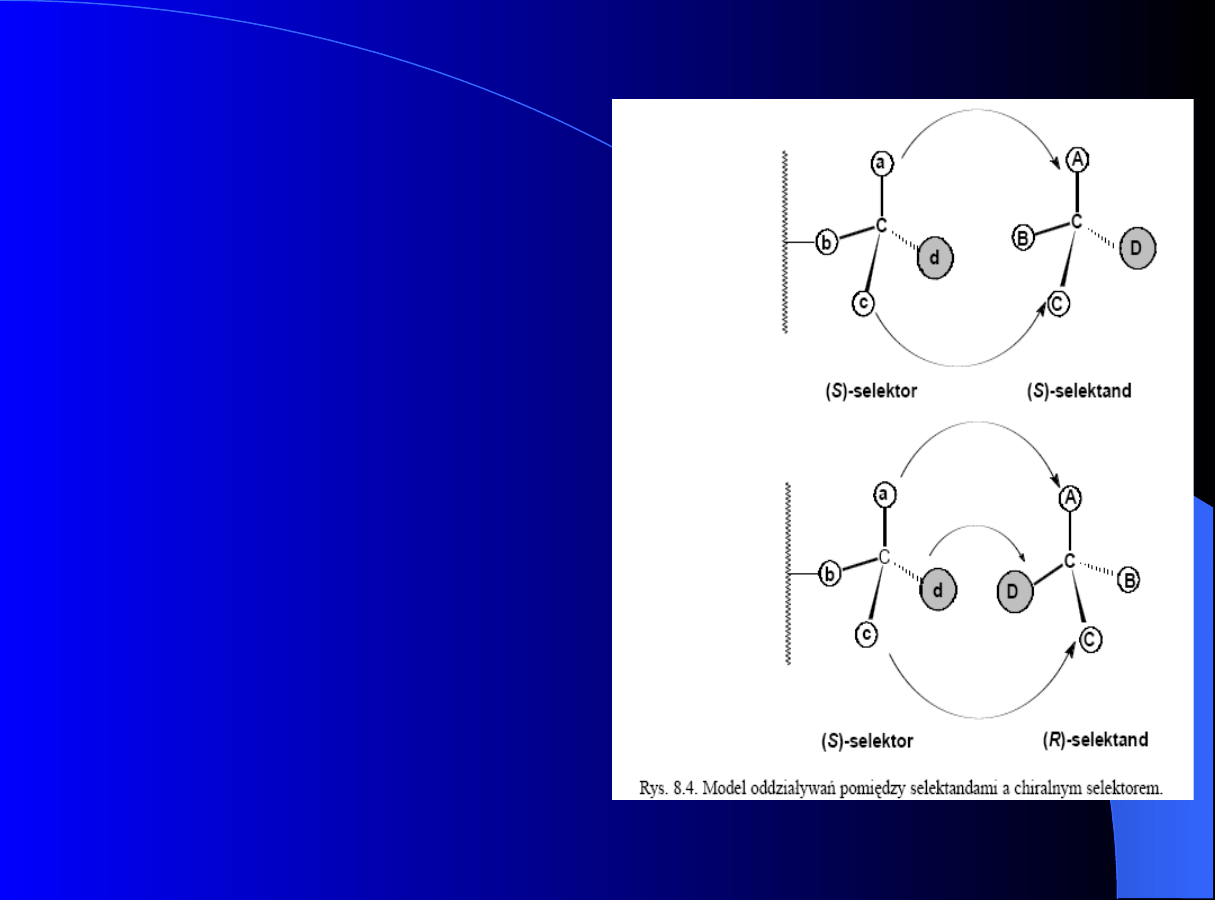
Chromatografia chiralna

Podstawowe pojęcia

Zasada Pirkle

:

aby nastąpiło

chromatograficzne różnicowanie
racemicznych cząsteczek na danej
fazie, niezbędne jest wystąpienie
minimum trzech oddziaływań
pomiędzy enencjomerami a
chiralnym selektorem, przy czym
minimum jedno z tych oddziaływań
powinno być stereochemicznie
zależne, to znaczy zależne od
konfiguracji centrum chiralnego
danego enencjomeru.

Rozdzielenie enancjomerów z
wykorzystaniem techniki HPLC przy
użyciu chiralnych faz stacjonarnych
(CSP - (Chiral Stationary Phases)) lub
chiralnych dodatków do fazy
ruchomej, oparte jest na tworzeniu
się przejściowych
diastereoizomerycznych kompleksów
pomiędzy cz¹steczką różnicującą
(selektorem), będącą elementem CSP
lub chiralnej fazy ruchomej, a
cząsteczką rozdzielanej substancji
(selektandem). Różnica w stabilności
tych kompleksów prowadzi do różnicy
czasów retencji.Enancjomer, który
tworzy mniej trwały kompleks,
szybciej wymywany jest z kolumny.

T0

T1

T2

T3

T4

D

S

L

e = r

D

S

L

T4

T3

T2

T1

T0

e

r

e

T0

T1

T2

T3

T4

e = r

T0

T1

T2

T3

T4

D

e = r

T4

T3

T2

T1

T0

e

r

e

P

2

T4

T3

T2

T1

T0

e

r

e

a)

b)

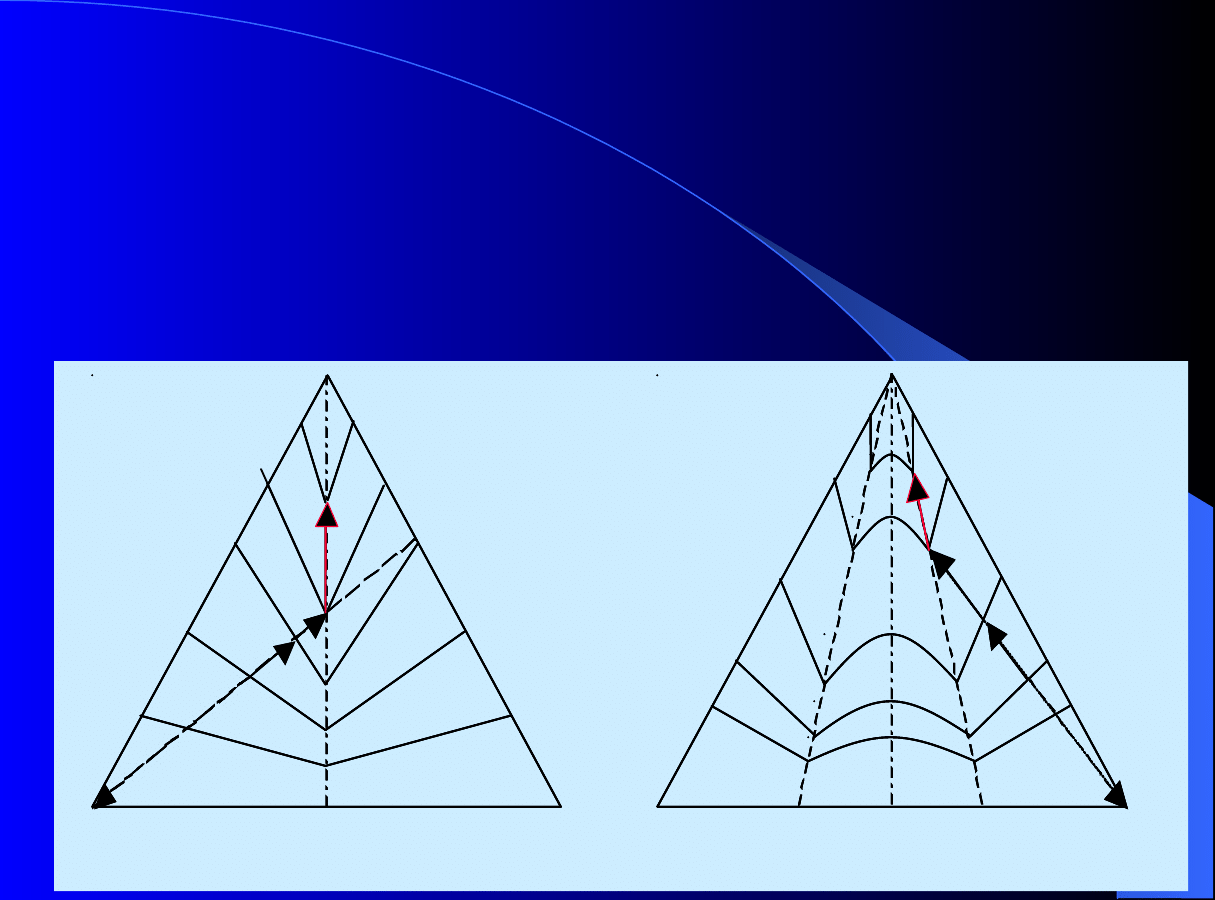
Odpowiednio:
a) układ tworzący

konglomerat

oraz
b) układ tworzący mieszaninę

racemiczną

P

0

P

2

P

3

P

4

P

3

P

4

P

0

P

1

.

.

.

.

Zasada krystalizacji

Zasada krystalizacji

czystego, pożądanego enancjomeru

czystego, pożądanego enancjomeru

poprzez och

poprzez och

ł

ł

odzenie

odzenie

Kompilacja chromatografii i krystalizacji

Podstawowe pojęcia

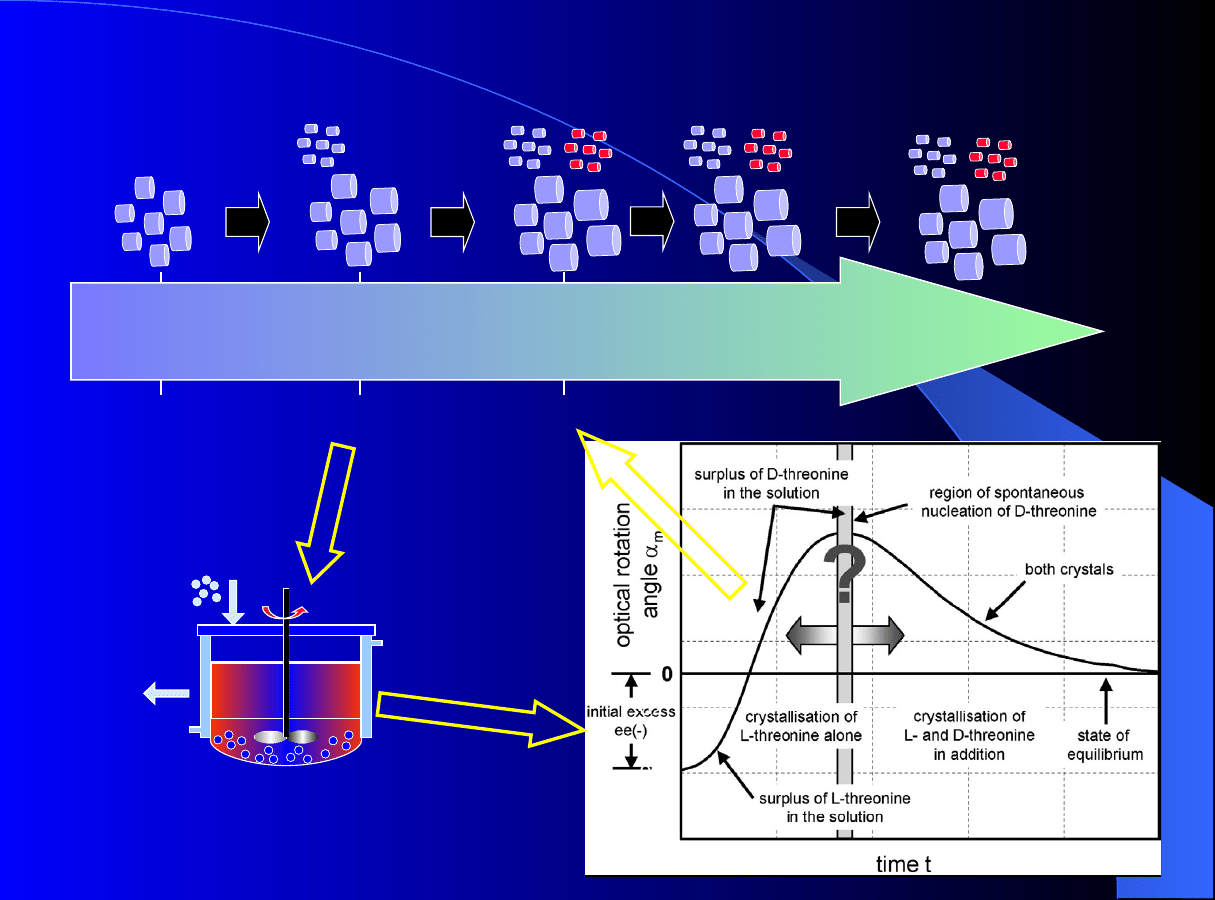
Zasady krystalizacji preferencyjnej

Zasady krystalizacji preferencyjnej

Wzrost

kryształów

E

1

Zarodkowani

e + wzrost

kryszt. E

1

Zarodkowani

e E

2

Wzrost

kryształów

E

1

, E

2

czas





0



1



2

E

1

E

1

Krystalizacja E

1

Krystalizator okresowy

Krystalizator okresowy

.



1



2

.

Żele NIPA

Podstawowe pojęcia

Żele NIPA

Żele NIPA

- hydrożele podlegające przejściom fazowym

związanym z dużą zmianą objętości.
Zmiany zachodzące pod wpływem temperatury w obrębie fazy
polimerowej mogą być wykorzystane w wielu dziedzinach współczesnej
chemii i technologii, czego przykładem są zastosowania takich
polimerów w medycynie, np. w kontrolowanym uwalnianiu leków czy
jako nośników białek i peptydów.
W większości przypadków są to termoczułe hydrożele usieciowane
głównie
N’N’-metylenobisakryloamidem,

a

także

dihydroksyetylenobisakryloamidem

i

dimetakrylanem

glikolu

etylenowego lub liniowe polimery tzw. poli(NIPAAm). Innym przykładem
jest szczepienie liniowego poli(NIPAAm) na powierzchni kapsułek i
sterowanie uwalnianiem leku za pomocą otwierania/zamykania porów
membrany

kapsułki

dzięki

rozkłębieniu/skłębieniu

liniowego

poli(NIPAAm) ze zmianami temperatury.
„Inteligentne polimery” są wykorzystywane ponadto w procesach
separacyjnych,

np.

odwadnianie

roztworów

białek

i

innych

wielkocząsteczkowych substancji biologicznie czynnych.

Produktywność 1 – 10 kg czystej
subst./dzień.

80 cm SMB
system

2 m średnicy

0.5 m wysokości
złoża

1,570 L objetości

12,000 kg wagi

(Amersham
Biosciences)

Podsumowanie

Podsumowanie

Chromatografia jest praktycznie jedyną metodą rozdziału tzw.
mieszanin „trudnych”, które nie dają się rozdzielić
alternatywnymi metodami rozdziału np. za pomocą krystalizacji,
ekstrakcji itp.

• Chromatografia jest często najszybszą oraz pewną drogą do
otrzymywania

pożądanych

enancjomerów

–

farmacja,

biotechnologia;

• Chromatografia może być z punktu widzenia ekonomiki procesu
najważniejszą drogą do produkcji substancji czynnych - farmacja.

Sprawność pojedynczej kolumny chromatograficznej okresowej
jest bardzo wysoka przy jednoczesnej wysokiej czystości
produktu kluczowego.

Jednocześnie produktywność procesu chromatografii okresowej
jest bardzo niska w porównaniu do altermatywnych metod
rozdziału.

Zastosowanie chromatografii ciągłej (SMB) pozwala znacząco
zredukować tę różnicę produktywności.

Cykl monotematycznych publikacji b

Cykl monotematycznych publikacji b

ę

ę

d

d

ą

ą

cych podstaw

cych podstaw

ą

ą

rozprawy habilitacyjnej:

rozprawy habilitacyjnej:

1. Piątkowski W., Antos D., Kaczmarski K., „Comparing simulations of

adsorption on heterogeneous surfaces by two kinetic models, the
transport-dispersive and Langmuir kinetic models”, Acta Chrom., 10
(2000), 23-38

2. Piątkowski, W., Antos D., Kaczmarski, K., “Modeling of preparative

chromatography processes with slow intraparticle mass transport
kinetics”, J.Chrom. A, 988 (2003), 219-231

3. Piątkowski W., Gritti, F., Kaczmarski, K., Guiochon, G., ”Influence of

the particle porosity on chromatographic band profiles”, J.Chrom. A,
989, (2003), 207-219

4. Piątkowski, W., Antos D., Gritti, F., Guiochon, G., ”Study of the

competitive isotherm model and the mass transfer kinetics for a BET
binary system”,
J.Chrom. A, 1003, (2003), 73-89

5. Piątkowski W., Petrushka I., Antos D., „Adsorbed solution model for

prediction of normal-phase chromatography process with varying
composition of the mobile phase”, J.Chrom. A, 1092 (2005) 65

6. Piątkowski W., “Problemy przenoszenia skali w procesie

chromatografii preparatywnej”, Inż. Chem. i Proc. 26, (2005), 605-
630

7. Piątkowski W., “Optimization problems of preparative

chromatography process illustrating by the separation of real mixture
of isomers”, Acta Chromatographica 16 (2006), 92-118

DZIĘKUJĘ ZA UWAGĘ

DZIĘKUJĘ ZA UWAGĘ