Automatyka,

sterowanie oraz

eksploatacja urządzeń

technicznych

Prowadzący : dr inż.Daniel Liberacki

SZCZEGÓŁOWY PROGRAM NAUCZANIA

Kierunek studiów: Inżynieria Środowiska

Specjalność: Ochrona i Kształtowania Środowiska

Cel nauczania

•

Zapoznanie

studentów

z

podstawowymi

pojęciami

z

zakresu

automatyki

oraz

zastosowaniem jej w sterowaniu urządzeniami i

systemami wodno- melioracyjnymi.

Szczególna uwaga będzie zwrócona na procesy

wykorzystania automatyzacji w systemach rozrządu

wody, automatyzacji budowli wodnych, pompowni

oraz zastosowaniu automatyzacji w nawodnieniach.

Treść nauczania

•

Zasadnicze pojęcia i określenia związane z automatyką.

•

Klasyfikacja układów automatyki. Podział układów

sterowania automatycznego.

•

Liniowe układy sterowania automatycznego. Sygnały

wejściowe i wyjściowe, sterujące sygnały zakłócające w

układach sterowania automatycznego.

•

Człony podstawowe układów sterowania automatycznego,

ich klasyfikacja oraz rodzaje połączeń.

• Typowe sygnały występujące w układach sterowania

automatycznego.

• Pojęcie transmitancji układu – funkcji przejścia (przepustowości).

• Transmitancja układu otwartego i zamkniętego.

• Pojęcia stabilności układów sterowania automatycznego.

• Warunek konieczny oraz dostateczny stabilności asymptotycznej

układów sterowania automatycznego.

• Badanie stabilności układów sterowania automatycznego.

.

• Pojęcie regulatora i jego rola w układach sterowania.

• Rodzaje regulatorów w układach zamkniętych

sterowania automatycznego.

• Regulatory proporcjonalne (typu P),

• Regulatory całkujące (typu I)).

• Prawo regulacji. Podstawowe właściwości regulatorów

o działaniu ciągłym.

• Regulatory cyfrowe.

Literatura

•

Chochowski A., Osianka E. (1990) :

Ćwiczenia laboratoryjne

z podstaw automatyki

. Wyd. SGGW, Warszawa

•

Urbaniak A. (1991) :

Automatyzacja w inżynierii sanitarnej.

Wyd. Politechnika Poznańska, Poznań

•

Mikulczyński T. (1998):

Podstawy automatyki

. Politechnika

Wrocławska.

•

Greblicki W. (2001) :

Teoretyczne podstawy automatyki

.

Politechnika Wrocławska.

•

KOWAL J. (2006) -

Podstawy Automatyki

- tom 1, UWND, Kraków;

•

KOWAL J. (2007) -

Podstawy Automatyki

- tom 2, UWND, Kraków;

•

Urbaniak A. (2007) – Podstawy automatyki. Wyd. Polit.

Poznańskiej.

POJĘCIA PODSTAWOWE

Początek temu, co dziś ogólnie nazywamy

automatyką

, dały

udane i praktycznie zrealizowane pomysły układów, dzięki którym

uzyskano samoczynną regulację, np. obrotów maszyn parowych,

napięć generatorów elektrycznych czy poziomów cieczy w

zbiornikach.

AUTOMATYKA – jest więc nauką techniczną która obejmuje

zarówno teorię jak i zasady konstrukcji oraz użytkowania urządzeń

automatycznych.

Natomiast

podstawy automatyki

to dyscyplina naukowa, która

porozrzucany w różnych działach techniki, dorobek, zebrała,

usystematyzowała i co najważniejsze, uogólniła, a przez to

radykalnie uprościła.

Umożliwiło to uzyskanie szerszego spojrzenia na zagadnienie

automatyzacji, a łącznie z rozwojem aparatury technicznej

zadecydowało o obecnym rozwoju automatyzacji procesów

jednostkowych,

czyli

tak

zwanej

automatyzacji

konwencjonalnej

.

Od automatyzacji prostych procesów jednostkowych, w którym

układy regulacji zastępują człowieka, w jego najprostszych

czynnościach nadzoru i kontroli, przeszło się do

automatyzacji

procesów

kompleksowych

,

polegającej

na

tym,

że

prace

poszczególnych regulatorów zainstalowanych w jakimś procesie

kompleksowym

zaczyna

się

podporządkowywać

układowi

centralnemu,

sterującemu

całością

złożonego

procesu

kompleksowego, według ustalonych kryteriów ekonomicznych,

technicznych czy ekonomiczno-technicznych.

Podstawy automatyki

– są więc odrębną

dyscypliną naukową o własnych specyficznych

pojęciach podstawowych.

Są to pojęcia o charakterze bardzo ogólnym,

wynikające ze specyfiki zakresu rozpatrywanych

zagadnień, a więc np.: sygnał, informacja,

przesyłanie sygnału, element układu automatyki

regulator, obiekt regulacji, proces kompleksowy.

Sygnałem – określamy w automatyce ogólnie

przebieg

dowolnej

wielkości

fizykalnej

występującej w procesie regulacji.

Jeżeli dwie wielkości fizykalne są jednoznacznie od

siebie zależne, to z przebiegu jednej z nich

możemy wynosić o przebiegu drugiej, czyli

inaczej mówiąc – jeden sygnał zawiera informacje

o drugim.

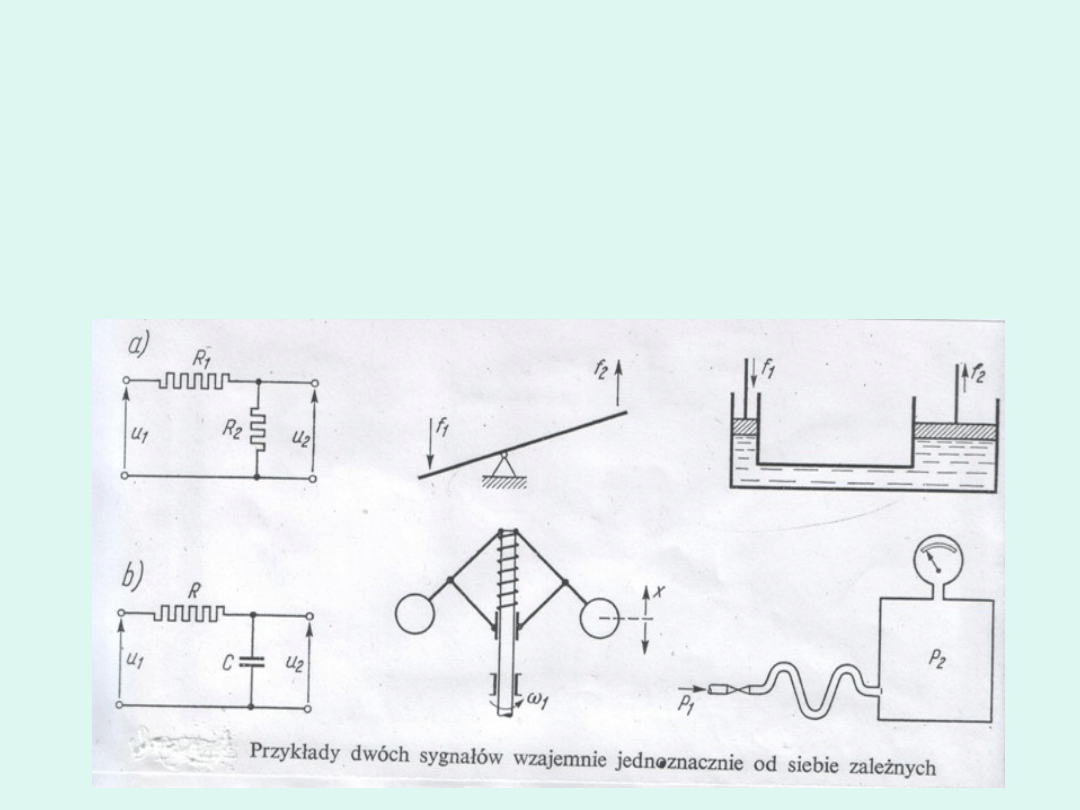
Przykłady kilku par sygnałów wzajemnie jednoznacznych od siebie

zależnych

Przy czym podzielono je na dwie grupy :

Grupa pierwsza to przypadki zależności proporcjonalnej.

u

2

= k·u

1

, f

2

= c·f

1

k i c – współczynniki o wartościach stałych niezależnych od

przebiegu sygnałów u

1

, f

1

Grupa druga to przypadki zależności bardziej skomplikowanej, którą

określa

równanie

różniczkowe

podające

zależność

sygnału

wyjściowego

od

sygnału

wejściowego.

W takich przypadkach przebieg sygnału wyjściowego nie jest

proporcjonalny do przebiegu sygnału wejściowego, lecz ulega on

pewnym

zmianom.

O wielkościach i rodzaju tych zmian decydują dynamiczne własności

układu, za pomocą, którego sygnał jest przesyłany czy też, jak

mówimy – przez który sygnał przechodzi.

Zadaniem regulacji jest uzyskanie pewnej z góry

przewidzianej

wartości

określonej

wielkości

fizycznej i podtrzymywanie jej, bądź realizowanie

z góry przewidzianego przebiegu tej wielkości.

Wielkość tę nazywamy wielkością (sygnałem)

regulowaną. Jest to więc wielkość, która

podlega regulacji w danym procesie (obiekcie).

Sygnał

to

abstrakcyjny

model

dowolnej

mierzalnej wielkości zmieniającej się w czasie,

generowanej przez zjawiska fizyczne lub systemy.

Tak jak wszystkie zjawiska może być opisany za

pomocą aparatu matematycznego, np. poprzez

podanie pewnej funkcji zależnej od czasu.

Ponieważ sygnał niesie informację o naturze

badanych zjawisk lub systemów, w niektórych

dziedzinach nauk jest on traktowany jak nośnik

informacji.

Sygnał oznacza zatem przepływ strumienia

informacji, przy czym przepływ może odbywać

się w jednym lub w wielu wymiarach.

Sygnały można przedstawić w postaci:

•analitycznej - za pomocą wzoru

matematycznego, który definiuje

funkcję

opisującą zmiany wartości sygnału np. w

dziedzinie

czasu

,

częstotliwości

itp.,

•graficznej - za pomocą

wykresu

lub

grafu

.

Każdy sygnał może być opisany przez jedną z
następujących wielkości:

•czas trwania, który może być ograniczony jakimś

przedziałem czasowym, formalnie przedstawionym

jako różnica pomiędzy końcem przedziału T2 i

początkiem przedziału T1,

•wartość

chwilową

sygnału,

mierzoną

w

jednostkach

właściwych dla danej wielkości,

•funkcję opisującą przebieg sygnału, przy czym

sygnał może być funkcją jednej

zmiennej

lub wielu

zmiennych niezależnych,

•specyficzne własności opisujące naturę danego

sygnału, takie jak:

amplituda

, częstotliwość,

energia

,

moc

,

okresowość

, itp.

Element układu automatyki

Jeżeli

przebiegi

wielkości

fizykalnych,

oznaczonych

indeksami

1

, zaczniemy zmieniać według dowolnej funkcji

x(t)

, gdzie

t

oznacza czas, to znając własności dynamiczne

poszczególnych układów możemy obliczyć przebiegi

odpowiadających im wielkości, oznaczonych indeksami

2

.

Przebiegi oznaczone indeksami 1 nazywamy

sygnałami

wejściowymi

umownie oznaczane symbolem

x

, natomiast

przebiegi oznaczone indeksem 2 nazwano

sygnałami

wyjściowymi

i oznacza się je umownie symbolem

y

.

Układ, w którym wyróżniamy sygnał wejściowy i

wyjściowy nazywamy

elementem

i

oznaczamy

w sposób umowny tak jak na rysunku .

Do wywołania sygnału x potrzebna jest pewna

energia na wejściu danego elementu. Energia

doprowadzona do ich wejścia jest większa od energii

otrzymywanej na wyjściu. Wynika to bezpośrednio z

ich konstrukcji (tarcie, opory) i zasady zachowania

energii.

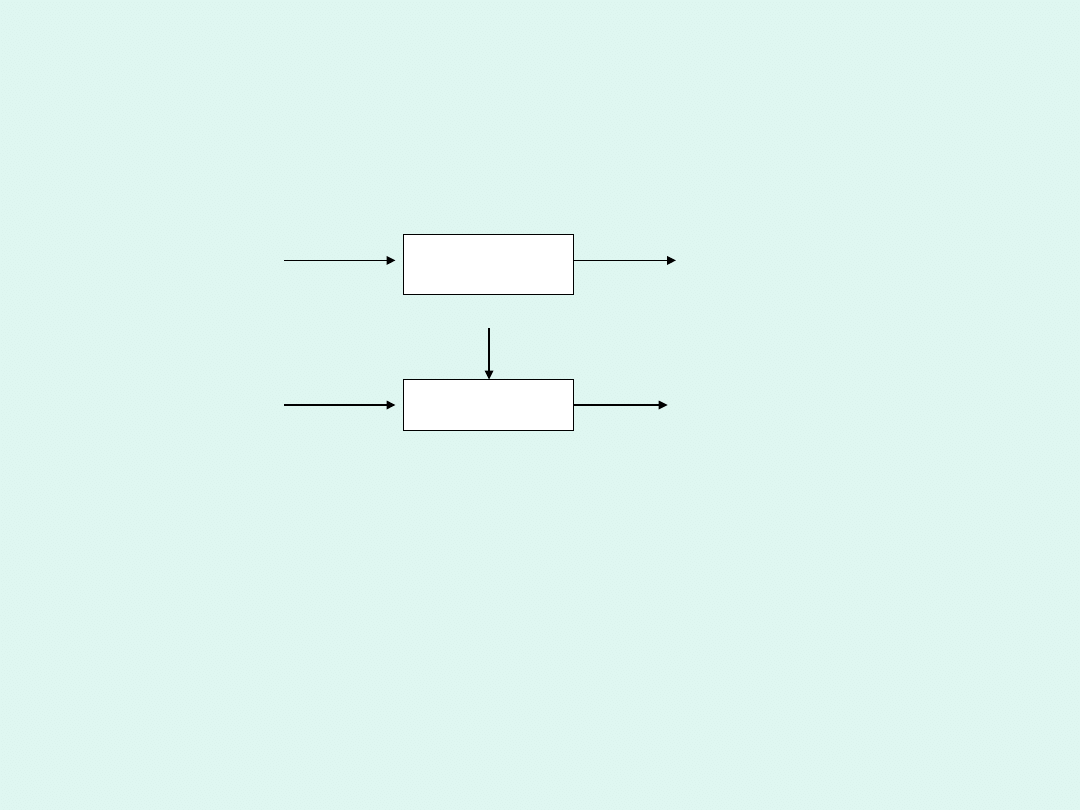
Taki element, w którym energia otrzymywana na wyjściu

jest większa od energii doprowadzanej do wejścia

nazywamy

elementem wzmacniającym

.

x

y

x

y

E

Aby energia otrzymywana na wyjściu była większa od

energii na wejściu, konieczne jest doprowadzenie energii

dodatkowej z zewnątrz.

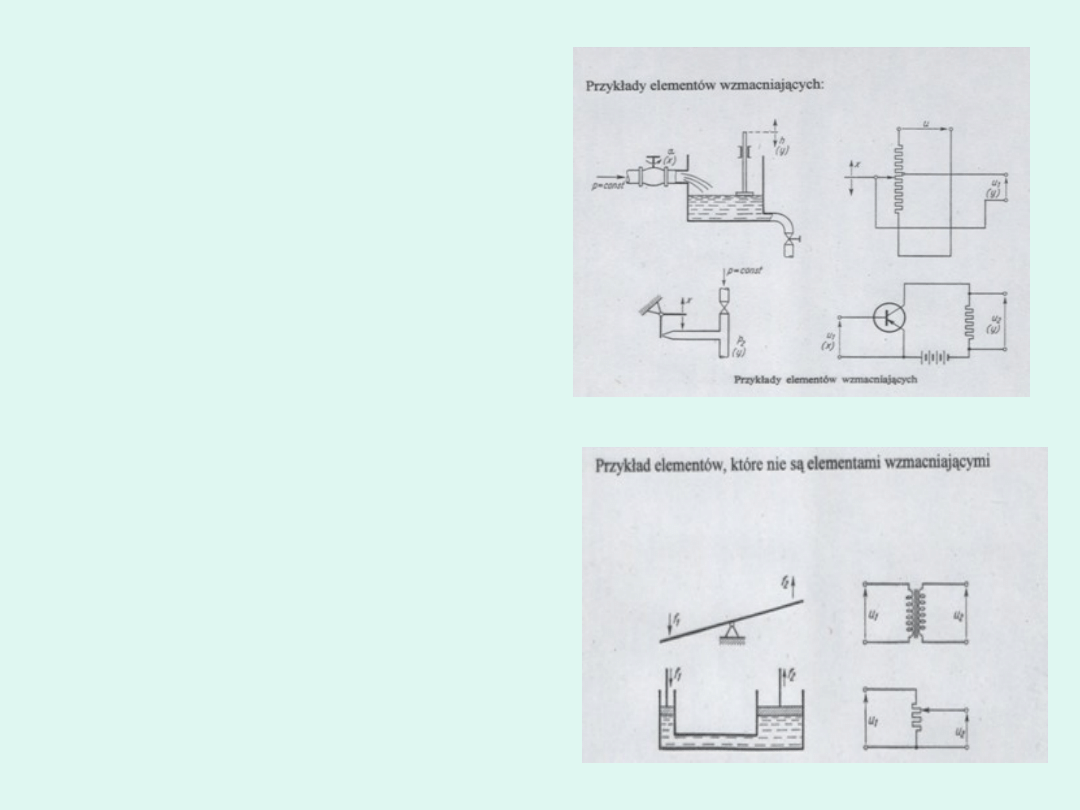
Przykłady

elementów

wzmacniających przedstawiono na

rysunku 1.

Symbole x i y w nawiasach wskazują,

który sygnał należy uważać za

wejściowy, a który za wyjściowy.

Na

rysunku

2.

przedstawiono

niektóre elementy, które nie są

elementami wzmacnianymi.

W

omawianych

dotychczas

elementach

wyróżniliśmy

jeden

sygnał wejściowy i jeden wyjściowy.

Są to przypadki najprostsze.

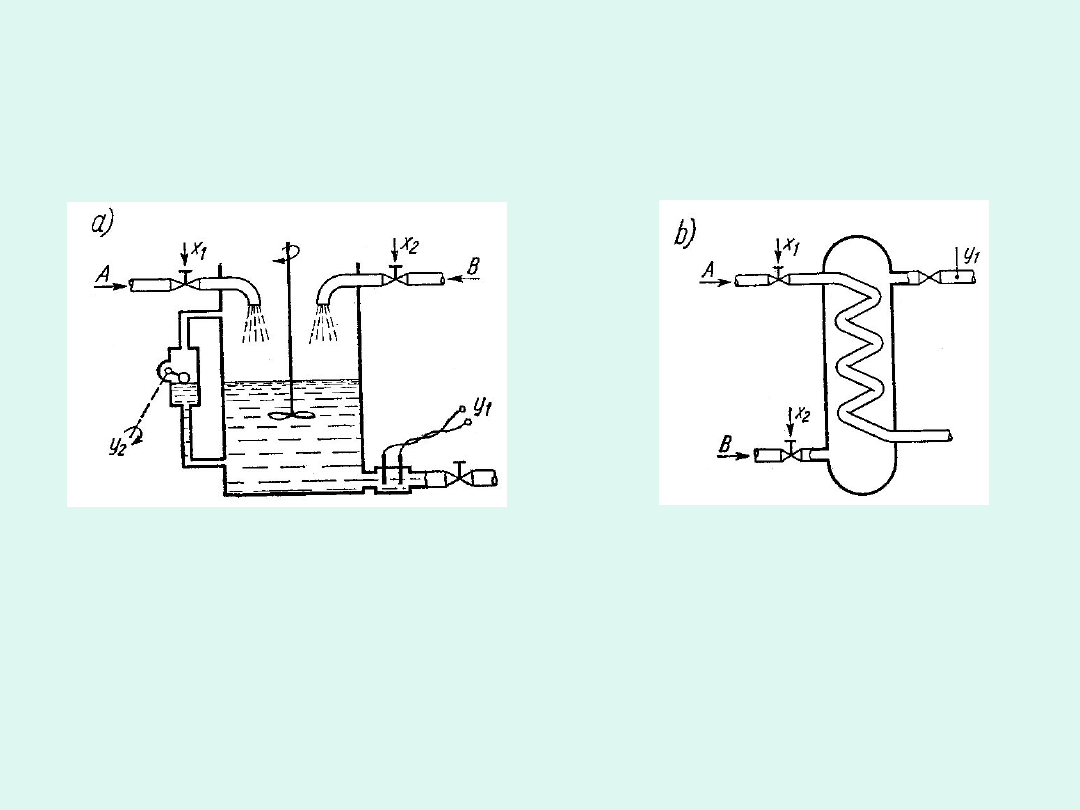
W praktyce spotykamy najczęściej elementy bardziej złożone, w których

występuje kilka sygnałów wejściowych i kilka wyjściowych. Przykłady takich

elementów przedstawiono na rysunku a i b

Liczba sygnałów wejściowych nie musi być równa liczbie sygnałów

wyjściowych. Dlatego liczbę sygnałów wejściowych oznaczono jako

n a liczbę sygnałów wyjściowych jako m. W większości przypadków

zachodzących w praktyce n = m. (schematy za Węgrzyn 1974)