Program przedmiotu

“Opracowywanie danych w

chemii”

1.

Wprowadzenie: przegląd rodzajów danych oraz

metod ich opracowywania.

2.

Podstawowe pojęcia rachunku

prawdopodobieństwa i statystyki matematycznej.

3.

Podstawy analizy wyników pomiarów. Statystyczna

weryfikacja hipotez. Analiza wariancji.

4.

Dopasowywanie modeli

a) Regresja liniowa pojedyncza i wielokrotna.
b) Regresja nieliniowa.
c) Analiza konfluentna.
d) Porównywanie modeli.
e) Metoda największej entropii.

5.

Analiza skupień: grupowanie podobnych obiektów.

6.

Analiza czynnikowa.

Literatura

• J. Czermiński i współautorzy, Metody

statystyczne w doświadczalnictwie

chemicznym. PWN, Warszawa.

• S. Brand, Analiza danych, PWN, Warszawa.

• A. Strzałkowski, A. Śliżyński,

Matematyczne metody opracowywania

wyników pomiarów, PWN, Warszawa.

• C. R. Rao, Modele liniowe statystyki

matematycznej, PWN, Warszawa.

• R.G. Brereton, Chemometrics, Wiley.

• Sieber,Wild, Nonlinear regression, Wiley.

Pochodzenie danych

• Pomiar (np. pomiary

fizykochemiczne)

• Obserwacja (np. zapis zmiany

liczebności populacji na określonym
terenie)

• Symulacja (np. symulacje dynamiki

molekularnej ewolucji czasowej
zespołów cząsteczek)

Metody analizy danych

• Analiza statystyczna (obliczanie średnich i

rozrzutu, ocena wiarygodności pomiarów,

ocena istotności różnic wielkości

zmierzonych w różnych miejscach)

• Dopasowywanie modeli matematycznych

do danych pomiarowych (np.analiza

regresyjna i konfluentna)

• Analiza skupień (znajdowanie skupisk

obiektów o podobnych cechach)

• Analiza czynnikowa (wyławianie czynników

określających większość właściwości zbioru

danych lub zjawiska)

Zastosowania

• Analiza statystyczna wyników pomiarów:

chemia analityczna, chemia medyczna,
technologia chemiczna.

• Dopasowywanie modeli: chemia fizyczna,

chemia organiczna, krystalochemia i inne
metody określania struktury cząsteczek,
chemia teoretyczna, technologia chemiczna.

• Analiza skupień: analiza konformacyjna,

QSAR.

• Analiza czynnikowa: QSAR, spektroskopia.

Rachunek

prawdopodobieństwa

A – zdarzenie
E – przestrzeń wszystkich zdarzeń
P(A) – prawdopowobieństwo zdarzenia

A; liczba nieujemna określająca
częstość jego występowania.

P(E)=1
P(A+B)=P(A)+P(B) dla zdarzeń

wykluczających się.

Prawdopodobieństwo

warunkowe i niezależność

zdarzeń

P(A|B)=P(AB)/P(B)
P(AB)=P(A|B)P(B)

Zdarzenia A i B są niezależne jeżeli

P(A|B)=P(A)
czyli
P(AB)=P(A)P(B)

Zmienne losowe i ich

rozkłady

Zmienna losowa: liczba

przyporządkowana zdarzeniu

Dystrybuanta:
F(x)=P(yx)
Gęstość prawdopodobieństwa:
f(x)=dP(x)/dx
Funkcja zmiennej losowej jest też

zmienną losową.

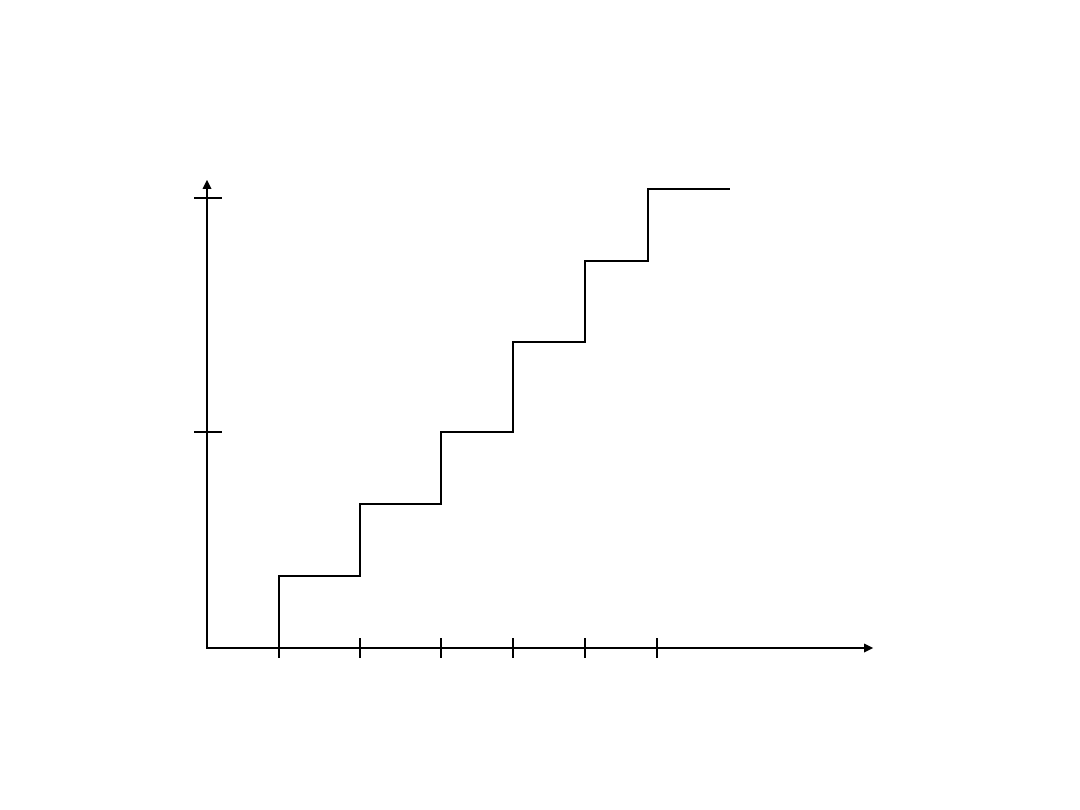
1 2 3 4 5
6

F(x)

x

0.5

1

Dystrybuanta liczby oczek na jednej ścianie kostki dla rzutów
idealnie symetryczną kostką.

Momenty rozkładu









  



















n

1

i

i

i

n

1

i

i

i

x

x

P

x

H

)

x

(

H

E

x

x

P

x

})

x

({

E

 

 

 





   























dx

x

f

x

H

x

H

E

dx

x

xf

xˆ

}

x

{

E

Dla zmiennych
ciągłych:

Jeżeli H(x)=(x-x

c

)

n

to E{H(X)} nazywa się n-

tym momentem x względem c; jeżeli c=

to E

jest n-tym momentem centralnym, 

n

({x}).

xˆ

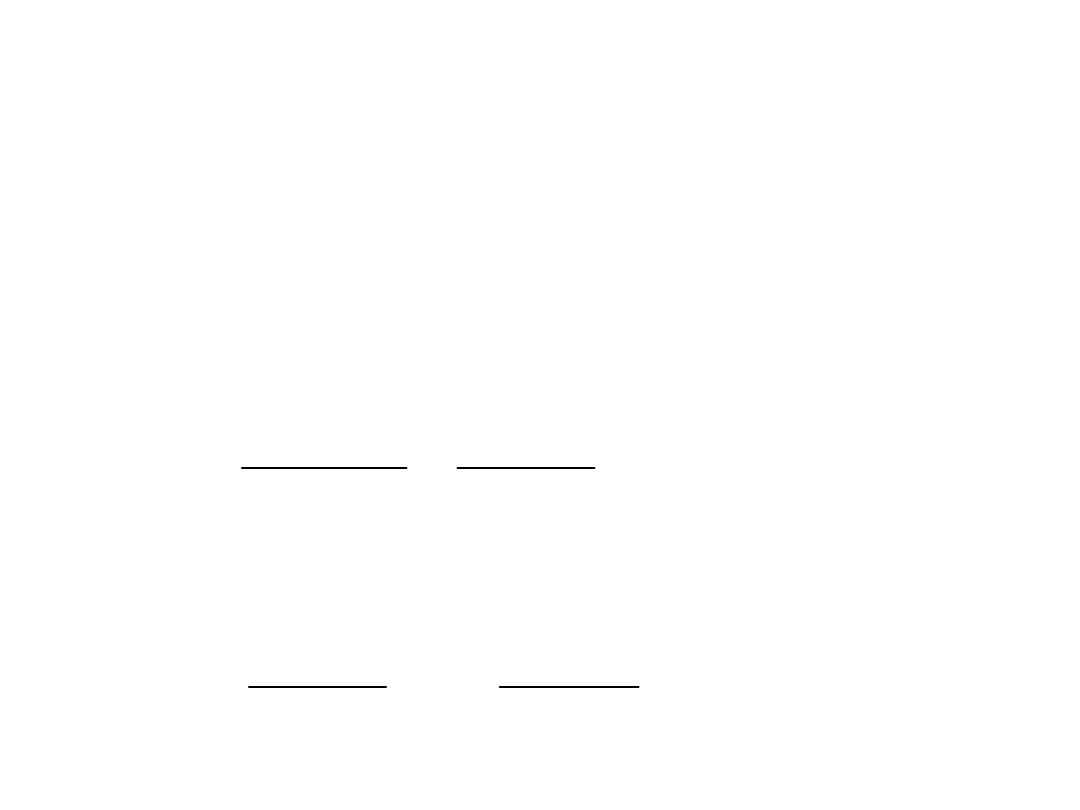
Użyteczne momenty

centralne

Wariancja

 

 

 

 



  



















dx

x

f

xˆ

x

x

x

2

2

2

Skrzywienie

 

 

 

 

 

 

 

  

  























dx

x

f

xˆ

x

x

1

x

x

x

3

3

2

/

3

2

3

Kurtoza

 

 

 

 

 

 

 

  

  

3

dx

x

f

xˆ

x

x

1

3

x

x

x

4

4

2
2

4



























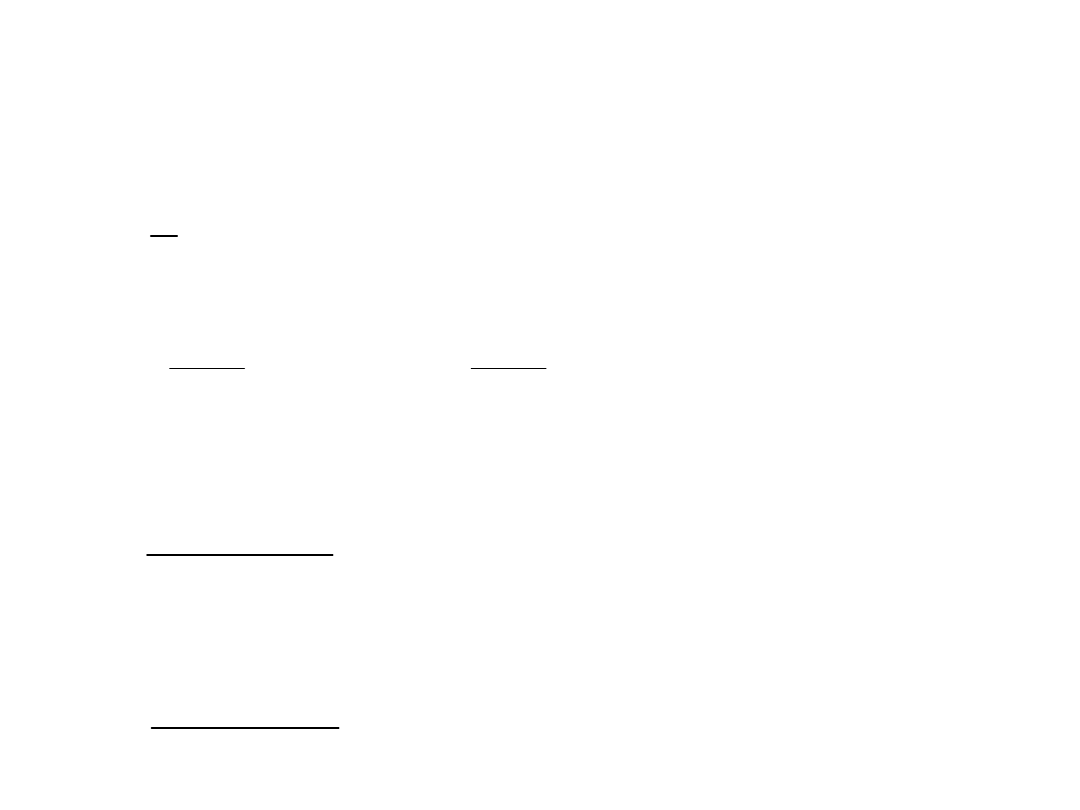
Obliczanie momentów

centralnych zbioru punktów













3

)

1

n

(

xˆ

x

)

1

n

(

xˆ

x

x

x

n

1

n

1

xˆ

x

1

n

1

x

n

1

xˆ

4

n

1

i

4

i

3

n

1

i

3

i

2

n

1

i

i

n

1

i

2

i

n

1

i

2

i

2

n

1

i

i

























































































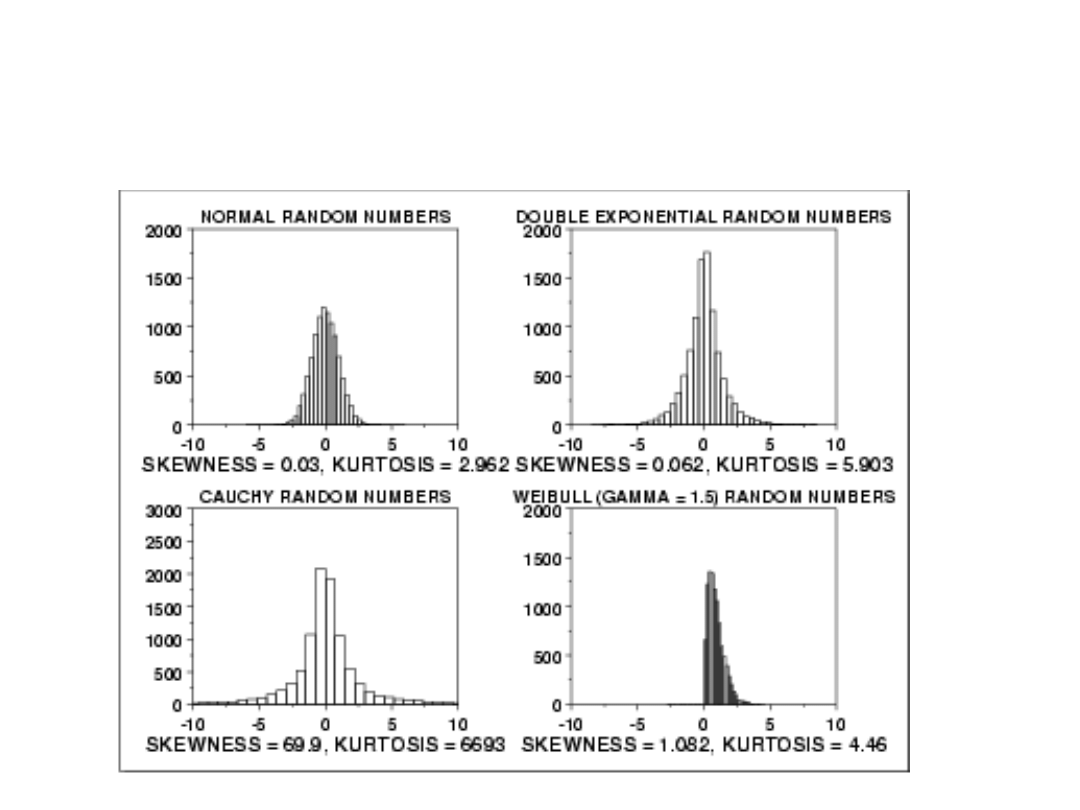
Przykłady momentów

centralnych paru rozkładów

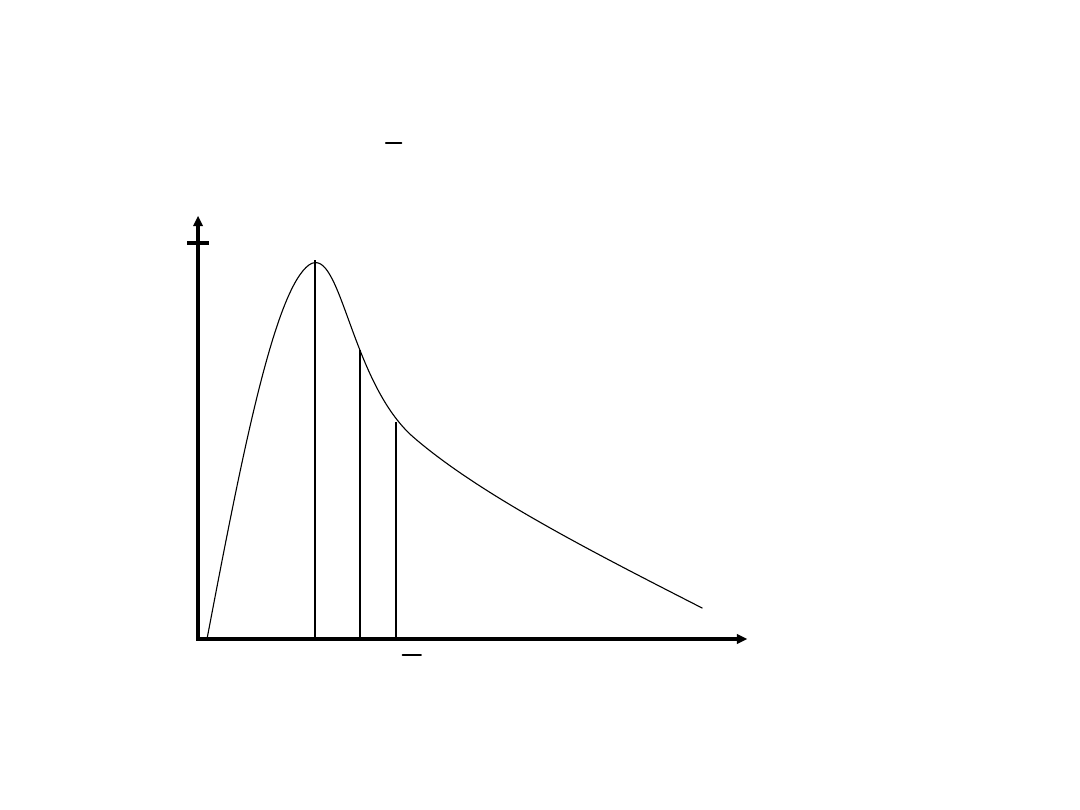
x

f(x)

x

x

x

.

m

5

0

Wartość najbardziej prawdopodobna (modalna): x

m

: f’(x

m

)=0,

f’’(x

m

)<0

Mediana: x

0.5

: P(x<x

0.5

)=0.5

Wartość średnia:

 











dx

x

xf

x

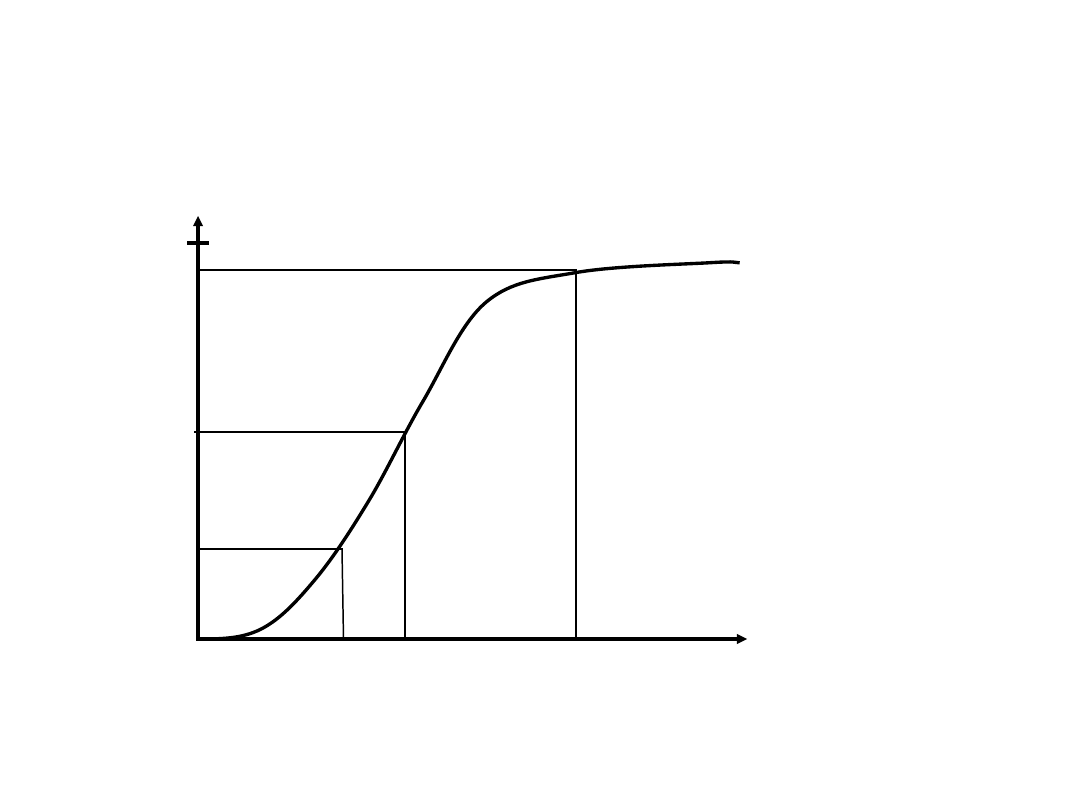
Mediana i kwantyle

1.0

0.5

0.2

x

0.5

x

0.2

x

F(x)

median
a

 

 











q

x

q

q

dx

x

f

x

F

x

0.9

Rozkład dwóch zmiennych i

kowariancja

 

 









 









 











 

 

 

   

y

x

y

,

x

cov

y

,

x

y

,

x

cov

yˆ

y

xˆ

x

E

y

yˆ

y

E

x

xˆ

x

E

yˆ

y

E

xˆ

x

E

11

2

2

02

2

2

20

01

10



















































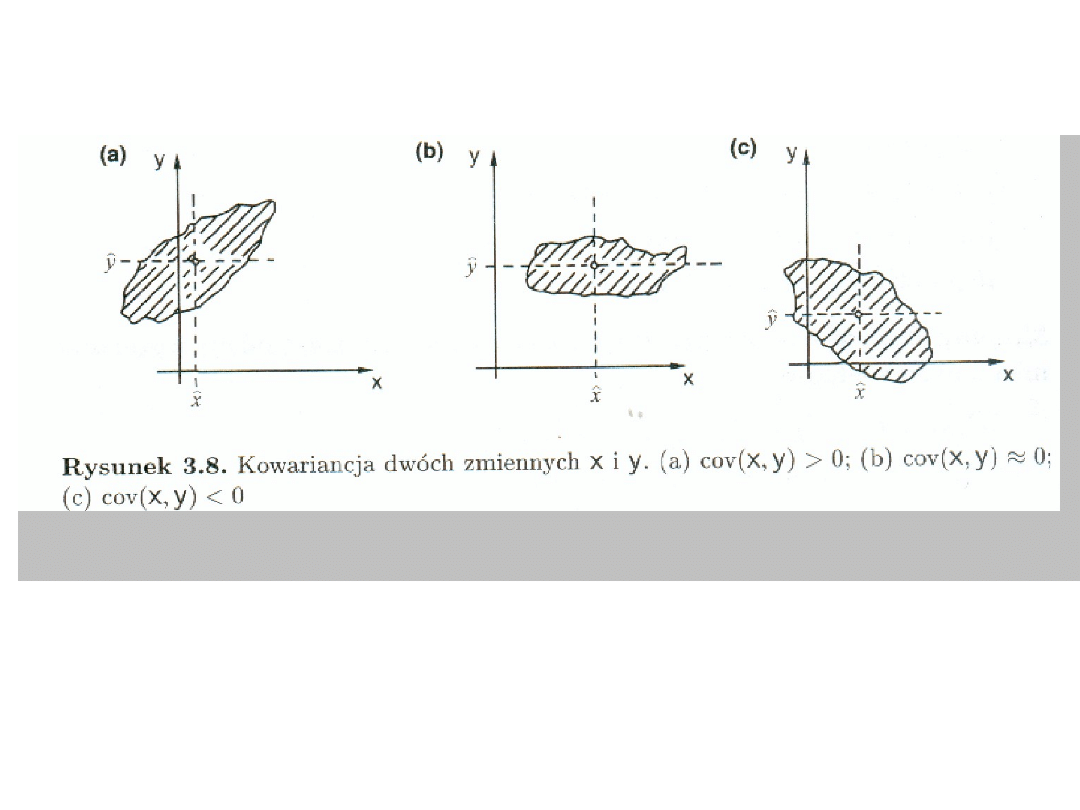
Sposoby przedstawiania rozkładów zmiennych

losowych:

1. Wykresy liniowe (rozkłady jednowymiarowe).

2. Wykresy „rozproszone” (scatter plots)

(dwuwymiarowe)

3. Histogramy

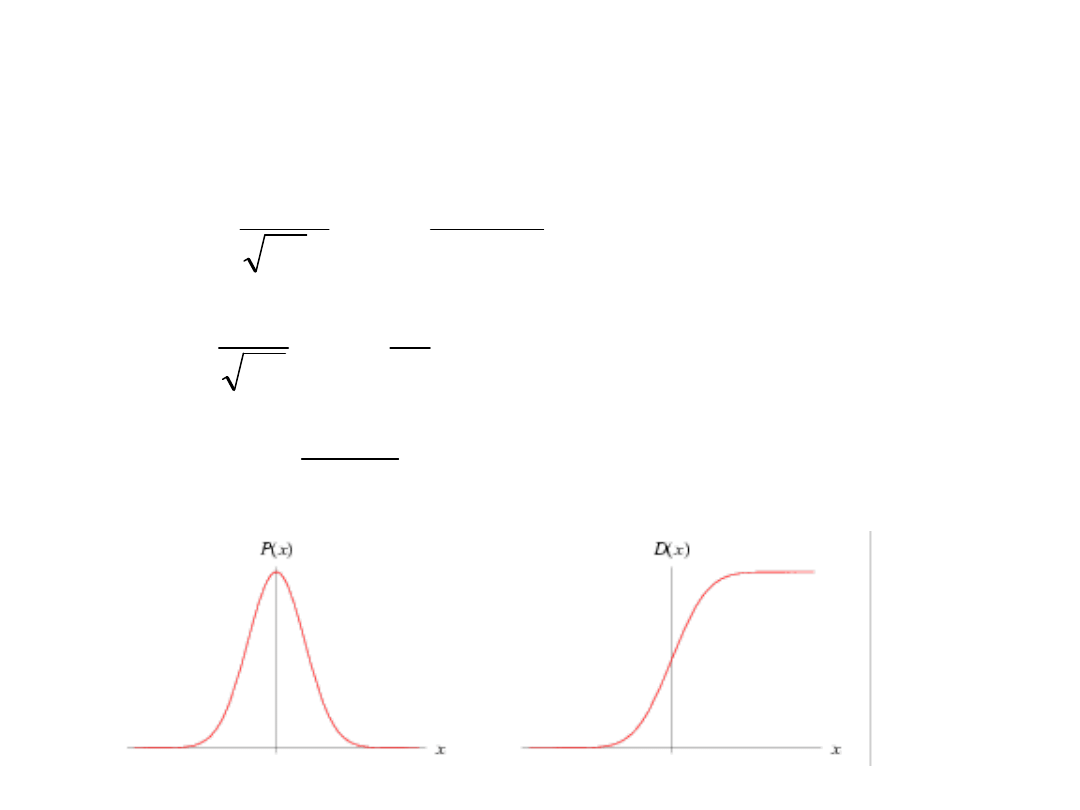
Rozkład normalny





























































































x

erf

,

;

x

F

2

x

exp

2

1

0

,

1

;

u

f

2

x

exp

2

1

,

;

x

f

2

2

2

U = zmienna
stadardyzowana

Wielowymiarowy rozkład

normalny

 



 





































x

A

x

2

1

exp

2

)

A

det(

)

x

(

f

)

x

,...,

x

,

x

(

f

T

2

/

n

n

2

1

Centralne twierdzenie

graniczne

Jeżeli x jest zmienną losową o wartości

średniej a i wariancji b

2

, to zmienna













n

1

i

i

n

x

lim

n

1

Ma rozkład normalny o wartości średniej a i

wariancji b

2

/n.